Pandemic modelling for regions implementing an elimination strategy

Abstract

During the COVID-19 pandemic, some countries, such as Australia, China, Iceland, New Zealand, Thailand, and Vietnam successfully implemented an elimination strategy, enacting strict border control and periods of lockdowns to end community transmission. Atlantic Canada and Canada’s territories implemented similar policies, and reported long periods with no community cases. In Newfoundland and Labrador (NL), Nova Scotia, and Prince Edward Island a median of 80% or more of daily reported cases were travel-related from July 1, 2020 to May 31, 2021. With increasing vaccination coverage, it may be appropriate to exit an elimination strategy, but most existing epidemiological frameworks are applicable only to situations where most cases occur in the community, and are not appropriate for regions that have implemented an elimination strategy. To inform the pandemic response in regions that are implementing an elimination strategy, we extend importation modelling to consider post-arrival travel restrictions, and pharmaceutical and non-pharmaceutical interventions in the local community. We find that shortly after the Omicron variant had begun spreading in Canada, the expected daily number of spillovers, infections spread to NL community members from travellers and their close contacts, was higher than any time previously in the pandemic. By December 24, 2021, the expected number of spillovers was 44% higher than the previous high, which occurred in late July 2021 shortly after travel restrictions were first relaxed. We develop a method to assess the characteristics of potential future community outbreaks in regions that are implementing an elimination strategy. We apply this method to predict the effect of variant and vaccination coverage on the size of hypothetical community outbreaks in Mount Pearl, a suburb of the St. John’s metropolitan area in NL. Our methodology can be used to evaluate alternative plans to relax public health restrictions when vaccine coverage is high in regions that have implemented an elimination strategy. This manuscript was submitted as part of a theme issue on “Modelling COVID-19 and Preparedness for Future Pandemics”.

1. Introduction

To manage SARS-CoV-2 infections, countries including Australia, China, Iceland, New Zealand, Thailand, and Vietnam used an elimination approach (also known as a zero-COVID policy). This approach combines strong border control to diminish travel-related cases with pharmaceutical (PIs) and non-pharmaceutical interventions (NPIs) that reduce or completely end community transmissions if border measures fail (Baker et al., 2020b, Heywood and Macintyre, 2020). Elimination differs from eradication in that its intended region of influence is localized, typically to the jurisdiction pursuing the goal. This policy was also used in infranational jurisdictions such as Atlantic Canada and Canada’s territories (Bignami, 2021, Contandriopoulos, 2021, Department of Health and Community Services, N.L., 2022).

Until the end of 2021, countries that used an elimination strategy had less SARS-CoV-2 mortality (Baker et al., 2020a, Nam et al., 2020) and less stringent local restrictions when there were no community cases, which resulted in less psychological distress (Aknin et al., 2022). Regions that implemented elimination strategies may have also had stronger economies (König and Winkler, 2021). Newfoundland and Labrador (NL), which implemented a containment approach (Department of Health and Community Services, N.L., 2022), achieved prolonged periods with no community cases and low SARS-CoV-2 mortality: 3.6 SARS-CoV-2 deaths per 100,000 people in NL, compared to 78.1 SARS-CoV-2 deaths per 100,000 people in Canada from the beginning of the pandemic until December 31, 2021 (NL: 19 deaths (Government of Newfoundland and Labrador, 2021a) for a provincial population of 521,854 people (Statistics Canada, 2021); Canada: 30,024 SARS CoV-2 deaths (Public Health Agency of Canada, 2022) for a national population of 38,426,473 (Statistics Canada, 2021). Success similar to that of NL occurred throughout Atlantic Canada and in Canada’s territories.

The feasibility of an elimination strategy depends on vaccine availability and uptake. Hong Kong had low numbers of SARS-CoV-2 cases through strict border control, quarantine and NPIs, but did not vaccinate abundantly, which exposed the population to severe disease outcomes when the Omicron variant emerged (Ma and Parry, 2022). The feasibility of an elimination strategy may depend on variant characteristics and jurisdictional geographic and social characteristics (Silver, 2022, Martignoni and Hurford, 2022, Department of Health and Community Services, N.L., 2022). In early 2022, following the establishment of the Omicron variant, NL shifted from a containment to a mitigation approach (Department of Health and Community Services, N.L., 2022), with many of the jurisdictions that had implemented an elimination strategy responding similarly (a notable exception is China who continued to pursue an elimination strategy). The elimination strategy is most likely appropriate in specific locations and for specific periods of time as the costs and benefits of the strategy likely depend on complex interactions between regional characteristics, public health policy, community behavioural responses, and variant epidemiological characteristics.

While implementing an elimination strategy, it is important to develop tools to assess the risk of community outbreaks, to evaluate whether border controls should be upscaled or released. In the following, we define an importation as an individual who arrives in the local jurisdiction from another jurisdiction while infected with SARS-CoV-2. An importation occurs when a traveller is infected at the point of origin, or during travel to their destination. A travel-related infection refers to both an importation and close contacts who become infected by the traveller. A spillover is an infection from an individual with a travel-related infection to a community member that is not a close contact of the traveller, and a community infection is when a community member is infected either as a spillover, or from another community member. We note that this terminology differs from that used in NL Public Service Advisories, which reported cases as ‘related to international (or domestic) travel’ or ‘close contacts of a known case’. Infections and cases differ in that cases are the infections that are reported.

Travel-related and community infections arise through different processes, and therefore carry different risks and occur at different rates. The rate of arriving importations is dependent on the prevalence of infection at the travellers’ points of origin, the risk of infection during travel, and the rates of inbound travel to the local community (Russell et al., 2021). The rate that travel-related infections generate subsequent infections depends on contact rates with community members and can be reduced through post-arrival travel restrictions (Arino et al., 2020, Chen et al., 2021, Dickens et al., 2020). When travellers are to self-isolate post-arrival, infections can be spread to household members. In regions with few community cases of SARS-CoV-2, it is necessary to distinguish between importations, close contacts who were infected by an imported infection, and community infections (see Price et al., 2020 for related comments).

Here, we develop an approach to estimate the potential future impact of SARS-CoV-2 in communities that have experienced long periods with a high percentage of cases that are travel-related. Many models focus on community spread, without distinguishing between travel-related and community cases, and are not suitable for this purpose. During the pandemic, new SARS-CoV-2 variants emerged (Otto et al., 2021), and our framework considers this evolving risk. Our approach uses two models in a pipeline, expected spillovers and community spread, rather than only a single model that couples both. Our first model predicts the expected number of community members that are infected by travellers (i.e., spillovers) and considers three categories of public health measures: post-arrival travel restrictions, NPIs in the local community, and vaccination. Our second model describes a hypothetical future community outbreak and considers different variants and levels of vaccine coverage. The first model, describing the expected number of spillovers, is not coupled to the second model, describing a community outbreak, because community outbreaks might hypothetically begin on any given day, and averages taken across hypothetical outbreak start dates obscure key information (Juul et al., 2021). Considering a pipelined uncoupled framework is useful because some decisions that public health officials make are conditional on whether a community outbreak has been detected (notably the implementation of NPIs as part of an elimination strategy), while other decisions are better informed by the average across community outbreaks with all possible hypothetical start dates (i.e., generally applicable measures, such as provincial mask mandates when surveillance is low and importations are frequent).

In July 2021, most Canadians had received at least one dose of a SARS-CoV-2 vaccine, and there was a need to transition to a sustainable approach for SARS-CoV-2 management should high immunity levels be maintained. After vaccination, continued isolation of regions that implemented elimination strategies might be unrealistic, particularly given the economic and social impacts of these strategies (Committee for the Coordination of Statistical Activities, 2021). At this time, there was a need to develop guidelines to advise regions with zero or low SARS-CoV-2 prevalence in exiting elimination strategies (Lokuge et al., 2021, Open Society Common Purpose Taskforce, 2021). This remains an important topic even as most Canadian provincial governments have relaxed COVID-19 control measures. Indeed, vaccine coverage still lags in a large proportion of the world, and the emergence risk of novel variants remains high (Otto et al., 2021).

2. Materials and methods

2.1. Data

Our analysis combines data from multiple sources (summarized in Table 1) including the Public Health Agency of Canada (PHAC), and the Newfoundland and Labrador Centre for Health Information (NLCHI). A data source for travel-related cases was the COVID-19 Canada Open Data Working Group (CCODWG) (Berry et al., 2020, Berry et al., 2021), a group of volunteers who curated data from government and non-government sources. We validated the CCODWG data with travel-related cases as reported by the NL and NB provincial governments and found that the CCODWG data accurately describes the number of travel-related cases in NL and NB (Figure S1). Another data source was the Bank of Canada NPI stringency index (Cheung et al., 2021), which was used to measure the severity of NPIs implemented in NL. All modelling was performed in R (R Core Team, 2022). All data and code are archived at https://github.com/ahurford/pandemic-COVID-zero. Parameter estimates are summarized in Table 2, Table 3.

Table 1.

Data sources.

Data source	Variables	Timeframe	Jurisdictions	Figures
COVID Canada Open Data Working Group	Travel-related cases (daily) Close contact cases (daily)	July 1, 2020–May 31, 2021	NB, PEI, NS, NL, YT, NWT	Figs. 1; 2; and S1
Newfoundland and Labrador Centre for Health Information	Travel-related cases (daily)	July 1, 2020–December 24, 2021	NL	Figs. 2; 3A, E; and S1
Government of New Brunswick public releases	Travel-related cases (daily)	January 1, 2021–May 31, 2021	NB	Fig. S1
Public Health Agency of Canada public data	New cases (daily)	March 15, 2020–December 24, 2021	All Canadian provinces	Explanatory variable for model fit in Fig. 2
Public Health Agency of Canada public data	Variant frequency (weekly) Vaccination levels (weekly)	March 14, 2020–December 24, 2021	Canada Canada and NL	Fig. 3A, E; and S2A Fig. 3C, E; and S2B
Newfoundland and Labrador Centre for Health Information	Community cases (daily) Close contacts infected per travel-related case Number of cases and symptom onset date for the Mt. Pearl outbreak	March 14, 2020–December 24, 2021 February 8–24, 2021	NL	Fig. 3E Fig. 3E Fig. 4
Bank of Canada	NPI stringency (daily)	July 1, 2020–December 24, 2021	NL	Fig. 3D

The line list for CCODWG (Berry et al., 2020) was discontinued on May 31, 2021, and as such, no data on travel-related cases or close contacts of travellers are available from CCODWG after this date.

Table 2.

Parameter estimates.

Description	Value	Details
The number of close contacts infected per imported infection of the Original variant	c${}_{\mathrm{OR}}$=0.149	Estimated from NLCHI data as: (the number of close contacts)/(the number of importations) on any day. Estimate is the average, weighted by the Original variant prevalence in Canada, when this prevalence was greater than 1%.
The number of close contacts infected per imported infection of the Alpha variant	c${}_{\alpha }$=0.114	Same estimation method and data as c${}_{\mathrm{OR}}$
The number of close contacts infected per imported infection of the Delta variant	c${}_{\delta }$=0.266	Same estimation method and data as c${}_{\mathrm{OR}}$
The number of close contacts infected per imported infection of the Omicron variant	c${}_{\mathrm{o}}$=0.756	Same estimation method and data as c${}_{\mathrm{OR}}$
Probability of no infection given exposure for unvaccinated individuals	z${}_{0,\mathrm{k}}$ = 0	Assumed. Constraint is 0 $\le$z${}_{0,\mathrm{k}}$$\le$1.
Probability of no infection given exposure for individuals with 1 dose of vaccine (original, Alpha and Delta variant)	z${}_{\mathrm{1,OR}}$=z${}_{\mathrm{1},\alpha }$ =z${}_{\mathrm{1},\delta }$ =0.49	Based on Pfizer vaccine efficacy against symptomatic infection (Bernal et al., 2021). Original variant same as Alpha variant (Khateeb et al., 2021). Constraint is 0 $\le$z${}_{1,\mathrm{k}}$$\le$1.
Probability of no infection given exposure for individuals with 1 dose of vaccine (Omicron variant)	z${}_{1,\mathrm{o}}$ = 0	Assumed. Constraint is 0 $\le$z${}_{1,\mathrm{k}}$$\le$1.
Probability of no infection given exposure for individuals with 2 or 3 doses of vaccine (original and Alpha variant)	z${}_{\mathrm{2,OR}}$ = z${}_{\mathrm{2},\alpha }$ = z${}_{\mathrm{3,OR}}$ = z${}_{\mathrm{3},\alpha }$ = 0.93	Based on Pfizer vaccine efficacy against symptomatic infection (Bernal et al., 2021). Original variant same as Alpha variant (Khateeb et al., 2021). Constraint is 0 $\le$z${}_{2,\mathrm{k}}$$\le$1.
Probability of no infection given exposure for individuals with 2 or 3 doses of vaccine (Delta variant)	z${}_{\mathrm{2},\delta }$=z${}_{\mathrm{3},\delta }$ =0.88	Based on Pfizer vaccine efficacy against symptomatic infection (Bernal et al., 2021). Constraint is 0 $\le$z${}_{2,\mathrm{k}}$$\le$1.
Probability of no infection given exposure for individuals with 2 doses of vaccine (Omicron variant)	z${}_{\mathrm{2,o}}$=0.09	Andrews et al. (2022). Based on Pfizer vaccine efficacy against symptomatic infection after 25 weeks. Constraint is 0 $\le$z${}_{2,\mathrm{k}}$$\le$1.
Probability of no infection given exposure for individuals with 3 doses of vaccine (Omicron variant)	z${}_{\mathrm{3,o}}$=0.67	Andrews et al. (2022). Based on Pfizer vaccine efficacy against symptomatic infection. Constraint is 0 $\le$z${}_{3,\mathrm{k}}$$\le$1.
Transmission rate	$\beta$ = 0.287	Calibrated
Multiplicative change in transmission for Alpha variant relative to original variant	b${}_{\alpha }$=1.77	Model 1a estimate from Table 1 in Davies et al. (2021)
Multiplicative change in transmission for Delta variant relative to original variant	b${}_{\delta }$=1.97	Campbell et al. (2021)
Multiplicative change in transmission for Omicron variant relative to original variant	b${}_{\mathrm{o}}$=2.97	Relative risk for unvaccinated primary cases (1.51) from Table 1 in Jalai et al. (2022)
Proportion of travellers that comply with self-isolation requirements	$\rho$=0.7	Assumed. Constraint is 0 $\le$$\rho$$\le$1.
Probability the traveller is infectious after completing x days of self-isolation	Figure S3E	See Supplementary Material for details
Probability a PCR test a days after arrival is a false negative	Figure S3F	See Supplementary Material for details
Probability 5 Rapid Antigen Tests are all false negatives	$\sigma$=0.1	Assumed. Constraint is 0 $\le$$\sigma$$\le$1.

All parameters are unitless.

Table 3.

Post-arrival travel restrictions in NL.

Reopening step	Dates, t	New measures	Value
SMO (Travel Exemption Order), May 5 2020	t${}_1$ = May 4, 2020–June 30, 2021	All travellersself-isolate for 14-days	m${}_0$(t${}_1$) = f${}_1$(14) = 0.153 m${}_1$(t${}_1$) = 0.153 m${}_2$(t${}_1$) = 0.153
SMO Reopening – Travel – Step 1, July 1, 2021	t${}_2$ = July 1, 2021–July 31, 2021	Partially vaccinatedtravellers must have a negative PCR test result at entry Fully vaccinated travellers have no restrictions	m${}_0$(t${}_2$) = 0.153 m${}_1$(t${}_2$) = f${}_2$(0,0) = 0.384 m${}_2$(t${}_2$) = f${}_1$(0) = 0.509
SMO Reopening – Travel – Step 2 - August 1, 2021	t${}_3$ = Aug 1, 2021–Sept 29, 2021	Unvaccinatedtravellers complete a Polymerase Chain Reaction (PCR) test on day 7–9 of self-isolation, and can exit self-isolation if negative. Partially vaccinated travellers have no restrictions	m${}_0$(t${}_3$) = 0.156 m${}_1$(t${}_3$) = f${}_2$(8,8) = 0.509 m${}_2$(t${}_3$) = 0.509
SMO Reopening – Travel – Step 2 – UPDATED, Sept 30, 2021	t${}_4$= Sept 30–Dec 20, 2021	Partially vaccinatedtravellers complete a PCR test on day 7–9 of self-isolation, and can exit self-isolation if negative.	m${}_0$(t${}_4$) = 0.156 m${}_1$(t${}_4$) = 0.156 m${}_2$(t${}_4$) = 0.509
SMO Reopening – Travel – Step 2 – December 21, 2021 Update	t${}_5$= Dec 21–24, 2021	All travellersself-isolate for 5-days and complete a rapid antigen test each day	m${}_0$(t${}_5$) = 0.1f${}_1$(5) = 0.022 m${}_1$(t${}_5$) = 0.022 m${}_2$(t${}_5$) = 0.022

The restrictions for travellers with 3 doses of vaccine are the same as for 2 doses of vaccine. For the calculations, 1 dose of vaccine and partially vaccinated were considered equivalent. When a vaccination status is not listed under a Special Measures Order (SMO), the new SMO does not change the measures that apply to that vaccination status. The functions $f_1\left(s\right)$ and $f_2(s,\tau )$ are defined in the Supplementary Material.

2.2. Modelling framework

Central to our approach where we develop a method to quantify the expected number of spillovers are two quantities: $n_{j,k}\left(t\right)$, the number of travel-related infections, and $p_{j,k}\left(t\right)$, the probability that a traveller or their close contacts infects a community member, where both quantities depend on the date, $t$. Travellers and their close contacts are indexed by their vaccination status, i.e., the number of vaccination doses completed, $j$ which can be $0,1,2$, or $3$, and the infecting variant, $k$, referring to the Original ($OR$), Alpha ($\alpha$), Delta ($\delta$), or Omicron ($o$; BA.1 subvariant) variants. Post-arrival travel restrictions, NPIs and vaccine coverage in the local community, and variant transmissibility are all considered to calculate $p_{j,k}\left(t\right)$.

2.3. Statistical model of imported cases to NL

To model the daily number of imported cases arriving to NL, we used a Poisson regression. Explanatory variables were time series of the mean new cases per 10,000 population over the last 14 days for (from east to west) Nova Scotia, Quebec, Ontario, Manitoba, Saskatchewan, Alberta and British Columbia. Provincial population sizes were based on Statistics Canada estimates for the first quarter of 2021. Fitted coefficients were constrained to be non-negative because we hypothesized that high infection prevalence in other provinces should have a positive relationship with the number of imported cases arriving in NL from that province.

2.4. Model 1: Expected number of spillovers

2.4.1. Characteristics of travel-related cases

To estimate the expected number of travellers or their close contacts that infected NL community members (referred to as ‘spillovers’), we first obtain the number of travellers and their close contacts with vaccination status $j$ and infected with variant $k$ as

$$n_{j,k}\left(t\right)=(1+c_k)D\left(t\right)T_{j,k}\left(t\right),$$ (1)

where $c_k$ is the number of close contacts infected per imported infection of the variant, $k$, and $D\left(t\right)$ is the number of imported infections reported on date $t$. We assume all infected travellers are identified and reported. Eq. (1) assumes a similar frequency of vaccination statuses for travellers and their close contacts. Given a travel-related infection, $T_{j,k}\left(t\right)$ is the probability that the traveller has vaccination status $j$ and is infected with variant $k$, where

$$T_{j,k}=\frac{v_k\left(t\right)x_j^T\left(t\right)z_{j,k}}{\sum _{j,k}{v}_k\left(t\right)x_j^T\left(t\right)z_{j,k}}.$$ (2)

Here, $x_j^T\left(t\right)$ is the fraction of travellers with vaccination status $j$ at time $t$, $v_k\left(t\right)$ is the frequency of the variant $k$ at the origin sites of travellers, and $z_{j,k}$ is the probability that a traveller with vaccination status $j$ is infected with the variant $k$, where we assume no changes in $z_{j,k}$ over time, i.e., as might occur due to waning of the vaccination.

As data on variant frequencies is not reliably available for jurisdictions within Canada, we parameterize $v_k\left(t\right)$ as the variant frequency in Canada. To parameterize $z_{j,k}$, we equate reported vaccine efficacies against symptomatic infection with the probability of infection (see Table 2) . Realistically, vaccines prevent less against infection and transmission than symptomatic infection, however, data for vaccine efficacies against infection and transmission are less available.

2.4.2. Post-arrival travel restrictions

Post-arrival travel restrictions may include self-isolation for a specified number of days after arrival, and Polymerase Chain Reaction (PCR) or Rapid Antigen Tests (RATs). In NL, different post-arrival travel restrictions were implemented through Special Measures Orders at different times during the SARS-CoV-2 public health emergency and depended on the vaccination status of the travellers (Table 3). We let $m_j\left(t\right)$ describe the efficacy of travel restrictions for a traveller with the vaccination status $j$, given the post-arrival travel restrictions on a given date $t$.

To estimate $m_j\left(t\right)$, we assumed that the efficacy of self-isolation for a given number of days could be calculated from the generation interval of SARS-CoV-2 (Ferretti et al., 2020), which was estimated for the Original variant. We assumed the generation interval was the same for all variants, although data suggests shorter generation times for the Delta variant (Hart et al., 2022). We felt this assumption was reasonable as our conclusions are likely more sensitive to other parameter estimates (as described in the Discussion). We estimated the probability of a false negative PCR test by considering (Hellewell et al., 2021). The complete details of how we parameterized the effect of post-arrival travel restrictions are provided in the Supplementary Material. We had no information on compliance with self-isolation requirements, or when travellers are usually infected prior to arrival, and so we assumed 70% compliance with self-isolation, and that infected travellers were exposed between zero and ten days prior to arrival, with exposure times following a uniform distribution.

We assumed that the travel restrictions that applied to travellers also applied to their close contacts (i.e., household members). Our assumption is an over-simplification because in NL sometimes household members of travellers were subject to restrictions and other times they were not. If close contacts were infected from a traveller the timing of the close contact’s infectious period would be later than that of the traveller, and potentially after even a long period of self-isolation that began when the traveller arrived. This suggests that our assumption that the same restrictions apply to the traveller and their close contacts could under-estimate the spillover risk. However, in NL during the period of this study, if the traveller tested positive or if the close contacts developed symptoms, the close contacts were required to complete a PCR test. If the PCR test was positive, the close contacts were required to self-isolate, and in this respect, our assumptions regarding the probability that a close contact of a traveller infects a community member are an under-estimate.

2.4.3. NPIs and vaccination in the local community

We let the susceptibility of the local community to infection be determined by NPIs and vaccination (PIs). We let $\omega \left(t\right)$ be the stringency of NPIs in the local community on a given date $t$. We used the Bank of Canada COVID-19 stringency index estimated for NL. The Bank of Canada COVID-19 stringency index is calculated from 12 sub-indices which include policy related to school and workplace closures, restrictions on public and private gathering, travel restrictions, enforcement mechanisms, and public information campaigns (Cheung et al., 2021). We let $\beta$ be a transmission rate parameter, and we let $b_k$ be a multiplier reflecting the relative transmission rates for different variants.

The susceptibility of the local community to infection when considering vaccination is,

$$x^C\left(t\right)=z_{0,k}{x}_0^C\left(t\right)+z_{1,k}{x}_1^C\left(t\right)+z_{2,k}{x}_2^C\left(t\right)+z_{3,k}{x}^C\left(t\right),$$ (3)

where the fraction of the community with different vaccination statuses is $x_j^C\left(t\right)$ and $z_{j,k}$ is the probability of infection given vaccination status $j$ and the infecting variant $k$ as previously defined. We assume four factors act independently to determine the probability that a traveller infects a local community member: (i) the efficacy of travel restrictions, $m_j\left(t\right)$; (ii) the stringency of NPIs, $\omega \left(t\right)$; (iii) the transmissibility of different variants; and (iv) the susceptibility of the local community after considering vaccination, $x^C\left(t\right)$. As such,

$$p_{j,k}\left(t\right)=\beta b_k{m}_j\left(t\right)x^C\left(t\right)(1-\omega \left(t\right)).$$ (4)

We assume that spillovers occur following a Binomial distribution with probability $p_{j,k}\left(t\right)$ and $n_{j,k}\left(t\right)$ trials. Then, on each date $t$, the expected number of community members infected by a traveller or their close contact is

$$\overline{\sigma }\left(t\right)=\sum _j\sum _k{n}_{j,k}\left(t\right)p_{j,k}\left(t\right),$$ (5)

which is the expectation of a Binomial distribution summed across all vaccination and variant types.

This quantity, $\overline{\sigma }\left(t\right)$, describes the daily expected number of community members infected by travellers and their close contacts (spillovers). Quantifying SARS-CoV-2 risks in regions that do not have SARS-CoV-2 community cases was an area of need during the first 18 months of the SARS-CoV-2 pandemic, and Eq. (5) addresses this need.

2.5. Model 2: Modelling outbreaks in regions implementing an elimination strategy

The second model for quantifying SARS-CoV-2 risk in regions that do not have community cases is to answer the question ‘if a community outbreak is established, how will the number of cases change over time, and how many cases will occur in the outbreak?’ To illustrate this modelling for a region that had few community cases of SARS-CoV-2, we consider Mount Pearl, NL.

Prior to December 15, 2021 in NL, the largest community outbreak of SARS-CoV-2 occurred due to the Alpha variant, with symptom onset dates from February 1 to 27, 2021, and with spread predominately in the Mount Pearl region. Mount Pearl is a suburb of St. John’s, and is part of the St. John’s metropolitan area which in 2016 had a population size of 205,955 (Statistics Canada, 2017). In response to the outbreak, on February 11, a Special Measures Order enacted the strictest level of NPIs (Alert level 5) in the St. John’s region. Contacts of cases were traced and tested, and many cases were associated with Mount Pearl Senior High School (Government of Newfoundland and Labrador, 2021b). No new cases associated with the outbreak were reported with symptom onset dates after February 28, 2021.

We calibrated a stochastic Susceptible–Infected–Recovered (SIR) model to data describing daily new reported cases and their symptom onset dates for cases belonging to the Mount Pearl outbreak (see Supplementary Material for details). This parameterized model is then the basis to explore the dynamics of hypothetical future outbreaks in Mount Pearl, NL.

For comparison, hypothetical scenarios retain the pattern of NPI implementation that occurred in the actual Mount Pearl outbreak, i.e., implementation of strict NPIs 10 days after the start of the outbreak, although it is possible to explore scenarios without this assumption. We consider future scenarios where vaccination coverage may have changed, and where a different variant may have caused the outbreak. For simplicity in interpreting the results of vaccination scenarios, we assume that all individuals in the community are either unvaccinated or have had two doses of vaccine.

3. Results

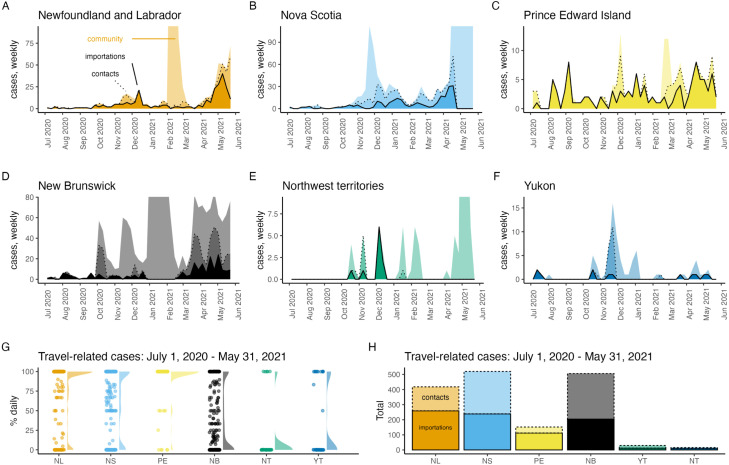
Most of the SARS-CoV-2 cases reported in Atlantic Canada and Canada’s territories were travel-related from July 1, 2020 to May 31, 2021 (Fig. 1). The period prior to July 1, 2020 was not considered because very few cases of any type were reported during this time. Notable differences that occur between these jurisdictions are that a much lower percentage of travel-related cases was reported each day in NB (mean = 36.7%, median = 13.4%), NT (mean = 12.8%, median = 0%) and YT (mean = 30.1%, median = 0%), as compared to NL (mean = 76.6%, median = 100%), NS (mean = 61.2%, median = 80%), and PE (mean = 91.3%, median = 100%) (Fig. 1G). The values reported for NB are likely still much higher than the provinces west of NB, which had community spread and likely near 0% of reported cases were travel-related on most days.

Fig. 1.

In Atlantic Canada and Canada’s territories most SARS-CoV-2 cases were importations and close contacts of these travellers from July 1, 2020 to May 31, 2021. Panels A–F show imported cases (dark shading, solid line), their close contacts (medium shading, dashed line), and community cases (light shading, no line) with the vertical axis limit as 20% more than the maximum number of reported weekly travel-related cases so that brief periods of large community outbreaks do not dominate the graphs. From July 1, 2020–May 31, 2021, panels G–H show the percentage of reported daily cases that were travel-related (dots; also shown as a shaded density plot, G), and the total number of imported cases and their close contacts (H).

During the same period, the total number of travel-related cases also differed between jurisdictions with NL (importations = 259, close contacts of travellers = 159), NS (importations = 239, close contacts = 281), and NB (importations 204, close contacts = 302) having reported at least 2.75 times more travel-related cases than PE (importations = 112, close contacts = 40), and with YT (importations = 12, close contacts = 18) and NT (importations = 10, close contacts = 6) having reported very few travel-related cases at all (Fig. 1H). Other Canadian provinces and Nunavut (NU) were not considered because travel-related case data was not reliably reported for these jurisdictions.

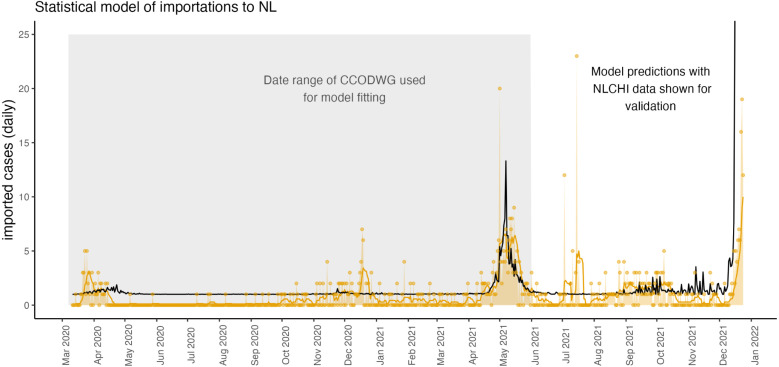
We found that the daily number of importations to NL was predicted as 1.12 times the mean number of new cases per 10,000 population in NS, where the mean is taken over the last 14 days (Fig. 2). Estimated coefficients for the contribution of other provinces to the prediction of daily imported cases to NL were not different than zero, and the estimated intercept was zero. This statistical relationship is reasonable since a pre-pandemic survey reported 26% of travel into NL was from the Maritimes, second only to Ontario (Government of Newfoundland Labrador, 2018). The island of Newfoundland was the destination for 93% of travellers into NL (Government of Newfoundland Labrador, 2018), the ferry to Newfoundland departs from NS, and many flights to Newfoundland are routed with layovers in NS.

Fig. 2.

From March 15, 2020–December 24, 2021, the daily number of imported cases to NL is reliably predicted as 1.12 times the mean number of new cases per 10,000 population in NS, where the mean is taken over the last 14 days. This relationship was fit using the publicly available CCODWG data, where curation of these data ended on May 31, 2021 before the end of the study period. The model-predicted daily number of imported cases to NL (black line) extends beyond the time period of model fitting (grey shaded region) because data describing new cases in NS was available through to the end of the study period. To validate the predictions of the statistical model, we show the number of daily imported cases reported by NLCHI (yellow dots and yellow shading), and the 7-day rolling mean of daily imported cases (yellow line) where these data span the full study period.

The agreement of the model (Fig. 2, black line) with the data (yellow line) is good since the model was only parameterized with data to May 31, 2021 (grey shaded region), but the model predictions still agree with the validation data from June 1 to December 24, 2021 and the model predicts the rise in importations that occurred in early December 2021. Few importations were reported and so chance events disrupt the agreement between the model predictions and the data. For example, in July 2021, a Portuguese fishing boat anchored in Conception Bay, NL and 31 crew members tested positive for SARS-CoV-2 (Smelie, 2021). This event may explain the 23 imported cases reported on July 15, 2021. The arrival of such boats with SARS-CoV-2 positive crew members is a chance event rather than a regularly occurring event that can be predicted by a model.

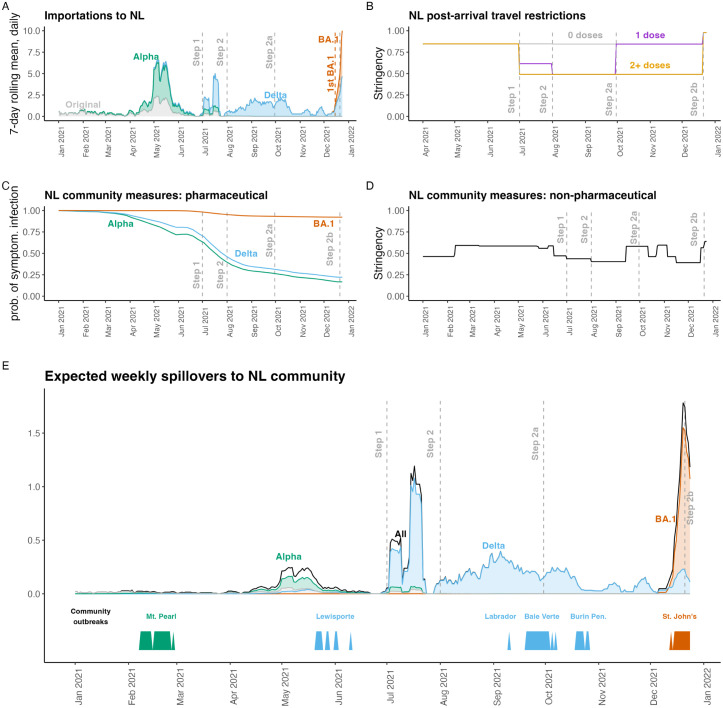
By December 24, 2021 (Fig. 3E), the expected number of spillovers, infections spread from travellers and their close contacts to NL community members, was as high as it had ever been (as calculated by Eq. (5)). At this time, a community outbreak involving the Omicron variant was already occurring, with the first Omicron variant case in NL reported in St. John’s on December 15, 2021. The expected number of spillovers in mid-December was 44% higher than the previous highest value, and due to both the high number of imported cases (Fig. 3A) and the reduced efficacy of two vaccine doses in protecting the NL community from infection with the Omicron variant (Fig. 3C). In late July 2021, the expected number of spillovers was also high (Fig. 3E). This was after NL relaxed entry requirements for Canadian travellers on July 1, 2021 (Fig. 3B; Table 3), but before most Newfoundlanders and Labradorians were fully vaccinated (Figure S2C). The peak in the expected number of spillovers due to the Alpha variant (early May 2021; Fig. 3E) was due to an increased number of importations occurring at that time (Fig. 3A). The expected number of spillovers occurring due to the Delta variant was higher than that of the Alpha variant for two reasons: (1) after July 1, 2021 travel restrictions into NL for Canadians were relaxed (Fig. 3B; Table 3), and (2) the Delta variant is more transmissible than the Alpha variant (Table 2).

Fig. 3.

In mid-December 2021, the expected number of spillovers to NL community members was the highest it had ever been. High spillover risk in mid-December 2021 was due to the establishment of the Omicron BA.1 variant in Canada and high numbers of imported cases (A), and low vaccine efficacy for NL community members with two doses of vaccine exposed to the Omicron variant (C). (A) Imported cases, $D\left(t\right)$. (B) The stringency of post-arrival travel restrictions, $1-m_j\left(t\right)$. (C) The probability of a symptomatic infection given exposure when considering vaccination of NL community members, $x^C\left(t\right)$. (D) The stringency of NPIs implemented in the NL community, $\omega \left(t\right)$. (E) The expected number spillovers, NL community members infected by travellers and their close contacts, $\overline{\sigma }\left(t\right)$ (black - Eq. (5); with variant-specific numbers shown with colours). The timing of actual community outbreaks with more than 5 cases are shown along the bottom bar. Grey dashed vertical lines show post-arrival travel restrictions due to different Special Measures Orders (see Table 3).

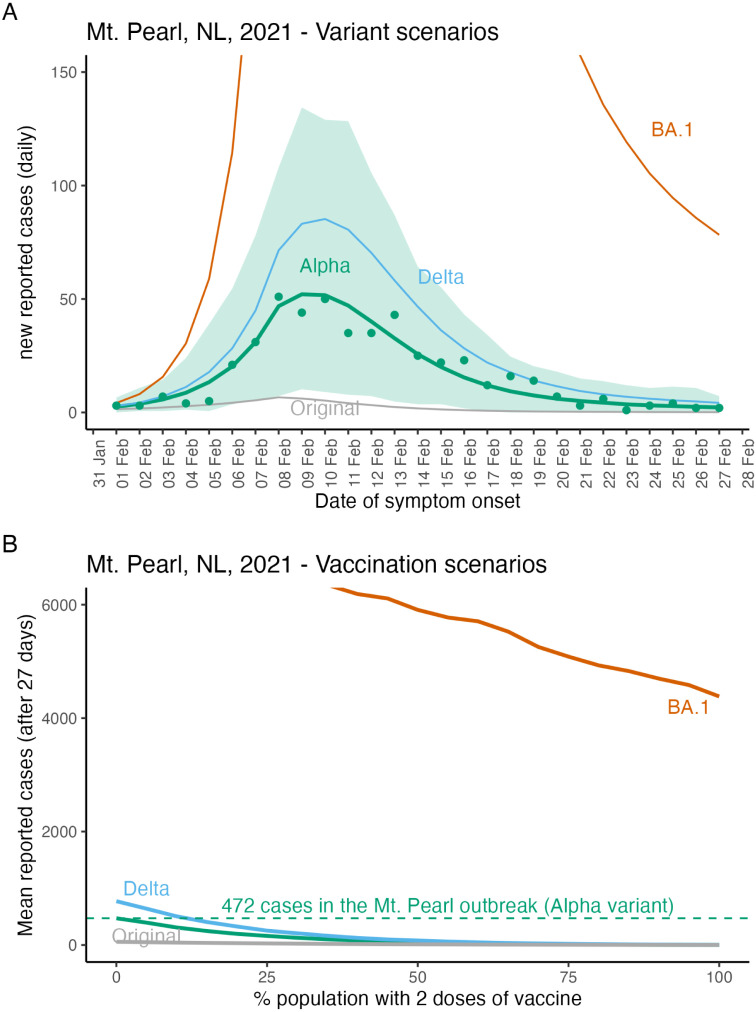
The stochastic SIR model (Fig. 4A, green lines and shading) shows close agreement with the data from the Mount Pearl outbreak in February, 2021 (Fig. 4A, green dots). When the Mount Pearl outbreak occurred few NL community members were vaccinated or had been infected, such that all the scenarios shown in Fig. 4A assume a fully susceptible community. The Omicron variant (BA.1 subvariant) is much more transmissible than the other variants, and a hypothetical BA.1 variant outbreak in a fully susceptible Mount Pearl, NL community (Fig. 4A, red line) cannot be completely shown given the vertical axis limits that were set to emphasize the actual Mount Pearl Alpha variant outbreak. Fig. 4A does not consider the arrival of imported cases. This is because the Mount Pearl data was strictly for cases known to belong to this outbreak.

Fig. 4.

Epidemiological model fit and hypothetical future variant and vaccination scenarios for Mount Pearl, NL. The Mount Pearl outbreak was due to the Alpha variant and the vertical axis limits of panel (A) were selected to show the Alpha variant (green line), and the Mount Pearl data (green dots) which meant that large values for the BA.1 variant are not shown. Lines show the mean and the shaded region shows the minimum and maximum values for 1000 simulations. The peak number of reported daily new cases for the BA.1 variant is 806 (not shown). In panel (B) vaccination scenarios assume community members are either unvaccinated or vaccinated with 2 doses. After 27 days of a BA.1 outbreak in a fully unvaccinated community, we estimate 7852 reported cases (not shown due to truncation). For more details describing parameter estimates see Table 2, and for model details see the Supplementary Material.

The number of cases reported in the Mount Pearl outbreak was 472 (Fig. 4B, green dashed line). For the simulations, the mean total number of reported cases after 27 days (the duration of the Mount Pearl outbreak) when the community is fully susceptible are Original variant, 56, Alpha variant, 472, Delta, 773, and Omicron variant, 7852. We assumed that community members could be either unvaccinated or have two doses of vaccine. The effect of vaccination is to substantially reduce the number of reported cases in the outbreak after 27 days for all variants (Fig. 4B).

4. Discussion

In regions that have extended periods with few community cases of SARS-CoV-2, for example, regions that effectively implemented an elimination strategy, travel-related cases are a high percentage of reported cases (Arino et al., 2021, Godin et al., 2021), and modelling importations is particularly important (Zhang et al., 2022). Here, we extend such importation modelling to incorporate post-arrival travel restrictions, community vaccination coverage, and NPIs into the risk assessment frameworks for regions with few community SARS-CoV-2 infections.

Atlantic Canada and Canada’s territories experienced few SARS-CoV-2 cases prior to June 2021, however, there were some differences between these jurisdictions. NT and YT reported few travel-related cases, while NL, NS, and NB reported similar numbers of travel-related cases, but with NB reporting a much lower percentage of daily cases that were travel-related (Fig. 1). Finally, while NL and NS had similar epidemiology until May 31, 2021, NL had enacted strict travel restrictions (Hurford et al., 2021), while NS enacted an extensive community testing program (Johnson-León et al., 2021). The YT implemented strict travel restrictions, but experienced an outbreak of the Gamma variant that overwhelmed hospital capacity (McPhee-Knowles et al., 2022).

We considered a statistical model describing the daily number of reported importations arriving in NL. During the pandemic response it was helpful to use this approach to forecast importations so that future risk could be assessed using Eq. (5). That was not done in this manuscript because such an exercise would never be current, but this could be valuable to assess border measures, the threat of a new variant, or the impacts of waning immunity. We found that importations to NL could be predicted from the mean new cases per 10,000 people in NS over the last 14 days (Fig. 2). These data were publicly available and regularly updated, but more generally better access to data describing travel volumes, travellers’ points of origin, reasons for travel, and granting of travel exemptions would aid real time importation modelling and risk quantification.

We applied our framework (Eq. (5)) to inform the potential for community outbreaks in NL. The estimated risk is somewhat consistent with the actual community outbreaks that occurred in NL (Fig. 3). Generally, it seems difficult to predict when community outbreaks might occur in regions without community cases even given the vast amounts of data that were available during the SARS-CoV-2 pandemic.

Our analysis considers only known travel-related infections, such that estimates per infected traveller equate to per known infected traveller. In NL, for the pandemic until July 1, 2021, testing of arriving travellers was intensive (owing to few ports of entry, reduced travel volumes (Hurford et al., 2021), testing requirements for rotational workers (Department of Health and Community Services, N.L., 2022), and requests for travellers potentially exposed during inbound flights to report for asymptomatic testing). This intensive testing, combined with few occurrences of community cases, suggests that a high proportion of imported cases were detected in NL during this time.

The main limitation of our analysis is parameter estimation and uncertainty. It is difficult to estimate the change in relative transmissibility due to a new variant because these data are estimated in different regions (or pooled across regions), and as the susceptible population changes owing to vaccination, infection, and waning of immunity during the time period that the estimation is made. We used 77% as the estimate of increased transmissibility of the Alpha variant relative to the Original variant (Table 2), however, the source of this estimate (Davies et al., 2021) gives a range of values from 43% to 90% depending on the population and assumptions of the estimation procedure. Vaccine efficacies are estimated in specific populations, and application to other regions assumes no differences in population structure with regard to age and immunity, and does not estimate protection against infection and onward transmission, which is a critical parameter for epidemiological models. Finally, the impact of NPIs on transmission is difficult to assess, and the impact of new variant characteristics on the effectiveness of NPIs is unknown. In some instances data were not available to estimate parameters, for example, we assumed 70% compliance with self-isolation requirements, and the transmission rate parameter was calibrated (Table 2).

Our work was motivated by a need for regions that successfully implemented an elimination strategy during the first 18 months of the COVID-19 pandemic to quantify the risk of SARS-CoV-2 spread in their communities, and a need for guidelines to exit an elimination strategy when high vaccination coverage has been achieved. While guidelines for reopening have been developed by many jurisdictions, those using criteria expressed as the number of observed community cases (Anderson et al., 2021, Nali et al., 2021) are not helpful for regions that are reopening when there are few community cases.

Existing theory applicable to developing such guidelines is importation modelling (i.e., considering infection prevalence at travellers’ origins and travel volumes into a destination, e.g. Russell et al., 2021) and branching process modelling that calculates the probability of a major outbreak (i.e., Allen, 2008). Extensions of classic branching process models consider the probability of an outbreak in age-structured populations with NPIs (Lovell-Read et al., 2022), and when importations occur (Ball et al., 2017). A related concept is the ‘event reproduction number’, a quantity that describes the number of secondary infections arising from one infected person attending an event (Tupper et al., 2020), since this quantity measures outbreak risk rather than simulating the entire outbreak. Some modelling studies have considered the efficacy of pre- and post-arrival travel restrictions (Steyn et al., 2021, Wells et al., 2021), but without linking to importation modelling as we have done. Future work to inform guidelines to exit an elimination strategy should further bridge these different research areas.

There is a need to communicate reasonable expectations to the public in regions where elimination has been implemented as relaxation of measures might have little or no impact on reported case numbers when infection prevalence is already high (Russell et al., 2021, Chen et al., 2020), but might bring risk in populations with zero or low SARS-CoV-2 prevalence (Russell et al., 2021, Chen et al., 2020, Arino et al., 2021). In regions that have implemented an elimination strategy, an increase in reported case numbers may occur even when measures are carefully and reasonably relaxed, and particularly if the prevalence of variants of concern is higher outside the jurisdiction than in (Wells et al., 2020, Grépin et al., 2021).

Prior to May 31, 2021, Atlantic Canada and Canada’s territories had experienced prolonged periods with few community SARS-CoV-2 cases. In this manuscript, we characterize differences within these jurisdictions, and distinguish between travel-related and community cases (Fig. 1). We illustrate a type of epidemic modelling that is useful in these regions. This framework extends importation modelling such that border restrictions, variants, NPIs and vaccination in the local community are considered. Additionally, hypothetical future outbreaks are considered by simulating variant and vaccination scenarios. Our framework can be used to inform the risk associated with different candidate reopening plans when vaccination coverage is high in regions that have experienced prolonged periods with few SARS-CoV-2 cases, and help inform plans to exit an elimination strategy.

CRediT authorship contribution statement

Amy Hurford: Developed the modelling framework, Wrote the code, Made the figures, Wrote the manuscript. Maria M. Martignoni: Wrote the manuscript. J. Concepción Loredo-Osti: Wrote the code, Comments on manuscript drafts. Francis Anokye: Wrote the code, Comments on manuscript drafts. Julien Arino: Wrote the manuscript, Comments on manuscript drafts. Bilal Saleh Husain: Collected data, Comments on manuscript drafts. Brian Gaas: Comments on manuscript drafts. James Watmough: Comments on manuscript drafts.

Appendix A. Supplementary data

The following is the Supplementary material related to this article.

MMC S1

Additional details describing the data, model parameterization, and model formulation.