Joint inference of physiological network and survival analysis identifies factors associated with aging rate

Summary

We describe methodology for joint reconstruction of physiological-survival networks from observational data capable of identifying key survival-associated variables, inferring a minimal physiological network structure, and bridging this network to the Gompertzian survival layer. Using synthetic network structures, we show that the method is capable of identifying aging variables in cohorts as small as 5,000 participants. Applying the methodology to the observational human cohort, we find that interleukin-6, vascular calcification, and red-blood distribution width are strong predictors of baseline fitness. More important, we find that red blood cell counts, kidney function, and phosphate level are directly linked to the Gompertzian aging rate. Our model therefore enables discovery of processes directly linked to the aging rate of our species. We further show that this epidemiological framework can be applied as a causal inference engine to simulate the effects of interventions on physiology and longevity.

Graphical abstract

Highlights

• •Bayesian framework linking physiological network to Gompertzian survival function
• •The framework captures critical aging parameters in real world datasets
• •Aging rate in human cohorts is associated with levels of phosphate, RBCs, and creatinine
• •Model enables simulations of what-if interventional hypotheses

Motivation

The physiological processes that determine the longevity and the aging rate of our species are poorly understood. In principle, it should be possible to use deeply phenotyped data from long-term observational studies to identify key biological pathways involved in the aging process. In practice, however, the development of an epidemiological framework capable of capturing the full complexity of physiology and the effect of its decline on survival outcomes remains both theoretically and computationally challenging.

Sethi and Melamud describe a general methodology for joint inference of the physiological-survival network to identify physiological variables associated with Gompertzian aging parameters, i.e., the baseline hazard and aging rate of an organism. They apply this methodology to reconstruct physiological networks and to simulate the effects of interventions.

Introduction

In humans, the probability of death at age twenty is approximately 1 in 10,000 and it increases exponentially, doubling every eight years. This relationship was first discovered by Benjamin Gompertz in 1825 (Kirkwood, 2015) when modeling actuarial life tables of England, and since has been demonstrated to be an accurate model of mortality generalizable to all human populations. The hazard function described by Gompertz takes a mathematical form of $\lambda$ (t) = $\alpha$∗exp($\beta$∗t) where the alpha parameter captures the time-independent probability of failure of an individual at the baseline (t = 0), and the beta parameter captures a time-dependent increase in failure for an individual (i.e., the aging rate of an organism).

Despite the success of the Gompertz equation in describing the shape of the mortality hazard, remarkably little is known about what biological factors determine the aging rate (Moffitt et al., 2017). At the individual level, an age-dependent increase in the probability of mortality is a consequence of the decline in physiological robustness (Dent et al., 2016). Underlying this loss in robustness are gradual declines in functions of tissues/organs and ultimately a failure of homeostatic mechanisms to maintain a functional state (López-Otín et al., 2013; Muñoz-Espín and Serrano, 2014). In principle, given broad multi-function multi-organ measurements, it should be possible to determine which biological pathways influence the aging rate. However, in practice, this is difficult for three reasons.

The first is a practical data limitation. To identify longevity factors, we need information from deeply phenotyped longitudinal cohorts, optimally profiled starting at a young age, before the onset of significant pathologies. Acquiring such data is difficult if not impossible over the complete human lifespan. Consequently, most longitudinal cohorts span only a fraction of the human lifespan and usually focus on elderly individuals with pre-existing conditions. Although some of these limitations are partially addressed in general population longitudinal cohorts such as the Framingham Heart Study (Tsao and Vasan, 2015), Baltimore Longitudinal Study of Aging (Ferrucci, 2008), Cardiovascular Health Study (Fried et al., 1991), Health Aging Body and Composition Study (Sutton-Tyrrell et al., 2005), Osteoporotic Fractures in Men (MrOS) Study (Orwoll et al., 2005), Study of Osteoporotic Fractures (SOF) (Cummings et al., 1995), these cohorts are relatively small, limiting our power to detect time-dependent interactions (Schmoor et al., 2000).

The second limitation is methodological. To date, there are no computational models capable of describing the full complexity of interactions between multiple layers of biology and time-dependent components of the survival function. Most epidemiological techniques rely on statistical approximations with a selected set of variables. Indeed, many commonly used epidemiological regression techniques such as Cox proportional hazards model explicitly factor out time-dependent contributions of the hazard function, focusing specifically on time-invariant contribution of covariates (Cox, 1972; Stensrud and Hernán, 2020). Furthermore, most multivariate regression techniques assume only direct effects of variables on survival, neglecting second-order indirect effects and time-dependent interactions when modeling survival outcomes.

The third limitation is an incomplete description of the physiological network architecture. The robustness of a biological system is determined by a complex set of stabilizing interactions, and we currently lack a full description of these interactions for humans, as well as how this network responds to environmental perturbations and changes as a function of age (Cannon, 1929; Pomatto and Davies, 2017). Over many years, researchers have developed smaller dynamic models of subsets of physiology, such as glucose-insulin regulation, calcium-phosphate homeostasis, or iron homeostasis (Chifman et al., 2012; Makroglou et al., 2006; Peterson and Riggs, 2010). However, these models do not capture long-term steady-state behavior and the full dynamic model of human physiology is yet to be developed. Although it is currently infeasible to capture the complete dynamic state of physiological systems, it is possible to build network models capturing the long-term steady-state behavior of key variables that affect survival.

Graphical networks can be used as high-level representations of biological systems (Barabási and Oltvai, 2004; Freund, 2019; Stelzl et al., 2005). It is possible to approximate the steady-state behavior of physiological networks with directed acyclic graphs (DAGs) in which no feedback loops or cycles are allowed. In these networks, each node captures the state of biological variables, and each edge or connection captures the influence of one node on another. The connectivity can be thought of as directional if changes in one node (parent) propagate to another node (child). These types of models are direct analogs of graphical representations that are used for inference in causal inference (Pearl, 2000; Spirtes et al., 2000). Here we are adopting methods from the field of causal inference (Glymour et al., 2019) to study the influence of physiological variables on survival. In this representation, variables that influence human health are captured by measurements such as glucose levels, inflammation, hematology, etc. and the structure of their connectivity is inferred from underlying data.

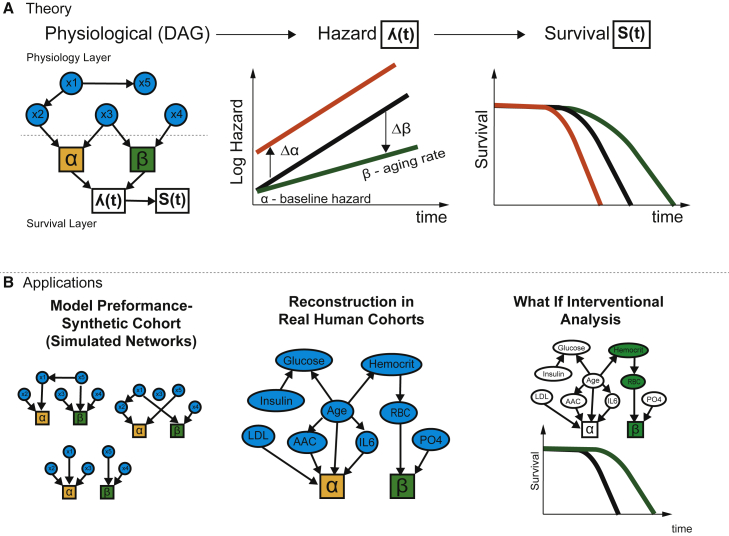
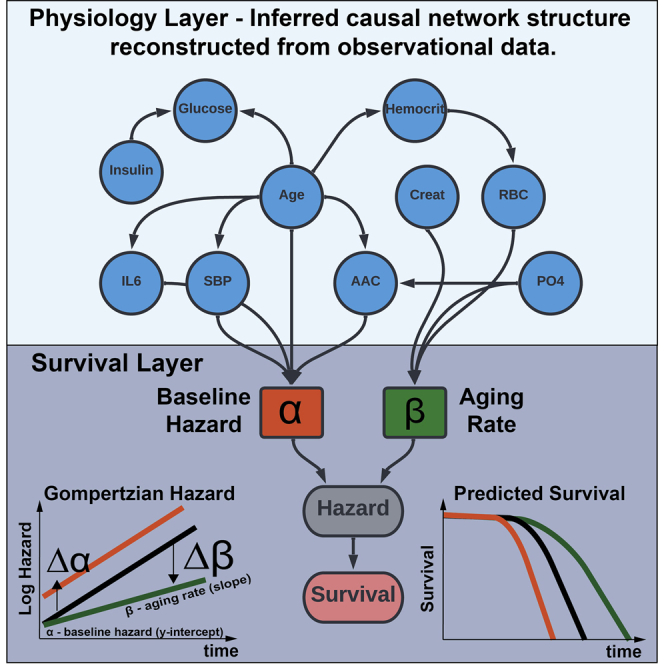
The key utility of these methods is that they can be used to reconstruct physiological network DAG and to identify variables directly affecting survival in absence of any prior information. These networks can be used to understand the causal structure of relationships, identify confounding, and confirm previously known relationships. More important, such methods allow us to uncover heretofore unknown causal relationships and to propose experiments and interventions to test these hypotheses. As a proof of concept, we have applied this model to the MrOS longitudinal cohort, and demonstrate unique insight afforded by the methodology (Figure 1).

Figure 1.

Overview of theoretical framework and applications to real human datasets

Physiological DAG captures causal relationships between physiological variables and their effects on Gompertz survival function.

(A) The variables can affect hazard at the baseline, as well as the aging rate of an organism. For example, changing variable x2 will change the baseline fitness (orange curve), while changing variable x4 changes the aging rate (green curve). In the illustration, x1 affects survival indirectly by modifying x2 while changing x5 does not affect survival even though it may be correlated with survival.

(B) We construct simulations with synthetic networks to determine the power of the methodology to identify survival covariates in realistic settings. Applying this method to human cohort physiological datasets, allows us to reconstruct the network model of human physiology and its connectivity to survival. We can also simulate potential longevity interventions by propagating information through physiological networks to survival outcomes.

Results

Identification of optimal methodology for variable selection

The computational strategy to select survival variables and physiological network inference is highly dependent on the size of the cohort, the number of input variables, and their variability. We evaluated several multivariate and univariate approaches to identify a method with the best performance in cohort sizes between 1,000 and 50,000 individuals.

Using 17 years of survival data, we generated two sets of simulations (1,000 simulations in total) to determine the accuracy of different methods for inferring covariates and the corresponding effect sizes associated with survival (see STAR Methods). In each simulation, we evaluated the performance of three methods to recover correct associations with latent Gompertz parameters: univariate, multivariate greedy hill-climbing algorithm, and multivariate LASSO (least absolute shrinkage and selection operator). The first set of simulations was used to evaluate the accuracy of different methods for identifying the causal covariates directly influencing the Gompertz parameters ($\alpha$ and $\beta$). The second set of simulations extended the first set of simulations by including a physiological DAG, thus simulating the effects of confounding (i.e., causal relationships within different survival-related parameters), and indirect effects on the Gompertz terms. The setup of simulations is illustrated in Figure 2. We evaluated power and accuracy by running simulations with cohort sizes of N = 1,000, 5,000, 10,000, 25,000, and 50,000. For the full description of the setup of simulations, variable→α, variable→β selection, as well as the inference methods, see STAR Methods.

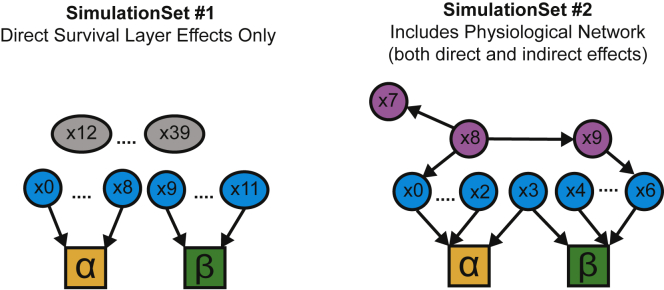
Figure 2.

Setup of the theoretical network to estimate effects of variables on survival with and without physiological network layer

Set #1 survival layer: X0 to X8 connected to alpha; X9 to X11 connected to beta; X12 to X39 are connected to survival. Set #2 survival layer with physiological DAG: X0 to X3 connected to alpha; X3 to X6 connected to beta; X7 to X9 are only connected to physiological network.

Inference of survival-associated variables

The results of our simulations are shown in Figures S1–S6 and Table 1. In the absence of confounding in simulation set #1, univariate methods performed reasonably well, but as expected, the presence of confounding significantly reduced the specificity of the method in simulation set #2. Variable selection in multivariate methods is partly able to take confounding into account. Both multivariate methods showed high sensitivity and specificity for the identification of variables directly connected to the survival layer in both simulation sets #1 and #2.

Table 1.

Accuracy of inference methods based on simulations (N = 5,000)

Inference method	Sensitivity	Specificity	PPV	NPV
Parameters affecting baseline fitness (α)
Univariate (set #1)	0.94	0.75	0.52	0.98
Hill climbing (set #1)	0.88	0.92	0.77	0.96
LASSO (set #1)	0.64	1	0.99	0.91
Univariate (set #2)	0.95	0.12	0.42	0.77
Hill climbing (set #2)	0.8	0.79	0.71	0.86
LASSO (set #2)	0.5	1	0.99	0.75
Parameters affecting aging rate (β)
Univariate (set #1)	0.69	0.61	0.13	0.96
Hill climbing (set #1)	0.51	0.92	0.35	0.96
LASSO (set #1)	0.35	0.92	0.27	0.95
Univariate (set #2)	0.88	0.1	0.39	0.55
Hill climbing (set #2)	0.32	0.85	0.59	0.65
LASSO (set #2)	0.17	0.91	0.54	0.62
All parameters affecting survival
Univariate (set #1)	0.9	0.69	0.55	0.94
Hill climbing (set #1)	0.87	0.89	0.78	0.94
LASSO (set #1)	0.66	0.99	0.96	0.87
Univariate (set #2)	0.94	0.11	0.71	0.43
Hill climbing (set #2)	0.73	0.7	0.85	0.52
LASSO (set #2)	0.42	0.99	0.99	0.42

PPV, positive predictive value; NPV, negative predictive value.

As expected, the sensitivity (or power to identify the true covariates) of all methods increases with cohort size, as a larger number of observations provides more power to pick up true effects (Figures S2 and S3). We found that we have more power to identify $\alpha -$ covariates in comparison with $\beta$-covariates (Figures S2 and S6). This is probably because $\beta$-covariates are identified through their interaction with time while the effects of $\alpha$-covariates are constant throughout time. As a result, most of the variation (R²) in alpha is explained across all simulations, but we do not have the power to explain most of the variation in beta (Figure S4). With a cohort size of 5,000, our simulations show that most of the variation in alpha is explained using the hill-climbing model (mean R² = 0.94) while the variation in beta is only partially explained using any of the models (mean R² = 0.42 in the hill-climbing model).

Results for a medium-size cohort with approximately ∼5,000 individuals are shown in Table 1 and results for all cohort sizes are shown in Figures S2–S6. Overall, the univariate method has the highest sensitivity but the least specificity, producing the highest number of false positive associations. On the other hand, although the multivariate LASSO regression method was much more specific, additional accuracy comes at the cost of reduced sensitivity. Overall, the greedy hill-climbing inference method offered the best compromise between sensitivity and specificity, and thus is the most practical method for medium-size cohorts. In very large cohorts with N > 50,000, we find multivariate LASSO regression catches up to the performance of the hill-climbing algorithm.

Inference of physiological network architecture

To evaluate the performance of different causal inference approaches for physiological network reconstruction, we compared multiple published methods including incremental association Markov blanket (IAMB) (Tsamardinos et al., 2003), grow-shrink (GS) (Margaritis and Thrun, 1999), Peter Clark (PC) (Spirtes and Glymour, 1991), max-min parents and children (MMPC) (Tsamardinos et al., 2006), and inductive causation (Verma and Pearl, 1991) algorithms (Figure S7). We compared methods that use score-based or constraint-based metrics to identify the network structure. The score-based methods optimize the network architecture on the basis of goodness of fit after penalizing for the number of parameters. The constraint-based method determines conditional independence between variables and creates a Bayesian network structure based on this. For a more complete description see STAR Methods.

Although performance varied, we observed that the accuracy of these methods saturates at cohort sizes of around 5,000. This is probably due to the limitations of these algorithms when applied to observational data as they can only identify Markov equivalent causal networks without interventional experiments (Guo et al., 2020). Of all algorithms, the IAMB algorithm produced the most precise causal structure while also giving reasonable recall (Figure S7).

On the basis of this evaluation, we decided to use the following three-step approach for the construction of a hybrid physiology-survival network in the MrOS cohort:

• 1.Identify variables associated with survival outcomes using univariate analysis.
• 2.Construct the physiological network using the IAMB causal inference method.
• 3.Identify a subset of variables directly connected to survival using a multivariate hill-climbing approach.

Univariate analysis of survival in MrOS cohort

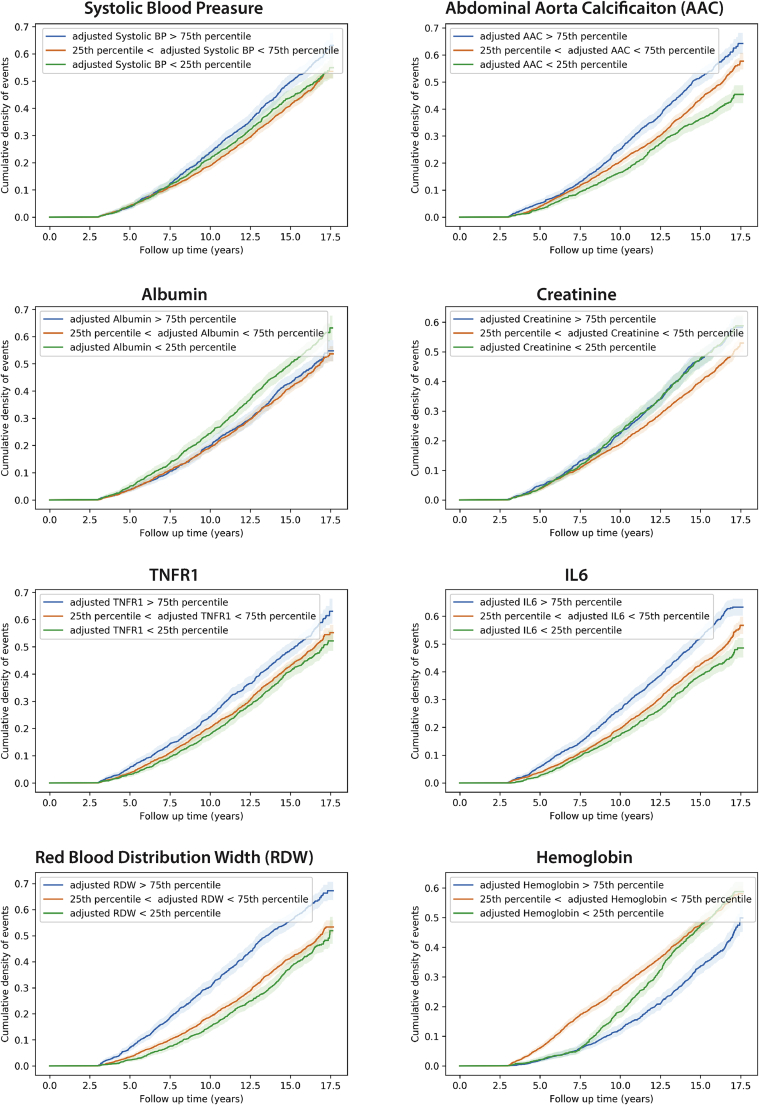
The MrOS cohort is a multi-center prospective, longitudinal, observational cohort study designed to examine risk factors of osteoporosis in older men (≥64 years) and has more than 17 years of survival data (baseline characteristics in Table S1). The cohort is well characterized at baseline providing us with an excellent opportunity to identify biomarkers and physiological markers associated with long-term survival within humans. We performed a univariate survival analysis for 164 variables measured at baseline and found 34 variables associated with long-term survival in the MrOS cohort (see STAR Methods). All univariate survival models were created after adjusting for the age of the participant at baseline. The cumulative density and Kaplan Meier (KM) plots for some of the most significant associations are shown in Figures 3 and S8. In addition to age at baseline, the most significant associations in MrOS include:

• 1.diabetes (glucose and insulin),
• 2.kidney health (creatinine and cystatin C),
• 3.inflammation (immune cell counts in complete blood cell counts, interleukin-6 [IL-6], and C-reactive protein [CRP]),
• 4.anthropometric measurements such as body mass index (BMI),
• 5.cardiovascular health (systolic blood pressure and abdominal aorta calcification [AAC]), and
• 6.iron homeostasis measures (red blood cell [RBC] count, hematocrit, RBC distribution width [RDW], mean corpuscular hemoglobin concentration [MCHC]).

Figure 3.

Cumulative density of event plots for selected biomarkers

Age-adjusted cumulative density of event plots for selected biomarkers associated with survival in MrOS are plotted after adjusting biomarker differences for age (see STAR Methods). BP, blood pressure; AAC, abdominal aortic calcification; TNFR1, tumor necrosis factor (TNF)-alpha receptor 1; RDW, red blood cell distribution width; IL-6, interleukin-6.

Most of these associations consist of well-established risk factors, but we were particularly surprised by the strength of association between AAC and all-cause mortality in the MrOS cohort (age-adjusted hazard ratio [HR] of ∼1.2; Figure S8). AAC is a measure of the amount of hydroxyapatite buildup in the abdominal arteries and is a well-known prognostic indicator of cardiovascular disease (Budoff et al., 2007; Prabhakaran et al., 2007; Sethi et al., 2020). Our analyses show that vascular calcification is one of the largest risk factors for mortality of ≥65-year-old men, and its presence at baseline can be used as a prognostic indicator of poor long-term outcomes.

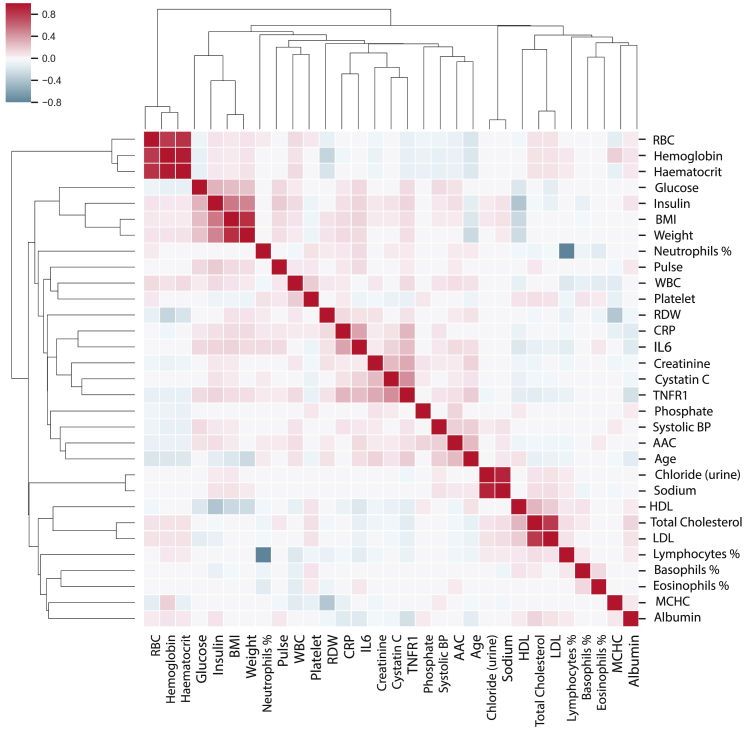
Although univariate associations with survival are informative, they cannot be interpreted as causal to the survival outcome, as these associations could be due to correlation with unaccounted factors missing from the model (see Table 1). The presence of confounding can be seen in the clustered heatmap of correlation patterns of 34 survival-associated biomarkers as shown in Figure 4. There is a high degree of correlation between multiple survival-associated biomarkers. These correlation patterns arise through a set of shared biological processes, suggesting that it should be possible to reconstruct the underlying physiological network structure. To go beyond simple univariate associations, we will need to use more rigorous multivariate inference methods.

Figure 4.

Correlation of survival-associated physiological variables

The correlation matrix between the 34 variables associated with survival in a univariate model (after age correction) in the MrOS cohort is shown. Red indicates a high correlation between the markers, while blue represents anticorrelation between the markers. Biomarkers are ordered on the basis of a similarity in correlation profiles across the MrOS cohort. Interpretation of these highly correlated patterns is possible only by reconstruction of underlying causal relationships.

Multivariate inference of survival layer

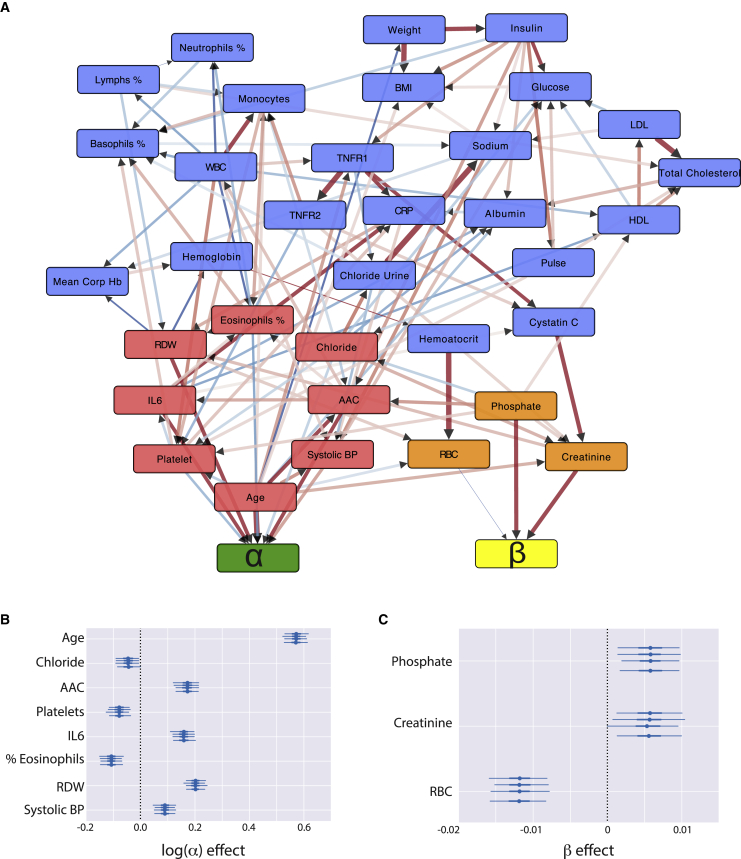
To identify a set of variables jointly associated with survival, we implemented a multivariate greedy hill-climbing algorithm (Spirtes and Glymour, 1991) (see STAR Methods). The algorithm tests for the association of each variable with the baseline fitness ($\alpha$) and/or the aging rate ($\beta$) by exploring various network architectures (creating and removing edges between variables and latent parameters) while optimizing the Watanabe-Akaike information criterion (WAIC) that maximizes the likelihood of the Gompertz survival function while penalizing for the number of parameters in the model. This procedure is critical to our analysis as it implements both feature selection: identification of a minimal set of survival-associated variables, as well as provides information on how each variable influences survival. Running the algorithm on the MrOS cohort, starting with 34 survival variables, the algorithm identified a minimal set of 11 independent variables. Most variables (8 of 11) directly associated with survival were found to contribute to the baseline fitness, with three variables associated with the aging rate (Figure 5).

Figure 5.

MrOS hybrid physiological and survival network

(A) Inferred hybrid physiology-survival network from MrOS observation cohort. Nodes in the network represent biomarkers associated with survival in a univariate model (after adjusting for baseline age). The arrows represent inferred causal relationships learned through the causal structure discovery method (IAMB). The Gompertz survival latent parameters are represented by green and yellow nodes. The nodes directly influencing Gompertz parameters in the network are colored red (α) and orange (β), while the rest of the nodes in the physiological network are colored blue. Biomarker-survival layer α or β associations are learned with the hill-climbing procedure. Red arrows represent correlated links, while blue arrows represent anticorrelated links. The edge thickness and shade represent the causal effect size of one node on another.

(B and C) The mean effect size (circle) of each relevant node to the two Gompertz parameters is displayed along with their 95% credible intervals (horizontal lines). These median effect sizes and credible intervals (95% [thin line] and interquartile range [thick line]) are estimated using four Monte Carlo Markov-chain simulations (error bars are shown for each chain).

Variables associated with the aging rate (β)

The decline in the robustness of the physiological system can be observed as an increased hazard of mortality as a function of time, which reads as characteristic latent parameter beta in the Gompertz equation. By definition, factors that affect the aging rate (β) change the slope of the hazard trajectory (Figure 1A). In the MrOS cohort, the strongest association we see with the aging rate is the protective effect of high RBC counts. According to our model, maintenance of high RBC counts can slow the aging rate by ∼6% per SD increase in RBCs. Previous reports have established that loss of ability to maintain steady production of RBC is strongly associated with a variety of disease outcomes, but the effects of RBC on aging rate were not analyzed (Weiss and Goodnough, 2005). On the other hand, an increase in creatinine and serum phosphate levels, which are associated with reduced kidney function and bone maintenance respectively, accelerate the aging process by ∼3%. High levels of serum phosphate and creatinine are known to be associated with adverse outcomes (Eddington et al., 2010; Kestenbaum et al., 2005; Wannamethee et al., 1997), but were previously not linked to an increase in the aging rate. In addition, the concentration of serum phosphate is well known to be a predictor of lifespan across different species even after taking body size into consideration (Kuro-o, 2010). To our knowledge, this is the first time that these biomarkers were directly linked to the aging rate of our species.

Variables associated with baseline fitness (α)

The age of individuals at the baseline in the MrOS cohort ranges from 64 to 100 (mean 73 ± 5.9). As a consequence, the majority of the cohort has pre-existing conditions, and variables associated with baseline fitness are strong predictors of their long-term survival outcome. As expected, baseline age has the largest effect on survival as it broadly captures the physiological fitness of each participant (connectivity of age within the network in Figure 5). Following baseline age, the red blood cell distribution width had the largest effect on baseline fitness. RDW is the measure of variability in the volume and size of the red blood cells. Higher RDWs indicate an alteration in the erythropoietic system, which is suggestive of several pathological conditions. Higher RDW values are strongly associated with cardiovascular events (Tonelli et al., 2008; Zalawadiya et al., 2010) and are prognostic of heart failure (Allen et al., 2010; Felker et al., 2007), aging related outcomes (Kim et al., 2021) and pulmonary hypertension (Hampole et al., 2009; Tanindi et al., 2012). Moreover, elevated RDW levels are strongly associated with all-cause mortality within the general population (Patel et al., 2009; Perlstein et al., 2009).

Abdominal aortic calcification had the second biggest effect on baseline fitness within the MrOS cohort. AAC is caused by the formation of hydroxyapatite crystals in the arteries and is associated with multiple types of cardiovascular events (Leow et al., 2021; Sethi et al., 2020). There are multiple possible mechanisms by which calcification of arteries can occur, such as chronic kidney disease, diabetes, and loss of calcium phosphate homeostasis. In particular, because phosphate has been associated with the aging rate in MrOS, the association of baseline fitness with AAC may reflect the accelerated reduction in fitness due to exposure of elevated phosphate prior to baseline.

In addition, higher systolic blood pressure and inflammatory marker IL-6 are also associated with adverse mortality risk. High blood pressure is a significant risk factor for a variety of cardiovascular and renal events, including myocardial infarction, stroke, atherosclerosis, aortic aneurysm, hypertensive heart disease, heart failure, peripheral artery disease, and end-stage renal disease (Rahimi et al., 2015). IL-6 signaling is associated with increased cardiovascular events while anti-IL-6 therapy is associated with a reduction of the risk for cardiovascular events (Ridker et al., 2018).

Overall, our single-layer multivariate survival model with just 11 variables performed well for the prediction of 17-year survival outcome (concordance index = 0.78) and is capable of distinguishing between α and β covariates. However, this single-layer survival model does not consider the physiological network that accounts for covariation within the variables (see Figure 4), a problem that will be addressed in the next section.

Construction of physiological network

On the basis of our simulations, we used the IAMB algorithm to create a physiology DAG of physiological measures with 34 unique survival-associated variables identified using univariate analysis. Each variable is represented as a node in the network. On average every node is connected to approximately six other nodes in the network (∼6 edges per node). All the nodes form a single connected component.

As expected, the baseline age of individuals has a high degree of influence on various physiological processes. In our network reconstruction, age directly influences ten other variables:

• (1)increase in systolic blood pressure (Pinto, 2007),
• (2)changes in body composition (reduction in weight [Seidell and Visscher, 2000] and increase in BMI),
• (3)decrease in red blood cell count,
• (4)increase in red-blood distribution width (Salive et al., 1992),
• (5)accumulation of abdominal aortic calcification (Kiel et al., 2001; Sethi et al., 2020),
• (6)reduction in the serum concentration of albumin (Cooper and Gardner, 1989),
• (7)increase in inflammation (TNF-R1) (Stowe et al., 2010),
• (8)reduction in immune function reduction in platelet count (Jones, 2016),
• (9)increased monocyte counts (Hearps et al., 2012), and
• (10)reduced kidney function (increase in creatinine) (Tiao et al., 2002).

Interestingly, nearly all the nodes in the physiological network (28 of 33 nodes) are connected to the baseline age within two steps (neighbor of a neighbor), capturing a broad influence of age on multiple physiological systems.

The network consists of several densely connected subnetworks such as the cholesterol subnetwork (low-density lipoprotein [LDL], high-density lipoprotein [HDL], and cholesterol), glucose subnetwork (glucose and insulin), the kidney homeostasis subnetwork (cystatin C and creatinine), haemopoietic system (monocytes, lymphocytes, neutrophils, basophils, RBCs, and RDW), and the inflammation markers (TNF receptors TNF-R1 and TNF-R2 and C-reactive protein).

The connectivity of the reconstructed physiological networks recapitulates known physiological relationships but also suggests previously unidentified relationships. A presence of an edge between two nodes suggests a potentially causal relationship between the two variables. Although it may not be possible to test all these hypotheses, some are supported by epidemiological studies. For example, it is known that changes in cholesterol are associated with changes in sodium and glucose concentrations (Parhofer, 2015) and albumin concentrations (Gillum, 1993) in the serum. Changes in concentrations of inflammatory proteins are intricately associated with changes in immune cell types (Rea et al., 2018). The concentration of CRP and IL-6 changes in response to changes in platelet cell counts (Burstein, 1994; Semple, 2015) while TNF-R1 is predicted to change in response to changes in white blood cell (WBC) count (He et al., 2010). In addition to these known associations, our analysis suggests potentially novel relationships.

Our models predict that an increase in insulin concentration can increase resting pulse, calcification of arteries (AAC), inflammation (TNF-R1), serum sodium concentration, albumin concentration, and immune cell composition (percentage of basophil cells). An increase in phosphate levels is predicted to increase HDL, platelet cell count, creatinine, calcification of arteries (AAC), and decrease chloride. Overall, in absence of randomized clinical trials (RCTs), it is infeasible to test all these statistical connections, but they serve as useful mechanisms for generating hypotheses and further experimental validation.

Simulating effect of physiological perturbations on median survival time

In the absence of randomized clinical trials, it is hard to know the effect of an intervention on overall survival. Unfortunately, RCTs are often impractical and technically difficult. As an alternative, our models allow us to carry out such simulations by carrying out hypothetical “what if” scenarios, where the effects of perturbation are propagated throughout the physiological network to a survival layer. This is exactly the problem of counterfactual inference in the causal analysis of observational data (Pearl, 2009; Prosperi et al., 2020).

We compared the effects of perturbation on a median survival time in the MrOS cohort between the survival layer and hybrid physiological-survival network. In our in silico intervention experiments on physiological DAG, when the perturbation is applied to a particular node, it is assumed that the effects of the biomarker are only felt downstream of that node (i.e., only children of the intervened node feel the effect of the intervention). The hybrid physiological-survival network captures both indirect and direct effects on survival while the survival network only captures the direct effects of a covariate on survival.

Direct effects: Intervention on nodes without including physiology network effects

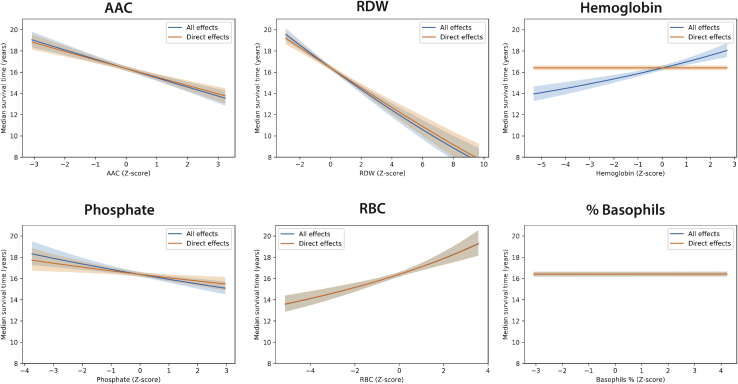
We evaluate the effect of intervening on each node within the network using counterfactual simulations (Figures 6 and S9). For example, while considering counterfactual intervention on phosphate, which is directly connected to the aging rate, we simulate the median survival time on the basis of modulating changes in phosphate without considering how phosphate affects any other physiological parameters, that is, all other parameters are maintained at mean levels (i.e., ∼74-year-old man). On the basis of these counterfactual simulations, a decrease in phosphate levels by 3 SDs leads to an increase of ∼1 year in estimated median survival time. Simulating effects on intervention, a decrease in AAC and RDW levels by 3 SDs has the largest effects on median survival time (∼2–3 years increase in expected lifespan) (Figure 6). It is important to note that for nodes connected to the aging rate, the effect of an intervention is non-linear. For example, $\beta$-associated covariates like RBC and phosphate lead to non-linear effects on median survival time because of its interaction with time in our model (Figure 6).

Figure 6.

Counterfactual plots: Simulation of interventional effects

Effect of an intervention on a variable in hybrid physiology-survival networks on survival outcome (years gained). The median survival time was calculated for different interventions on the basis of the extremes of these biomarkers within the MrOS cohort. In the network structure, hemoglobin is not connected directly to latent Gompertz parameters in the survival model; as such, the direct effect of hemoglobin on survival is 0. However, once the network is taken into consideration, indirect effects of hemoglobin on other nodes (hemoglobin → hematocrit → RBC → β) and (hemoglobin → glucose → SBP → α) can be observed as non-zero survival effect.

All effects: Intervention on nodes including physiological network effects

For a node that is not directly connected to the survival layer, a simulated intervention can also lead to changes in other physiological nodes, and those changes can further change the survival outcome. In this scenario, we include indirect effects that approximate how changes propagate in biological networks. Figure 6 shows differences between direct and overall effects if the effect of the interventional node on survival is mediated by a node that is directly linked to the Gompertz parameters. For example, phosphate not only changes the aging rate directly, but also affects the rate of calcification of arteries, thereby changing levels of AAC, which in turn reflects in decreased baseline fitness of individuals ($\alpha$). In another example, an imbalance in iron homeostasis can lead to problems in the production of hemoglobin, which further leads to a reduction in RBC counts, thereby increasing RDW measurements (Salive et al., 1992). These events are then reflected in increased baseline fitness and higher aging rate. The models suggest that interventions that restore normal phosphate or RBC counts levels may have additional indirect benefits on median survival time in the MrOS cohort.

It is also worth pointing out that there are nodes in the network without any children, and therefore one would predict that intervention would not change the outcome of interest. For example, the percentage of basophil cells has a negligible effect on survival in either the multivariate survival model or the physiological network because it does not affect any other variable in the network (Figure 6). Hence, the physiological network provides clues as to which interventions will be most beneficial.

Discussion

The question of which factors determine the remarkably long lifespan of our species has been the subject of intense research in the field of aging epidemiology. At the heart of this question is a necessity to compile a comprehensive catalog of molecular changes over a large portion of a human lifespan, as well as the difficult task of developing novel modeling techniques capable of capturing the full complexity of their physiological interactions and declines. There are a wide array of statistical techniques available to aging researchers, such as Cox proportional hazard models (Cox, 1972), biological age predictions (Horvath, 2013; Levine et al., 2018; Lu et al., 2019), and frailty indices (Clegg et al., 2013). However, these models do not capture interdependence between different variables, their interactions with time, as well as their effect on the aging rate of the biological system. As aging is a process that involves time-dependent changes, it is essential to also identify molecular changes that accelerate or decelerate the aging rate (Margolick and Ferrucci, 2015).

Here we set out to address these modeling challenges. We asked two questions. First, is it possible to build an interpretable model of survival that considers the complexity of physiological network interactions and can provide insight into which factors directly contribute to the aging rate of our species? Second, is it possible to identify variables that affect the aging rate in human cohort data? To answer these questions, we developed a fully parametric Bayesian framework for inference of the physiological network that is linked to the Gompertz survival function. In this framework, variables that are linked to beta components of the hazard function can be interpreted as interacting with time, and variables that are linked to alpha components are said to be present at the baseline and their effects stay constant throughout follow-up time.

To our knowledge, this is the first attempt to combine both physiological and Gompertz survival analysis to model how the steady state levels of different markers affect survival. Prior work has focused on incorporating Gompertzian behavior within kinetic models to predict biomass growth rate or physiological behavior of different species (Boshagh and Rostami, 2021; Stevenson et al., 2008). To achieve our goal, we not only model the networks but perform causal structure discovery, without any prior assumptions on the connectivity of different biomarkers to latent parameters. To test the accuracy of these network inference methods, we have carried out extensive simulations with synthetic cohorts, as well as a variety of physiological network structures with and without confounding factors. This framework provides a powerful methodology to identify survival parameters. We find that it is substantially more difficult to identify variables influencing aging rate compared with identifying variables that affect fitness at baseline. Beta covariates by definition interact with time and are harder to detect, but with larger cohorts, we expect that the power to detect aging rate biomarkers will increase. Furthermore, the length of the follow-up time is a critical parameter for the identification of variables that affect aging rates. On the other hand, alpha covariates are easier to detect, because they measure the historical dysregulation of different processes within individuals up to the point of entry into the study. For example, in the MrOS cohort, these covariates reflect a cumulative 65–90 years of individuals’ health history.

Using simulations, we evaluated the trade-offs of three different causal inference methods to identify biomarkers that affect alpha and/or beta. We find that although univariate models offer the highest sensitivity, they produce incorrect inferences in the presence of confounding variables (Figure S5). Multivariate models do much better, but at the cost of false negatives, and not surprisingly performance depends on the details of the implementation of variable selection. For example, hill-climbing variable selection works best in small cohort sizes, while LASSO variable selection technique performs best on larger datasets. The main advantage of using causal graph algorithms is that they work well in moderate to large cohort settings, capture connectivity in physiology, and provide clues to interventions that might be most beneficial for longevity.

Applying the method to the MrOS cohort revealed several interesting findings. We observed that the age of individuals at the first visit was strongly linked to the alpha baseline component of the Gompertz hazard function. This is consistent with the Gompertz model that predicts that the hazard of a person increases exponentially with baseline age, as the age variable captures a lifetime reduction of fitness in participants before they enter the study. We also checked if baseline age influences the aging rate itself. In the MrOS cohort, the model showed that baseline age does not change aging rate significantly. On the basis of our power simulations, we believe that this cohort is sufficiently powered to detect the interaction between the baseline age and aging rate if such interaction existed.

We also find that most biomarkers and physiological measures that determine the lifespan of individuals are already present at the baseline. These biomarkers include parameters such as arterial health (blood pressure and AAC), inflammation (IL-6), hematology (RDW and eosinophils), kidney function (cystatin C, chloride), and liver function (albumin). Many of these variables are seen in the first layer of physiology-survival network and are linked directly to the alpha component of hazard in Figure 5. In addition to these direct connections, many variables indirectly contribute to survival through multiple interactions with each other. These variables include BMI (5 connections), HDL (3 connections), CRP (4 connection), total cholesterol (5 connections), and LDL (4 connections).

Perhaps the most interesting aspect of these graphical models is that they allow us to simulate what-if interventional hypotheses (Pearl, 2000). Unlike simpler multivariate models, the physiological-survival network hybrid model can consider indirect effects of an intervention, by propagating effects throughout the physiological layer to the survival layer. For example, we predict that reducing elevated phosphate levels would decrease the aging rate directly, as well as indirectly by reducing progression of vascular calcification, thus resulting in a significant extension of lifespan in elderly individuals. A similar association between levels of phosphate and aging rates has been observed in other species (Kuro-o, 2010). We believe that this powerful methodology can be further extended by taking into consideration genetic effects, use of medications, and pre-existing conditions. The technique could be further extended to include an additional biomarker-disease layer before the survival layer.

Limitations of the study

There are several critical limitations in this methodology that should be considered when interpreting our results. First, the DAG network structures do not take into account the cyclical nature of physiological systems. Our networks were constructed at the baseline of the study and thus represented a snapshot of physiological systems, under the assumption that physiological networks are approximately at a steady state. Given longitudinal data, it is possible to extend the methodology to construct cyclic causal networks that capture the dynamics of physiological systems.

Second, the correctness of network skeleton and edge directionally depends on many factors such as the presence of unmeasured confounding, linearity of response, and a number of independent measurements (statistical power). Unmeasured confounding is assumed to be absent, which is unrealistic in complex biological systems. Although some of these issues could be resolved with increased depth and breadth of biomarker sampling, accommodating non-linear effects would require further development.

Third, it is important to recognize that causal structure discovery is a computationally difficult NP-hard problem. Heuristic-based methods are not guaranteed to find an optimal solution and the robustness of the result may depend on the nature of the confounding variable. Recent advances in feature selection techniques such as “stability selection” could be used to evaluate the stability of network architecture through bootstrapping techniques (Pfister et al., 2021), however, even the most robust computational associations will ultimately require experimental interventions to confirm causal connectivity. In addition, the application of genetic variants as instrumental variables could help identify the directionality of some of the causal links in the physiological network (Sanderson et al., 2022).

Finally, caution is warranted when interpreting the results of the what-if interventional analysis. Our method assumes that the network structure is correct, that there is an absence of confounders in the children downstream of the intervention node, and that the network does not change on intervention (i.e., that there is no rewiring and feedback in the network). Furthermore, the current implementation removes all incoming edges of a node on the intervention. Softer interventions are possible by targeting a particular edge for intervention (a single protein’s function).

STAR★Methods

Key resources table

RESOURCE	SOURCE	IDENTIFIER
MrOS Data	https://mrosonline.ucsf.edu/DataRelease/ReleasedDatasets	dbGaP Study Accession: phs000373.v1.p1
Software -Bayesian Survival Analysis	This study	https://doi.org/10.5281/zenodo.7186584

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Anurag Sethi anurag@calicolabs.com.

Materials availability

This study did not generate new unique reagents.

Experimental model and subject details

We received all deidentified baseline and survival data from the MrOS cohort.

Method details

Parametric Gompertz approach to survival analysis

The Gompertz survival model describes a fully parametric form of survival, in which the hazard increases exponentially with time. Hazard is a measure of an instantaneous probability of an event for an individual that survived to a certain time t

$${\lambda }_i\left(t\right)={\alpha }_i\times exp\left({\beta }_{i}t\right)$$ (Equation 1)

where ${\alpha }_i$ is a measure of fitness at baseline and ${\beta }_i$ is the aging rate of individual $i$. These latent variables are estimated based on best fit of the survival curve to the mortality curve. It is well known that a combination of genetics and environment can lead to heterogeneity in these latent parameters. For example, in the Center of Disease Control and Prevention mortality dataset, survival analysis after stratifying by gender shows that gender is significantly associated with the aging rate in addition to being associated with the baseline fitness (data not shown). Unlike the commonly used Cox Proportional Hazards (CoxPH), where a baseline hazard function is eliminated (Cox, 1972), we formulate the Gompertz function with a covariate structure, allowing us to evaluate both constant hazard as well time-dependent hazard.

Given the hazard in equation (1), the probability of individual $i$ surviving beyond time $t$ can be calculated using the equation (Collett, 2015):

$$S_i\left(t\right)=exp(-\underset{0}{\overset{t}{\int }}{\lambda }_i\left(u\right)du)=exp\left(\frac{{\alpha }_i}{{\beta }_i}\right(exp\left({\beta }_{i}t\right)-1)$$ (Equation 2)

Given a set of measured covariates such as physiological parameters or biomarkers at some fixed time point t, it is not known a priori which covariates are associated with changes in baseline-fitness ($\alpha$) and/or the aging rate ($\beta$) component of survival. To make such an inference, we developed a Bayesian network that can test for the association of factors with alpha and beta terms of survival function, as well as model second-order interactions between various factors. We assume that the individual $i$ survival parameters vary linearly with an individual’s covariates $x_i$:

$$log\left({\alpha }_i\right)=log\left(a^0\right)+\sum _j{a}^j{x}_{i,j}$$

$${\beta }_i=b^0+\sum _j{b}^j{x}_{i,j}$$ (Equation 3)

where $x_{i,j}$ refers to the baseline measurement of covariate $j$ for individual $i$, and $a^0$ and $b^0$ are shared whole cohort-level parameters representing mean baseline fitness levels and aging rate.

Parametric bayesian approach

To identify survival parameters we use Bayesian models. The overall likelihood of observing survival time distribution in a cohort is given as product of individual survival time probabilities (Equation 2)

$${L=\prod _{i=1}^N{S}_i\left(t_i\right)\times {{\lambda }_i}^{C_i}\left(t_i\right)=\prod _{i=1}^{N}exp\left(\frac{{\alpha }_i}{{\beta }_i}(exp\left({\beta }_{i}t\right)-1)\right)\times ({\alpha }_i\times exp\left({\beta }_{i}t\right))}^{C_i}$$ (Equation 4)

where ti is the time of an event, Ci = 1 if death was observed, and Ci = 0 if the individual was right censored.

The priors for the parameters in equation 3 are assumed to be:

$$log\left(a^0\right)\sim N\left(\mathrm{0,30}\right)$$

$$a^j\sim N(0,{\sigma }_{a^s}\times {\sigma }_{a^j})$$

$${\sigma }_{a^s}=HN\left(\mathrm{0,10}\right)$$

$${\sigma }_{a^j}=HN\left(\mathrm{0,10}\right)$$

$$b^0\sim N\left(\mathrm{0,10}\right)$$

$$b^j\sim N(0,{\sigma }_{b^s}\times {\sigma }_{b^j})$$

$${\sigma }_{b^s}=HN\left(\mathrm{0,10}\right)$$

$${\sigma }_{b^j}=HN\left(\mathrm{0,10}\right)$$ (Equation 5)

where $N(\mu ,\sigma )$ and $HN(\mu ,\sigma )$ represent the normal and half-normal distribution with mean $\mu$ and standard deviation $\sigma$ respectively. All the covariates have a common factor ${\sigma }_{a^s}$ or ${\sigma }_{b^s}$ while they have individual variances ${\sigma }_{a^j}$ or ${\sigma }_{b^j}$. To ensure that the Bayesian inference is stable, $log\left(a^0\right)$ is constrained to be negative between 0 and -30 as $a^0$ represents the baseline probability of the event occurring while $a^j$ is bound between +3 and −3 based as each risk factor typically has a small effect on the baseline fitness in our experience.

In addition, $b^0$ is the aging rate and is a measure of how fast the risk of event occurring increases with time and is constrained to be a positive value between 0 and 0.5. Typically, the aging rate calculated from mortality data for human populations is $\sim$ 0.08 per year for adult populations. Finally, $b^j$ is constrained between +0.1 and −0.1. All the covariates are transformed to such that their means are 0 and standard deviations are 1 and the biomarkers are log-transformed before the transformation so that they obey close to a normal distribution.

Inference of survival parameters in synthetic cohorts

Identification of variables that affect survival depends on baseline characteristics of the cohort, size of the cohort, length of the follow-up, censorship rates, technical variability of measurement, etc. To gain a better understanding of limitations of the methodology, we performed a number of power simulation aimed at answering the following questions:

• 1.Power: what is the cohort size/effect size required to identify variables associated with $\alpha$ or $\beta$ components of survival?
• 2.Directionality: Is it possible to identify the correct directionality of the effects?
• 3.Effect sizes: Is it possible to accurately estimate coefficients of association?
• 4.Correlation versus causation: Can causal variables be identified accurately from other correlated variables in the survival network?
• 5.Network architecture: Is it possible to accurately connect components of a physiological network?

To address these questions, we carried out theoretical simulations with a variety of synthetic network architectures where covariate structure and effect sizes were predetermined. The follow-up time period of these synthetic networks was similar to the follow-up time in the MrOS cohort. To evaluate the effect of cohort size on the statistical power and accuracy of various causal inference techniques, we ran the simulations with cohort sizes of N=1000, 5000, 10000, 25000, and 50000 participants. To evaluate the impact of confounding, our synthetic networks include large numbers of covariates that did not affect survival parameters, as well as covariates correlated with survival outcomes but not causally linked to survival.

Given known synthetic network architectures, we evaluated the ability of three different algorithms to correctly recover the structure, directionality, and effect sizes of covariates.

• 1.Univariate association between covariates and survival parameters.
• 2.Greedy Hill-climbing algorithm for multivariate structure inference.
• 3.Regularized LASSO approach for multivariate structure inference.

We performed two sets of simulations, evaluating inference with and without a physiological DAG.

Simulation Set 1 - Survival analysis in the absence physiological network

In a simple model of survival, all the variables are independent of each other and have a direct impact on survival. To simulate this scenario. we generated a single layer networks with 40 independent variables of which 9 variables affect $\alpha$ while 3 variables affect $\beta .$ The parameters for these simulations are chosen based on our observations within MrOS cohort with ∼40 variables taken in the physiological DAG, 8 of which directly affect alpha while 3 variables affect beta. All variables follow a standardized normal distribution, and none of the variables affect $\alpha$ and $\beta$ simultaneously.

$$log\left({\alpha }_i\right)=log\left(a^0\right)+\sum _{j=0}^8{a}^j{x}_{i,j}$$

$${\beta }_i=b^0+\sum _{j=9}^{11}{b}^j{x}_{i,j}$$ (Equation 6)

The effect sizes $a^j$ for each of the covariates $x_j$ on variation in $\alpha$ is randomly chosen in the interval [-0.5, 0.5] while the effect sizes $b^j$ for each of the covariates $x_j$ on variation in $\beta$ is randomly chosen in the interval [-0.01, 0.01]. We simulated 17 years of follow up, 100 times for each cohort size assuming baseline $log\left(a^0\right)$ = -4.5 and ${\beta }^0$ = 0.083 such that there were 40% events observed within the follow up time. These settings were chosen to match observed censorship in the MrOS dataset.

Simulation Set 2 - Survival analysis in presence of physiological network

To simulate a more realistic scenario that captures the complexity of physiological networks, we simulated random DAGs where variables can regulate each other, as well as impact survival parameters directly and indirectly. In these simulations, we generated 10 variables of which 4 variables affect $\alpha$ while 4 variables affect $\beta .$ The variables were generated using a randomly generated DAG with 0.5 probability for the relationship between variables and all variables follow a standardized normal distribution (i.e., mean of 0 and standard deviation of 1). The density of edges was set based on observed density in the MrOS cohort. The correlations in the DAG are randomly chosen in the range [-1, 1]. To evaluate the sensitivity of our methods to identify covariates that affect both alpha and beta we include a covariate with a joint effect ($x_3$). We generated the simulations with the following conditions:

$$log\left({\alpha }_i\right)=log\left(a^0\right)+\sum _{j=0}^3{a}^j{x}_{i,j}$$

$${\beta }_i=b^0+\sum _{j=3}^6{b}^j{x}_{i,j}$$ (Equation 7)

All other parameters were the same as in Simulation Set #1. Here, the presence of regulation between variables, allows us to investigate the accuracy of physiological DAG reconstruction and its impacts on survival.

Methods for identifying variables that directly impact survival

We utilized Markov Chain Monte Carlo (MCMC) sampling (Gilks et al., 1995) with the No U-Turn Sampler (NUTS) (Hoffman and Gelman, 2011) to infer the parameters that affect survival outcomes. Each MCMC run consists of 4 chains with 2000 steps (1000 burn-in) and is checked for convergence using Rhat<1.04 (https://mc-stan.org/users/documentation/).

We evaluate three modeling techniques (univariate, LASSO, greedy hill climbing) for their ability to identify the true causal relationship between covariates and the latent Gompertz parameters (Equations 6 and 7 and STAR Methods). Reconstruction of the physiological network is done independently of the survival layer (method described in the next section).

In a univariate model, the covariate j directly affects survival of individual i by influencing either alpha or beta in the absence of covariate structure. Variable selection is based on the Watanabe-Akaike information criterion (WAIC) (Watanabe, 2013) as compared to the null model without a covariate.

$$log\left({\alpha }_i\right)=log\left(a^0\right)+a^j{x}_{i,j}{\beta }_i=b^0+b^j{x}_{i,j}$$ (Equation 8)

Second, we evaluated the multivariate model with Bayesian LASSO regularization as a means of identifying variables that affect survival. In this model, the effect sizes ${\alpha }^j$ and ${\beta }^j$ for each of the covariates $x_j$ on the Gompertz parameters are assumed to have regularized Laplace priors.

Third, we used a Greedy-Hill climbing algorithm. In this approach, variables are selected sequentially, by measuring improvement in statistical fit (WAIC) after adding or deleting each variable from multivariate. During each iteration, we accepted the addition or deletion of a covariate to ${\alpha }_i$ or ${\beta }_i$ that produced the most significant improvement in the fit. We repeat this process until convergence. We also utilized leave one out cross validation (Vehtari et al., 2015) as a criterion for convergence and obtained consistent results with WAIC-based convergence.

Methods for identifying physiological network interaction and their impact on survival

The connectivity of a biological system can be represented as a network of state variables (nodes) and their interactions (vertices), where changes in one variable are propagated to other variables of the network through a complex set of functional relationships. The propagation of changes between nodes in a realistic physiological network is hard to model computationally, as the structure of the network is typically unknown. With that in mind, we have chosen to represent a physiological network as a simple directed acyclic graph (DAG) with a linear set of relationships between nodes. Of course, even in this simple model most connectivity is not known and needs to be discovered.

The structure of the Physiology DAG can be discovered by searching all possible permutations of connectivity and selecting the architecture that has the highest probability of explaining data. The joint probability of observing all variables in a particular state for an individual is given in the formula below:

$$P(X_1,X_2,\mathrm{....},X_n)=\prod _{i=1}^{n}G\left(X_i\right|X_{j\mathrm{...}})$$ (Equation 9)

where $n$ represents the number of nodes, X are state variables, and the network G is represented as a set of all conditional dependencies between children and parents. Finding the most likely architecture G (learning structure) can be carried out by a set of search algorithms that maximize the probability of observing the data across all individuals after taking model complexity into account. There are a number of algorithms that have been developed for this task (Glymour et al., 2019; Guo et al., 2020).

Construction of physiological networks in simulations

In Simulation Set #2, we generated 10 variables that were generated using a randomly generated DAG with 0.5 probability for a relationship between variables and all variables follow a standardized normal distribution (i.e., mean of 0 and standard deviation of 1). We generated the variables based on the DAG with the following conditions:

$$x_{i,j}\sim N({\mu }_{i,j},{\sigma }_j)$$

$${\mu }_{i,j}=\sum _{k\in p{a}_j}{\gamma }_{kj}{x}_{i,k}$$

$${\sigma }_j=\sqrt{1-\sum _{k\in p{a}_j}{\gamma }_{kj}^2}$$

where the correlations in the DAG (${\gamma }_{kj}$) are randomly chosen in the range [-1, 1]. The simulation was rejected if the standard deviation for any variable was imaginary. The parents of each variable ($x_j$) within the DAG are denoted by $p{a}_j$. The standard deviation in these simulations placed additional constraints on the causal effect sizes (${\gamma }_{kj}$) within the network. Of the 10 variables, 4 of these variables affect $\alpha$ while 4 variables affect $\beta .$$\alpha$ and $\beta$ share a single covariate ($x_3$) in these simulations.

Methods to infer physiological network

We evaluated different algorithms from the causal structure discovery literature for inferring the network connectivity structure of the synthetic physiological network. In particular, we compared methods that used score-based or constraint-based metrics to identify the network structure in the physiological network. The tested methods include:

• 1)Greedy Equivalence Search (GES) uses Bayesian information criterion (BIC) as the score to optimize.
• 2)Incremental Association Markov Blanket (IAMB) algorithm identifies the Markov blanket or variables that can be used to predict a variable locally before identifying the global connectivity of the network.
• 3)Grow-Shrink (GS) algorithm also identifies the local Markov structure to build up the network structure.
• 4)Peter Clark (PC) algorithm identifies the conditional independencies from the data to build up the network structure.
• 5)Max-Min Parents and Children (MMPC) algorithm identifies the parent-children set, for each node that contains all variables that are a parent or a child of the node.
• 6)Inductive Causation (IC) algorithm creates a Bayesian network structure based on constraints identified from conditional independence between variables.

In this work, we build upon these methods and evaluate six different algorithms for structure discovery. Using simulations, we calculated the accuracy of incremental association Markov blanket (IAMB) (Tsamardinos et al., 2003), Grow-Shrink (GS) (Margaritis and Thrun, 1999), Peter Clark (PC) (Spirtes and Glymour, 1991), Max-Min Parents and Children (MMPC) (Tsamardinos et al., 2006), and inductive causation (IC) (Verma and Pearl, 1991) algorithms from the constraint-based algorithms and compared it to the accuracy of the score-based algorithm - Greedy Equivalence Search Algorithm (GES) (Chickering, 2002). All algorithms were tested with default settings as implemented in bnlearn (Scutari, 2010).

Accuracy of parameter and effect size identification in simulations

We estimate the accuracy of physiological network reconstruction and the accuracy of identification of variables with direct connectivity to survival parameters. We also evaluate the impact of correctly selecting a variable given its true effect size. For this, we simulated a range of effect sizes on both alpha and beta covariates as detailed in the simulated networks set#1 and set#2 sections above (Equations 6 and 7). We compared the inferred effect size in the final survival model to the actual effect size in the simulation.

We calculate the following measures. A true positive (TP) is a true causal relationship in the simulated dataset (either between survival parameters and covariates or between different simulated variables within the simulated network). A false positive (FP) is an edge that was identified by an algorithm but does not exist in simulated data. A false negative (FN) is the missing identification of a causal edge that exists within the network, and a true negative (TN) is the correct prediction of the absence of an edge. For the evaluation of physiological network reconstruction, we measured precision and recall. The definition of these measures is as follows:

Sensitivity (recall) measures the ability of the algorithm to detect the true positives. Defined as:

$$Sensitivity=\frac{TP}{TP+FN}$$ (Equation 10)

Specificity measures the ability of the algorithm to detect the true negatives. Defined as:

$$Specificity=\frac{TN}{TN+FP}$$ (Equation 11)

Positive Predictive Value (precision or PPV) is the fraction of predicted positives that are true positives. PPV is defined as:

$$PPV=\frac{TP}{TP+FP}$$ (Equation 12)

Negative Predictive Value (NPV) is the fraction of predicted negatives that are true negatives. NPV is defined as:

$$NPV=\frac{TN}{TN+FN}$$ (Equation 13)

Bayesian inference of survival layer

We applied and compared three methods for Bayesian inference. We utilized Markov Chain Monte Carlo (MCMC) simulations (Gilks et al., 1995) with the No U-Turn Sampler (NUTS) (Hoffman and Gelman, 2011) to infer the parameters given the structure of the network. Each simulation was run for 1000 steps with 1000 steps of burn-in time and 4 chains were run per simulation to check for convergence of the simulations. Except for LASSO fit, in all other inference methods, the goodness of fit during structural inference was measured using the Watanabe-Akaike Information Criterion (WAIC) with lower values of WAIC considered to be better fits (Vehtari et al., 2015). WAIC is based on an estimate of the predictive distribution of individual observations. WAIC tries to predict the accuracy of the model for out of sample prediction (also called cross-validation) based on the log likelihood of the observations within the training sample and contains a penalty for the effective number of parameters used within the model.

Univariate association between covariates and survival parameters

The goal of univariate association methods is to identify all the covariates that are associated with either Gompertz parameter. The fit is applied with each individual covariate applied to either affect baseline fitness or aging rate. We run 2 simulations per covariate using either fit:

$$log\left({\alpha }_i\right)=log\left(a^0\right)+a^j{x}_{i,j}$$

or

$${\beta }_i=b^0+b^j{x}_{i,j}$$

Using MCMC simulations, all variables that show improved fit for the survival model (lower WAIC as compared to null model) are taken for further analysis. The null model for univariate variable selection is the model in which the Gompertz parameters are independent of all covariates (i.e., X0-X39 in set 1 and X0-X9 in set 2).

Regularized LASSO approach for multivariate structure inference

LASSO is a regularized approach to identify all the relevant variables associated with survival in a single iteration (Tibshirani, 1996). In this approach, the effect sizes ${\alpha }^j$ and ${\beta }^j$ for each of the covariates $x_j$ on the Gompertz parameters are assumed to have regularized Laplace priors. The hyperparameters on the Laplace distribution are also learned from the data:

$${\alpha }_j=L(0,\lambda )$$

$${\beta }_j=L(0,\lambda )$$

$$\lambda =HC\left(\mathrm{0,1}\right)$$

where $L(0,\lambda )$ represents the Laplace distribution with the location at 0 and $\lambda$ is the scale parameter while $HC\left(\mathrm{0,1}\right)$ represents the Half Cauchy distribution with location at 0 and a scale parameter of 1. During the simulation, a variable is selected if the 95% credible interval of the corresponding coefficient does not overlap with 0.

Greedy hill-climbing algorithm for multivariate structure inference

This model is a multivariate version of the Gompertz survival function, where feature selection is based on incremental improvement in WAIC.

$$log\left({\alpha }_i\right)=log\left(a^0\right)+\sum _{j=0}^3{a}^j{x}_{i,j}$$

$${\beta }_i=b^0+\sum _{j=3}^6{b}^j{x}_{i,j}.$$

The covariates chosen for the hill climbing procedure are the variables that passed the univariate variable selection. In the greedy hill-climbing algorithm, we learn the structure using multiple iterations. During each iteration, the method explores the space of models in which one of two steps can be taken:

• a)A new covariate can be associated with either alpha or beta (single edge addition).
• b)A pre-existing association of covariates with either alpha or beta can be removed from the model (single edge deletion).

At the end of each iteration, the model with the best WAIC (minimum) is chosen. The iterative hill climbing is performed until no further improvement in WAIC is possible.

Application of models to human cohorts

Selection of variables for inclusion into physiological networks

The Osteoporotic Fractures in Men (MrOS) cohort is a multi-center prospective, longitudinal, observational cohort study designed to examine the extent to which fracture risk is related to bone mass, bone geometry, lifestyle, anthropometric and neuromuscular measures, and fall propensity, as well as to determine how fractures affect the quality of life in men. The MrOS study population consists of ambulatory men aged 64 years or older at baseline. The study was designed to study osteoporosis in elderly men (Orwoll et al., 2005).

In this study, there were hundreds of biomarkers and physiological parameters measured. We focused on biomarkers associated with long-term survival within the MrOS cohort and removed individuals that died within the first 3 years, or were deemed unhealthy. The unhealthy participants were unable to complete at least one of the following tasks: (i) climb ten steps, (ii) walk two blocks, (iii) perform a narrow walk trial, or (iv) complete 5 stands. To identify variables that are potentially associated with survival outcomes, we carried out a univariate analysis with age adjustment to identify all covariates associated with survival using Gompertz analyses.

After removing highly correlated biomarkers, we identified 34 covariates in the MrOS cohort that improved the prediction of survival and were chosen for multivariate survival analyses and for the construction of physiological networks. The complete list of selected variables can be found in Figure 5 and age-adjusted hazard ratios for some of the selected variables can be found in Figure S8. All details of the preprocessing steps and variable selection are in the methods.

Baseline measurements

At baseline, a comprehensive assessment of physiological and biochemical measures was conducted This includes skeletal measurements such as bone mineral density (BMD) using dial energy X-ray absorptiometry (DEXA) and quantitative computed tomography (QCT) as well as lifestyle, medical, and nutritional factors using surveys as well as a physical activity using self-reported surveys. In addition, they also made physical and anthropometric measurements such as weight, height, body mass index (BMI) as well as measured the cognitive, visual, and neuromuscular function by measuring grip strength, walking speed, as well as the ability of the participant to rise from the chair and the Modified Mini-Mental Status (3MS) examination. Blood and urine samples were collected after fasting for biochemical measurements.

Baseline characteristics of MrOS

In order to identify biomarkers associated with baseline fitness and aging rate under realistic scenarios, we applied Gompertz survival analyses to a human cohort with ∼17 years of follow up time. The Osteoporotic Fractures in Men (MrOS) Study is a multi-center prospective, longitudinal, observational study designed to examine risk factors associated with longer term health outcomes in elderly individuals.

To focus on biomarkers associated with long-term survival, we removed participants that died in the first two years of a study or had clear indications of poor health. This resulted in a subset of 4,864 participants (MrOS) as shown in the baseline table. We focused on biochemical and physiological measures collected in Year 1 and Year 2 of this study, as these years had the most complete biochemical characterization.

Event outcomes

Study participants received a one-page Tri-Annual Questionnaire every four months. This instrument is used to update contact information and to ascertain the incidence of falls and fractures and back pain. Vital status and cause of death during the study are verified through state death certificates. The February 2018 release was used for all analyses in this manuscript.

Data preprocessing

All survival analyses were performed with respect to all cause mortality within this manuscript. We removed unhealthy participants at baseline to focus on early predictive biomarkers of aging. All variables were normalized to Z-scores before survival regression. The log of all biochemical measurements were taken before Z-score normalization.

Univariate association with survival

We initially performed univariate analysis with age adjustment to identify all covariates associated with survival using Gompertz analyses. Before testing for a univariate association, we removed all outliers from the data (modified Z-score > 3.5).

We performed a univariate analysis with anthropometric measurements, abdominal aortic calcification measured using DEXA scans, serum biochemistry panel, serum and urine bone marker assay, cytomegalovirus seropositivity assay, serum cytokine assay, serum glucose assay, serum FGF23 and uric acid assay, vascular endothelial growth factor assay, medical inventory form, vitamin D assay, PTH assay, osteocalcin assay, renal function assay, thyroid assay, and urine mineral assay for association with either Gompertz parameter after adjusting for age.

Some of these measurements were not made for all participants in the cohort but we did not impute missing values during univariate association tests. We identified the subset of physiological markers and/or biomarkers that contributed significantly to either of the latent Gompertz parameters ${\alpha }_i$ or ${\beta }_i$ after age and sex correction based upon the survival data for the different cohorts.

To identify the biomarker $\left(x\right)$ that significantly affect survival of the cohort, we ran Markov Chain Monte Carlo (MCMC) with No U-Turn Sampler (NUTS) with the following model:

$$log\left({\alpha }_i\right)=log\left(a^0\right)+a^{Age}Ag{e}_i+a^x{x}_i$$

$$log\left({\beta }_i\right)=log\left(b^0\right)+b^x{x}_i$$

Each chain was run for 1000 steps with 1000 steps of burn-in time and 4 chains were run per simulation to check for convergence of the simulations. The contribution of a biomarker to survival was considered significant if its inclusion improved the WAIC measure relative to the null model.

Construction of physiological and survival networks

In the first step, the physiological networks were constructed using the Incremental Association Markov Blanket (IAMB) algorithm (Tsamardinos et al., 2003) followed by a greedy hill climbing algorithm (Tsamardinos et al., 2006) to find the directionality of undirected edges. The Markov blanket of a variable X is defined as the smallest set of variables in the network that improve the accuracy of predicting variable X. The Markov blanket of X includes the variables that are directly connected to X in the DAG as well as variables that have a common successor (i.e., collider variables). IAMB is a two-step variable selection process, where first all variables that predict X are identified (forward phase) and then this set is pruned (reverse phase) based on conditional independencies in the data. Following this, we used a hill climbing algorithm to identify the directionality of edges within the DAG.

In the second step, we utilize a greedy hill climbing algorithm to identify which covariates from the physiological network are associated with alpha or beta using a multivariate survival model. Once the survival regression converges, we then merge the edges in the physiological and survival networks within a single causal network.

Assessment of accuracy of survival regression

We measured the goodness of fit using the concordance index or C-index. The C-index is a generalization of the area under the ROC curve (AUC) that can take into account censored data. It represents the global assessment of the model discrimination power: this is the model’s ability to correctly provide a reliable ranking of the survival times based on the individual risk scores. To estimate the C-index for the Gompertz model, we simulated 18 years of survival data with each participant having the mean hazard predicted by the multivariate survival model identified in this study. Then we compared the order of simulated events with the order of real events as implemented in the lifelines package v0.26.0⁴.

Modeling effect of intervention in physiological networks

There are two types of questions one can ask of joined physiology - survival network. First, what is the effect of an intervention on physiology nodes directly connected to survival nodes? Second, what is the indirect effect of an intervention on the physiology layer? The second question can be modeled by propagating changes on one node to all its successors within the physiology layer, and ultimately modeling how that information propagates into the survival layer. Simulating these hypothetical scenarios, can be thought of as counterfactuals – what if there was a treatment that modulated physiological variables and what effect would the treatment have on median survival in the individuals?

Direct effects

In the multivariate survival model, the effect of modifying a single covariate X on survival time was measured by keeping all other covariates at the mean value (Z-score = 0) and only modifying X. The range of Z-scores for X was based on the range of X observed within the cohort. The coefficients of ${\alpha }_j$ & ${\beta }_j$ from the MCMC trajectory of the multivariate survival model was used to measure the uncertainty in predicted median survival time under this model (Equation 14). The median survival time ($T_{1/2}$) was calculated based on the Gompertz survival quantile function:

$$T_{1/2}=\frac{1}{\beta }log(\left(\frac{\beta }{e^{\alpha }}\right)\ast log\left(2\right)+1)$$ (Equation 14)

where the Gompertz parameters are calculated using the counterfactual condition.

Total effects

During the counterfactual calculations with the combined physiological-survival networks, we used do-calculus for estimating the median survival time for each covariate (Pearl, 2000) based on the optimized DAG. During do-calculus, the variable under consideration X is changed to a particular value and the edges from its parents are removed. In the modified network, all descendants of X are updated to a new value based on their relationship with X. This update ensures that information is propagated to descendants of X, and ultimately their effects on survival. The median survival time is calculated using the same formula as with the direct effects above. The advantage of this methodology is that indirect effects are allowed during the counterfactual calculation, which is not possible with the simple multivariate survival model.

Quantification and statistical analysis

The statistical approach used in this article is described in method details. All Bayesian models were implemented using PyMC3, and Kaplan-Meier curves were constructed using Lifelines python package.

Published: December 2, 2022

Data and code availability

• •Data for MrOS study is available through University of California San Francisco and California Pacific Medical Center Research Institute: https://mrosonline.ucsf.edu/. dbGaP study accession numbers are listed in the key resources table.
• •Code is available at https://github.com/calico/Bayesian_Survival_Analysis/. All original code has been deposited at Zenodo and is publicly available as of the date of publication. DOIs are listed in the key resources table.
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.