Simulated filament shapes in embedded 3D printing

Abstract

Embedded 3D printing, wherein fluid inks are extruded into support baths, has enabled the manufacture of complex, custom structures ranging from cell-laden tissue analogues to soft robots. This method encompasses two techniques: embedded ink writing (EIW), where filaments are extruded, and embedded droplet printing (EDP), where droplets are suspended. Materials for embedded 3D printing can be Newtonian, but often both the ink and the support bath are yield stress fluids, following elastic behavior below the yield stress and shear-thinning, viscous behavior above the yield stress. The effect of surface tension on print quality has been debated, as inks have been printed into supports at high and low surface tensions. In order to guide material selection for embedded 3D printing and identify key scaling relationships that influence print quality, this study investigates the role of ink rheology, support rheology, and surface tension on the morphology of single filaments. Numerical simulations in OpenFOAM demonstrate that at low viscosities, surface tension controls the filament morphology. Where capillarity is suppressed, the ratio of the local ink and support viscosities and the shape of the yield surface in the support control the filament shape. Herschel–Bulkley support fluids (yield stress fluids) produce more stable, accurately positioned filaments than Newtonian supports. In the short term, non-zero surface tensions can suppress filament shape defects in EIW and are essential for producing droplets in EDP.

1. Introduction

3D printing has enabled the fabrication of structures with complex geometries and composition gradients which cannot be achieved with conventional processes. This complexity enables advanced therapies including personalized medical devices and tissue analogues. The most popular method for printing biomaterials is direct ink writing (DIW), wherein a fluid ink is extruded out of a nozzle as a continuous filament and solidified after deposition.¹ Direct ink writing is amenable to a wide range of materials, enabling diverse functionalities, mechanical behaviors, and solidification methods.^2,3

Recently, techniques integrating support baths with direct ink writing have emerged. Support baths can hold the form of the printed structure, preventing slumping and enabling fully three-dimensional print paths, as opposed to layer-by-layer printing.⁴ As such, baths expand the direct ink writing space to include low-viscosity materials, many of which are essential for printing tissue analogues and other soft materials. Support baths can also serve functional purposes by providing nutrients to a cell-laden print⁵ or introducing a cross-linker to the printed structure.^6,7 We refer to this technique as embedded ink writing (EIW),⁸ to denote that this technique focuses on extrusion of continuous filaments, and that one material is printed into another material. Here, we focus only on the extrusion process, not the removal process, so this study can apply to inks and supports which are sacrificial or permanent. This work can be applied to a range of overlapping techniques including “3D printing with sacrificial materials,”⁹ “bath-enabled extrusion 3D printing,”¹⁰ “direct ink writing in a supporting viscous liquid,”¹¹ “embedded 3D printing,”^12-15 “freeform printing,”^16-18 “freeform reversible embedding (FRE),”^19-21 “guest–host writing (GHost writing),”⁷ “omnidirectional printing,”²² “printing in liquid-like solids,”^5,23 “printing-then-gelation” or “printing-then-solidification,”^17,24,25 “printing liquids in solution,”²⁶ “sacrificial writing into functional tissue (SWIFT),”²⁷ “suspended layer additive manufacturing (SLAM),”^28,29 and “writing in granular gels.”^30,31 Additionally, this study covers a material space that is applicable to “embedded droplet printing,”^5,32-34 where ink droplets are generated within a viscoplastic bath.

Materials used in EIW span a wide range of rheological behaviors and interfacial properties. One of the central considerations in material selection for EIW is the suppression of Plateau-Rayleigh instabilities, wherein surface tension causes the filament to break up into droplets. In yield stress fluid supports, design strategies have focused on balancing a filament diameter l against surface tension σ and yield stress τ_y, where filaments rupture if l < σ/τ_y.^9,17 In these simulations, the critical diameter is 4 mm, which is larger than the simulated filaments. In non-yielding fluids, design strategies have focused on delaying instabilities, where the time scale of breakup is t = αη_sl/σ, where η_s is the support viscosity, and α is a scaling factor that depends on the viscosity ratio between the ink and support.²⁶ Understanding these fundamental relationships, there are several strategies to make printing possible across a wide range of ink and support viscosities. Most studies have used ink–support combinations with low surface tensions.³⁰ Because most biomaterials are hydrophilic, most bioprinting studies use hydrophilic support baths.^12,16,18 Similarly, amphiphilic polymers such as Pluronic F127 can be printed into hydrophobic yield stress fluids.¹³ Alternatively, hydrophobic inks can be printed into hydrophilic supports by printing into a support with a high yield stress.²⁰ In lieu of yield stress fluids, low-viscosity Newtonian water-based inks can be printed into low-viscosity Newtonian oil-based supports by introducing nanoparticle surfactants which jam at the ink-support interface.²⁶

While there have been numerous studies on the effect of the ink-support viscosity ratio and surface tension on filament breakup during injection into a static bath,^35-37 there is little reporting on the cross-sectional shape and placement of the filament in a 3D printing context. Understanding how material properties influence the cross-sectional shape and placement of a filament is critical for toolpath design. To set layer heights and interfilament spacings, the toolpath designer or slicing software must know where a filament will end up relative to the nozzle tip (x–y positioning and z positioning), how much space it will fill, and what shape the filament will take. Further, sharp edges and surface asperities on an individual filament will translate to surface roughness on the printed part. Understanding how to suppress those sharp edges is thus critical for controlling the part finish. Reported cross-sectional shapes have ranged from circular^6,7 to oblong,^6,30 where filaments tend to be elongated vertically. Critically, Uchida et al. find that the height/width increases with decreasing ink viscosity and increasing support viscosity.¹¹ This paper directly examines the effect of the viscosity ratio, or the ink viscosity divided by the support viscosity, on the filament aspect ratio.

In this work, we use simulations to directly probe the effects of ink rheology, support rheology, and surface tension on the cross-sectional shape of printed filaments. By using numerical methods, we can isolate variables which would be difficult to isolate in experiments. For example, it is difficult to change the viscosity of a fluid without changing its surface tension. Simulations are particularly useful when isolating aspects of yield stress fluids. Experimentally, it is difficult to change the yield stress of a Herschel–Bulkley fluid without changing its zero shear viscosity, but simulations let us isolate the effect of yielding from the behavior of unyielded fluids. Additionally, numerical methods allow us to simulate three-dimensional flow fields for which no analytical models have been presented. We investigate four scenarios: a Newtonian ink and Newtonian support, a Newtonian ink and Herschel–Bulkley support, a Herschel–Bulkley ink and Newtonian support, and a Herschel–Bulkley ink and Herschel–Bulkley support. In each scenario, we vary the viscosity or plateau (unyielded) viscosity of each fluid and the surface tension between the fluids. We find that the local viscosity ratio of the fluids and the surface tension control the shape of the filament, and interactions between those variables are critical.

2. Methods

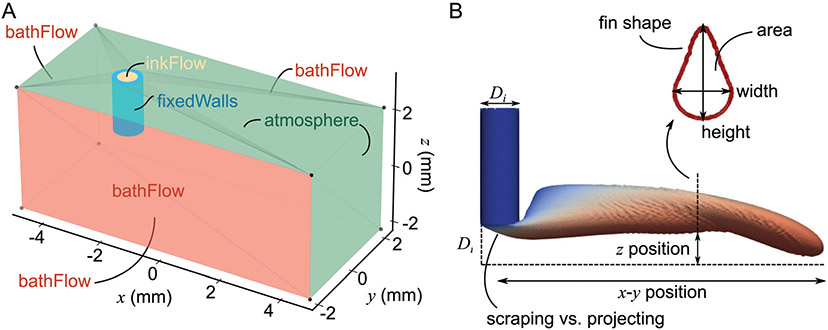
Simulations were conducted in OpenFOAM v1912 and OpenFOAM 8.^{38-40 §} The nozzle was assumed to be a 20 gauge blunt tipped needle with an inner diameter (D_i) of 0.603 mm and a wall thickness of 0.152 mm (Fig. 1A). All following dimensions are in terms of the nozzle inner diameter D_i. The nozzle was oriented vertically along the z axis, and the surface of the bath flowed in the positive x direction. The bath was 16D_i long in the x direction, 7D_i wide in the y direction and 7D_i tall in the z direction. The center of the bottom of the nozzle was placed 1/2D_i above the z center of the bath, in the y center, and 4D_i from the negative x limit of the bath. The ink extrusion velocity at the nozzle inlet was fixed at 10 mm s⁻¹, and the bath translation velocity at the edges of the simulated volume was fixed at 10 mm s⁻¹.

Fig. 1.

(A) Simulation geometry. Boundaries used to define boundary conditions are labeled. Gray lines are from the mesh used to define the surface. (B) Filament quality metrics. The blue column is the ink inside of the nozzle.

Boundaries are shown in Fig. 1A, and initialization files are listed in the ESI‡ (Section S1). The inkFlow boundary is at the nozzle inlet. It imposes a fixed velocity of ink into the top of the nozzle and imposes zero pressure flux over the boundary, such that the flux of ink is constant, and the pressure can evolve to fit the flux. The bathFlow boundary is on the positive and negative y faces, negative x face, and negative z face. It imposes a fixed velocity of support downstream on the surfaces of the volume and imposes zero pressure flux over the boundary. This implies that support fluid is moving into the front face of the volume and along the sides and bottom of the volume at a fixed velocity, and the pressure field can evolve. The atmosphere boundary is on the positive x and positive z faces. This mixed boundary establishes that the atmosphere outside of the simulated volume is composed of support fluid. It imposes a zero gradient condition on the composition and a total pressure of zero over the surface, allows ink and support to leave the volume, and allows support to flow back into the volume. As such, this is a quasi-free surface, where the pressure condition mimics a free surface, but rather than allowing inflow of air,²³ which would make this a more complex three-phase system, the surface allows inflow of support. One could view this surface as being near the bath-air interface. Section S1 (ESI‡) discusses the differences between this quasi-free surface and a zero-gradient surface, which would simulate a deeper bath. The fixedWalls boundary is imposed on the inner and outer walls of the nozzle and the bottom edge of the nozzle wall. It imposes no slip on the velocity and a zero gradient condition on the composition and pressure. The bulk of the volume was initialized with a velocity of 0 mm s⁻¹, which reflects a condition where the stage starts moving at the beginning of extrusion. In other words, the bath is standing still right before printing begins.

The mesh was created using snappyHexMesh^38,39 with dynamic mesh refinement at the ink-support interface. The initial mesh has a cell size of 0.2 mm with snapping refinement up to 2 levels, with 10 cells between levels. Dynamic remeshing was imposed at the ink-support interface where the ink volume fraction was between 0.001 and 0.999, where mesh refinement can occur once every five time steps. Remeshing allowed the mesh to be refined down to 4 levels of a finer mesh and up to 5 levels of a coarser mesh, from the original mesh (Fig. S6, ESI‡).

Simulations were solved using interFoam,^38,39,41 where the solver solved for the volume fraction of ink within cells of the two-phase ink and support system. Simulations ran for up to 5 s, with an initial time step of 0.001 s and time step updating based on a maximum Courant number of 1, where the Courant number is the velocity magnitude multiplied by the time step size divided by the mesh cell length.⁴² Where filaments are produced, and the amount of interface isn’t continually changing, the solve residuals converge within the simulation time (Fig. S7, ESI‡).

Transport properties were defined for the ink and support. Newtonian fluids were defined as Newtonian, while non-Newtonian fluids were defined as Herschel–Bulkley fluids. Densities ρ of both ink and support were defined as 1 g mL⁻¹ in order to suppress buoyancy. In OpenFOAM, the dynamic viscosity η of a Herschel–Bulkley fluid is defined as:

$$\eta =\text{min}({\eta }_0,{\tau }_0∕\stackrel{.}{\gamma }+k{\stackrel{.}{\gamma }}^{n-1})$$ (1)

where η₀ is the plateau viscosity, τ₀ is the yield stress, γ is the shear rate, k is the consistency index, and n is the flow index. Unless otherwise noted, τ₀ is set to 10 Pa, k is set to 3.75 Pa sⁿ, and n is set to 0.45, based on reported values for Carbopol suspensions.⁴³ These values are comparable to values reported in the literature for embedded 3D printing supports (Table S1, ESI‡). Newtonian fluid viscosities and Herschel–Bulkley plateau viscosities in this study range from 10⁻² Pa s to 10⁵ Pa s. Reported viscosities for Newtonian fluids range from 10⁻³ Pa s to 10² Pa s (Table S1, ESI‡), but comparing the more viscous end of the simulated range to the viscous end of the simulated Herschel–Bulkley materials enables isolation of viscous dissipation from yielding behavior. Reported zero shear viscosities for Herschel–Bulkley supports range from 10 Pa s to 10⁷ Pa s, but simulating the low-viscosity range provides insight into the lower limits of the material space. The flow speed V_∞ is 10 mm s⁻¹, the nozzle inner diameter D_i is 0.603 mm, and the nozzle outer diameter D_o is 0.907 mm.

For Newtonian fluids, the Reynolds number is defined as Re = ρV_∞D/η. For ink inside the nozzle, Re is 6.03 × 10⁻⁸ to 6.03 × 10⁻¹. For support flowing around the nozzle, Re is 9.07 × 10⁻⁸ to 9.07 × 10⁻¹. For Herschel–Bulkley fluids flowing inside the nozzle, Re = 0.019, as defined in ref. 44. For Herschel–Bulkley fluids flowing around the nozzle, Re and the Oldroyd number Od are defined as:⁴⁵

$$\text{Od}=\frac{{\tau }_0{D}_{\mathrm{o}}^n}{k{V}_{\infty }^n},\text{Re}=\frac{V_{\infty }^{2-n}{D}_{\mathrm{o}}^n\rho }{k}$$ (2)

For these fluids, Od = 0.906, and Re = 0.00906. The Ohnesorge number, which is relevant for droplet formation, is defined as $\text{Oh}=\eta ∕\sqrt{\rho \sigma D_{\mathrm{i}}}$.⁴⁶ For Newtonian fluids in this study, Oh ranges from 6.4 × 10⁻² to 6.4 × 10⁵.

Results were processed using Paraview 5.8.0.⁴⁷ OpenFOAM initialization files were generated, Paraview scripts were run, and data were processed using Python 3.7⁴⁸ using code that is available at ref. 49 The data associated with this paper is available at ref. 50.

3. Results

Simulation rates within this study varied from [0.41 to 11569] computing hours per simulation second (Fig. S5, ESI‡). Using a Python script, rates were monitored while the simulations ran. Simulations with rates higher than 120 h s⁻¹ were aborted instantly, and simulations with rates higher than 60 h s⁻¹ were aborted once the simulation reached 1 s. As such, while full sweeps across plateau viscosities from 10⁻² Pa s to 10⁵ Pa s were initiated, some figures in this paper contain regions of “no data”’ due to untenable computation times. These slow computation rates tend to occur where there is a high contrast in viscosity between the ink and support. Some of these high computation times occur because of “spraying,”’ where the nozzle generates many small droplets. Because the mesh is refined at the ink–support interface, sprays result in fine meshes that explode computation times both by increasing the number of mesh cells and reducing the time step size via Courant number limits.

3.1. General filament shape

One of the most obvious characteristics to consider is the overall extrudate shape. Ideally, EIW produces a continuous filament. While a non-circular cross-sectional shape could be beneficial, most toolpath designs and printing techniques are tailored to circular cross-sections, so in this study, we will consider the ideal filament shape to be a circular cylinder. There should be no variation in cross-sectional shape or position along the length of the filament. Variations could lead to interfilament porosity or other morphological defects. Alternatively, in embedded droplet printing, droplets should be generated.³² Although there are a variety of applications for embedded droplet printing, most are tailored to spheres, so droplets should be spherical and should not cling to the nozzle.

Filament positioning is an essential print quality metric. Here, we define two ways to characterize the position of a filament. First is the z position, or the vertical position within the bath (Fig. 1B). If the z position is too high, the nozzle needs to dig into existing lines to print a new line. Ideally, the filament is deposited just below the nozzle, so the top of the filament touches the bottom of the nozzle. The lowest position achieved within this study is close to the ideal position. Related to the vertical position is the depth of the filament at the nozzle exit. In some cases, it protrudes deeply into the bath, and in other cases, it is scraped downstream (Fig. 1B). The next position characteristic is the x–y position (Fig. 1B). Ideally, if the part design asks for a 10 mm line, and the nozzle or stage travels 10 mm, a 10 mm line should be extruded. However, there are many cases in this study where that line would be shorter than 10 mm, resulting in poor x–y positioning. There are a few ways to measure x–y positioning accuracy. One is to simulate a large volume, extrude a long line, and measure the difference between the actual filament endpoint and the intended filament endpoint. The present simulation geometry is sufficiently large to identify deficiencies in x–y positioning accuracy within 1 s, for many of the simulated filaments. Another indicator of x–y positioning accuracy is the filament velocity. If the stage translates at 10 mm s⁻¹, the filament should travel at 10 mm s⁻¹. If the filament is too slow, the extruded line will be too short. Another proxy for x–y positioning is the filament area, since it is correlated with the interface speed. Ideally, the cross-sectional area should be constant and equal to the ink flux divided by the translation speed.⁹ Variations in area over the length of the line can lead to defects, and areas that are larger than ideal will reduce the resolution of the print and correlate with slow speeds, i.e. poor x–y positioning.

The objective of this section is to identify the controlling variables that influence the overall filament shape. Here, many interactions between variables are present. Surface tension is only relevant on these time scales at low viscosities. The viscosity ratio (the ink viscosity divided by the support viscosity) is only relevant where both materials behave like Newtonian fluids, or where the viscosity ratio is defined using local viscosities, not unyielded viscosities. The viscosity of the ink alone is only relevant when the support follows Herschel–Bulkley behavior, and the viscosity of the support alone is only relevant when the ink follows Herschel–Bulkley behavior. These simulations were conducted with surface tensions of 0 and 40 mJ m⁻². 40 mJ m⁻² is within the range of oil–water interfacial energies. This work sweeps through inks and supports with Newtonian viscosities ranging from 10⁻² Pa s to 10⁵ Pa s. Throughout this discussion, results are plotted as a function of ink viscosity and support viscosity. Most maps can be broken into four regions: (i) at high ink and support viscosities; (ii) at low ink and support viscosities; (iii) at low ink viscosities and high support viscosities; and (iv) at high ink viscosities and low support viscosities. These regions are defined by which independent variables, e.g., surface tension and viscosity ratio, control the considered metric. Depending on which dependent variable is being considered, the borders between these regions may shift. In some cases, regions will be combined to highlight similarities in controlling variables. For example, in Fig. 2A, region i expands to include some parts of region iii and iv because the viscosity ratio dominates the region. In no case are the boundaries between these regions sharp; usually, a controlling variable gradually becomes less effective, and another controlling variable becomes more effective, across these boundaries. When Herschel–Bulkley fluids are included, the boundaries between regions are largely defined by yielding. Where Newtonian fluids are included, the boundaries between regions are largely defined by a balance between viscous dissipation and interfacial tension.

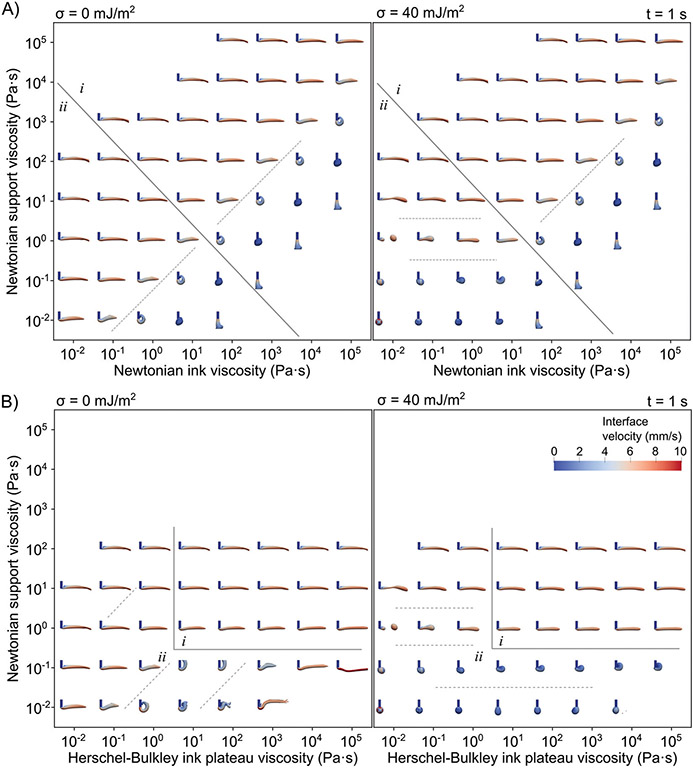
Fig. 2.

Views of extruded filaments from the +y direction after 1 s of extrusion, where the support is Newtonian. Surfaces indicate the interpolated interface between ink and support, where the volume fraction of ink is 0.5. Colors indicate the magnitude of the velocity at the interface. Blue vertical cylinders represent the ink inside of the nozzle. (i) Viscosity ratio dominates. (ii) Surface tension dominates. Dashed lines indicate trends in controlling variables (viscosity ratio or support viscosity). (A) Newtonian ink. (B) Herschel–Bulkley ink.

3.1.1. Newtonian ink, newtonian support.

First, consider a Newtonian ink and Newtonian support. In reality, many of these inks and supports would not be printable, because the inks would be too viscous to extrude through a nozzle, and the supports would be too viscous to allow the nozzle to travel through the bath. Newtonian–Newtonian combinations have only been demonstrated at very low viscosities.^26,51 However, these simulations let us isolate viscous dissipation. In viscoplastic fluids, it is difficult to disentangle viscous dissipation from plasticity.

Fig. 2A shows the ink–support interface after 1 s of flow. In the ink viscosity–support viscosity map, two regions are apparent. In region i, where the ink and support viscosities are high, the viscosity ratio controls the filament shape. In region ii, where the ink and support viscosities are low, surface tension has a larger effect. The boundary between regions i and ii is related to the balance between viscous dissipation and surface tension. Note that at zero surface tension, there is no distinction between regions i and ii.

First, consider region i (Fig. 2A). Within this viscous regime, capillarity does not influence the filament shape. At a very high viscosity ratio, where the ink is 10⁴ times more viscous than the support, the filament jets directly to the base of the simulated volume, even though the bath support is flowing downstream (Fig. S8, ESI‡). Where the ink is 10³ times more viscous, the filament interacts with the support, forming a round shell around the ejected jet (Fig. S9, ESI‡). Where the ink is 10² times more viscous, the filament starts to move downstream, still ejecting deeply in z into the support, and then it curls over itself and makes contact with the nozzle (Fig. S10, ESI‡). Where the ink is 10 times more viscous than the support, filaments start to form. Similarly to the curled morphology, the filament protrudes into the support below the nozzle, then drifts upward, but eventually stabilizes into a filament (Fig. S11, ESI‡). As the viscosity ratio continues to decrease and the support becomes more viscous than the ink, the filament is scraped downstream underneath the nozzle instead of protruding into the support (Fig. 1B). This leads to a wide, flat filament tip (Fig. 1B and Fig. S12, ESI‡). Additionally, the filament x–y positioning is more accurate at low viscosity ratios. Where the simulated volume extends around 7.25 mm downstream of the nozzle, and the bath is moving at 10 mm s⁻¹, the filament should travel past the end of the simulated volume before 1 s. As the viscosity ratio decreases, the filament tip travels farther.

Second, consider region ii (Fig. 2A). Within this low-viscosity regime, capillarity influences the filament shape. At zero surface tension, the filament shapes continue to follow the same viscosity ratio dependence demonstrated in region i, with slight variations at a low support viscosity of 10⁻² Pa s. However, at a surface tension of 40 mJ m⁻², the filament shape does not simply depend on viscosity ratio, and every filament simulated within this region is distinct. At a non-zero surface tension, the dominant rheological variable in region ii is the support viscosity. In more viscous supports, the 40 mJ m⁻² filaments are similar to the 0 mJ m⁻² filaments, but with rounded filament tips. At intermediate support viscosities, filaments rupture downstream of the nozzle (Fig. S13, ESI‡). Filaments break up faster at lower ink viscosities. As the support viscosity decreases, the rupture point draws closer to the nozzle. At low support viscosities, droplets form and break at the nozzle tip, and rather than traveling downstream with the bath, they travel up the side of the nozzle to the top of the bath (Fig. S14, ESI‡). The density of the ink and support are set to be equal in these experiments, so this is not a buoyancy effect. At very low support viscosities, the ink balls around the filament tip, forming a droplet that clings to the nozzle.

3.1.2. Herschel–Bulkley ink, Newtonian support.

Next, replace the Newtonian ink with a Herschel–Bulkley ink. In this case, the inks have a yield stress and shear-thinning behavior above yield. Again, many of these Newtonian supports would be too viscous to allow the nozzle to travel, but this configuration allows us to isolate the effects of ink yielding on filament morphology.

Fig. 2B shows the ink–support interface after 1 s of flow. Two regions are apparent. In region i, where the support viscosity is at least 1 Pa s and the ink plateau viscosity is at least 10 Pa s, the support viscosity controls the filament morphology. In region ii, where the support viscosity is less than 1 Pa s or the ink plateau viscosity is less than 10 Pa s, surface tension dominates. A Herschel–Bulkley ink allows for filaments where a Newtonian ink does not, at high ink plateau viscosities. The vertical boundary between region i and ii is related to whether the ink can yield, and the horizontal boundary is related to whether the support is viscous enough to yield the ink, which is discussed later.

First, consider region i, at high viscosities (Fig. 2B). The filament morphology is controlled by the viscosity of the Newtonian support. Increasing the viscosity of the support lengthens the filament, improving its x–y positional accuracy. At higher support viscosities, the ink directly underneath the nozzle is scraped downstream, like the low viscosity ratio Newtonian inks in Fig. 2A. A non-zero surface tension introduces some tip rounding at the lower support viscosities. The ink plateau viscosity has little effect on the filament shape within region i.

Second, consider region ii, at low viscosities (Fig. 2B). The filament morphology is dominated by surface tension, where a non-zero surface tension causes filaments to break into droplets at high support viscosities and causes ink to ball up onto the nozzle at low support viscosities. The non-zero surface tension filament shape depends primarily on support viscosity. The zero surface tension filament shape depends primarily on the viscosity ratio. At low ink plateau viscosities, the Herschel–Bulkley inks behave like Newtonian inks. At zero surface tension and high ink plateau viscosities, the Herschel–Bulkley inks produce irregular filaments where the Newtonian inks produced shells or vertical jets. Defects in these filaments include spirals along the flow direction (Fig. S15, ESI‡), large vertical displacements (Fig. S16, ESI‡), and splattering (Fig. S17, ESI‡).

3.1.3. Newtonian ink, Herschel–Bulkley support.

Next, return to a Newtonian ink and introduce a Herschel–Bulkley support. In this case, the support bath now has a yield stress and shear-thinning behavior above yield. Recall that many of the simulated Newtonian inks would be too viscous to extrude, but this map isolates the effect of support yielding on filament morphology.

Fig. 3A shows the ink–support interface after 1 s of flow. Here, three regions are present. In region i, where the ink viscosity is 100 Pa s or greater, filaments are not produced, and capillarity is suppressed. In region ii, where the ink viscosity is less than 100 Pa s and the support plateau viscosity is less than 10 Pa s, surface tension dominates. In region iii, where the ink viscosity is less than 100 Pa s and the support plateau viscosity is greater than 1 Pa s, the filament shape depends on the viscosity of the Newtonian ink. Herschel–Bulkley support baths enable continuous filaments where Newtonian supports do not, where the ink viscosity is low and the support plateau viscosity is high. However, Herschel–Bulkley support baths also lose the ability to produce filaments where Newtonian supports did, where both the ink and support are at high viscosities. The vertical boundary between region i and the other two regions is related to the local viscosity ratio between the ink viscosity and the yielded support viscosity. The horizontal boundary between regions ii and iii is related to whether the support yields.

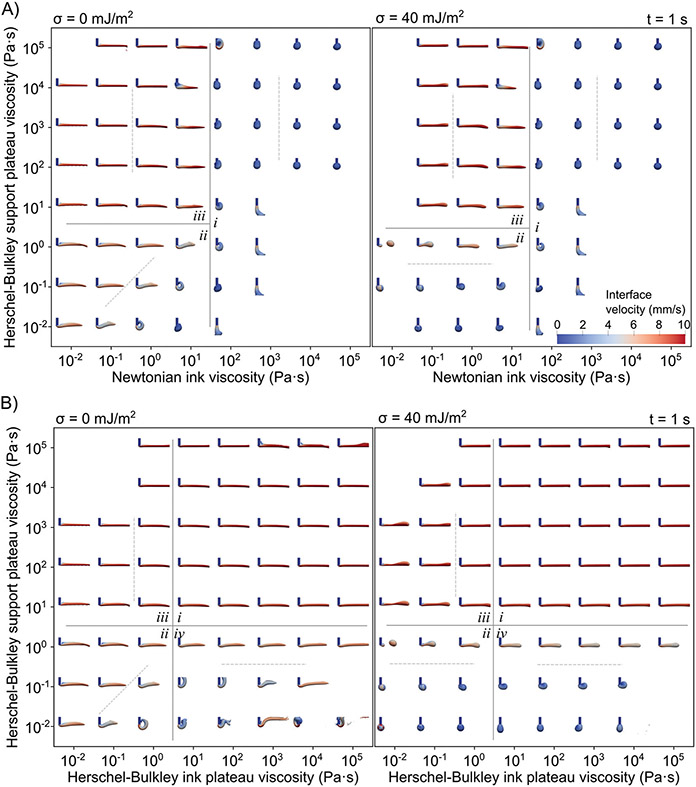
Fig. 3.

Where the support is a Herschel–Bulkley fluid, views of extruded filaments from the +y direction after 1 s of extrusion. Surfaces indicate the interpolated interface between ink and support, where the volume fraction of ink is 0.5. Colors indicate the magnitude of the velocity at the interface. Blue vertical cylinders represent the ink inside of the nozzle. Dashed lines indicate trends. (ii) Surface tension dominates. (iii) Ink viscosity dominates. (A) Newtonian ink. (i) Ink viscosity dominates. (B) Herschel–Bulkley ink. (i) Filaments are consistent. (iv) Support viscosity dominates.

First, consider region i, at high ink viscosities (Fig. 3A). Here, the surface tension has a negligible effect. Above a support plateau viscosity of 10 Pa s, shells are produced. The shell edge climbs higher on the nozzle with decreasing ink viscosity. At a support plateau viscosity at or below 10 Pa s, filaments curl, shell, or jet, depending on ink viscosity, with deviations from ink viscosity dependency at low support plateau viscosities.

Second, consider region ii, at low ink and support viscosities (Fig. 3A). In this region, the filament morphology is the same as the equivalent filament morphology in a Newtonian bath (Fig. 2A). Again, the surface tension dominates and causes filaments to break into droplets, either downstream of the nozzle or at the nozzle tip. At zero surface tension, the viscosity ratio dominates, where here the viscosity ratio is the ink viscosity divided by the support plateau viscosity.

Third, consider region iii, at low ink viscosities and high support viscosities (Fig. 3A). The filament morphology is similar throughout the region, where a continuous filament extends downstream. The Newtonian ink viscosity is the dominant variable that influences the filament shape, but there are variations between filaments of the same ink viscosity. The dominant differences are present at the filament tip and at the nozzle exit. At low ink viscosities, the ink is scraped downstream under the nozzle tip like the filaments printed into low viscosity ratio Newtonian baths (Fig. 2A). At higher ink viscosities, the ink projects into the bath like filaments printed into high viscosity ratio Newtonian baths. At low ink viscosities, the filament x–y positioning is most accurate, where filaments travel the farthest in 1 s. At higher ink viscosities, the filament barely reaches the end of the simulated region in 1 s, indicating that the printed filament will be shorter than intended. Overall, compared to the Newtonian baths, the Herschel–Bulkley baths produce more accurate x–y positioning. However, whereas Newtonian baths at high viscosities suppress capillarity, Herschel–Bulkley baths of comparable plateau viscosities allow rounded filament tips at non-zero surface tensions.

3.1.4. Herschel–Bulkley ink, Herschel–Bulkley support.

Finally, allow both the ink and support to be Herschel–Bulkley fluids. This is the most experimentally relevant combination, as these inks are extrudable, and these supports allow the nozzle to travel.

Fig. 3B shows the ink–support interface after 1 s of flow. Four regions are present in these maps. In region i, where the ink and support plateau viscosities are 10 Pa s or greater, the filament shape is very weakly dependent on rheology, and surface tension has a small effect on filament shape. In region ii, where the ink and support plateau viscosities are below 10 Pa s, capillarity dominates, and the viscosity ratio controls the filament shape at zero surface tension. In region iii, where the ink plateau viscosity is at least 10 Pa s and the support plateau viscosity is less than 10 Pa s, capillarity dominates, and the support plateau viscosity is a secondary controlling variable. In region iv, where the ink plateau viscosity is less than 10 Pa s and the support plateau viscosity is at least 10 Pa s, capillarity dominates, and the ink plateau viscosity is a secondary controlling variable. The boundaries between these four regions are related to whether the fluids yield.

First, consider region i, at high ink and support viscosities (Fig. 3B). The trends in this region are only found in Fig. 3B, where both the ink and support are Herschel–Bulkley fluids. Throughout this region, continuous filaments are always generated. The filament surface flows at nearly 10 mm s⁻¹, which is the intended velocity. As such, these filaments exhibit better x–y positioning than filaments printed with Newtonian supports and filaments printed in regions ii and iv. There are minor variations in filament shape within region i. Filaments at zero surface tension bend downward slightly compared to the filaments at a surface tension of 40 mJ m⁻². At zero surface tension within region i, the lowest viscosity ink and support produce less accurate positioning than the more viscous inks and supports. At very high support plateau viscosities at zero surface tension, some ink is initially pushed upstream of the nozzle (in the negative x direction), then wraps around the nozzle, leading to the defects visible in Fig. 3B.

Second, consider region ii, at low ink and support viscosities (Fig. 3B). In this region, the Herschel–Bulkley ink and support behave like Newtonian fluids, such that this region looks the same in Fig. 2A, B and 3A, B. Capillarity dominates in this region. At zero surface tension, the filament morphology depends on the viscosity ratio. At non-zero surface tension, the filament morphology depends primarily on the support viscosity and secondarily on the ink viscosity.

Third, consider region iii, at low ink viscosities and high support viscosities (Fig. 3B). In this region, the Herschel–Bulkley ink behaves like a Newtonian ink, mirroring Fig. 3A, where the support is a Herschel–Bulkley fluid and the ink is Newtonian. Here, capillarity has the largest effect on filament shape. At non-zero surface tensions, the end of the filament rounds, and the middle of the filament starts to narrow, mirroring Plateau–Rayleigh instabilities. This instability is most severe at low ink plateau viscosities. As a secondary effect, there are minor differences in filament morphology within this region, mostly varying as a function of the ink plateau viscosity. These differences are most obvious just underneath the nozzle tip, where ink is scraped downstream at low ink viscosities and projects into the bath at high ink viscosities.

Fourth, consider region iv, at high ink viscosities and low support viscosities (Fig. 3B). In this region, the Herschel–Bulkley support behaves like a Newtonian support, so region iii looks like Fig. 2B, where the support is Newtonian and the ink is a Herschel–Bulkley fluid. Within this region, surface tension dominates. At high support viscosities, filaments are generated at zero surface tension, but at 40 mJ m⁻², surface tension rounds the filament tip and draws the filament back toward the nozzle, which is detrimental to x–y positioning. At lower support viscosities, secondary trends are present. At a surface tension of 40 mJ m⁻², the support plateau viscosity controls the droplet morphology. At zero surface tension, the viscosity ratio controls the filament morphology. Because these simulations are faster than the simulations in Fig. 2B, a new defect is visible, where the ink initially curls upstream of the nozzle, then is pushed onto the nozzle (Fig. S18, ESI‡). At an even higher viscosity ratio, the filament curls downstream of the nozzle and splashes (Fig. S19, ESI‡).

3.2. Qualifying cross-sections

Close examination of filament cross-sections can inform toolpath design and material selection for EIW (Fig. 4). The shape of the cross-section can inform strategies for tiling filaments via toolpath design, and it can provide some indication of the surface roughness of the printed part. If filaments exhibit irregularities or sharp edges such as the fin shape in Fig. 1B, those could translate into surface roughness. Fig. 4 also demonstrates z positioning accuracy, but those measurements are discussed in more quantitative detail in Section 3.3.

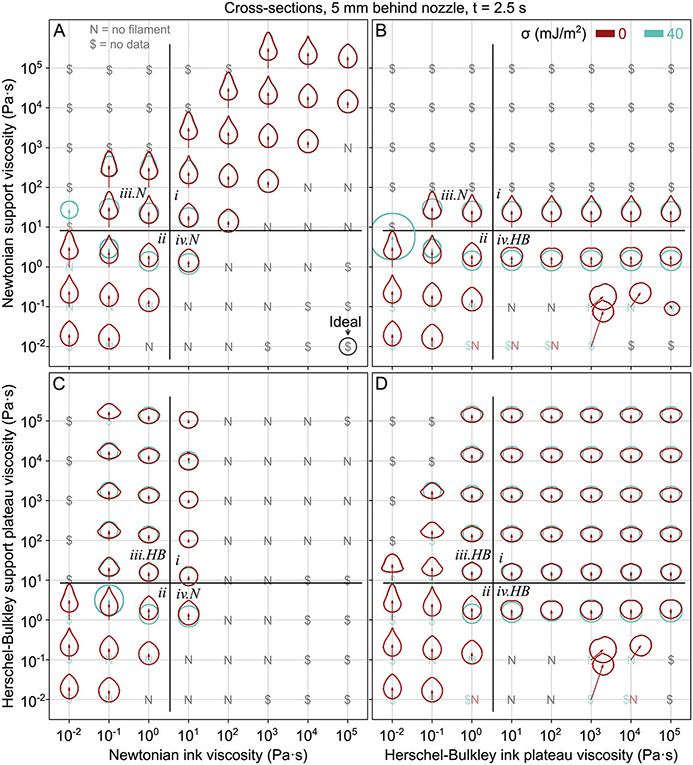
Fig. 4.

Cross-sections of filament interfaces, 5 mm behind the nozzle after 2.5 s of extrusion. Arrows indicate the displacement between the intended center of the filament and the actual centroid. Regions i, ii, iii, and iv indicate trends in controlling variables. iii.N contains Newtonian supports, and iii.HB contains Herschel–Bulkley supports. iv.N contains Newtonian inks, and iv.HB contains Herschel–Bulkley inks. If there is no “$” or “N”, the 40 mJ m⁻² cross-section is behind the 0 mJ m⁻² cross-section. (A) Newtonian ink and support. The “ideal” cross-section is a circle with the inner diameter of the nozzle, where the top of the filament is at the bottom of the nozzle. This ideal applies to all four quadrants of the figure. (B) Herschel–Bulkley ink and Newtonian support. (C) Newtonian ink and Herschel–Bulkley support. (D) Herschel–Bulkley ink and support.

Fig. 4 shows cross-sections of filaments collected 5 mm behind the nozzle after 2.5 s of flow. For many of these simulations, the cross-section changes over time and over the length of the filament, so these cross-sections should not be considered to be at steady state. Steady state is discussed in greater detail in Section 3.4. These cross-sections are collected at a position that is far enough from the nozzle that most filaments have left the region near the nozzle where the filament changes rapidly.

Many of the trends discussed in Section 3.1 are reflected in Fig. 4. As such, it is possible to slice these maps into the same regions from Fig. 3B. In region i, at high ink and support viscosities, each map exhibits different cross-sections (Fig. 4A-D). In region ii, at low ink and support viscosities, all maps show the same cross-sections (Fig. 4A-D). In region iii, at low ink viscosities and high support viscosities, the Newtonian supports produce the same cross-sections (Fig. 4A and B: iii.N), and the Herschel–Bulkley supports produce the same cross-sections (Fig. 4C and D: iii.HB). In region iv, at high ink viscosities and low support viscosities, the Newtonian inks produce the same cross-sections (Fig. 4A and C: iv.N), and the Herschel–Bulkley inks produce the same cross-sections (Fig. 4B and D: iv.HB). Across all regions, non-zero surface tensions produce more circular cross-sections, particularly at low viscosities or with Herschel–Bulkley fluids.

In region i in Newtonian supports (Fig. 4A and B) and in region ii for all materials (Fig. 4A-D), most filaments exhibit fin-shaped cross-sections, where the top of the filament is pinched and elongated vertically. This produces a sharp edge at the top of the filament which could result in surface roughness on the final part. With decreasing viscosity ratio, the top of the filament becomes taller, but not monotonically sharper. In region i in Herschel–Bulkley supports, most filaments exhibit rounder cross-sections, with a shallow point at the top of the filament at zero surface tension (Fig. 4C and D).

In region iii, Herschel–Bulkley inks behave like Newtonian inks, but Herschel–Bulkley supports behave differently from Newtonian supports. In region iii.N, where the support is Newtonian, all inks produce the same fin-shaped cross-sections at zero surface tension and rounder cross-sections at non-zero surface tension (Fig. 4A and B). In region iii.HB, where the support is Herschel–Bulkley, all inks produce the same short and wide cross-sections (Fig. 4C and D). At zero surface tension, there is either a shallow sharp edge at the top of the filament (in viscous inks) or sharp edges at the sides at the filament (in low-viscosity inks). At non-zero surface tension, cross-sections are nearly circular. One could imagine the filaments in region iii.HB as if the filaments in region iii.N had been dropped into a half-pipe.

In region iv, Herschel–Bulkley supports behave like Newtonian supports, but Herschel–Bulkley inks behave differently from Newtonian inks. In region iv.N, where the ink is Newtonian, most of the region contains defects like curling and jetting. However, the one filament that is generated has a pointed top edge at zero surface tension and a round cross-section at non-zero surface tension (Fig. 4A and C). In region iv.HB, where the ink is Herschel–Bulkley, most of the region is still composed of defects including spiraling and excessive z displacement. However, the filaments that are generated are round with a flat top at zero surface tension and round at non-zero surface tension (Fig. 4B and D). One could imagine the filaments in region iv.HB as if a plate had been placed on top of the filaments in region iv.N.

3.3. Quantifying cross-sections

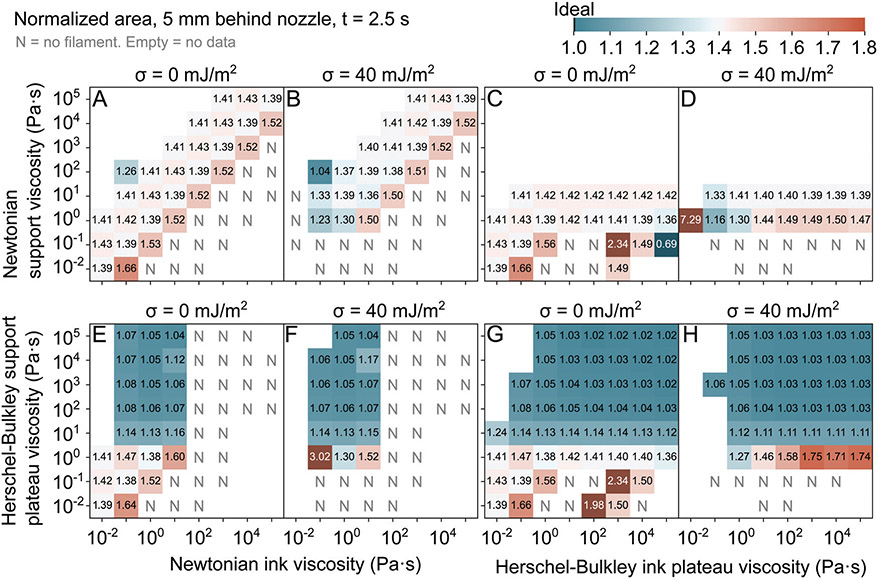
There are a few ways to directly quantify the cross-sections shown in Fig. 4. One is the velocity of the filament, which is an indicator of the x–y positioning accuracy of the filament. Fig. S20 (ESI‡) shows the average velocity throughout the filament cross-section, normalized by the translation speed of the bath. A related metric is the cross-sectional area, which is indicative of printing resolution. Toolpath designs must take into account the actual cross-sectional area of the printed filament in order to avoid printing too much or too little ink to fill the intended space. Fig. 5 shows the area of the cross-sections shown in Fig. 4, normalized by the area of the inside of the nozzle. The normalized area follows an inverse relationship with the normalized cross-section speed, with some exceptions (Fig. S21, ESI‡). As such, within this discussion, wherever the area is ideal, the speed is also ideal, and where the area is large, the speed is slow. Cross-sectional areas far behind the nozzle are shown in Fig. 5. The most ideal cross-sectional areas occur where both the ink and support are Herschel–Bulkley fluids with high plateau viscosities (Fig. 5G and H).

Fig. 5.

Cross-sectional area of filaments, normalized by the inner area of the nozzle. (A and B) Newtonian ink and support at surface tensions of (A) 0 mJ m⁻² and (B) 40 mJ m⁻². (C and D) Herschel–Bulkley ink and Newtonian support at surface tensions of (C) 0 mJ m⁻² and (D) 40 mJ m⁻². (E and F) Newtonian ink and Herschel–Bulkley support at surface tensions of (E) 0 mJ m⁻² and (F) 40 mJ m⁻². (G and H) Herschel–Bulkley ink and support at surface tensions of (G) 0 mJ m⁻² and (H) 40 mJ m⁻².

Where both fluids are Newtonian, all cross-sectional areas are larger than ideal, mostly between 1.3 to 1.5 times the intended area (Fig. 5A and B). Trends in area are consistent with the trends observed in Sections 3.1 and 3.2. The cross-sectional area depends on viscosity ratio (Fig. 5A and B). Cross-sectional areas are largest at a high viscosity ratio (ink viscosity/support viscosity = 10). Cross-sectional areas do not change at viscosity ratios from 10⁻² to 10⁰. Although there is limited data below viscosity ratios of 10⁻², the one measured area is the smallest within the Newtonian–Newtonian regime. Where the surface tension is 40 mJ m⁻², the cross-sectional area also decreases with decreasing support viscosity and ink viscosity (Fig. 5B). These trends continue in the low-viscosity region (ii) for all maps (Fig. 5C-H).

Where the ink is a Herschel–Bulkley fluid, and the support is Newtonian, all cross-sectional areas are still larger than ideal, between 1.4 to 1.5 times the intended area (Fig. 5C and D). At high ink plateau viscosities, cross-sectional areas depend weakly on the ink viscosity, support viscosity, and surface tension. At zero surface tension, all simulated cross-sectional areas are similar (Fig. 5C). At a surface tension of 40 mJ m⁻², the cross-sectional area is lower in more viscous supports, and it decreases with decreasing ink viscosity (Fig. 5D). In some cases, increasing the surface tension increases the cross-sectional area, and in other cases, it decreases the area. It is possible that at higher support viscosities where the simulation was too expensive, filaments could have smaller areas like those produced in Newtonian inks at low viscosity ratios.

Where the ink is Newtonian and the support is a Herschel–Bulkley fluid, at high support plateau viscosities, cross-sectional areas are close to ideal, with areas ranging from 1.04 to 1.17 times the intended area (Fig. 5E and F). Cross-sectional areas primarily vary with the viscosity of the ink and do not vary considerably with surface tension. Where both the ink and support are Herschel–Bulkley fluids, the cross-sectional areas in the high-viscosity region are smallest out of all simulated filaments, with areas ranging from 1.02 to 1.14 times the intended cross-sectional area (Fig. 5G and H). Above a support plateau viscosity of 10 Pa s (region i), cross-sectional areas are very consistent, regardless of ink viscosity, support viscosity, and surface tension. At high support plateau viscosities and low ink plateau viscosities (region iii), the cross-sectional area slightly increases (Fig. 5G). At low support plateau viscosities and high ink plateau viscosities (region iv), areas increase greatly, particularly for the non-zero surface tension (Fig. 5G and H).

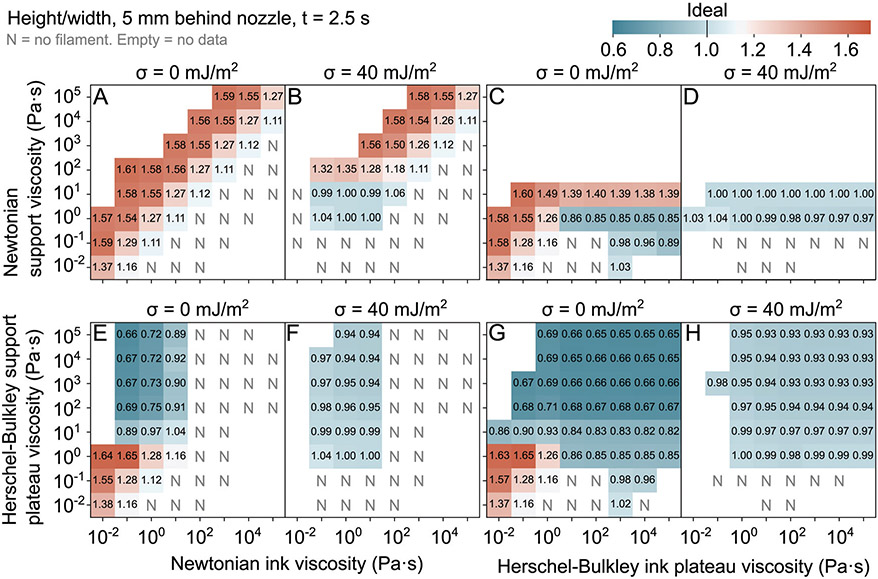
Another way to quantify the cross-section is the aspect ratio, defined here as the height of the filament divided by the width (Fig. 1B). The aspect ratio provides useful information about the inter-layer and intra-layer resolution. A large aspect ratio will provide finer resolution within a layer than between layers. A small aspect ratio will provide finer resolution between layers than within the layer. As such, because interfaces between filaments influence the mechanical properties of the part, and functional properties of the part could depend on resolution, an aspect ratio of 1 should produce the most isotropic material.

Aspect ratios are shown in Fig. 6. The most ideal aspect ratios occur in Herschel–Bulkley supports or at low Newtonian support viscosities, with a non-zero surface tension (Fig. 6B, D, F and H). Again, familiar themes emerge. In most cases, Herschel–Bulkley fluids behave like Newtonian fluids at low plateau viscosities (region ii), leading to similarities in aspect ratio across Fig. 6. In Fig. 6A and B and the Newtonian-like regimes, the filament aspect ratio increases with decreasing viscosity ratio. At a surface tension of 40 mJ m⁻², the aspect ratio decreases to 1 at low support viscosities. In Herschel–Bulkley inks, the aspect ratio depends on the support viscosity and surface tension (Fig. 6C and D). The non-zero surface tension produces an aspect ratio of 1 (Fig. 6D). At zero surface tension, the aspect ratio increases with increasing support viscosity, where some aspect ratios are too low, and others are too high (Fig. 6C).

Fig. 6.

Aspect ratio of filaments, defined as maximum height divided by maximum width. (A and B) Newtonian ink and support at surface tensions of (A) 0 mJ m⁻² and (B) 40 mJ m⁻². (C and D) Herschel–Bulkley ink and Newtonian support at surface tensions of (C) 0 mJ m⁻² and (D) 40 mJ m⁻². (E and F) Newtonian ink and Herschel–Bulkley support at surface tensions of (E) 0 mJ m⁻² and (F) 40 mJ m⁻². (G and H) Herschel–Bulkley ink and support at surface tensions of (G) 0 mJ m⁻² and (H) 40 mJ m⁻².

Herschel–Bulkley supports produce low aspect ratios. At high support plateau viscosities, with Newtonian inks, at a surface tension of 40 mJ m⁻², nearly circular filaments are produced (Fig. 6F). At zero surface tension, aspect ratios decrease with decreasing ink viscosity and are consistently too low (Fig. 6E). The most ideal aspect ratios occur at moderate support plateau viscosities, at 10 Pa s. Where both fluids are Herschel–Bulkley, aspect ratios are very consistent across the high-viscosity region (Fig. 6G and H). At zero surface tension, filaments are short and wide, with an aspect ratio of 2/3. With decreasing support viscosity, the aspect ratio increases, not quite to 1 (Fig. 6G). At a surface tension of 40 mJ m⁻², aspect ratios are nearly 1 in the high-viscosity region, increasing slightly to 1 at a support plateau viscosity of 1 Pa s (Fig. 6H).

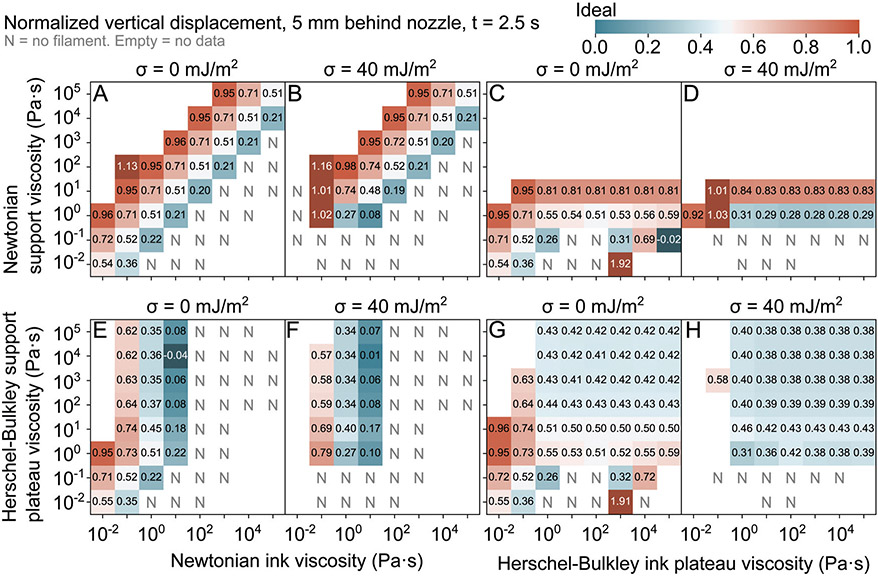
The final way we will quantify the cross-section is the vertical displacement, shown in Fig. 7. Here, the vertical displacement is defined as the vertical distance between the bottom of the filament and the intended bottom of the filament, normalized by the inner diameter of the nozzle (Fig. 1B). The ideal displacement is zero, but almost all simulated filaments rise above the intended position. A displacement greater than 1 nozzle diameter would be catastrophic, as the nozzle would need to dig into existing layers to write new layers. A lesser displacement could be workable, depending on how the flow field around the nozzle interacts with existing written layers.

Fig. 7.

Vertical z displacement of filaments, defined as the vertical distance between the bottom of the filament and the ideal position of the bottom of the filament, normalized by the nozzle diameter. (A and B) Newtonian ink and support at surface tensions of (A) 0 mJ m⁻² and (B) 40 mJ m⁻². (C and D) Herschel–Bulkley ink and Newtonian support at surface tensions of (C) 0 mJ m⁻² and (D) 40 mJ m⁻². (E and F) Newtonian ink and Herschel–Bulkley support at surface tensions of (E) 0 mJ m⁻² and (F) 40 mJ m⁻². (G and H) Herschel–Bulkley ink and support at surface tensions of (G) 0 mJ m⁻² and (H) 40 mJ m⁻².

The best vertical displacement occurs with Newtonian inks with a 10 Pa s viscosity and a Herschel–Bulkley support with a high plateau viscosity (Fig. 7E and F). Elsewhere, displacements are too high. Again, familiar patterns occur. When both fluids are Newtonian or follow Newtonian behavior, the vertical displacement increases with decreasing viscosity ratio (Fig. 7A and B). At a surface tension of 40 mJ m⁻², the vertical displacement decreases with decreasing support viscosity (Fig. 7B). When the ink follows Herschel–Bulkley behaviors and the support is Newtonian, increasing the support viscosity increases the vertical displacement (Fig. 7C and D). At the lower support viscosity, increasing the surface tension decreases the vertical displacement.

In Herschel–Bulkley supports with Newtonian inks, the vertical displacement decreases with increasing ink viscosity. At the highest ink viscosity that produces filaments, at high support viscosities, the vertical displacement is close to ideal (Fig. 7E and F). Surface tension does not have a large effect in this regime. When both fluids are Herschel–Bulkley fluids, above a support plateau viscosity of 10 Pa s and an ink plateau viscosity of 100 Pa s, all vertical displacements are similar, around 0.4 nozzle diameters (Fig. 7G and H). Increasing the surface tension slightly decreases the vertical displacement.

Summarizing the four quantitative metrics, one can establish critical values where each cross-section can be considered ideal. If we establish that “ideal” corresponds to a normalized velocity between 0.9 to 1, a normalized area between 1 to 1.1, an aspect ratio between 0.9 to 1.1, and a normalized vertical displacement between −0.1 to 0.1, there is a very small region where all four criteria are met (Fig. S22, ESI‡). This occurs where the ink is Newtonian and has a viscosity of 10 Pa s, and the support is Herschel–Bulkley and has a plateau viscosity above 10 Pa s, excluding 10⁴ Pa s. Alternatively, three criteria are met (all except vertical displacement) where the support is Herschel–Bulkley and has a plateau viscosity above 10 Pa s, the surface tension is 40 mJ m⁻², and either the ink is Newtonian and has a viscosity below 10² Pa s, or the ink is Herschel–Bulkley.

3.4. Filament stability

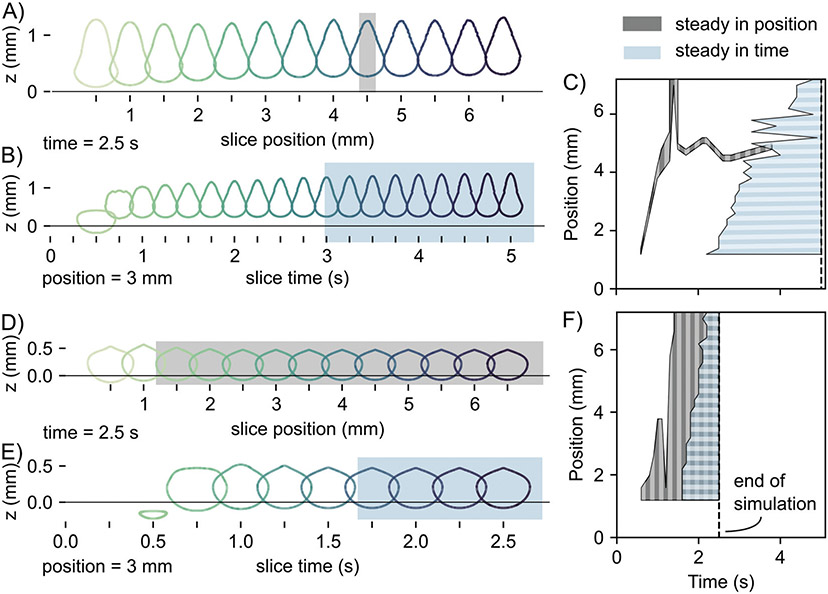
Recall that the cross-sections collected in Fig. 4-7 are taken at an arbitrary position along the filament and time after extrusion. These cross-sections are not collected at a position or time where filaments reach steady state because many filaments never reach a steady state. Consider Fig. 8A and B, which shows cross-sections of a single filament collected at varying positions and times. It is apparent that at a given time, the cross-sections are not consistent across the entire length of the filament, and at a given position, the cross-sections are not consistent across all times. Here, we systematically quantify stability by tracking one variable, the vertical filament position (as plotted in Fig. 7). Stability is measured here using two qualifiers: “steady in time” and “steady in position.” At a given position and time, the filament is steady in time if the range of vertical positions is less than 1% of the nozzle diameter within a span of 1 s centered around the given time (blue regions in Fig. 8). The filament is steady in position if the range of the vertical positions is less than 1% of the nozzle diameter within a span of 1 mm centered around the given position (gray regions in Fig. 8). In short, “steady in time” means that the filament isn’t changing over time, and “steady in distance” means that the filament is consistent along its length. Of course, these designations are arbitrary. It is possible for a region to be labeled steady, even though the cross-sections change considerably over the entire region, either because they vary slowly, or because they vary in some other metric like aspect ratio (e.g., in Fig. 8B). This analysis is only meant to give some indication of the relative stability of different filaments.

Fig. 8.

Stability of two example filaments printed at a surface tension of 0 mJ m⁻², a support Newtonian or plateau viscosity of 10² Pa s, and a Newtonian ink viscosity of 10⁰ Pa s. Stability is defined here using the position of the bottom of the filament. (A–C) Newtonian support (D–F) Herschel–Bulkley support. (A and D) Filament cross-sections at 2.5 s as a function of position along the length of the filament. Highlighted regions indicate where the filament is steady in position. (B and E) Filament cross-sections 3 mm behind the nozzle as a function of extrusion time. Highlighted regions indicate where the filament is steady in time. (C and F) Regions where the filament is steady. Steady in position means that at a given time, the filament cross-section doesn’t change within the plotted span in position. Steady in time means that at a given position, the filament cross-section doesn’t change over the plotted span in time.

The main variable that influences stability is whether the support is Newtonian or a Herschel–Bulkley fluid (Fig. S23-S30, ESI‡). In Fig. 8A-C, the support is Newtonian. There is a very narrow region in position–time space where the filament is steady in position, and the filament does not start to become steady in time until around 2.5 s. There is a very small region where the filament is both steady in position and steady in time. In contrast, in Fig. 8D-F, the Newtonian support is replaced by a Herschel–Bulkley support. There is a large region in position–time space where the filament is steady in position, extending to the end of the filament by 1.5 s. The region where the filament is steady in time starts earlier, around 2 s, and the steady-in-time region extends to the end of the filament sooner. As such, yielding in the sheared support results in a filament that is more consistent over time and position. Increasing the surface tension can also slightly expand the steady zone within the simulated timescale, most clearly visible in Fig. S29 and S30 (ESI‡). This small improvement in reaching an arbitrary steady-state does not mean that the filament is energetically stable at non-zero surface tension. At non-zero surface tensions, the filament can still rupture over long time scales due to Plateau–Rayleigh instabilities. The greater significance is that the non-zero surface tension helps the filament to overcome the difficult barrier of short term consistency over time and the length of the filament.

3.5. Spatial variations in speed and viscosity

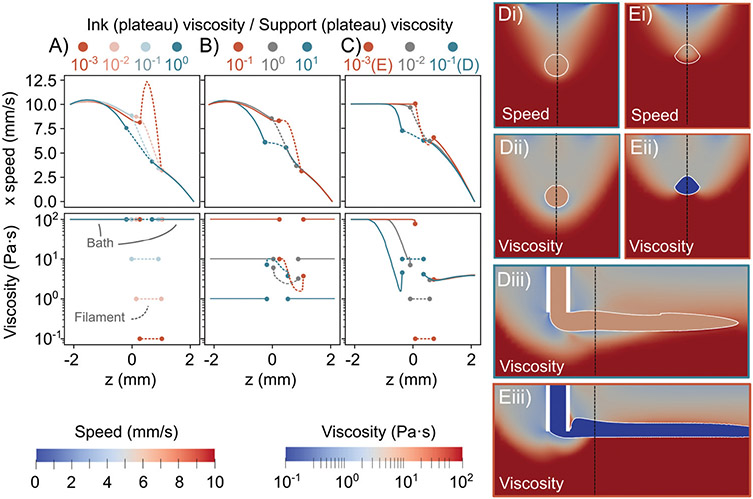
Spatial variations in speed within the print bath can help to explain variations in x–y positioning accuracy between filaments. The boundary conditions of these simulations establish that the bottom of the bath has a fixed speed of 10 mm s⁻¹, and the top of the bath can be any speed. Without the nozzle, the velocity of the bath would decay from the bottom to the top due to momentum diffusion.⁵² Simulations without the nozzle show a decay in speed from the bottom to the top, with the bath approaching a constant velocity with increasing time (Fig. S47, ESI‡). However, the speed decay near the nozzle is not solely due to momentum diffusion in the bath. If we assume that the bath is an infinite fluid bounded only on its bottom plane by a moving plate, the velocity of the fluid at a given point in the bath would depend on the bath viscosity, the distance of the point from the plate, and the time since the plate began to move.⁵² Fig. 9A-C shows the x component of the fluid velocity collected along line traces from the bottom of the bath to the top, 1.5 mm behind the nozzle. Even where the bath viscosity is held constant, the speed profiles vary (Fig. 9). Thus, the nozzle and filament influence the speed profiles within the bath.

Fig. 9.

(A–C) Line profiles of the velocity along the stage translation direction (x) and viscosity, from the bottom to the top of the bath, 1.5 mm behind the nozzle after 1 s of flow, where the surface tension is 0 mJ m⁻². The plateau viscosity is used for the viscosity ratio in Herschel–Bulkley fluids. (A) Newtonian ink and support. (B) Herschel–Bulkley ink and Newtonian support. The ink plateau viscosity is 10¹ Pa s. (C) Newtonian ink and Herschel–Bulkley support. The support plateau viscosity is 10² Pa s. (D and E) Speed (i) and viscosity (ii, iii) cross-sections in the y–z plane (i, ii) and x–z plane (iii) for a Newtonian ink and Herschel–Bulkley support with a plateau viscosity of 10² Pa s at an ink viscosity of (D) 10¹ Pa s and (E) 10⁻¹ Pa s. Dashed lines indicate locations of slices and of line profiles. White regions indicate the ink–support interface and nozzle.

Below the filament, where the support is Newtonian (Fig. 9A and B), the support slightly accelerates, then decelerates toward the printed filament. In contrast, in Herschel–Bulkley supports, the velocity stays constant from the bottom of the bath, then steeply drops just below the filament (Fig. 9C). Drops in velocity are the largest at the highest viscosity ratios, i.e. where the ink is more viscous than the support (Fig. 9A-C). Correspondingly, the Herschel–Bulkley support viscosity decreases below the filament (Fig. 9C). At the highest plotted viscosity ratio (10⁻¹), the support viscosity drops below the ink viscosity and then steeply increases toward the ink viscosity just below the filament.

Within the filament, the speed further decays. Opposite of the decay below the filament, the decay within the filament becomes steeper as the viscosity ratio decreases, i.e. the support is much more viscous than the ink (Fig. 9A-C). At a low viscosity ratio of 10⁻³ where both fluids are Newtonian, the speed actually peaks at the center of the filament (Fig. 9A). In contrast, in the Herschel–Bulkley support at the same low viscosity ratio, the speed reaches a local minimum at the center of the filament (Fig. 9C). For Herschel–Bulkley inks, the ink viscosity also varies within the filament (Fig. 9B). In all cases for these profiles close to the nozzle, the local ink viscosity is lower than the ink plateau viscosity throughout the filament. If the ink plateau viscosity is greater than the support viscosity, the center of the filament is more viscous than the surface. Otherwise, the surface is more viscous than the center.

Above the filament, velocities decay to 0 (Fig. 9A-C). Velocities for all plotted Newtonian supports of various viscosities converge to the same profile above the filament (Fig. 9A and B). In Herschel–Bulkley supports, the velocities decay more steeply above the filament than in Newtonian supports (Fig. 9C). Regardless of the ink viscosity, Herschel–Bulkley supports of the same plateau viscosity converge to the same viscosity profile above the filament, where the viscosity decreases slightly above the filament, then increases slightly but not all the way to the plateau viscosity (Fig. 9C). Note that speeds do not decrease to zero everywhere on the top plane of the bath; only in the wake of the nozzle (Fig. S39-S46, ESI‡). The wake is correlated with a downward flux of support behind the nozzle for the quasi-free surface and occurs with and without injected ink (Section S1, ESI‡). In the deep bath, the wake is much smaller, and fluid flows upwards behind the nozzle (Section S1, ESI‡).

The variations in viscosity shown in the line profiles in Fig. 9B and C can be further contextualized by examining the bath yield surface. In Fig. 9D and E, velocity maps and yielded zones are shown in the y–z plane and in the x–z plane, where the ink is Newtonian, and the support is Herschel–Bulkley. In Fig. 9D, where the ink viscosity is high, the low-velocity zone and yielded zone extend below the filament. In Fig. 9E, where the ink viscosity is low, the low-velocity zone begins within the filament, and the yielded zone is dimpled around the filament. The yielded zone can also be viewed from the side, along the length of the filament. The zone directly around the nozzle is yielded, and after some length, the bottom of the yielded zone intersects with the bottom of the filament. In the lower-viscosity ink, the bottom of the yielded zone hits the filament sooner (Fig. 9D and E). This smaller yielded zone is beneficial for maintaining filaments; if the yielded zone is very large, a droplet forms at the nozzle tip (Fig. S36, ESI‡).

Yielding could help to explain differences in cross-sectional shape between the two filaments. Within the yielded zone, the support viscosity is between 1 and 10 Pa s, with local variations. In Fig. 9D, the filament is more viscous than the yielded support, and as such, it can transfer stress to the yielded zone. In Fig. 9E, the filament is less viscous than the yielded support and dissipates stress. Because it is not transferring stress to the support below the filament, the yielded zone shrinks and dimples underneath the filament. Note that because the dimple in Fig. 9E also appears when the surface tension is 40 mJ m⁻² and the filament cross-section is round, the dimple in the yield surface comes from viscous dissipation, not from the filament shape (Fig. S32, ESI‡). Further, because the yield surface shape is independent from the support plateau viscosity but dependent on the local ink viscosity (Fig. S32 and S34, ESI‡), the yielded zone shape depends on viscous dissipation in the ink. While there is a direct correlation between the yielded zone shape and the filament shape at a single surface tension, capillarity can also influence the filament shape (Fig. S32 and S34, ESI‡).

4. Discussion

This paper examines how printing performance depends on yielding, the viscosity ratio, the support viscosity, the ink viscosity, and surface tension. First, consider yielding. The Herschel–Bulkley fluids in this study yield to a viscosity between 1 Pa s to 10 Pa s, with local variations. Notably, if the strain rate is assumed to be the translation speed divided by the nozzle outer diameter, or the flow speed divided by the nozzle inner diameter, the strain rate is between 11 s⁻¹ and 17 s⁻¹, and the yielded viscosity is between 1.4 Pa s and 1.9 Pa s. As such, any Herschel–Bulkley fluid that has a plateau viscosity at or below 1 Pa s never yields, so it behaves like a Newtonian fluid. Hence, region ii, at low viscosities, is the same for every map in this paper (Fig. 2-7), with only minor variations observable in the quantitative measurements (Fig. 5-7).

Likewise, in region iii, at low ink viscosities and high support viscosities, the Herschel–Bulkley ink does not yield. As a result, the two Newtonian supports behave the same (Fig. 2 and 4A, B: iii.N), and the two Herschel–Bulkley supports behave the same (Fig. 3 and 4C, D: iii.HB). Again, there are minor variations observable in the quantitative measurements at the viscous edge of region iii, at an ink viscosity of 1 Pa s (Fig. 5-7). Ample yielding in the bath further simplifies this region. When a nozzle travels through a viscoelastic bath, it produces a yielded zone, and the bath velocity is matched to the nozzle velocity near the nozzle.^13,30,53 Below the nozzle, the printed filament also yields the bath, as demonstrated by the change in yielded zone size with ink viscosity (Fig. S36, ESI‡). At the print speed used in these simulations, the yielded zone in the support is large and tends to reach a viscosity of 1 Pa s to 10 Pa s, so within region iii.HB, the Herschel–Bulkley supports within this region all tend to behave like supports with a plateau viscosity of 10 Pa s to 100 Pa s. As such, while one could view region iii.HB as depending primarily on the ink viscosity, one could also view region iii.HB as depending on the viscosity ratio, defined as the ink viscosity divided by the yielded support viscosity. Further, the lack of support plateau viscosity dependence in region iii.HB indicates that while the shape of the yielded zone might matter, the properties of the unyielded support do not influence the filament shape. However, high support plateau viscosities result in earlier filament stability, so the properties of the unyielded support are still relevant to print quality (Fig. S27 and S28, ESI‡).

Region iv, at high ink viscosities and low support viscosities, is more complicated than region iii. The ink does not yield as broadly as the support, so this region cannot be simplified as easily. Inside the nozzle, the ink yields to 1 Pa s to 10 Pa s near the nozzle wall, where the shear rate is high, but the ink only yields to 10 Pa s to 100 Pa s at the center of the nozzle where the shear rate is low, so the yielded ink comes out of the nozzle at a higher viscosity than the yielded Herschel–Bulkley support (Fig. S37 and S38, ESI‡). While the support is stressed by a rigid nozzle, the extruded ink must be stressed by the support. If the support is not viscous enough, it does a poor job of transferring stress to the ink, so the center of the extruded filament remains close to its plateau viscosity (Fig. S37 and S38, ESI‡). As a result, while region iv is like region iii because it can be split into iv.HB and iv.N based on the ink rheology, the behaviors within iv.HB are more complicated than the behaviors in iii.HB. Unlike the Herschel–Bulkley supports in region iii.HB, Herschel–Bulkley inks in region iv.HB do not all behave like Newtonian inks of a certain viscosity. Rather, region iv.HB could be further split into two sub-regions based on support viscosity. At a support viscosity of 1 Pa s, most of the filament yields, so all Herschel–Bulkley inks at this support viscosity behave similarly (Fig. 2B and 3B). One could view this row as having inks that all have similar viscosities, and as such, similar viscosity ratios, where the viscosity ratio is defined as the yielded ink viscosity divided by the support viscosity. At the lower support viscosities, the filaments do not fully yield, so all filaments have different viscosities. One could view this region as following the viscosity ratio, defined roughly as the ink plateau viscosity divided by the support viscosity (Fig. 2B and 3B).

Having examined the yielding in the bath and filament, one can understand why region i, at high viscosities, is different in every map (Fig. 4). Where both fluids are Newtonian, the viscosity ratio behavior established at low viscosities is still valid. In a Newtonian support, Herschel–Bulkley inks behave differently from Newtonian inks because the high-viscosity support yields the ink, such that all inks behave as if their viscosity ratio is the yielded ink viscosity divided by the support viscosity, although in some cases, the yielding is minimal. With a Newtonian ink, Herschel–Bulkley supports behave differently from Newtonian supports because the nozzle and filament yield the support, such that all supports trend as if their viscosity ratio is the ink viscosity divided by the yielded support viscosity, and the shape of the yield surface influences the flow field and thus the filament shape. When both ink and support are Herschel–Bulkley, they behave differently from the other three cases because the nozzle and filament yield the support, and the support yields the ink in return, such that both fluids reach 1 Pa s to 10 Pa s and locally match each other’s viscosities in region i (Fig. S34 and S38, ESI‡). As such, throughout region i where both fluids are Herschel–Bulkley, the local viscosity ratio is 1, and the shape of the yield surface is consistent, resulting in consistent filament shapes.

The four quadrants of Fig. 2-4 can guide estimation of filament morphology where the simulation was too computationally expensive to run (Fig. S49, ESI‡). For example, in region iii.N, most of the region is too computationally expensive to simulate when the ink is Herschel–Bulkley, but more filaments are simulated when the ink is Newtonian. If we assume that the Herschel–Bulkley ink continues to behave like a Newtonian ink in this region, we can assume that all of iii.N is the same between Fig. 4A and B. Further, in a Newtonian support and Herschel–Bulkley ink, because region i follows the filament morphology in region iii.N at an ink plateau viscosity of 1 Pa s, one could assume that the next two rows of region i in Fig. 4B at support viscosities of 10² and 10³ Pa s are also filaments, following the filament shapes at viscosity ratios of 10⁻² and 10⁻³ in Fig. 4A.

Understanding the relationship between yielding and the viscosity ratio, let’s move on to the influence of viscosity ratio, support viscosity, ink viscosity, and surface tension. Here, “viscosity ratio” always refers to the viscosity of the injected phase (ink) divided by the viscosity of the encapsulating phase (support). Previous work on injection of fluids into immiscible, non-zero surface tension fluids (without the moving bath) has shown that the viscosity ratio and the Weber number control the morphology of the injected material.³⁵ At moderate Weber numbers, high viscosity ratios produce droplets attached to the nozzle, moderate viscosity ratios produce filaments that break into droplets, and low viscosity ratios produce continuous filaments.³⁵ Similarly, numerical analysis of cylindrical filaments has shown that the filaments retract toward the nozzle with a speed that scales with the surface tension divided by the support viscosity, and the filament ruptures sooner as the viscosity ratio decreases.³⁶ Both of these trends are consistent with the results in this paper. Consider region ii, where the support is Newtonian and the surface tension is 40 mJ m⁻² (Fig. 2). Consider the vertical columns in region ii. At non-zero surface tension, the filament retracts toward the nozzle, and it retracts faster at lower support viscosities. Consider the columns or downward sloping diagonals in region ii. As the viscosity ratio increases, extrudates transition from continuous filaments, to filaments that rupture, to droplets that cling to the nozzle. As such, these trends in rupture and retraction can be explained by previously established theory,^35,36 without considering movement of the bath. Note that the surface tension divided by the support viscosity is a component of the capillary number, indicating that the retraction speed may depend on a balance between viscous forces and surface tension. However, the capillary number and viscosity ratio alone cannot explain all of the effects in this work, as is visible in Fig. S50 (ESI‡).

In contrast, some other trends require consideration of the 3D printing geometry. Much of the zero surface tension filament geometry can be explained intuitively using the viscosity ratio (Fig. 2). If the support is much more viscous than the ink, the ink cannot penetrate the bath and is instead scraped along the underside of the nozzle and forced upwards, leading to flat filament ends and high vertical displacements at low viscosity ratios. Similar, large vertical displacements have been reported in experimental studies conducted at low viscosity ratios.^11,17,23,33 Additionally, scraping under the nozzle is apparent in experimental studies of filaments²³ and droplets.³² As the ink becomes much more viscous than the support, it drives deeper into the bath, until it hits the bottom of the bath. This is consistent with previous reports that filaments drag with the nozzle rather than extruding into the bath at high viscosity ratios.^11,13 However, the filament does not monotonically displace lower and lower into the bath with increasing viscosity ratio. At a viscosity ratio of 10², the filament curls over on itself. Spatial variations in velocity and pressure help to explain this (Fig. S1 and S43, ESI‡). Below the nozzle, the bath is confined, which causes the bath to accelerate (Fig. 9A and B). In the nozzle’s wake, very close to the nozzle and the top of the bath, the bath velocity decays to zero (Fig. 9A-C). As such, the support on top of the filament moves slowly, and the support below moves quickly, curling the filament. Additionally, there is a pressure differential across the nozzle, such that the pressure is lower in the nozzle wake than below and ahead of the nozzle. The pressure differential would pull fluid toward the back of the nozzle. This low pressure zone on the back of the nozzle may be why droplets travel up the back of the nozzle at low support viscosities. If the filament drives deeply into the bath, it confines the bath more and causes a greater acceleration and thus larger speed difference between the support below and above the nozzle, so the filament curls into the low pressure zone just behind the nozzle. If the filament does not penetrate as deeply, the acceleration in the gap under the filament is lower, and the filament curls less, never entering the low pressure zone just behind the nozzle, so the support material outside of the low pressure zone is able to catch the filament and redirect it downstream.

The fin shape that occurs at low viscosity ratios could come from the shape of the flow field. As the nozzle travels through the bath, the support fluid is displaced. In Newtonian supports, the support flows around the nozzle in the x–y plane and converges behind the nozzle (Fig. S48, ESI‡).⁵⁴ If the filament is in that space, particularly if it is already displaced upward due to squeezing below the nozzle at low viscosity ratios, the converging support compresses the filament. If the support is much more viscous than the ink, the support compresses the filament more. Because some of the support near the bottom of the nozzle is able to displace under the nozzle instead of around the sides, this compression is stronger higher up in the bath. Thus, filaments at low viscosity ratios are squeezed into a fin shape. Filaments in Herschel–Bulkley fluids escape this fate because local yielding changes the shape of the flow field. Instead of flowing within the x–y plane and converging behind the nozzle to squeeze the filaments horizontally, streamlines in Herschel–Bulkley fluids deflect in z, flowing upward ahead of the nozzle and downward behind the nozzle, compressing the filaments vertically (Fig. S48, ESI‡). Because this streamline shape is not described in two-dimensional simulations,^54,55 these three-dimensional simulations are necessary for understanding 3D printing, particularly in Herschel–Bulkley fluids. One might also note that because some of the simulated filaments break symmetry along the x–z plane (region iv.HB), i.e. they bend left and right, the full volume must be simulated, and symmetry along the center of the filament cannot be assumed. Consistent with these findings, Uchida, et al. demonstrated that the aspect ratio of printed filaments increases with increasing support viscosity and decreasing ink viscosity.¹¹ Similarly, in ref. 7, filaments printed into “self-healing” hydrogels are short and wide, like the cross-sections in Fig. 4C and D. Previous work which reported aspect ratios greater than one may have been conducted at small local viscosity ratios, although high extrusion speed to translation speed ratios could have played larger roles.^6,17,30 Notably, circular filaments are achieved in yield stress fluid supports in ref. 20 and in ref. 6, where the flow speed is close to the translation speed.

The shape of the flow field can also help to explain stability, cross-sectional areas, and x–y positioning. The nozzle wake is smaller in Herschel–Bulkley supports than Newtonian supports. The full-speed support fluid above the filament in the Herschel–Bulkley fluid could help to stabilize the filament by removing the velocity gradient across the filament. Naturally, fast-moving support would help to draw the filament at the bath translation speed, ensuring accurate x–y positioning and cross-sectional areas. Alternatively, one might note that the cross-sectional area decreases at low viscosity ratios in Newtonian baths (Fig. 5A and B). In this case, the interior of the filament travels much faster than its surface (Fig. 9A and Fig. S43, ESI‡), mirroring the parabolic flow profile inside of the nozzle. While this flow profile does not help with stability, it does improve x–y positioning.

Capillarity has a straightforward influence on filament shape, but its implications for stability place an important caveat on all of the noted benefits of a non-zero surface tension. Where the local viscosities of the ink and support at the filament–bath interface are sufficiently low, capillarity overcomes viscous dissipation, and the filament cross-section becomes circular, reducing the filament surface area. Particularly at lower ink viscosities and support viscosities, the filament starts to break into droplets (Fig. 3). However, where the critical filament diameter to overcome capillarity is l = σ/τ_y, all of the simulated filaments have a diameter smaller than the critical diameter of 4 mm, so after the simulated time scale, all of the simulated filaments at a surface tension of 40 mJ m⁻² will eventually rupture. This could be overcome using in situ curing via ionic cross-linking²⁵ or surface stabilization via jammed particles.^26,51 Although non-zero surface tension filaments are unstable, this does not mean that zero surface tension filaments are more stable. Most notably in Newtonian supports, filaments continue to grow taller over time and over the length of the filament at zero surface tension due to the shape of the flow field (Fig. S12, ESI‡), while equivalent filaments at non-zero surface tension at a moderate support viscosity remain round due to capillarity. Thus, filaments at zero surface tension, particularly if they exhibit minimal yielding, may also benefit from in situ curing.

5. Conclusions

This paper describes a suite of simulations that predict the shapes of filaments extruded into support baths. We simulated Newtonian and Herschel–Bulkley inks and supports, across a wide range of plateau viscosities, at zero surface tension and an oil–water surface tension. We established quantitative metrics to define filament position and filament shape, which are key indicators of print quality. Critically, we make the following recommendations:

• For cylindrical filaments, use a non-zero surface tension and a high plateau viscosity Herschel–Bulkley ink and/or support.

• For accurate filament positioning in the horizontal x–y plane and most consistent shape along the length of the filament, use a Herschel–Bulkley support.

• For accurate filament positioning in the vertical z direction, use a Herschel–Bulkley support and Newtonian ink.

• To write spherical droplets, use a non-zero surface tension, low-viscosity ink and slightly higher viscosity support.

Alternatively, these results can guide selection of support materials, given a certain ink. If the ink is hydrophilic and has a low viscosity, like many bio-inks, then a viscous, Herschel–Bulkley, hydrophobic support (with an appropriate yield stress) will produce the most circular, consistent filaments. However, because the plateau viscosity tends to increase with yield stress, it may be necessary to instead use a low-viscosity hydrophilic support. If the ink is viscous and Newtonian, then a Newtonian support of the same or slightly lower viscosity and any surface tension will produce the most circular filaments. If the ink is hydrophilic, Herschel–Bulkley, and has a high plateau viscosity, a hydrophobic Herschel–Bulkley support with a high plateau viscosity will produce the most circular filaments.

Of course, there are bounds to the scope of this study. Buoyancy was suppressed, so the few benefits of low-viscosity supports may be outweighed by the loss of viscous drag that would prevent extrudates from sinking or floating. On the other hand, a dense ink could combat the vertical displacement caused by the flow field, improving vertical z positioning. Likewise, these simulations prohibited mixing, but at zero surface tension, diffusion between the ink and support is likely.^25,29 The dimensions of the simulated bath could also limit the scope of these results. The two boundaries that are fixed to the bath flow velocity (the bottom plane and the plane upstream of the nozzle) are close to the nozzle, compared to the typical size of a print bath.³⁰ As such, the flow field ahead of and below the nozzle may vary in larger print baths, resulting in different filament shapes. Surface functionalization of the nozzle or alternative nozzle shapes (e.g., conical) could also alter the flow field. Varying the print speeds could also alter the flow field. All of these simulations were conducted at a low Reynolds number (≈0.01). Higher Reynolds numbers could induce vortices which could disturb the deposited filament.⁹ Furthermore, varying the ratio of the extrusion speed to translation speed could change the relationship between the flow field and the filament, altering the filament shape. Additionally, in this study the post-yielding behavior was held constant. Future work on Herschel–Bulkley fluids could investigate the several axes of yielding by changing the yield stress, power law index, and consistency index, and importantly, varying them separately for ink and support. Of course, in real life, it is difficult to only manipulate one of these variables at a time, but simulations could help to extract key scaling relationships. Additionally, because OpenFOAM approximates Herschel–Bulkley fluids through purely viscous behavior, future studies could incorporate the elastic behavior present in many DIW inks and supports. Elasticity has been proposed both as a mechanism for crevice formation and relaxation in the bath,⁵⁶ as a driver of die swell,⁵⁷, and a critical form holding mechanism.⁵⁸ Work on models including the Carreau or power law models would further expand the scope of known scaling behaviors. Finally, this study only examined single filaments. Studying filament extrusion in the context of existing filaments, to examine fusion between neighboring filaments and distortion of existing filaments, will be critical for guiding material selection, particularly regarding surface tension. Scaling up to larger structures will be important for understanding how previously-printed ink can change the behavior of the bath and lead to residual stresses in the final part.

In conclusion, this study identifies the critical variables that control extrudate shape. At low ink viscosities and/or support viscosities, surface tension is the key variable that controls filament shape or filament breakup. Where the surface tension is zero, or at high viscosities, the viscosity ratio, or the ink viscosity divided by the support viscosity, controls the filament shape and placement. If the ink or support is a Herschel–Bulkley fluid and yields fully during printing, the yielded viscosity should be used in the viscosity ratio.