Multiple mechanisms regulate statistical learning of orthographic regularities in school-age children: Neurophysiological evidence

Abstract

Using event-related potentials (ERPs), this study investigated how the brains of Chinese children of different ages extract and encode relational patterns contained in orthographic input. Ninety-nine Chinese children in Grades 1-3 performed an artificial orthography statistical learning task that comprised logographic components embedded in characters with high (100%), moderate (80%), and low (60%) positional consistency. The behavioral results indicated that across grades, participants more accurately recognized characters with high rather than low consistency. The neurophysiological results revealed that in each grade, the amplitude of some ERP components differed, with a larger P1 effect in the high consistency condition and a larger N170 and left-lateralized P300 effect in the low consistency condition. A smaller N170 effect occurred in Grade 3 than in Grade 1, and a larger P300 effect occurred in Grade 1 than in either Grade 2 or 3. These findings suggest the dynamic nature of statistical learning by showing that neural adaptation associated with N170, and attention and working memory related to P1 and P300, regulate different types of structural input, and that children’s abilities to prioritize these mechanisms vary with context and age.

Highlights

• •How multiple mechanisms regulate statistical learning remains unknown.
• •EEG recorded children’s learning of high-, moderate- and low-positional consistencies.
• •An attenuated N170 for high-consistency reflects neural adaptation.
• •An enhanced P1 and P300 for low-consistency indicate attention and working memory.
• •Statistical learning is supported by adaptation, attention and working memory.

Previous behavioral studies have demonstrated that statistical learning—the ability to involuntarily extract and encode relational patterns of environmental input—plays a critical role in reading acquisition (for a review, see Lee et al., 2022). This is partly because many orthographies contain myriad statistical patterns that can be detected and learned by young children through mere repeated exposure (e.g., Frost et al., 2013; Treiman and Kessler, 2022). Also, individual's implicit orthographic processing, defined as sensitivity to the untaught distribution of print patterns (e.g., the co-occurring frequency of letters or letter clusters in English, and the position of occurrence of radicals/stroke patterns in Chinese), determines initial reading success (e.g., Apel, 2011; Tong et al., 2019, Tong et al., 2020a). For example, using sperate measures of statistical learning and implicit orthographic processing, a recent study has suggested a potential direct link between visual statistical learning and the acquisition of orthographic regularities (e.g., Tong et al., 2019). However, due to the constraints of behavioral approach and the lack of a unified paradigm for tapping directly into the processes of statistical learning of orthographic regularities, what the neural mechanisms underpin, and the possible developmental changes affecting statistical learning of orthographic regularities remain less well understood. Thus, by employing event-related potentials (ERPs) to record continuous neural signals evoked by cognitive processes before the behavioral response (e.g., Sommer et al., 2022), this study synergized statistical learning with orthographic regularity acquisition in an artificial logography learning paradigm to examine the neural correlates of statistical learning of orthographic regularities and the possible developmental changes at the neural level of Chinese first-, second-, and third-graders.

As a logographic script, Chinese compound characters exhibit orthographic regularities by the position and function of radicals and stroke patterns, which are the constituent components of characters. For example, the left-right structured, semantic-phonetic compound character 情/qing2/ (affection) comprises a left-sided phonetic radical 青 /qing1/ providing a sound cue and a right-sided semantic radical 忄(heart-related) indicating a clue to meaning. Positional consistency refers to the probability of a radical appearing at a given position within characters (Tong et al., 2020a). Since the radical 忄always appears on the left, its left positional consistency is 100%, but zero for other locations. However, unlike 忄, the positional regularities of radicals and stroke patterns are not exclusively regular/rule-basedbut more quasi-regular. For example, among a corpus of 3,764 characters learned by Chinese primary school students, 42 contain the component "目", which appears on the left in 29 (e.g., 瞇, 睫, 瞅, 瞞, 瞄, 盯, 瞎, 睜, 瞼, 瞪, 睡, 眼, 睛. 眨, 睹, 瞧, 盼, 瞭, 眠, 眺, 瞻, 瞰, 睬, 矚, 瞬, 眶, 眈, 瞌, 睦), on the right in one (i.e., 相), at the top in one (e.g., 鼎), at the bottom in 10 (e.g., 看, 督, 眉, 冒, 盲, 省, 盾, 瞥, 眷, 着), and in the middle in one (i.e., 算). Thus, the distribution of the occurrence frequency of "目" is 69.05%, 2.38%, 2.38%, 23.81%, and 2.38% for left, right, top, bottom, and middle, respectively.

In fact, several behavioral studies have demonstrated that Chinese children are sensitive to the untaught distributional patterns of positional regularities of radicals and stroke patterns. For example, using an implicit orthographic regularity elicitation paradigm, Tong and McBride (2014) showed that even 5-year-old Chinese kindergarteners were sensitive to the distributional patterns of character components. Similarly, Yin and McBride (2015) found that Chinese kindergartners’ accuracy was higher when reading pseudocharacters with phonetic cues or with radicals in their legal, rather than illegal, position. A recent study corroborated these findings by showing that Chinese children with dyslexia can statistically extract positional regularities of radicals, but were influenced by distributional patterns of left-right and top-bottom structured characters (Tong et al., 2020b). Together, these behavioral studies indicate that Chinese children can extract statistical regularities at a very young age and manifest them in their reading behavior. However, none of these studies elucidate the neural processes that enable these children to cope with quasi-regularity of the positional occurrence of radicals, and establish the representation for further learning and reading.

Recently, Conway (2020) proposed a multicomponent model encompassing two primary cortical systems, with the first comprising a set of implicit, unconscious learning mechanisms based on the general principle of cortical plasticity, while the second is an explicit, conscious process mediated by attentional and working memory networks. In the implicit system, statistical learning’s plasticity of processing reflects the adaptation of neural networks to statistical structures (Reber, 2013), which is associated with reduced neural activity (Grill-Spector et al., 2006). According to the second system, statistical learning also involves consciousness, including attention and working memory, to learn complex regularities through accumulated experience (e.g., Daltrozzo and Conway, 2014; Hendricks et al., 2013). Similarly, Mano (2016) assumed sensitivity to orthographic regularities as a two-process framework involving statistical learning, task-driven attentional control, and their dynamic interplay in sublexical processing, that mainly activated the posterior occipitotemporal sulcal region (i.e., visual word form area; Cohen and Dehaene, 2004).

Aligning with the multicomponent views, several ERP studies provided initial evidence for the possible involvement of multiple cognitive processes during statistical learning. For example, using a short interstimulus interval adaptation paradigm, Cao et al. (2014) compared the N170 effects elicited by two adaptor-test pairs and found that test characters with the same adaptor (vs. a foil adaptor) produced a smaller N170, reflecting an increased efficiency in neural adaptation (Reber, 2013). Meanwhile, Turk-Browne et al. (2005) found that while statistical regularities could be automatically and implicitly learned, this process was controlled by selective attention as evidenced by slower responses in the attended stream condition but not in the unattended condition.

Indeed, past studies suggested that attentional levels affected all ERP components corresponding to statistical learning (Daltrozzo and Conway, 2014). For example, P300 reflects the extent of attentional resource allocation and the depth of input processing (Peisch et al., 2021) and is a neural indicator of working memory load during conscious visual processing (Koivisto et al., 2018). Also, P1, a positive ERP component recorded at 90–130 ms after stimulus onset in occipital sites, is related to children’s visual processing and spatial location (e.g., Taylor et al., 2003). Baldwin and Kutas (1997) demonstrated that P300 effects were evoked by sequence violations in both explicit and implicit statistical learning. Neural imaging studies further revealed that implicit learning tasks triggered the caudate nucleus, a brain area that was activated in explicit rule learning and working memory (e.g., Lieberman et al., 2004; Seger and Cincotta, 2002). Together, these prior neuroscience studies reinforce our hypothesis that statistical learning of orthographic regularities may be supported by multiple neural mechanisms operating at different stages of learning. We tested this hypothesis with developing Chinese children.

Our second aim is to address another unresolved issue concerning a developmental change in statistical learning: namely, how age affects neural mechanisms of statistical learning (Daltrozzo and Conway, 2014). The developmental invariance model assumes that implicit statistical learning is an age-independent cognitive process (Reber, 1993). An ERP study using a predictor-target task on adults, older children (aged 9–12), and younger children (aged 6–8) showed that high predictors evoked a similar P300 effect across all three groups, indicating no age difference for visual statistical learning (Jost et al., 2015). However, the age-variant model claims that children’s performance improves as they age (e.g., Arciuli and Simpson, 2011). Employing the visual triplet statistical learning paradigm on 5- to 12-year-olds, Arciuli and Simpson (2011) demonstrated that older children outperformed younger children. Furthermore, Raviv and Arnon (2018) found that the age effect was modality-specific such that visual but not auditory statistical learning improved with age. Subsequently, Shufaniya and Arnon (2018) reported that both learning patterns in different perceptual modalities improved with age, resulting in age invariance for the input’s linguistic feature.

In sum, our study examined 1) when and to what extent children’s brains were activated during statistical learning of orthographic regularities, and 2) the developmental differences of this process in first-, second-, and third- graders. Specifically, by detecting the temporal course of each ERP indicator and comparing the activated ERP differences among three position consistency levels (i.e., high, moderate, and low), we clarified the neural mechanism underpinning statistical learning of orthographic regularities in children from 7 to 9. As in study of Tong et al. (2020a) showing N170 as the ERP indicator of adults’ statistical learning of positional consistency, we hypothesize a larger N170 effect in low versus high condition. Furthermore, since younger children’s processing is less automatic than older children's, their statistical learning of orthographic regularities demands more explicit attention and working memory. We thus hypothesize the attenuated N170 response elicited by high condition relative to moderate and low conditions (reflecting implicit process), and that the P300 becomes smaller as age increases (indicating explicit process).

1. Method

1.1. Participants

One hundred healthy native Chinese first- (17 boys, 15 girls; Mean age = 7 years, 2 months, SD = 4.69 months), second- (17 boys, 19 girls; Mean age = 8 years, 3 months, SD = 4.12 months), and third-graders (13 boys, 19 girls; Mean age = 9 years, 6 months, SD = 7.68 months) participated in this study. One second-grader whose accuracy rate in the learning phase was 2.5 standard deviations below the individual mean was removed from the final analysis. Data for two second-graders in the recognition test were non-existent since they completed the EEG recording in the learning phase only. Therefore, 99 children’s EEG data were used for final EEG data analysis and 97 children’s data were used for the recognition data analysis. All participants had normal or corrected-to-normal vision and were right-handed. Ethical approval for this study was obtained from the Research Ethics Committee of the corresponding author’s university.

1.2. Materials

Stimuli were adopted and modified from a past study (He and Tong, 2017). For the learning phase, stimuli consisted of 30 artificial pseudocharacters combining six target radicals with five control radicals adopted from Geba and Dongba characters used by the Naxi minority in Western China. Participants in this study were unfamiliar with these two scripts. The target radicals appeared in two positions (i.e., half at the top, half at the bottom) and were manipulated to carry different levels of positional consistency: high (100%), moderate (80%), and low (60%), according to orthographic regularity in Chinese radicals. The high consistency radicals (e.g., ) were manipulated to appear in the same top or bottom position in all five pseudocharacters (e.g., 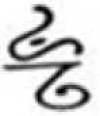,,,,). The moderate radicals (e.g., ) were manipulated to appear at the top or bottom in four pseudocharacters with 20% in the opposite position (e.g., ,,,,). The low consistency radicals (e.g., ) were manipulated to appear at the top or bottom in three pseudocharacters with 40% in the opposite position (e.g., ,,,,). The control radical carried no positional preference among items. Thirty pseudocharacters (10 for each condition) were ultimately created in the learning phase.

The visual complexity of all pseudocharacters was matched through cosine similarity to control for visual difference among items in the three conditions. Widely used in machine learning to extract critical words from a text to show high sensitivity between two characters, cosine similarity assesses similarity according to the cosine of the angle between the vectors of two items (Korenius et al., 2007, Xia et al., 2015). The similarity between two characters, c₁ and c₂, is defined as:

$$d=\frac{{\sum }_{i=1}^d{c}_1\times c_2}{\sqrt{{\sum }_{i=1}^d{c}_1^2}\times \sqrt{{\sum }_{i=1}^d{c}_2^2}},$$

where c₁ and c₂ are the value of pixels on the binary images of character c₁ and c₂, respectively. The similarity score between two characters ranges from zero to one, with higher scores indicating higher levels of similarity. Using the cosine similarity measure, three 10 × 10 matrixes for every two consistency levels (each contains 10 items) were obtained in this study. Results show that the averaged visual similarities for every two consistency levels are matched (high vs. moderate: M = 0.911; high vs. low: M = 0.912; moderate vs. low: M = 0.912). Fig. 1 displays the averaged similarity scores of 100 paired comparisons for every two conditions.

Fig. 1.

The similarity scores of 100 paired comparisons for every two conditions. The averaged similarities are in the lower left.

1.3. Procedure

All participants were involved in the learning and recognition phases. During the learning phase, participants were exposed to a continuous sequence of pseudocharacters in a fixed pseudo-randomized order at the center of the monitor (e.g., He and Tong, 2017). Stimuli were displayed using E-Prime 2.0 software (Psychology Software Tools, Pittsburgh, PA). For each trial, a fixation “+ ” was shown at the center of the monitor for 500 ms, followed by a blank screen for 500 ms. Then, a pseudocharacter appeared for 800 ms, followed by a blank screen for 1000 ms. Participants were required to press the SPACEBAR key when two identical stimuli appeared continuously. Each stimulus was repeated 24 times resulting in 720 trials.

The recognition phase contained 30 stimuli, half of which were original stimuli used in the learning phase, and the other half novel stimuli created by reversing the positions of target and control radicals. Participants were required to press corresponding keys if they recognized stimuli from the learning phase. Items remained visible until the participants responded. Children’s reaction time and accuracy rate were recorded for both the learning and recognition phases. The experiment lasted approximately 40 minutes.

1.4. EEG recording and data analysis

While children performed the statistical learning task in the learning phase, the Brain Product 32-channel Ag/AgCl system (Brain Products Inc) recorded EEG at a sample rate of 500 Hz with the FCz electrode as the online reference. Electrode impedances were kept below 15 kΩ. EEG data were preprocessed with EEGLAB (Delorme and Makeig, 2004) and re-referenced to the average reference with ICA employed to correct for eye-blink artifacts. The continuous EEG was segmented into epochs from − 100–600 ms and time-locked to the target stimuli with a 2–30 Hz band-pass filter. The baseline of each epoch was corrected from − 100–0 ms, and ERPs were averaged within each condition.

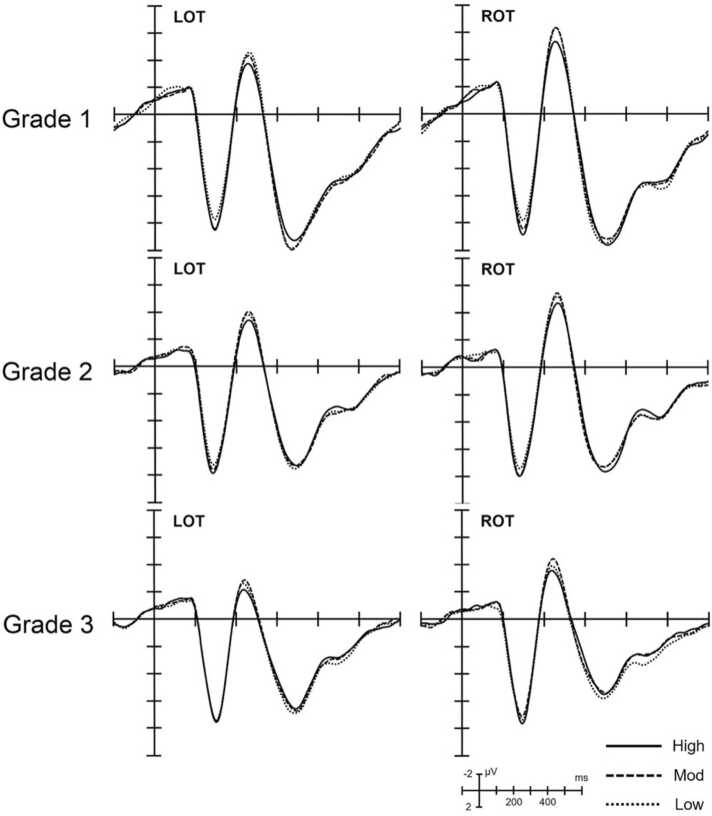
Using Global Field Power (GFP), ERP components were identified based on their peak. Within each grade, peaks were similar for each component. Thus, the average GFP in all participants determined the time window of each component. As shown in Fig. 2, a large positive waveform, i.e., the P1 component, was observed at 146 ms. A large negative waveform, i.e., the N170 component, was found at 230 ms. Another large positive waveform, the P300 component, was observed at 344 ms. Therefore, three ERP components, i.e., P1 (120–180 ms), N170 (210–250 ms), and P300 (320–370 ms), were identified. Past studies have suggested that orthographic processing is located in the occipital-temporal area (Tong et al., 2020a, Tong et al., 2020b). We thus selected four electrodes (i.e., P7, P8, O1, and O2) in the occipital-temporal areas based on the topographic maxima over both hemispheres across different conditions. We averaged the ERPs within the left (LOT) and right (ROT) occipital-temporal areas in order to increase the signal-to-noise ratio. Bonferroni correction was applied to protect from Type-I error in multiple comparisons. Finally, we applied Greenhouse-Geisser correction to overcome the effect when the assumption of sphericity in repeated measures analysis of variance (ANOVA) was violated.

Fig. 2.

GFP for the whole process across the entire group. The vertical gray columns indicate three microstates reflecting P1, N170, and P300. Note. GFP is defined as the spatial standard deviation quantifying the amount of neural activity from all electrodes at each time point (Skrandies, 1990). Therefore, the peak of N170 here is positive.

2. Results

2.1. Behavioral results

Table 1 shows the reaction times and accuracy rates from the learning phase and recognition test for three conditions among the three grades. Trials with incorrect response and 2.5 standard deviations more than the individual mean were removed from the final analysis in the recognition test. For the learning phase, children’s mean response accuracy was 61.6%, 61.4%, and 58.2% for Grades 1, 2, and 3, respectively.

Table 1.

Reaction Time and Accuracy Rate in the Learning Phase and Recognition Test for Three Conditions among Three Grades.

Conditions	Learning phase		Recognition test
	Reaction time	Accuracy rate	Reaction time	Accuracy rate
Grade 1
High	967.813(140.122)	0.624(0.205)	2015.462(640.588)	0.681(0.133)
Moderate	960.874(144.827)	0.608(0.193)	1776.324(808.110)	0.531(0.120)
Low	928.534(104.640)	0.616(0.180)	1760.964(607.180)	0.613(0.186)
Grade 2
High	889.591(142.697)	0.598(0.201)	1824.167(586.519)	0.682(0.155)
Moderate	881.843(134.280)	0.626(0.218)	1609.469(641.614)	0.536(0.156)
Low	855.420(127.432)	0.619(0.178)	1841.021(767.402)	0.570(0.133)
Grade 3
High	855.321(161.235)	0.584(0.217)	1484.867(601.916)	0.716(0.176)
Moderate	863.070(188.855)	0.560(0.213)	1426.795(556.112)	0.581(0.142)
Low	826.994(179.431)	0.602(0.192)	1460.593(643.145)	0.572(0.130)

Note: Standard deviations are in parentheses. The reaction time and accuracy rate in the learning phase are based on children’s performance of filler trials in the cover task. As the cover task is to ensure participants’ pay attention to learning stimuli, we did not interpret the behavioral results in the learning phase.

For the recognition test in Grade 1, the mean recognition accuracy was 60.8%, significantly higher than chance (50%; t₍₃₁₎ = 7.35, p < 0.001). One-sample t-tests revealed significant differences between recognition accuracy and chance for the high-consistency condition (Mean = 68.12%; t₍₃₁₎ = 7.71, p < 0.001) and the low-consistency condition (Mean = 61.25%; t₍₃₁₎ = 3.42, p = 0.002). However, no significant difference between recognition accuracy and chance occurred for the moderate-consistency condition (Mean = 53.13%; t₍₃₁₎ = 1.47, p = 0.152).

For the recognition test in Grade 2, the mean recognition accuracy was 59.6%, significantly higher than chance (50%; t₍₃₂₎ = 5.70, p < 0.001). One-sample t-tests revealed significant differences between recognition accuracy and chance for the high consistency condition (Mean = 68.18%; t₍₃₂₎ = 6.74, p < 0.001) and the low-consistency condition (Mean = 56.97%; t₍₃₂₎ = 3.00, p = 0.005). However, no significant difference between recognition accuracy and chance occurred for the moderate-consistency condition (Mean = 53.64%; t₍₃₂₎ = 1.34, p = 0.189).

For the recognition test in Grade 3, the mean recognition accuracy was 62.3%, significantly higher than chance (50%; t₍₃₁₎ = 7.71, p < 0.001). One-sample t-tests revealed significant differences between recognition accuracy and chance for the high-consistency condition (Mean = 71.56%; t₍₃₁₎ = 6.92, p < 0.001), the moderate-consistency condition (Mean = 58.12%; t₍₃₁₎ = 3.23, p = 0.003), and the low-consistency condition (Mean = 57.19%; t₍₃₁₎ = 3.13, p = 0.004).

Two separate mixed ANOVAs with consistency (high, moderate, and low conditions) as a within-factor and grade (1, 2, and 3) as a between-factor were performed on accuracy rate and response time for the recognition test. For accuracy rate, the main effect of consistency was significant (F_{(2, 188)} = 25.41, p < 0.001, ${\eta }_p^2$ = 0.213). Follow-up comparisons showed that children were more accurate in the high-consistency condition than in the moderate- and low-consistency conditions (ps < 0.001). However, no statistically significant difference occurred between the moderate and low conditions (p = 0.301). For reaction time, the effect of consistency was significant (F_{(2, 188)} = 5.17, p = 0.008, ${\eta }_p^2$ = 0.052). Follow-up comparisons showed that children showed faster responses in the moderate-consistency condition than in the high-consistency condition (p = 0.010). However, no statistical difference occurred between the high and low conditions (p = 0.360), nor between the moderate and low conditions (p = 0.219). The effect of grade was significant (F_{(2, 94)} = 4.01, p = 0.021, ${\eta }_p^2$ = 0.079). Follow-up comparisons showed that third-graders had a shorter reaction time than first-graders (p = 0.024). However, no statistical difference occurred between the first- and second-graders (p = 1.0), nor between the second- and third-graders (p = 0.119). No other main effects and interactions were found to be significant (ps > 0.05).

2.2. ERP results

The mean amplitude and comparisons across conditions in both LOT and ROT are shown in Table 2 and Fig. 3. Topographical maps of different conditions for three grade groups in each time window are shown in Fig. 4, Fig. 5, Fig. 6. The results of the statistical analyses in three ERP components are summarized in Table 1s (see Supplemental Tables).

Table 2.

Mean Amplitudes of Three ERP Components (P1, N170, and P300) for Each Consistency Condition in the Left Occipital-temporal (LOT) and Right Occipital-temporal (ROT) Regions.

	ROI
	LOT	ROT
P1
High	6.343(3.970)	6.409(3.695)
Moderate	6.193(3.752)	6.149(3.578)
Low	5.913(3.675)	5.922(3.598)
N170
High	-2.631(3.803)	-4.003(3.820)
Moderate	-3.190(3.695)	-4.745(3.486)
Low	-3.126(3.839)	-4.510(3.846)
P300
High	7.378(3.699)	7.251(3.452)
Moderate	7.611(3.626)	7.056(3.451)
Low	7.721(3.511)	7.302(3.498)

Note: Standard deviations are in parentheses.

Fig. 3.

Grand averaged ERP waveforms of high-, moderate-, and low-consistency conditions at LOT and ROT for three grade groups.

Fig. 4.

Topographical maps of different conditions in the 120–180 ms time windows for three Grade groups. H-L: the voltage difference between high and low consistency conditions; H-M: the voltage difference o between high and moderate consistency conditions; M-L: the voltage difference between moderate and low consistency conditions.

Fig. 5.

Topographical maps of different conditions in the 210–250 ms time windows for three Grade groups. M-H: the voltage difference between moderate and high consistency conditions; M-L: the voltage difference between moderate and low consistency conditions; L-H: the voltage difference between low and high consistency conditions.

Fig. 6.

Topographical maps of different conditions in the 320–370 ms time windows for three Grade groups. L-H: the voltage difference between low and high consistency conditions; L-M: the voltage difference between low and moderate consistency conditions; M-H: the voltage difference between moderate and high consistency conditions.

2.2.1. P1 (120–180 ms time window)

A mixed ANOVA with consistency (high, moderate, and low conditions) and ROI (LOT and ROT) as within-subject factors, and grade (1, 2, and 3) as a between-subject factor revealed that the main effect of consistency was significant (F_{(2, 192)} = 9.04, p < 0.001, ${\eta }_p^2$ = 0.086). Follow-up comparisons showed that the mean amplitude for the high-consistency condition was more positive than for the low-consistency condition (p < 0.001). However, the difference between high- and moderate-consistency conditions (p = 0.110 ) and between moderate- and low-consistency conditions (p = 0.074) was not significant. No other main effects and interactions were found to be significant (ps > 0.1).

2.2.2. N170 (210–250 ms time window)

A mixed ANOVA with consistency (high, moderate, and low conditions) and ROI (LOT and ROT) as within-subject factors, and grade (1, 2, and 3) as a between-subject factor showed that the main effect of consistency was significant (F_{(2, 192)} = 18.41, p < 0.001, ${\eta }_p^2$ = 0.161). Follow-up comparisons showed that the mean amplitude for the low-consistency condition was more negative than for the high-consistency condition (p < 0.001), and the mean amplitude for the moderate-consistency condition was more negative than for the high-consistency condition (p < 0.001). However, the difference between the moderate-consistency condition and the low-consistency condition was not significant (p = 0.628). The main effect of ROI was significant (F_{(1, 96)} = 22.52, p < 0.001, ${\eta }_p^2$ = 0.190). The following comparison showed that the mean amplitude for ROT was more negative than for LOT (p < 0.001). Moreover, the main effect of Grade was significant (F_{(2, 96)} = 3.18, p = 0.046, ${\eta }_p^2$ = 0.062). The mean amplitude for Grade 1 was marginally more negative than for Grade 3 (p = 0.050); however, the difference was not significant between Grade 1 and Grade 2 (p = 1.0), nor between Grade 2 and Grade 3 (p = 0.224). No other interaction was observed in our analysis (ps > 0.1).

2.2.3. P300 (320–370 ms time window)

A mixed ANOVA with consistency (high, moderate, and low conditions) and ROI (LOT and ROT) as within-subject factors, and grade (1, 2, and 3) as a between-subject factor revealed that the main effect of grade was significant (F_{(2, 96)} = 10.57, p < 0.001, ${\eta }_p^2$ = 0.180). Follow-up comparisons showed that the mean amplitude for Grade 1 was more positive than for Grade 3 (p < 0.001), and the mean amplitude for Grade 1 was more positive than for Grade 2 (p = 0.017). However, the difference between Grade 2 and 3 was not significant (p = 0.211). The interaction of consistency by ROI was significant (F_{(2, 192)} = 5.36, p = 0.005, ${\eta }_p^2$ = 0.053). Further analysis showed a significant effect of consistency at LOT (F_{(2, 192)} = 4.16, p = 0.017, ${\eta }_p^2$ = 0.042). The mean amplitude for the low consistency condition was more positive than for the high-consistency condition (p = 0.014). However, no significant difference occurred between the moderate- and high-consistency conditions (p = 0.199) or between the low- and moderate-consistency conditions (p = 1.0). The effect of consistency was not significant at ROT (F_{(2, 192)} = 2.45, p = 0.089, ${\eta }_p^2$ = 0.025). No other main effects and interactions were significant (ps > 0.1).

2.2.4. Time-point-wise TANOVA analysis

To compare the consistent difference of scalp fields among the three conditions, a time-point-wise Topographic Analysis of Variance (TANOVA) was conducted by computing a nonparametric randomization test based on the GFP of difference maps. The time-point-wise TANOVA analyses for ERP effects of consistency are shown in Fig. 7. T-map series across three grade groups are summarized in Table 5s (see supplemental analysis). Results revealed a significant difference of orthographic statistical learning between the low- and high-consistency conditions in four time windows: N170 with a P1/N170 transition (164–242 ms), P300 time range (260–356 ms), and two small time windows (402–434 ms, and 446–500 ms). Process differed between the moderate- and high-consistency conditions during two time ranges: a P1 and N170 duration (116–250 ms) and a time window of P300 (268–414 ms). The comparison of the moderate and low conditions suggested process differences in a brief time window within the N170 duration (214–218 ms) and P300 time range (276–342 ms). Each t-map for the significant TANOVA time windows is displayed on the right of Fig. 7. The t-maps of both the low-high and moderate-high comparisons were significant in the P1-N170 segment at the occipital-temporal and parietal electrodes. A contrast of low- versus high-consistency conditions was observed at the left occipital-temporal electrodes in the time window of 402–434 ms, and at the right occipital-temporal electrodes in the time window of 446–500 ms.

Fig. 7.

Time-point-wise ERP effects of consistency. The TANOVA results of low versus high and moderate versus high contrasts showed differences in the P1-N170 component and the other two time ranges (dark grey frames are from 164 to 242 ms, 402–434 ms, and 446–500 ms, respectively. T-maps are displayed on the right).

Fig. 8 displays the time-point-wise TANOVA analyses of grade effects. Results revealed that grade effects significantly differed during statistical learning of orthographic regularities between first- and third-graders, and between first- and second-graders in three time windows: P1 (116–188 ms), N170 (206–260 ms), and P300 (300–490 ms). However, no statistically significant difference occurred in the three time windows between second- and third-graders.

Fig. 8.

Time-point-wise ERP effects of grade. The TANOVA results of Grade 1 versus Grade 3 and Grade 1 versus Grade 2 contrasts showed differences in the P1, N170, and P300 components (dark grey frames are from 116 to 188 ms, 206–260 ms, and 300–490 ms, respectively. T-maps are displayed on the right).

3. Discussion

Many studies have demonstrated that the human brain can detect orthographic regularities in a language through statistical learning (e.g., Gingras and Sénéchal, 2019; He and Tong, 2017; Samara and Caravolas, 2014). However, the neural mechanisms underlying, and the developmental patterns affecting this learning process, remain largely unknown. Using the ERP technique with an artifical orthographic statistical learning paradigm, this study investigated neurophysiological correlates and developmental patterns of statistical learning of orthographic regularities in Chinese first-, second-, and third-graders. In conjunction with behavioral results, the ERP data demonstrated that children from all three grades could extract positional regularities of radicals embedded in artificial pseudocharacters using statistical learning. The statistical learning process of orthographic regularities is accompanied by rapid changes in neural activation, indicated by three ERP components (i.e., P1, N170, and P300). Specifically, in each grade, the amplitude of some ERP components differed, with a larger P1 effect in the high consistency condition and a larger N170 and left-lateralized P300 effect in the low consistency condition. Also, a smaller N170 amplitude occurred in Grade 3 than in Grade 1, and a larger P300 amplitude occurred in Grade 1 than in either Grade 2 or 3. These findings suggest statistical learning is subserved by at least two mechanisms: a neural adaptation triggered by high consistency inputs, and a cognitive control process (i.e., attention or working memory) triggered by low consistency inputs.

Consistent with previous behavioral studies, all first-, second-, and third-graders were able to extract and learn the orthographic regularities (i.e., the position of radicals) through occurance frequency patterns embedded in the artificial pseudocharacters (e.g., He and Tong, 2017; Tong et al., 2020a, Tong et al., 2020b; Yin & McBride, 2015). This finding supports the experience-dependent mechanism (e.g., Canale, 2022; Saffran et al., 1996), which might be domain-general (Thiessen and Saffran, 2007) since it applies to a broad range of learning processes, including visual perception (e.g., Turk-Browne et al., 2010), motor skill learning (e.g., Robertson, 2007), speech segmentation (e.g., Saffran et al., 1996), and even social intuition (Lieberman, 2000). Our finding extends previous studies by demonstrating that this mechanism may be essential for learning quasi-regularities of Chinese character orthography.

Regarding the neural mechanisms related to children’s statistical learning, this study demonstrated a larger P1 amplitude in the high-consistency condition compared to the low-consistency condition. As the P1 effect is sensitive to the violation of radical positions in Chinese characters (Lo et al., 2019, Yum et al., 2015), the P1 activation produced by high-consistency condition in the current study may indicate that children were unaware of the legality of the artificial radicals embedded in the pseudocharacters; thus, the P1 effect was entirely attributed to visual statistical learning. Additionally, the effect of positional consistency can be explained by top-down attentional modulation (Taylor et al., 2003) in which the larger P1 effect elicited by stimuli in the high-consistency condition reflects stronger attentional control from top-down modulatory processing associated with more consistent features in orthographic regularities.

However, the peak between low- and high-consistency conditions shifted in the N170 component. That is, an attenuated N170 effect was found for the high-consistency level compared to the low-consistency level, suggesting a neural adaptation to familiar and consistent statistical input (e.g., Peter et al., 2019; Taylor et al., 2003) in which the neurocognitive processes of perceiving, encoding, and acting upon a given stimulus change adaptively as the experience of external input increases (Conway, 2020). This is exemplified by neuronal activity decay during the repetition of identical or similar stimuli (Benda, 2021). Of relevance to our study is that the high-, moderate-, and low-consistency conditions for radicals embedded in artificial pseudocharacters were manipulated by varying the frequency of same-position target radicals across different pseudocharacters. High consistency meant that the same radical appeared in the same position across stimuli every time. With the accumulation of repeated exposure to the stimuli, participants became more familiar with the position of the radicals in the high-consistency condition than in the low- consistency condition. This greater familiarity leads to a decreased neuronal response to radicals appearing in the same position—hence, the observed attenuated N170 effect.

The orthographic regularity hypothesis offers an alternative explanation: namely, that stimuli carrying greater orthographic regularity should be associated with less negative N170 responses (McCandliss et al., 1997, Tong et al., 2020a, Tong et al., 2020b). In this study, orthographic regularity was the positional consistency of target radicals appearing in artificial pseudocharacters. The more consistently a target radical appeared in more learned materials, the greater the orthographic regularity of that radical. Thus, a less negative N170 effect was found for the high-consistency condition than for the low-consistency condition (see item analysis in Supplemental Analyses), suggesting that during a long-term learning process, children more efficiently extract and encode high condition orthographic regularities and more rapidly distinguish low positional consistency. However, in the moderate condition, detecting regularities was puzzling for the children, leading to larger N170 amplitudes, lower accuracy, and shorter reaction times. Our results extend this hypothesis to artificial orthography learning by showing that N170 is not specific to a real orthography but applies to visual materials encoding regularity information. Future research needs to further verify this hypothesis using different sets of artificial materials.

Furthermore, this study detected an enhanced P300 amplitude in the low-consistency condition compared to the high-consistency condition. P300 in the learning phase suggested that children need to focus their attention on encoding the artificial stimuli and allocate attentional resources to acquire statistical patterns of artificial orthography. The enhanced P300 effect indicates that increased attentional control is triggered by the inconsistent inputs with higher uncertainty (Carrión and Bly, 2007, Johnson, 1986), which might be attributed to the limitation of young learners’ attentional resources for the more complicated regularities extracted from the low-consistency condition (Forest et al., 2021). This explanation is supported by Mano’s (2016) two-process framework in which attention control interacts with statistical learning during the orthographic learning process. The two-process framework assumed that, in addition to the need for statistical learning, the processing of certain types of orthographic regularities might require unique amounts of attention and cognitive control. Conway (2020) further explained that some aspects of statistical learning, especially for rule-based information, reflect conscious processes that rely on attention and working memory.

An alternative explanation for the P300 effect is the working memory load hypothesis. As suggested by Koivisto et al. (2018), P300 indicates that visual consciousness and working memory share resources at the relatively late maintenance stage. Consistent with this hypothesis, children need to constantly encode while consolidating the extracted orthographic regularities. As each positional consistency condition occupies different working memory resources, a significant difference in P300 amplitudes was observed between the low- and high-consistency conditions over the left occipitotemporal scalp. However, working memory load was associated more with maintenance than the encoding process (Shucard et al., 2009). As the current experimental design cannot distinguish the encoding and maintenance processes, future research is needed to investigate how and to what extent working memory load influences the process of encoding and long-term maintenance during orthographic statistical learning. The results of all three ERP components indicate that young children can acquire complex regularities from domain-general statistical learning and language recoding mechanisms (Rey et al., 2019).

Our study observed a developmental progression among children from 7 to 9 years old, with first-graders evoking larger N170 and P300 effects than third-graders. More specifically, the analysis of time-point-wise TANOVA indicated a developmental profile of children’s first few years of primary school: at the start of learning to read, children required more effort to process statistical patterns of orthographic regularity, as indicated by larger P1, N170, and P300 responses. After more reading training, children from at least 8 years old improved during the entire stage of orthographic processing, as manifested by each ERP indicator. These findings were consistent with previous studies (Ho et al., 2003, Tong and McBride, 2014) showing a gradual development in children’s ability to acquire orthographic regularities. Thus, first-graders acquired the orthographic information of radicals (Ho et al., 2003), which produced further improvement after one year of maturation and training (Anderson et al., 2013, Pacton et al., 2001).

Additionally, the absence of interaction between consistency and grade at the behavioral and neural levels suggested that developmental difference in statistical learning is not apparent enough for children during the first three years of primary school. This finding corroborated the claim by Reber (1993) and other statistical learning studies (e.g., Amso and Davidow, 2012; Jost et al., 2015; Janacsek et al., 2012), suggesting that statistical learning of orthographic regularities is age invariant from the start of reading development. However, since our study manipulated only positional regularities, further reserach is needed to determine whether statistical learning of other types of orthographic regularities, such as semantic or phonetic consistency of radicals, relies on the same sets of mechanism. In fact, past behavioral developmental studies have demonstrated that Chinese children acquire positional regularities of radicals earlier than the functional regularities (e.g., Ho et al., 2003; Tong et al., 2016). Moreover, considering that the children’s age range was only 7–9 years old, further studies on primary school children, as well as testing the difference of functional connections based on activation of brain regions among three age groups, would be of value.

Notably, a discrepancy exists between the behavioral results and ERP results. Specifically, first- and second-graders' accuracy rates for the behavioral recognition test did not exceed the chance level though a significant difference between high and moderate conditions was observed at N170. One explanation is the nature of the measurement with ERPs reflecting the neural activities that occurred during learning phase, while the accuracy for the recognition task occurred during the retrieval process of learning outcomes. Furthermore, as orthographic statistical learning might occur after only a few minutes of exposure (Chetail, 2017), the behavioral performance could results from a combination of learning and memory consolidation. These results may indicate that ERPs are moresensitive than behavioral measures for online statistical learning process.

Additionally, the the first- and second- graders' chace-level behavioral recognition accuracy in moderate, but above chance-level in high- and low-consistency conditions, could reflect that the recognition of high- and low-consistency items is dominated by a single mechanism while the retrieval of moderate consistency items may activate two competing mechanisms. Specifically, during the learning phase, two types of representation are formed: an abstract statistical structure representation of the target radicals' positional regularities, and an item-specific pseudocharacter representation. Although both representations are available during the testing phase, abstract statistical structure representation dominates the retrieval of high-consistency condition items (100%), while item-specific representation is more active in the retrieval of low-consistency items due to more violated position items in low than moderate conditions. In contrast, two types of representations are equally active in the moderate consistency-condition and compete for cognitive resources, resulting in a lower recognition accuracy rate than high- and low-consistency conditions (see results of item regularity analysis in supplementary material). Future research is needed to further warrant this explanation.

Nevertheless, our ERP results of N170, P1 and P300 align well with the multicomponent view of statistical learning, suggesting that high and low consistency inputs elicit two learning systems (see developmental difference analysis in supplemental analyses). Specifically, the attenuated N170 could be a neural index of the adaptation of familiar and repeated input, and the effects under high consistency condition (i.e., the target radical always appears in one position) are qualitatively different from moderate and low conditions (i.e., the target radical can appear in two positions). In contrast, the P1 and P300 components reflect the attentional processing triggered by items with various distributional statistics. One possibility is that the difference between 100% and 80% consistency is not large enough to elicit attentional effects, but between 100% and 60% consistency is.

Despite the robust results showing the neural activities of statistical learning of positional regularities of target radicals, it should be noted that the target radicals were not counterbalanced across low, moderate, and high conditions. However, becuase our experimental stimuli were created from Dongba and Geba characters and not exposed to our particiants before, we were able to more effectively eliminate the influence of individuals’ preference and prior knowledge. Thus, it is unlikely that the strong effect observed in the present study is related to the repeated visual features of the stimuli.

In sum, this study advances our understanding of the neurophysiological markers of statistical learning of orthographic regularities and the associated developmental patterns. Specifically, the P1, N170, and P300 components of ERPs can be used in conjunction with reaction time to identify the cognitive process of statistical learning of orthographic regularities in Chinese children. N170 reflects the extraction and encoding of orthographic regularities in the occipitotemporal region with neural adaptation, while P1 and P300 relate to multiple cognitive mechanisms underlying the process of statistical learning. The grade effect was significant, i.e., the smaller N170 amplitude in Grade 3 than Grade 1 and the larger P300 amplitude in Grade 1 than either Grade 2 or 3. These findings underscore the multiple mechanisms underlying statistical learning and indicate the developmental invariance of statistical learning of orthographic regularities in Chinese children.

CRediT authorship contribution statement

Conceptualization and experimental design: S-XT and XT; Data collection: RD and YY; Formal data analysis: RD and XT; Final writing and revision: S-XT, RD and XT; Equipment and Resources: WS and ST. Supervision of the Investigation: XT. Shelley Xiuli Tong and Rujun Duan contributed equally to this paper. All authors approved the final version of the mansucript.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary material

Supplementary material

.

Data availability

Data will be made available on request.