Mechanistic Study of Alkyne Insertion into Cu–Al and Au–Al Bonds: A Paradigm Shift for Coinage Metal Chemistry

Abstract

In this work, the mechanism of the insertion reaction of 3-hexyne into Cu–Al and Au–Al bonds in M–aluminyl (M = Cu, Au) complexes is computationally elucidated. The mechanism is found to be radical-like, with the Cu–Al and Au–Al bonds acting as nucleophiles toward the alkyne, and predicts a less efficient reactivity for the gold–aluminyl complex. The proposed mechanism well rationalizes the kinetic (or thermodynamic) control on the formation of the syn (or anti) insertion product into the Cu–Al bond (i.e., dimetallated alkene) which has been recently reported. A comparative analysis of the electronic structure reveals that the reduced reactivity at the gold site—usually showing higher efficiency than copper as a “standard” electrophile in alkyne activation—arises from a common feature, i.e., the highly stable 6s Au orbital. The relativistic lowering of the 6s orbital, making it more suitable for accepting electron density and thus enhancing the electrophilicity of gold complexes, in the gold–aluminyl system is responsible for a less nucleophilic Au–Al bond and, consequently, a less efficient alkyne insertion. These findings demonstrate that the unconventional electronic structure and the electron-sharing nature of the M–Al bond induce a paradigm shift in the properties of coinage metal complexes. In particular, the peculiar radical-like reactivity, previously shown also with carbon dioxide, suggests that these complexes might efficiently insert/activate other small molecules, opening new and unexplored paths for their reactivity.

Short abstract

The electron-sharing Au−Al and Cu−Al bonds in coinage metal−aluminyl complexes act as nucleophilic sites for the alkyne insertion, leading to a radical-like metal−aluminyl reactivity. The generally accepted factor determining superior “standard” electrophilic reactivity of gold complexes of [LAu]⁺ type in activating alkynes toward nucleophilic addition (i.e., the relativistic contracted and stabilized empty 6s orbital) is found here to be responsible for a less nucleophilic Au−Al bond (where the valence Au configuration is close to 6s¹), which enables an Au > Cu to a Cu > Au shift for coinage metal reactivity.

Introduction

Recently, the CO₂ insertion into M–Al bonds (M = Cu, Ag, Au) of coinage metal–aluminyl complexes has been reported.¹⁻⁴ Depending on the group 11 metal nature, the product of carbon dioxide insertion, featuring the CO₂ carbon atom coordinated to M and the two oxygen atoms bonded to the aluminyl moiety (4-Au, 5-Ag, 6-Cu), is stable to further reaction for the [^tBu₃PAuAl(NON)] (NON = 4,5-bis(2,6-diisopropylanilido)-2,7-di-tert-butyl-9,9-dimethylxanthene) complex 1-Au, whereas for the silver analogue [^tBu₃PAgAl(NON)] complex 2-Ag, the insertion product leads to the corresponding carbonate complex 7-Ag (and CO), and for the copper system [^tBu₃PCuAl(NON)] 3-Cu, it proceeds rapidly to the carbonate 8-Cu even at low temperatures (see Scheme 1).

Scheme 1. Reactions of Gold–Aluminyl 1-Au, Silver–Aluminyl 2-Ag, and Copper–Aluminyl 3-Cu Complexes with CO₂ Leading to Corresponding 4-Au, 5-Ag, and 6-Cu Insertion Products.

For complex 1-Au, we have demonstrated that the nucleophilic behavior of the electron-sharing, weakly polarized Au–Al bond combined with Al acting as an electrophile is the driving force for the CO₂ insertion reactivity occurring via a cooperative radical-like mechanism.⁵⁻⁸ The main interaction in the CO₂ insertion process has been shown to be electron donation from the Au–Al σ bond toward the CO₂ LUMO, assisted by a secondary interaction where electron donation occurs from the CO₂ HOMO toward the Al center (mostly an empty 3p_z orbital). These unique Au–Al electron-sharing bond nature and radical-like mechanism features, which are uncommon in gold(I) chemistry, make these species suitable candidates for insertion chemistry. In the same context, we have also analyzed the Cu–Al bond in 3-Cu, which has been found to have an analogous electron-sharing nature with, however, a slight Cu(δ⁺)–Al(δ^–) polarization that may lead to subtle differences in their reactivity.⁵

More recently, internal alkyne insertion into the Cu–Al bond of the copper–aluminyl complex 3-Cu has been experimentally reported, producing (aluminylalkenyl)copper compounds which possess different reactivity at the two derived M–C functions.⁹ Complex 3-Cu is able to control the nature of the formed (syn or anti) dimetallated alkenes, with syn isomers accessible through a kinetic control with high selectivity and anti isomers isolable through a thermodynamic control (Scheme 2). The syn dimetallated alkenes (9-Cu, 11-Cu) can give a selective insertion of CO leading to the formation of copper acyl compounds.⁹

Scheme 2. Reactions of Copper–Aluminyl 3-Cu and Gold–Boryl 13-Au-B Complexes with Internal Alkynes Leading to Corresponding Insertion Products (9–12 Cu) and Assumed Intermediates (14-Au-B and 16-Au-B).

Strictly related gold silyl^10,11 and boryl¹² complexes have been also experimentally reported to insert alkynes into Au–Si and Au–B bonds. Amgoune and Bourissou reported that alkynes can be activated via insertion into the Au–Si bond of the gold silyl (R₃P)AuSiR’Ph₂ (R = Ph, Me; R’ = ^tBu, Ph) systems with exclusively syn stereochemistry. Similarly, Yamashita et al. very recently reported an isomerization of a cis-(2-borylalkenyl)gold complex via a retro-1,2-metalate shift, where the first step is syn insertion of an internal alkyne into the Au–B bond of the [IPrAuB(Ar)₂] (IPr = N,N’-bis(2,6-di-iso-propylphenyl)imidazole-2-ylidene; Ar = o-tolyl) gold boryl 13-Au-B complex (Scheme 2).¹²

We have recently demonstrated that the Au–Al and Au–B bonds in [LAuX] (L = phosphine, N-heterocyclic carbene (NHC); X = Al(NON), B(o-tol)₂) complexes possess a similar electron-sharing nature, with diarylboryl complexes displaying a slightly more polarized bond as Au(δ⁺)–B(δ^–), which is responsible for a reduced radical-like reactivity toward CO₂⁸ (consistent with the reaction of complex [IPrAuB(o-tol)₂] with carbon dioxide having not been experimentally reported).¹³ The ancillary ligand of gold (phosphine or carbene) has been shown to have a negligible electronic trans effect on the Au–X bond and only a minor impact on the formation of the insertion product, although modification of the steric hindrance at the carbene site may exert a sizable control over the reaction.⁸

In this framework, one might surmise that the electron-sharing nature of the Au–Al bond in complex 1-Au which allowed to rationalize its reactivity with CO₂ may favor the reaction of complex 1-Au with alkynes analogous to that of complex 3-Cu. A comparative investigation of alkyne insertion in complexes 1-Au and 3-Cu would be relevant to shed light on the metal effect on this reactivity by a detailed comparison between Au–Al and Cu–Al bond nature and reaction mechanisms. As mentioned, a radical-like reactivity is new in gold chemistry, substantially differing from the well-known strong carbophilic Lewis acid behavior of gold complexes toward alkynes.¹⁴ Most of the reactions in which gold catalysts are involved can be classified as nucleophilic additions to a carbon–carbon unsaturated bond (alkynes, alkenes, and allenes), proceeding in a stepwise manner. In typical gold complexes of LAuX type (L = phosphine, carbene; X = counterion), the facile substitution of X with the alkyne substrate (pre-equilibrium step) allows for a η² coordination of the CC triple bond to the Au center which, acting as an electrophile, activates it for the subsequent nucleophilic attack by Nu–H (for instance, alcohols, water, amines, etc.), with the formation of vinyl gold intermediates and subsequent cleavage of the gold–carbon bonds by a proton (protodeauration step), to give the desired products and regenerate the catalyst.¹⁵⁻¹⁹ Remarkably, the nucleophilic attack commonly occurs on the Au–CC π complex anti to gold, affording an organogold complex with trans arrangement of the nucleophile and gold center (outer-sphere mechanism, Scheme 3), as supported by several experimental and computational studies.¹⁵⁻²⁷

Scheme 3. Schematic Representation of the (a) Outer-Sphere, (b) Inner-Sphere, and (c) Radical-like Mechanisms for the Nucleophilic Attack Step on the Alkyne Triple Bond.

Alternatively, the nucleophilic attack has been proposed to involve coordination of the nucleophile to gold and syn insertion of the substrate into the Au–Nu bond, leading to cis vinyl gold intermediates (inner-sphere mechanism, Scheme 3). However, no direct unambiguous evidence for the inner-sphere mechanism has been reported to date.²⁸⁻³² Cu-catalyzed reactions of internal alkynes for the synthesis of different valuable alkenes and heterocycles have also appeared in the literature in the last decade and they follow analogous mechanisms, with the functionalization occurring via both an inner- and an outer-sphere mechanism.³³

However, the M–alkyne (M = Cu, Au) bond energies vary generally in the order Cu < Au, indicating a more efficient activation of the triple bond by gold complexes, due to their higher electrophilicity. In addition, dinuclear gold (and heterobimetallic Cu/Au) complexes and their use in catalysis have recently received significant attention and comparative studies of the controversial mono- vs dual-metal-catalyzed pathways have appeared in the literature.³⁴⁻³⁹

From a more general perspective, insertion reactions of organic molecules into heterobimetallic M–M’ or M–E (E = B, Si) bonds represent an attractive approach to synthetic organic chemistry and industrial catalysis, although examples of this heterobimetallic reactivity are still scarce.^{10−12,40,41} One challenge in heterobimetallic catalysis is identifying a metal cooperative effect (if any) and its origin through mechanistic investigation, which can provide the necessary insight to understand how these catalysts work and possibly how modifications can be planned to increase both the activity and selectivity.

In this work, we computationally elucidate the mechanism of the experimentally observed alkyne (3-hexyne) insertion reaction into the Cu–Al bond in complex 3-Cu which is compared to that of the analogous model insertion reaction into the Au–Al bond in complex 1-Au. Detailed mechanistic analysis highlights the superior ability of the copper–aluminyl complex in activating (and inserting) the alkyne, leading to a more efficient formation of the syn product. The superior activity of 3-Cu with respect to 1-Au is found to be consistent with the relativistic stabilization of the gold valence atomic orbitals, in particular the 6s orbital, which is commonly known to enhance the electrophilicity of gold complexes and which, in this case, is responsible for a less efficient nucleophilic behavior of the gold–aluminum electron-sharing bond, thus inducing a paradigm shift in the coinage metal chemistry.

Results and Discussion

Reaction Mechanism of the Alkyne Insertion into the Cu–Al Bond

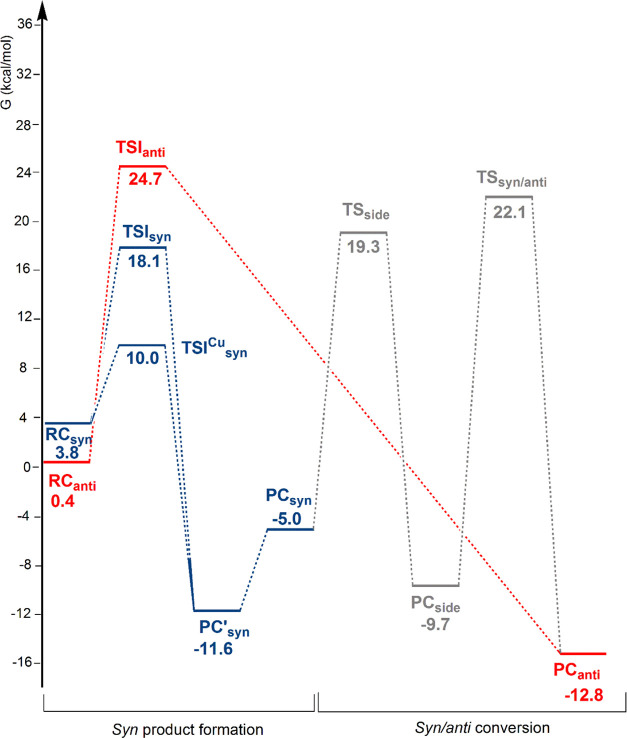
The free-energy profile for 3-hexyne insertion into the Cu–Al bond of complex 3-Cu is illustrated in Figure 1. It has been calculated using the same computational setup as that employed in ref (5) for the insertion reaction of CO₂ into the Au–Al bond in complex 1-Au (see the Computational Details Section). Optimized structures of stationary points along the paths are also sketched with selected geometrical parameters in Figure 2.

Figure 1.

Free-energy reaction profile for the 3-hexyne insertion into the Cu–Al bond in [^tBu₃PCuAl(NON)] (3-Cu) complex: the anti insertion path (red lines), the syn insertion path (blue lines), and the syn/anti conversion path (gray lines). ΔG values refer to the energy of the separated reactants taken as zero.

Figure 2.

Sketched stationary point structures along the paths of Figure 1 with selected interatomic distances (Å) and bond angles (°). Values in parentheses refer to experimentally available data taken from ref (9).

Starting from the reactant complex RC_anti, where the substrate CC triple bond is oriented perpendicular to the Cu–Al bond, alkyne insertion occurs with an activation free-energy barrier ΔG^≠ = 24.3 kcal/mol (via TSI_anti) leading directly to the formation of the anti insertion product (PC_anti) (red line profile). The process is exergonic with ΔG = −12.8 kcal/mol.

Reactant complex RC_syn, featuring the CC triple bond parallel to the Cu–Al bond, allows for alkyne insertion (blue line profiles) occurring both at the Al (via TSI_syn, ΔG^≠ = 14.3 kcal/mol) and at the Cu (via TSI_syn^Cu, ΔG^≠ = 6.2 kcal/mol) sites and leading to a stable intermediate species PC’_syn (ΔG = −11.6 kcal/mol) which, upon Cu–Al bond stretching, yields a less stable syn insertion product (PC_syn, ΔG = −5.0 kcal/mol). This reaction mechanism is in good agreement with the experimental finding that formation of the syn dimetallated alkenes is under kinetic control (lower activation barriers are calculated for syn insertion). Notably, in the TSI_syn and TSI_syn^Cu structures (Figure 2), both the Cu and Al sites are involved in a concerted mechanism, preferentially starting at the Cu site. As for the thermodynamic control for the formation of the anti isomer, comparison of the PC_syn main geometrical parameters with available X-ray crystallography data (see Figure 2) shows that this species is in good agreement with experimentally reported parameters, thus representing the isolated species, although PC_syn is found to be less stable than PC_anti by 7.8 kcal/mol (and PC’_syn by 6.6 kcal/mol). The interconversion of PC_syn to PC_anti has been proposed to occur through a C-to-Al migration of an Et group based on the isolated and structurally characterized (NON)AlEt species⁹ and in analogy with the reactivity of the boryl gold compound reported by Yamashita et al.¹² Access to anti dimetallated alkene has been investigated through a two-step process via TS_side and TS_syn/anti transition states (gray line, Figure 1), i.e., thorough isomerization of the PC_syn species. The calculated barrier for the first step (denoted as “side reaction”) leading to (NON)AlEt and copper acetylide co-product PC_side is ΔG^≠ = 24.3 kcal/mol, indicating that the migration of the Et group is viable from PC_syn along the path for the syn/anti conversion. Formation of PC_side is exergonic by 4.7 kcal/mol and dissociation into (NON)AlEt and [^tBu₃PCuCCEt] separated species requires only 2.0 kcal/mol (see Figure S1). The PC_side conversion to PC_anti involves the Et group migration to the alkyne (via TS_syn/anti) with a high activation energy ΔG^≠ = 31.8 kcal/mol. These results indicate that the rate-determining step is the isomerization from PC_side to PC_anti, which is consistent with the more forcing experimental conditions (heating to 45 °C for 6 h) needed to access the anti insertion product and with the experimental observation that (NON)AlEt can be isolated from the reaction mixture, whereas assignment of anti dimetallated alkene (PC_anti) could not be confirmed crystallographically for 3-hexyne.

The preferential formation of PC_syn via TSI_syn^Cu with respect to the other pathways described above can be rationalized by analyzing the evolution of the electronic structure along the reaction path. In particular, the analysis of the alkyne–complex interaction at the three initial transition states for each path (i.e., TSI_syn, TSI_syn^Cu, and TSI_anti) using energy decomposition analysis (EDA),⁴² natural orbitals for chemical valence (NOCV),⁴³ and charge-displacement (CD)⁴⁴⁻⁴⁶ approaches, in combination with the activation strain model⁴⁷⁻⁴⁹ (ASM, see the Methodology section in the SI for details on these approaches), allows to gain quantitative insights into the factors controlling the reported reactivity.

As depicted in Figures 3 and S2–S7 and Table S1 in the SI, the alkyne–complex interaction at TSI_syn, TSI_syn^Cu, and TSI_anti for the copper–aluminyl complex is, on a qualitative ground, of analogous nature.

Figure 3.

Main results of the NOCV analysis (Δρ₁’ component) of the [EtCCEt]−[^tBu₃PCuAl(NON)] interaction at TSI_syn, TSI_syn^Cu, and TSI_anti. The isosurfaces for the Δρ_1’ component at TSI_syn, TSI_syn^Cu, and TSI_anti (a, b, and c, respectively) are shown together with the associated orbital interaction energy and the corresponding main molecular orbitals contributions (d, e, and f for TSI_syn, TSI_syn^Cu, and TSI_anti, respectively). The charge flux is red → blue. Isovalue is 2 me/a₀³ for (a–c), while it is 20 me/a₀³ for (d–f). See Figures S2–S7 in the SI for the complete NOCV analysis.

Despite a different geometrical rearrangement of both the complex and alkyne moieties, the NOCV analysis reveals a qualitatively analogous interaction at the three TSs, where the main component Δρ₁’ identifies a charge transfer arising from the electron-sharing Cu–Al bond (as it can be inferred by the large contribution of the σ Cu–Al centered HOMO of the complex in all cases) toward the π* LUMO of the alkyne fragment (Figures S2, S4, and S6). A second significant component of the complex–alkyne interaction for all TSs can be observed (Δρ₂’), which is also qualitatively analogous in all cases and features a reverse alkyne-to-complex charge transfer toward an unoccupied molecular orbital of the complex with large contributions from the empty Al 3p_z atomic orbital (Figures S3, S5, and S7). It is worth noting that the alkyne–complex interaction scheme discussed here is highly reminiscent of that previously reported for the [^tBu₃AuAl(NON)]–CO₂ interaction,⁵⁻⁸ indicating a general scheme for the interaction of this class of complexes with small molecules.

Despite these evident qualitative analogies, on a quantitative ground, the ASM approach (Table S2 in the SI and Figure 4) helps to rationalize the relevant differences between the disfavored anti pathway via TSI_anti and the syn pathway, particularly the preferential reactivity via TSI_syn^Cu.

Figure 4.

Activation strain model (ASM) decomposition of the relative energy (ΔE) of TSI_syn^Cu (left) and TSI_anti (right) into distortion (ΔE_dist) and interaction (ΔE_int) contributions.

Although the interaction energy between the alkyne and the complex appears to favor TSI_anti with respect to TSI_syn^Cu (ΔE_int is −82.9 and −72.2 kcal/mol, respectively, see Figure 4), thus apparently suggesting a more stable TSI_anti, the ASM results indicate that the balance between these favorable interactions and the disfavoring distortion penalty is key. As shown in Figure 4, the distortion penalty is much larger in the case of TSI_anti (89.4 kcal/mol), while it is lower by almost 30 kcal/mol in the case of TSI_syn^Cu (62.6 kcal/mol), leading to TSI_syn^Cu being more stable than TSI_anti in terms of relative electronic energy (−9.2 vs 6.4 kcal/mol, respectively), in agreement with the lower free-energy barrier associated with the syn path (see Figure 1) which determines the kinetic control discussed earlier.

The reason behind the reduced distortion destabilization at TSI_syn^Cu can be found by inspection of the geometry of the two transition states in Figure 2. While at TSI_syn^Cu the syn approach of the alkyne leads to a transition state in which the Cu–Al bond is unbroken (the Cu–Al bond length is 2.385 Å), at TSI_anti the copper–aluminum bond is cleaved (the Cu–Al bond length is 3.135 Å). Since the Cu–Al bond is a fairly strong bond (the calculated dissociation energy is −78.4 kcal/mol), this leads to a distortion penalty associated with the deformation of the complex which is clearly higher for TSI_anti (26.6 kcal/mol, Table S2) with respect to that for TSI_syn^Cu (14.9 kcal/mol, Table S2). This difference, combined with the higher energy penalty at the alkyne site (ΔE_dist^alkyne is 47.7 and 62.7 kcal/mol for TSI_syn^Cu and TSI_anti, respectively) due to the higher degree of alkyne deformation (the C–C bond length is 1.321 vs 1.383 Å for TSI_syn^Cu and TSI_anti, respectively), explains the preferential syn formation from a kinetic standpoint.

Finally, it is worth exploring the nature of the reactivity in relation to the formed products, especially considering that gold–aluminyl complexes have been reported to react with CO₂ with a radical-like reactivity, i.e., with gold and aluminyl fragments behaving as doublet species when capturing CO₂.⁵⁻⁸ Based on the scheme previously used for gold–aluminyl complexes,⁵⁻⁸ we describe the formation of PC_syn, PC_syn’, and PC_anti from both radical doublet [^tBu₃PCu]· and [Al(NON)]· and closed shell charged [^tBu₃PCu]⁺ and [Al(NON)]⁻ fragments (see Scheme S1 in the SI). The results, reported in Table S3 in the SI, strongly suggest that a similar radical-like reactivity is also observed for copper–aluminyl reacting with the alkyne. Indeed, the overall formation energy of the products (ΔE) is found to be lower starting from radical fragments (−102.2, −106.9, and −106.9 kcal/mol for PC_syn, PC_syn’, and PC_anti, respectively) with respect to that from the corresponding closed shell fragments (−131.6, −136.3, and −136.3 kcal/mol for PC_syn, PC_syn’, and PC_anti, respectively), thus indicating the higher stability of the radical fragments, in strict analogy with the reaction of 1-Au with CO₂. This finding further elucidates that (i) the alkyne insertion occurs neither with an outer- nor an inner-sphere but more properly via a radical-like mechanism relying on a nucleophilic Cu–Al bond as the driving force and (ii) the reactivity mode previously found for gold–aluminyl complexes with CO₂ (i.e., a cooperative radical-like reactivity) emerges here as a more general paradigm for coinage metal–aluminyl complexes (and electron-sharing M–Al bonds) efficiently reacting with small molecules.

Reaction Mechanism of the Alkyne Insertion into the Au–Al Bond

The free-energy profile for 3-hexyne insertion into the Au–Al bond of complex 1-Au is illustrated in Figure 5, with the optimized structures of stationary points along the paths sketched with selected geometrical parameters in Figure 6.

Figure 5.

Free-energy reaction profile for the 3-hexyne insertion into the Au–Al bond in [^tBu₃PAuAl(NON)] (1-Au) complex: the anti insertion path (red lines), the syn insertion path (blue lines), and the syn/anti conversion paths (direct path: green lines; two-step path: gray lines). ΔG values refer to the energy of the separated reactants taken as zero.

Figure 6.

Sketched stationary point structures along the paths in Figure 5 with selected interatomic distances (Å) and bond angles (°).

The reaction paths are qualitatively similar to those for 3-Cu, with some relevant quantitative differences. Alkyne anti insertion occurs with an activation free-energy barrier of 32.3 kcal/mol (via TSI_anti) leading directly to the formation of the anti insertion product (PC_anti) (red line profile, ΔG = −5.8 kcal/mol). Analogously, the syn insertion via TSI_syn (ΔG^≠ = 16.9 kcal/mol) or via TSI_syn^Au (ΔG^≠ = 27.4 kcal/mol) leads to a stable intermediate species PC’_syn (ΔG = −6.6 kcal/mol) which, upon Au–Al bond stretching, yields a less stable syn insertion product (PC_syn, ΔG = −0.3 kcal/mol). As a result, formation of the syn dimetallated alkenes occurring at the Au–Al site is similarly predicted under kinetic control, with a higher activation barrier compared to that calculated for 3-Cu (16.9 vs 6.2 kcal/mol). Similarly, in the TSI_syn and TSI_syn^Au structures (Figure 6), both the Au and Al sites are involved, reflecting again a cooperative effect of the two centers in the alkyne insertion, with a more relevant role of Al. Notably, in the RC_syn structure, the Au–Al bond distance (2.418 Å) is close to the experimental value reported for complex 1-Au (2.402 Å)¹ and slightly shorter than the sum of the single-bond covalent radii of Au and Al (2.50 Å).⁵⁰ Preferential formation of the syn product via kinetic control can be explained on the basis of what was discussed in the previous section for 3-Cu, i.e., the enhanced distortion penalty at TSI_anti due to a substantially broken Au–Al bond (Au–Al bond length is 3.212 Å, see Figure 6) leading to a higher activation barrier (see Table S5 in the SI for the ASM results).

Analogously to 3-Cu, PC_syn has a lower stability than PC_anti (by 5.5 kcal/mol) and PC’_syn (by 6.3 kcal/mol), and, remarkably, the RC_syn-to-PC_syn conversion is practically thermoneutral, thus suggesting a possibly reversible reaction with a PC_syn that experimentally may be hardly isolable.

Interestingly, the formation of the syn products is predicted to occur via different paths for 3-Cu and 1-Au. Whereas the former is predicted to form more favorably the corresponding PC’_syn via TSI_syn^Cu (i.e., via a transition state where the alkyne is coordinated to the metal in a roughly η² fashion) with an activation barrier of 6.2 kcal/mol, the kinetically favored path for 1-Au is predicted to be via TSI_syn, which features a lower activation barrier (ΔG^≠ = 16.9 kcal/mol) with respect to that via TSI_syn^Au (ΔG^≠ = 27.4 kcal/mol), thus suggesting that the alkyne η²-like coordination to Au leads to a less stable transition state.

EDA, CD, NOCV, and ASM approaches help to shed light on these differences (see Tables S4, S5, and Figures S8–S13 in the SI for the complete results). On a qualitative ground, the alkyne–complex interaction appears to be unaffected by replacing the copper metal center with gold, coherently with the very similar reported M–Al bond features. The main NOCV component of the interaction of the substrate with 1-Au at all TSs (Δρ₁’) consists of a charge transfer from the Au–Al σ-bonding orbital toward the LUMO of the alkyne (see Figures S8, S10, and S12 in the SI). In all cases, a second component (Δρ₂’) is observed which consists of a charge transfer from the alkyne HOMO toward the LUMO of the complex (see Figures S9, S11, and S13 in the SI).

On a quantitative ground, however, the differences concerning the stability of TSI_syn^Cu and TSI_syn^Au, which determine the different preferential paths for 3-Cu and 1-Au, respectively, become evident. In particular, comparison of ASM results (see Tables 1, S2, and S5 in the SI) clarifies that the interaction between the substrate and the complex contribution (ΔE_int) is found to be the determining factor driving their different stability.

Table 1. Most Relevant ASM (Top) and EDA-NOCV (Bottom) Results for TSI_syn^Cu and TSI_syn^Au1.

	TSIsynCu	TSIsynAu
ASM decomposition of ΔE
ΔE	–9.6	14.2
ΔEdist	62.6	64.0
ΔEint	–72.2	–49.8
EDA decomposition of ΔEint
ΔEPauli	346.1	357.0
ΔEelst	–217.7	–218.5
ΔEsteric	128.4	138.5
ΔEoi	–187.6	–176.0
ΔEoi1	–140.4	–127.2
ΔEoi2	–20.1	–22.9
ΔEdisp	–13.0	–12.3

¹See Tables S2 and S5 in the SI for detailed ASM results and Tables S1 and S4 in the SI for detailed EDA-NOCV and CD results. All energies are reported in kcal/mol.

As shown in Table 1, while both TSI_syn^Cu and TSI_syn^Au feature analogous distortion penalties (62.6 and 64.0 kcal/mol, respectively), the stabilizing interaction contribution is different (−72.2 vs −49.8 kcal/mol, respectively), favoring an overall more stable TSI_syn^Cu (ΔE is −9.6 and 14.2 kcal/mol, respectively). The EDA-NOCV approach allows to decompose the interaction energy term ΔE_int, showing in detail that the complex–alkyne interaction mainly differs at the two TSs due to an orbital interaction increase (ΔE_oi is −187.6 vs −176.0 kcal/mol for TSI_syn^Cu and TSI_syn^Au, respectively) and, in particular, to a more energetically stabilizing complex-to-alkyne charge transfer (ΔE_oi¹ is −140.4 vs −127.2 kcal/mol for TSI_syn^Cu and TSI_syn^Au, respectively). The Pauli repulsion component also differs in the two TSs, being significantly lowered at TSI_syn^Cu (ΔE_Pauli is 346.1 vs 357.0 kcal/mol for TSI_syn^Cu and TSI_syn^Au, respectively).

The larger Pauli repulsion contribution at TSI_syn^Au may be rationalized on the basis of the more spatially extended 5d Au compared to the 3d Cu orbitals, as recently highlighted by Toste, Head-Gordon and co-workers.⁵¹ On the other hand, the increased orbital energy stabilization coming from the increased ΔE_oi (and in particular ΔE_oi¹) at TSI_syn^Cu with respect to TSI_syn^Au can be explained by analyzing the HOMO (i.e., the main filled molecular orbital of the complexes involved in the Δρ₁’ component) of the metal–aluminyl complexes at their corresponding transition state structure, as shown in Figure 7.

Figure 7.

Atomic orbital contributions to the HOMO of 3-Cu (a) and 1-Au (b) at the TSI_syn^Cu and TSI_syn^Au structures, respectively, and HOMO energy. Spin density distribution in the radical [^tBu₃M]· (M = Cu, Au) fragments at the TSI_syn^Cu and TSI_syn^Au geometry (c, d, respectively) (isodensity value 3 me/a₀³) and Mulliken population on M and P.

From Figure 7a, the composition of the 3-Cu HOMO at the TSI_syn^Cu structure features contributions from copper 4s, 4p_x, and 3d_xz atomic orbitals which sum up to 33.6% (8.4, 14.7, and 10.5% contributions from Cu 4s, 4p_x, and 3d_xz orbitals, respectively). Coupled with contributions from Al (20.3%), overall the 3-Cu HOMO at TSI_syn^Cu is mostly centered on the two metals (53.9%), quantitatively rationalizing the cooperative behavior of the two metals in the reported reactivity. Concerning 1-Au (Figure 7b), while the Al orbitals give analogous contributions (20.5%), the 1-Au HOMO at TSI_syn^Au has less coinage metal character (overall 26.2%, with 8.7, 9.4, and 8.1% contributions from Au 6s, 6p_x, and 5d_xz atomic orbitals, respectively). This different composition leads to an overall lower bimetallic character of the HOMO (46.7%). As a result, the reactivity of 1-Au via TSI_syn^Au is less efficient and this can be quantitatively inferred also by the energy of the HOMO, which is more stable (and thus, according to the frontier molecular orbital theory, less reactive) for 1-Au (−3.922 eV) than for 3-Cu (−3.787 eV, see Figure 7a,b).

These results can be rationalized on the basis of the radical-like reactivity of the metal (and aluminyl) fragments and metal’s atomic orbitals. As shown in Scheme S1 and Tables S3 and S6 in the SI, the product formation is favored by starting from [^tBu₃PM]· (M = Cu, Au) and [Al(NON)]^· radical fragments, suggesting a radical-like reactivity of both gold– and copper–aluminyl complexes, also consistent with gold’s valence 5d¹⁰6s¹ configuration in gold–aluminyl complexes we recently discussed.⁵² Upon spin density analysis on the two isolated metal fragments at the geometry they have in TSI_syn^Cu and TSI_syn^Au (Figure 7c,d), clear differences emerge between gold and copper. The unpaired electron in the radical [^tBu₃PCu]^· fragment is highly localized on Cu (0.89 e) with only a small delocalization on P (0.10 e). Conversely, the unpaired electron on [^tBu₃PAu]^· is less localized on Au (0.78 e) and more delocalized on P (0.21 e). As a result, the unpaired electron on Au is less available for the reactivity with 3-hexyne at the nucleophilic site, leading to a reduced bimetallic character and to a lower-energy and less reactive HOMO with respect to Cu. This decreased availability of the 6s¹ electron on gold is consistent with the relativistic stabilized 6s orbital in Au (−5.678 eV), which is remarkably close in energy to the 3p_x atomic orbital of the ligand’s phosphorus (−5.506 eV), leading to an efficient overlap and delocalization of the unpaired electron. By contrast, the copper 4s orbital is at higher energy (−4.640 eV), which reduces the overlap with the P orbital and the delocalization toward the ligand, and, consequently, it makes the electron at the copper site more available for the reaction with 3-hexyne.

Interestingly, the picture we describe here is well known in the framework of coinage metal chemistry. It is widely accepted that many of the unique properties of gold complexes, such as the high electrophilicity and carbophilicity, can be ultimately attributed to the relativistic enhanced stability of the 6s orbital of Au, at a variance with the less remarkable electrophilicity of analogous linear copper complexes, featuring higher-lying 4s orbitals.¹⁴ However, since copper– and gold–aluminyl complexes display a nucleophilic reactivity, where the M center also plays an active role, here the same features penalize gold with respect to copper and explain the more favorable reactivity of 3-Cu with the alkyne substrate.

This unconventional situation is not uniquely related to the first part of the syn path, but it affects the whole reaction path. For instance, the reduced ability of gold in the aluminyl complex to interact with the alkyne has been investigated by optimizing a “reactant-like” species with the alkyne coordinated to Au and Cu in a η² mode (see RC^Cu and RC^Au in Figure S1 in the SI) which shows a much more unstable complex (ΔG = 18.0 kcal/mol with respect to the separated reactants) formed by 1-Au compared to that formed by 3-Cu (ΔG = 8.0 kcal/mol).

Furthermore, at variance with 3-Cu, for 1-Au isomerization of the PC’_syn to PC_anti species can directly occur via the TS’_syn/anti transition state (green line, Figure 5) with a free-energy barrier ΔG^≠ = 16.2 kcal/mol, remarkably close to that for the formation of PC’_syn (ΔG^≠ = 16.9 kcal/mol). Attempts to calculate a similar direct path for 3-Cu have led to a minimum energy species with a similar structure to that of TS’_syn/anti (see PC’_anti in Figure S1 in the SI), representing an additional isomer product of the alkyne insertion reaction.

For the syn/anti conversion through the two-step path, a higher activation barrier for the first step (“side reaction”) leading to (NON)AlEt and gold acetylide co-product PC_side has been calculated (ΔG^≠ = 31.1 kcal/mol), indicating that the migration of the Et group is not the preferred route to PC_anti. In addition, formation of PC_side is endoergonic by 6.2 kcal/mol and dissociation into (NON)AlEt and [^tBu₃PAuCCEt] separated species releases 2.5 kcal/mol (see Figure S1). Comparison between the corresponding PC_side thermodynamic stabilities for 3-Cu and 1-Au (−9.7 vs +5.9 kcal/mol) gives further indirect evidence supporting a less reactive gold site at 1-Au, while 3-Cu is capable of more strongly interacting with unsaturated CC bonds in this uncoventional nucleophilic reactivity. Finally, the PC_side conversion to PC_anti involving the Et group migration to the alkyne (via TS_syn/anti) has an activation energy of ΔG^≠ = 25.1 kcal/mol. As a result, one can expect that alkyne insertion into 1-Au would furnish a possibly isolable anti insertion product, with the syn product and the side (NON)AlEt product which could be more difficult to isolate and characterize, unless more forcing experimental conditions (higher temperatures and longer reaction times) are used.

This detailed mechanistic and orbital picture provides evidence that the exceptional gold Lewis acid standard reactivity (i.e., the ability of gold to promote insertion of π substrate through an inner-sphere or outer-sphere mechanism, see Scheme 3a,b) is switched in the nucleophilic M–Al scenario. This is consistent with neither an inner- or an outer-sphere mechanism, but it is best described as a cooperative radical-like mechanism (see Scheme 3c), where the actual nucleophile is the metal–aluminyl bond, analogously to what happens in the reactivity with carbon dioxide. This new mode of chemical reactivity by coinage metal complexes toward small molecules opens new perspectives beyond the framework of conventional properties, reactivity, and chemical behavior of coinage metal complexes.

Conclusions

In this work, the reaction mechanism of the alkyne insertion into the Cu–Al bond has been computationally investigated, based on the reported experimental characterization of the reactivity of a copper–aluminyl complex toward 3-hexyne.

The reaction mechanism we find here for the Cu–Al complex nicely agrees with the experimental observations. The calculations predict the activation barrier leading to the syn insertion product, where the alkyne approaches the complex closely to the copper site, to be significantly lower than that leading to the anti insertion product, in agreement with the experimentally observed kinetic control over syn product formation. Electronic structure analysis rationalizes the preferential syn formation, showing that the anti path is disfavored due to the substantial copper–aluminyl bond breaking occurring at the first transition state, which increases the distortion penalty and, consequently, the associated activation barrier.

The reaction mechanism calculated for the gold–aluminyl complex is qualitatively similar, predicting analogous kinetic control and preferential syn product formation due to energy penalty associated to early Au–Al bond breaking along the anti reaction path. However, alkyne insertion into the Au–Al bond is expected to furnish a less stable syn product, via an almost thermoneutral step, which could be more difficult to isolate and characterize. Interestingly, the mechanism reported here shows that the reaction is predicted to be less efficient for gold than for copper, in sharp contrast with the more efficient electrophilic reactivity of gold complexes toward unsaturated substrates. Extensive electronic structure analysis demonstrates that, in strict analogy with the reactivity reported for gold–aluminyl complexes toward CO₂, the driving force of the complex–alkyne interaction is the charge transfer from the electron-sharing copper– and gold–aluminyl bonds toward the π* LUMO of the alkyne. The Cu–Al and Au–Al bonds act as actual nucleophilic sites for the reaction, leading to a cooperative radical-like metal–aluminyl reactivity.

This nucleophilic behavior of M–Al bonds leads to a switch in the well-established paradigm for “standard” electrophilic reactivity at the coinage metal site toward unsaturated substrates. Upon thorough analysis, the generally accepted factor determining superior electrophilicity of gold complexes in this context (i.e., the relativistic stabilized valence 6s orbital) is found to lead here to a less nucleophilic Au–Al bond (where the valence Au configuration is close to 6s¹), leading to a less efficient charge transfer toward the alkyne and, in turn, to a less efficient reactivity.

These findings show that these new classes of copper and gold complexes bearing new-generation aluminyl ligands represent a new chapter in the coinage metal chemistry, where the nucleophilic behavior of the metal–aluminyl bonds induces a paradigm switch of established electronic features and, consequently, different trends in the reactivity with well-known substrates such as alkynes. Furthermore, the results reported here, showing a cooperative radical-like reactivity of the M–Al complexes toward 3-hexyne analogous to that toward carbon dioxide, suggest that these complexes may efficiently react with a range of other small molecules, opening new and unexplored paths for the reactivity of coinage metal complexes.

Computational Details

All geometry optimizations and frequency calculations on optimized structures (minima with zero imaginary frequencies and transition states with one imaginary frequency) for the alkyne insertion into the [^tBu₃PMAl(NON)] (M = Cu,Au) complexes have been carried out using the Amsterdam Density Functional (ADF) code^53,54 in combination with the related Quantum-regions Interconnected by Local Description (QUILD) program.⁵⁵ The PBE⁵⁶ GGA exchange-correlation (XC) functional, the TZ2P basis set with a small frozen core approximation for all atoms, the ZORA Hamiltonian⁵⁷⁻⁵⁹ for treating scalar relativistic effects, and the Grimme’s D3-BJ dispersion correction were used.^60,61 Solvent effects were modeled employing the conductor-like screening model (COSMO) with the default parameters for toluene as implemented in the ADF code.⁶² The same computational setup has also been used for the EDA, CD-NOCV, and ASM calculations and for computing the radical reactions between [Al(NON)], [EtCCEt], and [^tBu₃PM] fragments. This protocol has been used successfully in refs (1, 5) to study the [^tBu₃PAuAl(NON)] and [^tBu₃PAuCO₂Al(NON)] complexes reactivity. For further details and description of the methods used in this work, see the “Methodology” section in the Supporting Information.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.inorgchem.2c03713.

• Methodology, supporting tables (EDA results for 3-Cu and 1-Au, ASM results for 3-Cu and 1-Au, and analysis of the products formation from copper and aluminyl fragments and from gold and aluminyl fragments), figures (optimized structures with Cu/Au–alkyne direct interaction and NOCV isosurfaces of the main interactions at the TSs for 3-Cu and 1-Au) and scheme for the products formation via metal fragments, and xyz coordinates of all structures (PDF)

This work is funded by the Ministero dell’Università e della Ricerca (MUR, project AMIS, through the program “Dipartimenti di Eccellenza – 2018-2022”).

The authors declare no competing financial interest.