Abstract
Cytokine release syndrome (CRS) is a lethal adverse event in chimeric antigen receptor (CAR) T-cell therapy, hindering this promising therapy for cancers, such as B-cell acute lymphoblastic leukemia (B-ALL). Clinical management of CRS requires a better understanding of its underlying mechanisms. In this study, a computational model of CRS during CAR T-cell therapy is built to depict how the cellular interactions among CAR T-cells, B-ALL cells, and bystander monocytes, as well as the accompanying molecular interactions among various inflammatory cytokines, influence the severity of CRS. The model successfully defines the factors related to severe CRS and studied the effects of immunomodulatory therapy on CRS. The use of the model is also demonstrated as a precision medicine tool to optimize the treatment scheme, including personalized choice of CAR T-cell products and control of switchable CAR T-cell activity, for a more efficient and safer immunotherapy. This new computational oncology model can serve as a precision medicine tool to guide the clinical management of CRS during CAR T cell therapy.
Keywords: CAR T-cell therapy, computational model, cytokine release syndrome, leukemia
Graphical Abstract
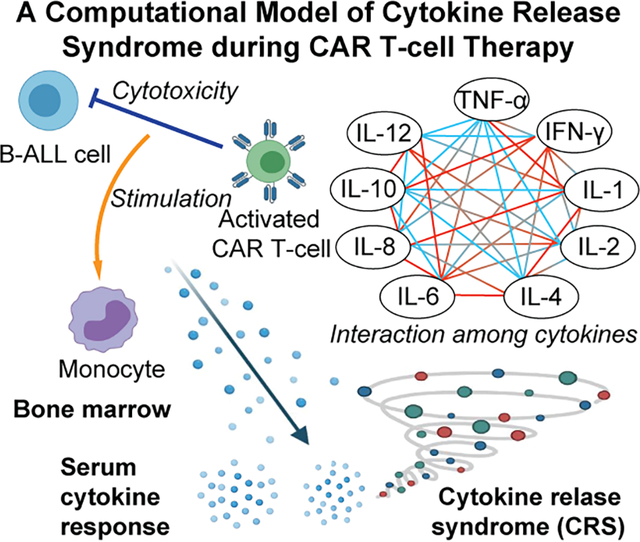
Cytokine release syndrome (CRS) is a lethal adverse event in chimeric antigen receptor (CAR) T-cell therapy for B-cell acute lymphoblastic leukemia. A computational model of CRS during CAR T-cell therapy is established using clinical data to faithfully recapitulate the whole picture of cellular and molecular interactions in CRS, which can be used for guiding clinical management of CRS.
1. Introduction
CAR (chimeric antigen receptor) T-cell therapy is a promising immunotherapy for B-cell acute lymphoblastic leukemia (B-ALL); however, its major adverse effect, cytokine release syndrome (CRS), frequently occurs and compromises its therapeutic potential [1]. Clinically, CRS is a systemic inflammatory reaction that includes fever, coagulopathy, renal insufficiency, and hypotension, and is caused by excessive pro-inflammatory cytokines in blood serum, typically within the first 14 d after CAR T-cell infusion [2]. CRS is commonly observed in 70–80% of patients receiving CAR T-cell therapy, and approximately 30% experience severe CRS [2–3]. Thus, addressing CRS is an important requirement for the safer utilization of CAR T-cell therapy.
Clinical monitoring of CRS is typical during CAR T-cell therapy, whereby a series of factors correlated with CRS and the corresponding statistical relationships can be used to guide clinical practice [4]. For example, statistical methods have demonstrated that the risk of experiencing severe CRS is affected by the tumor burden of patients and CAR T-cell dose [3b, 4–5], and is characterized by clinical laboratory parameters, such as body temperature and cytokine concentrations in blood serum [4, 5b]. These statistical methods fit the parameters and the risk of CRS into a regression expression [4, 5b] or decision tree [4, 5b] without a complete understanding of the underlying immunological mechanisms, and give an estimation of CRS for new patients based on the presumption that they are well represented by the previous patients. However, such a representation is doubtful when novel or personalized treatments are used, as no precedent comparable data is available. Thus, statistical methods are not the ideal choice to allow clinicians to take effective preemptive measures against adverse effects, such as CRS in immunotherapy. To assist in the development of new preemptive measures, a model must refer to how these measures work, namely, looking into the biological mechanism. Recently, computational models of immunotherapy have served as valuable tools for dissecting the pathophysiological mechanisms of CRS. For instance, quantitative models have been developed to depict the release of cytokines such as IFN-γ, IL-6, and IL-10 during CRS [6] and further grade the severity of CRS [7]. Various cytokines promote or suppress each other during CRS, forming an interaction network [8]; however, such a depiction is lacking in existing models with cellular mechanisms. Critically, the cellular mechanisms causing CRS, for example, how activated CAR T-cell cells trigger bystander immune cells, such as monocytes in the bone marrow, to secrete excessive cytokines that diffuse into the serum and provoke a systemic inflammatory response [9], are understudied in current CRS models. Thus, new models that can recapitulate key cellular and cytokine networks and dynamics are critical for identifying potential risk factors and screening for effective mitigation strategies for severe CRS.
In this study, we developed a computational model of CRS to mechanistically describe the critical cellular interactions between CAR T-cells and B-ALL cells, as well as bystander monocytes, which are a prominent source of cytokines in CRS [10] in the bone marrow during immunotherapy treatment. Based on existing clinical data, we in silico studied how these cellular interactions trigger the activation of monocytes and cause the release of excessive cytokines, and how the molecular network among cytokines regulates CRS. Our novel computational CRS model based on the cellular-molecular interactions provides a practical tool for understanding, estimating, mitigating, and managing CRS clinically. Based on the model, we estimated the probabilities of patients experiencing severe CRS and studied how anti-IL-6R immunomodulatory therapy can mitigate CRS severity. We also demonstrated that our model can be used to guide clinical practice, for example, the choice of 4-1BB or CD28 costimulatory CAR T-cell products and control of switchable CAR T-cell activity for more efficient and safer immunotherapy.
2. Results
2.1. Computational modeling of CRS on cellular and molecular levels
During CAR T-cell therapy, infused CAR T-cells are activated by B-ALL cells, with enhanced expansion and tumor elimination activities. Activated CAR T-cells trigger bystander immune cells such as monocytes in the bone marrow to secrete excessive cytokines that diffuse into the blood circulation and provoke the systemic inflammatory response of CRS [9]. To capture the cellular-level interactions among CAR T-cells, B-ALL cells, and monocytes and the molecular-level cytokine dynamics during CAR T-cell therapy, a multicompartmental model was established using ordinary differential equations (ODEs) (Fig 1; Details see ‘Formulation of the model’ in Methods). The cellular interaction model features the growth, activation, and apoptosis of CAR T-cells, the expansion and loss of the CD19 antigen on B-ALL cells, B-ALL elimination by CAR T-cells, and the stimulation of monocytes by the lysis activity of CAR T-cells. Furthermore, we modeled the release of nine key cytokines (TNF-α, IFN-γ, IL-1, IL-2, IL-4, IL-6, IL-8, IL-10, and IL-12) from activated CAR T-cells and monocytes. We assumed that the release rates of these cytokines into the serum were associated with the number of activated CAR T-cells and monocytes. Moreover, we accounted for the alteration of secretion and degradation of one cytokine due to the presence and change in other cytokines by describing the systemic response with an interactive feedback network. Such an interaction was previously modeled based on serum cytokine measurements in a clinical trial in which a single dose stimulation of a medicine induced a cytokine storm in adults [8b]. Using the computational model, we mapped the serum cytokine concentrations to the probability of severe CRS (see next subsection) to provide a complete modeling of CRS.
Fig 1. A scheme of the CRS model showing key cellular and cytokine interactions in the bone marrow and serum.
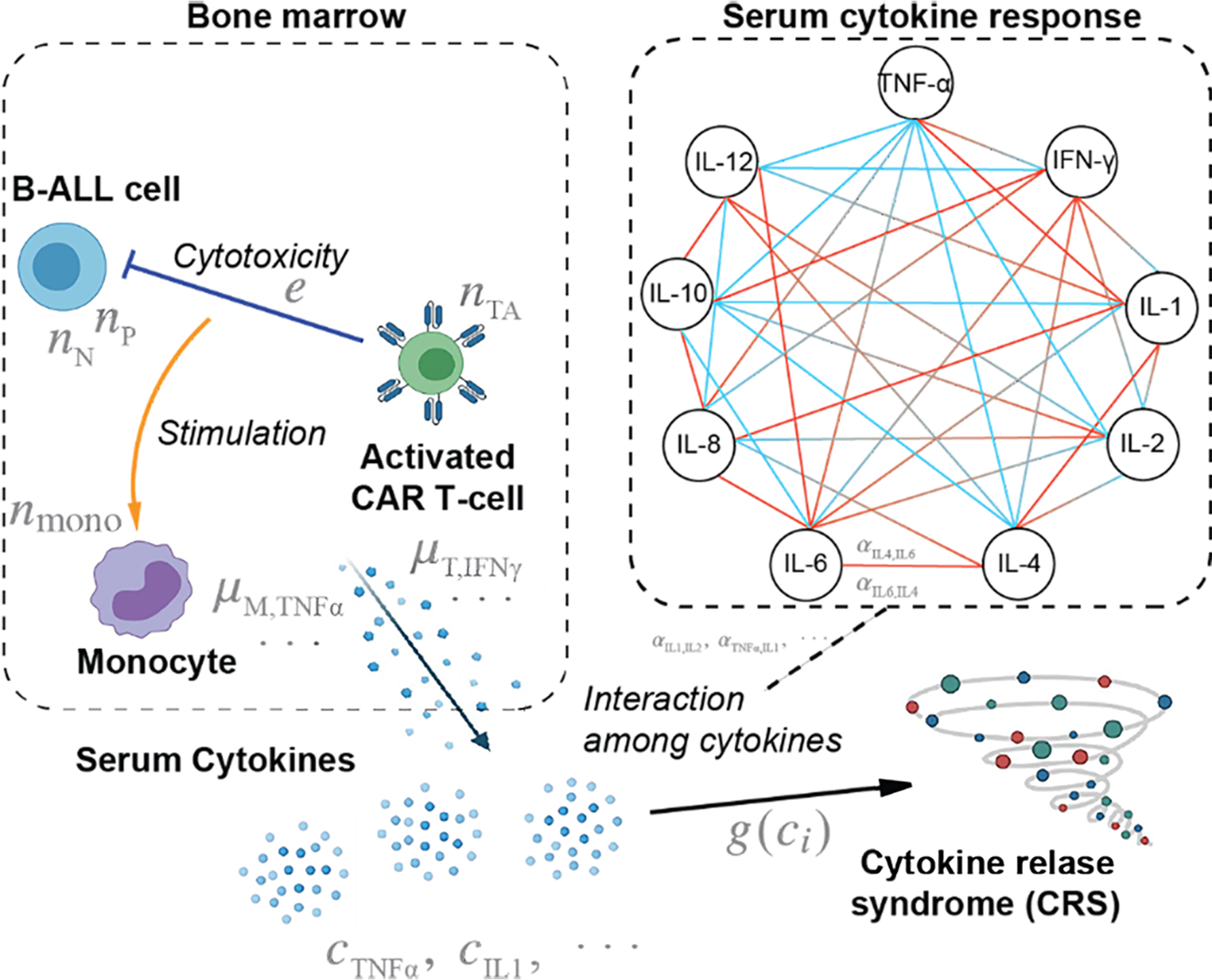
For the cytokine interaction network scheme on the right panel, red ends denote promotion, whereas blue ends denote inhibition. Briefly, activated CAR T-cells kill B-ALL cells through cytotoxic activity, and this killing process stimulates monocytes in the microenvironment. The monocytes secrete multiple cytokines in response, whereas the activated CAR T-cells also secrete cytokines. These cytokines, from local inflammation in bone marrow, then enter blood circulation in excessive amounts and induce systematic reaction, leading the body to respond with altered cytokine secretion and degradation, which is seen as interactions among cytokines. The excessive cytokines from bone marrow, with such interactions, accounts for the high cytokine level in the serum, which demonstrates CRS.
The model was calibrated as a nonlinear mixed effect (NLME) model based on the clinical data of 17 patients (see ‘Collection of clinical data’ in Methods). To ensure robustness, we kept the number of parameters as low as possible (nine parameters vs. 17 patients), and we calibrated the population level parameters to represent the general population to avoid overfitting. This population-level calibration provided an estimation of the probabilistic distribution of parameters of the population and individual patients (see ‘Model Calibration’ in Methods). Then, we applied the Monte Carlo method to obtain an estimation of the time series profile of the characteristic cytokines IL-6, IL-2, and IL-1 in CRS, which was consistent with clinical measurements (Fig 2A–C), justifying our use of the population level parameters in further development of the model. Additionally, as a trade-off with model robustness under limited data availability and quality, we did not target fitting our model to match individual patient results (Supplementary Fig S2), but aimed to obtain the overall trends of these real-time results (Fig 2D–G) during CRS. We defined an equivalent monocyte number, which was assumed to be proportional to the number of activated monocytes in the bone marrow (see Equation (7) in Methods). After calibration, we inspected the real-time dynamic results provided by the model, such as the numbers of CAR T-cells and equivalent monocytes in the bone marrow (Fig 2D), cytokine release rates in the bone marrow (Fig 2E) and serum (Fig 2F), and concentrations of different cytokines in the serum (Fig 2G) of individual patients. Notably, the distinct IL-6 release rate profiles of patients #1 and #2 in the bone marrow (Fig 2E) and serum (Fig 2F), arising from the distinct setting of the two clinical trials, and the fact that patient #1 is a pediatric patient, whereas #2 is not, justified our choice to trade off individual fitting closeness to compensate for the data source availability and quality. In contrast, the similarity between patients #2 and #3, obtained from the same clinical trial, demonstrated that our strategy preserved the robustness of the model, as expected.
Fig 2. Calibration and simulation results of the CRS model.
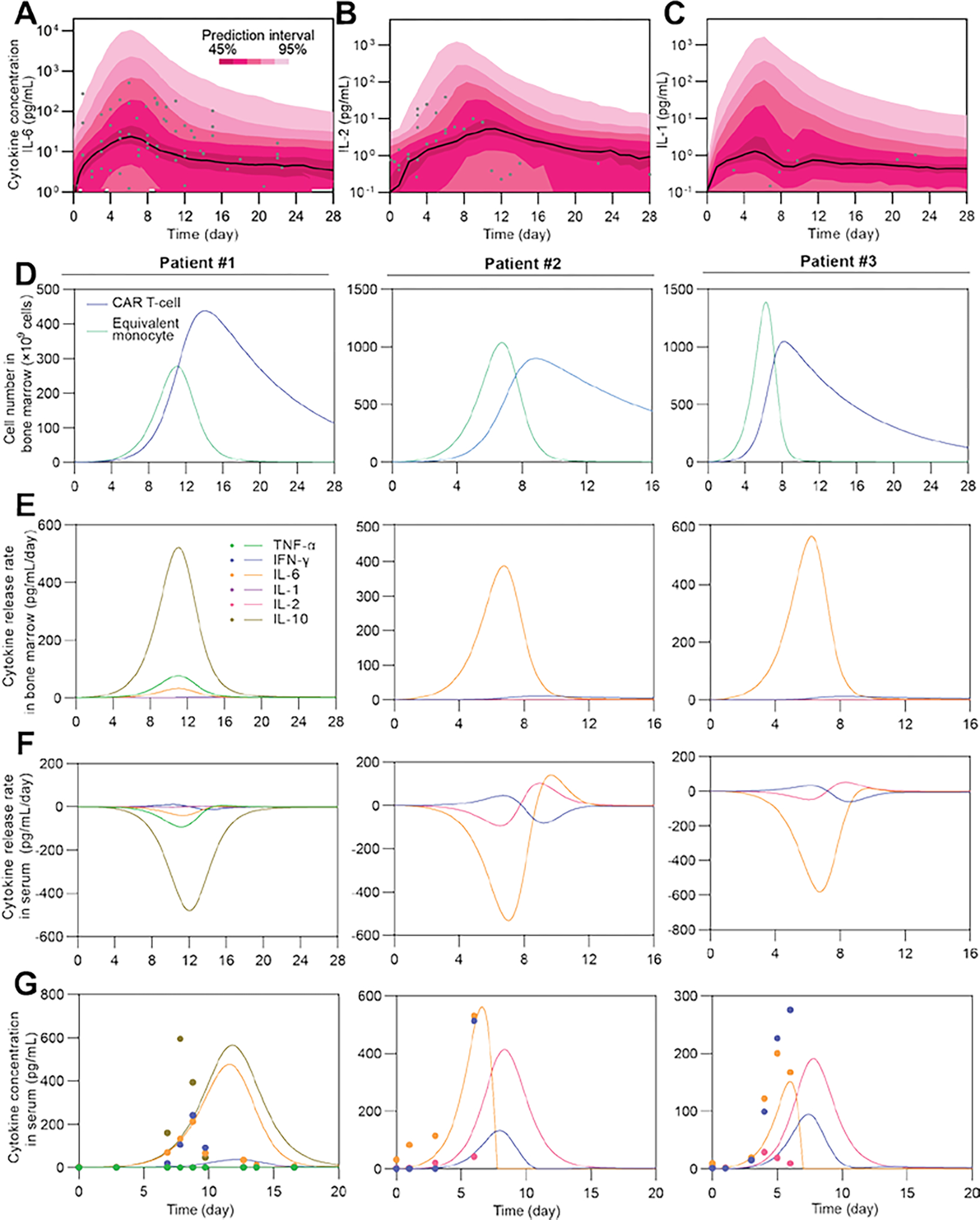
(A–C) Calibration results and simulation using Monte Carlo method to estimate the distribution of IL-6 time series of the population. Black lines show median, color bands show prediction intervals with different probabilities, and dots show clinical observations. Patient number = 17. (D–F) Simulated time series of CAR T-cell and equivalent monocyte number in bone marrow (D), and cytokine release rates in bone marrow (E) and serum (F). Negative release rate in F means clearance of cytokines. (G) Experimental (dot) and simulated (line) time series results of concentrations of different cytokines in serum.
2.2. Risk factors of severe CRS
A high tumor burden is clinically associated with a higher risk of CRS [3b, 5]. The proposed model captured the correlation between the initial tumor burden and the peak concentrations of cytokines, such as IFN-γ, IL-8, and IL-6, validating the clinical observations (Fig 3A). Our simulation results also showed that the amount of CAR T-cells and monocytes in the first 7 d after CAR T-cell infusion, defined as the area-under-curve of time series amount of CAR T-cells and monocytes from day 0 to day 7 (AUC7), were positively correlated with the initial tumor burden, reflecting the stimulation of B-ALL cells to CAR T-cell cells and monocytes (Fig 3B).
Fig 3. Factors affecting the cytokine dynamics and probability of severe CRS.
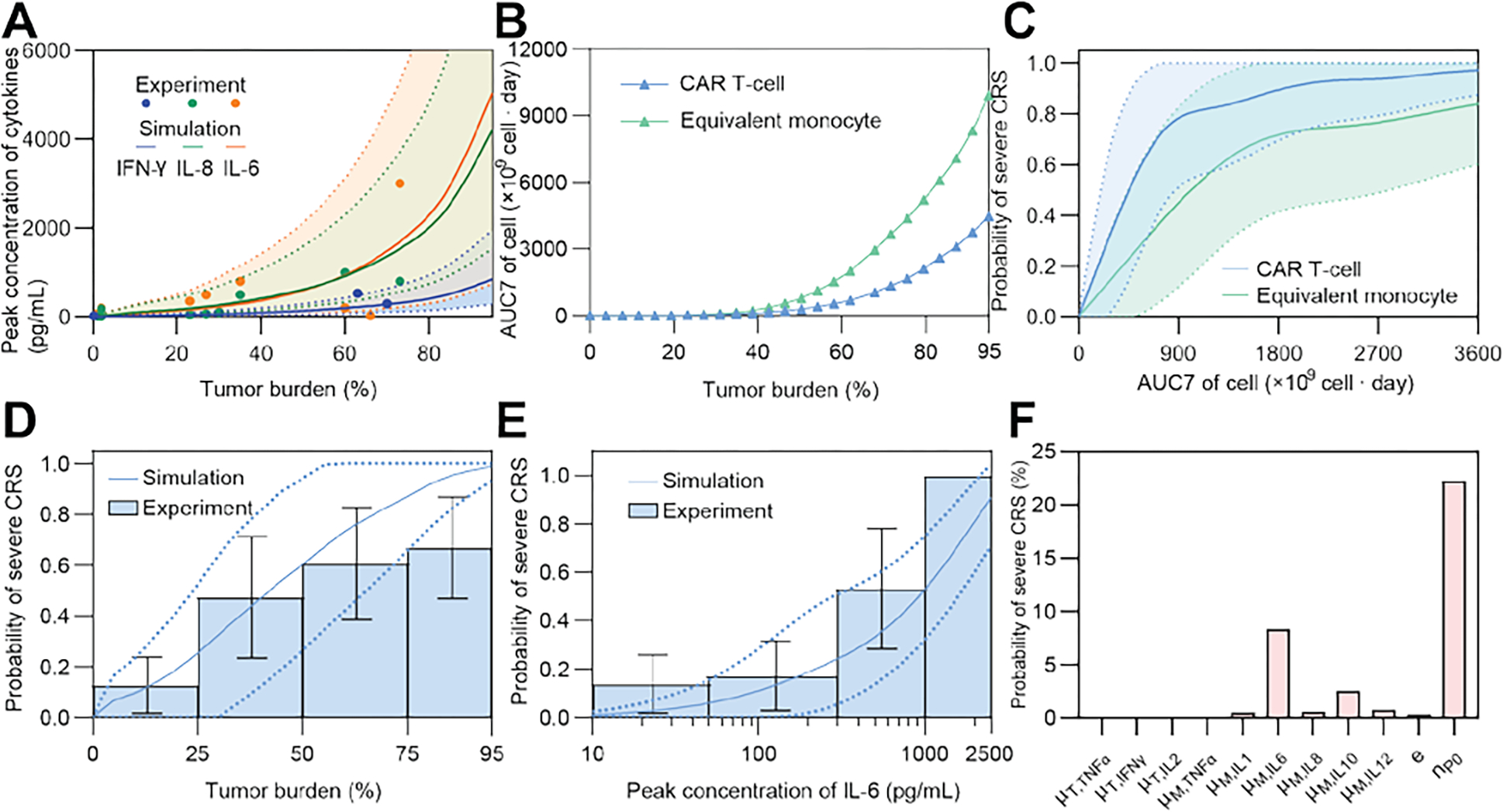
(A) The relationship between tumor burden and peak concentration of cytokines (IFN-γ, IL-6, and IL-8) of the population through a virtual patient cohort generated using Monte Carlo simulation. Data of IFN-γ were from the previous calibration process, and data of IL-6 and IL-8 were for validation. Solid lines represent the median of simulated results, whereas dotted lines denote quartile boundaries. Cohort size = 2000. (B) The relationship between AUC7 of CAR T-cells and equivalent monocytes and the tumor burden. (C) The relationship of the probability of severe CRS and AUC7 of CAR T-cells and monocytes of the population through a virtual patient cohort generated using Monte Carlo simulation. Solid lines show the median and bands show quartile boundaries. Cohort size = 4000. (D, E) Variation of the probability of severe CRS of the population through a virtual patient cohort (size = 1000) generated using Monte Carlo simulation as tumor burden (D) and peak concentration of IL-6 (E) change, validated against clinical data (patient number = 60(D), 95(E)). Solid lines show the median and dotted lines show quartile boundaries. Histogram shows clinical data in different tumor burden intervals; error bars denote standard mean ± standard deviation (SD). (F) Sensitivity analysis of parameters illustrated by changing each parameter +10%. Bars show the corresponding changes of the probability of severe CRS.
In our model, we estimated the probability of severe CRS, which is equivalent to grade 3 or above CRS graded based on clinical symptoms, by calculating the difference between the concentrations of various cytokines with their typical values for severe or mild CRS (equivalent to grade 2 or below CRS) (see ‘Estimation of the probability of severe CRS’ in Methods). To validate the estimation, considering that the number of clinical samples is limited, we generated virtual patient cohorts based on lognormal distribution of the population level secretion coefficients of cytokine calibrated from clinical data to simulate the distribution of outputs of interest, such as the probability of severe CRS (see ‘Monte Carlo simulation of virtual patient cohorts’ in Methods).
The modeling results showed that the probability of severe CRS was positively correlated with the AUC7 of CAR T-cells and equivalent monocytes (Fig 3C). In addition, the probability of severe CRS increased with increasing initial tumor burden (Fig 3D) and peak concentration of IL-6 (Fig 3E), recapitulating the experimentally observed proportion of severe CRS among a collection of 155 patients (95 with IL-6 data and 60 with tumor burden data) (see ‘Collection of clinical data’ in Methods). This clinical observation was confirmed by our sensitivity analysis of the model, which indicated the key role of the initial tumor burden (nP0) and the release rate of IL-6 (μM,IL6) in invoking CRS (Fig 3F).
In addition, the simulation results indicated that as the initial tumor burden increased, the IL-6 concentration peaked earlier (Fig 4A). The peak concentration of IL-6 in the serum was negatively correlated with the time for IL-6 to reach a peak (Fig 4B). This implies that if a patient with a high tumor burden has an increase in IL-6 at an early stage, the patient may have more severe CRS, and additional measures may be necessary to mitigate the CRS risk. We further found that the release rate of IL-6 from equivalent monocytes and the initial number of B-ALL cells were two key risk factors that synergistically induced severe CRS (Fig 4C).
Fig 4. Influence of IL-6 on the development of severe CRS.
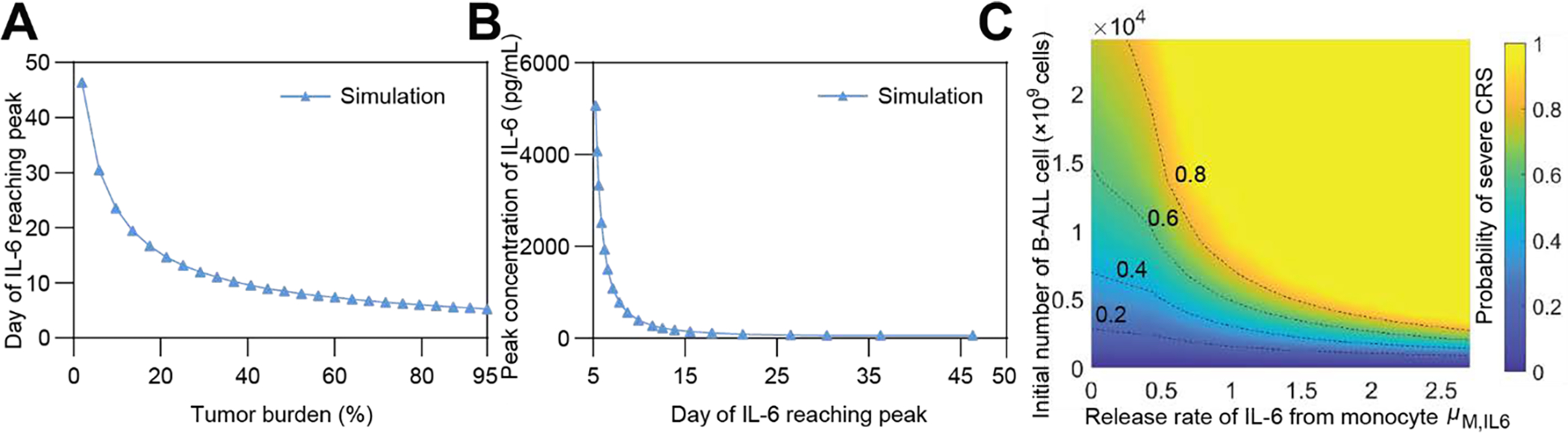
(A) Negative correlation between the day of IL-6 reaching peak and initial tumor burden. (B) Negative correlation between the peak IL-6 concentration and the day of IL-6 reaching peak. (C) Variation of the probability of severe CRS as the initial number of B-ALL cells (equivalent to tumor burden) and the release rate of monocytes of IL-6, μM,IL6 change.
A more comprehensive evaluation of CRS risk needs to include cytokines other than IL-6 [4, 5b]. Thus, we proposed a CRS factor, FCRS, that depends only on the release rate of each cytokine, the killing efficiency of CAR T-cells, and the initial tumor burden to depict the extent of CRS (see ‘CRS factor’ in Methods). Based on the fitting results of individual patients, a positive correlation between FCRS and the probability of severe CRS was observed (Fig 5A). A similar trend was verified by simulation results of a virtual patient cohort based on the Monte Carlo method (Fig 5B). As the initial tumor burden and the release rate of IL-6 from equivalent monocytes, μM,IL6, increased, FCRS also increased (Fig 5C), showing the same trend as the probability of severe CRS (Fig 4C), further confirming the consistency of the findings. Therefore, FCRS is a valuable patient-specific CRS function factor capable of providing implications for the risk of developing severe CRS and the necessity of mitigation measures against CRS for a B-ALL patient in the early stage of CAR T-cell therapy.
Fig 5. The patient-specific CRS factor predicts the probability of severe CRS.
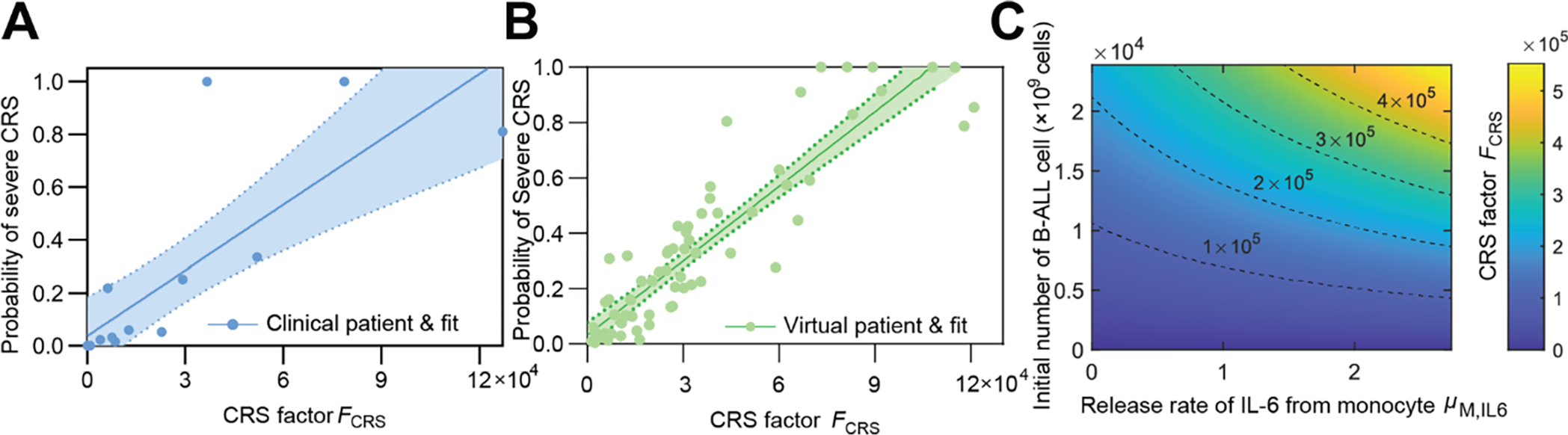
(A) The CRS factor, FCRS, shows linear correlation to the probability of severe CRS. Dots show data of individual patients and line shows linear fit. Band denotes 95% confidence interval. Patient number = 17. (B) Monte Carlo simulation of a virtual patient cohort showed similar correlation between FCRS and estimated probability of CRS. Dots show virtual patients and line shows linear fit. Band denotes 95% confidence interval. For A and B, the probability of severe CRS saturated with too large FCRS, trivially not obedient to the linear correlation, which was neither included by the plot nor used in linear correlation. Cohort size = 100. (C) The variation of CRS Factor FCRS as the initial number of B-ALL cell (equivalent to tumor burden) and the release rate of IL-6 from monocytes, μIL6,M changed.
2.3. In Silico modeling of CRS mitigation
One common measure to mitigate CRS is the use of tocilizumab, a monoclonal antibody targeting the IL-6 receptor, IL-6R [11]. To mechanistically understand such treatment, we included the competitive binding process of tocilizumab and IL-6 to IL-6R (see ‘Modeling of tocilizumab effect’ in Methods) into our computational model: tocilizumab decreases the number of IL-6 and IL-6R complexes formed by binding with free IL-6R. Our simulated results demonstrated a decrease in the probability of severe CRS by 0.25 with preemptive tocilizumab starting from the day of CAR T-cell infusion, which was consistent with the trend shown in clinical trials [12] (Fig 6A). Based on the simulation of virtual patient cohorts, it was shown that the reduced CRS severity is largely due to the decreased effective bioavailability of IL-6, which is defined as the equivalent concentration of IL-6 affected by the competition between tocilizumab and IL-6 in binding with IL-6R (Fig 6B). The characteristics of CAR T-cell therapy after tocilizumab application were depicted and compared with those of the control group (Fig 6C–F). The concentration of IL-6 increased after adding tocilizumab because of the negative feedback after IL-6R was bound to the drug (Fig 6C). The risk of severe CRS after tocilizumab application decreased in various initial tumor burdens (Fig 6D) and peak IL-6 concentrations (Fig 6E). The decreased slope of the linear correlation between the probability of severe CRS and the CRS factor confirmed the tendency of a lower risk of CRS with the application of tocilizumab (Fig 6F).
Fig 6. Mitigation of CRS with tocilizumab.
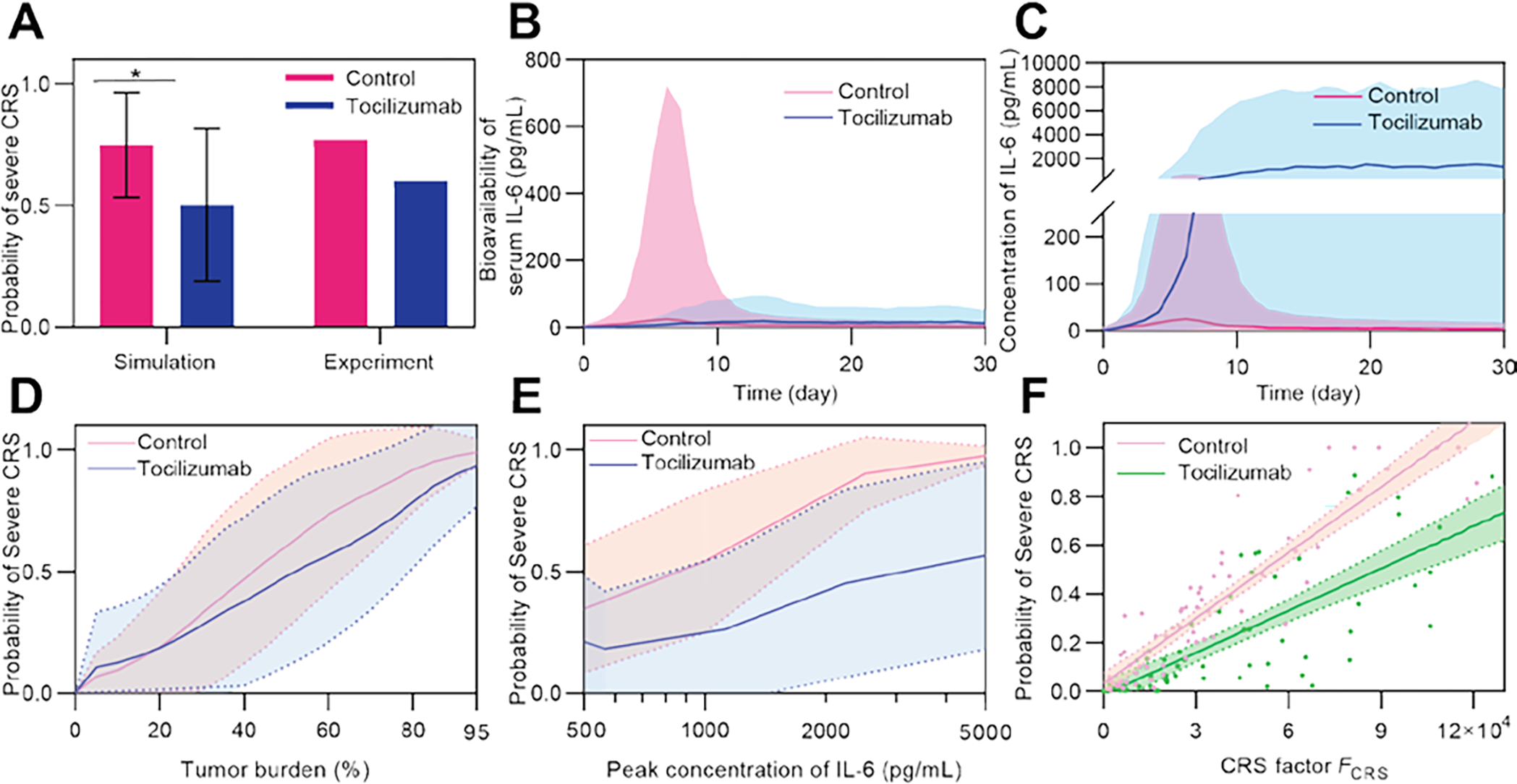
(A) Simulated probability of CRS in the control and tocilizumab treatment groups. Simulation was conducted among a virtual cohort (size = 1500) with high tumor burden of 40–95% to match the high tumor burden cohorts (≥ 40%) in clinical trials [12] (patient number = 15 (tocilizumab) and 26 (control)). Error bars denote mean ± SD. P-values were calculated using Student’s t-test. *p<0.05. (B) Comparison of simulated bioavailability and (C) concentration of IL-6 between the control and tocilizumab treatment groups. Lines denote median and bands denote quartile boundaries. Cohort size = 200. (D, E) Variation of probability of severe CRS as tumor burden (D) and peak concentration of IL-6 (E) changed, and comparison between the control and tocilizumab treatment groups. Solid lines show median and dotted lines show quartile boundaries. Cohort size = 400. (F) Monte Carlo simulation of two virtual patient cohorts show decreased probability of severe CRS with tocilizumab treatment compared to the control group. Dots show virtual patients, lines show linear fit, and bands denote 95% confidence interval. Cohort size = 100.
2.4. In-silico selection of CAR T-cell products
Current CAR T-cell products targeting CD19 for B-ALL have a costimulatory domain of either 4-1BB or CD28, whereas 4-1BB products respond slower than CD28 products, but more persistently [13]. This slower response may help reduce the risk of severe CRS but has also raised concerns about tumor escape from CAR T-cell treatments. We modeled this difference between the two CAR T-cell products by tuning CAR T-cell activation, proliferation, and death rates. Since there are no published clinical data quantifying the extent to which 4-1BB products respond more slowly than CD28 products, we tested through the range of two, five, or ten times slower responses (for example, two times slower response means the CAR T-cell activation, proliferation, and death rates were all divided by a factor of two). By testing in a virtual cohort, we found that the slower the response, the later the probability of severe CRS would peak, and the lower the peak would be (Fig 7A). This indicated that the 4-1BB CAR T-cell product, which had a relatively slower CAR T-cell response, demonstrated later and milder CRS symptoms compared to the CD28 CAR T-cell products, in accordance with clinical observations [13]. However, such an improvement in terms of CRS came at the cost of delayed tumor elimination (Fig 7B). Moreover, as we examined two patients with different initial tumor burdens and cytokine release rates treated with the same 4-1BB CAR T-cell product (assumed to be five times slower CAR T-cell response), we found distinct treatment outcomes and CRS responses. Our simulation results showed that patient #1 presented a significant improvement in severe CRS probability (blue lines in Fig 7B), whereas patient #2 presented only minor improvement. This indicated that the optimal choice of CAR T-cell products, such as CD28, 4-1BB, or other novel products under development, may vary between patients. In this instance, our model is valuable for personalized precision medicine. We demonstrated this concept by determining the change in D60 tumor burden (efficacy of product) and peak probability of severe CRS (safety of product) with control and five times slower CAR T-cells in a virtual cohort (Fig 7C). With our model, we were able to identify patients who benefited from a reduction in severe CRS probability without compromising efficacy, and those who benefitted little, but showed a large decrease in efficacy.
Fig 7. In-silico modeling and comparison of 4-1BB and CD28 CAR T-cell products.
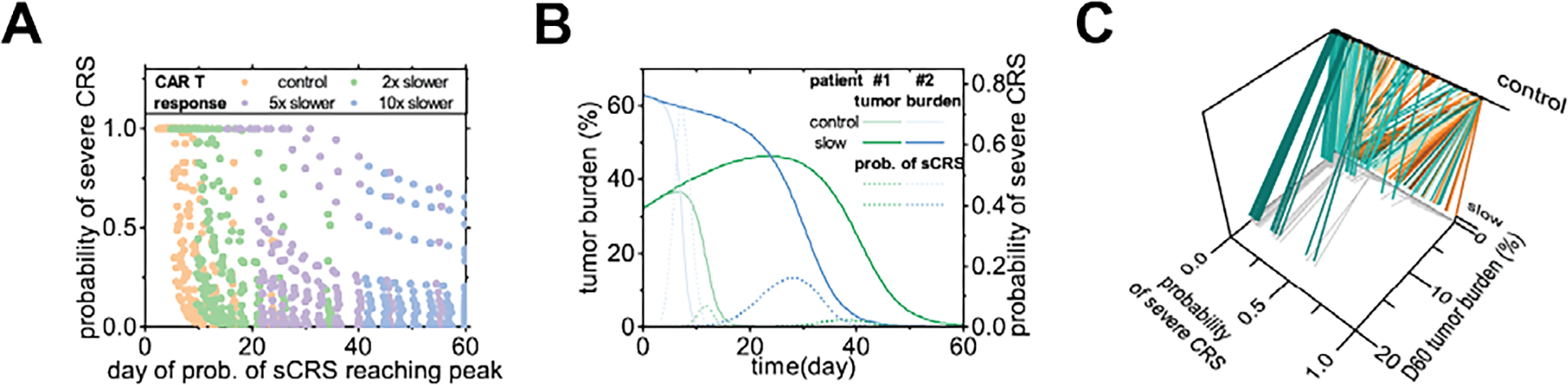
(A) Peak probability of severe CRS and the day of the peak, for a virtual cohort of 200 virtual patients, with CAR T-cell response two, five, and ten times slower. Cohort size = 200. (B) Time series of tumor burden and probability of severe CRS of patients #1 and #2, with control or five times slower CAR T-cell response. (C) In a virtual cohort of 200 patients, the peak probability of severe CRS and the tumor burden at day 60 with control or five times slower CAR T-cell response. Lines link individual virtual patients. Cohort size = 200.
2.5. Optimizing the treatment scheme of switchable CAR T-cell products
For better management of the safety of CAR T-cell therapy, novel CAR T-cell products with switchable activity have been developed. After infusion, these CAR T-cells can be switched on and off through external signals, such as small molecules or optical signals (Fig 8A) [14]. Currently, such products are still under development, and periodic switching has been experimentally tested [14a]. It is also possible to switch off the activity once the clinical assay determines that the risk of CRS reaches a certain level and resumes CAR T-cell activity after the risk decreases, that is, switching is conditionally triggered. Generally, periodic switching can be characterized by the period and duty cycle, whereas a conditionally triggered switching can be characterized by the time needed from taking the sample to decision of switching (denoted “assay lag” here), and the threshold of the assay indices to switch on or off (Fig 8B). With our model, we simulated the tumor burden and the probability of severe CRS in a patient, with periodic switching or conditionally triggered switching (Fig 8C). By varying the duty cycle and the period of the switching (Fig 8D), we found that the duty cycle influenced the outcome most significantly; a suitable duty cycle balances the efficacy (by D30 tumor burden) and safety (by peak severe CRS probability). More frequent switching with a shorter period also slightly improved the peak severe CRS probability without compromising efficacy. In addition, by simulating different assay lags and severe CRS probability cut-offs, we found that both factors significantly influenced the outcome (Fig 8E). A suitable cutoff would reduce the risk of CRS without compromising anti-tumor efficacy, and the shorter the assay lag, the greater the benefit. By plotting both methods with the D30 tumor burden and peak probability of severe CRS, we found that the triggered scheme has the potential to outperform the periodic scheme. This urges rapid feedback monitoring of indices such as cytokines, for flexible and timely switching of CAR T-cells, when the developing switchable CAR T-cell products come into clinical use.
Fig 8. In-silico modeling of the treatment schemes and outcomes of switchable CAR T-cell products.
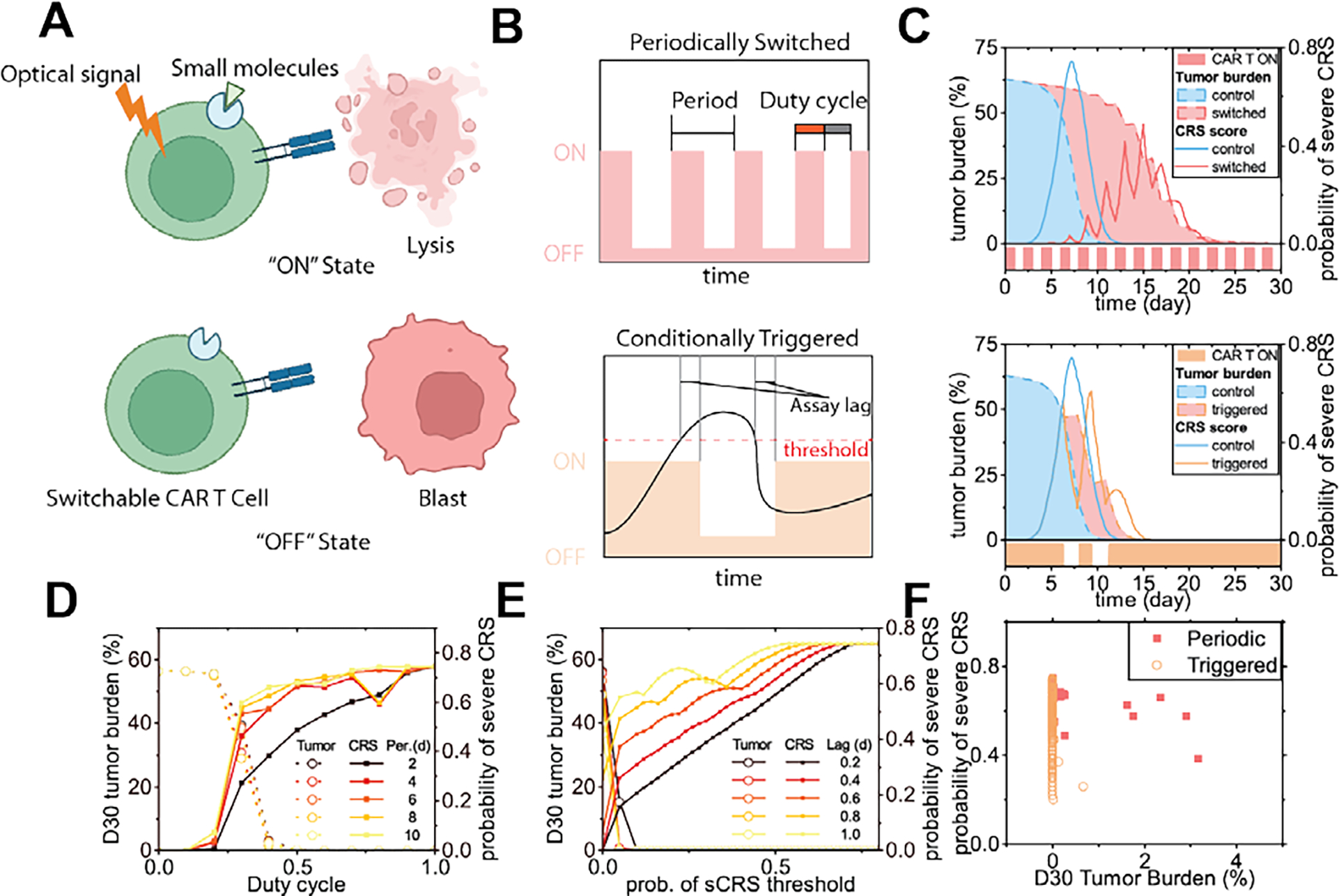
(A) Scheme of switchable CAR T-cells. (B) Two possible switching schemes. (C) Tumor burden and probability of severe CRS responding to switching of the CAR T-cells through two different schemes (patient #2). (D) Tumor burden at day 30 and peak CRS probability of the periodic switching scheme, as the duty cycle and the period changed. (E) Tumor burden at day 30 and peak CRS probability of the conditionally triggered scheme, as the severe CRS probability threshold and the assay lag changed. (F) Peak probability of severe CRS and D30 tumor burden, as the factors of the two controlling schemes were varied.
3. Discussion
In this study, a mechanistic model of CRS was built to depict the key cellular mechanisms and cytokine responses that drive and influence CRS severity. The inclusion of cellular level information together with the cytokine interaction network in our model enabled it to describe the pathogenesis of CRS in detail, making it superior to current phenomenological approaches that rely on clinical laboratory parameters such as body temperature and blood cytokine concentrations. This computational model was calibrated with clinical data collected from various clinical trials and validated the clinical observations that the initial tumor burden and IL-6 level are two major factors that positively correlate with the severity of CRS. We established that the cellular interactions among B-ALL, CAR T-cells, and monocytes in the bone marrow and their associated excessive secretion of cytokines, including IL-6, are responsible for CRS progression. By defining the CRS factor, FCRS, based on the parameters of initial tumor burden, killing efficiency of CAR T-cell, and release rates of key cytokines, our model was able to accurately estimate the probability of severe CRS for individual patients. Moreover, we successfully simulated CRS intervention using a monoclonal antibody, tocilizumab, targeting IL-6R as a proof of concept. Such a clinical input-informed CRS model can thus guide the clinical management of CRS during CAR T-cell therapy, screen effective and personalized mitigation strategies for patients with severe CRS, and serve as a precision medicine tool to help select more suitable CAR T-cell products and optimize treatment schemes for individual patients.
Limited data availability and quality posed a challenge to the robustness of our model. During the development of our model, we merged data from various clinical trials to enlarge the dataset to compensate for the challenge that there was only limited clinical cytokine data available in current CAR T-cell therapy trials. However, the data originated from various clinical trials with different settings, including differences in age, CAR T-cell type, source and dose, and pretreatment. This gave rise to the concern of overfitting of parameters with a small number of patients available and the large noise from differences in conditions among clinical trials. In general, we kept our model robust by limiting the number of parameters to fit to avoid an overfitting problem. For example, in the modeling of cytokine release from the bone marrow, we directly associated cytokine release with the number of cells in the bone marrow. This simplification was possible because the process of excessive cytokines entering the blood is fast, owing to the low volume and high vessel density of the bone marrow. Such simplification reduced the number of free parameters in the model (otherwise dedicated parameters should have been included to depict the volume of the bone marrow, the rate of the transport of cytokines from bone marrow, and the nonlinear terms of the secretion, such as Michaelis-Menten terms), providing the model with a more robust structure. Similarly, when defining the CRS factor, the weights of different cytokine release rates should ideally be calibrated with clinical data; however, that calibration requires data of all related cytokine concentrations in comparable clinical trials, preferably with cellular cytokine secretion measured by phenotyping. However, few clinical trials with all cytokine concentrations have been published to date. Therefore, we had to simplify our definition and assign the weights of cytokine release rates by empirical experience, such as assigning a higher weight to IL-6 for its pivotal role. By determining the probability of severe CRS and other factors, we showed that although this definition was imperfect, it was a functional prototype of a comprehensive factor that can estimate the risk of CRS for each patient before the start of therapy.
Although many types of cytokines in CRS have been studied in previous computational models [6, 8a], the extent to which each cytokine group contributes to CRS has not been well defined. A mathematical model was recently proposed to study the interaction of multiple cytokines in CRS [7]. Similarly, our model established a cytokine interaction network of nine cytokines for more accurate estimation of the risk of developing severe CRS. In the model, the estimation of severe CRS probability was influenced by the scope of cytokines considered, which was limited to the few types of cytokines in current studies. This is largely because of the lack of relevant clinical data. In addition to the current measured cytokine concentrations in serum, a large-scale and single-cell profiling of dynamic cytokine secretion and the phenotype of immune cells in bone marrow [15] may better validate our model to depict the mechanism underlying CRS. Because our model is structured in matrix form, it can be expanded easily to include more cytokines and mitigations when more sufficient clinical data become available in the future. For example, IL-1 has recently attracted attention as an important cytokine in CRS [16] and as a potential target for CRS mitigation (for example, Anakinra [17]). However, as IL-1 has not been a routinely measured cytokine for CRS before its importance has been recognized, there is limited serum data and response to mitigation data of IL-1 for B-ALL available to date, which is insufficient to build and validate a model. As the data accumulate in ongoing clinical trials (e.g., NCT04148430), we will be able to add mitigations such as Anakinra in our model and compare the IL-1 response with the experiment. Furthermore, whereas current models of CRS on CAR T-cell therapy mainly use data collected from single clinical trials [6] or animal model studies [8a] and various CRS grading standards have been proposed based on different clinical symptoms [18], our model incorporated clinical data from various trials and estimated the occurrence of CRS with quantitative standards, providing a broader implication for CRS pathogenesis.
CRS, typically interchangeable with the term ‘cytokine storm’, is observed in several scenarios apart from CAR T-cell therapy. Our method that combines both the cytokine interaction model and the cellular model may not be limited to CAR T-cell therapy. By modifying the cellular interactions with immune cells, host cells, and viruses, our modeling framework can be adapted to the scenario of viral infection, such as the cytokine storm during the infection of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2). Similarly, our modeling of mitigation can also be generalized to assist in comparing the use of mitigations, such as tocilizumab in CAR T-cell-induced CRS and SARS-CoV-2-induced CRS [19].
In conclusion, we built a computational model depicting the cellular mechanism and cytokine response of CRS to estimate the severity of CRS, studied the effect of immunomodulatory therapy, and used the model to optimize the treatment scheme to balance the risk of CRS and the efficacy of therapy. We believe that this model can provide insights into the cause of occurrence and the estimation of CRS during CAR T-cell therapy, as well as other cytokine-related toxicities such as the cytokine storm observed during SARS-CoV-2 infection in the pandemic.
4. Methods
4.1. Collection of clinical data
Time-series clinical data of cytokine concentrations of TNF-α, IFN-γ, IL-1, IL-2, IL-6, and IL-10, used for the calibration of the model, as shown in Figure 2, were acquired from multiple references[20] using plot digitalization (Table 1). Cytokine concentrations were subtracted from baseline concentrations (the concentration on day 0 or the lowest concentration if the clinical data decreased over time). The simulation results were zero-clipped (Fig S1). The data of grade or CRS severity with initial tumor burden and/or peak serum IL-6 concentration, used for validation of the probability of CRS, as shown in Figure 3D&E, were acquired from multiple references using plot digitalization (Table 2). As shown in Figure 3A, IFN-γ data from [20a] were used for calibration, and IL-6 and IL-8 data from [20b] were used for validation. All plot digitalizations were performed using WebPlotDigitizer (https://automeris.io/WebPlotDigitizer/) [21].
Table 1.
Data for calibration of the model
Table 2.
Validation data for the CRS reported against tumor burden and IL6
4.2. Formulation of the model
4.2.1. Modeling the cellular interactions between CAR T-cells and B-ALL cells
The modeling of the cellular dynamics of CAR T-cells and B-ALL cells can be found in our previous study [10]. Briefly, the study addressed the growth and apoptosis of activated and non-activated CAR T-cells, CD19+, and CD19− B-ALL cells; elimination of B-ALL cells by CAR T-cells; activation of CAR T-cells; and loss of CD19 in B-ALL cells, as described by Equations (1)–(4).
| (1) |
| (2) |
| (3) |
| (4) |
The number of cells in the bone marrow was denoted nP and nN for CD19+ and CD19− B-ALL cells, respectively, and nTA and nTN for activated and non-activated CAR T-cells, respectively. The growth of B-ALL cells was determined using the logistic growth Equation (1), with growth rates of rP and rN for CD19+ and CD19− B-ALL cells, respectively, and the maximal capacity of nc. The proliferation of activated CAR T-cells was determined using Equation (2), with the maximal growth rate rTA with B-ALL cell stimulation in a Michaelis-Menten form with constant Kr. CAR T-cell activation was determined with a maximal activation rate kA and B-ALL cell stimulation with a constant KA. The natural death of CAR T-cell was determined using Equation (3), with death rates lTA and lTN for activated and nonactivated cells, respectively. B-ALL cell elimination by CAR T-cells was determined using Equation (4), with maximal elimination rates e and e/kb, with Menten-Michaelis constants KP and KN for CD19+ and CD19− B-ALL cells, respectively. The parameters in Equations (1)–(4) are cited from our previous study [10].
4.2.2. Modeling bone marrow cytokine response
The release of cytokines from the bone marrow is caused by immune activities induced by CAR T-cell therapy in the bone marrow. First, it was assumed that the rate of cytokine release by CAR T-cells in the bone marrow is proportional to the number of CAR T-cells as follows:
| (5) |
where nTA is the number of activated CAR T-cells. CAR T-cells release cytokine i at a rate of μT,i. The number of CAR T-cells in the bone marrow was derived from Equations (1)–(4). ‘BM’ represents ‘bone marrow’, ‘T’ represents ‘T-cells’, and ‘M’ represents ‘macrophages’.
Monocytes have been suggested to be a major source of cytokines released during CRS. The cytokines released by monocytes was modeled as follows:
| (6) |
where μM,i is the release rate of cytokine type i, and nmono is the number of monocytes. It has also been reported that the release of cytokines is stimulated by certain molecules produced during CAR T-cell killing of B-ALL cells [20j]. Thus, the number of monocytes releasing cytokines was assumed to be proportional to the rate of CAR T-cell-mediated killing of B-ALL cells. Similar to a previous model [22], the number of equivalent monocytes is expressed as follows:
| (7) |
where we associated the equivalent monocytes with the killing activity (terms including the killing rate, e), and the activation of CAR T-cells (the number of activated CAR T-cells, nTA).
Activated T-cells have been reported to release TNF-α [23], IFN-γ [24], and IL-2 [25], and monocytes release TNF-α [26], IL-1 [27], IL-6 [28], IL-8 [29], IL-10 [30], and IL-12 [31]. Therefore, we only counted these cytokines with release coefficients and
4.2.3. Modeling serum cytokine response
The CRS cytokine interaction network model was modified from a previous method [7]. Specifically, the concentration of cytokines derived from the interaction in the serum is expressed as follows:
| (8) |
where i and j are indices for the species of cytokines, and is the serum concentration of cytokine i. Cytokine j leads to a response to cytokine i by a coefficient of ij, and the change rate of cytokine i exhibits feedback on itself with a coefficient si. The coefficients si and ij were obtained from an original study [7]. The ‘I’ subscription was used to mark the interaction of cytokines.
Considering the cytokine responses from both the release in bone marrow and the interaction in serum, the final equation for cytokine concentration in serum could be expressed by substituting Equation (7) into (6), and then adding Equations (5), (6), and (8), as follows:
| (9) |
It has been shown that the cytokines released by CAR T-cells and monocytes in the bone marrow diffused into the serum and elevated the concentration of cytokines in the serum, where cytokines interact with each other. These processes are summed up in Equation (9) to depict the overall concentration of cytokines in the serum. The parameters si and αij for cytokine dynamics in serum were obtained from Yiu’s original model [7]. The secretion rates of cytokines by cells from the bone marrow (μ…) were fitted with Equations (1)–(4).
4.3. Model Calibration
The calibration of the NLME model was performed using the stochastic approximation of expectation maximization (SAEM) algorithm provided by Monolix software (2020R1; Lixoft, France). The initial tumor burden was described as a regressor and cytokine data were described as observations. To prevent overfitting, the population standard deviation was assumed to be 1.25 for all cytokine secretion coefficients. We adopted population-level fitting results at the cellular level (Table 3) from our previous study [10] that were calibrated based on clinical data. In addition, the molecular-level parameters were fitted (Tables 4 and 5).
Table 3.
Population-level fitted parameters and initial values of CAR T-cells and B-ALL cells (cellular level modeling)
| Parameter | Description | Unit | Value |
|---|---|---|---|
|
| |||
| r P | Growth rate of CD19+ B-ALL cells | day−1 | 0.071 |
| r TA | Growth rate of activated CAR T-cells | day−1 | 1.5 |
| l TA | Apoptosis rate of activated CAR T-cells | day−1 | 0.11 |
| l TN | Apoptosis rate of non-activated CAR T-cells | day−1 | 2e-7 |
| n C | B-ALL cell-carrying capacity | 2585.74 | |
| e | Killing rate of activated CAR T-cells | day−1 | 19.34 |
| K P | Saturation constant to CAR T-cell killing rate | 11040.05 | |
| K r | Saturation constant to CAR T-cell growth rate | 1360.54 | |
| K A | Saturation constant to CAR T-cell activation rate | 11883.73 | |
| k A | Activation rate of CAR T-cells | day−1 | 0.58 |
| r N | Growth rate of CD19− B-ALL cells | day−1 | 0.1 |
| k m | Mutation factor | day−1 | 1.5e-7 |
| k b | Bystander killing scaling factor | 7.9 | |
| K N | Saturation rate of CD19− B-ALL cells to killing efficacy | 16956.03 | |
| n P0 | Initial value of CD19+ B-ALL cells | ×109 cells | 1467.01 |
| n N0 | Initial value of CD19− B-ALL cells | ×109 cells | 19.89 |
| n TN0 | Initial value of non-activated CAR T-cells | ×109 cells | 8.97 |
Table 4.
Population-level fitted release rates of various cytokines (molecular level modeling)
| Parameter | Description | Unit | Value |
|---|---|---|---|
|
| |||
| μ T,TNFα | Release rate of TNF-α from CAR T-cells into serum | pg mL−1 day−1(109 cell)−1 | 0.0004 |
| μ T,IFNγ | Release rate of IFN-γ from CAR T-cells into serum | pg mL−1 day−1(109 cell)−1 | 0.0116 |
| μ T,IL2 | Release rate of IL-2 from CAR T-cells into serum | pg mL−1 day−1(109 cell)−1 | 0.0015 |
| μ M, TNFα | Release rate of TNF-α from monocytes stimulated by tumor lysis into serum | pg mL−1 (109 cell)−1 | 0.4618 |
| μ M,IL1 | Release rate of IL-1 from monocytes stimulated by tumor lysis into serum | pg mL−1 (109 cell)−1 | 0.4133 |
| μ M,IL6 | Release rate of IL-6 from monocytes stimulated by tumor lysis into serum | pg mL−1 (109 cell)−1 | 1.8253 |
| μ M,IL8 | Release rate of IL-8 from monocytes stimulated by tumor lysis into serum | pg mL−1 (109 cell)−1 | 0.5683 |
| μ M,IL10 | Release rate of IL-10 from monocytes stimulated by tumor lysis into serum | pg mL−1 (109 cell)−1 | 6.1396 |
| μ M,IL12 | Release rate of IL-12 from monocytes stimulated by tumor lysis into serum | pg mL−1 (109 cell)−1 | 1.8594 |
Table 5.
Individual-level fitted release rates of various cytokines (molecular level modeling)
| Pat. No. | μ T,TNFα | μ T,IFNγ | μ T,IL2 | μ M, TNFα | μ M,IL1 | μ M,IL6 | μ M,IL8 | μ M,IL10 | μ M,IL12 |
|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||
| 1 | 0.000446 | 0.003592 | 0.001152 | 0.275235 | 0.119008 | 1.85297 | 0.536542 | 1.87497 | 2.01872 |
| 2 | 0.000394 | 0.011354 | 0.001517 | 0.473093 | 0.373535 | 1.65234 | 0.466915 | 15.6379 | 4.67181 |
| 3 | 0.000395 | 0.01175 | 0.001519 | 0.432445 | 0.4088 | 0.411243 | 0.792654 | 5.58148 | 1.8618 |
| 4 | 0.000395 | 0.011613 | 0.001527 | 0.461807 | 0.413271 | 1.82473 | 0.568253 | 6.13907 | 1.85965 |
| 5 | 0.000294 | 0.012866 | 0.002191 | 0.618077 | 4.35899 | 3.26738 | 1.06832 | 0.43901 | 17.3246 |
| 6 | 0.000395 | 0.011612 | 0.001527 | 0.461257 | 0.413134 | 1.81435 | 0.568487 | 108.931 | 1.86407 |
| 7 | 0.000372 | 0.013243 | 0.001336 | 0.402073 | 0.347817 | 0.973329 | 0.66982 | 14.2192 | 1.95262 |
| 8 | 0.000396 | 0.011674 | 0.001522 | 0.455337 | 0.384914 | 0.771902 | 0.560472 | 1.9066 | 1.73366 |
| 9 | 0.000395 | 0.01161 | 0.001527 | 0.462083 | 0.414387 | 84.4419 | 0.568791 | 118.87 | 1.8536 |
| 10 | 0.000382 | 0.016063 | 0.001523 | 0.971001 | 0.349997 | 0.686622 | 0.431895 | 0.142302 | 0.851897 |
| 11 | 0.000404 | 0.013388 | 0.001484 | 0.484646 | 0.477202 | 0.619983 | 0.617316 | 1.12084 | 2.4544 |
| 12 | 0.000395 | 0.011611 | 0.001527 | 0.462529 | 0.415349 | 51.5049 | 0.568627 | 106.164 | 1.86779 |
| 13 | 0.000395 | 0.011612 | 0.001527 | 0.461877 | 0.413437 | 1.84092 | 0.568305 | 6.17834 | 1.85983 |
| 14 | 0.000395 | 0.011641 | 0.001527 | 0.44469 | 0.385164 | 0.715483 | 0.5659 | 6.9142 | 1.80477 |
| 15 | 0.000395 | 0.011614 | 0.001527 | 0.461835 | 0.413313 | 1.82805 | 0.568284 | 6.10506 | 1.85932 |
| 16 | 0.000395 | 0.011613 | 0.001527 | 0.461825 | 0.413327 | 1.83195 | 0.568292 | 6.1365 | 1.8595 |
| 17 | 0.000395 | 0.011514 | 0.001518 | 0.423723 | 0.390628 | 1.00856 | 0.552313 | 11.6701 | 1.85441 |
4.4. Estimation of the probability of severe CRS
Clinically, the severity of CRS is described by grade, which is evaluated by clinical symptoms such as body temperature and categorized into four or five grades according to various grading standards [18]. To make the clinical data graded by different standards available in our model, we divided CRS into two levels: severe CRS, which is equivalent to level 3 or above CRS graded based on clinical symptoms, and mild CRS, which is equivalent to level 2 or below CRS according to references [32].
Similar to the method in [7], we estimated the probability of severe CRS by comparing the concentrations of different types of cytokines with corresponding typical values of severe or mild cases of CRS. The probability of severe CRS increases when the concentrations of cytokines are closer to the typical values of severe CRS but far from mild CRS. When the concentration of cytokines was lower than the typical value of the concentration of mild CRS, the probability of severe CRS was set to 0. When the concentration of cytokines was higher than the typical concentration of severe CRS, the probability of severe CRS was set to 1. The model was constructed using a piecewise but continuous function to express the probability of severe CRS (g) as follows:
| (10) |
where
| (11) |
Here, i denotes cytokine species (TNF-α, IL-6, IL-8, or IL-10), ci is the concentration of cytokine i in the serum, and and are reference cytokine concentrations for severe and mild CRS cases, respectively. ci was compared with the severe and mild CRS reference concentrations to determine how close the cytokine profile was to the two cases, thus providing an estimation of the probability of severe CRS. Considering the distinct order of magnitude and biological significance of different cytokines, γi, , and were defined as the normalized cytokine concentration against the reference concentration of mild CRS; γ, γs, and γm are the vector magnitudes of the concentrations.
In the estimation, the reference concentration of cytokines for mild CRS was set as the cut-off to define the probability of severe CRS as 0. In the expression of g0, the first bracket denotes the extent to which the total concentration of cytokines deviates from the mild case in the sense that a higher overall concentration leads to a more severe reaction. The second bracket denotes the closeness between the magnitude of the concentration of cytokines and that of the severe case, whereas the third bracket denotes the closeness in the angle between Euclidean vectors, both in the sense that a cytokine profile similar to the severe case indicates severe CRS.
The reference cytokine concentration was defined to reflect the typical concentrations of cytokines in severe or mild CRS patients. The reference concentrations of the four cytokines included in the estimation were selected from Fig 6A–D of [5b] and are listed in Table 6. Specifically, the reference value was selected as the doubled peak concentrations of the ≥Grade 4 CRS lines, and the mild reference was selected as half the concentrations of the Grade 0 CRS lines.
Table 6.
Reference cytokine concentration (pg/mL)
| TNF-α | IL-6 | IL-8 | IL-10 | |
|---|---|---|---|---|
|
| ||||
| Severe | 250 | 2820 | 790 | 561 |
| Mild | 0.3138 | 2.475 | 8.842 | 3.124 |
4.5. CRS Factor
We performed a local partial derivative-based sensitivity analysis instead of using regression-based or variance-based global methods as the global methods were not reliable because the sensitivity of each parameter varies drastically at different regions of the parameter space. For example, there are low sensitivity to cytokine secretion rates when there is not enough initial tumor burden to provoke a strong inflammation, but when the initial tumor burden is high enough, the sensitivity to secretion rate of IL-6 is prominent. With such heterogeneity, a rational local condition is more meaningful. The local condition was selected as the population level parameter, with the average tumor burden of the calibration cohort (used in Fig 2). Through this sensitivity analysis we found that the secretion coefficient of the IL-6 cytokine by monocytes and the tumor burden are most important in driving CRS (Fig 3C). The CRS process is a consequence of the killing of tumor cells by CAR T-cells, which is determined by the B-ALL cell elimination rate of CAR T-cells (e). Additionally, clinical experience has suggested that the initial tumor burden [3b, 5] and various cytokines including IL-6 [33] and others [2, 34] such as TNF-α, IFN-γ, IL-1, IL-2, IL-6, IL-8, IL-10, and IL-12 influence the risk of CRS or related toxicity in CAR T-cell therapy. Thus, we defined the CRS factor, FCRS, in Equation (14) based on the B-ALL cell elimination rate of CAR T-cell, e, the number of initial B-ALL cells, nP0, and the release rates of various cytokines (μT,TNFα, μT,IFNγ, μT,IL2, μM,TNFα, μM,IL1, μM,IL6, μM,IL8, μM,IL10, and μM,IL12) from CAR T-cells and monocytes. Ideally, release rates should be weighted based on the importance of each cytokine, as determined by clinical data. However, as clinical data measuring and comparing all these factors are limited, weights were empirically assigned based on the importance of each cytokine. As IL-6 plays a pivotal role in CRS, we weighted μM,IL6 by a factor of 5, where factor 5 was roughly selected by comparing the sensitivity of μM,IL6 with the second most sensitive factor: μM,IL10. It was not selected with precision because changing it to approximately 4–8 did not significantly affect the correlation of FCRS with the probability of severe CRS. For the other cytokines, we assigned their uniform release rates to 1. Our choice of weights yielded a better correlation with the probability of severe CRS than the choice of IL-6 alone (Fig S3). The CRS factor FCRS overall represents the probability of severe CRS as follows:
| (12) |
4.6. Monte Carlo simulation of virtual patient cohorts
Virtual patient cohorts were generated using MATLAB code (MATLAB R2021a) using the population mode and deviation of parameters of interest (that is, the secretion coefficients), calculated from the calibration of the NLME model using the SAEM algorithm (Table 4) while keeping the parameters for cellular interaction shown in Table 3 fixed. Thus, the secretion coefficients of cytokines were distributed randomly to simulate variations among the general population. The distribution was set as a lognormal distribution in accordance with the assumption of the NLME model, that is, the distribution of the lognormal was generated with the populational mode (Table 4) and deviation (1.25) from the Monolix software. A cohort of virtual patients was then generated using pseudorandom numbers simulating the distribution for each plot in Fig 3, 5, and 6. The measurement error estimated from the calibration was also simulated for comparison with calibration data points.
4.7. Modeling of tocilizumab effect
The biological function of IL-6 is mediated by its binding of IL-6 to its receptor, IL-6R. Binding can be assumed to be proportional to the concentrations of IL-6 and IL-6R, since IL-6R forms a complex with IL-6 once bound, as follows:
| (13) |
where cIL6 is the concentration of IL-6, cIL6R_free is the concentration of free IL-6R, and cIL6_IL6 is the concentration of the bound form of the IL6-IL6R complex.
Tocilizumab is a monoclonal antibody that binds IL-6R to block its binding to IL-6. The binding of IL-6R to tocilizumab is an antigen-antibody binding process, which can be described as follows:
| (14) |
where cIL6R_all is the concentration of total IL-6R and cTCZ is the concentration of tocilizumab. KD is the dissociation constant for tocilizumab on IL-6R as used from [35] and set to 0.37 μg/mL. The tocilizumab concentration was determined using a pharmacokinetic model.
Collectively,
| (15) |
Therefore, we defined an equivalent bioavailability of IL-6, denoted as γIL6, in place of IL-6 concentration, for comparison between the control and tocilizumab treatment groups. In the absence of tocilizumab, the bioavailability of IL-6 depends on its concentration, represented as follows:
| (16) |
The pharmacokinetics of tocilizumab was adapted from [36], which consists of a bicompartmental model that considers a central volume V1 and a peripheral volume V2. Intravenously injected tocilizumab starts from the central volume and distributes to the peripheral volume to take effect, as follows:
| (17) |
The parameters in the equation can be found in [36]. Tocilizumab is typically used at a dose of 8 mg/kg, which is approximately 160 μg/mL in serum concentration. Thus, we used an 8 mg/kg Q2W IV dose starting on the day of infusion in our simulation, as this is a common choice of dose according to [35–36].
4.8. Modeling of different CAR T-cell products and switchable CAR T-cells
To model a slower CAR T-cell response, the parameters for CAR T-cell response (rP, kA, and lTA, but not e) were divided by a factor of two, five, or ten for a two, five, and ten times slower response, respectively. The killing rate (e) was not changed because the literature suggested no significant difference in anticancer activity [13b].
To model the switchable CAR T-cells, kA and e was set to 0 for the “OFF” state and their original values for the “ON” state, as the activation and killing process required recognition of tumor cells by the switchable CAR molecule.
4.9. Statistical Analysis
P-values were calculated using the Student’s t-test with Prism 9 software (GraphPad Software Inc., CA, USA). Statistical significance was set at p < 0.05, and sample sizes are indicated in all figure legends. Error bars denote mean ± standard deviation (SD) in histograms. In figures with a central line and band, the band denotes quartile boundaries and the line denotes median. Only in Fig 5A and B and Fig 6F the line denotes the linear fitting and the band denotes the 95% confidence interval determined by the fitting.
Supplementary Material
Acknowledgements
This work was supported by the National Science Foundation (CBET2103219), US National Institutes of Health (R35GM133646), and Cancer Research Institute Irvington Postdoctoral Fellowship (CRI4018).
Footnotes
Conflict of Interests
The authors declare no conflict of interests.
Supporting Information
Supporting information is available from the Wiley Online Library or from the author.
Contributor Information
Zhuoyu Zhang, Department of Mechanical and Aerospace Engineering, New York University, Brooklyn, NY 11201, USA.
Lunan Liu, Department of Mechanical and Aerospace Engineering, New York University, Brooklyn, NY 11201, USA.
Chao Ma, Department of Mechanical and Aerospace Engineering, New York University, Brooklyn, NY 11201, USA.
Weiqiang Chen, Department of Mechanical and Aerospace Engineering, New York University, Brooklyn, NY 11201, USA; Department of Biomedical Engineering, New York University, Brooklyn, NY 11201, USA; Laura and Isaac Perlmutter Cancer Center, NYU Langone Health, New York, NY 10016, USA.
Data Availability Statement
The code for the computational model is available at https://github.com/ZZY-NYU/CART_CRS_MODEL. Source data for fitting the computational model are available from the references listed in the Methods section. All the parameters used in the modeling to generate the main figures are listed in Tables 1–6. Any further information can be obtained from the corresponding author upon reasonable request.
References
- [1].Almasbak H, Aarvak T, Vemuri MC, J Immunol Res 2016, 2016, 5474602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Brudno JN, Kochenderfer JN, Blood Rev 2019, 34, 45–55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].a) Chou CK, Turtle CJ, Bone Marrow Transplant 2019, 54, 780–784; [DOI] [PubMed] [Google Scholar]; b) Aldoss I, Khaled SK, Budde E, Stein AS, Curr Oncol Rep 2019, 21, 4. [DOI] [PubMed] [Google Scholar]
- [4].Teachey DT, Lacey SF, Shaw PA, Melenhorst JJ, Maude SL, Frey N, Pequignot E, Gonzalez VE, Chen F, Finklestein J, Barrett DM, Weiss SL, Fitzgerald JC, Berg RA, Aplenc R, Callahan C, Rheingold SR, Zheng Z, Rose-John S, White JC, Nazimuddin F, Wertheim G, Levine BL, June CH, Porter DL, Grupp SA, Cancer Discov 2016, 6, 664–679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].a) Liu D, Zhao J, J Hematol Oncol 2018, 11, 121; [DOI] [PMC free article] [PubMed] [Google Scholar]; b) Hay KA, Hanafi LA, Li D, Gust J, Liles WC, Wurfel MM, Lopez JA, Chen J, Chung D, Harju-Baker S, Cherian S, Chen X, Riddell SR, Maloney DG, Turtle CJ, Blood 2017, 130, 2295–2306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Hardiansyah D, Ng CM, Clin Transl Sci 2019, 12, 343–349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Hopkins B, Pan Y, Tucker M, Huang Z, Processes 2018, 7. [Google Scholar]
- [8].a) Waito M, Walsh SR, Rasiuk A, Bridle BW, Willms AR, in Mathematical and Computational Approaches in Advancing Modern Science and Engineering (Eds.: Bélair J, Frigaard IA, Kunze H, Makarov R, Melnik R, Spiteri RJ), Springer International Publishing, Cham, 2016, pp. 331–339; [Google Scholar]; b) Yiu HH, Graham AL, Stengel RF, PLoS One 2012, 7, e45027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].a) Mueller KT, Maude SL, Porter DL, Frey N, Wood P, Han X, Waldron E, Chakraborty A, Awasthi R, Levine BL, Melenhorst JJ, Grupp SA, June CH, Lacey SF, Blood 2017, 130, 2317–2325; [DOI] [PMC free article] [PubMed] [Google Scholar]; b) Norelli M, Camisa B, Barbiera G, Falcone L, Purevdorj A, Genua M, Sanvito F, Ponzoni M, Doglioni C, Cristofori P, Traversari C, Bordignon C, Ciceri F, Ostuni R, Bonini C, Casucci M, Bondanza A, Nat Med 2018, 24, 739–748. [DOI] [PubMed] [Google Scholar]
- [10].Liu L, Ma C, Zhang Z, Chen W, medRxiv 2021, 2021.2009.2021.21263913. [Google Scholar]
- [11].Kotch C, Barrett D, Teachey DT, Expert Rev Clin Immunol 2019, 15, 813–822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Kadauke S, Myers RM, Li Y, Aplenc R, Baniewicz D, Barrett DM, Barz Leahy A, Callahan C, Dolan JG, Fitzgerald JC, Gladney W, Lacey SF, Liu H, Maude SL, McGuire R, Motley LS, Teachey DT, Wertheim GB, Wray L, DiNofia AM, Grupp SA, J Clin Oncol 2021, 39, 920–930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].a) Neelapu SS, Tummala S, Kebriaei P, Wierda W, Gutierrez C, Locke FL, Komanduri KV, Lin Y, Jain N, Daver N, Westin J, Gulbis AM, Loghin ME, de Groot JF, Adkins S, Davis SE, Rezvani K, Hwu P, Shpall EJ, Nat Rev Clin Oncol 2018, 15, 47–62; [DOI] [PMC free article] [PubMed] [Google Scholar]; b) Cappell KM, Kochenderfer JN, Nat Rev Clin Oncol 2021, 18, 715–727. [DOI] [PubMed] [Google Scholar]
- [14].a) Mestermann K, Giavridis T, Weber J, Rydzek J, Frenz S, Nerreter T, Mades A, Sadelain M, Einsele H, Hudecek M, Sci Transl Med 2019, 11; [DOI] [PMC free article] [PubMed] [Google Scholar]; b) Wu CY, Roybal KT, Puchner EM, Onuffer J, Lim WA, Science 2015, 350, aab4077; [DOI] [PMC free article] [PubMed] [Google Scholar]; c) Nguyen NT, Huang K, Zeng H, Jing J, Wang R, Fang S, Chen J, Liu X, Huang Z, You MJ, Rao A, Huang Y, Han G, Zhou Y, Nat Nanotechnol 2021, 16, 1424–1434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].An X, Sendra VG, Liadi I, Ramesh B, Romain G, Haymaker C, Martinez-Paniagua M, Lu Y, Radvanyi LG, Roysam B, Varadarajan N, PLoS One 2017, 12, e0181904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Giavridis T, van der Stegen SJC, Eyquem J, Hamieh M, Piersigilli A, Sadelain M, Nat Med 2018, 24, 731–738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Strati P, Ahmed S, Kebriaei P, Nastoupil LJ, Claussen CM, Watson G, Horowitz SB, Brown ART, Do B, Rodriguez MA, Nair R, Shpall EJ, Green MR, Neelapu SS, Westin JR, Blood Adv 2020, 4, 3123–3127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].a) Porter D, Frey N, Wood PA, Weng Y, Grupp SA, J Hematol Oncol 2018, 11, 35; [DOI] [PMC free article] [PubMed] [Google Scholar]; b) Frey NV, Porter DL, Hematology Am Soc Hematol Educ Program 2016, 2016, 567–572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Hoiland RL, Stukas S, Cooper J, Thiara S, Chen LYC, Biggs CM, Hay K, Lee AYY, Shojania K, Abdulla A, Wellington CL, Sekhon MS, Br J Haematol 2020, 190, e150–e154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].a) Brentjens RJ, Davila ML, Riviere I, Park J, Wang X, Cowell LG, Bartido S, Stefanski J, Taylor C, Olszewska M, Borquez-Ojeda O, Qu J, Wasielewska T, He Q, Bernal Y, Rijo IV, Hedvat C, Kobos R, Curran K, Steinherz P, Jurcic J, Rosenblat T, Maslak P, Frattini M, Sadelain M, Sci Transl Med 2013, 5, 177ra138; [DOI] [PMC free article] [PubMed] [Google Scholar]; b) Cai YX, Zhu JY, He JC, Yang W, Ma C, Xiong F, Li F, Chen WQ, Chen PY, Adv Healthc Mater 2019, 8, e1801478; [DOI] [PMC free article] [PubMed] [Google Scholar]; c) Grupp SA, Kalos M, Barrett D, Aplenc R, Porter DL, Rheingold SR, Teachey DT, Chew A, Hauck B, Wright JF, Milone MC, Levine BL, June CH, N Engl J Med 2013, 368, 1509–1518; [DOI] [PMC free article] [PubMed] [Google Scholar]; d) Lee DW, Kochenderfer JN, Stetler-Stevenson M, Cui YK, Delbrook C, Feldman SA, Fry TJ, Orentas R, Sabatino M, Shah NN, Steinberg SM, Stroncek D, Tschernia N, Yuan C, Zhang H, Zhang L, Rosenberg SA, Wayne AS, Mackall CL, The Lancet 2015, 385, 517–528; [DOI] [PMC free article] [PubMed] [Google Scholar]; e) Li S, Zhang J, Wang M, Fu G, Li Y, Pei L, Xiong Z, Qin D, Zhang R, Tian X, Wei Z, Chen R, Chen X, Wan J, Chen J, Wei X, Xu Y, Zhang P, Wang P, Peng X, Yang S, Shen J, Yang Z, Chen J, Qian C, Br J Haematol 2018, 181, 360–371; [DOI] [PubMed] [Google Scholar]; f) Heng G, Jia J, Li S, Fu G, Wang M, Qin D, Li Y, Pei L, Tian X, Zhang J, Wu Y, Xiang S, Wan J, Zhu W, Zhang P, Zhang Q, Peng X, Wang L, Wang P, Wei Z, Zhang Y, Wang G, Chen X, Zhang C, Sun Y, Zhao W, Fan Y, Yang Z, Chen J, Qian C, Clin Cancer Res 2020, 26, 1606–1615; [DOI] [PubMed] [Google Scholar]; g) Ghorashian S, Kramer AM, Onuoha S, Wright G, Bartram J, Richardson R, Albon SJ, Casanovas-Company J, Castro F, Popova B, Villanueva K, Yeung J, Vetharoy W, Guvenel A, Wawrzyniecka PA, Mekkaoui L, Cheung GW, Pinner D, Chu J, Lucchini G, Silva J, Ciocarlie O, Lazareva A, Inglott S, Gilmour KC, Ahsan G, Ferrari M, Manzoor S, Champion K, Brooks T, Lopes A, Hackshaw A, Farzaneh F, Chiesa R, Rao K, Bonney D, Samarasinghe S, Goulden N, Vora A, Veys P, Hough R, Wynn R, Pule MA, Amrolia PJ, Nat Med 2019, 25, 1408–1414; [DOI] [PubMed] [Google Scholar]; h) Curran KJ, Margossian SP, Kernan NA, Silverman LB, Williams DA, Shukla N, Kobos R, Forlenza CJ, Steinherz P, Prockop S, Boulad F, Spitzer B, Cancio MI, Boelens JJ, Kung AL, Khakoo Y, Szenes V, Park JH, Sauter CS, Heller G, Wang X, Senechal B, O’Reilly RJ, Riviere I, Sadelain M, Brentjens RJ, Blood 2019, 134, 2361–2368; [DOI] [PMC free article] [PubMed] [Google Scholar]; i) Fitzgerald JC, Weiss SL, Maude SL, Barrett DM, Lacey SF, Melenhorst JJ, Shaw P, Berg RA, June CH, Porter DL, Frey NV, Grupp SA, Teachey DT, Crit Care Med 2017, 45, e124–e131; [DOI] [PMC free article] [PubMed] [Google Scholar]; j) Hu Y, Wu Z, Luo Y, Shi J, Yu J, Pu C, Liang Z, Wei G, Cui Q, Sun J, Jiang J, Xie J, Tan Y, Ni W, Tu J, Wang J, Jin A, Zhang H, Cai Z, Xiao L, Huang H, Clin Cancer Res 2017, 23, 3297–3306. [DOI] [PubMed] [Google Scholar]
- [21].Rohatgi A, WebPlotDigitizer: Version 4.5, https://automeris.io/WebPlotDigitizer, accessed: Nov 2021.
- [22].Chen X, Kamperschroer C, Wong G, Xuan D, Clin Transl Sci 2019, 12, 600–608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Mehta AK, Gracias DT, Croft M, Cytokine 2018, 101, 14–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].de Araujo-Souza PS, Hanschke SCH, Nardy A, Secca C, Oliveira-Vieira B, Silva KL, Soares-Lima SC, Viola JPB, J Leukoc Biol 2020, 108, 1329–1337. [DOI] [PubMed] [Google Scholar]
- [25].Liao W, Lin JX, Leonard WJ, Curr Opin Immunol 2011, 23, 598–604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Joyce DA, Steer JH, Abraham LJ, Inflamm Res 1997, 46, 447–451. [DOI] [PubMed] [Google Scholar]
- [27].Kaneko N, Kurata M, Yamamoto T, Morikawa S, Masumoto J, Inflamm Regen 2019, 39, 12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Tanaka T, Narazaki M, Kishimoto T, Cold Spring Harb Perspect Biol 2014, 6, a016295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Waugh DJ, Wilson C, Clin Cancer Res 2008, 14, 6735–6741. [DOI] [PubMed] [Google Scholar]
- [30].Sabat R, Grutz G, Warszawska K, Kirsch S, Witte E, Wolk K, Geginat J, Cytokine Growth Factor Rev 2010, 21, 331–344. [DOI] [PubMed] [Google Scholar]
- [31].Zheng H, Ban Y, Wei F, Ma X, Adv Exp Med Biol 2016, 941, 117–138. [DOI] [PubMed] [Google Scholar]
- [32].a) Hong R, Zhao H, Wang Y, Chen Y, Cai H, Hu Y, Wei G, Huang H, Bone Marrow Transplantation 2021, 56, 570–580; [DOI] [PMC free article] [PubMed] [Google Scholar]; b) Schuster SJ, Maziarz RT, Rusch ES, Li J, Signorovitch JE, Romanov VV, Locke FL, Maloney DG, Blood Advances 2020, 4, 1432–1439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Frey N, Porter D, Biol Blood Marrow Transplant 2019, 25, e123–e127. [DOI] [PubMed] [Google Scholar]
- [34].Gofshteyn JS, Shaw PA, Teachey DT, Grupp SA, Maude S, Banwell B, Chen F, Lacey SF, Melenhorst JJ, Edmonson MJ, Panzer J, Barrett DM, McGuire JL, Ann Neurol 2018, 84, 537–546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Mihara M, Ohsugi Y, Kishimoto T, Open Access Rheumatol 2011, 3, 19–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Frey N, Grange S, Woodworth T, J Clin Pharmacol 2010, 50, 754–766. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The code for the computational model is available at https://github.com/ZZY-NYU/CART_CRS_MODEL. Source data for fitting the computational model are available from the references listed in the Methods section. All the parameters used in the modeling to generate the main figures are listed in Tables 1–6. Any further information can be obtained from the corresponding author upon reasonable request.


