Abstract
High-dimensional -omics data such as genomic, transcriptomic, and metabolomic data offer great promise in advancing precision medicine. In particular, such data have enabled the investigation of complex diseases such as cancer at an unprecedented scale and in multiple dimensions. However, a number of analytical challenges complicate analysis of high-dimensional -omics data. One is the growing recognition that complex diseases such as cancer are multifactorial and may be attributed to harmful changes on multiple -omics levels and on the pathway level. When individual genes in an important pathway have relatively weak signals, it can be challenging to detect them on their own, but the aggregated signal in the pathway can be considerably stronger and hence easier to detect with the same sample size. To address these challenges, there is a growing body of literature on knowledge-guided statistical learning methods for analysis of high-dimensional -omics data that can incorporate biological knowledge such as functional genomics and functional proteomics. These methods have been shown to improve predication and classification accuracy and yield biologically more interpretable results compared with statistical learning methods that do not use biological knowledge. In this review, we survey current knowledge-guided statistical learning methods, including both supervised learning and unsupervised learning, and their applications to precision oncology, and we discuss future research directions.
INTRODUCTION
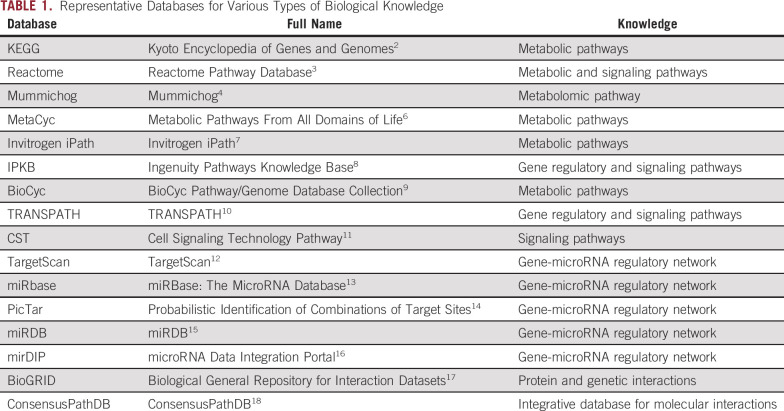
Rapid advances in technologies have led to generation of high-dimensional -omics data, such as genomics, transcriptomics, and metabolomics data, in many biomedical studies. Such data offer great promise in advancing precision medicine. They have been used to build prediction models for disease risk or progression and for adaptive response to treatment, uncover molecular signatures associated with a disease that provide insights about disease mechanism, and identify potential therapeutic targets. At the same time, they also present many analytical challenges. Many advanced statistical learning methods1 have been developed to address these analytical challenges. For example, regularized regression methods have been developed for building prediction model and identifying important molecular signatures for disease risk or prognosis. These methods have many appealing features from a methodologic point of view. In particular, they achieve simultaneous variable selection and model estimation and can be used to analyze data where the sample size is less than the number of -omics features. However, they also have some important limitations when used to analyze -omics data for complex diseases such as cancer. There is growing recognition that complex diseases are multifactorial and may be attributed to harmful changes on multiple -omics levels and on the pathway level. For example, when expression levels of individual genes in an important pathway associated with cancer risk have relatively weak signals, it can be challenging to detect them on their own, but the aggregated signal in the pathway can be considerably stronger and hence easier to detect with the same sample size. The vast majority of existing statistical learning methods are entirely data driven and fail to incorporate biological knowledge such as functional genomics and functional proteomics that can be represented by a graph (Table 1).
TABLE 1.
Representative Databases for Various Types of Biological Knowledge
Extensive research in the past has yielded ever-deepening knowledge of biological functions of genes and gene products, which have been shown to function through pathways and networks. Major efforts have been undertaken to structure and store accumulated biological knowledge on pathways and networks in multiple public or commercial databases, including, but not limited to, Kyoto Encyclopedia of Genes and Genomes (KEGG),2 Gene Ontology,19 BioCarta (www.biocarta.com),20 and Cell Signaling Technology Pathway.11 Such biological knowledge sheds important insight on regulatory relationships between genes and gene products that are often associated with disease risk or progression. It has been shown to be highly valuable to incorporate such biological knowledge into analysis of gene expression data in relation to disease risk. For example, Costello et al21 demonstrated that use of biologic pathway information improved drug sensitivity prediction. In addition, a two-step approach,22 conducting clustering analysis followed by annotating clusters by a gene set enrichment analysis, has been shown to improve power in clustering analysis of gene expression data. Similar biological knowledge is also available for other types of -omics data, and Table 1 lists representative databases for such biological knowledge.
CONTEXT
Key Objective
To review advances in knowledge-guided statistical learning methods for analysis of -omics data and spur wider and more frequent applications of such methods in basic, translational, and clinical research toward the goal of advancing precision oncology.
Knowledge Generated
The knowledge-guided analysis strategy offers a number of advantages. It enables selection of important pathways instead of individual -omics features and improves power in uncovering important features and accuracy of prediction models. The results from such analyses are biologically more meaningful and interpretable and can provide deeper insights about molecular mechanism and underpinning of complex diseases such as cancer. The strategy can also facilitate the integration of multimodal -omics data through the incorporation of biological knowledge about the functional relationship between different modalities.
Relevance
Knowledge-guided statistical learning methods can be used to construct accurate models for predicting cancer risk, prognosis, and response; uncover molecular signatures that are predictive of cancer risk, disease progression, or patient response to treatment, which can inform novel targets for therapeutic development; and identify cancer subtypes related to molecular differences, which offers insights about optimizing treatment strategy for each subtype, an important step toward precision oncology.
Recent methodologic research23-25 has also provided strong evidence about the advantages of knowledge-guided statistical learning methods that can incorporate the aforementioned biological knowledge, compared with statistical learning methods that do not use such biological knowledge. Knowledge-guided statistical learning methods enable selection of important pathways instead of individual -omics features and improve power in uncovering important features, particularly those with weak signals. The results from such analyses are biologically more meaningful and interpretable and can provide insights about molecular mechanism and underpinning of complex diseases. In addition, such a strategy can also facilitate the integration of multimodal -omics data through the incorporation of biological knowledge about the functional relationship between different modalities (eg, expression quantitative trait loci and metabolomic quantitative trait loci). As such, this knowledge-guided data-driven approach is particularly powerful and useful for analysis of -omics data in complex diseases such as cancer.
Knowledge-guided statistical learning methods have wide applications in precision medicine, including precision oncology. The knowledge-guided supervised learning methods can be used to construct prediction models for disease risk and prognosis, which can then be used to identify higher risk groups more accurately and tailor interventions to individual patients.26 They can also be used to uncover molecular signatures that are predictive of disease risk, disease progression, or patient response to treatment, which can inform novel targets for therapeutic development. The knowledge-guided unsupervised learning methods, such as biclustering, can be used to identify disease subgroups and important pathways associated with each subgroup.27 Identification of subgroups related to molecular differences offers insights about optimizing treatment strategy for each subgroup and is an important step toward developing a precision medicine approach for complex diseases such as cancer.
In this review, we survey advances in knowledge-guided statistical learning methods for analysis of high-dimensional -omics data in precision medicine, many of which have been applied to analysis of cancer data. We organize our presentation in two broadly defined categories, knowledge-guided supervised statistical learning methods and knowledge-guided unsupervised statistical learning methods.
KNOWLEDGE-GUIDED SUPERVISED STATISTICAL LEARNING METHODS
The majority of the statistical learning tasks on cancer genomics studies focus on investigating the relationship between the high-dimensional complex genomic features and certain clinical outcomes. Depending on the type of clinical outcomes, methods have been proposed to handle binary data (eg, the disease status), continuous data (eg, time to death), categorical data (eg, cancer subtypes), and censored data (eg, time to cancer recurrence). Through this learning procedure, we can identify important genomic features that are highly associated with clinical end points, build a prediction rule that will be crucial for future clinical practice, or even achieve both simultaneously. Correspondingly, prior biological or structure knowledge is supposed to be incorporated within feature selection or the prediction process to refine the model for a more accurate and interpretable result.
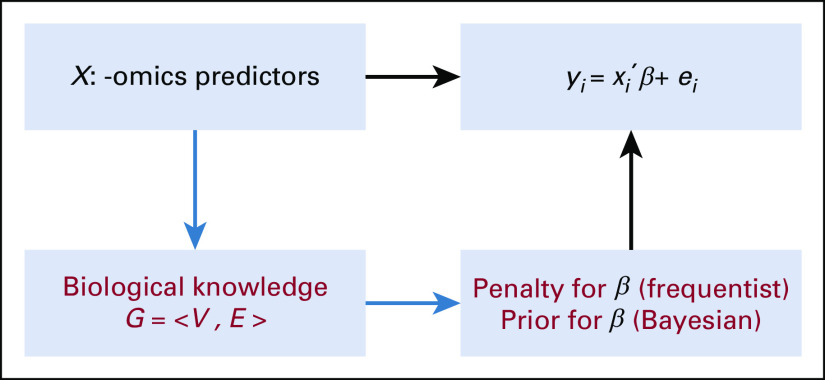
For ease of illustration, we introduce a few notations without loss of generality. Suppose a study recruits n patients with an outcome of interest (eg, disease status) and p predictors (ie, confounders and genomics features) collected for each patient. Under high-dimensional case, the number of predictors is larger than the sample size (ie, p > n), and we denote the outcome as Y and a collection of -omics predictors as X. The existing biological knowledge (eg, pathway information, gene-gene network) among predictors is represented as a direct or indirect graph among genomics features, denoted as G. The goal of the supervised learning is to build a prediction model for Y using X, which also allows us to assess how X influences Y. A knowledge-guided supervised learning approach allows the incorporation of the information in G. In this section, we broadly categorize current knowledge-guided supervised learning methods into two types of approaches, the frequentist approach and the Bayesian approach. Figure 1 provides an example of a knowledge-guided linear regression model in both the frequentist and Bayesian frameworks.
FIG 1.
Knowledge-guided linear regression model where Y is the clinical outcome of interest and X is the set of high-dimensional -omics features or predictors, and G = <V, E> is the graph containing the biological knowledge about -omics predictors with V denoting the set of nodes (ie, -omics features) and E denoting the set of edges. To incorporate G = <V, E>, a penalty for β is used in a frequentist framework, and a prior distribution for β is used in a Bayesian framework.
The main distinction between the frequentist and Bayesian approaches is their view on probability. In short, frequentist approaches try to solve the exact value of probability on the basis of the event they observed, whereas Bayesian methods do not assume there is fixed probability of the event but treat this probability itself also as random. In terms of model fitting, frequentist models do not assign prior distribution for the unknown parameters and eventually end up with a point estimate for them, whereas Bayesian models need such a prespecified prior and produce a posterior distribution for each parameter. The difference in the modeling scheme results in their differences in how to incorporate biological knowledge, computation, and interpretation of analysis results.
Frequentist Approach
The majority of knowledge-guided frequentist methods for analysis of high-dimensional -omics data are based on a regression framework to study the association between -omics features X and an outcome of interest Y [ie, Y ≈ f(X, β)], with β being the set of p unknown regression coefficients to be estimated. Under a high-dimensional setting, β are typically assumed to be sparse, with many of them being zero. This essentially translates to a feature selection process by keeping important -omics features with nonzero coefficients in the model while excluding unimportant ones. To induce sparsity or shrinkage for the regression coefficients, a penalty function, p(β), is often introduced, leading to the so-called penalized regression. In the case where biological knowledge among predictors X is available and can be represented by a graph G, we can also use p(β) to incorporate such biological knowledge (Fig 1). Specifically, when there is an edge between features i and j in G, a common strategy is to induce similar shrinkage effects between their corresponding parameters βi and βj.
The work of Li and Li23 represents one of the earliest attempts to incorporate gene network information into feature selection for cancer genomics application. The work tackles the problem of predicting time to death among patients with glioblastoma using microarray gene expression markers under a classic linear regression model. To incorporate the pathway information in KEGG, they proposed a network-constrained penalty on the basis of the following two assumptions: first, genes connected by an edge have similar functions and, therefore, are expected to have smoothed regression parameters; and second, the connected genes have higher probability to be selected or not selected simultaneously. The penalty itself consists of an L1-norm to achieve global sparsity as the usual penalization procedure does, as well as a quadratic form on the network Laplacian matrix to induce smoothness across the biological graph. Using this method, they identified gene subnetworks that were highly correlated with survival time of patients with glioblastoma (see Fig 2 in the article by Li and Li23), and some of these subnetworks were not identified by other existing learning methods that did not use pathway information. Although some of the subnetworks were supported by previously published work, some have not been reported in the literature, and these novel gene signatures can inform the molecular underpinnings of glioblastoma prognosis or even novel targets for therapeutic development.
After Li and Li,23 a number of extensions have been proposed. To handle binary outcome, Zhang et al28 adopted the network-constrained penalty under a logistic regression model that was used to predict a specific breast cancer subtype on the basis of gene expression data from The Cancer Genome Atlas (TCGA) consortium while incorporating protein-protein interactions. Sun et al29 proposed a Cox regression model with the network-constrained penalty for survival outcome. Their method was applied to a breast cancer study to identify genes and subnetworks that are predictive of survival while incorporating biologic network from KEGG.
Besides extensions to handle different outcome types, Pan et al24 proposed a new penalty on the basis of Lr-norm. It reduces the computational costs with a smaller number of tuning parameters and allows two connected genes to both up- and downregulate one another’s expression while maintaining the grouping effect. A few subsequent extensions include those by Kim et al30 to modify the penalty by removing the constraint of a similar magnitude of the connected biomarkers, which is biologically more meaningful, and Tian et al31 to use a multinomial logit model for cancer subtype prediction. Overall, these works focus on incorporating individual-level relationships between -omics biomarkers under the assumption that connected biomarkers are more likely to affect clinical outcome in a coordinated way.
More recently, for analysis of gene and microRNA biomarkers, Zhao et al26 proposed a hierarchical group penalty, which incorporates pathway membership, gene network, and microRNA-gene regulatory network information into a semiparametric accelerated failure time model to predict prostate cancer recurrence after surgery. Compared with previous works, hierarchical group penalty further allows a group-level sparsity (ie, genes in the same pathway are also more likely to be associated or not associated with clinical outcome at the same time). Zhao et al26 were among the first to include both group-level membership and within-group connectivity and induce sparsity at both the pathway level and gene level. Another novelty in the work by Zhao et al26 is the incorporation of the microRNA regulatory network or, more generally, a partially known biological graph. The article by Zhao et al26 treats the unknown component of the biological graph as missing data and proposes a multiple-imputation approach for handling missing edges in the graph. The analysis of prostate cancer data using their method yielded a more accurate prediction model for prostate cancer recurrence after prostatectomy, which can be used to help determine whether adjuvant therapy is needed after surgery.
A number of other supervised learning methods have also been proposed to analyze high-dimensional biomedical data while incorporating biological knowledge, including support vector machine (SVM)32 for binary classification and linear discriminant analysis33 for general classification. For both methods, similar to the regression setting, biological knowledge represented by graph is incorporated into the model using penalty functions, where the sparsity and grouping effects are also expected. The knowledge-guided SVM has been used to predict clinical outcome of patients with glioblastoma using genomic biomarkers.32
Bayesian Approach
Although frequentist models are traditionally considered canonical, Bayesian approaches have attracted increasing interest in recent years as a result of their ease in incorporating prior information and quantifying uncertainty. As such, they have played an important role in the development of knowledge-guided supervised learning methods.
When analyzing high-dimensional -omics data, prior distributions that lead to variable selection or shrinkage are used in a Bayesian model to improve prediction and identify important features. There is an extensive body of literature on Bayesian variable selection.34 Different from variable selection achieved through a penalty in a frequentist paradigm, Bayesian variable selection can be achieved in two ways, namely, selection on the basis of a point-mass mixture prior or regularization through a shrinkage prior. The former35 directly includes or excludes a predictor in the model by introducing a binary selection indicator. However, the computation to fit such a Bayesian model can become prohibitively expensive for analysis of high-dimensional -omics data. A shrinkage prior36 is analogous to a penalty on regression coefficients in a frequentist model and requires much less computation. Thus, it is more attractive for high-dimensional data. The downside with a shrinkage prior is that it does not directly provide results on feature selection; in addition, a subsequent truncation step, often ad hoc, is required to obtain the final set of selected predictors.
Similar to existing frequentist methods, the majority of knowledge-guided Bayesian supervised learning methods are developed for regression models. Prior distributions for β are carefully designed to incorporate biological knowledge represented by a graph G (Fig 1). One earlier work by Li and Zhang37 proposed to use the Ising model38 combined with the point-mass mixture for incorporating graph information under a linear regression model. This idea has been used widely in subsequent applications. As an extension of the work by Li and Zhang,37 Stingo et al39 proposed a Bayesian hierarchical variable selection regression model incorporating both pathway membership and gene network information with application to breast cancer microarray data. Their method, similar to that of Zhao et al,26 enables selection of important pathways as well as important genes within the selected pathways. After the work by Stingo et al,39 the general idea of Bayesian hierarchical variable selection at both the group level and individual level has gained increasing popularity. Zhe et al40 tackled the following limitation of the method from Stingo et al39: all the pathways that a selected gene belongs to are also selected, which is overly restrictive and may not always be meaningful. To remove this restriction as well as reduce the computation, they proposed a Bayesian joint pathway and gene selection model that uses a graph Laplacian matrix to encode biological knowledge and a variational Bayesian algorithm for model estimation. The analyses of a gene expression data set using their method yielded a more accurate prediction model for survival time in patients with diffuse large B-cell lymphoma than several existing learning methods that did not use biological information.
Beyond genomics, Zhang et al41 analyzed molecular inversion probe data to identify genes and probes that are associated with clinically relevant subtypes of breast cancer. Their method uses information on biological grouping of gene and probe-within-gene levels to define a hierarchical selection procedure through a point-mass mixture prior for gene selection and a shrinkage prior for probe selection. As the dimension of -omics data increases, there is a growing interest in using Bayesian shrinkage priors for knowledge-guided variable selection and prediction as a result of potential computational savings. Rockova and Lesaffre42 developed a Bayesian model for hierarchical feature selection at the pathway level and gene level on the basis of Bayesian lasso.36 Subsequently, Chang et al25 developed a novel adaptive structured shrinkage prior to incorporate biological knowledge in a Bayesian regression model. They also developed a computationally efficient expectation-maximization algorithm that is scalable to analysis of hundreds of thousands or even millions of predictors. Applied to a TCGA glioblastoma data set, Chang et al25 identified a set of risk genes along with enriched pathways that were predictive of patient survival. Kundu et al43 adopted similar ideas to incorporate gene network information in an integrative analysis for gene, copy number, and methylation data. In general, with the computational advantage of the Bayesian shrinkage prior, this research direction is expected to become even more active for analysis of large-scale -omics data.
Besides regression, knowledge-guided Bayesian methods have also been developed for discriminant analysis44 and SVM45 for analysis of high-dimensional genomics data. In both of these methods, the combination of a point-mass mixture prior and an Ising prior has been used to facilitate a knowledge-guided selection procedure where the gene network information is obtained from one of the databases listed in Table 1.
KNOWLEDGE-GUIDED UNSUPERVISED STATISTICAL LEARNING METHODS
Compared with the rich literature in knowledge-guided supervised learning methods, there has been fairly limited work on incorporating biological knowledge in an unsupervised learning framework. Unsupervised learning methods are typically used as a data mining approach to help explore and visualize large-scale data; see Chapter 14 in Hastie et al.1 The existing knowledge-guided unsupervised learning methods have been focused in two areas, namely, clustering analysis and dimension reduction, for which either a frequentist or a Bayesian approach can be used.
Clustering Analysis
The goal of clustering analysis is to group patients on the basis of their similarities in, for example, genomic features. In terms of application to cancer -omics, clustering analysis has been widely used to uncover cancer subtypes, which is essential to understand tumor heterogeneity and optimize prevention and treatment strategy accordingly. There has also been a great deal of interest in incorporating biological knowledge in clustering to improve subtyping accuracy and yield biologically more interpretable results. Liu et al46 and Yu et al47 developed network-assisted biclustering algorithms to simultaneously group patients with cancer and gene features into meaningful clusters. They mainly used the number of edges connected with each gene to define weights in the clustering procedure.
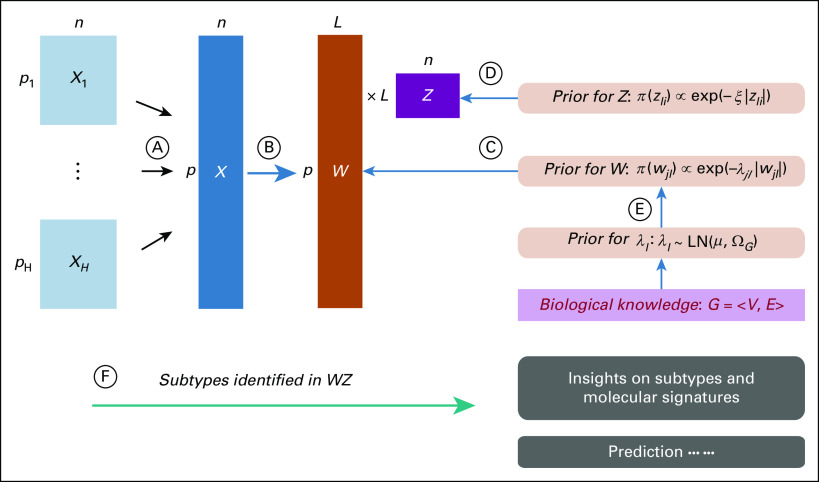
Recently, more advanced integrative clustering methods have been proposed to jointly analyze multimodality cancer -omics data while incorporating biological information. Li et al48 proposed a generalized Bayesian biclustering approach (Fig 2). Their method is able to jointly handle different data types (continuous and discrete), which is well suited to analyze multiomics data sets in cancer, including gene expression, copy number, RNA sequencing, and single nucleotide polymorphism. To incorporate biological knowledge, a Bayesian adaptive structured shrinkage prior is placed on the factor loading matrix, which encourages the -omics features connected in a graph to have zero or nonzero loading simultaneously in the same factor. Their method was used to conduct biclustering analysis of gene expression data, DNA methylation data, and DNA copy number data from a TCGA glioblastoma data set. The subgroups identified by their method had a higher correlation with survival outcome of patients with glioblastoma than those identified by other biclustering methods. As such, these subgroups, if validated, may be clinically more relevant. Similar in spirit, Min et al49 proposed a generalized Bayesian factor analysis for integrative clustering of multiomics data. Different from Li et al,48 a point-mass mixture prior combined with an Ising model was used to incorporate biological knowledge. To reduce heavy computation, they developed an efficient variational expectation-maximization algorithm for estimation, making their method scalable to the analysis of high-dimensional -omics data.
FIG 2.
Knowledge-guided Bayesian generalized biclustering analysis.48 (A) Integrate data from H -omics modalities, X1, …, XH. (B) X is linked to loading W and latent factors Z. (C and D) Prior for W and Z, respectively. (E) Prior for incorporating biological knowledge. (F) Biclusters identified in the product W*Z provide insight on disease subgroups and associated molecular signatures. This method was used to conduct biclustering analysis of gene expression data, DNA methylation data, and DNA copy number data from a glioblastoma data set from The Cancer Genome Atlas. The subgroups identified by the method had a higher correlation with survival outcome of patients with glioblastoma than those identified by other biclustering methods.
Dimension Reduction
Dimension reduction methods can be used to project high-dimensional -omics features into a lower dimension space either to better understand or visualize the data structure or to facilitate assessing dependence between two sets of data. Incorporation of biological knowledge could also play a vital role in improving the performance of dimension reduction, and a few recent publications have made attempts in this direction. Li et al27 incorporated biological knowledge into the sparse principal component analysis, a popular dimension reduction tool for high-dimensional data, to identify genes associated with glioblastoma cancer subtypes. They extended and investigated two network-based penalties, the grouped penalty by Pan et al24 and the fused lasso penalty by Tibshirani et al.50 The resulting sparse principal component analysis algorithm is able to incorporate biological network information in the principal component loadings and achieve more accurate and biologically meaningful dimension reduction. Similarly, biologic knowledge has also been incorporated into the canonical correlation analysis51 and the coinertia analysis (CIA)52 for assessing dependence between two -omics data sets. Applied to analysis of gene expression data and protein abundance data in the NCI-60 cell line data set, the knowledge-guided CIA52 method was able to project the high-dimensional -omics feature to a lower dimensional space in which the 10 different types of cancers were clearly separated (see Fig 1 in article by Min et al52). It selected a sparse subset of genes and proteins that may inform key molecular underpinnings that distinguish these cancers. Of note, both canonical correlation analysis and CIA are popular multivariate statistical methods for integrative analysis and have become popular in analysis of multimodality -omics data in cancer studies.
In addition, Liu et al53 developed a knowledge-guided approach to use expression data and coexpression network information to improve de novo discovery of driver pathways in cancer on the basis of mutation data. Analyses of three cancer data sets using their method revealed new driver pathways that were not uncovered by other methods including, particularly, driver genes with less frequent mutations that are much more difficult to detect. These new driver pathways may offer insights about cancer biology and inform novel targets for screening and for therapeutic development.
DISCUSSION
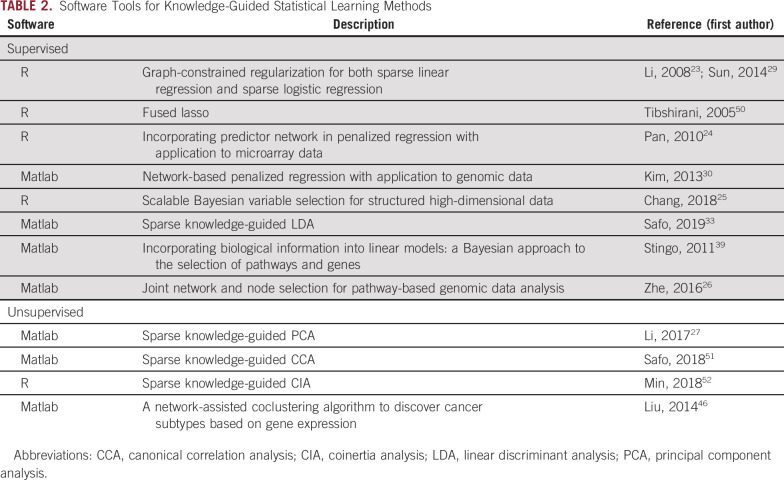
Statistical learning methods have been proven powerful for analysis of high-dimensional -omics data in modern biomedical research but have some important limitations. To address these limitations, the knowledge-guided strategy, as reviewed here, has drawn increasing interest in recent years and has been shown to yield biologically more interpretable and meaningful results. Software tools for many of the methods reviewed earlier have been made publicly available (Table 2).
TABLE 2.
Software Tools for Knowledge-Guided Statistical Learning Methods
Although substantial progress has been made in the development of knowledge-guided statistical learning methods, there is still much room for additional methodologic developments and improvements. One area for future research is to assess robustness of knowledge-guided methods to mis-specification of biological knowledge, because in practice, biological knowledge represented by a graph G is known to be incomplete and include false edges. Existing work27 has demonstrated that some knowledge-guided supervised learning methods are fairly robust to mis-specified biological knowledge G, but more research is needed for other types of statistical learning methods. To further enhance robustness, it is also of significant interest to combine knowledge-guided methods with learning biological knowledge graphs from observed data, for which there is little research besides that by Zhao et al.26 In addition, most of the existing knowledge-guided Bayesian methods may not be scalable to analysis of big -omics data that can have hundreds of thousands or even millions of features, and more research on efficient computation algorithms is needed.
Although knowledge-guided statistical learning methods have drawn growing interest in methodologic communities, they have not been widely used by cancer researchers, and the findings from the methods publications reviewed in this article largely remain to be validated in subsequent studies. Our hope is that this review will raise the awareness and spur wider and more frequent applications of knowledge-guided methods in basic, translational, and clinical research in order to advance precision medicine, particularly for complex diseases such as cancer. This will generate more compelling evidence on how such methods can catalyze cancer research and subsequently improve cancer prevention, screening, and treatment. It will also offer exciting opportunities to extensively assess and validate these methods in real data settings and identify potential methodologic gaps for additional refinement.
Supplementary Material
AUTHOR CONTRIBUTIONS
Conception and design: All authors
Collection and assembly of data: Yize Zhao, Qi Long
Data analysis and interpretation: Yize Zhao, Qi Long
Manuscript writing: All authors
Final approval of manuscript: All authors
Accountable for all aspects of the work: All authors
AUTHORS' DISCLOSURES OF POTENTIAL CONFLICTS OF INTEREST
The following represents disclosure information provided by authors of this manuscript. All relationships are considered compensated. Relationships are self-held unless noted. I = Immediate Family Member, Inst = My Institution. Relationships may not relate to the subject matter of this manuscript. For more information about ASCO's conflict of interest policy, please refer to www.asco.org/rwc or po.ascopubs.org/site/ifc.
Qi Long
Research Funding: Bayer
Travel, Accommodations, Expenses: Intelmed Tech
No other potential conflicts of interest were reported.
REFERENCES
- 1.Hastie T, Tibshirani R, Friedman J: The Elements of Statistical Learning. New York, NY, Springer, 2001 [Google Scholar]
- 2.Kanehisa M, Goto S: KEGG: Kyoto Encyclopedia of Genes and Genomes. Nucleic Acids Res 28:27-30, 2000 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Croft D, O’Kelly G, Wu G, et al. : Reactome: A database of reactions, pathways and biological processes. Nucleic Acids Res 39:D691-D697, 2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Li S, Park Y, Duraisingham S, et al. : Predicting network activity from high throughput metabolomics. PLOS Comput Biol 9:e1003123, 2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Reference deleted.
- 6.Karp PD, Riley M, Paley SM, et al. : The metacyc database. Nucleic Acids Res 30:59-61, 2002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.https://pathways.embl.de/ Invitrogen: iPath I.
- 8.Qiagen : Ingenuity Pathway Analysis (IPA). https://www.qiagenbioinformatics.com/products/ingenuity-pathway-analysis/
- 9.https://biocyc.org/ BioCyc Database Collection: Homepage.
- 10.Krull M, Voss N, Choi C, et al. : TRANSPATH: An integrated database on signal transduction and a tool for array analysis. Nucleic Acids Res 31:97-100, 2003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Cell Signaling Technology: CST Pathways. https://www.cellsignal.com/contents/science/cst-pathways/science-pathways.
- 12.Agarwal V, Bell GW, Nam J-W, et al. : Predicting effective microRNA target sites in mammalian mRNAs. Elife 4:e05005, 2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Griffiths-Jones S: miRBase: The microRNA sequence database. Methods Mol Biol 342:129-138, 2006 [DOI] [PubMed] [Google Scholar]
- 14.Krek A, Grün D, Poy MN, et al. : Combinatorial microRNA target predictions. Nat Genet 37:495-500, 2005 [DOI] [PubMed] [Google Scholar]
- 15.Wong N, Wang X: miRDB: An online resource for microRNA target prediction and functional annotations. Nucleic Acids Res 43:D146-D152, 2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Shirdel EA, Xie W, Mak TW, et al. : NAViGaTing the micronome: Using multiple microRNA prediction databases to identify signalling pathway-associated microRNAs. PLoS One 6:e17429, 2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Stark C, Breitkreutz B-J, Reguly T, et al. : BioGRID: A general repository for interaction datasets. Nucleic Acids Res 34:D535-D539, 2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kamburov A, Stelzl U, Lehrach H, et al. : The ConsensusPathDB interaction database: 2013 update. Nucleic Acids Res 41:D793-D800, 2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ashburner M, Ball CA, Blake JA, et al. : Gene ontology: Tool for the unification of biology. Nat Genet 25:25-29, 2000 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Nishimura D: BioCarta. Biotech Softw I Rep 2:117-120, 2001 [Google Scholar]
- 21.Costello JC, Heiser LM, Georgii E, et al. : A community effort to assess and improve drug sensitivity prediction algorithms. Nat Biotechnol 32:1202-1212, 2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Subramanian A, Tamayo P, Mootha VK, et al. : Gene set enrichment analysis: A knowledge-based approach for interpreting genome-wide expression profiles. Proc Natl Acad Sci USA 102:15545-15550, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Li C, Li H: Network-constrained regularization and variable selection for analysis of genomic data. Bioinformatics 24:1175-1182, 2008 [DOI] [PubMed] [Google Scholar]
- 24.Pan W, Xie B, Shen X: Incorporating predictor network in penalized regression with application to microarray data. Biometrics 66:474-484, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Chang C, Kundu S, Long Q: Scalable Bayesian variable selection for structured high-dimensional data. Biometrics 74:1372-1382, 2018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Zhao Y, Chung M, Johnson BA, et al. : Hierarchical feature selection incorporating known and novel biological information: Identifying genomic features related to prostate cancer recurrence. J Am Stat Assoc 111:1427-1439, 2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Li Z, Safo SE, Long Q: Incorporating biological information in sparse principal component analysis with application to genomic data. BMC Bioinformatics 18:332, 2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Zhang W, Wan YW, Allen GI, et al. : Molecular pathway identification using biological network-regularized logistic models. BMC Genomics 14:S7, 2013. (suppl 8) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Sun H, Lin W, Feng R, et al. : Network-regularized high-dimensional Cox regression for analysis of genomic data. Stat Sin 24:1433-1459, 2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kim S, Pan W, Shen X: Network-based penalized regression with application to genomic data. Biometrics 69:582-593, 2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Tian X, Wang X, Chen J: Network-constrained group lasso for high-dimensional multinomial classification with application to cancer subtype prediction. Cancer Inform 13:25-33, 2015 (suppl 6) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Zhu Y, Shen X, Pan W: Network-based support vector machine for classification of microarray samples. BMC Bioinformatics 10:S21, 2009. (suppl 1) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Safo SE, Long Q: Sparse linear discriminant analysis in structured covariates space. Stat Anal Data Mining 12:56-59, 2019 [Google Scholar]
- 34.O’Hara RB, Sillanpää MJ: A review of Bayesian variable selection methods: What, how and which. Bayesian Anal 4:85-117, 2009 [Google Scholar]
- 35.George EI, McCulloch RE: Variable selection via Gibbs sampling. J Am Stat Assoc 88:881-889, 1993 [Google Scholar]
- 36.Park T, Casella G: The Bayesian lasso. J Am Stat Assoc 103:681-686, 2008 [Google Scholar]
- 37.Li F, Zhang NR: Bayesian variable selection in structured high-dimensional covariate spaces with applications in genomics. J Am Stat Assoc 105:1202-1214, 2010 [Google Scholar]
- 38.Brush SG: History of the Lenz-Ising model. Rev Mod Phys 39:883-893, 1967 [Google Scholar]
- 39.Stingo FC, Chen YA, Tadesse MG, et al. : Incorporating biological information into linear models: A Bayesian approach to the selection of pathways and genes. Ann Appl Stat 5:1978-2002, 2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Zhe S, Naqvi SA, Yang Y, et al. : Joint network and node selection for pathway-based genomic data analysis. Bioinformatics 29:1987-1996, 2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Zhang L, Baladandayuthapani V, Mallick BK, et al. : Bayesian hierarchical structured variable selection methods with application to molecular inversion probe studies in breast cancer. J R Stat Soc Ser C Appl Stat 63:595-620, 2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Rockova V, Lesaffre E: Incorporating grouping information in Bayesian variable selection with applications in genomics. Bayesian Anal 9:221-258, 2014 [Google Scholar]
- 43.Kundu S, Cheng Y, Shin M, et al. : Bayesian variable selection with graphical structure learning: Applications in integrative genomics. PLoS One 13:e0195070, 2018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Stingo FC, Vannucci M: Variable selection for discriminant analysis with Markov random field priors for the analysis of microarray data. Bioinformatics 27:495-501, 2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Sun W, Chang C, Zhao Y, et al. : Knowledge-guided Bayesian support vector machine for high-dimensional data with application to genomic data. Presented at the 2018 IEEE International Conference on Big Data (Big Data), Seattle, WA, 2018, pp 1484-1493 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Liu Y, Gu Q, Hou JP, et al. : A network-assisted co-clustering algorithm to discover cancer subtypes based on gene expression. BMC Bioinformatics 15:37, 2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Yu G, Yu X, Wang J: Network-aided bi-clustering for discovering cancer subtypes. Sci Rep 7:1046, 2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Li Z, Chang C, Kundu S, et al. : Bayesian generalized biclustering analysis via adaptive structured shrinkage. Biostatistics 10.1093/biostatistics/kxy081 [epub ahead of print on December 31, 2018] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Min EJ, Chang C, Long Q: Generalized Bayesian factor analysis for integrative clustering with applications to multi-omics data. Presented at the 2018 IEEE 5th International Conference on Data Science and Advanced Analytics, Turin, Italy, October 1-3, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Tibshirani R, Saunders M, Rosset S, et al. : Sparsity and smoothness via the fused lasso. J R Stat Soc Series B Stat Methodol 67:91-108, 2005 [Google Scholar]
- 51.Safo SE, Li S, Long Q: Integrative analysis of transcriptomic and metabolomic data via sparse canonical correlation analysis with incorporation of biological information. Biometrics 74:300-312, 2018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Min EJ, Safo SE, Long Q: Penalized co-inertia analysis with applications to-omics data. Bioinformatics 35:1018-1025, 2019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Liu B, Wu C, Shen X, et al. : A novel and efficient algorithm for de novo discovery of mutated driver pathways in cancer. Ann Appl Stat 11:1481-1512, 2017 [DOI] [PMC free article] [PubMed] [Google Scholar]