Correlations between complex human phenotypes vary by genetic background, gender, and environment

Summary

We develop a closed-form Haseman-Elston estimator for genetic and environmental correlation coefficients between complex phenotypes, which we term HEc, that is as precise as GCTA yet ∼20× faster. We estimate genetic and environmental correlations between over 7,000 phenotype pairs in subgroups from the Trans-Omics in Precision Medicine (TOPMed) program. We demonstrate substantial differences in both heritabilities and genetic correlations for multiple phenotypes and phenotype pairs between individuals of self-reported Black, Hispanic/Latino, and White backgrounds. We similarly observe differences in many of the genetic and environmental correlations between genders. To estimate the contribution of genetics to the observed phenotypic correlation, we introduce “fractional genetic correlation” as the fraction of phenotypic correlation explained by genetics. Finally, we quantify the enrichment of correlations between phenotypic domains, each of which is comprised of multiple phenotypes. Altogether, we demonstrate that the observed correlations between complex human phenotypes depend on the genetic background of the individuals, their gender, and their environment.

Graphical abstract

Highlights

• •An estimator of genetic correlation generalizes the Pearson correlation estimator
• •Fractional genetic correlation quantifies genetic fraction of a phenotypic correlation
• •Genetic correlations between phenotypes vary by genetic and environmental determinants

Elgart et al. develop a closed-form estimator for genetic correlation between phenotypes called HEc, generalizing the Pearson estimator. Fractional correlation estimates that quantify contributions of genetics and environment to the overall phenotypic correlation demonstrate that both genetics and environment contribute to phenotypic correlation differences between groups of individuals.

Introduction

Both genetics and environment determine human phenotypes and the correlations between them.^1,2 Correlations can arise due to multiple forms of causal relationships including common genetic and environmental determinants, (bi)directional causal associations and others. The correlations between phenotypes can reveal genetic architecture, help uncover gene functions and disease mechanisms, improve diagnosis, and aid in therapeutic interventions.³ Given appropriate data, phenotypic correlations can be decomposed into genetic and environmental components by estimating corresponding measures, such as genetic correlation.⁴

Several studies have leveraged the data generated by large studies with genotyped individuals and multiple measured phenotypes (e.g., BioBank Japan⁵ and UK Biobank⁶), to estimate genetic correlations between various phenotypes.^7,8,9,10 Dozens of pairwise correlations between phenotypes were estimated and reported, mostly based on studies with participants of European or East Asian ancestries^9,10 and of mixed genders. Genetic ancestry, as well as biological sex and sociocultural roles of gender, all contribute to differences in phenotypic distributions between different groups of people due to both underlying genetics and different environmental exposures.^11,12,13 The genetic background manifests in allele frequencies, effect sizes, and, more generally, genetic architectures.^14,15 Sociocultural measures, captured in part by self-reported race/ethnicity, are related to behavioral, environmental, and psychosocial exposures such as smoking, alcohol, nutrition, physical activity, and stress,^16,17 modifying the effect of genetic variants. In this work, we refer to the collective characteristics of a studied race and ethnicity-based group as a “background” to reflect the fact that no single genetic or social measure can be used to define the group, although its individuals may self-identify using a specific, pre-defined label, whether by choice or by the set of options presented to them. Notably, these background groups are enriched with patterns of both genetics and sociodemographic (and environmental and cultural) similarity, and all factors may ultimately affect the expression of genetic effects. However, we cannot, using existing data, separate these different influences. While a handful of studies reported differences in genetic correlation across different background groups,^18,19,20 these are limited in the number of studied phenotypes and backgrounds. Similarly, while biological sex-specific heritabilities of complex phenotypes have been reported previously,^21,22,23 gender-specific correlations between phenotypes have not been comprehensively studied. Genetic correlations between phenotypes can be leveraged for prediction of health conditions²⁴ and differences between these correlations across groups may affect the application of prediction models. An environmental correlation between two phenotypes may suggest the possibility of a lifestyle change to alleviate the burden of disease related to these phenotypes.

The two main computational approaches that are used to estimate genetic correlation are the genetic restricted maximum likelihood analysis (GREML),^25,26,27 which requires individual-level genotypes and is computationally challenging when analyzing datasets with thousands of individuals; and the linkage disequilibrium score regression (LDSC),²⁸ which uses genome-wide association study (GWAS) summary statistics. LDSC requires reliable GWASs, and can be inaccurate when there is genetic heterogeneity between the target sample and reference linkage disequilibrium (LD) panel,^29,30 and thus cannot be used reliably for admixed or multi-ancestry analyses. Thus, both GREML and LDSC approaches are limited when analyzing datasets that include tens of thousands of genetically diverse individuals.

Here, we estimated the heritabilities, as well as genetic and environmental correlations between phenotypes in joint as well as background- and gender-stratified analysis. First, we derived a closed-form solution for the estimation of genetic and environmental correlation coefficients within the Haseman-Elston regression framework, which we termed HEc (Haseman-Elston closed form). Second, we applied the algorithm to study heritabilities and genetic correlations for 28 phenotypes in the Trans-Omics in Precision Medicine (TOPMed) program^31,32 dataset, with a large representation of individuals of White, Black, and Hispanic/Latino backgrounds. We then focused on Hispanics/Latinos from the Hispanic Community Health Study/Study of Latinos (HCHS/SOL) cohort,³³ and utilized available data on shared household (representing shared environmental exposure) and compared gender-specific genetic and environmental correlations across a larger panel of 61 phenotypes. Finally, we performed domain-level enrichment analysis to identify genetic and environmental correlations between phenotypic domains.

Results

HEc is a fast and precise estimator for genetic correlation

We developed an estimator, HEc, for genetic correlation within the Haseman-Elston regression framework (see STAR Methods for detailed derivation). The HEc estimator generalizes the Pearson correlation coefficient, and it has the closed-form formula:

$${\hat{\rho }}_k=\frac{\widehat{ϵ}{}_1^T{\mathit{S}}_{\mathit{k}}{\widehat{ϵ}}_2}{\sqrt{\left(\widehat{ϵ}{}_1^T{\mathit{S}}_{\mathit{k}}{\widehat{ϵ}}_1\right)\left(\widehat{ϵ}{}_2^T{\mathit{S}}_{\mathit{k}}{\widehat{ϵ}}_2\right)}}$$

where ${\widehat{ϵ}}_1,{\widehat{ϵ}}_2$ are the residuals of traits $y_1,y_2$ after regression on covariates, and ${\mathit{S}}_{\mathit{k}}$ is a matrix that depends on the genetic relationship between individuals in the dataset and potentially other matrices used to model correlation between individuals (e.g., matrices modeling shared environmental influences). The reader may see that it generalizes the standard Pearson estimator since replacing the matrix ${\mathit{S}}_{\mathit{k}}$ by the identity matrix and by assuming that the residuals are those obtained by regressing the traits on intercepts (i.e., subtracting their mean), reduces the estimate to the Pearson correlation coefficient.

We evaluated the performance of HEc in simulations across multiple parameters and background groups and compared it with the GREML algorithm⁴ implemented in the GCTA (Genome-wide Complex Trait Analysis) software³² (Figures 1A and S2–S5).

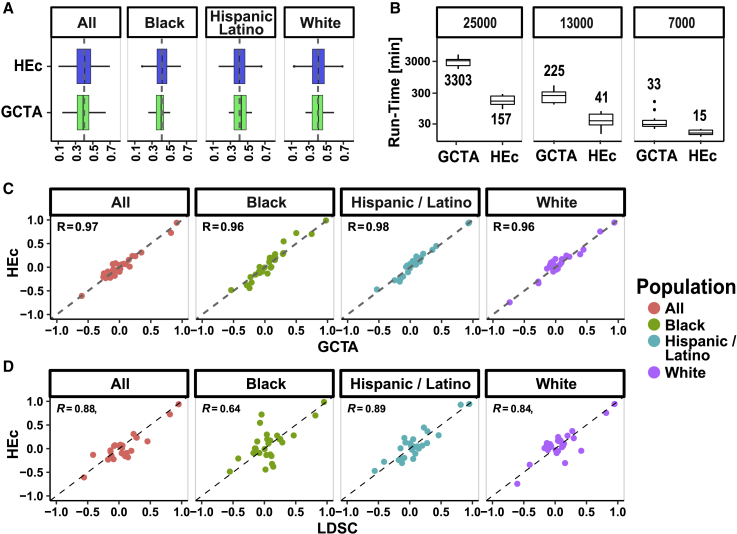
Figure 1.

Closed-form HEc is as accurate as GCTA on diverse and admixed populations while being up to 20× faster

Comparison of accuracy and computation speed between our HEc method, GCTA-GREML, and an LD-score-based method (LDSC) based on simulations and the TOPMed dataset. Relatedness data from three self-reported TOPMed backgrounds as well as a combined group of the same size consisting of equal number of all three (n = 7,706) were used to simulate phenotype pairs with known genetic correlation coefficients (${\rho }_k$).

(A) Boxplots of distributions of estimated ${\rho }_k$ from HEc (blue color) and GCTA-GREML (green) when we set ${\rho }_k$ = 0.4. See Figure S1 and S2 for multiple simulation values.

(B) Comparison of runtime between HEc and GCTA-GREML for samples comprised of increasing number of individuals (note the log scale).

(C) Comparison of ${\rho }_k$ estimates between HEc and GCTA-GREML for all pairs of eight phenotypes selected from the diverse TOPMed cohort either joint or stratified by self-reported background.

(D) Comparison of ${\rho }_k$ estimates between HEc and LDSC for all pairs of eight phenotypes from the diverse TOPMed cohort either joint or stratified by self-reported background. See supplemental information and STAR Methods for description of the methods and GWAS used.

Figure S1 visualizes TOPMed and HCHS/SOL individuals in the space generated by the first two genetic principal components (PCs). One can see that the White, Black, and Hispanic/Latino background groups are only partly separated in PC space, and individuals from Hispanic/Latino background, who are admixed with high proportions of European, Amerindian, and, to lower extent, African genetic ancestries, are represented throughout the PC space. In Figure S1B that focuses on HCHS/SOL, we also highlight finer self-reported Hispanic/Latino backgrounds, including Mexican, Puerto Rican, etc., which show some clustering, indicating some genetic structure within Hispanic/Latino individuals (as is known). This figure demonstrates that individuals within the background groups are on average more similar to each other in their genetic patterns compared with individuals in other background groups. However, the separation in the figure is far from perfect, as background groups capture self-identification, which does not precisely correlate with genetic patterns. Self-identified background also captures shared culture and systematic environmental exposures, which modify genetic effects, and which motivated us to use these grouping rather than ones based on genetic ancestry.

To simulate realistic data, we used kinship matrices from participants of the different self-reported backgrounds (Black, Hispanic/Latino, White) and a joint group of same size comprised of people from each group (n = 7,706, which is the also the size of the smallest subgroup from the TOPMed dataset). We evaluated the time required for each algorithm as a function of the number of individuals (Figure 1B). In all cases, HEc matched or exceeded the accuracy of GCTA while improving the speed up to 20-fold and beyond (Figure 1B).

HEc outperforms existing approaches on complex real-world data

We selected eight phenotypes from the TOPMed cohort (height, BMI, diastolic blood pressure, systolic blood pressure, total cholesterol, HDL cholesterol, LDL cholesterol, triglycerides) to compare the performance of HEc with existing algorithms (GCTA and LDSC; Figures 1C and 1D). We estimated the heritabilities of the eight phenotypes using GCTA and LDSC and estimated genetic correlations between all phenotype pairs using HEc and GCTA. Estimates were computed based on the combined TOPMed cohort (Figure 1, “All”) as well as on the different background groups. While we see excellent agreement of HEc and GCTA estimates (Figure 1C; correlation above 0.96 for all groups), there is lower agreement between HEc and LDSC (Figure 1D; same for GCTA versus LDSC). This is especially evident for the self-reported Black group where the correlation is only 0.64 (Figure 1D). We also performed comparisons to a method called cov-LDSC, which was reported to account for population structure in admixed populations when estimating heritability³⁴ (Figure S5). Although the method indeed resulted in a lesser bias for heritability (Figure S5D), when extending the method for estimating genetic correlation there was little improvement (Figure S5B).

A compendium of genetic correlations and heritabilities in the multi-ethnic TOPMed dataset

We next expanded the number of analyzed phenotypes and calculated phenotypic and genetic correlations between 28 harmonized phenotypes in 33,959 TOPMed individuals. Results are provided in Figure 2 and Data S1. There were 378 phenotype pairs in the dataset. Of these, 270 (∼71%) had phenotypic correlations $R$ with p < 0.05 (Figure 2A), and 66 (18%) had genetic correlations (p < 0.05; Figure 2B, and inset).

Figure 2.

Genetic basis of observed phenotypic correlations between phenotypes in the combined TOPMed dataset

Correlation matrices where each column and row represent one of the 28 phenotypes in the TOPMed dataset (n = 33,959), and the intersection is the estimated correlation magnitude. Size and color of circle indicates the correlation strength: dark orange, positive; dark purple, negative correlation.

(A) Phenotypic correlations between the phenotypes. Inset: number of positive and negative correlated phenotype pairs with p < 0.05.

(B) Estimated genetic correlations (${\rho }_k$) (shown only for phenotype pairs with p < 0.05 between the phenotypes). Inset: number of phenotype pairs with both phenotypic and genetic correlations with p < 0.05 in this dataset.

(C) Estimated heritabilities for the studied phenotypes.

(D) Fractional genetic correlations (${\rho }_{fk})$ between the phenotypes (shown only for phenotype pairs with p < 0.05). Inset: example of phenotypic and genetic correlation where the absolute value of the genetic correlation is larger than that of the phenotypic correlation which complicates interpretability.

Our results in the multi-ethnic dataset agree well with previous reports. For example, we estimated a genetic correlation of ${\hat{\rho }}_k=0.23(95\%\text{CI}0.07-0.4)$ between body mass index (BMI) and triglycerides, while Bulik-Sullivan et al. estimated it at 0.26¹⁰ and Zhang et al. at 0.2³⁰ in European populations. We also identified potentially clinically relevant genetic correlations, including between white blood cell types and blood pressure, that are consistent with literature implicating a biological association between inflammation and hypertension^35,36 (Table S2 in Data S3).

We also estimated heritabilities for all the phenotypes in our combined dataset (Figure 2C; Table S3). The most highly heritable phenotypes are height (${\hat{h}}^2=$ 0.56, SE = 0.02) as well as multiple blood cell measurements, such as neutrophil counts (Figure 2C; ${\hat{h}}^2=$ 0.4, SE = 0.04) and total white blood cell (WBC) counts (Figure 2C; ${\hat{h}}^2=$ 0.45, SE = 0.03) similar to previous estimates.^37,38

Fractional genetic correlation quantifies the contribution of genetics to phenotypic correlations

We identified multiple instances where the genetic correlation coefficient is larger than the phenotypic correlation (Figure 2D, inset). For example, for lymphocytes and platelets the estimated phenotypic correlation is $\hat{R}=0.23$ but the estimated genetic correlation is larger: $\widehat{{\rho }_k}=0.37(95\%\text{CI}0.2-0.6)$. This emphasizes that the genetic correlation coefficient is not directly related to the phenotypic correlation.³⁹,⁴⁰ To address this, we introduce the concept of “fractional genetic correlation” (${\rho }_{fk}$), which we define as the fraction of the observed phenotypic correlation $R$ explained by genetics in the decomposition $\hat{R}={\hat{\rho }}_{fk}+{\hat{\rho }}_{fϵ}$ (see STAR Methods (Equation 34), (Equation 35), (Equation 36)), where ${\hat{\rho }}_{fϵ}$ is the estimated fractional residual correlation. In the example of lymphocytes and platelets, the estimated fractional genetic correlation is $\widehat{{\rho }_{fk}}=0.13$, and we conclude that 56% of the observed phenotypic correlation is due to genetics ($\widehat{{\rho }_{fk}}=0.13$ out of $\hat{R}=$ 0.23).

We estimated ${\rho }_{fk}$ for all the pairs of phenotypes in our dataset (Figure 2D; Table S4 in Data S3). Of phenotype pairs with genetic correlation with p < 0.05, 58% had substantial $\widehat{{\rho }_{fk}}$, defined as $\left|\widehat{{\rho }_{fk}}\right|>0.1$, corresponding to 19% of phenotypic correlations with p < 0.05. For most of the phenotype pairs, $\widehat{{\rho }_{fk}}$ is much lower than $\widehat{{\rho }_k}$ and is lower than the estimated $R$ (by construction).

Genetic correlations and heritabilities differ between self-reported background groups

Out dataset includes 8,054 Black, 17,143 White, and 8,762 Hispanic/Latino participants (Table S2). We estimated heritability, phenotypic, and genetic correlations within these groups and compared them with the estimates of the combined group (Figures 3 and S7; Data S1).

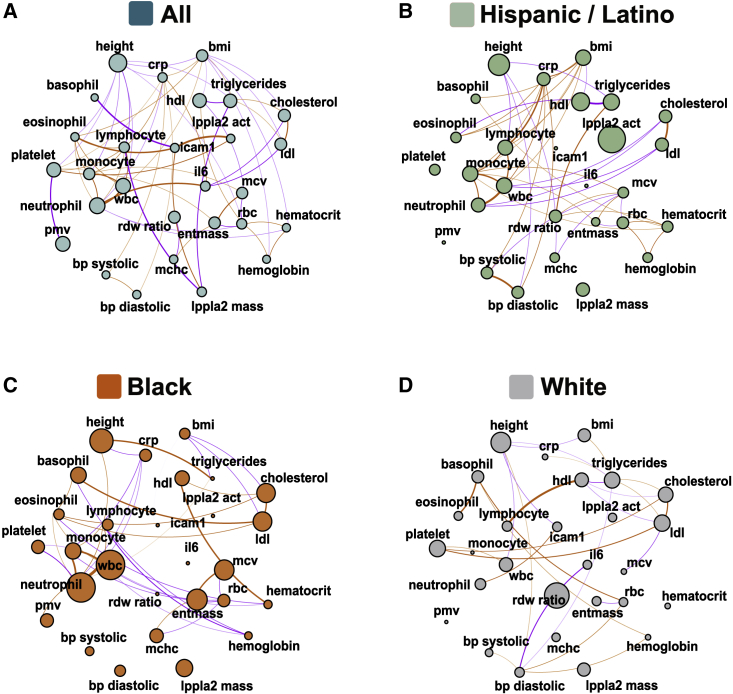
Figure 3.

Many genetic correlations and heritabilities vary by self-reported background

Fractional genetic correlation plots where each phenotype is represented by a node and the fractional genetic correlations are represented by connections (edges) between nodes. The size of the node is proportional to the phenotype heritability. The thickness of the edge is proportional to the magnitude of the fractional genetic correlation and the color represents direction: orange represents positive and purple negative correlation.

(A) Fractional genetic correlations (${\rho }_{fk})$ between the 28 phenotypes in the combined TOPMed dataset (p < 0.05, n = 33,959).

(B–D) Fractional genetic correlations (${\rho }_{fk}$) between the 28 phenotypes in subsets of TOPMed individuals grouped by self-reported race/ethnic background: Hispanic/Latino (B) (marine, n = 8,762), Black (C) (orange, n = 8,054), and White (D) (gray, n = 17,143).

While some phenotypes, such as HDL and eosinophil counts, have similar heritabilities across self-reported background groups (Figures 3 and S4), many other heritabilities vary by group. For example, CRP is similarly heritable in the Black and Hispanic/Latino backgrounds ($\widehat{h_2}=0.34,\text{SE}=0.13$ and 0.38 $,\text{SE}=0.07$, respectively), but much less so in White individuals ($\widehat{h_2}=0.09,\text{SE}=0.1)$. In contrast, neutrophil counts are very heritable in Black individuals ($\widehat{h_2}>0.99,\text{SE}=0.06)$, but are less so in White individuals ($\widehat{h_2}=0.29,\text{SE}=0.21)$ and Hispanic/Latino individuals ($\widehat{h_2}=0.41,\text{SE}=0.08$).

Similarly, multiple phenotype pairs, such as systolic and diastolic blood pressure are genetically correlated across backgrounds (Figures 3 and S6). However, many other ${\hat{\rho }}_k$ differ by background (Figure 3). For example, lymphocyte counts and height have estimated genetic correlation $\widehat{{\rho }_k}=0.68(95\%\text{CI }0.1-0.99)$ in individuals from a Black background, but an opposite estimate $\widehat{{\rho }_k}=-0.34(95\%\text{CI}-0.5\text{to}-0.17)$ of genetic correlation in individuals from an Hispanic/Latino background (p = 0.02 for correlation coefficients difference), and genetic correlation with p > 0.05 in individuals from a White background $\widehat{{\rho }_k}=-0.22(95\%\text{CI}-0.99-0.7)$ (Figures 3 and S6; Data S1). Overall, out of the 378 examined phenotype pairs, in 211 (55%) we detect a difference in genetic correlation values (p < 0.05) for at least two of the background groups in the multi-ethnic TOPMed dataset.

Genetics and shared household differentially affect phenotypic correlations in Hispanic/Latino individuals

We next studied genetic correlations among a larger panel of 61 phenotypes in n = 12,565 self-reported Hispanic/Latino individuals from the HCHS/SOL.^33,41 The phenotypes represent 11 phenotypic domains: diabetes, cardiovascular disease, blood pressure, kidney function, lipids, lung function, sleep, anthropometrics, iron, RBC (red blood cell), and WBC (Figures 4 and S8; Table S1). HCHS/SOL also has information about household sharing between participants, allowing for estimation of both genetic and environmental correlations between phenotypes.

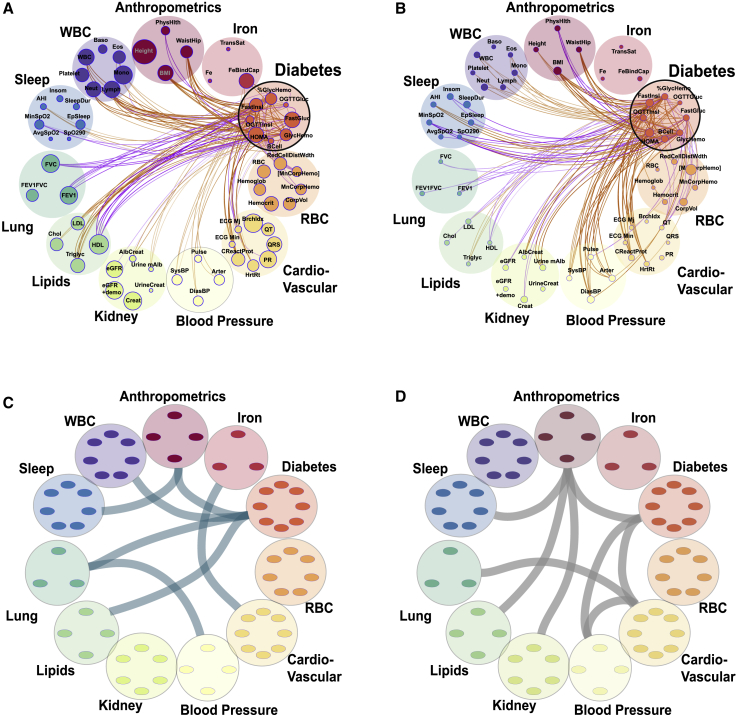
Figure 4.

Genetics and shared household factors contribute to associations between phenotypes

(A and B) Correlation plots between phenotypes in the HCHS/SOL dataset (n = 12,565). Each phenotype is represented by a node (colored small circles) with the size of the circle proportional to the phenotype heritability. The correlations are represented by connections (edges) between nodes (phenotypes). The nodes are grouped into phenotypic domains (colored semi-transparent circles labeled anthropometrics, iron, etc.). The thickness of the edge is proportional to the strength of correlation and the color represents magnitude: orange represents positive and purple negative correlation. A focused look on the diabetes phenotype domain showing fractional genetic (A) and fractional household (B) correlations with all other phenotypes (see Figure S7 for full graph).

(C and D) Same as (A and B) but connections represent enriched correlations between phenotypic domains. (C) Represents genetic correlations (teal) and (D) household correlations (gray).

We estimated ${\rho }_k$ and ${\rho }_{fk}$ in conjunction with the corresponding household correlation measures ${\rho }_h$ and ${\rho }_{fh}$ for all the 1,830 pairs of phenotypes (Figures 4 and S8). Out of the 1,830 phenotype pairs, 1,499 (or ∼81%) have phenotypic correlations with p < 0.05 (Data S2). Of these, 427 (∼28%) also have genetic correlations with p < 0.05 (Figure 3A) and 380 (∼25%) have household correlations with p < 0.05. An interesting contrast between the genetic and household correlations can be seen for multiple phenotype pairs. For example, the diabetes domain (Figures 4A and 4B) has many household correlations with p < 0.05 with blood pressure domain phenotypes (but less so for genetic correlations) and has many genetic correlations with p < 0.05 with lung and lipid domain phenotypes (but not household correlations).

Domain enrichment analysis highlights associations between phenotypic domains

The genetic correlations are distributed non-uniformly with regard to the phenotypic domains. Domain enrichment analysis, in which we measured over-abundance of correlations with p < 0.05 between phenotypes within domain-pairs, showed a strong enrichment of the number of intra-group correlations for all the 11 phenotype domains (Data S2). Figures 4C and 4D visualize the estimated between-domain enrichment (p < 0.05). While some observed correlations, such as the ones between anthropometrics and diabetes or sleep, are driven both by genetics and shared household, many other domain-level correlations due to shared household do not mirror the genetic ones (Figure 4D). For example, shared household affects the correlations between diabetes and the blood-pressure and cardiovascular domains (but not genetic); however, the correlations between diabetes and lung and lipids domains are driven by genetics.

Heritabilities and genetic correlations differ across gender groups

The HCHS/SOL dataset of 12,565 participants has 5,175 males and 7,390 females (both self-identified genders and identified by sex chromosome checks using genetic data). Thus, we estimated heritabilities and genetic correlations stratified by gender. We identify a large number of differences between genders (Figures 5 and S9) in both genetic and environmental correlations. For example, the phenotype pair DiasBP (diastolic blood pressure) and FEV1FVC (forced expiratory volume to forced vital capacity ratio) has a negative estimated $\widehat{{\rho }_k}=-0.77(95\text{\% CI}-0.99--0.18)$ in males but a positive genetic correlation $\widehat{{\rho }_k}=0.43(95\text{\% CI}0.13-0.84)$ in females. Similarly, the household correlation for lymphocyte count and height is $\widehat{{\rho }_h}=0.68(95\%\text{CI}0.02-0.99)$ in males but $\widehat{{\rho }_h}=-0.39(95\%\text{CI}-1\text{to}-0.03)$ in females (Figures 5 and S9; Data S2).

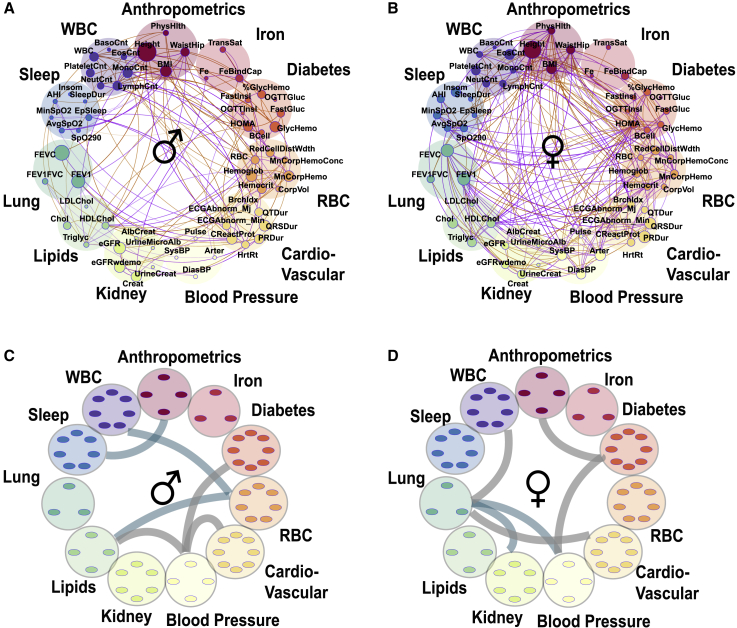
Figure 5.

Gender differences in genetic correlations and heritabilities

(A and B) Correlation plots where each phenotype is represented by a node and the correlations are represented by connections (edges) between nodes. The size of the node is proportional to the phenotype heritability. The thickness of the edge is proportional to the strength of correlation and the color represents magnitude: orange represents positive and purple negative correlation. Shown are fractional genetic correlations (${\rho }_{fk})$ between the 61 phenotypes in the extended HCHS/SOL dataset (p < 0.05) in males (A) (n = 5,175) and females (B) (n = 7,390).

(C and D) Enriched (p < 0.05) correlations between the phenotypic domains. Teal represents genetic correlations and gray represents household correlation in males (C) and females (D).

Overall, out of 363 phenotype pairs with either male or female genetic correlation with p < 0.05, there were 128 phenotype pairs (35%) in which the correlations were detected only in one gender groups (Figure S9C). Similarly, out of 349 phenotype pairs with either male or female household correlation with p < 0.05, there were 214 phenotype pairs (61%) in which the correlations were detected only in one gender group (Figure S9F).

These differences were also apparent at the domain level (Figures 5C and 5D). For example, while the correlations between blood pressure and diabetes domains are predominantly environmental in both gender groups (Figures 5C and 5D), the correlations between anthropometrics and sleep domains are enriched for genetic correlations only in the male group (Figure 5C and 5D). Figure S10 and Table S5 further provide similar results from gender-stratified genetic correlation analysis in the TOPMed White background group.

Discussion

We sought to study how observed correlations between complex human phenotypes can vary by socially constructed groups, and their characterization using both genetics and shared environment. To achieve that, we developed and implemented a computationally efficient framework HEc to estimate genetic and environmental correlations between phenotypes. We validated our method in simulations guided by data from multiple TOPMed background groups. HEc showed similar accuracy to GCTA while being up to 20 times faster. The GCTA speed dropped significantly with increased number of people, and it took up to 55 h to calculate a single genetic correlation for the combined TOPMed dataset (∼30k people), while it took ∼2.5 h for HEc.

We also compared HEc with GCTA and LDSC genetic correlation estimates using real data on a number of phenotypes in different background groups. While HEc and GCTA results were highly concordant, HEc and LDSC results differed. This is expected, as LDSC uses summary statistics from GWAS and relies on a reference panel for computing LD, assuming that the LD matches that of the population used for GWAS. Here, we implemented LDSC on summary statistics from the pan-UKBB GWAS, a population of mostly European genetic ancestry, and our target TOPMed background groups for LD. Thus, differences in LDSC-estimated genetic correlations across backgrounds are only due to differences in LD, and differences between HEc (and GCTA) and LDSC for the same TOPMed group are due to mismatch in the underlying genetic associations with the phenotypes. Notably, there are currently no available high-powered GWAS for either the Black or Hispanic/Latino groups that could be used by LDSC in lieu of the pan-UKBB GWAS summary statistics for any of the phenotypes analyzed here. We also adapted and studied a more recent algorithm (cov-LDSC³⁴) that was developed to estimate heritability in admixed populations using summary statistics. While it did improve estimated heritability across backgrounds, its estimated genetic correlations were similar to those from LSDC (Figure S3). Finally, while LDSC was indeed very fast when calculating genetic correlations (which takes only several minutes) after preparation of the LD reference, it is important to note that it required a very long preprocessing: over 5 days for calculating a group-specific LD panel for each background group. In this case, methods that use individual-level data, such as GCTA and HEc, are advantageous, especially given that preparation of the LD panel needs to be adapted for both the summary statistics and the genetic data used by matching on available genotypes and on effect alleles.

We next employed HEc to systematically interrogate factors that may affect the observed correlation between complex human phenotypes, including shared genetics and shared environment. We assessed differences by self-reported background, capturing a combination of genetic patterns and sociocultural and environmental exposures that may modify genetic effects; and gender, capturing both biological sex effects and downstream sociocultural-related modifications; all affecting the underlying determinants of phenotypic distributions. We identified differences in some of the correlations and heritabilities across groups, agreeing with some previous reports of differences in phenotypic distributions and disease prevalence across race/ethnicities^11,12,13 (Figure S7). Overall, we identified 26 phenotype pairs that had different genetic correlations (p < 0.05) between the Hispanic/Latino background and other backgrounds, 41 such phenotype pairs for the White background and 39 phenotype pairs with genetic correlation p < 0.05 only in the Black background group (Figure S6A).

We estimated high heritabilities of some of the blood phenotypes specifically in the Black background group. The heritabilities of neutrophil counts ($\widehat{h_2}>0.99,\text{SE}=0.07),\text{WBC counts}(\widehat{h_2}>0.99,\text{SE}=0.05),MC{V}_{EntVol}\left(\widehat{h_2}=0.64,\text{SE}=0.14\right);\text{and monocytes }(\widehat{h_2}=0.5\pm 0.16)$ in the Black background were much higher than in the White background, with $\text{neutrophil}\left(\widehat{h_2}=0.3,\text{SE}=0.21\right),WBC\left(\widehat{h_2}=0.4,\text{SE}=0.1\right),MC{V}_{EntVol}(\widehat{h_2}=0.1,\text{SE}=0.25\text{and Monocytes}(\widehat{h_2}=0,\text{SE}=0.28)$. Similarly high heritabilities were previously reported for Black individuals based on 236 African American pedigrees from the GeneSTAR study,⁴² and are usually attributed to the Duffy antigen receptor for chemokine gene, which accounts for ∼20% of total variation in the blood measures.^43,44 The differences in the distribution of the Duffy antigens in population were first reported in 1954, when it was found that the overwhelming majority of people of African descent had the erythrocyte phenotype Fy(a-b-) which is rare in European genetic ancestries, and therefore in individuals of White background, who have predominately European ancestry. This region was shown to confer protection against malaria while inducing benign neutropenia. This genotype likely has high influence on estimated heritabilities and genetic correlations related to blood counts.

Traditionally in the GWAS era, such analyses have been performed for groups with clearly defined genetic ancestry, typically European. An important difference now is that we have been using whole-genome sequencing (WGS) data, with joint estimation of PCs and kinship matrix. Thus, our analysis does not suffer from limitations from focusing on sets of SNPs with differing LD patterns in different genetic ancestries and with different imputation qualities, which may affect analyses using genotyping array and imputed data. In principle, it is therefore appropriate to attempt to use these data to characterize the population in aggregate. However, we still see differences between estimates in the aggregated analysis and in the background-stratified analyses. These differences are likely driven by gene-environment interactions, where individuals from different backgrounds are exposed differently to modifiers of genetic effects. Such modifiers may include lifestyle factors such as smoking, sleep, nutrition,^45,46 and although less studied, structural determinants such as the built environment and access to health care. Another potential reason for differences between backgrounds are gene-gene interactions leading to different genetic effects in haplotypes of different genetic ancestries.⁴⁷ Although group differences reduce our ability to interpret the estimates in the combined group, we think that it was important to demonstrate the places where such differences are observed, as these are likely areas where there are stronger environmental effects on genetic effects and therefore policy or lifestyle interventions may be more useful to improve health.

We used a few measures of correlation throughout. The phenotypic correlation is the correlation between phenotypes without further modeling of contribution of specific factors. The genetic and household correlations measure the similarity between the contribution of genetic factors and household environment, respectively, to the phenotypes. Although genetic correlation could, by some statistical models, be traced to additive effects of a set of genetic variants, the household correlation was not developed under the same modeling assumption. Yet, they are estimated in the same manner, as different parameters corresponding to different matrices, once defined based on a statistical model that relies on measures of similarity of genetics (genetic relationship) and of household environment (household sharing) between individuals. Both of types of correlations are not restricted by the phenotypic correlation, where the phenotypic correlation may be very low while the genetic (or household) correlation can be large. This motivated the concept of “fractional genetic correlation coefficient” ${\rho }_{fk}$ that we introduced, defined as the fraction of the observed phenotypic correlation $R$ explained by genetics: $R={\hat{\rho }}_{fk}+{\hat{\rho }}_{fϵ}$. The fractional genetic correlation ${\rho }_{fk}$ is the genetic correlation normalized by the two traits’ heritabilities ((Equation 34), (Equation 35), (Equation 36)) and is algorithm-agnostic, i.e., it does not depend on which algorithm is used to estimate heritabilities and genetic correlations. It addresses the limitations of the genetic correlations where (1) it is sometimes higher than the phenotypic correlation, and (2) it can have high estimate when the estimated heritabilities are low. The fractional genetic correlation allows for identification of phenotype pairs where genetics is a large contributor to the overall observed correlations. Fractional genetic correlations are typically lower than genetic correlations and are more highly correlated with the observed phenotypic correlations (e.g., correlations of 0.92 between the phenotype and fractional genetic correlations estimated in the TOPMed White background compared with correlation of 0.67 between the estimated phenotypic and genetic correlations; similarly 0.84 versus 0.52 between estimated phenotype and fractional versus genetic correlation in the Black background group). We believe that this measure is useful as it is interpretable with respect to its relationship to phenotypic correlation, and we report it for all correlations estimated in this work.

We next assess the contribution of genetics and environment to the correlations between phenotypes using the rich data collected in the HCHS/SOL cohort, including measurements from a wide range of phenotypes along with genetics and information on shared households. We estimated genetic and environmental (due to shared household) correlations between 61 phenotypes from diabetes, cardiovascular, blood pressure, kidney, lipids, lung, sleep, anthropometrics, iron, RBC, and WBC domains. While shared household does not capture all of the contribution of the environment to the correlations between phenotypes, it does contribute substantially to 22% of all the 1,830 phenotype pairs (p < $0.05$, Figure 4; Figure S8). Moreover, the contribution of the shared household to phenotypic correlations varies by phenotype pairs. In some cases, estimated genetic and household correlation are in opposite directions. For example, for albumin-creatinine ratio and PR duration (an echocardiogram measure of heart rate) $\widehat{{\rho }_k}=0.31(95\%\text{CI}0.12-0.67)\text{ while }\widehat{{\rho }_H}=-0.65(95\%\text{CI}(-0.99\text{to}-0.17)$; and for major ECG abnormalities and BMI $\widehat{{\rho }_k}=-0.33\left(95\text{\% }\text{CI}-0.88\text{to}-0.07\right)\text{and}\widehat{{\rho }_H}=0.75(95\text{\%}\text{ CI}0.04-1)$).

We also performed domain-level enrichment analysis. We defined domains as sets of phenotypes that capture similar underlying “latent” phenotypes, with the limitations that groups of phenotypes assigned for the same domain may still capture complex underlying biology, i.e., are not measures of exactly the same latent phenotype (e.g., insomnia and mean oxygen saturation during sleep, while correlated in individuals with obstructive sleep apnea, may capture different pathophysiological disorders). While more study is needed, domain analysis should be less sensitive to individual variation in any particular phenotype. The results of this analysis highlight the domains and their mode of association (genetic and/or environmental) and, in the case of the correlations that are driven by the shared household, present a way to increase or disrupt the correlation via lifestyle changes. Interestingly, it seems that some domains have multiple phenotypes that are correlated with phenotypes in another domain predominantly via genetics or shared household. For example, the interactions between diabetes and blood pressure and cardiovascular domains are strongly influenced by shared household and therefore are a possible target for lifestyle interventions. On the other hand, the diabetes domain has an abundance of genetically correlated phenotypes with the lung and anthropometrics domains.

Finally, we stratified participants from the Hispanic/Latino background by gender and analyzed genetic and household correlations. We found multiple differences between the genders such that there were 35% phenotype pairs with genetic correlations and 61% phenotype pairs with household correlations with p < 0.05 only in one gender group but not the other. For example, eosinophil counts versus PhysHealth (Aggregate Physical Health Scale) had a high $\widehat{{\rho }_k}=0.98$ (95% CI. 0.19–1) in males but $\widehat{{\rho }_k}=-0.46(95\text{\%}\text{ CI }-0.99\text{to}-0.09)$ in females. Similarly, the estimated household correlation between lymphocyte counts and height was $\widehat{{\rho }_h}=0.68$ (95% CI, 0.02–1) in males but was reversed and equal to $\widehat{{\rho }_k}=-0.39$ (95% CI, $-1$ to $-0.03$). Multiple correlations between phenotypic domains were also gender specific. Other recent studies considered gender differences in genetic determinants of phenotypes, focusing on UK Biobank participants of European ancestries.^48,49 Both studies computed genetic correlations between male and female genetic effects for the same phenotype, which we will denote here by ${\rho }_{gender}$ to differentiate it from ${\rho }_k$, and found that often this genetic correlation is different than 1, indicating differences in genetic architecture between the gender groups. Zhu et al. further showed that gender differences are often due to “amplification effects,” where genetic associations in one gender group, e.g., females, on average, are the same as the effects in males, multiplied by a constant, suggesting different regulations, for example, due to hormone levels, in males and females. In contrast, our analysis focused on gender differences in genetic correlation ${\rho }_k$ between pairs of phenotypes. While mathematical modeling is needed to study whether the amplification model is consistent with downstream large differences in ${\rho }_k$ between a pair of phenotypes in males compared with females, it is possible that differences in the systematic regulation of sets of genes between males and females will lead to such observed differences.

In interpreting such gender-stratified genetic and household correlations, we note that gender is a social construct that is related to sex, and drivers of some of the estimated quantities depend on complex interactions between biological determinants of sex and the gendered environment. Thus, both genetic and environmental correlations may differ between genders due to sociocultural differences between them (differences in environmental exposures may lead to differences in genetic effects via gene-environment interactions). Here, we were not able to assess specific sociocultural contributions related to gender roles to the estimated correlations, but we think that observed differences in household correlations are largely driven by them.

A specific strength of our study is the use of high-quality phenotypic and genotyping data from the diverse multi-ethnic TOPMed program. Furthermore, all participating studies are population-based cohort studies, reducing the likelihood of selection and other biases, which may arise in studies following selected populations, such as case-control studies. Other strengths are the investigation of a large panel of phenotypes, evaluation of both genetic and environmental correlations, stratification by both self-reported background and gender, and the domain-level enrichment analysis.

Nevertheless, this study also has several limitations. For example, the use of self-reported background rather than strata defined by genetic ancestry is also somewhat imprecise, as self-reported background may change over time.⁵⁰ Still, we chose to proceed with these groupings; first, to reflect on currently used groups in medical research, and second, because individuals of Hispanic/Latino background are highly admixed and there is no natural grouping that is based on genetic ancestry. We also note that socially constructed background groups may be meaningful due to differences in exposures across groups, which may translate to differences in the expression of genetic effects via gene-environment interactions. As the field of genetic medicine grapples with the use of genetic ancestry and social definition of race/ethnicity,⁵¹ both potentially leading to the wrong and harmful reification of the biological basis of race,⁵² it would be important to re-consider models for genetic correlation analyses. Finally, while our results are consistent with other studies^14,15 that demonstrated that genetic effects on specific traits vary by age, gender, and other environmental exposures, additional data and mathematical models are needed to untangle how specific factors influence measures of genetic and environmental correlations.

In summary, in this work we establish that multiple factors, including genetics, gender, sociocultural environment, and household environment, all shape the correlations between complex human phenotypes. We demonstrate how stratification by groups that encapsulate these factors, such as background groups capturing both genetic patterns and social race/ethnicity constructs, and gender groups capturing biological sex effects and gendered environment, uncovers differences in heritabilities and genetic correlations between them. We report thousands of genetic and environmental correlations between phenotypes. This work should lay the foundation for additional research in identifying personalized treatment and intervention strategies in understudied populations. Future work includes the application of approaches from the graph analysis field, such as Gaussian graphical models^53,54,55 to discover directionality and causality, utilizing genetically correlated phenotypes to improve polygenic risk prediction models,⁵⁶ and studying genetic correlations by categories of genetic variants to capture the contributions of rare variants.

Limitations of the study

One limitation of this study is the somewhat limited sample sizes. Larger sample sizes, especially within stratified analyses, would enable stronger inferences. Another limitation is imperfect definitions of phenotypic domains, which may not accurately capture underlying pathophysiology. Next, although the use of population-based studies reduces the likelihood of bias in estimation of heritabilities and genetic correlations, additional biases could remain as all studies employed some preferential sampling, e.g., of specific age ranges, geographic regions, etc., and therefore none of the studies, separately or combined, accurately represents a random sample from a specific US population. Lastly, we note that because the p values were derived via a bootstrap procedure (which is quite slow), and there were thousands of estimated genetic correlations in this paper, we are limited by the resulting p values with regard to FDR correction (which we provide for all calculated correlation values in Data S1. Phenotypic and genetic correlations between all harmonized phenotypes in the TOPMed dataset combined and separated by group, Data S2. Phenotypic and genetic correlations between all phenotypes in the HCHS/SOL dataset combined and separated by self-reported gender, Data S3. Supplemental Table 2: TOPMed phenotypes’ characteristics across backgrounds, related to Figures 2 and 3, Data S4. Supplemental Table 4: HCHS/SOL phenotypes’ characteristics across self-reported genders, related to Figures 4 and 5).

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
Summary statistics, PAN-UK BioBank	Pan-UKB team. https://pan.ukbb.broadinstitute.org. 2020	https://pan.ukbb.broadinstitute.org/
TOPMed data, by study	Taliun et al.31	Amish: phs000956, ARIC: phs001211, CARDIA: phs001612, CHS: phs001368, FHS: phs000974, HCHS_SOL: phs001395, JHS: phs000964, MESA: phs001416
Software and algorithms
All original computer code	This paper	https://github.com/tamartsi/HE_Genetic_Correlation
Principal Components, kinship matrices, unrelated individuals	This paper	TOPMed DCC pipeline https://github.com/UW-GAC/analysis_pipeline
GCTA	Yang et al.57	https://yanglab.westlake.edu.cn/software/gcta/#Overview
R package: igraph	Csardi et al.58	https://igraph.org/r/
R package: qgraph	Epskamp et al.59	https://cran.r-project.org/web/packages/qgraph/index.html
R package: corrplot	Friendly60	https://cran.r-project.org/web/packages/corrplot/vignettes/corrplot-intro.html
ldsc package	Bulik-Sullivan28	https://github.com/bulik/ldsc
cov-LDSC	Luo34	https://github.com/immunogenomics/cov-ldsc

Resource availability

Lead contact

Further information and requests should be directed to the lead contact, Dr. Tamar Sofer (tsofer@bwh.harvard.edu).

Materials availability

This study did not generate new, unique reagents.

Experimental model and subject details

The Trans-Omics for Precision Medicine (TOPMed) program

We used harmonized phenotype data from eight cohort studies participating in TOPMed (9) Freeze 8 [https://www.nhlbiwgs.org/topmed-whole-genome-sequencing-methods-freeze-8], which included 33,959 genotyped individuals from the Amish Study (n = 1,105), JHS (n = 2,807), FHS (n = 3,658), HCHS/SOL (n = 7,693), ARIC (n = 7,479), CHS (n = 3,482), MESA (n = 4,665), and CARDIA (n = 3,070) with available self-reported race/ethnic identification, which we refer to as “background”. Descriptions of each of these studies are provided in the Supplemental information. This dataset included 8,054 Black participants, 17,143 White participants and 8,762 participants of Hispanic/Latino background. All participants provided informed consent and the study was approved by IRBs in each of the participating institutions. For TOPMed WGS data acquisition and QC report see ncbi.nlm.nih.gov/projects/gap/cgi-bin/GetPdf.cgi?id=phd006969.1. The phenotype harmonization was performed by TOPMed Data Coordinating Center (DCC) as described in.³² The phenotype names and description, exclusion criteria and transformations are described in Table S1. Phenotypes’ characteristics across backgrounds are reported in Table S2 (Data S3). All analyses were adjusted for age, gender, study, and reported race/ethnicity as well as 11 first principal components (PCs) to adjust for population structure. The PCs, kinship matrices, and unrelated individual pools were computed by TOPMed DCC via a robust pipeline [https://github.com/UW-GAC/analysis_pipeline] via a combination of KING,⁶¹ PC-AiR,⁶² and PC-Relate.⁶³

The Hispanic community health study/study of latinos

The HCHS/SOL is a community-based cohort study of Hispanic individuals from four field centers across the US^33,41 with almost 13,000 genotyped participants. A two-stage sampling scheme for participant selection was employed, with sampled community block units followed by households. Correlation matrices to model environmental variance due to households and community block units were generated so that the i, j entry of a given matrix was set to 1 if the i and j individuals live in the same household (or community block unit), and 0 otherwise. This study was approved by the institutional review boards at each field center, where all participants gave written informed consent. Genotyping and quality control for HCHS/SOL have been described in detail elsewhere.⁶² In brief, DNA extracted from blood was genotyped on the HCHS Custom 15,041,502 array (Illumina Omni2.5M + custom content). Genotyping and downstream quality-control procedures yielded 2 232 944 genetic variants for genotyped HCHS/SOL participants. These were used for genotype imputation with the 1000 Genomes Project phase 3 reference panel⁶⁴ as previously described.⁶⁵ Variants with at least two copies of the minor allele and present in any of the four 1000 Genomes continental panels were imputed yielding about 50 million imputed variants prior to quality filtering. A subset of 7,693 individuals from HCHS/SOL participated in TOPMed and was used in the first part of this study (with the whole dataset used in the latter parts), with additional phenotypes that were not harmonized across other TOPMed studies. HCHS/SOL phenotype names and description are described in Table S3. The number of participants with non-missing information per phenotype as well as means and standard deviations per phenotype per gender are reported in Table S4 (Data S3). We estimated genetic correlations between phenotypes from the following domains: anthropometric, blood pressure, lipids, blood cell counts, and inflammation markers. All analyses were adjusted for age, gender, sampling weights and 11 first principal components to account for population structure.

Method details

Statistical model when genetic relatedness in the only modeled source of correlation

Consider the linear model

$$y_i=x_i^T\beta +g_{i,1}{\alpha }_1+\dots +g_{i,d}{\alpha }_d+{ϵ}_i^0,i=1,\dots ,n$$ Model 1

in which the quantitative outcome $y_i$ is modeled by a regression on covariates $x_i$ and the additive effects of d genetic variants $g_1,\dots ,g_d$; and ${ϵ}_i^0\sim \mathcal{N}\left(0,{\sigma }_e^2\right)$ are normally distributed errors across $n$ participants. Assuming that the genetic variants are independent random variables, each centered and scaled to have mean 0 and variance 1, the mean and variance of $y_i$ are

$$E\left[y_i\right]=x_i^T\beta$$ (Equation 1)

$$var\left(y_i\right)=var\left(g_1\right)\times {\alpha }_1^2+\dots +var\left(g_d\right)\times {\alpha }_d^2+{\sigma }_e^2=$$

$$=\sum _{j=1}^d{\alpha }_j^2+{\sigma }_e^2={\sigma }_k^2+{\sigma }_e^2$$ (Equation 2)

Here, ${\sigma }_k^2,{\sigma }_e^2$ are the genetic and error variance components. Accordingly, narrow-sense heritability, which is the proportion of trait variance that is due to additive genetic factors is:

$${\hat{h}}^2=\frac{{\sigma }_k^2}{{\sigma }_k^2+{\sigma }_e^2}$$ (Equation 3)

To model genetic correlation, we extend Model 1 into a two-trait model. For person i:

$$y_{i,1}=x_i^T{\beta }_1+g_{i,1}{\alpha }_{\mathrm{1,1}}+\dots +g_{i,d}{\alpha }_{1,d}+{ϵ}_{i,1}^0$$ (Equation 4)

$$y_{i,2}=x_i^T{\beta }_2+g_{i,1}{\alpha }_{\mathrm{2,1}}+\dots +g_{i,d}{\alpha }_{2,d}+{ϵ}_{i,2}^0$$ (Equation 5)

with error terms ${ϵ}_{i,1}^0,{ϵ}_{i,2}^0$ satisfying ${ϵ}_{i,l}^0\sim \mathcal{N}\left(0,{\sigma }_{ϵ,l}^2\right),cor\left({ϵ}_{i,1}^0,{ϵ}_{i,2}^0\right)={\rho }_{ϵ},{ϵ}_{i,1}^0\perp {ϵ}_{j,2}^0$ for $k\in \left\{\mathrm{1,2}\right\},i=1,\mathrm{..},n$.

Thus, the errors of the same person may be correlated for the two traits, but for different traits the error of person i is independent of the error of person j. Consider the covariance between the two traits, again while making the simplifying assumption of independence between genetic variants:

$$cov\left(y_{i,1},y_{i,2}\right)=cov\left(x_i^T{\beta }_1+g_{i,1}{\alpha }_{\mathrm{1,1}}+\dots +g_{i,d}{\alpha }_{1,d}+{ϵ}_{i,1}^0,x_i^T{\beta }_2+g_{i,1}{\alpha }_{\mathrm{2,1}}+\dots +g_{i,d}{\alpha }_{2,d}+{ϵ}_{i,2}^0\right)$$

$$=cov\left(g_{i,1}{\alpha }_{\mathrm{1,1}}+\dots +g_{i,d}{\alpha }_{1,d}+{ϵ}_{i,1}^0,g_{i,1}{\alpha }_{\mathrm{2,1}}+\dots +g_{i,d}{\alpha }_{2,d}+{ϵ}_{i,2}^0\right)$$

$$=\sum _{k=1}^d{\alpha }_{1,k}{\alpha }_{2,k}+{\sigma }_1{\sigma }_2{\rho }_e={\sigma }_{g_1}{\sigma }_{g_2}{\rho }_k+{\sigma }_{ϵ,1}{\sigma }_{ϵ,2}{\rho }_e$$ (Equation 6)

where ${\rho }_k$ is the correlation between the genetic effect of the k-th variant on the two outcomes, and ${\rho }_e$ is the correlation between the residual errors of the two outcomes. Note that the transition to using ${\rho }_k$ at the final step treats the vectors of causal genetic effects ${\alpha }_1={({\alpha }_{\mathrm{1,1}}\dots {\alpha }_{1,d})}^T,{\alpha }_2={({\alpha }_{\mathrm{2,1}}\dots {\alpha }_{2,d})}^T$ as random variables with mean 0, i.e., $E\left[{\alpha }_{i,j}\right]=0,var\left({\alpha }_{i,j}\right)={\sigma }_{g,i}^2,i\in \left\{\mathrm{1,2}\right\},j=1,\dots ,d$.

Noting that for individuals $i,l,$ $cov\left(g_{i,j},g_{l,j}\right)=k_{i,l}$, the probability of the two individuals sharing the same allele identically-by-decent,^61,63 an equivalent formulation supposes that the genetic effects can be modeled via K, the $n\times n$ kinship matrix, tabulating the measure of genetic relationship between the i and j participants in its i,j entry. Consider the vector form of the model for the l outcome with correlated errors of trait l = 1,2:

$$\begin{array}{ll}{y}_l=X{\beta }_l+{ϵ}_l,\hfill & l=\mathrm{1,2}\hfill \end{array}$$ Model 2

$$cov\left({ϵ}_l\right)={\sigma }_{ϵ,l}^2{\mathit{I}}_{n\times n}+{\sigma }_{k,l}^2\mathit{K}$$

$$cov\left({ϵ}_1,{ϵ}_2\right)={\sigma }_{ϵ,1}{\sigma }_{ϵ,2}{\rho }_{ϵ}{\mathit{I}}_{n\times n}+{\sigma }_{k,1}{\sigma }_{k,2}{\rho }_k\mathit{K}$$

Now the genetic correlation can be estimated using mixed model with two traits. However, this is computationally demanding, especially for very large datasets. Recently,⁶⁶ discussed the Haseman-Elston regression for variance components estimation, and demonstrated that the genetic variance components estimator corresponding to the kinship matrix, if it is independent of all other correlation matrices in a model with potentially multiple sources of correlation (which holds here, because we only have a single correlation matrix, the kinship matrix) are given by ${\hat{\sigma }}_{ϵ,l}^2=\frac{\widehat{ϵ}{}_l^T{\mathit{K}}^{-}{\widehat{ϵ}}_l}{tr\left({\mathit{K}}^{-}{\mathit{K}}^{-}\right)}$, where ${\mathit{K}}^{-}$ is the kinship matrix with all diagonal values set to zero.

An estimator of genetic correlation between two phenotypes

We extend the Haseman-Elston approach for modeling the genetic correlations between two phenotypes. For the errors of persons i and j, and phenotypes 1 and 2, under Model 2 we get:

$$E\left[{ϵ}_{1,i},{ϵ}_{2,i}\right]={\sigma }_{ϵ,1}{\sigma }_{ϵ,2}{\rho }_{ϵ}+{\sigma }_{k,1}{\sigma }_{k,2}{\rho }_k$$ (Equation 7)

$$E\left[{ϵ}_{1,i},{ϵ}_{2,j}\right]={\sigma }_{k,1}{\sigma }_{k,2}{\rho }_k{k}_{i,j}$$ (Equation 8)

Suppose for now that ${\sigma }_{k,1}=\left|\sqrt{{\sigma }_{k,1}^2}\right|$ and ${\sigma }_{k,2}=\left|\sqrt{{\sigma }_{k,2}^2}\right|$ are known. For estimating the genetic correlation between the two phenotypes, we take all pairs ${\widehat{ϵ}}_{1,i}{\widehat{ϵ}}_{2,j}$ of residuals (estimating the error terms) after regression on mean-model covariates for $i\ne j$, and regress them against the “covariate” ${\sigma }_{k,1}{\sigma }_{k,2}{k}_{i,j}$. From properties of linear regression, we get:

$${\hat{\rho }}_k=\frac{{\sum }_{i=1}^n{\sigma }_{k,1}{\sigma }_{k,2}{k}_{i,j}{\widehat{ϵ}}_{1,i}{\widehat{ϵ}}_{2,j}}{{\sum }_{i=1}^n{\sigma }_{k,1}^2{\sigma }_{k,2}^2{k}_{i,j}^2}=\frac{{\sum }_{i=1}^n{k}_{i,j}{\widehat{ϵ}}_{1,i}{\widehat{ϵ}}_{2,j}}{{\sigma }_{k,1}{\sigma }_{k,2}{\sum }_{i=1}^n{k}_{i,j}^2}=\frac{\widehat{ϵ}{}_1^T{\mathit{K}}^{-}{\widehat{ϵ}}_2}{{\sigma }_{k,1}{\sigma }_{k,2}tr\left({\mathit{K}}^{-}{\mathit{K}}^{-}\right)}$$ (Equation 9)

Now we can plug-in the estimators of ${\sigma }_{k,1},{\sigma }_{k,2}$ to get:

$${\hat{\rho }}_k=\frac{\widehat{ϵ}{}_1^T{\mathit{K}}^{-}{\widehat{ϵ}}_2}{tr\left({\mathit{K}}^{-}{\mathit{K}}^{-}\right)\sqrt{\left(\frac{\widehat{ϵ}{}_1^T{\mathit{K}}^{-}{\widehat{ϵ}}_1}{tr\left({\mathit{K}}^{-}{\mathit{K}}^{-}\right)}\right)\left(\frac{\widehat{ϵ}{}_2^T{\mathit{K}}^{-}{\widehat{ϵ}}_2}{tr\left({\mathit{K}}^{-}{\mathit{K}}^{-}\right)}\right)}}=\frac{\widehat{ϵ}{}_1^T{\mathit{K}}^{-}{\widehat{ϵ}}_2}{\sqrt{\left(\widehat{ϵ}{}_1^T{\mathit{K}}^{-}{\widehat{ϵ}}_1\right)\left(\widehat{ϵ}{}_2^T{\mathit{K}}^{-}{\widehat{ϵ}}_2\right)}}$$ (Equation 10)

This estimator resembles that of the Pearson correlation parameter between the variables ${\widehat{ϵ}}_1$ and ${\widehat{ϵ}}_2$, as can be seen if one replaces the matrix ${\mathit{K}}^{-}$ by the identify matrix $\mathit{I}$. Interestingly, this estimator does not involve the unknown variance parameters. It does include the estimated kinship parameters, which are treated as fixed.

Extension to multiple correlation matrices and generalization

We can use multiple relatedness matrices $(A,\mathrm{...},K)$ with elements $\left(a_{i,j}\mathrm{..}{k}_{i,j}\right)$ indicating the measure of relatedness between the i-th and j-th participants in its i,j entry to model the variance. We can then estimate the variance components obtained from expressions of the form

$$E\left[{ϵ}_i,{ϵ}_j\right]={\sigma }_{ϵ}^2\times 1_{\left(i=j\right)}+{\sigma }_a^2{a}_{i,j}+\dots +{\sigma }_k^2{k}_{i,j}$$ (Equation 11)

(corresponding to Model 2 above) via a residual regression, i.e. by taking the vector all pairs of residuals ${\widehat{ϵ}}_{1,i}{\widehat{ϵ}}_{2,j}$ for all $i,j$. The HE design matrix, now re-defined (compared to⁶⁶) to include rows corresponding to ${\widehat{ϵ}}_{1,i}{\widehat{ϵ}}_{2,j}$ with $i=j$, is given by:

$$X_{\sigma }=\left(\begin{array}{llll}1\hfill & a_{\mathrm{1,1}}\hfill & \dots \hfill & k_{\mathrm{1,1}}\hfill \\ 0\hfill & a_{\mathrm{1,2}}\hfill & \dots \hfill & k_{\mathrm{1,2}}\hfill \\ ⋮\hfill & ⋮\hfill & \dots \hfill & ⋮\hfill \\ 0\hfill & a_{1,n}\hfill & \dots \hfill & k_{1,n}\hfill \\ 0\hfill & a_{\mathrm{2,1}}\hfill & \dots \hfill & k_{\mathrm{2,1}}\hfill \\ 1\hfill & a_{\mathrm{2,2}}\hfill & \dots \hfill & k_{\mathrm{2,2}}\hfill \\ ⋮\hfill & ⋮\hfill & \dots \hfill & ⋮\hfill \\ 0\hfill & a_{2,n}\hfill & \dots \hfill & k_{2,n}\hfill \\ ⋮\hfill & ⋮\hfill & \dots \hfill & ⋮\hfill \\ 1\hfill & a_{n,n}\hfill & \dots \hfill & k_{n,n}\hfill \end{array}\right)$$ (Equation 12)

Similarly, the design matrix for estimating genetic correlation, obtained from expression of the form

$$E\left[{ϵ}_{1,i},{ϵ}_{2,j}\right]={\sigma }_{ϵ,1}{\sigma }_{ϵ,2}{\rho }_{ϵ}{1}_{i=j}+{\sigma }_{a,1}{\sigma }_{a,2}{\rho }_a{a}_{i,j}+\dots +{\sigma }_{k,1}{\sigma }_{k,2}{\rho }_k{k}_{i,j}$$ (Equation 13)

Can be written (if the variance parameters were known) as:

$$X_{\rho }=\left(\begin{array}{llll}{\sigma }_{ϵ,1}{\sigma }_{ϵ,2}\hfill & {\sigma }_{a,1}{\sigma }_{a,2}{a}_{\mathrm{1,1}}\hfill & \dots \hfill & {\sigma }_{k,1}{\sigma }_{k,2}{k}_{\mathrm{1,1}}\hfill \\ 0\hfill & {\sigma }_{a,1}{\sigma }_{a,2}{a}_{\mathrm{1,2}}\hfill & \dots \hfill & {\sigma }_{k,1}{\sigma }_{k,2}{k}_{\mathrm{1,2}}\hfill \\ ⋮\hfill & ⋮\hfill & \dots \hfill & ⋮\hfill \\ 0\hfill & {\sigma }_{a,1}{\sigma }_{a,2}{a}_{1,n}\hfill & \dots \hfill & {\sigma }_{k,1}{\sigma }_{k,2}{k}_{1,n}\hfill \\ 0\hfill & {\sigma }_{a,1}{\sigma }_{a,2}{a}_{\mathrm{2,1}}\hfill & \dots \hfill & {\sigma }_{k,1}{\sigma }_{k,2}{k}_{\mathrm{2,1}}\hfill \\ {\sigma }_{ϵ,1}{\sigma }_{ϵ,2}\hfill & {\sigma }_{a,1}{\sigma }_{a,2}{a}_{\mathrm{2,2}}\hfill & \dots \hfill & {\sigma }_{k,1}{\sigma }_{k,2}{k}_{\mathrm{2,2}}\hfill \\ ⋮\hfill & ⋮\hfill & \dots \hfill & ⋮\hfill \\ 0\hfill & {\sigma }_{a,1}{\sigma }_{a,2}{a}_{2,n}\hfill & \dots \hfill & {\sigma }_{k,1}{\sigma }_{k,2}{k}_{2,n}\hfill \\ ⋮\hfill & ⋮\hfill & \dots \hfill & ⋮\hfill \\ {\sigma }_{ϵ,1}{\sigma }_{ϵ,2}\hfill & {\sigma }_{a,1}{\sigma }_{a,2}{a}_{n,n}\hfill & \dots \hfill & {\sigma }_{k,1}{\sigma }_{k,2}{k}_{n,n}\hfill \end{array}\right)$$ (Equation 14)

Noting that:

$$X_{\rho }=X_{\sigma }\left(\begin{array}{llll}{\sigma }_{ϵ,1}{\sigma }_{ϵ,2}\hfill & 0\hfill & \dots \hfill & 0\hfill \\ 0\hfill & {\sigma }_{b,1}{\sigma }_{b,2}\hfill & \dots \hfill & 0\hfill \\ ⋮\hfill & ⋮\hfill & \ddots \hfill & ⋮\hfill \\ 0\hfill & 0\hfill & \dots \hfill & {\sigma }_{k,1}{\sigma }_{k,2}\hfill \end{array}\right)=X_{\sigma }{D}_{\sigma }$$ (Equation 15)

We get that:

$$X_{\rho }^T{X}_{\rho }=D_{\sigma }{X}_{\sigma }^T{X}_{\sigma }{D}_{\sigma }$$ (Equation 16)

$${\left(X_{\rho }^T{X}_{\rho }\right)}^{-1}=D_{\sigma }^{-1}{\left(X_{\sigma }^T{X}_{\sigma }\right)}^{-1}{D}_{\sigma }^{-1}$$ (Equation 17)

We also note the outcome matrices for estimating variance components and correlation parameters are:

$$Y_{\sigma ,1}=\left(\begin{array}{l}{ϵ}_{\mathrm{1,1}}{ϵ}_{\mathrm{1,1}}\hfill \\ {ϵ}_{\mathrm{1,1}}{ϵ}_{\mathrm{1,2}}\hfill \\ ⋮\hfill \\ {ϵ}_{\mathrm{1,1}}{ϵ}_{1,n}\hfill \\ {ϵ}_{\mathrm{1,2}}{ϵ}_{\mathrm{1,1}}\hfill \\ {ϵ}_{\mathrm{1,2}}{ϵ}_{\mathrm{1,2}}\hfill \\ ⋮\hfill \\ {ϵ}_{\mathrm{1,2}}{ϵ}_{1,n}\hfill \\ ⋮\hfill \\ {ϵ}_{1,n}{ϵ}_{1,n}\hfill \end{array}\right),Y_{\sigma ,2}=\left(\begin{array}{l}{ϵ}_{\mathrm{2,1}}{ϵ}_{\mathrm{2,1}}\hfill \\ {ϵ}_{\mathrm{2,1}}{ϵ}_{\mathrm{2,2}}\hfill \\ ⋮\hfill \\ {ϵ}_{\mathrm{2,1}}{ϵ}_{2,n}\hfill \\ {ϵ}_{\mathrm{2,2}}{ϵ}_{\mathrm{2,1}}\hfill \\ {ϵ}_{\mathrm{2,2}}{ϵ}_{\mathrm{2,2}}\hfill \\ ⋮\hfill \\ {ϵ}_{\mathrm{2,2}}{ϵ}_{2,n}\hfill \\ ⋮\hfill \\ {ϵ}_{2,n}{ϵ}_{2,n}\hfill \end{array}\right),Y_{\rho }=\left(\begin{array}{l}{ϵ}_{\mathrm{1,1}}{ϵ}_{\mathrm{2,1}}\hfill \\ {ϵ}_{\mathrm{1,1}}{ϵ}_{\mathrm{2,2}}\hfill \\ ⋮\hfill \\ {ϵ}_{\mathrm{1,1}}{ϵ}_{2,n}\hfill \\ {ϵ}_{\mathrm{1,2}}{ϵ}_{\mathrm{2,1}}\hfill \\ {ϵ}_{\mathrm{1,2}}{ϵ}_{\mathrm{2,2}}\hfill \\ ⋮\hfill \\ {ϵ}_{\mathrm{1,2}}{ϵ}_{2,n}\hfill \\ ⋮\hfill \\ {ϵ}_{1,n}{ϵ}_{2,n}\hfill \end{array}\right)$$ (Equation 18)

Therefore:

$$\left(\begin{array}{l}{\sigma }_{ϵ,1}^2\hfill \\ {\sigma }_{a,1}^2\hfill \\ ⋮\hfill \\ {\sigma }_{k,1}^2\hfill \end{array}\right)={\left(X_{\sigma }^T{X}_{\sigma }\right)}^{-1}{X}_{\sigma }^T{Y}_{\sigma ,1},\left(\begin{array}{l}{\sigma }_{ϵ,2}^2\hfill \\ {\sigma }_{a,2}^2\hfill \\ ⋮\hfill \\ {\sigma }_{k,2}^2\hfill \end{array}\right)={\left(X_{\sigma }^T{X}_{\sigma }\right)}^{-1}{X}_{\sigma }^T{Y}_{\sigma ,2}$$ (Equation 19)

and:

$$\left(\begin{array}{l}{\sigma }_{ϵ,1}^2\hfill \\ {\sigma }_{a,1}^2\hfill \\ ⋮\hfill \\ {\sigma }_{k,1}^2\hfill \end{array}\right)={\left(X_{\rho }^T{X}_{\rho }\right)}^{-1}{X}_{\rho }^T{Y}_{\rho }$$ (Equation 20)

$$=D_{\sigma }^{-1}{\left(X_{\sigma }^T{X}_{\sigma }\right)}^{-1}{D}_{\sigma }^{-1}{D}_{\sigma }{X}_{\sigma }^T{Y}_{\rho }$$ (Equation 21)

$$=D_{\sigma }^{-1}{\left(X_{\sigma }^T{X}_{\sigma }\right)}^{-1}{X}_{\sigma }^T{Y}_{\rho }$$ (Equation 22)

Because the l_th entry of $D_{\sigma }$ is ${\sigma }_{1,l}{\sigma }_{2,l}$ we have then for ${\rho }_l$:

$${\rho }_l=\frac{{\left[{\left(X_{\sigma }^T{X}_{\sigma }\right)}^{-1}{X}_{\sigma }^T{Y}_{\rho }\right]}_l}{{\sigma }_{1,l}{\sigma }_{2,l}}$$ (Equation 23)

$$=\frac{{\left[{\left(X_{\sigma }^T{X}_{\sigma }\right)}^{-1}{X}_{\sigma }^T{Y}_{\rho }\right]}_l}{{\sqrt{{\left[{\left(X_{\sigma }^T{X}_{\sigma }\right)}^{-1}{X}_{\sigma }^T{Y}_{\sigma ,1}\right]}_l\left[{\left(X_{\sigma }^T{X}_{\sigma }\right)}^{-1}{X}_{\sigma }^T{Y}_{\sigma ,2}\right]}}_l}$$ (Equation 24)

To prove that this is a generalized Pearson correlation, we only need to show that ${\left[{\left(X_{\sigma }^T{X}_{\sigma }\right)}^{-1}{X}_{\sigma }^T{Y}_{\rho }\right]}_l$ is a bilinear form, with the matrix completely defined by the l_th row of ${\left(X_{\sigma }^T{X}_{\sigma }\right)}^{-1}{X}_{\sigma }^T$. This is simple to see, because the entries of $X_{\sigma }^T{Y}_{\rho }$ are:

$$X_{\sigma }^T{Y}_{\rho }=\left(\begin{array}{l}{ϵ}_1^T\mathit{I}{ϵ}_2\hfill \\ {ϵ}_1^T\mathit{A}{ϵ}_2\hfill \\ ⋮\hfill \\ {ϵ}_1^T\mathit{K}{ϵ}_2\hfill \end{array}\right)$$ (Equation 25)

Similarly:

$$X_{\sigma }^T{Y}_{\sigma ,1}=\left(\begin{array}{l}{ϵ}_1^T\mathit{I}{ϵ}_1\hfill \\ {ϵ}_1^T\mathit{A}{ϵ}_1\hfill \\ ⋮\hfill \\ {ϵ}_1^T\mathit{K}{ϵ}_1\hfill \end{array}\right),X_{\sigma }^T{Y}_{\sigma ,2}=\left(\begin{array}{l}{ϵ}_2^T\mathit{I}{ϵ}_2\hfill \\ {ϵ}_2^T\mathit{A}{ϵ}_2\hfill \\ ⋮\hfill \\ {ϵ}_2^T\mathit{K}{ϵ}_2\hfill \end{array}\right)$$ (Equation 26)

and the l_th row of ${\left(X_{\sigma }^T{X}_{\sigma }\right)}^{-1}$ determines the weights in the following expression:

$${\left[{\left(X_{\sigma }^T{X}_{\sigma }\right)}^{-1}{X}_{\sigma }^T{Y}_{\rho }\right]}_l={ϵ}_1^T\left[{\omega }_{ϵ,l}\mathit{I}+{\omega }_{a,l}\mathit{A}+\dots +{\omega }_{k,l}\mathit{K}\right]{ϵ}_1$$ (Equation 27)

Thus for

$${\mathit{S}}_{\mathit{l}}={\omega }_{ϵ,l}\mathit{I}+{\omega }_{a,l}\mathit{A}+\dots +{\omega }_{k,l}\mathit{K}$$ (Equation 28)

We get

$${\hat{\rho }}_l=\frac{\widehat{ϵ}{}_1^T{\mathit{S}}_{\mathit{l}}{\widehat{ϵ}}_2}{\sqrt{\left(\widehat{ϵ}{}_1^T{\mathit{S}}_{\mathit{l}}{\widehat{ϵ}}_1\right)\left(\widehat{ϵ}{}_2^T{\mathit{S}}_{\mathit{l}}{\widehat{ϵ}}_2\right)}}$$ (Equation 29)

Deriving confidence intervals for estimated correlation coefficients; We propose two methods to compute confidence intervals for the estimated correlation coefficients. First, using the Fisher’s transformation, which was developed to estimate confidence intervals for the standard Pearson correlation coefficient, and second, using block bootstrap.

Confidence intervals using the Fisher’s transform

Fisher’s transformation converts the distribution of the correlation coefficients to a normal one and thus allows us to calculate confidence intervals (and corresponding p values) for the correlation coefficient using the values of the correlation coefficient and the sample size.^67,68 Since we show that calculating genetic correlation is equal to calculating standard correlation for adjusted phenotypes (Equation 29), the Fisher method is equally applicable for genetic correlation coefficient with the modification of plugging-in “effective sample size” to account for the modeled correlation structure between the two traits. Specifically, Fisher’s z-transformation of a correlation coefficient $\rho$ is defined as:

$$z=\frac{1}{2}\ln \left(\frac{1+\rho }{1-\rho }\right)=arctanh\left(\rho \right)$$ (Equation 30)

If the two variables for which the correlation is measured have a bivariate normal distribution and are independent and identically distributed, then $z$ is approximately normally distributed with mean $\text{μ}$ and SE $\text{σ}$ given by:

$$\mu =\frac{1}{2}\ln \left(\frac{1+\rho }{1-\rho }\right)$$ (Equation 31)

$$\sigma =\frac{1}{\sqrt{N_{eff}-3}}$$ (Equation 32)

and $N_{eff}$ being the effective sample size of our sample equal to:

$$N_{eff}=\sqrt{tr\left({\mathit{S}}_{\mathit{l}}{\mathit{S}}_{\mathit{l}}^{\mathit{T}}\right)}$$ (Equation 33)

where ${\mathit{S}}_{\mathit{l}}$ is the weighted matrix described in Equation 28. The coverage of this approach was verified in simulations via comparisons to the block Bootstrap method described below (see Figure S1).

Confidence intervals using block bootstrap

Multiple participants in our datasets are genetically related (and thus correlated), which violates the assumption of the standard bootstrap method. We thus performed the block bootstrap procedure to derive the confidence intervals and p values as described in.⁶⁹ Briefly, related individuals were grouped into blocks (via third degree kinship) and the sampling procedure was at the level of blocks. We applied the Fisher’s transformation on each correlation value estimated in the bootstrap. Standard deviations and consequently confidence intervals and p values were calculated based on the Fisher’s transformed values. Finally, to obtain confidence intervals on the original genetic correlation scale we applied the inverse transformation of the Fisher’s transform (given by $f\left(x\right)=(e^{2x}-1)/(e^{2x}+1)$) to the endpoints of the confidence intervals obtained on the Fisher’s transformation scale. In addition, we used the quantiles method to derive 95% confidence interval from the bootstrap results and report whether the corresponding p value is < 0.05 based on the null value being in the confidence interval.

Testing for difference of two correlation coefficients

To compare two correlation coefficients, we transform both correlations using the Fisher-z transformation (as described in Equation 30). Once the correlations have been converted into z values, the normal distribution is used to conduct the test of $Z_1-Z_2$.

Fractional genetic correlation

For simplicity, focus on the single correlation matrix settings (the derivation here naturally extends to multiple sources of correlation). Recall Model 2 - the phenotypic correlation coefficient $\mathit{R}$ is equal to:

$$R=\frac{cov\left({ϵ}_1,{ϵ}_2\right)}{\sqrt{cov\left({ϵ}_1\right)cov\left({ϵ}_2\right)}}=\left(\frac{{\sigma }_{ϵ,1}{\sigma }_{ϵ,2}}{\sqrt{{\sigma }_{ϵ,1}^2+{\sigma }_{k,1}^2}\sqrt{{\sigma }_{ϵ,2}^2+{\sigma }_{k,2}^2}}\times {\rho }_{ϵ}\right)+\left(\frac{{\sigma }_{k,1}{\sigma }_{k,2}}{\sqrt{{\sigma }_{ϵ,1}^2+{\sigma }_{k,1}^2}\sqrt{{\sigma }_{ϵ,2}^2+{\sigma }_{k,2}^2}}\times {\rho }_k\right)$$ (Equation 34)

We then define Fractional Genetic Correlation (${\rho }_{fk}$) as

$${\rho }_{fk}=\left(\frac{{\sigma }_{k,1}{\sigma }_{k,2}}{\sqrt{{\sigma }_{ϵ,1}^2+{\sigma }_{k,1}^2}\sqrt{{\sigma }_{ϵ,2}^2+{\sigma }_{k,2}^2}}\times {\rho }_k\right)$$ (Equation 35)

and Fractional Residual Correlation as

$${\rho }_{fϵ}=\frac{{\sigma }_{ϵ,1}{\sigma }_{ϵ,2}}{\sqrt{{\sigma }_{ϵ,1}^2+{\sigma }_{k,1}^2}\sqrt{{\sigma }_{ϵ,2}^2+{\sigma }_{k,2}^2}}\times {\rho }_{ϵ}$$

.

This is a natural decomposition of phenotypic correlation into two components:

$$R={\rho }_{fk}+{\rho }_{fϵ}$$ (Equation 36)

Unlike standard genetic correlation, ${\rho }_{fk}$ is the genetic correlation adjusted (fractional) for both traits’ heritabilities and variances and crucially it represents a fraction of the phenotypic correlation that is due to genetics. As expected, the fractional correlation terms are never larger than the phenotypic correlation $R$, because they sum to $R$.

Quantification and statistical analysis

Simulation studies

We studied the accuracy of the proposed method for estimating genetic correlations and for calculating confidence intervals in simulations. We used correlation matrices from the HCHS/SOL representing kinship and shared household to generate realistic correlation structures. In all simulations, data were generated by first sampling two uncorrelated error vectors $\left({ϵ}_1,{ϵ}_2\right)$ from a standard normal distribution. We next simulated the covariance structure according to our model:

$$cov\left({ϵ}_l\right)={\sigma }_{ϵ,l}^2{\mathit{I}}_{n\times n}+{\sigma }_{k,l}^2\mathit{K}+{\sigma }_{h,l}^2\mathit{H}cov\left({ϵ}_1,{ϵ}_2\right)={\sigma }_{ϵ,1}{\sigma }_{ϵ,2}{\rho }_{ϵ}{\mathit{I}}_{n\times n}+{\sigma }_{k,1}{\sigma }_{k,2}{\rho }_k\mathit{K}+{\sigma }_{h,1}{\sigma }_{h,2}{\rho }_h\mathit{H}$$

The matrix K represents kinship, and H represents shared household. All simulations were performed 1,000 times with different sample sizes (1000, 4000, and 7706, the latter is sample size of HCHS/SOL individuals in TOPMed freeze 8 which is the smallest subgroup in this study) and values of ${\rho }_k$ and ${\rho }_h$ ranging from 0 to 1 in increments of 0.1. The variance components reported here were set to typical values for phenotypes from our dataset and equal to $\sigma =\left({\sigma }_{k,1}{\sigma }_{k,2},{\sigma }_{h,1},{\sigma }_{h,2}\right)=(0.6,0.7,0.4,0.3)$ (corresponding to HDL, height, fasting glucose levels and eosinophil counts accordingly). The confidence intervals and p values were calculated from the block bootstrap method using the Fisher’s transformation and the percentile method (Figure S1).

We repeated all the simulations for a single kinship matrix on different self-reported background groups using kinship matrices from TOPMed participants from the available background groups (Black, Hispanic/Latino, and White). We also simulated a joint group in which we sampled an equal number of TOPMed individuals from each of the background groups, and used the corresponding kinship matrix. The number of participants was kept at 7706, and we compared the performance of HEc method (1000 repeats per group per ${\rho }_k$) to GCTA-GREML (with 40 repeats due to the slow computation speeds).

Heritability and genetic/environment correlation estimation via HEc and GCTA-GREML

The relatedness between individuals is modeled via a kinship (K) matrix, and an additional household matrix (H) for modeling environmental effects (available only for the HCHS/SOL cohort). Each phenotype was regressed on age, gender, sampling weights and 11 first principal components (and race/ethnicity and study for TOPMed combined cohorts) and the residuals were rank-normalized. We estimated the correlation coefficients corresponding to the relatedness matrices for all trait pairs by plugging in the normalized residuals to Equation 29. This was implemented via R scripts provided in GitHub repository [https://github.com/tamartsi/HE_Genetic_Correlation]. The genetic and environment variance components as well as the corresponding heritabilities were calculated via the GCTA software.⁵⁷ Following sensitivity analysis for the presence of related individuals in the cohorts (Figure S5) we removed all individuals related at third degree or more for the calculation of heritabilities, however as we did not see any substantial effects of relatives on the estimated genetic correlations (Figure S2B), the relatives were kept in for genetic and environmental correlation coefficients estimation. We provide the confidence intervals for both the Fisher Method and the two Bootstrap-Based approaches in the supplementary data files. Visualizations were performed via the R packages igraph,⁵⁸ qgraph,⁵⁹ ggplot2⁷⁰ and corrplot⁶⁰ followed by Adobe Illustrator. The figures are based on uncorrected p values. FDR-corrected p values are provided in the Supplementary Data files.

Heritability and genetic correlation estimation via LD-based methods

Summary statistics for 8 selected phenotypes (Table S5) were downloaded from PAN-UK BioBank (https://pan.ukbb.broadinstitute.org/). The GWAS underwent further cleanup and quality control as recommended by the ldsc package (https://github.com/bulik/ldsc).^10,28 LD scores were computed for each of the TOPMed self-reported background groups as well as for the joint dataset as recommended by the ldsc software. Alternatively, covariate-adjusted LD scores were calculated via cov-LDSC (https://github.com/immunogenomics/cov-ldsc)³⁴ using 11 principal components (calculated as described in section 2.4). Finally, genetic correlations and heritabilities were estimated using the computed LD scores.

Domain-level enrichment analysis

We calculated the enrichment of inter-domain correlation via a permutation approach. Specifically, for 1000 repeats, we generated random connections between nodes in our correlation graph such that each node will receive a same number of connections as in the real dataset as well as keeping the overall number of connections identical. We then calculated the distribution of number of connections between each pair of domains and used it to obtain a domain enrichment p value as follows:

$$\text{p}\text{-}\text{value}(\text{domain}1,\text{domain}2)=\frac{1}{1000}\sum _{i=1}^{1000}1(N_i^c>N^c)$$

where $N^c$ is the number of connections between domains 1 and 2, and $N_i^c,i=1,\dots ,1000$ is the number of connections between domains 1 and 2 in the $i$ th permutation. We considered two domains to be enriched if their enrichment p value was <0.05.

Additional resources

No additional resources were used.

Published: December 12, 2022

Data and code availability

• •The data is publicly available upon request from the TOPMed consortium (https://topmed.nhlbi.nih.gov/), and all original code used in this work is freely available at https://github.com/tamartsi/HE_Genetic_Correlation.
• •Any additional information required to reanalyze the data reported in this work paper is available from the lead contact upon request.