A new measure of hygiene inequality applied to urban-rural comparison

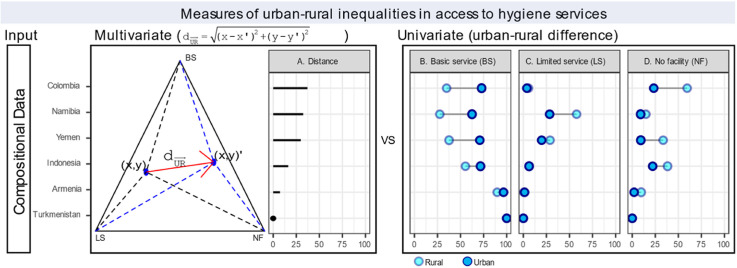
Abstract

Access to hygiene services remains one of the most urgent challenges facing countries, especially low-income ones. This has become much more critical in the current context of the COVID-19 pandemic. The WHO/UNICEF Joint Monitoring Program globally monitors access to hygiene service levels. As data are in three parts with a constant sum and a positive value, they are compositional data. Inequality is monitored in disaggregated data; in the urban–rural case, this is done through a simple difference between the urban and rural service levels. However, this simple form of calculation does not take into account the characteristics of the data, which can lead to erroneous interpretations of the results. Therefore, we propose an alternative measure of inequality that uses a ternary diagram and does not infringe on the data properties.

The results of the new urban–rural inequality measure show spatial heterogeneity. The highest inequality occurs in Colombia, with a value of 37.1 percentage points, and the lowest in Turkmenistan, with a value of zero. Our results also show that 73 of the 76 countries evaluated have higher basic hygiene services in urban areas than in rural areas. This means that urban households have more availability of a handwashing facility on-premises with soap and water than rural households. Likewise, by subdividing the ternary diagram into ternary parcels, we could group and rank the countries based on hygiene service conditions in a hierarchical order using tripartite information. Finally, our study finds that a multivariate measure of inequality can be important for the public policies of the sector with a general vision, which underscores the value of making evidence-based decisions.

Graphical abstract

1. Introduction

The 2030 Agenda is an ambitious action plan promoted by the United Nations and has the spirit of “leaving no one behind” (United Nations General Assembly, 2015). The inclusion of all people to reach the global goal in 2030 is the engine that drives all adhering countries. It addresses 17 sustainable development goals (SDGs); this study addresses SDG 6, and specifically, the section on hygiene in SDG 6.2.

Hand hygiene with soap and water is a high-impact, low-tech practice that correlates with good quality of public health and is a simple and effective way to reduce diseases. The reported benefits of handwashing are broad; for instance, as it can: reduce the transmission of viruses that cause common diseases; reduce the risk and incidence of diarrheal diseases (Shahid et al., 1996; Curtis and Cairncross, 2003); reduce the risk of respiratory infection (Rabie and Curtis, 2006); and provide economic benefits (Townsend et al., 2017). It acquires more relevance due to the novel severe acute respiratory syndrome coronavirus-2 (SARS-CoV-2), which caused the COVID-19 pandemic in 2020 (Pal et al., 2020; Synowiec et al., 2021). Currently, one of the main recommendations for reducing the risk of SARS-CoV-2 infection (besides vaccination) is the continuous practice of handwashing with soap and water (World Health Organization [WHO], 2020a). The remaining uncertainties about the transmission routes of SARS-CoV-2 (airborne in aerosol, surface contact, fecal-oral transmission (Heller et al., 2020; Pandey et al., 2021), etc.), and the fact that asymptomatic persons can have a high viral shedding (e.g., be infectious), underscores the importance of using handwashing as an essential measure (WHO, 2020b). For instance, a study under laboratory conditions shows that SARS-CoV-2 can remain viable and infectious in aerosols for hours, and on surfaces for up to days, depending on the spilled inoculum (van Doremalen et al., 2020).

Global monitoring of hygiene services has been incorporated into SDG 6.2 and has been carried out since 2015. The aim of Goal 6.2 is “by 2030, to achieve access to adequate and equitable sanitation and hygiene services for all … ". Proper hygiene is related to households having handwashing facilities with soap and water. The WHO/UNICEF Joint Monitoring Program (JMP) conducts global monitoring of households with or without handwashing facilities and classifies them into the three categories of the so-called handwashing ladder: basic, limited, and no facilities. The number of cases in each category is counted in a given household set (e.g., a country), after which three numerical variables are calculated; once divided by the total number of households, these form a constant sum proportion of one (or 100% if they are percentages); these are therefore compositional data (Aitchison, 1986, Egozcue and Pawlowsky-Glahn, 2011, Filzmoser et al., 2018, van den Boogaart and Tolosana-Delgado, 2013a).

The separate analysis of each percentage corresponds to the univariate analysis and is very common in the sector. The joint analysis of the three variables is a multivariate analysis. As the three hygiene variables have a constant sum constraint and are implicitly related to a predefined total or complementary parts, no variable can be interpreted independently of the others; rather, they must be interpreted as compositions (van den Boogaart and Tolosana-Delgado, 2013b). In global monitoring, the application of statistical techniques for compositional data in water, sanitation, and hygiene (WASH) began with Pérez-Foguet et al. (2017) and was expanded by Ezbakhe and Pérez-Foguet (2019), who incorporate the uncertainty of data into the analysis; however, its practical application to the global data set was not possible until Quispe-Coica and Pérez-Foguet (2020) introduced data preprocessing with zero values, missing data, and outliers. These analyzes have also recently been extended to the health domain related to child mortality (Ezbakhe and Pérez-Foguet, 2020).

Inequality of access to any service is one of the main obstacles to universal coverage. Therefore, as for water and sanitation, the JMP also monitors urban–rural inequality in hygiene. This information can help national and international actors in the sector to target interventions. In this sense, experts have recommended disaggregating the information and measuring inequalities from different aspects (Economic and Council, 2016, WHO/UNICEF, 2015). Hence, JMP currently monitors WASH inequality on data disaggregated by wealth quintiles, urban and rural residence, sub-national regions, and ladder service levels (see https://washdata.org/monitoring/inequalities). The wealth quintiles are based on an analysis of household assets, and the final result expressed in proportions is also represented by place of residence. Therefore, in any of the follow-up alternatives described, a measure of urban–rural inequality can be applied.

The current alternative used by the JMP for global reporting is to use the simple difference between the ratio of urban and rural service levels. For hygiene, this is carried out in the three categories of the handwashing ladder (WHO/UNICEF, 2016), giving three measures of inequality. This implies that, in an inequality ranking, countries are likely to have different positions depending on the category of analysis. As compositional data have a constant sum, a part or the rest will also be affected if one of the parts varies. Consequently, when interpreting a category, the rest of the categories must also be taken into account. In fact, the compositional data are multivariate by nature (van den Boogaart and Tolosana-Delgado, 2013b), thus reinforcing the idea of interpreting one category by considering the rest.

Knowing the space in which these data operate is also an important part, as it allows us to calculate inequality by selecting among the different multivariate alternatives that exist, using the one that best adapts to the data. The sample space in which the compositional data operates is the simplex S^D, and the vector space structure is called Aitchison geometry or the Aitchison simplex (which is a different geometric frame from the Euclidean vector space). Therefore, before applying any classical statistical technique, it is first necessary to perform log-ratio transformations (Aitchison, 1982, 1986; Egozcue et al., 2003). However, when data are in three or four parts, it is possible to represent them graphically in the same simplex space. If data are in three parts, the graphical representation in simplex is made through a ternary diagram; if in four parts, through a regular tetrahedron. If data are greater than four parts, the graphical representation in simplex is not possible; however, everything related to the operations, definitions, and interpretations of compositional data are valid for any number of parts (Pawlowsky-Glahn and Egozcue, 2006, Von Eynatten et al., 2002). It is also possible to reduce the number (n) of parts, independently of the dimensions, by an amalgamation process, a particular case being the dichotomous analysis, where the n parts are reduced to two.

That said, when the information is tripartite with a constant sum and is positive, as in the case of hygiene data, there are few multivariate alternatives that allow us to calculate urban–rural inequality in the simplex sample space. For our purpose, information is limited to the ternary diagram. Recall that everything ternary can be amalgamated and converted to binary, to then compare the inequality between two populations through arithmetic differences, a common practice carried out by the JMP to compare dichotomous variables (WHO/UNICEF, 2019a). The application of the ternary diagram to graphically represent data is very common in other areas of science, including the earth sciences, geochemistry, and chemistry (Miller, 2002; Graham et al., 2020; Verma, 2020). Lately, it has also been applied in epidemiology (Dumuid et al., 2020) and waste management, for both dynamic and static visualization (Bartl, 2014; Pomberger et al., 2017). Other studies present proposals for ternary graphical representation in centered data, which allows the graphical visualization and interpretation of the data structure to be improved (Von Eynatten et al., 2002).

On the other hand, in the literature in the WASH sector, it is very common to use univariate thematic maps of any of the categories of services accessed by the population, grouping (by color) those that are within a certain range (we will call this “amplitude” in this study). The global reports carried out by WHO/UNICEF are a clear example that the reading and interpretation of results are also univariate (WHO/UNICEF, 2019a, 2020). However, if the country data points are represented on the ternary diagram, each point represents a three-part composition, and they will have one reading or another, depending on their location on the ternary diagram.

A main objective of this study is to propose a multivariate measure of urban–rural inequality, taking into account the compositional characteristics of the data. For this, we first discretized the ternary diagram to represent the urban and rural data points in it, and then we calculated the distance between the two points as an overall measure of inequality. Another aim is to represent tripartite information on a thematic map. Finally, we applied this to a global data set on hygiene in urban and rural settings.

2. Materials and methods

2.1. Data analysis: input

For this study, the information was obtained from the JMP platform (www.washdata.org). Countries with data from 2017 were filtered, as they were the most up-to-date. As a result, the analysis is limited to data from 77 countries in the rural residence area, and the data from 76 countries in the urban residence area. The difference of one unit between urban and rural is due to Peru, which only presents information for rural and non-urban hygiene facilities. The breakdown of the number of countries by region (of a total of 76) is: 10 countries of the Central and Southern Asia (CSA) region, 9 countries of the Eastern and South-Eastern Asia (ESEA) region, 12 countries of Latin America and the Caribbean (LAC) region, 8 countries of the Northern Africa and Western Asia (NAWA) region, 3 countries of the Oceania region, and 34 countries of the Sub-Saharan Africa (SSA) region. Note that countries in several regions (Australia, New Zealand, Europe, and Northern America) were not included in the analysis, as no hygiene information for 2017 was found on the JMP website.

The information source provides disaggregated data on the presence or absence of a handwashing facility in the three levels of service: basic service (BS), limited service (LS), and no facility (NF). The BS level refers to the availability of an on-premise handwashing facility with soap and water; LS refers to the availability of an on-premise handwashing facility lacking soap and/or water; and NF refers to no on-premise handwashing facility. This information is represented in a three-part composition vector $S^{D=3}=\left\{x=(x_1,x_2,x_3):\forall x_i>0,{\sum }_{i=1}^3{x}_i=100\right\}$, which is subsequently represented in the ternary diagram.

2.2. Ternary diagram basics concepts

The ternary diagram is a diagram that graphically represents the proportions of the three compositions in an equilateral triangle. The mathematical basis of the equilateral triangle is the well-known Viviani theorem (Abboud, 2010), and it has the potential to express the compositional data of three parts as one. This is advantageous when doing a multivariate analysis of tripartite information.

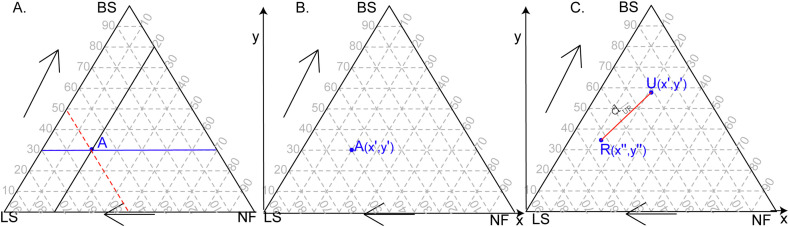
Location of the data points on the ternary diagram can be determined in several ways. Here, we illustrate two ways. The first option is to draw lines parallel to the basis of the ternary diagram opposite the vertex (Fig. 1 A). In the depicted example, a random value of 30% for BS, and of 20% for NF, is given. The first step is to plot the BS value with a straight line whose value is 30% (solid blue line in Fig. 1A); the NF value is then drawn with a solid black line whose value is 20%. The intersection of these two lines will be the location of data point “A" (BS = 30%, NF = 20%) on the ternary diagram. It should be noted that it is not necessary to draw the third line (dashed red line) to locate the data point of “A”; as there is a closing value of 100%, the result of LS will simply be a difference (i.e., LS = 100 - NF–BS). Consequently, it is possible to plot two-dimensional observations within a triangle.

Fig. 1.

Location of data points on the ternary diagram (plots A, B) and distance measurement (plot B). Plot A: BS value on solid blue line, NF value on solid black line, and LS value on dashed red line. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)

The second option is related to the conversion between the ternary diagram and the XY coordinates (see Pomberger et al. (2017)). Briefly, the three-part composition must be converted to XY coordinates using Eq. (1) and Eq. (2); this transformation allows the distance between two points to be calculated in a classical way (Fig. 1B and C).

$$\text{x}\text{'}=\text{NF}+\text{BS/}2$$ (1)

$$\text{y}\text{'}=\text{BS×}\sqrt{3}/2$$ (2)

The Pomberger et al. (2017) procedure is followed to construct the ternary diagram from the cited alternatives. The main justification is to ease capturing the data points in the ternary diagram through computational calculations; additionally, this allows the distance between two points (${\text{d}}_{\overrightarrow{\text{UR}}}$) to be easily calculated.

2.3. Plotting and reading a ternary parcel

The construction of a colored thematic map, like the univariate ones, requires the underlying data to be ordered. This is accomplished by first discretizing the ternary diagram into the ternary parcel.

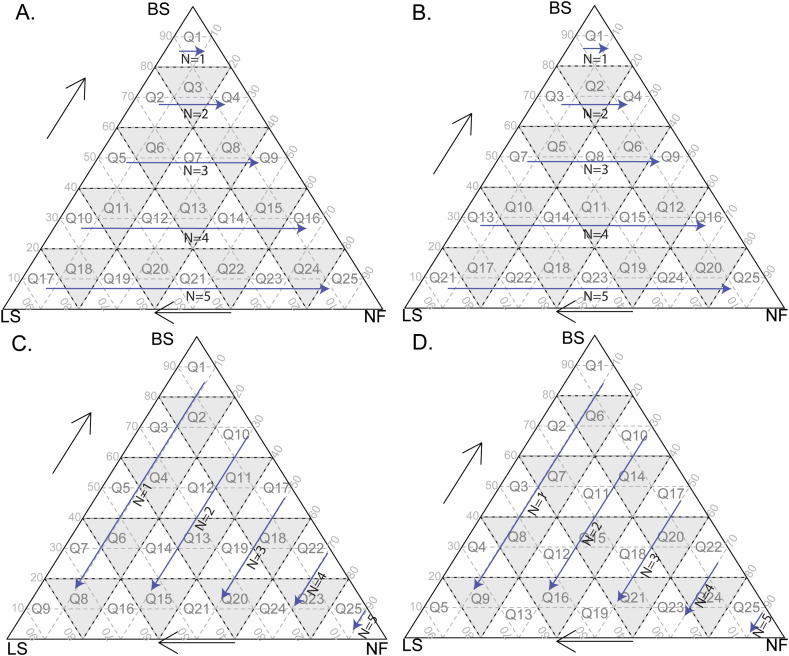
Ternary parcels can have different amplitudes. For example, if the ternary diagram is not delimited, the amplitude of the ternary parcel will be 100 (see Fig. 1A), and therefore the ternary reading would be BS ≤ 100, LS ≤ 100, and NF ≤ 100. If we limit the amplitude of the ternary parcel to 50, the number of ternary parcels will be 4, and the ternary reading of the plot located in the ternary center would be BS ≥ 50, LS ≤ 50, and NF ≤ 50. If we limit the amplitude of the ternary parcel to 20, the number of ternary parcels will be 25 (such as shown in Fig. 2 A), and the reading of one of the ternary parcels will be BS > 80, LS < 20, and NF < 20 (see reading of Q1, Fig. 2A). If the amplitude of the ternary parcel is 10, the number of ternary parcels that will be formed will be 100. The ternary parcel's amplitude is related to the precision of the reading. In this study, we selected an initial amplitude of 20 to analyze data, which represented an equilibrium between reading and ordering the parcels. We discuss the influence of the amplitude and the relationship with reading precision in the next sections.

Fig. 2.

(A–C) Three alternative routes to classify countries by groups: horizontally from left to right (A), vertically from top to bottom, with priority at shaded areas and then the white areas, from left to right (B), and diagonally from right to left, and diagonally from top to bottom with priority at white areas and then the shaded areas (C). N: level number.

On the other hand, to order the groups of countries (parcels), we define countries that have values close to the BS vertex as those that have a high coverage of handwashing facilities with soap and water on-premises as the ones in the best position. Countries that have values close to the NF vertex are those that have a high percentage of households that do not have handwashing facility and are shown as the last ones. Note that the order may have the four different classification alternatives (shown in Fig. 2):

• i)the first classification alternative is the one shown in subfigure A. It follows the logic of classifying countries with a high degree of coverage of basic hygiene services facilities, and then from left to right to prioritize access to limited hygiene services, and finally closing with the worst group of countries in Q25;
• ii)in the second alternative (subfigure B), the groups are arranged vertically from top to bottom, giving a higher value to countries that have a high coverage of basic hygiene services, and then from left to right to prioritize access to services of limited hygiene, and finally closing with the most unfavorable group of countries in Q25;
• iii)in the third alternative (subfigure C), the groups are ordered diagonally from top to bottom and by levels. The first level is when NF ≤ 20, and the last level, when 80 < NF. This order follows the criterion of first classifying countries with a low level of NF coverage (i.e., Q1 to Q9) and ending the classification with the group of countries with high NA values (i.e., Q25). Internally, for N = 1, it goes in descending order, giving priority to the basic level and ending in the LS vertex;
• iv)the fourth alternative (subfigure D) is a variant of the third alternative; the only change is the internal order of each level (first the white ternary parcels, and then the colored ones). The criterion used to define the order at each level is used to give a higher value to the group of countries with the lowest NF, and diagonally from higher BS to lower BS, both in the white ternary parcel and in the gray ternary parcel.

For this analysis, we chose the fourth alternative (Fig. 2D), which ensures that the first five ranking orders (i.e., Q1-Q5) include the value of zero for NF compared to the other alternatives. In the first and second alternatives, the group of countries captured by Q4 are those that do not have an NF value of zero; for the third alternative, countries that have a value of zero are more likely to be in Q3 or Q5 than in Q2 or Q4. In summary, by selecting the fourth (Fig. 2D), we place the group of countries with the lowest NF value in the first eight ranking orders (i.e., N = 1), and the group of countries with the highest NF value (i.e., N = 5) in the last order. This criterion is related to the vision of the 2030 Agenda of “leaving no one behind.”

2.4. Urban–rural inequality in a ternary diagram

Urban–rural inequality is measured through distances ${\text{d}}_{\overrightarrow{\text{UR}}}$ in the ternary diagram through Eq. (3). The greatest inequality will be presented by the countries with the greatest distance, and the lowest inequality, by the countries with the least distance. A value of zero indicates that there is no urban–rural inequality, while a value of 100 percentage points (p.p.) indicates a maximum inequality between urban–rural.

$${\text{d}}_{\overrightarrow{\text{UR}}}=\sqrt{{\left(\text{x}\text{'}-\text{x}\text{'}\text{'}\right)}^2+{\left(\text{y}\text{'}-\text{y}\text{'}\text{'}\right)}^2}$$ (3)

where x ', y' are the values of the urban residence area, and x '', y '' are the values of the rural residence area.

The proposal is compared with the standard way of measure of inequality, i.e., one inequality value calculated with Eq. (3) versus three inequality values calculated through the absolute value of the urban–rural difference in terms of the proportion for each dimension; this strategy is currently being used by WHO/UNICEF as part of the comparison of the proportion of the population with access to WASH services between urban and rural areas and reported in global reports (WHO/UNICEF, 2019a). The ternary amalgamated in two gives a result of differences between urban and rural that is exactly proportional to the differences between the magnitudes of the dichotomous variables (see Appendix B).

Finally, a graphical representation of thematic maps, ternary diagrams, and box plots was built into the R Core Team (2020) (v.4.0.3) platform, for which the following R packages were used: ggplot2 (v3.3.5; Wickham, 2016), tidyverse (v1.3.1; Wickham et al., 2019), and pgirmess (v1.7.0; Giraudoux et al., 2021) for building the ternary diagram; and tmap (v3.3–2; Tennekes, 2018) and sf (v1.0-1; Pebesma, 2018) for thematic maps. The database and R scripts are presented in Quispe-Coica and Pérez-Foguet (2021).

3. Results

3.1. Ternary classification of the hygiene service ladders in urban and rural

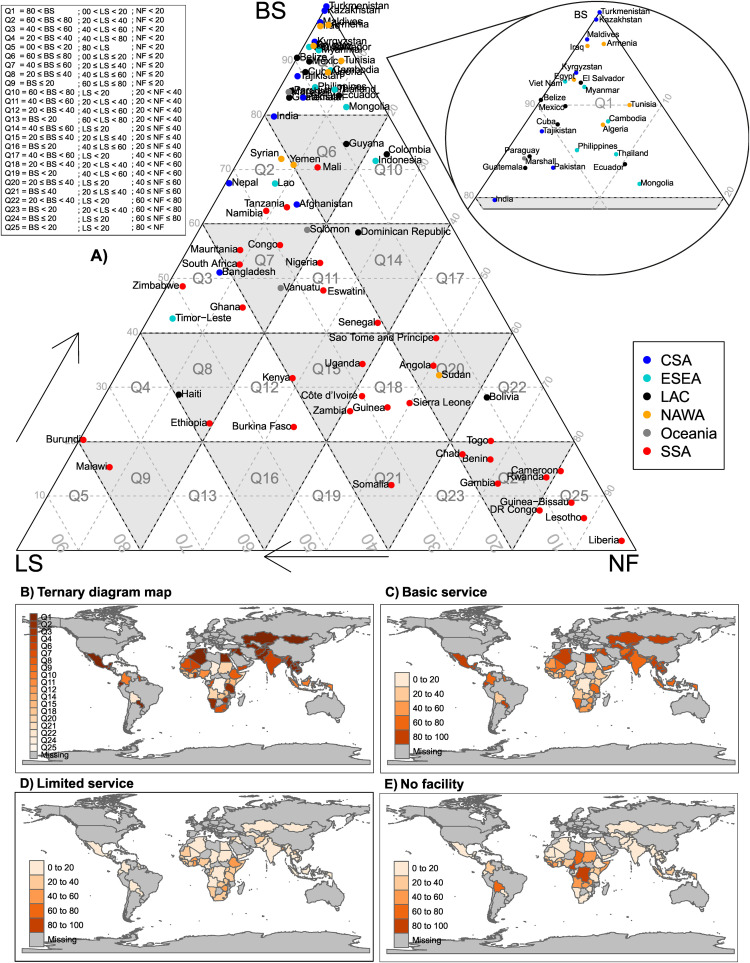
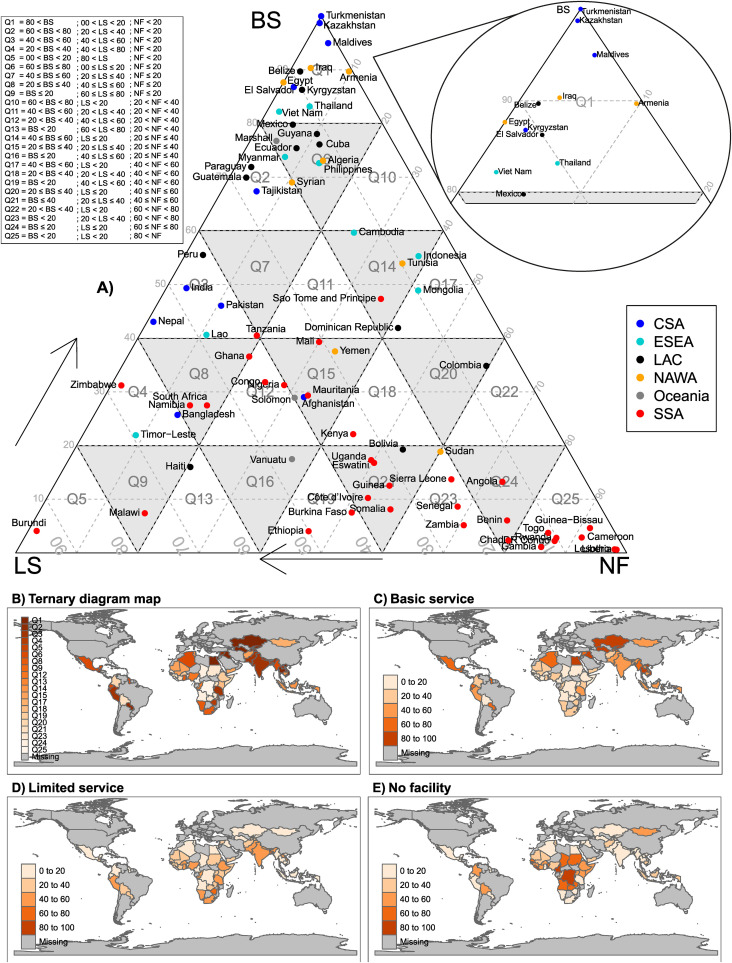
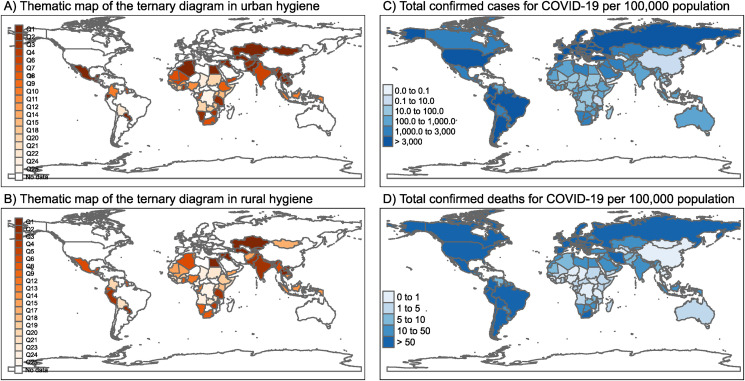
The countries' information on access to hygiene facilities is presented in Fig. 3, Fig. 4 for urban and rural residences, respectively. Twenty-five ternary parcels are used, with no information given for six ternary parcels in the urban area, and four in the rural area. The ternary diagrams and the corresponding classification in ternary parcels are presented in subfigure A and as thematic map in subfigure B. The univariate thematic map of the three hygiene categories is shown in subfigures C, D and E. The list with the classification of all the countries is presented in Table A1, and the summary of the number of countries found in each ternary parcel is shown in Table 1 .

Fig. 3.

Access to urban hygiene services in 2017. A: diagram ternary. B: ternary diagram map. C–E: univariate diagram.

Fig. 4.

Access to rural hygiene services in 2017. A: diagram ternary. B: ternary diagram map. C–E: univariate diagram.

Table 1.

Quantification of the number of countries according to their classification in the ternary parcel. N, level number of Fig. 2D; Qn, ternary parcel of order n.

N	Qn	Urban							Rural
		Global	Regional						Global	Regional
			CSA	ESEA	LAC	NAWA	Oceania	SSA		CSA	ESEA	LAC	NAWA	Oceania	SSA
1	Q1	25	6	6	7	5	1		11	4	2	2	3
	Q2	6	2	1		1		2	4	1		2	1
	Q3	4	1	1				2	6	3	1	1			1
	Q4	1						1	3	1	1				1
	Q5								1						1
	Q6	4	1		1	1		1	8		2	4	1	1
	Q7	5					2	3
	Q8	2			1			1	3						3
	Q9	1						1	1						1
2	Q10	2		1	1
	Q11	3						3
	Q12	1						1	2						2
	Q13								1			1
	Q14	1			1				4		2		1		1
	Q15	2						2	5	1			1	1	2
	Q16								1					1
3	Q17								2		1	1
	Q18	4						4	1						1
	Q19								2						2
	Q20	3				1		2	1			1
	Q21	1						1	6			1			5
4	Q22	2			1			1
	Q23								4				1		3
	Q24	4						4	3						3
5	Q25	5						5	8						8
	Total	76	10	9	12	8	3	34	77	10	9	13	8	3	34

Our classification method grouped 25 countries for urban residence, and 11 countries for rural residence, in Q1. The regional breakdown of Q1 shows that 7 LAC countries, 6 ESEA and CSA countries, 5 NAWA countries, and 1 Oceania country corresponded to urban residence, and 4 CSA countries, 3 NAWA countries, 2 LAC countries, and 2 ESEA countries corresponded to rural residence. No country from the SSA region appeared in this group, but they did from Q2 onwards.

The group of countries in the ternary parcel Q1 (i.e., 80 < BS, LS < 20, and NF < 20) are characterized by having the best conditions for on-site handwashing practice, as they have high coverage of basic services (BS > 80), low coverage of households with limited services (LS < 20), and low coverage of households without handwashing facilities (NF < 20). Their representation on the thematic map has the most intense color, and the intensity decreases in the order from Q1 to Q25. The difference between urban and rural in the number of countries captured by Q1 shows that there is a higher probability of having better handwashing conditions in urban residence than in rural residence, both in the total and in the regional breakdown.

The group of countries from Q2 to Q9 are characterized by having relatively better conditions for handwashing practice, as they have low coverage of households without on-site handwashing facilities (i.e., NF ≤ 20%), BS ≤ 80%, and LS from 0 to 100%. Note that rural Burundi is the only country in Q5 and is very close to the LS vertex, which implies that it has high coverage of LS (>80%), low coverage of BS (<20%), and low coverage of households with NF (<20%). Also noteworthy is the appearance for the first time of two countries in the SSA region in urban Q2 (Tanzania and Namibia).

The ternary parcels captured 9 urban countries and 13 rural ones in Q10 to Q16. This group of countries is characterized by having NF values that are within the range of 20%–40%, while the BS and LS values are between zero and 80%. Compared to Q1 to Q9, there is a higher concentration of rural than urban in Q10–Q16, with 13 vs. 9 countries, respectively; this pattern is observed also in the following classification levels (from N3 to N5).

Following the sequence, the group of countries that were classified in Q17 to Q21 have the common characteristic of having NF values from 40% to 60%, and BS and LS values from 0 to 60%. In the regional breakdown, there is a predominance of countries in the SSA region over the rest. For urban cases, there are 7 countries in SSA as compared to 1 in NAWA. For rural cases, there are 8 countries in SSA as compared to 3 in LAC and 1 in ESEA.

In the following order of classification, from Q22 to Q24, the situation is similar to the previous one: there is a predominance of countries from the SSA region over the rest. This is more drastic in the ternary parcel Q24, which contained only SSA countries, both in the urban and the rural categories.

The last sorting order corresponds to Q25. As for Q24, all the countries captured by this ternary parcel belong to the SSA region. The group of countries that are in this ternary parcel are characterized by low coverage of households with BS (<20), low coverage of LS (<20), and high coverage of households with NF (>80). Their representation on the thematic map has the lowest color in intensity, which means that countries in this group (of the total of countries analyzed) have the most unfavorable conditions for handwashing.

On the other hand, we note that interpreting the univariate thematic map can lead to an erroneous interpretation of the information. Using Burundi as an example, if we only interpret the BS value (of 4.1%) expressed in the thematic map in Fig. 4C, we observe that it is represented with the lowest color in intensity, giving the impression that Burundi has very unfavorable conditions for handwashing. However, in our classification alternative, Burundi is in Q5 and is represented in the thematic map in Fig. 4B with the most intense color. This means that it has relatively better conditions for handwashing, as it has a high value of LS (94.5%) and a low value of NF (1.4%). Consequently, a univariate analysis does not show what is going on in the other parts, highlighting the value of using an alternative way of exploring closed data with a ternary thematic map.

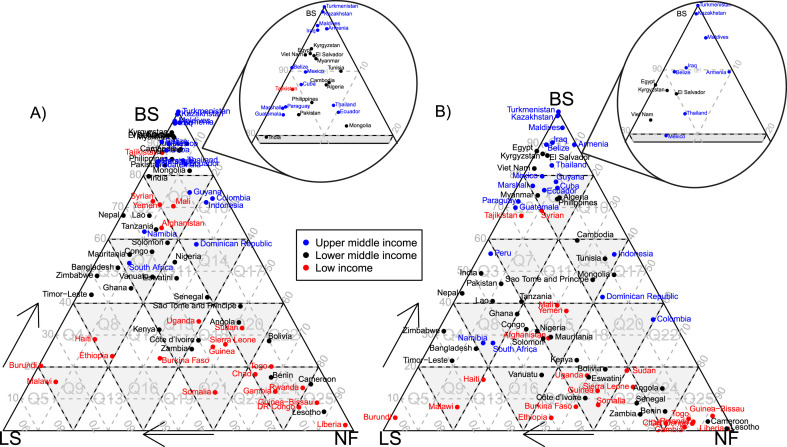
Finally, when crossing the classification of the countries with their income level (Figure A3), we observe that in the order of classification from Q1 to Q9, there is a greater concentration of upper-middle-income countries than of lower and lower-middle-income countries, both in the urban and rural categories. This decreases in the higher levels; for example, at level 2 (i.e., N2; from Q10 to Q16), there are only three upper-middle-income countries in the urban residence areas, and only one in rural; at the next level (N3; from Q17 to Q21), there are only two upper-middle-income countries in rural areas and none in urban. At the highest levels, ternary parcels have not captured any upper-middle-income countries. In general, the results show that the upper-middle-income countries are concentrated at the top of the ternary diagram, and the lower-middle-income and low-income countries, at the bottom.

3.2. Urban–rural inequality in access to hygiene facilities

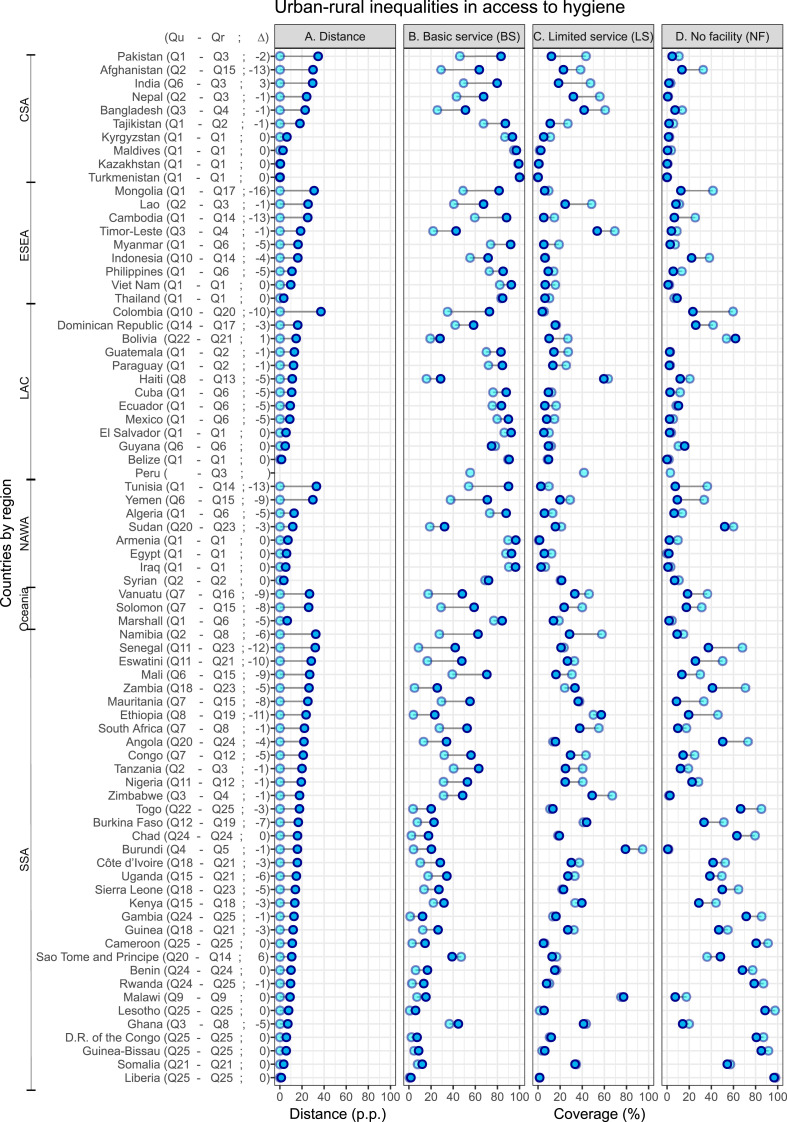
The results of the urban–rural inequality vectors are shown in the ternary diagram of Fig. 5 A and spatially in Fig. 5B. The vectors use the urban residence area as the starting point, and the rural residence area as the end point. The distance between these two points, the module of the vector, represents urban–rural inequality.

Fig. 5.

Urban–rural inequality of the ternary diagram, expressed as distance (A) or map (B). The starting point of the vector is the urban position, and the ending point of the vector is the rural position.

In the ternary diagram, the vector directions do not have a defined order, indicating a differentiated behavior of inequality between countries; further, expressed as a thematic map, the results show spatial heterogeneity (Fig. 5B). However, common patterns are repeated in 73/76 countries, such as the direction of the vector from top to bottom (diagonally to the right or to the left). This indicates that there is a higher level of BS in urban than rural settings. In contrast, in Sao Tome and Principe and Guyana, the direction is from bottom to top (diagonally to the left), which means that the level of BS is higher in the rural than in the urban setting (see also Fig. 6 B).

Fig. 6.

A) A measure of inequality expressed in terms of distance. The blue circle represents the upper limit of the distance of the ternary diagram. B–D: Urban–rural inequality graph used by UNICEF and WHO (2020). A blue circle denotes urban, and a light blue circle, rural. Δ indicates the change of order between urban (Qu) and rural (Qr) in the ternary parcel (e.g., in Pakistan Δ = Q_u=1 – Q_r=3 = −2). (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)

For LS, the urban–rural difference has a negative value in 57/76 countries, indicating that households in the rural residence area have greater coverage of hygiene facilities lacking soap or water than households in the urban residence area. Finally, in the case of NF, the urban–rural difference has a negative value in 68/76 countries, which means that households in the rural residence area have greater NF coverage than those in the urban ones.

The urban–rural inequality result expressed in terms of distance is shown in Fig. 6A and the summary statistics by quartiles in Table 2 (boxplot in Figure A1). We complement the inequality value illustrated in Fig. 6A with the results obtained from the urban (Qu) and rural (Qr) classification in the ternary diagram. The uppercase delta value (Δ) indicates a change of order between urban and rural in the ternary parcel (i.e., Δ = Qu - Qr). A negative value of Δ means that, in the classification, urban is in a higher order than rural; a positive value of Δ indicates the reverse process. A value of Δ equal to zero means that there is no change and, therefore, urban and rural are in the same ternary parcel.

Table 2.

Statistical summary of the measure of inequality by quartiles. Values are expressed as a percentage and rounded to one decimal place.

Region	Minimum (p.p.)	Quartile 1 (p.p.)	Quartile 2 (p.p.)	Quartile 3 (p.p.)	Maximum (p.p.)
Central and Southern Asia (CSA)	0	3.7	20.5	28.3	34.6
Eastern and South-Eastern Asia (ESEA)	3.5	10.9	16.4	25.2	31.0
Latin America and the Caribbean (LAC)	1.5	8.1	11.0	13.5	37.1
Northern Africa and Western Asia (NAWA)	3.6	5.7	9.5	21.3	33.1
Oceania	6.6	16.3	26.0	26.4	26.8
Sub-Saharan Africa (SSA)	1.2	10.2	15.8	21.6	32.5
Global	0	8.7	14.4	23.1	37.1

Globally, 19/76 countries were identified as belonging to the first quartile with inequality distances ≤8.7 p.p. (with a minimum value of zero in Turkmenistan), and with inequality distances >8.7 p.p. in 75% of the remaining countries. In the third quartile, the inequality distances are ≤23.1 p.p. for 75% of the countries, and >23.1 p.p. for the remaining 25% of the countries, with a maximum value of 37.1 p.p. in Colombia. The zero-value found in Turkmenistan is based on having both NF and LS equal to null, with the BS service category at 100%; therefore, when applying Eq. (3), a vector with null distance is obtained. The meaning of the zero value is that there is equality between urban and rural in access to the hygiene service facilities and, in the particular case of Turkmenistan, the hygiene facilities also have soap and water.

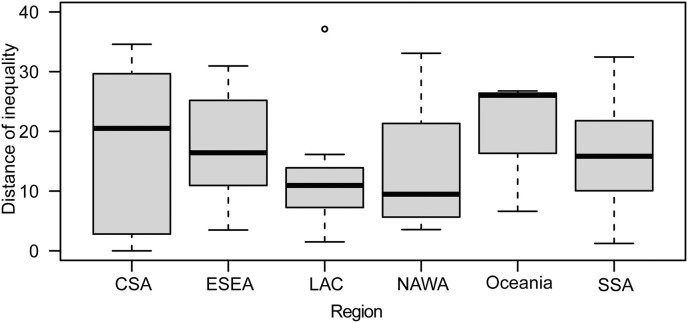
From a regional perspective, the inequality measures show high heterogeneity. In the LAC region, Colombia is the country with the highest urban–rural inequality (with a value of 37.1 p.p.), and Belize is the country with the lowest inequality (with a value of 1.5 p.p.) (Fig. 6A). Colombia's inequality value deviates greatly from the normal behavior of the region, where 75% of the countries have inequality distances ≤13.5 p.p.; therefore, it is considered an atypical behavior. The LAC region also has the lowest interquartile range (IQR; 5.4 p.p.) with respect to the rest of the regions, which translates into less dispersion of data.

In contrast, the CSA region has the highest IQR value, of 24.6 p.p., which translates into a greater dispersion of data. Likewise, in CSA, 75% of the countries have an inequality distance of ≤28.3 p.p., with a value of zero in Turkmenistan; the remaining 25% the distances have an inequality distance of >28.3 p.p., with a maximum value of 34.6 p.p. in Pakistan.

In the ESEA region, 7/9 countries have inequality distances ≤25.2 p.p., with a minimum value of 3.5 p.p. in Thailand; in the remaining two countries, the inequality distances are >25.2 p.p., with a maximum value of 31.0 p.p. in Mongolia. In the Oceania region, distances could only be calculated for three countries; the minimum value is 6.6% in Marshall, and the maximum value is 26.8 p.p. in Vanuatu. In the SSA region, 75% of the countries have an inequality distance ≤21.6 p.p., with a minimum value of 1.2 p.p. in Liberia, and the remaining 25% of countries have distances >21.6 p.p., with a maximum value of 32.5 p.p. in Namibia.

Note that a low value in the inequality measure does not necessarily imply that the best conditions are present for handwashing with soap and water. For example, in the CSA, ESEA, LAC, and NAWA regions, a delta with a zero value corresponds to the countries with less inequality but is also present when urban and rural are in the same ternary parcel of Q1, Q2, or Q6. Q1 countries have the best conditions for handwashing with soap and water. However, in the SSA region, the four countries with the lowest inequality are in Q21 or Q25, yet at the same time have a Δ value equal to zero, which translates into countries with the most unfavorable conditions for handwashing with soap and water; indeed, they present high NF values (>80% in Q25, and between 40% and 60% in Q21). Consequently, to avoid an erroneous interpretation of the value of inequality, it is necessary that this magnitude be accompanied by the ternary classification.

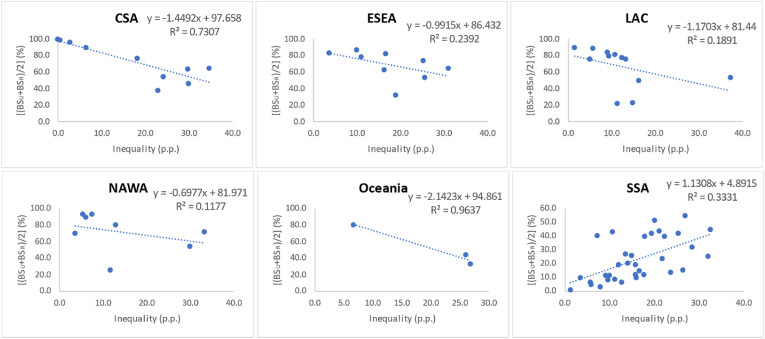
Our results also show that the multivariate measure of inequality has a dual behavior with respect to BS hygiene: it has a direct relationship in the SSA region (i.e., the magnitude of inequality decreases and the average of the urban and-rural BS also decreases), and an inverse relationship in the remaining regions (i.e., the magnitude of inequality decreases, while the average of the urban-rural BS increases). This affirmation is supported by the result of the linear fit between the inequality measure obtained and the average urban and rural BS, which has a negative slope in the CSA, ESEA, LAC, NAWA, and Oceania regions, while the SSA region has a positive slope (see Figure A4).

The univariate graphs in Fig. 6B–D allow a very intuitive visualization of urban–rural inequality in access to hygiene services, facilitating the reading of each category. However, it is not possible to know the level of inequality in the country as a whole, since the three categories contain information on inequality and can score better or worse depending on the category of analysis. For instance, ordering the absolute value of inequality in descending order (e.g., with the highest inequality in the first order, and the lowest in the last order) leads to India being ranked 12th based only on the BS category, ranked 3rd based only on the LS category, and ranked 64th based on the NF category. However, the unique measure proposed in this study give India a value of 29.7 p.p., placing it in 9th place.

Another detail to take into account is that the sum of the inequality values of the three categories results in a value of zero (i.e., 30.4 p.p. (BS) – 28.8 p.p. (LS) – 1.6 p.p. (NF) = 0). This is because, for both urban and rural areas of residence, the sum of the parts has a constant value of 100% and, therefore, the difference between urban and rural results in zero. The constant closing value is a peculiarity of composition data, and it is also one of the reasons why it requires a particular statistical approach.

Finally, it can be inferred from the results obtained that access to basic service facilities —such as to hygiene facilities with soap and water— is a privilege of mainly households located in urban areas. Sao Tome, Principe, and Guyana are the only cases in which basic service was higher in rural than in urban areas. Meanwhile, limited hygiene and NF service are higher in rural than in urban areas.

4. Discussion

4.1. Urban–rural inequality in a ternary diagram

We constructed twenty-five ternary parcels with a reading precision of twenty, which allowed us to group the countries with similar behaviors in order from the ternary parcel Q1 to the ternary parcel Q25. We obtained results that show a greater concentration of countries with urban households (e.g., 25/76 countries in Q1) than rural (e.g., 11/77 countries in Q1) in the BS vertex. This translates into greater availability of handwashing facilities with soap and water in urban households than in rural ones. In contrast, countries in the ternary parcels Q24 and Q25, both urban and rural, correspond only to countries belonging to the SSA region.

For some country analyses, the amplitude of twenty was not beneficial, as it generates misleading results in the ranking order. For example, in the urban residence area (Fig. 3A), Kenya (BS = 31.7%, LS = 39.6%, NF = 28.7%) has better indicators than Burkina (BS = 22.7%, LS = 43.9%, NF = 33.4%) and is therefor, better; nonetheless, according to our ranking, it is at Q15, while Burkina is at Q12. However, if we adjust the reading precision to a magnitude of ten, Kenya would rank at Q48, and Burkina at Q56, in the new classification. This allows us to affirm that one of the limitations of the method has to do with the adequate selection of the reading precision.

The method is also limited when the data point is very close to the boundary of the subdivided ternary parcel or to its vertices; by not taking into account the uncertainty of the data, they are very likely to be in either one or both. Taking the same previous case above as an example, the Kenyan data point is very close between the limit of Q12 and Q15 (the limit between both has the value of 40 in LS), so if we add the uncertainty of the data, it is very likely that Kenya is doubly classified. Another more drastic case is shown for rural Tanzania: the data point is very close to one of the vertices of Q3, implying that if its uncertainty is added, it could also be in any of these (Q7, Q8, Q11, Q12, or Q15). This underscores the need to incorporate data uncertainty (Ezbakhe and Pérez-Foguet, 2019) to obtain greater precision in the order of classification.

Further, the values of the service stairs have a tendency to go to the upper limit of one, which expressed in the ternary diagram, indicates that the data points are very close to the vertices. This is relevant as SDG 6.2 seeks " … by 2030, achieve access to adequate and equitable sanitation and hygiene for all and end open defecation … ". Therefore, as the BS progress rate increases, the data points of the countries will tend to the BS vertex. This implies that it will be more relevant to capture data points when they are in Q1 under multivariate behavior.

Our method allows adjustments to the new conditions to be made, giving a more accurate reading. For this, it will only be necessary to adjust the amplitude of the ternary parcel to a value lower than twenty, which generates an increase in the number of subdivided ternary parcels.

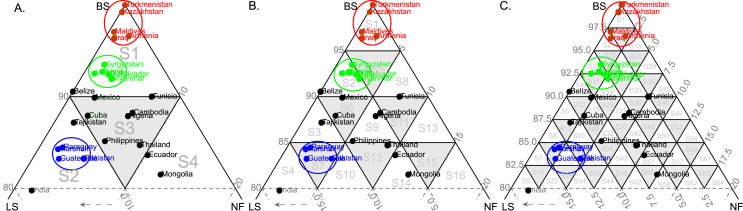
However, an excessive increase in the breadth may not be beneficial to the grouping and ranking order of countries. To illustrate this situation, we carried out a Q1 zoom of the urban residence area (Fig. 3A) and then subdivided it into ternary parcels with three levels of reading precision (of 10, 5, and 2.5; Fig. 7 A–C). Here, subfigure A was subdivided from a ternary parcel with an amplitude of twenty, to four ternary parcels with an amplitude of ten. The order of the classification follows the same logic outlined in Fig. 2D and goes from S1 as the best, to S4 as the least favorable. We also intuitively delimited three possible similar groups (colored red, green, and blue; Fig. 7), which should capture the following subdivisions as the reading precision increases.

Fig. 7.

Zoom of Q1 in the urban residential area subdivided into ternary parcels with different reading precision measures. Left: When the reading precision is 10, the subdivision of Q1 results in 4 ternary parcels. Center: When the reading precision is 5, the subdivision of Q1 results in 16 ternary parcels. Right: When the reading precision is 2.5, the subdivision of Q1 results in 64 ternary parcels. (Note that, to reduce confusion, the internal subdivisions are indicated with Sn).

By increasing the reading precision to five (Fig. 7B), the group of countries shown in red and blue are perfectly captured by the ternary parcels S1 and S7, respectively, while S2 captures the group of countries shown in green and has added Belize. If we continue to increase the reading accuracy to a 2.5 ternary delimitation, as shown in Fig. 7C, there is a greater dispersion of the group of intuitively delimited points: the group of countries in green is now distributed in S3, S11, and S18; the groups of countries in red and blue also have multiple distributions. The order of classification is also altered as the ternary reading amplitude increases, as seen for Myanmar (BS = 91.95%, LS = 5.25%, and NF = 2.80%) and El Salvador (BS = 92.41%, LS = 5.31%, and NF = 2.28%), shown in green. Both countries are in the same ternary parcel in subfigure A and B; in subfigure C, however, Myanmar is in S18 and El Salvador in S11, despite having very close data points.

Therefore, an excessive increase in the reading precision has a dispersion effect in the group of countries, which is not beneficial for the grouping or ordering of classification, in addition to the order uncertainty previously mentioned. Therefore, the precision of the ternary reading has to be limited, taking into account data uncertainty and the desired level of clustering of the final results.

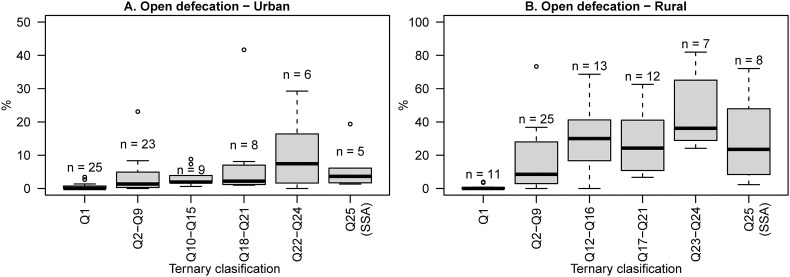
Along the same lines as SDG 6.2, which seeks to end open defecation (OD) and provide adequate hygiene, our method allows us to explore the relationship between levels of hygiene service and a sanitation service category. For this, we used a boxplot to cross the ternary classification obtained for each country with the proportion of people who continue open defecation (Fig. 8 ). The boxplot shows that OD rate is lower for countries in Q1, and higher for those in Q25; this trend is more drastic in rural areas than in the urban ones. This shows that there is a relationship to a greater or lesser extent between those without handwashing facilities with soap and water and OD; i.e., households with sanitation facilities that do not practice OD are more likely to also have handwashing facilities with soap and water.

Fig. 8.

Ternary classification vs open defecation, both in urban and rural areas. Open defecation (OD) refers to the disposal of human faeces in fields, forests, bushes, open bodies of water, beaches, other open spaces, or with solid waste. In rural regions, Syria was excluded from the analysis, as it did not have information from OD.

The countries in Q23, Q24 and Q25 belong mainly to the SSA region; according to Fig. 8, this group of countries has high values of OD and NF (NF > 60%). These conditions in the SSA region lead to diseases related to inadequate WASH services, with diarrhea the main one. In SSA, improvements in sanitation were responsible for a reduction of more than 10% in the mortality rate from diarrhea in children under 5 years of age (Troeger et al., 2018). In the same region, Zerbo et al. (2021) found that 7.75% (5.99–9.7%) of all deaths due to diarrheal diseases are attributed to unsafe WASH. Systemic review of the effect of handwashing with soap on the risk of diarrhea in the community found that handwashing with soap can reduce the risk of diarrheal diseases by 42–47% (Curtis and Cairncross, 2003). Therefore, an intervention aimed at reducing OD and NF in households in the SSA region will have a positive effect on their public health.

SDG 6.2 also seeks equitable access; in that sense, our method gives an integrated measure of a three-part service ladder. The measure is for analyzing the difference between urban and rural, which allows the public policies of the sector to be differentiated with a general vision. This differs from the simple difference between the proportion of urban and rural that the JMP performs (WHO/UNICEF, 2016), which has also been used in other studies. Our methodology also incorporates calculations of common distances, which facilitates the understanding of each result obtained, allows comparison between countries (either on a thematic map or in distance measures), and allows an inequality ranking of urban–rural inequality of the countries.

However, expressing inequality in a single, multidimensional measure hides information from the parties, which does not allow for specific sectoral interventions. This is one of the main disadvantages of a comprehensive measure, as noted in other studies (Giné-Garriga et al., 2017, Giné-Garriga and Pérez-Foguet, 2010, Hsiao et al., 2005). Therefore, the obtained inequality measure is further strengthened if it is also accompanied by the usual measure of the simple difference between urban and rural between the parties or with the ternary classification obtained. For example, an inequality value of 3.5 p.p. in Thailand is not the same as a value of 3.5 p.p. in Somalia. This can be better visualized by adding the ternary parcel to which they belong: Thailand is in Q1 (i.e., it has 80 < BS, LS < 20, NF < 20), and Somalia is in Q21 (i.e., it has BS ≤ 20, 20 ≤ LS ≤ 40, 40 ≤ NF ≤ 60). This will help to provide a global magnitude for policies with a general vision and disaggregated magnitudes for targeted interventions.

In this study, we could not calculate urban–rural inequality for some countries due to a lack of information. However, for countries with available information, our results show that urban–rural inequalities can differ in magnitude from one country to another, from a minimum value of zero to a maximum value of 37.1 p.p. With regional geographic variation, the urban–rural inequality in CSA has a minimum value of zero and a maximum value of 34.6 p.p.; in ESEA, the minimum value of 3.5 p.p. and a maximum value of 31.0 p.p.; in LAC, a minimum of 1.5 p.p. and a maximum of 37.1 p.p.; and in NAWA, a minimum of 3.6 p.p. and a maximum of 33.1 p.p., in Oceania, the minimum is 6.6 p.p. and the maximum is 26.8 p.p., and in SSA, the minimum is 1.2 p.p. and the maximum is 32.5 p.p. The inequality measures obtained justify differentiated management strategies for both urban and rural areas, with greater emphasis on rural households as well as on the countries that are in the Q25 ternary parcel, which are the countries with the highest proportions of NF.

4.2. Hygiene facilities and COVID

Our results are based on information from 2017. However, we consider that the analysis by ternary parcels with an amplitude of twenty helps to compensate the brief changes that have been generated to date in analysis, which allows us to cross the information obtained from hygiene with the data of cases and death due to the COVID-19 disease. Hygiene cross-information corresponds only to countries that with urban and rural in the same ternary parcel or in the classification range of ternary parcels (e.g., in Fig. 6, Ghana has urban in Q3 and rural in Q8 and therefore is considered in the classification from Q2 to Q9); countries that do not meet this condition were excluded from this analysis. In any case, this discussion is informative for helping national and international actors to understand the link between hygiene and public health.

We were not able to calculate urban–rural inequality or the realities of some countries in terms of hygiene. The main reason is little or no information. It is more drastic in high-income regions, such as Europe, Northern America, Australia, and New Zealand, for which there is no ternary hygiene information for the year 2017. A recent study by Brauer et al. (2020) reaffirms the hypothesis that there is little global data on hygiene. Even so, with complementary information, they were able to estimate the proportion of the population with no facilities for washing hands with soap and water for the year 2019. They show that high-income countries have low levels of the proportion of the population without access to a handwashing station with soap and water. Having almost all basic services covered is probably one of the reasons why information gathering is taking a back seat. However, most of these countries also have the highest number of confirmed cases and deaths from COVID-19 according to the WHO (see Figure A2). The case of the USA is the most illustrative, especially as the estimates by Brauer et al. (2020) suggested that the proportion of the population without access to a handwashing station with soap and water was 0.4% value [lower = 0.3%, upper = 0.5%] in 2019. However, as of 15 March 2021, the USA is in the 9th place in the ranking of confirmed COVID-19 cases per 100,000 population and in the 13th place in the ranking of deaths from COVID-19 per 100,000 population.

Notably, Ahmad et al. (2020) showed that counties with a higher percentage of substandard housing households had a higher incidence and mortality associated with COVID-19. Homes that have any of the following four problems are considered precarious conditions: overcrowding, high housing cost burden, incomplete kitchen facilities, and incomplete plumbing facilities. Incomplete plumbing is related to homes that lack hot and cold running water, a flushing toilet, or a bath/shower. The scarcity of water, lack of water, or water insecurity at homes (Stoler et al., 2021) makes hand hygiene difficult, which translates into an increased risk of infection by the SARS-COV2 virus. That said, it is likely that in homes without the necessary conditions to practice hand hygiene, there will be a greater increase in infection rate. Therefore, obtaining data, even if it is only low amounts of data, is still relevant for targeting interventions.

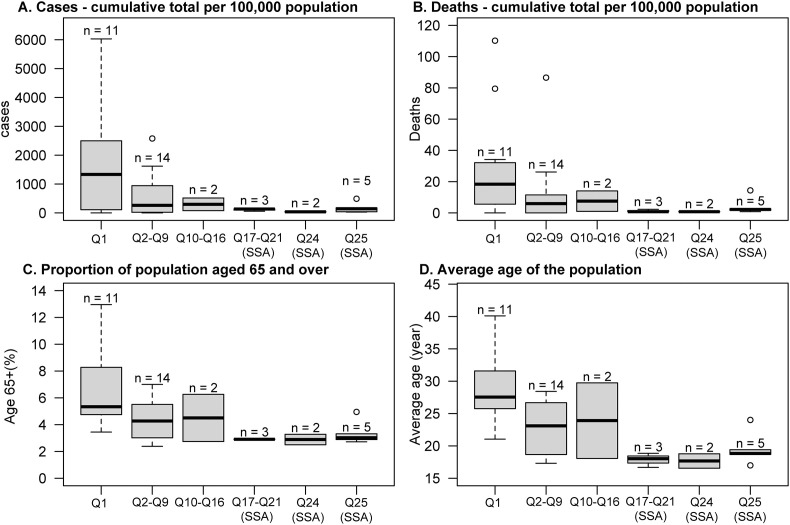
For the results obtained by crossing our ternary classification with confirmed cases and deaths from COVID-19, the median of the countries that are within the Q1 group is higher than the median of the rest of the groups in both confirmed cases and deaths from COVID-19 (Fig. 9 A and B). This means that some countries that have higher rated levels of hygiene service (i.e., belong to 80 < BS, LS < 20, NF < 20) and have higher confirmed cases and deaths from COVID-19 (cumulative total per 100,000 population; as of 15 March 2021). In turn, the lowest values of the median of confirmed cases and deaths from COVID-19 are presented in the range of ternary parcels from Q17 to Q25 and, at the same time, the countries that are in this range of ternary parcels all belong to the SSA region.

Fig. 9.

A–D) Graphs based on level of service, e.g., countries in Q1 to Q9 belong to Level 1 (N1 to N5; see also Fig. 2D). Cases (A) and deaths (B) from COVID-19 per 100,000 population. Proportion of population that is ≥ 65-years old (C) and average age of the population (D); information obtained from United Nations Department of Economic and Social Affairs Population Division (2019).

It is paradoxical that, with low levels of BS hygiene, there is also a low rate of confirmed cases and deaths from COVID-19 (per 100,000 population). It would be expected that lower proportions of BS would lead to a higher contagion rate. We further assume that available figures represent the actual number of deaths more or less approximately, but with the same accuracy regardless of the country; however, some international news at the time of writing this research casts doubts about this hypothesis (ANDINA, 2021, GESTION, 2021). Nonetheless, possible explanations are emerging in the literature about this phenomenon, which is occurring in some countries of the SSA region. One explanation is that SSA countries have younger populations, which could act as a protective factor against COVID-19. Another possible explanation is related to the low proportion of older adults in SSA, given that older adults have a higher risk of hospitalization or death when contracting the COVID-19 disease (CDC, 2019, Shahid et al., 2020). According to the Centers for Disease Control and Prevention (CDC), as compared with 5–17-year-olds, the rate of hospitalization is 40 times higher in 65–74-year-olds, 65 times higher in 75–84-year-old, and 95 times higher in ≥85-year-olds (CDC, 2019). To contrast these statements, we crossed the classification of the countries into ternary parcels obtained with the average age of the population and the proportion of the population aged ≥65-year-olds (Fig. 9C and D). The results show that the median age in SSA is lower than the median age of the countries that are in the ternary parcel Q1; the same occurs for the proportion of the population aged ≥65-year-olds.

Other explanations have been suggested in the literature, such as the role of climate (Adedokun et al., 2020; Huang et al., 2020), vaccination against Bacillus Calmette-Guerin (BCG) (that might have a protective role against COVID-19) (Curtis et al., 2020; Miller et al., 2020), population density (Tcheutchoua et al., 2020), and others (Lalaoui et al., 2020; Mbow et al., 2020; Tcheutchoua et al., 2020). Of these, the most prominent is probably the lessons learned from dealing with diseases, such as ebola, malaria, HIV, and others, given that the infrastructures built and the response management systems in place have rapidly adapted to cope with the current pandemic (Lumu, 2020; Nachega et al., 2020; Payne, 2020).

All this could partly explain that even being in the ternary parcels from Q17 to Q25, some countries in the SSA region have low values of confirmed cases and deaths from COVID-19. The most striking thing is that the countries that are in Q25, such as Cameroon, Lesotho, DR Congo, Guinea-Bissau, and Liberia, also have low values of confirmed cases and deaths from COVID-19 and, at the same time, represent the countries with the conditions most unfavorable for practicing hand hygiene, i.e., BS < 20, 80 < NF, LS < 20.

Finally, it is highly possible that, despite having access to a facility, handwashing with soap and water is being practiced poorly (Wolf et al., 2019), thus further increasing the likelihood of contracting COVID-19 disease.

5. Conclusions

To our knowledge, this is the first time that a measure of inequality was applied to the hygiene sector that takes into consideration the multivariate characteristics of the data. Furthermore, this is also the first attempt to classify the countries into ternary parcels that can later be represented on a thematic map, with the potential application of a spatial analysis.

The construction of the thematic map with each ternary parcel (Qn) offers a better visualization and interpretation of the results, either grouped by region or individually for each country. It is necessary that each ternary parcel (Qn) is read as ternary delimitations, or (in the individual case of a country represented by data in the ternary diagram) as data with tripartite information. Omitting any of the categories in the reading can contribute to inaccuracies in the interpretation of the results. Consequently, in this article, we provide another way to explore and interpret hygiene data in its space, which is the simplex.

Likewise, we propose an alternative measure of urban–rural inequality when the characteristic of the data is compositional and ternary, without infringing on the properties of the data (i.e., scale invariance, subcompositional coherence). This new measure of inequality is different from the simple urban–rural difference that is widely used in global monitoring of household access to drinking water and sanitation services. It has the potential to be applied to the monitoring of urban-rural inequality of the JMP service ladders on estimates of water, sanitation, hygiene, waste management and environmental cleaning in health care facilities (WHO/UNICEF, 2019b), which have tripartite information (basic service, limited service, and no service). It can also be used to monitor urban-rural inequality in the JMP service ladders on drinking water, sanitation, and hygiene in schools (UNICEF and WHO, 2020), which also has tripartite information.

The results we obtained highlight the need to continue to make efforts in rural households, in order to reduce the urban–rural gap that was evidenced in 2017, as they have less availability of basic facilities for handwashing than urban households. This translates into leaving no one behind. On the other hand, Colombia is proof that an upper-middle-income country is not necessarily a guarantee of equality in access to on-premise handwashing facilities, given that we identified it as the country with the greatest inequality in 2017.

Achieving universal access to hygiene facilities with soap and water by 2030 will continue to be a challenge, mainly in the countries of the SSA region that were classified in the ternary parcel Q24 (urban: Chad, Benin, Gambia, Rwanda; rural: Angola, Benin, Chad) and Q25 (urban: Cameroon, DR Congo, Guinea-Bissau, Lesotho, Liberia; rural: Cameroon, DR Congo, Guinea-Bissau, Lesotho, Liberia, Togo, Rwanda, Gambia), as they are within the ternary parcels with the worst conditions. In addition, the current pandemic has highlighted the need for households to have facilities to wash their hands with soap and water; continuous hand hygiene will act as a protective barrier, thus reducing the risk of contagion of the SARS-CoV-2 virus or other common diseases.

Finally, it is possible to explore and measure the urban–rural inequality of the compositional data in the ternary diagram when these are tripartite data. When they are in four parts, it can also be calculated in the regular tetrahedron, a subject that is not addressed in this study. For five or more parts, it is necessary first to perform logarithmic ratio transformations to apply any usual statistical technique, a topic that is also not addressed in this research. Therefore, future research should address new methodologies to measure urban–rural inequality when compositional data has four or more parts. We recommend that greater emphasis be placed on the five-part inequality measures, as SDGs 6.1 and 6.2 have five levels of service in the water and sanitation ladders.

Appendix A.

Fig. A1.

Boxplot of urban–rural inequality by region

Fig. A2.

Urban (A) and rural (B) hygiene service of 2017. Thematic map of confirmed cases (C) and deaths (D) from COVID-19, obtained March 15, 2021 from the WHO platform (see https://covid19.who.int/)

Fig. A3.

Urban (left) and rural (right) graphical representation of the countries in the ternary diagram by income. Information on the classification of countries according to their level of wealth was obtained from World Bank (2021).

Fig. A4.

Linear fit, in the six regions analyzed, between the inequality measure obtained and the average urban and rural BS. The CSA, ESEA, LAC, NAWA and Oceania regions have a negative slope, while the SSA region has a positive slope.

Table A1.

Urban and rural classification of countries in the ternary diagram

ID	Urban	Rural
Q1	Algeria, Armenia, Belize, Cambodia, Cuba, Ecuador, Egypt, El Salvador, Guatemala, Iraq, Kazakhstan, Kyrgyzstan, Maldives, Marshall, Mexico, Mongolia, Myanmar, Pakistan, Paraguay, Philippines, Tajikistan, Thailand, Tunisia, Turkmenistan and Vietnam	Armenia, Belize, Egypt, El Salvador, Iraq, Kazakhstan, Kyrgyzstan, Maldives, Thailand, Turkmenistan and Vietnam
Q2	Afghanistan, Laos, Namibia, Nepal, Syria and Tanzania	Guatemala, Paraguay, Syria and Tajikistan
Q3	Bangladesh, Ghana, Timor-Leste, Zimbabwe	India, Laos, Nepal, Pakistan and Tanzania
Q4	Burundi	Bangladesh, Timor-Leste and Zimbabwe
Q5		Burundi
Q6	Guyana, India, Mali and Yemen	Algeria, Cuba, Ecuador, Guyana, Marshall, Mexico, Myanmar and Philippines
Q7	Congo, Mauritania, Solomon, South Africa and Vanuatu
Q8	Ethiopia and Haiti	Ghana, Namibia and South Africa
Q9	Malawi	Malawi
Q10	Colombia and Indonesia
Q11	Eswatini, Nigeria and Senegal
Q12	Burkina Faso	Congo and Nigeria
Q13		Haiti
Q14	Dominican Republic	Cambodia, Indonesia, Sao Tome and Principe and Tunisia
Q15	Kenya and Uganda	Afghanistan, Mali, Mauritania, Solomon and Yemen
Q16		Vanuatu
Q17		Dominican Republic and Mongolia
Q18	Côte d'Ivoire, Guinea, Sierra Leone and Zambia	Kenya
Q19		Burkina Faso and Ethiopia
Q20	Angola, Sao Tome and Principe and Sudan	Colombia
Q21	Somalia	Bolivia, Côte d'Ivoire, Eswatini, Guinea, Somalia and Uganda
Q22	Bolivia and Togo
Q23		Senegal, Sierra Leone, Sudan and Zambia
Q24	Benin, Chad, Gambia and Rwanda	Angola, Benin and Chad
Q25	Cameroon, DR Congo, Guinea-Bissau, Lesotho and Liberia	Cameroon, DR Congo, Gambia, Guinea-Bissau, Lesotho, Liberia, Rwanda and Togo

Appendix B.

As is known, the n parts of the composition can only be represented geometrically in the simplex when they are three and four parts. It is also possible to do a bivariate analysis, for this it is necessary to first merge the n parts of the composition into two as shown in Eq. (B.1). In statistical analysis of compositional data, this procedure is called amalgamation (Greenacre, 2020, Greenacre et al., 2021, Mateu-Figueras and Daunis-i-Estadella, 2008).

$$S^n=\left\{x=(x_1,x_2,\mathrm{...},x_n):\forall x_i>0,{\sum }_{i=1}^n{x}_i=100\right\}\to S^2=\left\{x=(x_1,x_2):\forall x_i>0,x_1+x_2=100\right\}$$ (B.1)

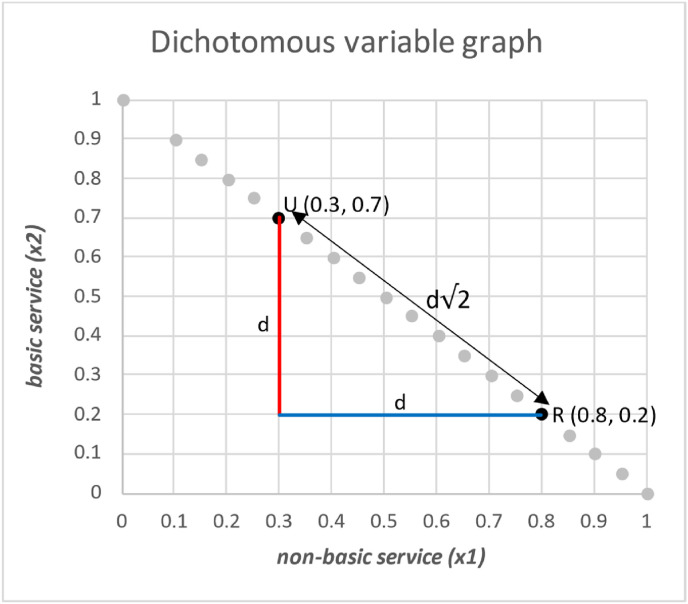
The geometric figure is a 45° isosceles right triangle. In this geometry, the percentages of the categories can be directly compared and this is a common practice in the WASH sector. To be more explicit, we illustrate the dichotomous variable in Figure B1. The graph has been constructed with a series of dichotomous points that have a constant sum with a value of one. The data points are on the hypotenuse of the triangle.

Fig. B.1.

d: distance measurement. U: urban. R: rural.

The inequality is calculated by the difference between the vector ${\overrightarrow{\text{U}}}_{(x1,x2)}$ and ${\overrightarrow{\text{R}}}_{(x1,x2)}$, the result of which is shown in Table B1. The result of the vector difference always gives the same value (i.e., │ ${\text{U}}_{\mathit{x}1}$ - ${\text{R}}_{\mathit{x}1}$ │= │ ${\text{U}}_{\mathit{x}2}$ - ${\text{R}}_{\mathit{x}2}$ │). As an example, we compare the two dichotomous points and the result in both is equal to 0.5 (see Table B1).

Table B.1.

Comparison of the urban-rural inequality measure for a dichotomous variable. │Δ│: Absolute value of the urban-rural difference

Urban (${\overrightarrow{\text{U}}}_{(x1,x2)}$)		Rural (${\overrightarrow{\text{R}}}_{(x1,x2)}$)		Δ (Urban - Rural)
Ux1	Ux2	Rx1	Rx2	│${\text{U}}_{\mathit{x}1}$ - ${\text{R}}_{\mathit{x}1}$│	│${\text{U}}_{\mathit{x}2}$ - ${\text{R}}_{\mathit{x}2}$│
0.3	0.7	0.8	0.2	0.5	0.5

Now, if we take into account the distance between the two points as a measure of inequality (i.e., d√2), we can observe that when normalizing the measure of inequality between the value of zero and one (i.e., divide d√2 by √2, a result is obtained d ∈ [0–1]), in magnitude, the result is equal to that obtained by the simple difference between the dichotomous variables of urban and rural.

In summary, for dichotomous variables, obtaining a single measure of inequality according to our approach is equal to the simple difference between the parts, as the JMP already does. The interpretation is also the same as that commonly done in the WASH sector. Therefore, in this paper we have focused on the ternary diagram because there was not yet an alternative way of measuring inequality in tripartite data that was consistent with the definitions of compositional data.