Implementation of the Theoretical Coulometric Titration Curve in the Determination of the Amount of Substance of Potassium Hydrogen Phthalate: the Search for a Better Metrological Approach

Abstract

In metrology, the certification of potassium hydrogen phthalate (KHP) as a reference material is made using the potential primary method of coulometric titration. Usually, this titration is performed in three steps at constant current, where two endpoint (EP) times are determined from the nonlinear regression that fits the empirical W-function (eWf) to the experimental data. As an alternative, we propose the implementation of the theoretical coulometric titration curve (TC). The TC allowed us to compute the KHP amount of substance, the influence of CO₂ in the system, the acid dissociation constants for carbonic and phthalic acids, assuming that those species are the only acids present during titration, and the EP times. The amount of substance of KHP estimated with the EP time and obtained from the TC was compared with the results of the eWf, and no statistical difference was found, while the amount of substance, when estimated directly as a parameter of the nonlinear regression of the TC, was lower. Therefore, the traditional method finds the total acidity of the dissolution, and our method finds the KHP purity. In addition, the acid dissociation constants for H₂CO₃ and phthalic acid estimated in this work agreed with the data reported in the literature. Finally, the description of the coulometric system using the theoretical TC has a solid and well-known chemical support that is not present in the eWf; this fact is essential for the uncertainty budget and the scientific support for coulometry as a potential primary method.

1. Introduction

Coulometry is one of the measurement techniques in chemical metrology to determine the amount of substance,¹⁻³ and it is defined as a potential primary method for quantification by the Consultative Committee for Amount of Substance (CCQM).^2,4,5 Furthermore, coulometry relates to three of the seven base units of the International System of Units (SI): the amount of substance (moles), time (s), and electrical current (A).⁵⁻⁷ According to the latter facts, coulometry is helpful in the certification of reference materials,^2,4,5,8−10 and it is widely used in the National Metrology Institutes (NMIs).

One of the most important reference materials in chemistry is potassium hydrogen phthalate (KHP) because it is a primary standard for the typical acid–base titrations.^11,12

The coulometric cell is represented as follows (generator electrodes)

1

In this electrolytic cell, hydronium ions are reduced (and also water if the potential difference applied is big enough) on the surface of the Pt electrode, increasing the HO^– ion concentration, and silver is oxidized to produce silver chloride (AgCl). Also, it can happen that the HO^– ions neutralize the H⁺ ions from the KHP in the bulk of the dissolution, Scheme 1.

Scheme 1. Neutralization Reaction between the Hydrogen Phthalate Ion and the Hydroxide Ion.

As with any titration, the endpoint (EP) calculation is a challenge in order to get the highest accuracy and reliability,¹³ particularly when it is required to certify reference materials. In coulometry, the estimation of the titration EP is made, usually by a nonlinear regression that fits the empirical W-function (eWf) eq 2

2

or a third-grade polynomial to the experimental data but only near to the EP.^7,11,14−16 The eWf (eq 2) was introduced for the first time in 1995 by the CCQM as an empirical function for determining the EP times in coulometry.⁴ In eq 2, y is the potentiometric response of the pH sensor, and a, b, c, and k are empirical adjustable parameters to fit the model to the experimental data. It is important to note that these last parameters do not have any relationship with the chemical process. Only q has a chemical meaning, being the EP time. Finally, in eq 2, “Error” is the error of the model. A graphical representation of this function is shown in Figure 1, together with a set of experimental data, which were measured only close to the EP in one of our typical coulometric titrations of KHP.

Figure 1.

Graphical representation of the eWf (eq 2).¹⁷ The open black circles are the experimental data of our experiment 1 of a total of 10 (see below), and the dashed red line is the nonlinear regression using eq 2 with a = 13.98, b = −0.15, c = −0.10, k = −0.06, and q = 179.11 as parameters.

On the other hand, one of the biggest challenges in metrology is uncertainty determination. The latter requires establishing a mathematical model that describes the entire physical or chemical process of the experiment according to the evaluation of measurement data—a guide to the expression of uncertainty in measurement (GUM).¹⁸ Then, in this research, we propose the implementation of the theoretical titration curve (TC) as an alternative model to estimate the amount of substance directly and to improve the performance of coulometry as a primary method of quantification, especially by the detailed understanding of the chemical processes involved.

2. Experimental Section

2.1. Instrumentation

A high-precision coulometer from APPLIED PRECISION, Stavitelska 1, 833104 Bratislava, Slovakia (AP), is used in this work, connected to a vertical cell type with main, auxiliary, and intermediate compartments. The generator electrodes are a Pt wire spiral (800 × 3 mm), >99.95% pure, around a pH sensor (Metrohm Unitrode), and a Ag wire spiral (100 × 0.5 cm), >99.9% pure, both from Tecnoincol, Cali, Colombia. An agar–agar gel with KCl 1 mol kg_dsln^–1 separates the cathode from the anode.

2.2. Reagents

The supporting electrolyte, KCl, was made by dissolving 37.22 g of KCl (Reag. USP for analysis, ACS, ISO Panreac) in 500 g of water type I. The agar–agar salt bridge was made by dissolving 1 g of agar (Merck) and 2.2 g of KCl in 40 mL of water type I. The latter mixture was heated to get a homogeneous gel; then, 2 cm of the height of the intermediate compartment was filled with this dissolution and cooled at room temperature for at least 2 h.

KHP was purchased from Merck EMSURE Reag. Ph Eur. It is ground and homogenized on an agate mortar; then, it is dried at 110 °C in a moisture analyzer (Mettler Toledo HC103). The KHP is cooled to room temperature (19 °C) in a desiccator.¹⁹

The KCl supporting electrolyte was acidified with HCl 0.01 mol kg_dsln^–1 dissolution made from a 0.1 M HCl (Titripur, Reag. Ph. Eur., Reag. USP Merck) dissolution. Ar (grade 5) gas was bubbled during the whole experiment, except in the main titration.

2.3. Coulometric Titration

A mass of 262.23 g (250 mL) of KCl 1 mol kg_dsln^–1 is added to the coulometric cell. The pH of this dissolution is between 5.2 and 6.2. Then, 20 drops of HCl 0.01 mol kg_dsln^–1 (around 0.4 g) are added to acidify the dissolution, and Ar (grade 5) is bubbled during the whole experiment into the coulometric cell to eliminate gases (mainly CO₂).

The coulometry starts with the initial titration (IT): pulses of 2.000000(1) mA are added for 2.04000000(5) s, and pH values are recorded after the current pulses. During the IT, the software detects the biggest change in pH with respect to the added charge, (dpH/dQ), and the IT finishes with five additional current pulses and pH measurements.

The main titration is performed after the IT: a sample of KHP close to 0.500000(8) g is measured in a Mettler Toledo XPE56 comparator and added to the main compartment of the coulometric cell where an electrical current of 200.0000(17) mA is applied to titrate 99.8% of the sample.

During the final titration (FT), the remaining analyte is titrated with pulses of 10.000000(85) mA for 4.92000000(5) s. In the same way as the IT, the FT finishes when five additional points are taken after detecting the biggest change in pH with respect to the added charge, see Figure 2.

Figure 2.

Scheme of the coulometric titration of KHP and the TC estimated for our experiment 1. The blue line corresponds to the TC at the IT, where CO₂ and HCl are titrated; the green line is the TC estimated for the titration of 99.98% of the analyte, and the red line is the TC at the FT where the remaining analyte is titrated. The black circles are the corresponding experimental data at the IT and FT.

2.4. Computation of the Endpoint Times

This work compared two ways to compute the EP times: the one that comes with the AP instrument, which uses the eWf, and the theoretical TC.

2.4.1. AP Instrument and the Empirical W-Function

The software of the AP instrument calculates the EP times for the IT and FT and the amount of KHP in mol kg^–1 based on the experimental data. The AP software uses the eWf, eq 2, for the nonlinear regression and the Levenberg–Marquardt algorithm to estimate the EP times.¹¹

2.4.2. Theoretical Titration Curve

The theoretical TC requires several functions for the IT and FT. In the IT, the acid–base equilibrium relies on the concentration of HCl and CO₂ (as total inorganic carbon: CO₂ = CO_2(aq) + HCO₃^– + CO₃), and we consider the following reactions²⁰⁻²²

3

4

5

6

This work uses equilibrium (eqs 4–6) for calculations, which are presented in detail in Section S1 of the Supporting Information. Subsequently, eq 7 obtained from mass and charge balances allowed us to determine the pH as a function of time.

7

In eq 7, [H₃O⁺] is the concentration in mol kg_dsln^–1 of the hydronium ions; [HCl]₀ is the initial concentration in mol kg_dsln^–1 of hydrochloric acid; and [CO₂]₀ is the concentration in mol kg_dsln^–1 of the carbonic species present in the dissolution.

K_ap:CO2 is the apparent dissociation constant of carbonic acid; K_a2:CO2 is the second dissociation constant of carbonic acid; K_w is the water ionization constant;²³i is the electrical current in amperes; t is the time in seconds; n is the number of moles of electrons exchanged; F is the Faraday’s constant; and kg_dsln is the mass in kilograms of the dissolution.

In the case of the FT, KHP is added to the dissolution, and then two new equilibria are considered

8

9

Likewise, as shown in eq 7, we obtained the mass balance, the charge balance, and the following function for the FT, eq 10.

10

where K_a1:H2P is the first dissociation constant of phthalic acid (H₂P); K_a2:H2P is the second dissociation constant of phthalic acid; and [KHP]₀ is the total concentration of the phthalic species added to the coulometric cell. Notice that [KHP]₀ is the value we are looking for.

Functions (eqs 7 and 10) were used for nonlinear regressions and implemented in R (version 4.1.2) software,²⁴ for Windows. The R function nlsLM based on the Levenberg–Marquardt algorithm^17,25,26 was chosen for nonlinear regressions. The mathematical development to obtain functions (eqs 7 and 10) is found in Sections S1 and S2 of the Supporting Information, and the respective R scripts are available at http://ciencias.bogota.unal.edu.co/index.php?id=3053.

2.5. Amount of Substance

Once the EP times were estimated using either eWf or TC, the amount of substance of KHP in mol kg^–1 was calculated using eq 11.^7,11,27

11

where i₁ is the electrical current flowing during the IT, t_totalini is the total time of the current flowing during the IT, t₁ is the EP time at the IT, t_cor is the correction in time given by the instrument, i_main is the electrical current flowing during the main titration, t_main is the total time of the current flowing during the main titration, i₂ is the electrical current flowing during the FT, t₂ is the EP time at the FT, n is the number of moles of electrons that are transferred in the reaction, F is the Faraday constant, m is the mass in grams of KHP added to the system, and h_cor is the correction factor for air buoyancy. In eq 11, the current is in amperes (A), and time is in seconds (s).

A total of 10 experiments were performed, and the results obtained were evaluated with a normality test (Shapiro–Wilk²⁸) and a homogeneity of the variance test (Levene’s test²⁹). The results of the previous two statistical tests allowed us to apply the t-Student test at a level of significance of α = 0.05^30,31 to compare the amount of substance resulted from the eWf with that from the TC.

3. Results and Discussion

The implementation of the TC allows the computation of the amount of substance of KHP with or without the explicit estimation of the EP times. The TC also gives us the concentrations of CO₂, HCl, and the acid dissociation constants of CO₂ and H₂P under our experimental conditions, something which is not possible using the eWf. We compare the eWf and TC results in the following sections and discuss the TC advantages.

3.1. Statistical Significance of the Estimated Parameters in Nonlinear Regression

Table 1 shows the parameters obtained using the eWf, along with their standard errors, t-values, and p-values. Here, the standard error will be considered as the uncertainty of the estimated parameter;^26,32 the t-value is the t-Student statistic value calculated at 95% confidence, establishing the null hypothesis as β = 0, where β is the estimated parameter and the p-value is the probability of β = 0. Observe that if the standard error is greater than the parameter itself, the t-value is smaller than 1 and the p-value is larger than 0.05.³³ Therefore, the parameter will not be significant in nonlinear regression, and it is unnecessary to include it to fit the experimental data well.²⁶

Table 1. Estimated Parameters a, b, c, k, and q from the Nonlinear Regression of the eWf to the Experimental Data for Our Experiment 1 of a Total of 10^a.

parameter	estimate	standard error	t-value	p-value
initial titration
a	14.0	86.32	0.16	0.88
b	–0.15	0.82	–0.18	0.86
c	–0.10	43.17	0.00	1.00
k	–0.06	0.13	–0.46	0.66
q	179.11	0.25	713.88	<2 × 10–16
final titration
a	6.14 × 10–1	0.39 × 10–1	15.63	1.95 × 10–5
b	1.24 × 10–2	0.06 × 10–2	21.25	4.27 × 10–6
c	7.95	0.02	408.05	1.68 × 10–12
k	–1.18 × 10–1	0.04 × 10–1	–26.89	1.33 × 10–6
q	1440.00	0.09	15907.20	<2 × 10–16

^aThe significance level used was α = 0.05. Notice that the no-significance parameters are in bold.

According to the results in Table 1, the values of the parameters found by the nonlinear regression with the eWf can be statistically not significant as in the IT case or significant as in the FT case. The only exception is the q parameter, which was significant in all experiments. Observe that the parameters and their statistical significance do not have a chemical meaning because they are not directly related to the studied chemical phenomenon.

On the contrary, when the IT is studied using the TC, all parameters have a chemical meaning and are statistically significant, as is seen in Table 2. Notably, during the IT, the TC allows us to study the acid dissociation constants of CO₂, also presented in Table 2.

Table 2. Computed Parameters by the Nonlinear Regression of the TC for the Initial Titration in Experiment 1 of a Total of 10^a.

parameter	estimate	standard error	t-value	p-value
[CO2]0/mol kgdsln–1	2.07 × 10–6	0.35 × 10–6	5.84	1.64 × 10–4
[HCl]0/mol kgdsln–1	1.18 × 10–5	0.03 × 10–5	36.50	5.68 × 10–12
Kap:CO2	1.87 × 10–6	0.35 × 10–6	5.39	3.08 × 10–4
Ka2:CO2	2.10 × 10–8	0.69 × 10–8	3.05	0.01

^aThe significance level used was α = 0.05.

In the case of the FT, as a first attempt, we made the nonlinear regression, estimating both dissociation constants for CO₂ and H₂P according to eq 12.

12

Table 3 shows that the parameters 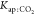for CO₂ and 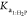for H₂P are not statistically significant because their p-values are 0.59 and 0.96, respectively. Also, their standard errors are closer to or higher than the parameters themselves. The latter is explained by the low influence of the species CO_2(aq), HCO₃^–, H₂P, and HP^– in the acid–base equilibrium established in the FT and close to the EP, which is in the pH range of 7.8 to 8.8. In this pH range, CO_2(aq), HCO₃, H₂P, and HP^– have insignificant concentrations as it is demonstrated with the Bjerrum diagrams in Figure 3a,b. Figure 3 also shows that close to the EP of the FT, the prevalent species are CO₃^2– for carbonic acid equilibrium and phthalate ion (P^2–) for the H₂P equilibrium.

Table 3. Chemical Parameters Estimated from the Data of the Final Titration in Experiment 1 (from a Total of 10) by the Nonlinear Regression of the TC^a.

parameter	estimate	standard error	t-value	p-value
CO2 parameters
[CO2]0/mol kgdsln–1	1.50 × 10–5	0.29 × 10–5	5.11	6.95 × 10–3
Kap:CO2	3.93 × 10–4	0.68 × 10–4	0.579	0.59
Ka2:CO2	4.78 × 10–10	1.47 × 10–10	3.24	0.03
KHP parameters
[KHP]0/mol kgdsln–1	9.2500 × 10–3	0.0004 × 10–3	24731	<2 × 10–16
Ka1:H2P	58.7	995.2	0.059	0.96
Ka2:H2P	1.37 × 10–5	0.13 × 10–5	10.17	1.91 × 10–5

^aThe significance level was α = 0.05. Notice that the no-significance parameters are in bold.

Figure 3.

Species distribution diagrams (Bjerrum diagrams) for CO₂ and H₂P as a function of time during the experimental titration of KHP (FT). Data from experiment 1 of a total of 10 replicas. The orange data are the experimental pH values and the EP time estimated by the nonlinear regression.

Having noticed this little influence of 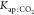and 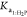on the pH values in the TC of the FT of KHP, only the second acid dissociation constants, 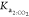from CO₂ and 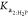from H₂P, were considered as parameters to estimate in the nonlinear regression, as shown in eq 13; then, the values for 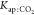and 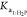used were those found in the literature.^20,34

13

The results from the nonlinear regression using eq 13 for the FT of KHP are in Table 4, where all the chemical parameters are statistically significant. Then, the importance of removing the non-significant parameters from the function to obtain a good performance in the data fitting is clear; otherwise, unreasonable values of the acid dissociation constants could be obtained.

Table 4. Chemical Parameters Estimated in Experiment 1 (from a Total of 10) by Nonlinear Regression Using TC According to eq 13 at the Final Titration^a.

parameter	estimate	standard error	t-value	p-value
CO2 parameters
[CO2]0/mol kgdsln–1	1.94 × 10–5	0.21 × 10–5	9.30	8.68 × 10–5
Ka2:CO2	3.30 × 10–10	0.48 × 10–10	6.83	4.85 × 10–4
KHP parameters
[KHP]0/mol kgdsln–1	9.227 × 10–3	0.002 × 10–3	4552	2.00 × 10–16
Ka2:H2P	1.96 × 10–5	0.01 × 10–5	194	1.28 × 10–12

^aThe significance level used was α = 0.05.

Therefore, the results presented in the following sections use eq 13.

It is important to observe in Tables 2 and 4 that [CO₂]₀ as total inorganic carbon in mol kg_dsln^–1 is 2.07 × 10^–6 for the IT, while for the FT, it is 1.94 × 10^–5. Comparing these concentrations with the solubility of CO₂ under salinity conditions similar to ours (3.154 × 10^–2 mol kg_dsln at 20 °C and a salinity of 40 g Cl^– kg_dsln^–1 reported by Weiss(1974)³⁵), it has been found that they are 4 (for IT) and 3 (for FT) orders of magnitude lower. Thus, it can be said that the concentrations of CO₂ estimated are reasonable values, but they change during the experiment.

It is necessary to take into account that the total elimination of CO_2(g) from the atmosphere and then from the dissolution in the coulometric cell is not possible in practice because the system is not hermetic. Then, the fact that there is a higher concentration of the carbonic species in the FT, with respect to the IT, can be associated with two factors: (i) the elimination of a considerable part of CO_2(aq) due to the reaction with HCl at the beginning of the experiment and (ii) the solubilization in the coulometric test dissolution of the environmental CO_2(g) during the long time that the main titration requires (the main plus the FT takes about 2 hours, while the first titration takes just 40 min). Besides, during the main titration, the Ar bubbler is removed from the dissolution to avoid sample dispersion over the wall cell. The latter fact increases the CO₂ concentration at the FT compared to the IT.

Notice from the previous discussion that the results obtained from the TC allow us to understand the chemical processes of the KHP coulometric titration. The latter is crucial at the metrological level and is impossible to determine using the eWf results.

3.2. Acid Dissociation Constants Estimated with the Theoretical Titration Curve

The use of the TC allows us to compute the acid dissociation constants of CO₂ and H₂P, as was presented in the previous section. The reliability of those parameters and their agreement with literature values are shown in Table 5.

Table 5. Mean of the pK_a Values (10 Experiments) Estimated by the Nonlinear Regression Using the TC in the Coulometric Titration of KHP^a.

	estimatedb	literature valuec	difference in %
pKap:CO2	5.701(0.096)	5.86820	–2.9
pKa2:H2P	4.701(0.007)	4.711(0.017)36	–0.2
pKa2:CO2 at IT	7.582(0.089)	8.89320	–14.7
pKa2:CO2 at FT	9.292(0.078)	8.89320	4.5

^aIT: initial titration. FT: final titration. Reference values found in literature for pK_a of CO₂ and H₂P are also shown.

^bStandard deviation (SD) is given in parentheses.

^cThe literature reference.

The literature values for the acid dissociation constants of CO₂, pK_ap:CO2 and pK_a2:CO2, were computed making use of the polynomials in eqs 14 and 15 proposed by Millero et al. 2002,²⁰ and considering our working conditions, salinity S = 66 g Cl^–/kg_dlsn and T = 20.36 °C.

14

15

The reference value for K_a2:H2P of H₂P was taken at 293.15 K and KCl was 1.0612 mol kg^–1 (Ferra et al. 2009³⁶), which are the closest experimental conditions to our laboratory, 291.15 to 294.15 K and KCl 0.929 mol kg_dsln^–1.

Then, the results in Table 5 confirm that the implementation of TC is reliable because the values estimated by acid dissociation constants are close enough to those reported in similar conditions. Nonetheless, it is important to notice the discrepancy found for the 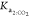of CO₂ at IT and FT, a fact that continues under study, but it is probably related to the statistical significance of this parameter during the IT and the possible resolubilization of the atmospheric CO₂ in the dissolution during the main and FT.

3.3. Computed Endpoint Times

The EP times computed by the nonlinear regression using the eWf and the TC are shown in Table 6. The EP time in the eWf corresponds to the estimation of the q parameter of eq 2. On the contrary, the EP time with TC is estimated considering eq 16.

16

Table 6. Computed EP Times (t₁ and t₂) from the Nonlinear Regressions Using the eWf and the TC^a.

endpoint time / s
experiment	empirical W-function,teWf	theoretical curve, tTC(t)	Applied Precision, AP	% difference
initial titration
1	179.11	177.71	178.78	–0.78
2	228.47	226.64	230.1	–0.80
3	167.52	165.93	166.99	–0.95
4	160.42	158.01	159.91	–1.50
5	218.86	217.57	218.31	–0.59
6	169.82	166.51	170.04	–1.94
7	252.77	250.09	252.35	–1.06
8	231.09	229.44	230.46	–0.71
9	79.87	77.71	79.24	–2.70
10	101.54	100.14	101.32	–1.37
final titration
1	62.17	61.64	61.89	–0.88
2	62.44	61.28	62.31	–1.86
3	58.51	58.38	58.43	–1.92
4	59.21	58.02	59.18	–2.02
5	59.41	58.43	59.35	–1.65
6	62.74	61.58	62.68	–1.85
7	62.33	61.10	62.26	–1.98
8	61.59	60.57	61.50	–1.66
9	59.83	58.71	59.72	–1.88
10	59.56	58.51	59.44	–1.77

^aThe EP times given by the software of the Applied Precision instrument (AP) are also given as a reference value. The percentage of difference (% difference) is calculated with respect to the value obtained with the eWf as 100*(t_TC(t) – t_eWf)/t_eWf.

In eq 16, 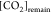is the remaining species of CO₂ in mol kg_dsln^–1 titrated in the FT, at FT – 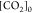at IT, 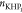i the number of moles of KHP titrated with the excess of HO^– produced in the IT, and 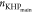is the number of moles of KHP titrated in the main titration. Equation 16 comes from the data structure of the AP instrument and how the TC was implemented.

The percentages of difference between the EP times with TC and the eWf are lower than −2.70% for the IT (mean = −1.24 s, SD = 0.66 s, and % CV = −53.3), while for the FT, these are lower than −2.02% (mean = −1.75 s, SD = 0.33 s, and % CV = 18.9).

Figure 4 shows the EP times computed for experiment 1 of a total of 10, including the first numerical derivative of the experimental data (green dots) used as a reference value for the location of the EP time. Observe, in Figure 4, that the three ways to compute the EP time give consistent values and are close between them. The discrepancies found are related to the magnitude of uncertainty in determining the EP times.

Figure 4.

Calculation of the EP times for the IT (a) and the FT (b). Experimental data (black asterisk) for experiment 1 of 10. Nonlinear regression fitting with eWf (continuous red line) and with TC (dashed blue line). These lines overlap with the experimental data. The numerical first derivative of the experimental data (green dots) is presented as a reference guide. Vertical lines correspond to EP times, and horizontal lines correspond to the pH at those EPs.

3.4. Amount of Substance

In order to compare the results from eWf and TC, the amount of substance, in mol kg^–1, was calculated using eq 11 and the respective estimated EP times. The eWf results were obtained in two ways. The first one is the result given by the software of the AP. The second is our script in R, which uses the pH versus time data given using the AP instrument. We implemented the R script to verify the correctness of our computations and as a way to understand what the AP instrument does. The two ways of computation give us non-different statistical results according to the t-Student test. The discrepancies are attributed to the round and truncation errors that are unavoidable in computers. Then, in the following discussion, we only use the results from our R script labeled as eWf. Figure 5 shows the results for the 10 replicates.

Figure 5.

Box plot of the amount of substance in mol kg^–1 of KHP for 10 experiments. The amount of substance in the first three boxplots from left to right was calculated using eq 11 after estimating the EP times. Results are ordered from left to right as nonlinear regression using the eWf with our R script (eWf), Applied Precision (AP) software, and the theoretical TC TC(t). Also, the results of the KHP amount of substance obtained directly from the parameter estimated with TC, TC(NLR), are shown in the last boxplot on the right.

Observe that the amount of substance estimated with the eWf or TC EP computation, TC(t), is similar. The TC(t) is only −0.003% lower than the eWf, as is expected from the negative differences found for EP times; see Figure 4. However, that difference is not statistically significant according to the t-Student test. The fact that both the amount of substances from eWf and TC(t) are the same statistically verifies the reliability of our implementation of the theoretical TC.

At this point, it is essential to remember that the amount of substance calculated using t₁ and t₂ and the eWf does not distinguish the acidic species in the dissolution. However, when t₂ is estimated using the TC in the FT, see eq 16, both KHP and CO₂ (as total inorganic carbon) concentrations must be considered explicitly in the titration. Otherwise, the estimated EP time does not fit with the inflection point of the experimental data, see Figure 6.

Figure 6.

Nonlinear regression fitting with TC to experiment 1 of a set of 10. The vertical red line is the EP time, determined when both concentrations are used: [KHP]₀ and 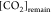, and the blue vertical line is the EP time, determined when only [KHP]₀ is used.

This is a significant result because it indicates that both species, KHP and CO₂, are present and must be considered for determination of the EP time in the FT.

Observe that the amount of substance of KHP given directly as a parameter from the nonlinear regression of the TC, TC(NLR), gives us lower and more dispersed values than those from EP times, see Figure 5. The amount of substance of KHP from the TC(NLR) is significantly lower than the results obtained with the eWf because the first does not include the [CO₂]₀ dissolved in the dissolution. According to the latter, the amount of substance could be reported in two ways: (i) as total acidity when the EP times are calculated with eq 11 with eWf or TC(t), which considers both species CO₂ and KHP or (ii) only as the amount of KHP found as a parameter from the TC(NLR), which clearly will be lower.

Observe also that the TC, as shown above, involves more variables than eWf, each one full of chemical meaning but also adding additional uncertainty to the computation. In addition, the TC computation estimates values for the 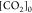, which are low values that unavoidably produce a higher dispersion. As a consequence, the standard deviation of the TC(NLR) results has a higher value than the eWf, as confirmed by the experimental results in Figure 5. Then, it is clear that a simple and empirical function, such as the eWf, underestimates the SD, and the TC(NLR) results are more realistic and significant than those from the eWf.

3.5. Advantages of the Theoretical Titration Curve

The calculation of the EP time in coulometric titrations at the metrological level has not changed in a long time,^4,17 and the eWf is assumed as the best way to obtain the EP time of those titrations. However, taking into account the GUM guide for estimation of uncertainty, sections 3.1.6, 3.4.2, and 4.1.2, the mathematical model proposed for any calculation must describe in detail the phenomenon of the experiment in order to have a good knowledge of the uncertainty sources during the measurement.¹⁸ The TC is a mathematical model that describes in detail the chemistry behind the coulometric titration of KHP. The latter is a significant advantage over the eWf, which has no chemical meaning. For example, some error sources come from insufficient knowledge of minimal changes in experimental conditions (the temperature, the atmospheric pressure, the relative humidity, or the ionic force).^10,37 These errors are corrected, in part, by the estimation of the dissociation constants of carbonic and phthalic acids.¹⁸ On the other hand, our results show that those acid dissociation constants are in good agreement with those estimated in the literature,^20,36 which means that our TC works fine.

Furthermore, the parameters obtained from nonlinear regression using the TC give us additional information on the influence of CO₂ on the entire course of the titration and on the EP time. Remarkably, the TC can estimate the amount of substance of KHP directly as a parameter, while the eWf calculates the total acidity of the test solution. It means that TC can discriminate KHP from CO₂ in the coulometry titration, something impossible using the eWf.

Besides, the eWf fits well to the experimental data but only near the EP; in the case of the TC, the data can be fitted at any stage of the titration as the theoretical TC was constructed considering all the species in the dissolution, and it can predict the pH values at any stage of the titration.

All the previously mentioned arguments make the TC a better model than the eWf in determining the amount of substance of KHP.

4. Conclusions

The theoretical TC was implemented as an alternative model for determining the amount of substance of KHP in coulometric titration. It was demonstrated that the implementation of TC gives additional information not provided by the eWf, such as the effect of carbon dioxide as an impurity on the whole titration and the value of the acid dissociation constants of CO₂ and phthalic acid.

The successful implementation of the TC was verified by comparing its results with those from the well-established and commonly used eWf. The difference in the amount of substance between the two mentioned methods is only −0.003%, and according to the statistical t-test, they are equivalent. In this latter case, the TC was used to estimate the EPs of the titrations as the eWf made it. However, the TC can also give us the amount of substance of KHP directly without the estimation of the EPs and without the residual CO₂, which is always present in the non-hermetic coulometric cell. Moreover, the TC gives us the acid dissociation constants of the carbonic and phthalic acids, which are in good agreement with the equivalent values reported in the literature. This valuable information is not available from the eWf and allows us to include, implicitly, the effects of temperature and salinity (ionic strength) in the computation of the SDs of our results.

The implementation of the theoretical TC model based on the chemistry of the acid–base equilibrium enhances the performance of the coulometric titration as a primary method in the metrological determination of the amount of substance of KHP.

Glossary

Abbreviations

KHP

potassium hydrogen phthalate

H₂P

phthalic acid

HP^–

hydrogen phthalate ion

P^2–

phthalate ion

CO₂ = CO_2(aq) + HCO₃^– + CO₃

mass balance for total inorganic carbon

[CO₂]₀

total inorganic carbon in concentration, mol kg_dsln^–1

CRM

certified reference material

TC

potassium hydrogen phthalate acid–base theoretical titration curve

eWf

empirical W-function

AP

high-precision coulometry equipment from Applied Precision company

INM

Instituto Nacional de Metrología de Colombia

NMI

National Metrology Institute

mol kg_dsln^–1

mol per kilogram of dissolution

SD

standard deviation

% CV

coefficient of variation percentage

EP

endpoint

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.2c05642.

• Mathematical development of the theoretical titration curve and complete results from the nonlinear regression analysis (PDF)

The authors declare no competing financial interest.