Abstract
Magnetic iron oxide nanoparticles have multiple biomedical applications in AC-field hyperthermia and magnetic resonance imaging (MRI) contrast enhancement. Here, two cubic particle suspensions are analyzed in detail, one suspension displayed strong magnetic heating and MRI contrast efficacies, while the other responded weakly. This is despite them having almost identical size, morphology, and colloidal dispersion. Aberration-corrected scanning transmission electron microscopy, electron energy loss spectroscopy, and high-resolution transmission electron microscopy analysis confirmed that the spinel phase Fe3O4 was present in both samples and identified prominent crystal lattice defects for the weakly responding one. These are interpreted as frustrating the orientation of the moment within the cubic crystals. The relationship between crystal integrity and the moment magnitude and dynamics is elucidated for the case of fully dispersed single nanocubes, and its connection with the emergent hyperthermia and MRI contrast responses is established.
Introduction
Magnetic iron oxide nanoparticles (MNPs) are under intensive scrutiny for biomedical applications due to their responses to: (i) static homogeneous DC-magnetic fields in which the strong moments can provide contrast enhancement for magnetic resonance imaging (MRI);1 (ii) DC-magnetic field gradients which provide magnetophoretic particle motion;2,3 and (iii) AC-fields in the kilohertz range which generate localized heating applicable for cancer ablation4 or thermally triggered drug release.5 Next-generation magnetic nanomaterials are expected to involve combinations of these functions.6,7
However, while the understanding of how the internal particle structure determines the strength and dynamics of the moments is quite advanced,8 the impact of structure on both the AC-field heating and MRI contrast efficacies, i.e., the specific absorption rate (SAR) and the relaxivities (r1 and r2), is missing, and this limits development of the dual magnetic function. Significant practical challenges also remain to reproducibly process MNPs into stable suspensions at the application scale with appropriate crystallinity, size, and colloidal dispersion to provide strong moments with appropriate internal dynamics to control the responses.9 It is also well known that repeated syntheses using the favored thermal decomposition approaches can produce samples with rather different magnetic properties, reflecting high sensitivity of the final nanocrystals to minor differences/fluctuations in particle nucleation and growth during the process.
Suspensions of spherical MNPs usually show a SAR of ≤100 W g–1 under typical field conditions. The field strength and frequency dependence of the SAR can be significant and should be borne in mind when making performance comparisons;10 however, most measurements are in the range νAC 200–700 kHz and IAc 5–20 kA m–1.11,12 High SAR values have been reported, usually due to more open room temperature AC-field hysteresis loops under the field conditions used, arising from increased magnetocrystalline anisotropy energy, ΔEanis. This can be generated through Co- or Mn-doping of the oxide;13 through formation of ordered (low particle number) chains,14 which can also be extracted from magnetosomes;15 or through particle shape anisotropy. All three approaches are synthetically challenging and difficult to upscale, with shape control perhaps the most amenable to optimization.
In this regard cubic MNPs have shown significant promise. Guardia et al. described SAR dependence on size, demonstrating a higher SAR of ca. 2300 W g–1 (at 700 kHz and 24 kA m–1) for 19 nm than for 12, 25, or 38 nm cubes.16 Nogues and co-workers showed an ∼74% increase in the SAR to ca. 192 W g–1 and ca. 40% enhancement in the spin–spin relaxivity, r2, on increasing size from 13 to 19 nm.12 Nemati et al. reported a threefold higher SAR under similar field conditions for cubic as compared to spherical MNPs of the same volume,17 and similarly, Martinez-Boubeta et al. showed that 20 nm nanocubes exhibited 20% higher SAR compared to the spherical counterparts of the same diameter.14 Significant issues emerge including: (i) the complexity of size control in these systems. Much of this literature details efforts to control average size, polydispersity, shape, crystallinity, and magnetic properties; (ii) again, few details are provided on batch-to-batch variability; and (iii) the dual, hyperthermic, and MRI functionalities have not been rationalized in the context of nanocrystal microstructural analysis.
Pellegrino and co-workers correlated low SAR (in toluene and water) for spherical MNPs in the size (dTEM) range from 10 to 18 nm with crystal structure and lattice distortions.11 High-resolution transmission electron microscopy (HR-TEM) coupled with peak pair analysis was employed for poorly responsive spherical 18 nm MNPs only, from which it was suggested that lower heating efficacies are associated with strained regions (magnetically frustrated layers) within the lattice that adversely affect dynamic alignment of the moments.
Here, a systematic study was performed on two heptane suspensions of cubic MNPs prepared in apparently identical fashion which showed very similar particle size, morphology, and critically, full particle dispersion. The final suspensions, unsurprisingly for thermal decomposition synthesis, differed strikingly in their SAR and spin–lattice relaxivity, r1. This difference enabled the first comparative assessment of the role of crystal structure integrity on the magnetic properties. Aberration-corrected scanning transmission electron microscopy (STEM) and electron energy loss spectroscopy (EELS) elemental analysis of cubic MNPs demonstrated indistinguishable chemical composition and phase. Microstructural analysis revealed crystal defects for the weakly responsive materials which are interpreted as frustrating moment reorientation.
There have been reports on the relaxivity of MNPs of different shapes, including spheres,18 cubes,12 and nanoflowers,19 and structure–relaxivity relationships in MNPs for MR imaging have been recently reviewed.20 For particles in the size range of this study, large moments generate high r2, and so dephasing (local image suppression due to rapid 1H spin–spin relaxation) overwhelms any T1-weighting effects (local image enhancement due to rapid 1H spin–lattice relaxation). The more complex field shape generated by the cubic particles has been reported to exacerbate this effect.20 For these reasons, r1 and r2 values in the clinical MRI frequency range are usually reported. In contrast, in this study, we exploit measurement of the 1H Larmor frequency dependence of r1. The low-frequency relaxivity in particular reveals changes in the moment dynamics, arising from the presence of defects, which largely determine the SAR achieved. To the best of our knowledge, this is the first report establishing how crystallinity influences the moment magnitude and dynamics which determine the hyperthermic and contrast efficacies for fully dispersed single crystals.
Experimental Section
Synthesis
Iron oleate (FeOl) is one of the key precursors to synthesize iron oxide MNPs having a cubic morphology. MNP formation using FeOl involves two main stages; precursor synthesis and then MNP synthesis. To synthesize the precursor, Fe(III) chloride hexahydrate (10.8 g, 40 mmol) and sodium oleate (36.5 g, 120 mmol) were added into a mixture of 80 mL of ethanol, 60 mL of deionized water, and 140 mL of heptane in a 500 mL three-necked round-bottomed flask and stirred vigorously overnight (minimum 12 h). The next day, the reaction mixture was refluxed (at ca. 70 °C) for 7 h under nitrogen flow. Once the reaction mixture cooled down, it was transferred to a separating funnel. The mixture separates into two distinct phases, the lower (aqueous phase) was removed and disposed of. The upper organic phase that contains FeOl was washed with hot deionized water (∼80 °C) and the bottom aqueous phase was discarded repeatedly. The main purpose of this washing was to get rid of salts and aqueous-based impurities from the organic phase. This washing step was repeated 60 times. MNPs synthesized with unwashed FeOl showed two distinct morphologies: cubes and relatively smaller (∼12.3 nm) nanospheres. The fraction of cubes increased with the number of washes, but a noncubic fraction remained at 10 times washed. With 30 and 60 times washed precursors nearly perfectly cubic-shaped MNPs were formed. Afterward, the organic phase was dried over magnesium sulfate and then concentrated by a rotary evaporator. Thereafter, a viscous brown liquid was obtained which was stored under ambient conditions under nitrogen.
The cubic MNP synthesis is based on the protocol given by Shavel et al.;21 1.5 g of iron oleate, 250 mg of sodium oleate, 543 μL of oleic acid, and 20 mL of squalene (CAS: 111-02-4, C30H50) were added to a 100 mL round-bottom flask. First, the reaction mixture was degassed for 2 h at 120 °C with vigorous nitrogen flow. This step eliminates traces of moisture and dissolved oxygen in the reaction mixture. Then, the mixture was kept at reflux for 2 h. After this period, and once the reaction mixture had cooled to room temperature, the MNPs were precipitated by ethanol and any of the original solvent and other impurities were removed by centrifugation (SIGMA Laborzentrifugen GmbH) operated at 8000 rpm for 10 min. This process was repeated three times by sequential dispersal in heptane/ethanol precipitation added in proportion of 1:4 by volume, after which the MNPs were stabilized in heptane.
AC-Field Hyperthermia
The efficacy of MNPs is quantified using the SAR, which has units of W g–1 and which quantifies the ability of the material to convert magnetic energy provided by an AC-field into heat energy.17 In this study, a calorimetric approach was used in which an AC-field was applied and the suspension temperature was continuously monitored. A NanoTherics NAN201003 magneTherm AC-field generator (NanoTherics Ltd.; Newcastle-under-Lyme, United Kingdom) was used throughout. Typically, 1.0 mL of MNP suspension (∼20 mm height), having Fe concentration ranging between 30 and 120 mM, was transferred to a “cylindrical” eppendorf tube and placed in a thermally insulating polystyrene sample holder to provide close-to-adiabatic conditions. The sample temperature was measured by using a nonmetallic temperature sensor (Opsens Ltd., Canada). The probe was typically placed at a 15 mm depth from the suspension surface. The temperature of the sample was equilibrated in the instrument before the AC-field was applied. All measurements were undertaken at νAC 535 kHz and IAc 16.0 kA m–1. The temperature increase over time on application of the field was recorded and the SAR value was calculated using eq 1:
| 1 |
where C is the volumetric specific heat capacity of the solvent (J mL–1 °C–1), Vs is the sample volume (mL), mFe is the mass of Fe in the suspension (g), and 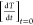 is the initial slope of the curve (°C
s–1) extracted here as the coefficient of the linear
term in a fourth-order polynomial fit. The error associated with the
individual SAR measurements was ∼5% for high heating MNPs.
The iron content was measured following digestion22 using flame atomic absorption spectroscopy.
is the initial slope of the curve (°C
s–1) extracted here as the coefficient of the linear
term in a fourth-order polynomial fit. The error associated with the
individual SAR measurements was ∼5% for high heating MNPs.
The iron content was measured following digestion22 using flame atomic absorption spectroscopy.
Atomic Absorption Spectrometry
For AAS analysis a Varian SpectrAA 55B atomic absorption spectrometer equipped with a single slit burner was used. A Fe cathode lamp operating at a wavelength of 248.3 nm was used as the light source and the flame was maintained with a mixture of air and acetylene. For a typical measurement, standards of Fe concentration between 0.1 and 7.0 ppm were prepared by diluting a Fe standard solution of known concentration 1000 ppm from Sigma-Aldrich (CAS: 10421484) in 1 M HNO3. The absorbances were measured for these standards to obtain a calibration curve. Aliquots of known volume were taken from the MNP suspensions diluted appropriately to ensure that the Fe concentration would fall within the calibrated range. These aliquots were digested in HCl (12 M, 1.5 mL) for 2 h prior dilution with 1 M HNO3 in a volumetric flask.
Dynamic Light Scattering
Colloidal properties were measured by dynamic light scattering (DLS) using a Malvern NanoZS (Malvern Instruments, Malvern, UK) instrument. This instrument uses a 3 mW He–Ne laser working at a wavelength of 633 nm with the scattered light detected at 173°. For a typical DLS measurement, around 1 mL of suspension of 0.5–5 mM Fe concentration was used. Measurements were carried out at 25 °C. The Z-average size and polydispersity index (PDI) were obtained from cumulant analysis through the analysis of the correlation functions using Dispersion Technology software (v. 4.10, Malvern Instruments; Worcestershire, UK). All distributions were unimodal, the PDI values were low, and there were no longer time features in the correlation functions; hence, the Z-average size is used throughout as a measure of the average hydrodynamic size, dhyd.
Fast-Field-Cycling Nuclear Magnetic Resonance (FFC-NMR)
The spin–lattice relaxivity (r1, expressed in mM–1 s–1) is defined as the 1H spin–lattice relaxation rate enhancement per millimolar of Fe in the suspensions and is calculated by using following equation:
| 2 |
where R1, sus and R1, sol are the spin–lattice relaxation rates (units, s–1) of the MNP suspension and pure solvent, respectively, and CFe is the mM Fe concentration of the suspension. Hence, the numerator in eq 2 is the relaxation enhancement. The dependence of r1 on the applied field (and hence frequency, νL = γB0/2π, where γ is the gyromagnetic ratio for 1H or 2.6575 × 108 rad T–1 s–1) for the MNP suspensions was measured by fast-field-cycling NMR relaxometry (FFC-NMR) using a Stelar Spinmaster FFC2000. This instrument employs a fast-cycling electromagnet to vary the applied field across a range corresponding to the 1H Larmor frequencies from 0.01 to 40 MHz. The system operated at a measurement frequency of 16.3 MHz for 1H, with a 90° pulse of 7 μs using standard pulse sequences.23 The temperature of the suspensions was maintained at 25 °C using a thermostat airflow system.
Low-Magnification Transmission Electron Microscopy
MNPs were characterized at low magnification using a FEI Tecnai G2 20 TWIN 200 kV TEM microscope. Typical sample preparation for imaging involved spotting ∼3 μL of an MNP suspension of Fe concentration 2–5 mM onto a formvar-coated copper grid and allowing natural drying. The images were analyzed using ImageJ software to measure n ≥ 100 particle sizes, which were averaged to calculate, dTEM.
High-Resolution Transmission Electron Microscopy
An aberration-corrected JEOL ARM200CF electron microscope in the TEM mode operating at 200 kV was utilized to acquire atomic resolution (HR-TEM) micrographs of cubic iron oxide MNPs. A beam current condition of 15 μA was maintained throughout.
Selected Area Electron Diffraction
Selected area electron diffraction (SAED) bulk crystal structure analysis of MNPs was performed using a JEOL JEM-3010 transmission electron microscope operating at 300 keV. A camera length of 20 cm was selected for data acquisition.
X-ray Diffraction
MNP suspension in heptane were dried for X-ray diffraction (XRD) characterization. The analysis was performed using an X-ray diffractometer (Siemens D500), with data acquired in the 25–70° 2θ range, with an exposure time of 7 s and accelerating voltage and current 40 kV and 30 mA, respectively.
STEM-Energy-Dispersive X-ray Spectroscopy and STEM-EELS
To evaluate the elemental distribution of the synthesized iron oxide nanoparticles, STEM-EDS was performed using an aberration-corrected JEOL ARM200CF 200 kV electron microscope in the STEM mode. Elemental mapping was performed using an Oxford EDS system in the drift corrector acquisition mode. Qualitative chemical analysis of MNPs was carried out using STEM-EELS analysis. A GATAN annular dark-field (ADF) STEM detector with a collection semiangle of 53.4 mrad and 0.3 eV/ch energy dispersion with a step size of 1 nm was utilized for the dual-EELS spectral acquisition.
Results and Discussion
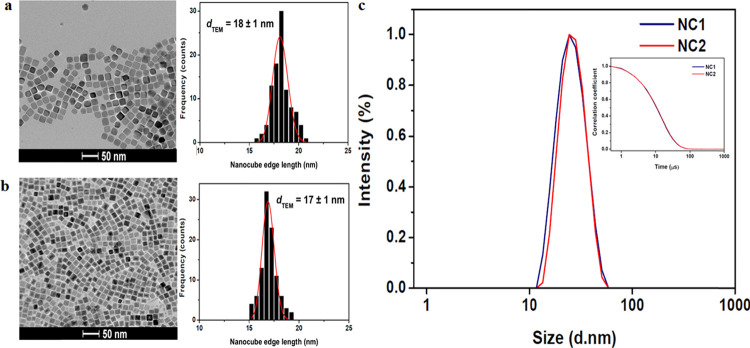
Two stable suspensions of cubic MNPs in heptane were selected from a large number of otherwise identical suspensions prepared using the thermal decomposition approach described in the Experimental Section. There were no apparent differences in the progress of the reaction in any case. The samples selected showed strong and weak hyperthermic responses, see below. TEM analysis Figure 1a,b demonstrated the expected morphological similarities between the two samples. In both cases square shapes are apparent in the images; average nanocube sizes, dTEM, of 18 ± 1 and 17 ± 1 nm were measured for samples NC1 and NC2, respectively both with an average aspect ratio of 1.0 ± 0.1. The distributions are unimodal for both samples with almost no smaller particles or aggregates evident. As our focus was on the effect of crystal integrity on the magnetic properties of the suspensions, cubic MNPs surface-stabilized with oleic acid in the organic solvent heptane were prepared to ensure full particle dispersion. This approach has been adopted by others.12,21,24 The colloidal properties were assessed by DLS (see Figure 1c) in the typical Fe concentration range of ∼0.5–5.0 mM also used for FFC-NMR (see below). The dhyd values were 24.5 nm (PDI 0.08) and 25.2 nm (0.05), for NC1 and NC2, respectively. The correlation functions were completely superimposable, demonstrating effectively indistinguishable hydrodynamic sizes.
Figure 1.
Primary magnetic nanocube characterization. Representative TEM images of cubic MNPs along with their respective size histograms for (a) NC1 and (b) NC2. A lognormal distribution was confirmed by fitting the dTEM values given are the sample (n = 100) averages. (c) DLS characterization (intensity size distribution) of the same samples in heptane at 25 °C. Inset: correlation functions.
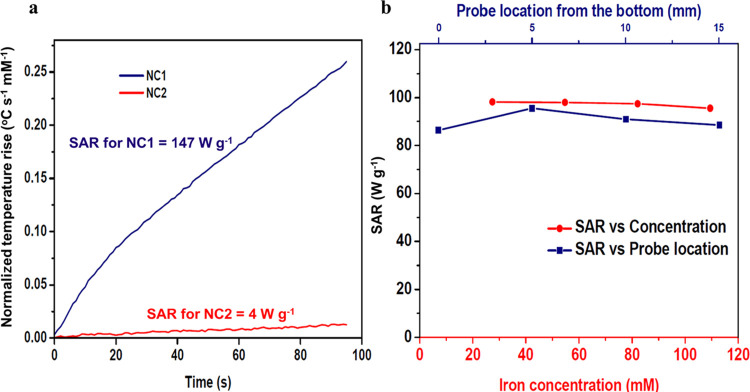
The AC-field hyperthermic efficacy of the suspensions was measured at νAC 535 kHz and IAc 16.0 kA m–1, Figure 2a, with SAR values of 147 and 4 W g–1 obtained at Fe concentrations of 55 and 43 mM for NC1 and NC2, respectively. It is well known that magnetic properties of MNP suspensions are largely determined by particle size, shape,7 and dispersion; hence, this great difference in the SAR is initially surprising.
Figure 2.
AC-field hyperthermic efficacy of cubic MNP suspensions in heptane at νAC 535 kHz and IAC 16.0 kA m–1. (a) AC-field-induced temperature increases for suspensions NC1 and NC2. (b) SAR values of a representative cubic MNP suspension (NC3, dTEM 18 ± 1 nm) as a function of: (i) Fe concentration between 27 and 109 mM at probe location 5 mm from the bottom of the sample holder and (ii) probe location between 0 to 15 mm for a suspension of Fe concentration 109 mM.
A collective particle scenario (arising from reversible aggregation) which increased the SAR has been described for suspensions in this Fe concentration range.25 To confirm the validity of the measured values, the concentration dependence of the SAR was subsequently measured for a different representative strongly heating cubic MNP suspension, NC3 (dTEM = 18 ± 1 nm, dhyd 26.0 nm, PDI 0.04) in the Fe concentration range from 27 to 109 mM. The conditions used to synthesize NC3 were identical, in so far as is possible, to those for NC1 and NC2. The initial heating rates were found to increase in proportion to concentration, with an average SAR of 97 W g–1 (std. dev. of 1 W g–1 for the four concentrations) obtained, Figure 2b. This demonstrates robustness in extraction of the initial slope and that there is no particle aggregation in this range. The effect of the thermal probe location was also varied from 0 to 15 mm from the bottom of the eppendorf tube, at Fe concentration 109 mM, and the SAR values remained within 5% of the average. This demonstrates that the suspensions are homogeneous and there are no convective patterns. Hence, the huge variability in SAR is real and, given the full dispersion, it must arise due to differences in the internal structure of the cubic MNPs and how these alter the moment magnitude and/or dynamics.
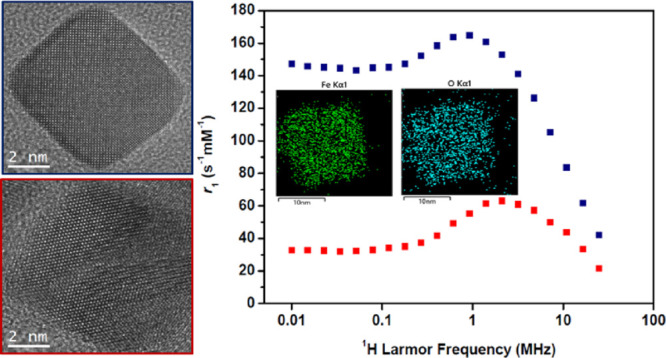
The magnetic properties of the suspensions were further evaluated by measuring the spin–lattice relaxivities (r1) as a function of 1H Larmor frequency, νL (and hence field strength), by fast field-cycling NMR relaxometry.26 The FFC-NMR profiles obtained are commonly used for evaluating MRI contrast efficacy and for interrogating the moment dynamics.27,28 Experimental profiles obtained for NC1 and NC2 are shown in Figure 3, along with profiles simulated using the accepted SPM model26 that satisfactorily reproduce the experimental data. Note that these measurements were performed in the low millimolar Fe concentration range in which DLS demonstrates full dispersion.
Figure 3.
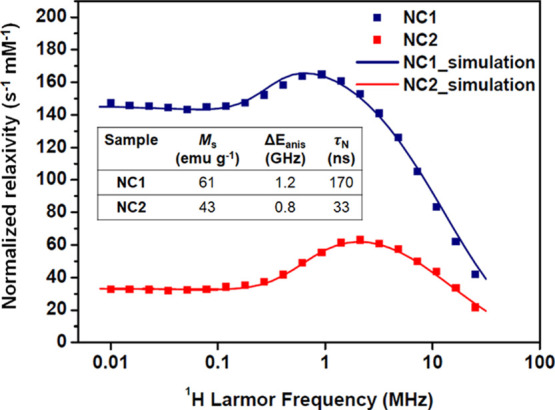
FFC-NMR profiles (r1 as a function of νL) recorded at 25 °C for NC1 and NC2 suspensions in heptane. The Fe concentrations were 1.0 and 0.9 mM, respectively. The solid lines show the simulated profiles for which the parameters are indicated in the inset table.
The profile for NC2 (low SAR) shows the characteristic response of superparamagnetic MNP suspensions, with decreasing r1 in the high-frequency (clinical MRI) range, a mid-frequency maximum with r1 decreasing substantially to a low-frequency plateau, which are as expected for superparamagnetic MNPs in suspension. This observation further confirms full particle dispersion. Profiles have been previously described for water26 and heptane suspensions29 of spherical MNPs; this is, to the best of our knowledge, the first report of the profile for nanocube dispersions. The low-frequency relaxation is known to be dominated by the Néel process (moment reorientation in the magnetocrystalline field), and the high frequency part by the particles’ Brownian motion (as in this range the moments are locked to the external field). It is interesting that despite the distinct cubic shape, the profile is so similar to those recorded for spherical MNPs.23 This demonstrates that the Brownian correlation time, τB, and the Néel correlation time, τN, are comparable to those for similarly sized spheres. Superparamagnetism is generally associated with closed hysteresis loops under DC-field conditions at room temperature. In AC-fields, the delay between reversal of the applied field direction and dynamic realignment of the MNP moments results in heat dissipation.27 Longer delays correspond to a greater area enclosed by the AC-hysteresis loop, which is proportional to the SAR.30 Our interpretation is that for NC2, τN is too short (motion too fast) for there to be a significant SAR contribution at νAC 535 kHz.
For NC1 on the other hand, while the high frequency part of the profile converges toward that of NC2 (which has identical dhyd), as expected, below 10 MHz, the profiles differ substantially due to increased τN associated with greater internal magnetocrystalline anisotropy energy, ΔEanis, i.e., higher average barrier to moment reorientation within the cubes. Increased low-frequency r1 is well documented and is usually associated with the formation of clusters (and hence dipolar interactions) that retard the moment dynamics,27,28,31 although that is not the case here. The r1 value of 147 s–1 mM–1 measured at 0.01 MHz is extraordinarily high for a fully dispersed, and field-stable, suspension of identical dhyd to NC2. The high relaxivity can be unambiguously attributed to slower average moment reorientation in NC1, the longer τN at room temperature also gives rise to increased hysteresis (open loops) and a high SAR at 535 kHz.
Simulations were undertaken using the accepted SPM model developed by Muller and co-workers.26 Initial attempts to simulate the experimental profiles assuming a nonmagnetic surface layer of thickness 0.5 nm (comprising pinned or canted spins) did not reproduce the experimental r1 maximum, or high frequency response, irrespective of the other parameters used. It was found that using the TEM edge lengths reproduced the experimental profiles (in particular, the frequency of the r1 maxima), and the other parameters could then be varied to obtain the best agreement, Figure 3. The NMR size obtained reflects the accessible surface sensed by the solvent molecules during the MNP encounter that drives 1H relaxation, rather than the core or magnetic size. We have previously shown the NMR size to be slightly larger than the core size for glycopeptide-stabilized spheres in H2O18 and for oleyl-stabilized spheres in heptane,29 suggesting the ligands prevent close access. The necessity of using the edge length for oleyl-stabilized cubes may reflect geometric issues, i.e., the distribution of distances of the closest approach. The simulations were found to be highly sensitive to the saturation magnetization (Ms), adjusting it after fixing the size was the most important factor in reproducing the experimental profile, so the uncertainty in this parameter is small. The Ms and τN values obtained from the simulations are consistent with expectation for MNPs in this size range27 and with the XRD and microstructural analysis below. The ΔEanis and τN values were then adjusted to provide almost perfect agreement in the mid-frequency range. The success of the simulations shows that the different chemical environments of the 1H in heptane have no measurable effect on the relaxivity.
The SPM model has several assumptions (including a uniaxial magnetocrystalline field and perfect size monodispersity), so while interpretation of the trends for the suspensions may be instructive, the absolute values of the extracted parameters should be viewed with some caution. Nevertheless, it is interesting that the simulations show Ms values in the expected range and with a much higher value, by a factor of 1.4, for NC1 and also higher τN (and ΔEanis) for this suspension, as is also shown by the SAR analysis. Given the similarity in size (the “cubic” nanocrystal volume of NC1 is only ca. 19% higher than NC2), the significantly higher Ms for NC1 must be associated with better crystallinity, which is confirmed by the microstructural analysis presented below.
For cubic MNPs, the magnetocrystalline easy axis is generally accepted to be along the [111] direction, pointing toward a corner.32 On careful inspection of TEM images recorded for NC1 and NC2, Figure 1b, sharper corners are evident for NC2. These would be expected to generate deeper local energy minima for the moment (and hence longer τN) for NC2; however, the experiments and simulations suggest otherwise. We suggest that NC2 defects in the crystals prevent orientation of the moment toward the corners (however sharp), effectively reducing ΔEanis and τN. While this explanation would be equally applicable for any other orientation of the easy axis (toward an edge or face), the divergence in the hyperthermic and relaxometric properties for the two suspensions strongly suggest lattice distortions as the underlying cause for the low SAR and r1 in NC2.
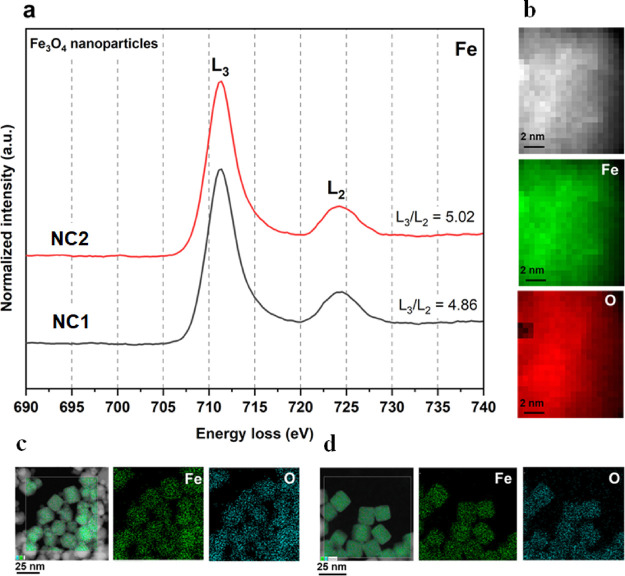
Microstructural analysis of NC1 and NC2 was undertaken, focusing first on the sample’s chemical composition. Iron oxide MNPs are typically composed of magnetite (Fe3O4), maghemite (γ-Fe2O3), or intermediate phases sometimes associated with a more oxidized outer layer. Oxidation can progress after extended exposure to air,33 which can lead to changes in the magnetic responses.34 Oxidation state and crystal structure analysis were performed using STEM and HR-TEM. STEM-EELS and STEM-EDS were used to evaluate the elemental composition and chemical oxidation states of cubic nanoparticles, the results for NC1 and NC2 are shown in Figure 4.
Figure 4.
STEM-EELS and STEM-EDS analysis of cubic iron oxide nanoparticles obtained from NC1 and NC2 confirming the uniform elemental composition. (a) STEM-EELS analysis (0.3 eV/ch) representing the iron L2,3 ionization edge of the spinel phase of NC1 and NC2. (b) STEM-EELS localized nanometer scale elemental mapping. (c) STEM-EDS mapping of nanocubes from NC1. (d) STEM-EDS mapping of nanocubes from NC2, indicating the uniform presence of iron and oxygen for both samples.
Figure 4a shows the STEM-EELS chemical analysis representing the L2,3 ionization edges of Fe as acquired for the cubic MNPs. For transition metals, L2,3 ionization edges appear due to the transitions of electrons from the 2p state to the unoccupied 3d state.35 Ionization edges L3 and L2 were observed due to transitions from 2p3/2 and 2p1/2 core states, respectively, to unoccupied 3d states localized in Fe species.36 The integrated intensity ratio of white lines (L3/L2) can be correlated with the Fe valence state. The Fe L2,3 ionization edges of both cubic MNP suspensions confirmed the characteristic energy difference ΔE(L2 – L3) of 12.93 eV corresponding to iron oxide.37 Furthermore, the L3/L2 was evaluated as 4.86 for NC1 and 5.02 for NC2, which correspond to magnetite.37,38 The absence of a low-frequency feature (prepeak) for the L3 edge and of a high-frequency feature (postpeak) for the L2 edge, which are characteristic features of maghemite,39 confirm the predominance of magnetite in both samples. The Fe3O4 spinel crystal structure consists of both Fe2+ and Fe3+ oxidation states with possible tetrahedral (Fe3+) and octahedral sites (Fe2+ and Fe3+).40Figure 4b shows the STEM-EELS elemental mapping localized on the nanometer scale confirming the uniform presence of iron and oxygen. Figure 4c,d shows the complementary STEM-EDS elemental mapping of cubic MNPs from NC1 and NC2, respectively. Overall, the results indicate that the variation in the magnetic properties of NC1 and NC2 is not associated with variation in the chemical oxidation states. Both batches of cubic MNPs possessed identical chemical composition associated with Fe3O4.
The microstructural characteristics of NC1 and NC2 were evaluated using SAED bulk characterization. Detailed analysis of SAED patterns is shown in Figure S1a,b for NC1 and NC2, respectively. The spinel Fe3O4 phase was confirmed with characteristic lattice planes (202), (222), (400), (242), (333), and (404) observed having d-spacings of 2.95, 2.47, 2.07, 1.69, 1.60, and 1.48 Å, respectively, for NC1. Similarly, for NC2, the characteristic lattice planes (202), (311), (400), (242), and (404), associated with the spinel Fe3O4 phase, can be observed. However, the diffraction ring associated with the (333) lattice plane was absent in the SAED pattern of NC2. XRD bulk analyses for NC1 and NC2 are shown in Figure S1c. The intensities of the (202), (311̅), and (400) lattice planes corresponding to d-spacings of 2.98, 2.54, and 2.10 Å, respectively, are lower for NC2 than NC1. Using the Scherrer equation, the evaluated crystallite sizes for NC1 and NC2 are 12.49 and 7.12 nm, respectively. For cubic MNPs, a shape factor of 0.94 was considered for calculating crystallite size.41 The calculated FWHM from the (311̅) highest intensity XRD peaks are 0.012175 and 0.0213173 radians for NC1 and NC2, respectively. These results further validate the interpretation of the FFC-NMR results and are complemented by HR-TEM analysis that follows, suggesting greater prevalence of lattice defects in NC2.
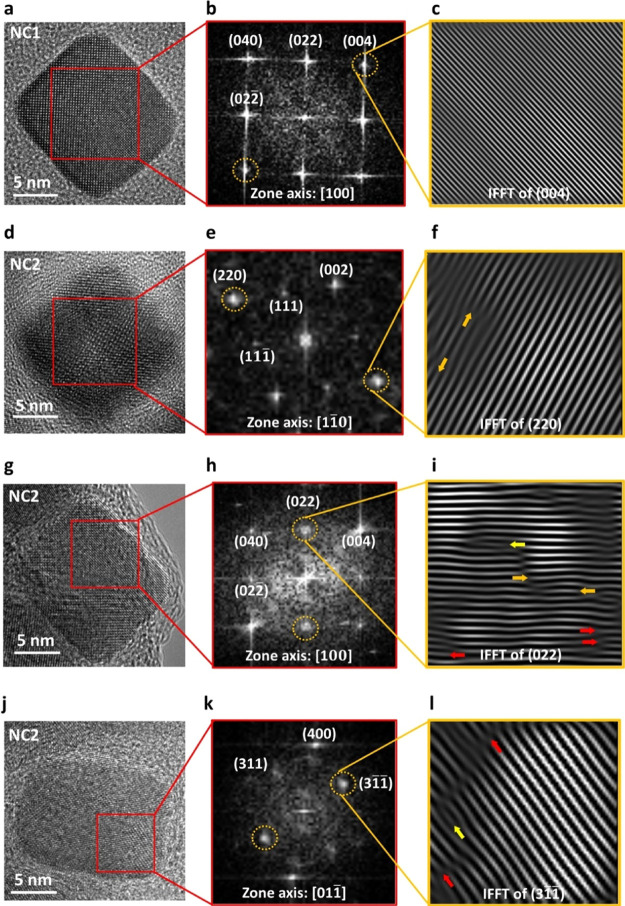
The lattice distortions indicated by the XRD analysis for NC2 were further investigated using HR-TEM. Figure 5 shows HR-TEM and associated fast Fourier transform (FFT) and inverse-FFT (IFFT) analyses for representative NC1 and NC2 MNPs. Figure 5a shows the HR-TEM micrograph of a representative NC1 particle; the corresponding FFT analysis from the identified region is shown in Figure 5b indicating lattice planes (040), (022), (004), and (002̅) associated with 2.09, 2.98, 2.09, and 2.98 Å d-spacings, respectively, in the [100] zone axis. Figure 5c shows the IFFT pattern of the (004) lattice plane confirming the absence of lattice dislocations.
Figure 5.
High-resolution TEM analysis of cubic MNPs from NC1 (a–c) and NC2 (d–l) demonstrating greater prevalence of lattice distortions in NC2. HR-TEM micrographs (a,d,g,j) of representative cubic MNPs from NC1 and NC2. The corresponding FFT patterns acquired from the localized crystal regions indicating the lattice planes along [100], [11̅0], [100], and [011̅] zone axes are represented in panels (b,e,h,k), respectively. (c) Inverse-FFT acquired from the (004) lattice plane confirming the absence of lattice dislocations in the representative NC1 crystal. Panels (f,i,l) showing inverse-FFT acquired from (220), (022), and (31̅1̅) major lattice planes, respectively, confirm the presence of planar lattice dislocations in the representative NC2 crystals. Orange arrows indicate interstitial extra half planes, yellow arrows indicate specifically extrinsic stacking faults, and red arrows indicate intrinsic stacking faults.
Figure 5d shows the HR-TEM micrograph of a representative particle from NC2. The corresponding FFT analysis from the identified region is shown in Figure 5e indicating lattice planes (220), (002), (111), and (111̅) associated with 2.98, 4.23, 4.98, and 4.98 Å d-spacings, respectively, in the [11̅0] zone axis. Figure 5g shows the HR-TEM micrograph of another NC2 particle, and the FFT analysis, Figure 5h, shows lattice planes (040), (022), (004), and (002̅) associated with 2.09, 2.98, 2.09, and 2.98 Å d-spacings, respectively, in the [100] zone axis. Figure 5j shows the HR-TEM micrograph of a third representative NC2 crystal. The FFT analysis, Figure 5k, indicates lattice planes (400), (311), and (31̅1̅), in this case, associated with 2.12, 2.57, and 2.57 Å d-spacings, respectively, in the [011̅] zone axis. Figure 5f,i,l represents IFFT patterns of (220), (022), and (31̅1̅) lattice planes, respectively, confirming the presence of stacking faults. These are planar defects which can appear extrinsically, due to the inclusion of an additional atomic layer, or intrinsically, due to a missing intermediate atomic layer.42 Such stacking faults can originate during crystal growth from point defects or localized dislocations.43 Stacking fault defects associated with partial dislocations play a critical role in cross-slip and gliding of dislocations.44 Extra half planes apparent in Figure 5f,i, represented by orange arrows, are clear evidence of edge dislocations indicating interstitial-type stacking faults.45 In Figure 5i,l extrinsic and intrinsic stacking faults are represented by yellow and red arrows, respectively. Furthermore, analysis of additional NC2 crystals confirmed the presence of a twin boundary and an edge dislocation, see Figure S2a,b, respectively. Formation of twin boundaries is highly sensitive to the chemical environment and events during the MNP synthesis.46 Edge dislocations can induce local strain fields in the lattice.47 It is clear that distinct defects are present in NC2 cubic MNPs.
We suggest that these localized defects adversely affect the moments’ magnitude and dynamics, resulting in poor collective magnetic characteristics, as observed for NC2. Similar observations were reported by Pellegrino and co-workers11 based on microstructural analysis of a single low SAR spherical iron oxide MNP. The comparative structural analysis presented here along with the evaluation of both the MRI and hyperthermic responses, for samples that are identical in all other respects, confirms the role of crystal integrity. For the low SAR suspension (NC2), crystal defects prevent moment orientation toward the corners, and clearly, the particles have reduced magnetic volume and hence lower magnetization and lower magnetocrystalline anisotropy, giving fast moment reorientation, as determined by FFC-NMR.
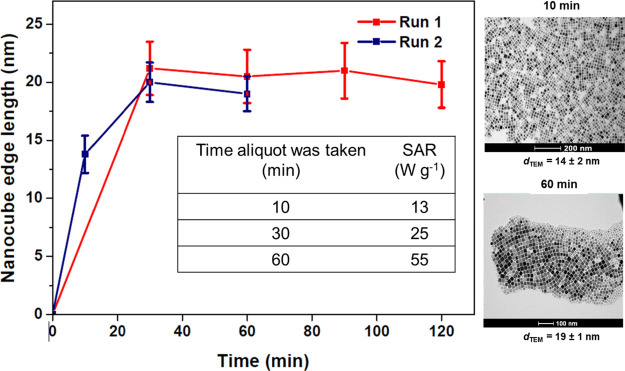
Finally, the causes of batch-to-batch variability in crystal integrity were evaluated by studying the evolution of a suspension’s characteristics during synthesis. Multiple samples were drawn from a reaction at different times for TEM and hyperthermia analysis, see Figure 6. Time zero is defined as the start of reflux. It is clear that within 10 min, good cubic morphology was achieved, and the dTEM value was already found to be 14 ± 1 nm with an aspect ratio of 1.00 ± 0.02. Hence, the system was in the growth phase by this time and the measured SAR was low. Over the full hour of the reaction, the size increased to 19 ± 2 nm and the SAR to 55 W g–1. Hence, this is a reasonably high heating sample, akin to NC1 albeit with the efficacy somewhat suppressed, most likely due to the disturbance caused by taking aliquots. It is clear that the SAR evolves throughout the growth phase due primarily, we suggest, to improving crystallinity. However, as a subpopulation of small particles is evident at 60 min, it is not possible to eliminate the possibility of a significant number of smaller nonheating particles contributing to the low SAR for the aliquot experiment. No such subpopulations are present for NC1 and NC2, for which we suggest that differences in crystallinity give rise to the hugely differing SAR values.
Figure 6.
Temporal size evolution of cubic MNPs synthesized using FeOl in squalene with L/P = 1. Aliquots were drawn at the times indicated after the onset of reflux. All the aliquots were stabilized in heptane for SAR measurement and TEM preparation. The dTEM values given are the sample (n = 100) averages. Inset table, the SAR measurements for Run 2.
It was also found that in this case, extending the reaction for a greater time did not further improve the SAR. It can be concluded that high SAR suspensions are associated with successful annealing due to elevated temperature (∼285 °C) that relieves magnetic frustration. It is not possible to demonstrate whether the partially annealed defects arise from predominantly twinned nuclei, or if all particles grow only by monomer addition. In either case the outcome is unpredictable, its extent varies from reaction to reaction despite identical synthesis conditions for NC1 and NC2. Therefore, to tailor the magnetic characteristics of the MNPs, it would be interesting to investigate the stochasticity associated with the MNP growth phase and how it influences crystal structure integrity.
Conclusions
Clear differences in the microstructural characteristics of the nanocube samples pinpoint better crystallinity and the absence of defects as responsible for high hyperthermic and relaxometric efficacies for fully dispersed nanocubes. Interestingly, the presence of defects is found to be more important than the sharpness of the corners or surface layer effects in determining the depth of the magnetocrystalline energy minima. Samples with higher prevalence of planar lattice defects are found to have both lower Ms and τN. These two effects, which are revealed by the difference in low-frequency r1, combine to greatly reduce the SAR for otherwise identical nanocrystals. Hence, this work contributes to understanding of how crystallinity determines both the strength and the dynamics of the magnetic moments and demonstrates the importance of defect-free crystals. It also identifies that exceptionally high low-frequency r1 is possible for relatively small defect-free fully dispersed nanocubes. Such materials may have applications for T1-weighted imaging in ultralow field MRI. It is anticipated that with the emerging possibility of identifying easy axes for individual crystals, through magnetic force microscopy,48 new possibilities for understanding the effect of different types of defects on the ensemble magnetic properties may soon be realized. Finally, the potential of process optimization and crystal engineering of cubic MNPs, and in particular of the conditions during the growth phase, is identified as key for realizing higher and more consistently reproducible hyperthermic and relaxometric responses.
Acknowledgments
The authors acknowledge support from Science Foundation Ireland (16/IA/4584). R.S-Y. acknowledges the financial support from the U.S. National Science Foundation (NSF) award number DMR-1809439. A.H.P.’s efforts were supported by NSF award number DMR-1710049. The authors thank Dr. Gita Singh for her assistance with XRD measurements and Dr. Tony Keene for stimulating discussions.
Glossary
Abbreviations
- AAS
Atomic absorption spectroscopy
- dhyd
Average hydrodynamic size
- dTEM
Average TEM size
- τB
Brownian correlation time
- EDS
Energy-dispersive X-ray spectroscopy
- EELS
Electron energy loss spectroscopy
- FFC-NMR
Fast-field-cycling nuclear magnetic resonance
- FFT
Fast Fourier transform
- HR-TEM
High-resolution transmission electron microscopy
- L2,3
Ionization edges of iron (white lines)
- FeOl
Iron oleate
- MNP
Magnetic nanoparticle
- MRI
Magnetic resonance imaging
- ΔEanis
Magnetocrystalline anisotropy energy
- τN
Néel correlation time
- PDI
Polydispersity index
- STEM
Scanning transmission electron microscopy
- SAED
Selected area electron diffraction
- SAR
Specific absorption rate
- r1
Spin–lattice relaxivity
- XRD
X-ray diffraction.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.chemmater.2c00708.
Crystal structure analysis of NC1 and NC2 based on SAED and XRD measurements and additional high-resolution TEM analysis of cubic MNPs from NC2 (PDF)
Author Contributions
S.D.S. synthesized cubic iron oxide MNPs and performed low-resolution TEM, DLS, and magnetic hyperthermia measurements and FFC-NMR simulations. S.D.S. and D.F.B. wrote the manuscript. A.H.P. performed HR-TEM, SAED, STEM-EELS, and STEM-EDS characterization. E.M.K. carried out FFC-NMR measurements. K.N. completed materials characterization and contributed to preparation of the revised manuscript. R.S-Y. supervised the HR-TEM/STEM materials characterization. S.F. supervised the project. D.F.B. conceptualized and supervised the project. The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.
The authors declare no competing financial interest.
Supplementary Material
References
- Lee N.; Hyeon T. Designed synthesis of uniformly sized iron oxide nanoparticles for efficient magnetic resonance imaging contrast agents. Chem. Soc. Rev. 2012, 41, 2575–2589. 10.1039/C1CS15248C. [DOI] [PubMed] [Google Scholar]
- Lyons S.; Mc Kiernan E. P.; Dee G.; Brougham D. F.; Morrin A. Electrostatically modulated magnetophoretic transport of functionalised iron-oxide nanoparticles through hydrated networks. Nanoscale 2020, 12, 10550–10558. 10.1039/D0NR01602K. [DOI] [PubMed] [Google Scholar]
- Tarn M. D.; Peyman S. A.; Robert D.; Iles A.; Wilhelm C.; Pamme N. The importance of particle type selection and temperature control for on-chip free-flow magnetophoresis. J. Magn. Magn. Mater. 2009, 321, 4115–4122. 10.1016/j.jmmm.2009.08.016. [DOI] [Google Scholar]
- Liu X.; Zhang Y.; Wang Y.; Zhu W.; Li G.; Ma X.; Zhang Y.; Chen S.; Tiwari S.; Shi K. Comprehensive understanding of magnetic hyperthermia for improving antitumor therapeutic efficacy. Theranostics 2020, 10, 3793. 10.7150/thno.40805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hervault A.; Dunn A. E.; Lim M.; Boyer C.; Mott D.; Maenosono S.; Thanh N. T. Doxorubicin loaded dual pH-and thermo-responsive magnetic nanocarrier for combined magnetic hyperthermia and targeted controlled drug delivery applications. Nanoscale 2016, 8, 12152–12161. 10.1039/C5NR07773G. [DOI] [PubMed] [Google Scholar]
- Lee N.; Yoo D.; Ling D.; Cho M. H.; Hyeon T.; Cheon J. Iron oxide based nanoparticles for multimodal imaging and magnetoresponsive therapy. Chem. Rev. 2015, 115, 10637–10689. 10.1021/acs.chemrev.5b00112. [DOI] [PubMed] [Google Scholar]
- Wu K.; Su D.; Liu J.; Saha R.; Wang J.-P. Magnetic nanoparticles in nanomedicine: a review of recent advances. Nanotechnology 2019, 30, 502003. 10.1088/1361-6528/ab4241. [DOI] [PubMed] [Google Scholar]
- Muscas G.; Yaacoub N.; Peddis D.. Magnetic disorder in nanostructured materials. In Novel Magnetic Nanostructures; Elsevier, 2018; pp 127–163. [Google Scholar]
- Vreeland E. C.; Watt J.; Schober G. B.; Hance B. G.; Austin M. J.; Price A. D.; Fellows B. D.; Monson T. C.; Hudak N. S.; Maldonado-Camargo L.; Bohorquez A. C.; Rinaldi C.; Huber D. L. Enhanced nanoparticle size control by extending LaMer’s mechanism. Chem. Mater. 2015, 27, 6059–6066. 10.1021/acs.chemmater.5b02510. [DOI] [Google Scholar]
- Dutz S.; Hergt R. Magnetic particle hyperthermia—a promising tumour therapy?. Nanotechnology 2014, 25, 452001 10.1088/0957-4484/25/45/452001. [DOI] [PubMed] [Google Scholar]
- Levy M.; Quarta A.; Espinosa A.; Figuerola A.; Wilhelm C.; García-Hernández M.; Genovese A.; Falqui A.; Alloyeau D.; Buonsanti R.; Cozzoli P. D.; García M. A.; Gazeau F.; Pellegrino T. Correlating magneto-structural properties to hyperthermia performance of highly monodisperse iron oxide nanoparticles prepared by a seeded-growth route. Chem. Mater. 2011, 23, 4170–4180. 10.1021/cm201078f. [DOI] [Google Scholar]
- Muro-Cruces J.; Roca A. G.; López-Ortega A.; Fantechi E.; del -Pozo-Bueno D.; Estradé S.; Peiró F.; Sepúlveda B.; Pineider F.; Sangregorio C.; Nogues J. Precise size control of the growth of Fe3O4 nanocubes over a wide size range using a rationally designed one-pot synthesis. ACS Nano 2019, 13, 7716–7728. 10.1021/acsnano.9b01281. [DOI] [PubMed] [Google Scholar]
- Lee J.-H.; Jang J.-T.; Choi J.-S.; Moon S. H.; Noh S.-H.; Kim J.-W.; Kim J.-G.; Kim I.-S.; Park K. I.; Cheon J. Exchange-coupled magnetic nanoparticles for efficient heat induction. Nat. Nanotechnol. 2011, 6, 418–422. 10.1038/nnano.2011.95. [DOI] [PubMed] [Google Scholar]
- Martinez-Boubeta C.; Simeonidis K.; Makridis A.; Angelakeris M.; Iglesias O.; Guardia P.; Cabot A.; Yedra L.; Estradé S.; Peiró F. Learning from nature to improve the heat generation of iron-oxide nanoparticles for magnetic hyperthermia applications. Sci. Rep. 2013, 3, 1–8. 10.1038/srep01652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alphandery E.; Faure S.; Seksek O.; Guyot F.; Chebbi I. Chains of magnetosomes extracted from AMB-1 magnetotactic bacteria for application in alternative magnetic field cancer therapy. ACS Nano 2011, 5, 6279–6296. 10.1021/nn201290k. [DOI] [PubMed] [Google Scholar]
- Guardia P.; Riedinger A.; Nitti S.; Pugliese G.; Marras S.; Genovese A.; Materia M. E.; Lefevre C.; Manna L.; Pellegrino T. One pot synthesis of monodisperse water soluble iron oxide nanocrystals with high values of the specific absorption rate. J. Mater. Chem. B 2014, 2, 4426–4434. 10.1039/c4tb00061g. [DOI] [PubMed] [Google Scholar]
- Nemati Z.; Das R.; Alonso J.; Clements E.; Phan M.; Srikanth H. Iron oxide nanospheres and nanocubes for magnetic hyperthermia therapy: a comparative study. J. Electron. Mater. 2017, 46, 3764–3769. 10.1007/s11664-017-5347-6. [DOI] [Google Scholar]
- Borase T.; Ninjbadgar T.; Kapetanakis A.; Roche S.; O’Connor R.; Kerskens C.; Heise A.; Brougham D. F. Stable aqueous dispersions of glycopeptide-grafted selectably functionalized magnetic nanoparticles. Angew. Chem., Int. Ed. 2013, 52, 3164–3167. 10.1002/anie.201208099. [DOI] [PubMed] [Google Scholar]
- Lartigue L.; Hugounenq P.; Alloyeau D.; Clarke S. P.; Levy M.; Bacri J.-C.; Bazzi R.; Brougham D. F.; Wilhelm C.; Gazeau F. Cooperative organization in iron oxide multi-core nanoparticles potentiates their efficiency as heating mediators and MRI contrast agents. ACS Nano 2012, 6, 10935–10949. 10.1021/nn304477s. [DOI] [PubMed] [Google Scholar]
- Zhou Z.; Yang L.; Gao J.; Chen X. Structure–relaxivity relationships of magnetic nanoparticles for magnetic resonance imaging. Adv. Mater. 2019, 31, 1804567 10.1002/adma.201804567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shavel A.; Rodríguez-González B.; Spasova M.; Farle M.; Liz-Marzán L. M. Synthesis and characterization of iron/iron oxide core/shell nanocubes. Adv. Funct. Mater. 2007, 17, 3870–3876. 10.1002/adfm.200700494. [DOI] [Google Scholar]
- Monks P.; Wychowaniec J. K.; McKiernan E.; Clerkin S.; Crean J.; Rodriguez B. J.; Reynaud E. G.; Heise A.; Brougham D. F. Spatiotemporally Resolved Heat Dissipation in 3D Patterned Magnetically Responsive Hydrogels. Small 2021, 17, 2004452 10.1002/smll.202004452. [DOI] [PubMed] [Google Scholar]
- Meledandri C. J.; Brougham D. F. Low field magnetic resonance techniques in the development of nanomaterials for biomedical applications. Anal. Methods 2012, 4, 331–341. 10.1039/c2ay05420e. [DOI] [Google Scholar]
- Dehsari H. S.; Ribeiro A. H.; Ersöz B.; Tremel W.; Jakob G.; Asadi K. Effect of precursor concentration on size evolution of iron oxide nanoparticles. CrystEngComm 2017, 19, 6694–6702. 10.1039/C7CE01406F. [DOI] [Google Scholar]
- Conde-Leboran I.; Baldomir D.; Martinez-Boubeta C.; Chubykalo-Fesenko O.; del Puerto Morales M.; Salas G.; Cabrera D.; Camarero J.; Teran F. J.; Serantes D. A single picture explains diversity of hyperthermia response of magnetic nanoparticles. J. Phys. Chem. C 2015, 119, 15698–15706. 10.1021/acs.jpcc.5b02555. [DOI] [Google Scholar]
- Roch A.; Muller R. N.; Gillis P. Theory of proton relaxation induced by superparamagnetic particles. J. Chem. Phys. 1999, 110, 5403–5411. 10.1063/1.478435. [DOI] [Google Scholar]
- Laurent S.; Forge D.; Port M.; Roch A.; Robic C.; Vander Elst L.; Muller R. N. Magnetic iron oxide nanoparticles: synthesis, stabilization, vectorization, physicochemical characterizations, and biological applications. Chem. Rev. 2008, 108, 2064–2110. 10.1021/cr068445e. [DOI] [PubMed] [Google Scholar]
- Stolarczyk J. K.; Meledandri C. J.; Clarke S. P.; Brougham D. F. Size selectable nanoparticle assemblies with magnetic anisotropy tunable across the superparamagnetic to ferromagnetic range. Chem. Commun. 2016, 52, 13337–13340. 10.1039/C6CC05871J. [DOI] [PubMed] [Google Scholar]
- Meledandri C. J.; Stolarczyk J. K.; Ghosh S.; Brougham D. F. Nonaqueous magnetic nanoparticle suspensions with controlled particle size and nuclear magnetic resonance properties. Langmuir 2008, 24, 14159–14165. 10.1021/la8018088. [DOI] [PubMed] [Google Scholar]
- Garaio E.; Collantes J. M.; Garcia J. A.; Plazaola F.; Mornet S.; Couillaud F.; Sandre O. A wide-frequency range AC magnetometer to measure the specific absorption rate in nanoparticles for magnetic hyperthermia. J. Magn. Magn. Mater. 2014, 368, 432–437. 10.1016/j.jmmm.2013.11.021. [DOI] [Google Scholar]
- Meledandri C. J.; Ninjbadgar T.; Brougham D. F. Size-controlled magnetoliposomes with tunable magnetic resonance relaxation enhancements. J. Mater. Chem. 2011, 21, 214–222. 10.1039/C0JM01061H. [DOI] [Google Scholar]
- Singh G.; Chan H.; Baskin A.; Gelman E.; Repnin N.; Král P.; Klajn R. Self-assembly of magnetite nanocubes into helical superstructures. Science 2014, 345, 1149–1153. 10.1126/science.1254132. [DOI] [PubMed] [Google Scholar]
- Wu W.; Jiang C. Z.; Roy V. A. Designed synthesis and surface engineering strategies of magnetic iron oxide nanoparticles for biomedical applications. Nanoscale 2016, 8, 19421–19474. 10.1039/C6NR07542H. [DOI] [PubMed] [Google Scholar]
- Santoyo Salazar J.; Perez L.; De Abril O.; Truong Phuoc L.; Ihiawakrim D.; Vazquez M.; Greneche J.-M.; Begin-Colin S.; Pourroy G. Magnetic iron oxide nanoparticles in 10–40 nm range: composition in terms of magnetite/maghemite ratio and effect on the magnetic properties. Chem. Mater. 2011, 23, 1379–1386. 10.1021/cm103188a. [DOI] [Google Scholar]
- Wang Z.; Yin J.; Jiang Y. EELS analysis of cation valence states and oxygen vacancies in magnetic oxides. Micron 2000, 31, 571–580. 10.1016/S0968-4328(99)00139-0. [DOI] [PubMed] [Google Scholar]
- Laffont L.; Gibot P. High resolution electron energy loss spectroscopy of manganese oxides: Application to Mn3O4 nanoparticles. Mater. Charact. 2010, 61, 1268–1273. 10.1016/j.matchar.2010.09.001. [DOI] [Google Scholar]
- Cavé L.; Al T.; Loomer D.; Cogswell S.; Weaver L. A STEM/EELS method for mapping iron valence ratios in oxide minerals. Micron 2006, 37, 301–309. 10.1016/j.micron.2005.10.006. [DOI] [PubMed] [Google Scholar]
- Maher B. A.; Ahmed I. A.; Karloukovski V.; MacLaren D. A.; Foulds P. G.; Allsop D.; Mann D. M.; Torres-Jardón R.; Calderon-Garciduenas L. Magnetite pollution nanoparticles in the human brain. Proc. Natl. Acad. Sci. U. S. A. 2016, 113, 10797–10801. 10.1073/pnas.1605941113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Almeida T. P.; Kasama T.; Muxworthy A. R.; Williams W.; Nagy L.; Hansen T. W.; Brown P. D.; Dunin-Borkowski R. E. Visualized effect of oxidation on magnetic recording fidelity in pseudo-single-domain magnetite particles. Nat. Commun. 2014, 5, 1–6. 10.1038/ncomms6154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang C.; Baer D. R.; Amonette J. E.; Engelhard M. H.; Antony J.; Qiang Y. Morphology and electronic structure of the oxide shell on the surface of iron nanoparticles. J. Am. Chem. Soc. 2009, 131, 8824–8832. 10.1021/ja900353f. [DOI] [PubMed] [Google Scholar]
- Langford J. I.; Wilson A. Scherrer after sixty years: a survey and some new results in the determination of crystallite size. J. Appl. Crystallogr. 1978, 11, 102–113. 10.1107/S0021889878012844. [DOI] [Google Scholar]
- Hiroshi N.Defects in Metals. In Physical Metallurgy; Elsevier, 2014; pp 561–637. [Google Scholar]
- Hilhorst J.; Wolters J. R.; Petukhov A. V. Slanted stacking faults and persistent face centered cubic crystal growth in sedimentary colloidal hard sphere crystals. CrystEngComm 2010, 12, 3820–3826. 10.1039/c0ce00022a. [DOI] [Google Scholar]
- Han F.; Yuan F.; Li G.; Zhang Y.; Ali M.; Guo W.; Ren J.; Liu C.; Gu H. Atypical U-shape micro-stacking faults within body-centered tetragonal Zr2Si nanoparticle in silicon modified Zircaloy-4 alloy. Scr. Mater. 2021, 203, 114051 10.1016/j.scriptamat.2021.114051. [DOI] [Google Scholar]
- Li B.; Liu H.; Lu X.; Kang L.; Sheng Y.; Xiong A. Atomic configurations of basal stacking faults and dislocation loops in GaN irradiated with Xe20+ ions at room temperature. Appl. Surf. Sci. 2019, 486, 15–21. 10.1016/j.apsusc.2019.04.213. [DOI] [Google Scholar]
- Carnis J.; Kshirsagar A. R.; Wu L.; Dupraz M.; Labat S.; Texier M.; Favre L.; Gao L.; Oropeza F. E.; Gazit N. Twin boundary migration in an individual platinum nanocrystal during catalytic CO oxidation. Nat. Commun. 2021, 12, 1–10. 10.1038/s41467-021-25625-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mouritz A. P.Introduction to Aerospace Materials; Elsevier, 2012. [Google Scholar]
- Moya C.; Iglesias-Freire Ó.; Pérez N.; Batlle X.; Labarta A.; Asenjo A. Direct imaging of the magnetic polarity and reversal mechanism in individual Fe3–xO4 nanoparticles. Nanoscale 2015, 7, 8110–8114. 10.1039/C5NR00592B. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.