Big Data in a Nano World: A Review on Computational, Data-Driven Design of Nanomaterials Structures, Properties, and Synthesis

Abstract

The recent rise of computational, data-driven research has significant potential to accelerate materials discovery. Automated workflows and materials databases are being rapidly developed, contributing to high-throughput data of bulk materials that are growing in quantity and complexity, allowing for correlation between structural–chemical features and functional properties. In contrast, computational data-driven approaches are still relatively rare for nanomaterials discovery due to the rapid scaling of computational cost for finite systems. However, the distinct behaviors at the nanoscale as compared to the parent bulk materials and the vast tunability space with respect to dimensionality and morphology motivate the development of data sets for nanometric materials. In this review, we discuss the recent progress in data-driven research in two aspects: functional materials design and guided synthesis, including commonly used metrics and approaches for designing materials properties and predicting synthesis routes. More importantly, we discuss the distinct behaviors of materials as a result of nanosizing and the implications for data-driven research. Finally, we share our perspectives on future directions for extending the current data-driven research into the nano realm.

Introduction

The predictive power of quantum mechanics combined with the efficiency of density functional theory has revolutionized our ability to describe microscopic phenomena in materials. During past decades, first-principles computations have become an indispensable part of materials design, with applications ranging from energy harvesting, conversion, and storage, to quantum information and drug design.¹⁻⁵ With the advancement of modern supercomputers, computational capacity today enables high-throughput screening and data-driven in silico exploration of novel materials. At the same time, there has been a corresponding increase in scientific publications and a remarkable amount of data which fuels the application of artificial intelligence to interpret patterns, predict properties, and steer the directions of materials design. Materials science has entered the fourth paradigm: data-intensive scientific discovery.

Today, automated workflows empower the growth of materials databases, e.g., Materials Project, NOMAD, and the Open Quantum Materials Database (OQMD), and others (Table 1).⁶⁻¹⁰ These databases have expanded their capacity from basic properties like structure, total energy, formation energy, and band structures, to evaluating phase behavior, vibrational, dielectric, elastic, and spectral properties. In turn, such data are used in data-driven approaches, where machine learning models are trained to map the composition and structure to the targeted properties. While much of the data are obtained within the mean-field approximation of density functional theory (DFT), such as generalized gradient approximation (GGA) and extensions thereof, more accurate methodologies such as GW and time-dependent DFT (TDDFT) can complement the large data sets which together provide useful trends and descriptors. Robust, predictive models require a large, systematic, and diverse set of high-quality input data covering the target properties, emphasizing the urgency and importance of curating databases containing such information. However, the majority of data-driven explorations have focused on crystalline bulk materials or molecular crystals, where periodic DFT codes run efficiently.

Table 1. General Open-Source Databases for Solids^a.

General databases	Electronic structure	Thermodynamics	Mechanical	Spectra	Synthesis/surface
Materials Project;6materialsproject.org;API available	Band structure, DOS, magnetic moment, charge densities, bonding and chemical environment, Fermi surfaces dielectric tensor	Phonon dispersion, Hull stability, formation energy, phase diagram, Pourbaix diagram (aqueous stability)	Elastic tensor, piezoelectric tensors, equation of states	XANES, XAFS, EXAFS, absorption spectra XRD	Surface energies, Wulff shape, suggested substrates, synthesis recipe
MPContribs(community-contributed data including experimental data); mpcontribs.org;API available	Band structure (including GW), effective masses, electronic transport, band alignment, DOS, Hubbard U/J	Formation energy, disordered structures, experimental phase and formation energies	Elastic constant		Surfaces, adsorbates
NOMAD;7nomad-lab.eu;API available	Band structure, DOS, eigenvalues, angular spin momentum	Phonon dispersion, heat capacity, Helmholtz free energy	Stress tensor	Oscillator strength, transition dipole moment
AFLOW;18aflowlib.org;API available	Band structure, DOS, magnetic properties	Formation energy, Debye temperature, vibrational free energy, heat capacity	Bulk modulus, Poisson ratio, elastic anisotropy
OQMD;8oqmd.org;API available	Band gap	Phase diagrams, formation energy
Materials Cloud;19www.materialscloud.org;API available	Band structure, DOS, magnetization, Wannier functions, band inversion strength,20 (anti)ferromagnetism	Phonon dispersion		Molecular IR/Raman spectroscopy	Exfoliation energy (2D mat.)21,22
NREL Materials Database;23−25materials.nrel.gov	Band gap (including GW), VBM/CBM, effective masses, magnetic moment	Formation energy, Hull stability		XRD
Computational Materials Repository;26cmr.fysik.dtu.dk	Band structure (including GW), effective masses, polarizabilities, band alignment	Formation energy, Hull stability	Elastic constant	Absorption spectra	Adsorption energy, surface energy
JARVIS;27jarvis.nist.gov;API available	Band gap, effective masses, magnetic moments, dielectric constants	Formation energy	Elastic tensor, piezoelectric tensors, equation of states	Frequency-dependent dielectric function, infrared intensities, spectroscopy limited maximum efficiency, XRD	Exfoliation energies
MatCloud;28http://matcloud.cnic.cn;API available	Band structure, DOS, dielectric constant	Formation energy, vibrational entropy,Gibbs free energy, heat capacity	Elastic tensor, shear modulus, Young’s modulus		Adsorption
MPDS29 (including experimental data);mpds.io;API available	Band structure, DOS, effective mass, electrical conductivity, charge transfer, superconductivity, magnetic properties	Entropy thermal conductivity, Debye temperature, heat capacity, thermal expansion, Seebeck coefficient, phase transition temperature	Elastic moduli, sound velocity, compressibility	Optical absorption, work functions, refractive index	Decomposition
Materiae;30,31materiae.iphy.ac.cn;API available	Band structure (SOC), DOS (SOC), SOC band gap, topological class
phonondb;31,32phonondb.mtl.kyoto-u.ac.jp		Phonon dispersion, phonon DOS, entropy, free energy, heat capacity, Gruneisen parameters
MatNavi 33 (literature and experimental data);mits.nims.go.jp	Band structure, DOS, charge density	Phase diagrams (T), thermal capacity, diffusion coefficient	Tensile strength (metal), proof stress	XRD, XAS	Surface tension

^aThe list of properties intends to be as exhaustive as possible, but due to the high diversity of data, we only listed properties with more than 500 data points. Databases are marked if they include experimental results or an API (Application Programming Interface) for programmatic access.

Owing to the rapid development in materials synthesis and imaging techniques, materials at the nanometer scale—including quantum dots, atomically thin nanoplates, nanowires, and nanocrystalline thin films (Figure 1)—have generated tremendous excitement and are impacting a range of technological applications including optoelectronics, catalysis, and energy storage. While such nanomaterials, spanning 1–100 nm, can offer precise control¹¹ over composition, size, and shape, they also exhibit large surface areas, a range of morphologies, structural reconstruction, defects, and associated quantum confinement effects which result in behaviors distinct from their bulk counterparts.¹²⁻¹⁷ The increased complexity, as well as the lack of long-range order, has posed challenges for traditional first-principles methods. However, recent data-driven approaches have proven effective in navigating the vast parameter space, aiding structure determination and property predictions. In this review, we discuss the progress on functional nanomaterials design, including structure, properties, and synthesis, specifically focusing on data-intense research. We summarize the commonly used computational methods, high-throughput studies, descriptors, and machine learning approaches, discuss the challenges brought by the complexities of nanomaterials, and comment on the opportunities for future direction.

Figure 1.

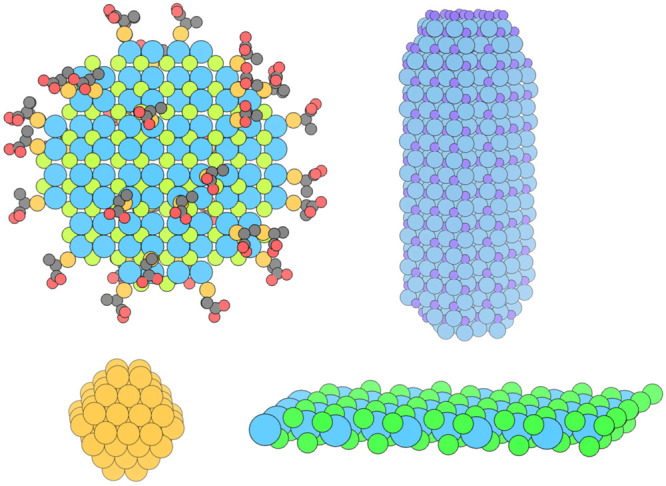
Common model nanomaterials. Top left, nanocrystals with ligands; top right, nanorods; bottom left, nanoclusters; bottom right, 2D nanoplatelets.

Data-Driven Design of Nanomaterials

Nanostructured materials, including nanocrystals, nanorods, nanoplates, nanoclusters, and nanocrystalline thin films, have gained prominence in recent years due to rapid advancements in materials synthesis techniques. This class of materials offers great physical and chemical tunability with enhanced performance across systems ranging from inorganic semiconductors to metals and molecular crystals.³⁴⁻³⁶ As a result of the large surface area-to-bulk ratio as well as strong interactions with the external environment,^37,38 nanomaterials, as compared to the bulk, are more prone to defects and surface reconstruction.^39,40 To passivate the material, surface surfactants and ligands as well as core–shell architectures are employed; however, these techniques in turn introduce additional complexity as well as tunability. For traditional first-principles modeling and associated property screens, where the cost of computation scales rapidly with the number of atoms necessary to describe the material, such chemical and structural complexity presents challenges.

While periodic DFT codes perform efficiently on reasonably well-ordered bulk materials with up to hundreds of atoms/unit cell, many nanomaterials require a much larger number of atoms to account for, e.g., hybrid, defective, and disordered structures, as well as complex surface chemistry, depending on the details of the environment (pH, chemical potential, salts, and solvent).

In the following, we discuss the current status of data-driven approaches to predicting materials structure and functionality, specifically focusing on bridging the gap between bulk to nanomaterials (Figure 2).

Figure 2.

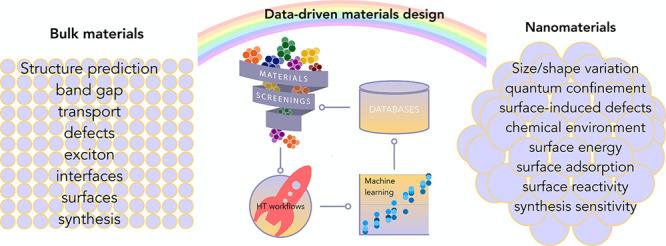
Properties relevant for general bulk materials and additional properties that are unique to nanomaterials as a result of nanosizing. We note that the properties in bulk are also native to the nanomaterials. The middle panel is the data-driven methods including database query, materials screening, HT workflows, and machine learning.

Nanomaterials Structure Prediction

In nanomaterials, the size and morphology provide extra degrees of freedom that add tunability of properties as well as complexity of the available phase space. To explore and direct synthesis efforts in this phase space, computational structure prediction can provide a map of stable, low-energy synthesizable configurations.

Nanoparticles are one class of nanomaterials that have a wide range of shapes and sizes. Nanoclusters are a subclass of nanoparticles, delineated as such due to their ultrasmall sizes. Nanoclusters comprise up to 100–150 atoms (<1 nm), while nanoparticles generally refer to larger structures between 1 and 100 nm. This distinction originates from the irregularity of nanoclusters, which have stronger quantum confinement effects, off-lattice atomic arrangements, variable bond lengths, and more diversity in their resulting properties. On the other hand, nanoparticles typically exhibit atomic configurations and symmetries that resemble the bulk crystal structure, which in turn correlates with more predictable properties.

Identifying stable nanocluster geometries computationally is important for comparing to experimental measurements and directing synthesis efforts; however, the time and length scales will generally determine the level of theory that is computationally tractable. Nanoclusters are small enough to be calculated with DFT, including dispersion corrections, hybrid exchange–correlation functionals, spin–orbit coupling, implicit/explicit solvation, and stabilizing ligands for increased accuracy. Typically, however, DFT is too expensive to consider for calculating a nanoparticle, an array of nanoclusters, or a simulation over many time steps. For this reason, less computationally expensive methods are typically used to estimate the structure and energies, including semi-empirical tight binding methods or interatomic potentials.⁴¹

The potential energy surface (PES) of a nanostructure dictates the global minima, i.e., the most stable atomic configurations given the composition. Sampling the entire PES via first-principles methods in the complex geometry is computationally infeasible; hence, a number of structure generation methods have been developed. The major techniques to generate plausible structures are genetic algorithms,⁴² basin hopping,⁴³ random structure searching,^? and simulated annealing.⁴⁴ Less standard methods include particle swarm algorithms⁴⁴ and other variants of these broad methods including tree growth algorithms,⁴⁵ Tabu (“taboo”) algorithms,⁴⁶ and ab initio random structure searching (AIRSS).⁴⁷ Several reviews have previously highlighted these techniques and their advantages for certain systems.⁴⁸⁻⁵⁰ Furthermore, some of these algorithms have been adapted to screen for properties beyond thermodynamic stability, such as vertical electron affinity.^51,52

An efficient method to rapidly generate structures is to simply reuse and recalculate structures that were previously found for similar elements. As an example of this approach, Sokol et al. conducted a data mining study with the idea that binary heteropolar materials have similar energy orderings to one another and showed that the low-energy structures of (ZnO)_n clusters exhibit similar energy orderings when applied to other binary heteropolar materials such as (AlN)_n.⁵³ The tendency of certain elements to behave similarly at the nanoscale can be quantified by comparing the relative ordering of stabilities for structures with each element. The similarity of different elements at the nanoscale was quantified by comparing the energy rankings of clusters with similar atomic arrangements at the nanoscale for all elements in the Quantum Cluster database.⁵⁴ A study conducted by Chaves et al. is another example of a systematic study of transition metal nanoclusters, where they used structures from literature as a starting point and then conducted a Revised Basin Hopping Monte Carlo structure search.⁵⁵⁻⁵⁷

An interatomic potential (IAP) is an empirical parametrization of a potential energy surface that can be fitted to nanoparticles. Recently, machine-learned potentials (MLPs) specifically applied to nanoparticle systems have become increasingly sophisticated and can rival traditional atomistic methods. Machine learning potential regression methods bring benefits over more traditional physics-based methods in that the models can be built agnostically to the material, applied to a diverse set of input systems, and have been shown to improve the topology of the PES.^41,58,59 It is important to note that, like any parametrized model, MLPs are fundamentally limited by the quality of their training data. Many, on the order of 50000, first-principles calculations of nanoclusters, including their structures, energies, and forces, are required to fit IAP models with very good accuracy,^59,60 with the possibility of reducing that number to ∼500 calculations by using active learning that iteratively queries the energy landscape in regions of failure and updates the training pools.⁶¹ IAPs excel at small structures for which we can sample many configurations, and large structures in which bulk-like behavior and surface facets dominate. On the other hand, medium-sized structures, on the order of a few hundred atoms large, are challenging because they fall between the two regimes—they are typically too large for first-principles approaches and too disordered to model as a bulk crystal with surface facets. Bridging the data gap between these two length scales will be the key to future developments in nanoparticle structure prediction.

Cluster expansions, methods typically applied to bulk crystals with well-defined lattices, have emerged as a possible approach to rapidly estimate the energies of nanoparticles. Cluster expansions have effectively modeled the surface and adsorbates of nanoparticles.^62,63 An off-lattice cluster expansion formalism, the Atomic Cluster Expansion (ACE), has recently been developed by Drautz.⁶⁴ PACE, the performant open-source implementation of ACE, has exhibited comparable accuracy and performance for small Cu and Si clusters as other MLPs.⁶⁰ Other equivariant MLPs that have recently emerged and show excellent accuracy include the Neural Equivariant Interatomic Potential (NeQuip),⁶⁵ Allegro,⁶⁶ and MACE⁶⁷ (a message-passing variant of ACE).

We emphasize the usefulness of diligent data reporting standards, as combining data from several individual studies can provide a superior starting point for further development by furnishing informed guesses of stable structures when considering a new system. Curating quality data on the energies and geometries of nanoparticles will act as innovation multipliers across the broad range of nanomaterial design efforts. Furthermore, the record of prior tuned/trained IAP speeds up the development of potentials, thus improving the efficiency of structure prediction. We note here the example of OpenKIM and NIST interatomic potential repositories, which have archives of previously fitted potentials for many systems.⁶⁸⁻⁷⁰ Databases such as these provide excellent avenues to build on existing work and close the gap from bulk to nanostructures.

Design Metrics of Materials: Bulk to Nanomaterials

In searching for materials with favorable properties for a specific application, generally, multiple metrics are of importance. A consideration of computational cost and robustness/accuracy is optimized typically through a funnel-type investigation where multiple filtering steps are needed, applying increasingly strict criteria and/or computationally intense properties toward the end. In the following, we discuss several commonly used criteria used in data-driven searches for materials in applications where nanosizing is prevalent (Figure 4). We note the use of nanocrystals (NCs) as model nanomaterials throughout the discussion.

Figure 4.

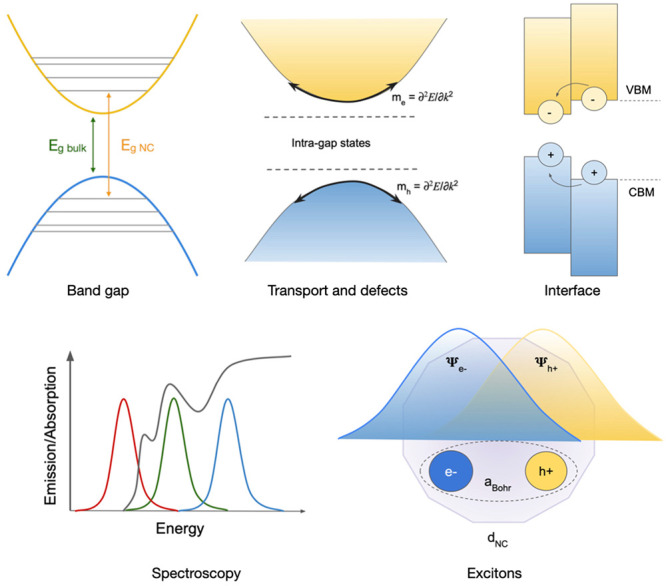
Schematics of relevant design metrics in electronic structure screening of solid materials. E_g stands for band gap, and NC stands for nanocrystals. m_e and m_h are the effective mass of electrons and holes, respectively. VBM and CBM refer to the valence band minimum and conduction band maximum. Ψ_e and Ψ_h refer to the electron and hole wave functions, respectively; and a_Bohr is the Bohr radius of the exciton. d_NC stands for the nanocrystal size.

Stability

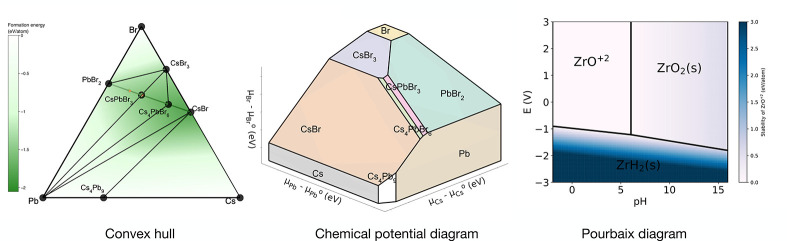
Stability commonly provides the first screening metric in high-throughput (HT) materials design and can be employed for both bulk and nanomaterials. Relevant quantities for stability include formation energy ΔH_f and E_hull (energy above convex hull) where the formation energies ΔH_f are calculated using elemental chemical potentials to determine if the compound is favored to form from the constituent elements. In contrast, the energy above hull (E_hull) determines the distance between the energy of the compound and the geometric, bounded shape consisting of all phases within the relevant chemical space that exhibit energy lower than any other phase or linear combination of phases at the respective compositions (Figure 3). E_hull is a more demanding metric than the formation energy and hence is often used as a descriptor for stability against decomposition to other phases.⁷¹⁻⁷³ A similar metric to E_hull is the decomposition enthalpy ΔH_d to measure the stability against other phases.⁷⁴ Phase transitions into alternative structures at fixed composition can be elucidated via the occurrence of phonon imaginary frequencies,⁷⁵ and solid–solid polymorphic phase transition may occur when the external conditions enable a low activation energy barrier.^76,77

Figure 3.

Diagrams for finding stable compounds. The convex hull diagram denotes the relative energy (shown as a color map) of a composition with respect to the lowest energy boundary of other phases or linear combinations of those phases. The chemical potential diagram looks at the same phase stability by tuning the chemical potential of the constituent elements, indicating the relative stability of a phase at a certain chemical environment. Both the convex hull and chemical potential diagram are generated for CsPbBr₃ using the Materials Project phase diagram tool. The Pourbaix diagram is a way to identify stable nanostructures in an aqueous environment as the pH and voltage vary (example generated using the Pourbaix diagram app on Materials Project for Zr).

While these quantities provide a basic understanding of the energetics, they do not always translate to synthesizability. DFT calculations are carried out at 0 K, and at elevated T, vibrational and configurational entropy contribute toward the free energy. Recently, Aykol et al.⁷⁸ showed that synthesis of any material, nanometric or bulk, is subject to the enthalpy limit of the analogous amorphous state, a useful result as many nanomaterials exhibit high enthalpies of formation. Indeed, the prolific existence of diverse carbon nanostructures is enabled by the abnormally high enthalpy of amorphous carbon, allowing for a large window of metastability.

Since nanocrystals possess large surface-to-volume ratio, specific surface facets relevant to the morphology, size, and polymorph will impact stability as well as functionality,^17,79−81 and large surface areas lend themselves to the stabilization by a chemical environment (Figure 3), e.g., chemical potential, surface reconstruction, and/or ligation. For instance, Singh et al. used Pourbaix diagrams as a filtering tier for photocathodes, removing over 95% of the materials under consideration, thus highlighting the importance of including aqueous stability metrics (Figure 3).^73,82,83 Finally, while entropic differences between bulk solids are often neglected, increased defect populations and various atomic configurations in nanostructures can contribute to significant entropy effects, leading to improved thermodynamic stability.^84,85 Overall, the stability of nanomaterials is closely related to the size, shape, and surface chemistry and must be understood for individual materials. To the best of our knowledge, HT studies for the stability of nanostructures are rare.⁸⁶ As a step in the right direction, the construction of phase diagrams, including a chemical environment and the corresponding surface energies of the underlying bulk materials,¹⁷ will be highly beneficial for the initial screening.

Band Gap

In optoelectronics and photocatalysis applications, the ideal band gap is one of the most determining descriptors for functionality. For solar cells, in particular, the thermodynamic limit states that the theoretical efficiency of a light absorber reaches its maximum at a band gap of 1.3–1.4 eV.⁸⁷ A direct band gap is commonly favored over an indirect band gap for more efficient absorption or emission as it does not require phonons to compensate for the momentum transfer. In other optoelectronic applications, band gap requirements can differ widely; e.g., a band gap across the whole visible light range (1.65–3 eV) is considered desirable for LEDs, while, for transparent conductors, band gaps larger than the energy of visible light threshold (3 eV) are preferred.^88,89

HT computational studies generally use band gaps calculated by the efficient and low-cost functional GGA-PBE as the first step, with subsequent corrections to account for the underestimation of E_g,^90,91 or followed by additional screening of more expensive hybrid functional calculations to narrow down the candidates.^71,72,92,93 While hybrid functionals or GW-theory-based approaches offer improved accuracy, the computational cost is orders of magnitude higher and requires expert knowledge to converge co-dependent parameters. While some work has used GW band gaps either as the middle or the last step in the screening process, there are—to the best of our knowledge—no robust automated workflows.^94,95 Recently, van Setten et al. identified a correlation between the number of empty bands and energy cutoffs in the self-energy, and a better description of the experimental band gap by the G₀₀^GN@PBE (with plasmon-pole approximation) than the linear model.⁹⁶ Rasmussen et al. further investigated numerical methods to correct the error in the linearized quasi-particle self-energy.⁹⁷ Both these efforts toward an HT GW workflow stress the importance of an accurate starting point at the Kohn–Sham energy.

With large amounts of theoretically calculated band gaps, machine learning help elucidate the structure–property relation. Emphasizing the importance of physically meaningful descriptors, various studies⁹⁸⁻¹⁰⁰ have shown excellent mapping of bulk band gaps onto compositional representations for the materials. Single-value scalars such as band gap, ionization energy, and electron affinity are commonly used descriptors,¹⁰¹ and even the densities of states have been used as a complex input feature for mapping the relationship between materials and their electronic structure.^102−104

In nanostructures, increased band gaps are expected as a result of quantum confinement,¹⁰⁵ which follows the relation of ΔE_g ∼ 1/R² for an infinite well (Figure 4).^106−108 Different schemes are applied depending on whether the regime of confinement is weak, intermediate, or strong, as the size of the NC approaches the size of the exciton Bohr radius, resulting in different relations of ΔE_g with respect to the size.^{16,17,109−111} The dimensionality of the nanostructure also affects how the band gap behaves with regard to size. For example, in 2D materials, the band gap is confined in the out-of-plane direction but remains bulk-like in-plane, offering an extended design space.¹¹² These works show the value of developing physics-based descriptors that connect bulk properties to the specifics of the nanocrystal symmetry and dimensionality.

Transport

The flow of charged carriers are crucial in determining the efficiency of an operating semiconductor (Figure 4). The quantum mechanics of carrier mobility are described by the transport equations with different levels of approximations from semiempirical to fully first-principles.^113−119 In the simplest Drude model, the mobility is inversely proportional to the effective mass: 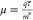, where q is the charge, τ̅ is the mean free time, and m* is the effective mass.¹²⁰ While multiple scattering mechanisms, including phonon, impurity, defect, and surface scattering, are responsible for slowing down the mean free time, effective masses are a key element in determining the intrinsic carrier mobilitiy, μ. The effective masses of electrons and holes in semiconductors are derived from the dispersion of the electronic structure, precisely, the inverse of the second derivative of the energy with respect to wavenumber, e.g., the effective mass of the carriers, m_e^* and m_h, for electrons and holes, respectively: 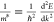, in the parabolic approximation. In a charge-based device, m* should ideally be small as light carrier mass facilitates carrier mobility, and thus more efficient carrier extraction in the case of a light absorber, or fast recombination in the case of a light emitter. In thermoelectrics, small m* and band degeneracy are favored to deliver a high power factor.^88,121,122 Many studies have considered effective mass in the screening steps as an additional filter to band gap, with m* ≤ 0.1m₀, in which m₀ refers to the free electron mass.^88,92,93

In nanostructures where quantum confinement effects are present, the effective masses derived from the bulk band structures can be inaccurate (or undefined) due to the modified band structure.¹²³ When the crystal size is limited, the electron (hole) wave functions are confined within the crystal boundaries and the effective mass becomes energy-dependent^124,125 As a general trend, the effective mass is expected to increase as crystal size decreases due to reduced dispersion at band edges; however, as shown in a literature comparison of ZnS NCs, this is not always the case experimentally due to crystal orientations, impurities, and other factors.¹²³ Carrier mobilities have been shown to decrease with NC size,¹²⁶ most likely due to enhanced surface scattering; in these cases, surface passivation is useful to reduce carrier trapping.¹²⁷ It is also noted that many thin films grown with low-cost methods introduce nanocrystalline domains or grains, both within the film and at surfaces or interfaces, and the nanostructure of these films can dominate properties such as electronic transport and optical absorption. For example, in many nanocrystalline thin films (e.g., Ag,¹²⁸ CdSe,¹²⁹ and ZnO,¹³⁰ among others) conductivity is decreased from that expected in a bulk material due to variable range hopping, in which thermally activated charge carriers “hop” between localized states in different crystalline domains.^131,132 Hence, multiple factors contribute to carrier scattering in nanomaterials; therefore, the effective masses derived from the parent bulk can only be used as an estimation rather than a prediction for the final transport.

Defects

While the electronic structure of the parent crystal serves as the foundation for understanding the electronic behavior of materials, defects should not be overlooked, as they are ubiquitously present in any material—both bulk and nanomaterials (Figure 4). Point defects, including vacancies, substitutional defects, and impurities can introduce charge transition levels either within the band or in the gap. The latter is considered a “deep” defect that acts as a recombination center that traps electrons or holes, hindering the energy conversion process, and hence deteriorating the device performance. To determine the configuration, concentration, and charge transition levels of these defects present by no means trivial tasks, requiring large supercell calculations to simulate the dilute limit.¹³³ In the case of charged defects, various charge states need to be considered for which additional corrections are needed to account for the periodic image effect.^134,135 Due to the increased complexity of such calculations, defect levels are usually present at the last step of the high-throughput screening projects.^93,94,136 Computationally less demanding methods such as the atomic-orbital-based method (LCAO) was used by Kuhar et al. to investigate the electronic structure, and specifically, the density of states (DOS), in the presence of vacancies. Compounds with mid-gap energy states were ruled out, aiming at filtering out those with detrimental intrinsic defects.⁹³ Another study by Hinuma et al. examined more specifically the formation energy diagram in crystalline Ca₂ZnN₂, CaZn₂N₂, and CaMg₂N at the last step of the screening process and provided guidance for synthesis conditions to achieve favorable defect concentrations. Kumagai et al. developed codes for HT point-defect calculations to characterize oxygen vacancies in oxides and were able to identify electronic structure characteristics that affect the defect formation energy.¹³⁶ We note that high-throughput descriptors such as the hydrogen interstitial defect energy (i.e., the “hydrogen descriptor”)¹³⁷ and the branch point energy^138−140 have been proposed to assess doping type in semiconductors.

There has been excellent recent progress in the automation of defect calculations. Several packages provide point-defect calculation workflows, for instance, PyCDT, PyLada and PyDEF, which enable the automatic calculation of defect formation energy with image charge corrections.^141−143 With the help of these computational frameworks, broader and systematic defect calculations are made possible, which in turn enables future databases of charged defect properties across chemical systems and structures. Collection of defect information will lead to improved understanding and trends of how to rationally design functional materials, e.g., in optoelectronics and quantum materials applications. The Quantum Point Defect (QPOD) database is an example that contains more than 1900 defect systems comprising various charge states of intrinsic point defects in a set of 2D semiconductors and insulators.¹⁴⁴

For NCs, the large surface-to-bulk ratio and often nonstoichiometry composition further induce more defects in addition to the ones existing in bulk, where trap states are often formed within the band gap.^37,38,145 It is nontrivial to directly compare the defect formation energies calculated for the bulk to nanostructures, but we note a few key differences. First, unlike bulk materials, the defect formation energies in NCs are location-dependent, where the defect concentrations are likely higher on the surface than in the core.¹⁴⁶ This means that the defect levels may be tuned by merely changing the size of the NCs.¹⁴⁷ Second, dangling bonds on the surface introduce localized surface states that are often deep traps, which are not captured by the bulk defect calculation.^37,148,149 Third, the formation of NCs typically happens in colloidal solutions, meaning the chemical potentials may be considered as ion pairs instead of solid precipitates.³⁸ These different behaviors present challenges for directly using bulk defect energetics, and additional considerations for surface defects must be given as materials approach the nanoscale.

Exciton Binding Energy

Another design-relevant electronic structure property is the exciton binding energy, E_b, which is the minimum energy required to separate an electron and hole pair. Depending on the application, the ideal E_b differs. While a small E_b is beneficial for the separation of electron–hole pairs in a solar cell for efficient carrier extraction,¹⁵⁰ a large E_b may be preferred for a larger quantum yield in a light-emitting diode.¹⁵¹ Formally computing the exciton energy involves calculating the bound states of the electron–hole pair via Bethe–Salpeter equation (BSE), a computationally demanding method that is challenging to automate. In the hydrogen-like Wannier–Mott approximation assuming band edge excitation, the exciton binding energy is simplified as 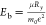, where R_y is the Rydberg constant, μ is the reduced mass of the electron and hole 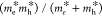, and ϵ is the dielectric constant (often ϵ_∞, the high-frequency dielectric constant, is used). The exciton radius equals m₀ϵa_H/μ, where a_H is the hydrogen Bohr radius. The quantity ϵ, including ϵ₀ (static dielectric constant) and ϵ_∞, can be obtained from density functional perturbation theory (DFPT) calculation. Currently, ϵ calculated for >7000 materials are tabulated on Materials Project, allowing for analyses of bulk trends over structure and composition.¹⁵² Furthermore, optical spectral information, e.g., photoluminescence emission and UV/vis absorption spectra, are often used for inferring the exciton binding energy. Computational spectra that include many-body interaction (GW plus BSE) generally compare well with experimentally measured spectra for semiconductors, where the energy difference between the absorption onset and electronic band gap determines the exciton binding energy: E_b = E_g – E_opt.^153−158 Study by Yang et al. also showed that the band-to-band vertical optical transitions obtained at the independent-particle approximation with an HSE band gap correction compare well with experiments, providing a good starting point for accurate high-throughput optical spectra.¹⁵⁹

Transferring trends in exciton binding energy between bulk and nanosized materials should be exercised with caution. In structures that are smaller than the Bohr radius of the exciton, the wave functions of the electrons and holes become spatially confined, and thus the overlap is strengthened, leading to increased exciton binding energy (Figure 4).^16,160−162 Furthermore, the exciton fine structures caused by exchange interaction depends closely on the size and shape of the crystals,^160,163,164 and can reverse the energy order of the dark/bright states.¹⁶⁵ Notably, the dielectric constant also changes due to reduced screening in the finite-size system, resulting in enhanced exciton binding energy.¹⁶⁶

Interfaces

Interfacial alignment in nanomaterials has a fundamental impact on materials performance and device functionality; however, the electronic structure of an interface is intimately connected to the stability of a given nanomaterial with respect to its external environment. One simple yet useful metric of thermodynamic and chemical stability in bulk interfaces is the Materials Project’s Interfacial Reaction Calculator,^6,167 in which “reactants” are the materials in contact with one another. The reaction energy descriptor E_rxn indicates whether a stable solid–solid interface is favorable to form under canonical thermodynamic conditions, as well as the degree of instability of any unintentional product. This descriptor has been predictive in polycrystalline and nanocrytalline thin film interfaces such as CdTe–Cu_xZn_1–xS,¹⁶⁸ determining an unstable interface and accurately predicting the products observed experimentally, and has promise for assessing the stability of other nanocrystalline interfaces.

In electronic devices, sufficient alignment of band extrema (CBM and VBM) between neighboring materials is crucial to ensure efficient charge transfer (Figure 4). In semiconductor heterojunctions and metal–semiconductor junctions, the relative energies of the CBM, VBM, and work functions dictate whether electrons and holes can flow efficiently across the interface. For instance, for a water splitting reaction to occur, the CBM should be higher than the proton reduction potential and VBM lower than the oxidation potential of water.^169,170

DFT slab calculations are often used to compute band offsets; however, the approach comes with caveats that are exacerbated in nanomaterials.^171−173 Since detailed knowledge of chemical as well as structural features of interfaces is rarely available, results based on explicit first-principles calculations should be interpreted with caution, employing reliable reference states. Within DFT, the absolute values of the eigenstates should not be directly compared as they depend on the pseudopotentials, basis sets, and functionals. The vacuum should be the common reference level to compare across different codes and databases.

Band alignment in real materials is surface-specific and hence highly dependent on the facet of the exposed surface, the surface morphology, and interfacial defects; however, there is not yet a consensus among the DFT community about how to treat nanocrystalline thin film interfaces.¹⁷⁴ Additionally, in solid–liquid interfaces the direct comparison of reference levels ignores the fact that the surface dipoles between the semiconductor and liquid can impact the band edges and qualitatively alter the comparison with experimental results.¹⁷⁵ State-of-the-art computational frameworks have recently been developed to take into account the aqueous–solid interface to obtain the correct electrostatic alignment.^176,177 However, these approaches rely on a case-by-case examination of a specific system, hence difficult to apply in HT workflows for systematic data production.

Surface Adsorption

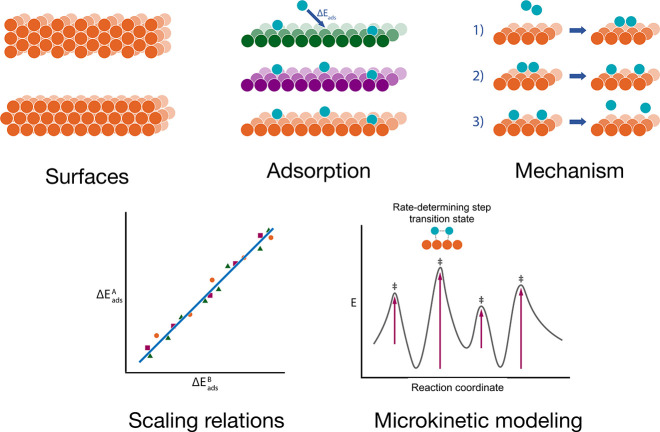
The adsorption of a molecule to a solid surface is relevant for many applications including catalysis and sensors, thus providing one of the most widely used descriptors of surface reconstruction, reactivity, and catalytic activity. The adsorption energy is essential in determining the mechanism of formation and breaking of the bonds, and it depends on the geometries as well as on the electronic properties of the surface and adsorbates (Figure 5).¹⁷⁸ Therefore, mapping out the adsorption energy for different sites and adsorbates using computational methods provides rich information on the geometrical and chemical determinants for active adsorption sites. Indeed, we have seen a steady growth of HT workflow development and data of adsorption energy for transition metal surfaces for catalyst design.^179−181

Figure 5.

Schematics of relevant phenomena and modeling approaches for surface reactivity: identifying relevant surfaces, adsorption sites, and energies; elucidating reaction mechanisms; scaling relations in adsorption energy; and microkinetic modeling by investigating the transition states.

Standardized and reproducible workflows can expedite the screening. An HT workflow for computing adsorption energies on solid surfaces was developed by Montoya et al.¹⁸² using the codes Atomate and Pymatgen.^6,183−185 The workflow allows for (i) generation of slabs corresponding to all of the unique terminations in a bulk, (ii) identification of adsorption sites using a triangulation network of surface sites, and (iii) DFT geometry optimizations with automated error corrections^6,185 for all of the empty slabs and adsorption structures. Adsorption energies computed using the workflow with the revised PBE (RPBE) functional¹⁸⁶ for a series of transition metals showed close quantitative agreement with experimental values.

Inorganic semiconductors are widely used as photocatalysts, and their surface chemistries are more complex than metals due to less homogeneous electronic density at the surface, dipole formation, and strong site dependence. An automated DFT adsorption workflow was developed by Andriuc et al.¹⁸⁷ This workflow, while building on the previous Atomate version,¹⁸² features computational improvements in efficiency and robustness using relaxed structures, frozen core slabs, and a slab–adsorbate distance optimization step. The computed metrics include semiconductor-specific properties for photocatalysis (e.g., the p-band center, or the elemental makeup of the conduction band minimum and the valence band maximum).

Compared to inorganic systems, hybrid materials often exhibit more complex structures, with nonhomogeneous electron densities at surfaces that require more careful handling. An HT DFT framework for screening metal–organic frameworks (MOFs) was developed by Rosen et al. for heterogeneous catalysis applications, where two different methods are used to identify adsorbate sites: a geometry-based one meant to identify adsorption sites on undercoordinated atoms and a potential energy grid method designed to find low-energy adsorption sites.¹⁸⁸

Despite these advances, challenges remain pertaining to (i) rotational degrees of freedom for larger, more complex adsorbate molecules, (ii) concentration-dependent behavior associated with the adsorbate coverage, and (iii) the high computational cost of DFT for larger systems.

To accelerate learning at a reduced cost, machine learning methods are being rapidly developed.^189−194 For instance, Tran et al. developed GASpy (Generalized Adsorption Simulator for Python), a dynamic workflow for DFT adsorption data.¹⁹⁵ Their “smart database” approach implemented surrogate-based optimization and active machine learning concepts which allow for the exploration of a broader chemical space at a reduced cost. Each adsorption site was represented by a vector of the atomic number, Pauling electronegativity, coordination number, and median adsorption energy of the adsorbate on the pure element.^195,196 Among other noteworthy data resources, The Open Catalyst Project¹⁹⁷ was designed as a community effort toward developing machine learning models. The database (OC20) contains 1.2 million DFT relaxations of adsorption structures built from different adsorbates and surfaces of metallic materials, including relaxation trajectories, charge analyses, and orbital information. Using these data, including randomly perturbed structures, the Project aims to use machine learning to replace or augment DFT simulations. Notably, the performed baseline graph neural network (GNN) models would require 10 orders of magnitude larger data set to achieve the desired accuracy in predicting the total energy against DFT, proving the necessity of both increasing the data quantity and improving the physics-informed representations.¹⁹⁷ The recently released OC22 data set, including more than 60K oxides calculated by DFT, improved in accuracy in the prediction of total energies and forces by joint training of the OC20 data set, suggesting the importance of including a variety of data sets of complex systems.¹⁹⁸

These challenges call for further development in building comprehensive data sets: the surface energy and adsorption energy are the most essential information in determining the exposed facets, the shape of the nanocrystal, and the possible active sites, providing valuable descriptors for compositions in training ML models. Standardized workflows and data sets for these properties will be instrumental.

Surface Reactivity

Surface reactivity can be described by microkinetic modeling (Figure 5), which requires the thermodynamic properties of absorbed species and the rate constants.^199−201 The rate of surface-mediated bond disassociation rely on computing adsorption and transition-state energies, a computationally demanding parameter if using traditional quantum chemical methods. These energies then propagate in physical models to predict the rates of reactive events. The large parameter space involved in these processes can be reduced to low-dimensional “descriptor space” via scaling relations of the adsorption energy, thereby enabling HT screening based on a few metrics such as adsorption energies and electronic structure properties (Figure 5).^202−204 Automated methods based on machine learning have been shown to be efficient in navigating reaction pathways by combining DFT adsorption energies and scaling relations.²⁰⁵

Despite recent advances, there are challenges in modeling nanomaterials surface reactivity. First, surface reactivity is highly affected by particle size. A study by Li et al. showed there exists an optimal chemical ratio and size of a FePt nanoparticle for CO oxidation using DFT.²⁰⁶ In another computational study, Yudanov et al. elucidated that the CO adsorption energy is correlated with the Pd nanocluster size.²⁰⁷ It was found that CO interaction weakens as particle becomes smaller up to a critical size and that CO adsorption energy approaches the bulk adsorption energy as the size increases. Second, the specificity of active sites and the chemical environment influences surface reactions. Understanding of site activity requires a priori knowledge of the atomic structure and reaction site calculated by DFT, which can deviate substantially from real materials interfaces, where surface passivation, reconstruction, and defects are prevalent. A wide span of parameters, from pressure, temperatures, and pH, to reactants/products species and concentration, and to solvents and electrolytes can influence the surface chemistry and topology, making it extremely difficult to derive one prediction which holds for all conditions.^169,203 Hence, surface reactivity trends with surface and interfacial conditions may prove more useful, as exact information about the surface states may not be available. For data-driven design of materials with target reactivity, there is a pressing need for well-structured and transferable databases with reliable metadata that reports surface- and site-related properties, as well as chemical environments and kinetics.^208−210

In summary, designing functional nanomaterials present challenges as well as opportunities for data-driven research. Current HT studies mostly consider bulk material properties due to computational constraints, and hence one must bear in mind their limitations when transferring the knowledge into the nano domain. Indeed, one set of materials/properties may respond differently to nanosizing than others. To accurately describe the nano phenomena can be computationally demanding even for one system, much less in high-throughput fashion. In order to overcome this challenge, systematic reporting and curation of experimentally measured nanostructure data, including but not limited to shape-, size-, surface-, and defect-dependent properties, are needed. A few databases of experimental characterization at the nanoscale are available, such as electron energy loss spectrum^211,212 and refractive index²¹³ etc., but these resources are often for small sets of materials. Indeed, the development of robust, efficient, and accurate computational workflows is hampered by the lack of systematic, well-curated public experimental data to benchmark against for determination of a reasonable level of theory and numerical parameters. Therefore, progress in systematic reports of experiment synthesis and characterization will facilitate data-driven materials research, both from an experimental and a computational perspective.

Toward Predictive Synthesis

While the modeling and data-driven predictions of materials properties and their correlations with the underlying structure have made significant advances in the past decade, predictive synthesis is still in its nascency. The phase space of possible structures is high-dimensional, and the reaction pathways between competing phases are driven by both thermodynamic and kinetic factors. Minor changes in the intricate interplay of experimental conditions, including reactants, concentrations, temperature, pressure, humidity, etc., can translate to distinct phases and unwanted byproducts.

As noted in Section Stability, the thermodynamic energy surface of all phases and multiphase equilibrium can be inferred from a computed convex-hull phase diagram (Figure 6). Phases that are calculated to be close to or on the convex hull are predicted to be thermodynamically metastable/stable at low temperatures but may not be easily synthesized, for a variety of reasons. In this context, a survey of the ICSD entries showed that the experimentally found compounds can exhibit energies greater than 100 meV/atom above the convex hull, depending on the anion chemistry. Some of these materials are synthesized under conditions where the environmental parameters competitively lower their free energy and then remain kinetically trapped at lower temperatures.²¹⁵ Thus, the proximity to the convex hull provides a guide to synthesizability, but environmental factors as well as kinetics influence the final results.

Figure 6.

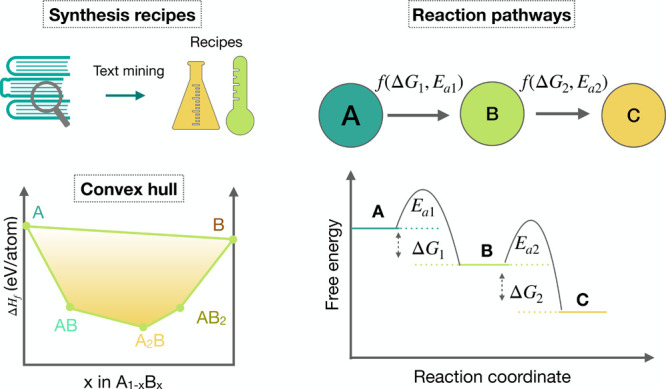
Schematic for data-driven methods for guided synthesis in inorganic solids, including natural language processing, convex hull stability, and reaction pathway prediction. ΔG represents free energy difference, and E_a represents activation barriers. Right panel adapted with permission from ref (214). Copyright 2021 The Authors under Creative Commons Attribution 4.0 International License, published by Springer Nature.

Combining the timeline of experimentally discovered compounds with their stability determined by the convex-hull diagram, the likelihood of synthesis of a target material can be approximated using graph networks and machine learning models.²¹⁶ Via the application of pathfinding algorithms, McDermott et al. predicted the most probable reaction pathways to a target material using the DFT-calculated ground-state bulk energy including a machine-learned vibrational entropy²¹⁷ of all stable phases for the particular chemical systems (Figure 6).²¹⁴ Selectivity rules based on chemical potential maps²¹⁸ have been shown to inform the selection of precursors to maximize the yield of the target materials. Information about competing phases, such as the amorphous limit⁷⁸ or entropically favored materials,²¹⁹ can help to exclude materials from consideration that are unlikely to be successfully synthesized.

While a reaction pathway determines whether the synthesis route is possible, a synthesis recipe must also include environmental conditions. While the formation of crystal is controlled by nucleation and growth, the process depends on many factors, such as nucleation barrier, surface free energy, and the free energy of the reaction pathway.²²⁰ Information about the synthesis environment, such as solution salts and impurity ions, has been shown to impact the kinetics of structure selection.²²¹ Often times, the description of the synthesis conditions is embedded in the literature, making it difficult to directly mine the data. To unravel the vast information, efforts using natural language processing are underway to harness the treasure trove of published synthesis recipes.^222−225 These machine-learning-based approaches have the potential to deconvolute kinetic and thermodynamic factors, especially when combined with thermodynamic predictions of phase competition. However, notably, published work is highly biased toward successful outcomes²²⁶, and greater efforts to capture the entire experience of experimental synthesis are needed.

Successful predictions resulting in synthesized materials are still limited. The reasons are 2-fold. First, it remains unclear in experiments which factors precisely determine successful synthesis outcomes. A wide range of experimental synthesis methods exist, and the determining parameters may differ in each method. Second, compared to extensive research on understanding their properties, materials modeling has paid less attention to how materials are made in the real world, resulting in a knowledge gap between the theory and experiments.

Rationalizing synthesis is an area of materials science and chemistry that is in dire need of harnessing the knowledge that is today largely embedded as human experience. Automated robotics laboratories and associated data infrastructure will become a crucial component toward this goal, delivering standardized, consistent, and successful as well as unsuccessful “dark reactions” synthesis data and results.^226−234 Availability of such data enables the correlation between conditions and outcomes, which can be analyzed via, e.g., classification methods.²²⁴ Ontology, as a branch of computer science, has also been applied to semantically represent materials informatics for machine interpretability.^235,236 The HT capabilities of robot-driven laboratories will contribute large amounts of quality synthesis data to the aforementioned models, enabling the predictive simulation of possible scenarios.

Data-Driven Nanomaterials Synthesis

In addition to bulk synthesis, nanomaterials pose another set of synthesis parameters including but not limited to size, shape, and ligand chemistry.^237,238 Experimental observations show that the phase stabilities of NCs are dependent on sizes, where the metastable bulk phases can be stabilized by a more favorable surface energy as compared to the bulk ground state.^17,239−242 Questions associated with bulk materials synthesis still exist for nanomaterials, adding complexity with regard to controlling these parameters. Minor changes in synthesis conditions (e.g., temperature, mole ratio, and the length of alkyl chains) of nanomaterials can lead to significant variations in composition, dimensionality, morphology, short-range order, etc., all of which impact the electronic and optical properties.^243−246

How to easily access this information becomes the accelerator for nanomaterials synthesis. Nanoparticle databases have emerged in an effort to assemble a vast collection of metadata that includes both experimental and theoretical data. Among multiple databases (Table 2), we highlight a few as excellent sources of data. The NOMAD (Novel Materials Discovery) Laboratory is a curated database of shared data from both experimental and computational studies and includes a search engine, a Python API, and over 2 M clusters in the database.⁷ The Open Catalysis Project is a computational database for catalyst structures, with 1.3 million molecular relaxations that are open-source for training purposes.²⁴⁷ The Cambridge structure database (CSD) contains experimentally observed and computationally verified small-molecule organic and metal–organic structures that have been growing steadily since 1965 and now have over 1 M structures, with over 50% of those involving at least one metal atom.²⁴⁸ The Quantum Cluster Database is an online repository of DFT calculated pure element nanoclusters with over 50K total clusters containing between 3 and 55 atoms.⁵⁴ The clusters comprise a collection of clusters found in literature in addition to clusters generated with a genetic algorithm. An extensive list can be found in a review by Panneerselvam and Choi.²⁴⁹

Table 2. Nanostructure Focused Databases.

Nanomaterial databases	Data sets
Cambridge Structure Database248	Small-molecule organic and metal–organic crystal structures
Quantum Cluster Database54	50k total DFT calculated structures for nanoclusters with 3–55 atoms
Catalysis-Hub263	100k DFT adsorption and reaction energies
Open Catalyst Project197	1.2 M DFT adsorption structures
Materials Cloud22,264,265	2D materials and porous materials
Quantum Point Defect144	Point defects in 2D materials

On the other hand, while there are experimental databases (e.g., caNanoLab,²⁵⁰ NR,²⁵¹ and eNanoMapper²⁵²) specifically for biological/medical applications, including physicochemical properties such as size, shape, composition, purity, surface area, toxicity, and environmental effects (reviews can be found in refs (253) and (254)), a similar resource is not available for the purpose of materials science.

Nanomaterials databases face the challenges of variability in information and how to represent each structure with the appropriate metadata. A theoretically calculated database could include the following: atomic species, atomic coordinates, effective charge, implicit solvent, calculation software, functional, basis set, energy, forces, band gap, electronic structure, etc. An experimentally observed nanoparticle entry in a database could include atomic species, atomic coordinates, counterions present, stabilizing ligands, synthesis recipe, concentrations of reagents, temperature, and percent yield and likely contains information on the average particle size and distribution of sizes. The large available space of features and descriptors adds challenges to the already daunting task of materials synthesis data curation.

Efforts have been made to create universal descriptors. Yan et al. have made efforts to normalize the annotations of nanoparticle databases by creating a procedure to generate 2142 nanodescriptors for each nanomaterial in their open database, Pubvinas.²⁵⁵ These descriptors include physicochemical properties and bioactivities like cytotoxicity and protein adsorption. While Pubvinas has created fixed descriptors for their database, NOMAD has created a posteriori data sorting technique, meaning that their database can continue adding descriptors if necessary depending on the added data.⁷ The challenges associated with general materials data, volume, variety, velocity, and veracity, call for efficient approaches in its exchange and usage, and we encourage the reader to explore references by Draxl and Scheffler^7,256 for more details. We note that the data challenge becomes even more pronounced in nanomaterials, where data-driven research is nascent and the property–synthesis–characterization landscape increases in complexity. This field should also benefit from careful handling of expanding data sets by using the “FAIR” data principles (Findable, Accessible, Interoperable, and Repurposable), a guideline in major databases to enhance data reusability as it becomes crucial infrastructure for physics, chemistry, and materials science.²⁵⁷

The ultimate goal, for experiments, is to provide a highly interpretable set of guidelines that indicate how different tunable factors will influence the products. For synthesis, the most important descriptors are the reaction conditions that led to the experimentally synthesized product and the relative thermodynamic energies of candidate structures. Phase diagrams and intelligent data visualization are great tools for this purpose. In these phase diagrams, partial pressure, chemical potentials, pH, temperature, etc., provide tuning knobs, enabling the identification of promising regions in high-dimensional parameter space for fabricating a target compound.^258−261

There is an opportunity for more development of easily interpretable guidelines on a larger scale. As an example, bulk materials databases like the Materials Project have made significant strides in providing synthesis-relevant data using Phase Diagram and Pourbaix Diagram analysis applications.^6,83,262 Similar analysis applications to facilitate searches through reaction space for nanomaterials would be highly desirable; however, the underlying data are today unavailable. With the rise of data-driven research in nanomaterial synthesis, we expect a rise in the quantity, quality, accessibility, and interpretability of data for nanomaterials synthesis and properties.

Conclusion

The development in data-driven materials research has surged in the past decade, creating an interdisciplinary domain of physics, chemistry, software, and data science. Materials databases are collecting more complex data with far-reaching potentials for functional materials design and guided synthesis.

Nanomaterials, on the other hand, exhibit behaviors distinct from underlying bulk structures, which originates from the confined nature and large surface area. The electronic structure and chemical activity of nanomaterials are controlled by the size and morphology of the crystals, the active surface sites, and the chemical environment. Synthesis is controlled by both thermodynamics and kinetic processes, both of which are highly sensitive to the external environment. There is a nontrivial gap to bridge between bulk and nanomaterials predictive modeling, which data-driven approaches are well-suited for, given the multidimensional, complex landscape. For future development of materials data, the information particularly helpful will be size-, surface-, and environment-specific properties, including surface energies, adsorption sites, various phase diagrams, and reaction networks.

As large-scale computational methods and high-throughput automated laboratories with data curation investments become more mainstream, we believe progress in the accessibility, quantity, accuracy, and complexity of nanomaterials data will profoundly advance this field. We note the opportunities in curating and disseminating experimental results with annotated metadata, as complementary to existing computational resources. The large number of raw data generated by automated laboratories contains highly reproducible parameters and includes a variety of information such as synthesis conditions, which can then be used by machine learning approaches and feeds back into the design process. Given the paradigm shift toward data-centric computational materials research, we are optimistic about the outlook for nanomaterials research in utilizing big data to its fullest potential.

Glossary

Vocabulary

convex hull

energy diagram that connects all ground state polymorphs of a specific chemical system, where points on the connected lines indicate thermodynamically stable phases, while points above the hull indicate thermodynamic instability

nanomaterial

material consisting of particles or constituents of nanoscale dimensions, in which typically at least one dimension is between 1 and 100 nm

quantum confinement

phenomena observed when the size of the particle is too small to be comparable to the wavelength of the electron, described by the quantum well model, and results in discrete energy levels in the valence band and conduction band and an increase of the band gap

reaction network

network of interlinking phases with the nodes representing a combination of phases and the edges representing the reaction pathways, being a complex thermodynamic phase space, where the reaction pathways can be represented by cost functions that combine thermodynamic and kinetic features

scaling relation

correlation between the adsorption energies of different adsorbates on various catalytic surfaces and often used to understand the reactivity of catalysts and to identify promising new catalysts

Author Contributions

The team put together this review collaboratively. In particular: R.X.Y. wrote the Introduction, the electronic structure part of section Design Metrics of Materials: Bulk to Nanomaterials, part of section Data-Driven Nanomaterials Synthesis, and Conclusion, and was responsible for editing the final manuscript. C.A.M. wrote the section Nanomaterials Structure Prediction and part of the section Data-Driven Nanomaterials Synthesis; O.A. and M.S. wrote Surface Adsorption and Surface Reactivity in section Design Metrics of Materials: Bulk to Nanomaterials. R.W.-R. edited the subsections Interfaces and Transport, and M.K.H. edited the general text, particularly with regard to the general databases. K.A.P. conceptualized the scope of the review and edited the manuscript extensively.

The authors declare no competing financial interest.