Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2022 Dec 2;16(12):20222–20228. doi: 10.1021/acsnano.2c05645

Low Power In-Memory Computation with Reciprocal Ferromagnet/Topological Insulator Heterostructures

Hamed Vakili †,*, Samiran Ganguly ‡,, George J de Coster §, Mahesh R Neupane §,∥, Avik W Ghosh †,‡
PMCID: PMC9798907  PMID: 36459145

Abstract

graphic file with name nn2c05645_0005.jpg

The surface state of a 3D topological insulator (3DTI) is a spin-momentum locked conductive state, whose large spin hall angle can be used for the energy-efficient spin–orbit torque based switching of an overlying ferromagnet (FM). Conversely, the gated switching of the magnetization of a separate FM in or out of the TI surface plane can turn on and off the TI surface current. By exploiting this reciprocal behavior, we can use two FM/3DTI heterostructures to design an integrated 1-transistor 1-magnetic tunnel junction random access memory unit (1T1MTJ RAM) for an ultra low power Processing-in-Memory (PiM) architecture. Our calculation involves combining the Fokker–Planck equation with the Nonequilibrium Green Function (NEGF) based flow of conduction electrons and Landau–Lifshitz–Gilbert (LLG) based dynamics of magnetization. Our combined approach allows us to connect device performance metrics with underlying material parameters, which can guide proposed experimental and fabrication efforts.

Keywords: spintronics, quantum transport, 3D topological insulator, ferromagnetic heterostructures, in-memory computing

In-memory computing or Processing-in-Memory (PiM)1,2 is an important emerging architectural design that reduces data movement between the memory and the processor. PiM operates by performing simple intermediate steps along a long chain of compute processes within the memory array itself, as far as possible. The memory layout in a typical PiM architecture is in the form of a grid. Each row and column of the grid is driven by selectors, which enable the cells for a read or write operation. A sense amplifier reads an entire row of the memory cell by comparing its state against a known reference voltage, current, or charge.3 While such a local computing paradigm leads to a significantly reduced footprint, this, however, needs to be traded off against material integration complexity as well as overall switching costs. Recent experiments on spin–orbit torque (SOT) based switching4−9 in FM/3DTI heterostructures suggest TIs as a promising alternative to heavy metal underlayers, because of their higher spin Hall angle. Conversely, the ability of a FM to turn current On or Off in a TI by breaking time reversal symmetry through its orientation10,11 offers an option for a gate tunable selector, atop the intrinsic energy efficiency of a gate-tunable bandgap.12,13 This brings up intriguing possibilities of using the reciprocal interactions between a FM and a TI to realize energy-efficient device configurations.

In this paper we present a 1-transistor 1-magnetic tunnel junction random access memory unit (1T1MTJ-RAM) that can function as a potentially compact, energy-efficient building block of a PiM (Figure 1). The proposed device has two FM/3DTI heterostructures, one functioning as a row-column selector switch, the other as a nonvolatile memory unit. Switching in the second MTJ memory unit (FM2) is based on conventional SOT, with the required spin current at the FM2–3DTI interface provided by the spin momentum locking at the 3DTI surface. The FM that acts as the selector unit (FM1) needs to be electrically switched from out-of-plane to in-plane and back. There are a number of mechanisms to achieve this switching, such as a gated piezoelectric clamped on a magnetostrictive material sitting on the TI14−19 or Voltage Controlled Magnetic Anisotropy (VCMA) at the FM/3DTI20 to control the polarization of the FM1. Another mechanism is to tune the interface induced anisotropy of a FM/3DTI by changing the free energy of the heterostructure using an applied gate voltage.21,22 Although the electrical switching of ferromagnets in FM/3DTI remains challenging, this proposal could encourage more experimental efforts in this direction.

Figure 1.

Figure 1

Open in a new tab

(a) Schematic 1T1MTJ cell using FM/3DTI heterostructures sitting well within a spin scattering length. The first ferromagnet (FM1) is the selector unit while the second (FM2) is the memory unit. In the off state, FM1 is oriented perpendicular to the TI plane to open a gap in its top surface states (Figure 2). The large red arrow shows the FM polarization and the spheres with small arrows show the spin current. (b) In the On state, ungapped metallic states on the top surface and surface current are restored by rotating FM1 into the TI plane. (c) Simulated current flows on top and bottom layers, connected by current flowing along the ungapped side walls. Note that the oxide does not need to be between the FM1 and the TI surface.

One of the known challenges for the FM1–3DTI is a low On/Off ratio compared to competing CMOS technologies. In this paper we show that as a selector for low power PiM, the On/Off ratio does not need to be very high. In fact, our proposed device is naturally suited for compact PiM designs, as it directly incorporates a selection transistor in the first FM1–3DTI combination. Using an enhanced sense-amplifier for each column with programmable sensing thresholds, it is possible to implement basic Boolean operations (AND, OR, XOR, Majority, and their complements). We describe a possible scheme of building such a PiM toward the end.

Results

Switching Mechanism

The SOT is calculated from the in-plane and out-of-plane components of the polarization current applied to the FM2 Jp = Jin + iJout, obtained by adding phenomenological scattering terms within FM2 of thickness tFM(23−25) on top of the NEGF calculated (eq 5a) spin current Js in the TI

graphic file with name nn2c05645_m001.jpg 1a
graphic file with name nn2c05645_m002.jpg 1b

where α is the Gilbert damping, m is the FM magnetization vector, and the net scattering length L = (1/λsr2 + 1/λϕ2 – i/λj2)−1/2. λsr, λϕ, and λj are spin relaxation and the precessional and decoherence lengths of the FM, while p is the interface dependent spin transfer efficiency from TI to FM2 (assumed to be 0.5). Note that due to spin precession in FM2, an out-of-plane component arises in the SOT, denoted by the imaginary part of τSOT.

A gate tunable anisotropy (through strain or VCMA) switches FM1 from out-of-plane to in-plane, which changes the magnetic exchange energy. Note that when the FM1 is in-plane, it does not need to be polarized in any specific direction as long as the out-of-plane component is negligible. The band structure of the 3DTI below FM1 is modified accordingly, shifting locally relative to the Fermi energy (Figure 2). We shift the bottom surface 0.5 times the top surface under the applied gate voltage Vg and assume the magnet covers the full TI width laterally. The corresponding NEGF calculated torque τSOT with phenomenological corrections (eq 1b) is then fed into the Landau–Lifshitz–Gilbert (LLG) equation26 self-consistently and quasi-statically, assuming the electron transit speed is orders of magnitude faster than the magnet’s resonant frequency.

Figure 2.

Figure 2

Open in a new tab

Band structure of the 3DTI at various points. Red lines in (a–c) emphasize the top surface states and, in (d), the side surfaces. Dashed lines show the bottom surface states. (a) FM/3DTI bandstructure with in-plane magnet (in the y direction). (b) Magnet in the z direction with on-site voltage energy at the top at −0.1 and bottom at −0.05 V. (c) Band structure of the pristine (magnet free) 3DTI channel discretized in the z direction (top to bottom). (d) 3DTI side surface (with magnet) bands discretized in the transport direction, showing ungapped states even when the FM1’s exchange coupling extends to a few top TI layers.

The voltage control of the FM1 anisotropy can arise from the VCMA effect driven by a vertical electric field across an oxide(MgO)-FM stack, ΔK = ξV/toxtFM, with VCMA coefficient ξ and oxide thickness tox and ΔK the change in the anisotropy. Alternatively, if we use strain as a switching mechanism for FM1, the applied effective field can be added to H as ζ(u·m)u, where ζ is the strain coefficient that needs to cancel out the effective anisotropy field HK. u is the strain direction that needs to be along z (perpendicular to the TI) in this case. For the VCMA mechanism, assuming a thickness of 1 nm for the capped oxide and FM1 layers, a ΔK/V = 33–100 kJ/m3 (change in anisotropy volume density) for CoFeB of 1 nm thickness has been reported,27−29 whereas by doping FM/oxide interface a larger ΔK/V has been achieved as well.29,31 The effect of oxide on the FM1/3DTI interface is ignored here as it is on the other side of the FM1 (not sandwiched between FM1 and 3DTI), and the effect of the FM1 and FM2 on the band structure of the 3DTI is assumed to be limited to the magnetic exchange. For the strain mechanism, ΔK/V of 200–300 kJ/m3 has been reported. For both the VCMA and strain, the free energy change from the applied gate Vg can potentially lower the voltage requirements. The required voltage to change the anisotropy of a reliable FM1 with thermal barrier ΔT = 40 of size 40 × 40 × 1 nm3 would be 0.3–1 V. Although this is relatively large compared to the applied bias, since there is negligible current in the FM1 heterostructure (we assume a thin insulating buffer), the energy consumption is still small (∼100–300 aJ). Most of the energy consumption comes from the current dissipation in the 3DTI. Using the material parameters reported for room temperature 3DTI switching of ferromagnet,32 the energy consumption from the current in the 3DTI is estimated to be around 10 fJ.

We set up a tight binding Hamiltonian that describes the 3DTI, the Zeeman energy term HZ (magnetic exchange) originating from the FM/3DTI exchange and the on-site energy term HV from the applied gate voltage at FM1, with parameters fitted to ab initio calculations (details in the Methods section).

Figures 2 panels a and b show the band structure of the 3DTI at the location of the FM1, for the On (magnet in-plane of TI) and Off (magnet out-of-plane) states, respectively. For the On state (a), we see a shift in the Dirac point away from the Γ point, relative to the pristine (magnet-free) TI states (Figure 2c). For the Off state (b), however, the degeneracy is lifted and a corresponding energy gap is created for the top surface states (red solid lines), while at the same time keeping the bottom surface states (dashed lines) intact. We also present the side surface states (Figure 2d), and as expected (Figure 1b), they stay gapless for both On and Off states, as the FM only affects part of the top surface. This would mean that for an electrical transistor based on FM/3DTI, the side current would play a crucial role. However, using FM1/TI as a selector as proposed, we avoid dealing with the side current as only the top surface states can apply any appreciable spin–orbit torque to FM2.

Reliability

For a competitive transistor-memory device based on the FM/3DTI stack, we outline requirements in this paper. The first is the On/Off ratio β. For deterministic switching of an in-plane ferromagnet with a given thermal barrier ΔT, the critical spin current Ic = (4qαkBTΔT/ℏ)(1 + HD*/2HK)33 with HD being the effective demagnetization field which we take to be twice HK. We also need to make sure that, when FM1 is out-of-plane in the Off state, the surface leakage current is small enough to not accidentally switch FM2. The probability P of switching FM2 can be approximated using the Fokker–Planck equation34−36

graphic file with name nn2c05645_m003.jpg 2

When the TI is not gapped (FM1 in-plane, P ≈ 1), the write error WER ≈ 1 – P, while when locally gapped (FM1 out-of-plane, P ≈ 0), the error is WER ≈ P. For simplicity we take our target WER in both cases to be identical. For thermally assisted switching (Off) we can solve the Fokker–Planck equation or use the empirical equation P = exp(−tf0 exp(−ΔT(−ι)c)), where t is the switching time and ι = Is/Ic – 1 is the spin current overdrive. c is an empirical constant, assumed to be 1 for in-plane FM2, 2 for out-of-plane FM2, and in between for imperfections.

The Zeeman term HZ = M0S·σ, which breaks time reversal symmetry to open a surface gap must be large enough to allow a small WER for accidental switching. For the Off state, t should be ∼μs for cache memory and years for long-term memory. Equation 3 connects WER to material parameters, and Figure 3a shows that, depending on Vg and M0, the device can be used in different regimes. For long-term storage, we assume ΔT = 40, WER = 10–7, and c = 1.238,39 and attempt frequency f0 = 1 GHz.40 When the FM1 is in-plane, the required ON Is/Ic is ∼0.2. For short-term memory, the Off state will need Is/Ic to be <0.2 to avoid accidentally switching FM2 with the above WER. This means that a modest On/Off ratio of 10 would make the device work. For longer memory applications (hours to days), a larger On/Off ratio (Figure 3a), log10 β > 3 is needed. M0 of up to 100 meV has been reported in the MnBi2Se4/Bi2Se3 heterostructure,41,42 which is in the range for up to 102 cache memory.

Figure 3.

Figure 3

Open in a new tab

(a) The color plot shows the logarithm of the On/Off ratio β of nonequilibrium spin current Js at the FM2/3DTI interface with respect to the Zeeman energy coefficient M0 and applied gate bias Vg. The contours show different memory regimes in which the device can operate, ranging from cache memory (operating in μs up to longer term memory, like a computer with RAM 103 s). The dashed red line is the Vg equal to the applied bias VDD. As explained in the text, the red circles show the minimum required M0 for each contour. (b) The image shows the 0 and 300 K LLG simulation of the FM2 magnetization dynamics. Applied voltage bias and Vg are 100 mV. The Zeeman exchange energy for FM2 is taken to be 10 meV. λsr, λϕ, λj are taken to be 1, 10, and 1 nm, respectively. Source, drain, FM1, and FM2 lengths are 20 nm each. 3DTI thickness is 5 nm (6 layers), and the magnet thickness t is 2 nm. The total length of the channel is 140 nm. Gilbert damping α is 0.1. (c) The image shows the current flow with and without electric coupling between FM1 and 3DTI at Vg = 0 (diamond) and −0.1 V. The coupling between the FM1 and 3DTI top surface is taken to be 0.3 eV, which corresponds to effective mass of m* = 0.48me, where me is the electron mass.37

In Figure 2c,d we see an energy offset between the TI side and top surface bands, implying different surface conductivities at any given energy. To achieve minimum required magnetic exchange M0, the applied gate voltage should be approximately equal to the applied bias VDD, Vg ≈ VDD. This matches Figure 3a (VDD = −0.1 eV, VDD = 0 eV), where the minimum M0 required for short-term (∼μs) memory occurs when Vg is near the midpoint (red dashed line). This implies that without a magnetization, when the chemical potential is tuned to the top or side Dirac point to reduce its conductivity, the other surface will retain a large density of states (DOS), providing a shunting conduction channel between top and bottom. For long-term (103 s) memory, a higher On/Off ratio is needed which requires a bigger bandgap, hence a larger M0. Due to the sizable gap opening for long-term memory, the critical Vg values for the minimum M0 (red circles) deviate from the midpoint. In Figure 3c, we performed the simulation with and without any electric coupling between FM1 and 3DTI, which shows that, at Vg = 0, the required M0 is only increased by 5–10%. At higher Vg, there is no noticeable difference.

Note that the On/Off ratio would be larger if we used a simplified 2D Hamiltonian that only considers surface states. This is because in a realistic TI structure, a significant amount of the current shunts into the bulk of the TI stack, which our 3D geometry naturally takes into account (Figure 1c). The shunting allows the surface current to go around the gapped region, reducing the On/Off ratio. To have a faster working memory, using a perpendicular ferromagnet such as FM2 is preferred, as the switching mechanism would be determined by a field-like torque, which is faster than an antidamping torque. However, for a perpendicular ferromagnet an assisting external field is required. This assisting field can originate from the stray field of a capping magnetic layer or the exchange bias of a coupled antiferromagnet–ferromagnet stack.43−45

Proposal for a Processor-in-Memory (PiM) Design

In Figure 4a we show a possible approach for performing in-memory compute functions using an array built out of the presented memory cell. The relation between the voltage lines in Figures 4 and 1 are as follows: WR, VDD; WR′, VSS; WE, Vg; RL, Vout. The cell (Figure 4b) contains a selection transistor, which acts as a write enable (WE) signal. The current flowing in the TI acts as the write signal, with the two ends designated as WR and WR′. Since a spintronic memory cell requires bipolar currents for programming, we can either use a bipolar current generating selector to drive the WR signal with WR′ grounded or reverse the polarities of WR, WR′ pairs between 0/1 and 1/0, respectively.

Figure 4.

Figure 4

Open in a new tab

(a) Memory array for the presented cell. (b) Cell and its position in the array indicated. (c) Truth table for the array operations.

The read is performed at the reader MTJ with a voltage divider, which changes the output voltage at the read line (RL), shared column-wise over the array cells. The reader is charged through the RD line. We include one transistor in the cell for a read enable functionality (RE) that provides the load resistance for adequate current to the read line per cell depending on the voltage at the divider, critical for the read and PiM functionalities as we describe next. We choose to arrange the read to be done row-wise, whereas the write is done column-wise. This is by no means a necessary condition for designing this architecture but simply one of the choices we make that allows us the option of simultaneous read and write, if necessary. The read is performed by sensing the current in the read line and comparing with a reference current in the sense amplifier (SA), which then reports the value stored at a specific cell addressed via RD and RE signals. The truth table of these operations is shown in Figure 4c.

The PiM functions are also arranged within the SA over each column. We can build in reference currents that enable Boolean operations over the whole array, by enabling multiple rows at a time. Consider a two-bit AND operation over any two rows. In this case, the two specific rows are enabled using RE and all the RD over the rows are enabled as well. Each of the SA reference currents for the AND operation is set to 1.8IR, where IR is the read current of a cell when it is storing ‘1’. In this case both of the cells being read simultaneously by a single SA will have to be ‘1’ to trigger the SA to report ‘1’, in all other combinations it will report ‘0’. Similarly for the OR case, the reference current can be set as 0.8IR to trigger ‘1’ from SA for even one of the cells being ‘1’. An XOR gate can be implemented by a two threshold SA where the thresholds are 0.8IR and 1.8IR and it is configured to report ‘1’ when reading values in between these two references. The complement functions are easily implemented by using an additional inverter. All these functionalities are built within a single SA and, per the requirements of the computation, the SA can be configured to perform a given operation.

Comparison With Existing Technology

The in-memory computation is also possible to be performed with existing technologies such as SRAM and DRAM. Note that in order for our proposed device to be competitive, the interface roughness between FM2 and TI must be minimized to have α as small as possible (smaller than 0.1). Our proposed device has the lowest energy consumption (Table 1). However, the speed of operation is also lower than the rest, with the energy-delay product (EDP) being the lowest. For low energy applications, the low energy cost is a higher priority.

Table 1. Energy Consumption of Proposed Device Compared to Existing Technologies46a.

technology energy (fJ) latency (ns)
proposed device 10 5
SRAM 50 2.7
DRAM 65 3.4
SOT-MRAM 40 2.6
Open in a new tab
a

For SRAM and DRAM the 45 nm transistor technology is used.

Conclusion

In this article we proposed an in-memory processing device based on the reciprocal interactions in FM-3DTI heterostructures. The main advantage was the integration of the selector-memory units onto a shared transport channel and hence a compact design. Using DFT-calibrated 3D tight binding, NEGF-LLG and Fokker–Planck, we connected the material parameters to switching delay and WER. We showed that a modest On–Off suffices for selector action in cache memory, even in the presence of current shunting through the sides and bulk. We also showed that as long as the FM1 is not connected to the circuit (no incoming or outgoing current), a modest electric coupling or tunneling between FM1 and 3DTI has only a minor negative effect on the performance. We assumed an in-plane FM2 (type y FM, parallel to the spin current polarization) in this work which, to be efficient, needs low damping. This would mean a high-quality interface is crucial. One alternative way is to have FM2 be perpendicular to the spin current polarization, which needs an assisting in-plane magnetic field perpendicular to the spin polarization to break the symmetry. Methods such as adding a second FM layer to use its demagnetization field to act as the assisting magnetic field is shown to work. Other methods, such as structural asymmetry and crystal dependent spin current geometry, have also been proposed.47 To have SOT switching with 3DTI, a type x ferromagnet, in-plane polarization but (anti)parallel to the electric current48 should be more efficient than out-of-plane FM2 as the magnetic exchange between an out-of-plane FM2 and 3DTI will lower the efficiency of the current generation by the 3DTI. Improvements in the magnetic exchange between FM1 and 3DTI can make even long-term memory applications possible at a low energy cost. Finally, there are experimental challenges in the electrical switching of a ferromagnet in FM/3DTI heterostructures, and further improvements in the voltage controlled switching of ferromagnet methods are needed.

Methods

In the 3D atomistic grid {i, j, k}, the Hamiltonian looks like49−52

graphic file with name nn2c05645_m004.jpg 3

where the onsite energies ε3DTI = (C0 + 2C1 + 4C2)I4×4 + (M + 2M1 + 4M2)I2×2 ⊗ τz and the hopping terms Tx,y = −M2I2×2 ⊗ τz – C2I4×4 + (iA0/2)σx,y ⊗ τx and Tz = −M1I2×2 ⊗ τz + C1I4×4 + (iB0/2)σz ⊗ τx. For Bi2Se3, we use M = −0.28 eV, A0 = 0.8 eV, B0 = 0.32 eV, C1 = 0.024 eV, C2 = 1.77 eV, M1 = 0.216 eV, M2 = 2.6 eV, and C0 = −0.0083 eV. τ and σ are the Pauli matrices in orbital and spin subspaces, respectively, while I is the identity matrix. One layer each of the source and drain is included in the Hamiltonian. The fixed FM in the MTJ is not included in the simulation. Our 3D model allows us to separate the bulk and interfacial components of the charge and current densities (Figure 1).

We employ the Non-Equilibrium Green Function (NEGF) formalism to analyze electron transport and the overall performance of the device. The retarded Gr and correlation Green functions Gn are53,54

graphic file with name nn2c05645_m005.jpg 4

with fS,D the source/drain Fermi–Dirac distributions. We assume a uniform cross-section that allows us to Fourier transform the transverse y–z hopping terms into 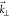Inline graphic. The self-energies ΣS,D are calculated recursively for each E and Inline graphic. ΓS,D are the corresponding energy broadening matrices. The spin and charge current densities from site i to j and SOT torque are calculated as

graphic file with name nn2c05645_m008.jpg 5a
graphic file with name nn2c05645_m009.jpg 5b

We solve the stochastic LLG equation (1 + α2)∂tm = γ(m × H + αm × (m × H) + τSOT) within a macroscopin model, H = HK + HTh + HD. HD is the demagnetization field. The effective anisotropy field HK = (2ΔTkBT/MsV)(u0·m)u0, where ΔT is the ferromagnet’s thermal stability related to anisotropy K, ΔT = KV/kBT. u0 is the effective field pointing along the ẑ and ŷ directions for FM1 and FM2, respectively, at the start of the simulation. For thermal fluctuations, we add a stochastic field HTh = (η/μ0)Inline graphic,55 where η is a random vector following a normal distribution with zero average. μ0 is vacuum permeability, kB is the Boltzmann constant, T is temperature, Ms is the saturation magnetization, γ is the electron gyromagnetic ratio, and V and Δt are the volume of FM2 and the simulation time step.

Acknowledgments

We acknowledge useful discussions with Patrick Taylor (ARL), Joe Poon, Md Golam Morshed (UVA) and Supriyo Bandyopadhyay (VCU). This work is supported by the Army Research Lab (ARL) and in part by the NSF I/UCRC on Multifunctional Integrated System Technology (MIST) Center (IIP-1439644, IIP-1439680, IIP-1738752, IIP-1939009, IIP-1939050, and IIP-1939012).

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

The authors declare no competing financial interest.

Notes

The preprint draft of this paper is available on arXiv.56

References

  1. Chi P.; Li S.; Xu C.; Zhang T.; Zhao J.; Liu Y.; Wang Y.; Xie Y.. PRIME: A Novel Processing-in-Memory Architecture for Neural Network Computation in ReRAM-Based Main Memory; ACM/IEEE Annual International Symposium on Computer Architecture (ISCA); ACM/IEEE, 2016; pp 27–39. [Google Scholar]
  2. Ghose S.; Boroumand A.; Kim J. S.; Gómez-Luna J.; Mutlu O. Processing-in-memory: A workload-driven perspective. IBM J. Res. Dev. 2019, 63, 3:1–3:19. 10.1147/JRD.2019.2934048. [DOI] [Google Scholar]
  3. Fong X.; Kim Y.; Yogendra K.; Fan D.; Sengupta A.; Raghunathan A.; Roy K. Spin-Transfer Torque Devices for Logic and Memory: Prospects and Perspectives. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems 2016, 35, 1–22. 10.1109/TCAD.2015.2481793. [DOI] [Google Scholar]
  4. Tang C.; Chang C.-Z.; Zhao G.; Liu Y.; Jiang Z.; Liu C.-X.; McCartney M. R.; Smith D. J.; Chen T.; Moodera J. S.; Shi J. Above 400-K robust perpendicular ferromagnetic phase in a topological insulator. Science Advances 2017, 3, e1700307 10.1126/sciadv.1700307. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Mellnik A. R.; Lee J. S.; Richardella A.; Grab J. L.; Mintun P. J.; Fischer M. H.; Vaezi A.; Manchon A.; Kim E.-A.; Samarth N.; Ralph D. C. Spin-transfer torque generated by a topological insulator. Nature 2014, 511, 449–451. 10.1038/nature13534. [DOI] [PubMed] [Google Scholar]
  6. Wang Y.; Zhu D.; Wu Y.; Yang Y.; Yu J.; Ramaswamy R.; Mishra R.; Shi S.; Elyasi M.; Teo K.-L.; Wu Y.; Yang H. Room temperature magnetization switching in topological insulator-ferromagnet heterostructures by spin-orbit torques. Nat. Commun. 2017, 8, 1364. 10.1038/s41467-017-01583-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Han J.; Richardella A.; Siddiqui S. A.; Finley J.; Samarth N.; Liu L. Room-Temperature Spin-Orbit Torque Switching Induced by a Topological Insulator. Phys. Rev. Lett. 2017, 119, 077702. 10.1103/PhysRevLett.119.077702. [DOI] [PubMed] [Google Scholar]
  8. Han J.; Liu L. Topological insulators for efficient spin–orbit torques. APL Materials 2021, 9, 060901. 10.1063/5.0048619. [DOI] [Google Scholar]
  9. Wu H. Magnetic memory driven by topological insulators. Nat. Commun. 2021, 12, 6251. 10.1038/s41467-021-26478-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Semenov Y. G.; Duan X.; Kim K. W. Electrically controlled magnetization in ferromagnet-topological insulator heterostructures. Phys. Rev. B 2012, 86, 161406. 10.1103/PhysRevB.86.161406. [DOI] [Google Scholar]
  11. Taniyama T. Electric-field control of magnetism via strain transfer across ferromagnetic/ferroelectric interfaces. J. Phys.: Condens. Matter 2015, 27, 504001. 10.1088/0953-8984/27/50/504001. [DOI] [PubMed] [Google Scholar]
  12. Sajjad R.; Ghosh A. W. Manipulating Chiral Transmission by Gate Geometry: Switching in Graphene with Transmission Gaps. ACS Nano 2013, 7, 9808. 10.1021/nn403336n. [DOI] [PubMed] [Google Scholar]
  13. Wang K.; Elahi M. M.; Wang L.; Habib K. M. M.; Taniguchi T.; Watanabe K.; Hone J.; Ghosh A. W.; Lee G.-H.; Kim P. Graphene transistor based on tunable Dirac fermion optics. Proc. Natl. Acad. Sci. U. S. A. 2019, 116, 6575–6579. 10.1073/pnas.1816119116. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Vaz C. A. F.; Walker F. J.; Ahn C. H.; Ismail-Beigi S. Intrinsic interfacial phenomena in Manganite heterostructures. J. Phys.: Condens. Matter 2015, 27, 123001. 10.1088/0953-8984/27/12/123001. [DOI] [PubMed] [Google Scholar]
  15. Trassin M. Low energy consumption spintronics using multiferroic heterostructures. J. Phys.: Condens. Matter 2016, 28, 033001. 10.1088/0953-8984/28/3/033001. [DOI] [PubMed] [Google Scholar]
  16. Manchanda P.; Singh U.; Adenwalla S.; Kashyap A.; Skomski R. Strain and Stress in Magnetoelastic Co–Pt Multilayers. IEEE Trans. Magn. 2014, 50, 1–4. 10.1109/TMAG.2014.2325396. [DOI] [Google Scholar]
  17. De Ranieri E.; Roy P. E.; Fang D.; Vehsthedt E. K.; Irvine A. C.; Heiss D.; Casiraghi A.; Campion R. P.; Gallagher B. L.; Jungwirth T.; Wunderlich J. Piezoelectric control of the mobility of a domain wall driven by adiabatic and non-adiabatic torques. Nat. Mater. 2013, 12, 808–814. 10.1038/nmat3657. [DOI] [PubMed] [Google Scholar]
  18. Verba R.; Lisenkov I.; Krivorotov I.; Tiberkevich V.; Slavin A. Nonreciprocal Surface Acoustic Waves in Multilayers with Magnetoelastic and Interfacial Dzyaloshinskii-Moriya Interactions. Phys. Rev. Applied 2018, 9, 064014. 10.1103/PhysRevApplied.9.064014. [DOI] [Google Scholar]
  19. Bandyopadhyay S.; Atulasimha J.; Barman A. Magnetic straintronics: Manipulating the magnetization of magnetostrictive nanomagnets with strain for energy-efficient applications. Applied Physics Reviews 2021, 8, 041323. 10.1063/5.0062993. [DOI] [Google Scholar]
  20. Manipatruni S.; Nikonov D. E.; Lin C.-C.; Prasad B.; Huang Y.-L.; Damodaran A. R.; Chen Z.; Ramesh R.; Young I. A. Voltage control of unidirectional anisotropy in ferromagnet-multiferroic system. Science Advances 2018, 4, eaat4229 10.1126/sciadv.aat4229. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Semenov Y. G.; Duan X.; Kim K. W. Electrically controlled magnetization in ferromagnet-topological insulator heterostructures. Phys. Rev. B 2012, 86, 161406. 10.1103/PhysRevB.86.161406. [DOI] [Google Scholar]
  22. Duan X.; Li X.-L.; Li X.; Semenov Y. G.; Kim K. W. Highly efficient conductance control in a topological insulator based magnetoelectric transistor. J. Appl. Phys. 2015, 118, 224502. 10.1063/1.4937407. [DOI] [Google Scholar]
  23. Manchon A.; Matsumoto R.; Jaffres H.; Grollier J. Spin transfer torque with spin diffusion in magnetic tunnel junctions. Phys. Rev. B 2012, 86, 060404. 10.1103/PhysRevB.86.060404. [DOI] [Google Scholar]
  24. Ndiaye P. B.; Akosa C. A.; Fischer M. H.; Vaezi A.; Kim E.-A.; Manchon A. Dirac spin-orbit torques and charge pumping at the surface of topological insulators. Phys. Rev. B 2017, 96, 014408. 10.1103/PhysRevB.96.014408. [DOI] [Google Scholar]
  25. Fischer M. H.; Vaezi A.; Manchon A.; Kim E.-A. Spin-torque generation in topological insulator based heterostructures. Phys. Rev. B 2016, 93, 125303. 10.1103/PhysRevB.93.125303. [DOI] [Google Scholar]
  26. Slonczewski J. Current-driven excitation of magnetic multilayers. J. Magn. Magn. Mater. 1996, 159, L1–L7. 10.1016/0304-8853(96)00062-5. [DOI] [Google Scholar]
  27. Kanai S.; Yamanouchi M.; Ikeda S.; Nakatani Y.; Matsukura F.; Ohno H. Electric field-induced magnetization reversal in a perpendicular-anisotropy CoFeB-MgO magnetic tunnel junction. Appl. Phys. Lett. 2012, 101, 122403. 10.1063/1.4753816. [DOI] [Google Scholar]
  28. Xue F.; Sato N.; Bi C.; Hu J.; He J.; Wang S. X. Large voltage control of magnetic anisotropy in CoFeB/MgO/OX structures at room temperature. APL Materials 2019, 7, 101112. 10.1063/1.5101002. [DOI] [Google Scholar]
  29. Rana B.; Otani Y. Towards magnonic devices based on voltage-controlled magnetic anisotropy. Commun. Phys. 2019, 2, 90. 10.1038/s42005-019-0189-6. [DOI] [Google Scholar]
  30. Nozaki T.; Yamamoto T.; Miwa S.; Tsujikawa M.; Shirai M.; Yuasa S.; Suzuki Y. Recent Progress in the Voltage-Controlled Magnetic Anisotropy Effect and the Challenges Faced in Developing Voltage-Torque MRAM. Micromachines 2019, 10, 327. 10.3390/mi10050327. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. DC M.; Grassi R.; Chen J.-Y.; Jamali M.; Reifsnyder Hickey D.; Zhang D.; Zhao Z.; Li H.; Quarterman P.; Lv Y.; Li M.; Manchon A.; Mkhoyan K. A.; Low T.; Wang J.-P. Room-temperature high spin–orbit torque due to quantum confinement in sputtered BixSe(1–x) films. Nat. Mater. 2018, 17, 800–807. 10.1038/s41563-018-0136-z. [DOI] [PubMed] [Google Scholar]
  32. Sun J. Z. Spin-current interaction with a monodomain magnetic body: A model study. Phys. Rev. B 2000, 62, 570–578. 10.1103/PhysRevB.62.570. [DOI] [Google Scholar]
  33. Li Z.; Zhang S. Thermally assisted magnetization reversal in the presence of a spin-transfer torque. Phys. Rev. B 2004, 69, 134416. 10.1103/PhysRevB.69.134416. [DOI] [Google Scholar]
  34. Butler W. H.; Mewes T.; Mewes C. K. A.; Visscher P. B.; Rippard W. H.; Russek S. E.; Heindl R. Switching Distributions for Perpendicular Spin-Torque Devices Within the Macrospin Approximation. IEEE Trans. Magn. 2012, 48, 4684–4700. 10.1109/TMAG.2012.2209122. [DOI] [Google Scholar]
  35. Chen E.; et al. Progress and Prospects of Spin Transfer Torque Random Access Memory. IEEE Trans. Magn. 2012, 48, 3025–3030. 10.1109/TMAG.2012.2198451. [DOI] [Google Scholar]
  36. Sankey J. C.; Cui Y.-T.; Sun J. Z.; Slonczewski J. C.; Buhrman R. A.; Ralph D. C. Measurement of the spin-transfer-torque vector in magnetic tunnel junctions. Nat. Phys. 2008, 4, 67–71. 10.1038/nphys783. [DOI] [Google Scholar]
  37. Bedau D.; Liu H.; Bouzaglou J.-J.; Kent A. D.; Sun J. Z.; Katine J. A.; Fullerton E. E.; Mangin S. Ultrafast spin-transfer switching in spin valve nanopillars with perpendicular anisotropy. Appl. Phys. Lett. 2010, 96, 022514. 10.1063/1.3284515. [DOI] [Google Scholar]
  38. Liu H.; Bedau D.; Sun J.; Mangin S.; Fullerton E.; Katine J.; Kent A. Dynamics of spin torque switching in all-perpendicular spin valve nanopillars. J. Magn. Magn. Mater. 2014, 358–359, 233–258. 10.1016/j.jmmm.2014.01.061. [DOI] [Google Scholar]
  39. Breth L.; Suess D.; Vogler C.; Bergmair B.; Fuger M.; Heer R.; Brueckl H. Thermal switching field distribution of a single domain particle for field-dependent attempt frequency. J. Appl. Phys. 2012, 112, 023903. 10.1063/1.4737413. [DOI] [Google Scholar]
  40. Hirahara T.; et al. Large-Gap Magnetic Topological Heterostructure Formed by Subsurface Incorporation of a Ferromagnetic Layer. Nano Lett. 2017, 17, 3493–3500. 10.1021/acs.nanolett.7b00560. [DOI] [PubMed] [Google Scholar]
  41. Kaveev A. K.; Suturin S. M.; Golyashov V. A.; Kokh K. A.; Eremeev S. V.; Estyunin D. A.; Shikin A. M.; Okotrub A. V.; Lavrov A. N.; Schwier E. F.; Tereshchenko O. E. Band gap opening in the BiSbTeSe2 topological surface state induced by ferromagnetic surface reordering. Phys. Rev. Materials 2021, 5, 124204. 10.1103/PhysRevMaterials.5.124204. [DOI] [Google Scholar]
  42. Krizakova V.; Garello K.; Grimaldi E.; Kar G. S.; Gambardella P. Field-free switching of magnetic tunnel junctions driven by spin–orbit torques at sub-ns timescales. Appl. Phys. Lett. 2020, 116, 232406. 10.1063/5.0011433. [DOI] [Google Scholar]
  43. Kong W. J.; Wan C. H.; Wang X.; Tao B. S.; Huang L.; Fang C.; Guo C. Y.; Guang Y.; Irfan M.; Han X. F. Spin–orbit torque switching in a T-type magnetic configuration with current orthogonal to easy axes. Nat. Commun. 2019, 10, 233. 10.1038/s41467-018-08181-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Zheng Z.; et al. Field-free spin-orbit torque-induced switching of perpendicular magnetization in a ferrimagnetic layer with a vertical composition gradient. Nat. Commun. 2021, 12, 4555. 10.1038/s41467-021-24854-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Angizi S.; He Z.; Reis D.; Hu X. S.; Tsai W.; Lin S. J.; Fan D.. Accelerating Deep Neural Networks in Processing-in-Memory Platforms: Analog or Digital Approach?; IEEE Computer Society Annual Symposium on VLSI (ISVLSI), IEEE, 2019; pp 197–202. [Google Scholar]
  46. Shao Q.; et al. Roadmap of Spin–Orbit Torques. IEEE Trans. Magn. 2021, 57, 1–39. 10.1109/TMAG.2021.3078583. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Fukami S.; Anekawa T.; Zhang C.; Ohno H. A spin–orbit torque switching scheme with collinear magnetic easy axis and current configuration. Nat. Nanotechnol. 2016, 11, 621–625. 10.1038/nnano.2016.29. [DOI] [PubMed] [Google Scholar]
  48. Liu C.-X.; Qi X.-L.; Zhang H.; Dai X.; Fang Z.; Zhang S.-C. Model Hamiltonian for topological insulators. Phys. Rev. B 2010, 82, 045122. 10.1103/PhysRevB.82.045122. [DOI] [Google Scholar]
  49. Götte M.; Paananen T.; Reiss G.; Dahm T. Tunneling Magnetoresistance Devices Based on Topological Insulators: Ferromagnet–Insulator–Topological-Insulator Junctions Employing Bi2Se3. Phys. Rev. Applied 2014, 2, 054010. 10.1103/PhysRevApplied.2.054010. [DOI] [Google Scholar]
  50. Sengupta P.; Kubis T.; Tan Y.; Klimeck G. Proximity induced ferromagnetism, superconductivity, and finite-size effects on the surface states of topological insulator nanostructures. J. Appl. Phys. 2015, 117, 044304. 10.1063/1.4906842. [DOI] [Google Scholar]
  51. Liu J.; Hesjedal T. Magnetic Topological Insulator Heterostructures: A Review. Adv. Mater. 2021, 2102427. 10.1002/adma.202102427. [DOI] [PubMed] [Google Scholar]
  52. Datta S.Lessons from Nanoelectronics. Lessons from Nanoscience: A Lecture Notes Series, Vol. 5; World Scientific, 2012; Vol. 2. [Google Scholar]
  53. Ghosh A. Nanoelectronics A Molecular View. World Scientific Series in Nanoscience and Nanotechnology, Vol. 13; World Scientific, 2016. [Google Scholar]
  54. Vakili H.; Xie Y.; Ganguly S.; Ghosh A. W.. Anatomy of nanomagnetic switching at a 3D Topological Insulator PN junction. arXiv,2110.02641; 2021; 10.48550/arXiv.2110.02641. [DOI] [PMC free article] [PubMed]
  55. Vakili H.; Ganguly S.; de Coster G. J.; Neupane M. R.; Ghosh A. W.. Low power In Memory Computation with Reciprocal Ferromagnet/Topological Insulator Heterostructures. arXiv2203.14389; 2022 10.48550/arXiv.2203.14389. [DOI] [PMC free article] [PubMed]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Articles from ACS Nano are provided here courtesy of American Chemical Society

RESOURCES