Abstract
Nearly all diseases are caused by different combinations of exposures. Yet, most epidemiological studies focus on estimating the effect of a single exposure on a health outcome. We present the Causes of Outcome Learning approach (CoOL), which seeks to discover combinations of exposures that lead to an increased risk of a specific outcome in parts of the population. The approach allows for exposures acting alone and in synergy with others. The road map of CoOL involves (i) a pre-computational phase used to define a causal model; (ii) a computational phase with three steps, namely (a) fitting a non-negative model on an additive scale, (b) decomposing risk contributions and (c) clustering individuals based on the risk contributions into subgroups; and (iii) a post-computational phase on hypothesis development, validation and triangulation using new data before eventually updating the causal model. The computational phase uses a tailored neural network for the non-negative model on an additive scale and layer-wise relevance propagation for the risk decomposition through this model. We demonstrate the approach on simulated and real-life data using the R package ‘CoOL’. The presentation focuses on binary exposures and outcomes but can also be extended to other measurement types. This approach encourages and enables researchers to identify combinations of exposures as potential causes of the health outcome of interest. Expanding our ability to discover complex causes could eventually result in more effective, targeted and informed interventions prioritized for their public health impact.
Keywords: Causes of effects, sufficient component cause model, inductive–deductive, machine learning, neural networks, explanations, precision public health, complex epidemiology, interactions, supervised clustering
Key Messages.
Most diseases are caused by a combination of multiple exposures but most epidemiological studies focus on one single exposure and one single health outcome.
Using causal inference and machine learning, the Causes of Outcome Learning approach addresses explorative questions such as ‘Given a particular health outcome, what are the most common combinations of exposures, which might have been its causes?’.
Using simulated data and real-life data, we demonstrate the usefulness of the approach.
A tutorial is included in the Supplementary material of this paper (available as Supplementary data at IJE online) and the R package ‘CoOL’ is available to assist researchers with the computational phase.
Introduction
Most diseases are multifactorial and exposures may act together and lead to combined effects that exceed the sum of the individual effects on an additive scale, which is called synergism.1–3 A classic example is how the combined effect of smoking and asbestos on lung cancer exceeds the sum of their individual effects.4 The most established theoretical framework for understanding synergism in epidemiology is the sufficient cause model. This model uses causal pie illustrations of components of causes to indicate that when all components of one cause are present it is sufficient to cause disease.5 Assessing synergisms may lead to improved public health in two ways: (i) better disease prevention and treatment through insight into the causation of a disease (aetiology) and (ii) quantification of the disease burden in high-risk subgroups who may benefit from risk-mitigating interventions. For decades, these points have been appreciated for effective preventive strategies. Rose, for example, said that ‘risk assessment must consider all relevant factors together rather than confine attention to a single test, for nearly all diseases are multifactorial’ when discussing effective policy decisions.6
Few epidemiological studies try to identify larger combinations of causes for specific outcomes despite the policy relevance. We suspect that the apparent lack of epidemiological studies into causes of outcomes has several reasons: (i) frequently taught frameworks for epidemiologists that warn against type 1 errors from multiple testing (false-positive findings),7 (ii) various confounding structures for each exposure complicate causal interpretation,8 (iii) the overwhelming number of combinations among exposures challenges the model fitting,9 (iv) insufficient statistical power in small data samples hides true phenomena and (v) the lack of theoretically founded approaches.9,10 Frameworks for identifying component causes exist, though they are not commonly applied in epidemiology. These frameworks select on either outcome11 or exposure.12 Unfortunately, these frameworks can only consider a few exposures at a time and they do not allow for the estimation of risk, which is often of public health interest. In the social sciences, configurational comparative methods deal with sufficient causes (referencing earlier work13). The most famous of these methods is the qualitative comparative analysis,14,15 which has been applied in the public health domain.16 Qualitative comparative analysis works by analysing all combinations of exposures and uses a top-down search of exposure combinations that fulfil some chosen criteria, such as a risk threshold.15 Using pre-defined risk thresholds has advantages as transparent protocols and disadvantages as being threshold-sensitive and confined to unadjusted tabular data.
Moreover, assessing exposure synergisms through standard approaches based on calculating all possible combinations of exposures is rarely feasible in practice. First, such analysis would be based on a large number of parameters requiring large sample sizes and posing computational challenges. Second, the numerous parameters returned from regression are not interpretable and potentially misleading as demonstrated in Supplementary Comparison 1 (available as Supplementary data at IJE online).
We introduce a causal inference-inspired machine learning approach called the Causes of Outcome Learning (CoOL) approach. CoOL is aimed at generating insights regarding questions like ‘Given a particular health outcome, what are the most common combinations of exposures, which might have been its causes?’. It utilizes the flexibility of a tailored machine learning model and an explanation technique to discover meaningful combinations of exposures while avoiding certain causal biases. Examples of questions to ask using CoOL could be ‘What are the most common combination of environmental and household exposures measured before 6 weeks of age causing child mortality in Guinea-Bissau between 6 weeks of age to 3 years of age?’ or ‘What are the most common combination of stressful events in childhood causing a high disease burden in early adult life in Denmark?’. To answer these questions well, we must explore many combinations of exposures. Targeting subgroups for interventions aimed at these combinations of exposures may provide a large public health impact. We present the approach assisted by a simple simulated example solely for pedagogical purposes but CoOL also works on complex scenarios with higher-order interacting synergy. A step-by-step tutorial and six simulations of various complexity are included in Supplementary Simulations 1–6 (available as Supplementary data at IJE online). Three robustness checks are found in Supplementary Simulations 7–9 (available as Supplementary data at IJE online). A six-page real-life application using cohort data from the Center of Disease Control and Prevention is available in the Supplementary real-life analysis (available as Supplementary data at IJE online). A glossary can be found in Supplementary Table 1 (available as Supplementary data at IJE online).
Simulated example
We generate a healthy study population of 10 000 individuals (half men and women); 20% are exposed to Drug A and 20% are exposed to Drug B. Sex, Drug A and Drug B are independent. In this scenario, all individuals have a baseline risk of developing any atopic disease of 5% throughout a 10-year follow-up period; men who are exposed to Drug A have a 15% higher risk of developing atopy and so do women who are exposed to Drug B. The simulated example uses two two-way interactions as a pedagogical example but CoOL can identify any higher-order interacting synergy if it exists in data and the data set is large enough.
The CoOL approach
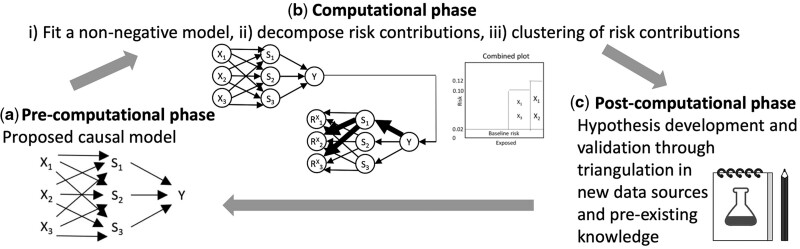
CoOL is enabled by recent advances in understanding why machine learning models produce the results they do [explainable artificial intelligence such as layer-wise relevance propagation (LRP)17–19] and by the science of causal structures for causal inference.20 CoOL is a three-phase inductive–deductive scientific process (Figure 1). The bulk of our method’s contribution is related to the second phase. The goal of CoOL is to generate hypotheses for further testing. The road map for applying CoOL is as follows:
Figure 1.
The phases of CoOL towards inference to the best explanation
(a) Pre-computational phase: scoping the research question and causal structure assumptions. (b) Computational phase: (i) A non-negative model as close to the assumed causal model is fitted, (ii) risk contributions are decomposed and (iii) individuals are clustered into subgroups. (iv) Manual validation of the results is suggested in an internal validation data set to assess the stability of the results. (c) Post-computational phase: the results are held against existing evidence in order to develop new hypotheses that can be tested in new studies. New understandings will update our initial assumed causal model
The pre-computational phase: Propose a causal model using a directed acyclic graph (DAG) of the exposures and the outcome based on prior domain expertise of selected actionable exposures and contextual factors. This phase aids the identification of exposure variables to include in the analysis.
-
The computational phase: The goal of this phase is to identify subgroups of the population who have certain combinations of exposures that together were found to elevate their risk for the health outcome [we provide the R package ‘CoOL’ (Supplementary Information 1, available as Supplementary data at IJE online)]:
-
Training data:
Fit a non-negative model on an additive scale based on the features from the assumed causal model. We suggest a tailored neural network that can capture synergistic effects using activation functions, which allows combinations of covariates interacting to predict higher risks.
Decompose the risk contributions.
Cluster individuals based on the risk contributions.
-
Internal validation data:
Ensure the robustness of the findings in an internal validation data set.
-
Post-computational phase: Based on learnings from the computational phase and existing knowledge, develop hypotheses to be assessed in further (intervention) studies on new temporal or external validation data. The approach focuses on common high-risk subgroups and directs researchers towards potentially large public health impact. The outcome of this phase is to suggest one or several sound hypotheses by combining the empirical findings from one’s own data with a critical assessment.
Inference from CoOL relies on how risk contributions cluster in subgroups of the population. These risk contributions rely on causal assumptions specified in the pre-computational phase but they are not counter-factual estimates, i.e. reflecting what would have happened had the exposure been absent. The main challenges for a causal interpretation in CoOL as well as in standard approaches are first that the measured covariates may be insufficient to adjust for confounding, second as the total effects of exposures are diluted if mediators are included in the model, and third because the effect of synergistically co-acting exposures is divided between the risk contributions estimated via CoOL. However, CoOL is designed to avoid biases the following ways: (i) guiding the inclusion of relevant exposures through expertise-based knowledge in the pre-computational phase, (ii) using a relaxed monotonic model to prevent the introduction of collider bias9 when clustering risk contributions (Supplementary Comparison 2, available as Supplementary data at IJE online), (iii) adjusting for calendar effects to prevent spurious time-trend associations (Supplementary Method 1, available as Supplementary data at IJE online), (iv) re-weighting the study population if some individuals are censored during follow-up to prevent selection bias9 (Supplementary Method 2, available as Supplementary data at IJE online) and (v) designing the model set-up on an additive scale to allow us to identify synergisms, which a multiplicative model could not.
We use the following notation in the next sections: denotes exposures, denotes the outcome and denotes j unknown sets of sufficient causes for the outcome (inspired by the notation by VanderWeele and Robins21). USCi and U denote different types of unmeasured (including unmeasurable and unknown) causes. USCi denotes the unmeasured component causes of SCj, whereas U denotes unmeasured causes of Y. denotes a baseline risk assumed to affect all individuals. Activation functions are denoted as . Connection parameters from the exposures to the activation functions are denoted as . Intercepts are denoted as . + denotes restrictions to non-negative values (≥0, positive or zero) and − denotes restrictions to non-positive values (≤0, negative or zero).
Pre-computational phase
Causal structures are commonly depicted with DAGs,22 which allow a causal interpretation of associations given a set of causal assumptions: exchangeability, positivity, consistency, no measurement error and no model misspecification.9
The intuition of CoOL is to link exposures to unknown sufficient causes21 (with probabilistic effects, not deterministic) as illustrated in Figure 2a and c. The theoretical DAG in Figure 2c makes no assumptions about the existence of causal effects between exposures and outcomes, and the computational steps aim at reducing these causal effects towards the minimal sets of component causes. The assumed causal model assists in exposure selection: actionable exposures that we can intervene on, such as drug intake, and contextual factors, which describe subgroups in risk. It also helps to decide whether proximal non-actionable exposures should be excluded if they mediate effects of actionable exposures and thus mask their effects. Further, the assumed causal model is used for the interpretation of the results because only direct and joint effects are returned.8
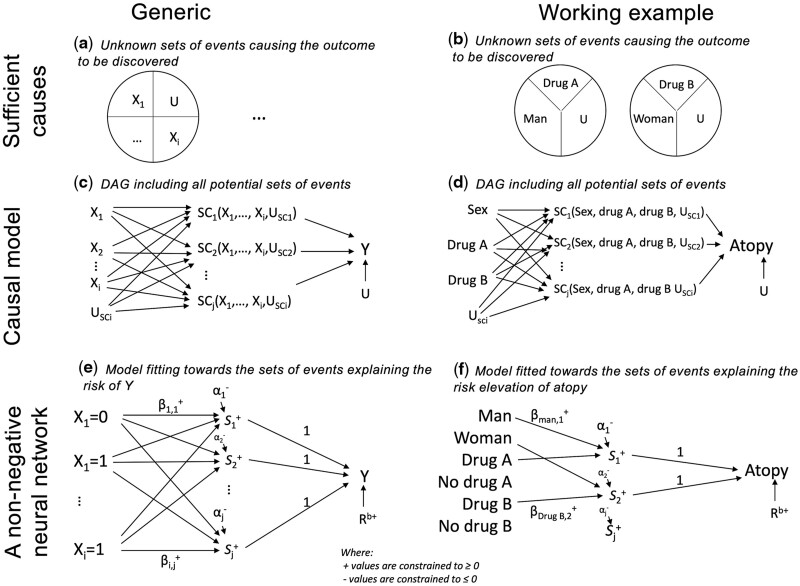
Figure 2.
Sufficient causes, causal model and non-negative neural network
The pictogram shows the relation between epidemiological theory, structural models and a non-negative neural network. The left column is a generic presentation and the right column shows the simulated example. (a) and (b) An illustration of sufficient causes. The example to the right shows that a certain disease occurs if men are exposed to Drug A and some unknown factors and if women are exposed to Drug B and some unknown factors. (c) and (d) An assumed causal model illustrated using a directed acyclic graph, where denotes the exposures, USCi denotes the unmeasured causes of the sufficient causes, U denotes the unmeasured causes of Y assumed to affect all individuals, denotes hidden sufficient causes and denotes the outcome. (e) and (f) A non-negative neural network resembling the assumed causal model. denotes exposures, denotes non-negative parameters, denotes hidden activation functions, denotes non-positive intercepts acting as activation thresholds for activation functions and denotes the baseline risk
A common drawback of existing synergistic risk estimation models is their positive monotonicity assumption, i.e. exposures either have no effect or always act in the same direction on the outcome.1,23 The proposed non-negative model (next section) relaxes the monotonicity assumption by letting us explore all directions of exposures on the outcome simultaneously for which effects act independently or synergistically with others (e.g. if there exist exposures that are especially harmful for men and other exposures that are especially harmful for women). If we had applied a model with both positive and negative parameters, the risk contributions would also take both negative and positive values, which would be difficult to interpret. Further, since the risk contributions are conditioned on the outcome, clustering risk contributions from a model with positive and negative parameters could lead to collider bias stratification9 and thus result in spuriously inversely correlated risk contributions (Supplementary Comparison 2). Using monotonicity (including the relaxed version) by applying a non-negative model prevents collider bias in the computational phase Step 3 when clustering the risk contributions.
In causal inference studies, inclusion of covariates causing confounding is solely for adjustment.9 In CoOL, all potential causes of the outcome are of relevance (i.e. covariates are also considered as potential exposures of interest) and including them carefully allows quantification of individual and joint direct exposure effects adjusted for when individual exposures confound the effect of another exposure (due to being on the latter exposure's backdoor path to the outcome).20 However, researchers need to consider issues with unmeasured confounding, selection or collider bias and measurement bias. In studies, where data are gathered over a longer time span, calendar time may introduce spurious correlations if changes occur in exposure prevalence and in diagnosis criteria. The model can be adjusted for calendar time without attributing it a risk contribution (Supplementary Method 1, available as Supplementary data at IJE online). Also, selection bias may occur if at-risk individuals become systematically censored. To prevent selection bias due to censoring during follow-up, the model can be adjusted using inverse probability of censoring weights assuming a correct model specification of the probability of not being censored during follow-up (Supplementary Method 2, available as Supplementary data at IJE online).
For our motivating example, we assume that sex, Drug A and Drug B do not share a common cause. Ideally, we want to identify the sufficient causes shown in Figure 2b and the DAG showing our scientific interest has been drawn in Figure 2d. Had other information been available, we may have included it or not, depending on the assumed causal structure for developing atopy.
Computational phase
The many potential combinations of exposures increase the risk of identifying spurious associations. To manually validate the findings before developing hypotheses, data are split into a training data set and an internal validation data set. We suggest fitting the model on the training data (with regularization to reduce overfitting to noise, which could produce ungeneralizable predictions) until it converges based on the error function. A training scheme using k-fold splits of the training data may be useful in very large data sets but needs further investigation.
Fitting a non-negative model
We suggest a non-negative, single-hidden layer, neural network on an additive scale (Figure 2e) as the mathematical model designed to mimic our assumed causal model (Figure 2c). This model resembles a linear regression model estimating risk differences but with two key modifications. First, the model includes a series of latent interactions that can combine the effects of various exposures. The latent interactions are estimated using what is known in machine learning as activation functions, , represented in the hidden layer between the exposures and the outcome. Second, we restrict all connection parameters to have non-negative values (≥0, positive or zero)24 so that exposures can only increase the occurrence of the outcome.1 Further, each category of the variable is binary/one-hot encoded into one new variable each with 0 if not present and 1 if present and thereby meets a relaxed version of the monotonicity assumption. The disease outcome is coded 0 and 1. The activation functions return the non-negative (≥0, positive or zero) sum of its input value. The intercepts can only take non-positive (≤0, negative or zero) values and act as an activation threshold that only allows combinations of exposures with large -weighted sum to pass . The baseline risk can only take non-negative (≥0, positive or zero) values. The non-negative and non-positive restrictions are made to decompose and cluster the risk contributions without suggesting spurious subgroups due to collider bias (Supplementary Comparison 2, available as Supplementary data at IJE online). If a person has no risk contribution of any exposures, the person is assumed to have a risk equal to the baseline risk. The connection parameters between the activation functions and the outcome have a fixed value of 1. The model estimates the risk on an additive scale so that synergisms are defined as combined effects that are larger than the sum of individual effects.5
This model can be formulated as below and satisfies the assumption that the added risk is independent of the baseline risk or is formulated as an ‘independent of background’ model according to Beyea and Greenland: 25
Fitting the model is done using stochastic gradient descent on the training data set: in a step-wise procedure run on one individual at a time, the model estimates the individual’s risk of the disease outcome, , calculates the squared prediction error and adjusts the model parameters to minimize this error.26 By iterating through all individuals for multiple epochs, we obtain model parameters, which minimizes the sum of prediction errors across the entire population. The initial values, derivatives, learning rates and regularization parameter are described in Supplementary Information 2 (available as Supplementary data at IJE online).
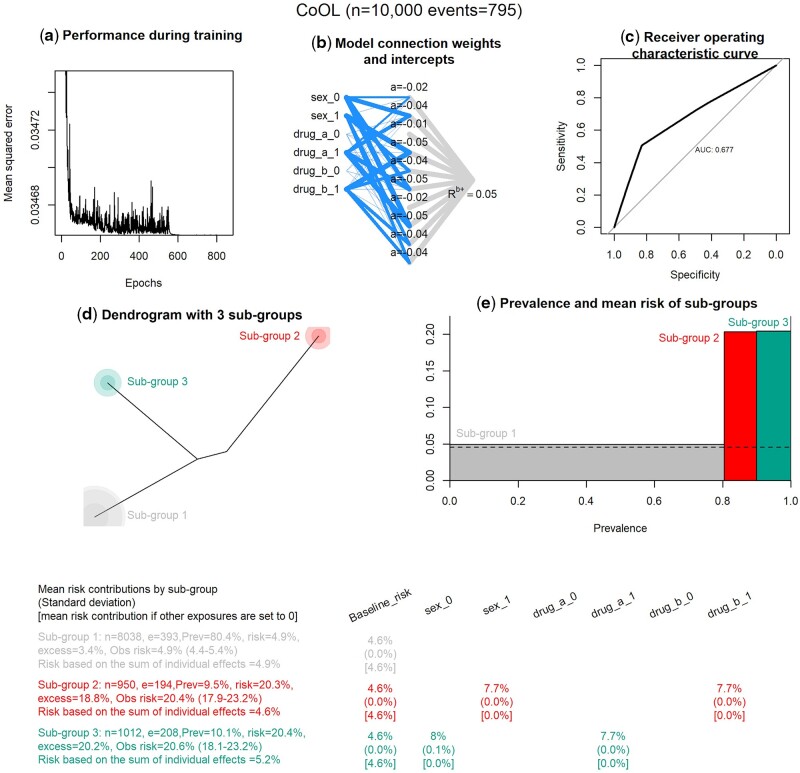
Our simulated example data are split into a training data set and an internal validation data set. Figure 2f presents the model for our motivating example. We binary-encode new variables for each possible category of each exposure, such that sex (coded 0 if man, 1 if women) becomes two factors: man (coded 1 if man, 0 if not man) and woman (coded 1 if woman, 0 if not woman) and so forth for Drug A and Drug B. If, for example, we had strong expertise knowledge that Drug B could only be harmful (and never beneficial), we could have used this causal information to limit the degrees of freedom in the model and decrease the chance of discovering false-positive findings. The training data set is used to fit the proposed non-negative model with 10 hidden activation functions. Figure 4a–c shows how the error decreases by each epoch; it visualizes the neural network connections and receiver operating characteristic curve. Although the predictive performance measured by the area under the receiver operating characteristic curve (AUC) provides a useful metric for evaluating model discriminatory performance across the entire population, a model with low AUC can still capture important sets of causes for particular subgroups.27
Figure 4.
Results of the computational phase of CoOL
The main results are combined in one plot. (a) Prediction performance measured by the mean squared error by epoch. (b) A visualization of the fitted non-negative neural network. The width of the line indicates the strength of each connection. (c) A plot on prediction performance as measured by the area under the receiver operating characteristic curve. (d) A dendrogram of the three subgroups. (e) The mean risk and prevalence by subgroups. (f) The table with the main results for the working example. ‘n’ is the total number of individuals in the subgroup, ‘e’ is the number of events/individuals with the outcome in the subgroup, ‘prev’ is the prevalence of the subgroup, ‘risk’ is the mean risk in the subgroup based on the model, ‘excess’ is the excess fraction being the proportion out of all cases that are more than expected (more than the baseline risk) in this subgroup (see Supplementary Information 4, available as Supplementary data at IJE online), ‘obs risk’ is the observed risk in this subgroup (95% CI is calculated using the Wald method in 74), ‘risk based on the sum of individual effects’ is the risk summed up where all other exposures are set to zero. For the three estimates presented at each variable by each subgroup, the first estimate is the mean risk contribution, the estimate in parentheses is the standard deviation and the estimate in brackets is the risk contribution had all other exposures been set to zero. The baseline risk is by definition the same for all groups
Decomposing risk contributions
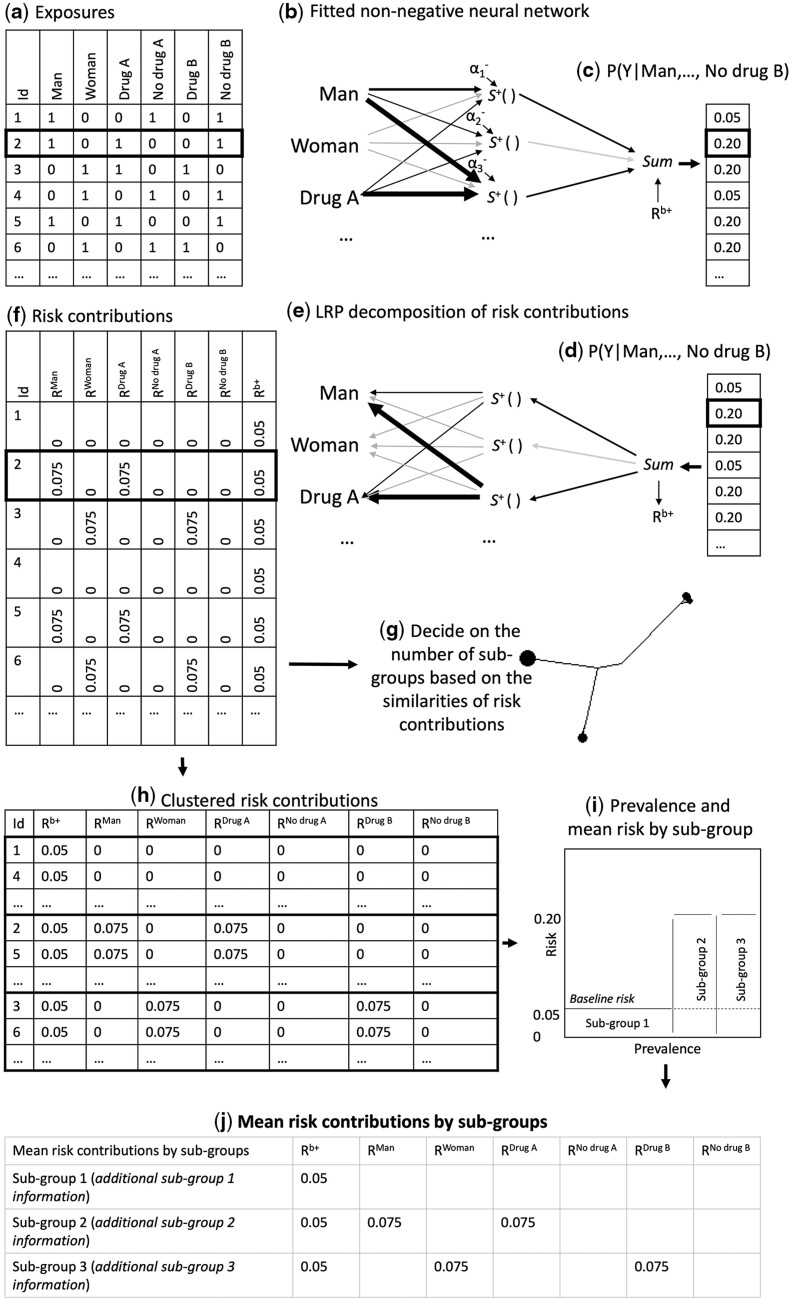
Machine learning models are commonly referred to as black boxes due to the limited interpretability of their parameters and the way they interact with the input variables.28 Instead of attempting to interpret the model parameters directly, we use LRP17–19 to decompose the risk of the outcome to risk contributions for each individual (in particular, we use the LRPalpha=1, beta=0 rule). LRP was introduced by Bach et al. in 201517 as a decomposition technique for pre-trained neural networks and was later justified via Deep Taylor Decomposition.29 As opposed to other explanation techniques for neural networks, LRP is aimed at conserving the information such that all relevance measures sum to the probability of the outcome. In CoOL, the predicted risk of the outcome, is decomposed into a baseline risk, , and the risk contributions by each exposure, (where can take values between 0 and 1):
These risk contributions may be interpreted as an expression of the exposures’ positive contribution to the risk given the model and the individual’s set of exposures. The estimation is designed to prevent spurious associations and direct researchers in identifying combinations of exposures associated with elevated risk of a specific health outcome, but they cannot directly be interpreted as the counter-factual effect of what would have happened had the exposure been absent. No risk contributions are decomposed to the intercepts, . The below procedure is conducted for all individuals in a one-by-one fashion. The baseline risk, , is represented by its own parameter (Figure 2e) and is therefore estimated as part of fitting the non-negative neural network. More precisely, the decomposition of the risk contributions for exposures, , takes three steps:
Step 1: Subtract the baseline risk, :
Step 2: Decompose risk contributions to the hidden activation functions, where is the value returned by each of the activation functions given the exposure distribution , parameters, and intercepts, :
Step 3: Decompose risk contributions from the hidden activation functions to the exposures:
As a result of the risk decomposition, each individual is assigned a set of risk contributions, , one for each exposure plus a baseline risk, . The decomposition of risk contributions have been illustrated in Figure 3e and f using the motivating example and explanation in the figure legend.
Figure 3.
Workflow of the computational phase of CoOL
The flowchart of how subgroups are identified as part of the computational phase of Causes of Outcome Learning. (a) The expanded data set of sex (one variable for man, one for woman), Drug A (one variable for Drug A, one for no Drug A) and Drug B (one variable for Drug B, one for no Drug B). (b) The fitted non-negative model is illustrated. Wide edges indicate large connection parameters. (c) and (d) The predicted risk, . (e) The predicted risk is decomposed using LRP to risk contributions of the baseline, , and exposures, . (f) The risk contribution matrix. (g) A dendrogram to help decide on the number of subgroups. (h) Clustered risk contribution matrix into subgroups. (i) Prevalence and mean risk by subgroup plot. This plot indicate areas for greater public health impact. (j) A table with the mean of risk contributions by subgroups. It can hold more information that can be useful when developing hypotheses, such as quantifications of the excess proportion of all cases found in this subgroups when considering the prevalence of the subgroup, the risk in the subgroup and the baseline risk
Clustering of risk contributions
We suggest to subgroup the individuals based on risk contributions using Manhattan distances and Ward’s method.30,31 A dendrogram may help decide the number of relevant subgroups (Figure 3g).32 Plotting the prevalence and mean risk of each subgroups can help researchers to identify the subgroups with the highest public health impact (Figure 3i).33 A table of mean risk contributions and standard deviations by subgroups may illuminate which exposures are associated with elevated risk in each subgroup (Figure 3j). An indication of synergism is when the combined risk contribution of a set of exposures is higher than the sum of stand-alone risk contributions of each of the exposures (Supplementary Information 3, available as Supplementary data at IJE online, but deviations may occur in noisy data sets). Final reporting of synergism should be using the yet unseen internal validation data set before developing hypotheses in the post-computational phase.34
Given the combined risk contributions causally affect the outcome and meet the assumption of positive monotonicity, the excess fraction (also referred to as grouped partial attributable risks35 or formally as the attributable proportion in the population23) is the area within a subgroup above the baseline risk (Figure 3i) and can be defined for a subgroup Z as:
where denotes eliminating risk contributors in subgroup Z and is calculated as (Supplementary Information 4, available as Supplementary data at IJE online):
Yet, as the inductive–deductive process of CoOL aims to identify causes and test hypotheses, the excess fractions may be cautiously interpreted as the potential for a public health impact if the hypothesis is true.
Analysing our motivating example, we apply the fitted non-negative model, decompose the risk contributions using LRP and show a dendrogram of how similar the populations are (Figure 4d), which suggests three groups. Figure 4e shows the risk and prevalence of the three subgroups, where one subgroup has a risk of 5%, a second subgroup has a risk of ∼20% with a prevalence of 10% and a third subgroup has a risk of ∼20% with a prevalence of 10%. Figure 4f shows us that we correctly identified that men (sex_0) who are exposed to Drug A (drug_a_1) have a 5% baseline risk, which reaches a near 20% risk through the contributions from being a man and Drug A. Similar are the findings for women (sex_1) and Drug B (drug_b_1). In general, we expect that the predicted risks are slightly underestimated due to regularization.
Post-computational phase
The results of the computational step may provide learnings about different sets of exposures, which may have led to a higher risk of the outcome in specific subgroups. When exploring causes of outcomes, some findings may be spurious. Therefore, the combination of appropriately selected exposures, a well-defined study-design, the use of regularization parameters for model fitting, critically selecting findings and ensuring the replicability in internal validation data is important before developing new hypotheses. This evidence for hypothesis development should be interpreted in light of the domain expertise formalized in the assumed causal model (the pre-computational phase). New hypotheses about multifactorial aetiology may be denoted in an updated DAG.21 In contrast to other machine learning approaches, CoOL allows us to identify subgroups through combinations of risk contributions that are easily communicated with words.
New learnings may be formulated as a hypothetical intervention and assessed using established methodological frameworks for causal inference modelling.9,21 The post-computational phase for triangulating the hypotheses is conducted in external populations (in temporal validation data or more desirably, external validation data). If replicable, the researchers should provide sufficient evidence that the replicated finding is causal (and not due to similar bias structures). This may be done using various triangulation approaches with orthogonal bias structures (i.e. designs with biases in different directions) including studies outside the epidemiological field.36 Eventually and if possible, the hypotheses generated using CoOL need to be tested using a randomized set-up.
In our example, we now have some learnings to inform two hypotheses: men taking Drug A seem to be at a higher-than-normal risk and women taking Drug B seem to be at a higher-than-normal risk. We may test the findings in observational data from other populations before we eventually intervene (stop exposure to Drug A for men and Drug B for women) possible in a randomized way if justified by equipoise.
Real-life application
Below is a summary of an application of CoOL on publicly available real-life data that focuses on demonstrating the computational phase and highlighting the importance of the pre-computational and post-computational phases.
Pre-computational phase
In a cohort study conducted by the Center for Disease Control and Prevention, we follow 7539 individuals <50 years of age at baseline in 1971–75, of which 739 individuals die during the follow-up period until 1992. We ask the research question: ‘What are the different common sets of circumstances, which might have caused young Americans to die prematurely?’ We use the baseline information sex, age, body mass index (BMI) and systolic blood pressure. Based on prior knowledge and literature, we assume the causal structure shown in Supplementary Real-life Data AnalysisFigure 1. Only selected baseline factors are included for pedagogical reasons.
Computational phase
We analyse a 50% random sub-sample as training data using the CoOL approach. The CoOL analysis reveals that among men in their 40s with high systolic blood pressure, an inverse dose–response association with BMI and mortality is observed (a four-way interaction). We validate this finding in the remaining 50% internal validation data set.
Post-computational phase
The finding from both the training data and the internal validation data is also reported in another study.37 Thus, we may have a similarly complex subgroup of high-risk individuals, who may be targeted for risk-mitigating efforts. Naturally, any causal conclusions require thorough consideration of bias, e.g. confounding due to the presence of unmeasured underlying chronic illnesses decreasing BMI and increasing mortality.38 Still, the strong indication of synergy suggested in the joint exposure group warrants further investigations in future studies.
We discuss this application example in more detail in the Supplementary material, available as Supplementary data at IJE online (real-life data analysis).
Discussion
We have introduced CoOL, which investigates common combinations of exposures that may have caused a health outcome. This approach essentially provides a formalized approach to data exploration, which may lead to new and relevant hypotheses to eventually be tested using traditional epidemiological approaches. We used a simple simulation in the presentation; however, CoOL translates to complex scenarios (see how CoOL performs on nine different data simulations and a real-life analysis in the Supplementary material, available as Supplementary data at IJE online).
So far, the sufficient cause model and the way of thinking about causes of an outcome have, de facto, mostly been a theoretical framework and not a practical approach for applied data analysis in epidemiology.9 Fully explaining an outcome seems far-fetched in epidemiology39 since these sets of events will interplay with multiple unknown or unmeasurable causes. However, CoOL is particularly suited towards common and public health relevant exposures in subpopulations, which is important for learning aetiology for preventive interventions40—or at least identify vulnerable subgroups who may benefit from risk-mitigating interventions.
Limitations and extensions
Inference
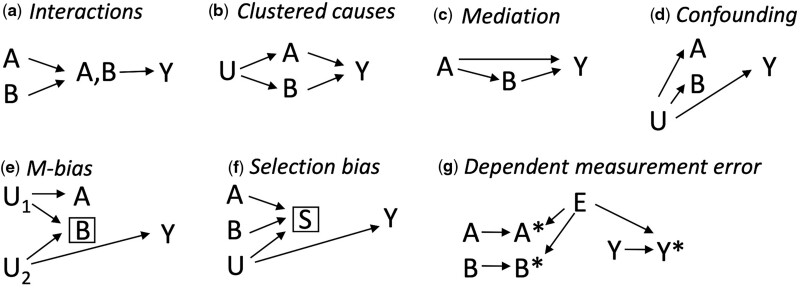
Co-occurring associations between the exposures and the outcome can be due to various causal structures such as interactions,34 clustered causes (exposures sharing a common cause), mediation,34 uncontrolled confounding,9 conditioning on a common effect (collider-stratification or selection bias)41 and measurement error42 (Figure 5). Collider bias should not be introduced by using a neural network compared with standard approaches since all causes of the latent interactions are included in the model.21 ‘Interactions’ (Figure 5a) entail a combined structural effect that is beyond the sum of the individual effects of the putative causes, and thus some inference about the underlying structures may be suggested by CoOL and confirmed by formal interaction analysis.34 Importantly, certain measurement errors can produce spurious appearances of interactions43 and by dichotomizing continuous exposures, synergistic results may be an indicator of those individuals with the most extreme values who are also exposed to additional unmeasured risk factors. The latter may be useful when identifying high-risk groups but misleading for understanding co-acting causes of disease. In real life, complex combinations of all these structures cannot be excluded and researchers need to assess various hypotheses through triangulation—and if possible through randomization—to support their explanatory contribution.36 Very large data sets may be needed to illuminate complex structures.
Figure 5.
Seven causal structures causing co-occurring associations
A and B denote measured exposures of interest, U denotes an unmeasured cause of A and B, Y denotes the outcome and S denotes a selection mechanism. All seven causal structures result in an increased co-occurrence of A and B in the Causes of Outcome Learning approach. It only applies for interactions that the combined effect is larger than the sum of the individual effects as well as some measurement error structures.43 (a) Interaction—A and B jointly affect Y and thus occur often together when assessing risk contributions (see also 34). (b) Clustered causes—A and B occur more often together due to U. (c) Mediation—since B is caused by A, A and B often occur together (see also 34). (d) Confounding—if U is a cause of A, B and Y, all variables occur often together (see also 9). (e) M-bias—selection on B can cause a non-causal association between A and B, and A and Y (see also 41). (f) Selection bias—conditioning on S creates a non-causal association between A, B and Y (see also 41). (g) Dependent measurement error—the measured A (A*), B (B*) and Y (Y*) occur more often together if they share E as cause (see also 42)
Rose described chains of causes by separating causes into distal and proximal causes: proximal causes, e.g. infectious agents, dietary deficiencies, smoking, toxic exposures and allergens, are close to the outcome and distal causes, e.g. social and economic positions, are causes of causes and thus distal to the outcome.6 The fitted effects of proximal causes may mask effects of distal causes (if their effects are mediated through the proximal causes) and the included exposures should therefore be carefully selected according to appropriate actionable exposures and contextual factors. An individualized focus on proximal causes may misdirect attention away from structural public health interventions and could in the worst-case scenario stigmatize parts of the population without offering preventive interventions.44
Model
The presented version of CoOL deals with binary exposures and outcomes, similarly to the sufficient cause model.10 However, the approach can be extended to continuous outcomes, where the value 0 has a meaningful interpretation (e.g. loss of disease-free years, and in contrast to e.g. BMI). Multiple other extensions of CoOL may be possible, e.g. incorporating time, such as time-varying variables and complex confounding scenarios. Future work should explore simultaneous analysis of ‘outcome-wide’ approaches45 since co-morbidity may share underlying sufficient component causes (e.g. atopic diseases as asthma, dermatitis and nasopharyngitis) and thus may be a multi-task learning problem. The parameter restriction to non-negative values limits the model to focus on synergistic structures, thus antagonistic structures that can have public health relevance may be overlooked.
Robustness checks
Sparse data may result in type 1 (false-positive findings) and type 2 errors (false-negative findings). Robustness checks should be conducted to challenge the stability of the approach.46 It may give insight to change the number of activation functions (Supplementary Simulation 7, available as Supplementary data at IJE online), rerun the analysis with subsamples of the study population (Supplementary Simulation 8, available as Supplementary data at IJE online) and change the regularization parameters (Supplementary Simulation 9, available as Supplementary data at IJE online). Risk probabilities of >1 as well as a baseline risk above the crude risk of the outcome or equal to 0 indicate model misspecification (warnings will be shown if using the R package, CoOL). It is important to ensure that the mean predicted risk in each subgroup is approximately equivalent to the actual risk in the subgroup.
Theoretical comparison with other approaches
Based on epidemiology textbooks, one may assess the independent and joint effects of all possible combinations of all exposures (two-way interactions, three-way interactions, etc.).47 This approach is, however, in practice, often not feasible because it requires a very high number of parameters and may become uninterpretable—or even misleading—as shown in the comparison with CoOL in Supplementary Comparison 1 (available as Supplementary data at IJE online). Our suggested approach utilizes the advantages of neural networks to discover the relevant combinations of exposures and make them interpretable using LRP while avoiding certain causal biases.
LRP properties of CoOL can be compared to decomposition approaches of mediated and interactive effects in epidemiology;48,49 however, more work is needed to assess the extent of these similarities.
Approaches such as the exposome50–52 and exposure-wide or environment-wide association studies (EWAS)53,54 assess multiple exposures simultaneously but few applied studies include interactions.53–56 The few that do consider interactions tend to investigate interaction of pre-selected factors only57 or with methods generally restricted to pairwise interactions.58 Such studies have been discussed in relation to their potential, especially in light of successes of genome-wide association studies,59 and limitations such as a challenging causal interpretation.8
LRP has been successfully demonstrated in image, text and biological data classification60–62 as well as for health records to explain clinical decisions on therapy assignment.63 In this latter case, neither a baseline risk was estimated nor was there interest in identifying subgroups. The computational phase of CoOL has similarities to work on explaining and correcting computer vision64,65 but takes its depart from a causal question. CoOL may be viewed as a supervised clustering approach based on an additive feature attribution method guided by a causally inspired model. It should be investigated to which degree other additive feature attribution methods approximate similar results; 66 however, we suspect that the use of negative attributions used in many other approaches may mislead the search for true causes due to the introduction of collider bias since clustering is based on a common effect (Supplementary Comparison 2, available as Supplementary data at IJE online).
Alternative methods to LRP for decomposing neural network predictions were proposed recently, such as DeepLIFT67 and Integrated Gradients.68 However, only LRP and its Deep Taylor Decomposition theoretical framework29 fit our assumption of a non-negative neural network with non-positive activation–function intercepts. Using non-negative models for sets of explanations within certain aims was proposed decades ago69 but not in relation to causal questions. We did not want to consider sensitivity-based, perturbation-based or surrogate-based explanation techniques, since our question of interest relates to the causes of an outcome posed as ‘Given a particular health outcome, what are the most common sets of exposures, which might have been its causes?’ rather than effects of causes posed as ‘What would have occurred if a particular factor were intervened upon and thus set to a different level than it in fact was?’. These distinctions have previously been discussed in the causal inference literature10 and the literature on LRP.18
Conclusion
We have introduced the CoOL approach with the aim of disentangling common combinations of exposures that could have caused a specific health outcome. The approach is based on prior knowledge of the causal structure, the flexibility of a non-negative neural network, the LRP explanation technique for decomposing risk contributions and clustering and, finally, hypothesis development and testing. These are steps towards building better transparency and causal reasoning into hypothesized causal findings from machine learning methods in the health sciences.70,71 The proposed approach links to the sufficient cause model;5 it may help disentangle structures in the ‘syndemics’ (synergistic epidemics) literature72 and add a tool for holistic approaches to ‘precision’ public health.73 We stress that CoOL is an inductive–deductive approach and that researchers need to carefully consider the most appropriate set-up for fair public health actions. CoOL encourages and enables epidemiologists to examine common combinations of exposures as causes of the outcome of interest. This could eventually inform the development of more effective, targeted and impactful public health interventions.
Ethics approval
Ethics approval is not needed for this study as it includes simulated data and publicly available anonymous data.
Data availability
All code and simulated examples can be found at https://cran.r-project.org/package=CoOL and https://github.com/ekstroem/cool. The data for the real-life application can be found at https://wwwn.cdc.gov/nchs/nhanes/ and pre-processed at https://github.com/suinleelab/treeexplainer-study/tree/master/notebooks/mortality.
Supplementary data
Supplementary data are available at IJE online.
Author contributions
A.R. conceived of the idea. A.R., P.D. and C.T.E. developed the proof of principle. A.R., P.D., L.A., S.L., W.S. and C.T.E. contributed to the machine learning aspects. A.R., O.A.A., N.H.R. and C.T.E. contributed to the causal inference aspects. A.R., P.D., L.A. and C.T.E. developed the R package. All authors contributed significantly to the conceptualization of the approach and writing of the manuscript. All authors have approved the final version of the manuscript and are accountable for all aspects of the work.
Funding
A.R. was supported by an international post-doc grant by the Independent Research Fund Denmark (9034-00006B). P.D. was supported by a research grant from the Danish Diabetes Academy funded by the Novo Nordisk Foundation. L.A., S.L. and W.S. are supported by the German Ministry for Education and Research as BIFOLD (refs. 01IS18025A and 01IS18037A) and TraMeExCo (ref. 01IS18056A). O.A.A. was supported by a grant (R01EB0276502) from the National Institute of Biomedical Imaging and Bioengineering (NIBIB) and a grant (UL1TR001881) from the National Center for Advancing Translational Sciences (NCATS), both at the National Institutes of Health (NIH).
Supplementary Material
Acknowledgements
The authors would like to thank the colleagues at the Section of Epidemiology, Department of Public Health, University of Copenhagen for valuable comments and suggestions on the idea throughout the development. The authors are grateful to Rasmus Wibæk Christensen, Stine Byberg and Douglas Ezra Morrison for comments on the manuscript; to Tue Kjærgaard Nielsen for assistance with the implementation of dendrograms; and to Thorkild IA Sørensen for guidance on literature regarding BMI, blood pressure and mortality.
Conflict of interest
None declared.
Contributor Information
Andreas Rieckmann, Section of Epidemiology, Department of Public Health, University of Copenhagen, Copenhagen, Denmark.
Piotr Dworzynski, Novo Nordisk Foundation Center for Basic Metabolic Research, University of Copenhagen, Copenhagen, Denmark.
Leila Arras, Department of Artificial Intelligence, Fraunhofer Heinrich Hertz Institute, Berlin, Germany.
Sebastian Lapuschkin, Department of Artificial Intelligence, Fraunhofer Heinrich Hertz Institute, Berlin, Germany.
Wojciech Samek, Department of Artificial Intelligence, Fraunhofer Heinrich Hertz Institute, Berlin, Germany; BIFOLD—Berlin Institute for the Foundations of Learning and Data, Berlin, Germany.
Onyebuchi Aniweta Arah, Department of Epidemiology, Fielding School of Public Health, University of California, Los Angeles, CA, USA; Department of Statistics, UCLA College of Letters and Science, Los Angeles, CA, USA.
Naja Hulvej Rod, Section of Epidemiology, Department of Public Health, University of Copenhagen, Copenhagen, Denmark.
Claus Thorn Ekstrøm, Section of Biostatistics, Department of Public Health, University of Copenhagen, Copenhagen, Denmark.
References
- 1. VanderWeele TJ, Robins JM.. The identification of synergism in the sufficient-component-cause framework. Epidemiology 2007;18:329–39. [DOI] [PubMed] [Google Scholar]
- 2. Rothman KJ, Greenland S, Lash TL.. Modern Epidemiology. Philadelphia: Wolters Kluwer Heal. Williams Wilkins, 2008. [Google Scholar]
- 3. Rothman KJ, Greenland S, Walker AM.. Concepts of interaction. Am J Epidemiol 1980;112:467–70. [DOI] [PubMed] [Google Scholar]
- 4. Ngamwong Y, Tangamornsuksan W, Lohitnavy O. et al. Additive synergism between asbestos and smoking in lung cancer risk: a systematic review and meta-analysis. PLoS One 2015;10:e0135798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Rothman KJ. Causes. Am J Epidemiol 1976;104:587–92. [DOI] [PubMed] [Google Scholar]
- 6. Rose G, Khaw KT, Marmot M.. Rose’s Strategy of Preventive Medicine: The Complete Original Text. Oxford: Oxford University Press, 2008. [Google Scholar]
- 7. Brankovic M, Kardys I, Steyerberg EW. et al. Understanding of interaction (subgroup) analysis in clinical trials. Eur J Clin Invest 2019;49:e13145. [DOI] [PubMed] [Google Scholar]
- 8. VanderWeele TJ. Outcome-wide epidemiology. Epidemiology 2017;28:399–402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Hernán M, Robins JM.. Causal Inference: What If. Boca Raton: Chapman & Hall/CRC, 2020. [Google Scholar]
- 10. VanderWeele TJ, Hernán MA.. From counterfactuals to sufficient component causes and vice versa. Eur J Epidemiol 2006;21:855–58. [DOI] [PubMed] [Google Scholar]
- 11. Reiber GE, Vileikyte L, Boyko EJ. et al. Causal pathways for incident lower-extremity ulcers in patients with diabetes from two settings. Diabetes Care 1999;22:157–62. [DOI] [PubMed] [Google Scholar]
- 12. Alrawahi AH. New approaches to disease causation research based on the sufficient-component cause model. J Public Health Res 2020;9:1726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Mackie JL. Causes and conditions. Am Philos Q 1965;2:245–64. [Google Scholar]
- 14. Baumgartner M, Falk C.. Configurational causal modeling and logic regression. Multivar Behav Res 2021;1–19. [DOI] [PubMed] [Google Scholar]
- 15. Ragin CC. Using qualitative comparative analysis to study causal complexity. Health Serv Res 1999;34:1225–39. [PMC free article] [PubMed] [Google Scholar]
- 16. Warren J, Wistow J, Bambra C.. Applying qualitative comparative analysis (QCA) in public health: a case study of a health improvement service for long-term incapacity benefit recipients. J Public Health (Oxf) 2014;36:126–33. [DOI] [PubMed] [Google Scholar]
- 17. Bach S, Binder A, Montavon G, Klauschen F, Müller K-R, Samek W.. On pixel-wise explanations for non-linear classifier decisions by layer-wise relevance propagation. PLoS One 2015;10:e0130140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Montavon G, Samek W, Müller K-R.. Methods for interpreting and understanding deep neural networks. Digit Signal Process A Rev J 2018;73:1–15. [Google Scholar]
- 19. Montavon G, Binder A, Lapuschkin S, Samek W, Müller K-R.. Layer-wise relevance propagation—an overview [Chapter 10]. Explain AI Interpret Explain Vis Deep Learn 2019;193–206. [Google Scholar]
- 20. Pearl J, Glymour M, Jewell NP.. Causal Inference in Statistics: A Primer. Chichester: John Wiley & Sons, 2016. [Google Scholar]
- 21. VanderWeele TJ, Robins JM.. Directed acyclic graphs, sufficient causes, and the properties of conditioning on a common effect. Am J Epidemiol 2007;166:1096–104. [DOI] [PubMed] [Google Scholar]
- 22. Tennant PW, Harrison WJ, Murray EJ. et al. Use of directed acyclic graphs (DAGs) in applied health research: review and recommendations. Int J Epidemiol 2021;50:620–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Suzuki E, Yamamoto E, Tsuda T.. On the relations between excess fraction, attributable fraction, and etiologic fraction. Am J Epidemiol 2012;175:567–75. [DOI] [PubMed] [Google Scholar]
- 24. Kallus N. Classifying treatment responders under causal effect monotonicity. Int Conf Mach Learn 2019;3201–10. [Google Scholar]
- 25. Beyea J, Greenland S.. The importance of specifying the underlying biologic model in estimating the probability of causation. Health Phys 1999;76:269–74. [DOI] [PubMed] [Google Scholar]
- 26. LeCun YA, Bottou L, Orr GB, Müller K-R.. Efficient BackProp BT—Neural Networks: Tricks of the Trade. Berlin: Springer, 2012. [Google Scholar]
- 27. Janssens ACJW, Martens FK.. Reflection on modern methods: revisiting the area under the ROC Curve. Int J Epidemiol 2020;49:1397–403. [DOI] [PubMed] [Google Scholar]
- 28. Pearl J. The seven tools of causal inference, with reflections on machine learning. Commun ACM 2019;62:54–60. [Google Scholar]
- 29. Montavon G, Lapuschkin S, Binder A, Samek W, Müller K-R.. Explaining nonlinear classification decisions with deep Taylor decomposition. Pattern Recognit 2017;65:211–22. [Google Scholar]
- 30. Strauss T, Maltitz MV.. Generalising ward’s method for use with manhattan distances. PLoS One 2017;12:e0168288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Chavent M, Kuentz-Simonet V, Labenne A, Saracco J.. ClustGeo: an R package for hierarchical clustering with spatial constraints. Comput Stat 2018;33:1799–822. [Google Scholar]
- 32. Yu G, Smith DK, Zhu H, Guan Y, Lam TTY.. GGTree: an R package for visualization and annotation of phylogenetic trees with their covariates and other associated data. Methods Ecol Evol 2017;8:28–36. [Google Scholar]
- 33. Eide GE, Heuch I.. Attributable fractions: fundamental concepts and their visualization. Stat Methods Med Res 2001;10:159–93. [DOI] [PubMed] [Google Scholar]
- 34. VanderWeele TJ. Explanation in Causal Inference: Methods for Mediation and Interaction. New York: Oxford University Press, 2015. [Google Scholar]
- 35. Land M, Vogel C, Gefeller O.. Partitioning methods for multifactorial risk attribution. Stat Methods Med Res 2001;10:217–30. [DOI] [PubMed] [Google Scholar]
- 36. Lawlor DA, Tilling K, Smith GD.. Triangulation in aetiological epidemiology. Int J Epidemiol 2016;45:1866–86. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Hong HY, Qiong WN, Feng LX. et al. Body mass index and prognosis in patients with systolic heart failure. Zhonghua xin xue guan bing za zhi. Chinese J Cardiovasc Dis 2009;37:870–74. [PubMed] [Google Scholar]
- 38. Sudharsanan N, Ho JY.. Rural–urban differences in adult life expectancy in Indonesia: a parametric g-formula–based decomposition approach. Epidemiology 2020;31:393–401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Smith GD. Epidemiology, epigenetics and the ‘gloomy prospect’: embracing randomness in population health research and practice. Int J Epidemiol 2011;40:537–62. [DOI] [PubMed] [Google Scholar]
- 40. Olsen J. What characterises a useful concept of causation in epidemiology? J Epidemiol Community Health 2003;57:86–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Arah OA. Analyzing selection bias for credible causal inference. Epidemiology 2019;30:517–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. VanderWeele TJ, Hernán MA.. Results on differential and dependent measurement error of the exposure and the outcome using signed directed acyclic graphs. Am J Epidemiol 2012;175:1303–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Greenland S. Basic problems in interaction assessment. Env Heal Perspect 1993;101:59–66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Kee F, Taylor-Robinson D.. Scientific challenges for precision public health. J Epidemiol Community Health 2020;74:311–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. VanderWeele TJ, Mathur MB, Chen Y.. Outcome-wide longitudinal designs for causal inference: a new template for empirical studies. Stat Sci 2020;35:437–66. [Google Scholar]
- 46. Lange T, Roth V, Braun ML, Buhmann JM.. Stability-based validation of clustering solutions. Neural Comput 2004;16:1299–323. [DOI] [PubMed] [Google Scholar]
- 47. Kleinbaum DG, Kupper LL, Morgenstern H.. Epidemiologic Research: Principles and Quantitative Methods. New York: John Wiley & Sons, 1991. [Google Scholar]
- 48. VanderWeele TJ. A three-way decomposition of a total effect into direct, indirect, and interactive effects. Epidemiology 2013;24:224–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Huang YT, Tai AS, Chou MY, Lin GX, Lin SH.. Six-way decomposition of causal effects: Unifying mediation and mechanistic interaction. Stat Med 2020;39:4051–68. [DOI] [PubMed] [Google Scholar]
- 50. Wild CP. The exposome: from concept to utility. Int J Epidemiol 2012;41:24–32. [DOI] [PubMed] [Google Scholar]
- 51. Rappaport SM, Smith MT.. Environment and disease risks. Science 2010;330:460–61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Rappaport SM. Implications of the exposome for exposure science. J Expo Sci Environ Epidemiol 2011;21:5–9. [DOI] [PubMed] [Google Scholar]
- 53. Patel CJ, Bhattacharya J, Butte AJ.. An environment-wide association study (EWAS) on type 2 diabetes mellitus. PLoS One 2010;5:e10746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Patel CJ, Bhattacharya J, Ioannidis JPA, Bendavid E.. Systematic identification of correlates of HIV infection: an X-wide association study. AIDS 2018;32:933–43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Tzoulaki I, Patel CJ, Okamura T. et al. A nutrient-wide association study on blood pressure. Circulation 2012;126:2456–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Patel CJ, Cullen MR, Ioannidis JP, Butte AJ.. Systematic evaluation of environmental factors: persistent pollutants and nutrients correlated with serum lipid levels. Int J Epidemiol 2012;41:828–43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57. Patel CJ, Ioannidis JPA, Cullen MR, Rehkopf DH.. Systematic assessment of the correlations of household income with infectious, biochemical, physiological, and environmental factors in the United States, 1999-2006. Am J Epidemiol 2015;181:171–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. Barrera-Gómez J, Agier L, Portengen L. et al. A systematic comparison of statistical methods to detect interactions in exposome-health associations. Environ Heal A Glob Access Sci Source 2017;16:1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Ioannidis JPA. Exposure-wide epidemiology: revisiting Bradford Hill. Stat Med 2016;35:1749–62. [DOI] [PubMed] [Google Scholar]
- 60. Samek W, Binder A, Montavon G, Bach S, Müller K-R.. Evaluating the visualization of what a Deep Neural Network has learned. IEEE Trans Neural Netw Learn Syst 2017;28:2660–73. [DOI] [PubMed] [Google Scholar]
- 61. Arras L, Horn F, Montavon G, Müller K-R, Samek W. ‘What is relevant in a text document?’: an interpretable machine learning approach. PLoS One 2017;12:e0181142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62. Sturm I, Lapuschkin S, Samek W, Müller K-R.. Interpretable deep neural networks for single-trial EEG classification. J Neurosci Methods 2016;274:141–45. [DOI] [PubMed] [Google Scholar]
- 63. Yang Y, Tresp V, Wunderle M, Fasching PA.. Explaining therapy predictions with layer-wise relevance propagation in neural networks. Proc—2018 IEEE Int Conf Healthc Informatics, ICHI 2018;152–62. [Google Scholar]
- 64. Lapuschkin S, Wäldchen S, Binder A, Montavon G, Samek W, Müller K-R.. Unmasking Clever Hans predictors and assessing what machines really learn. Nat Commun 2019;10:1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65. Anders CJ, Weber L, Neumann D, Samek W, Müller K-R, Lapuschkin S.. Finding and removing Clever Hans: using explanation methods to debug and improve deep models. Inf Fusion 2022;77:261–95. [Google Scholar]
- 66. Lundberg SM, Lee SI.. A unified approach to interpreting model predictions. Proc 31st Int Conf Neural Inf Process Syst 2017;4768–77. [Google Scholar]
- 67. Shrikumar A, Greenside P, Kundaje A.. Learning important features through propagating activation differences. 34th Int Conf Mach Learn ICML 2017;3145–53. [Google Scholar]
- 68. Sundararajan M, Taly A, Yan Q.. Axiomatic attribution for deep networks. 34th Int Conf Mach Learn ICML 2017;3319–28. [Google Scholar]
- 69. Lee DD, Seung HS.. Learning the parts of objects by non-negative matrix factorization. Nature 1999;401:788–91. [DOI] [PubMed] [Google Scholar]
- 70. Beam AL, Manrai AK, Ghassemi M.. Challenges to the reproducibility of machine learning models in health care. JAMA 2020;323:305–06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71. Holzinger A, Langs G, Denk H, Zatloukal K, Müller H.. Causability and explainability of artificial intelligence in medicine. Wiley Interdiscip Rev Data Min Knowl Discov 2019;9:e1312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72. Tsai AC. Syndemics: A theory in search of data or data in search of a theory? Soc Sci Med 2018;206:117–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73. Olstad DL, McIntyre L.. Reconceptualising precision public health. BMJ Open 2019;9:e030279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74. Vollset SE. Confidence intervals for a binomial proportion. Stat Med 1993;12:809–24. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All code and simulated examples can be found at https://cran.r-project.org/package=CoOL and https://github.com/ekstroem/cool. The data for the real-life application can be found at https://wwwn.cdc.gov/nchs/nhanes/ and pre-processed at https://github.com/suinleelab/treeexplainer-study/tree/master/notebooks/mortality.