Theoretical investigation on resonance characteristics of a vapor bubble based on Laplace transform method

Abstract

In the present paper, resonance characteristics of the vapor bubble oscillating in an acoustic field are investigated analytically. The analytical solution of the non-dimensional perturbation of the instantaneous bubble radius during the transient process in the initial oscillation stage is explicitly obtained and physically analyzed at the resonance situation based on the Laplace transform method. And the typical oscillation behaviors obtained from the analytical solution are thoroughly exhibited and analyzed in the time and frequency domains. In addition, the corresponding oscillation behaviors at the non-resonance situation are also investigated for the purpose of comparisons. Through our investigation, several essential conclusions can be drawn as follows: (1) The analytical solution of the non-dimensional perturbation of the instantaneous bubble radius can be divided into four terms according to the physical meaning. Among them, it is the term related to the acoustic field that causes the progressively violent bubble oscillation. (2) The vapor bubble with a smaller equilibrium radius could respond faster and more significantly to the acoustic field during the oscillation. (3) The bubble oscillation characteristics always exhibit significant differences at the resonance and non-resonance situations in both the time and frequency domains, even if the difference between the natural frequency of the oscillating vapor bubble and the angular frequency of the acoustic field is greatly small.

Nomenclature

Roman letters

$c_{\text{pl}}$

the specific heat of the liquid at the constant pressure (J/(kg·K))

$D_{\text{l}}$

the thermal diffusivity of the liquid (m²/s)

$h_{\text{lv}}$

the latent heat of the liquid vaporization (J/kg)

$p_0$

the ambient pressure (Pa)

$p_{\text{a}}$

the pressure amplitude of the acoustic field (Pa)

$p_{\text{v}}$

the pressure of the vapor inside the bubble (Pa)

R

the instantaneous vapor bubble radius (m)

$\dot{R}$

the first derivative of R with respect to the time (m/s)

$\ddot{R}$

the second derivative of R with respect to the time (m/s²)

$R_0$

the equilibrium bubble radius (m)

s

the independent variable in the complex field

t

the time (s)

t*

the non-dimensional time

$T_0$

the ambient temperature (K)

x

the non-dimensional perturbation of the instantaneous bubble radius

$\ddot{x}$

the second derivative of x with respect to the time (s⁻²)

$x_0$

the initial value of x

${\dot{x}}_0$

the initial value of $\dot{x}$ (s⁻¹)

$x_{\text{n}}$

the non-dimensional perturbation of the instantaneous bubble radius at the non-resonance situation

$x_{\text{r}}$

the non-dimensional perturbation of the instantaneous bubble radius at the resonance situation

${\stackrel{\sim }{x}}_{\text{n-low}}$

the lower oscillation envelope at the non-resonance situation

${\stackrel{\sim }{x}}_{\text{n-up}}$

the upper oscillation envelope at the non-resonance situation

${\stackrel{\sim }{x}}_{\text{r-low}}$

the lower oscillation envelope at the resonance situation

${\stackrel{\sim }{x}}_{\text{r-up}}$

the upper oscillation envelope at the resonance situation

${\stackrel{\sim }{x}}_{\text{n-up}}^{\text{'}}$

the derivative of ${\stackrel{\sim }{x}}_{\text{n-up}}$ with respect to the time (s⁻¹)

${\stackrel{\sim }{x}}_{\text{r-up}}^{\text{'}}$

the derivative of ${\stackrel{\sim }{x}}_{\text{r-up}}$ with respect to the time (s⁻¹)

$\mathrm{\Delta }{\stackrel{\sim }{x}}_{\text{n/r-up}}$

the non-dimensional difference between ${\stackrel{\sim }{x}}_{\text{r-up}}^{}$ and ${\stackrel{\sim }{x}}_{\text{n-up}}$

Greek letters

${\rho }_{\text{l}}$

the liquid density (kg/m³)

${\rho }_{\text{v}}$

the density of the vapor inside the bubble (kg/m³)

σ

the surface tension coefficient (kg/s²)

τ

an integral variable (s)

ω

the angular frequency (s⁻¹)

${\omega }_0$

the natural frequency of the oscillating vapor bubble (s⁻¹)

${\omega }_{\text{a}}$

the angular frequency of the acoustic field (s⁻¹)

${\omega }_{\text{r}}$

the resonance frequency of the oscillating vapor bubble (s⁻¹)

$\omega \text{*}$

the non-dimensional ω

$\mathrm{\Delta }\omega \text{*}$

the non-dimensional difference between ${\omega }_0$ and ${\omega }_{\text{a}}$

Subscript

ℒ

the symbol of the Laplace transform operation

*

the symbol of the convolution operation

1. Introduction

Vapor bubbles exist in natural environment and production extensively, which have a wide range of applications. Generally speaking, vapor bubbles play an important role in chemical change [1], [2], ultrasonic cleaning [3], [4], ultrasonic enhanced boiling heat transfer [5], [6], [7] and other scenarios. In the above application, the resonance situation of vapor bubbles is regarded as an important working condition frequently [8], which is always employed to greatly enhance the cavitation intensity and increase the degree of liquid turbulence [9], [10]. Specifically, in the ultrasonic cleaning field, the cleaning effect can be significantly improved by applying the ultrasonic with frequencies near the resonance frequency of vapor bubbles [11]. And in the medical field, the resonance characteristics of intravascular microbubbles can be employed for ultrasonic diagnosis of specific targets [12]. Therefore, it is necessary to investigate the resonance characteristics of the vapor bubbles driven by acoustic fields.

During the oscillating process of the vapor bubble, the volume and temperature in the bubble are constantly changing, resulting in the vapor pressure in the bubble always changing between the supersaturated and undersaturated. Therefore, during this process, the evaporation and condensation processes always occur on the bubble surface, which is one of the main differences between the vapor bubble and gas bubble dynamics. Due to the condensation rate is limited, it is always difficult to keep up with the decrease rate of the bubble volume, and the vapor in the bubble would behave like a non-condensable gas last stage [13]. This non-equilibrium condensation effect could buffer the collapse process and significantly affects the dynamic behaviors of the vapor bubble. Fujikawa et al. [13] systematically investigated the evaporation and condensation processes at the vapor–liquid interface of the vapor bubble by assuming that there is a thin and finite non-equilibrium region at the phase interface. In this region, the phase transformation process continues, and the transformation rate can be expressed according to the classic expression proposed by Schrage [14].

In the existing literature, the research on the resonance of the vapor bubble mainly focuses on its nonlinear oscillation characteristics during the steady state stage of the oscillation. And considerable progress has been made in the research, such as the oscillation curve and frequency response. To be specific, Lauterborn [15] investigated the nonlinear oscillation response curve of vapor bubbles in the incompressible liquid and summarized the characteristics of main resonance, harmonic resonance, subharmonic resonance and ultra-harmonic resonance during the oscillation. Zhang and Li [16] studied the nonlinear oscillation of bubbles under the dual-frequency acoustic excitation and found that bubbles have two special resonance forms (i.e. of combination resonance and simultaneous resonance) under the dual-frequency excitation. And Hao and Prosperetti [17] found that there are two resonance radii and a limit bubble size during the nonlinear bubble oscillation at the given amplitudes and frequencies. Furthermore, Hegedűs et al. [18] studied a dual-frequency driven single spherical bubble, and exhaustive analyzed the effects of the pressure amplitude, frequency, phase shift between the two harmonic components and the bubble size. And it is found that for a relatively low active cavitation threshold, the application of the giant response combined with the main resonance can significantly increase the bubble collapse strength. In addition to the above regular resonance properties of the bubble caused by the external acoustic field, the parametric resonance properties of the bubble induced by the vibrating fluid have also been discussed. The parametric resonance obviously differs from the regular resonance as it is always linked to the phenomenon of the bubble instability. Specifically, based on the parametric resonance theory, Nabergoj and Francescutto [19] obtained the radial motion amplitude and pressure amplitude threshold of the bubble spherical instability. Lyubimov et al. [20] found that the vibrating fluid could cause coupled oscillations of two neighboring modes. Meanwhile, viscous effect would cause a shift in the non-zero threshold and frequency of resonance excitation and could expand the resonance region. On this basis, Konovalov et al. [21] further developed a rigorous method based on the multiscale method to study the viscous effect on the parametric resonance, and revealed the relations governing the resonance modes evolution around the instability excitation threshold.

In addition, in order to further obtain analytical expressions of important oscillation characteristic parameters of the vapor bubble, the research on the linearized bubble wall motion equations has also made some progress, mainly focusing on the natural frequency of the vapor bubble. Specifically, Khabeev [22] derived two natural frequencies and two resonance dimensions for the vapor bubble oscillating in a certain range of acoustic field frequencies. Prosperetti [23] established a relatively complete linearized oscillation model for the vapor bubble oscillating in the acoustic field, and obtained the explicit expression of the natural frequency based on the model. And Zhang and Lin [24] obtained the resonance frequency of the bubbles in the cylindrical bubble group according to the linearized bubble wall motion equations, and further analyzed the influence of several essential parameters on the resonance frequency of the cylindrical bubble group.

However, the research on the transient process in the initial stage of the vapor bubble resonance is relatively scarce in the previous work. Specifically, the detailed evolution process and its physical mechanism of the instantaneous radius of the vapor bubble have not been fully explored and discussed. And the exact difference between the bubble oscillation at the resonance and non-resonance situations, as well as the analytical reasons for the difference have not yet been clearly revealed. Therefore, the linearized bubble wall motion equations of the vapor bubble are greatly worth to be further solved analytically at the resonance situation to reveal the resonance characteristics.

In order to obtain the analytical solution of the vapor bubble at the resonance situation, several solution methods for solving linearized bubble wall motion equations are briefly introduced and evaluated here. Firstly, the method of complex variable function is one of the most popular mathematical methods for solving linearized equations due to its simplicity. And it has been widely employed to solve the linearized bubble wall motion equation [25], [26]. Nevertheless, this method is not always satisfactory especially at the resonance situation. Specifically speaking, when the bubble oscillation damping is small enough to be ignored, the method cannot obtain the correct bubble resonance oscillation curve due to the existence of singularities. Then, to solve the analytical solution at the resonance situation, another solving method based on the Laplace transform is introduced as follows. In general, Laplace transform is a common transformation method in engineering, which can solve ordinary differential equations of arbitrary order with constant coefficients [27]. For example, the Laplace transform method has been widely employed in automatic control [28], [29], electrical engineering [30] and environmental engineering [31]. For the specific comparison between the Laplace transform method and the complex analysis method, readers can refer to Appendix I.

In the present paper, based on the linearized bubble wall motion equations and the Laplace transform method, the resonance characteristics of the vapor bubble oscillating in the acoustic field are exhaustively investigated in the time and frequency domains. And the corresponding oscillation characteristics at the non-resonance situation are also analyzed for the purpose of comparisons. The whole paper is organized as follows: In Section 2, the analytical solutions for the linearized bubble wall motion equations at the resonance and non-resonance situations are obtained respectively. In Section 3, the correctness of the analytical solution is verified numerically. In Section 4, the oscillation characteristics of the non-dimensional perturbation of the instantaneous bubble radius are analyzed at both the resonance and non-resonance situations. In Section 5, the oscillation characteristics at the resonance situation and the non-resonance situation near the resonance frequency are further compared. In Section 6, the main conclusions of the present paper are summarized. In Appendix I, the comparison between the Laplace transform method and the complex analysis method are discussed. In Appendix II, bubble oscillation characteristics at standing acoustic wave condition are exhibited. In Appendix III, the graphical method to find the resonance frequency of the vapor bubble are introduced. And In Appendix IV, the oscillation envelopes at two situations are derived and shown.

2. Theoretical model

In this section, the critical equations and the specific solving procedures are exhibited in detail. Particularly, in Section 2.1, the basic bubble wall motion equations of a single spherical vapor bubble driven by an acoustic field are introduced. In Section 2.2, the general procedures of the Laplace transform method to solve the linearized bubble wall motion equations are derived. Furthermore, in 2.3, 2.4, the analytical solutions of the non-dimensional perturbation of the instantaneous bubble radius at the resonance and non-resonance situations are revealed respectively.

2.1. Bubble wall motion equations

For the oscillation of a single spherical vapor bubble driven by a single-frequency acoustic field, if the compressibility and the viscosity of the liquid are small enough to be neglected, the bubble wall motion can be expressed by the classical Rayleigh-Plesset equation [32]. Moreover, the bubble size is considered to be much smaller than the wavelength of the acoustic wave, and the spatially inhomogeneous part of the acoustic pressure around the bubble is negligible for both the simple sinusoidal wave and the standing acoustic wave. In the subsequent analysis, the condition of the simple sinusoidal wave is considered emphatically. For the condition of the standing wave, readers can refer to Appendix II. On this basis, the bubble oscillation can be described as follows [32]:

$$R\ddot{R}+\frac{3}{2}{\dot{R}}^2=\frac{p_{\text{ext}}\left(R,t\right)-p_{\text{s}}\left(t\right)}{{\rho }_{\text{l}}}$$ (1)

where

$$p_{\text{ext}}\left(R,t\right)=p_{\text{v}}-\frac{2\sigma }{R}$$ (2)

$$p_{\text{s}}\left(t\right)=p_0+p_{\text{a}}\sin \left({\omega }_{\text{a}}t\right)$$ (3)

Here, $R$ is the instantaneous vapor bubble radius. $\ddot{R}$ is the second derivative of $R$ with respect to the time. $\dot{R}$ is the first derivative of $R$ with respect to the time. ${\rho }_{\text{l}}$ is the liquid density. $p_{\text{v}}$ is the pressure of the vapor inside the bubble. $\sigma$ is the surface tension coefficient. $p_0$ is the ambient pressure. $p_{\text{a}}$ is the pressure amplitude of the acoustic field. ${\omega }_{\text{a}}$ is the angular frequency of the acoustic field. $t$ is the time.

Since the small-amplitude oscillations of the bubble in the early stage of oscillation are mainly focused in the present paper, the complex nonlinear phenomenon is out of consider. And further ignoring the oscillation dissipation, Eq. (1) can be linearized as follows [23]:

$$\ddot{x}+{\omega }_0^{2}x=f$$ (4)

where

$$x=\frac{R-R_0}{R_0}$$ (5)

$$f=-\frac{p_{\text{a}}}{{\rho }_{\text{l}}{R}_0^2}\sin \left({\omega }_{\text{a}}t\right)$$ (6)

Here, $\ddot{x}$ is the second derivative of the non-dimensional perturbation of the instantaneous bubble radius with respect to the time. ${\omega }_0$ is the natural frequency of the oscillating vapor bubble. $x$ is the non-dimensional perturbation of the instantaneous bubble radius (referred to as the non-dimensional radius for short). $R_0$ is the equilibrium bubble radius. To closed the model, the expression of the natural frequency applying to the vapor bubble is introduced as follows [23]:

$${\omega }_0^2=\frac{1}{{\rho }_{\text{l}}{R}_0^2}\left(S-\frac{2\sigma }{R_0}\right)$$ (7)

where

$$S=\frac{2h_{\text{lv}}^2{\rho }_{\text{v}}^2}{{\rho }_{\text{l}}{c}_{\text{pl}}{T}_0}·\frac{{\left({\omega }_{\text{a}}{R}_0^2/2D_{\text{l}}\right)}^{3/2}}{{\left(\sqrt{{\omega }_{\text{a}}{R}_0^2/2D_{\text{l}}}+1\right)}^2+{\omega }_{\text{a}}{R}_0^2/2D_{\text{l}}}$$ (8)

Here, $h_{\text{lv}}$ is the latent heat of the liquid vaporization. ${\rho }_{\text{v}}$ is the density of the vapor inside the bubble. $c_{\text{pl}}$ is the specific heat of the liquid at the constant pressure. $T_0$ is the ambient temperature. $D_{\text{l}}$ is the thermal diffusivity of the liquid. For the linearized equation with the damping, readers can refer to Appendix I.

2.2. General solving procedures

In the present paper, the Laplace transform method is selected to solve the linearized differential bubble wall motion equations shown in Eq. (4). When solving differential equations, the general procedures of the Laplace transform method are as follows. Firstly, Laplace transform is employed to change the given differential equation into algebraic equation. Secondly, the algebraic equation is solved and the result is factored. Then the inverse Laplace transform of the result of the factorization is carried out. Lastly, the convolution operation of the non-homogeneous part of the differential equation is carried out and the solution of the differential equation can be obtained. Whether at the resonance or non-resonance situation, the corresponding analytical solution can be obtained as long as the above procedures are followed. And the difference between them only reflected in the forms of the integrand in the convolution. Therefore, the Laplace transform method can be advisably employed to solve the analytical solution of the vapor bubble driven by an acoustic field at both the resonance and non-resonance situations. Next, the general solving process will be shown as follows.

Firstly, by taking the Laplace transform on Eq. (4), one can obtain:

$$\mathcal{L}\left\{\ddot{x}+{\omega }_0^{2}x\right\}=\mathcal{L}\left\{f\right\}$$ (9)

Here, $\mathcal{L}$ is the symbol of the Laplace transform operation. And the independent variable of the function $L\{\}$ is s which is in the complex field. According to the law of the linearity of the Laplace transform [27], Eq. (9) can be transformed into:

$$\mathcal{L}\left\{\ddot{x}\right\}+{\omega }_0^2\mathcal{L}\left\{x\right\}=\mathcal{L}\left\{f\right\}$$ (10)

Then, applying the differential law of Laplace transform [27], Eq. (10) can be organized as follows:

$$s^2\mathcal{L}\left\{x\right\}-x_{0}s-{\dot{x}}_0+{\omega }_0^2\mathcal{L}\left\{x\right\}=\mathcal{L}\left\{f\right\}$$ (11)

Here, $x_0$ and ${\dot{x}}_0$ are the initial values of x and $\dot{x}$ respectively. And the solution of Eq. (11) is

$$\mathcal{L}\left\{x\right\}=\frac{x_{0}s+{\dot{x}}_0}{s^2+{\omega }_0^2}+\frac{\mathcal{L}\left\{f\right\}}{s^2+{\omega }_0^2}$$ (12)

Subsequently, by factoring Eq. (12), one can obtain:

$$\begin{array}{c}\mathcal{L}\left\{x\right\}=\frac{x_0}{2}\left(\frac{1}{s-\text{i}{\omega }_0}+\frac{1}{s+\text{i}{\omega }_0}\right)\\ +\frac{{\dot{x}}_0}{2\text{i}{\omega }_0}\left(\frac{1}{s-\text{i}{\omega }_0}-\frac{1}{s+\text{i}{\omega }_0}\right)\\ +\frac{\mathcal{L}\left\{f\right\}}{2\text{i}{\omega }_0}\left(\frac{1}{s-\text{i}{\omega }_0}-\frac{1}{s+\text{i}{\omega }_0}\right)\end{array}$$ (13)

According to the exponential and linearity law of the Laplace transform [27], Eq. (13) can be transformed into:

$$\begin{array}{c}\mathcal{L}\left\{x\right\}=\mathcal{L}\left\{\frac{x_0}{2}\left({\text{e}}^{\text{i}{\omega }_{0}t}{\text{+ e}}^{-\text{i}{\omega }_{0}t}\right)\right\}\\ \text{+}\mathcal{L}\left\{\frac{{\dot{x}}_0}{2\text{i}{\omega }_0}\left({\text{e}}^{\text{i}{\omega }_{0}t}-{\text{e}}^{-\text{i}{\omega }_{0}t}\right)\right\}\\ +\mathcal{L}\left\{f\right\}·\mathcal{L}\left\{\frac{1}{2\text{i}{\omega }_0}\left({\text{e}}^{\text{i}{\omega }_{0}t}-{\text{e}}^{-\text{i}{\omega }_{0}t}\right)\right\}\end{array}$$ (14)

Furthermore, relying on the convolution and linearity law of the Laplace transform [27], Eq. (14) can be expressed as follows:

$$\mathcal{L}\left\{x\right\}=\mathcal{L}\left\{x_0·\frac{{\text{e}}^{\text{i}{\omega }_{0}t}{\text{+ e}}^{-\text{i}{\omega }_{0}t}}{2}+{\dot{x}}_0·\frac{{\text{e}}^{\text{i}{\omega }_{0}t}-{\text{e}}^{-\text{i}{\omega }_{0}t}}{2\text{i}{\omega }_0}+f*\frac{{\text{e}}^{\text{i}{\omega }_{0}t}-{\text{e}}^{-\text{i}{\omega }_{0}t}}{2\text{i}{\omega }_0}\right\}$$ (15)

Here, “*” is the symbol of the convolution operation. Due to the uniqueness of the Laplace transform [27], the Laplace transform operation symbol in Eq. (15) can be directly removed. One can obtain:

$$x=x_0·\frac{{\text{e}}^{\text{i}{\omega }_{0}t}{\text{+ e}}^{-\text{i}{\omega }_{0}t}}{2}+{\dot{x}}_0·\frac{{\text{e}}^{\text{i}{\omega }_{0}t}-{\text{e}}^{-\text{i}{\omega }_{0}t}}{2\text{i}{\omega }_0}+f*\frac{{\text{e}}^{\text{i}{\omega }_{0}t}-{\text{e}}^{-\text{i}{\omega }_{0}t}}{2\text{i}{\omega }_0}$$ (16)

Moreover, according to the Euler's formula [27], ${\text{e}}^{\pm \text{i}{\omega }_{0}t}=\cos {\omega }_{0}t\pm \text{i}\sin {\omega }_{0}t$ can be established. Hence, Eq. (16) can be transformed into

$$x=x_0·\cos {\omega }_{0}t+\frac{{\dot{x}}_0}{{\omega }_0}·\sin {\omega }_{0}t+f*\frac{\sin {\omega }_{0}t}{{\omega }_0}$$ (17)

Finally, by taking the convolution operation on the last term in Eq. (17), and combining Eqs. (6), (17), the result can be obtained as follows:

$$x=x_0·\cos {\omega }_{0}t+\frac{{\dot{x}}_0}{{\omega }_0}·\sin {\omega }_{0}t-\frac{p_{\text{a}}}{{\rho }_{\text{l}}{R}_0^2}\frac{1}{{\omega }_0}{\int }_0^t\sin {\omega }_{\text{a}}\tau ·\sin {\omega }_0\left(t-\tau \right)d\tau$$ (18)

Here, τ is an integral variable. And Eq. (18) is the general analytical expression of the dimensionless radius of the oscillating vapor bubble. For the solution of the linearized equation with the damping, readers can refer to Appendix I.

2.3. Analytical solution at resonance situation

At the resonance situation, the relationship between ${\omega }_0$ and ${\omega }_{\text{a}}$ is

$${\omega }_0={\omega }_{\text{a}}$$ (19)

And the value of ${\omega }_{\text{a}}$ at this situation can be called the resonance frequency of the oscillating vapor bubble, which is defined as a new parameter ${\omega }_{\text{r}}$. According to Eq. (7), (8), ${\omega }_0$ varies with ${\omega }_{\text{a}}$, so the resonance frequency ${\omega }_{\text{r}}$ can be solved approximately by using the graphical method. For the specific solution process and the values of ${\omega }_{\text{r}}$ corresponding to the different equilibrium radii $R_0$, readers can refer to Appendix III.

At this situation, according to the product-to-sum identity of the trigonometric functions, one can obtain:

$$\sin {\omega }_{\text{a}}\tau ·\sin {\omega }_0\left(t-\tau \right)=\frac{1}{2}\left[\cos \left(2{\omega }_{\text{a}}\tau -{\omega }_{\text{a}}t\right)-\cos {\omega }_{\text{a}}t\right]$$ (20)

Then bring Eq. (20) into Eq. (18) and representing all ${\omega }_0$ as ${\omega }_{\text{a}}$, the resonance solution of the vapor bubble oscillating in the acoustic field can be expressed as follows:

$$x_{\text{r}}=x_{\text{r1}}+x_{\text{r2}}+x_{\text{r3}}+x_{\text{r4}},{\omega }_0={\omega }_{\text{a}}$$ (21)

where

$$x_{\text{r1}}=x_0·\cos {\omega }_{\text{a}}t$$ (22)

$$x_{\text{r2}}=\frac{{\dot{x}}_0}{{\omega }_{\text{a}}}·\sin {\omega }_{\text{a}}t$$ (23)

$$x_{\text{r3}}=-\frac{p_{\text{a}}}{{\rho }_{\text{l}}{R}_0^2}\frac{\sin {\omega }_{\text{a}}t}{2{\omega }_{\text{a}}^2}$$ (24)

$$x_{\text{r4}}=\frac{p_{\text{a}}}{{\rho }_{\text{l}}{R}_0^2}\frac{t\cos {\omega }_{\text{a}}t}{2{\omega }_{\text{a}}}$$ (25)

Here, $x_{\text{r}}$ is the non-dimensional perturbation of the instantaneous bubble radius at the resonance situation (referred to as the non-dimensional radius at the resonance situation for short).

Eqs. (21)–(25) shows the resonance solution $x_{\text{r}}$ consists of four terms with the different and clear physical meaning. Among them, the first term $x_{\text{r1}}$ is determined by the initial non-dimensional perturbation of the bubble radius. The second term is determined by the initial change rate of the non-dimensional radius. And the last two terms $x_{\text{r3}}$ and $x_{\text{r4}}$ are both mainly related to the amplitude and the frequency of the acoustic field. Nevertheless, the difference between $x_{\text{r3}}$ and $x_{\text{r4}}$ is still significant. Comparatively, $x_{\text{r3}}$ is bounded, while $x_{\text{r4}}$ is unbounded. For $x_{\text{r4}}$, its amplitude is a function of the time t and will continuously increase over time. Predictably, the amplitude of $x_{\text{r4}}$ will be much larger than the other three bounded terms when the oscillation time is large enough. Hence, it can be considered that $x_{\text{r4}}$ is the root cause of the violent oscillation of the vapor bubble.

2.4. Analytical solution at non-resonance situation

Corresponding to Section 2.3, the analytical solution at the non-resonance situation is introduced in this section. At this situation, the relationship between ${\omega }_0$ and ${\omega }_{\text{a}}$ is

$${\omega }_0\ne {\omega }_{\text{a}}$$ (26)

According to Eqs. (7), (8), the natural frequency ${\omega }_0$ cannot be equal to the resonance frequency ${\omega }_{\text{r}}$ at this situation.

Similarly, at this situation, according to the product-to-sum identity of the trigonometric functions, one can obtain

$$\sin {\omega }_{\text{a}}\tau ·\sin {\omega }_0\left(t-\tau \right)=\frac{1}{2}\left[\cos \left(\left({\omega }_{\text{a}}+{\omega }_0\right)\tau -{\omega }_{0}t\right)-\cos \left(\left({\omega }_{\text{a}}-{\omega }_0\right)\tau +{\omega }_{0}t\right)\right]$$ (27)

Bring Eq. (27) into Eq. (18), the non-resonance solution of the vapor bubble oscillating in the acoustic field can be expressed as follows:

$$x_{\text{n}}=x_{\text{n1}}+x_{\text{n2}}+x_{\text{n3}}+x_{\text{n4}},{\omega }_0\ne {\omega }_{\text{a}}$$ (28)

where

$$x_{\text{n1}}=x_0·\cos {\omega }_{0}t$$ (29)

$$x_{\text{n2}}=\frac{{\dot{x}}_0}{{\omega }_0}·\sin {\omega }_{0}t$$ (30)

$$x_{\text{n3}}=-\frac{p_{\text{a}}}{{\rho }_{\text{l}}{R}_0^2}\frac{\sin {\omega }_{\text{a}}t+\sin {\omega }_{0}t}{2{\omega }_0\left({\omega }_{\text{a}}+{\omega }_0\right)}$$ (31)

$$x_{\text{n4}}=\frac{p_{\text{a}}}{{\rho }_{\text{l}}{R}_0^2}\frac{\sin {\omega }_{\text{a}}t-\sin {\omega }_{0}t}{2{\omega }_0\left({\omega }_{\text{a}}-{\omega }_0\right)}$$ (32)

Here, $x_{\text{n}}$ is the non-dimensional perturbation of the instantaneous bubble radius at the non-resonance situation (referred to as the non-dimensional radius at the non-resonance situation for short).

Eq. (28) shows the non-resonance solution $x_{\text{n}}$ also composed of four terms. Among them, the first three terms in $x_{\text{n}}$ is basically the same as those in the resonance solution $x_{\text{r}}$ in terms of the form and the physical meaning. And the fundamental difference between the two situations is mainly reflected in the fourth terms of $x_{\text{r}}$ and $x_{\text{n}}$. For $x_{\text{n4}}$ at the non-resonance situation, its essence is the sum of the two trigonometric functions with a bounded and constant amplitude. However, for the non-resonance situation near the resonance situation, the value of $x_{\text{n4}}$ can reach considerable large. To be specific, the effects of $x_{\text{n1}}$ and $x_{\text{n2}}$ are relatively small, and the amplitude of $x_{\text{n4}}$ is much larger than $x_{\text{n3}}$, because $\left|{\omega }_{\text{a}}+{\omega }_0\right|$ is always much larger than $\left|{\omega }_{\text{a}}-{\omega }_0\right|$ in Eqs. (31), (32) at this situation. And it is foreseeable that the closer ${\omega }_{\text{a}}$ and ${\omega }_0$ are, the more dominant $x_{\text{n4}}$ is and the larger amplitude of the non-dimensional radius can reach.

3. Numerical verification

In this section, the analytical results obtained in Section 2 are verified numerically based on the Keller-Miksis equation for the vapor bubble [33]. And in order to close the Keller-Miksis equation model, the specific expression of $p_{\text{v}}$ in the equation is also obtained from Ref. [23], which is consist with that in Eq. (2). As a result, the viscous dissipation due to liquid viscosity, the acoustic dissipation due to the compressibility of the liquid and the heat dissipation due to the thermodynamic processes of the vapor inside the bubble [23] are naturally included in the Keller-Miksis equation. Hence, the corresponding analytical solution of the linear equation with the oscillation damping (i.e. Eq. (46)) is chosen as the object to be verified.

Fig. 1 shows the comparison between the analytical and the numerical results. In Fig. 1, the red solid and blue dash lines refer to the results based on the Laplace transform method from Eq. (46) and the Keller-Miksis equation respectively. And the oscillation initial conditions and the equilibrium radius of the bubble are as follows: $x_0=0.005$, ${\dot{x}}_0=500{\text{s}}^{-1}$ and $R_0={10}^{-4}\mathrm{m}$. And the amplitude and frequency of the acoustic field are as follows: $p_{\text{a}}=100\text{Pa}$ and ${\omega }_{\text{a}}={10}^5\text{Hz}$. As shown in Fig. 1, for the condition of the bubble oscillation under the small perturbation, the analytical result exhibits great consistency with the numerical results for both the transient state process at the initial oscillation stage and the steady state process at the subsequent oscillation. Therefore, the nonlinear effect is quite weak and the nonlinear terms can be safely ignored. Of course, inevitably, when the oscillation amplitude is large enough, nonlinear effects will show up.

Fig. 1.

The comparison between the analytical and the numerical results. The red solid and blue dash lines refer to the analytical results from Eq. (46) and the numerical result from the Keller-Miksis equation. $x_0=0.005$, ${\dot{x}}_0=500{\text{s}}^{-1}$. $R_0={10}^{-4}\mathrm{m}$.

4. Typical oscillation characteristics

In this section, the typical oscillation characteristics of the non-dimensional radius are comprehensively analyzed in the time and frequency domains based on the analytical solutions in Section 2. Specifically, in Section 4.1, the oscillation characteristics at the resonance situation are analyzed. And in Section 4.2, the corresponding oscillation characteristics at the non-resonance situation are analyzed.

Before the analysis, several important information is given as follows. Firstly, the water and the water vapor are selected as the liquid media and the vapor bubble content respectively. Then, the ambient temperature and the pressure amplitude of the acoustic field are set to $T_0=373.15\mathrm{K}$ and $p_{\text{a}}=100\mathrm{Pa}$ respectively. In addition, the values of the physical parameters corresponding to 373.15 K are selected.

Subsequently, several new non-dimensional parameters are introduced for convenience of the subsequent analysis. Firstly, $\mathrm{\Delta }\omega \text{*}$ is introduced as follows:

$$\mathrm{\Delta }\omega \text{*}=\frac{{\omega }_0-{\omega }_{\text{a}}}{{\omega }_{\text{r}}}$$ (33)

Here, ${\omega }_{\text{r}}$ is the resonance frequency which has been defined in Section 2.3. And the $\mathrm{\Delta }\omega \text{*}$ can be employed to characterize the non-dimensional difference between ${\omega }_0$ and ${\omega }_{\text{a}}$. Specifically, $\mathrm{\Delta }\omega \text{*}=0$ corresponds to the resonance situation, and $\mathrm{\Delta }\omega \text{*}\ne 0$ corresponds to the non-resonance situation. In addition, the effect of the sign of $\mathrm{\Delta }\omega \text{*}$ is discussed. According to Eqs. (28)–(32), whether $\mathrm{\Delta }\omega \text{* > 0}$ or $\mathrm{\Delta }\omega \text{* < 0}$, the oscillation characteristics and their changing trends of the bubble are basically the same. Therefore, only the conditions of $\mathrm{\Delta }\omega \text{*}⩾\text{0}$ are exhibited and analyzed. Then, $\omega \text{*}$ is defined as follows:

$$\omega \text{*}=\frac{\omega }{{\omega }_{\text{r}}}$$ (34)

Here, $\omega$ is the angular frequency. And $\omega \text{*}$ can be employed to represent the non-dimensional independent variable in the analysis of the frequency domain.

4.1. Resonance situation

In this section, the oscillation characteristics of the non-dimensional radius at the resonance situation are analyzed from the time and frequency domains. Moreover, the influence of the equilibrium bubble radius $R_0$ on the oscillation characteristics is also investigated.

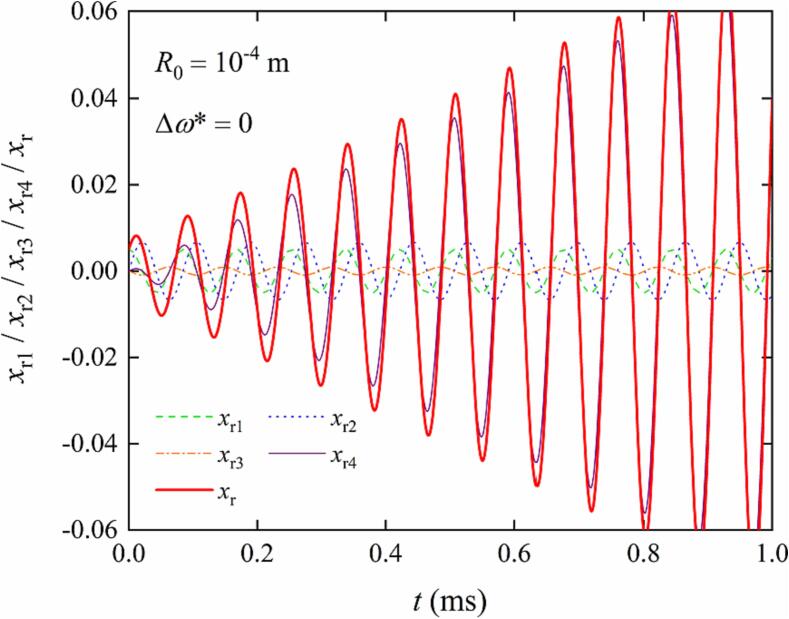
Fig. 2 shows the oscillation characteristics of the non-dimensional radius $x_{\text{r}}$ and its four terms at the resonance situation in the time domain. In Fig. 2, the green dash, blue dot, orange dot dash and purple solid curves refer to $x_{\text{r1}}$, $x_{\text{r2}}$, $x_{\text{r3}}$ and $x_{\text{r4}}$ in Eqs. (22)-(25) respectively. And the red thick solid curve refers to $x_{\text{r}}$ in Eq. (21). In addition, the equilibrium bubble radius and the non-dimensional initial conditions of the bubble are set as follows:$R_0={10}^{-4}\text{m}$. $x_0=0.005$. And ${\dot{x}}_0=500{\text{s}}^{-1}$.

Fig. 2.

The oscillation characteristics of the non-dimensional radius and its four terms at the resonance situation in the time domain. The green dash, blue dot, orange dot dash and purple solid curves refer to $x_{\text{r1}}$, $x_{\text{r2}}$, $x_{\text{r3}}$ and $x_{\text{r4}}$ respectively. And the red thick solid curve refers to the non-dimensional radius at the resonance situation $x_{\text{r}}$. $R_0={10}^{-4}\text{m}$. $x_0=0.005$. ${\dot{x}}_0=500{\text{s}}^{-1}$.

As shown in Fig. 2, the oscillation amplitude of the non-dimensional radius gradually increases over time at the resonance situation. As for the its four terms, the curves referring to $x_{\text{r1}}$, $x_{\text{r2}}$, $x_{\text{r3}}$ always oscillate periodically with fixed amplitudes, the same frequency and different phases. While the curve referring to $x_{\text{r4}}$ oscillates non-periodically with a linear increasing amplitude over time. According to the dominant effect of the four terms on $x_{\text{r}}$, the oscillation process can be divided into two stages roughly. Specifically, at the initial stage when about $t<0.1\text{ms}$, the oscillation characteristics of $x_{\text{r}}$ are dominated by $x_{\text{r1}}$ and $x_{\text{r2}}$ primarily. While the effects of $x_{\text{r3}}$ and $x_{\text{r4}}$ are relatively weak, because the values of them is relatively small and even offset each other out due to the difference in phase. Later, the influence of each term on $x_{\text{r}}$ significantly changes compared with the initial stage. At this stage, $x_{\text{r4}}$ becomes the dominant term and the dominant effect keep stronger over time, because its amplitude increases linearly over time and is gradually much larger than that of $x_{\text{r1}}$, $x_{\text{r2}}$ and $x_{\text{r3}}$. Physically speaking, at the quite short initial oscillation stage, initial conditions of the oscillating bubble dominate the oscillation characteristics of the vapor bubble, decisively affect the oscillation amplitude, frequency and phase. But soon after, the acoustic field becomes the primary cause of the constant growth of the oscillation amplitude, which means the resonance of the bubble begin to emerge and prosper. Admittedly, the amplitude of the bubble will certainly not always maintain this linear increase trend, because the nonlinear effect will gradually become significant when the amplitude is large enough. But for the early stage of the resonance with the tiny oscillation amplitude, the linear increasing trend of the amplitude obtained based on the Laplace transform has a certain rationality.

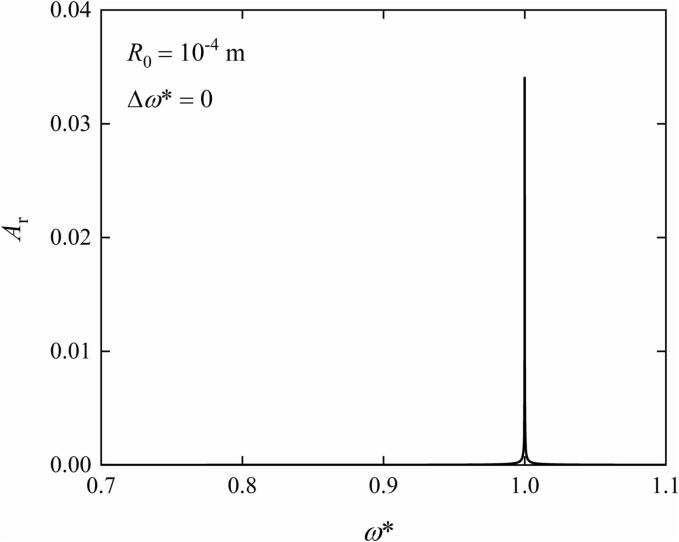
Subsequently, Fig. 3 shows the oscillation characteristics of the non-dimensional radius at the resonance situation in the frequency domain. In Fig. 3, $A_{\text{r}}$ represents the amplitude at the resonance situation. And the equilibrium bubble radius, the initial conditions and the other parameters are all consistent with those in Fig. 2. In addition, the time range is selected as 0–10⁻³ s in the fast Fourier transform operation in order to obtain a smooth curve of $A_{\text{r}}$. As shown in Fig. 3, there is only one obvious peak at $\omega \text{*}=1$. That is to say, there is only one characteristic angular frequency in the oscillation process at the resonance situation, which is equal to the resonance frequency ${\omega }_{\text{r}}$.

Fig. 3.

The oscillation characteristics of the non-dimensional radius at the resonance situation in the frequency domain. $R_0={10}^{-4}\text{m}$. $x_0=0.005$. ${\dot{x}}_0=500{\text{s}}^{-1}$.

Moreover, Fig. 4 shows the oscillation characteristics of the non-dimensional radius with different equilibrium bubble radii at the resonance situation in the time domain. In Fig. 4, the blue solid, red dash and green dot curves refer to $R_0=1\times {10}^{-3}\text{m}$, $R_0=2\times {10}^{-3}\text{m}$ and $R_0=5\times {10}^{-3}\text{m}$ respectively. And the initial conditions are all ignored in these three cases in order to directly compare the effects of $R_0$. As shown in Fig. 4, the amplitude growth rate of the non-dimensional radius shows obvious negative correlation with the change of the equilibrium bubble radius. To be specific, the vapor bubble with a smaller equilibrium radius will respond faster and more significantly to the acoustic field at the resonance situation.

Fig. 4.

The oscillation characteristics of the non-dimensional radius with different equilibrium bubble radii at the resonance situation in the time domain. The blue solid, red dash and green dot curves refer to $R_0=1\times {10}^{-3}\text{m}$, $R_0=2\times {10}^{-3}\text{m}$ and $R_0=5\times {10}^{-3}\text{m}$ respectively. $x_0=0$. ${\dot{x}}_0=0{\text{s}}^{-1}$. $\mathrm{\Delta }\omega \text{*}=0$.

4.2. Non-resonance situation

In this section, the oscillation characteristics of the non-dimensional radius at the non-resonance situation are analyzed from the time domain and the frequency domain correspondingly. And the influence of the equilibrium bubble radius $R_0$ is also explored. In addition, the difference between the non-resonance situation and the resonance situation are briefly discussed during the analysis.

Firstly, Fig. 5 shows the oscillation characteristics of the non-dimensional radius and its four terms at the non-resonance situation in the time domain. In Fig. 5, the green dash, blue dot, orange dot dash and purple solid curves refer to $x_{\text{n1}}$, $x_{\text{n2}}$, $x_{\text{n3}}$ and $x_{\text{n4}}$ in Eqs. (29)–(32) respectively. And the red thick solid curve refers to $x_{\text{n}}$ in Eq. (28). Moreover, the angular frequency of the acoustic field and the corresponding natural frequency of the oscillating vapor bubble are 58,842 s⁻¹ and 70,010 s⁻¹ respectively. In addition, the equilibrium radius and the initial conditions of the oscillating vapor bubble are the same as those in Fig. 2. According to Appendix III, the resonance frequency corresponding to this equilibrium radius is 74,457 s⁻¹, and $\mathrm{\Delta }\omega \text{*}=0.15$ can be calculated in this case.

Fig. 5.

The oscillation characteristics of the non-dimensional radius and its four terms at the non-resonance situation in the time domain. The green dash, blue dot, orange dot dash and purple solid curves refer to $x_{\text{n1}}$, $x_{\text{n2}}$, $x_{\text{n3}}$ and $x_{\text{n4}}$ respectively. And the red thick solid curve refers to the non-dimensional radius at the non-resonance situation $x_{\text{n}}$. $R_0={10}^{-4}\text{m}$.$x_0=0.005$. ${\dot{x}}_0=500{\text{s}}^{-1}$. $\mathrm{\Delta }\omega \text{*}=0.15$.

As shown in Fig. 5, the oscillation amplitude of the non-dimensional radius periodically increases first and then decreases at the non-resonance situation. As for the four terms of the non-dimensional radius, the curves referring to $x_{\text{n1}}$, $x_{\text{n2}}$, $x_{\text{n3}}$ and $x_{\text{n4}}$ all oscillate periodically and boundedly. Among them, only the oscillation amplitude of the curve referring to $x_{\text{n4}}$ exhibits obvious periodic change over time, and always grows from zero to a fixed maximum and then back to zero in a unit period. That is to say, $x_{\text{n4}}$ is the critical cause for the periodically changing amplitude of $x_{\text{n}}$. While the contributions of $x_{\text{n1}}$, $x_{\text{n2}}$, $x_{\text{n3}}$ on the amplitude of $x_{\text{n}}$ always keep constant, and these influence mainly reflected at the beginning and end of each oscillation period of $x_{\text{n}}$. In general, compared with the oscillation characteristics at the resonance situation in Fig. 2, the amplitude of the non-dimensional radius at the non-resonance situation cannot increase indefinitely.

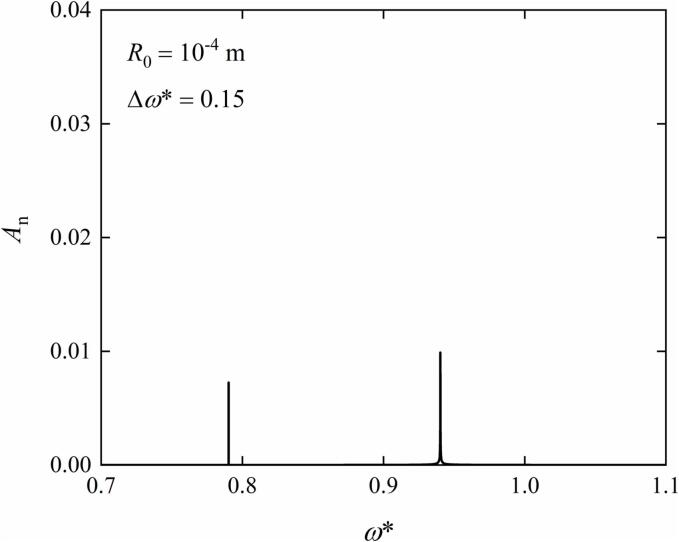
Moreover, Fig. 6 shows the oscillation characteristics of the non-dimensional radius in the frequency domain. In Fig. 6, $A_{\text{n}}$ represents the amplitude at the non-resonance situation. The equilibrium bubble radius, the initial conditions of the oscillation and the other parameters all corresponds to those in Fig. 5. As shown in Fig. 6, there are two obvious characteristic angular frequencies with the different peaks of the amplitude. Specifically, the values of the two characteristic angular frequencies respectively correspond to the angular frequency of the acoustic field ${\omega }_{\text{a}}$ and the natural frequency of the oscillating vapor bubble ${\omega }_0$. Among them, the smaller one and the bigger one refer to ${\omega }_{\text{a}}$ and ${\omega }_0$ respectively. In addition, according to Eqs. (29)–(32), $x_{\text{n1}}$ and $x_{\text{n2}}$ have only a partial contribution to the peak amplitude referring to ${\omega }_0$. Nevertheless, $x_{\text{n3}}$ and $x_{\text{n4}}$ have the same contribution to both the peak amplitudes referring to ${\omega }_0$ and ${\omega }_{\text{a}}$. Therefore, the peak amplitude referring to ${\omega }_{\text{a}}$ is relatively lower than that referring to ${\omega }_0$.

Fig. 6.

The oscillation characteristics of the non-dimensional radius at the non-resonance situation in the frequency domain. $R_0={10}^{-4}\text{m}$. $x_0=0.005$. ${\dot{x}}_0=500{\text{s}}^{-1}$. $\mathrm{\Delta }\omega \text{*}=0.15$.

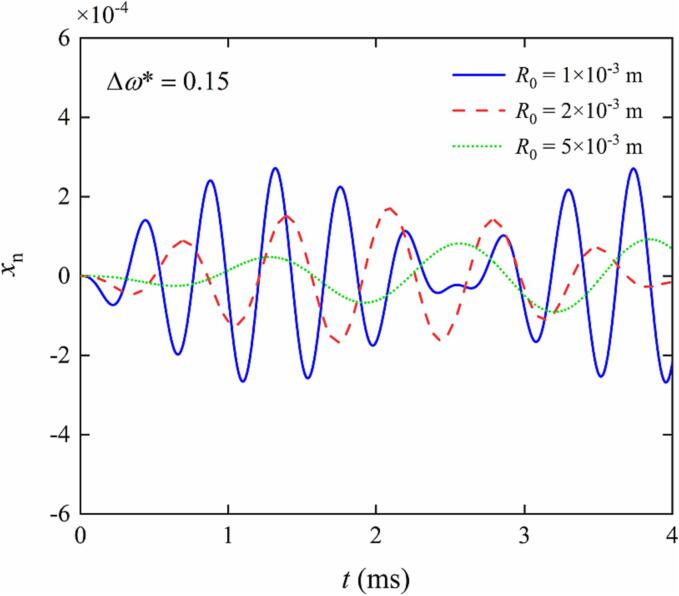
Furthermore, Fig. 7 shows the oscillation characteristics of the non-dimensional radius with different equilibrium bubble radii at the non-resonance situation in the time domain. In Fig. 7, the blue solid, red dash and green dot curves represent the cases of $R_0=1\times {10}^{-3}\text{m}$, $R_0=2\times {10}^{-3}\text{m}$ and $R_0=5\times {10}^{-3}\text{m}$ respectively. In addition, the initial conditions are all ignored in the figure. As shown in Fig. 7, it can be seen that $x_{\text{n}}$ in the three cases are all bounded, and the period of the oscillation significantly shortens and the maximum peak of $x_{\text{n}}$ gradually decreases as $R_0$ increases. That is to say, the vapor bubble with a smaller equilibrium radius will respond faster and more dramatically to the acoustic field.

Fig. 7.

The oscillation characteristics of the non-dimensional radius with different equilibrium bubble radii at the non-resonance situation in the time domain. The blue solid, red dash and green dot curves represent the cases of $R_0=1\times {10}^{-3}\text{m}$, $R_0=2\times {10}^{-3}\text{m}$ and $R_0=5\times {10}^{-3}\text{m}$ respectively. $x_0=0$. ${\dot{x}}_0=0{\text{s}}^{-1}$. $\mathrm{\Delta }\omega \text{*}=0.15$.

5. Comparison of resonance and non-resonance situations

In this section, the comparison of the oscillation characteristics at the resonance situation and the non-resonance situation near the resonance frequency is logically investigated from three aspects. Among them, in Section 5.1, the difference between the two situations in the time domain is comparatively analyzed. In Section 5.2, the difference in the frequency domain is mainly compared. And in Section 5.3, the difference in the oscillation envelope of the non-dimensional radius is further discussed.

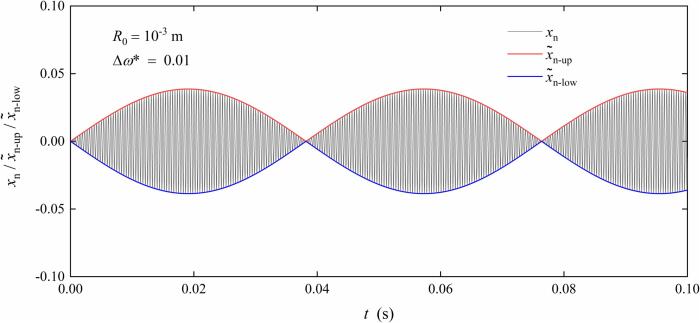
Firstly, the non-resonance situation near the resonance frequency is briefly introduced. At this situation, ${\omega }_0$ and ${\omega }_{\text{a}}$ are very close, and both of them are also quite close to ${\omega }_{\text{r}}$ with the same equilibrium bubble radius. Predictably, the non-dimensional radius would also dramatically increase during the bubble oscillation at this situation, which seems to be particularly similar to the resonance characteristic. As a result, this situation is frequently employed to approximately investigate the bubble resonance characteristics. Therefore, it is well worth to analyze the oscillation characteristics at this situation and compare those with resonance characteristics.

Subsequently, the bubble oscillation model employed for the comparison is simplified and introduced. Specifically, only the dominant term determining the non-dimensional radius oscillation characteristics is preserved, and the non-dimensional radii at the two situations are respectively simplified as follows:

$$x_{\text{r}}=\frac{p_{\text{a}}}{2{\rho }_{\text{l}}{R}_0^2{\omega }_{\text{a}}}t\cos {\omega }_{\text{a}}t,{\omega }_0={\omega }_{\text{a}}$$ (35)

$$x_{\text{n}}=\frac{p_{\text{a}}}{2{\rho }_{\text{l}}{R}_0^2{\omega }_0\left({\omega }_{\text{a}}-{\omega }_0\right)}\left(\sin {\omega }_{\text{a}}t-\sin {\omega }_{0}t\right),{\omega }_0\ne {\omega }_{\text{a}}$$ (36)

Here, $x_{\text{r}}$ and $x_{\text{n}}$ are approximated as $x_{\text{r4}}$ and $x_{\text{n4}}$ respectively. According to Eq. (36), the extremum of $x_{\text{n}}$ can be significantly improved by simply adjusting the angular frequency of the acoustic field ${\omega }_{\text{a}}$ and making it closer to the natural frequency ${\omega }_0$. And in this section, all values of $\mathrm{\Delta }\omega \text{*}$ at the non-resonance situation are not greater than 10⁻² in order to be close enough to the resonance situation.

5.1. Time domain

Fig. 8 shows the oscillation characteristics of the non-dimensional radius at both the resonance situation and the non-resonance situation near the resonance frequency in the time domain. In Fig. 8, the black curve represents the case at the resonance situation. The blue and red curves represent the cases at the non-resonance situation near the resonance frequency with $\mathrm{\Delta }\omega \text{*}=0.003$ and $\mathrm{\Delta }\omega \text{*}=0.010$ respectively.

Fig. 8.

The oscillation characteristics of the non-dimensional radius at the resonance situation and the non-resonance situation near the resonance frequency in the time domain. The black curve represents the case at the resonance situation. The blue and red curves represent the cases at the non-resonance situation near the resonance frequency with $\mathrm{\Delta }\omega \text{*}=0.003$ and $\mathrm{\Delta }\omega \text{*}=0.010$ respectively. $R_0={10}^{-3}\text{m}$.

As shown in Fig. 8, there are still significant differences between the two situations on a relatively long time although $\mathrm{\Delta }\omega \text{*}$ is quite small. Among them, the oscillation amplitude of the non-dimensional radius maintains linear growth over time at the resonance situation, and the increase will be unbounded if the bubble oscillation time is long enough. While the oscillation amplitude at the non-resonance situation near the resonance frequency still shows the periodic changes. Furthermore, the period and the amplitude peak with different $\mathrm{\Delta }\omega \text{*}$ at the non-resonance situation are also different significantly. Specifically, the period and the amplitude peak both become much longer with the decrease of $\mathrm{\Delta }\omega \text{*}$. However, the strong similarity between the resonance situation and the non-resonance situation near the resonance frequency can be found when the initial stage of the oscillation is focused on. To be specific, the oscillations of the non-dimensional radius referring to $\mathrm{\Delta }\omega \text{*}=0$ and $\mathrm{\Delta }\omega \text{*}=0.010$ have almost uniform oscillation frequency and amplitude when $t<0.010\text{s}$. And the similar oscillation phenomenon referring to $\mathrm{\Delta }\omega \text{*}=0$ and $\mathrm{\Delta }\omega \text{*}=0.003$ can be further maintained until $t=0.025\text{s}$. That is to say, the same oscillation phenomenon of the bubble non-dimensional radius at the resonance and non-resonance situations can be persisted for a longer time with the decrease of $\mathrm{\Delta }\omega \text{*}$.

5.2. Frequency domain

Fig. 9 shows the oscillation characteristics of the non-dimensional radius at the resonance situation and the non-resonance situation near the resonance frequency in the frequency domain. In Fig. 9, the three cases all correspond to those in Fig. 8.

Fig. 9.

The oscillation characteristics of the non-dimensional radius at the resonance situation and the non-resonance situation near the resonance frequency in time frequency domain. The black curve represents the case at the resonance situation. The blue and red curves represent the cases at the non-resonance situation near the resonance frequency with $\mathrm{\Delta }\omega \text{*}=0.003$ and $\mathrm{\Delta }\omega \text{*}=0.010$ respectively. $R_0={10}^{-3}\text{m}$.

As shown in Fig. 9, the difference in the characteristic frequencies of the oscillating non-dimensional radius at the two situations still obviously exist although $\mathrm{\Delta }\omega \text{*}$ is quite small. Specifically, there is only one main characteristic frequency equal to ${\omega }_{\text{r}}$ at the resonance situation. While two notable characteristic frequencies exist at the non-resonance situation near the resonance frequency with the same peak amplitude. In addition, by comparing the cases at the non-resonance situation with the different $\mathrm{\Delta }\omega \text{*}$, it can be found that the two characteristic frequencies gradually get close to ${\omega }_{\text{r}}$ and the amplitude peak corresponding to the characteristic frequencies also gradually increases with the decrease of $\mathrm{\Delta }\omega \text{*}$.

5.3. Oscillation envelope

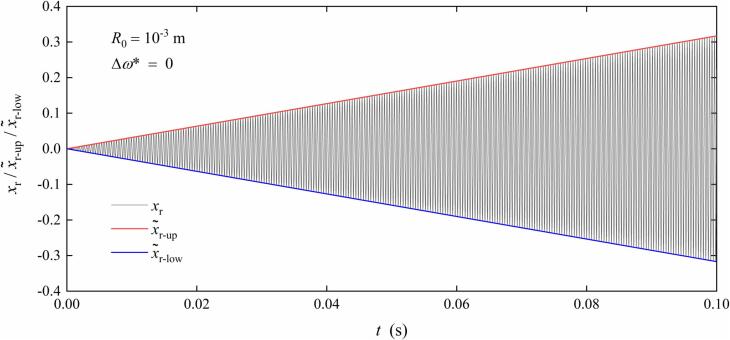
In this section, the oscillation envelopes of the non-dimensional radius are analytically introduced and quantitatively analyzed to further discuss the difference of the oscillation characteristics between the resonance situation and the non-resonance situation near the resonance frequency.

Firstly, the expressions of the envelopes corresponding to the two situations are briefly introduced. Since the oscillations are symmetric about $x_{\text{r}}=0$ and $x_{\text{n}}=0$ at the resonance situation and the non-resonance situation respectively, only the upper envelopes are selected for analysis, which can be introduced as follows:

$${\stackrel{\sim }{x}}_{\text{r-up}}=\frac{p_{\text{a}}}{2{\rho }_{\text{l}}{R}_0^2{\omega }_{\text{a}}}t,{\omega }_0={\omega }_{\text{a}}$$ (37)

$${\stackrel{\sim }{x}}_{\text{n-up}}=\frac{p_{\text{a}}}{{\rho }_{\text{l}}{R}_0^2{\omega }_0}\left|\frac{\sin \left(\left({\omega }_{\text{a}}-{\omega }_0\right)t/2\right)}{{\omega }_{\text{a}}-{\omega }_0}\right|,{\omega }_0\ne {\omega }_{\text{a}}$$ (38)

Here ${\stackrel{\sim }{x}}_{\text{r-up}}$ and ${\stackrel{\sim }{x}}_{\text{n-up}}$ are the upper oscillation envelopes at the resonance and non-resonance situations respectively. The values of the envelopes can be employed to represent the amplitude variation of the non-dimensional radius over time. For the derivation and schematic of the oscillation envelopes, readers can refer to Appendix IV.

Subsequently, based on Eqs. (37), (38), the time derivatives of the oscillation envelopes at the two situations are obtained as follows:

$${\stackrel{\sim }{x}}_{\text{r-up}}^{\text{'}}=\frac{p_{\text{a}}}{2{\rho }_{\text{l}}{R}_0^2{\omega }_{\text{a}}},{\omega }_0={\omega }_{\text{a}}$$ (39)

$${\stackrel{\sim }{x}}_{\text{n-up}}^{\text{'}}=\frac{p_{\text{a}}}{2{\rho }_{\text{l}}{R}_0^2{\omega }_0}·\left|\cos \left(\left({\omega }_{\text{a}}-{\omega }_0\right)t/2\right)\right|,{\omega }_0\ne {\omega }_{\text{a}}$$ (40)

Here ${\stackrel{\sim }{x}}_{\text{r-up}}^{\text{'}}$ and ${\stackrel{\sim }{x}}_{\text{n-up}}^{\text{'}}$ are the derivatives of the envelopes at the resonance and non-resonance situations with respect to the time respectively. Among them, ${\stackrel{\sim }{x}}_{\text{r-up}}^{\text{'}}$ is time-invariant, while ${\stackrel{\sim }{x}}_{\text{n-up}}^{\text{'}}$ is time-varying with a trigonometric structure. That is to say, the amplitude at the resonance situation always keeps linear growth, while the amplitude at the non-resonance resonance is always changing periodically, which can properly correspond and interpret the results in Fig. 8.

Furthermore, in order to further quantitatively analyze the envelope difference at the two situations, several new non-dimensional parameters are introduced here. Firstly, the non-dimensional difference of the envelopes between the resonance and the non-resonance situations is defined as follows:

$$\mathrm{\Delta }{\stackrel{\sim }{x}}_{\text{n/r-up}}=\frac{{\stackrel{\sim }{x}}_{\text{r-up}}-{\stackrel{\sim }{x}}_{\text{n-up}}}{{\stackrel{\sim }{x}}_{\text{r-up}}}$$ (41)

Then, the non-dimensional time is defined as follows:

$$t*=\frac{t}{2\pi /{\omega }_{\text{r}}}$$ (42)

Subsequently, Fig. 10 shows the non-dimensional difference in the envelopes of the non-dimensional radius between the two situations with the different $\mathrm{\Delta }\omega \text{*}$ in the time domain. In Fig. 10, the magenta dot, red dot dash, blue dash and green solid curves represent the cases with $\mathrm{\Delta }\omega \text{*}=1\times {10}^{-4}$, $\mathrm{\Delta }\omega \text{*}=5\times {10}^{-4}$, $\mathrm{\Delta }\omega \text{*}=1\times {10}^{-3}$ and $\mathrm{\Delta }\omega \text{*}=5\times {10}^{-3}$ respectively. And the black dot line refers to $\mathrm{\Delta }{\stackrel{\sim }{x}}_{\text{n/r - up}}=1$. In addition, the singular points at $t*=0$ are all ignored at the two situations.

Fig. 10.

The non-dimensional difference in the envelopes of the non-dimensional radius between the two situations in the time domain. The magenta dot, red dot dash, blue dash and green solid curves represent the cases with $\mathrm{\Delta }\omega \text{*}=1\times {10}^{-4}$, $\mathrm{\Delta }\omega \text{*}=5\times {10}^{-4}$, $\mathrm{\Delta }\omega \text{*}=1\times {10}^{-3}$ and $\mathrm{\Delta }\omega \text{*}=5\times {10}^{-3}$ respectively. The black dot line refers to $\mathrm{\Delta }{\stackrel{\sim }{x}}_{\text{n/r-up}}=1$. $R_0={10}^{-3}\text{m}$.

As shown in Fig. 10, $\mathrm{\Delta }{\stackrel{\sim }{x}}_{\text{n/r-up}}$ is always non-negative. That is to say, the amplitude of the non-dimensional radius at the resonance situation is not less than that at the non-resonance situation for the same moment. Specifically, the difference in the oscillation characteristics between the two situations has not yet emerged considerably at the initial stage. Then, the difference gradually increases and reaches to the maximum for the first time when the first oscillation period of ${\stackrel{\sim }{x}}_{\text{n-up}}$ ends up. Subsequently, the difference constantly fluctuates below the maximum and would gradually stabilize at the maximum if the oscillation time is long enough. In addition, it can also be found that the growth rate of $\mathrm{\Delta }{\stackrel{\sim }{x}}_{\text{n/r-up}}$ at the initial stage increases significantly with the increase of $\mathrm{\Delta }\omega \text{*}$ by comparing the four cases in the figure. In other words, the difference in amplitude at the two situations will appear faster as $\mathrm{\Delta }\omega \text{*}$ increases.

Moreover, in order to quantitatively analyze the corresponding moments when the considerable difference appears at the two situations in Fig. 10, a new non-dimensional time threshold parameter is introduced as $t_{\text{th}}^{\ast }$. And $t_{\text{th}}^{\ast }$ is equal to the value of $t^{\text{*}}$ when a certain non-dimensional difference $\mathrm{\Delta }{\stackrel{\sim }{x}}_{\text{n/r-up}}$ appears for the first time.

Based on this, Fig. 11 shows the influence of $\mathrm{\Delta }\omega \text{*}$ on $t_{\text{th}}^{\text{*}}$ when $\mathrm{\Delta }{\stackrel{\sim }{x}}_{\text{n/r-up}}$ reaches a certain threshold for the first time. In Fig. 11, the black curve with the squares, the red curve with the rounds and the blue curve with the triangles represent the cases with $\mathrm{\Delta }{\stackrel{\sim }{x}}_{\text{n/r-up}}=0.05$, $\mathrm{\Delta }{\stackrel{\sim }{x}}_{\text{n/r-up}}=0.10$ and $\mathrm{\Delta }{\stackrel{\sim }{x}}_{\text{n/r-up}}=0.20$ respectively. As shown in Fig. 11, $t_{\text{th}}^{\ast }$ gradually declines and approaches zero with the increase of $\mathrm{\Delta }\omega \text{*}$, and the decline rate also slows down during this process. To be specific, $t_{\text{th}}^{\ast }$ is greatly sensitive when $\mathrm{\Delta }\omega \text{*}$ is small (referring to $\mathrm{\Delta }\omega {\text{* < 10}}^{-2}$). In addition, it can be seen that $t_{\text{th}}^{\ast }$ gradually increases as $\mathrm{\Delta }{\stackrel{\sim }{x}}_{\text{n/r-up}}$ increases by comparing the cases with the different $\mathrm{\Delta }{\stackrel{\sim }{x}}_{\text{n/r-up}}$, and the influence of $\mathrm{\Delta }{\stackrel{\sim }{x}}_{\text{n/r-up}}$ is mainly reflected when $\mathrm{\Delta }\omega \text{*}$ is small (referring to $\mathrm{\Delta }\omega {\text{* < 10}}^{-2}$).

Fig. 11.

The influence of $\mathrm{\Delta }\omega \text{*}$ on $t_{\text{th}}^{\text{*}}$ when $\mathrm{\Delta }{\stackrel{\sim }{x}}_{\text{n/r-up}}$ reaches a certain threshold for the first time. The black curve with the squares, the red curve with the rounds and the blue curve with the triangles represent the cases with $\mathrm{\Delta }{\stackrel{\sim }{x}}_{\text{n/r-up}}=0.05$, $\mathrm{\Delta }{\stackrel{\sim }{x}}_{\text{n/r-up}}=0.10$ and $\mathrm{\Delta }{\stackrel{\sim }{x}}_{\text{n/r-up}}=0.20$ respectively. $R_0={10}^{-3}\text{m}$.

6. Conclusion

In the present paper, the resonance characteristics of the vapor bubble oscillating in the acoustic field are investigated analytically. Firstly, the bubble wall motion equations are linearized and solved analytically based on the Laplace transform method at both the resonance and non-resonance situations. And each term in the solutions is also analyzed in detail at the two situations. Subsequently, the typical oscillation behaviors of the non-dimensional perturbation of the instantaneous bubble radii and the contribution of each term to the behaviors are exhibited and analyzed adequately at the two situations. Moreover, the oscillation behaviors at the non-resonance situation near the resonance frequency are further investigated from the time domain, frequency domain and the oscillation envelope, which is employed to compare to the oscillation behaviors at the resonance situation. Through the research, several essential conclusions have been drawn as follows:

• (1)The analytical solution of the non-dimensional perturbation of the instantaneous bubble radius can be divided into four terms according to the physical meaning. Among them, two terms are directly related to the initial position and the initial velocity of the vapor bubble respectively. While the other two terms are both mainly related to the amplitude and the frequency of the acoustic field. In addition, one of the terms related to the acoustic field causes the violent bubble oscillation.
• (2)The vapor bubble with a smaller equilibrium radius could respond faster and more dramatically to the acoustic field, and have a larger oscillation frequency during the oscillation at both resonance and non-resonance situations.
• (3)The bubble oscillation characteristics always exhibit significant differences at the two situations in both the time and frequency domains as long as the oscillation time is long enough, even if the difference between ${\omega }_0$ and ${\omega }_{\text{a}}$ is greatly small. And the time required for the considerable difference appearing would significantly decrease as the non-dimensional difference between ${\omega }_0$ and ${\omega }_{\text{a}}$ increases.

In addition, the analysis thought based on the Laplace transform method can be further employed to investigate the oscillation characteristics of the vapor bubble oscillating in the non-simple-harmonic excitation, such as the rectangular and triangular waves.

CRediT authorship contribution statement

Xiaoyu Wang: Conceptualization, Methodology, Investigation, Software, Writing – original draft. Xuan Du: Investigation, Formal analysis, Validation. Dan Gao: Writing – review & editing, Supervision. Yuning Zhang: Writing – review & editing, Project administration, Funding acquisition. Ting Chen: Writing – review & editing, Funding acquisition.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix I: Comparison between Laplace transform method and complex analysis method

In this Appendix, the terms related to the oscillation damping are taken into account on the basis of Eq. (4), in order to ensure that the two methods can find the solution smoothly. And the linearized bubble wall motion equation of the vapor bubble with the oscillation damping based on the Rayleigh-Plesset equation can be expressed as follows [23]:

$$\ddot{x}+2\zeta {\omega }_0\dot{x}+{\omega }_0^{2}x=f$$ (43)

Here, ζ is the damping ratio. And the specific expression of $2\zeta {\omega }_0$ can be expressed as follows [23]:

$$2\zeta {\omega }_0=D+\frac{4{\mu }_{\text{l}}}{{\rho }_{\text{l}}{R}_0^2}+\frac{{\omega }^2{R}_0}{c_{\text{l}}}$$ (44)

where

$$D=\frac{h_{\text{lv}}^2{\rho }_{\text{v}}^2}{{\rho }_{\text{l}}^2{D}_{\text{l}}{c}_{\text{pl}}{T}_0}·\frac{\sqrt{{\omega }_{\text{a}}{R}_0^2/2D_{\text{l}}}+1}{{\left(\sqrt{{\omega }_{\text{a}}{R}_0^2/2D_{\text{l}}}+1\right)}^2+{\omega }_{\text{a}}{R}_0^2/2D_{\text{l}}}$$ (45)

Firstly, the Laplace transform method is applied to solve Eq. (43). According to its general solution process in Section 2.2, the solution of Eq. (43) can be expressed as follows:

$$\begin{array}{c}{x}_{\text{L}}=x_0·e^{-\zeta {\omega }_{0}t}·\cos \left(\sqrt{1-{\zeta }^2}{\omega }_{0}t\right)\\ +\frac{\zeta x_0·e^{-\zeta {\omega }_{0}t}}{\sqrt{1-{\zeta }^2}}·\sin \left(\sqrt{1-{\zeta }^2}{\omega }_{0}t\right)\\ +\frac{{\dot{x}}_0·e^{-\zeta {\omega }_{0}t}}{\sqrt{1-{\zeta }^2}{\omega }_0}·\sin \left(\sqrt{1-{\zeta }^2}{\omega }_{0}t\right)\\ -\frac{p_{\text{a}}}{2{\rho }_{\text{l}}{R}_0^2\sqrt{1-{\zeta }^2}{\omega }_0}\left(\sin {\omega }_{\text{a}}t·\left(A_1+A_2\right)-\cos {\omega }_{\text{a}}t·\left(A_3-A_4\right)\right)\end{array}$$ (46)

where

$$\begin{array}{c}{A}_1\\ =\left(e^{-\zeta {\omega }_{0}t}\left(-\zeta {\omega }_0\sin \left(\sqrt{1-{\zeta }^2}{\omega }_0+{\omega }_{\text{a}}\right)t\right)\right)\\ \left(-\left(\sqrt{1-{\zeta }^2}{\omega }_0+{\omega }_{\text{a}}\right)\cos \left(\sqrt{1-{\zeta }^2}{\omega }_0+{\omega }_{\text{a}}\right)t\right)\\ \left(+\left(\sqrt{1-{\zeta }^2}{\omega }_0+{\omega }_{\text{a}}\right)\right)/\left({\left(-\zeta {\omega }_0\right)}^2+{\left(\sqrt{1-{\zeta }^2}{\omega }_0+{\omega }_{\text{a}}\right)}^2\right)\end{array}$$ (47)

$$\begin{array}{c}{A}_2\\ =\left(e^{-\zeta {\omega }_{0}t}\left(-\zeta {\omega }_0\sin \left(\sqrt{1-{\zeta }^2}{\omega }_0-{\omega }_{\text{a}}\right)t\right)\right)\\ \left(-\left(\sqrt{1-{\zeta }^2}{\omega }_0-{\omega }_{\text{a}}\right)\cos \left(\sqrt{1-{\zeta }^2}{\omega }_0-{\omega }_{\text{a}}\right)t\right)\\ \left(+\left(\sqrt{1-{\zeta }^2}{\omega }_0-{\omega }_{\text{a}}\right)\right)/\left({\left(-\zeta {\omega }_0\right)}^2+{\left(\sqrt{1-{\zeta }^2}{\omega }_0-{\omega }_{\text{a}}\right)}^2\right)\end{array}$$ (48)

$$\begin{array}{c}{A}_3\\ =\left(e^{-\zeta {\omega }_{0}t}\left(-\zeta {\omega }_0\cos \left(\sqrt{1-{\zeta }^2}{\omega }_0-{\omega }_{\text{a}}\right)t\right)\right)\\ \left(+\left(\sqrt{1-{\zeta }^2}{\omega }_0-{\omega }_{\text{a}}\right)\sin \left(\sqrt{1-{\zeta }^2}{\omega }_0-{\omega }_{\text{a}}\right)t\right)\\ \left(+\zeta {\omega }_0\right)/\left({\left(-\zeta {\omega }_0\right)}^2+{\left(\sqrt{1-{\zeta }^2}{\omega }_0-{\omega }_{\text{a}}\right)}^2\right)\end{array}$$ (49)

$$\begin{array}{c}{A}_4\\ =\left(e^{-\zeta {\omega }_{0}t}\left(-\zeta {\omega }_0\cos \left(\sqrt{1-{\zeta }^2}{\omega }_0+{\omega }_{\text{a}}\right)t\right)\right)\\ \left(+\left(\sqrt{1-{\zeta }^2}{\omega }_0+{\omega }_{\text{a}}\right)\sin \left(\sqrt{1-{\zeta }^2}{\omega }_0+{\omega }_{\text{a}}\right)t\right)\\ \left(+\zeta {\omega }_0\right)/\left({\left(-\zeta {\omega }_0\right)}^2+{\left(\sqrt{1-{\zeta }^2}{\omega }_0+{\omega }_{\text{a}}\right)}^2\right)\end{array}$$ (50)

If $\zeta =0$, Eq. (46) can be simplified to Eq. (18). Besides, when time is long enough, $e^{-\zeta {\omega }_{0}t}$ tends to 0, the four integrals of Eqs. (47)-(50) can be further simplified. Then Eq. (46) can be transformed into:

$$\begin{array}{c}{x}_{\text{L}}=-\frac{p_{\text{a}}}{{\rho }_{\text{l}}{R}_0^2}·\frac{\left[\left({\omega }_0^2-{\omega }_{\text{a}}^2\right)\sin {\omega }_{\text{a}}t-2\zeta {\omega }_0{\omega }_{\text{a}}\cos {\omega }_{\text{a}}t\right]}{{\omega }_0^4+{\omega }_{\text{a}}^4-2{\omega }_0^2{\omega }_{\text{a}}^2+4{\zeta }^2{\omega }_0^2{\omega }_{\text{a}}^2}\\ =-\frac{p_{\text{a}}}{{\rho }_{\text{l}}{R}_0^2}·\frac{\sin \left({\omega }_{\text{a}}t-\phi \right)}{\sqrt{{\omega }_0^4+{\omega }_{\text{a}}^4-2{\omega }_0^2{\omega }_{\text{a}}^2+4{\zeta }^2{\omega }_0^2{\omega }_{\text{a}}^2}}\end{array}$$ (51)

where

$$\phi =\arccos \left(\frac{{\omega }_0^2-{\omega }_{\mathrm{a}}^2}{\sqrt{{\omega }_0^4+{\omega }_{\mathrm{a}}^4-2{\omega }_0^2{\omega }_{\mathrm{a}}^2+4{\zeta }^2{\omega }_0^2{\omega }_{\mathrm{a}}^2}}\right)$$ (52)

According to Eq. (51), it is easy to find the relationship between ${\omega }_0$ and ${\omega }_{\text{a}}$ satisfying the resonance situation (i.e. the situation that $x_{\text{L}}$ can reach the maximum) as follows:

$${\omega }_{\text{a}}=\sqrt{1-2{\zeta }^2}{\omega }_0$$ (53)

Then, the complex analysis method is utilized to solve Eq. (43) for comparison. According to the solution of ordinary differential equation, the solution of Eq. (43) can be expressed as follows:

$$x_{\text{C}}=x_1+x_2$$ (54)

Here, $x_1$ and $x_2$ correspond to the general solution and the particular solution of Eq. (43) respectively. Among them, since the bubble oscillation is always underdamped, the general solution is given by the following equation:

$$x_1=e^{-\zeta {\omega }_{0}t}\left[C_1\cos \left({\omega }_0\sqrt{1-{\zeta }^2}\right)t+C_2\sin \left({\omega }_0\sqrt{1-{\zeta }^2}\right)t\right]$$ (55)

Here, $C_1$ and $C_2$ are constants determined by the initial conditions. Furthermore, to solve $x_2$, Eq. (43) can be expressed in the form of complex variable as follows:

$${\ddot{x}}_2+2\zeta {\omega }_0{\dot{x}}_2+{\omega }_0^2{x}_2=-\frac{p_{\text{a}}}{{\rho }_{\text{l}}{R}_0^2}{\text{e}}^{\text{i}\left({\omega }_{\text{a}}t-\frac{\mathrm{\pi }}{2}\right)}$$ (56)

Then the solution of Eq. (56) can be artificially set as follows:

$$x_2=C_3·{\text{e}}^{\text{i}\left({\omega }_{\text{a}}t-\frac{\mathrm{\pi }}{2}\right)}$$ (57)

Here $C_3$ is an undetermined coefficient. Substituting Eq. (57) into Eq. (56), one can solve

$$C_3=-\frac{p_{\text{a}}}{{\rho }_{\text{l}}{R}_0^2\left({\omega }_0^2-{\omega }_{\text{a}}^2+2\zeta {\omega }_0{\omega }_{\text{a}}\text{i}\right)}$$ (58)

Hence,

$$x_2=-\frac{p_{\text{a}}}{{\rho }_{\text{l}}{R}_0^2\left({\omega }_0^2-{\omega }_{\text{a}}^2+2\zeta {\omega }_0{\omega }_{\text{a}}\text{i}\right)}·{\text{e}}^{\text{i}\left({\omega }_{\text{a}}t-\frac{\mathrm{\pi }}{2}\right)}$$ (59)

Combine Eq. (55) and Eq. (59), and bring in the initial conditions $x_0$ and ${\dot{x}}_0$, the solution of Eq. (43) can be obtained as follows:

$$\begin{array}{c}{x}_{\text{C}}=x_0·{\mathrm{e}}^{-\zeta {\omega }_{0}t}·\cos \left(\sqrt{1-{\zeta }^2}{\omega }_{0}t\right)\\ +\frac{\zeta x_0·{\mathrm{e}}^{-\zeta {\omega }_{0}t}}{\sqrt{1-{\zeta }^2}}·\sin \left(\sqrt{1-{\zeta }^2}{\omega }_{0}t\right)\\ +\frac{{\dot{x}}_0·{\mathrm{e}}^{-\zeta {\omega }_{0}t}}{\sqrt{1-{\zeta }^2}{\omega }_0}·\sin \left(\sqrt{1-{\zeta }^2}{\omega }_{0}t\right)\\ -\frac{p_{\text{a}}}{{\rho }_{\text{l}}{R}_0^2\left({\omega }_0^2-{\omega }_{\text{a}}^2+2\zeta {\omega }_0{\omega }_{\text{a}}\text{i}\right)}·{\text{e}}^{\text{i}\left({\omega }_{\text{a}}t-\frac{\mathrm{\pi }}{2}\right)}\end{array}$$ (60)

If $\zeta =0$, Eq. (60) can be further simplified. However, for this condition, it cannot be employed to analyze the resonance situation (i.e. ${\omega }_0={\omega }_{\text{a}}$). because the last term of $x_{\text{C}}$ will become singular.

Finally, by comparing $x_{\text{L}}$ and $x_{\text{C}}$ in Eqs. (46), (60) respectively, it can be found that both methods have successfully obtained the analytical solution of Eq. (43). But the form of the solution is obviously different, especially for the terms related to the external acoustic field. To be specific, the terms in $x_{\text{L}}$ all consist of real numbers, while the terms in $x_{\text{C}}$ contain imaginary numbers. Therefore, it can be considered that the solution obtained by the Laplace transform method has a clearer physical meaning, while the solution form obtained by the complex analysis method seems to be more concise. In addition, if the damping is ignored (i.e. $\zeta =0$), for the resonance situation (i.e. ${\omega }_0={\omega }_{\text{a}}$), it can be found that Eq. (46) is still bounded, while Eq. (60) will behave singularly since the denominator of the last term is zero. Hence, it can be thought that the Laplace transform method has a larger scope of application.

Appendix II. Bubble oscillation at standing acoustic wave condition

For the condition of the standing acoustic wave, the effect of the acoustic field on the bubble is related to the bubble location. And the bubble size is still considered to be much smaller than the standing wave wavelength, so that the spatially inhomogeneous part of the pressure around the bubble can also be neglected in this appendix. Then, take the one-dimensional standing acoustic wave as an example for analysis, which is formed by the interference of two acoustic waves with the same wavelength, frequency and pressure amplitude. According to Eq. (6), the standing acoustic wave effect on the bubble can be expressed as follows:

$$f_{\text{s}}=-\frac{2p_{\text{a}}}{{\rho }_{\text{l}}{R}_0^2}\sin \left({\omega }_{\text{a}}t\right)\sin \left(2\mathrm{\pi }\frac{l_{\text{b}}}{\lambda }\right)$$ (61)

Here, λ is the wavelength, and l_b represents the distance between the bubble and the wave node.

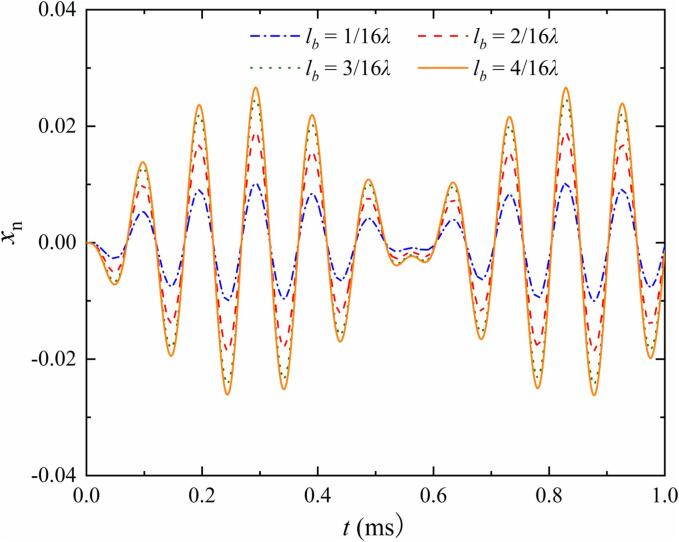
On this basis, oscillation characteristics at the non-resonance situation are selected to analyze the effect of the bubble position in the standing acoustic wave field. Fig. 12 shows the oscillation characteristics of the non-dimensional radius with the different l_b at the non-resonance situation in the time domain. In Fig. 12, the initial conditions are set to zero. The blue dot dash, red dash, green dot and orange solid curves refers to $l_{\text{b}}=1/16\lambda$, $l_{\text{b}}=2/16\lambda$, $l_{\text{b}}=3/16\lambda$ and $l_{\text{b}}=4/16\lambda$. $R_0=1\times {10}^{-4}\text{m}$. And the values of other related parameters are consistent with those in Fig. 7. As shown in Fig. 12, the relative position of the bubble and the standing wave would obviously affect the amplitude of the bubble oscillation, but will not change the frequency of the oscillation. Specifically, as $l_{\text{b}}$ increases, the bubble position gradually approaches the antinode of the standing wave. In this process, the acoustic pressure amplitude of the liquid around the bubble caused by the standing wave gradually increases, which leads to a larger amplitude of the bubble oscillation. And the oscillation amplitude reaches the maximum when the bubble is located at the antinode.

Fig. 12.

The oscillation characteristics of the non-dimensional radius with the different $l_{\text{b}}$ at the non-resonance situation in the time domain. The blue dot dash, red dash, green dot and orange solid curves refers to $l_{\text{b}}=1/16\lambda$, $l_{\text{b}}=2/16\lambda$, $l_{\text{b}}=3/16\lambda$ and $l_{\text{b}}=4/16\lambda$. $R_0=1\times {10}^{-4}\text{m}$. And the values of other parameters are all consistent with those in Fig. 7.

Appendix III. Graphical method to find resonance frequency

In this appendix, the process of the graphical method to find the resonance frequency and the results of the resonance frequency with the different equilibrium bubble radii are introduced in detail.

Firstly, the natural frequency of the vapor bubble shown in Eqs. (7), (8) can be simply expressed as a single argument function of the angular frequency of the acoustic field, which can be expressed as follows:

$${\omega }_0=h\left({\omega }_{\text{a}}\right)$$ (62)

Here h is a functional relationship from ${\omega }_{\text{a}}$ to ${\omega }_0$. In addition, at the resonance situation, there is the relationship as follow:

$${\omega }_0={\omega }_{\text{a}}$$ (63)

Based on Eqs. (62), (63), the approximate value of the resonance frequency ${\omega }_{\text{r}}$ can be obtained at the resonance situation by employed the graphical method. Fig. 13 shows the schematic of the graphical method to solve the resonance frequency. In Fig. 13, the black solid line represents the relationship between ${\omega }_0$ and ${\omega }_{\text{a}}$ shown in Eq. (62). The black dash line represents the equality of ${\omega }_0$ and ${\omega }_{\text{a}}$ shown in Eq. (63). The point I represents the intersection of the two black lines. And the coordinate of the point I can be represented as $\left({\omega }_{\text{r}},{\omega }_{\text{r}}\right)$. Here, the value of ${\omega }_{\text{r}}$ is the resonance frequency to be sought. As shown in Fig. 13, the resonance frequency ${\omega }_{\text{r}}$ of the oscillating vapor bubble with a certain $R_0$ can be obtained by finding the coordinate corresponding to the intersection of the two lines representing Eqs. (62), (63) respectively.

Fig. 13.

The schematic of the graphical method to solve the resonance frequency. The black solid line represents the relationship between ${\omega }_0$ and ${\omega }_{\text{a}}$ obtained by Prosperetti [23]. The black dash line represents ${\omega }_{\text{a}}={\omega }_0$. The point $I\left({\omega }_{\text{r}},{\omega }_{\text{r}}\right)$ represents the intersection of the two black lines. And the value of ${\omega }_{\text{r}}$ is the resonance frequency to be sought.

In addition, a series of resonance frequencies corresponding to the different equilibrium bubble radii can be obtained based on this method. Here, Table 1 shows the partial typical results corresponding to the different equilibrium bubble radii.

Table 1.

The resonance frequencies corresponding to the different equilibrium bubble radii.

Equilibrium bubble radius $R_0$ (m)	Resonance frequency ${\omega }_{\text{r}}$ (s−1)
1 × 10−4	74,457
2 × 10−4	47,634
5 × 10−4	26,056
1 × 10−3	16,454
2 × 10−3	10,379
5 × 10−3	5639
1 × 10−2	3554
2 × 10−2	2239
5 × 10−2	1215
1 × 10−1	765
2 × 10−1	482
5 × 10−1	261

Appendix IV. Oscillation envelopes at two situations

In this appendix, the mathematical expressions and the schematics of the envelopes referring to the non-dimensional perturbation of the instantaneous bubble radius during the oscillation are clearly shown at both the resonance and the non-resonance situations.

Firstly, at the resonance situation, the expression of the non-dimensional perturbation of the instantaneous bubble radius has been shown in Eq. (35). Since the equation contains only one trigonometric function term, the envelope expressions can be obtained by directly replacing the trigonometric function term with unity. Hence, the upper and lower envelopes at the resonance situation can be expressed as follows:

$${\stackrel{\sim }{x}}_{\text{r-up}}=\frac{p_{\text{a}}}{2{\rho }_{\text{l}}{R}_0^2{\omega }_{\text{a}}}t,{\omega }_0={\omega }_{\text{a}}$$ (64)

$${\stackrel{\sim }{x}}_{\text{r-low}}=-\frac{p_{\text{a}}}{2{\rho }_{\text{l}}{R}_0^2{\omega }_{\text{a}}}t,{\omega }_0={\omega }_{\text{a}}$$ (65)

Here ${\stackrel{\sim }{x}}_{\text{r-up}}$ and ${\stackrel{\sim }{x}}_{\text{r-low}}$ are the upper and lower envelopes at the resonance situation respectively.

In addition, at the non-resonance situation, the expression of the non-dimensional perturbation of the instantaneous bubble radius is shown in Eq. (36). Since the equation contains the product of two trigonometric functions, it is necessary to do some preprocessing before obtaining the envelope expressions. According to the product-to-sum identity of trigonometric functions, Eq. (36) can be transformed into

$$x_{\text{n}}=\frac{p_{\text{a}}}{{\rho }_{\text{l}}{R}_0^2{\omega }_0\left({\omega }_{\text{a}}-{\omega }_0\right)}\cos \left(\left({\omega }_{\text{a}}+{\omega }_0\right)t/2\right)\sin \left(\left({\omega }_{\text{a}}-{\omega }_0\right)t/2\right)$$ (66)

For the non-resonance situation near the resonance frequency, ${\omega }_{\text{a}}+{\omega }_0\gg {\omega }_{\text{a}}-{\omega }_0$ can be established. Therefore, the angular frequency of the cosine function is much greater than that of the sine function in Eq. (66). In this situation, the term with the smaller angular frequency can characterize the amplitude and periodicity of the oscillation envelope. And the term with the larger angular frequency can be set to unity to construct the envelope expressions. According to the above analysis, the upper and lower envelopes at the non-resonance situation near the resonance frequency can be expressed as follows:

$${\stackrel{\sim }{x}}_{\text{n-up}}=\left|\frac{p_{\text{a}}}{{\rho }_{\text{l}}{R}_0^2{\omega }_0\left({\omega }_{\text{a}}-{\omega }_0\right)}\sin \left(\left({\omega }_{\text{a}}-{\omega }_0\right)t/2\right)\right|,{\omega }_0\ne {\omega }_{\text{a}}$$ (67)

$${\stackrel{\sim }{x}}_{\text{n-up}}=-\left|\frac{p_{\text{a}}}{{\rho }_{\text{l}}{R}_0^2{\omega }_0\left({\omega }_{\text{a}}-{\omega }_0\right)}\sin \left(\left({\omega }_{\text{a}}-{\omega }_0\right)t/2\right)\right|,{\omega }_0\ne {\omega }_{\text{a}}$$ (68)

Here ${\stackrel{\sim }{x}}_{\text{n-up}}$ and ${\stackrel{\sim }{x}}_{\text{n-low}}$ are the upper and lower envelopes at the non-resonance situation respectively.

Moreover, Fig. 14, Fig. 15 show the envelopes of the non-dimensional perturbation of the instantaneous bubble radius at the resonance and non-resonance situations respectively. In Fig. 14, Fig. 15, the red and blue lines represent the upper and lower envelopes respectively.

Fig. 14.

The envelopes at the resonance situation. The black curve represents the non-dimensional perturbation of the instantaneous bubble radius at the resonance situation. The red and blue lines represent the upper and lower envelopes at the resonance situation respectively. $R_0={10}^{-3}\text{m}$.

Fig. 15.

The envelopes at the non-resonance situation. The black curve represents the non-dimensional perturbation of the instantaneous bubble radius at the non-resonance situation. The red and blue curves represent the upper and lower envelopes at the non-resonance situation respectively. $R_0={10}^{-3}\text{m}$.