Predictive QM/MM modeling of modulations in protein-protein binding by lysine methylation

Abstract

Lysine methylation is a key regulator of protein-protein binding. The amine group of lysine can accept up to three methyl groups, and experiments show that protein-protein binding free energies are sensitive to the extent of methylation. These sensitivities have been rationalized in terms of chemical and structural features present in the binding pockets of methyllysine binding domains. However, understanding their specific roles requires an energetic analysis. Here we propose a theoretical framework to combine quantum and molecular mechanics methods, and compute the effect of methylation on protein-protein binding free energies. The advantages of this approach are that it derives contributions from all local non-trivial effects of methylation on induction, polarizability and dispersion directly from self-consistent electron densities, and at the same time determines contributions from well-characterized hydration effects using a computationally efficient classical mean field method. Limitations of the approach are discussed, and we note that predicted free energies of fourteen out of the sixteen cases agree with experiment. Critical assessment of these cases leads to the following overarching principles that drive methylation-state recognition by protein domains. Methylation typically reduces the pairwise interaction between proteins. This biases binding toward lower methylated states. Simultaneously, however, methylation also makes it easier to partially dehydrate proteins and place them in protein-protein complexes. This latter effect biases binding in favor of higher methylated states. The overall effect of methylation on protein-protein binding depends ultimately on the balance between these two effects, which is observed to be tuned via several combinations of local features.

Introduction

Protein methylation¹ is a ubiquitous post translational modification that controls protein-protein bind-ing.^2–4 Methylation-induced changes in protein-protein binding produce downstream effects essential to many cellular processes, including gene expression, apoptosis and DNA repair. Here we focus on N-methylation of lysines in which lysine’s side chain amine group is methylated. Lysine’s amine group can accept up to three methyl groups, leading to four different methylated states, namely Me0, Me1, Me2 and Me3. Methylation does not alter lysine’s positive charge, and in fact, lysine’s positive charge is important to protein-protein complex-ation.^5,6 Lysine methylation is tightly regulated in eukaryotic cells, and aberrations in lysine methylation have been implicated in several physiological disorders, including neurodegenerative diseases, cardiovascular diseases and cancer.^2–4,7–9

Experiments show that lysine methylation can change protein-protein binding free energies by several units of thermal energy, kT, where k is the Boltzmann constant and T is the temperature.^10–26 Binding free energies have also been shown to depend on the extent of methylation, and for a given protein-protein complex, progressive methylation can lead to either tighter or weaker binding.

These results have been rationalized in terms of several chemical and structural features in methyllysine binding pockets.^10–26 Preferences for lower methylated states are considered to be due to cavity size constraints that prevent binding site expansion to accommodate bulkier methylated-lysines,^{13–16,22,23,26} and due to breakage of strong hydrogen bonds made by amine hydro-gens.^{13–15,22,23,25,26} Selectivity toward higher methylated states is considered to be due to enhanced disper-sion from methylation,^10,19 cavity size constraints that prevent binding site aromatic cages from collapsing and appropriately coordinating lower methylated states,^11,13 and increased weak hydrogen bonding in higher methylated states,^27–29,19

Understanding the relative contributions of these effects and constructing mechanistic models requires an energetic analysis. Early experiments demonstrated that mono-methylation of ammonium ion does not strengthen its interaction with benzene,³⁰ and so the mere presence of cation-π interactions in lysine bind-ing pockets does not explain their role in selecting higher methylated states. It is also been suggested that preferences for higher methylated states may be related to the effect of methylation on lysine’s hydration en-ergy.^30–32 Specifically, experiments show that ammonium mono-methylation reduces its hydration energy substantially by 14.7 kT.³³ A corresponding reduction in lysine’s hydration energy would decrease the cost of partially dehydrating it, which would make it easier to place in protein-protein complexes. However, specific contributions from this hydrophobic effect in methylation-dependent protein-protein binding remain unknown. In fact, this also makes it difficult to assess the relative roles of the various local chemical and structural features discussed above in driving methylation-state selectivity.

Molecular simulation methods can, in principle, provide the necessary quantitative insight. Key challenges, however, remain. Perturbative methods employing classical molecular mechanics potential energy functions can be used to compute the effect of methylation on protein-protein binding free energies.³⁴ However, their predictive accuracies depend strongly on how well they describe ion-ligand interactions, which remains an area of active research.^35–37 In addition, lysine methylation is expected to alter inductive effects,^38–40 polarization^41,42 and vdW dispersion,⁴³ which can contribute substantially to energetics.^40,42,43 In fact, these forces contribute nontrivially to local interactions, and due to unavailability of classical Hamiltonians to describe their interdependencies self-consistently in the context of lysine methylation, a first-principles approach is currently required. At the same time, first-principles approaches are computationally prohibitive for estimating methylation-effects on hydration free energies, however, such effects can be described adequately using classical electrostatics methods.

To address these challenges, here we propose a theoretical framework to combine results from quantum and classical methods, and compute the effect of lysine methylation on protein-protein binding free energies. In this framework, local effects of methylation are obtained from benchmarked quantum methods, and effects on hydration energies are estimated from classical methods, but after calibration and benchmarking on model systems against experiment. We apply this method to sixteen experimentally studied cases for which both structural and binding free energy data is available.^{10–16,18,19,17,21–26} We find that predicted free energies of fourteen of these sixteen cases agree with experiment. Limitations of this approach are also discussed. By examining relative contributions of the different energetic terms in fourteen separate cases,^{10–16,18,19,17,21–26} we also construct a general mechanistic model of how protein-protein complexation is modulated by lysine methylation.

Results and discussion

We consider sixteen different cases for which structural and thermodynamic data are available simultaneously from experiment.^{10–12,14,13,15,20,18,21,24–26}. Experimental binding free energy changes associated with lysine methylation are determined from the ratios of protein-peptide dissociation constants $\left(k_d^1/k_d^0\right)$ in two methylated states (‘1’ and ‘0’) of the peptide, that is, $\text{Δ}{G}_{\text{expt}}=-kT\ln \left(k_d^1/k_d^0\right)$. We note that for ten of these sixteen cases experiments were not conducted at sufficiently high concentrations needed for determining k_d in the relatively weakly-bound methylated state. Therefore, for these ten cases, we only have information on the sign of $\text{Δ}{G}_{\text{expt}}$. Nevertheless, for some of these cases, we were also able to determine lower limits on $\text{Δ}{G}_{\text{expt}}$ using the highest concentration of peptide used in experiments. Finally, note we that we do not apply our method to compute the effect of tri-methylation in the H3/K4–BPTF/PHD case.¹³ This is because our current implementation does not handle cases in which complexes of methylated states differ in the numbers of interfacial structural waters.

Comparison between predicted and experimental ΔG

Table 1 compares the predicted methylation-induced changes in protein-peptide binding free energies against experiment. We note that for all cases, the sign of the predicted ΔG agrees with experiment. Next, we examine the six cases for which exact ΔG values are available from experiment. We find that for one of these six cases (H4/K20–L3MBTL1/MBT complex) the predicted ΔG differs substantially from experiment (by 26.8 kT), and for the remaining five cases, the average error is 1.0 kT. We also find another case (H4/K20–53BP1/TD) for which the predicted ΔG seems to be exceptionally high. We, therefore, consider H4/K20–53BP1/TD and H4/ K20–L3MBTL1/MBT complexes to be the two cases for which the approach does not perform well.

Table 1.

Effects of methylation change (ΔMe) on protein-peptide binding free energy (ΔG) and its energetic components, $\text{Δ}{E}_{\text{Me}}$ and ${\text{ΔΦ}}_{\text{Me}}$. ${\text{ΔΦ}}_{\text{Me}}$ are estimated with and without explicit descriptions of crystallographic waters in Poisson models, and those obtained with explicit descriptions are provided in brackets. Predicted ΔG are also compared against experimental estimates ($\text{Δ}{G}_{\text{expt}}$). $\text{Δ}{E}_{\text{Me}}^{\text{vdW}}$ is the dispersion contribution to $\text{Δ}{E}_{\text{Me}}$. The H3/K4-BPTF/PHD(Y17E) case flagged by the dagger denotes a scenario in which cavity size constraints are partially removed, and is discussed in the main text. The H4/K20-L3MBTL1/MBT and H4/K20-53BP1/TD cases flagged by the asterisk sign, are cases where structural constraints on Asp residues are removed, and discussed in the main text.

Host/Residue	Receptor	PDB ID/Resolution (A)	ΔMe	$\text{Δ}{E}_{\text{Me}}$	$\text{Δ}{E}_{\text{Me}}^{\text{vdW}}$	${\text{ΔΦ}}_{\text{Me}}$	ΔG	$\text{Δ}{G}_{\text{expt}}$
H3/K9	HP1/CD	1KN(A/E)/2.1/2.4	2 → 3	0.4	−9.7	−2.8 (−2.8)	−2.4 (−2.4)	−1.0b
H3/K4	BPTF/PHD (Y17E)	2RI7/1.5	2 → 3	16.5	−4.6	−13.3	3.2	0.6k
				14.2†	−7.3†	−13.3	0.9†	0.6k
H3/K4	BAF45C/PHD1-PHD2	5SZC/1.2	0 → 1	3.5	−7.5	−3.2 (−4.0)	0.3 (−0.5)	0.9c
H3/K4	CHD1/DCD	2B2W/2.4	1 → 3	−0.8	−6.1	−1.4 (0.6)	−2.2 (−0.2)	−1.2d
H4/K20	53BP1/TD	2IG0/1.7	0 → 2	6.6	−8.3	−18.7	−12.1	< −4.0a
H3/K4	BPTF/PHD	2FSA/1.9	0 → 2	5.1	−7.6	−6.1 (−10.2)	−1.0 (−5.1)	< 0e
H3/K9	HP1/CD	1KNA/2.1	0 → 2	0.9	−4.5	−7.4 (−11.9)	−6.5 (−10.9)	< 0b
H3/K9	ZMET2/CD	4FT2/3.2	0 → 2	0.4	−7.1	−12.4	−12.0	< −4.5f
KDM1A/K114	CHD1/DCD	5AFW/1.6	0 → 2	−0.3	−5.6	−11.8 (−16.6)	−12.1 (−16.9)	< 0g
H3/K9	ZMET2/BAH	4FT4/2.7	0 → 2	−3.3	−4.8	−3.2	−6.5	< −6.0f
H3/K4	SGF29/TD	3ME9/1.4	0 → 3	7.0	−15.1	−11.2	−4.2	−3.9h
H3/K4	CHD1/DCD	2B2W/2.4	0 → 3	0.8	−12.5	−10.4 (−8.9)	−9.6 (−8.1)	< 0d
H3/K27	CBX7/CD	2L1B/NMR	0 → 3	4.4	−16.7	−12.5	−8.1	< 0i
H3/K27 mimic	CBX7/CD	4MN3/1.5	0 → 3	8.1	−12.0	−16.1 (−12.0)	−8.0 (−3.9)	< 0j
H4/K20	53BP1/TD	2IG0/1.7	2 → 3	28.7	−4.1	−2.4	26.3	> 4.0a
				7.4*	−2.2*	−2.4	5.0*	> 4.0a
H4/K20	L3MBTL1/MBT	2PQW/2.0	2 → 3	29.3	−3.1	−8.0	21.3	3.5k
				30.3*	−2.9*	−8.0	22.3*	3.5k

^ais taken from Ref. ¹⁴,

^bfrom Ref. ¹¹,

^cfrom Ref. ²⁶,

^dfrom Ref. ¹²,

^efrom Ref. ¹³,

^ffrom Ref. ²¹,

^gfrom Ref. ²⁵,

^hfrom Ref. ²⁰,

ⁱfrom Ref. ¹⁸ and

^jis taken from Ref. ²⁴. Acronyms of protein and domain names are expanded in Table S3 of the Supplementary Information. All energies are in kT units with T=298 K.

In both cases, H4/K20–53BP1/TD and H4/K20–L3MBTL1/MBT, we note that ΔE_Me is exceptionally large in comparison to other cases. This means that the Me3 states are relatively under-stabilized. Since the Me3 states in both cases were constructed from the Xray structures of their respective Me2 states, it seems plausible that the under-stabilization of the Me3 states could be due to the application of restraints on the backbone atoms that prevented the Me3 state from expanding to accommodate the third methyl group. In both these cases, the third methyl group on lysine replaces the hydrogen atom involved in hydrogen bonding with binding site Asp residue, and perhaps restraints on Asp backbone prevent Asp from moving away to accommodate the methyl group. To test this, we release the backbone restraints on these Asp residues, and then re-optimize geometries and recompute $\text{Δ}{E}_{\text{Me}}$. These calculations are flagged by the asterisk sign in Table 1. Note that since backbone constraints are removed only for the Me3 state, and not the Me2 state, we add a backbone relaxation correction to $\text{Δ}{E}_{\text{Me}}$ as $\text{Δ}{E}_{\text{corr}}=E_{\text{constr}}-E_{\text{free}}$, where $E_{\text{constr}}$ and $E_{\text{free}}$ are the energies of Asp computed in isolation, but in geometries adopted in clusters relaxed with and without constraints. Removal of backbone restraints does alter structures (Figure S1 of Supplementary Information). However, it improves predictions only for the H4/K20–53BP1/TD case, but not the H4/K20-L3MBTL1/MBT case. Clearly, a more detailed investigation is required to address these two cases.

Note that for eight cases, we report two predicted values. These represent two different treatments of crystallographic waters in implicit solvent calculations of ${\text{ΔΦ}}_{\text{Me}}$. For the remaining cases, where only one value is provided, X-ray structures did not report any resolved waters in methylation sites. Explicit descriptions of crystallographic waters in implicit solvent models have shown improvements in predictions of pKa values,⁴⁴ but this empirical finding may not be transferable to our ΔG predictions. Therefore, we provide two estimates, one in which crystallographic waters are described explicitly in ${\text{ΔΦ}}_{\text{Me}}$ calculations, and the other in which crystallographic waters are omitted in ${\text{ΔΦ}}_{\text{Me}}$ calculations. We find no specific trend in the effect of this treatment on ${\text{ΔΦ}}_{\text{Me}}$ estimates. Additionally, in half of the cases, it does affect ${\text{ΔΦ}}_{\text{Me}}$ substantially (> 2 kT), however, due to limited experimental data it is unclear as to which treatment yields better predictions of ΔG. Nevertheless, none of our conclusions depend on this choice, and in the analysis and discussions that follow, we refer to only the set obtained without explicit treatment of crystallographic waters in ΔΦ_Me calculations.

Analysis of ΔG components

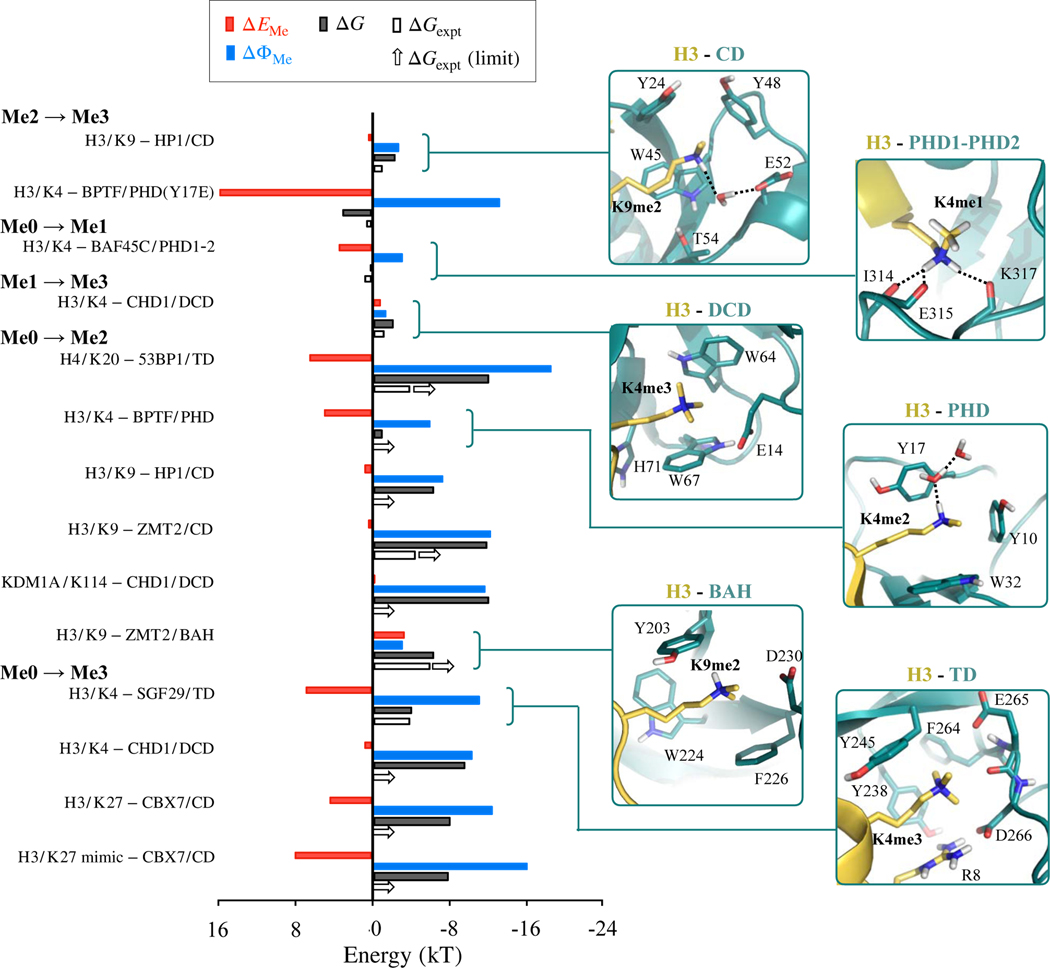
Figure 1 shows the effect of methylation on the two components of ΔG (Equation 3). The first component, $\text{Δ}{E}_{\text{Me}}$ is the effect of methylation on the mutual interaction between the protein and methylated peptide. The second component, ${\text{ΔΦ}}_{\text{Me}}$ is the combined effect of methylation on the interactions of the complex and peptide with solvent. Note that only those fourteen cases are shown in Figure 1 for which our predictions compare well against experiment. We note two clear trends.

Figure 1.

Comparison between predicted (ΔG) and experimental (ΔG_expt) values of the effect of methylation on protein-peptide binding free energies. ΔG_expt denoted by unfilled arrows indicate cases in which experimental dissociation constant were available for only one lysine methylation-state, and for the other state only limiting values were available. Also shown are contributions to ΔG from ΔE_Me and ΔΦ_Me. Binding sites of selected cases are provided in insets on the right, and those of remaining cases are provided in Figure S2 of the Supplementary Information. All energies are in kT units with T=298 K.

Firstly, we observe that for all cases, ${\text{ΔΦ}}_{\text{Me}}$ < 0. We know that for both the peptide and the protein-peptide complex, methylation will weaken favorable interactions with the solvent as well as the entropy of the solvent. Peptide methylation will, therefore, make it easier to partially dehydrate the peptide and place it in a complex. This will positively impact complex formation. At the same time, methylation will also weaken the hydration energy of the resulting complex, which will negatively impact complex formation. The observation that ΔΦ_Me < 0, therefore, implies that the energy gained in dehydrating a methylated peptide to place it in a complex exceeds the energy lost in complex hydration. This enhanced hydrophobic effect is, therefore, observed to drive specificity in favor of higher methylated states.

The second trend we note is that, in most cases, $\text{Δ}{E}_{\text{Me}}$ > 0, which implies that methylation weakens mutual interaction between protein and methylated peptide. This methylation-induced change drives specificity in favor of lower methylated states.

The overall magnitude and sign of ΔG depends ultimately on the relative contributions of $\text{Δ}{E}_{\text{Me}}$ and ${\text{ΔΦ}}_{\text{Me}}$, which seems to be tuned via several different combinations of local features in the various methyllysine binding domains illustrated in Figure 1. To understand how these local binding site features contribute to methylation-state preferences, we examine next the relationships between our computed energetics and the various features, including cavity size or topological constraints in binding sites, dispersion, hydrogen bond numbers and solvent accessible areas.

Chemical and structural features driving methylation-state specificity Dispersion

Expectedly, methylation enhances stabilization from dispersion regardless of whether methylation weakens or strengthens protein-peptide interactions (Table 1). However, there is no correlation between the extent of dispersion change and $\text{Δ}{E}_{\text{Me}}$. Even in the H3/K9–ZMET2/BAH case where methylation stabilizes protein-peptide interactions by −3.3 kT, the dispersion contribution is comparable to cases that exhibit a $\text{Δ}{E}_{\text{Me}}$ > 0. Therefore, at least for the cases studied here, dispersion cannot be a unique determinant of methylation-state selectivity.

Increased intermolecular distances

In all, but the H3/K4–BAF45C/PHD1-PHD2 case, we note that methylation interferes directly with interactions of lysines with binding site residues and increases distances between them (Figure S2 of Supplementary Information). Therefore, in all but one case, methylation-induced weakening of mutual interactions between protein and peptide can be attributed partly to increased distance between lysine and binding site. In the one exception – H3/K4–BAF45C/PHD1-PHD2 complex – methylation neither breaks hydrogen bonds, nor does it change distances between lysine and binding site, and yet it destabilizes interactions by 3.5 kT. This destabilization may be due to altered inductive effects^38–40 that could increase electron density on the amine nitrogen, although a systematic study of this effect is required, especially in the context of polarization that can counter this effect.^41,42

Strong hydrogen bonds

Weakened interaction between protein and peptide can also be partly attributed to methylation-induced breakage of strong hydrogen bonds. This is noted in five out of the fourteen cases (Table S2 of Supplementary Information). Breakage of strong hydrogen bonds is associated with both minor as well as large $\text{Δ}{E}_{\text{Me}}$, such as 0.4 kT in H3/K4–ZMET2/CD and 7.0 kT in H3/K4–SGF29/TD complexes. Surprisingly, though, breakage of strong hydrogen bonds is noted even in cases that prefer higher methylated states. These include the H3/K4–BPTF/PHD and H3/K9–ZMET2/CD complexes that prefer the higher Me2 state over the Me0 state. Therefore, breakage of strong hydrogen bonds is not a sufficient condition for driving preferences toward lower methylated states. Additionally, we note that specificity for lower methylation states can also be achieved without breakage of strong hydrogen bonds, such as in H3/K4–BAF45C/PHD1-PHD2 complexation.

Weak hydrogen bonds

Formation of CH...O type weak hydrogen bonds between methyl groups of lysines and binding site oxygen atoms is suggested to drive specificity toward higher methylated states.^29,19 Certainly, in the H3/K9–ZMET2/BAH and H3/K27–CBX7/CD cases, where methylation strengthens pairwise interaction between protein and pep-tide, we do note that methylation increases weak hydrogen bonds (Table S2 of Supplementary Information). So strengthened mutual interactions in these two cases could be due partly to increase in weak hydrogen bonds. But at the same time, we also note that increased weak hydrogen bonds does not always warrant an overall strengthening of pairwise interactions between protein and peptide. Additionally, we note increased weak hydrogen bonding in cases that actually prefer lower methylated states. Therefore, increased weak hydrogen bonding is not a sufficient condition for driving preferences toward higher methylated states.

Cavity size constraints

Cavity size constraints are considered to play a dual role. Firstly, they could prevent the binding site from expanding to accommodate bulkier (methylated) lysines. This would help drive specificity toward lower methylated states.^{13–16,22,23,26} In the fourteen cases considered here, there are two that prefer lower methylated states. In H3/K4–BAF45C/PHD1-PHD2, mono-methylation does not interfere with any existing interactions of lysine in the Me0 state (see inset in Fig. 1). Therefore, the cavity size constraint model does not apply to this case. In the other case, H3/K4–BPTF/PHD(Y17E), lysine tri-methylation of the Me2 state will break lysine’s hydrogen bond with residue E17, and E17 will also have to move away to accommodate the additional methyl group (see inset in Fig. 1). To understand the role of constraints on E17, we release its backbone constraints, and then reoptimize geometries and recompute ΔE_Me. Removal of backbone constraints indeed expands the binding site in the Me3 state (Figure S2 of Supplementary Information), and reduces $\text{Δ}{E}_{\text{Me}}$ from 16.5 to 14.2 kT (Table 1). The computed ΔG also reduces from 3.2 to 0.9 kT, and, in fact, gets closer to the experimental estimate of 0.6 kT. In other words, releasing constraints improves predictions, and reduces selectivity toward the Me3 state, which is the opposite of the expected role of cavity size constraints.

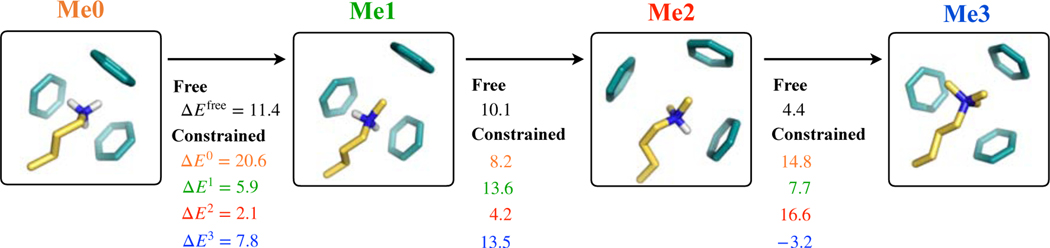
The second way in which cavity size constraints are expected to drive selectivity is that they prevent aromatic cages in binding sites from appropriately coordinating lower methylated states. This it typically considered to drive selectivity in favor of Me2/Me3 states over Me0/Me1 states.^11,13 To understand the role of topological constraints in this context, we consider a system in which lysine interacts with a three-benzene cage, as shown in Fig. 2. This system represents the binding sites aromatic cages present in almost all proteins that select Me3/Me2 states over Me1/Me0 states.^31,45,46 When no constraints are placed on any atoms, we find that progressive methylation of lysine weakens its interactions with the benzene cage. Mono-, di- and tri-methylation of lysine lead to $\text{Δ}{E}_{\text{Me}}$ of 11.4, 21.5 and 25.9 kT, respectively. Additionally, we note that the optimized geometries of the lysine-benzene clusters in the four states differ from each other (Fig. 2). Differences are noted in cage diameter, which expands with methylation, and also in the relative orientations of benzenes around lysine. We take each of these four geometries, and recompute $\text{Δ}{E}_{\text{Me}}$ with constraints on benzene carbons. These $\text{Δ}{E}_{\text{Me}}$ are also shown in Fig. 2. We make the following key observations. It is not surprising that preferences for a given state increase when its optimized geometry is employed. What is interesting is that lysine-age interactions are extremely sensitive to changes in cage geometry. Finally, we note that under certain structural constraints, methylation can strengthen lysine-cage interactions. Specifically, we note that when the geometry optimized in the Me3 state is employed, methylation of the Me2 state strengthens lysine-cage interaction energy. These observations provide direct support to the idea that cavity size constraints can bias selectivity in favor of higher methylated states.

Figure 2.

Effect of lysine methylation and topological constraints on its interaction with a three-benzene cluster. ΔE_Me computed without any restraints are shown in black ink and denoted by ΔE^free. ΔE⁰, ΔE¹, ΔE² and ΔE³ are the ΔE_Me obtained with benzene carbons restrained to positions in the three-benzene geometries that were relaxed without constraints in the presence of lysines in, respectively, their Me0, Me1, Me2 and Me3 states. All energies are in kT.

Solvent accessible areas

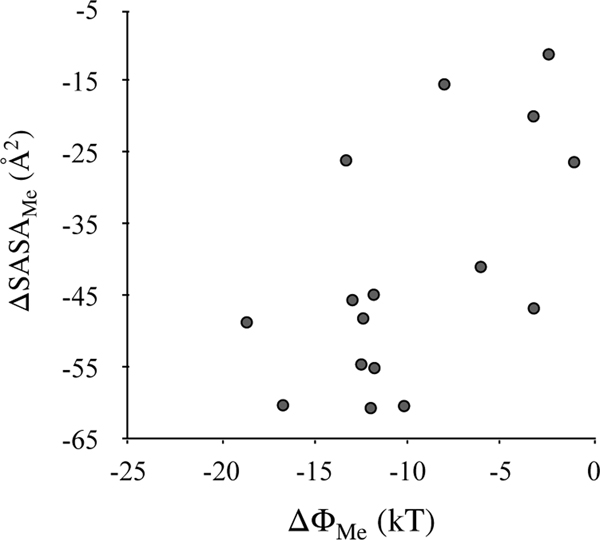
Variations in ${\text{ΔΦ}}_{\text{Me}}$ will essentially depend on the extent of methylation as well as the structure and chemistry of protein-peptide complexes. The expectation is that the more the methylation, the larger the $\left|{\text{ΔΦ}}_{\text{Me}}\right|$. Indeed, these two quantities are related, but the correlation is small (Pearson correlation = 0.42). We can also expect that the more a lysine’s methyl group is buried inside the binding site, the lesser it would decrease the hydration energy of the complex. Consequently, it will lead to a more negative ${\text{ΔΦ}}_{\text{Me}}$ that would increase preferences toward the methylated state. To examine this relationship quantitatively, we determine how methylation changes solvent accessible surface areas (SASA) of peptides and protein-peptide complexes, ${\text{ΔSASA}}_{\text{Me}}=\left({\text{SASA}}_{A{P}_1}-{\text{SASA}}_{A{P}_0}\right)-\left({\text{SASA}}_{P_1}-{\text{SASA}}_{P_0}\right)$. Here AP₁ and AP₀ refer to the protein-peptide complexes in two methylated states, and P₁ and P₀ refer to the peptide in the same two methylated states. By this deffinition, a larger $\left|{\text{ΔSASA}}_{\text{Me}}\right|$ will correspond to a greater burial of the methyl groups in the binding site. We _nd a moderate negative correlation of 0.56 between these quantities (Fig. 3). This means that for many cases, a smaller change in surface area translates into a larger $\left|{\text{ΔΦ}}_{\text{Me}}\right|$, that is, the more a methyl group is buried inside the binding site, the stronger is the binding site’s specificity toward the higher methylated state. For example, methyl groups of H3/K9 are more buried in its complex with HP1/CD compared to ZMT2/BAH, leading to a larger $\left|{\text{ΔΦ}}_{\text{Me}}\right|$, and a relatively stronger preference for the Me2 state over the Me0 state (Figure S2 of the Supplementary Information).

Figure 3.

Correlation between ${\text{ΔΦ}}_{\text{Me}}$ and ${\text{ΔSASA}}_{\text{Me}}$. ${\text{ΔΦ}}_{\text{Me}}$ is the net effect of methylation on interactions of the complex and peptide with solvent and ${\text{ΔSASA}}_{\text{Me}}$ is the net effect of methylation on the solvent accessible surface areas of the complex and peptide.

Conclusions

Toward understanding molecular mechanisms of how methylation alters protein-protein binding, we propose a new approach to predict its effect on protein-protein binding free energies. The approach combines best practices from quantum and classical methods where all local non-trivial effects of methylation are obtained from electronic-level descriptions and the well-established solvation effects are obtained efficiently from classical methods. We apply it to predict the effect of lysine methylation on binding free energies in many different cases, and we note that predicted values of most cases are in excellent agreement with experiment. Certainly, improvements are needed in treating interfacial waters and modeling structural rearrangements in response to methylation, which we expect will be the subjects of future studies.

Collective assessments of energetics in different cases leads to the following overarching principles that drive methylation-state selectivity. Firstly, we note that in most cases methylation weakens the pairwise interaction between proteins, which biases binding toward lower methylated states. Secondly, in all cases we note that lysine’s enhanced hydrophobicity makes it easier to partially dehydrate proteins and place them into protein-protein complexes. Consequently, this biases binding toward higher methylated states. The overall binding preference toward a specific methylated state depends ultimately on the balance between these two contributions.

Selective binding of lysine methylation-states is generally rationalized in terms of specific chemical and structural features in methyllysine binding pockets. Analysis of such features in the context of computed energetics reveals several new insights. (i) Enhanced dispersion cannot be a standalone determinant of selectivity because, at least for the cases studied here, its contribution is not correlated with methylation-induced changes in protein-protein mutual interactions or binding free energies. (ii) Methylation-induced weakening of mutual interactions between proteins is observed to be associated with breakage of strong hydrogen bonds and increased distances between lysines and their binding pockets. Specific roles of altered induction and polarization in modulating protein-peptide interactions, however, remain to be determined. (iii) Reduction in strong hydrogen bonds numbers is not a sufficient condition for driving preferences toward lower methylated states, as they are noted in cases that prefer higher methylated states. Similarly, increased weak hydrogen bonding is also not a sufficient condition for driving preferences toward higher methylated states, although they do stabilize higher methylated states. (iv) There is a moderate correlation between the extent to which a methyl group is buried inside a binding site, and binding site’s specificity toward a higher methylated state. In addition to these observations, we also provide direct evidence supporting that cavity size constraints on aromatic cages can bias selectivity in favor of higher methylated states.

In general, this study provides a new approach to understand the mechanism of how post-translational modifications modulate protein-protein interactions. In the context of lysine methylation, it provides new mechanistic insights, which we expect will have direct implications in designing therapeutic molecules targeting methyl-lysine binding proteins.^47,48

Methods

Theory

Experiments measuring the effect of methylation on dissociation constants of protein-protein complexes^{10–16,18,19,17,20–26} treat methylated proteins as short peptides that contain the target lysine in different methylated states. To compute the effect of methylation on protein-peptide binding free energies, we consider the following substitution reaction in the aqueous phase:

$$A{P}_0+P_1\rightleftharpoons A{P}_1+P_0.$$ (1)

Here A refers to a methyllysine binding protein and P refers to the peptide that is methylated. The subscript ‘1’ refers to some higher methylated state of a lysine in the peptide relative to ‘0’. The Helmholtz free energy change associated with this reaction is

$$\text{Δ}G=G_{A{P}_1}-G_{A{P}_0}-\left(G_{P_1}-G_{P_0}\right).$$ (2)

Expanding in terms of internal energy (U) and entropy (S), and writing the internal energy as a sum of intra-protein, protein-solvent and solvent-solvent terms, that is, $U_X\sim U_{XX}+U_{Xsol}+U_{Xsolsol}$, we can express ΔG as a sum of two terms,

$$\text{Δ}G=\text{Δ}{E}_{\text{Me}}+{\text{ΔΦ}}_{\text{Me}}.$$ (3)

The first term quantifies the effect of methylation on protein-peptide interaction energy,

$$\text{Δ}{E}_{\text{Me}}=\left(\langle E_{A{P}_{1}A{P}_1}\rangle -\langle E_{P_1{P}_1}\rangle \right)-\left(\langle E_{A{P}_{0}A{P}_0}\rangle -\langle E_{P_0{P}_0}\rangle \right),$$ (4)

where internal energies are expressed as potential energy averages. The second term

$${\text{ΔΦ}}_{\text{Me}}={\text{ΔΦ}}_{AP}-{\text{ΔΦ}}_P,$$ (5)

where

$${\text{ΔΦ}}_{AP}=\left[U_{A{P}_{1}sol}+U_{A{P}_{1}solsol}-U_{A{P}_{0}sol}-U_{A{P}_{0}solsol}-T\text{Δ}{S}_{AP}\right]$$ (6)

and

$${\text{ΔΦ}}_P=\left[U_{P_{1}sol}+U_{P_{1}solsol}-U_{P_{0}sol}-U_{P_{0}solsol}-T\text{Δ}{S}_P\right],$$ (7)

is the net effect of methylation on the interactions of the complex and peptide with solvent. This term also includes entropic changes, and we assume in this partition that the majority of the entropic change comes from solvent re-organization. This is supported by the observation that for the cases studied so far, methylation has little effect on structures of protein-peptide complexes.^31,21,25,26

Implementation

To determine $\text{Δ}{E}_{\text{Me}}$ in Equ. 4, we consider that distant effects of methylation on protein-peptide interaction energies will be relatively minor and can be neglected.⁴² We, therefore, consider $E_{A{P}_{1}A{P}_1}$ and $E_{A{P}_{0}A{P}_0}$ to be potential energies of methyllysine binding sites, including methyllysine, instead of being potential energies of entire protein-peptide complexes. Similarly, $E_{P_1{P}_1}$ and $E_{P_0{P}_0}$ are potential energies of isolated lysines in their two methylated states. This reduces system size and makes feasible estimation of $\text{Δ}{E}_{\text{Me}}$ directly from first-principles methods.

We define an amino acid to be part of a lysine’s binding site if any of its atoms are within 6 Å from the lysine amine nitrogen, and the cluster could include amino acids from both the protein and the peptide. Increasing the cutoff to 8 Å and 10 Å for selected test cases had negligible effects on $\text{Δ}{E}_{\text{Me}}$. We compute $\langle E_{A{P}_{1}A{P}_1}\rangle$ and $\langle E_{A{P}_{0}A{P}_0}\rangle$ after adding missing hydrogens, capping the non-contiguous backbones and then relaxing geometries. Geometries are relaxed after applying positional constraints on backbone heavy atoms, while side chains and hydrogens are free to move during relaxation. This strategy is supported by experimental structural studies that show that methylation does not affect the secondary structure of the protein-peptide complex.^31,21,25,26 As an exception to this strategy, when salt bridges are present in clusters, positional constraints are also placed on amine/guanidine nitrogens and carboxyl carbons to prevent their charge neutralization through proton transfer. Optimized geometries are shown in Figures S1 and S2 of the Supplementary Information.

$\langle E_{P_1{P}_1}\rangle$ and $\langle E_{P_0{P}_0}\rangle$ are computed once, and the same values are used for all protein-peptide substitution reactions, as they do not depend on protein-peptide complex. We obtain them by taking the lowest energy structure from a set of twenty random structures after subjecting each one of them to separate geometry relaxation.

Note that for the one case where we use NMR structural data (K3/K27–CBX7/CD complex), we use all twenty structural conformations to compute $\text{Δ}{E}_{\text{Me}}$. For this, we first extract clusters from each conformation using a 6 Å cutoff, and create a superset of amino acids present in these clusters. We then remake these twenty clusters by choosing all amino acids in this superset and neglecting the cutoff distance criteria. This makes the twenty clusters chemically identical and permits cross-comparison of electronic energies. We then subject seven of these twenty clusters, which are structurally different from each other, to ab initio optimization, which gives us seven values for $E_{A{P}_{1}A{P}_1}$ and $E_{A{P}_{0}A{P}_0}$. We Boltzmann average these values to get $\langle E_{A{P}_{1}A{P}_1}\rangle$ and $\langle E_{A{P}_{0}A{P}_0}\rangle$.

We compute ${\text{ΔΦ}}_{\text{Me}}$ from solutions to Poisson’s equations.^49,50 Poisson’s equations are set up numerically by describing atoms using the ParSE (Parameters for Solvation Energy) parameter set,⁴⁹ and defining dielectric boundaries using a solvent probe radius of 1.4 Å about the ParSE atomic radii. The protein interior is assigned a dielectric 2, consistent with ParSE parameterization. In the gas phase, the solvent is assigned an ϵ = 1, and in the condensed phase, the solvent has a dielectric ϵ =78.5. The Poisson’s equation is solved using a multigrid approach implemented in the APBS v 1.3 package,⁵⁰ with a finest grid spacing smaller than 0.5 Å. For each system, convergence is examined against the size of the outer grid and the spacing of the finer grid.⁵¹

PDB2PQR,⁵² with in-house modifications to describe methylated lysines, is used for assigning ParSE parameters to protein atoms, adding missing hydrogens, building missing side-chains and optimizing hydrogen bond networks. For all, but one case, we use X-ray structures that are available at their respective highest resolutions. The resolutions of the X-ray structures used are noted in Table 1 in the Results and Discussion section. For the one case, K3/K27–CBX7/CD, where we use NMR structure instead of X-ray structure, the reported ${\text{ΔΦ}}_{\text{Me}}$ is an average over all twenty conformations.

We acknowledge that calculations of ${\text{ΔΦ}}_{\text{Me}}$ could benefit from a more rigorous treatment involving explicit solvent, however, we note that applications of explicit solvent simulations in computing hydration energies remain limited to small molecules and peptides, and even for small molecules, they require substantial computational resources.^34,53

Benchmarking and calibration

All terms in $\text{Δ}{E}_{\text{Me}}$ are computed using the vdW-corrected PBE0 functional PBE0+vdW,⁵⁴ implemented in the all-electron, localized basis FHI-aims program package.^55,56 We use the “very tight” settings for integration grids and basis sets, as described by Blum et al., ⁵⁵ which yield converged energy differences and negligible basis set superposition errors. Among the DFT+vdW methods, PBE0 performs well against the S22 dataset, exhibiting a mean absolute error of 0.5 kT,⁵⁷ and also performs well against our new reference data on charged clusters^35–37 obtained from “gold standard” quantum Monte Carlo and coupled cluster single double and perturbative triple excitation (CCSD(T)) theory.

To further examine the performance of PBE0+vdW, especially in the context of lysine methylation, we compute the effect of ammonium methylation on ammonium’s dimerization energy with water, formate and benzene, that is, we determine $\text{Δ}{E}_{\text{Me}}=\text{Δ}{E}_{\text{NH}3\text{CH}3}-\text{Δ}{E}_{\text{NH}4}$. Here $\text{Δ}{E}_{\text{NH}3\text{CH}3}=E_{\text{dimer}}-E_{\text{X}}-E_{\text{NH}3\text{CH}3}$ and $\text{Δ}{E}_{\text{NH}4}=E_{\text{dimer }}-E_{\text{X}}-E_{\text{NH}4}$ are the dimerization energies of methylammonium and ammonium ions with small molecule X. In the expressions above E_NH4 and E_NH3CH3 are the electronic energies of isolated ammonium and methylammonium ions, E_X are the electronic energies of water, formate or benzene, and E_dimer are the electronic energies of the dimers of ammonium and methylammonium ions with water, formate or benzene. Prior to calculating E, all individual molecules as well as dimers are energy minimized separately using PBE0+vdW, and these optimized geometries are used for calculations by all quantum methods. Table 2 shows that PBE0+vdW performs excellently against CCSD(T). We note that PBE0+vdW⁵⁴ approximates dispersion as a sum of two-body terms, and so here we also test this approximation by comparing against the PBE0+MBD method⁵⁸ that includes many-body dispersion contributions (Table 2). The CCSD(T) interaction energies are established from complete basis set extrapolation of total energies, computed with Dunning’s correlation consistent aug-cc-pVTZ and aug-cc-pVQZ basis sets. The total energies are corrected for basis set superposition error with counterpoise corrections.⁵⁹ To accelerate CCSD(T) calculations, we employ the local coupled cluster method that is based on domain-based local pair natural orbital (PNO) approach,⁶⁰ as implemented in ORCA v 4.0.1,⁶¹ which is used with so-called TightPNO thresholds.

Table 2.

Performance of vdW-corrected PBE0 density functionals against CCSD(T) in predicting the effect of ammonium methylation on ammonium’s dimerization energies with small molecules. All energies are in kT (T=298 K).

Molecule	CCSD(T)	PBE0+MBD	PBE0+vdW
H2O	3.5	4.1	4.1
HCOO−	6.9	6.4	6.5
C6H6	1.7	1.4	1.4

We also develop ParSE parameters of methylated lysines for use in computation of ${\text{ΔΦ}}_{\text{Me}}$. These parameters are calibrated against experimental and quantum mechanical data. First, the integral equation formalism variant of the polarizable continuum model (PCM),⁶² implemented in Gaussian 09,⁶³ is calibrated to reproduce experimental hydration free energy changes associated with ammonium ion methylation (Table 3). The experimental values are taken from Ref. ³³ Note that while estimation of individual hydration free energies of ions from experiments involves extrathermodynamic assumptions, the estimation of relative solvation free energies of two ions is independent of extrathermodynamic assumptions as long as the same counter ion is used.^64,33 In the PCM model, we describe electron densities at the MP2/aug-cc-pVDZ level of theory, and define the dielectric boundary, with water dielectric being 78.5, using the following atomic radii: r_N = 1.83 Å, r_C = 1.925 Åand r_H = 1.443 Å. The electrostatic scaling factors for the three atoms, which are calibrated to reproduce experimental hydration free energy differences, are α_N = 1.00, α_C = 1.12 and α_H = 0.88. The PCM model is then used for computing the effect of lysine side chain methylation on its hydration free energy, and the values obtained are then used as targets to calibrate methylated lysine parameters in the ParSE model (Table 3). The calibrated ParSE parameters are provided in Table S1 of the Supplementary Information.

Table 3.

Comparison between experimental³³ and computed hydration free changes associated with ammonium ion and lysine methylation. All energies are in kT, with T=298 K.

	Ammonium ion		Lysine side chain
	Expt.	PCM	PCM	ParSE
Me0 → Me1	14.7	15.9	11.3	11.2
Me0 → Me2	28.0	28.6	20.4	20.3
Me0 → Me3	40.5	39.4	25.6	25.8
Me1 → Me2	13.3	12.7	9.1	9.1
Me2 → Me3	12.5	10.8	5.2	5.5

Research highlights.

1. Method to predict effect of methylation on protein-protein binding free energy

2. Strength of the method lies in description of local interactions at the QM level

3. Predicts fourteen out of sixteen free energy changes in agreement with experiment

4. Critical assessment of cases yields overarching principles that drive selectivity