Abstract
Lysine methylation is a key regulator of protein-protein binding. The amine group of lysine can accept up to three methyl groups, and experiments show that protein-protein binding free energies are sensitive to the extent of methylation. These sensitivities have been rationalized in terms of chemical and structural features present in the binding pockets of methyllysine binding domains. However, understanding their specific roles requires an energetic analysis. Here we propose a theoretical framework to combine quantum and molecular mechanics methods, and compute the effect of methylation on protein-protein binding free energies. The advantages of this approach are that it derives contributions from all local non-trivial effects of methylation on induction, polarizability and dispersion directly from self-consistent electron densities, and at the same time determines contributions from well-characterized hydration effects using a computationally efficient classical mean field method. Limitations of the approach are discussed, and we note that predicted free energies of fourteen out of the sixteen cases agree with experiment. Critical assessment of these cases leads to the following overarching principles that drive methylation-state recognition by protein domains. Methylation typically reduces the pairwise interaction between proteins. This biases binding toward lower methylated states. Simultaneously, however, methylation also makes it easier to partially dehydrate proteins and place them in protein-protein complexes. This latter effect biases binding in favor of higher methylated states. The overall effect of methylation on protein-protein binding depends ultimately on the balance between these two effects, which is observed to be tuned via several combinations of local features.
Keywords: protein-protein interactions, methylation, polarization, electrostatics, quantum mechanics
Introduction
Protein methylation1 is a ubiquitous post translational modification that controls protein-protein bind-ing.2–4 Methylation-induced changes in protein-protein binding produce downstream effects essential to many cellular processes, including gene expression, apoptosis and DNA repair. Here we focus on N-methylation of lysines in which lysine’s side chain amine group is methylated. Lysine’s amine group can accept up to three methyl groups, leading to four different methylated states, namely Me0, Me1, Me2 and Me3. Methylation does not alter lysine’s positive charge, and in fact, lysine’s positive charge is important to protein-protein complex-ation.5,6 Lysine methylation is tightly regulated in eukaryotic cells, and aberrations in lysine methylation have been implicated in several physiological disorders, including neurodegenerative diseases, cardiovascular diseases and cancer.2–4,7–9
Experiments show that lysine methylation can change protein-protein binding free energies by several units of thermal energy, kT, where k is the Boltzmann constant and T is the temperature.10–26 Binding free energies have also been shown to depend on the extent of methylation, and for a given protein-protein complex, progressive methylation can lead to either tighter or weaker binding.
These results have been rationalized in terms of several chemical and structural features in methyllysine binding pockets.10–26 Preferences for lower methylated states are considered to be due to cavity size constraints that prevent binding site expansion to accommodate bulkier methylated-lysines,13–16,22,23,26 and due to breakage of strong hydrogen bonds made by amine hydro-gens.13–15,22,23,25,26 Selectivity toward higher methylated states is considered to be due to enhanced disper-sion from methylation,10,19 cavity size constraints that prevent binding site aromatic cages from collapsing and appropriately coordinating lower methylated states,11,13 and increased weak hydrogen bonding in higher methylated states,27–29,19
Understanding the relative contributions of these effects and constructing mechanistic models requires an energetic analysis. Early experiments demonstrated that mono-methylation of ammonium ion does not strengthen its interaction with benzene,30 and so the mere presence of cation-π interactions in lysine bind-ing pockets does not explain their role in selecting higher methylated states. It is also been suggested that preferences for higher methylated states may be related to the effect of methylation on lysine’s hydration en-ergy.30–32 Specifically, experiments show that ammonium mono-methylation reduces its hydration energy substantially by 14.7 kT.33 A corresponding reduction in lysine’s hydration energy would decrease the cost of partially dehydrating it, which would make it easier to place in protein-protein complexes. However, specific contributions from this hydrophobic effect in methylation-dependent protein-protein binding remain unknown. In fact, this also makes it difficult to assess the relative roles of the various local chemical and structural features discussed above in driving methylation-state selectivity.
Molecular simulation methods can, in principle, provide the necessary quantitative insight. Key challenges, however, remain. Perturbative methods employing classical molecular mechanics potential energy functions can be used to compute the effect of methylation on protein-protein binding free energies.34 However, their predictive accuracies depend strongly on how well they describe ion-ligand interactions, which remains an area of active research.35–37 In addition, lysine methylation is expected to alter inductive effects,38–40 polarization41,42 and vdW dispersion,43 which can contribute substantially to energetics.40,42,43 In fact, these forces contribute nontrivially to local interactions, and due to unavailability of classical Hamiltonians to describe their interdependencies self-consistently in the context of lysine methylation, a first-principles approach is currently required. At the same time, first-principles approaches are computationally prohibitive for estimating methylation-effects on hydration free energies, however, such effects can be described adequately using classical electrostatics methods.
To address these challenges, here we propose a theoretical framework to combine results from quantum and classical methods, and compute the effect of lysine methylation on protein-protein binding free energies. In this framework, local effects of methylation are obtained from benchmarked quantum methods, and effects on hydration energies are estimated from classical methods, but after calibration and benchmarking on model systems against experiment. We apply this method to sixteen experimentally studied cases for which both structural and binding free energy data is available.10–16,18,19,17,21–26 We find that predicted free energies of fourteen of these sixteen cases agree with experiment. Limitations of this approach are also discussed. By examining relative contributions of the different energetic terms in fourteen separate cases,10–16,18,19,17,21–26 we also construct a general mechanistic model of how protein-protein complexation is modulated by lysine methylation.
Results and discussion
We consider sixteen different cases for which structural and thermodynamic data are available simultaneously from experiment.10–12,14,13,15,20,18,21,24–26. Experimental binding free energy changes associated with lysine methylation are determined from the ratios of protein-peptide dissociation constants in two methylated states (‘1’ and ‘0’) of the peptide, that is, . We note that for ten of these sixteen cases experiments were not conducted at sufficiently high concentrations needed for determining kd in the relatively weakly-bound methylated state. Therefore, for these ten cases, we only have information on the sign of . Nevertheless, for some of these cases, we were also able to determine lower limits on using the highest concentration of peptide used in experiments. Finally, note we that we do not apply our method to compute the effect of tri-methylation in the H3/K4–BPTF/PHD case.13 This is because our current implementation does not handle cases in which complexes of methylated states differ in the numbers of interfacial structural waters.
Comparison between predicted and experimental ΔG
Table 1 compares the predicted methylation-induced changes in protein-peptide binding free energies against experiment. We note that for all cases, the sign of the predicted ΔG agrees with experiment. Next, we examine the six cases for which exact ΔG values are available from experiment. We find that for one of these six cases (H4/K20–L3MBTL1/MBT complex) the predicted ΔG differs substantially from experiment (by 26.8 kT), and for the remaining five cases, the average error is 1.0 kT. We also find another case (H4/K20–53BP1/TD) for which the predicted ΔG seems to be exceptionally high. We, therefore, consider H4/K20–53BP1/TD and H4/ K20–L3MBTL1/MBT complexes to be the two cases for which the approach does not perform well.
Table 1.
Effects of methylation change (ΔMe) on protein-peptide binding free energy (ΔG) and its energetic components, and . are estimated with and without explicit descriptions of crystallographic waters in Poisson models, and those obtained with explicit descriptions are provided in brackets. Predicted ΔG are also compared against experimental estimates (). is the dispersion contribution to . The H3/K4-BPTF/PHD(Y17E) case flagged by the dagger denotes a scenario in which cavity size constraints are partially removed, and is discussed in the main text. The H4/K20-L3MBTL1/MBT and H4/K20-53BP1/TD cases flagged by the asterisk sign, are cases where structural constraints on Asp residues are removed, and discussed in the main text.
| Host/Residue | Receptor | PDB ID/Resolution (A) | ΔMe | ΔG | ||||
|---|---|---|---|---|---|---|---|---|
| H3/K9 | HP1/CD | 1KN(A/E)/2.1/2.4 | 2 → 3 | 0.4 | −9.7 | −2.8 (−2.8) | −2.4 (−2.4) | −1.0b |
| H3/K4 | BPTF/PHD (Y17E) | 2RI7/1.5 | 2 → 3 | 16.5 | −4.6 | −13.3 | 3.2 | 0.6k |
| 14.2† | −7.3† | −13.3 | 0.9† | 0.6k | ||||
| H3/K4 | BAF45C/PHD1-PHD2 | 5SZC/1.2 | 0 → 1 | 3.5 | −7.5 | −3.2 (−4.0) | 0.3 (−0.5) | 0.9c |
| H3/K4 | CHD1/DCD | 2B2W/2.4 | 1 → 3 | −0.8 | −6.1 | −1.4 (0.6) | −2.2 (−0.2) | −1.2d |
| H4/K20 | 53BP1/TD | 2IG0/1.7 | 0 → 2 | 6.6 | −8.3 | −18.7 | −12.1 | < −4.0a |
| H3/K4 | BPTF/PHD | 2FSA/1.9 | 0 → 2 | 5.1 | −7.6 | −6.1 (−10.2) | −1.0 (−5.1) | < 0e |
| H3/K9 | HP1/CD | 1KNA/2.1 | 0 → 2 | 0.9 | −4.5 | −7.4 (−11.9) | −6.5 (−10.9) | < 0b |
| H3/K9 | ZMET2/CD | 4FT2/3.2 | 0 → 2 | 0.4 | −7.1 | −12.4 | −12.0 | < −4.5f |
| KDM1A/K114 | CHD1/DCD | 5AFW/1.6 | 0 → 2 | −0.3 | −5.6 | −11.8 (−16.6) | −12.1 (−16.9) | < 0g |
| H3/K9 | ZMET2/BAH | 4FT4/2.7 | 0 → 2 | −3.3 | −4.8 | −3.2 | −6.5 | < −6.0f |
| H3/K4 | SGF29/TD | 3ME9/1.4 | 0 → 3 | 7.0 | −15.1 | −11.2 | −4.2 | −3.9h |
| H3/K4 | CHD1/DCD | 2B2W/2.4 | 0 → 3 | 0.8 | −12.5 | −10.4 (−8.9) | −9.6 (−8.1) | < 0d |
| H3/K27 | CBX7/CD | 2L1B/NMR | 0 → 3 | 4.4 | −16.7 | −12.5 | −8.1 | < 0i |
| H3/K27 mimic | CBX7/CD | 4MN3/1.5 | 0 → 3 | 8.1 | −12.0 | −16.1 (−12.0) | −8.0 (−3.9) | < 0j |
| H4/K20 | 53BP1/TD | 2IG0/1.7 | 2 → 3 | 28.7 | −4.1 | −2.4 | 26.3 | > 4.0a |
| 7.4* | −2.2* | −2.4 | 5.0* | > 4.0a | ||||
| H4/K20 | L3MBTL1/MBT | 2PQW/2.0 | 2 → 3 | 29.3 | −3.1 | −8.0 | 21.3 | 3.5k |
| 30.3* | −2.9* | −8.0 | 22.3* | 3.5k |
is taken from Ref. 14,
from Ref. 11,
from Ref. 26,
from Ref. 12,
from Ref. 13,
from Ref. 21,
from Ref. 25,
from Ref. 20,
from Ref. 18 and
is taken from Ref. 24. Acronyms of protein and domain names are expanded in Table S3 of the Supplementary Information. All energies are in kT units with T=298 K.
In both cases, H4/K20–53BP1/TD and H4/K20–L3MBTL1/MBT, we note that ΔEMe is exceptionally large in comparison to other cases. This means that the Me3 states are relatively under-stabilized. Since the Me3 states in both cases were constructed from the Xray structures of their respective Me2 states, it seems plausible that the under-stabilization of the Me3 states could be due to the application of restraints on the backbone atoms that prevented the Me3 state from expanding to accommodate the third methyl group. In both these cases, the third methyl group on lysine replaces the hydrogen atom involved in hydrogen bonding with binding site Asp residue, and perhaps restraints on Asp backbone prevent Asp from moving away to accommodate the methyl group. To test this, we release the backbone restraints on these Asp residues, and then re-optimize geometries and recompute . These calculations are flagged by the asterisk sign in Table 1. Note that since backbone constraints are removed only for the Me3 state, and not the Me2 state, we add a backbone relaxation correction to as , where and are the energies of Asp computed in isolation, but in geometries adopted in clusters relaxed with and without constraints. Removal of backbone restraints does alter structures (Figure S1 of Supplementary Information). However, it improves predictions only for the H4/K20–53BP1/TD case, but not the H4/K20-L3MBTL1/MBT case. Clearly, a more detailed investigation is required to address these two cases.
Note that for eight cases, we report two predicted values. These represent two different treatments of crystallographic waters in implicit solvent calculations of . For the remaining cases, where only one value is provided, X-ray structures did not report any resolved waters in methylation sites. Explicit descriptions of crystallographic waters in implicit solvent models have shown improvements in predictions of pKa values,44 but this empirical finding may not be transferable to our ΔG predictions. Therefore, we provide two estimates, one in which crystallographic waters are described explicitly in calculations, and the other in which crystallographic waters are omitted in calculations. We find no specific trend in the effect of this treatment on estimates. Additionally, in half of the cases, it does affect substantially (> 2 kT), however, due to limited experimental data it is unclear as to which treatment yields better predictions of ΔG. Nevertheless, none of our conclusions depend on this choice, and in the analysis and discussions that follow, we refer to only the set obtained without explicit treatment of crystallographic waters in ΔΦMe calculations.
Analysis of ΔG components
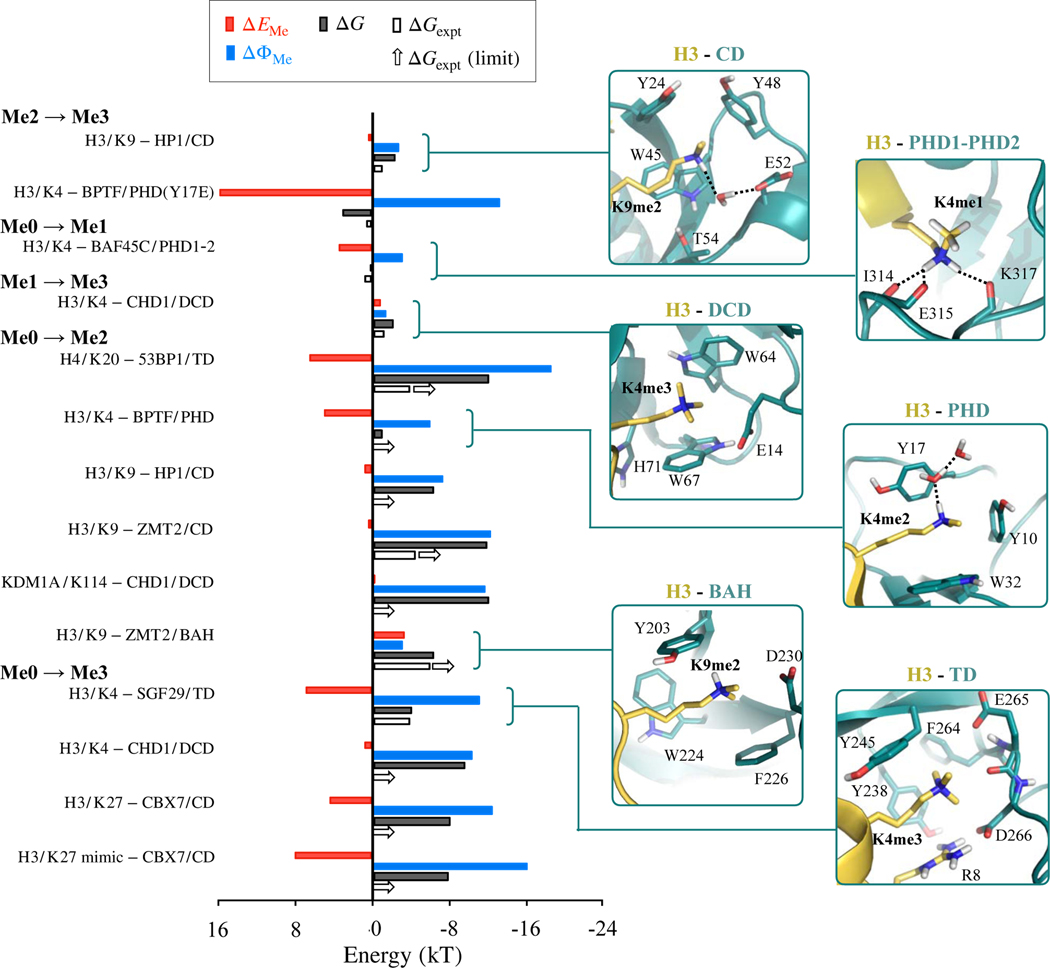
Figure 1 shows the effect of methylation on the two components of ΔG (Equation 3). The first component, is the effect of methylation on the mutual interaction between the protein and methylated peptide. The second component, is the combined effect of methylation on the interactions of the complex and peptide with solvent. Note that only those fourteen cases are shown in Figure 1 for which our predictions compare well against experiment. We note two clear trends.
Figure 1.
Comparison between predicted (ΔG) and experimental (ΔGexpt) values of the effect of methylation on protein-peptide binding free energies. ΔGexpt denoted by unfilled arrows indicate cases in which experimental dissociation constant were available for only one lysine methylation-state, and for the other state only limiting values were available. Also shown are contributions to ΔG from ΔEMe and ΔΦMe. Binding sites of selected cases are provided in insets on the right, and those of remaining cases are provided in Figure S2 of the Supplementary Information. All energies are in kT units with T=298 K.
Firstly, we observe that for all cases, < 0. We know that for both the peptide and the protein-peptide complex, methylation will weaken favorable interactions with the solvent as well as the entropy of the solvent. Peptide methylation will, therefore, make it easier to partially dehydrate the peptide and place it in a complex. This will positively impact complex formation. At the same time, methylation will also weaken the hydration energy of the resulting complex, which will negatively impact complex formation. The observation that ΔΦMe < 0, therefore, implies that the energy gained in dehydrating a methylated peptide to place it in a complex exceeds the energy lost in complex hydration. This enhanced hydrophobic effect is, therefore, observed to drive specificity in favor of higher methylated states.
The second trend we note is that, in most cases, > 0, which implies that methylation weakens mutual interaction between protein and methylated peptide. This methylation-induced change drives specificity in favor of lower methylated states.
The overall magnitude and sign of ΔG depends ultimately on the relative contributions of and , which seems to be tuned via several different combinations of local features in the various methyllysine binding domains illustrated in Figure 1. To understand how these local binding site features contribute to methylation-state preferences, we examine next the relationships between our computed energetics and the various features, including cavity size or topological constraints in binding sites, dispersion, hydrogen bond numbers and solvent accessible areas.
Chemical and structural features driving methylation-state specificity Dispersion
Expectedly, methylation enhances stabilization from dispersion regardless of whether methylation weakens or strengthens protein-peptide interactions (Table 1). However, there is no correlation between the extent of dispersion change and . Even in the H3/K9–ZMET2/BAH case where methylation stabilizes protein-peptide interactions by −3.3 kT, the dispersion contribution is comparable to cases that exhibit a > 0. Therefore, at least for the cases studied here, dispersion cannot be a unique determinant of methylation-state selectivity.
Increased intermolecular distances
In all, but the H3/K4–BAF45C/PHD1-PHD2 case, we note that methylation interferes directly with interactions of lysines with binding site residues and increases distances between them (Figure S2 of Supplementary Information). Therefore, in all but one case, methylation-induced weakening of mutual interactions between protein and peptide can be attributed partly to increased distance between lysine and binding site. In the one exception – H3/K4–BAF45C/PHD1-PHD2 complex – methylation neither breaks hydrogen bonds, nor does it change distances between lysine and binding site, and yet it destabilizes interactions by 3.5 kT. This destabilization may be due to altered inductive effects38–40 that could increase electron density on the amine nitrogen, although a systematic study of this effect is required, especially in the context of polarization that can counter this effect.41,42
Strong hydrogen bonds
Weakened interaction between protein and peptide can also be partly attributed to methylation-induced breakage of strong hydrogen bonds. This is noted in five out of the fourteen cases (Table S2 of Supplementary Information). Breakage of strong hydrogen bonds is associated with both minor as well as large , such as 0.4 kT in H3/K4–ZMET2/CD and 7.0 kT in H3/K4–SGF29/TD complexes. Surprisingly, though, breakage of strong hydrogen bonds is noted even in cases that prefer higher methylated states. These include the H3/K4–BPTF/PHD and H3/K9–ZMET2/CD complexes that prefer the higher Me2 state over the Me0 state. Therefore, breakage of strong hydrogen bonds is not a sufficient condition for driving preferences toward lower methylated states. Additionally, we note that specificity for lower methylation states can also be achieved without breakage of strong hydrogen bonds, such as in H3/K4–BAF45C/PHD1-PHD2 complexation.
Weak hydrogen bonds
Formation of CH...O type weak hydrogen bonds between methyl groups of lysines and binding site oxygen atoms is suggested to drive specificity toward higher methylated states.29,19 Certainly, in the H3/K9–ZMET2/BAH and H3/K27–CBX7/CD cases, where methylation strengthens pairwise interaction between protein and pep-tide, we do note that methylation increases weak hydrogen bonds (Table S2 of Supplementary Information). So strengthened mutual interactions in these two cases could be due partly to increase in weak hydrogen bonds. But at the same time, we also note that increased weak hydrogen bonds does not always warrant an overall strengthening of pairwise interactions between protein and peptide. Additionally, we note increased weak hydrogen bonding in cases that actually prefer lower methylated states. Therefore, increased weak hydrogen bonding is not a sufficient condition for driving preferences toward higher methylated states.
Cavity size constraints
Cavity size constraints are considered to play a dual role. Firstly, they could prevent the binding site from expanding to accommodate bulkier (methylated) lysines. This would help drive specificity toward lower methylated states.13–16,22,23,26 In the fourteen cases considered here, there are two that prefer lower methylated states. In H3/K4–BAF45C/PHD1-PHD2, mono-methylation does not interfere with any existing interactions of lysine in the Me0 state (see inset in Fig. 1). Therefore, the cavity size constraint model does not apply to this case. In the other case, H3/K4–BPTF/PHD(Y17E), lysine tri-methylation of the Me2 state will break lysine’s hydrogen bond with residue E17, and E17 will also have to move away to accommodate the additional methyl group (see inset in Fig. 1). To understand the role of constraints on E17, we release its backbone constraints, and then reoptimize geometries and recompute ΔEMe. Removal of backbone constraints indeed expands the binding site in the Me3 state (Figure S2 of Supplementary Information), and reduces from 16.5 to 14.2 kT (Table 1). The computed ΔG also reduces from 3.2 to 0.9 kT, and, in fact, gets closer to the experimental estimate of 0.6 kT. In other words, releasing constraints improves predictions, and reduces selectivity toward the Me3 state, which is the opposite of the expected role of cavity size constraints.
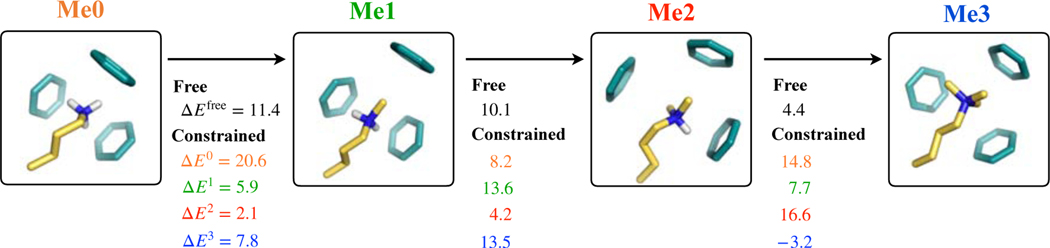
The second way in which cavity size constraints are expected to drive selectivity is that they prevent aromatic cages in binding sites from appropriately coordinating lower methylated states. This it typically considered to drive selectivity in favor of Me2/Me3 states over Me0/Me1 states.11,13 To understand the role of topological constraints in this context, we consider a system in which lysine interacts with a three-benzene cage, as shown in Fig. 2. This system represents the binding sites aromatic cages present in almost all proteins that select Me3/Me2 states over Me1/Me0 states.31,45,46 When no constraints are placed on any atoms, we find that progressive methylation of lysine weakens its interactions with the benzene cage. Mono-, di- and tri-methylation of lysine lead to of 11.4, 21.5 and 25.9 kT, respectively. Additionally, we note that the optimized geometries of the lysine-benzene clusters in the four states differ from each other (Fig. 2). Differences are noted in cage diameter, which expands with methylation, and also in the relative orientations of benzenes around lysine. We take each of these four geometries, and recompute with constraints on benzene carbons. These are also shown in Fig. 2. We make the following key observations. It is not surprising that preferences for a given state increase when its optimized geometry is employed. What is interesting is that lysine-age interactions are extremely sensitive to changes in cage geometry. Finally, we note that under certain structural constraints, methylation can strengthen lysine-cage interactions. Specifically, we note that when the geometry optimized in the Me3 state is employed, methylation of the Me2 state strengthens lysine-cage interaction energy. These observations provide direct support to the idea that cavity size constraints can bias selectivity in favor of higher methylated states.
Figure 2.
Effect of lysine methylation and topological constraints on its interaction with a three-benzene cluster. ΔEMe computed without any restraints are shown in black ink and denoted by ΔEfree. ΔE0, ΔE1, ΔE2 and ΔE3 are the ΔEMe obtained with benzene carbons restrained to positions in the three-benzene geometries that were relaxed without constraints in the presence of lysines in, respectively, their Me0, Me1, Me2 and Me3 states. All energies are in kT.
Solvent accessible areas
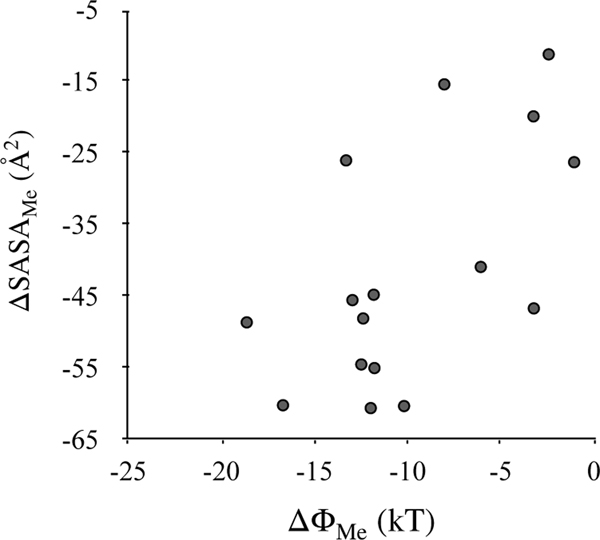
Variations in will essentially depend on the extent of methylation as well as the structure and chemistry of protein-peptide complexes. The expectation is that the more the methylation, the larger the . Indeed, these two quantities are related, but the correlation is small (Pearson correlation = 0.42). We can also expect that the more a lysine’s methyl group is buried inside the binding site, the lesser it would decrease the hydration energy of the complex. Consequently, it will lead to a more negative that would increase preferences toward the methylated state. To examine this relationship quantitatively, we determine how methylation changes solvent accessible surface areas (SASA) of peptides and protein-peptide complexes, . Here AP1 and AP0 refer to the protein-peptide complexes in two methylated states, and P1 and P0 refer to the peptide in the same two methylated states. By this deffinition, a larger will correspond to a greater burial of the methyl groups in the binding site. We _nd a moderate negative correlation of 0.56 between these quantities (Fig. 3). This means that for many cases, a smaller change in surface area translates into a larger , that is, the more a methyl group is buried inside the binding site, the stronger is the binding site’s specificity toward the higher methylated state. For example, methyl groups of H3/K9 are more buried in its complex with HP1/CD compared to ZMT2/BAH, leading to a larger , and a relatively stronger preference for the Me2 state over the Me0 state (Figure S2 of the Supplementary Information).
Figure 3.
Correlation between and . is the net effect of methylation on interactions of the complex and peptide with solvent and is the net effect of methylation on the solvent accessible surface areas of the complex and peptide.
Conclusions
Toward understanding molecular mechanisms of how methylation alters protein-protein binding, we propose a new approach to predict its effect on protein-protein binding free energies. The approach combines best practices from quantum and classical methods where all local non-trivial effects of methylation are obtained from electronic-level descriptions and the well-established solvation effects are obtained efficiently from classical methods. We apply it to predict the effect of lysine methylation on binding free energies in many different cases, and we note that predicted values of most cases are in excellent agreement with experiment. Certainly, improvements are needed in treating interfacial waters and modeling structural rearrangements in response to methylation, which we expect will be the subjects of future studies.
Collective assessments of energetics in different cases leads to the following overarching principles that drive methylation-state selectivity. Firstly, we note that in most cases methylation weakens the pairwise interaction between proteins, which biases binding toward lower methylated states. Secondly, in all cases we note that lysine’s enhanced hydrophobicity makes it easier to partially dehydrate proteins and place them into protein-protein complexes. Consequently, this biases binding toward higher methylated states. The overall binding preference toward a specific methylated state depends ultimately on the balance between these two contributions.
Selective binding of lysine methylation-states is generally rationalized in terms of specific chemical and structural features in methyllysine binding pockets. Analysis of such features in the context of computed energetics reveals several new insights. (i) Enhanced dispersion cannot be a standalone determinant of selectivity because, at least for the cases studied here, its contribution is not correlated with methylation-induced changes in protein-protein mutual interactions or binding free energies. (ii) Methylation-induced weakening of mutual interactions between proteins is observed to be associated with breakage of strong hydrogen bonds and increased distances between lysines and their binding pockets. Specific roles of altered induction and polarization in modulating protein-peptide interactions, however, remain to be determined. (iii) Reduction in strong hydrogen bonds numbers is not a sufficient condition for driving preferences toward lower methylated states, as they are noted in cases that prefer higher methylated states. Similarly, increased weak hydrogen bonding is also not a sufficient condition for driving preferences toward higher methylated states, although they do stabilize higher methylated states. (iv) There is a moderate correlation between the extent to which a methyl group is buried inside a binding site, and binding site’s specificity toward a higher methylated state. In addition to these observations, we also provide direct evidence supporting that cavity size constraints on aromatic cages can bias selectivity in favor of higher methylated states.
In general, this study provides a new approach to understand the mechanism of how post-translational modifications modulate protein-protein interactions. In the context of lysine methylation, it provides new mechanistic insights, which we expect will have direct implications in designing therapeutic molecules targeting methyl-lysine binding proteins.47,48
Methods
Theory
Experiments measuring the effect of methylation on dissociation constants of protein-protein complexes10–16,18,19,17,20–26 treat methylated proteins as short peptides that contain the target lysine in different methylated states. To compute the effect of methylation on protein-peptide binding free energies, we consider the following substitution reaction in the aqueous phase:
| (1) |
Here A refers to a methyllysine binding protein and P refers to the peptide that is methylated. The subscript ‘1’ refers to some higher methylated state of a lysine in the peptide relative to ‘0’. The Helmholtz free energy change associated with this reaction is
| (2) |
Expanding in terms of internal energy (U) and entropy (S), and writing the internal energy as a sum of intra-protein, protein-solvent and solvent-solvent terms, that is, , we can express ΔG as a sum of two terms,
| (3) |
The first term quantifies the effect of methylation on protein-peptide interaction energy,
| (4) |
where internal energies are expressed as potential energy averages. The second term
| (5) |
where
| (6) |
and
| (7) |
is the net effect of methylation on the interactions of the complex and peptide with solvent. This term also includes entropic changes, and we assume in this partition that the majority of the entropic change comes from solvent re-organization. This is supported by the observation that for the cases studied so far, methylation has little effect on structures of protein-peptide complexes.31,21,25,26
Implementation
To determine in Equ. 4, we consider that distant effects of methylation on protein-peptide interaction energies will be relatively minor and can be neglected.42 We, therefore, consider and to be potential energies of methyllysine binding sites, including methyllysine, instead of being potential energies of entire protein-peptide complexes. Similarly, and are potential energies of isolated lysines in their two methylated states. This reduces system size and makes feasible estimation of directly from first-principles methods.
We define an amino acid to be part of a lysine’s binding site if any of its atoms are within 6 Å from the lysine amine nitrogen, and the cluster could include amino acids from both the protein and the peptide. Increasing the cutoff to 8 Å and 10 Å for selected test cases had negligible effects on . We compute and after adding missing hydrogens, capping the non-contiguous backbones and then relaxing geometries. Geometries are relaxed after applying positional constraints on backbone heavy atoms, while side chains and hydrogens are free to move during relaxation. This strategy is supported by experimental structural studies that show that methylation does not affect the secondary structure of the protein-peptide complex.31,21,25,26 As an exception to this strategy, when salt bridges are present in clusters, positional constraints are also placed on amine/guanidine nitrogens and carboxyl carbons to prevent their charge neutralization through proton transfer. Optimized geometries are shown in Figures S1 and S2 of the Supplementary Information.
and are computed once, and the same values are used for all protein-peptide substitution reactions, as they do not depend on protein-peptide complex. We obtain them by taking the lowest energy structure from a set of twenty random structures after subjecting each one of them to separate geometry relaxation.
Note that for the one case where we use NMR structural data (K3/K27–CBX7/CD complex), we use all twenty structural conformations to compute . For this, we first extract clusters from each conformation using a 6 Å cutoff, and create a superset of amino acids present in these clusters. We then remake these twenty clusters by choosing all amino acids in this superset and neglecting the cutoff distance criteria. This makes the twenty clusters chemically identical and permits cross-comparison of electronic energies. We then subject seven of these twenty clusters, which are structurally different from each other, to ab initio optimization, which gives us seven values for and . We Boltzmann average these values to get and .
We compute from solutions to Poisson’s equations.49,50 Poisson’s equations are set up numerically by describing atoms using the ParSE (Parameters for Solvation Energy) parameter set,49 and defining dielectric boundaries using a solvent probe radius of 1.4 Å about the ParSE atomic radii. The protein interior is assigned a dielectric 2, consistent with ParSE parameterization. In the gas phase, the solvent is assigned an ϵ = 1, and in the condensed phase, the solvent has a dielectric ϵ =78.5. The Poisson’s equation is solved using a multigrid approach implemented in the APBS v 1.3 package,50 with a finest grid spacing smaller than 0.5 Å. For each system, convergence is examined against the size of the outer grid and the spacing of the finer grid.51
PDB2PQR,52 with in-house modifications to describe methylated lysines, is used for assigning ParSE parameters to protein atoms, adding missing hydrogens, building missing side-chains and optimizing hydrogen bond networks. For all, but one case, we use X-ray structures that are available at their respective highest resolutions. The resolutions of the X-ray structures used are noted in Table 1 in the Results and Discussion section. For the one case, K3/K27–CBX7/CD, where we use NMR structure instead of X-ray structure, the reported is an average over all twenty conformations.
We acknowledge that calculations of could benefit from a more rigorous treatment involving explicit solvent, however, we note that applications of explicit solvent simulations in computing hydration energies remain limited to small molecules and peptides, and even for small molecules, they require substantial computational resources.34,53
Benchmarking and calibration
All terms in are computed using the vdW-corrected PBE0 functional PBE0+vdW,54 implemented in the all-electron, localized basis FHI-aims program package.55,56 We use the “very tight” settings for integration grids and basis sets, as described by Blum et al., 55 which yield converged energy differences and negligible basis set superposition errors. Among the DFT+vdW methods, PBE0 performs well against the S22 dataset, exhibiting a mean absolute error of 0.5 kT,57 and also performs well against our new reference data on charged clusters35–37 obtained from “gold standard” quantum Monte Carlo and coupled cluster single double and perturbative triple excitation (CCSD(T)) theory.
To further examine the performance of PBE0+vdW, especially in the context of lysine methylation, we compute the effect of ammonium methylation on ammonium’s dimerization energy with water, formate and benzene, that is, we determine . Here and are the dimerization energies of methylammonium and ammonium ions with small molecule X. In the expressions above ENH4 and ENH3CH3 are the electronic energies of isolated ammonium and methylammonium ions, EX are the electronic energies of water, formate or benzene, and Edimer are the electronic energies of the dimers of ammonium and methylammonium ions with water, formate or benzene. Prior to calculating E, all individual molecules as well as dimers are energy minimized separately using PBE0+vdW, and these optimized geometries are used for calculations by all quantum methods. Table 2 shows that PBE0+vdW performs excellently against CCSD(T). We note that PBE0+vdW54 approximates dispersion as a sum of two-body terms, and so here we also test this approximation by comparing against the PBE0+MBD method58 that includes many-body dispersion contributions (Table 2). The CCSD(T) interaction energies are established from complete basis set extrapolation of total energies, computed with Dunning’s correlation consistent aug-cc-pVTZ and aug-cc-pVQZ basis sets. The total energies are corrected for basis set superposition error with counterpoise corrections.59 To accelerate CCSD(T) calculations, we employ the local coupled cluster method that is based on domain-based local pair natural orbital (PNO) approach,60 as implemented in ORCA v 4.0.1,61 which is used with so-called TightPNO thresholds.
Table 2.
Performance of vdW-corrected PBE0 density functionals against CCSD(T) in predicting the effect of ammonium methylation on ammonium’s dimerization energies with small molecules. All energies are in kT (T=298 K).
| Molecule | CCSD(T) | PBE0+MBD | PBE0+vdW |
|---|---|---|---|
| H2O | 3.5 | 4.1 | 4.1 |
| HCOO− | 6.9 | 6.4 | 6.5 |
| C6H6 | 1.7 | 1.4 | 1.4 |
We also develop ParSE parameters of methylated lysines for use in computation of . These parameters are calibrated against experimental and quantum mechanical data. First, the integral equation formalism variant of the polarizable continuum model (PCM),62 implemented in Gaussian 09,63 is calibrated to reproduce experimental hydration free energy changes associated with ammonium ion methylation (Table 3). The experimental values are taken from Ref. 33 Note that while estimation of individual hydration free energies of ions from experiments involves extrathermodynamic assumptions, the estimation of relative solvation free energies of two ions is independent of extrathermodynamic assumptions as long as the same counter ion is used.64,33 In the PCM model, we describe electron densities at the MP2/aug-cc-pVDZ level of theory, and define the dielectric boundary, with water dielectric being 78.5, using the following atomic radii: rN = 1.83 Å, rC = 1.925 Åand rH = 1.443 Å. The electrostatic scaling factors for the three atoms, which are calibrated to reproduce experimental hydration free energy differences, are αN = 1.00, αC = 1.12 and αH = 0.88. The PCM model is then used for computing the effect of lysine side chain methylation on its hydration free energy, and the values obtained are then used as targets to calibrate methylated lysine parameters in the ParSE model (Table 3). The calibrated ParSE parameters are provided in Table S1 of the Supplementary Information.
Table 3.
Comparison between experimental33 and computed hydration free changes associated with ammonium ion and lysine methylation. All energies are in kT, with T=298 K.
| Ammonium ion | Lysine side chain | |||
|---|---|---|---|---|
| Expt. | PCM | PCM | ParSE | |
| Me0 → Me1 | 14.7 | 15.9 | 11.3 | 11.2 |
| Me0 → Me2 | 28.0 | 28.6 | 20.4 | 20.3 |
| Me0 → Me3 | 40.5 | 39.4 | 25.6 | 25.8 |
| Me1 → Me2 | 13.3 | 12.7 | 9.1 | 9.1 |
| Me2 → Me3 | 12.5 | 10.8 | 5.2 | 5.5 |
Supplementary Material
Research highlights.
Method to predict effect of methylation on protein-protein binding free energy
Strength of the method lies in description of local interactions at the QM level
Predicts fourteen out of sixteen free energy changes in agreement with experiment
Critical assessment of cases yields overarching principles that drive selectivity
Acknowledgments
The authors acknowledge the use of computer time from Research Computing at USF and UL. Authors thank Profs. Gary Daughdrill, Eric Jakobsson and Libin Ye for helpful comments and discussions. Funding for this work was provided by NIH grant number R01GM118697.
Footnotes
Declaration of interests
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
CRediT Author Statement
Sanim Rahman: Conceptualization, Methodology, Investigation, Writing – original draft
Vered Wineman-Fisher: Investigation, Validation
Yasmine Al-Hamdani: Investigation
Alexandre Tkatchenko: Conceptualization, Validation, Writing – review & editing,
Sameer Varma: Conceptualization, Methodology, Investigation, Project administration, Validation, Writing – original draft
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Ambler RP, Rees MW, (1959). ϵ-n-methyl-lysine in bacterial flagellar protein. Nature. 184. 56–57. [DOI] [PubMed] [Google Scholar]
- 2.Lee DY, Stallcup MR, Strahl BD, Teyssier C, (2005). Role of protein methylation in regulation of transcription. Endocr. Rev. 26. 147–170. [DOI] [PubMed] [Google Scholar]
- 3.Paik WK, Paik DC, Kim S, (2007). Historical review: the field of protein méthylation. Trends Diochem. Sd. 32. 146–152. [DOI] [PubMed] [Google Scholar]
- 4.Murn J, Shi Y„ (2017). The winding path of protein methylation research: milestones and new frontiers. Nature Rev. Moi Cell Bio!. 18, 517–527. [DOI] [PubMed] [Google Scholar]
- 5.Hughes RM, Wiggins KR, Khorasanizadeh S, Waters ML, (2007). Recognition of trimethyllysine by a chromodomain is not driven by the hydrophobic effect. Proc. Natl. Acad. Sci. 104. 11184–11188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Kamps JJAG et al. ,. (2015). Chemical basis for the recognition of tri methyl lysine by epigenetic reader proteins. Nature Commun., 6, 8911. 10.1038/ncomms9911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Han D. et al. , (2019). Lysine methylation of transcription factors in cancer. Cell Death Dis., 10. 290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Rowe EM Xing V, Biggar KK (2019). Lysine methylation: Implications in neurodegenerative disease. Brain Res. 1707, 164–171. [DOI] [PubMed] [Google Scholar]
- 9.Luo M, (2018). Chemical and biochemical perspectives of protein lysine methylation. Chem. Rev, 118. 6656–6705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Jacobs SA, Khorasanizadeh S, (2002). Structure of hp1 chromodomain bound to a lysine 9-methylated histone h3 tail. Sdence. 295. 2080–2083. [DOI] [PubMed] [Google Scholar]
- 11.Nielsen PR et al. , (2002). Structure of the hp1 chromodomain bound to histone h3 methylated at lysine 9. Nature, 416. 103–107. [DOI] [PubMed] [Google Scholar]
- 12.Flanagan JF et al. , (2005). Double chromodomains cooperate to recognize the methylated histone h3 tail. Nature. 438, 1181–1185. [DOI] [PubMed] [Google Scholar]
- 13.Li H. et al. , (2006). Molecular basis for site-specific read-out of histone h3k4me3 by the bptf phd finger of nurf. Nature, 442, 91–95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Botuyan MV et al. , (2006). Structural basis for the methylation state-sped fie recognition of histone h4-k20 by 53bp1 and crb2 in dna repair. Cell, 127. 1361–1373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Li H. et al. , (2007). Structural basis for lower lysine methylation state-specific readout by mbt repeats of I3mbtl1 and an engineered phd finger. Mol. CeS, 28. 677–691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Collins RE et al. , (2008). The ankyrin repeats of g9a and glp histone methyl transfera ses are mono- and dimethyl lysine binding modules. Nature Struct. Mol. Biol. 15. 245–250. 10.1038/nsmb.1384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Schalch T. et al. , (2009). High-affinity binding of chpl chromodomain to k9 methylated histone h3 is required to establish centromeric heterochromatin. Mol. Cell, 34, 36–46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kaustov L. et al. , (2011). Recognition and specificity determinants of the human cbx chromodomains. J. Biol. Chem, 286,521–529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Iwase S. et al. , (2011). Atrx add domain links an atypical histone methylation recognition mechanism to human mental-retardation syndrome. Nature Struct. Mol. Biol, 18. 769–776. 10.1038/nsmb.2062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Bian C. et al. (2011). Sgf29 binds histone h3k4me2/3 and is required for saga complex recruitment and histone h3 acetylation. EMBO J. 30. 2829–2842 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Du J. et al. , (2012). Dual binding of chromomethylase domains to h3k9me2-containing nucleosomes directs dna methylation in plaits. CeS, 151. 167–180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kuo AJ et al. , (2012). The bah domain of orc1 links h4k20me2 to dna replication licensing and meier-gorlin syndrome. Nature. 484. 115–119. 10.1038/nature10956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Cui GEP et al. , (2012). Phf20 is an effector protein of p53 double lysine méthylation that stabilizes and activates p53. Nature Struct. Mol. Biol, 19. 916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Simhadri C. et al. (2014). Chromodomain antagonists that target the pdycomb-group methyllysine reader protein chromobox homolog 7 (cbx7). J. Med. Chem, 57. 2874–2883. [DOI] [PubMed] [Google Scholar]
- 25.Metzger EEP et al. , (2016). Assembly of methylated kdm1a and chd1 drives androgen receptor-dependent transcription and translocation. Nature Struct. Mol. Biol, 23, 132. [DOI] [PubMed] [Google Scholar]
- 26.Local A. et al. , (2018). Identification d h3k4me1-associated proteins at mammalian enhancers. Nature Genet., 50. 73–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Cordier F, Barfield M, Grzesiek S, (2003). Direct observation of Cα –hα…o=c hydrogen bonds in proteins by inter residue h3jcαc scalar couplings. J. Am Chem. Soc, 125. 15750–15751. [DOI] [PubMed] [Google Scholar]
- 28.Ratajczyk T, Czerski I, Kamienska-Trela K, Szymanski S, Wojcik J, (2005). 1j(c, h) couplings to the individual protons in a methyl group: Evidence of the methyl protons’ engagement in hydrogen bonds. Angew. Chem. Int. Ed, 1230–1232 [DOI] [PubMed]
- 29.Horowitz S, Yesselman JD, Al-Hashimi HM Trievel, R.C., (2011). Direct evidence for methyl group coordination by carbon-oxygen hydrogen bonds in the lysine methyltransferase SET7/9. J. Biol. Chem, 286. 18658–18663. arXiv: 1011.1669v3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ma JC, Dougherty DA (1997). The cation-xinteraction. Chem. Rev, 97. 1303–1324. 10.1021/C19603744. [DOI] [PubMed] [Google Scholar]
- 31.Tavemam SD, U H. Ruthenburg AJ, Allis CD, Patel DJ, (2007). How chromatin-binding modules interpret histone modifications: Lessons from professional pocket pickers. Nature Struct. Mol. Biol, 14 (1025–1040). 15334406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Daze KD, Hof F, (2013). The cation-.rinteraction at protein-protein interaction interfaces: Developing and learning from synthetic mimics of proteins that bind methylated lysines. Acc. Chem. Res. 46. 937–945. 10.1021/ar300072g. [DOI] [PubMed] [Google Scholar]
- 33.Carvalho NF Pliego JR, (2015). Cluster-continuum quasichemical theory calculation of the lithium ion solvation in water, acetonitrile and dimethyl sulfoxide: an absolute single-ion solvation free energy scale. Pliys. Chem. Chem Phys„ 17. 26745–26755. [DOI] [PubMed] [Google Scholar]
- 34.Cournia Z, Allen B, Sherman W, (2017). Relative binding free energy calculations in drug discovery: Recent advances and practical considerations. J. Chem. Inf Model, 57, 2911–2937. 10.1021/acs.jcim.7b00564. [DOI] [PubMed] [Google Scholar]
- 35.WinemarvFisher V, Al-Hamdani Y, Addou I, Tkatchenko A, Varma S, (2019). lon-hydroxyl interactions: from high-level quantum benchmarks to transferable polarizable force fields. J. Chem Theory Comput, 15. 2444–2453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.WinemarvFisher V, Al-Hamdani Y, Nagy PR, Tkatchenko A, Varma S, (2020). Improved description of ligand polarization enhances transferability of ion-ligand interactions. J. Chem. Phys, 153, 094115. 10.1063/5.0022058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Wineman-Fisher V. et al. , (2020). Transferable interactions of li+ and mg2+ ions in polarizable models. J. Chem. Phys, 153, 101113. 10.1063/5.0022060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Huheey JE, (1965). The electronegativity of groups. J. Phys. Chem. 69. 3284–3291. [Google Scholar]
- 39.Richard Weaver J, Parry RW, Dipole moment studes. IV. Trends in dipole moments. Inorgan. Chem. 5 (1966) 718–723. [Google Scholar]
- 40.Teixidor F. et al. (2005). Are methyl groups electron-donating or electron-withdrawing in boron dusters? Permethylation of o-carborane. J. Am. Chem. Soc, 127, 10158–10159. [DOI] [PubMed] [Google Scholar]
- 41.Lide DR, CRC Handbook of Chemistry and Physics, 88th, 2007.
- 42.Rossi M, Tkatchenko A, Rempe SB, Varma S, (2013). Role of methyl-induced polarization in ion bindng. Proc. Natl. Acad. Sci. USA. 110. 12978–12983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Gobre VV, Tkatchenko A. (2013). Scaling laws for van der waals interactions in nanostructured materials. Nature Commun, 4, 2341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Kelly CP, Cramer CJ, Trnhlar DG, (2006). Adding explicit solvent molecules to continuum solvent calculations for the calculation of aqueous acid dissociation constants. J. Phys. Chem A, 110, 2493–2499. 10.1021/jp055336f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Patel DJ, (2016). A strudural perspective on readout of epigenetic histone and dna methylation marks. Cold Spring Harb Perspect Biol., 8. a018754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Beaver JE, Waters ML, (2016). Molecular recognition of lys and arg methylation. ACS Chem. Biol, 11, 643–653. [DOI] [PubMed] [Google Scholar]
- 47.Copeland RA, Solomon ME, Richon VM, (2009). Protein methyltransferases as a target class for drug discovery. Nature Rev. Drug Discov, 8. 724–732. [DOI] [PubMed] [Google Scholar]
- 48.Kaniskan HU, Martini ML, Jin J, (2018). Inhibitors of protein methyltransferases and demethylases. Chem. Rev, 118. 989–1068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Sitkoff D, Sharp KA, Honig B, (1994). Accurate calculation of hydration free energies using macroscopic solvent models. J. Phys. Chem, 98. 1978–1988. [Google Scholar]
- 50.Baker NA Sept D. Joseph S. Holst MJ, McCammon JA (2001). Electrostatics of ranosystems: Application to microtubules and the ribosome. Proc. Natl. Acad. Sd. 98. 10037–10041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Varma S, Jakobsson E, (2004). Ionization states of residues in ompf and mutants: Effects of dielectric constant and interactions between residues. Biopliys. J, 86, 690–704. http://www.sciencedirect.com/science/article/pii/S000634950474148X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Ddinsky TJ et al. , (2007). PDB2PQR: expanding aid upgrading automated preparation d biomdecular structures lor moleciJar simulations. Nucleic Acids Res., 35, W522–W525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Rizzi A. et al. , (2018). Overview of the sampl6 host-guest binding affinity prediction challenge. J. Comput-aided Mol. Des, 32, 937–963. https://pubmed.ncbi.nlm.nih.gov/30415285, [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Tkatchenko A, Scheffler M, (2009). Accurate molecular van der Waals interactions from ground-state electron density and free-atom reference data Phys. Rev. Letters, 102 6–9. [DOI] [PubMed] [Google Scholar]
- 55.Blum V. et al. , (2009). Ab initio molecular simulations with numeric atom-centered orbitals. Comput. Phys. Commai, 180. 2175–2196. 161200733. [Google Scholar]
- 56.Havu V, Blum V, Havu P, Scheffler M, (2009). Efficient O (N) integration for all-electron electronic structure calculation using numeric basis functions. J. Comput. Phys, 228. 8367–8379. [Google Scholar]
- 57.Marom N, et al. , (2011). Dispersion interactions with density-finctional theory: Benchmarking semiempirical and interatomic pairwise corrected density functionals. J. Chem. Theory Comput, 7. 3944–3951. [DOI] [PubMed] [Google Scholar]
- 58.Tkatchenko A. Distasio RA, Car R, Schelfler M, (2012). Accurate and efficient method for many-body van der Waals interactions, Phys. Rev. Letters, 108 [DOI] [PubMed] [Google Scholar]
- 59.Boys SF, Bernardi F, (1970). The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced enors. Mol. Phys
- 60.Riplinger C, Neese F, (2013). An efficient and near linear scaling pair natural orbital based local coupled cluster method. J. Chem. Phys,. [DOI] [PubMed]
- 61.Neese F, (2012). The ORCA program system. Wiley Interdiscipl. Rev. Comput. Mol. Sd. 2. 73–78. [Google Scholar]
- 62.Scalmani G, Frisch MJ, (2010). Continuous surface charge polarizable continuum models of solvation. I. General formalism. J. Chem. Phys, 132. 114110. [DOI] [PubMed] [Google Scholar]
- 63.Frisch M. et al. Gaussian 09 Revision A.1. 2009. [Google Scholar]
- 64.Asthagiri D. et al. , (2010). Ion selectivity from local configurations of ligands In solutions and ion channels. Chem. Phys. Letters, 485. 1–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.