Abstract
Tailoring magnetic orders in topological insulators is critical to the realization of topological quantum phenomena. An outstanding challenge is to find a material where atomic defects lead to tunable magnetic orders while maintaining a nontrivial topology. Here, by combining magnetization measurements, angle-resolved photoemission spectroscopy, and transmission electron microscopy, we reveal disorder-enabled, tunable magnetic ground states in MnBi6Te10. In the ferromagnetic phase, an energy gap of 15 meV is resolved at the Dirac point on the MnBi2Te4 termination. In contrast, antiferromagnetic MnBi6Te10 exhibits gapless topological surface states on all terminations. Transmission electron microscopy and magnetization measurements reveal substantial Mn vacancies and Mn migration in ferromagnetic MnBi6Te10. We provide a conceptual framework where a cooperative interplay of these defects drives a delicate change of overall magnetic ground state energies and leads to tunable magnetic topological orders. Our work provides a clear pathway for nanoscale defect-engineering toward the realization of topological quantum phases.
Keywords: magnetic topological insulator, MnBi6Te10, ferromagnetism, antiferromagnetism, defects
The first intrinsic magnetic topological insulator MnBi2Te4 (MBT)1−16 integrates topology with magnetism, and provides a fertile ground for realizing fascinating topological phases. Importantly, MBT exhibits intralayer ferromagnetism and interlayer antiferromagnetism. The compensated magnetic moments in even-layer MBT and the uncompensated ones in odd-layer counterparts give rise to axion insulators1 and quantum anomalous Hall (QAH) insulators,14 respectively. The key to tuning and optimizing these topological phases is to precisely control the interlayer magnetic interactions.
A promising route is to construct MnBi2nTe3n+1 superlattices, where Bi2Te3 (BT) buffer layers are inserted between the MBT layers. Previous studies have revealed that superlattices with n ≤ 3 exhibit interlayer antiferromagnetism,17−23 whereas those with n > 3 display ferromagnetism.23−25 On the other hand, for higher order superlattices the interlayer magnetic interactions become progressively weaker,23 which puts a strong limit on the tunability of magnetic interactions and subsequently on the onset temperatures of the resulting topological phases. Notably, previous studies on powder MnBi6Te1026 or hydrostatically pressurized MnBi6Te1027 revealed the possibility of tunable magnetic ground states, yet the nature of these samples disallowed angle-resolved photoemission spectroscopy (ARPES) to directly determine the band topology.
An alternative route is to explore the prevalent disorder effects in MBT and related compounds,28−33 and potentially use disorder to control the interlayer magnetic interactions. Recent experiments on MnSb2Te4 (MST) and Sb-doped MnBi2nTe3n+1 have demonstrated that the Mn/Sb and Mn/Bi antisite defects play an important role in tuning the system between antiferromagnetic (AFM) and ferromagnetic (FM) phases.29,34 However, no direct evidence has been found in the momentum space for the broken-symmetry gap in these materials. Moreover, the topological nature of MST is still under intense debates due to the reduced spin–orbit coupling (SOC) effect.12,35,36 It is thus an intriguing question whether such disorder-mediated magnetic interactions can be realized in the MBT-derived compounds without compromising the SOC effect, which potentially enables tunable topological phases by a sensitive control of the disorder.
In this Letter, we report a delicate FM topological insulator state in MnBi6Te10, which is attributed to disorder-mediated magnetic interactions. We employ high-resolution laser-based ARPES to detail the electronic structures of the FM and AFM phases, respectively. In the FM phase, a broken-symmetry gap is unambiguously observed on the topological surface state (TSS) of the MBT termination, with a gap onset temperature coinciding with the Curie temperature. In stark contrast, all terminations of the AFM phase of MnBi6Te10 exhibit negligible energy gaps on the TSS. Furthermore, our structural and magnetic characterizations reveal that Mn vacancies in MBT layers and Mn migration from MBT to BT layers are prevalent in FM MnBi6Te10. We provide a conceptual framework where a delicate interplay of Mn vacancies and Mn migration leads to the tunable magnetic phases in MnBi6Te10. Our work not only establishes the first unequivocal FM topological insulator phase in MnBi6Te10, but also demonstrates one of the highest FM Tc’s (13 K) among all MBT-derived compounds.24,25,37 The proposed new scheme of disorder-mediated ferromagnetism provides a pathway toward sensitive nanoscale tuning of topological phases and future topological quantum devices.
The MnBi6Te10 single crystals were synthesized through a self-flux method.20 So far, only the AFM phase was reported in MnBi6Te10, which is the ground state for MnBi2nTe3n+1 (n ≤ 3). The FM phase has 0.05 meV higher total energy per Mn atom that may be compensated by introducing certain type of defects.23,38 To meet this challenge, we increased the growth temperature window by 5 °C for FM samples comparing with the growth temperature for AFM samples in order to create Mn/Bi antisites and Mn vacancies, as both types of defects can weaken the interlayer AFM exchange coupling.
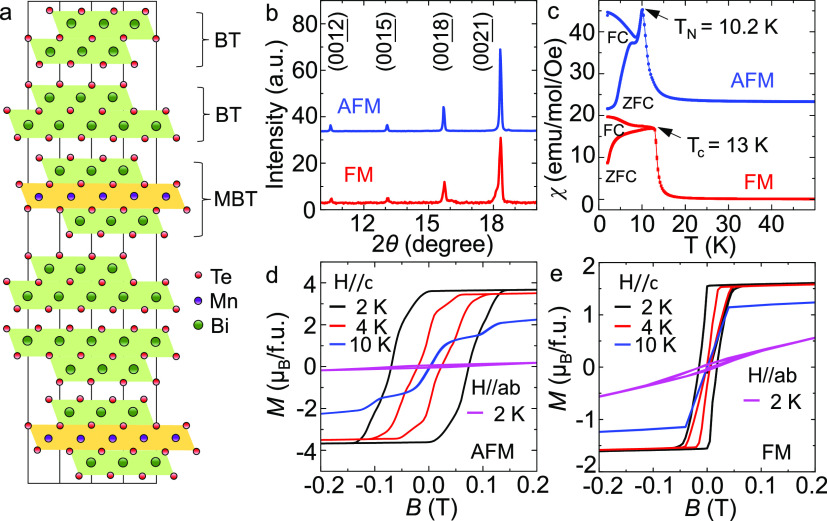
As shown in Figure 1b, the X-ray diffraction (XRD) patterns for the two magnetic phases exhibit the same (00l) diffraction peaks in good agreement with previous studies.20,39,40Figure 1c displays the zero-field-cooled (ZFC) and field-cooled (FC) magnetic susceptibilities measured with a c-axis applied field H = 100 Oe. A sharp Λ-like peak at 10.2 K is observed in the magnetic susceptibility of AFM MnBi6Te10, which indicates an AFM transition.20,23,25 The ZFC-FC bifurcation below 8 K seen in the AFM sample can be attributed to the evolution from a long-range AFM order to a cluster spin glass state,23 which is likely driven by the magnetic frustration caused by competing FM and AFM interactions. In contrast, the magnetic susceptibility for the FM material shows signatures of a typical FM transition: a rapid increase and plateauing of the susceptibility below the Curie temperature of 13 K. For FM MBT-derived materials, magneto-optical imaging has demonstrated that the ZFC-FC bifurcation in magnetic susceptibilities is likely due to the movement of FM domains.41 The FM phase is further confirmed by the isothermal magnetization curves in Figure 1e: a typical hysteresis loop expected for FM materials is revealed. In contrast, a spin-flop-like transition is observed in the AFM phase (Figure 1d), in agreement with previous reports on AFM MnBi4Te7.19
Figure 1.
Structural and magnetic characterizations of MnBi6Te10. (a) Schematic crystal structure of MnBi6Te10. (b) X-ray diffraction of ferromagnetic (FM, red) and antiferromagnetic (AFM, blue) MnBi6Te10. (c) Temperature dependent zero-field-cooled (ZFC) and field-cooled (FC) magnetic susceptibilities of FM (red) and AFM (blue) MnBi6Te10 using an external field H = 100 Oe along the c-axis. The results corresponding to the AFM samples are offset vertically for clarity. (d,e) Isothermal magnetization curves with the magnetic field applied along the c-axis and in the ab plane at various temperatures in (d) AFM and (e) FM MnBi6Te10.
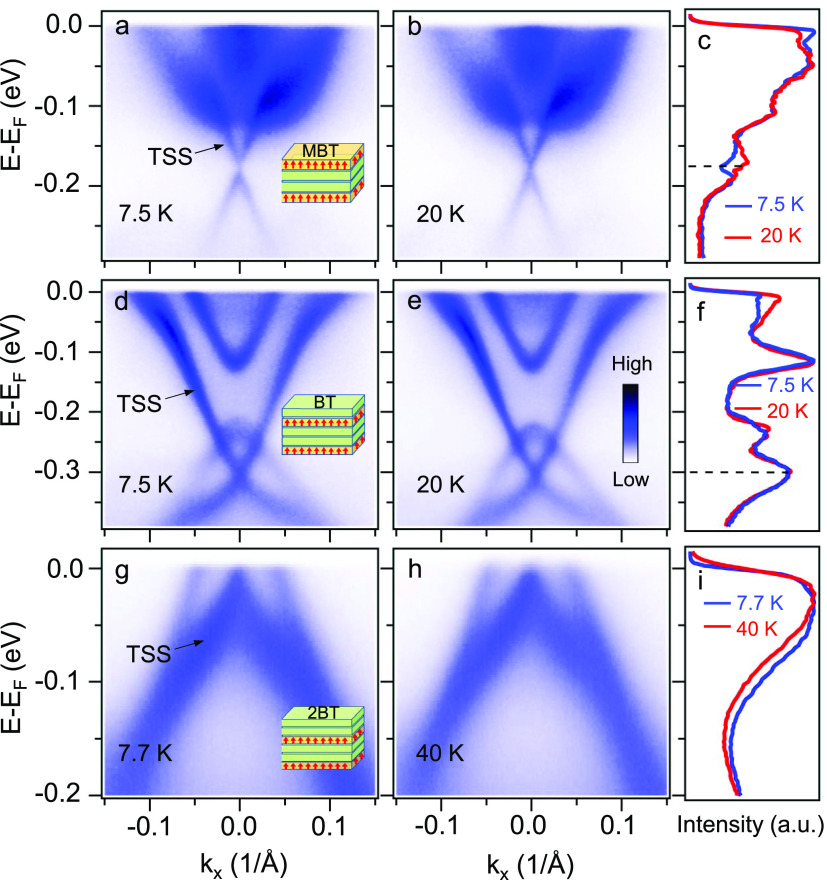
High-resolution ARPES results on FM MnBi6Te10 are presented in Figure 2. Three possible terminations are expected after cleaving, denoted by the top layer as MBT, single BT (1-BT), or double BT (2-BT) terminations. It is crucial to employ micron-scale laser beams to distinguish different terminations. Figure 2 presents three types of electronic structures found on FM MnBi6Te10. First, we point out that the termination assignment cannot be based on direct comparison between ARPES data and first-principles calculations, as the latter is often unable to properly model the impacts of defects and quantum confinement in MnBi2nTe3n+1 materials.16,40,42 A common spectroscopic feature characteristic of the MBT termination for all MnBi2nTe3n+1 superlattices is a Dirac surface state hybridized with parabolic Rashba bands.16,40,43 Hence, we associate the electronic structure in Figure 2a with the MBT termination. We assign the spectrum in Figure 2d to the 1-BT termination due to its strong resemblance with the counterpart on the 1-BT termination of FM Mn(Bi0.85Sb0.15)4Te7.37 Finally, since our material is phase-pure as demonstrated by the transmission electron microscopy measurement (Figure 3), we can only assign the last type of ARPES spectrum (Figure 2g) to the 2-BT termination. The two different types of BT-derived terminations exhibit electron (Figure 2d) and hole (Figure 2g) dopings, respectively. We notice that the qualitative trend is consistent with the previous ARPES data on the BT-derived terminations of AFM MnBi6Te1040 and FM MnBi8Te13,25 where electron doping systematically decreases as the number of BT layers increases. Nevertheless, the doping change from the 1-BT to the 2-BT terminations in FM MnBi6Te10 is much more dramatic, which may be due to its specific defect configuration [Supporting Information (SI) Note 1].
Figure 2.
Electronic structure of ferromagnetic MnBi6Te10. Energy-momentum spectra along Γ̅ – Μ̅ at (a) 7.5 K, and (b) 20 K. The insert in (a) illustrates the MnBi2Te4 (MBT) termination. (c) Comparison of energy distribution curves at Γ̅ . An energy gap is observed at the Dirac point (black dashed line) at 7.5 K. The counterpart results for the 1-Bi2Te3 (1-BT) termination are plotted in (d–f): (d,e) energy-momentum spectra, and (f) energy distribution curves at Γ̅ . The counterpart results for the 2-Bi2Te3 (2-BT) termination are plotted in (g–i): (g,h) energy-momentum spectra, and (i) energy distribution curves at Γ̅ .
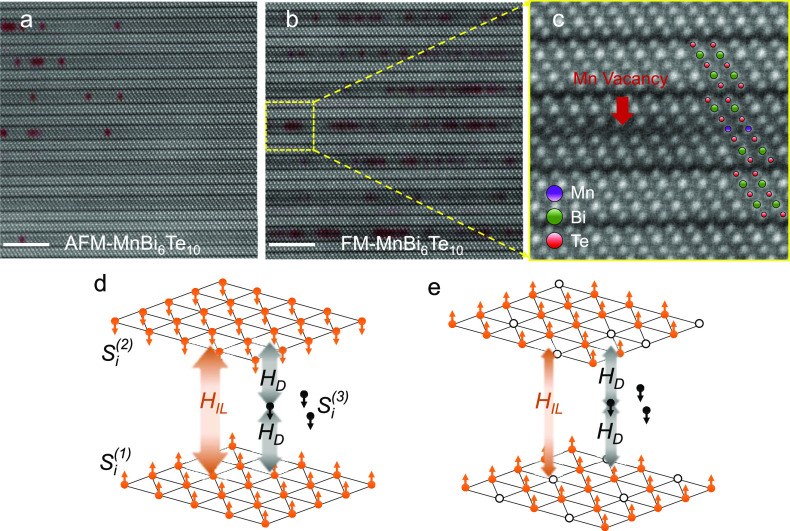
Figure 3.
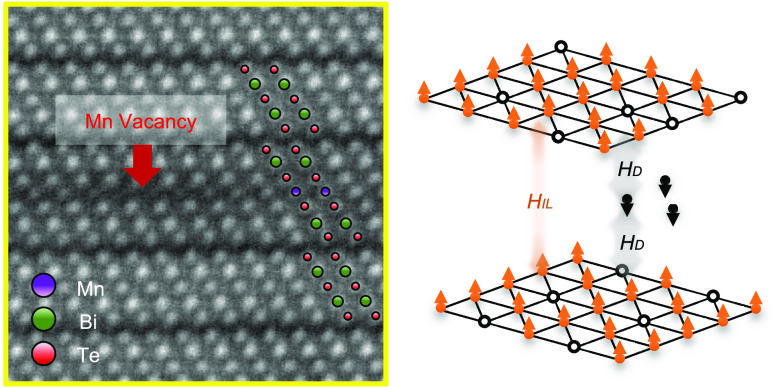
Structural characterizations of MnBi6Te10. Annular dark-field scanning transmission electron microscopy (ADF-STEM) images of (a) AFM and (b) FM MnBi6Te10. Scale bar indicates 5 nm. Mn vacancies are highlighted by red shading, where the intensity for the atomic column of Mn is lower than the value of two standard deviations below the Mn mean intensity. (c) Magnified image (yellow box in (b)). (d) A cartoon illustration showing HIL > HD in the AFM phase. (e) With increased Mn vacancies, HIL < HD in the FM phase.
We focus on the MBT and 1-BT terminations as their Dirac points are clearly resolvable below the Fermi level. Circular dichroism in ARPES measurements exhibits antisymmetric patterns near the Dirac point for both terminations (SI Figure 1). A helical circular dichroism (CD) pattern in ARPES has been successfully used to identify the topological surface state in MnBi2nTe3n+1 compounds.11,43 For the MBT termination, an energy gap of ∼15 meV at the Dirac point is visible in the ARPES data at 7.5 K and this gap disappears at 20 K (Figure 2a,b). The comparison of energy distribution curves (EDCs) taken at Γ̅ further highlights this temperature-dependent energy gap: a spectral peak at −0.18 eV at 20 K evolves into a dip upon cooling to 7.5 K. A temperature-dependent band dispersion analysis on the MBT termination yields a gap-closing temperature at 12.7 ± 1.4 K (SI Note 2 and SI Figure 2), yet we cannot completely rule out the existence of a finite gap above Tc. For the 1-BT termination, the spectra taken at both temperatures exhibit gapless Dirac cones (Figure 2d–f).
AFM MnBi6Te10 exhibits three types of ARPES spectra on three terminations (SI Figure 3 and SI Figure 4).21,40,44,45 The energy gaps at the Dirac points are negligible on all terminations of AFM MnBi6Te10, consistent with previous reports.22,40,43 While it is not the focus of our work, we point out that a likely scenario for the gapless TSS on the MBT termination of AFM MnBi6Te10 is that the Mn–Bi antisite defects may cause the TSS wave function to be relocated into the space between two adjacent MBT septuple layers.46 Both the nonmagnetic BT layers and the opposite magnetic moments from the two adjacent MBT layers may reduce the magnetic gap.
We thus establish the spectroscopic evidence of a magnetically induced broken-symmetry gap in FM MnBi6Te10 for the first time. This gap originates from strong interactions between the TSS electrons and the magnetic moments in the MBT layer. In contrast, the TSS electrons on the 1-BT termination are localized to the top BT layer and spatially separate from the magnetic MBT layer, leading to a gapless Dirac point. Gap opening in the MnBi2nTe3n+1 compound family has been highly controversial.2,3,6,7,11,16,22,23,25,40,44,47−50 Specifically on MnBi6Te10, a 60 meV gap was reported in the AFM phase44 in contrast to the results from all other ARPES studies on MnBi6Te1022,23,25,40 including ours. However, this gap persists well above the magnetic ordering temperature and is likely due to extrinsic reasons such as local impurities. On the contrary, our clear spectroscopic gap in FM MnBi6Te10 which onsets at the magnetic ordering temperature clarifies the physics picture of a broken time-reversal symmetry. In addition, our resolved gap in FM MnBi6Te10 is fully consistent with previous observations on FM MnBi8Te13.24,25 The crucial new discovery is that the magnetic phase of MnBi6Te10 can be controllably tuned between AFM and FM.
We proceed to investigate the microscopic mechanism leading to tunable magnetic phases. Notably, Mn-doped BT can host ferromagnetism,51−54 yet the distinct XRD and ARPES results from our FM MnBi6Te10 compared to those from Mn-doped BT51−53 suggest that the proportion of the latter phase in our materials is negligible. Furthermore, structural characterizations by annular dark field scanning transmission electron microscopy (ADF-STEM) do not find any observable impurity phases for AFM or FM samples, as shown in Figure 3. The atomic resolution images exhibit an interleaved structure composed of MBT septuple layers and 2 BT quintuple layers, which is consistent with the crystal structures determined by XRD in Figure 1b. The selected-area electron diffraction (SAED) patterns, determined by the atomic stacking sequences and periodicity along the c-axis (SI Figure 5), further confirm the single phase of the FM and AFM MnBi6Te10 samples.
Mn vacancies are observed in both AFM and FM MnBi6Te10, as highlighted in red in Figure 3a–c. Strikingly, the concentration of Mn vacancies in the FM samples (Figure 3b) is much higher than that in the AFM samples (Figure 3a). The quantitative percentages of Mn vacancies are hard to determine from ADF-STEM since the intensity is formed by atoms in the projection of the entire atomic columns perpendicular to the imaging plane. The energy dispersive X-ray (EDX) analysis confirms the higher concentration of Mn vacancies in the FM samples (SI Table 1).
Another important type of disorder is Mn migration. This effect is manifested as the ferrimagnetic order induced by the “antisite defects” in MnSb2Te428,29 and Sb-doped MnBi4Te7.34,55 Measurements of magnetic moments at low and high magnetic fields can be used to estimate the density of Mn migration.32 Using our measured magnetic moments at 0.2 T (Figure 1) and 7 T (SI Figure 6), we obtain that 8.1% and 11.8% of Mn atoms in FM and AFM MnBi6Te10, respectively, have migrated from the original Mn sheets to the neighboring layers. Here we use the chemical formula of Mn1–y-6x(Bi1–xMnx)6Te10, where 6x and y indicate the densities of Mn migration and Mn vacancies, respectively. The comparable densities of Mn migration in FM and AFM MnBi6Te10 suggest that the true physical picture for the FM order is more complex than a simple migration-induced ferrimagnetism.29
We construct a conceptual model to illustrate that it is the delicate interplay of Mn vacancies and Mn migration that leads to the tunable magnetic phases in MnBi6Te10. We consider two Mn sheets where the intralayer and interlayer magnetic interactions are FM and AFM, respectively. An intermediate layer of migrated Mn ions interacts with the original Mn sheets antiferromagnetically. We obtain the energy difference between the FM and AFM alignments of the original Mn sheets (SI Note 3)
| 1 |
Here JIL,ij is the interlayer magnetic coupling between site i and j in the two original Mn sheets; JD,ij is the defect-induced magnetic coupling across the original Mn sheets and the defect layer. Importantly, the scenarios of HIL > HD and HIL < HD lead to the AFM and FM alignment of the two original Mn sheets, respectively.
To evaluate the energy balance in the presence of Mn vacancies and Mn migration, we consider the scaling laws of HIL and HD in terms of the Mn density in the original sheets (no) and in the migrated space (nm): HIL ∝ no2 and HD ∝ nonm. These scaling laws are rooted in the microscopic nature of magnetic interactions (SI Note 4), and independent of the numerical details of JD,ij and JIL,ij. Subsequently
| 2 |
Equation 2 reveals the
microscopic mechanism for defect-induced ferromagnetism
in MnBi6Te10. First, with substantial Mn vacancies
in the MBT layer, both HIL and HD decrease (Figure 3e). The energy balance is determined by nm/no. Notably, the
saturated magnetic moments at low and high magnetic fields (M1 and M2, respectively)
allow us to estimate this ratio:32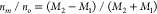 . Our measurements lead to nm/no = 0.2 and 0.13 for the
FM and AFM samples, respectively (SI Note 4). The values of nm/no for all the AFM MnBi6Te10 materials
in the literature are smaller than 0.1.20,25,38 The > 50% increase of nm/no tips the energy balance between HD and HIL, stabilizing
a ferromagnetic phase (Figure 3e). We remark that the more accurate nm/no can be >0.2 for FM MnBi6Te10 due to the potentially unsaturated M2 at 7 T.32
. Our measurements lead to nm/no = 0.2 and 0.13 for the
FM and AFM samples, respectively (SI Note 4). The values of nm/no for all the AFM MnBi6Te10 materials
in the literature are smaller than 0.1.20,25,38 The > 50% increase of nm/no tips the energy balance between HD and HIL, stabilizing
a ferromagnetic phase (Figure 3e). We remark that the more accurate nm/no can be >0.2 for FM MnBi6Te10 due to the potentially unsaturated M2 at 7 T.32
We emphasize that the simple Ising model neglects other types of magnetic interactions and should only serve as a conceptual framework. Nevertheless, it offers powerful scaling laws under which the delicate adjustment of Mn vacancies and Mn migration leads to tunable magnetic phases in MnBi6Te10. We emphasize that this disorder tuning leads to a change of the “global” magnetic ground state, which is to be distinguished from the more trivial disorder effect resulting in local changes of magnetism.36 Our new insight of quantitatively considering the ratio of nm/no is a substantial advance compared to previous studies which qualitatively pointed out the importance of disorder36,56 and the theoretical modeling whose predictions sensitively depend on numerical details.55 This insight, importantly, is obtained by the multimodal measurements combining magnetization, laser-based μARPES, and atomic-resolution TEM on the same batch of samples. Notably, FM MnBi6Te10 exhibits a Tc of 13 K, which is higher than the Tc of 10.5 K for FM MnBi8Te1324,25 and the Tc < 9 K for hydrostatically pressured MnBi6Te10,27 suggesting that the disorder-induced ferromagnetism may be more robust than that induced by superlattice stacking or by hydrostatic pressure. The delicate ferromagnetism revealed in this work will serve as a general framework to understand the phenomenology in all MnBi2nTe3n+1 superlattices.
We hope that our work will serve as a milestone to motivate further theoretical and experimental studies, in particular spectroscopy and microscopy studies with atomic resolutions to resolve what defects form under what growth conditions in disordered FM MnBi2nTe3n+1. The defect engineering via controlling the growth temperature can potentially be adapted in thin film deposition of MnBi2nTe3n+1 as well. Understanding how to tune the magnetism and topological states without introducing new chemical elements in the same MBT system through delicately controlling the defects, allows us to selectively realize exotic phases such as the axion insulator state and the quantum anomalous Hall insulator state, paving the road toward functional topological quantum devices at realistic cryogenic temperatures.
Methods
Sample Growth and Characterization
MnBi6Te10 single crystals were synthesized using the self-flux method,20 in which Mn, Bi, and Te powders were mixed with a stoichiometric molar ratio and sealed in a carbon-coated quartz tube under high vacuum. For the synthesis of ferromagnetic (FM) MnBi6Te10, the mixture was heated to 900 °C in a furnace and held for 10 h for homogeneous melting. The mixture then underwent a series of cooling and annealing stages: from 900 to 595 °C in 5 h, from 595 to 580 °C at a rate of 0.1 °C/h, annealed at 580 °C for 48 h, and finally quenched in water at 0 °C. For the synthesis of antiferromagnetic (AFM) MnBi6Te10, the same melting was adopted. It was followed by cooling from 900 to 590 °C in 5 h and then from 590 to 575 °C at a rate of 0.1 °C/h, annealed at 575 °C for 48 h and then quenched in water at 0 °C. The as-grown single crystals were found to be plate-like with luster and lateral dimensions of 2 × 2 mm2.
The crystallization of the grown single crystals was verified by the sharp (00L) XRD peaks using a Malvern Panalytical Empyrean diffractometer (Cu Kα radiation), as shown in Figure 1b. Magnetization of crystals was measured by the MPMS3 SQUID magnetometer (Quantum Design).
The TEM specimens were prepared using ThermoFisher Helios 660 dual beam system. The specimens were thinned down to electron transparency using 30 kV and 5 kV Ga ion beam and cleaned with 2 kV and 1 kV ion beam. The aberration-corrected STEM imaging was performed using ThermoFisher Titan G2 S/TEM equipped with image and probe correctors. The operating voltage for the STEM imaging was 200 kV. The STEM images have been drift corrected using the nonlinear drift correction algorithm. The elemental mapping was acquired with energy dispersive X-ray spectroscopy (EDS) with STEM mode.
Ultrahigh Resolution Laser-Based Angle-Resolved Photoemission Spectroscopy (ARPES)
Our laser-based ARPES setup was based on a Coherent MIRA Ti:sapphire oscillator. With a 5 W, 532 nm continuous wave seed laser, the oscillator output >9 nJ pulses with a central wavelength at 820 nm, a bandwidth of 7.6 nm, a pulse duration of 130 fs, and a repetition rate of 80 MHz. One mm beta barium borate (BBO) crystals were used to generate the second harmonic (410 nm) and fourth harmonic (205 nm), the latter of which was used for ARPES measurements. The optical bandwidth of the 6 eV beam was expected to be 2.7 meV due to the finite BBO thicknesses. The overall energy resolution incorporating the ARPES analyzer resolution was characterized as 4 meV.57 The beam waist at the optical focal point was less than 10 μm.57
Acknowledgments
The ARPES work was in part supported by the US Department of Energy (DOE), Office of Science, Basic Energy Sciences, Materials Science and Engineering Division, under contract No. DE-AC02-06CH11357, and in part supported by NSF DMR-2145373. The financial support for sample preparation was provided by the National Science Foundation through the Penn State 2D Crystal Consortium-Materials Innovation Platform (2DCC-MIP) under NSF cooperative agreement DMR-1539916 and DMR-2039351. Z.Q.M. acknowledges the support from the US National Science Foundation under grant DM-1917579. C.X.L. and R.B.M. acknowledge the support of the U.S. Department of Energy (Grant DESC0019064). B.Y. acknowledges the financial support by the Willner Family Leadership Institute for the Weizmann Institute of Science, the Benoziyo Endowment Fund for the Advancement of Science, Ruth and Herman Albert Scholars Program for New Scientists, the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (Grant 815869). N.A. and L.M acknowledge the support by NSF through the Pennsylvania State University Materials Research Science and Engineering Center DMR-2011839 (2020–2026). L.M and N.A. acknowledge the Air Force Office of Scientific Research (AFOSR) program FA9550-18-1-0277 as well as GAME MURI, 10059059-PENN for support.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.2c02500.
Defects and doping, circular dichroism in the ARPES spectra of ferromagnetic MnBi6Te10, side-by-side comparison of FM and AFM MnBi6Te10 using the temperature evolutions of the TSS’s on the MBT termination, electronic structure of antiferromagnetic MnBi6Te10, circular dichroism in the ARPES spectra of antiferromagnetic MnBi6Te10, selected area electron diffraction (SAED) patterns of MnBi6Te10, high-field magnetization measurements of AFM and FM MnBi6Te10, estimates of the chemical concentrations of MnBi6Te10 based on the scanning transmission electron microscopy–energy dispersive X-ray (STEM-EDX) analysis, magnetic interactions, and the determination of the Mn density ratio between different layers (PDF)
Author Contributions
C.Y., S.M., E.G., and S.Y. performed the ARPES measurements. Y.Z. and Z.M. grew the samples and performed the magnetization measurements. L.M. and N.A. performed the STEM measurements. All authors discussed the results and commented on the paper. C.Y. and S.Y. wrote the paper with input from all authors.
The authors declare no competing financial interest.
Supplementary Material
References
- Liu C.; Wang Y.; Li H.; Wu Y.; Li Y.; Li J.; He K.; Xu Y.; Zhang J.; Wang Y. Robust Axion Insulator and Chern Insulator Phases in a Two-Dimensional Antiferromagnetic Topological Insulator. Nat. Mater. 2020, 19, 522. 10.1038/s41563-019-0573-3. [DOI] [PubMed] [Google Scholar]
- Otrokov M. M.; Klimovskikh I. I.; Bentmann H.; Estyunin D.; Zeugner A.; Aliev Z. S.; Gaß S.; Wolter A. U. B.; Koroleva A. V.; Shikin A. M.; Blanco-Rey M.; Hoffmann M.; Rusinov I. P.; Vyazovskaya A. Y.; Eremeev S. V.; Koroteev Y. M.; Kuznetsov V. M.; Freyse F.; Sánchez-Barriga J.; Amiraslanov I. R.; Babanly M. B.; Mamedov N. T.; Abdullayev N. A.; Zverev V. N.; Alfonsov A.; Kataev V.; Büchner B.; Schwier E. F.; Kumar S.; Kimura A.; Petaccia L.; Di Santo G.; Vidal R. C.; Schatz S.; Kißner K.; Ünzelmann M.; Min C. H.; Moser S.; Peixoto T. R. F.; Reinert F.; Ernst A.; Echenique P. M.; Isaeva A.; Chulkov E. V. Prediction and Observation of an Antiferromagnetic Topological Insulator. Nature 2019, 576 (7787), 416–422. 10.1038/s41586-019-1840-9. [DOI] [PubMed] [Google Scholar]
- Rienks E. D. L.; Wimmer S.; Sánchez-Barriga J.; Caha O.; Mandal P. S.; Růžička J.; Ney A.; Steiner H.; Volobuev V. V.; Groiss H.; Albu M.; Kothleitner G.; Michalička J.; Khan S. A.; Minár J.; Ebert H.; Bauer G.; Freyse F.; Varykhalov A.; Rader O.; Springholz G. Large Magnetic Gap at the Dirac Point in Bi2Te3/MnBi2Te4 Heterostructures. Nature 2019, 576 (7787), 423–428. 10.1038/s41586-019-1826-7. [DOI] [PubMed] [Google Scholar]
- Gong Y.; Guo J.; Li J.; Zhu K.; Liao M.; Liu X.; Zhang Q.; Gu L.; Tang L.; Feng X.; Zhang D.; Li W.; Song C.; Wang L.; Yu P.; Chen X.; Wang Y.; Yao H.; Duan W.; Xu Y.; Zhang S.-C.; Ma X.; Xue Q.-K.; He K. Experimental Realization of an Intrinsic Magnetic Topological Insulator. Chin. Phys. Lett. 2019, 36 (7), 076801. 10.1088/0256-307X/36/7/076801. [DOI] [Google Scholar]
- Zeugner A.; Nietschke F.; Wolter A. U. B.; Gaß S.; Vidal R. C.; Peixoto T. R. F.; Pohl D.; Damm C.; Lubk A.; Hentrich R.; Moser S. K.; Fornari C.; Min C. H.; Schatz S.; Kißner K.; Ünzelmann M.; Kaiser M.; Scaravaggi F.; Rellinghaus B.; Nielsch K.; Hess C.; Büchner B.; Reinert F.; Bentmann H.; Oeckler O.; Doert T.; Ruck M.; Isaeva A. Chemical Aspects of the Candidate Antiferromagnetic Topological Insulator MnBi2Te4. Chem. Mater. 2019, 31 (8), 2795–2806. 10.1021/acs.chemmater.8b05017. [DOI] [Google Scholar]
- Swatek P.; Wu Y.; Wang L.-L.; Lee K.; Schrunk B.; Yan J.; Kaminski A. Gapless Dirac Surface States in the Antiferromagnetic Topological Insulator MnBi2Te4. Phys. Rev. B 2020, 101 (16), 161109. 10.1103/PhysRevB.101.161109. [DOI] [Google Scholar]
- Hao Y.-J.; Liu P.; Feng Y.; Ma X.-M.; Schwier E. F.; Arita M.; Kumar S.; Hu C.; Lu R.; Zeng M.; Wang Y.; Hao Z.; Sun H.-Y.; Zhang K.; Mei J.; Ni N.; Wu L.; Shimada K.; Chen C.; Liu Q.; Liu C. Gapless Surface Dirac Cone in Antiferromagnetic Topological Insulator MnBi2Te4. Phys. Rev. X 2019, 9 (4), 041038. 10.1103/PhysRevX.9.041038. [DOI] [Google Scholar]
- Chen Y. J.; Xu L. X.; Li J. H.; Li Y. W.; Wang H. Y.; Zhang C. F.; Li H.; Wu Y.; Liang A. J.; Chen C.; Jung S. W.; Cacho C.; Mao Y. H.; Liu S.; Wang M. X.; Guo Y. F.; Xu Y.; Liu Z. K.; Yang L. X.; Chen Y. L. Topological Electronic Structure and Its Temperature Evolution in Antiferromagnetic Topological Insulator MnBi2Te4. Phys. Rev. X 2019, 9 (4), 041040. 10.1103/PhysRevX.9.041040. [DOI] [Google Scholar]
- Li H.; Gao S.-Y.; Duan S.-F.; Xu Y.-F.; Zhu K.-J.; Tian S.-J.; Gao J.-C.; Fan W.-H.; Rao Z.-C.; Huang J.-R.; Li J.-J.; Yan D.-Y.; Liu Z.-T.; Liu W.-L.; Huang Y.-B.; Li Y.-L.; Liu Y.; Zhang G.-B.; Zhang P.; Kondo T.; Shin S.; Lei H.-C.; Shi Y.-G.; Zhang W.-T.; Weng H.-M.; Qian T.; Ding H. Dirac Surface States in Intrinsic Magnetic Topological Insulators EuSn2As2 and MnBi2nTe3n+1. Phys. Rev. X 2019, 9 (4), 041039. 10.1103/PhysRevX.9.041039. [DOI] [Google Scholar]
- Vidal R. C.; Bentmann H.; Peixoto T. R. F.; Zeugner A.; Moser S.; Min C.-H.; Schatz S.; Kißner K.; Ünzelmann M.; Fornari C. I.; Vasili H. B.; Valvidares M.; Sakamoto K.; Mondal D.; Fujii J.; Vobornik I.; Jung S.; Cacho C.; Kim T. K.; Koch R. J.; Jozwiak C.; Bostwick A.; Denlinger J. D.; Rotenberg E.; Buck J.; Hoesch M.; Diekmann F.; Rohlf S.; Kalläne M.; Rossnagel K.; Otrokov M. M.; Chulkov E. V.; Ruck M.; Isaeva A.; Reinert F. Surface States and Rashba-Type Spin Polarization in Antiferromagnetic MnBi2Te4 (0001). Phys. Rev. B 2019, 100 (12), 121104. 10.1103/PhysRevB.100.121104. [DOI] [Google Scholar]
- Nevola D.; Li H. X.; Yan J.-Q.; Moore R. G.; Lee H.-N.; Miao H.; Johnson P. D. Coexistence of Surface Ferromagnetism and a Gapless Topological State in MnBi2Te4. Phys. Rev. Lett. 2020, 125 (11), 117205. 10.1103/PhysRevLett.125.117205. [DOI] [PubMed] [Google Scholar]
- Chen B.; Fei F.; Zhang D.; Zhang B.; Liu W.; Zhang S.; Wang P.; Wei B.; Zhang Y.; Zuo Z.; Guo J.; Liu Q.; Wang Z.; Wu X.; Zong J.; Xie X.; Chen W.; Sun Z.; Wang S.; Zhang Y.; Zhang M.; Wang X.; Song F.; Zhang H.; Shen D.; Wang B. Intrinsic Magnetic Topological Insulator Phases in the Sb Doped MnBi2Te4 Bulks and Thin Flakes. Nat. Commun. 2019, 10, 4469. 10.1038/s41467-019-12485-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Otrokov M. M.; Rusinov I. P.; Blanco-Rey M.; Hoffmann M.; Vyazovskaya A. Yu.; Eremeev S. V.; Ernst A.; Echenique P. M.; Arnau A.; Chulkov E. V. Unique Thickness-Dependent Properties of the van Der Waals Interlayer Antiferromagnet MnBi2Te4 Films. Phys. Rev. Lett. 2019, 122 (10), 107202. 10.1103/PhysRevLett.122.107202. [DOI] [PubMed] [Google Scholar]
- Deng Y.; Yu Y.; Shi M. Z.; Guo Z.; Xu Z.; Wang J.; Chen X. H.; Zhang Y. Quantum Anomalous Hall Effect in Intrinsic Magnetic Topological Insulator MnBi2Te4. Science 2020, 367 (6480), 895–900. 10.1126/science.aax8156. [DOI] [PubMed] [Google Scholar]
- Estyunin D. A.; Klimovskikh I. I.; Shikin A. M.; Schwier E. F.; Otrokov M. M.; Kimura A.; Kumar S.; Filnov S. O.; Aliev Z. S.; Babanly M. B.; Chulkov E. V. Signatures of Temperature Driven Antiferromagnetic Transition in the Electronic Structure of Topological Insulator MnBi2Te4. APL Mater. 2020, 8 (2), 021105. 10.1063/1.5142846. [DOI] [Google Scholar]
- Yan C.; Fernandez-Mulligan S.; Mei R.; Lee S. H.; Protic N.; Fukumori R.; Yan B.; Liu C.; Mao Z.; Yang S. Origins of Electronic Bands in the Antiferromagnetic Topological Insulator MnBi2Te4. Phys. Rev. B 2021, 104 (4), L041102. 10.1103/PhysRevB.104.L041102. [DOI] [Google Scholar]
- Hu C.; Gordon K. N.; Liu P.; Liu J.; Zhou X.; Hao P.; Narayan D.; Emmanouilidou E.; Sun H.; Liu Y.; Brawer H.; Ramirez A. P.; Ding L.; Cao H.; Liu Q.; Dessau D.; Ni N. A van Der Waals Antiferromagnetic Topological Insulator with Weak Interlayer Magnetic Coupling. Nat. Commun. 2020, 11, 97. 10.1038/s41467-019-13814-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu J.; Liu F.; Sasase M.; Ienaga K.; Obata Y.; Yukawa R.; Horiba K.; Kumigashira H.; Okuma S.; Inoshita T.; Hosono H. Natural van Der Waals Heterostructural Single Crystals with Both Magnetic and Topological Properties. Sci. Adv. 2019, 5 (11), eaax9989 10.1126/sciadv.aax9989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vidal R. C.; Zeugner A.; Facio J. I.; Ray R.; Haghighi M. H.; Wolter A. U. B.; Corredor Bohorquez L. T.; Caglieris F.; Moser S.; Figgemeier T.; Peixoto T. R. F.; Vasili H. B.; Valvidares M.; Jung S.; Cacho C.; Alfonsov A.; Mehlawat K.; Kataev V.; Hess C.; Richter M.; Büchner B.; van den Brink J.; Ruck M.; Reinert F.; Bentmann H.; Isaeva A. Topological Electronic Structure and Intrinsic Magnetization in MnBi4Te7: A Bi2Te3 Derivative with a Periodic Mn Sublattice. Phys. Rev. X 2019, 9 (4), 041065. 10.1103/PhysRevX.9.041065. [DOI] [Google Scholar]
- Shi M. Z.; Lei B.; Zhu C. S.; Ma D. H.; Cui J. H.; Sun Z. L.; Ying J. J.; Chen X. H. Magnetic and Transport Properties in the Magnetic Topological Insulators MnB2Te4(Bi2Te3)n (N = 1,2). Phys. Rev. B 2019, 100 (15), 155144. 10.1103/PhysRevB.100.155144. [DOI] [Google Scholar]
- Tian S.; Gao S.; Nie S.; Qian Y.; Gong C.; Fu Y.; Li H.; Fan W.; Zhang P.; Kondo T.; Shin S.; Adell J.; Fedderwitz H.; Ding H.; Wang Z.; Qian T.; Lei H. Magnetic Topological Insulator MnBi6Te10with a Zero-Field Ferromagnetic State and Gapped Dirac Surface States. Phys. Rev. B 2020, 102 (3), 035144. 10.1103/PhysRevB.102.035144. [DOI] [Google Scholar]
- Hu Y.; Xu L.; Shi M.; Luo A.; Peng S.; Wang Z. Y.; Ying J. J.; Wu T.; Liu Z. K.; Zhang C. F.; Chen Y. L.; Xu G.; Chen X.-H.; He J.-F. Universal Gapless Dirac Cone and Tunable Topological States in (MnBi2Te4)m(Bi2Te3)n Heterostructures. Phys. Rev. B 2020, 101 (16), 161113. 10.1103/PhysRevB.101.161113. [DOI] [Google Scholar]
- Klimovskikh I. I.; Otrokov M. M.; Estyunin D.; Eremeev S. V.; Filnov S. O.; Koroleva A.; Shevchenko E.; Voroshnin V.; Rybkin A. G.; Rusinov I. P.; Blanco-Rey M.; Hoffmann M.; Aliev Z. S.; Babanly M. B.; Amiraslanov I. R.; Abdullayev N. A.; Zverev V. N.; Kimura A.; Tereshchenko O. E.; Kokh K. A.; Petaccia L.; Di Santo G.; Ernst A.; Echenique P. M.; Mamedov N. T.; Shikin A. M.; Chulkov E. V. Tunable 3D/2D Magnetism in the (MnBi2Te4)(Bi2Te3)m Topological Insulators Family. Npj Quantum Mater. 2020, 5 (1), 54. 10.1038/s41535-020-00255-9. [DOI] [Google Scholar]
- Lu R.; Sun H.; Kumar S.; Wang Y.; Gu M.; Zeng M.; Hao Y.-J.; Li J.; Shao J.; Ma X.-M.; Hao Z.; Zhang K.; Mansuer W.; Mei J.; Zhao Y.; Liu C.; Deng K.; Huang W.; Shen B.; Shimada K.; Schwier E. F.; Liu C.; Liu Q.; Chen C. Half-Magnetic Topological Insulator with Magnetization-Induced Dirac Gap at a Selected Surface. Phys. Rev. X 2021, 11 (1), 011039. 10.1103/PhysRevX.11.011039. [DOI] [Google Scholar]
- Hu C.; Ding L.; Gordon K. N.; Ghosh B.; Tien H.-J.; Li H.; Linn A. G.; Lien S.-W.; Huang C.-Y.; Mackey S.; Liu J.; Reddy P. V. S.; Singh B.; Agarwal A.; Bansil A.; Song M.; Li D.; Xu S.-Y.; Lin H.; Cao H.; Chang T.-R.; Dessau D.; Ni N. Realization of an Intrinsic Ferromagnetic Topological State in MnBi8Te13. Sci. Adv. 2020, 6 (30), eaba4275 10.1126/sciadv.aba4275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Souchay D.; Nentwig M.; Günther D.; Keilholz S.; de Boor J.; Zeugner A.; Isaeva A.; Ruck M.; Wolter A. U.; Büchner B.; Oeckler O. Layered Manganese Bismuth Tellurides with GeBi4Te7 and GeBi6Te10 Type Structures: Towards Multifunctional Materials. J. Mater. Chem. C 2019, 7 (32), 9939–9953. 10.1039/C9TC00979E. [DOI] [Google Scholar]
- Shao J.; Liu Y.; Zeng M.; Li J.; Wu X.; Ma X.-M.; Jin F.; Lu R.; Sun Y.; Gu M.; Wang K.; Wu W.; Wu L.; Liu C.; Liu Q.; Zhao Y. Pressure-Tuned Intralayer Exchange in Superlattice-Like MnBi2Te4/(Bi2Te3)n Topological Insulators. Nano Lett. 2021, 21 (13), 5874–5880. 10.1021/acs.nanolett.1c01874. [DOI] [PubMed] [Google Scholar]
- Liu Y.; Wang L.-L.; Zheng Q.; Huang Z.; Wang X.; Chi M.; Wu Y.; Chakoumakos B. C.; McGuire M. A.; Sales B. C.; Wu W.; Yan J. Site Mixing for Engineering Magnetic Topological Insulators. Phys. Rev. X 2021, 11 (2), 021033. 10.1103/PhysRevX.11.021033. [DOI] [Google Scholar]
- Murakami T.; Nambu Y.; Koretsune T.; Xiangyu G.; Yamamoto T.; Brown C. M.; Kageyama H. Realization of Interlayer Ferromagnetic Interaction in MnSb2Te4 toward the Magnetic Weyl Semimetal State. Phys. Rev. B 2019, 100 (19), 195103. 10.1103/PhysRevB.100.195103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hou F.; Yao Q.; Zhou C.-S.; Ma X.-M.; Han M.; Hao Y.-J.; Wu X.; Zhang Y.; Sun H.; Liu C.; Zhao Y.; Liu Q.; Lin J. Te-Vacancy-Induced Surface Collapse and Reconstruction in Antiferromagnetic Topological Insulator MnBi2Te4. ACS Nano 2020, 14 (9), 11262–11272. 10.1021/acsnano.0c03149. [DOI] [PubMed] [Google Scholar]
- Huang Z.; Du M.-H.; Yan J.; Wu W. Native Defects in Antiferromagnetic Topological Insulator MnBi2Te4. Phys. Rev. Mater. 2020, 4 (12), 121202. 10.1103/PhysRevMaterials.4.121202. [DOI] [Google Scholar]
- Lai Y.; Ke L.; Yan J.; McDonald R. D.; McQueeney R. J. Defect-Driven Ferrimagnetism and Hidden Magnetization in MnBi2Te4. Phys. Rev. B 2021, 103 (18), 184429. 10.1103/PhysRevB.103.184429. [DOI] [Google Scholar]
- Du M.-H.; Yan J.; Cooper V. R.; Eisenbach M. Tuning Fermi Levels in Intrinsic Antiferromagnetic Topological Insulators MnBi2Te4 and MnBi4Te7 by Defect Engineering and Chemical Doping. Adv. Funct. Mater. 2021, 31 (3), 2006516. 10.1002/adfm.202006516. [DOI] [Google Scholar]
- Hu C.; Lien S.-W.; Feng E.; Mackey S.; Tien H.-J.; Mazin I. I.; Cao H.; Chang T.-R.; Ni N. Tuning Magnetism and Band Topology through Antisite Defects in Sb-Doped MnBi4Te7. Phys. Rev. B 2021, 104 (5), 054422. 10.1103/PhysRevB.104.054422. [DOI] [Google Scholar]
- Chen L.; Wang D.; Shi C.; Jiang C.; Liu H.; Cui G.; Zhang X.; Li X. Electronic Structure and Magnetism of MnSb2Te4. J. Mater. Sci. 2020, 55 (29), 14292–14300. 10.1007/s10853-020-05005-7. [DOI] [Google Scholar]
- Wimmer S.; Sánchez-Barriga J.; Küppers P.; Ney A.; Schierle E.; Freyse F.; Caha O.; Michalička J.; Liebmann M.; Primetzhofer D.; Hoffman M.; Ernst A.; Otrokov M. M.; Bihlmayer G.; Weschke E.; Lake B.; Chulkov E. V.; Morgenstern M.; Bauer G.; Springholz G.; Rader O. Mn-Rich MnSb2Te4: A Topological Insulator with Magnetic Gap Closing at High Curie Temperatures of 45–50 K. Adv. Mater. 2021, 33 (42), 2102935. 10.1002/adma.202102935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guan Y. D.; Yan C. H.; Lee S. H.; Gui X.; Ning W.; Ning J. L.; Zhu Y. L.; Kothakonda M.; Xu C. Q.; Ke X. L.; Sun J. W.; Xie W. W.; Yang S. L.; Mao Z. Q. Ferromagnetic MnBi4Te7 Obtained with Low-Concentration Sb Doping: A Promising Platform for Exploring Topological Quantum States. Phys. Rev. Mater. 2022, 6 (5), 054203. 10.1103/PhysRevMaterials.6.054203. [DOI] [Google Scholar]
- Xie H.; Wang D.; Cai Z.; Chen B.; Guo J.; Naveed M.; Zhang S.; Zhang M.; Wang X.; Fei F.; Zhang H.; Song F. The Mechanism Exploration for Zero-Field Ferromagnetism in Intrinsic Topological Insulator MnBi2Te4 by Bi2Te3 Intercalations. Appl. Phys. Lett. 2020, 116 (22), 221902. 10.1063/5.0009085. [DOI] [Google Scholar]
- Aliev Z. S.; Amiraslanov I. R.; Nasonova D. I.; Shevelkov A. V.; Abdullayev N. A.; Jahangirli Z. A.; Orujlu E. N.; Otrokov M. M.; Mamedov N. T.; Babanly M. B.; Chulkov E. V. Novel Ternary Layered Manganese Bismuth Tellurides of the MnTe-Bi2Te3 System: Synthesis and Crystal Structure. J. Alloys Compd. 2019, 789, 443–450. 10.1016/j.jallcom.2019.03.030. [DOI] [Google Scholar]
- Ma X.-M.; Chen Z.; Schwier E. F.; Zhang Y.; Hao Y.-J.; Kumar S.; Lu R.; Shao J.; Jin Y.; Zeng M.; Liu X.-R.; Hao Z.; Zhang K.; Mansuer W.; Song C.; Wang Y.; Zhao B.; Liu C.; Deng K.; Mei J.; Shimada K.; Zhao Y.; Zhou X.; Shen B.; Huang W.; Liu C.; Xu H.; Chen C. Hybridization-Induced Gapped and Gapless States on the Surface of Magnetic Topological Insulators. Phys. Rev. B 2020, 102 (24), 245136. 10.1103/PhysRevB.102.245136. [DOI] [Google Scholar]
- Hu C.; Tanatar M. A.; Prozorov R.; Ni N. Unusual Dynamic Susceptibility Arising from Soft Ferromagnetic Domains in MnBi 8 Te 13 and Sb-Doped MnBi2nTe3n+1(n = 2, 3). J. Phys. Appl. Phys. 2022, 55 (5), 054003. 10.1088/1361-6463/ac3032. [DOI] [Google Scholar]
- Wu X.; Li J.; Ma X.-M.; Zhang Y.; Liu Y.; Zhou C.-S.; Shao J.; Wang Q.; Hao Y.-J.; Feng Y.; Schwier E. F.; Kumar S.; Sun H.; Liu P.; Shimada K.; Miyamoto K.; Okuda T.; Wang K.; Xie M.; Chen C.; Liu Q.; Liu C.; Zhao Y. Distinct Topological Surface States on the Two Terminations of MnBi4Te7. Phys. Rev. X 2020, 10 (3), 031013. 10.1103/PhysRevX.10.031013. [DOI] [Google Scholar]
- Vidal R. C.; Bentmann H.; Facio J. I.; Heider T.; Kagerer P.; Fornari C. I.; Peixoto T. R. F.; Figgemeier T.; Jung S.; Cacho C.; Büchner B.; van den Brink J.; Schneider C. M.; Plucinski L.; Schwier E. F.; Shimada K.; Richter M.; Isaeva A.; Reinert F. Orbital Complexity in Intrinsic Magnetic Topological Insulator MnBi4Te7 and MnBi6Te10. Phys. Rev. Lett. 2021, 126 (17), 176403. 10.1103/PhysRevLett.126.176403. [DOI] [PubMed] [Google Scholar]
- Jo N. H.; Wang L.-L.; Slager R.-J.; Yan J.; Wu Y.; Lee K.; Schrunk B.; Vishwanath A.; Kaminski A. Intrinsic Axion Insulating Behavior in Antiferromagnetic MnBi6Te10. Phys. Rev. B 2020, 102 (4), 045130. 10.1103/PhysRevB.102.045130. [DOI] [Google Scholar]
- Gordon K. N.; Sun H.; Hu C.; Linn A. G.; Li H.; Liu Y.; Liu P.; Mackey S.; Liu Q.; Ni N.; Dessau D.. Strongly Gapped Topological Surface States on Protected Surfaces of Antiferromagnetic MnBi4Te7 and MnBi6Te10. 2019, 1910.13943. arXiv. 10.48550/arXiv.1910.13943 (accessed June 24, 2022). [DOI] [Google Scholar]
- Tan H.; Yan B.. Distinct Magnetic Gaps between Antiferromagnetic and Ferromagnetic Orders Driven by Surface Defects in the Topological Magnet MnBi2Te4. 2022, 2207.13511. arXiv. 10.48550/arXiv.2207.13511 (accessed September 08, 2022). [DOI] [PubMed] [Google Scholar]
- Garnica M.; Otrokov M. M.; Aguilar P. C.; Klimovskikh I. I.; Estyunin D.; Aliev Z. S.; Amiraslanov I. R.; Abdullayev N. A.; Zverev V. N.; Babanly M. B.; Mamedov N. T.; Shikin A. M.; Arnau A.; de Parga A. L. V.; Chulkov E. V.; Miranda R. Native Point Defects and Their Implications for the Dirac Point Gap at MnBi2Te4(0001). Npj Quantum Mater. 2022, 7 (1), 1–9. 10.1038/s41535-021-00414-6. [DOI] [Google Scholar]
- Shikin A. M.; Estyunin D. A.; Klimovskikh I. I.; Filnov S. O.; Schwier E. F.; Kumar S.; Miyamoto K.; Okuda T.; Kimura A.; Kuroda K.; Yaji K.; Shin S.; Takeda Y.; Saitoh Y.; Aliev Z. S.; Mamedov N. T.; Amiraslanov I. R.; Babanly M. B.; Otrokov M. M.; Eremeev S. V.; Chulkov E. V. Nature of the Dirac Gap Modulation and Surface Magnetic Interaction in Axion Antiferromagnetic Topological Insulator MnBi2Te4. Sci. Rep. 2020, 10 (1), 13226. 10.1038/s41598-020-70089-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma X.-M.; Zhao Y.; Zhang K.; Kumar S.; Lu R.; Li J.; Yao Q.; Shao J.; Hou F.; Wu X.; Zeng M.; Hao Y.-J.; Hao Z.; Wang Y.; Liu X.-R.; Shen H.; Sun H.; Mei J.; Miyamoto K.; Okuda T.; Arita M.; Schwier E. F.; Shimada K.; Deng K.; Liu C.; Lin J.; Zhao Y.; Chen C.; Liu Q.; Liu C. Realization of a Tunable Surface Dirac Gap in Sb-Doped MnBi2Te4. Phys. Rev. B 2021, 103 (12), L121112. 10.1103/PhysRevB.103.L121112. [DOI] [Google Scholar]
- Shikin A. M.; Estyunin D. A.; Zaitsev N. L.; Glazkova D.; Klimovskikh I. I.; Filnov S. O.; Rybkin A. G.; Schwier E. F.; Kumar S.; Kimura A.; Mamedov N.; Aliev Z.; Babanly M. B.; Kokh K.; Tereshchenko O. E.; Otrokov M. M.; Chulkov E. V.; Zvezdin K. A.; Zvezdin A. K. Sample-Dependent Dirac-Point Gap in MnBi2Te4 and Its Response to Applied Surface Charge: A Combined Photoemission and Ab Initio Study. Phys. Rev. B 2021, 104 (11), 115168. 10.1103/PhysRevB.104.115168. [DOI] [Google Scholar]
- Hor Y. S.; Roushan P.; Beidenkopf H.; Seo J.; Qu D.; Checkelsky J. G.; Wray L. A.; Hsieh D.; Xia Y.; Xu S.-Y.; Qian D.; Hasan M. Z.; Ong N. P.; Yazdani A.; Cava R. J. Development of Ferromagnetism in the Doped Topological Insulator Bi2Te3. Phys. Rev. B 2010, 81 (19), 195203. 10.1103/PhysRevB.81.195203. [DOI] [Google Scholar]
- Lee J. S.; Richardella A.; Rench D. W.; Fraleigh R. D.; Flanagan T. C.; Borchers J. A.; Tao J.; Samarth N. Ferromagnetism and Spin-Dependent Transport in n-Type Mn-Doped Bismuth Telluride Thin Films. Phys. Rev. B 2014, 89 (17), 174425. 10.1103/PhysRevB.89.174425. [DOI] [Google Scholar]
- Vobornik I.; Panaccione G.; Fujii J.; Zhu Z.-H.; Offi F.; Salles B. R.; Borgatti F.; Torelli P.; Rueff J. P.; Ceolin D.; Artioli A.; Unnikrishnan M.; Levy G.; Marangolo M.; Eddrief M.; Krizmancic D.; Ji H.; Damascelli A.; van der Laan G.; Egdell R. G.; Cava R. J. Observation of Distinct Bulk and Surface Chemical Environments in a Topological Insulator under Magnetic Doping. J. Phys. Chem. C 2014, 118 (23), 12333–12339. 10.1021/jp502729u. [DOI] [Google Scholar]
- Teng J.; Liu N.; Li Y. Mn-Doped Topological Insulators: A Review. J. Semicond. 2019, 40 (8), 081507. 10.1088/1674-4926/40/8/081507. [DOI] [Google Scholar]
- Chen B.; Wang D.; Jiang Z.; Zhang B.; Cui S.; Guo J.; Xie H.; Zhang Y.; Naveed M.; Du Y.; Wang X.; Zhang H.; Fei F.; Shen D.; Sun Z.; Song F. Coexistence of Ferromagnetism and Topology by Charge Carrier Engineering in the Intrinsic Magnetic Topological Insulator Mn Bi4Te7. Phys. Rev. B 2021, 104 (7), 075134. 10.1103/PhysRevB.104.075134. [DOI] [Google Scholar]
- Sitnicka J.; Park K.; Skupinski P.ł; Grasza K.; Reszka A.; Sobczak K.; Borysiuk J.; Adamus Z.; Tokarczyk M.; Avdonin A.; Fedorchenko I.; Abaloszewa I.; Turczyniak-Surdacka S.; Olszowska N.; Kołodziej J.; Kowalski B. J; Deng H.; Konczykowski M.; Krusin-Elbaum L.; Wołos A. Systemic Consequences of Disorder in Magnetically Self-Organized Topological MnBi2Te4/(Bi2Te3) n Superlattices. 2D Mater. 2022, 9 (1), 015026. 10.1088/2053-1583/ac3cc6. [DOI] [Google Scholar]
- Yan C.; Green E.; Fukumori R.; Protic N.; Lee S. H.; Fernandez-Mulligan S.; Raja R.; Erdakos R.; Mao Z.; Yang S. An Integrated Quantum Material Testbed with Multi-Resolution Photoemission Spectroscopy. Rev. Sci. Instrum. 2021, 92 (11), 113907. 10.1063/5.0072979. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.