Ranking the information content of distance measures

Abstract

Real-world data typically contain a large number of features that are often heterogeneous in nature, relevance, and also units of measure. When assessing the similarity between data points, one can build various distance measures using subsets of these features. Finding a small set of features that still retains sufficient information about the dataset is important for the successful application of many statistical learning approaches. We introduce a statistical test that can assess the relative information retained when using 2 different distance measures, and determine if they are equivalent, independent, or if one is more informative than the other. This ranking can in turn be used to identify the most informative distance measure and, therefore, the most informative set of features, out of a pool of candidates. To illustrate the general applicability of our approach, we show that it reproduces the known importance ranking of policy variables for Covid-19 control, and also identifies compact yet informative descriptors for atomic structures. We further provide initial evidence that the information asymmetry measured by the proposed test can be used to infer relationships of causality between the features of a dataset. The method is general and should be applicable to many branches of science.

Significance Statement.

In real-world data sets many characteristics are often associated with each data point, and one can imagine different ways to define the similarity between 2 samples. For example, in a clinical database 2 patients might be compared based on their age, sex, or height, or on the results of specific clinical exams. In this work, we introduce a method which allows studying the relationship between different distances (or similarity) measures defined on the same dataset. One can find that 2 distances are unrelated, that they bring equal information, or that 1 of the 2 distances allows predicting the other, while the reverse is not true. This allows finding distances, which are maximally informative for a prediction, and detecting causality relationships.

Introduction

An open challenge in machine learning is to extract useful information from a database with relatively few data points, but with a large number of features available for each point (1–3). For example, clinical databases typically include data for a few hundred patients with a similar clinical history, but an enormous amount of information for each patient: the results of clinical exams, imaging data, and a record of part of their genome (4). In cheminformatics and materials science, molecules and materials can be described by a large number of features, but databases are limited in size by the great cost of the calculations or the experiments required to predict quantum properties (5, 6). In short, real-world data are often “big data”, but in the wrong direction: instead of millions of data points, there are often too many features for a few samples. As such, training accurate learning models is challenging, and even more so when using deep neural networks, which typically require a large amount of independent samples (7).

One way to circumvent this problem is to perform preliminary feature selection, and discard features that appear irrelevant or redundant (2,8–10). Alternatively, one can perform a dimensional reduction aimed at finding a representation of the data with few variables built as functions of the original features (11–13).

In some cases, explicit features are not available, as in the case of raw text documents or genome sequences. What one can always define, even in these cases, are distances between data points whose definition, however, can be rather arbitrary (14,15). How can one select, among an enormous amount of possible choices, the most appropriate distance measure for a given task? Finding the correct distance is of course as difficult as performing feature selection or dimensionality reduction. In fact, these tasks can be considered equivalent if explicit features are available, since in this case a particular choice of features naturally gives rise to a different distance function computed through the Euclidean norm.

In this work, we approach feature/distance learning through a novel statistical and information theoretic concept. We pose the question: given 2 distance measures A and B, can we identify whether one is more informative than the other? If distance A is more informative than distance B, even partial information on the distance A can be predictive about B, while the reverse will not necessarily be true. If this happens, and if the 2 distances have the same complexity, e.g. they are built using the same number of features, A should be generally preferred with respect to B in any learning model.

We introduce the concept of “information imbalance”, a measure able to quantify the relative information content of 1 distance measure with respect to another. We show how this tool can be used for feature learning in different branches of science. For example, by optimizing the information content of a distance measure, we are able to select from a set of more than 300 material descriptors, a subset of around 10, which is sufficient to define the state of a material system, and predict its energy. Moreover, we use the information imbalance to verify that the national policy measures implemented to contain the Covid-19 epidemic are informative about the future state of the epidemic. In this case, we also show that the method can be used to detect causality relationship between variables.

The information imbalance

Inspired by the widespread idea of using local neighborhoods to perform dimensional reduction (16) and classification (17), we quantify the relative quality of 2 distance measures by analyzing the ranks of the 1st neighbors of each point. For each pair of points i and j, the rank r_ij of point j relative to point i, is obtained by sorting the pairwise distances between i and rest of the points from smallest to largest. For example, if point j is the 1st neighbor of point i according to the distance d_A. The rank of 2 points will be, in general, different when computed using a different distance measures B, as illustrated in Fig. 1(a).

Fig. 1.

Distance ranks can be used to measure the relative informations contained in 2 distance measures. (a) Illustration of the distance rank of 2 points in different feature spaces A and B. The rank r_ij of point j relative to i is equal to 1 in space A, meaning that j is the 1st neighbor of i. This is not the case in space B, where point j is the 3rd neighbor of point i. (b) Illustration of how ranks can be used to verify that space x is less informative than space y. The figure shows how a distance bound in y automatically implies a distance bound in x. The opposite is not necessarily true: the 1st neighbor of a point in the x space can be very far in y.

The key idea of our approach is that distance ranks can be used to identify whether 1 metric is more informative than the other. Take the example given in Fig. 1(b), depicting a schematic representation of a noisy curved dataset. In this dataset, the distance along the y-axis is clearly more informative than the one along the x-axis since one could construct a function able to predict x from the knowledge of y, but not the opposite. This asymmetry is well-captured by the ranks between points. Take for example point i (red circle in the figure). Its 1st neighbor according to the y-distance is j (blue circle), while according to the x-distance (green lines) j is the 7th neighbor of i. Conversely, the nearest neighbor of i according to the x-distance is k (green circle), which is the 35th neighbor of i according to the y-distance (blue lines). We, hence find that 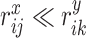, i.e. the rank in space x of the 1st neighbor measured in space y is much smaller than the rank in space y of 1st neighbor measured in space x.

To give a more quantitative example, let us consider a dataset of points harvested from a 3D Gaussian whose standard deviation along the z direction is a tenth of those along x and y. In this case, one can define a Euclidean distance between data points either using all the 3 features, 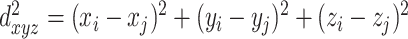, or using a subset of these features ( d_xy, d_yz, and so on).

Intuitively, d_xyz and d_xy are almost equivalent since the standard deviation along z is small, while there are information imbalances, say, between d_x and d_xy, which would allow saying that d_xy is more informative than d_x. In the first row of Fig. 2, we plot the ranks computed using 1 distance against the ranks computed using a second distance (for example the ranks in d_xy as a function of those in d_xyz for panel a). In the second row of the figure, we show the probability distribution p(r^A∣r^B = 1) of the ranks in space A restricted to those pairs (i, j) for which , namely to the nearest neighbors according to distance B. In panels (a) and (b), we compare the most informative distance containing all 3 coordinates to the one containing only the x and y coordinates. Given the small variance along the z direction, these 2 distance measures are practically equivalent, and this results in rank distributions strongly peaked around 1. In panels c and d, we compare the 2 metrics d_xy and d_x. In this case, the former is clearly more informative than the latter, and we find that the distribution of ranks when passing from d_xy to d_x is more peaked around small values than when going in the opposite direction. Finally, for 2 metrics built using independent coordinates (x and y, in panels c and f) the rank distributions are completely uniform.

Fig. 2.

Classifying and visualizing the relationship between any 2 distance measures using the information imbalance. (a), (c), and (e) scatter plots of the ranks between ordered pairs of points for different distance measures evaluated on a 3D Gaussian dataset with a small variance along z. The red and blue bands indicate, respectively, the points for which the rank on the x- and y-axis is equal to 1 (proportions were exaggerated for clarity). The histogram of the points inside each band is plotted in the bottom plots using the same color. (b), (d), and (f) probability of that 2 nearest neighbor points (r = 1) for 1 distance have rank r for the other distance. The 3 columns represent different pairs of representations. (g) The 4 different types of relationships that can characterize the relative information content of 2 spaces A and B. (h) Information imbalance plane for the discussed 3D Gaussian dataset with small z-axis variance (gray markers), and for a 4D isotropic Gaussian dataset (black star). The different colors (light blue, red, green, and orange) roughly mark the regions corresponding to the 4 types of relationships listed in panel (g).

We, hence propose to assess the relationship between any 2 distance measures d_A and d_B by using the properties of the conditional rank distribution p(r^B∣r^A = 1). The closer this distribution is to a delta function peaked at 1, the more information about space B is contained within space A.

This intuition can be made more rigorous through the statistical theory of copula variables. We can define a copula variable c_A as the cumulative distribution , where p_A(w∣x) is the of probability of sampling a data point within distance w from x in the A space. The value of c_A can be estimated from a finite dataset by counting the fraction of points that fall within distance d_A of point x, c_A ≈ r_A/N. Copula variables and distance ranks can be considered continuous-discrete analogues of each other. As a consequence, the distributions p(r^B∣r^A = 1) shown in Fig. 2 are nothing else but estimates of the copula distributions p(c_B∣c_A) with c_A conditioned to be very small. This is important, since Sklar’s theorem guarantees that the copula distribution p(c_A, c_B) contains the entire correlation structure of the metric spaces A and B, independently of any details of the marginal distributions p(d_A∣x) and p(d_B∣x) (18–20).

Using the copula variables, we define the “information imbalance” from space A to space B as

(1)

where we used the conditional expectation to characterize the deviation of p(c_B∣c_A = ϵ) from a delta function. In the limit cases where the 2 spaces are equivalent or completely independent, we have that 〈c_B∣c_A = ϵ 〉 = ϵ and 〈c_B∣c_A = ϵ 〉 = 1/2, respectively, so that the definition provided in Eq. (1) statistically confines Δ in the range (0,1). The information imbalance defined in Eq. (1) is estimated on a dataset with N data points as

(2)

We remark that the conditional expectation used in Eq. (1) is only one of the possible quantities that can be used to characterize the deviation of the conditional copula distribution from a delta function. Another attractive option is the entropy of the distribution. In S1.C (Supplementary Material), we show how these 2 quantities are related and we demonstrate that the specific choice does not substantially affect the results. In S1.B and Figure S1 (Supplementary Material), we also show how copula variables can be used to connect the information imbalance to the standard information theoretic concept of mutual information.

By measuring the information imbalances Δ(A → B) and Δ(B → A), we can identify 4 classes of relationships between the 2 spaces A and B. We can find whether A and B are equivalent or independent, whether they symmetrically share both independent and equivalent information, or whether one space contains the information of the other. These relationships are presented in Fig. 2(g). These relationships can be identified visually by plotting the 2 imbalances Δ(A → B) and Δ(B → A) against each other in a graph as done in Fig. 2(h). We will refer to this kind of graphs as information imbalance planes. In Fig. 2(h), we present the information imbalance plane of the 3D Gaussian dataset discussed so far, and used for Fig. 2(a)–(f). Looking at this figure, one can immediately verify that the small variance along the z axis makes the 2 spaces xyz and xy practically equivalent (gray circle). Similarly, one can verify that space x is correctly identified to be contained in xyz (gray square) and that the 2 spaces x and y are classified as orthogonal (gray triangle). The figure also includes a point corresponding to a different dataset sampled from a 4D isotropic Gaussian with dimensions 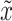, , , 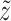and . 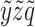This point (black star) shows that the spaces and are correctly identified as sharing symmetric information. Importantly, the information imbalance only depends on the local neighborhood of each point and, for this reason, it is naturally suited to analyze data manifolds, which are arbitrarily nonlinear. In S2.A and Figure S2 (Supplementary Material), we show that our approach is able to correctly identify the best feature for describing a spiral of points wrapping around 1 axis, and a sinusoidal function. More numerical tests are available online at (21) along with the corresponding code. In the examples discussed so far, we have chosen the Euclidean metric as distance measure for any subset of coordinates considered. We will make the same choice throughout the rest of this work.

Influence of national policy measures on the Covid-19 epidemic

We now use the information imbalance to analyze the “Covid-19 Data Hub”, a dataset which provides comprehensive and up to date information on the Covid-19 epidemic (22), including epidemiological indicators such as the number of confirmed infections and the number of Covid-19 related deaths for nations where this is available, as well as the policy indicators that quantify the severity of the governmental measures such as school and workplace closing, restrictions on gatherings and movements of people, testing, and contact tracing (23). More details on the dataset are available in S2.B.1 (Supplementary Material).

We first illustrate how the information imbalance can be used to recover the arrow of time from time series data. In Fig. 3(a), we show the information imbalance between the space [T_t, C_t], containing the number of tests T_t and the number of confirmed cases C_t in a given week t, and the space of the number of deaths occurring in week t + δt (D_{t + δt}). The imbalance is shown as a function of δt. All the points lay above the diagonal, indicating that, in the language of Fig. 2(h), the number of deaths is marginally contained in the 2 variables [T_t, C_t] if δ_t is small; and the optimal information imbalance occurs at δt = 1. Importantly, for each pair of opposite time lags (δt, −δt) we find that the 2 variables [T_t, C_t] always contain more information on future deaths than on past deaths. In this scenario, this result represents an obvious verification of the known arrow of time of the dataset, but it suggests that further dedicated investigations could bring to the development of accurate tests to detect nontrivial causality relationships (24).

Fig. 3.

The information imbalance allows for a straightforward verification of the impact of national policy measures on the Covid-19 epidemic. (a) Information imbalance between the space [T_t, C_t] of the number of tests and number of confirmed cases C_t in a given week t, and the number of deaths D_{t + δt} occurred in week t + δt. The time shift δt ranges from −5 (5 weeks before) to +5 (5 weeks after). (b) Minimum information imbalances from growing sets of policy variables P_t to the state of the epidemic after 2 weeks E_{t + 2}. (c) The corresponding information imbalance plane with the number of policy variables going from 1 to 10 reported in the gray circles. Point 10 is not visible as it lies below point 9. The figure shows that the policy measures space P_t can predict the state of the epidemic E_{t + 2}, while E_{t + 2} cannot predict P_t.

We now analyze the relationship between the space of policy measures P_t at week t, and the state of the epidemic E_{t + δt}, with δt = 2 (namely after 2 weeks). In S2.B.2 and Figure S3 (Supplementary Material), we show that the analysis with time lags of one or 3 weeks bring to similar results. While we consider several different choices for the policy space, the epidemic state is defined by the number of weekly deaths D_t and the ratio R_t = C_t/T_t of confirmed cases C_t over total number of tests performed T_t per week. We estimate the information imbalance Δ(P_t → E_{t + δt}) between the spaces defined by all the possible combination of policy measures P_t and the space of epidemiological variables E_{t + δt}. A low value of Δ(P_t → E_{t + δt}) means that P_t can predict E_{t + δt}. In Fig. 3(b), we present the minimum information imbalance Δ(P_t → E_{t + δt}) achievable with any set of d policy measures.

For d ≤ 2, Δ(P_t → E_{t + δt}) is close to 1, indicating that no single or couple of policy measure is significantly predictive about the state of the epidemic, consistently with (25). When 3 or more policy measures are considered, the information imbalance decreases rapidly reaching a value of about 0.28 when almost all policy measures are considered. This sharp decrease and the low value of the information imbalance clearly indicate that policy measures do contain information on the future state of the epidemic, and the more policy measures are considered, the more the future state of the epidemic can be considered as contained in the space of the policies. As a sanity check, a dummy policy variable was introduced for this test (blue hexagon). This variable is never selected by the algorithm, and its addition deteriorates the information content of the policy space.

The described analysis verifies that policy interventions have been effective in containing the spreading of the Covid-19 epidemic, a result which has been shown in a number of studies (25–28). In accordance with these studies, we also find that multiple measures are necessary to effectively contain the epidemic, with no single policy being sufficient on its own (29), and that the impact of policy measures increases monotonically with the number of measures put in place. We find that a small yet effective set of policy measures has been the combination of testing, stay home restrictions, and restrictions on international movement and gatherings. While our results are computed as averages over all nations considered, further analysis carried out in S2.B.3 and Figure S5 (Supplementary Material) on disjointed subsets of nations give results which are consistent with our main findings.

We finally note that the information imbalance Δ(E_{t + 2} → P_t) (shown in Fig. 3c) remains considerably high for any number of policy variables. This indicates that the state of the epidemic is not informative about past policy measures. Surprisingly, the state of the epidemic is not informative even on future policy measures (see S2.B.2 and Figure S4, Supplementary Material), a result which seems to indicate that that different nations have reacted to the epidemic through widely different strategies.

The information imbalance can also be used to optimally choose the relative scale of heterogeneous variables. For instance, in S2.B.4 and Figure S6 (Supplementary Material), we use the information imbalance to select the relative scale of heterogeneous epidemiological variables such as the total number of tests and the ratio of confirmed cases over total number of tests. This is important in real-world applications, where features are often characterized by different units of measure and different scales of variations.

Selection and compression of descriptors in materials physics

We now show that the information imbalance criterion can be used to assess the information content of commonly used numerical descriptors of the geometric arrangement of atoms in materials and molecules, as well as to compress the dimension (number of features) of a given descriptor with minimal loss of information. Such atomistic descriptors are needed for applying any statistical learning algorithm to problems in physics and chemistry (30–34), and the problem of choosing optimally informative atomic descriptors has recently attracted attention (35). We first consider a database consisting of an atomic trajectory of amorphous silicon generated from a molecular dynamics simulation at 500 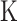(see S2.C.1 (Supplementary Material) for details). At each time step of this trajectory, we select a single local environment by including all the neighboring atoms within the cutoff radius of 4.5 Å; from a given central atom. In this simple system, which does not undergo any significant atomic rearrangement, one can define a fully informative distance measure as the minimum over all rigid rotations of the root mean square deviation (rmsd) of 2 local environments (details in S2.C.2 (Supplementary Material)).

In Fig. 4(a), this ground truth distance measure is compared with some of the descriptors most commonly used for materials modeling: the “Atom-centered Symmetry Functions” (ACSF) (36, 37), the “Smooth Overlap of Atomic Positions” (SOAP) (38, 39), and the 2- and 3-body kernels (40, 41). Unsurprisingly, all descriptors are contained in the ground truth distance measure. For ACSF and SOAP representations, one can increase the resolution by increasing the size of the descriptor in a systematic way, and we found that doing this allows both representations to converge to the ground truth.

Fig. 4.

The information imbalance can be used to perform an effective information-driven feature selection in materials systems. (a) Information imbalances between ground truth “rmsd” distance metric and standard atomistic descriptors. (b) Information imbalances between a full description and the most informative d-plet of components (d = 1, …, 4). (c) Convergence of the “symmetric” information imbalance with the number of components for 3 different compression strategies. The symmetric information imbalance is defined as ; more details can be found in S2.C.3 (Supplementary Material). (d) Force error on a validation set of a machine learning potential energy model built on the compressed descriptors.

A materials descriptor typically involves a few hundred components. Following a procedure similar to the one used in the last section to select policy measures, we use the information imbalance to efficiently compress these high-dimensional vectors with minimal loss of information (more details are given in S2.C.3 (Supplementary Material)). We perform this compression for a database consisting of complex geometric arrangements of carbon atoms (42). As illustrated in Fig. 4(b) and (c), the selection leads to a rapid decrease of the information imbalance, and converge much more quickly than other strategies such as random selection (blue squares) and standard sequential selection (green triangles). Figure 4(d) depicts the test error of a potential energy model constructed using a state-of-the-art Gaussian process regression model (43) (see S2.C.5 (Supplementary Material)) on the compressed descriptors, as a function of the size of the descriptors and for the different compression strategies considered. Remarkably, the graph shows that a very accurate model can be obtained using only 16 out of the 324 original components of the descriptor considered (39). Figures 4(c) and (d) show that when the information imbalance has converged, the validation error does not diminish further. This suggests that one can select the optimal descriptor dimension as the one for which no improvement in the information imbalance is observed. In S2.C.6 and Figure S8 (Supplementary Material), we show how a similar criterion can be also used to select the hyperparameters of materials descriptors, and we demonstrate how the order of the components selected by our procedure can be understood considering the fundamental structure of the descriptor. In S2.C.7 and Figure S7 (Supplementary Material), we show that, for this prediction task, the feature selection scheme based on the information imbalance is marginally more efficient than other well known compression schemes for materials descriptors.

Conclusions

In this work, we introduce the information imbalance, a new method to assess the relative information content between 2 distance measures. The key property which makes the information imbalance useful is its asymmetry: it is different when computed using a distance A as a reference and a distance B as a target, and when the 2 distances are swapped. This allows distinguishing 3 classes of similarity between 2 distance measures: a full equivalence, a partial but symmetric equivalence, and an asymmetric equivalence, in which 1 of the 2 distances is observed to contain the information of the other.

The potential applications of the information imbalance criterion are multifaceted. The most important one is probably the long-standing and crucial problem of feature selection (11–13). Low-dimensional models typically allow for more robust predictions in supervised learning tasks (2, 8). Moreover, they are generally easier to interpret and can be used for direct data visualization if sufficiently low dimensional. We design feature selection algorithm by selecting the subset of features which minimizes the information imbalance with respect to a target property, or to the original feature space.

As we have showcased, such algorithms can be “exact” if the distances to be compared are relatively few (as done for the Covid-19 database) or approximate, if one has to compare a very large number of distances (as done for the atomistic database). Such algorithms work well even when in the presence of strong nonlinearities and correlations within the feature space. This is exemplified by the analysis of the Covid-19 dataset, where 4 policy measures which appear similarly irrelevant when taken singularly, were instead identified as maximally informative when taken together with regards to the future state of the epidemic.

Other applications include dimensionality reduction schemes that directly use the information imbalance as an objective function. Admittedly, such function will in general be nondifferentiable and highly nonlinear, but efficient optimization algorithms could still be developed by exploiting recent results on the computation of approximate derivatives for sorting and ranking operations (44).

Another potentially fruitful line of research would be exploiting the information imbalance to optimize the performance of deep neural networks. For example, in S2.C.8 and Figure S9 (Supplementary Material), we show that one can reduce the size of the input layer of a neural network that predicts the energy of a material, yielding more computationally efficient and robust predictions. However, one can imagine to go much further, and compare distance measures built using the representations in different hidden layers, or in different architectures. This could allow for designing maximally informative and maximally compact neural network architectures. We finally envision potential applications of the proposed method in the study of causal relationships: we have seen that in the Covid-19 database the use of information imbalance makes it possible to distinguish the future from the past, as the former contains information about the latter, but not vice versa. We believe that this empirical observation can be made robust by dedicated theoretical investigations, and used in practical applications in other branches of science.

Notes

Competing Interest: The authors declare no competing interest. The views and opinions expressed in this paper are those of the authors and do not necessarily reflect the official policy or position of Banca d’Italia.

Funding

This work is supported in part by funds from the European Union’s Horizon 2020 research and innovation program (grant number 824143, MaX ’Materials design at the eXascale’ Centre of Excellence).

Authors' Contributions

A.G., G.C., B.C. and A.L. designed the research; A.G. performed the research; C.Z. and A.L. contributed to perform the research; and A.G., C.Z., B.C., G.C., and A.L. wrote the paper.

Preprints

A preprint of this article is published at https://doi.org/10.48550/arXiv.2104.15079.

Data availability

Details on the datasets used are available in the supplementary material.