SUMMARY
Single-cell RNA sequencing (scRNA-seq) quantifies gene expression for individual cells in a sample, which allows distinct cell-type populations to be identified and characterized. An important step in many scRNA-seq analysis pipelines is the annotation of cells into known cell types. While this can be achieved using experimental techniques, such as fluorescence-activated cell sorting, these approaches are impractical for large numbers of cells. This motivates the development of data-driven cell-type annotation methods. We find limitations with current approaches due to the reliance on known marker genes or from overfitting because of systematic differences, or batch effects, between studies. Here, we present a statistical approach that leverages public data sets to combine information across thousands of genes, uses a latent variable model to define cell-type-specific barcodes and account for batch effect variation, and probabilistically annotates cell-type identity from a reference of known cell types. The barcoding approach also provides a new way to discover marker genes. Using a range of data sets, including those generated to represent imperfect real-world reference data, we demonstrate that our approach substantially outperforms current reference-based methods, particularly when predicting across studies.
Keywords: Single-cell RNA-seq
1. Introduction
Single-cell RNA sequencing (scRNA-seq) quantifies gene expression at the level of individual cells, rather than measuring the aggregated gene expression in a biological sample containing millions of cells, as is done with bulk RNA-sequencing. This improved granularity permits the identification or discovery of distinct populations of cell types within the tissues under study. To effectively accomplish this, it is important to annotate cells reliably by known cell types, especially cells that are present in many tissues, such as immune system cells. Fluorescence-activated cell sorting (FACS) can be used prior to the sequencing step to physically sort cells from a mixed sample into their cell-type populations. While generally regarded as highly accurate, FACS-sorting has limited throughput and thus is impractical when sequencing large numbers of cells. As a result, there is a need for data-driven approaches to annotate cell types.
Current methods fall into one of two categories, which we will refer to as clustering-based and reference-based. In clustering-based methods, the more widely used approach, the target cells are first grouped using an unsupervised clustering algorithm (e.g., Kiselev and others, 2017; Lin and others, 2017; Ntranos and others, 2016; Stuart and others, 2018). Next, differential expression analysis is used to identify genes that are uniquely expressed in each group and compared to known cell-type-specific marker genes to annotate the group as a particular cell type.
Reference-based methods (e.g., Zhang and others, 2019; Pliner and others, 2019; Lieberman and others, 2018; Kiselev and others, 2018; de Kanter and others, 2019) use supervised learning approaches in which the target cells are compared to reliably annotated, such as by FACS-sorting, reference data for each cell-type of interest, and each target cell is annotated using the closest match. Approaches to defining the closest match vary. Many of these supervised methods are based on complex and hard-to-troubleshoot machine learning algorithms, such as XGBoost (Lieberman and others, 2018) and deep neural networks (Lopez and others, 2018). As a result, unexpected systematic differences between training and test sets may lead to overfitting. In addition, some of the most popular methods rely on marker genes to guide the determination of the closest match (Pliner and others, 2019; Zhang and others, 2019). However, reliable marker genes are not always known for every cell type of interest.
In this work, to avoid reliance on marker genes and minimize overfitting, we consider all genes as potentially informative and develop a latent variable model that characterizes cell types by the probabilities of genes being in expressed or not-expressed states, a probabilistic barcode. Other sources of within-state variabilities, such as that introduced by batch effects, are accounted for within our multilayer model. Exploratory data analysis, described in Section 4, demonstrates the need for these to be gene-specific distributions. We therefore implement a two-stage procedure: first, we estimate gene-specific parameters using a fixed public database, and second, we estimate cell-type-specific probabilities, the barcodes, for each cell type using training data. To classify cells into known cell types, we fit this model and use the resulting fit to compute posterior probabilities.
We start by describing the data sets used to build and assess our method, then provide a detailed description of our approach, and, finally, demonstrate its advantages over existing approaches. We chose existing methods to compare our approach to based on previously described results and popularity, with the goal of representing the full range of current approaches.
2. Data description
2.1. PanglaoDB database
To motivate and fit gene-specific distributions across tissues and cell types, we used the PanglaoDB database (Franzén and others, 2019), which provides publicly available scRNA-seq data from a diverse set of experiments. We considered only the data sets corresponding to nontumor samples from humans. This yielded 218 data sets comprising a total of 3, 389, 679 cells, with each data set representing one cell type or tissue type.
2.2. Assessment data
To benchmark our approach against existing methods, we constructed four assessment data sets. We selected data sets for which we were highly confident of the accuracy of assigned cell-type labels. In most cases, we chose to use data sets with experimentally (rather than computationally) derived labels, such as from FACS or MACS sorting. When not possible, we used subsets of data sets that contained well-established cell-type labels, as opposed to novel, rare, or otherwise poorly studied cell types, that were supported via additional analyses in the original study, such as leveraging spatial information. Note that our requirements made the construction of the assessment data sets challenging as annotations for most public data sets are computationally derived.
We considered four assessment data sets, which we refer to as the PBMC data set, the Colon data set, the Brain data set, and the Lung data set. For each of these data sets, we constructed a main data set from one or more published studies. This data set was split into a training set and a test set. For each main data set, a second test set was formed using data from a separate study not included in the main data set. We refer to the two test sets as the withheld and external test sets, respectively. Note that overtraining due to study-specific biases and batch effects will result in better performance in the withheld test set compared to the external test set. We also created three additional versions of the training set by altering the training set to mimic three scenarios commonly faced in practice. In the first additional version, we sampled 50 cells from each cell type to form a smaller training set. In the second version, we downsampled the counts to produce a training set with different coverage than the test set. Finally, in the third version, we introduced incorrect labels into the training set to mimic a situation with imperfect annotations. Details are in Note S1 of the Supplementary material available at Biostatistics online. Note that all results shown in the main text use the unaltered original training set.
3. Motivation
3.1. Clustering-based approaches identify more clusters with data set size
We used the Lung data set to investigate the relationship between the number of clusters and the data set size. In particular, we applied the Louvain clustering algorithm (Que and others, 2015), as implemented in version 3 of the Seurat package (Stuart and others, 2018), to successively subsetted versions of the Lung data set, ranging from a total of 100 cells to a total of 15, 000 cells in increments of 500 cells. We applied this clustering algorithm with three different resolution parameters (0.4, 0.8, and 1.2), where larger values are likely to lead to larger numbers of clusters. Although the cells are randomly sampled each time, and therefore, we expect approximately the same number of cell types to be represented in each subset, the number of clusters found ranges from 2 to 27, with a general increasing trend with data set size (Figure 1). This pattern persisted across all three resolution parameters tested. Moreover, the number of clusters found at each data set size differed with the resolution parameter, which shows that results can be highly sensitive to this value.
Figure 1.
Applying two popular clustering algorithms to successive subsets randomly sampled from the Lung reference data set identifies more clusters with increasing data set size. The number of clusters identified by Seurat at three different resolutions (0.4, 0.8, and 1.2) as well as SC3 is plotted against the number of cells included in the analysis on the log scale.
To ensure that this finding is not specific only to the Louvain algorithm and/or to the Seurat implementation, we also applied another popular clustering algorithm, SC3 (Kiselev and others, 2017), to the same data set using default parameters and the SC3’s built-in approach to determining the number of clusters. The number of clusters found ranged from 5 to 59, again with an increasing trend with data set size. It is notable as well that more clusters were found at each subset size than with Seurat (Figure 1).
3.2. Marker genes can be unreliable due to sparsity
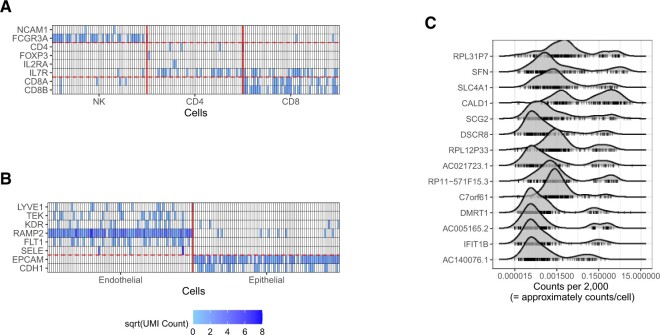
Clustering-based methods, as well as some reference-based methods, rely on marker genes. We therefore examined the reliability of such marker genes for labeling in scRNA-seq data. To do so, we used subsets of the reference PBMC data set and the reference Lung data set as examples and looked at the counts for marker genes for each cell type. We then selected the marker genes used in the publicly available Garnett classifiers (Pliner and others, 2019), which are popular, prebuilt cell-type classifiers based on marker genes, for PBMCs and lung as examples of markers that are likely to be used in practice. Specifically, in the PBMC data, we used the marker genes NCAM1 and FCGR3A for NK cells; CD4, FOXP3, IL2RA, and IL7R for CD4 cells; and CD8A and CD8B for CD8 cells. In the lung data, we used LYVE1, TEK, KDR, RAMP2, FLT1, and SELE for endothelial cells. We additionally used EPCAM and CDH1 for epithelial cells. Although epithelial markers were not provided by Garnett, these two genes have been validated as markers for lung epithelial cells (Xu and others, 2016).
If we examine the expression of these markers in random subsets of these cell types (Figures 2(A) and (B)), some markers appear to consistently have nonzero expression in the appropriate cell type, whereas others are much more unreliable. For example, RAMP2 and EPCAM have nonzero counts in almost every endothelial and epithelial cell respectively, and nearly all zero counts in the other cell type. Other markers, however, are more sparsely expressed, such as FCGR3A in NK cells and CD8A and CD8B in CD8 cells, and still others have nonzero counts in only very few cells, such as the gene CD4 in CD4 cells or SELE in endothelial cells. This is consistent with the fact that scRNAseq is sparse in a way that even genes known to be expressed can have majority nonzero counts.
Figure 2.
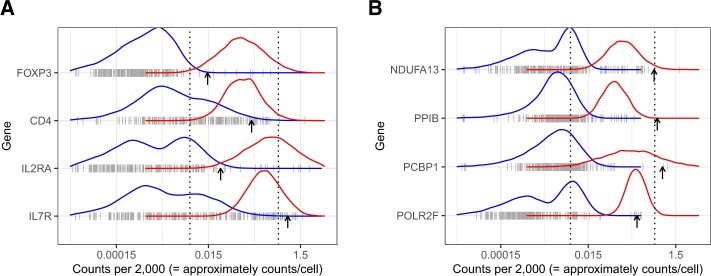
(A) Markers in NK, CD4, and CD8 cells from blood show that some are unlikely to be observed. (B) Markers in endothelial and epithelial cells from lung. (C) Example of density plots of genes with bimodal expression distributions across cell and tissue types. Every tick mark represents the rate of that gene in a particular cell type or tissue type. The centers of the on and off distributions can be seen to vary by gene.
4. Methods
4.1. Model-based probabilistic classifications provide substantial improvements
Given the limitations of clustering-based approaches, we considered reference-based approaches instead. We denote the unknown cell type for cell 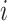 as
as 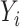 and the observed gene counts as
and the observed gene counts as 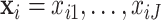 with
with 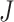 the total number of genes. For each cell
the total number of genes. For each cell 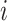 , our approach is to estimate the conditional probability
, our approach is to estimate the conditional probability 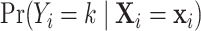 using Bayes rule and then select the cell type
using Bayes rule and then select the cell type 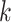 that maximizes it. While several statistical learning approaches are available to estimate this conditional probability, this is a particularly challenging problem because of the large number of genes, the sparsity of the data as demonstrated in Section 3.2, and systematic biases due to batch effects that make gene counts difficult to compare across studies (Cable and others, 2020). Here, we developed an approach that tackles these challenges by (i) using a conditional Poisson model to account for the sparsity and differences in coverage, (ii) introducing a parsimonious parametric model that assumes counts are independent across genes once we condition on cell type, and (iii) providing robustness to batch effects by assuming a latent state model for each gene that models within-state variability in a way that downweights its influence on prediction.
that maximizes it. While several statistical learning approaches are available to estimate this conditional probability, this is a particularly challenging problem because of the large number of genes, the sparsity of the data as demonstrated in Section 3.2, and systematic biases due to batch effects that make gene counts difficult to compare across studies (Cable and others, 2020). Here, we developed an approach that tackles these challenges by (i) using a conditional Poisson model to account for the sparsity and differences in coverage, (ii) introducing a parsimonious parametric model that assumes counts are independent across genes once we condition on cell type, and (iii) providing robustness to batch effects by assuming a latent state model for each gene that models within-state variability in a way that downweights its influence on prediction.
We start by using the Bayes rule to rewrite the posterior probability as:
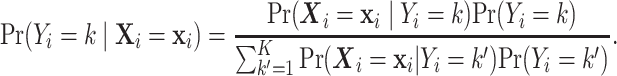 |
(4.1) |
We then assumed that each of the 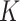 possible cell types is equally likely:
possible cell types is equally likely: 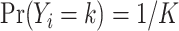 . To make the model parsimonious, we assumed that, conditional on the cell type, the
. To make the model parsimonious, we assumed that, conditional on the cell type, the 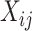 are independent across genes
are independent across genes 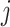 :
:
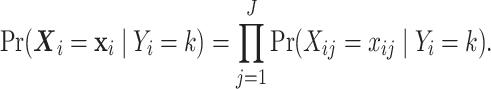 |
(4.2) |
To account for sparsity, we assumed that for any cell type 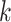 ,
, 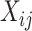 can be modeled as
can be modeled as
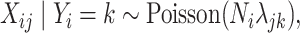 |
(4.3) |
with 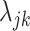 proportional to the expected gene expression for gene
proportional to the expected gene expression for gene 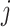 in cell type
in cell type 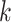 and
and 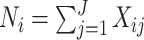 the total observed counts across all genes in cell
the total observed counts across all genes in cell 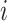 . A challenge is that estimating
. A challenge is that estimating 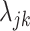 from data in the training set suffers from the limitations listed above: (i) we may have few cells available for estimation, (ii) data can be sparse, and (iii) batch effects result in systematic biased estimates that lead to unsuitable across-study performance. We developed an approach that tackled these limitations by (i) assuming that the biological information is represented by expressed (on) and not-expressed (off) latent states and (ii) accounting for other sources of variability with a random variable
from data in the training set suffers from the limitations listed above: (i) we may have few cells available for estimation, (ii) data can be sparse, and (iii) batch effects result in systematic biased estimates that lead to unsuitable across-study performance. We developed an approach that tackled these limitations by (i) assuming that the biological information is represented by expressed (on) and not-expressed (off) latent states and (ii) accounting for other sources of variability with a random variable 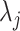 that follows a parametric distribution and assuming the
that follows a parametric distribution and assuming the 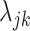 are realizations of this random variable. Next, we describe how we developed this parametric model.
are realizations of this random variable. Next, we describe how we developed this parametric model.
4.1.1. Count distributions are bimodal and gene-specific
To determine a parametric form for the gene-specific distributions of 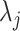 , we leveraged the fact that the PanglaoDB database offers large numbers of cells for each cell type
, we leveraged the fact that the PanglaoDB database offers large numbers of cells for each cell type 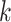 , defined estimates
, defined estimates
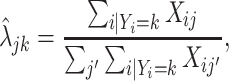 |
(4.4) |
and used exploratory data analysis. Specifically, we used 3, 389, 679 cells from 218 cell types and tissues from the PanglaoDB database to obtain precise estimates of the rates 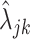 for
for 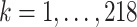 . We found that many genes showed a clear bimodal distribution for these rates when examined across cell types, consistent with our latent state model assumptions of off and on gene expression (Figure 2(C)). Furthermore, we noted that the centers of these off and on distributions vary by gene, consistent with results previously observed using gene expression data from the Gene Expression Omnibus and Array Express (McCall and others, 2010). This implies that observed gene count rates are not comparable across genes. For example, note that some values associated with the off distribution for RPL31P7 could be categorized as on for genes such as AC140076.1 (Figure 2(C)).
. We found that many genes showed a clear bimodal distribution for these rates when examined across cell types, consistent with our latent state model assumptions of off and on gene expression (Figure 2(C)). Furthermore, we noted that the centers of these off and on distributions vary by gene, consistent with results previously observed using gene expression data from the Gene Expression Omnibus and Array Express (McCall and others, 2010). This implies that observed gene count rates are not comparable across genes. For example, note that some values associated with the off distribution for RPL31P7 could be categorized as on for genes such as AC140076.1 (Figure 2(C)).
Further data exploration (Figure S1 of the Supplementary material available at Biostatistics online) led us to assume the off distribution was best modeled by a mixture of exponential and log-normal distributions, with the exponential accounting for counts that were mostly zeros, consistent with practically no expression, and the log-normal component accounting for low counts consistent with a nonzero background level of expression distinctly lower than the expressed state (Figure S2 of the Supplementary material available at Biostatistics online).
We therefore further divided the off state into two. We represented the latent structure by introducing the unobserved variable 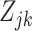 that can be one of three states, off-null, off-low, or on, for each gene
that can be one of three states, off-null, off-low, or on, for each gene 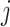 in each cell type
in each cell type 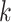 . For simplicity of exposition, we will refer to the off-low state as simply off. Note that if the
. For simplicity of exposition, we will refer to the off-low state as simply off. Note that if the 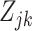 s were observed, the vector
s were observed, the vector 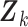 can be considered a gene expression barcode that uniquely identifies cell type
can be considered a gene expression barcode that uniquely identifies cell type 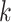 . The main challenge of our approach is estimating these
. The main challenge of our approach is estimating these 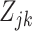 in a computationally efficient manner. We connect the unobserved
in a computationally efficient manner. We connect the unobserved 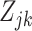 s to the observed
s to the observed 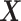 by modeling the distribution of
by modeling the distribution of 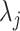 as
as
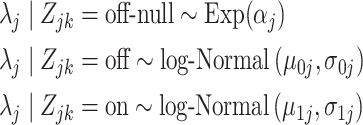 |
(4.5) |
based on our data exploration. Here, 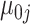 and
and 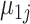 represent gene-specific means of the off and on distribution, respectively. The gene-specific standard deviations
represent gene-specific means of the off and on distribution, respectively. The gene-specific standard deviations 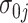 and
and 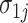 quantify the variability that accounts for the fact that we observe different rates for tissues within the same latent state. This includes variability introduced by batch effects.
quantify the variability that accounts for the fact that we observe different rates for tissues within the same latent state. This includes variability introduced by batch effects.
4.2. Estimating gene-specific parameters
Our approach to estimating this model is to first estimate the gene-specific parameters 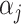 ,
, 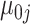 ,
, 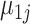 ,
, 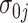 , and
, and 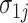 in model (4.5) using the PanglaoDB database (Figure S3 of the Supplementary material available at Biostatistics online). Because some genes had few tissues in the on state, and some genes, the housekeeping genes for example, had few tissues in the off state, to improve power, we borrowed strength across genes by imposing a prior distribution. Data exploration implied that gene-specific on and off means were correlated across genes, so we used a bivariate normal distribution with correlation
in model (4.5) using the PanglaoDB database (Figure S3 of the Supplementary material available at Biostatistics online). Because some genes had few tissues in the on state, and some genes, the housekeeping genes for example, had few tissues in the off state, to improve power, we borrowed strength across genes by imposing a prior distribution. Data exploration implied that gene-specific on and off means were correlated across genes, so we used a bivariate normal distribution with correlation 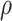 :
:
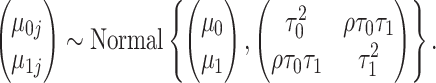 |
(4.6) |
Here, 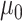 and
and 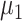 represent the overall expected log-rate for genes that are off and on, respectively, and
represent the overall expected log-rate for genes that are off and on, respectively, and 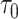 and
and 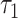 quantify the variability in the gene-specific shifts.
quantify the variability in the gene-specific shifts.
In the next step, we used the 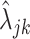 defined in (4.4) to estimate the parameters that define (4.5). We noted that the marginal distribution of the random variable
defined in (4.4) to estimate the parameters that define (4.5). We noted that the marginal distribution of the random variable 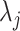 can be written as
can be written as
 |
(4.7) |
with 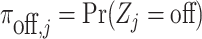 ,
, 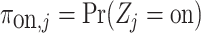 and the same parameters as those that defined the distributions in (4.5).
and the same parameters as those that defined the distributions in (4.5).
We selected prior parameters 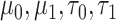 , and
, and 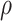 using an empirical approach. Specifically, we considered housekeeping genes (Eisenberg and Levanon, 2013), for which the microarray-based gene expression barcode (McCall and others, 2010) estimated nonzero probabilities of being on across all healthy tissues. We then took the mean of the log-rates
using an empirical approach. Specifically, we considered housekeeping genes (Eisenberg and Levanon, 2013), for which the microarray-based gene expression barcode (McCall and others, 2010) estimated nonzero probabilities of being on across all healthy tissues. We then took the mean of the log-rates 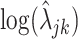 , as defined by (4.4), for these genes in the PanglaoDB database as
, as defined by (4.4), for these genes in the PanglaoDB database as 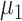 , and the sample standard deviation as
, and the sample standard deviation as 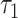 . We next took all genes for which the microarray-based gene expression barcode estimated zero probabilities of being on across all healthy tissues and used the Expectation–Maximization (EM) algorithm to fit a mixture of the off components, namely an exponential and a log-normal distribution, to all the rates
. We next took all genes for which the microarray-based gene expression barcode estimated zero probabilities of being on across all healthy tissues and used the Expectation–Maximization (EM) algorithm to fit a mixture of the off components, namely an exponential and a log-normal distribution, to all the rates 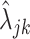 of this subset of genes in the PanglaoDB database. We used the mean of the log rates for genes with 95
of this subset of genes in the PanglaoDB database. We used the mean of the log rates for genes with 95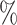 probability or higher of belonging to the log-normal distribution as
probability or higher of belonging to the log-normal distribution as 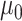 , and the sample standard deviation of these same genes as
, and the sample standard deviation of these same genes as 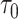 . We set
. We set 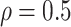 based on exploratory data analysis.
based on exploratory data analysis.
With the prior distribution in place, we then fit the model to 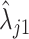 ,
, ,
, 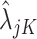 using the EM algorithm for each gene
using the EM algorithm for each gene 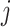 . To prevent label-switching and ensure interpretability of the model, we also set the constraints
. To prevent label-switching and ensure interpretability of the model, we also set the constraints 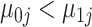 ,
, 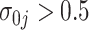 , and
, and 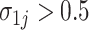 for all
for all 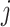 . Details of the algorithm are in Note S4 of the Supplementary material available at Biostatistics online, and we discuss convergence in Note S5 of the Supplementary material available at Biostatistics online. We considered the gene-specific parameters to be frozen going forward and denoted them with
. Details of the algorithm are in Note S4 of the Supplementary material available at Biostatistics online, and we discuss convergence in Note S5 of the Supplementary material available at Biostatistics online. We considered the gene-specific parameters to be frozen going forward and denoted them with 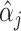 ,
, 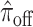 ,
, 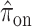 ,
, 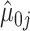 ,
, 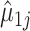 ,
, 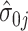 , and
, and 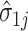 .
.
4.3. Estimating the probabilistic barcode from training data
With estimates of the gene-specific distributions (4.5) in place, all we need to produce a classification algorithm based on our estimate of the posterior probabilities (4.1) is an estimate of the 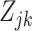 for each gene
for each gene 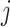 and cell type
and cell type 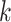 present in the training data. Note that any training data can be used, and the only requirement is they must have cell-type annotations for each cell.
present in the training data. Note that any training data can be used, and the only requirement is they must have cell-type annotations for each cell.
Due to the typically very large sizes of these data sets, it is critical to use computationally efficient approaches. Hence, for each cell type 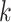 , we sum the cells of that type into a single pseudo-cell, and define
, we sum the cells of that type into a single pseudo-cell, and define 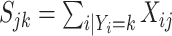 . We can show that if (4.3) and (4.5) hold, then for the pseudo-cell of cell type
. We can show that if (4.3) and (4.5) hold, then for the pseudo-cell of cell type 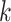 ,
,
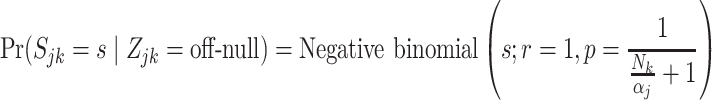 |
(4.8) |
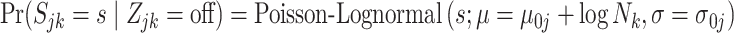 |
(4.9) |
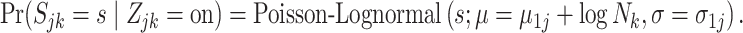 |
(4.10) |
In the equations above, we define 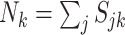 . Although each
. Although each 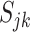 is often substantially larger than the individual
is often substantially larger than the individual 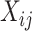 , the inclusion of
, the inclusion of 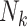 accounts for the total coverage across all cells, and this approach can be understood as analogous to modeling the rate of each gene across the cell type.
accounts for the total coverage across all cells, and this approach can be understood as analogous to modeling the rate of each gene across the cell type.
We can then plug-in our frozen estimates 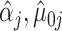 ,
, 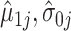 , and
, and 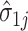 into (4.8) to define estimates of
into (4.8) to define estimates of 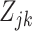 by computing
by computing 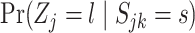 for each state
for each state 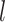 (off-null, off, on). These are found using the Bayes rule:
(off-null, off, on). These are found using the Bayes rule:
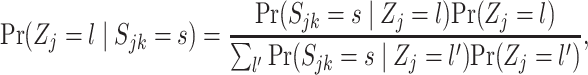 |
where 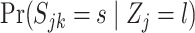 are computed as above, and we can plug-in our existing estimates
are computed as above, and we can plug-in our existing estimates 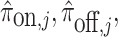 and
and 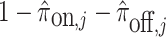 , respectively for
, respectively for 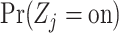 ,
, 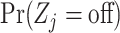 , and
, and 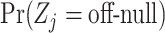 .
.
The resulting probabilities constitute our cell-type-specific barcode and can be interpreted as the probability of each gene belonging to each latent state for that given cell type. This can be computed for any cell type based on any annotated training data. We can plug-in our frozen estimates and rewrite (4.5) as
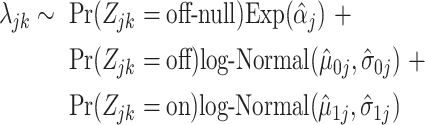 |
for each cell type 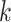 . This then fully specifies the distributions of the rates for each gene in cell type
. This then fully specifies the distributions of the rates for each gene in cell type 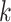 .
.
Finally, to classify each unknown cell, we first selected informative genes by considering only those exhibiting bimodal expression based on their gene-specific distributions. Specifically, we required a large enough difference between the off and on gene-specific means 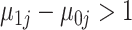 and that the probability of gene being always off or always on was less than 5
and that the probability of gene being always off or always on was less than 5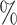 :
: 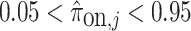 . This filter yielded a set of 6,996 genes. Considering only these informative genes, we can evaluate the posterior probability of each test cell belonging to each cell type of interest as in (4.1).
. This filter yielded a set of 6,996 genes. Considering only these informative genes, we can evaluate the posterior probability of each test cell belonging to each cell type of interest as in (4.1).
Evaluating this posterior probability requires computing Poisson-lognormal densities, which can be computationally inefficient. To improve the computational properties of our approach, we instead approximate the Poisson-lognormal densities with Poisson-gamma (i.e., negative binomial) densities, choosing parameters such that the gamma distribution has the same mean and variance as the lognormal distribution. In particular, if the lognormal distribution is parametrized by 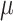 and
and 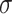 , a gamma distribution with parameters
, a gamma distribution with parameters 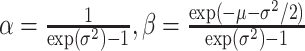 will have the same mean and variance. Hence, we would approximate the corresponding Poisson-lognormal density with the corresponding negative binomial density with parameters
will have the same mean and variance. Hence, we would approximate the corresponding Poisson-lognormal density with the corresponding negative binomial density with parameters 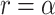 and
and 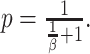
This approximation is motivated by the previous finding that in many analyses, similar results are achieved under either assumption of a lognormal or gamma distribution (McCullagh and Nelder, 2019). In practice, we find that this approximation at the classification step has minimal to no effect on the final results, while dramatically reducing the computational time. However, it should be noted that modeling the off and on distributions as Poisson-gamma from the start was found to be ineffective. The choice of lognormal was made based on the empirical distributions of real data, and in this case, was found to result in superior performance. The effectiveness of the gamma approximation in the classification step can be explained by the fact that we sum up the logarithms of these approximated densities for each gene to estimate the overall posterior probability for each cell type. This lessens the dependence on the accuracy of the density for any individual gene. By contrast, inaccurate modeling of any particular gene from the start can completely change all future learned barcodes with respect to that gene.
Optionally, it may be desired to detect if a test cell belongs to a cell type not represented in the training data. To do so, we construct an average cell type 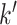 such that
such that 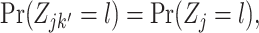 i.e. we use our existing estimates
i.e. we use our existing estimates 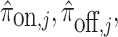 and
and 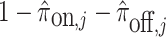 for
for 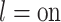 ,
, 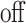 , and
, and 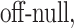 respectively. Note that these are the estimates learned from the PanglaoDB database as described in Section 4.2 and do not come from the training data; as a result, these can be thought of as the global probabilities that each gene is expressed across many cell types from many different tissues. The intuition is that if this average cell type represents a given test cell better than any of the cell types present in the training data, then the test cell is likely to not belong to any of the present cell types. Hence, we can also compute the posterior probability of the test cell belonging to this average cell type and report this result if the posterior probability is larger than those from all of the cell types under consideration.
respectively. Note that these are the estimates learned from the PanglaoDB database as described in Section 4.2 and do not come from the training data; as a result, these can be thought of as the global probabilities that each gene is expressed across many cell types from many different tissues. The intuition is that if this average cell type represents a given test cell better than any of the cell types present in the training data, then the test cell is likely to not belong to any of the present cell types. Hence, we can also compute the posterior probability of the test cell belonging to this average cell type and report this result if the posterior probability is larger than those from all of the cell types under consideration.
5. Results
5.1. Our approach improves current reference-based methods
We compared our method to eight leading classification methods: CHETAH (de Kanter and others, 2019), scmap (Kiselev and others, 2018), CaSTLe (Lieberman and others, 2018), SingleR (Aran and others, 2019), Garnett (Pliner and others, 2019), CellAssign (Zhang and others, 2019), SingleCellNet (Tan and Cahan, 2019), and SVM. The latter two were the top two methods from a benchmark of cell-type annotation approaches (Abdelaal and others, 2019), and the others are widely used methods that represent a range of current approaches. We provide more details about these methods in Note S2 of the Supplementary material available at Biostatistics online.
For each of these methods, we processed the reference and test data sets as recommended in their respective documentation, and for the methods requiring markers (Garnett and CellAssign), we identified six markers for each cell type using scran (Lun and others, 2016) on the reference data set. This was done for consistency because not every cell type under consideration had readily available, independently verified marker genes. For the runs with Garnett, we used Garnett’s built-in marker diagnostic function to assess the marker genes on the corresponding reference data, and we dropped any high ambiguity markers.
We applied each method to our assessment data sets. All the methods besides CaSTLe will call cells unassigned if a label cannot be given with sufficient certainty, so we report three metrics: (i) classification accuracy on the external test set among all cells that were assigned labels, (ii) the proportion of cells in the external test set that were assigned labels, and (iii) the ratio of accuracy among all assigned cells between the external test set and the withheld test set (Table 1). Ratios much lower than 1 in this third metric indicate overtraining due to batch effects. Note that methods have various names for their unassigned category; we considered any cell to be unassigned if it was given a label that does not correspond to one of the original training set labels. In particular, any intermediate or root node label from CHETAH is considered unassigned, as well as the “rand” label from SingleCellNet.
Table 1.
Comparison of leading methods to our approach on our assessment data sets. For each method and data set, we report the classification accuracy on the cells that are assigned labels, and in parentheses the proportion of cells that were assigned labels. We also report the ratio of accuracy among assigned cells between the external and withheld test sets
Accuracy (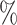 assigned) in external test set assigned) in external test set |
Ratio of accuracy in external to withheld test sets | |||||||
|---|---|---|---|---|---|---|---|---|
| Lung | Colon | Brain | PBMC | Lung | Colon | Brain | PBMC | |
| Barcode | 0.918 (84) | 0.998 (100) | 1.000 (73) | 0.986 (100) | 0.95 | 1.01 | 1.01 | 1.02 |
| SingleR | 0.824 (100) | 0.879 (100) | 0.964 (99) | 0.955 (100) | 0.84 | 0.88 | 0.96 | 1.00 |
| Garnett | 0.823 (85) | 0.905 (72) | 1.000 (100) | 1.000 (100) | 0.89 | 0.94 | 1.00 | 1.05 |
| CellAssign | 0.940 (49) | 0.994 (97) | NA (0) | 0.985 (99) | 0.97 | 1.01 | NA | 1.08 |
| CaSTLe | 0.633 (NA) | 0.677 (NA) | 0.136 (NA) | 0.984 (NA) | 0.65 | 0.68 | 0.14 | 1.00 |
| CHETAH | 0.968 (32) | 0.647 (72) | 1.000 (96) | 0.991 (97) | 0.98 | 0.66 | 1.00 | 1.00 |
| SingleCellNet | 0.640 (100) | 0.650 (100) | 1.000 (100) | 0.984 (100) | 0.66 | 0.65 | 1.00 | 1.02 |
| SVM | 1.000 (25) | 0.517 (96) | 1.000 (74) | 0.962 (22) | 1.01 | 0.52 | 1.00 | 0.97 |
| scmap | 0.988 (11) | 0.877 (82) | 1.000 (0.31) | 0.991 (78) | 1.02 | 0.88 | 1.00 | 1.02 |
The barcode approach performed well universally. On the Lung data set, which was the most challenging due to the inclusion of many similar cell types, the barcode had an accuracy of 91.8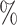 , and was able to assign labels to 84
, and was able to assign labels to 84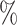 of cells. The methods that had higher accuracy (CellAssign, CHETAH, SVM, and scmap) were only able to assign labels to 49
of cells. The methods that had higher accuracy (CellAssign, CHETAH, SVM, and scmap) were only able to assign labels to 49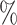 , 32
, 32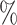 , 25
, 25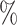 , and 11
, and 11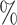 of the cells, respectively. Because the test set is imbalanced in the numbers of each cell type, we also report F1 scores, defined as the harmonic mean of precision and recall, for each cell type in Table S1 of the Supplementary material available at Biostatistics online. The barcode’s lowest F1 score for any cell type is 0.897, which is higher than the lowest F1 score for any other method that assigned labels to the majority of cells. The barcode approach achieved the highest accuracy on the Colon data set, tied the highest accuracy on the Brain data set, and obtained an accuracy of 98.6
of the cells, respectively. Because the test set is imbalanced in the numbers of each cell type, we also report F1 scores, defined as the harmonic mean of precision and recall, for each cell type in Table S1 of the Supplementary material available at Biostatistics online. The barcode’s lowest F1 score for any cell type is 0.897, which is higher than the lowest F1 score for any other method that assigned labels to the majority of cells. The barcode approach achieved the highest accuracy on the Colon data set, tied the highest accuracy on the Brain data set, and obtained an accuracy of 98.6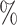 on the PBMC data set, which was within 1.5
on the PBMC data set, which was within 1.5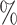 of the highest accuracy. Note that the test sets for Colon, Brain, and PBMC were all balanced, so we do not report F1 scores. In sum, the barcode was the only method to show strong performance on all four data sets. Our lowest accuracy in any data set was 91.8
of the highest accuracy. Note that the test sets for Colon, Brain, and PBMC were all balanced, so we do not report F1 scores. In sum, the barcode was the only method to show strong performance on all four data sets. Our lowest accuracy in any data set was 91.8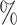 . The next best, among methods that assigned labels to the majority of cells, was SingleR with the lowest accuracy of 82.4
. The next best, among methods that assigned labels to the majority of cells, was SingleR with the lowest accuracy of 82.4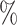 .
.
These results also show that the barcode is robust to overtraining. A method that overtrains typically has markedly worse performance in an external test set than in a withheld test. Hence, a ratio between external test set accuracy and withheld test sets accuracy that is much lower than 1 is suggestive of overtraining. Our approach is the only one among those that assigned labels to the majority of cells to have ratios above 0.90 across the four data sets. By contrast, other methods exhibit ratios farther from 1, especially on the more challenging Lung and Colon data sets.
It should be noted that our approach identified a relatively large proportion (27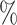 ) of the cells in the Brain data set as unassigned. These test cells are all purportedly microglia, which are present in the reference, but originate from an experimental procedure in which human-induced pluripotent stem cells (iPSCs) were differentiated into microglia within a mouse brain environment. While the original study validated this approach and showed that the resulting cells reproduce the expression profiles of endogenous human microglia, it was noted that some iPSCs appear to have differentiated into other similar cell types (Hasselmann and others, 2019). As a result, it is possible that our approach may be legitimately identifying a subset of cells with a distinct identity (Figure S4 of the Supplementary material available at Biostatistics online).
) of the cells in the Brain data set as unassigned. These test cells are all purportedly microglia, which are present in the reference, but originate from an experimental procedure in which human-induced pluripotent stem cells (iPSCs) were differentiated into microglia within a mouse brain environment. While the original study validated this approach and showed that the resulting cells reproduce the expression profiles of endogenous human microglia, it was noted that some iPSCs appear to have differentiated into other similar cell types (Hasselmann and others, 2019). As a result, it is possible that our approach may be legitimately identifying a subset of cells with a distinct identity (Figure S4 of the Supplementary material available at Biostatistics online).
We also evaluated each method using altered versions of the reference data to mimic realistic applications (Tables S2–S4 of the Supplementary material available at Biostatistics online). On each version of the data, the barcode achieved very similar accuracies as compared to using the unaltered reference data, with no drop in accuracy larger than 1.5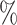 . This was close to SingleCellNet, whose largest drop in accuracy was 3.2
. This was close to SingleCellNet, whose largest drop in accuracy was 3.2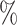 . Every other method had at least one drop of 5
. Every other method had at least one drop of 5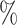 or more. The performance of these other methods varied substantially across the different versions.
or more. The performance of these other methods varied substantially across the different versions.
To evaluate the ability to correctly classify novel cell types as unassigned, we ran each method on the external test sets with one cell type removed at a time from the main reference data (details in Note S3 of the Supplementary material available at Biostatistics online). We summarized each method’s performance, pooling across all these comparisons, using three metrics: true positive rate, defined as the percentage of cells that should be called unassigned that were called unassigned; false positive rate, defined as the percentage of cells that should not be called unassigned that were called unassigned; and F1 score (Table S5 of the Supplementary material available at Biostatistics online). We found that our approach attains a true positive rate of 96.9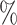 and a false positive rate of 5.8
and a false positive rate of 5.8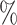 . Only one other method, CHETAH, had a higher true positive rate (99.9
. Only one other method, CHETAH, had a higher true positive rate (99.9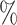 ) but also a much higher false positive rate (63.1
) but also a much higher false positive rate (63.1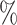 ). Our approach also had the highest F1 score at 0.962, with the next highest F1 score belonging to CellAssign (0.892).
). Our approach also had the highest F1 score at 0.962, with the next highest F1 score belonging to CellAssign (0.892).
Finally, we benchmarked the computational properties of each method on each external test set using median time, in minutes, reported by the R package bench and peak memory usage, in MiB, reported by the R package peakRAM. Since we used a Python implementation of SVM, timing and peak memory usage were assessed using the Python modules time and memory_profiler. We found that the barcode, scmap, SVM, and CHETAH were the fastest (Table 2). By far, the methods that had the least peak memory usage were CellAssign and CHETAH, and the methods with the highest peak memory usage were CaSTLe, SingleCellNet, and SVM. The barcode had similar peak memory usage as the remaining methods.
Table 2.
Median time, in minutes, and peak memory usage, in mebibytes, for each method to classify each external test set from the four main data sets (PBMC, Colon, Brain, and Lung)
| Time (min) | Peak memory (MiB) | |||||||
|---|---|---|---|---|---|---|---|---|
| PBMC | Colon | Brain | Lung | PBMC | Colon | Brain | Lung | |
| Barcode | 0.29 | 0.42 | 1.04 | 0.80 | 7603 | 9864 | 19 722 | 10 815 |
| SingleR | 1.17 | 4.66 | 0.528 | 4.36 | 9723 | 6633 | 2950 | 14 687 |
| Garnett | 3.35 | 7.71 | 13.19 | 54.72 | 8321 | 9331 | 3072 | 30 427 |
| CellAssign | 0.14 | 0.40 | 1.50 | 5.80 | 21 | 32 | 40 | 46 |
| CaSTLe | 5.52 | 5.16 | 0.97 | 31.26 | 22 636 | 28 432 | 15 248 | 32 615 |
| CHETAH | 0.98 | 0.43 | 0.86 | 0.28 | 697 | 526 | 832 | 1189 |
| SingleCellNet | 10.16 | 6.47 | 0.599 | 47.99 | 38 130 | 28 701 | 10 508 | 42 363 |
| SVM | 0.68 | 0.42 | 0.09 | 2.18 | 26 581 | 26 584 | 26 590 | 26 625 |
| scmap | 0.13 | 0.46 | 0.78 | 0.17 | 5738 | 4727 | 1118 | 11 069 |
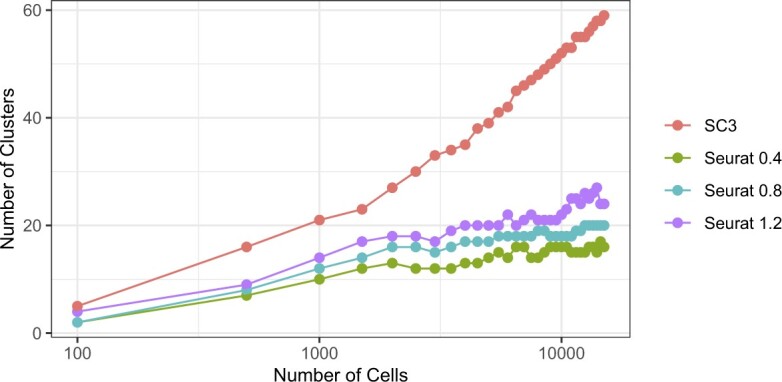
5.2. Model-based approach identifies predictive genes
Fitting model (4.3) permitted us to explain why some markers are more effective than others and to identify new marker genes. For example, note that for the FOXP3 gene, a marker we found to be reasonably effective for CD4 cells, the on distribution is clearly distinguishable from the off distribution (Figure 3(A)). In contrast, for the gene named CD4, which we found to be an ineffective marker despite having a larger rate than FOXP3 among CD4 cells in our PBMC data set, we see a less clear separation of the on and off distributions. Furthermore, markers such as IL7R have well-separated distributions but are on in many tissue types, which makes them less effective as well. Our method was also useful for defining new markers: for a given cell type 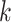 , we search for genes
, we search for genes 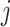 for which
for which 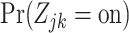 is high, but
is high, but 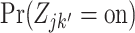 is low for most or all
is low for most or all 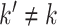 . Using this approach, we identified genes NDUFA13, PPIB, PCBP1, and POLR2F as potentially effective markers for CD4 cells (Figure 3(B)), for example.
. Using this approach, we identified genes NDUFA13, PPIB, PCBP1, and POLR2F as potentially effective markers for CD4 cells (Figure 3(B)), for example.
Figure 3.
Distributions of the rates of CD4 markers across cell- and tissue-types, against the fitted off and on components for each gene. Ticks show the rates of that gene in a particular cell- or tissue-type. Arrows indicate the rates in CD4 cells from the PBMC data set. (A) Four canonical CD4 markers. (B) Four CD4 markers we identified.
Our model also allows us to understand how the barcode approach is able to distinguish very similar cell types such as those in the most challenging Lung data set. We examined one very similar pair, capillary and artery, which was frequently mixed up under other approaches. After fitting our model to both cell types, we compared the probability of observing a nonzero count from each gene in a capillary cell versus an artery cell (Figure 4). This shows that there are very few dichotomous genes between the two, i.e., genes that will almost certainly have a nonzero count in one cell type and a zero count in the other. However, our probabilistic barcodes enable leveraging genes with more subtle differences between the two cell types, since we quantify the probability of a gene being on rather than using strictly binary expression. When we highlight the top genes contributing to the classification of withheld capillary cells, we can show that our approach is able to use many such genes with subtle differences.
Figure 4.
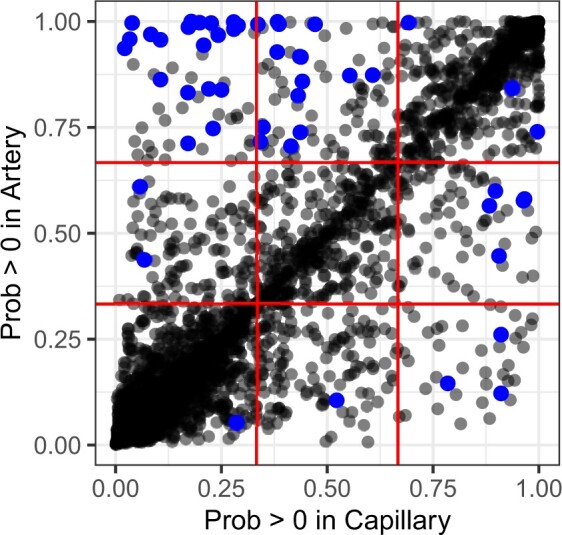
Probability of a nonzero count for each gene under our model for artery and capillary cells in the lung, assuming coverage of 2000 counts. Highlighted points indicate the top 50 genes contributing to the classification between artery and capillary in a set of 100 withheld capillary cells. These were identified as the genes with the highest average log-likelihood differences across the withheld capillary cells under the capillary barcode and the artery barcode.
6. Discussion
Currently, cell-type identification in scRNA-seq data sets is done with either clustering-based or reference-based methods. We showed that clustering-based methods can identify more clusters as the data set size increases, and that the number of clusters can be sensitive to algorithm parameters. This implies that overclustering can occur for large data set sizes, or that rare cell types are challenging to identify at small or medium data set sizes. As a result, clustering can sometimes result in ambiguous findings.
Moreover, clustering-based methods can depend on arbitrary user decisions such as the choice of marker genes, which is a problem for cell types that do not have well-established and widely accepted markers. Different users examining the same clusters might draw two different conclusions about the cell-type identities. We further showed that marker genes in scRNA-seq data can have varying reliability, even for well-studied cell types. This method of direct annotation by a user additionally implies that probabilistic classification is not possible; a given target cell is assigned to some particular cell type without any information about the certainty of this assignment. Finally, with clustering approaches, it is difficult to specify the desired granularity of the cell types. Since clusters are identified in an unsupervised manner, there is no differentiation between, for instance, a use case where it is enough to identify cells as T-cells and a use case in which identification at the level of T-cell subtypes is needed. With certain parameter settings, data set size, choice of marker genes, and other robust user decision-making, clustering approaches can yield strong results, but they are highly sensitive to all of these choices and can be difficult to validate. In other contexts, such as when the primary goal is the unsupervised discovery of distinct novel cell-type populations, this flexibility can be a strength. However, when the primary goal is the annotation of largely previously known cell types, which is the context we are concerned with, this sensitivity and large possible range of results is a significant challenge.
Reference-based methods avoid the pitfalls of clustering-based methods in this context. The supervised approach ensures that the desired granularity can be controlled with the choice of reference data and avoids artifacts such as the number of distinct cell types identified growing as the data set size increases. Because each cell is typically classified independently of the other cells in the data set, rare or fine classifications can be made no matter the size of the data. Nevertheless, we showed that many of the currently available algorithms are susceptible to overtraining due to study-to-study variability or batch effects. We introduced an approach that provides a solution to these challenges. First, we leverage thousands of genes, rather than only a few markers, to make the annotations, which provides robustness to the challenges introduced by sparsity. Second, we directly account for coverage in our model, allowing us to make reliable classifications even with varying coverage between the reference and test data. Finally, to account for study-specific biases and batch effects, we assume a latent variable model, model unwanted variability with gene-specific distributions across cell types and represent each reference cell type with a unique probabilistic barcode.
We demonstrated the advantages of our approach by assessing performance on several real-world data sets, in which our approach was successful at generalizing to external test sets. It is possible that the poor performance of the two marker-based methods (Garnett and CellAssign) on some of the data sets could be attributed to the choice of markers, and that a richer analysis to guide marker selection could have yielded better results. Even if better performance might be possible, this would require extra steps beyond what is part of the method. By contrast, our approach does not require additional inputs other than the reference data.
The fact that our method permits cells to be classified as unassigned offers the ability to detect unknown cell types in the test data. We demonstrated that our approach compares favorably to others on this challenge. In general, our approach will assign test cells to their closest cell type available in the reference, unless they are closer to the average cell-type profile. If a test cell belongs to a different subtype or cell state as a cell type in the provided reference, whether the test cell is classified as that reference cell type or as unassigned will depend on the relative closeness of the two profiles. As such, if the goal is specifically to identify particular subtypes or cell states, those should be provided in the reference.
Finally, we note that when classifying, our method assumes equal prior probabilities for each of the cell-type labels present in the training data. This means that the classifications are driven entirely by a comparison of the likelihoods of observing each cell’s profile under each possible cell type. In cases where one or more cell types may be very rare, our method consequently will always assign whichever label results in the highest likelihood, and will not discourage rare labels on the basis of this prior knowledge. This could result in assigning rare labels too often in cells that have similar likelihoods under both a rare label and a more common label. Because our method also returns the probabilities of each cell belonging to each cell type, in some cases it may be prudent to reweight these probabilities according to prior knowledge of cell-type abundance.
Supplementary Material
Acknowledgments
Conflict of Interest: None declared.
Contributor Information
Isabella N Grabski, Department of Biostatistics, Harvard T. H. Chan School of Public Health, Boston, MA, USA.
Rafael A Irizarry, Department of Biostatistics, Harvard T. H. Chan School of Public Health, Boston, MA, USA and Department of Data Science, Dana-Farber Cancer Institute, Boston, MA, USA.
Software
Software in the form of R code, together with a sample input data set and complete documentation is available at https://github.com/igrabski/scRNAseq-cell-type.
Supplementary material
Supplementary material is available at http://biostatistics.oxfordjournals.org.
Funding
Funding is provided by the National Institute of Health (NIH R35GM131802, R01HG005220) and the National Science Foundation (DGE1745303).
References
- Abdelaal, T., Michielsen, L., Cats, D., Hoogduin, D., Mei, H., Reinders, M. J. T. and Mahfouz, A. (2019). A comparison of automatic cell identification methods for single-cell RNA sequencing data. Genome Biology 20, 1–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aran, D., Looney, A. P., Liu, L., Wu, E., Fong, V., Hsu, A., Chak, S., Naikawadi, R. P., Wolters, P. J., Abate, A. R.. and others. (2019). Reference-based analysis of lung single-cell sequencing reveals a transitional profibrotic macrophage. Nature Immunology 20, 163–172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cable, D. M., Murray, E., Zou, L. S., Goeva, A., Macosko, E. Z., Chen, F. and Irizarry, R. A. (2020). Robust decomposition of cell type mixtures in spatial transcriptomics. Nature Biotechnology 40, 517–526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Kanter, J. K., Lijnzaad, P., Candelli, T., Margaritis, T. and Holstege, F. (2019). CHETAH: a selective, hierarchical cell type identification method for single-cell RNA sequencing. Nucleic acids research 47, e95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eisenberg, E. and Levanon, E. Y. (2013). Human housekeeping genes, revisited. Trends in Genetics 29, 569–574. [DOI] [PubMed] [Google Scholar]
- Franzén, O., Gan, L.-M. and Björkegren, J. L. M. (2019). Panglaodb: a web server for exploration of mouse and human single-cell RNA sequencing data. Database 2019, baz046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasselmann, J., Coburn, M. A., England, W., Velez, D. X. F., Shabestari, S. K., Tu, C. H., McQuade, A., Kolahdouzan, M., Echeverria, K., Claes, C.. and others. (2019). Development of a chimeric model to study and manipulate human microglia in vivo. Neuron 103, 1016–1033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiselev, V. Y., Kirschner, K., Schaub, M. T., Andrews, T., Yiu, A., Chandra, T., Natarajan, K. N., Reik, W., Barahona, M., Green, A. R.. and others. (2017). Sc3: consensus clustering of single-cell RNA-seq data. Nature Methods 14, 483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiselev, V. Y., Yiu, A. and Hemberg, M. (2018). scmap: projection of single-cell RNA-seq data across data sets. Nature Methods 15, 359. [DOI] [PubMed] [Google Scholar]
- Lieberman, Y., Rokach, L. and Shay, T. (2018). CaSTLe—classification of single cells by transfer learning: harnessing the power of publicly available single cell RNA sequencing experiments to annotate new experiments. PLoS One 13, e0205499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin, P., Troup, M. and Ho, J. W. K. (2017). CIDR: ultrafast and accurate clustering through imputation for single-cell RNA-seq data. Genome Biology 18, 59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lopez, R., Regier, J., Cole, M. B., Jordan, M. I. and Yosef, N. (2018). Deep generative modeling for single-cell transcriptomics. Nature Methods 15, 1053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lun, A. T., McCarthy, D. J., and Marioni, J. C. (2016). A step-by-step workflow for low-level analysis of single-cell RNA-seq data with Bioconductor. F1000Research, 5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCall, M. N., Uppal, K., Jaffee, H. A., Zilliox, M. J. and Irizarry, R. A. (2010). The gene expression barcode: leveraging public data repositories to begin cataloging the human and murine transcriptomes. Nucleic Acids Research 39(1), D1011–D1015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCullagh, P. and Nelder, J. A. (2019). Generalized Linear Models. Routledge. [Google Scholar]
- Ntranos, V., Kamath, G. M., Zhang, J. M., Pachter, L. and David, N. T. (2016). Fast and accurate single-cell RNA-seq analysis by clustering of transcript-compatibility counts. Genome Biology 17, 112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pliner, H. A., Shendure, J. and Trapnell, C. (2019). Supervised classification enables rapid annotation of cell atlases. Nature methods 16, 983–986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Que, X., Checconi, F., Petrini, F. and Gunnels, J. A. (2015). Scalable community detection with the Louvain algorithm. In: 2015 IEEE International Parallel and Distributed Processing Symposium. IEEE, pp. 28–37. [Google Scholar]
- Stuart, T., Butler, A., Hoffman, P., Hafemeister, C., Papalexi, E., Mauck III, W. M., Stoeckius, M., Smibert, P. and Satija, R. (2018). Comprehensive integration of single cell data. Cell, 177, 1888–1902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tan, Y. and Cahan, P. (2019). Singlecellnet: a computational tool to classify single cell RNA-seq data across platforms and across species. Cell Systems 9, 207–213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu, Y., Mizuno, T., Sridharan, A., Du, Y., Guo, M., Tang, J., Wikenheiser-Brokamp, K. A., Perl, A.-K. T., Funari, V. A., Gokey, J. J.. and others. (2016). Single-cell RNA sequencing identifies diverse roles of epithelial cells in idiopathic pulmonary fibrosis. JCI Insight 1, e90558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, A. W., O’Flanagan, C., Chavez, E. A., Lim, J. L. P., Ceglia, N., McPherson, A., Wiens, M., Walters, P., Chan, T., Hewitson, B.. and others. (2019). Probabilistic cell-type assignment of single-cell RNA-seq for tumor microenvironment profiling. Nature methods 16, 1007–1015. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.