Spectroscopic Study of the Br⁻+CH₃I→I⁻+CH₃Br S_N2 Reaction

Abstract

Mass spectrometry and anion photoelectron spectroscopy have been used to study the gas‐phase ${\mathrm{S}}_{\mathrm{N}}2$ reaction involving ${\mathrm{B}\mathrm{r}}^{-}$ and ${\mathrm{C}\mathrm{H}}_3\mathrm{I}$ . The anion photoelectron spectra associated with the reaction intermediates of this ${\mathrm{S}}_{\mathrm{N}}2$ reaction are presented. High‐level CCSD(T) calculations have been utilised to investigate the reaction intermediates that may form as a result of the ${\mathrm{S}}_{\mathrm{N}}2$ reaction along various different reaction pathways, including back‐side attack and front‐side attack. In addition, simulated vertical detachment energies of each reaction intermediate have been calculated to rationalise the photoelectron spectra.

The S_N2 reaction involving Br⁻ and CH₃I is investigated via anion photoelectron spectroscopy and mass spectrometry. Reaction intermediates pertaining to both Br⁻⋯CH₃I and I⁻⋯CH₃Br van der Waals complexes are observed. High‐level CCSD(T) calculations reaffirm the presence of these chemical species.

Introduction

Bimolecular nucleophilic substitution (${\mathrm{S}}_{\mathrm{N}}2$ ) reactions play a fundamental role in chemistry and have been studied extensively both experimentally[ ¹ , ² , ³ , ⁴ , ⁵ , ⁶ , ⁷ , ⁸ ] and computationally.[ ⁶ , ⁷ , ⁸ , ⁹ , ¹⁰ , ¹¹ , ¹² , ¹³ , ¹⁴ , ¹⁵ , ¹⁶ ] The simplest ${\mathrm{S}}_{\mathrm{N}}2$ reactions take the form of equation 1, where X and Y are often halogens but can also be other nucleophilic species such as OH and CN. ^[17]

$${\displaystyle {\mathrm{X}}^{-}+\mathrm{C}{\mathrm{H}}_3\mathrm{Y}\to {\mathrm{Y}}^{-}+\mathrm{C}{\mathrm{H}}_3\mathrm{X}}$$ (1)

In the gas‐phase, the typical mechanism associated with an ${\mathrm{S}}_{\mathrm{N}}2$ reaction involves the nucleophile ${\mathrm{X}}^{-}$ approaching the methyl group of the ${\mathrm{C}\mathrm{H}}_3\mathrm{Y}$ molecule, often referred to as a back‐side attack. ^[7] An ion‐dipole pre‐reaction adduct ${\mathrm{X}}^{-}\cdots {\mathrm{H}}_3\mathrm{C}\mathrm{Y}$ forms from this interaction, corresponding to a minimum on the potential energy surface, before a Walden inversion of the methyl group leads to a transition structure [$\mathrm{X}\cdots {\mathrm{C}\mathrm{H}}_3\cdots \mathrm{Y}$ ]${}^{-}$ .[ ¹⁸ , ¹⁹ ] The subsequent formation of the C−X bond and cleavage of the C−Y bond results in an ion‐dipole post‐reaction adduct ${\mathrm{Y}}^{-}\cdots {\mathrm{H}}_3\mathrm{C}\mathrm{X}$ , corresponding to another minimum on the potential energy surface, followed by the separation of the two substituents ${\mathrm{Y}}^{-}$ and ${\mathrm{C}\mathrm{H}}_3\mathrm{X}$ .

While the back‐side attack mechanism is the most commonly accepted, there are several other mechanisms pertaining to gas‐phase halide‐monohalomethane ${\mathrm{S}}_{\mathrm{N}}2$ reactions that have been described previously. A front‐side attack mechanism was first studied computationally by Glukhovtsev et al. for identity $({\mathrm{X}}^{-}+{\mathrm{C}\mathrm{H}}_3\mathrm{X}$ ) ${\mathrm{S}}_{\mathrm{N}}2$ reactions, ^[20] which was extended to non‐identity ${\mathrm{S}}_{\mathrm{N}}2$ reactions more recently by Bickelhaupt et al., ^[15] and through several studies by Czakó and co‐workers.[ ¹⁴ , ²¹ , ²² ] The front‐side attack features the nucleophile ${\mathrm{X}}^{-}$ appended linearly to the halogen Y, and requires overcoming a large central barrier before forming the ion‐dipole post‐reaction adduct ${\mathrm{Y}}^{-}\cdots {\mathrm{H}}_3\mathrm{C}\mathrm{X}$ . Czakó and co‐workers have previously described a double‐inversion mechanism, which involves overcoming a barrier where ${\mathrm{X}}^{-}$ interacts with one of the methyl hydrogens, before forming the ion‐dipole ${\mathrm{X}}^{-}\cdots {\mathrm{H}}_3\mathrm{C}\mathrm{Y}$ adduct similar to the back‐side attack. ^[23] When ${\mathrm{X}}^{-}$ is a fluoride anion, it has been shown that a hydrogen‐appended structure exists as a pre‐reaction adduct along the back‐side attack mechanism,[ ¹⁴ , ²⁴ ] however Czakó and co‐workers have also optimised this minimum for the ${\mathrm{C}\mathrm{l}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{I}$ complex. ^[25] To account for these additional mechanisms regarding gas‐phase ${\mathrm{S}}_{\mathrm{N}}2$ reactions, it is important that all species along each reaction coordinate are considered.

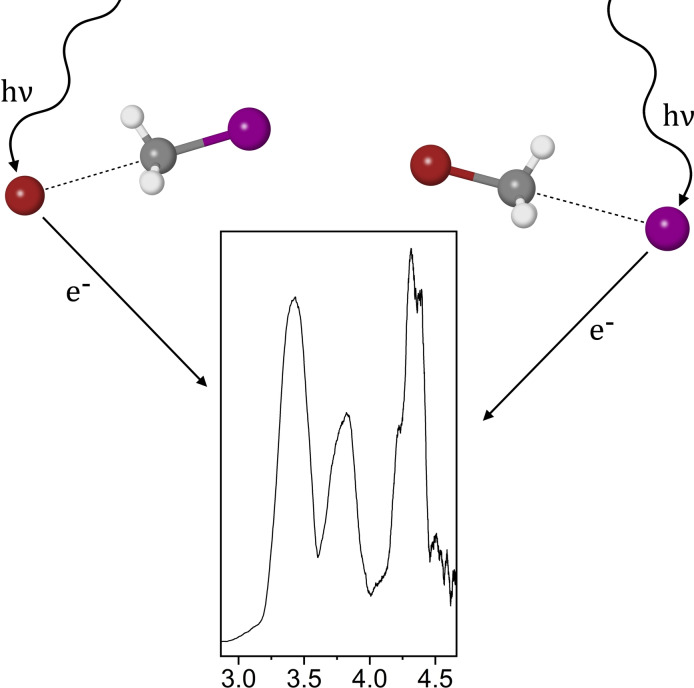
Anion photoelectron spectroscopy is an experimental technique that allows the study of gas‐phase van der Waals complexes that can be important in pre‐reaction or post‐reaction adducts on the potential energy surface. Anion photoelectron spectroscopy is useful in studying electronic structure.[ ²⁶ , ²⁷ , ²⁸ , ²⁹ ] In particular it has been used to investigate various ${\mathrm{S}}_{\mathrm{N}}2$ reaction pathways and intermediates, including ${\mathrm{X}}^{-}+{\mathrm{C}\mathrm{H}}_3$ I,[ ³⁰ , ³¹ ] ${\mathrm{I}}^{-}+{\mathrm{C}\mathrm{H}}_3$ X,[ ³² , ³³ , ³⁴ , ³⁵ ] and the ${\mathrm{I}}^{-}\cdots {\mathrm{C}\mathrm{F}}_3$ I complex. ^[36] The photoelectric effect is the main driving factor behind anion photoelectron spectroscopy, i. e. photons interact with an anionic species, resulting in the detachment of an electron. The kinetic energy of the detached electron is then measured to determine an electron binding energy (${\mathrm{e}}_{\mathrm{B}\mathrm{E}}$ ) of the anionic species, essentially deducing how tightly an electron is bound.

The ${\mathrm{e}}_{\mathrm{B}\mathrm{E}}$ can yield information about intermolecular interaction strength of a van der Waals complex. For example, the ${}^2{\mathrm{P}}_{3/2}$ and ${}^2{\mathrm{P}}_{1/2}$ photodetachment peaks in a bare bromide spectrum can be found at approximately 3.36 eV and 3.82 eV respectively, ^[37] however upon complexation with a molecule the two photodetachment peaks shift to higher energy.[ ³⁸ , ³⁹ , ⁴⁰ ] This shift in binding energy relative to the bare nucleophile is called a stabilisation energy ($E_{stab}$ ) and is indicative of the strength of the intermolecular forces binding the complex. Thus, a photoelectron spectrum of a halide ${\mathrm{X}}^{-}$ complexed with a solvent molecule can therefore be considered a perturbed photoelectron spectrum of the bare halide. ^[41] The ${\mathrm{e}}_{\mathrm{B}\mathrm{E}}$ can also aid in differentiating chemical species from one another due to physical properties such as spin‐orbit effects. For example, the spin‐orbit constant of atomic bromine is approximately 0.46 eV, ^[42] therefore the ${}^2{\mathrm{P}}_{3/2}$ and ${}^2{\mathrm{P}}_{1/2}$ spin‐orbit states of bromine will be separated by 0.46 eV, whereas the spin‐orbit constant of atomic iodine is approximately 0.94 eV. ^[43] This property allows isobaric species, such as two distinct halide complexes, to be distinguished using anion photoelectron spectroscopy.

Using computational methods such as ab initio calculations, it is possible to determine vertical detachment energies (VDE) that can be compared to experimental photodetachment peaks in a photoelectron spectrum, based on an optimised chemical structure. The Wild group has previously utilised anion photoelectron spectroscopy in conjunction with high‐level CCSD(T) calculations to elucidate the structure and binding motifs of van der Waals complexes observed in the gas‐phase, with good agreement to experimental data.[ ²⁸ , ²⁹ , ³⁸ , ³⁹ , ⁴⁰ ]

In this study, we present the photoelectron spectrum assigned to the ${\mathrm{S}}_{\mathrm{N}}2$ reaction intermediates ${\mathrm{B}\mathrm{r}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{I}$ and ${\mathrm{I}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{B}\mathrm{r}$ , formed from the bare constituents ${\mathrm{B}\mathrm{r}}^{-}$ and ${\mathrm{C}\mathrm{H}}_3\mathrm{I}$ . The pre‐reaction and post‐reaction adducts of the ${\mathrm{S}}_{\mathrm{N}}2$ reaction were observed and identified using a combination of mass spectrometry, anion photoelectron spectroscopy, and high‐level CCSD(T) calculations.

Results and Discussion

Geometries and Predicted Electron Detachment Energies

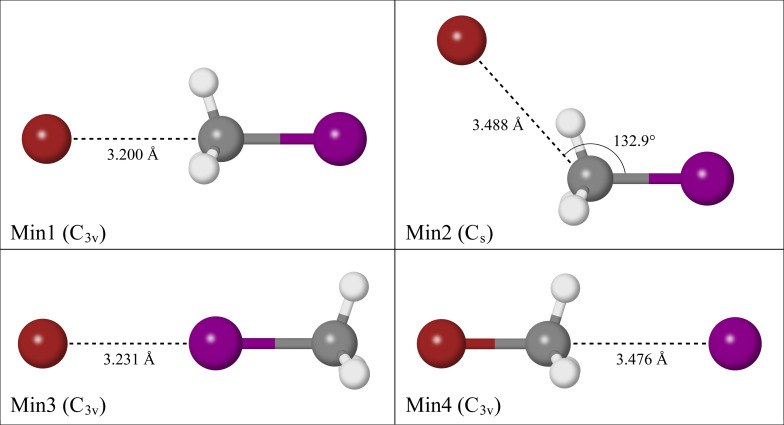
Four reaction intermediates were optimised at the CCSD(T)/AVTZ level of theory as shown in Figure 1. Three of the reaction intermediates are ${\mathrm{B}\mathrm{r}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{I}$ pre‐reaction adducts, one of which corresponds to the back‐side attack mechanism (Min1), another which features the bromide appended to one of the methyl hydrogens (Min2), and the last involves the bromide appended linearly to the iodine (Min3). The remaining reaction intermediate is a ${\mathrm{I}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{B}\mathrm{r}$ post‐reaction adduct where the iodide interacts with the methyl group of ${\mathrm{C}\mathrm{H}}_3\mathrm{B}\mathrm{r}$ (Min4). Another ${\mathrm{I}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{B}\mathrm{r}$ structure exists that is analogous to Min3, where the iodide is bound linearly to the bromine atom of ${\mathrm{C}\mathrm{H}}_3\mathrm{B}\mathrm{r}$ (Min5), however as this study is primarily interested in the forward reaction direction involving ${\mathrm{B}\mathrm{r}}^{-}$ and ${\mathrm{C}\mathrm{H}}_3\mathrm{I}$ , Min5 will not be discussed, but can be found in the supporting information. A structure analogous to Min2 was not identified for the ${\mathrm{I}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{B}\mathrm{r}$ complex.

Figure 1.

Reaction intermediates of the ${\mathrm{B}\mathrm{r}}^{-}+{\mathrm{C}\mathrm{H}}_3\mathrm{I}$ ${\mathrm{S}}_{\mathrm{N}}2$ reaction optimised at CCSD(T)/AVTZ theory.

Min1 and Min4 are both ion‐dipole bound structures that exhibit ${\mathrm{C}}_{3\mathrm{v}}$ symmetry. In Min1, the bromide interaction with the methyl group occurs at a C−Br distance of 3.200 Å, whereas in Min4 the iodide interaction occurs at a C−I distance of 3.476 Å due to the relative van der Waals radii of bromide and iodide respectively. Min2 exhibits ${\mathrm{C}}_{\mathrm{s}}$ symmetry, where the bromide interacts with one of the methyl hydrogens (${\mathrm{R}}_{\mathrm{B}\mathrm{r}\cdots \mathrm{C}}$ =3.488 Å), at an angle of 132.9° from the C−I bond. This interaction does not occur directly in‐line with the hydrogen atom, with the bromide lying at an angle of 146.9° from the C−H bond. For the iodine appended structure, Min3, the bromide‐iodine interaction occurs at a distance of 3.231 Å.

Simulated electron VDE values to the neutral halogen ${}^2{\mathrm{P}}_{3/2}$ and ${}^2{\mathrm{P}}_{1/2}$ electronic states are reported in Table 1 at the CCSD(T)/CBS level of theory, alongside zero‐point corrected dissociation energy (${\mathrm{D}}_0$ ) values. The reported energies for Min2 are all from CCSD(T)/AVTZ calculations, as a complete basis set extrapolation for this data yielded inconsistent results which will be discussed later. Min1 has the largest predicted VDE values, as well as the largest ${\mathrm{D}}_0$ of 47.6 kJ ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ . Relative to the simulatedCalculations predict that the respective ${}^2{\mathrm{P}}_{3/2}$ peaks for Min2 and Min3 are 0.08 eV and 0.13 eV less than the theoretical ${}^2{\mathrm{P}}_{3/2}$ peak of Min1. Min3 has a ${\mathrm{D}}_0$ value that is 11.9 kJ ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ less than Min1, while the dissociation of Min2 into its bare substituents requires 43.6 kJ ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ . Both the simulated VDE values and the ${\mathrm{D}}_0$ values indicate that Min1 is the most tightly bound complex of the three ${\mathrm{B}\mathrm{r}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{I}$ reaction intermediates, whereas the hydrogen bound nature of Min2 results in a stronger interaction than the iodine bound nature of Min3. The post‐reaction adduct corresponding to Min4 has the lowest ${}^2{\mathrm{P}}_{3/2}$ peak and the highest ${}^2{\mathrm{P}}_{1/2}$ peak of the four reaction intermediates, attributed to the large spin‐orbit constant of atomic iodine. ^[43] The ${\mathrm{D}}_0$ value calculated for Min4 is 5.4 kJ ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ less than Min1, indicative that the ion‐dipole structure for the ${\mathrm{B}\mathrm{r}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{I}$ complex is more tightly bound than the ion‐dipole structure for the ${\mathrm{I}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{B}\mathrm{r}$ complex.

Table 1.

Simulated electron vertical detachment energies and dissociation energies of the reaction intermediates from CCSD(T)/CBS results.

Complex	VDE		${\mathrm{D}}_0$ [kJ ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ ]
	${}^2{\mathrm{P}}_{3/2}$ [eV]	${}^2{\mathrm{P}}_{1/2}$ [eV]
${\mathrm{B}\mathrm{r}}^{-}\cdots {\mathrm{H}}_3\mathrm{C}\mathrm{I}$ (Min1)	3.84	4.30	47.6
${\mathrm{B}\mathrm{r}}^{-}\cdots {\mathrm{H}\mathrm{C}\mathrm{H}}_2\mathrm{I}$ (Min2)	3.76[*]	4.22[*]	43.6[*]
${\mathrm{B}\mathrm{r}}^{-}\cdots {\mathrm{I}\mathrm{C}\mathrm{H}}_3$ (Min3)	3.71	4.17	35.7
${\mathrm{I}}^{-}\cdots {\mathrm{H}}_3\mathrm{C}\mathrm{B}\mathrm{r}$ (Min4)	3.44	4.38	42.2

[*] Calculated at the CCSD(T)/AVTZ level of theory.

Photoelectron Spectroscopy

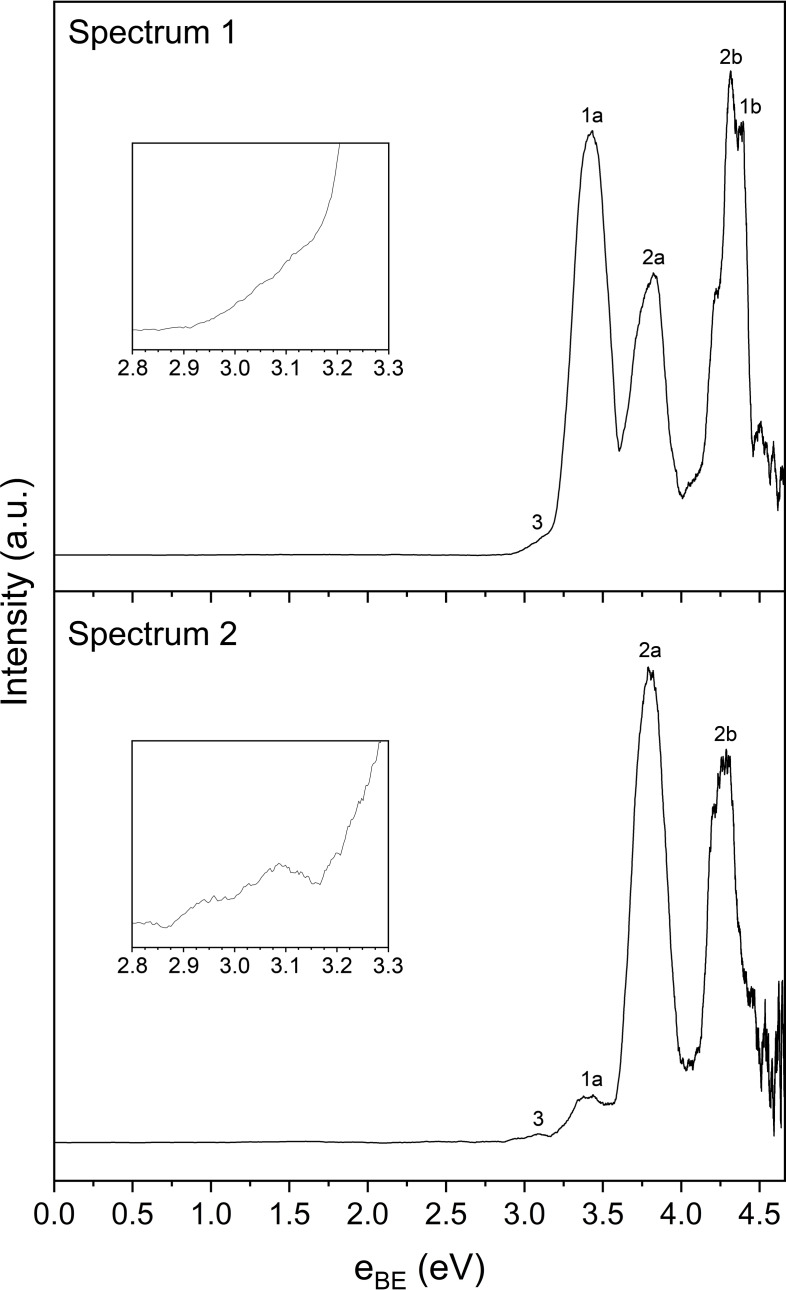
Two photoelectron spectra of the ${\mathrm{S}}_{\mathrm{N}}2$ reaction involving ${\mathrm{B}\mathrm{r}}^{-}$ and ${\mathrm{C}\mathrm{H}}_3\mathrm{I}$ have been recorded in this study, which result from the photodetachment of two different chemical species, namely ${\mathrm{B}\mathrm{r}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{I}$ and ${\mathrm{I}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{B}\mathrm{r}$ . The reaction intermediates were formed from a gas mixture containing ${\mathrm{C}\mathrm{H}}_2{\mathrm{B}\mathrm{r}}_2$ , ${\mathrm{C}\mathrm{H}}_3\mathrm{I}$ and Ar, a mass spectrum of which is provided in the supporting information. The two photoelectron spectra, as shown in Figure 2, were recorded under different experimental conditions; in spectrum 2, the ratio of ${\mathrm{C}\mathrm{H}}_2{\mathrm{B}\mathrm{r}}_2$ relative to ${\mathrm{C}\mathrm{H}}_3\mathrm{I}$ in the gas mixture was increased to test whether the ratio of the photodetachment peaks would differ when compared to spectrum 1. Both spectra result from photodetachment of the 223 m/z peak observed in the mass spectrum corresponding to the ${}^{81}$ Br isotopologue, a summary of the spectral features of which are found in Table 2.

Figure 2.

Photoelectron spectra of the ${}^{81}{\mathrm{B}\mathrm{r}}^{-}+{\mathrm{C}\mathrm{H}}_3\mathrm{I}$ ${\mathrm{S}}_{\mathrm{N}}2$ reaction intermediates, resulting from 4.661 eV laser radiation. The inset plots are a close‐up view of spectral feature 3, as annotated in the spectra.

Table 2.

Spectral features observed in the two photoelectron spectra from Figure 2, and assignment of chemical species to those spectral features. The VDE column refers to the theoretical vertical detachment energies for each species as shown previously in Table 1.

Spectral Feature	Spectrum 1 [eV]	Spectrum 2 [eV]	Average [eV]	Assignment	VDE [eV]
3[*]	3.10	3.09	3.10	${}^2{\mathrm{P}}_{3/2}$ ←${}^1{\mathrm{S}}_0$ of ${\mathrm{I}}^{-}$	3.06
1a	3.42	3.41	3.42	${}^2{\mathrm{P}}_{3/2}$ ←${}^1{\mathrm{S}}_0$ of ${\mathrm{I}}^{-}\cdots {\mathrm{H}}_3\mathrm{C}\mathrm{B}\mathrm{r}$ (Min4)	3.44
2a	3.82	3.80	3.81	${}^2{\mathrm{P}}_{3/2}$ ←${}^1{\mathrm{S}}_0$ of ${\mathrm{B}\mathrm{r}}^{-}\cdots {\mathrm{H}}_3\mathrm{C}\mathrm{I}$ (Min1)	3.84
2b	4.32	4.28	4.30	${}^2{\mathrm{P}}_{1/2}$ ←${}^1{\mathrm{S}}_0$ of ${\mathrm{B}\mathrm{r}}^{-}\cdots {\mathrm{H}}_3\mathrm{C}\mathrm{I}$ (Min1)	4.30
1b	4.39	$-$	4.39	${}^2{\mathrm{P}}_{1/2}$ ←${}^1{\mathrm{S}}_0$ of ${\mathrm{I}}^{-}\cdots {\mathrm{H}}_3\mathrm{C}\mathrm{B}\mathrm{r}$ (Min4)	4.38

[*] May arise from metastable dissociation of the ${\mathrm{I}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3$ Br complex after acceleration down the time‐of‐flight tube, or via a two‐photon photodissociation process, as discussed in the main text.

In spectrum 1, three distinct photoelectron peaks are observed, the first two of which are at 3.42 eV and 3.82 eV, while the third peak at 4.32 eV has the largest intensity and features a small shoulder peak at 4.39 eV. In spectrum 2, two major peaks at 3.80 eV and 4.28 eV are observed, with a minor peak at 3.41 eV. Another small spectral feature, annotated on the photoelectron spectra as feature 3, lies at approximately 3.10 eV in spectrum 1 and 3.09 eV in spectrum 2. This spectral feature has low intensity relative to the main photodetachment peaks, and while there appears to be a slight decrease in intensity of spectral feature 3 at approximately 3.15 eV in spectrum 2 before the onset of spectral feature 1a, the shape is notably similar between 3.00 and 3.10 eV in both spectra. A possible explanation for this spectral feature is that it may correspond to bare iodide. This could result either from metastable dissociation of the ${\mathrm{I}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{B}\mathrm{r}$ complex after acceleration down the time‐of‐flight tube but before photodetachment, ^[44] or it may result from a two‐photon process, where photodissociation of the ${\mathrm{C}\mathrm{H}}_3\mathrm{I}$ moiety within the ${\mathrm{B}\mathrm{r}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{I}$ complex occurs. ^[34] Similarly, bare bromide could be formed as a result of the two aforementioned processes, however as the two electronic states of atomic bromine (${}^2{\mathrm{P}}_{3/2}$ and ${}^2{\mathrm{P}}_{1/2}$ ) lie at approximately 3.36 eV and 3.82 eV respectively, both of these peaks would be convoluted within the main photodetachment peaks of the spectrum, therefore it cannot be stated whether bare bromide is actually present.

Rationalisation of Experimental Data

The theoretical VDE values calculated for each reaction intermediate can be compared to the experimental peaks to rationalise the photoelectron spectra. As there are two spectra, the theoretical VDE values will be compared to the average of each peak position. For Min1, the ion‐dipole ${\mathrm{B}\mathrm{r}}^{-}\cdots {\mathrm{H}}_3\mathrm{C}\mathrm{I}$ structure, the theoretical ${}^2{\mathrm{P}}_{1/2}$ peak of 4.30 eV is in good agreement with the experimental spectral feature 2b at 4.31 eV. Similarly, the theoretical ${}^2{\mathrm{P}}_{3/2}$ peak of 3.84 eV for Min1 is in agreement with spectral feature 2a at 3.81 eV. For Min4, the ion‐dipole ${\mathrm{I}}^{-}\cdots {\mathrm{H}}_3\mathrm{C}\mathrm{B}\mathrm{r}$ structure, the theoretical ${}^2{\mathrm{P}}_{3/2}$ and ${}^2{\mathrm{P}}_{1/2}$ peaks of 3.44 eV and 4.38 eV respectively agree with spectral feature 1a at 3.42 eV, and spectral feature 1b at 4.39 eV. These two peaks are in close agreement with previous photoelectron spectroscopic studies of the ${\mathrm{I}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{B}\mathrm{r}$ complex by Johnson and co‐workers, ^[32] and Mabbs and co‐workers, ^[34] which will be discussed in more detail later.

Regarding Min2, while it may seem as though the theoretical peak locations align closely with the spectral features also assigned to Min1, after further computational analysis which will be discussed later, it is evident that Min2 is a very weakly bound minimum electronically, and likely to not be a minimum when accounting for harmonic frequency modes, therefore there will be no assignment of the Min2 complex to experimental spectral features. As for the iodine‐bound structure, Min3, the theoretical VDE values do not align with any of the spectral features, and thus there appears to be no evidence of the formation of Min3. Further evidence to support the assignment of the Min1 ion‐dipole bound complex over the hydrogen‐bound and iodine‐bound complexes, Min2 and Min3 respectively, comes from the ${\mathrm{D}}_0$ values, which as stated previously was calculated to be the highest for Min1 at 47.6 kJ ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ , indicative that it is the most tightly bound, and therefore also the most stable of the three ${\mathrm{B}\mathrm{r}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{I}$ minima complexes.

The main difference between the two spectra is the relative size of the major photodetachment peaks. Spectral feature 2b is the largest peak in spectrum 1 due to the overlap of the ${}^2{\mathrm{P}}_{1/2}$ peaks of both pre‐reaction and post‐reaction intermediates, ${\mathrm{B}\mathrm{r}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{I}$ and ${\mathrm{I}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{B}\mathrm{r}$ respectively. In spectrum 2, the intensity of the peaks corresponding to the ${\mathrm{B}\mathrm{r}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{I}$ complex appears larger due to less formation of ${\mathrm{I}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{B}\mathrm{r}$ , and thus spectral feature 2a is the largest peak. Accounting for spin‐orbit effects, the difference between spectral features 1a and 1b is 0.97 eV, which is similar to the spin‐orbit constant of atomic iodine, ^[43] providing further evidence for the formation of ${\mathrm{I}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{B}\mathrm{r}$ . Likewise, the difference between spectral features 2a and 2b is 0.49 eV, which is similar to the spin‐orbit constant of atomic bromine, ^[42] hence providing more evidence to support the assignment of these peaks to the ${\mathrm{B}\mathrm{r}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{I}$ pre‐reaction intermediate. As the peaks between both spectra are consistent, the VDE values calculated for both the pre‐reaction and post‐reaction intermediates agree with the experimental data, and the gas mixtures in this study and those prior to it have not contained ${\mathrm{C}\mathrm{H}}_3\mathrm{B}\mathrm{r}$ , there is strong evidence to suggest that the ${\mathrm{S}}_{\mathrm{N}}2$ reaction involving ${\mathrm{B}\mathrm{r}}^{-}+{\mathrm{C}\mathrm{H}}_3\mathrm{I}$ has occurred. As for why the pre‐reaction and post‐reaction intermediates of the ${\mathrm{S}}_{\mathrm{N}}2$ reaction are observed in the spectra, a detailed explanation will be provided once the mechanism of the reaction is addressed.

Regarding the various ${\mathrm{S}}_{\mathrm{N}}2$ reaction mechanisms, evidence of the formation of Min1 and the lack of evidence of Min3 ultimately rules out the front‐side attack as the mechanism of which the ${\mathrm{S}}_{\mathrm{N}}2$ reaction occurs in this study. The formation of Min1 can either indicate the back‐side attack or the double‐inversion mechanism, however Czakó and co‐workers have previously reported that formation of Min1 from its bare substituents along the double‐inversion reaction pathway requires overcoming a large barrier of 53.0 kcal ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ (221.5 kJ ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ ). ^[23] In comparison, formation of Min1 along the back‐side attack reaction pathway is essentially barrierless, so while the double‐inversion mechanism cannot be ruled out as the reaction pathway that occurs in this study, it is energetically unfavourable relative to the back‐side attack mechanism.

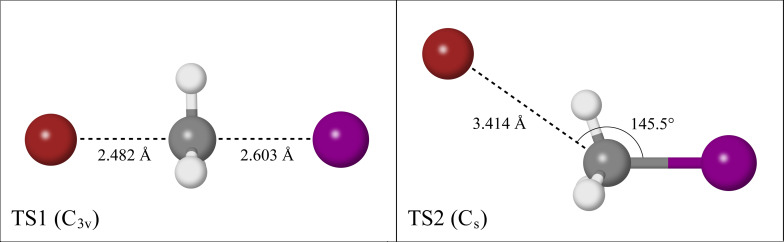
The hydrogen‐appended structure has previously been described as a pre‐reaction adduct before the formation of the ion‐dipole structure for numerous halide‐halomethane ${\mathrm{S}}_{\mathrm{N}}2$ reactions.[ ¹⁴ , ²⁴ , ²⁵ ] As this would imply that the hydrogen‐appended structure (Min2) is a pre‐cursor in the back‐side attack mechanism, which is the most likely reaction pathway that occurs in this study, it was imperative that additional computational analysis was performed. Two transition structures, one that links Min1 and Min4, and another that links Min1 and Min2, were optimised at CCSD(T)/AVTZ level of theory, as shown in Figure 3. The transition structure linking Min1 and Min4 involves the Walden inversion of the methyl group, which will be referred to as TS1. The transition structure linking Min1 and Min2 involves a hydrogen bound motif similar to Min2, which will be referred to as TS2.

Figure 3.

Transition structures along the back‐side attack reaction coordinate.

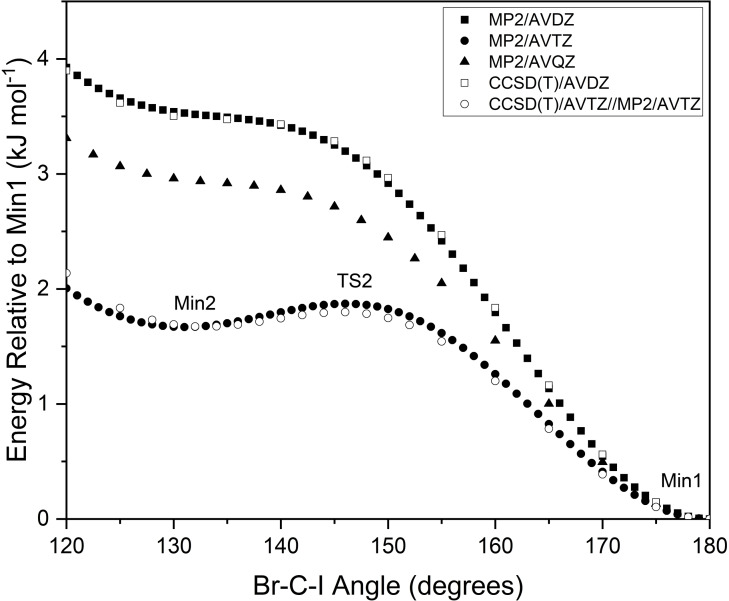
TS2 and Min2 both lie in a region of the potential energy surface that changes significantly depending on the level of theory used in the calculation. Figure 4 depicts multiple relaxed scans along the reaction coordinate that vary the ${\mathrm{B}\mathrm{r}}^{-}\cdots$ C−I angle. A preliminary scan at MP2/AVDZ theory yields only the ion‐dipole structure (Min1), however repeating this scan at MP2/AVTZ theory yields a local minimum that corresponds to Min2, and a local maximum that corresponds to TS2. Repeating the scan at MP2/AVQZ theory results in a potential energy surface similar to the MP2/AVDZ scan, with no presence of Min2 or TS2. A scan at CCSD(T)/AVDZ was performed, with results that are almost identical to the MP2/AVDZ scan, while a scan that calculated CCSD(T)/AVTZ energies from MP2/AVTZ geometries was also run to save on computational cost, giving results that emulate the MP2/AVTZ scan. Based on these results, it seems as though TS2 and Min2 are only able to be found when using Dunning's aug‐cc‐pVTZ basis sets with the pseudo‐potential derivatives on iodine and bromine.

Figure 4.

Relaxed scan of the potential energy surface along the back‐side attack pre‐reaction coordinate.

Attempting to perform a complete basis set (CBS) extrapolation of the single‐point energies of TS2 and Min2 yielded inconsistent results. The CCSD(T) energies calculated using AVDZ and AVQZ basis sets are both lower than the equivalent single‐point energies calculated for Min2, indicating that the potential energy surface located around TS2 is no longer a local maximum when using a different basis set, as is shown from the scans in Figure 4. When comparing the CCSD(T)/AVTZ energies of Min2 and TS2, the non‐zero‐point corrected barrier is only 0.12 kJ ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ . Correcting for zero‐point energies, this barrier reduces to −0.44 kJ ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ , indicating that TS2 is no longer a transition structure. Analysis of the harmonic frequency modes associated with Min2 reveal that modes ${\omega }_7$ and ${\omega }_8$ at 105 ${\mathrm{c}\mathrm{m}}^{-1}$ and 25 ${\mathrm{c}\mathrm{m}}^{-1}$ respectively, correspond to motion along the back‐side attack mechanism reaction coordinate. Accounting for the vibrational ground state ($\nu$ =0) of the complex, it would require approximately 0.63 kJ ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ and 0.15 kJ ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ for motion along these respective vibrational modes, both of which are higher than the previously mentioned 0.12 kJ ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ electronic barrier to TS2. Therefore, CCSD(T) calculations predict motion along the reaction coordinate from Min2 to form Min1 to be a transition that is barrierless, and so it is unlikely that Min2 is observed in the photoelectron spectra recorded in this study. This also highlights the difficulty that was encountered when attempting to optimise TS2 at the CCSD(T)/AVTZ level of theory, and may even explain why Szabó and Czakó were unable to optimise the equivalent transition structure for the ${\mathrm{C}\mathrm{l}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{I}$ system. ^[25]

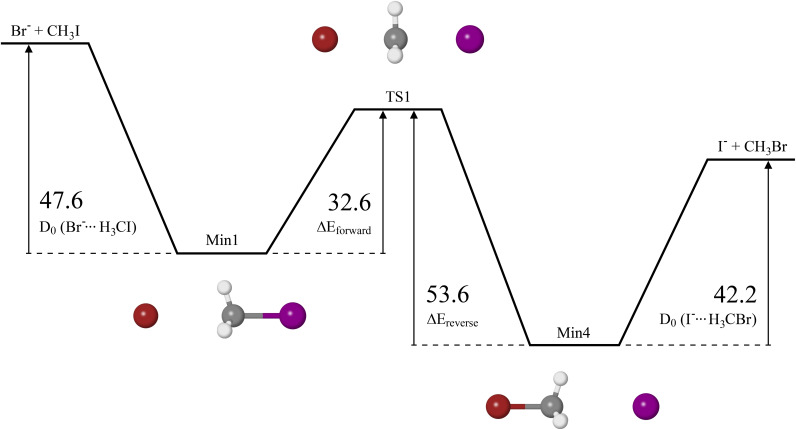
Figure 5 depicts the electronic potential energy surface for the back‐side attack mechanism of the ${\mathrm{B}\mathrm{r}}^{-}+{\mathrm{C}\mathrm{H}}_3\mathrm{I}\to {\mathrm{I}}^{-}+{\mathrm{C}\mathrm{H}}_3\mathrm{B}\mathrm{r}$ reaction, calculated at CCSD(T)/CBS level of theory. Similar to the ${\mathrm{D}}_0$ values, the central barrier height between Min1 and Min4 was zero‐point corrected. Min2 and TS2 are not included due to the CBS extrapolated energies predicting a barrierless transition from the reactants to Min1. In the forward direction, formation of Min1 has no barrier, upon which 32.6 kJ ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ is then required to overcome the central barrier to form Min4 (referred to as Δ${\mathrm{E}}_{\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{w}\mathrm{a}\mathrm{r}\mathrm{d}}$ ), followed by another barrier of 42.2 kJ ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ to dissociate into the products ${\mathrm{I}}^{-}$ and ${\mathrm{C}\mathrm{H}}_3$ Br. In the reverse direction, formation of Min4 is barrierless, and subsequent formation of Min1 requires overcoming a central barrier of 53.6 kJ ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ (referred to as Δ${\mathrm{E}}_{\mathrm{r}\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{e}}$ ), followed by another barrier of 47.6 kJ ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ to dissociate. Based on these results alone, the forward reaction will be favoured due to the energy of the products ${\mathrm{I}}^{-}$ and ${\mathrm{C}\mathrm{H}}_3$ Br and the central barrier both being lower than the energy of the reactants, ${\mathrm{B}\mathrm{r}}^{-}$ and ${\mathrm{C}\mathrm{H}}_3\mathrm{I}$ .

Figure 5.

Double‐well potential energy surface along the back‐side attack reaction coordinate calculated at the CCSD(T)/CBS level of theory, in kJ ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ .

The barrier heights for the ${\mathrm{B}\mathrm{r}}^{-}+{\mathrm{C}\mathrm{H}}_3\mathrm{I}\to {\mathrm{I}}^{-}+{\mathrm{C}\mathrm{H}}_3\mathrm{B}\mathrm{r}$ reaction have been reported in previous studies, a summary of which are shown in Table 3, as depicted in the potential energy surface diagram in Figure 5. Ervin and co‐workers calculated the barrier heights at the CCSD(T) level of theory using two different basis sets, one of which is the LanL2DZ basis set, and the other of which is the SDD basis set. ^[45] Czakó and co‐workers used CCSD(T)‐F12b/AVQZ theory in their respective study, ^[46] whereas Bickelhaupt and co‐workers used ZORA‐OLYP/TZ2P theory, ^[15] and Radom and co‐workers used G2(+) theory. ^[47] Compared to the CCSD(T)/CBS barrier heights reported in this study, the G2(+) barrier heights are in good agreement, with the largest difference being the ${\mathrm{D}}_0$ of the ${\mathrm{B}\mathrm{r}}^{-}\cdots {\mathrm{H}}_3\mathrm{C}\mathrm{I}$ complex at around 6.9 kJ ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ . At the CCSD(T)/LanL2DZ level of theory, the ${\mathrm{D}}_0$ of the ${\mathrm{B}\mathrm{r}}^{-}\cdots {\mathrm{H}}_3\mathrm{C}\mathrm{I}$ and ${\mathrm{I}}^{-}\cdots {\mathrm{H}}_3\mathrm{C}\mathrm{B}\mathrm{r}$ complexes reported by Ervin and co‐workers differ by less than 5.0 kJ ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ relative to the ${\mathrm{D}}_0$ values calculated in this study, however the Δ${\mathrm{E}}_{\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{w}\mathrm{a}\mathrm{r}\mathrm{d}}$ and Δ${\mathrm{E}}_{\mathrm{r}\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{e}}$ barrier heights reported are 18.8 kJ ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ and 18.3 kJ ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ less than those calculated in this study. The Δ${\mathrm{E}}_{\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{w}\mathrm{a}\mathrm{r}\mathrm{d}}$ barrier height calculated using the SDD basis set has better agreement with this study than the LanL2DZ basis set, however the other barrier heights calculated using the SDD basis set do not agree very well. All four barrier heights calculated for CCSD(T)‐F12b/AVQZ have good agreement with the respective barrier heights calculated in this study, the largest difference of which is 5.3 kJ ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ . The barrier heights reported by Bickelhaupt and co‐workers at the ZORA‐OLYP/TZ2P theory are all much lower than those reported in this study.

Table 3.

Comparison of the energies (kJ ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ ) calculated at 0 K in previous studies for the ${\mathrm{S}}_{\mathrm{N}}2$ reaction, relative to the reactants ${\mathrm{B}\mathrm{r}}^{-}+{\mathrm{C}\mathrm{H}}_3\mathrm{I}$ .

Barrier Height	$\mathrm{C}\mathrm{C}\mathrm{S}\mathrm{D}\left(\mathrm{T}\right)/{\mathrm{C}\mathrm{B}\mathrm{S}}^{\left[\mathrm{a}\right]}$	${\mathrm{C}\mathrm{C}\mathrm{S}\mathrm{D}\left(\mathrm{T}\right)/\mathrm{L}\mathrm{a}\mathrm{n}\mathrm{L}2\mathrm{D}\mathrm{Z}}^{\left[\mathrm{b}\right]}$	${\mathrm{C}\mathrm{C}\mathrm{S}\mathrm{D}\left(\mathrm{T}\right)/\mathrm{S}\mathrm{D}\mathrm{D}}^{\left[\mathrm{b}\right]}$	CCSD(T)‐F12b/${\mathrm{A}\mathrm{V}\mathrm{Q}\mathrm{Z}}^{\left[\mathrm{c}\right]}$	ZORA‐OLYP/${\mathrm{T}\mathrm{Z}2\mathrm{P}}^{\left[\mathrm{d}\right]}$	${\mathrm{G}2(+)}^{\left[\mathrm{e}\right]}$
${\mathrm{D}}_0$ (${\mathrm{B}\mathrm{r}}^{-}\cdots {\mathrm{H}}_3\mathrm{C}\mathrm{I}$ )	47.6	45.9	32.3	42.8	35.9	40.7
Δ${\mathrm{E}}_{\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{w}\mathrm{a}\mathrm{r}\mathrm{d}}$	32.6	13.8	28.3	30.9	15.0	38.4
Δ${\mathrm{E}}_{\mathrm{r}\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{e}}$	53.6	35.3	36.3	52.3	35.1	51.9
${\mathrm{D}}_0$ (${\mathrm{I}}^{-}\cdots {\mathrm{H}}_3\mathrm{C}\mathrm{B}\mathrm{r}$ )	42.2	37.6	31.1	36.9	28.0	36.3

[a] Calculated in this work in accordance with the W1w protocol. ^[48] [b] Ervin and co‐workers. ^[45] [c] Czakó and co‐workers. ^[46] [d] Bickelhaupt and co‐workers. ^[15] [e] Radom and co‐workers. ^[47]

The photoelectron spectra recorded in this study result from the photodetachment of two different chemical species, namely ${\mathrm{B}\mathrm{r}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{I}$ and ${\mathrm{I}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{B}\mathrm{r}$ . To the best of our knowledge, ${\mathrm{B}\mathrm{r}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{I}$ is a novel spectrum, however the photoelectron spectrum of ${\mathrm{I}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{B}\mathrm{r}$ has previously been recorded in two separate studies. Johnson and co‐workers were the first to publish a photoelectron spectrum of ${\mathrm{I}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{B}\mathrm{r}$ , however only the ${}^2{\mathrm{P}}_{3/2}$ peak at approximately 3.42 eV was visible due to the photon energy of the laser (3.875 eV) being less than the ${\mathrm{e}}_{\mathrm{B}\mathrm{E}}$ of the ${}^2{\mathrm{P}}_{1/2}$ state. ^[32] Mabbs and co‐workers published their ${\mathrm{I}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{B}\mathrm{r}$ photoelectron spectra more recently, with the focus being on tuning the wavelength of their laser to map out angular distributions, and were hence able to observe the ${}^2{\mathrm{P}}_{1/2}$ photodetachment peak at approximately 4.37 eV. ^[34] As was stated earlier, the ${\mathrm{I}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{B}\mathrm{r}$ photodetachment peaks in this study are in close agreement with the peaks observed in previous studies, providing further evidence that the ion‐dipole ${\mathrm{I}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{B}\mathrm{r}$ complex (Min4) is present in the photoelectron spectra.

As it appears that the back‐side attack mechanism is the reaction pathway that occurs in this study, an explanation can be provided as to why both the pre‐reaction and post‐reaction adducts of the ${\mathrm{B}\mathrm{r}}^{-}+{\mathrm{C}\mathrm{H}}_3\mathrm{I}$ ${\mathrm{S}}_{\mathrm{N}}2$ reaction are observed in this study. After dissociative electron attachment processes that allow the formation of ${\mathrm{B}\mathrm{r}}^{-}$ ions from ${\mathrm{C}\mathrm{H}}_2{\mathrm{B}\mathrm{r}}_2$ , any interactions of these ions with ${\mathrm{C}\mathrm{H}}_3\mathrm{I}$ will begin the ${\mathrm{S}}_{\mathrm{N}}2$ reaction without the need for additional energy, as shown in Figure 5 where the central barrier is lower than the energy of the reactants by 15.0 kJ ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ . It is also known that reactions involving ${\mathrm{B}\mathrm{r}}^{-}+{\mathrm{C}\mathrm{H}}_3\mathrm{I}$ occur rapidly in the gas phase with a rate constant of approximately $2.89\times {10}^{-11}$   ${\mathrm{c}\mathrm{m}}^3$   ${\mathrm{m}\mathrm{o}\mathrm{l}\mathrm{e}\mathrm{c}\mathrm{u}\mathrm{l}\mathrm{e}}^{-1}$   ${\mathrm{s}}^{-1}$ , ^[49] and given that the energy of the products is lower than the energy of the central barrier by 11.4 kJ ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ , it would typically be expected to observe the products of the ${\mathrm{S}}_{\mathrm{N}}2$ reaction, ${\mathrm{I}}^{-}$ and ${\mathrm{C}\mathrm{H}}_3\mathrm{B}\mathrm{r}$ . However, regarding the ion source used in the experimental apparatus, argon is present with a high partial pressure relative to ${\mathrm{C}\mathrm{H}}_2{\mathrm{B}\mathrm{r}}_2$ and ${\mathrm{C}\mathrm{H}}_3\mathrm{I}$ , so once the ${\mathrm{S}}_{\mathrm{N}}2$ reaction begins, collisions involving the argon and the nascent ${\mathrm{B}\mathrm{r}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{I}$ complexes occur, which stabilise the ${\mathrm{B}\mathrm{r}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{I}$ complexes before traversal over the central barrier, hence why ${\mathrm{B}\mathrm{r}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{I}$ is visible in the photoelectron spectra. Conversely, the argon may also stabilise the van der Waals complexes after overcoming the central barrier, but before forming the products ${\mathrm{I}}^{-}$ and ${\mathrm{C}\mathrm{H}}_3\mathrm{B}\mathrm{r}$ , which results in ${\mathrm{I}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{B}\mathrm{r}$ complexes being observed in the photoelectron spectra. If the ${\mathrm{S}}_{\mathrm{N}}2$ reaction goes to completion before acceleration down the time‐of‐flight tube, bare iodide will be formed and separated from the reaction adducts due to lower m/z ratio, so the majority of the iodide formed via the reaction will not be visible in the photoelectron spectra corresponding to the reaction adducts. Yet there does appear to be a small spectral feature at approximately 3.10 eV in the two spectra, which may correspond to bare iodide arising due to processes such as metastable dissociation of the ${\mathrm{I}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{B}\mathrm{r}$ complex after acceleration down the time‐of‐flight tube, or via two‐photon photodissociation of the ${\mathrm{C}\mathrm{H}}_3\mathrm{I}$ moiety within the ${\mathrm{B}\mathrm{r}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{I}$ complex. However, as this spectral feature has low intensity relative to the photodetachment peaks of the two complexes, it is believed that these other processes do not result in an appreciable amount of iodide being present in the spectra.

As for why Johnson and co‐workers, as well as Mabbs and co‐workers, did not observe any peaks corresponding to the ${\mathrm{B}\mathrm{r}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{I}$ complex in their respective studies, this requires discussing the reverse ${\mathrm{S}}_{\mathrm{N}}2$ reaction, i. e. the formation of ${\mathrm{B}\mathrm{r}}^{-}$ and ${\mathrm{C}\mathrm{H}}_3\mathrm{I}$ from ${\mathrm{I}}^{-}$ and ${\mathrm{C}\mathrm{H}}_3\mathrm{B}\mathrm{r}$ . As shown in Figure 5, 26.4 kJ ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ of energy is required for the reverse reaction to go to completion, and considering that the central barrier is higher than the energy of ${\mathrm{I}}^{-}$ and ${\mathrm{C}\mathrm{H}}_3\mathrm{B}\mathrm{r}$ by 11.4 kJ ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ , ${\mathrm{B}\mathrm{r}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{I}$ complexes stabilised by argon collisions in the ion source will be not be observed in the photoelectron spectra without sufficient energy input to traverse the central barrier.

Conclusions

In this study, anion photoelectron spectroscopy was utilised to study the gas‐phase ${\mathrm{B}\mathrm{r}}^{-}+{\mathrm{C}\mathrm{H}}_3\mathrm{I}$ ${\mathrm{S}}_{\mathrm{N}}2$ reaction, which has resulted in two distinct van der Waals complexes being observed, namely the pre‐reaction intermediate ${\mathrm{B}\mathrm{r}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{I}$ , and the post‐reaction intermediate ${\mathrm{I}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{B}\mathrm{r}$ . High‐level CCSD(T) calculations have been used in conjunction with mass spectrometry and anion photoelectron spectroscopy to provide evidence to support the occurrence of the ${\mathrm{S}}_{\mathrm{N}}2$ reaction. Three reaction intermediates pertaining to ${\mathrm{B}\mathrm{r}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{I}$ complexes, and one reaction intermediate pertaining to the ${\mathrm{I}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{B}\mathrm{r}$ complex were optimised at the CCSD(T)/AVTZ level of theory, with theoretical electron VDE values extrapolated to the complete basis set limit to provide accurate comparisons to the experimental data.

The photoelectron spectra recorded in this study result in three photodetachment peaks. Photodetachment peaks at 3.42 eV and 4.39 eV have been assigned to the respective ${}^2{\mathrm{P}}_{3/2}$ and ${}^2{\mathrm{P}}_{1/2}$ electronic states of the ion‐dipole ${\mathrm{I}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{B}\mathrm{r}$ complex, which agree with previous photoelectron spectroscopic studies of said complex, whereas to the best of our knowledge, photodetachment peak locations of the ${\mathrm{B}\mathrm{r}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{I}$ complex are being reported for the first time, observed at 3.81 eV and 4.30 eV. CCSD(T) calculations were also used to explore the possibility of various reaction pathways, of which the back‐side attack mechanism was considered to be the most likely pathway that the ${\mathrm{S}}_{\mathrm{N}}2$ reaction occurs in this study.

Experimental Section

The apparatus used to record the mass and photoelectron spectra comprises of a Wiley‐McLaren style time‐of‐flight mass spectrometer ^[50] to select the anions of interest, coupled to a photoelectron spectrometer with a magnetic bottle‐neck design. ^[51] The design and function of the spectrometer can be found in more detail in previous work.[ ⁵² , ⁵³ , ⁵⁴ ] The gas mixture required for the ${\mathrm{S}}_{\mathrm{N}}2$ reaction is comprised of trace amounts of ${\mathrm{C}\mathrm{H}}_3\mathrm{I}$ as the solvent species, and ${\mathrm{C}\mathrm{H}}_2{\mathrm{B}\mathrm{r}}_2$ as the bromide donor source. The remainder of the gas mixture is argon so that the total pressure is 400 kPa. A piezoelectric nozzle is used to pulse gas into the spectrometer, where it undergoes a supersonic expansion and is bombarded with energetic electrons originating from a hot rhenium filament. This allows the gas to undergo dissociative electron attachment processes which form various anion species, including van der Waals complexes. All anion species are accelerated along the time‐of‐flight axis to achieve mass separation. The desired anion species are intersected with a 266 nm (4.661 eV) laser pulse with a 10 Hz repetition rate, produced from the fourth harmonic of a Nd:YAG Spectra Physics Quantum Ray Pro. Detached photoelectrons are guided to a detector at the end of a 1.62 m flight tube by way of the previously mentioned bottle‐neck magnetic field, arising from the overlap of a divergent radial field with a homogeneous solenoid magnetic field applied along the length of the flight tube. The time‐of‐flight of the detached photoelectrons with respect to the laser pulse is recorded and then converted to electron kinetic energy (${\mathrm{e}}_{\mathrm{K}\mathrm{E}}$ ). Electron binding energy (${\mathrm{e}}_{\mathrm{B}\mathrm{E}}$ ) can then be determined using the known photon energy ($h\nu$ ) from the laser radiation, as shown via equation 2.

$${\displaystyle {\mathrm{e}}_{\mathrm{B}\mathrm{E}}=h\nu -{\mathrm{e}}_{\mathrm{K}\mathrm{E}}}$$ (2)

The conversion from electron time‐of‐flight to kinetic energy is a non‐linear process, and hence spectral intensities need to be readjusted. This involves a Jacobi transform, where the spectral intensities are multiplied by their time‐of‐flight cubed (${\mathrm{t}}^3$ ). An individual photoelectron spectrum is recorded over the course of 10000 laser shots, upon which a background spectrum is then recorded to substract from the main spectrum. Multiple background‐subtracted photoelectron spectra are summed together to form the final photoelectron spectrum. The spectra are also calibrated using the known bromine and iodine ${}^2{\mathrm{P}}_{3/2}$ and ${}^2{\mathrm{P}}_{1/2}$ peak positions to account for any drift in ${\mathrm{e}}_{\mathrm{K}\mathrm{E}}$ .

Computational Details

The Gaussian 09 program ^[55] was used for preliminary calculations and for the scans along the potential energy surface. The CFOUR computational chemistry program ^[56] was used for the geometry optimisations and energies of the individual substituents and complexes in this study, all of which were calculated at the CCSD(T) level of theory. All geometry optimisations and scans were performed using tighter convergence criteria ($1\times {10}^{-8}$   ${\mathrm{E}}_h$   ${\mathrm{a}}_0^{-1}$ ) given the loosely bound nature of van der Waals complexes. Dunning's augmented, correlation consistent basis sets were used for carbon and hydrogen (aug‐cc‐pVTZ), ^[57] while the effective core potential equivalents were used for bromine and iodine (aug‐cc‐pVTZ‐PP),[ ⁵⁸ , ⁵⁹ ] which are collectively referred to as AVTZ for simplicity. Following the geometry optimisations, vibrational frequency analysis calculations were performed at the same level of theory to test whether each structure was a minimum or a transition state on the potential energy surface. CCSD(T) single point energy calculations were performed for each structure using up to AVQZ basis sets in order to employ a two‐point complete basis set extrapolation in accordance with the W1w protocol. ^[48]

Vertical detachment energies (VDE) were calculated from the same geometry as their optimised anion structures, where the charge and multiplicity are altered to simulate the detachment of an electron. The predicted VDE values are then split into ${}^2{\mathrm{P}}_{3/2}$ and ${}^2{\mathrm{P}}_{1/2}$ spin‐orbit states based on the experimental spin‐orbit constants of bromine ^[42] for the ${\mathrm{B}\mathrm{r}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{I}$ complexes, and iodine ^[43] for the ${\mathrm{I}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{B}\mathrm{r}$ complex. A shift factor of −0.013 eV and −0.006 eV is applied to the simulated spin‐orbit states of the ${\mathrm{B}\mathrm{r}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{I}$ and ${\mathrm{I}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{B}\mathrm{r}$ complexes respectively, which is calculated based on the difference between the experimental and the simulated spin‐orbit states of each bare halogen,[ ³⁷ , ⁶⁰ ] shown in the supporting information.

Suppporting Information

• Structures and energetics of ${\mathrm{B}\mathrm{r}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{I}$ and ${\mathrm{I}}^{-}\cdots {\mathrm{C}\mathrm{H}}_3\mathrm{B}\mathrm{r}$ complexes, as well as vibrational modes and Cartesian coordinates

• Mass spectrum of gas mixture containing ${\mathrm{C}\mathrm{H}}_2{\mathrm{B}\mathrm{r}}_2$ , ${\mathrm{C}\mathrm{H}}_3\mathrm{I}$ and Ar, with a full assignment of mass spectral peaks

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supporting Information

H. T. Robinson, T. R. Corkish, C. T. Haakansson, P. D. Watson, A. J. McKinley, D. A. Wild, ChemPhysChem 2022, 23, e202200278.

Data Availability Statement

The data that support the findings of this study are available in the supplementary material of this article.