The Importance of Mg²⁺‐Free State in Nucleotide Exchange of Oncogenic K‐Ras Mutants

Abstract

For efficient targeting of oncogenic K‐Ras interaction sites, a mechanistic picture of the Ras‐cycle is necessary. Herein, we used NMR relaxation techniques and molecular dynamics simulations to decipher the role of slow dynamics in wild‐type and three oncogenic P‐loop mutants of K‐Ras. Our measurements reveal a dominant two‐state conformational exchange on the ms timescale in both GDP‐ and GTP‐bound K‐Ras. The identified low‐populated higher energy state in GDP‐loaded K‐Ras has a conformation reminiscent of a nucleotide‐bound/Mg²⁺‐free state characterized by shortened β2/β3‐strands and a partially released switch‐I region preparing K‐Ras for the interaction with the incoming nucleotide exchange factor and subsequent reactivation. By providing insight into mutation‐specific differences in K‐Ras structural dynamics, our systematic analysis improves our understanding of prolonged K‐Ras signaling and may aid the development of allosteric inhibitors targeting nucleotide exchange in K‐Ras.

Systematic structural and dynamic analysis of wildtype K‐Ras and its selected oncogenic mutations (G12C, G12D, and G12V) provides insight into mutation‐ and nucleotide‐specific differences aiding the development of allosteric inhibitors targeting K‐Ras signalling, in particular, the K‐Ras‐Sos interaction.

Introduction

K‐Ras, a prominent member of Ras superfamily among small GTPase proteins is responsible for approximately 20–30 % of all human cancers due to its oncogenic mutant variants frequently found in lung, colon, and pancreatic tumors.[ ¹ , ² ] Located in the cell membrane it acts as a ”molecular switch” involved in several signal transduction pathways (e. g. Ras‐Raf‐MEK‐ERK and Ras‐PI3‐K‐Akt) regulating cell growth, proliferation, and survival.[ ³ , ⁴ ] About 80 % of K‐Ras oncogenic mutations are found at the G12 position, ^[1] among which G12C, G12D, and G12V mutants are the most frequent ones (16 %, 40 %, and 26 % of all G12 mutants, respectively). ^[5] Ras proteins, with most known family members of H‐Ras, N‐Ras, and K‐Ras (translated in cells in two splice variants, K‐Ras4A and K‐Ras4B proteins), bind GTP in their active and GDP in their inactive form together with a Mg²⁺ cofactor in both states. ^[6] Their ”molecular switch” function is related to growth factors such as the epidermal growth factor (EGF) ^[7] inducing Ras to transform from the inactive GDP‐bound state to the active GTP‐bound state, accompanied by the ordering and exposure of its effector binding surface allowing the coordination and activation of downstream effectors including Raf kinase, PI3 K, and RalGDS. ^[8] The growth signal is switched off by the hydrolysis of GTP causing the transition to the inactive GDP‐bound form. The intrinsic nucleotide switching capacity of Ras proteins (activation through GDP→GTP exchange) as well as their GTP‐hydrolysis (inactivation) efficiency is poor, thus both of these steps are assisted by “factor” proteins, such as GEFs (Guanine nucleotide Exchange Factors, for example Sos) for activation and GAPs (GTPase Activating Proteins, for example p120 GAP) for the inactivation step. ^[9] GAP and GEF proteins also allow for the regulation of the entire Ras cycle. Oncogenic mutations affect the kinetics of elementary processes of the Ras cycle by either decreasing the rate of GTP‐hydrolysis or increasing the rate of nucleotide exchange (or both), thereby elevating the lifetime of the active GTP‐bound form maintaining cell growth, proliferation, and survival signals exaggeratedly. ^[10]

Ras proteins show a high degree of structural conservation in their guanosine nucleotide‐binding domain (G‐domain of ∼20 kDa; residues 1–166), however they markedly differ in the short hypervariable region (HVR, residues 167–188/189) at the C‐terminal end, responsible for membrane localization. ^[11] The G‐domain consists of a Rossmann‐fold‐like topology comprising six β‐strands, five α‐helices, and ten loops between them (Figure S1). ^[12] Its N‐terminal effector lobe (M1‐N86 residues), which is completely identical among Ras proteins, communicates with downstream effectors and contains the regions involved in GTP hydrolysis and nucleotide exchange: the P‐loop (G10‐S17) as well as switch‐I (Q25‐Y40) and switch‐II (D57‐G75) regions, ^[13] which undergo the most significant structural rearrangement along the catalytic cycle. The C‐terminal allosteric lobe (T87‐H166) is responsible for the regulation of the effector lobe through allosteric interaction networks, and it is more specific for each family member. ^[14]

As internal motions often participate in the formation of transiently appearing binding sites, communication networks coupled to the regulation of the catalytic cycle, membrane targeting, or determining the pliability of effector‐binding regions,[ ¹⁵ , ¹⁶ ] internal dynamics plays an important role not only in K‐Ras function, but also in the potential mechanisms of its inhibition. While experiments characterizing internal dynamics have extensively been carried out for H‐Ras,[ ¹⁷ , ¹⁸ , ¹⁹ , ²⁰ , ²¹ , ²² , ²³ , ²⁴ , ²⁵ , ²⁶ , ²⁷ , ²⁸ , ²⁹ , ³⁰ , ³¹ ] K‐Ras has come into the spotlight more recently due to the huge efforts to find applicable drugs against its oncogenic mutants.[ ³² , ³³ , ³⁴ , ³⁵ ]

Within the catalytic cycle, examination of the GTP‐bound form is especially challenging due to the intrinsic hydrolysis of GTP thereby preventing the performance of time‐consuming NMR relaxation measurements. To overcome this difficulty, non‐hydrolyzable GTP analogues (mostly GppNHp and GTPγS) have been used instead of native GTP. However, using non‐hydrolyzable GTP analogues has been shown to affect the dynamic properties of the complex. ^[26] A possible solution to the problem is accelerating GDP→GTP nucleotide exchange by adding GEF to Ras, ^[30] or by using a large excess of GTP after destabilizing the GDP‐bound form. Using the latter new methodology, we were able to investigate the fast dynamics of wildtype K‐Ras (wt) as well as its G12C and G12D mutants in their native GTP‐bound forms and established a new mechanism for GTP autohydrolysis, and the effect of oncogenic mutations on it. ^[36] In the present work, we extended the analysis to the investigation of yet another oncogenic P‐loop mutant, G12V K‐Ras, in its GDP‐ and native GTP‐bound forms (Figure S2–S3, Table S1–S3). Furthermore, as internal fluctuations on the μs‐ms time scale appear to be the most relevant to conformational transitions of the Ras‐cycle,[ ²² , ²⁶ , ²⁸ , ³⁷ , ³⁸ ] we present a systematic analysis of slow time scale dynamics of K‐Ras‐wt, G12C, G12D, and G12V in GDP‐ and native GTP‐bound states using Carr‐Purcell‐Meiboom‐Gill (CPMG) relaxation dispersion[ ³⁹ , ⁴⁰ ] and chemical exchange saturation transfer (CEST)[ ⁴¹ , ⁴² ] NMR measurements in combination with MD simulations. A dominant two‐state conformational exchange between a major and a low‐populated minor form is revealed on the ms timescale in both GDP‐ and GTP‐bound K‐Ras and using the Mg²⁺‐free state of G12C K‐Ras ⋅ GDP as a reference, we propose that Mg²⁺ release plays a significant role in forming the conformational landscape of Ras proteins. Mutation‐ and nucleotide‐specific differences of the exchange process revealed by our analysis improves the understanding of the role of oncogenic mutations in altering the dynamics of elementary processes in the Ras‐cycle.

Results and Discussion

Slow dynamics of GDP‐bound K‐Ras forms

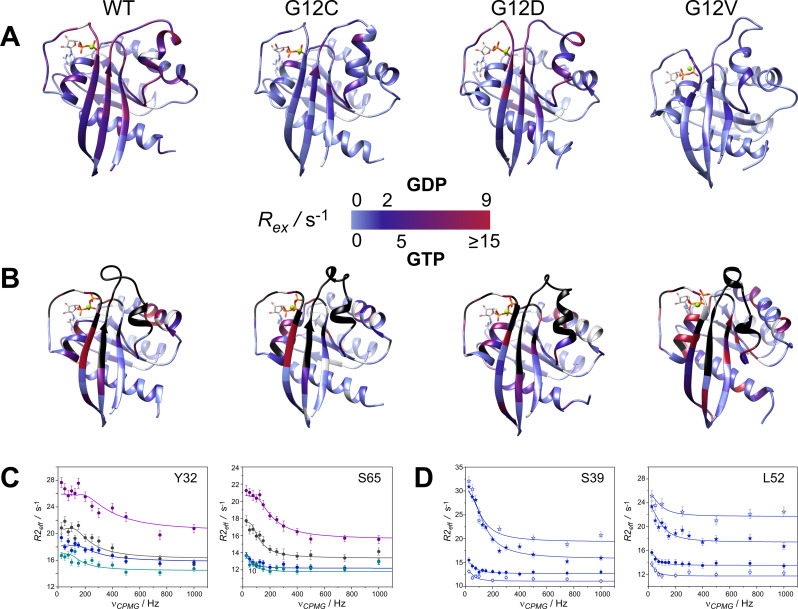
CPMG‐relaxation dispersion (R_ex)[ ³⁹ , ⁴⁰ ] NMR measurements probing the ms timescale motion of proteins are powerful tools for the analysis of conformational exchange processes with the advantage of providing kinetic, thermodynamic, and structural information on the exchanging states. To obtain a residue‐level analysis of slow dynamics in GDP‐ and cofactor‐bound K‐Ras variants and search for mutation‐specific differences, R_ex measurements have been performed on wt and oncogenic P‐loop K‐Ras mutants. According to our analysis, regions undergoing conformational fluctuations on the timescale amenable to CPMG R_ex measurements (∼0.3–10 ms) primarily include the β1‐L1 region comprising part of the P‐loop, L2‐β2 of switch‐I, β3, L4‐α2 of switch‐II continuing in L5 and part of α3 (Figure 1A). As judged by the number of residues exhibiting values of R_ex>2 Hz (Figure 1A, S4), conformational fluctuations are most pronounced in wt and G12D K‐Ras ⋅ Mg²⁺ ⋅ GDP. In G12C and G12V, the values of R_ex are considerably smaller in both the switch‐I and the switch‐II regions, whereas in G12D they approach or even exceed the ones observed in the wild‐type. Similar trends have been observed previously in backbone N−H chemical shift differences (Δδ) between wt and the three mutants ^[43] indicating that the dynamic features are related to structural differences. Representative transverse relaxation dispersions as a function of the CPMG field strength are plotted (Figure 1C). Residues with a non‐flat relaxation dispersion profile can be subjected to a global fit assuming a two‐state exchange with the kinetics of the exchange process and the population of the higher energy state being similar in wt and the mutants (Table 1). Values of k_ex range between ∼100–350 s⁻¹ with G12C being the slowest and G12D the fastest among the investigated variants. Population of the higher energy state ranges between 1.5–2.8 %, with lowest values observed for G12D and G12V. The chemical shift differences found for individual ¹⁵N spins between the ground and the higher energy states (|Δδ_EG|) are shown (Figure 2) and listed (Table S4). The largest structural differences between the two states are indicated in the C‐terminal half of switch‐I (e. g. Y32–D33, T35, E37–D38) and in switch‐II (e. g. T58), corresponding to a site where the two switch‐regions meet. Additionally, a highly dynamic segment on the ms‐timescale is observed in the C‐terminal half of α2 (T74–G75). This pattern is similar in each of the variants with subtle differences occurring between wt and the mutants.

Figure 1.

Values of ¹⁵ N R _ex (at 800 MHz for ¹H) of the investigated ¹⁵ N‐labeled (A) K‐Ras ⋅ Mg²⁺ ⋅ GDP and (B) K‐Ras ⋅ Mg²⁺ ⋅ GTP variants (25 °C, pH 7.4) mapped on the corresponding MD‐derived structures ([36] and current study) in a blue‐to‐red gradient. R _ex is estimated from the difference in R _2,eff at the lowest and highest ν _CPMG values. Note the slightly different scale for GTP‐bound complexes for better viewing the differences between the investigated variants. Prolines and amino acid positions exhibiting a flat dispersion profile are colored in grey. Unassignable residues due to severe line broadening in the GTP‐bound state are colored in black. Transverse relaxation dispersions of the backbone ¹⁵ N nuclei of representative residues of (C) the switch‐I (Y32) and the switch‐II (S65) regions in wild‐type (black), G12C (blue), G12D (magenta), and G12V (aqua) K‐Ras ⋅ Mg²⁺ ⋅ GDP and (D) the switch‐I region (S39) and β3 preceding switch‐II (L52) in GDP‐ (circle) and GTP‐bound (star) forms of G12C K‐Ras ⋅ Mg²⁺ as a function of CPMG B₁ field strength at static magnetic fields of 14.1 T (open symbols) and 18.8 T (closed symbols). Solid lines correspond to global two‐state exchange models with parameters listed in Table 1.

Table 1.

Kinetic and thermodynamic parameters of conformational exchange for the investigated K‐Ras variants in their GDP‐ and GTP‐bound forms deduced from a global fit analysis of ¹⁵ N backbone relaxation dispersion NMR measurements (T=25 °C, pH 7.4).

	K‐Ras‐wt	K‐Ras‐G12C	K‐Ras‐G12D	K‐Ras‐G12V
	GDP‐bound forms
k ex/s−1	164±28	99±26	345±47	172±35
p E/%	2.8±0.2	2.4±0.2	1.7±0.2	1.5±0.2
k GE/s−1	4.6±0.8	2.4±0.7	5.9±1.1	2.6±0.6
k EG/s−1	159±32	97±28	339±73	169±47
ΔG GE/kcal/mol	2.1±0.2	2.2±0.2	2.4±0.2	2.5±0.2

	GTP‐bound forms
k ex/s−1	404±54	500±67	332±42	312±51
p E/%	7.8±0.2	4.5±0.3	8.4±0.3	5.9±0.3
k GE/s−1	32±4	23±3	28±4	18±3
k EG/s−1	373±52	478±78	304±41	294±52
ΔG GE/kcal/mol	1.5±0.1	1.8±0.1	1.4±0.1	1.6±0.1

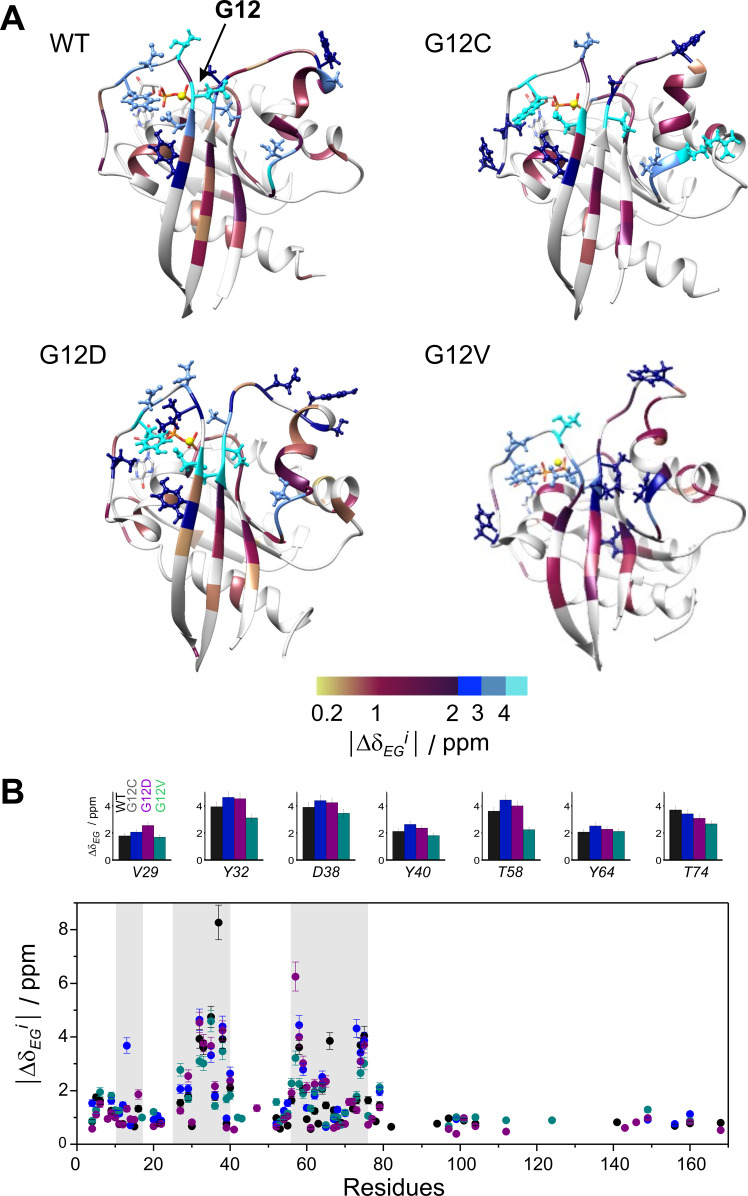
Figure 2.

Backbone ¹⁵ N chemical shift differences between the ground and higher energy state (|Δδ _EG ⁱ|) as derived from CPMG relaxation dispersion measurements of the investigated GDP‐bound K‐Ras variants with parameters listed in Table 1. (A) Values of |Δδ _EG ⁱ| are mapped on the ribbon diagram of the corresponding MD‐derived structures ([36] and current study). Residues exhibiting |Δδ _EG ⁱ| exceeding 2 ppm are highlighted in a ball‐and‐stick representation for better viewing. Prolines and amino acid positions exhibiting a flat dispersion profile or with no available data are colored in grey. The site of the mutation is indicated by arrow. (B) Values of |Δδ _EG ⁱ| as a function of amino acid sequence in wild‐type (black), G12C (blue), G12D (purple), and G12V (green) K‐Ras ⋅ Mg²⁺ ⋅ GDP. For representative residues, |Δδ _EG ⁱ| in the investigated K‐Ras variants are shown in large at the top. Regions of the P‐loop, switch‐I, and switch‐II are highlighted in a grey background.

To complement the CPMG relaxation dispersion analysis and check for the possibility of the presence of even smaller frequency motions, ¹⁵N ‐CEST measurements sensitive to motions on the ∼2–50 ms time scale were performed. Notably, CEST experiments are able to detect sporadic conformers well below 1 % population, that are not detectable during regular (e. g. ¹H,¹⁵N‐HSQC) NMR experiments. ^[44] Similar to the CPMG R _ex data, evaluation of the CEST experiments yielded a global fit of CEST curves for all four of the investigated GDP‐bound K‐Ras variants, using two‐state models. This is an indicator of the presence of concerted slow motions, with an additional benefit of observing the sign of chemical shift difference between the major and the minor conformers even by visual inspection. To avoid ambiguities, only a non‐overlapping subset of residues with a well‐defined main and minor peak has been included in the analysis for each variant. Residues included in the analysis are listed in Table 2 and S5 together with the obtained k _ex and p _E values. The obtained CEST curves are shown in Figure S5–S8. Despite the limited dataset, the CEST‐derived exchange rates and populations are in fairly good agreement with those obtained from the relaxation dispersion analysis indicating that there is a single dominant slow‐timescale motion in the GDP‐bound K‐Ras complex. Backbone ¹⁵N chemical shift differences obtained from the fitting (Table 2) for most residues are in good agreement with the R _ex‐derived values of |Δδ _EG|. Values of |Δδ _EG| could also be estimated by calculating the differences in ¹⁵ N‐chemical shifts of the two minima in the CEST curves giving an estimated value for those residues which could not be fitted (Table 2).

Table 2.

Comparison of ¹⁵N chemical shift differences between Mg²⁺‐bound and Mg²⁺‐free states as obtained directly from ¹H,¹⁵N‐HSQC spectra (Δδ _Mg(¹⁵N)) with the CEST‐derived chemical shift difference (Δδ _EG ^CEST) between the ground and higher energy state for the investigated GDP‐ and cofactor‐bound K‐Ras variants. In case of the CEST‐derived data, both fitted and estimated (from the difference between the two minima of the CEST curve) values are listed. Chemical shift differences for a given residue obtained from the two different experiments show a good agreement as indicated by the correlation factor (R ²). Exchange rates and population of the higher energy state obtained from the global fit of CEST curves for each variant are shown at the top. See text for details.

Res.	wt K‐Ras ⋅ Mg2+ ⋅ GDP k ex=267±20 s−1 p E=3.8±0.1 %			G12C K‐Ras ⋅ Mg2+ ⋅ GDP k ex=214±61 s−1 p E=1.3±0.1 %			G12D K‐Ras ⋅ Mg2+ ⋅ GDP k ex=668±60 s−1 p E=2.0±0.1 %			G12V K‐Ras ⋅ Mg2+ ⋅ GDP k ex=492±56 s−1 p E=1.5±0.1 %
	Δδ Mg/ppm	Δδ EG CEST/ppm		Δδ Mg/ppm	Δδ EG CEST/ppm		Δδ Mg/ppm	Δδ EG CEST/ppm		Δδ Mg/ppm	Δδ EG CEST/ppm
		estim.	fit		estim.	fit		estim.	fit		estim.	fit
Y32	−4.05	−4.50	−4.35	−4.64	−4.50	N/A	−4.04	−4.00	−4.49	−4.61	−4.50	−5.11
D33	−3.34	−3.00	−3.62	−3.43	−3.50	N/A	−3.12	−2.00	−3.70	−3.62	−3.50	N/A
T35	3.43	3.50	3.24	3.92	3.50	3.73	3.21	2.00	N/A	3.98	3.50	N/A
E37	−7.58	−7.50	−7.93	−8.50	−8.50	−8.77	−7.61	−8.00	−7.95	−8.43	−8.50	−8.95
D38	−3.65	−4.00	−4.22	−4.28	−4.50	−4.77	−3.52	−2.50	−4.11	−4.30	−4.50	−5.00
D57	−7.22	−7.00	−7.27	−7.23	−7.00	N/A	N/A	−7.00	−7.12	−7.28	−6.50	N/A
T58	4.03	4.00	3.69	4.34	4.50	4.27	3.98	2.50	N/A	4.70	4.50	N/A
Y64	−2.39	−2.50	−2.89	−2.55	−2.00	N/A	N/A	N/A	N/A	−2.51	−2.50	N/A
T74	2.71	2.00	2.39	2.71	2.50	N/A	2.94	2.50	2.57	2.62	2.00	2.05
G75	−3.34	−3.50	−3.75	−3.59	−3.50	N/A	−3.47	−3.00	−4.03	−3.63	−3.50	−4.02
R 2	–	0.994	0.999	–	0.997	0.999	–	0.968	0.996	–	0.994	0.997

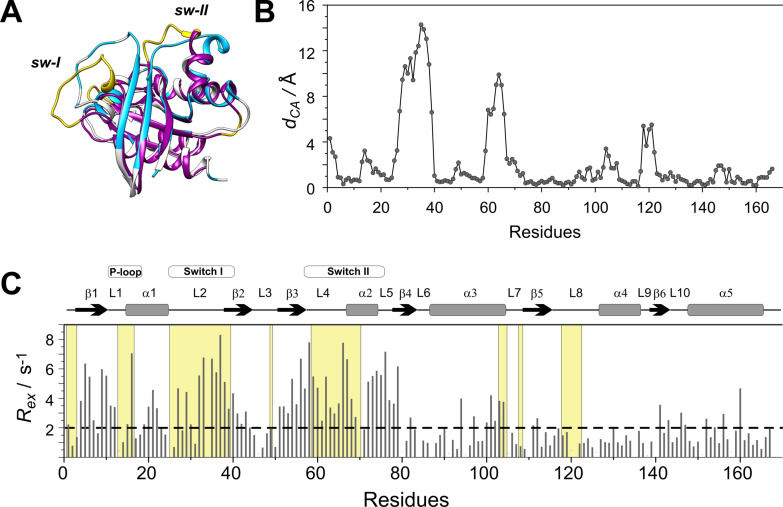
The segments involved in slow dynamics map to the regions undergoing a conformational remodeling upon interaction with Sos as GEF (Figure 3). The amino acid positions in nucleotide‐free H‐Ras displaying C^α positional changes larger than 2 Å upon Sos‐binding are highlighted. The match between the regions involved in ms timescale dynamics in K‐Ras ⋅ Mg²⁺ ⋅ GDP and those reorganized upon Sos‐binding indicates that the higher‐energy state inferred from the CPMG measurements may be reminiscent of a Sos‐bound state exhibiting a more open switch‐I region and a rearranged switch‐II. ^[13] Noteworthy, K‐Ras segments displaying a ms mobility overlap with regions of Ras displaying conformational differences upon the binding of small‐molecule inhibitors disrupting the Ras‐Sos interaction[ ⁴⁵ , ⁴⁶ , ⁴⁷ ] and with regions of Ras undergoing a global motion on the μs timescale. ^[28]

Figure 3.

(A) Superimposed structures of K‐Ras ⋅ Mg²⁺ ⋅ GDP (MD derived structure ^[36] ) (grey) and the nucleotide free H‐Ras ⋅ Sos compex (PDB: 1BKD, magenta). Regions displaying C^α positional differences larger than 2 Å between the two complexes are highlighted in yellow. Residues exhibiting a contribution to transverse relaxation of R _ex >2 Hz in K‐Ras ⋅ Mg²⁺ ⋅ GDP are depicted in blue. (B) C^α positional differences between K‐Ras ⋅ Mg²⁺ ⋅ GDP and H‐Ras ⋅ Sos along the amino acid sequence. (C) Values of ¹⁵ N R _ex (at 800 MHz for ¹H) of ¹⁵N‐labeled wild‐type K‐Ras ⋅ Mg²⁺ ⋅ GDP (T=25 °C, pH 7.4) as a function of amino acid sequence. R _ex is estimated from the difference in R _2,eff at the lowest and highest ν_CPMG values. Secondary structural elements are indicated at the top. Regions displaying d _CA>2 Å in (B) are shown in a yellow background.

Slow dynamics in GTP‐bound K‐Ras variants

In comparison to the GDP‐loaded form, in the presence of physiological GTP, values of R _ex become nearly an order of magnitude larger at many of the amino acid positions (Figure S9). Unfortunately, similarly to previous investigations on H‐Ras,[ ¹⁸ , ²² , ²⁹ , ³⁰ , ³¹ ] severe line broadening obscures the analysis of CPMG measurements in nearly the entirely length of switch‐II and in segments of switch‐I. However, values of R _ex>10 Hz in and the vicinity of the P‐loop and switch‐I indicate a dominant effect of ms timescale fluctuations throughout the effector lobe. Moreover, in comparison to the GDP‐complex, more intense slow motion is suggested in α3 and in other segments of the allosteric lobe including β5 and the β6‐L10‐α5 region. When comparing the GTP‐bound variants, values of R _ex estimated from the raw data in the analyzable regions tend to be the largest in wt and smallest in G12C, and most residues exhibiting an R _ex>10 Hz have been found in G12V K‐Ras ⋅ Mg²⁺ ⋅ GTP (Figure S9, Figure 1B). We note that on the basis of the raw data, many of the unassignable broad peaks exhibit large values of R _ex in each of the variants, suggesting that many of the ‘missing’ residues are part of the fluctuating network as well.

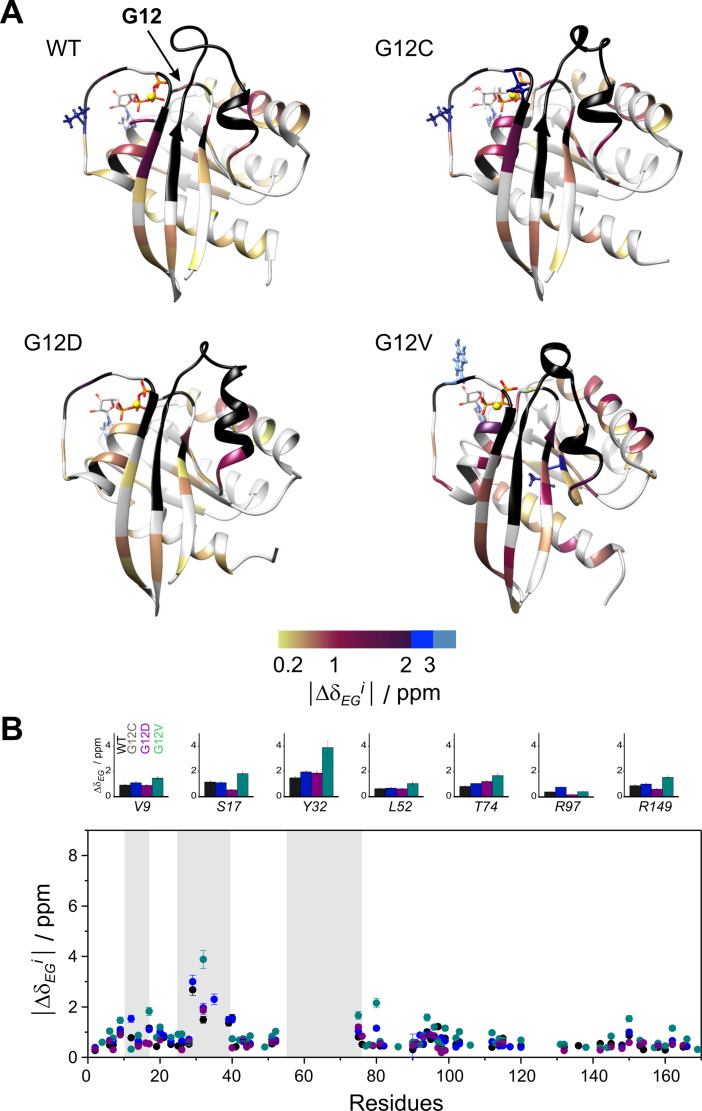
Similar to the GDP‐loaded state, residues with a non‐flat relaxation dispersion profile can be subjected to a global fit assuming a two‐state exchange with kinetics and thermodynamics similar in wt and the mutants (Table 1). The exchange process is fastest in G12C (500±67 s⁻¹) and slowest in G12V (312±51 s⁻¹) with population of the higher energy state ranging between 4.5±0.3 % (G12C) and 8.4±0.3 % (G12D). With the exception of G12D K‐Ras ⋅ Mg²⁺ ⋅ GTP (where k _ex is the same in the GTP‐ and the GDP‐bound forms), the exchange is 2–5 times faster than in the GDP‐bound forms. Representative transverse relaxation dispersions in comparison to the GDP‐bound form for one of the investigated mutants are plotted in Figure 1D. Chemical shift differences between the ground and the higher energy state indicative of the structural differences between the exchanging states are depicted in Figure 4 and listed in Table S6. In wt, values of |Δδ _EG| range between 0.3‐2.4 ppm, with most significant distinctions between the two states (|Δδ _EG|>1 ppm) observed at S17, V29, Y32, S39, Y40 (switch‐I), I93, and Y96 (α3) with most of switch‐I and switch‐II remaining exchange broadened. Noteworthy, most of the unassignable residues could be included in the global fit. When comparing the R _ex‐derived values of |Δδ _EG|, G12V appears to be the most distinct exhibiting considerably larger structural differences between the exchanging states than in wt in most segments of the protein (Figure 4).

Figure 4.

Backbone ¹⁵ N chemical shift differences between the ground and higher energy state (|Δδ _EG ⁱ|) as derived from CPMG relaxation dispersion measurements on the investigated GTP‐bound K‐Ras variants with parameters listed in Table 1. (A) Values of |Δδ _EG ⁱ| are mapped on the ribbon diagram of the corresponding MD‐derived structures ([36] and current study). Residues exhibiting |Δδ _EG ⁱ| exceeding 2 ppm are highlighted in a ball‐and‐stick representation for better viewing. Prolines and amino acid positions exhibiting a flat dispersion profile or with no available data are colored in grey. The site of the mutation is indicated by arrow. Unassignable residues due to severe line broadening are colored in black. (B) Values of |Δδ _EG ⁱ| as a function of amino acid sequence in wild‐type (black), G12C (blue), G12D (purple), and G12V (green) K‐Ras ⋅ Mg²⁺ ⋅ GTP. For representative residues, |Δδ _EG ⁱ| in the investigated K‐Ras variants are shown in large at the top. Regions of the P‐loop, switch‐I, and switch‐II are highlighted in a grey background.

Similarly to the GDP‐loaded form, the K‐Ras regions involved in slow dynamics evidenced either by exchange broadening or non‐flat R_ex profiles in GTP‐loaded K‐Ras overlap with those exhibiting the largest structural differences between the Sos‐bound and Sos‐free forms of H‐Ras (Figure S10). This suggests that the detected sparsely populated state might correspond to a pre‐existing conformation of the Sos‐bound K‐Ras. This is consistent with previous analysis of conformational exchange in GTP‐ (or non‐hydrolyzable analogue)‐bound Ras isoforms[ ¹⁹ , ²¹ , ²² , ²³ , ²⁵ , ²⁶ , ²⁷ , ³⁰ , ³¹ , ³⁷ ] indicating the presence of two dominating states differing primarily in the conformation of switch‐I, attributed to the effector binding 2(T) and to an exchange factor binding 1(T) states. Specifically, the relation of the low‐populated state to a GEF‐competent conformation has been suggested for GTP‐bound H‐Ras, with its ¹⁵N‐chemical shifts showing a good correlation with that of H‐Ras‐T35A‐GTP, which exhibits similar ³¹P chemical shifts as the effector‐incompetent state 1. ^[30] Of note, the GppNHp‐bound state of T35S H‐Ras, considered to be an appropriate representation of state 1, has been shown to exhibit an enhanced fluctuation in the switch‐I region sampling an open conformation of switch‐I ^[24] similar to the nucleotide‐free form found in the H‐Ras ⋅ Sos complex. ^[13]

Structural characterization and fast dynamics of Mg²⁺‐free G12C K‐Ras ⋅ GDP

Changes in Mg²⁺ saturation of Ras‐GDP complexes have been found to result in a coupled change in the effectiveness of nucleotide release. ^[48] Based on this observation, we hypothesized that Sos‐mediated nucleotide release and rebinding may be accomplished through a Mg²⁺‐free state. This inspired us to carry out a structural and dynamic characterization of the Mg²⁺‐free state of one of the most studied oncogenic mutant, G12C K‐Ras, whose nucleotide‐ and Mg²⁺‐bound forms we have analyzed previously.[ ³⁶ , ⁴³ ] The presence of GDP and the absence of Mg²⁺ in the complex have been confirmed by mass spectrometry.

Backbone and side chain ¹ H, ¹⁵ N, and ¹³ C resonances of Mg²⁺‐free G12C K‐Ras ⋅ GDP were assigned using a standard set of triple resonance NMR measurements leading to a near complete (96 %) assignment of the non‐proline residues (Figure S11A). Secondary structure elements were predicted by calculating secondary structure propensities (SSP) ^[49] relying on C^α, C^β, and H^α chemical shifts (Figure S11B). Overall, the general K‐Ras topology comprising six β‐strands and five α‐helices is well maintained in the absence of the cofactor as well. No structural change is indicated in the vicinity of nucleotide‐binding residues either. However, characteristic differences have been observed near the N‐terminal segment of β2 (D38, S39) and in the C‐terminal half of β3 (I55–T58), indicating a shortening of the two β‐strands in the Mg²⁺‐free form (Figure 5A). Among the affected residues, T58 indirectly participates in binding of the cofactor ‐ its carbonyl oxygen atom being H‐bonded to one of the water molecules in the coordination sphere of the Mg²⁺. ^[50] Besides this, the cofactor forms merely two direct interactions with the nucleotide‐loaded protein matrix, one with the side chain of S17 and one with the β‐phosphate of GDP. The remaining four positions of its coordination sphere are filled with water molecules reinforced in their positions by forming H‐bonds with backbone carbonyls of both switch‐I (Y32, D33, P34, I36) and switch‐II (T58) residues and the sidechain of D57. Comparison of the crystal structures of various forms of Ras proteins indicate that shortening of the β2 and β3 strands has thus far only been observed in the Sos complex of Ras (PDB: 1XD2). ^[51]

Figure 5.

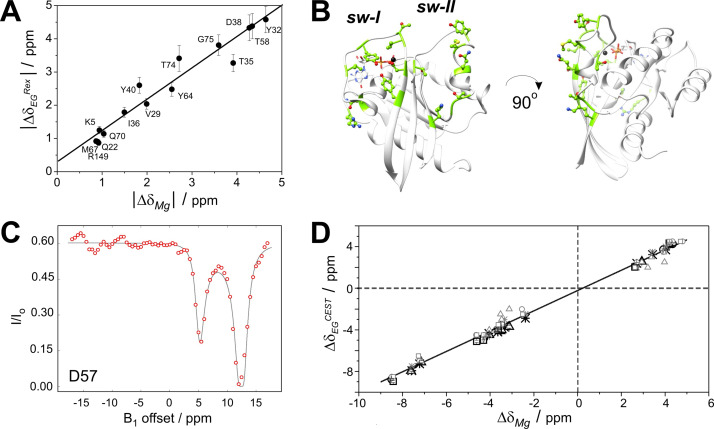
(A) Changes in secondary structure (based on SSP analysis, depicted in yellow), flexibility (based on Lipari‐Szabo model free analysis, depicted in orange), or both (depicted in red) upon Mg²⁺‐loss in G12C K‐Ras ⋅ GDP with respect to the cofactor‐bound form illustrated on the MD‐derived structure of G12C K‐Ras ⋅ Mg²⁺ ⋅ GDP. (B) Chemical shift perturbations (Δδ) of backbone amide ¹ H and ¹⁵ N nuclei between Mg²⁺‐bound and Mg²⁺‐free G12C K‐Ras ⋅ GDP. An arbitrary limit of 0.5 ppm is shown as a horizontal line. (C) Relaxation parameters (R ₁, R ₂, HetNOE) and (D) their analysis by Lipari‐Szabo model‐free formalism (S ², R _ex, τ _e) and reduced spectral density mapping (J(ω _h)) of G12C K‐Ras ⋅ GDP in its Mg²⁺‐free form as a function of the amino acid sequence. Regions of the P‐loop (red, residues 10–17), switch‐I (orange, residues 25–40), and switch‐II (blue, residues 57–75) are highlighted.

Residues exhibiting a significant chemical shift perturbation (Δδ>0.5 ppm, arbitrary limit) are found in the P‐loop (G13), switch‐I (V29, Y32, D33, T35, I36, E37, D38, S39, Y40), and switch‐II (D57, T58, Y64, T74, G75) regions (Figure 5B). Importantly, the affected residues are not limited to those involved directly in Mg²⁺ coordination but indicate the effect of the cofactor in additional regions. Remarkably, some of the residues exhibiting large Δδ between the two forms show a contribution of conformational exchange to transverse relaxation in G12C K‐Ras ⋅ Mg²⁺ ⋅ GDP (e. g. G13, D33, E37, D57, T58). ^[36] Among them, E37 exhibits an extreme value of both Δδ (2.3 ppm, while Δδ_avg=0.2 ppm) and R _ex (9.8 s⁻¹, while R _{ex, avg}=3.6 s⁻¹).

The summary of dynamic parameters inferred from Lipari‐Szabo model‐free analysis and reduced spectral densities are shown in Table S1 and Figure 5C and 5D (with experimental and calculated data given in Table S7 and S8). The tendencies in R ₁, R ₂, and HetNOE values are comparable to GDP‐bound G12C K‐Ras ⋅ Mg²⁺. ^[36] The most significant changes were found in the switch‐I region with the majority of residues (D30‐Y40) becoming highly flexible on the fast timescale in the Mg²⁺‐free form reflected in reduced values of R ₂/R ₁ (8.7 vs. global average of 14.8) and HetNOE (0.54 vs. global average of 0.77). Increased J(ω _H) in the region arises from ps motions (τ _e) as reported by modelfree analysis. Contribution from slow motions is not observed suggesting that in the absence of restricting interactions with the cofactor, they are channeled into increased flexibility on the ps timescale. The observed differences in structure and dynamics between the Mg²⁺‐bound and Mg²⁺‐free forms of GDP‐bound G12C K‐Ras are summarized in Figure 5A.

Structural characteristics of the higher energy state in K‐Ras ⋅ GDP

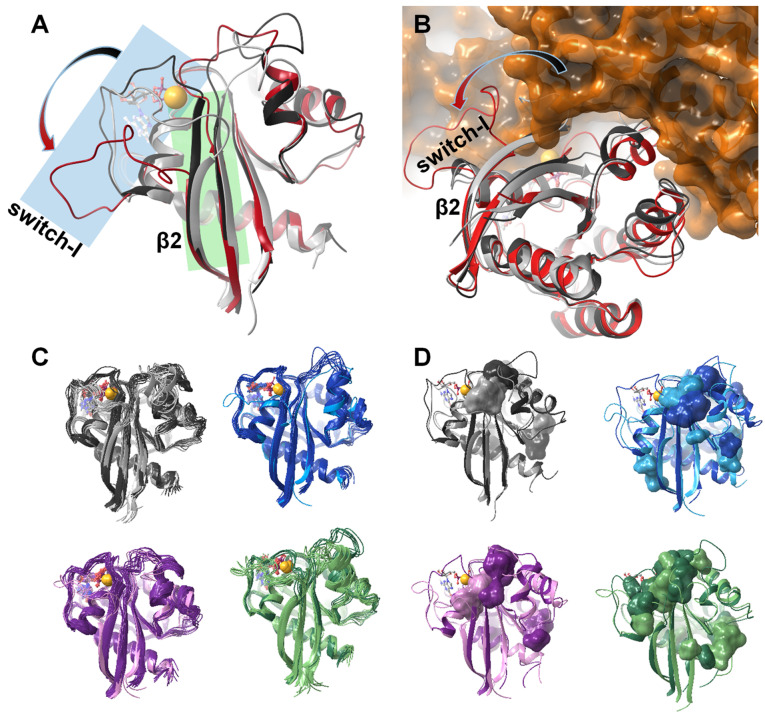
Obtaining the backbone assignment for the Mg²⁺‐free state of G12C K‐Ras ⋅ GDP allowed us a comparison of the ¹⁵ N‐chemical shift differences between the Mg²⁺‐bound and Mg²⁺‐free state of the GDP‐bound complex (|Δδ _Mg|) with the chemical shift difference between the CPMG‐derived ground and higher energy state in G12C K‐Ras ⋅ Mg²⁺ ⋅ GDP. A subset of residues located in the switch‐I (V29, Y32, T35, I36, D38, Y40) and switch‐II (T58, Y64, M67, Q70, T74‐G75) regions, together with additional amino acid positions in β1 (K5), α1 (Q22), and L10 (R149), shows a good correlation between |Δδ _Mg| and |Δδ _EG|, suggesting that the higher energy state may resemble a Mg²⁺‐free Sos‐bound state (Figure 6A−B). This is further supported by the comparison of CEST‐derived chemical shift differences between the ground and the excited state, Δδ _EG ^CEST (Figure S6–S9 and Figure 6C), with the chemical shift difference between the Mg²⁺‐bound and Mg²⁺‐free states of G12C K‐Ras ⋅ GDP (Δδ _Mg) obtained from the HSQC spectra indicating a good agreement in both the sign and the absolute value of the observed chemical shift change (Table 2). Based on the assignment of G12C K‐Ras ⋅ GDP, residues showing a significant role in slow dynamics and exhibiting a CEST effect have also been assigned in the Mg²⁺‐free spectra of wt, G12D, and G12V K‐Ras ⋅ GDP (Figure S12) allowing a similar comparison and yielding a similarly good correlation (Figure 6D and Figure S13).

Figure 6.

Conformational exchange in GDP‐loaded K‐Ras. (A) Correlation between ¹⁵ N backbone chemical shift differences deduced from relaxation dispersion measurements (CPMG) on G12C K‐Ras ⋅ Mg²⁺ ⋅ GDP (|Δδ _EG|) and those detected between the Mg²⁺‐bound and Mg²⁺‐free form (|Δδ _Mg|) of the complex. (B) Residues exhibiting a linear correlation between |Δδ _EG| and |Δδ _Mg| are indicated in green in a ball‐and‐stick representation on the ribbon diagram of G12C K‐Ras ⋅ Mg²⁺ ⋅ GDP. (C) Plot of the fit of the ¹⁵ N‐CEST experiment for a representative residue at the beginning of the switch‐II region (β3) in wt K‐Ras ⋅ Mg²⁺ ⋅ GDP. Numerical parameters of the fit are shown in Table 2. (D) Correlation between ¹⁵ N backbone chemical shift differences deduced from CEST experiments on wt (star), G12C (circle), G12D (triangle), and G12V (square) K‐Ras ⋅ Mg²⁺ ⋅ GDP (Δδ _EG ^CEST) and those detected between the corresponding Mg²⁺‐bound and a Mg²⁺‐free forms (Δδ _Mg). Fitted and estimated (based on the difference between the two minima of the CEST‐curve) values of Δδ _EG ^CEST are depicted in darker and lighter color, respectively.

Our findings regarding the role of the Mg²⁺‐free state in nucleotide‐exchange are consistent with the rearrangement of switch‐II residues affecting the coordination of Mg²⁺ and a partial occlusion of the magnesium binding site upon Sos‐binding in Ras. ^[13] Of note, destabilization of the N‐terminal segment (including switch‐I) of K‐Ras was recently shown to result in the loss of the Mg²⁺ cofactor in a study of N‐terminally truncated and N‐acetylated K‐Ras (2‐169)‐GDP and ‐GTP complexes. ^[52] This is in accordance with our ps‐ns dynamic analysis of Mg²⁺‐free K‐Ras‐G12C ⋅ GDP showing that the absence of cofactor increases the flexibility of the switch‐I region. Moreover, the authors report a repositioning of the side chain of E37 in the Mg²⁺‐free form pointing towards the solvent instead of switch‐II. Although this was observed for a GTP‐analogue‐bound form, ^[52] the extreme values of Δδ and R _ex obtained for E37 in our analysis suggest a similar large movement in Mg²⁺‐free G12C K‐Ras ⋅ GDP as well. Conformational exchange on the fast end of the ms timescale has also been found to be associated with Mg²⁺ affinity in Ras‐related C3 botulinum substrate 1 (Rac1), in which an oncogenic mutation in the switch‐I region (P29S) has been shown to shift a preexisting equilibrium towards a conformation with a distorted switch‐I region and a reduced affinity for Mg²⁺. ^[53]

Altogether, the CPMG R _ex and CEST measurements in conjunction with chemical shift perturbation and fast dynamic analysis of Mg²⁺‐free K‐Ras ⋅ GDP suggest that the low‐populated state in K‐Ras ⋅ Mg²⁺ ⋅ GDP with destabilized switch‐I/switch‐II regions represents a preformed snapshot of a Mg²⁺‐free K‐Ras with an exposed binding surface for Sos.

Mutation specific variations in the exchanging states in K‐Ras ⋅ GDP

The match between the regions exhibiting a global conformational exchange on the ms timescale and those affected by Sos‐binding as discussed above suggests that the low‐populated higher energy state is related to the GDP→GTP exchange on K‐Ras aiding the formation of the Ras‐Sos complex by a mechanism of conformational selection. While the overall core structure of K‐Ras in wt and the investigated oncogenic mutants is thought to be highly similar, ^[5] subtle structural and dynamic differences can affect the exchange process between the ground and the higher energy state with implications for misregulated GDP→GTP exchange and K‐Ras activation. As indicated by the R _ex‐ and CEST‐derived chemical shift differences between the exchanging states, the preceding and the first few residues of switch‐II (I55‐G60) exhibit larger structural differences between the two states in the mutants than in the wt form. This appears to be a general pattern in the mutants, which could be related to an increased plasticity in the region upon the mutation. Another markedly affected region involves the terminal residues of α2 (R73‐G75). Unlike the segment in β3, these few residues exhibit a decrease in |Δδ _EG| in comparison to wt, with most pronounced difference (∼1 ppm) occurring in G12V. Intriguingly, this is the region, where interaction network analysis of P‐loop mutants has indicated a structural rearrangement in G12V involving M72, a residue part of a hydrophobic network connecting P‐loop to switch‐II and the allosteric lobe. ^[54] MD simulations and Markov state modelling for G12V also indicate a distribution of metastable states with switch‐II orientation distinct from those observed in wt and G12D K‐Ras, ^[54] which might be related to the observed differences in |Δδ _EG| in the region. Importantly, G12V exhibits even larger differences from wt and the two other mutants in switch‐I, where a continuous stretch of residues (Y32‐I36) displays values of |Δδ _EG| smaller than in wt indicating that upon the mutation the structure of the ground and higher energy states become less distinct.

Unlike G12V, the two other mutants exhibit a slight increase in |Δδ_EG| with respect to wt in switch‐I, in particularly at V29, Y32, I36, and Y40 (Figure 2). A possible explanation for the observed differences with respect to wt (and G12V) in G12C and G12D might be a transient H‐bond interaction between the side chains of D12 (possibly C12 too) and Q61 (involved also in the interaction with GAP) restricting the conformational landscape for L4 and affecting the positioning of α2. By multiple H‐bond and van der Waals interactions, the distortion of switch‐II could be transmitted to β2/β3 and subsequently to switch‐I giving rise to larger structural differences than in wt between the ground and the excited state in the V29‐Y40 region as well. Rearrangement of the switch‐II region in G12D hypothesized by us is in agreement with residue pair distance calculations showing an overall expansion of K‐Ras upon the mutation affecting part of L4 (Q61–S65) and α3. ^[55] Specifically, formation of an H‐bond between E63 and Q99 has been shown to drive the protein to switch between a closed and an open conformers, and as a result of the mutation, the equilibrium is shifted in favor of a more disordered α2 with a deviation of its central segment towards α3. More recently, similar alteration in residue pair distances was found for GDP‐bound G12C K‐Ras, but not for the G12V mutant. ^[56]

Molecular dynamics analysis of the Mg²⁺‐bound and Mg²⁺‐free GDP‐bound state in wt and mutated K‐Ras

MD simulations were carried out to complement the NMR results and provide a molecular picture for the discussed states. In accordance with the NMR detected differences in chemical shifts between the Mg²⁺‐bound and Mg²⁺‐free states as well as between the ground and excited states of the Mg²⁺‐bound forms, we found that the removal of the cofactor affected mostly the switch‐I, switch‐II, and the allosteric regions (Figure S14). This supports our identification of the minor form present in the GDP‐ and Mg²⁺‐bound resting state of the Ras catalytic cycle as a conformation reminiscent of a Mg²⁺‐free or partially Mg²⁺‐free state. Upon loss of the Mg²⁺ cofactor, conformational changes of the protein matrix in the four studied variants of K‐Ras can be described by three distinct features:

1. Overall loosening of the structure characterized by an increased distance between the P‐loop and switch‐I as well as switch‐I and switch‐II (Figure S15). Structural changes (characterized by the distance between specific backbone amide N‐atoms in Mg²⁺‐bound vs. Mg²⁺‐free forms) were found to be most extensive in G12D and smallest in G12V, when averaged over the full‐sequence and followed the order of G12V<wt<G12D<G12C for the switch‐I region (Figure S14). For several key residues of switch‐I (V29, Y32, I36, Y38, Y40) and the proximate segment of switch‐II (T58, A59) this is in agreement with the observed mutation‐induced changes in the chemical shift differences between the ground and the higher energy state (Figure 2) indicated by the CPMG and CEST measurements supporting the hypothesis that the sparsely populated state is reminiscent of a Mg²⁺‐free, nucleotide‐bound state. We note that an overall loosening of the structure was previously suggested by MD simulations of several Mg²⁺‐free GDP‐bound small GTPases including H‐Ras, ^[50] but lacking an experimental evidence.

2. Shortening of the β2 strand (residues I36‐Y40) in the vicinity of the active site and the corresponding loss of backbone interactions between residues I36‐Y40 of switch‐I and residues L56–A59 of the β3 strand of switch‐II (Figure S16). This outermost segment of the hairpin‐like structural motif formed by strands β2 and β3 functions as a hub along the (P‐loop) – (active site‐proximal part of switch‐II) – (switch‐I) – (distal segment of switch‐II) interaction pathway. Thus, the absence of Mg²⁺ not only removes an important interaction partner of the nucleotide, but also contributes to the loosening of the protein structure by “unlocking” the β2/β3 hub. The observed shortening of the β2‐strand in the MD simulations is in full agreement with the SSP analysis of chemical shifts of Mg²⁺‐free G12C K‐Ras ⋅ GDP corroborating the results of the simulation.

3. Weakened association between the sugar ring of GDP and switch‐I, specifically with the backbone carbonyl groups of V29 and D30 residues (Figure S17 and S18). Both of them are located at a pivotal point between the effector and allosteric lobes of K‐Ras, therefore a loosening of interactions in the region should have a pronounced effect.

The described structural changes upon Mg²⁺ loss not only contribute to a weakened coordination of the nucleotide but also have implications for complex formation with GEF since the binding of the exchange factor initiates a similar change but of greater amplitude (Figure 7A–B). In GEF‐Ras complexes, the 929–944 helix (αF) of the exchange factor displaces completely the switch‐I region of Ras, effectively extruding GDP from the binding pocket. The observed shortening of the β2/β3‐strands and the coupled detachment of switch‐I from the core of the protein in the Mg²⁺‐free state prepares the protein matrix for the accommodation of GEF. Moreover, by comparing the MD‐derived K‐Ras structures to the crystal structure of GEF‐bound H‐Ras, it appears that the detachment of switch‐I with a concomitant shortening of the two β‐strands is, in fact, a necessary prerequisite of GEF‐binding. If GEF would simply dock to the surface of the intact Ras ⋅ Mg²⁺ ⋅ GDP complex, its αF helix would lock the nucleotide binding pocket hindering the exit of the cofactor. The partly released conformation of switch‐I, as indicated by the simulations, opens the nucleotide binding site for the approaching GEF allowing the insertion of its helix between switch‐I and the rest of the protein. This in turn leads to a complete disassembly of the nucleotide binding site. Similar conclusion was reached based on a detailed MD study of various RAS‐GEF complexes, where the authors proposed that en route from the GDP loaded state, displacement of switch‐I by the GEF helix (still in the presence of GDP) takes place. This leads to the dissociation of GDP and nucleotide‐free state, and eventual GTP coordination ^[57] by spontaneous nucleotide shuffle (shifted toward the GTP‐bound state by the over ten‐fold excess of GTP over GDP in cells) and the reattachment of switch‐I. Our results suggest that the detachment of switch‐I could arise from the low occupancy of the Mg²⁺ site. Accordingly, modulation of the Mg²⁺ concentration may provide a means to regulate the activation of Ras through attenuating the extent of GDP→GTP exchange.

Figure 7.

(A) Gradual shortening of the β2 strand (highlighted in green) and the opening of the switch‐I region (highlighted in blue) as the Mg²⁺ ion and the nucleotide is removed from the resting state of the Ras‐complex: comparing the structure of K‐Ras‐wt ⋅ Mg²⁺ ⋅ GDP fully intact complex (dark grey) with that of the GDP‐bound Mg²⁺‐free K‐Ras‐wt (light grey); in both cases the mid‐structure of the most populated cluster of the MD simulation is shown. The Mg²⁺‐free H‐Ras structure extracted from the crystal structure of the H‐Ras‐GEF (Sos1) complex (PDB code: 1xd2, ^[51] red) is shown for comparison. (B) Opening of the switch‐I region is a significant step of GDP release and the subsequent GDP↔GTP exchange: binding of GEF is only possible in the presence of the fully open conformer seen in the crystal structure of the H‐Ras‐GEF (Sos1) complex (PDB code: 1xd2, ^[51] H‐Ras shown in red, GEF in orange). The most populated cluster of the MD simulation of wt K‐Ras ⋅ Mg²⁺ ⋅ GDP (dark grey) and GDP‐bound Mg²⁺‐free K‐Ras‐wt (light grey) are also shown. (C) Comparison of the MD derived ensembles of GDP‐bound K‐Ras‐wt (grey), G12C (blue), G12D (purple), G12V (green) in the Mg²⁺‐bound (dark colors) and Mg²⁺‐free states (light colors); cluster mid structures of each cluster required for representing >95 % of the snapshots – thus the number of conformations shown corresponds to the heterogeneity of the equilibrium ensemble of each state. (D) Small‐molecule binding pockets (as calculated by the FTMap server ^[58] ) of each studied system illustrating the alteration of the surface landscape due both to Mg²⁺‐loss and the oncogenic mutations (colors are the same as in (C)).

The different internal dynamics and intrinsic reactivity of wt and each of the G12 mutants are not straightforward to decipher since mutations at the exposed P‐loop do not cause drastic structural changes. However, subtle rearrangement of local interaction preferences can be inferred. In our simulations, for example, in the Mg²⁺‐ and GDP‐bound state of the G12V variant, the tip of β2 (I36‐Y40) deviates significantly from the plane of the central β‐sheet (Figure S16), thus the shortening of β2 is already completed in this form. The removal of Mg²⁺ in G12V results only in an additional shortening of β3, which taken together provides an explanation for the smaller differences in chemical shifts between the ground and excited states in this mutant. Importantly, among the Mg²⁺‐free forms, the conformational heterogeneity of the G12V mutant exceeds by far that of the others, while the G12C and G12D variants remain the most well‐defined. This might be due to the preferred proximity of C12 and A59 (with C12‐Sγ…A59‐Cβ distance of 3.8±0.8 Å in ∼90 % of the snapshots) in case of the former and a transiently appearing H‐bond between residues D12 and Q61 (present in 35 % of the snapshots) in case of the latter providing extra stability for the switch‐II region in G12C and G12D K‐Ras, respectively. In case of the G12C variant, the conformational stability of the switch‐II region is also enhanced by a unique H‐bond network along K88‐D92‐Q61‐Y96‐A59 connecting switch‐II and the core region in more than half of the snapshots (54.9 %). In the G12V mutant, V12 displaces Q61 from this interaction‐chain, contributing to the increased flexibility of switch‐II and the structural heterogeneity of the complex. These examples illustrate that the Mg²⁺‐free form of wt and mutant variants of K‐Ras show characteristic differences in the switch regions. Thus, it is reasonable to assume that the minor conformers of each variant unveiled by our analysis holds new, targetable sites, which appear to be mutation‐state‐sensitive allowing the design of mutation‐state selective inhibitors according to a prediction by the FTMap server ^[58] (Figure 7C–D).

Conclusion

Due to the high affinity of GTP and GDP, direct targeting of the nucleotide binding site in oncogenic K‐Ras proteins poses a great challenge.[ ⁵⁹ , ⁶⁰ ] Alternative therapeutic strategies include the destabilization of interactions of K‐Ras with partner proteins such as GEFs, GAPs, and downstream effectors, involved in the signalling process.[ ³³ , ³⁴ , ³⁵ , ⁶¹ , ⁶² , ⁶³ , ⁶⁴ ] This has led to the concept of targeting inactive Ras states and blocking reactivation. ^[65] For efficient targeting, a mechanistic picture of K‐Ras interactions is necessary, requiring an atomic level understanding of the K‐Ras conformational energy landscape. Systematic analysis of internal motions of oncogenic P‐loop mutations in GDP‐ and GTP‐bound K‐Ras carried out in the current study highlights the importance of conformational dynamics in K‐Ras signalling. A dominant two‐state conformational exchange on the ms timescale is revealed in both GDP‐ and GTP‐bound K‐Ras encompassing most of the effector lobe and, to a smaller extent, some segments of the allosteric lobe. Similarities in the kinetics of the exchange and the affected regions in wt and the investigated mutants indicate that it is essentially the same process with subtle differences in the structural characteristics of the interconverting states. The affected regions show a similarity in GDP‐ and GTP‐bound K‐Ras mapping to the segments undergoing a remodelling upon Sos‐binding suggesting that the scarcely populated state may have implications for nucleotide exchange in both forms. Using the Mg²⁺‐free state of G12C K‐Ras ⋅ GDP as a reference, we show that the higher energy state of the GDP‐bound form corresponds to a state along the path connecting the Mg²⁺‐bound and Mg²⁺‐free forms of GDP−K‐Ras. As shown by MD, the Mg²⁺‐free state is characterized by a loosened β2/β3 hub region accompanied by an enlarged gap between switch‐I and switch‐II facilitating Sos‐binding (Figure 7A–B), and a weakened interaction between the sugar moiety of GDP and switch‐I preparing the protein for nucleotide release. Importantly, our joint NMR and MD analysis identifies transient opening of targetable pockets, which are sensitive to the presence or absence of P‐loop mutations (Figure 7D).

Although the kinetics and thermodynamics of the exchange process in the investigated variants are similar, chemical shift differences between the interconverting states indicate subtle mutation‐specific structural differences in the ground and/or the excited state in both GDP‐ and GTP‐bound K‐Ras. This includes G12V K‐Ras ⋅ Mg²⁺ ⋅ GDP, whose switch‐I conformation appears to be closer to the empty, Sos‐bound form in the ground state itself, and G12D K‐Ras ⋅ Mg²⁺ ⋅ GDP, which, on the contrary, exhibits a larger structural difference between the exchanging states than observed in wt. Importantly, while the regions involved in conformational exchange are similar in the GDP‐ and GTP‐bound forms, mutation‐related differences between the exchanging states differ significantly between the two forms. Taken together, our systematic analysis of the selected oncogenic mutations provides insight into mutation‐ and nucleotide‐specific differences in K‐Ras structural dynamics aiding the development of allosteric inhibitors targeting K‐Ras signalling, in particular, the K‐Ras‐Sos interaction.

Experimental Section

Protein expression and purification, NMR samples: Expression and purification of ¹⁵N‐labeled K‐Ras(1–169)‐wt, ‐G12C, ‐G12D, and G12V mutants as well as ¹³C,¹⁵N‐labeled K‐Ras‐G12C were performed in the Mg²⁺‐free form by using the methodology we published previously. ^[43] GDP and GTP were added subsequently during sample preparation. NMR samples contained the protein of interest in 1 mM concentration, 5 mM GDP (a minimum of five‐fold excess with respect to the protein) or 100 mM GTP (a minimum of 100‐fold excess with respect to the protein), 10 mM EDTA, 15 mM MgCl₂ (in 5 mM excess with respect to EDTA), 3 mM NaN₃ in PBS buffer, 10 % D₂O, and 1 % DSS, at pH 7.4. Due to the high excess of GTP, the native GTP‐bound form could be studied for 3–4 days, as we described earlier. ^[36] In case of Mg²⁺‐free ¹³C,¹⁵N‐labeled K‐Ras‐G12C, the sample contained 10 mM EDTA without the addition of MgCl₂.

NMR Spectroscopy: Resonance assignment of G12V K‐Ras ⋅ Mg²⁺ ⋅ GTP and Mg²⁺‐free G12C K‐Ras ⋅ GDP together with fast dynamic measurements were performed on a Bruker Avance III 700 MHz spectrometer (700.05 MHz for ¹H, 176.03 MHz for ¹³C, 70.94 MHz for ¹⁵N,) equipped with a 5 mm Prodigy TCI H&F−C/N−D, z‐gradient probe head and on a Bruker Avance Neo 700 MHz spectrometer (700.25 MHz for ¹H, 176.09 MHz for ¹³C, 70.96 MHz for ¹⁵N) equipped with a 5 mm Prodigy H&F−C/N−D, z‐gradient probe head. Relaxation dispersion and CEST measurements were carried out on Bruker Avance Neo 600 MHz and Bruker Avance III HD 800 MHz spectrometers equipped with 5 mm TCI H−C/N−D z‐gradient cryoprobe heads operating at 599.88 and 800.10 MHz for ¹H, 60.79 and 81.07 MHz for ¹⁵N, respectively. Measurements were performed at 298 K. Temperature was calibrated using a standard methanol solution. ¹H chemical shifts were referenced with respect to the ¹H‐resonance of internal DSS, whereas ¹³C and ¹⁵N‐chemical shifts were referenced indirectly using the corresponding gyromagnetic ratios according to IUPAC convention.

Sequence specific assignments of backbone ¹H‐ and ¹⁵N‐nuclei of GTP‐bound K‐Ras‐G12V were accomplished by 3D NOESY‐HSQC measurements (mixing time of 120 ms) and the assignment of wt, G12C, and G12D mutants obtained previously. ^[36] In the case of Mg²⁺‐free G12C K‐Ras ⋅ GDP, assignments were performed based on 3D BEST‐TROSY‐HNCO, BEST‐TROSY‐HN(CA)CO, BEST‐TROSY‐HNCA, BEST‐TROSY‐HN(CO)CA, BEST‐TROSY‐HNCACB, BEST‐TROSY‐HN(CO)CACB, and CC(CO)NH spectra. The assigned resonances were deposited in the BMRB database with the following entries: 50773 (G12V K‐Ras ⋅ Mg²⁺ ⋅ GTP), 50774 (Mg²⁺‐free G12C K‐Ras ⋅ GDP). Chemical shift perturbations (Δδ) upon Mg²⁺‐loss were calculated based on the backbone ¹H‐ and ¹⁵N‐chemical shifts of G12C K‐Ras ⋅ Mg²⁺ ⋅ GDP and Mg²⁺‐free G12C K‐Ras ⋅ GDP using the following equation: ^[66]

$${\displaystyle \Delta \delta =\sqrt{0.5\left[{\left(\Delta {\delta }_{\mathrm{H}}\right)}^2+{0.14\left(\Delta {\delta }_{\mathrm{N}}\right)}^2\right]}.}$$

¹⁵ N T ₁, T ₂ relaxation and ¹⁵N‐{¹H} heteronuclear NOE (HetNOE) measurements were performed for ¹⁵ N‐G12V K‐Ras in its GDP and GTP‐bound forms in the presence of the cofactor. A typical set of spectra in the 0.1–4.5 s and 0.017–0.678 s range were recorded in 10 points for T ₁ and T ₂ measurements, respectively. The longitudinal (R ₁) and transverse (R ₂) relaxation rates were determined by fitting the cross‐peak intensities as a function of the delay to a single‐exponential decay. The heteronuclear NOE values were obtained from the ratio of the peak intensities of saturated and unsaturated cross‐peaks. Overlapping peaks were omitted from the analysis. The obtained relaxation results were analyzed by reduced spectral density mapping ^[67] and the extended Lipari‐Szabo model‐free formalism[ ⁶⁸ , ⁶⁹ , ⁷⁰ ] using the isotropic approach, with N−H bond length of 1.02 Å and ¹⁵ N‐chemical shift anisotropy of −172 ppm. ^[71]

¹⁵ N relaxation dispersion (R _ex) measurements were carried out for wild‐type, G12C, G12D, and G12V K‐Ras in their GDP‐ and GTP‐bound forms in the presence of the cofactor using a relaxation compensated Carr‐Purcell‐Meiboom‐Gill (CPMG) dispersion experiment performed in a constant time manner.[ ³⁹ , ⁴⁰ ] The constant time delay (T_CP) was set to 40 ms. Spectra were collected as a series of 13 two‐dimensional data sets with CPMG field strengths (ν _CPMG) of 25, 50, 75, 100, 125, 150, 200, 250, 300, 400, 500, 750, and 1000 Hz. A reference spectrum was obtained by omitting the CPMG period in the pulse sequence. ^[72] Spectra (2 s interscan delay, 8 transients) were acquired in duplicate. Contributions to transverse relaxation rates of conformational exchange were analyzed assuming a two‐state exchange process using the all‐timescales multiple quantum Carver‐Richards‐Jones formulation. ^[73] Global fitting parameters were determined using a joint fit of 600 MHz and 800 MHz data sets. Overlapping peaks were omitted from the analysis.

¹⁵ N chemical exchange saturation transfer (CEST) experiments were run at 599.88 MHz ¹H frequency spectrometer using manufacturers’ hsqc_cest_etf3gpsitc3d pulse sequence. The ¹⁵ N B₁ field strength was 25 Hz with presaturation time of 400 ms. The ¹⁵ N chemical shift range was scanned in 0.5 ppm steps in between the 100–134 ppm range. A reference experiment was run with far off resonance offset and 1 ms irradiation time.

All spectra were processed with the Bruker TOPSPIN 3.6 program and analyzed using CARA. ^[74] Resonance assignment was accomplished by NMRFAM‐SPARKY. ^[75] Analysis of fast dynamics was performed using the FAST‐Modelfree software, ^[76] the automated version of Modelfree 4.2,[ ⁷⁷ , ⁷⁸ ] and Bruker Dynamics Center 2.5.4. Relaxation dispersion measurements were analyzed using GUARDD. ^[79] For the analysis of the CEST data, intensities in the output files obtained from Dynamics Center CEST processing routine were transformed by a Matlab code suitable for input for ChemEx program. ^[41] Exchange parameters (k _ex, p _e, Δδ _EG ^CEST) were optimized by fitting the experimental intensities as a function of the irradiation frequency while keeping the chemical shifts of the assigned main resonances fixed.

Molecular Dynamics Simulations: Starting models for the molecular dynamics (MD) simulations were built using the crystal structure of wt KRas‐GDP complex (4OBE) (introducing mutations and removing the Mg²⁺ ion manually). Trajectories of the wt‐GDP, G12C‐GDP, and G12D‐GDP systems were available from a previous study. ^[36] The simulations were carried out using GROMACS 4.5, ^[80] applying the AMBER‐ff99SBildnp* forcefield ^[81] with the parametrization of Steinbrecher et al. for the phosphate moieties ^[82] and the OPC water model. ^[83] The total charge of the system was neutralized, and physiological salt concentration was set using Na⁺ and Cl⁻ ions. Energy minimization of the starting structures was followed by relaxation of constraints on protein atoms in three steps, with an additional NVT step (all of 200 ps) to stabilize pressure. Trajectories of 600 ns (for the Mg²⁺ containing system) and 2000 ns (Mg²⁺‐free states) NPT simulations at 310 K and 1 bar were recorded for analysis (collecting snapshots at every 4 ps). Snapshots from the last 300 ns (Mg²⁺‐bound and Mg²⁺‐free states, respectively) of the simulation were clustered. Structures were fitted based on the conformation of the backbone of the core region of the protein and the clustering was carried out based on structural difference of the variable regions (also monitored at the backbone) using a 1 Å cutoff. The core region was selected based on the NMR measurements as those segments that show lowest flexibility or structural heterogeneity: residues 3–11, 18–26, 44–51, 80–84, 87–93, 111–117, 126–138, 141–143, 152–168. Ligand‐binding hotspots were identified using the FTMap server. ^[58]

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supporting Information

G. Pálfy, D. K. Menyhárd, H. Ákontz-Kiss, I. Vida, G. Batta, O. Tőke, A. Perczel, Chem. Eur. J. 2022, 28, e202201449.

Data Availability Statement

The data that support the findings of this study are available in the supplementary material of this article.