Pseudo‐Octahedral Iron(II) Complexes with Near‐Degenerate Charge Transfer and Ligand Field States at the Franck‐Condon Geometry

Abstract

Increasing the metal‐to‐ligand charge transfer (MLCT) excited state lifetime of polypyridine iron(II) complexes can be achieved by lowering the ligand's π* orbital energy and by increasing the ligand field splitting. In the homo‐ and heteroleptic complexes [Fe(cpmp)₂]²⁺ (1²⁺ ) and [Fe(cpmp)(ddpd)]²⁺ (2²⁺ ) with the tridentate ligands 6,2’’‐carboxypyridyl‐2,2’‐methylamine‐pyridyl‐pyridine (cpmp) and N,N’‐dimethyl‐N,N’‐di‐pyridin‐2‐ylpyridine‐2,6‐diamine (ddpd) two or one dipyridyl ketone moieties provide low energy π* acceptor orbitals. A good metal‐ligand orbital overlap to increase the ligand field splitting is achieved by optimizing the octahedricity through CO and NMe units between the coordinating pyridines which enable the formation of six‐membered chelate rings. The push‐pull ligand cpmp provides intra‐ligand and ligand‐to‐ligand charge transfer (ILCT, LL'CT) excited states in addition to MLCT excited states. Ground and excited state properties of 1²⁺ and 2²⁺ were accessed by X‐ray diffraction analyses, resonance Raman spectroscopy, (spectro)electrochemistry, EPR spectroscopy, X‐ray emission spectroscopy, static and time‐resolved IR and UV/Vis/NIR absorption spectroscopy as well as quantum chemical calculations.

Iron(II) complexes with 6,2’’‐carboxypyridyl‐2,2’‐methylamine‐pyridyl‐pyridine ligands possess low‐energy ¹MLCT states. ³MLCT and ^3/5MC excited states are nearly degenerate at the Franck‐Condon geometry. Expansion of the coordination sphere lowers the ^3/5MC energies shortening the ³MLCT lifetime. Cooling and solvent reorganization occurs within 33 ps to give the relaxed ⁵MC state with ca. 0.5 ns lifetime.

Introduction

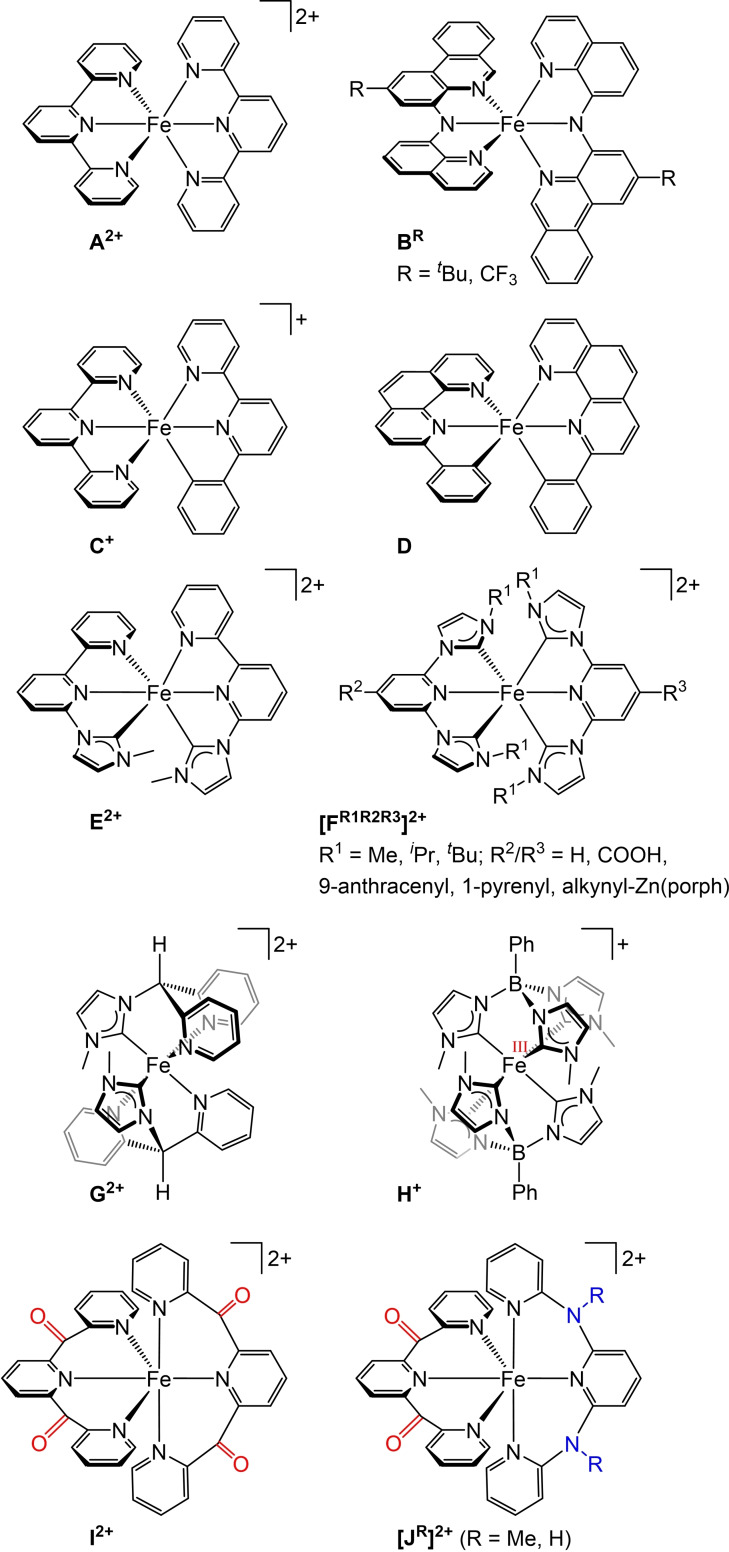
Polypyridine ruthenium(II) complexes like the prototypical complex [Ru(bpy)₃]²⁺ (bpy=2,2’‐bipyridine) are used as light harvesters in dye sensitized solar cells, as emitters in light emitting electrochemical cells and as photocatalysts thanks to their favorable redox and optical properties.[ ¹ , ² , ³ , ⁴ , ⁵ , ⁶ , ⁷ , ⁸ , ⁹ , ¹⁰ , ¹¹ , ¹² , ¹³ ] These properties encompass reversible ligand‐centered reduction and metal‐centered oxidation, strong visible light absorption via singlet metal‐to‐ligand charge transfer (¹MLCT) states, efficient intersystem crossing (ISC) to the ³MLCT state and a sufficiently high lifetime of the ³MLCT state enabled by high energy metal‐centered (MC) states.[ ¹ , ² , ³ , ⁴ , ⁵ , ⁶ , ⁷ , ⁸ , ⁹ , ¹⁰ , ¹¹ , ¹² , ¹³ ] Replacing the rare and expensive ruthenium by the earth abundant homologue iron is an attractive but challenging research target.[ ¹⁴ , ¹⁵ , ¹⁶ ] The ligand field splitting in 3d metal ions like iron is generally significantly smaller than in homologous 4d metal ions (primogenic effect), ^[17] which leads to a rapid non‐radiative decay of the potentially photoactive ³MLCT excited states to the singlet ground state (¹GS) via low‐energy ^3/5MC states.[ ¹⁴ , ¹⁵ , ¹⁶ ] While ruthenium(II) complexes usually exhibit phosphorescence from ³MLCT states as lowest energy excited states with lifetimes in the ns to μs range, non‐emissive ^3/5MC states are the lowest excited states in iron(II) complexes.[ ¹ , ¹⁴ , ¹⁵ , ¹⁶ ] This results in ultrafast internal conversion from ³MLCT to ³MC states followed by ISC to the ⁵MC state and finally non‐radiative relaxation to the ground state. The efficient MLCT→MC cascade decreases the ³MLCT lifetime to typically below 0.2 ps.[ ¹⁴ , ¹⁵ , ¹⁶ ]

For example, [Fe(tpy)₂]²⁺ A²⁺ (Scheme 1) populates the ⁵MC state within 0.7 ps after ¹MLCT excitation, ^[18] while the lifetime of its lowest ⁵MC state amounts to τ _5MC=5350 ps in acetonitrile. ^[19] Replacing terpyridine ligands in A²⁺ by amido donors yields iron(II) complexes B ^R with panchromatic absorption (Scheme 1). ^[20] A nanosecond excited state lifetime was assigned by the authors to a ³MLCT state, yet no emission has been reported for the complexes. ^[20] While a single cyclometalating ligand in C⁺ is not yet competent to sufficiently increase the ⁵MC state energies, ^[21] two rigidified cyclometalating ligands with low π* energies in D achieve a luminescent ³MLCT state (λ _emiss=1230 nm) with a lifetime of τ _3MLCT=1000 ps in benzene at room temperature (Scheme 1). ^[22] Similarly, the number of carbene donors[ ²³ , ²⁴ , ²⁵ , ²⁶ , ²⁷ , ²⁸ , ²⁹ , ³⁰ , ³¹ , ³² , ³³ , ³⁴ ] in place of pyridines in E²⁺ and F²⁺ increases the ³MLCT lifetime (Scheme 1). A hexacarbene complex with bidentate ligands achieves τ _3MLCT=528 ps. ^[35] The hexacarbene iron(II) complex H is rapidly oxidized to the iron(III) complex H⁺ , ^[36] while the bis(carbene) complex G²⁺ possesses a τ _3MLCT=9.2 ps, significantly higher than bis(carbene) iron(II) complexes with meridionally coordinating ligands. ^[37] In contrast to complexes A²⁺ – [F^R1R2R3]²⁺ , the tripodal tridentate ligands in G²⁺ and H⁺ form six‐membered chelate rings with the iron center resulting in complexes with high octahedricity. This is expected to increase the metal‐ligand orbital overlap and consequently the energies of the MC states. Similarly, the polypyridine iron(II) complexes I²⁺ and [J^R]²⁺ with meridional ligands are highly symmetric with respect to the [FeN₆] coordination sphere (Scheme 1).[ ¹⁹ , ³⁸ , ³⁹ , ⁴⁰ ] In addition, I²⁺ and [J^R]²⁺ possess low‐energy π* orbitals thanks to the dipyridyl ketone units to lower the MLCT state energies. The heteroleptic complexes [J^R]²⁺ feature additional electron donating (dipyridyl)amine moieties to increase the ligand field splitting and thus the MC state energies.[ ³⁸ , ³⁹ ]

Scheme 1.

Selected iron(II) complexes with tridentate N/C ligands with improved absorptivity and prolonged ³MLCT lifetimes via increasing the ^3/5MC state energies and/or lowering the ³MLCT state energies and the iron(III) complex H⁺ .

In this study, we employ the tridentate ligands 6,2’’‐carboxypyridyl‐2,2’‐methylamine‐pyridyl‐pyridine (cpmp) ^[41] and N,N’‐dimethyl‐N,N’‐di‐pyridin‐2‐ylpyridine‐2,6‐diamine (ddpd).[ ⁴² , ⁴³ ] These ligands provide large bite angles for an improved octahedricity and σ‐donating ability to increase the ligand field splitting and two or one dipyridyl ketone acceptor units as π‐accepting moieties to lower charge transfer states in the homo‐ and heteroleptic iron(II) complexes [Fe(cpmp)₂][PF₆]₂ (1[PF₆]₂ ) and [Fe(cpmp)(ddpd)][PF₆]₂ (2[PF₆]₂ ). In contrast to [M(tpy)₂]ⁿ⁺ complexes A²⁺ and topologically similar complexes B^R – [F^R1R2R3]²⁺ (Scheme 1), which possess orthogonal central donor units of the ligands (mostly pyridines) resulting in symmetry‐forbidden transitions between these moieties, the central pyridines of the cpmp and ddpd ligands are expected to be much closer to co‐planar with a torsion angle of ca. 30°. This should allow transitions with LL'CT character and improve the absorptivity in the visible spectral region.[ ¹⁹ , ³⁸ , ³⁹ , ⁴⁰ , ⁴¹ , ⁴² , ⁴³ ] Consequently, the electronic and structural situations in 1²⁺ and 2²⁺ shall provide low‐energy ^1/3ILCT, ^1/3LL'CT and ^1/3MLCT states along with up‐shifted ^3/5MC states. Ground and excited state properties of 1²⁺ and 2²⁺ were accessed by X‐ray diffraction analyses, resonance Raman spectroscopy, (spectro)electrochemistry, static and time‐resolved IR and VIS/NIR absorption spectroscopy as well as quantum chemical calculations (Density Functional Theory, DFT and time‐dependent DFT, TD‐DFT).

Results and Discussion

Syntheses and ground state structures

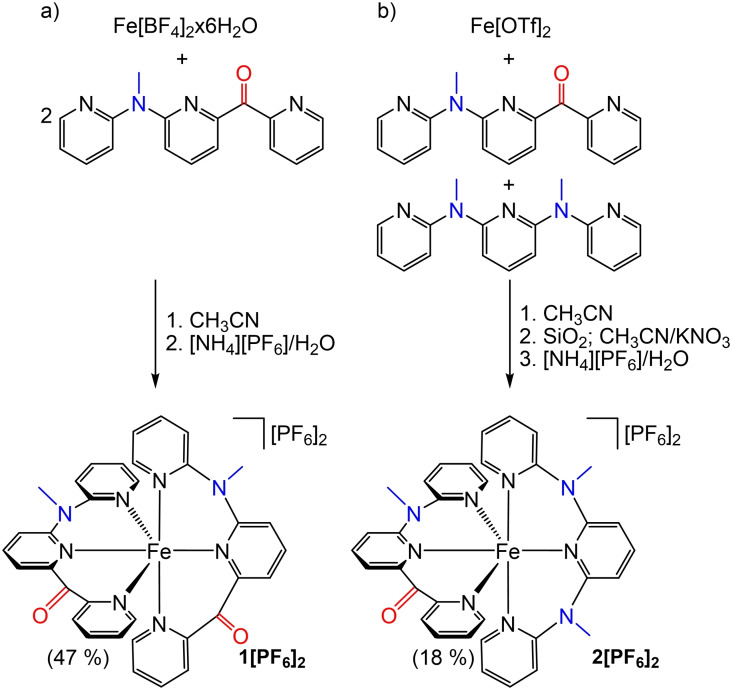
The blue homoleptic complex [Fe(cpmp)₂]²⁺ (1²⁺ ) is the sole product of the reaction of Fe[BF₄]₂x6H₂O with the ligand cpmp and can be straightforwardly purified by crystallization (Scheme 2a). In the presence of both ligands cpmp and ddpd in a 1 : 1 ratio, Fe[OTf]₂ forms both homo‐ and heteroleptic complexes (Scheme 2). The green heteroleptic complex [Fe(cpmp)(ddpd)]²⁺ (2²⁺ ) can be separated by column chromatography (Scheme 2b). However, ligand scrambling is observed for 2²⁺ over longer timescales in solution additionally forming the homoleptic complexes [Fe(ddpd)₂]^2+[38] and 1²⁺ .

Scheme 2.

Synthesis of the a) homoleptic and b) heteroleptic iron(II) complexes 1[PF₆] and 2[PF₆]₂ with the push‐pull ligand cpmp. Accepting CO and donating NMe units colored red and blue, respectively.

The combination of the py^a−py^b−py^c ligand nature and the helical arrangement of the meridional coordinated ligands (either P,P, or M,M)[ ⁴³ , ⁴⁴ ] furnishes both 1²⁺ and 2²⁺ as diastereomers with only one isomer depicted in Scheme 2 each. Flipping a cpmp ligand – formally exchanging C=O with N−Me and vice versa – yields the respective other diastereomer while maintaining the ligand helicity. The ¹H and ¹³C NMR resonances (400 MHz, 100 MHz) of the diastereomers appear indistinguishable but the diastereomers show up in the solid state structures (Figure 1). It is expected that these diastereomers form in an approximately 1 : 1 ratio (see below).

Figure 1.

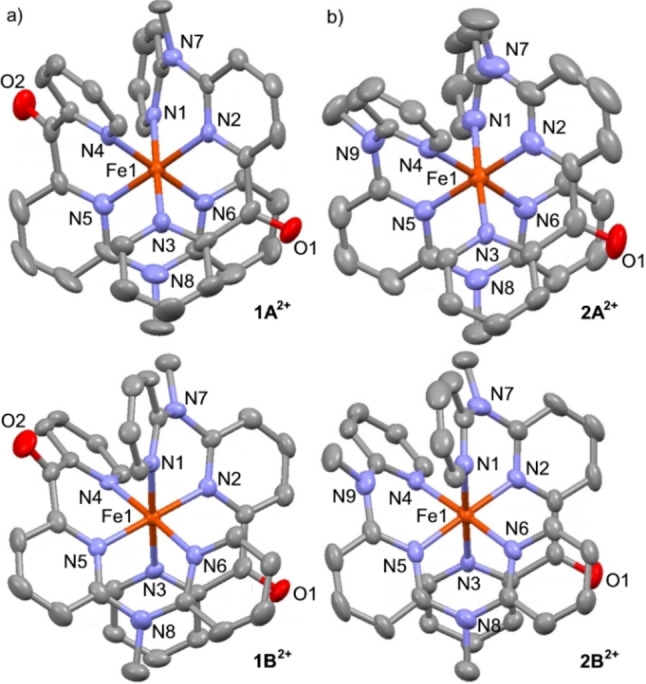
Molecular structures of a) 1²⁺ (1A²⁺ , 1B²⁺ ) and b) 2²⁺ (2A²⁺ , 2B²⁺ ) determined by single crystal XRD analyses. Thermal ellipsoids set at 50 % probability. Hydrogen atoms are omitted for clarity. Atom numbering differs from cif file numbering but fits to Table 1 for better comparability.

The compositions of 1[PF₆]₂ and 2[PF₆]₂ are confirmed by (high resolution) ESI mass spectrometry (Supporting Information, Figures S1–S2) and elemental analyses as well as multinuclear and correlation NMR spectroscopy (Supporting Information, Figures S3–S17). The NMR spectra display only a single set of ¹H and ¹³C NMR resonances for the isomers. The sharp NMR resonances indicate low‐spin 3d⁶ electron configurations in both cases.

The meridional coordination of the tridentate ligands is confirmed by single crystal X‐ray diffraction analyses (Figure 1, Table 1). The unit cells of 1[PF₆]₂×CH₃CN and 2[PF₆]₂×1.5CH₃CN contain the two diastereomers 1A²⁺ /1B²⁺ and 2A²⁺ /2B²⁺ , respectively. In the solid state, the second coordination sphere of the complexes is formed by hexafluorophosphate ions, co‐crystallized acetonitrile and the carbonyl group of a neighboring complex with closest contacts of Fe⋅⋅⋅[F(PF₅)]⁻, Fe⋅⋅⋅NCCH₃ and Fe⋅⋅⋅O ranging from 4.36 to 5.00 Å (1A²⁺ ), 4.59 to 5.56 Å (1B²⁺ ) and 4.42 to 6.11 Å (2A²⁺ ), 4.22 to 5.29 Å (2B²⁺ ) (Table 1).

Table 1.

Selected bond lengths (Å), angles (°), planarization PL (%) and continuous shape parameter S(OC‐6) ^[45] of 1²⁺ and 2²⁺ determined by XRD analyses (as [PF₆]⁻ salts) and by DFT calculations.

	1A2+ (DFT)	1A2+(XRD)	1B2+(XRD)	2A2+ (DFT)	2A2+(XRD)	2B2+(XRD)
Fe1‐N1	2.009	1.999(6)	1.985(5)	2.012	1.993(4)	1.997(3)
Fe1‐N2	1.978	1.963(5)	1.947(6)	1.972	1.953(4)	1.953(3)
Fe1‐N3	1.997	1.999(6)	1.973(6)	2.002	1.984(3)	1.964(3)
Fe1‐N4	2.005	1.974(6)	1.981(6)	2.003	1.983(3)	1.979(3)
Fe1‐N5	1.976	1.949(6)	1.950(6)	1.980	1.959(3)	1.964(3)
Fe1‐N6	2.002	1.984(6)	2.011(6)	2.002	1.986(3)	1.987(3)
N1‐Fe1‐N2	87.9	88.2(2)	87.7(2)	87.6	88.27(15)	87.76(13)
N2‐Fe1‐N3	90.5	90.3(2)	90.9(2)	90.9	90.19(14)	90.59(13)
N4‐Fe1‐N5	90.4	90.1(2)	90.5(2)	88.8	88.23(14)	88.74(14)
N5‐Fe1‐N6	87.6	89.1(3)	88.0(2)	88.8	89.15(14)	88.13(14)
PL(N7)	87.8	90.5	89.8	91.0	87.9	90.5
PL(C9)	98.0	95.2	97.8	97.9	95.6	98.1
PL(C10)	97.7	97.1	97.8	–	–	–
PL(N8)	90.3	87.6	89.2	87.8	87.6	89.2
PL(N9)	–	–	–	87.8	87.0	89.8
S(OC‐6)	0.04	0.04	0.04	0.06	0.05	0.06
Fe1⋅⋅⋅F1	–	4.36	4.72	–	4.42	4.42
Fe1⋅⋅⋅F2	–	4.73	4.84	–	6.11	4.22
Fe1⋅⋅⋅N1(CH3CN)	–	5.00	–	–	5.09	5.29
Fe1⋅⋅⋅O1(neighboring molecule)	–	4.76	4.59	–	4.78	4.62
Fe1⋅⋅⋅O2(neighboring molecule)	–	–	5.56	–	–	–

The [FeN₆] local coordination sphere is close to octahedral for all dications as shown by the shape parameter S(OC‐6) ^[45] being close to zero (Table 1). The Fe−N bond lengths of the central pyridine rings are only slightly shorter than of the terminal pyridine rings (Table 1), which is typically observed for complexes with py−X−py−X−py ligands, for example [M(ddpd)₂]²⁺, [M(dcpp)₂]²⁺ or [M(dcpp)(ddpd)]²⁺ complexes.[ ¹⁹ , ³⁸ , ⁴¹ , ⁴³ ] The N−Fe−N bond angles are very close to 90° for the dipyridyl ketone moieties and slightly smaller for the methyl(dipyridyl)amine moieties of the cpmp and ddpd ligands (Table 1). The degree of planarization PL=100×[Σ(X−A−Y)−3×109.5°]/[360°−3×109.5°] of 95–98 % for the dipyridyl ketone moieties and 88–91 % for the methyl(dipyridyl)amine moieties correlates inversely to the steric strain of the respective bridging groups. The torsion angles between the central pyridines of the two tridentate ligands are around 14° which should allow for LL'CT transitions. The geometries of 1A²⁺ /1B²⁺ and 2A²⁺ /2B²⁺ calculated by DFT methods on the CPCM(acetonitrile)‐B3LYP‐D3BJ‐ZORA/def2‐TZVP level of theory (Supporting Information, and Table 1) match the experimentally determined ones sufficiently well.

³¹P NMR spectra of 1[PF₆]₂ and 2[PF₆]₂ show the typical multiplet of the [PF₆]⁻ counter ions at −144.7 ppm (Supporting Information, Figures S8, S17) confirming the successful counter ion exchange which is also consistent with the characteristic PF vibrations of the counter ions around 831/557 cm⁻¹ in the IR spectra of 1[PF₆]₂ and 2[PF₆]₂ (Supporting Information, Figures S18–S19). The uncoordinated cpmp ligand displays a band of the C=O stretching vibration at 1679 cm⁻¹. ^[41] In the iron(II) complexes 1[PF₆]₂ and 2[PF₆]₂ , this band shifts to 1669 and 1672 cm⁻¹ (calculated as 1672 and 1667 cm⁻¹; scaled by 0.973), respectively, suggesting some π back‐donation of the low‐spin d⁶ iron(II) center into the π*(CO) orbitals. The homoleptic complex 1[PF₆]₂ with two cpmp ligands shows only a single CO stretching vibration indicating no coupling of the two C=O oscillators. The DFT calculated splitting of these bands of 1²⁺ is indeed below 3 cm⁻¹. The calculated energy differences between the isomers 1A²⁺ /1B²⁺ and 2A²⁺ /2B²⁺ are very small (<3 kJ mol⁻¹) and the respective calculated CO IR frequencies are essentially indistinguishable so that we consider only the A isomers in most parts of the following discussions. This is consistent with the experimental NMR and IR data.

Characterization of the electronic ground states

UV/Vis/NIR absorption spectra of 1[PF₆]₂ and 2[PF₆]₂ were measured in acetonitrile (Figure 2; Supporting Information, Figure S20 for full spectra). Time‐dependent DFT and charge transfer number analyses served to assign the character of the absorption bands (Supporting Information, Figures S21–S24). The band at 270 nm with a shoulder at 300 nm in the absorption spectrum of 1[PF₆]₂ is assigned to mainly ligand centered ππ* transitions. For the heteroleptic complex 2[PF₆]₂ these bands shift to 276 and 326 nm, respectively, with ¹ππ* and ¹LL'CT character. The 350 nm band of 1[PF₆]₂ can be assigned to mainly ¹MLCT transitions, while the shoulder at 410 nm is caused by ¹ILCT/¹LC and ¹LL'CT transitions. 2[PF₆]₂ shows the ¹MLCT band at 365 nm with a shoulder at 420 nm assigned to ¹ILCT/¹LC transitions. In both cases, ¹ILCT and ¹LL'CT states are higher in energy than the lowest ¹MLCT transitions.

Figure 2.

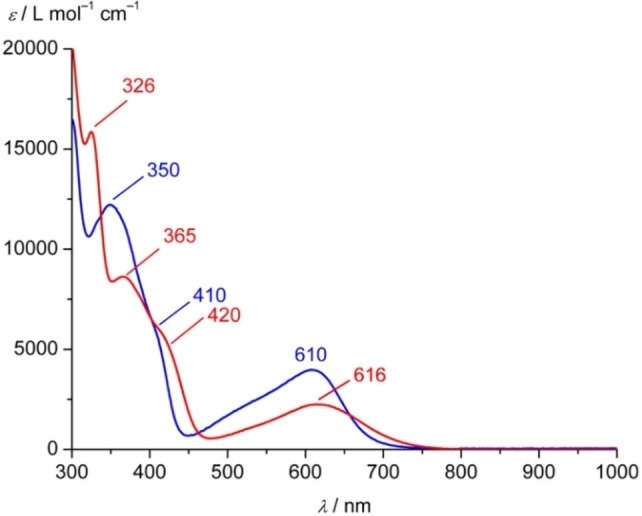
UV/Vis/NIR absorption spectra of 1[PF₆]₂ (blue) and 2[PF₆]₂ (red) in acetonitrile at 298 K.

The characteristic low‐energy ¹MLCT bands of 1[PF₆]₂ and 2[PF₆]₂ appear at 610 and 616 nm, respectively (Figure 2). The dipyridiyl ketone moieties act as the acceptor in the ¹MLCT transitions as seen in the difference densities (Supporting Information, Figures S22, S24). The ¹MLCT extinction coefficient of 1²⁺ is nearly twice as large as for 2²⁺ due to the presence of two acceptor sites instead of only one in 2²⁺ . The even higher extinction coefficient of [Fe(dcpp)₂]²⁺ I²⁺ with four dipyridyl ketone acceptor units fits to this trend.[ ¹⁹ , ³⁸ ] An analogous intensity change had been observed for the homologous ruthenium(II) complexes [Ru(cpmp)₂]²⁺ and [Ru(cpmp)(ddpd)]²⁺. ^[41] The number of donating methylamine units increases from [Fe(dcpp)₂]²⁺ (I²⁺ , Scheme 1) to 1²⁺ and 2²⁺ , which manifests itself in a bathochromic shift of the ¹MLCT absorption maximum from 606 nm over 610 nm to 619 nm.[ ¹⁹ , ³⁸ ] This effect mainly arises from an increased energy of the highest occupied orbitals (t _2g) by 0.26 eV and weaker increase in the LUMO energy (π*), so that the HOMO–LUMO energy gap decreases by 0.17 eV in 2²⁺ .

The nature of the low‐energy band of 1[PF₆]₂ was experimentally probed by resonance Raman spectroscopy in CH₃CN solution and in the solid state with excitation at 633, 532 and 473 nm, respectively, in comparison to the off‐resonance Raman spectrum with excitation at 785 nm (Supporting Information, Figures S25–S27). The spectra in solution normalized to the CN stretching band of the CH₃CN solvent allow for qualitative comparison of the different resonance enhanced Raman intensities of 1²⁺ . The most prominent enhancement is achieved with 633 nm excitation in particular at 1674 and 1198 cm⁻¹ corresponding to the C=O stretching and py‐C‐py deformation modes, respectively. Further bands with increased intensity at 1593, 1574, 1564, 1472, 1454, 1435 and 1416 cm⁻¹ belong to skeletal deformation modes of the pyridines (data given for the solid state; Supporting Information, Figures S26–S27). At higher excitation energies the enhancements are less pronounced suggesting less charge transfer character to the dipyridyl ketone unit at these excitation energies which qualitatively agrees with the TD‐DFT calculations and charge transfer number analysis (Supporting Information, Figures S21, S23), which predict decreasing MLCT character at the high energy tail of the absorption band.

Both complexes 1[PF₆]₂ and 2[PF₆]₂ are reversibly oxidized to the trications in their cyclic voltammograms at +0.79 and +0.55 V vs. ferrocene, respectively (Figure 3a). A DFT calculation on 1³⁺ confirms the metal centered nature of the oxidation (Figure 3b). The 1^3+/2+ oxidation potential is higher by 0.24 V than that of 2^3+/2+ due to the electron withdrawing effect of two carbonyl groups instead of a single one in 2²⁺ and the diminished donating effect of only two NMe groups in 1²⁺ instead of three in 2²⁺ . The even higher oxidation potential of [Fe(dcpp)₂]^3+/2+ I^3+/2+ (+1.29 V vs. ferrocene) with four CO groups is consistent with this trend.[ ¹⁹ , ³⁸ ] Compared to the ruthenium(II) homologues, the 1^3+/2+ and 2^3+/2+ potentials are lowered by 0.12 and 0.13 V, respectively. ^[41]

Figure 3.

a) Cyclic voltammograms of 1[PF₆]₂ (blue) and 2[PF₆]₂ (red), 1 mm in acetonitrile, 0.1 m [ ⁿ Bu₄N][PF₆], 100 mV s⁻¹ and DFT optimized geometries and spin densities (isosurface at 0.012 a. u.) of b) the iron(III) complex 1³⁺ and c) the radical ion 1⋅⁺ .

The homoleptic complex 1²⁺ exhibits two reversible reduction waves at −1.28 and −1.46 V that are assigned to the reduction of the individual cpmp ligands (Figure 3a, blue). The reduction wave of the single cpmp ligand in 2²⁺ appears at −1.36 V (Figure 3a, red). A second (irreversible) reduction appears at −2.03 V. On the timescale of the CV experiments, the 1^{2+ /} ⋅⁺ and 2^{2+ /} ⋅⁺ reductions are reversible, although the electron occupies π*_CO orbitals according to the spin densities obtained by DFT calculations on 1⋅⁺ (Figure 3c).

The chemical reversibility and stability of the redox products were explored by IR and UV/Vis/NIR spectroelectrochemistry, respectively (Figure 4; Supporting Information, Figure S28). 2⋅⁺ appeared less stable so the following experiments were only discussed for 1²⁺ derived redox products. The Fe^III/II oxidation of 1²⁺ is perfectly reversible on the timescale of IR and UV/Vis/NIR spectroelectrochemistry in CH₃CN/[ ⁿ Bu₄N][PF₆] (Figure 4; Supporting Information, Figures S29–S30). The (unresolved) CO stretching bands of the Fe^III complex 1³⁺ (Figure 3b) are shifted to higher energy by 18 cm⁻¹ compared to 1²⁺ (1684→1702 cm⁻¹; Figure 4a) suggesting a weaker π backbonding in the iron(III) complex than in the dication. This shift is excellently reproduced by the DFT calculations on 1³⁺ (18 cm⁻¹). Similarly, the evolution of the UV/Vis/NIR spectra during the 1²⁺ →1³⁺ oxidation displays several isosbestic points (Figure 4b). Characteristically, the low‐energy ¹MLCT band at 610 nm bleaches while a band at 962 nm appears. The latter band is assigned to ²LMCT transitions of the NMe moieties to low‐spin iron(III) according to TD‐DFT calculations on 1³⁺ (Supporting Information, Figures S31–S32). Chemical oxidation of 1²⁺ to 1³⁺ using one equivalent [NH₄]₂[Ce(NO₃)₆] yields a superimposable UV/Vis/NIR spectrum (Supporting Information, Figure S33).

Figure 4.

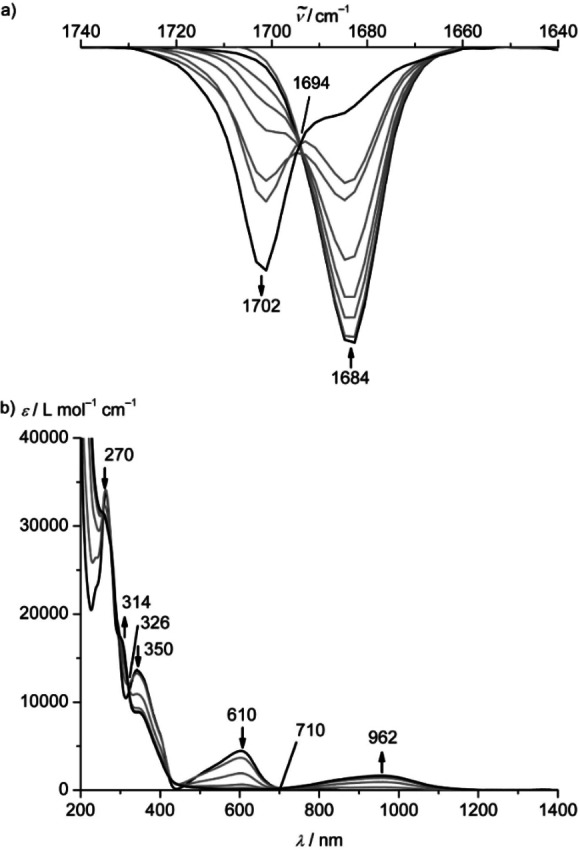
a) IR absorption spectra and b) UV/Vis/NIR absorption spectra of 1[PF₆]₂ in acetonitrile with 0.1 m [ ⁿ Bu₄N][PF₆] at 298 K collected during electrochemical oxidation.

Under reductive electrolysis 1²⁺ →1⋅⁺ , no clear isosbestic points are observed in the UV/Vis/NIR and IR spectra suggesting that follow‐up reactions occur on this timescale (Supporting Information, Figures S34–S35). Possibly pinacol coupling can occur at the reduced CO units after ligand dissociation on longer time scales, ^[46] similar to the quasireversible reduction of cpmp to cpmp⋅⁻ at −1.99 V. ^[41] Consequently, we resorted to faster chemical reduction using decamethylcobaltocene (E _1/2=−1.91 V in CH₃CN vs. ferrocene) ^[47] as reductant followed by immediate spectroscopic analysis. On this time scale, the band of the remaining C=O moiety shifts to lower energy from 1684 to 1681 cm⁻¹, while the band of the reduced CO unit has shifted into the fingerprint region. As a consequence, the CO band loses half its intensity (Supporting Information, Figure S36). A small shift of the remaining C=O band to lower energy is also predicted for 1⋅⁺ calculated by DFT (Figure 3c). The IR absorption of the reduced CO moiety of DFT‐optimized 1⋅⁺ has shifted into the fingerprint region, which results in a reduction of the original CO band intensity. This is fully consistent with the ligand centered reduction at a single dipyridyl ketone unit (Figure 3c).

To confirm the ligand and metal centered reduction and oxidation, we measured X‐band EPR spectra of the ions 1⋅⁺ and 1³⁺ in frozen solution. The redox products were prepared by chemical reduction of 1²⁺ with decamethylcobaltocene and oxidation of 1²⁺ with [NH₄]₂[Ce(NO₃)₆], respectively. The highly isotropic EPR resonance of 1⋅⁺ at g=2.0075 clearly confirms the ligand centered radical (Figure 5a). The EPR pattern of 1³⁺ is highly anisotropic with clearly discernible g ₁, g ₂ and g ₃ values diagnostic for low‐spin iron(III) complexes.[ ³⁸ , ⁴⁸ ] Interestingly, a double signal set is observed in a 1 : 1 intensity ratio (Figure 5b). We assign the two signal sets to the diastereomers 1A³⁺ and 1B³⁺ , respectively. This illustrates that EPR spectroscopy is the only spectroscopic method, that we employed, which can distinguish the A and B diastereomers (in the iron(III) state). However, assigning the individual resonances to 1A³⁺ and 1B³⁺ is impossible. The g ₂ values are very similar, while g ₁ and g ₃ values differ significantly. The anisotropy Δg=g ₁ – g ₃ of 1A³⁺ and 1B³⁺ hence ranges between 0.990 and 1.139. This is larger than that of the more symmetric complex [Fe(dcpp)₂]³⁺ I³⁺ (Δg=0.675) but smaller than that of the heteroleptic complex [Fe(dcpp)(ddpd)]³⁺ [J^Me]³⁺ (Δg=1.26). ^[38] This suggests that the g tensor is a very sensitive measure of the local symmetry around the low‐spin iron(III) center.

Figure 5.

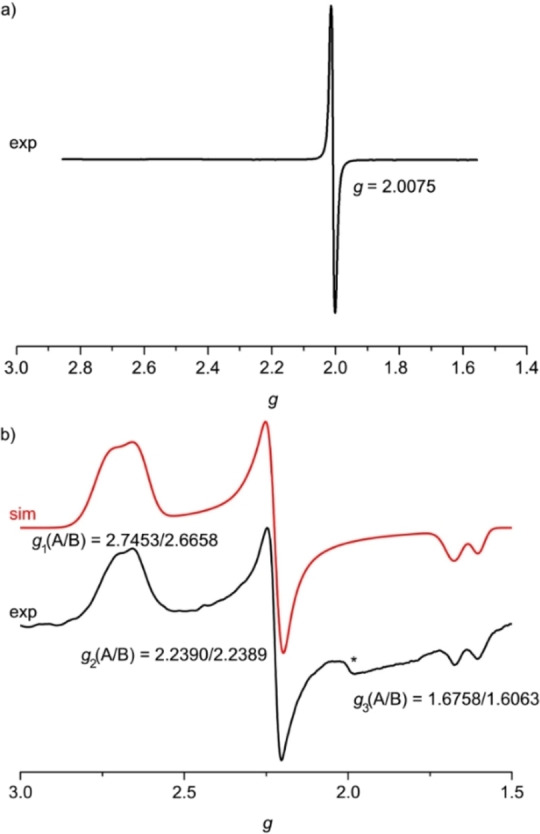
X‐band EPR spectra at 77 K of a) 1⋅⁺ in acetonitrile and b) 1³⁺ in butyronitrile. Simulation of the spectrum with the parameters indicated shown in red. The asterisk denotes a baseline artifact.

Core‐to‐core X‐ray emission spectroscopy ^[49] at 20 K in the solid state confirms the low‐spin states of the 3d⁶ iron(II) and 3d⁵ iron(III) complexes 1²⁺ and 1³⁺ with main line maxima at 7057.9 eV and 7058.1 eV, respectively, and a slightly increased Kβ’ satellite intensity for the d⁵ complex 1³⁺ (Supporting Information, Figure S37). ^[50] Fe K‐edge HERFD‐XANES measurements yield two pre‐edge features for 1²⁺ at 7113.3 eV (shoulder) and 7114.8 eV, while 1³⁺ shows four features at 7111.9, 7113.7, 7116.8 and 7115.4 eV (Supporting Information, Figures S38–S40). These features could be well reproduced by DFT calculations on low‐spin 1²⁺ and 1³⁺ confirming the low‐spin character of both ions similar to previous studies on carbene pyridine iron(II,III) complexes (Supporting Information, Figures S39–S40).[ ²⁷ , ⁵¹ ] Valence‐to‐core X‐ray emission spectra are also in agreement with the ones reported for carbene pyridine iron(II) complexes (Supporting Information, Figure S41). ^[27]

Excited state properties and dynamics

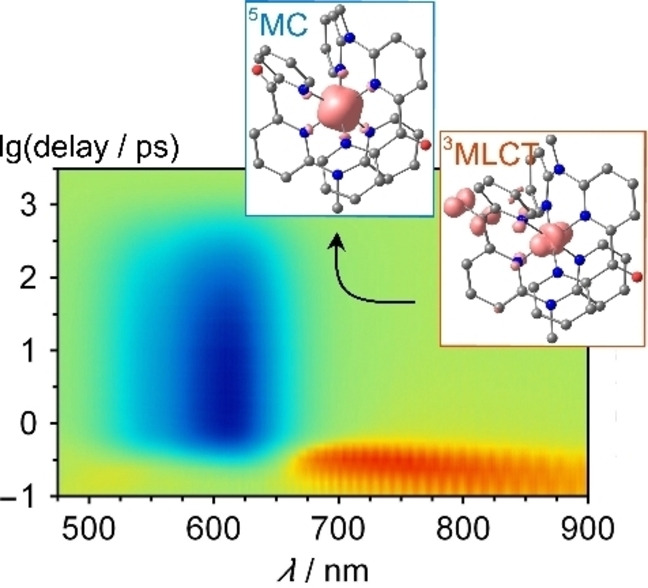
Ultrafast VIS‐pump/IR‐probe spectra of 1[PF₆]₂ in acetonitrile in the CO spectral region were obtained after optical excitation at 610 nm (¹MLCT absorption; Supporting Information, Figure S42). A negative transient absorption signal associated with the ground state bleach (GSB) is observed in the region around 1674 cm⁻¹ and a positive signal around 1685 cm⁻¹ from the CO stretch of an electronically excited state. Both features decay monoexponentially with a time constant τ _IR=(495±16) ps and an isosbestic point at 1681.5 cm⁻¹ (Supporting Information, Figure S42). The time constant τ _IR is assigned to the lifetime of the ⁵MC state of 1²⁺ . ⁵MC lifetimes in a similar range have been obtained by transient absorption spectroscopy for [Fe(dcpp)₂]²⁺ I²⁺ (τ _5MC=280 ps) and [Fe(dcpp)(ddpd)]²⁺ [J^Me]³⁺ (τ _5MC=548 ps), while the ⁵MC lifetimes of [Fe(bpy)₃]²⁺ (τ _5MC=960 ps) and [Fe(tpy)₂]²⁺ A²⁺ (τ _5MC=5350 ps) are significantly longer.[ ¹⁹ , ³⁸ ] Despite indications for a further, very short‐lived blue‐shifted contribution (Supporting Information, Figure S42), the time resolution of 142 fs impeded an unambiguous extraction from the experimental data and hence no clear signature of the ³MLCT state is observed, which should possess a significantly shifted CO stretching band with diminished intensity according to DFT calculations (1672 cm⁻¹→1683 cm⁻¹, scaled by 0.973). The predicted intensity loss of the CO stretching of the relaxed ³MLCT state occurs from the reduction of a single dipyridyl ketone unit, similar to the IR signature of 1⋅⁺ . On the other hand, the calculated CO bands of the ³MC and ⁵MC states of 1²⁺ are very similar to that of the ¹GS (all at 1672 cm⁻¹, scaled by 0.973). Hence, in good agreement with these calculations, analysis of the transient IR data (Supporting Information, Figure S42) reveals that it is comprised of the GSB signal of the CO band of the ¹GS and a slightly blue‐shifted absorption of the CO band in the ⁵MC state, which almost mutually cancel each other.

Consequently, we turned to fs UV/VIS‐pump‐VIS/NIR‐supercontinuum probe spectroscopy to investigate the ultrafast excited state kinetics of 1[PF₆]₂ (Supporting Information, Figures S43–S49). Figure 6 displays the TA spectra obtained upon laser excitation at 350 nm. The spectra are dominated by an intense negative band centered at 610 nm that can be assigned to the GSB. At sub picosecond delay times, two positive bands at ca. 500 nm and 760 nm are observed, which are attributed to the MLCT states. The comparison of the difference spectrum at 0.25 ps with the simulated MLCT spectrum obtained from spectroelectrochemical measurements supports this assignment (Supporting Information, Figure S47). The short‐lived positive band tails far into the NIR (Supporting Information, Figures S45–S46). Figure 6b depicts the corresponding decay traces at three wavelengths. A global lifetime analysis was performed for a quantitative analysis of the TA data. The entire dataset can be adequately fitted with three exponentials with lifetimes of τ ₁ <200 fs, τ ₂=33 ps and τ ₃=516 ps. The decay associated difference spectra as well as the evolution associated difference spectra and corresponding decay curves are shown in the Supporting Information, Figure S48. We attribute the ultrafast component τ ₁ to the ³MLCT lifetime. The τ ₂=33 ps component most likely originates from cooling and reorganization of the solvent cage as the dipole moment during the transition from ³MLCT to ^3/5MC states changes significantly. According to DFT calculations (see below) the dipole moment indeed decreases from 16.9/16.7 D (³MLC) to 6.1/6.6 D (³MC) and 6.4/6.9 D (⁵MC) for the isomers A/B, respectively. Finally, the τ ₃=516 ps component can be assigned to the ⁵MC lifetime as it shows no additional spectral features besides the GSB. This lifetime τ ₃ matches the lifetime τ _IR determined by fs VIS‐pump/IR‐probe spectroscopy. On the sub‐ps timescale, the low‐energy absorption assigned to the MLCT state narrows and shifts to higher energy suggesting a sub‐ps relaxation within the MLCT state (Supporting Information, Figure S49).

Figure 6.

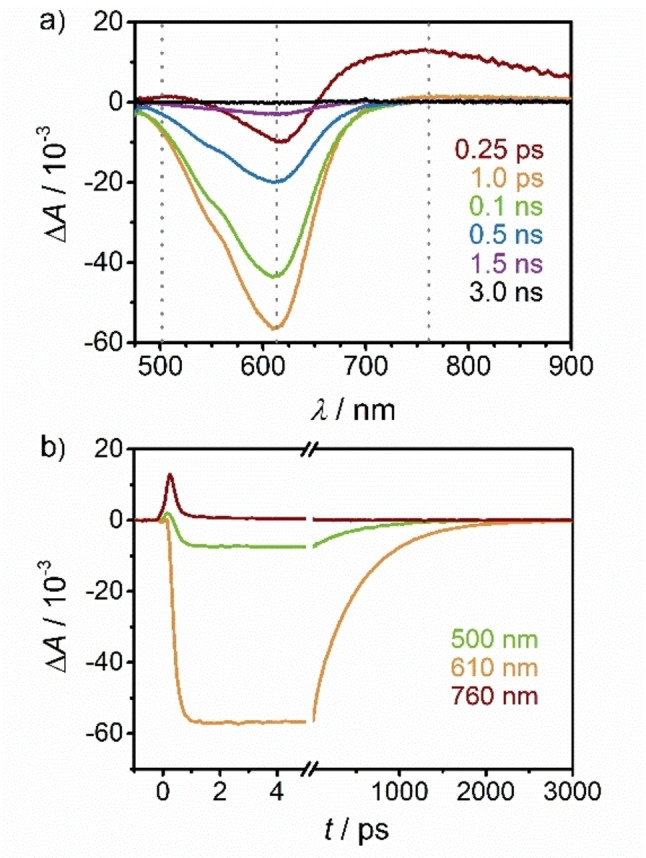
a) fs‐TA spectra of 1[PF₆]₂ in acetonitrile upon excitation at 350 nm (400 nJ/pulse) and b) corresponding time traces at 500 nm (green), 610 nm (orange) and 760 nm (red‐brown).

Excitation at 630 nm (direct excitation to the ¹MLCT state) yields qualitatively similar TA spectra, except for some artefacts such as scattered pump light (Supporting Information, Figure S43–S44). Global analysis delivers three components with very similar lifetimes (τ ₁<200 fs, τ ₂=45 ps, τ ₃=517 ps). Hence, there is no branching at higher energies and the evolution from the state(s) populated with 350 nm excitation to the ³MLCT state is completed in less than 200 fs. Global analysis reveals that the intermediate component is slightly more long‐lived in the case of 630 nm excitation. The observation of characteristic absorption bands of the MLCT state and the more detailed excited state dynamics of such highly symmetric [FeN₆] complexes seems unprecedented, as for the [FeN₆] complexes [Fe(dcpp)₂]²⁺ I²⁺ and [Fe(dcpp)(ddpd)]²⁺ [J^Me]³⁺ with high octahedricity merely the ground state recovery had been detected so far.[ ¹⁹ , ³⁸ , ⁴⁰ ]

To obtain deeper insight into the assignments of the states and dynamics[ ⁵² , ⁵³ ] we resorted to DFT calculations of the ¹GS, the ³MLCT, ³MC and ⁵MC states along a single symmetric Fe−N stretching mode (A_1g) to describe the expansion of the coordination sphere in the ⁵MC state for 1²⁺ (Figure 7a; for 2²⁺ see Supporting Information, Figure S50). The experimental ¹MLCT energy is indicated by a blue ⊗ in the diagram for illustration. Additionally, the ¹GS, the ³MLCT, ³MC and ⁵MC states were optimized without any constraints (Figure 7b–d; indicated in Figure 7a by black, green, orange and red ⊗, respectively). The description of the dynamics along a single breathing mode is highly simplified and the density of states in the relevant region is likely higher than only the reported optimized ³MLCT, ³MC and ⁵MC states. Sophisticated calculations on the singlet‐triplet dynamics of 1²⁺ with optimized functionals and including more degrees of freedom will be reported elsewhere. ^[54]

Figure 7.

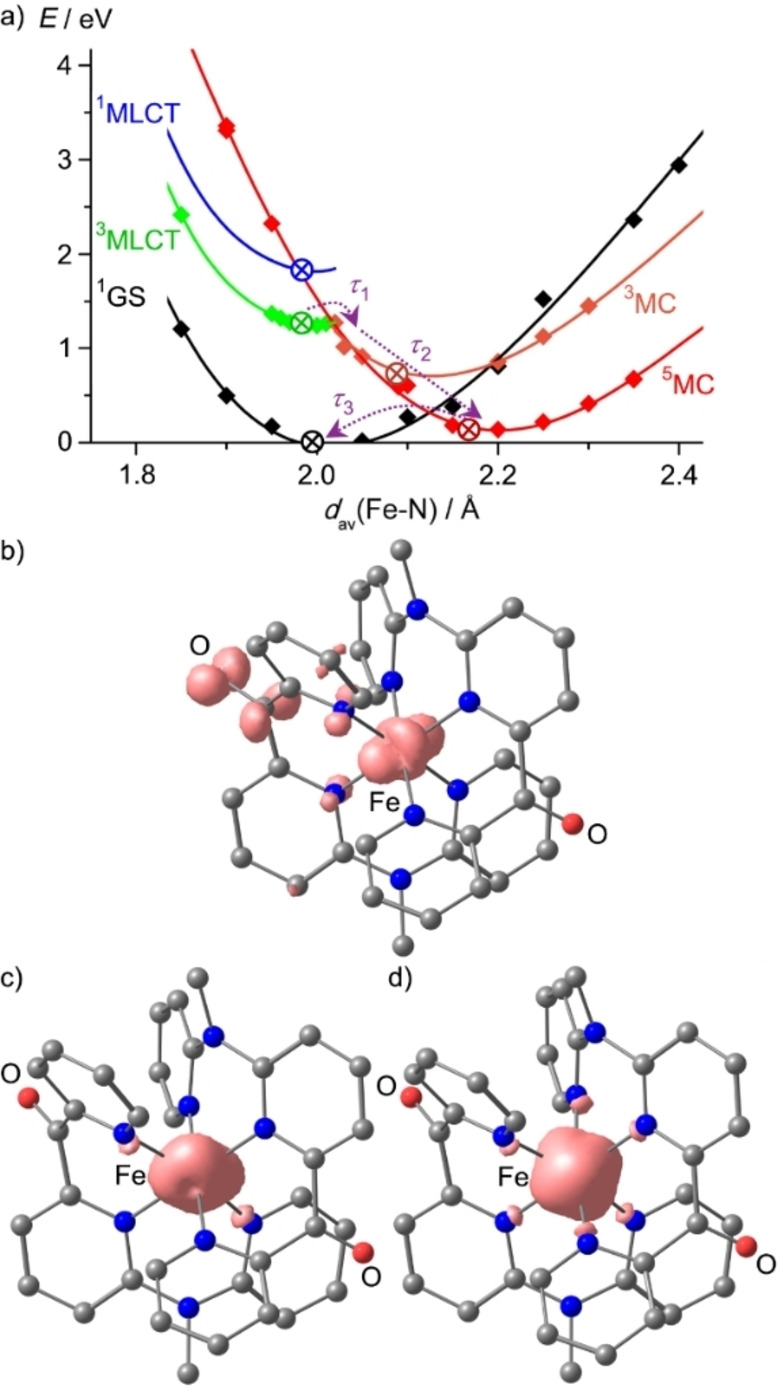
a) DFT calculated potential energy diagram of 1²⁺ including the ³MLCT (green), ³MC (orange), ⁵MC (red) and ¹GS (black) along the symmetric Fe−N stretching mode as simplified reaction coordinate. The ¹MLCT minimum is estimated from the experimental absorption spectrum (blue ⊗) and this curve parallels that of the ³MLCT state for illustration. The energies of fully optimized ¹GS, ³MLCT, ³MC and ⁵MC geometries are indicated by ⊗ in black, green, orange and red, respectively. Processes assigned to the experimental time constants τ ₁–τ ₃ are indicated with dashed purple arrows. Fully DFT optimized geometries and spin densities of b) the ³MLCT, c) the ³MC and d) the ⁵MC states of 1²⁺ are displayed at an isosurface value at 0.012 a.u.

Expectedly, the ³MLCT geometry is very similar to the GS geometry. The symmetric Fe−N stretch fits well to the expansion of the coordination sphere in the DFT optimized ⁵MC state (d(Fe−N)=2.193, 2.147, 2.164/2.194, 2.146, 2.161 Å). Yet, this symmetric mode does not perfectly describe the Jahn‐Teller distorted ³MC state (d(Fe−N)=2.226, 2.099, 2.192/1.993, 2.018, 1.999 Å). In this ³MC state, the Fe−N bonds to the terminal pyridines of a single cpmp ligand are elongated, which defines the Jahn‐Teller axis due to the population of the d_z2 orbital. Nevertheless, we used the simplified reaction coordinate along the symmetric A_1g Fe−N stretching mode to describe the overall process from the MLCT to the final ⁵MC state. At the Franck‐Condon geometry (d(Fe−N)≈2 Å), the ³MLCT, ³MC and ⁵MC states are very similar in energy on this level of theory (Figure 7a). The proximity of ³MLCT and ³MC can lead to efficient non‐radiative decay through coupling of states at conical intersections. Furthermore, this state ordering at the Franck‐Condon geometry/GS geometry suggests that indeed ³MC and ⁵MC are nearly degenerate which had been suggested for [Fe(dcpp)₂]²⁺ I²⁺ before, ^[19] yet the finally populated relaxed state of I²⁺ is the ⁵MC state as shown by time‐resolved K_α and K_β X‐ray emission spectroscopies. ^[40] Along the A_1g Fe−N mode, the energies of the ³MC and ⁵MC states drop significantly in the relevant regions from ca. 2.0 to 2.1 Å and 2.0 to 2.2 Å, respectively. Consequently, the ⁵MC state is lower than the ³MC state at their respective optimized geometries. Within this model, we assign τ ₁<200 fs to the ³MLCT→^3/5MC population transfer, τ ₂=33/45 ps to vibrational cooling and solvent reorganization within the MC states and τ ₃=516 ps to the ⁵MC→¹GS spin crossover.

The excited state landscape of the heteroleptic complex 2²⁺ is quite similar to that of 1²⁺ (Supporting Information, Figure S50; Figure 7a). The ⁵MC state of 2²⁺ is calculated a bit higher than in 1²⁺ so that ⁵MC/³MC inversion has occurred at the Franck‐Condon geometry at this level of theory. The fully optimized ³MC state is Jahn‐Teller distorted with elongated Fe−N bonds to the terminal pyridines of the ddpd ligand (2.292/2.194 Å) as well as to the central pyridine of ddpd (2.100 Å), while in the ¹GS all Fe−N bonds are close to 2 Å (Table 1). Expectedly, the ⁵MC state shows six elongated Fe−N bonds (ddpd: 2.154, 2.140, 2.157 Å; cpmp: 2.167, 2.150, 2.196 Å). At the respective optimized geometries the level ordering is ³MLCT > ³MC > ⁵MC. This ordering enables an efficient decay cascade ³MLCT→³MC→⁵MC with concomitant expansion of the coordination sphere preventing a long‐lived ³MLCT state similar to the situation in 1²⁺ .

Conclusions

The push‐pull ligand 6,2’’‐carboxypyridyl‐2,2’‐methylamine‐pyridyl‐pyridine (cpmp) was coordinated to iron(II) in the homo‐ and heteroleptic low‐spin complexes 1²⁺ and 2²⁺ with the aim to increase the ligand field splitting by a high octahedricity and thus lifting the ^3/5MC excited state energies and to decrease the ³MLCT states by low‐energy π* orbitals at the dipyridyl ketone units. The presence of accepting and donating units in cpmp additionally give rise to ¹LL'CT and ¹ILCT excited states to increase the absorption cross section. These states appear at comparably high energy (350/410 nm) so they do not seem to play a role for the excited state dynamics while the ¹MLCT states are at low energy (λ _max=610, 616 nm for 1²⁺ and 2²⁺ , respectively). The ³MLCT states are the lowest excited states at the Franck‐Condon geometry while the ³MC and ⁵MC states lower in energy upon Fe−N bond elongation. At the respective relaxed geometries, the ⁵MC state is the lowest state in 1²⁺ and 2²⁺ . The lifetime of the ⁵MC state of 1²⁺ has been determined by fs VIS‐pump/IR‐probe and fs UV/VIS‐pump‐VIS/NIR‐supercontinuum probe spectroscopies to 495 ps and 516 ps, respectively, identical within error. Clear signatures of the ³MLCT state of 1²⁺ were observed in fs‐transient absorption spectra in the sub‐picosecond regime at wavelengths above 650 nm, which are assigned to LMCT transitions from the NMe groups to the low‐spin iron(III) center. A kinetic model suggests a sequential population evolution of MLCT→^3/5MC states within 0.2 ps, while cooling and solvent relaxation occurs within 33 ps in the MC states. The expansion of the coordination sphere plays the dominant role in this decay to the ⁵MC state. To mitigate this expansion and the concomitant energy lowering of the ^3/5MC states, an even more rigid ligand environment might be helpful in future studies.

The dipyridyl ketone units provide useful IR probes for reductive and oxidative chemistry as the CO stretching bands significantly shift upon reduction or oxidation. Analogous strong CO shifts should occur in the MLCT states as predicted by DFT calculations. On the other hand, the CO stretching vibration in the ligand periphery is essentially unaffected by the spin state of 1²⁺ (¹GS, ³MC, ⁵MC) and thus gives no handle to probe the spin state in a time‐resolved manner. As vibrational probes for changes in the different spin states, Fe−N vibrations are the most suited ones but these are very challenging to observe by ultrafast IR or Raman spectroscopy.

Experimental Section

General Procedures: CH₃CN and Et₂O were distilled under argon atmosphere from CaH₂ and sodium, respectively. The ligands cpmp ^[41] and ddpd[ ⁴² , ⁵⁵ ] were synthesized according to literature. All other solvents and reagents were used as received from commercial suppliers (Acros, Alfa Aesar, Fischer and Sigma‐Aldrich).

Elemental analyses were performed by the microanalytical laboratory of the Department of Chemistry of the University of Mainz. Most NMR spectra were recorded on a Bruker Avance DRX 400 spectrometer. A Bruker Avance III HD 400 spectrometer was used for ¹H‐¹H COSY, ¹H‐¹³C‐HSQC and ¹H‐¹³C HMBC spectra of 2[PF₆]₂ . The measurements were performed at 400.31 MHz (¹H), 100.05 MHz (¹³C{¹H}), and 162.05 MHz (³¹P{¹H}). [CD₃CN (¹H, δ=1.94; ¹³C, δ=1.24 ppm)] ^[56] or versus external H₃PO₄ (85 %) (³¹P: δ=0 ppm); (s)=singlet, (d)=doublet, (t)=triplet, (sept)=septet, (m)=multiplet. Atom numbering is shown in the Supporting Information at the respective NMR spectra. ATR‐IR spectra were recorded with a Bruker ALPHA II FTIR spectrometer with a Platinum Di‐ATR module. ESI mass spectra were recorded on a Micromass Q‐TOF‐Ultima spectrometer. EPR spectra were collected on a Miniscope MS 300 (Magnettech GmbH, Germany) at a microwave frequency of 9.39 GHz with a frequency counter HP 5340 A (Hewlett Packard) (in frozen butyronitrile, 77 K, 1³⁺ ) and a frequency counter FC 400 (Magnettech GmbH, Germany) (frozen acetonitrile, 77 K, 1⋅⁺ ), respectively. Mn²⁺ in ZnS was used as external standard (g=2.118, 2.066, 2.027, 1.986, 1.946, 1.906). Simulations were performed with the program package Easyspin for MatLab (R2015a). ^[57] Electrochemical experiments were carried out on a BioLogic SP‐200 voltammetric analyzer using platinum wires as counter and working electrodes and 0.01 m Ag/AgNO₃ as the reference electrode. The measurements were carried out at a scan rate of 100 mV s⁻¹ for cyclic voltammetry experiments using 0.1 m [ ⁿ Bu₄][NPF₆] as the supporting electrolyte in CH₃CN. Potentials are referenced to the ferrocene/ferrocenium couple (E _1/2=85±5 mV under experimental conditions). UV/Vis/NIR spectroelectrochemical experiments were performed using a BioLogic SP‐50 voltammetric analyzer and a Specac omni‐cell liquid transmission cell with CaF₂ windows equipped with a Pt‐gauze working electrode, a Pt‐gauze counter electrode and a Ag wire as pseudo reference electrode, melt‐sealed in a polyethylene spacer (approximate path length 1 mm) in CH₃CN (0.3 mm and 0.9 mm for oxidation and reduction, respectively) containing 0.1 m [ ⁿ Bu₄N][PF₆]. ^[58] IR spectroelectrochemical experiments were performed using a BioLogic SP‐200 voltammetric analyzer with the same cell, electrodes and electrolyte as above (12 mm). UV/Vis/NIR spectra were recorded on a Varian Cary 5000 spectrometer using 1.0 cm cells (Hellma, Suprasil). A Horiba LabRAM HR Raman microscope was used for resonance Raman measurements with an object lens (10× NA 0.25) from Olympus. Samples were optically excited with a NIR laser (785 nm, 100 mW, air‐cooled diode laser), a red laser (633 nm, 17 mW, HeNe laser), a green laser (532 nm, 50 mW, air‐cooled frequency‐doubled Nd:YAG solid state laser), or a blue laser (473 nm, 20 mW, air‐cooled solid state laser). Samples were measured in the solid state and in CH₃CN solution. HERFD‐XANES (high energy resolution fluorescence detected X‐ray absorption near edge structure) and CtC‐XES (core‐to‐core X‐ray emission spectroscopy) experiments were conducted at beamline ID26 of the ESRF (European Synchrotron Radiation Facility). ^[59] During the experiments, the electron energy of the synchrotron was at 6.0 GeV, and its ring current varied between 180 and 200 mA. All measurements were carried out using the first harmonic of two u35 undulators. The incident photon energy was selected via the (311) reflection from a double Si crystal monochromator, leading to a photon flux of approximately 2×1013 photons ⋅ s⁻¹ on the sample position. The monochromator was calibrated using a Fe foil. All experiments were conducted with a Johann type spectrometer[ ⁶⁰ , ⁶¹ ] in a vertical Rowland geometry, using the (620) reflection of five spherically bent Ge crystal analyzers (with R=1 m). The emission was monitored by a photodiode installed at about 90° scattering angle and at 45° to the sample surface. Fe K‐edge HERFD‐XANES were obtained by recording the intensity of the Fe CtC XES maximum as a function of the incident energy. During each HERFD‐XANES scan, the undulator gap was kept at a fixed position and only the monochromator angle was changed. To minimize radiation damage, all measurements were carried out at 20 K using a He cryostat under vacuum conditions. Each HERFD‐XANES measurement was carried out in 60 seconds. To achieve a satisfying signal to noise ratio four spectra were averaged, each measured at a different spot of the homogeneous sample. Each sample is tested for radiation damage in the beginning by ten fast HERFD‐XANES scans over the pre‐edge and whiteline with a scan time of 10 seconds on one spot, starting with a 100‐times attenuated beam and ending with an unattenuated beam. Within these time frames, no radiation damage could be detected. CtC‐XES spectra were recorded off resonance at an excitation energy of 7300 eV in the range of 7030–7080 eV, with a step width of 0.2 eV. To observe reasonable data, three spectra (60 second per scan) were recorded, utilizing a different sample spot for each scan. Ultrafast Vis‐pump/IR‐probe spectra were measured using a flow cell (Specac Omni Cell with CaF₂ windows and 200 μm spacer) with a 8.6 mM acetonitrile solution at 295 K. A CPA laser system (Spectra‐Physics Spitfire Ace) with 100 fs pulses spectrally centered at 800 nm was used as laser source. The pump pulses centered at 610 nm were generated using a NOPA (Light Conversion TOPAS‐White). Every second pump pulse was blocked using a chopper to generate the difference spectra from two sequent spectra. The probe pulses were generated using a collinear OPA (Light Conversion TOPAS‐Prime with DFG extension) and detected using CPU[ ⁶² , ⁶³ ] and a CCD camera (Princeton Instruments PIXIS 2 K) connected to a spectrometer (Princeton Instruments Acton SpectraPro SP‐2500i). The lifetime was obtained from Global Target Analysis with TIMP. ^[64] Ultrafast pump‐VIS/NIR‐probe experiments were conducted using a Helios‐Fire pump‐probe setup (Ultrafast Systems) paired with a regeneratively amplified 1030 nm laser (Pharos, Light Conversion, 1030 nm, 200 fs, 200 μJ). The effective laser repetition rate of 1 kHz was set via an internal pulse picker. A small portion of the 1030 nm fundamental was directed to the optical delay line and was subsequently used to generate broadband probe light by focusing the beam onto a sapphire (visible range) or YAG (NIR range) crystal. The pump pulse was generated with an optical parametric amplifier (Orpheus‐F, Light Conversion). The samples were measured in a 1 mm quartz cuvette. For global analysis of the TA data the software Glotaran 1.5.1 was employed. ^[65] Intensity data for crystal structure determinations were collected with a Bruker AXS Smart1000 CCDC diffractometer with an APEX II detector using Mo−Kα radiation (λ=0.71073 Å). The diffraction frames were integrated using the SAINT software package ^[66] and were corrected for absorption with MULABS ^[67] of the PLATON software package. ^[68] The structures were solved with SHELXT ^[69] and refined by the full‐matrix method based on F ² using SHELXL ^[70] of the SHELX ^[71] software package and the ShelXle ^[72] graphical interface. All non‐hydrogen atoms were refined anisotropically while the positions of all hydrogen atoms were generated with appropriate geometric constraints and allowed to ride on their respective parent atoms with fixed isotropic thermal parameters.

Deposition Numbers 2125265 (for 1[PF ₆ ] ₂ ×CH ₃ CN) and 2125266 (for 2[PF ₆ ] ₂ ×1.5CH ₃ CN) contain the supplementary crystallographic data for this paper. These data are provided free of charge by the joint Cambridge Crystallographic Data Centre and Fachinformationszentrum Karlsruhe Access Structures service. Density functional theoretical calculations were carried out using the ORCA program package (version 4.0.1). ^[73] All calculations were performed using the B3LYP functional[ ⁷⁴ , ⁷⁵ , ⁷⁶ ] and employ the RIJCOSX approximation.[ ⁷⁷ , ⁷⁸ ] Relativistic effects were calculated at the zeroth order regular approximation (ZORA) level. ^[79] The ZORA keyword automatically invokes relativistically adjusted basis sets. To account for solvent effects, a conductor‐like screening model (CPCM) modeling acetonitrile was used in all calculations.[ ⁸⁰ , ⁸¹ ] Geometry optimizations were performed using Ahlrichs polarized valence triple‐zeta basis set def2‐TZVP.[ ⁸² , ⁸³ ] Atom‐pairwise dispersion correction was performed with the Becke‐Johnson damping scheme (D3BJ).[ ⁸⁴ , ⁸⁵ ] The presence of energy minima was checked by numerical frequency calculations. Explicit counterions and/or solvent molecules were not taken into account. The ³MC structures were found by constraining certain Fe−N bonds to longer distances and re‐optimizing the thus obtained structure without geometry constraints. All optimized geometries were ascertained as minima by numerical frequency analysis. For the potential diagrams, all Fe−N bonds were constrained to the respective averaged values. The assignment of the state characters has been done by dividing the molecule into three fragments (metal center and two ligands) and calculating charge transfer numbers, as implemented in the TheoDore software package.[ ⁸⁶ , ⁸⁷ ] TD‐DFT (XANES)[ ⁸⁸ , ⁸⁹ ] calculations were carried out using a modified TPSSh functional, with an adjusted Hartee‐Fock exchange of 12.5 %, which has been applied in previous studies on iron polypyridine complexes[ ²⁷ , ⁵¹ ] and has been shown to achieve a very good agreement between theory and experiment concerning the splitting of MC and MLCT transitions in the near‐edge to pre‐edge region. The def2‐TZVP ^[82] basis set (with a special integration accuracy of 5) was applied on all atoms except Fe, for which the expanded CP(PPP) basis set ^[90] is used (with a special integration accuracy of 7). All calculations were performed using the optimized structures. Inclusion of polar crystal environment effects were included via the conductor‐like polarizable continuum model (CPCM, ϵ=infinity).[ ⁸¹ , ⁹¹ ] All calculated XANES (TD‐DFT) transitions were broadened by 1.5 eV (fwhm). Calculated XANES were adjusted to experiment by shifting them by 151.3 eV. Kohn–Sham orbitals were visualized with the IboView program (version 20150427). ^[92]

Synthesis of 1[PF₆]₂ ([Fe(cpmp)₂][PF₆]₂). A solution of 200 mg (0.69 mmol) cpmp in acetonitrile (4 mL) was added to a solution of 116 mg Fe[BF₄]₂×6H₂O (0.34 mmol) in acetonitrile (1 mL). The blue solution was stirred for 16 h at room temperature. Addition of diethyl ether (200 mL) yielded a blue precipitate that was washed with diethyl ether (200 mL). The product was collected by filtration and dissolved in acetonitrile (1 mL). Addition of an aqueous solution of [NH₄][PF₆] (978 mg, 6 mmol, in 100 mL of H₂O) resulted in precipitation of a blue solid, which was collected by filtration and purified by slow diffusion of diethyl ether into a solution of 1[PF₆]₂ in acetonitrile to yield crystals suitable for single‐crystal X‐ray diffraction. The blue crystals were dried under reduced pressure. Yield: 131 mg (0.14 mmol, 47 %). Elem. anal. calcd. for C₃₄H₂₈F₁₂FeN₈O₂P₂×0.33 H₂O: C, 43.80; H, 3.10; N, 12.02. Found: C, 43.77; H, 3.22; N, 11.97. ¹H NMR (CD₃CN): δ=8.26 (dd, ³ J=7.9 Hz, 2 H, H⁹), 8.07 (m, 4 H, H³, H⁴), 8.01 (d, ³ J=7.3 Hz, 2 H, H⁸), 7.87 (dd, ³ J=8.4, 8.4 Hz, 2 H, H¹⁶), 7.56 (d, ³ J=8.5 Hz, 2 H, H¹⁰), 7.45 (d, ³ J=5.9 Hz, 2 H, H¹), 7.21 (dd, ³ J=7.5, ³ J=4.0 Hz, 2 H, H²), 7.10 (d, ³ J=8.8 Hz, 2 H, H¹⁷), 6.83 (d, ³ J=5.8 Hz, 2 H, H¹⁴), 6.77 (d, ³ J=6.8 Hz, 2 H, H¹⁵), 2.91 (s, 6 H, H⁶). ¹³C{¹H} NMR (CD₃CN): δ=179.9 (C¹²), 159.3 (C⁷), 158.6 (C¹³), 158.2 (C⁵), 157.3 (C¹), 156.8 (C¹¹), 154.4 (C¹⁴), 140.0 (C¹⁶), 139.4 (C⁹), 138.4 (C⁴), 126.2 (C²), 126.1 (C³), 124.4 (C⁸), 120.2 (C¹⁵), 117.5 (C¹⁰), 112.0 (C¹⁷), 37.4 (C⁶). ³¹P NMR (CD₃CN): δ=−144.7 (sept, ¹ J _PF=707 Hz). MS (ESI⁺) m/z (%)=318.05 (76, [Fe(cpmp)₂]²⁺), 365.05 (86, [Fe(cpmp)F]⁺), 655.16 (100, [Fe(cpmp)₂F]⁺), 781.8 (13, {[Fe(cpmp)₂][PF₆]}⁺), 1245.74 (23, {H[Fe(cpmp)₂]₃[PF₆]₄}²⁺), 1709.65 (25, {H₄[Fe(cpmp)₂]₄[PF₆]₆}²⁺). MS (HR‐ESI⁺): calcd. for C₃₄H₂₈F₆FeN₈O₂P⁺: m/z=781.1326, found: m/z=781.1309. IR (ATR): $\tilde{\upsilon }$ =1669 (m, CO), 1558(m), 1573 (m), 1482 (m), 1453 (m), 1435 (m), 1355 (m), 1320 (w), 1294 (vw), 1270 (w), 1244 (w), 1198 (vw), 1175 (w), 1154 (w), 1139 (w) 1122 (vw), 1090 (vw), 1067 (vw), 1020 (w), 972 (w), 833 (vs, PF), 793 (s), 754 (s), 713 (s), 673 (s), 649 (m), 633 (m), 578 (m), 559 (vs, PF₂), 516 (m), 448 (w), 434 (w), 414 (w) cm⁻¹. CV (CH₃CN): E _1/2=−1.46 (rev.), −1.28 (rev.), +0.78 (rev.) V vs. FcH/FcH⁺. UV/Vis/NIR (CH₃CN): λ _max (ϵ)=247 (20900, sh), 270 (28700), 300 (16500, sh), 350 (12200), 410 (5640, sh), 610 nm (3980 m ⁻¹cm⁻¹).

Synthesis of 2[PF₆]₂ ([Fe(cpmp)(ddpd)][PF₆]₂). A solution of 100 mg (0.34 mmol) cpmp and 100 mg (0.34 mmol) ddpd in dry acetonitrile (2 mL) was added to a suspension of 143 mg (0.40 mmol) Fe(OTf)₂ in dry acetonitrile (5 mL) under argon atmosphere. The yellow‐green solution was stirred for 30 minutes at room temperature. Addition of dry diethyl ether (200 mL) yielded in a green precipitate – containing [Fe(ddpd)₂]²⁺ and [Fe(cpmp)(ddpd)]²⁺.The product was purified by column chromatography on silica gel with acetonitrile/saturated aqueous solution of potassium nitrate (8 : 1) as eluent. The solvents were removed by freeze drying. The product was collected by filtration and dissolved in acetonitrile (1 mL). Addition of an aqueous solution of [NH₄][PF₆] (978 mg, 6 mmol, in 100 mL of H₂O) precipited a green solid, which was collected by filtration. The green crystals were dried under reduced pressure. Crystals suitable for single‐crystal X‐ray diffraction were yielded by slow diffusion of diethyl ether into a solution of 2[PF₆]₂ in acetonitrile. Yield: 67.1 mg (0.07 mmol, 18 %). Elem. anal. calcd. for C₃₄H₃₁F₁₂FeN₉OP₂×1.25 H₂O: C, 42.99; H, 3.55; N, 13.27. Found: C, 42.52; H, 3.04; N, 13.29. ¹H NMR (CD₃CN): δ=8.17 (t, ³ J=7.9 Hz, 1 H), 8.04 (m, 3 H), 7.92 (d, ³ J=7.4 Hz, 1 H), 7.83 (m, 3 H), 7.44 (m, 2 H), 7.14 (m, 5 H), 7.03 (d, ³ J=8.3 Hz, 1 H), 6.98 (d, ³ J=5.8 Hz, 1 H), 6.78 (m, 2 H), 6.69 (m, 1 H), 6.63 (d, ³ J=5.4 Hz, 2 H), 3.04 (s, 3 H), 3.02 (s, 3 H), 2.83 (s, 3 H). ¹³C{¹H} NMR (CD₃CN): δ=181.5, 162.4, 161.6, 161.4, 161.1, 160.9, 159.5, 158.7, 158.3, 156.5, 156.0, 155.2, 141.6, 141.3, 140.9, 140.8, 140.4, 139.5, 127.8, 127.2, 126.1, 125.7, 121.4, 121.2, 121.1, 117.9, 113.7, 113.5, 113.1, 113.0, 112.4, 40.0, 39.9, 39.2. The number of ¹H and ¹³C resonances, their intensity and multiplicity fit to the structure, yet the two ligand nuclei feature too similar chemical shifts to allow a detailed assignment. ³¹P NMR (CD₃CN): δ=−144.6 (sept, ¹ J _PF=706 Hz). MS (ESI⁺) m/z (%)=318.57 (96, [Fe(cpmp)(ddpd)]²⁺), 366.08 (100, [Fe(ddpd)F]²⁺), 656.20 (57, [Fe(cpmp)(ddpd)F]²⁺),782.82 (13, {[Fe(cpmp)(ddpd)][PF₆]}⁺),1246.75 (26, {H[Fe(cpmp)(ddpd)]₃[PF₆]₄}⁺), 1711.18 (33, {H₄[Fe(cpmp)(ddpd)]₄[PF₆]₆}²⁺}. MS (HR‐ESI⁺): calcd. for C₃₄H₃₁F₆FeN₉OP⁺: m/z=782.1643, found: m/z=782.1642. IR (ATR): $\tilde{\upsilon }$ =1672 (m, CO), 1593 (m), 1580 (m), 1567 (m), 1493 (m), 1450 (s), 1432 (s), 1358 (m), 1340 (m), 1320 (w), 1304 (vw), 1290 (vw), 1270 (vw), 1278 (w), 1238 (w), 1196 (vw), 1171 (w), 1142 (m), 1134 (w), 1096 (w), 1065 (vw), 1020 (vw), 974 (vw), 949 (vw), 915 (vw), 875 (m), 831 (vs, PF), 978 (vs), 777 (s), 747 (vs), 717 (m), 672 (m), 647 (vw), 634 (vw), 589 (w), 583 (w), 555 (s, PF₂), 516 (w), 446 (w), 414 (w) cm⁻¹. CV (CH₃CN): E _1/2=−2.03 (rev.), −1.36 (rev.), +0.55 (rev.) V vs. FcH/FcH⁺. UV/Vis/NIR (CH₃CN): λ_max (ϵ)=244 (21900), 276 (30100), 326 (15900), 365, (8630), 420 (5500, sh), 616 nm (2250 m ⁻¹cm⁻¹).

Chemical oxidation of 1[PF₆]₂ . 1[PF₆]₂ (100 mg, 0.11 mmol, 1.0 equiv.) was dissolved in CH₃CN (5 mL). [NH₄]₂[Ce(NO₃)₆] (95 mg, 0.17 mmol, 1.6 equiv.) was added as a solid. After 5 minutes of stirring at room temperature, the orange solid was collected by filtration and dried under reduced pressure. EPR (frozen PrCN, 77 K): g ₁(A/B)=2.7453/2.6658, g ₂(A/B)=2.2390/2.2389, g ₃(A/B)=1.6758/1.6063. UV/Vis/NIR (CH₃CN): λ _max=270, 314 (sh), 350, 962 nm. IR (ATR): $\tilde{\upsilon }$ =3112 (vw, sh), 3087 (vw), 3030 (vw, sh), 1695 (w, CO), 1649 (vw), 1595 (w), 1577 (vw), 1454 (s, sh), 1427 (vs, NO), 1322 (vs), 1298 (vs), 1267 (vs), 1250 (vs, sh), 1204 (w), 1168 (w), 1159 (w), 1143 (w), 1102 (w), 1070 (vw), 1038 (m), 1019 (m), 971 (w), 892 (w), 816 (s, NO), 788 (w), 780 (w), 761 (m), 734 (s, NO), 706 (w), 679 (w), 658 (vw), 634 (vw), 615 (vw), 574 (w), 525 (vw), 512 (vw), 474 (vw), 456 (vw), 446 (vw), 432 (vw), 405 (w) cm⁻¹.

Chemical reduction of 1[PF₆]₂ . 1[PF₆]₂ (2.65 mg, 2.86 μmol, 1.0 equiv.) was dissolved in CH₃CN (1.5 mL). Decamethylcobaltocene (0.63 mg, 1.91 μmol, 1.0 equiv.) was added to 1.0 mL of this solution as solid. EPR and IR spectra were directly measured after 5 minutes of stirring. EPR (frozen CH₃CN, 77 K): g=2.0075. IR (CH₃CN): $\tilde{\upsilon }$ =1681 (CO) cm⁻¹.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supporting Information

J. Moll, R. Naumann, L. Sorge, C. Förster, N. Gessner, L. Burkhardt, N. Ugur, P. Nuernberger, W. Seidel, C. Ramanan, M. Bauer, K. Heinze, Chem. Eur. J. 2022, 28, e202201858.

Data Availability Statement

The data that support the findings of this study are available in the supplementary material of this article.