Integrating eco‐evolutionary dynamics and modern coexistence theory

Abstract

Community ecology typically assumes that competitive exclusion and species coexistence are unaffected by evolution on the time scale of ecological dynamics. However, recent studies suggest that rapid evolution operating concurrently with competition may enable species coexistence. Such findings necessitate general theory that incorporates the coexistence contributions of eco‐evolutionary processes in parallel with purely ecological mechanisms and provides metrics for quantifying the role of evolution in shaping competitive outcomes in both modelling and empirical contexts. To foster the development of such theory, here we extend the interpretation of the two principal metrics of modern coexistence theory—niche and competitive ability differences—to systems where competitors evolve. We define eco‐evolutionary versions of these metrics by considering how invading and resident species adapt to conspecific and heterospecific competitors. We show that the eco‐evolutionary niche and competitive ability differences are sums of ecological and evolutionary processes, and that they accurately predict the potential for stable coexistence in previous theoretical studies of eco‐evolutionary dynamics. Finally, we show how this theory frames recent empirical assessments of rapid evolution effects on species coexistence, and how empirical work and theory on species coexistence and eco‐evolutionary dynamics can be further integrated.

Recent studies suggest that rapid evolution operating concurrently with competition may enable species coexistence. Such findings necessitate general theory that incorporates the coexistence contributions of eco‐evolutionary process in parallel with purely ecological mechanisms, and provides metrics for quantifying the role of evolution in shaping competitive outcomes in both modelling and empirical contexts. To foster the development of such theory, here we extend the interpretation of the two principal metrics of modern coexistence theory ‐ niche and competitive ability differences ‐ to systems where competitors evolve and show how this theory frames recent empirical assessments of rapid evolution effects on species coexistence, and how empirical work and theory on species coexistence and eco‐evolutionary dynamics can be further integrated.

INTRODUCTION

Increasing recognition that evolutionary change is fast enough to operate on contemporary time scales is forcing ecologists to consider rapid evolution as a major determinant of ecological dynamics (Ellner, 2013; Govaert et al., 2019; Hairston et al., 2005; Hendry, 2016; Schoener, 2011; Thompson, 1998). Particularly exciting are eco‐evolutionary feedbacks, where ecological and evolutionary processes reciprocally affect one another, generating interactions and dynamics unforeseen based on ecology or evolution alone (Post & Palkovacs, 2009). In the competition literature, ecologists have long understood that competition shapes the evolutionary trajectories of competitors and that the resulting niche partitioning reciprocally shapes opportunities for species coexistence (Barabás & D'Andrea, 2016; Brown & Wilson, 1956; de Mazancourt et al., 2008; Germain et al., 2018; Grant & Grant, 2006; Pastore et al., 2021; Slatkin, 1980). Meanwhile, a number of studies have shown that the evolution of interspecific competitive ability can favour cyclical coexistence by rescuing competitors threatened with competitive exclusion (Lankau, 2009, 2011; León, 1974; Levin, 1971; Mougi, 2013; Pease, 1984; Pimentel, 1968; Pimentel et al., 1965; Vasseur et al., 2011; Wittmann & Fukami, 2018; Yamamichi et al., 2020).

The ecological literature continues to accumulate mechanisms by which rapid evolution affects species coexistence. These include, for example, the evolution of a defence trait in a prey species that equalises the competitive ability of its consumers, and thereby promotes their coexistence (van Velzen, 2020). Rapid evolution can also promote fluctuation‐dependent coexistence by changing the functional response of consumers to resources (Yamamichi & Letten, 2021) or promote exclusion when local adaptation prevents the colonisation of later‐arriving competitors (Leibold et al., 2019; Loeuille & Leibold, 2008; Thompson & Fronhofer, 2019; Urban & De Meester, 2009). The breadth of results showing how evolution shapes competitive outcomes necessitates an integrated theoretical framework for understanding the eco‐evolutionary dynamics of species coexistence.

Of particular need is a framework that places eco‐evolutionary mechanisms alongside purely ecological mechanisms, and does so in the same currency, so that the magnitude of these mechanisms can be quantified and compared. Such a framework would be especially important for interpreting the cyclical coexistence that can emerge from the evolution of competitive ability (Lankau, 2009, 2011; Mougi, 2013; Vasseur et al., 2011). With this mechanism, evolution in response to changing species abundances feeds back to affect those abundances, continuing evolutionary change and making the competitive outcome impossible to predict with ‘ecology‐only’ approaches. In fact, unlike cases where eco‐evolutionary dynamics converge to a fixed point and evolution is only transient, the purely ecological dynamics at all points in a coexistence cycle may predict competitive exclusion (Vasseur et al., 2011).

To motivate future studies integrating rapid evolution and species coexistence, we considered how competitive dynamics in evolving systems could be incorporated into a prominent ecological framework—modern coexistence theory (Barabás et al., 2018; Chesson, 1994, 2000a, 2000b, 2018). In this theoretical framework, when two species compete, the outcome of competition can be decomposed into two ecological metrics that align with verbal concepts long held by those studying competition (Box 1, Chesson, 2000b). The first is the stabilising niche difference, which measures the degree to which species harm individuals of their own species more than they harm individuals of other species. It stabilises the interaction between two competing species by favouring the growth of species that drop to low relative abundance (i.e. negative frequency‐dependence in community dynamics). The second metric is the competitive ability difference (more technically termed the average fitness difference), a comparison of species' average abilities to compete, often measured as their ability to grow and maintain that growth under crowded conditions. Coexistence occurs when the stabilising niche difference is strong enough to overcome the competitive ability difference (Chesson, 2000b).

BOX 1. Review of contemporary coexistence theory.

Here, following modern coexistence theory, we show how to calculate the mutual invasibility condition, the stabilising niche difference and the competitive ability difference based on a Lotka–Volterra model of competition. This provides the basis for determining the eco‐evolutionary versions of these quantities in the main text.

In a two‐species Lotka–Volterra model, species i and j affect the per capita growth rate of species i (1/N _i ∙dN _i /dt) as follows:

$$\frac{1}{N_i}\frac{{\mathit{dN}}_i}{\mathit{dt}}=r_i\left(1-{\alpha }_{\mathit{ii}}{N}_i-{\alpha }_{\mathit{ij}}{N}_j\right),$$ (1.I)

where r _i is the intrinsic growth rate of species i and α _ij describes the per capita effect of species j on species i. With only species j in the system, this equilibrium will be achieved when $N_j^{*}=1/{\alpha }_{\mathit{jj}}$. The invasion condition for species i is determined by substituting $N_j^{*}$ for N _j in Equation 1.I and assuming that species i is at such low density as to not affect its own growth (N _i  = 0). Thus, the conditions for species i and j to have positive growth when rare are:

$$\frac{{\alpha }_{\mathit{ij}}}{{\alpha }_{\mathit{jj}}}<1\text{and}\frac{{\alpha }_{\mathit{ji}}}{{\alpha }_{\mathit{ii}}}<1.$$ (1.II)

In other words, the resident species must harm itself more than it harms the invader.

The invasion conditions for two species can be combined in ways that map onto common verbal concepts of the controls over coexistence including niche differences and competitive ability. Following Chesson and Kuang (2008), the niche overlap, ρ, is the average degree to which the two invasion conditions in Equation 1.II are met across the two species:

$$\rho =\sqrt{\frac{{\alpha }_{\mathit{ji}}{\alpha }_{\mathit{ij}}}{{\alpha }_{\mathit{ii}}{\alpha }_{\mathit{jj}}}}.$$ (1.III)

The greater the intraspecific interactions relative to the interspecific interactions, the less the niche overlap, and the greater the stabilising niche difference, which can be expressed as −ln(ρ).

Following Chesson (2013), the competitive ability difference (traditionally termed the ‘fitness difference’) is the ratio of the left‐hand sides of Equation 1.II and describes the degree to which species i more easily (or less easily if κ _i /κ _j  < 1) meets the invasion condition than species j:

$$\frac{{\kappa }_i}{{\kappa }_j}=\sqrt{\frac{{\alpha }_{\mathit{jj}}{\alpha }_{\mathit{ji}}}{{\alpha }_{\mathit{ii}}{\alpha }_{\mathit{ij}}}}.$$ (1.IV)

When species i is the fitness superior, the interaction coefficients subjecting it to competition (in the denominator of Equation 1.IV) are smaller than when species j is the recipient of competition (in the numerator).

The mutual invasion condition (Equation 1.II) can now be expressed, after some algebra (see Saavedra et al., 2017; Chesson, 2018 for overview):

$$\rho <\frac{{\kappa }_i}{{\kappa }_j}<\frac{1}{\rho }.$$ (1.V)

This condition states that when the competitive ability difference is closer to unity, the greater the niche overlap ρ can be and still allow coexistence. ρ << 1 almost guarantees coexistence, and if ρ > 1, coexistence is impossible as the system is destabilised, with the potential for priority effects if the competitive ability difference is sufficiently close to one (Ke & Letten, 2018). If species i is deemed the competitive superior, condition 1.V can be equivalently expressed as −ln(ρ) > ln(κ _i /κ _j ), meaning the stabilising niche difference exceeds the competitive ability difference.

This framework for coexistence has been instrumental in helping resolve questions about diversity maintenance, biological invasions, neutral theory, community assembly and trait‐based and phylogenetic community ecology (Adler et al., 2007; HilleRisLambers et al., 2012; Ke & Letten, 2018; Letten et al., 2017; Levine et al., 2017; Levine & HilleRisLambers, 2009; Mayfield & Levine, 2010; Saavedra et al., 2017; Song et al., 2020; Spaak & De Laender, 2020). It is therefore a natural starting place to incorporate evolutionary change into the rules for species coexistence. But before doing so, we must ensure that the fundamental structure of the framework still holds when species evolve. Niche and competitive ability differences, for example, can be readily derived from interaction coefficients in phenomenological models of competition (Lotka–Volterra competition model in continuous time (Lotka, 1932; Volterra, 1926) and Leslie–Gower competition model in discrete time (Leslie & Gower, 1958)) and are readily used to understand stable coexistence after transient evolution (Pastore et al., 2021). But if interaction coefficients continuously change in response to competition, what is the meaning of these metrics? More fundamentally, does the mutual invasibility criterion upon which modern coexistence theory is based (Box 1) even hold in evolving systems?

As we will show here, the niche and competitive ability concepts, and therefore much of modern coexistence theory, can indeed be successfully extended to evolving systems. This framework, therefore, has tremendous potential to translate the evolutionary effects of competitors into the currency of ecological models, helping formally unify the ecological and evolutionary literature on coexistence. Such a unification allows one to better understand complex eco‐evolutionary dynamics against the inevitable backdrop of purely ecological mechanisms one finds in nature. Aside from these theoretical benefits, developing a modern coexistence theory for evolving systems is important for properly framing empirical results about how evolution affects species diversity maintenance (Germain et al., 2020; Hart et al., 2019). For example, a number of recent studies have postulated or empirically examined how evolutionary change affects the ecological niche and competitive ability differences between pairs of competitors (Germain et al., 2020; Hart et al., 2019; Pastore et al., 2021). But without first demonstrating the applicability of the coexistence framework to evolving systems of competitors, interpreting such results is challenging. In a worst‐case scenario, quantifying how evolutionary change affects the ‘ecological’ stabilising niche and competitively ability differences could be misleading.

In this paper, we first define an eco‐evolutionary mutual invasion condition for species coexistence that accounts for trait evolution in response to species' competitive environments. We then use the eco‐evolutionary invasion growth rates to generate stabilising niche and competitive ability differences that jointly predict the outcome of the interaction between rapidly evolving competitors. We use a graphical interpretation of these metrics to show how the ecological dynamics at key points in the eco‐evolutionary trajectory of a system predict the interaction outcome under rapid or more gradual evolutionary change. Finally, we apply the eco‐evolutionary framework to simulations of several prior theoretical studies to re‐interpret their results from the perspective of modern coexistence theory. We conclude by discussing the implications of our framework for empirical tests of how evolution affects species coexistence, the parallels between the partitioning methods developed for coexistence theory and eco‐evolutionary dynamics, and extensions to more diverse communities.

THE ECO‐EVOLUTIONARY INVASION GROWTH RATE, NICHE OVERLAP AND COMPETITIVE ABILITY DIFFERENCE

The purely ecological mutual invasion condition for species coexistence specifies that each species can invade the system from low density when its competitor is at its single species carrying capacity (Box 1). The logic is that, regardless of the complexity of the dynamics away from the boundaries where one species is at near zero density, exclusion cannot occur if both species have a positive growth rate when depressed to very low density (Grainger et al., 2019). In other words, the equilibrium points where one species is at zero density and the other is at its carrying capacity are unstable and, as a result, neither species can be excluded if both are initially present. Satisfying the mutual invasion condition in a purely ecological model requires that both species exert greater effects on individuals of their own species than they do on one another (Box 1).

Now consider a system where the competitors have interactions dependent on traits (e.g. rooting morphology in plants, bill morphology in birds) that evolve as a function of the competitive environment in which they are found. One can still calculate an invasion condition that predicts eco‐evolutionary coexistence. Chesson (2000b) points out that even if the interaction coefficients of a Lotka–Volterra model (Box 1) are some function of species densities (e.g. α _ij  = f[N _i , N _j ]), the invasion conditions in Equation 1.II of Box 1 still hold for coexistence (if there are multiple carrying capacities, as possible in models more complex than Lotka–Volterra, the invasion growth rates need to be evaluated at all resident species equilibria) (Barabás et al., 2018). What is additionally required, however, is that the per capita effect of the resident species on itself (e.g. α _jj ) is evaluated at the resident equilibrium state, as is the interspecific effect of the resident on the invader.

This logic can be extended to understand the eco‐evolutionary invasion condition. We do this here for a Lotka–Volterra system of competitors (Box 1) where the interaction coefficients change with the competitive environment due to the evolution of some underlying trait. The conditions for coexistence in Box 1 still hold, but we must assume that rapid evolution is sufficiently fast and the adaptive landscape sufficiently simple that the traits that determine interaction coefficients are perfectly specified by the species' densities (following Chesson, 2000b). Of course, assuming much faster evolution than ecology (Cortez & Ellner, 2010) is the exact opposite of the time scale separation that has long justified the quasi‐independence of the subdisciplines (Hutchinson, 1965). But even under relatively ‘slow’ evolution, a population that spends long enough suppressed to low densities might eventually evolve to such conditions (see also the ‘Limitations of the eco‐evolutionary niche and competitive ability difference’ section). If we make this assumption, when calculating the condition for species i to invade the resident state for species j, the interaction coefficients α _jj and α _ij (Box 1) must take on the values they have after evolving to that resident state, which we denote α _jj | _j and α _ij | _j . The mutual invasion criterion for the coexistence of competitors that evolve becomes (Figure 1b):

$$\frac{{\left.{\alpha }_{\mathit{ij}}\right|}_j}{{\left.{\alpha }_{\mathit{jj}}\right|}_j}<1\text{and}\frac{{\left.{\alpha }_{\mathit{ji}}\right|}_i}{{\left.{\alpha }_{\mathit{ii}}\right|}_i}<1.$$ (1)

FIGURE 1.

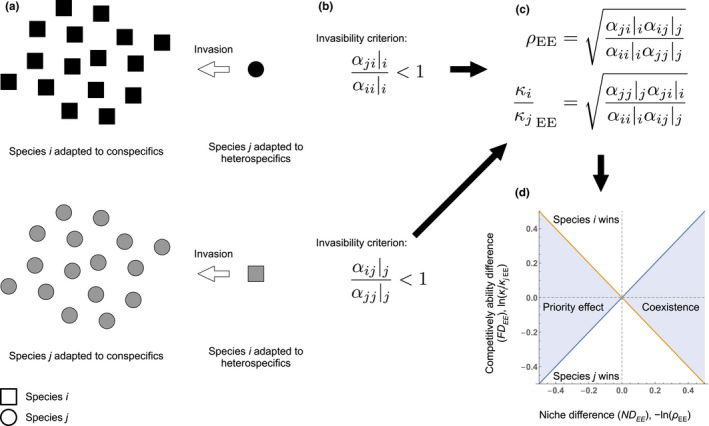
Definitions of eco‐evolutionary niche and competitive ability differences. (a) When rare species j (the single circle) invades a population of resident species i (squares), species i is adapted to conspecifics (the squares are black) and species j is adapted to heterospecifics (the circle is black). In the same way, when rare species i (single grey square) invades a population of resident species j (grey circles), species j is adapted to conspecifics and species i is adapted to heterospecifics. (b) The invasion growth rates need to be evaluated in the relevant evolutionary backgrounds for understanding mutual invasibility and stable coexistence. Rare species j can invade the community evolved to resident species i if ${\left.{\alpha }_{\mathit{ji}}\right|}_i/{\left.{\alpha }_{\mathit{ii}}\right|}_i<1$, where α _ji is a competition coefficient representing the per capita negative effects of species i on species j in the Lotka–Volterra competition model. The subscript after the vertical line represents the evolutionary background of the competition coefficients. (c) In this context, we can calculate the eco‐evolutionary niche difference (ND _EE ), −ln(ρ _EE), and competitive ability difference (FD _EE ), ln(κ _i /κ _jEE), based on the invasion growth rates for evaluating coexistence. (d) The calculated eco‐evolutionary niche and competitive ability differences can be used to predict the outcome of competition. Here, the x‐axis shows the eco‐evolutionary niche difference (ND _EE ), and y‐axis shows the eco‐evolutionary competitive ability difference (FD _EE ). Depending on the competition coefficients, there are four possible outcomes: (1) coexistence when ND _EE is positive and the absolute value of FD _EE is smaller than ND _EE , (2) priority effect, where an initially common species excludes an initially rare species, emerging when ND _EE is negative and the absolute value of FD _EE is smaller than that of ND _EE , (3) species i wins when FD _EE is positive and the absolute value of ND _EE is smaller than FD _EE , and (4) species j wins when FD _EE is negative and the absolute value of ND _EE is smaller than that of FD _EE .

Each species can increase when rare when the intraspecific effect of a resident species evolved to itself is greater than its effect on the invader evolved to that resident.

We can go further and specify the eco‐evolutionary niche and competitive ability differences from this mutual invasion condition. As noted in Box 1, the niche difference reveals how stabilised is the interaction between the species, whilst the competitive ability difference reveals the average competitive advantage or disadvantage of species i versus j. Paralleling the relationship of these metrics to the purely ecological invasion condition in Box 1, for a Lotka–Volterra model, the eco‐evolutionary (EE) niche overlap (the inverse of the niche difference) is:

$${\rho }_{\mathit{EE}}=\sqrt{\frac{{\left.{\alpha }_{\mathit{ji}}\right|}_i{\left.{\alpha }_{\mathit{ij}}\right|}_j}{{\left.{\alpha }_{\mathit{ii}}\right|}_i{\left.{\alpha }_{\mathit{jj}}\right|}_j}},$$ (2)

whilst the eco‐evolutionary competitive ability (of species i relative to j) is:

$${\frac{{\kappa }_i}{{\kappa }_j}}_{\mathit{EE}}=\sqrt{\frac{{\left.{\alpha }_{\mathit{jj}}\right|}_j}{{\left.{\alpha }_{\mathit{ii}}\right|}_i}\frac{{\left.{\alpha }_{\mathit{ji}}\right|}_i}{{\left.{\alpha }_{\mathit{ij}}\right|}_j}}.$$ (3)

Because of the way these metrics combine to determine competitive outcomes, it is useful to express them in log units, allowing us to represent them without square roots, products and quotients. We thus define the eco‐evolutionary niche difference (the inverse of the niche overlap), ND _EE , as −ln(ρ _EE ). We can define the eco‐evolutionary competitive ability difference (of species i relative to j), FD _EE , as $\ln \left({\frac{{\kappa }_i}{{\kappa }_j}}_{\mathit{EE}}\right)$. The relative magnitude of ND _EE and FD _EE defines the border between coexistence, exclusion and priority effects in a niche difference–competitive ability difference space as shown in Figure 1. Specifically, stable coexistence is possible when −ND _EE  < FD _EE  < ND _EE just like the purely ecological condition (Equation 1.V in Box 1).

INTERPRETING THE ECO‐EVOLUTIONARY COEXISTENCE METRICS

Whilst the above expressions for the eco‐evolutionary niche and competitive ability differences are useful for defining the outcome of competition between evolving competitors, they are perhaps most interesting in their comparison to the purely ecological versions of these quantities (i.e. the niche and competitive ability differences evaluated in a single evolutionary background). This comparison reveals the influence of coupling the ecology and evolution of the competitors to coexistence.

We can decompose the eco‐evolutionary niche difference into the following contributions (see Appendix S1 for the mathematical steps):

$${\mathit{ND}}_{\mathit{EE}}=\frac{{\left.\mathit{ND}\right|}_i+{\left.\mathit{ND}\right|}_j}{2}+\frac{{\left.\mathit{FD}\right|}_j-{\left.\mathit{FD}\right|}_i}{2}.$$ (4)

Here, the ND in the left‐hand side (ND _EE ) is an amalgam of competition coefficients under two types of evolutionary backgrounds—species evolved to i or j being dominant (as in Equation 2). By contrast, on the right‐hand side, each ND and FD has a single evolutionary background. Thus, the eco‐evolutionary niche difference is a simple function of the purely ecological versions of these metrics evaluated at different evolutionary end points. The first term on the right‐hand side quantifies the contributions of ecological mechanisms—the mean of the ecological niche differences when the competitors have evolved to species i being common versus species j being common. The second term describes the degree to which species i's competitive ability is greater when evolved to being rare versus common—the evolution of increased competitive ability. Thus, in an evolving system, there is a stabilising effect of species evolving greater competitive ability when rare, and a destabilising effect of species evolving poorer competitive ability when rare. These evolutionary effects combine with ecological niche differences (in the first term of the sum) to determine the degree to which species gain advantages when rare—the meaning of the stabilising niche difference.

Following Equation 4, even with no ecological stabilisation (ND| _i  = ND| _j  = 0) or even a destabilised interaction (e.g. ND| _i  = ND| _j  < 0), the system may still yield eco‐evolutionary stabilisation (ND _EE  > 0) if species become sufficiently better competitors at low relative abundance (the second term is large). Of course, if they evolve in the other direction, such that species become poorer competitors when rare, this will decrease ND _EE and favour alternative stable states. Our framework thereby positions within modern coexistence theory the classic idea termed the ‘evolution of increased competitive ability’, where coexistence is possible via the evolution of a rare species' competitive advantage (Pimentel, 1968; Pimentel et al., 1965).

We can similarly decompose the eco‐evolutionary competitive ability difference (advantage of species i relative to j) into its ecological components:

$${\mathit{FD}}_{\mathit{EE}}=\frac{{\left.\mathit{FD}\right|}_i+{\left.\mathit{FD}\right|}_j}{2}+\frac{{\left.\mathit{ND}\right|}_j-{\left.\mathit{ND}\right|}_i}{2}.$$ (5)

The first term of the right‐hand side quantifies the contributions of ecological competitive ability differences—the mean of those differences when the competitors have evolved to species i being common versus species j being common. The second term reveals that species i's eco‐evolutionary competitive advantage over species j increases with, for example, its ability to evolve different resource use than species j when it is in the invader state (or that ecological niche differences decline when species j evolves to a common species i). This makes sense in that ecological niche differences favour both species, but if this benefit changes with species' relative abundance, the species benefiting from greater niche differences when rare is favoured on average.

In sum, the expressions for the eco‐evolutionary stabilising niche and competitive ability differences are simple functions of the purely ecological versions of these metrics evaluated at two evolutionary extremes—(1) species have evolved to species i being common—the red point in Figure 2a and (2) species being evolved to species j being common—the blue point in Figure 2a. Because of the relatively simple relationships between these metrics and the eco‐evolutionary outcome, one can graphically locate this outcome (i.e. coexistence, priority effect or competitive exclusion) from the position of these values alone (Figure 2a).

FIGURE 2.

Calculating eco‐evolutionary niche and competitive ability differences. (a) Eco‐evolutionary niche and competitive ability differences (ND _EE and FD _EE , purple point) can be calculated from the purely ecological versions of these quantities at two evolutionary end points (Appendix S1). More specifically, these metrics must be measured for competitors after the traits underlying their competition coefficients have evolved to the resident state where species i or j is dominant (red and blue points, respectively). The blue and orange lines delineate the four regions of competitive outcome. (b) Following Equations (4), (5), for obtaining ND _EE , we first calculate the mean value of the ND values (the vertical black line). (c) Then, if the competitive ability of species i increases when evolved to resident species j (the blue point is above the red point), half of the difference in the FD values (the vertical distance between points) is added to the mean ND. (d) For obtaining FD _EE , we first calculate the mean value of the FD values (the horizontal black line). (e) Then, if the niche difference decreases when species i evolves to resident species j, half of the difference in the ND values (the horizontal distance between points) is subtracted from the mean FD.

For example, to determine the eco‐evolutionary stabilising niche difference, ND _EE , first locate the midpoint of the x‐axis projections of the red and blue points (where species have evolved to species i and j being common, respectively), yielding the average ecological niche difference (i.e. the first term of Equation 4: Figure 2b). If the competitive ability of species i increases when it evolves to the state where species j is common (the blue point is above the red point), move rightwards from that midpoint (towards the coexistence region) by half the vertical distance between the blue and red points (i.e. the second term of Equation 4: Figure 2c). This is the eco‐evolutionary niche difference. If instead, species i loses competitive ability when evolved to resident species j, move leftwards from the midpoint (towards the priority effect region). Similar methods can be used to locate the eco‐evolutionary competitive ability difference, FD _EE . First, locate the midpoint of the y‐axis projections of the red and blue points, yielding the average ecological competitive ability difference (i.e. the first term of Equation 5: Figure 2d). If the ecological niche difference decreases when species i evolves to the state where species j is common (the blue point lies to the left of the red point), move down from the midpoint (towards species j's dominance) by half the horizontal distance between the blue and red points (i.e. the second term of Equation 5: Figure 2e). This is the eco‐evolutionary competitive ability difference. If instead, the niche difference increases when species i evolves to resident species j, move up from the midpoint by the same amount.

GRAPHICAL INTERPRETATION OF ECO‐EVOLUTIONARY EFFECTS ON COEXISTENCE IN PRIOR STUDIES

Next, to demonstrate the utility of our framework, we show (1) how it can be used to interpret the eco‐evolutionary dynamics of species coexistence in prior theoretical work (Box 2, Figure 3), (2) how evaluating the potential for coexistence from a snapshot of competitive dynamics at any point in the eco‐evolutionary trajectory can be misleading and (3) how our metrics based on the eco‐evolutionary invasion growth rate can correctly predict stable coexistence. Although competitive dynamics are always a function of species' traits—attributes that have evolved over time in nature—an explicitly eco‐evolutionary framework of the type we develop here is not always needed to understand the outcome of competition. For example, if and when traits stop evolving, presumably in response to a stable abundance of the competitors, the purely ecological niche and competitive ability differences (at the evolutionary equilibrium) should reveal the coexistence outcome. Therefore, to properly test the validity of our eco‐evolutionary extension of modern coexistence theory, we evaluated its ability to predict the cyclical coexistence observed in models with the evolution of increased competitive ability. In such models, competitor evolution is persistent.

BOX 2. Eco‐evolutionary niche and competitive differences in a simple haploid model with intransitive competition.

Here, we show how to apply our framework to understand the dynamics of a simplified model of Levin (1971) (Appendix S4), where competition occurs amongst three asexually reproducing, clonal genotypes that are members of two distinct species. The dynamics at the genotype level are as follows:

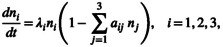(2.I)

where n _i is the density of genotype i, λ _i is its intrinsic growth rate and a _ij is the competition coefficient describing the effect of genotype j on i (i, j = 1, 2, 3). If we assume that the first two genotypes belong to a single ‘species 1’ (and hence λ ₁ = λ ₂) and represent its density as N ₁ = n ₁ + n ₂ and a species 2's density as N ₂ = n ₃, and the allele frequency within species 1 as p = n ₁/N ₁, Equation 2.I can be written at the species and allele frequency level as:

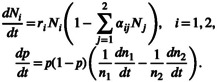(2.II)

Here, r ₁ = λ ₁ = λ ₂, r ₂ = λ ₃, ${\alpha }_{11}=a_{11}{p}^2+\left(a_{12}+a_{21}\right)p\left(1-p\right)+a_{22}{\left(1-p\right)}^2$, ${\alpha }_{12}=a_{13}p+a_{23}\left(1-p\right)$, ${\alpha }_{21}=a_{31}p+a_{32}\left(1-p\right)$, and ${\alpha }_{22}=a_{33}$.

When we assume parameter values such that the three genotypes have intransitive competitive relationships (Figure 3a), the system shows cyclic dynamics in species densities (depending on the initial condition: Figure 3c).

$$\left(\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\end{array}\right)=\left(\begin{array}{ccc}1& 0.5& 1.75\\ 1.25& 1& 0.25\\ 0.75& 1.5& 1\end{array}\right).$$ (2.III)

When species 2 (genotype 3) rises to dominance, this favours the increased frequency of genotype 2 (the better interspecific competitor genotype) over genotype 1 within species 1. This genotypic change favours species 1 over species 2, enabling its recovery. Meanwhile, when species 1 rises to dominance, this favours genotype 1 (the better intraspecific competitor genotype) over genotype 2, allowing species 2 (genotype 3) to recover.

The simplicity of this model allows one to directly calculate the eco‐evolutionary invasion growth rates of the two species. When species 1 is a resident species, intraspecific competition excludes genotype 2 so genotype 1 is at its carrying capacity, 1/a ₁₁. Thus, the invasion per capita growth rate of species 2 (genotype 3) is dN ₂/dt/N ₂ = r ₂(1 − a ₃₁/a ₁₁) and it is positive when a ₃₁/a ₁₁ < 1. On the other hand, when species 2 (genotype 3) is the resident, its density is at its carrying capacity, 1/a ₃₃. The invader species (species 1) has two genotypes, but adaptive evolution to interspecific competition in the resident community favours genotype 2 and excludes genotype 1. Hence, the invasion per capita growth rate of species 1 (genotype 2) is dN ₁/dt/N ₁ = r ₁(1 − a ₂₃/a ₃₃) and it is positive when a ₂₃/a ₃₃ < 1. From these invasion growth rates, we can determine the eco‐evolutionary niche difference and competitive ability difference as log‐transformed versions of the following:

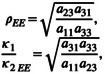(2.IV)

which falls in the region of ‘coexistence’ when parameterised with expression 2.III (the purple point in Figure 3b). Similar steps can be taken to calculate the niche and competitive ability difference when species 1 has evolved to being resident or the invader, generating the red and blue points in Figure 3b. When the dynamics of the full system are simulated, the ecological niche difference (ND), −ln(ρ), and competitive ability difference (FD), ln(κ ₁/κ ₂), at all points in the eco‐evolutionary cycle are shown by black curve in Figure 3b. Note that the system moves between regions where species 1 wins, where there is a priority effect, or where species 2 wins. This occurs along a trajectory between the niche and competitive ability differences observed when species 1 has evolved to being rare (blue point in Figure 3a,b) or common (the red point). Because of this variation in ecological outcomes over the trajectory, measurements of coexistence parameters at any point in time may indicate an outcome that differs from the true eco‐evolutionary outcome of coexistence, as predicted in our framework.

FIGURE 3.

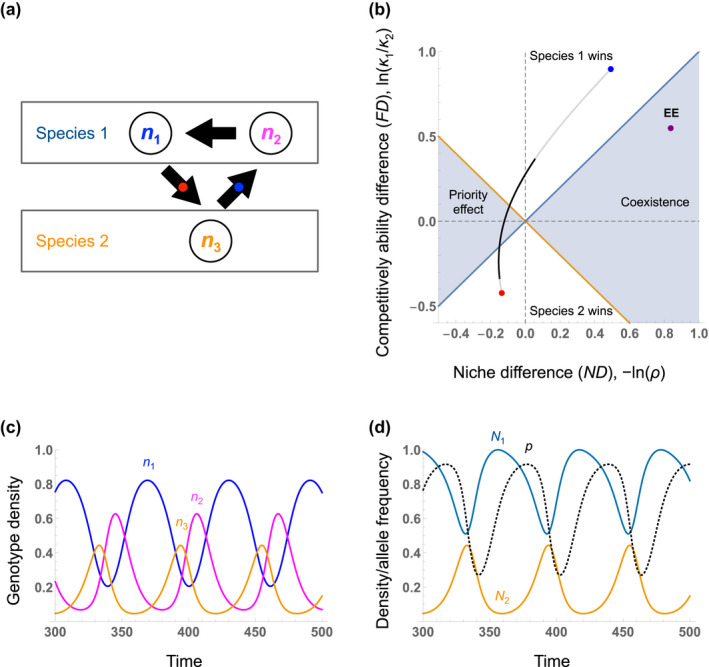
Eco‐evolutionary dynamics in a simple haploid model with intransitive competition. (a) Intransitive competition amongst three genotypes n _i , two of which belong to species 1, whilst the third belongs to species 2. n ₁ is competitively excluded by n ₃, n ₃ is excluded by n ₂, and n ₂ is excluded by n ₁ (the black arrows point to the pairwise competitive winner: Equations 2.I, 2.III). Arrows with embedded red and blue points show the competitive outcome at the two invader‐resident states shown in panel b in terms of niche and competitive ability differences. (b) Temporal shifts in the ecological niche and competitive ability differences in the simulated dynamics of the system are shown by the black curve. The coloured points connected by the grey curve indicate the ecological niche difference and competitive ability difference when species 1 has evolved to being the common resident (evolved to maximise intraspecific competition, red) or rare invader (evolved to maximise interspecific competition, blue), respectively. The right purple point EE represents the eco‐evolutionary niche difference (ND _EE ) and competitive ability difference (FD _EE ) predicting the competitive outcome. See Figure 2 and accompanying text for how to calculate the two metrices at the purple point from those at the red and blue points. Simulated time series of (c) the competing genotype densities, n_i , and (d) species densities, N_i (solid lines) and allele frequency, p = n ₁/N ₁ (dashed line).

This mechanism of cyclical coexistence can arise from a trade‐off between intraspecific (α _jj ) and interspecific (α _ji ) competitive ability, as was proposed by Pimentel (Pimentel, 1968; Pimentel et al., 1965) and has received empirical validation in fly and plant systems (Lankau & Strauss, 2007; Shaw et al., 1995). Building on these results, many theoretical studies now show coexistence with population cycles in systems with a trade‐off between intraspecific and interspecific competitive ability (Box 2, Lankau, 2009; León, 1974; Levin, 1971; Mougi, 2013; Pease, 1984; Vasseur et al., 2011; Wittmann & Fukami, 2018). However, it is often difficult to assess whether coexistence is driven by ecological, evolutionary or some combination of processes, and to compare mechanisms across models (but see Patel et al., 2018). In Box 2 and Figure 3, we illustrate the steps involved in applying our analysis to these problems for a simple model of coexistence between cycling species composed of asexual haploids (also see Appendix S4, Figure S3, Levin, 1971).

We use this approach to analyse the more complex models of Vasseur et al. (2011) and Mougi (2013), both of which were inspired by empirical studies on competition between two plant species mediated by toxic allelochemicals (Lankau, 2009; Lankau & Strauss, 2007). Both studies considered the behaviour of the continuous‐time Lotka–Volterra model with competitor evolution along a trade‐off between interspecific and intraspecific competitive ability. Adaptive evolution of a quantitative trait(s) underlying competition occurs along a fitness gradient (Abrams, 2001), such that higher conspecific relative to the heterospecific density favours better intraspecific competitive ability at the expense of interspecific competitive ability. Meanwhile, lower conspecific relative to the heterospecific density favours better interspecific competitive ability at the expense of intraspecific competitive ability. Although Vasseur et al. (2011) considered evolution of a single competitor whilst Mougi (2013) assumed coevolution, both result in evolving competitors coexisting whilst exhibiting population cycles.

Vasseur et al. (2011) considered competition between a non‐evolving species 1 and an evolving species 2, with a quantitative trait of species 2 evolving along the fitness gradient (Abrams, 2001) in response to the population densities (‘neighbour‐dependent selection’) (Figure 4). Specifically, adaptation to heterospecifics increased the trait value, which increased self‐regulation (${\overline{\alpha }}_{22}$) and suppression of the non‐evolving competitor (${\overline{\alpha }}_{12}$) whilst decreasing suppression from the non‐evolving competitor (${\overline{\alpha }}_{21}$) (Figure 4a, see Appendix S2 and Figure S1 for more details). In effect, these changes mean that the evolving species evolves greater interspecific competitive ability when it drops to rarity and becomes a poorer interspecific competitor when common. Various competitive outcomes are possible depending on the parameterisation, but in Figure 4, we show a case where the two species coexist (Figure 4b). However, they do so in a cyclical manner, with the evolving species' trait value changing as a function of its rarity and commonness in the system (Figure 4b).

FIGURE 4.

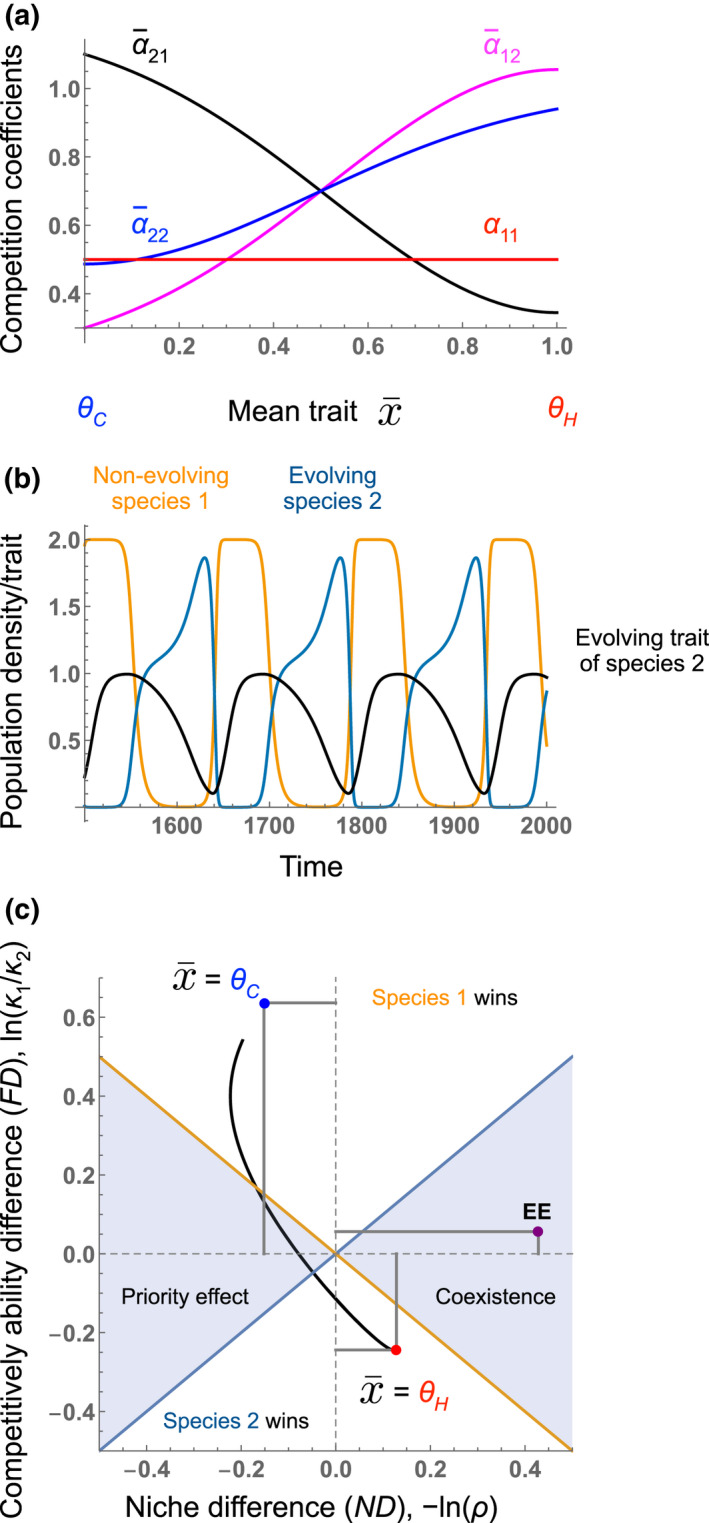
Eco‐evolutionary niche and competitive ability differences in the Vasseur et al. (2011) model of coexistence between an evolving species and non‐evolving species. (a) Based on empirical studies of plant competition mediated by allelochemicals (Lankau & Strauss, 2007), Vasseur et al. (2011) assumed adaptive evolution of one competitor's mean trait $\overline{x}$, determining where it falls along a trade‐off between intraspecific and interspecific competition. Trait values θ _C (= 0) and θ _H (= 1) indicate trait values adapted to conspecifics and heterospecifics, respectively. The intraspecific competition coefficient of the non‐evolving species 1 (α ₁₁: a red line) is constant, whereas the intraspecific competition coefficient of the evolving species 2 (${\overline{\alpha }}_{22}$: a blue curve) and interspecific competition coefficient of the non‐evolving species 1 (${\overline{\alpha }}_{12}$: a magenta curve) increase and the interspecific competition coefficient of evolving species 2 (${\overline{\alpha }}_{21}$: a black curve) decreases as the mean trait value increases. See Appendix S2 for details of the model and parameters. (b) Simulated time series of competing species densities and an evolving trait in Figure 5h of Vasseur et al. (2011). Black, orange and blue lines show the evolving trait and population densities of non‐evolving species 1 and evolving species 2, respectively. The mean trait of the evolving species 2 moves to θ _C when dominant, which allows the invasion of the non‐evolving species 1. The mean trait evolves to θ _H when rare, and it favours the increase of the evolving species 2. (c) Niche difference (ND), −ln(ρ), and competitive ability difference (FD), ln(κ ₁/κ ₂), in eco‐evolutionary cycles of the two competing species (b). The simulation trajectory in panel b, shown by the black curve in panel c, connects the blue and red points, which indicate the niche difference and competitive ability difference when one species is dominant ($\overline{x}$ = θ _C and θ _H , respectively).

The mechanisms behind the coexistence of Vasseur et al. (2011) are clarified when viewed through the lens of the framework developed here (Figure 4c). First, observe that the cyclical trajectory of the system in niche difference–competitive ability difference space moves on a path between the two eco‐evolutionary invasion states—(1) species 2 has evolved to being rare (the red point) and (2) species 2 has evolved to being a common resident (the blue point) (Figure 4 and Figure S1). Second, the trajectory never enters the coexistence region—meaning that at any point along that trajectory, one competitor wins. Third, note that despite this, the eco‐evolutionary niche and competitive ability differences accurately predict the coexistence of the species (a right purple point EE in Figure 4c). Whilst the average ecological niche difference (the first term in Equation 4) always favours exclusion or a priority effect, the fact that the evolving species 2 becomes a better competitor when evolved to a resident species 1, moves the eco‐evolutionary niche difference strongly in the direction of coexistence, matching the dynamics (Figure 4c). Thus, the rapid evolution of competitive ability difference (a hierarchical trait sensu [Stump et al., 2022]) contributes to the niche differences.

Coevolutionary dynamics in Mougi (2013)'s model show a similar dynamic (Figure 5, see Appendix S3 and Figure S2 for details). When species 1 is rare and species 2 is dominant, coevolution moves species' traits towards the blue point in Figure 5a, which maximises the rare species 1's growth rate. Conversely, when species 1 is dominant and species 2 is rare, coevolution moves the trait values to the red point of Figure 5a, which minimises the resident species 1′ growth rate. As in the model of Vasseur et al. (2011) where only one species evolves, coevolution favours the coexistence of cycling competitors (Figure 5b) and does so in a system where competitive exclusion is predicted at all points along the cyclical trajectory (Figure 5c). Mougi (2013)'s study also predicts the eco‐evolutionary trajectory when species only evolve in response to intraspecific competition, as shown by the black point in Figure 5a,c. Comparison between the dynamics at the black point and those where species evolve to the state where the other species is common provides an interesting way to quantify how evolution alters competitive dynamics, a point we return to in the ‘Empirical implications’ section.

FIGURE 5.

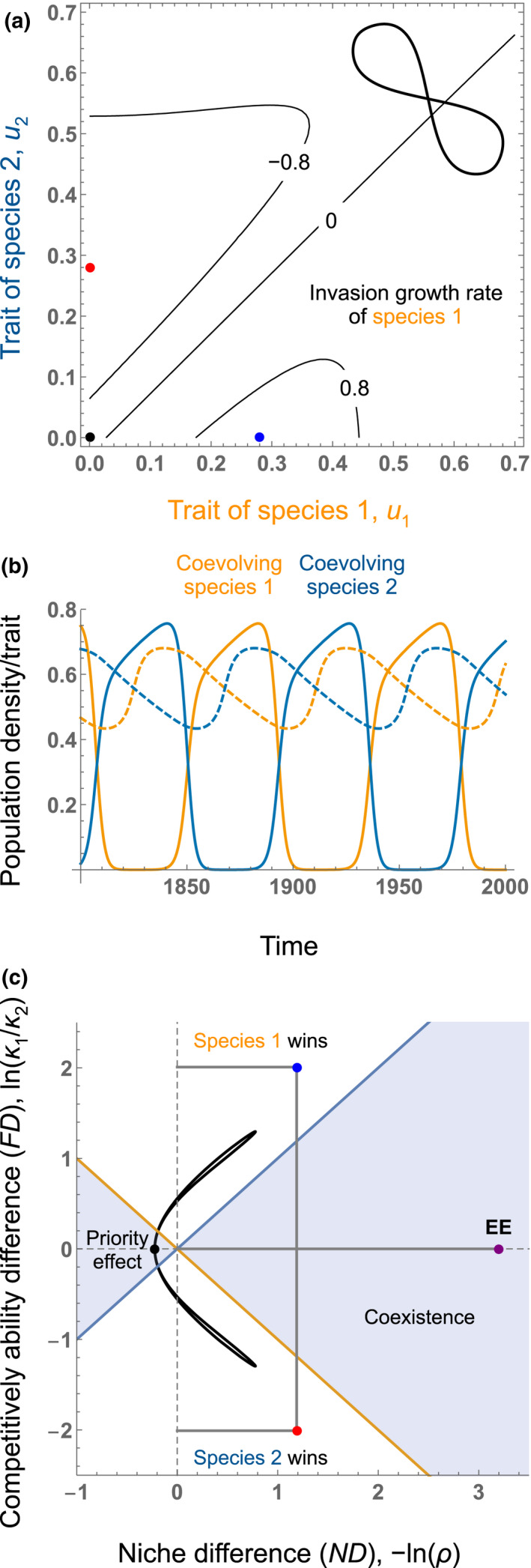
Eco‐evolutionary niche and competitive ability differences in Mougi (2013) where both species coevolve. Mougi (2013) modelled coevolution between two competing species, again assuming a trade‐off between intraspecific and interspecific competition (mediated by allelochemicals). (a) Invasion growth rate of species 1 as a function of the traits of two coevolving species. It is maximised when species have evolved to species 1 being rare (the blue point) because at this point, species 1 evolves to heterospecifics (u ₁ = u _H ; meaning species 1 produces more allelochemicals effective against species 2) and species 2 evolves to conspecifics (u ₂ = u _C ; meaning species 2 produces less allelochemicals, which are costly and only effective against species 1). Species 1's invasion growth rate is minimised when evolved to being common (the red point) because at this point, species 1 evolves to conspecifics (u ₁ = u _C ) and species 2 evolves to heterospecifics (u ₂ = u _H ). The black point at the origin indicates the optimal traits when the two species are not interacting. The simulated coevolving trait dynamics in panel b is reproduced in top‐right. (b) Simulated time series of competing species densities and coevolving traits in Figure 1a of Mougi (2013). Solid and dashed lines represent population densities and traits, respectively. Orange and blue lines represent species 1 and 2, respectively. Here, larger trait values mean adaptation to heterospecifics (u _H ) and smaller trait values indicate adaptation to conspecifics (u _C ). See Appendix S3 for details of the model and parameters. When one species is common, it evolves to trait values (u _C ) that favour the invasion of the other species. Species dropping to rarity also evolve trait values (u _H ) that favour their recovery, causing the system to exhibit cyclic eco‐coevolutionary dynamics. (c) Niche difference (ND), −ln(ρ) and competitive ability difference (FD), ln(κ ₁/κ ₂), along the eco‐evolutionary cycles of the two competing species. The blue and red points indicate the niche difference and competitive ability difference when species 2 and 1 are common, respectively. The purple EE point indicating the eco‐evolutionary niche and competitive ability differences (based on Equations (4), (5)) predicts the stable coexistence observed in simulation.

The eco‐evolutionary cyclic dynamics in the models explored here (Levin, 1971; Mougi, 2013; Vasseur et al., 2011) can be considered a product of intransitive competition amongst genotypes. Box 2 and Figure 3 show the simplest case: genotype 2 of species 1 beats species 2, species 2 beats genotype 1 of species 1, and genotype 1 beats genotype 2 within species 1. Such intransitive relationships have received some empirical support. Lankau and Strauss (2007), for example, show how allocation to growth versus allelochemicals in a mustard species sets up intransitive relationships with a heterospecific (Lankau, 2009). Meanwhile, recent theoretical studies have emphasised the potential importance of intransitive competition at the species level for coexistence (Gallien et al., 2017; Soliveres & Allan, 2018). Nonetheless, the empirical generality of intransitive competition as a basis for eco‐evolutionary mechanisms of coexistence remains to be explored. Given that intransitive relationships may not be the widespread basis of eco‐evolutionary coexistence, it should be noted that our theory can still incorporate non‐cycling cases with the limitations described next.

LIMITATIONS OF THE ECO‐EVOLUTIONARY NICHE AND COMPETITIVE ABILITY DIFFERENCE

In the above examples of coexistence between cycling competitors, the cycles emerge because one species is always being driven to exclusion, but trait change when rare allows the rare competitor to recover (i.e. sequential evolutionary rescue). If instead, the system tends towards coexistence at a fixed point, this fixed point is not predicted by the eco‐evolutionary niche and competitive ability differences. This is because the ecological dynamics predicted when each species has evolved to a community where both species are present, as occurs at a stable eco‐evolutionary equilibrium, should not match the ecological dynamics when each species has evolved to a community where their heterospecific competitor is common (as assumed in the eco‐evolutionary niche and competitive ability differences). Nevertheless, our eco‐evolutionary metrics still predict the qualitative outcome of the dynamics, even without population cycles—namely, whether or not the two species coexist. Because our theory of coexistence in eco‐evolutionary models must focus on the interactions at the invader‐resident state, it cannot simultaneously predict dynamics away from this regime. This can be seen when we change the parameter values of the models of Vasseur et al. (2011) and Levin (1971) (Figures S1 and S2), making it possible for the two species to coexist at a stable equilibrium (Levin, 1971; Vasseur et al., 2011). In this situation, the eco‐evolutionary niche and competitive ability differences still lie in the coexistence region, but the equilibrium state of the system lies elsewhere in that region. A similar pattern is observed with classical ecological character displacement (Barabás & D'Andrea, 2016; Pastore et al., 2021; Slatkin, 1980). Here, evolution increases the distance between two species along a one‐dimensional trait axis, which decreases interspecific interaction coefficients and thereby stabilises coexistence, albeit without population cycles (Appendix S5, Figure S4).

Another limitation of our approach is that it assumes that species dropping to low density eventually evolve to the state when they are rare and their competitor is common, or at least do so before exclusion. However, if the intraspecific genetic variation and heritability are small and evolution slow, dynamics may tend towards a stable equilibrium even when more rapid evolution would favour a different outcome (Vasseur et al., 2011). We acknowledge that it may be difficult for a rare invading species to adapt to new environments due to low genetic variation. Moreover, despite some recent studies suggesting surprisingly rapid adaptation in rare invading populations (Prentis et al., 2008), demographic stochasticity could drive a low‐density species extinct before it can evolve to the resident. Thus, our eco‐evolutionary niche and competitive ability differences should be regarded as the maximum potential invasion rate for a rare species. In other words, our analysis focuses on a limiting case of the full range of possible eco‐evolutionary dynamics, including situations where evolution can maximally promote coexistence. Thus, empiricists should be careful when interpreting our metrics, especially if genetic variation within the focal species is small. Future work can explore how demographic stochasticity affects adaptive evolution and coexistence (Schreiber et al., 2022) by considering models where selection is strong when population size is large and genetic drift is dominant when population size is small.

Finally, complex fitness landscapes may result in alternative stable eco‐evolutionary states (i.e. initial condition dependence) when more monotonic landscapes would favour coexistence (Schreiber et al., 2011). In this case, the invasion growth rate, and our approach more generally, would need to be adapted to this more complex scenario to make accurate predictions (Schreiber et al., 2019). For similar reasons, our invasion growth rate approach is particularly useful in a two‐species system because mutual invasibility exactly delineates when the species coexist. In more diverse systems, however, it is a more difficult problem to formulate a generalisation of mutual invasibility (Law & Morton, 1996; Schreiber, 2000).

EMPIRICAL IMPLICATIONS

Our analysis of how evolution shapes competitive dynamics between two species in past models of coexistence highlights the challenges associated with empirically quantifying this effect. For example, by working with models (and not empirical data), we were able to use math or simulation to show that coexistence was impossible at all points along the evolutionary trajectory of the competitors, and thereby demonstrate the key role of rapid evolutionary change in facilitating coexistence. In fact, this finding is one of several reasons it may be risky to infer the possibility of species coexistence from snapshots of competitive dynamics in the wild (e.g. measuring population growth rates over a year). This issue could be partly resolved by assessing competitive dynamics at multiple points in the evolutionary trajectory. However, whilst empirical studies can in principle predict competitive outcomes for populations adapted to different relative abundances of competitors, they cannot do so at all points, as we do with the theory. Thus, the empirical question becomes at what relative abundances should we assess evolutionary change and the subsequent ecological dynamics if we want to predict eco‐evolutionary coexistence? Our eco‐evolutionary metrics suggest a theoretically justified experimental design for predicting coexistence. An experimentalist needs only to measure the interactions at two points in the space of all relative abundances (the blue and red points in Figure 2a) to make predictions for the coexistence of two species across a broad range of abundances and possibly complicated dynamics (in the spirit of Lankau & Strauss, 2007). However, we acknowledge that an empiricist does not a priori know the carrying capacities of species, and outside of observational approaches, determining these requires considerable work.

Equally valuable is decomposing the evolutionary coexistence metrics into their component parts as in Equations 4 and 5. Equation 4, for example, provides a theoretically justified metric of the evolution of increased competitive ability (Pimentel, 1968; Pimentel et al., 1965), separate from character displacement, all in the units of ecological coexistence mechanisms. The pathway to empirically quantifying these metrics is logistically challenging (Godoy et al., 2014), but the approach of Lankau and Strauss (2007) where species are adapted to rarity and commonness before competition experiments (Figure 1) presents a promising way forward. Hess et al. (2022) essentially used this approach when evaluating how phenotypic plasticity influences invasion growth rates in a system of floating aquatic plants.

Interestingly, the approach advocated here is different than that of recent empirical studies, which address effects of evolution on coexistence by comparing the niche and competitive ability differences of species evolved in allopatry versus sympatry (Hart et al., 2019). Trait evolution under these two conditions is the critical comparison in classic studies of character displacement (Grant & Grant, 2006). Whilst these approaches certainly address how evolution to purely conspecifics (the black point in Mougi (2013)'s example—Figure 5a,c) versus a mixture of conspecifics and heterospecifics influences ecological outcomes, neither selective environment aligns with conditions experienced in an invader‐resident state. This may not be problematic if the eco‐evolutionary outcome is coexistence at a fixed point (Pastore et al., 2021). However, as we have shown here, in cases where coexistence depends on the coupling of evolution and ecology (e.g. Figures 3, 4, 5), only the ecological niche and competitive ability differences evolved at specific relative abundances reveals the true eco‐evolutionary outcome.

FUTURE DIRECTIONS

Here, we have provided a theoretical framework for integrating ecological and evolutionary mechanisms of species coexistence. It generates theoretically justified metrics of the eco‐evolutionary niche difference and competitive ability difference useful for evaluating the potential for species coexistence, even with eco‐evolutionary cycles. In cases where species coexist regardless of rapid evolutionary change, existing tools to measure coexistence metrics at different evolutionary end points are likely sufficient to predict the overall dynamics (Pastore et al., 2021). But for the most interesting cases, where evolutionary change coupled to ecological dynamics is essential for coexistence, the novel approach we have developed here should provide unique insights, complementary to recent stability analyses of the eco‐evolutionary equilibrium (Patel et al., 2018). Our approach will also be readily applicable to cases where species exhibit phenotypic plasticity in response to competition (Hess et al., 2022; Turcotte & Levine, 2016).

By quantifying evolutionary effects on species coexistence in the same units as ecological mechanisms, our work should inspire future efforts to integrate the approaches of modern coexistence theory and eco‐evolutionary dynamics. One promising path forward builds on an interesting parallelism between these approaches. Both decompose growth rates into useful components: Chesson's coexistence theory decomposes invasion growth rates into the contributions of various variation‐dependent and independent mechanisms (Barabás et al., 2018; Chesson, 1994, 2000b; Ellner et al., 2019). Meanwhile, researchers of eco‐evolutionary dynamics have developed methods for decomposing variation in growth rates into the contributions of ecological and evolutionary processes (Ellner et al., 2011; Govaert et al., 2016; Hairston et al., 2005; reviewed in Govaert, 2018). Though the data requirements for these methods have limited their application, other methods can also be used to isolate the contribution of ecological, evolutionary and eco‐evolutionary mechanisms to the focal processes of interest (Barbour et al., 2022; Gibert et al., 2022; Lion, 2018; Rudman et al., 2022). It may be possible to integrate these theories to quantify the relative importance of ecological and evolutionary processes within individual coexistence mechanisms.

In addition, whilst our focus here was the contribution of eco‐evolutionary process to the coexistence of two species, resolving its role in more complex communities (Godoy et al., 2018; Levine et al., 2017; Saavedra et al., 2017; Toju et al., 2017) is an important next step. Of course, we first need to carefully define eco‐evolutionary niche and competitive ability differences in systems with three or more species (Song et al., 2019), especially when the system shows oscillations (Huisman & Weissing, 1999). The theory on intransitive competitive relationships at the species level extend well beyond three species or genotypes (Gallien et al., 2017; Soliveres & Allan, 2018), and thus the genotype‐level competition in Box 2 and Figure 3 could be expanded to provide an important path forward. Further efforts of this type, which formally integrate evolutionary processes into coexistence theory, will help to unify ecological and evolutionary approaches to community ecology.

AUTHORSHIP

MY and JML conceived the study and analysed the model. MY conducted simulations and wrote the first draft of the manuscript. All authors contributed substantially to writing and revisions.

CONFLICT OF INTEREST

The authors declare no conflict of interest.

PEER REVIEW

The peer review history for this article is available at https://publons.com/publon/10.1111/ele.14078.

Supporting information

Appendix S1–S5

Figures S1–S4

Yamamichi, M. , Gibbs, T. & Levine, J.M. (2022) Integrating eco‐evolutionary dynamics and modern coexistence theory. Ecology Letters, 25, 2091–2106. Available from: 10.1111/ele.14078

DATA AVAILABILITY STATEMENT

This study did not generate new data.