Abstract
Genetic structure in host species is often used to predict disease spread. However, host and pathogen genetic variation may be incongruent. Understanding landscape factors that have either concordant or divergent influence on host and pathogen genetic structuring is crucial for wildlife disease management. Devil facial tumor disease (DFTD) was first observed in 1996 and has spread throughout almost the entire Tasmanian devil geographic range, causing dramatic population declines. Whereas DFTD is predominantly spread via biting among adults, devils typically disperse as juveniles, which experience low DFTD prevalence. Thus, we predicted little association between devil and tumor population structure and that environmental factors influencing gene flow differ between devils and tumors. We employed a comparative landscape genetics framework to test the influence of environmental factors on patterns of isolation-by-resistance (IBR) and isolation-by-environment (IBE) in devils and DFTD. Although we found evidence for broad-scale co-structuring between devils and tumors, we found no relationship between host and tumor individual genetic distances. Further, the factors driving the spatial distribution of genetic variation differed for each. Devils exhibited a strong IBR pattern driven by major roads, with no evidence of IBE. By contrast, tumors showed little evidence for IBR and a weak IBE pattern with respect to elevation in one of two tumor clusters we identify herein. Our results warrant caution when inferring pathogen spread using host population genetic structure and suggest that reliance on environmental barriers to host connectivity may be ineffective for managing the spread of wildlife diseases. Our findings demonstrate the utility of comparative landscape genetics for identifying differential factors driving host dispersal and pathogen transmission.
Introduction
Infectious diseases are a major driver of wildlife population dynamics and can contribute to extinction (De Castro & Bolker, 2005). Thus, considerable effort is devoted to detecting diseases and identifying the processes influencing their transmission and spread. Traditional epidemiological approaches rely on direct estimates of disease prevalence, host movement, and host contact rates for model parameterization, but these estimates are logistically challenging to obtain from wildlife populations (Craft, 2015; Craft, Volz, Packer, & Meyers, 2009; Hamede, Bashford, McCallum, & Jones, 2009). Further, there is often uncertainty as to whether observed contacts and movements reflect actual pathogen transmission and spread (Craft, 2015). In contrast, the spatial distribution of genetic variation contains signatures of past dispersal (in the case of the host) or spread (in the case of the pathogen) and often can be linked with environmental or ecological factors at fine spatial scales (Archie, Luikart, & Ezenwa, 2009; Biek & Real, 2010; Blanchong, Robinson, Samuel, & Foster, 2016; Hemming-Schroeder, Lo, Salazar, Puente, & Yan, 2018; Kozakiewicz et al., 2018). Knowledge of these relationships is critical to predicting the spread of wildlife diseases and can inform management strategies aimed at mitigating their impact.
Spatial patterns of genetic variation are routinely used to understand patterns of connectivity and movement in wildlife, and a number of studies have extended this framework for predicting the spread of wildlife diseases resulting from host movement. For example, estimates of host genetic variation have been used to explain and forecast the prevalence and distribution of pathogens (e.g., Blanchong et al., 2008; Guivier et al., 2011; Robinson, Samuel, Rolley, & Shelton, 2013), the transmission potential of different host species (e.g., Paquette, Talbot, Garant, Mainguy, & Pelletier, 2014; Vander Wal et al., 2013) or of different sexes within species (e.g., Cote, Garant, Robert, Mainguy, & Pelletier, 2012; Talbot, Garant, Paquette, Mainguy, & Pelletier, 2012), and to improve the predictive power of models of disease spread (e.g., Davy, Martinez-Nunez, Willis, & Good, 2015; Kozakiewicz et al., 2018; Robinson et al., 2013; Wilder, Kunz, & Sorenson, 2015). However, pathogen genetic structure does not necessarily reflect that of the host, and pathogen transmission may be disconnected from patterns of host gene flow. Such a disconnect may be due to factors including multiple host/vector species, pathogen persistence in environmental reservoirs, transmission via nonreproducing hosts, or host life history characteristics resulting in reduced susceptibility at dispersal age (Mazé-Guilmo, Blanchet, Mccoy, & Loot, 2016; Talbot, Vonhof, Broders, Fenton, & Keyghobadi, 2017). Therefore, comparative approaches, ideally incorporating the relative influence of environmental or ecological factors, are necessary for understanding the extent to which host and pathogen genetic structure are related and to disentangle the factors influencing each. One approach that is ideally suited for the comparative study of host and pathogen genetic variation is landscape genetics.
Landscape genetics is an analytical framework for testing the influence of environmental heterogeneity on patterns of gene flow and population genetic structure (Manel & Holderegger, 2013; Manel, Schwartz, Luikart, & Taberlet, 2003; Storfer et al., 2007). Most landscape genetics studies have focused on single species, but there are a growing number of comparative, multi-species studies (e.g., Cleary, Waits, & Finegan, 2017; Goldberg & Waits, 2010; Petren, Grant, Grant, & Keller, 2005; Trumbo, Spear, Baumsteiger, & Storfer, 2013; Zancolli, Rödel, Steffan-Dewenter, & Storfer, 2014). Even fewer multi-species studies have employed landscape genetics methods to study the dynamics of infectious diseases in wildlife systems (Biek & Real, 2010; Hemming-Schroeder et al., 2018; Kozakiewicz et al., 2018). Such comparative landscape genetics frameworks can provide valuable insights into how host-pathogen interactions shape patterns of disease transmission and spread across heterogeneous landscapes (Leo, Gonzalez, Millien, & Cristescu, 2016; Schwabl et al., 2017; Talbot et al., 2017).
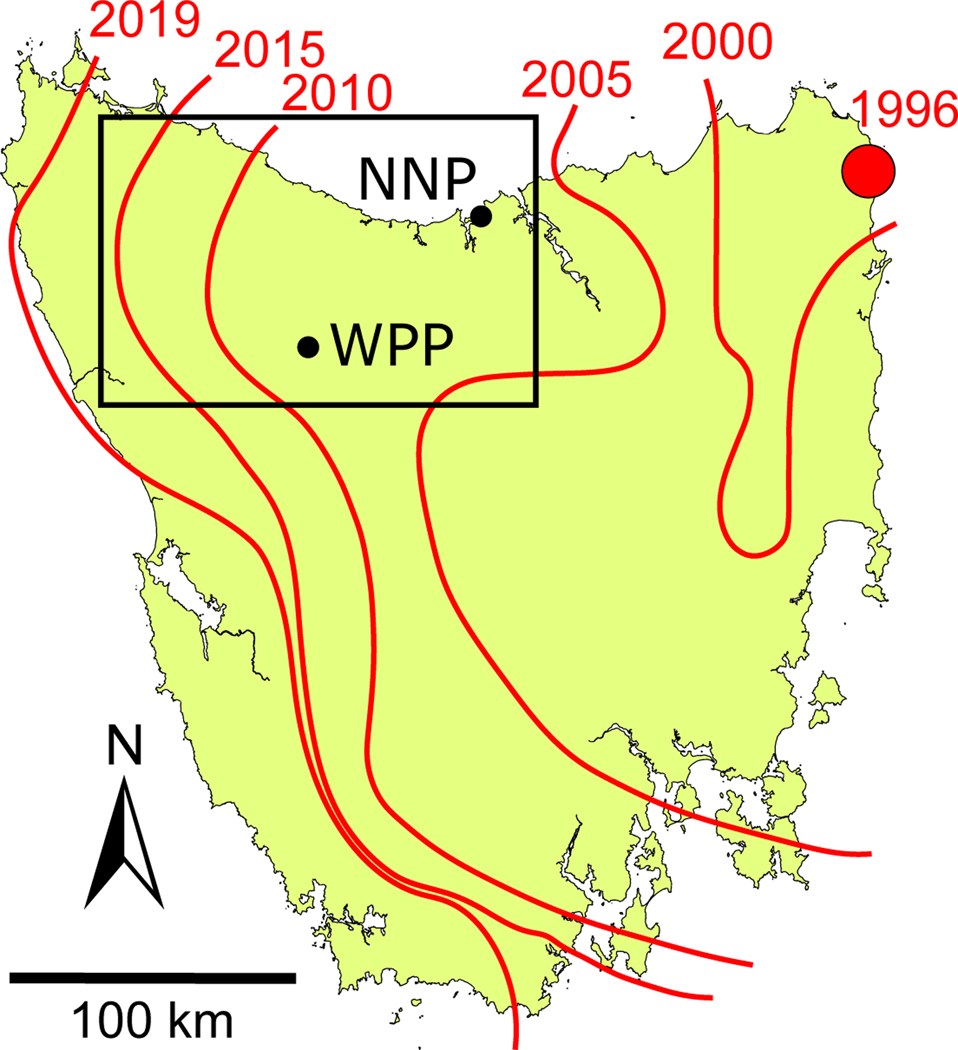
Tasmanian devils (Sarcophilus harrisii) and their transmissible cancer provide a highly appropriate study system to test for host-pathogen co-structuring in a comparative landscape genetics framework. In 1996, devil facial tumor disease (DFTD) was discovered in northeastern Tasmania, Australia. DFTD is one of only a few documented transmissible cancers (Metzger & Goff, 2016; Ostrander, Davis, & Ostrander, 2016; Storfer et al., 2017) and since its emergence, has spread across almost the entire geographic range of the Tasmanian devil (Save the Tasmanian Devil Programme, 2019) (Figure 1). With a nearly 100% mortality rate, DFTD has caused an estimated 80% population decline across the species range, with localized declines exceeding 90% (Lazenby et al., 2018; McCallum et al., 2007).
Figure 1.
The spread of DFTD across the island of Tasmania, with the approximate disease front over time depicted as red lines labelled by year. The site of the first documented case of DFTD is identified by the red circle. The 12,000 km2 study area is shown within the box, with Narawntapu National Park (NNP) and West Pencil Pine (WPP) indicated.
Devil facial tumors are transmitted as an allograft through biting, a common occurrence during social interactions among devils (Hamede, Mccallum, & Jones, 2013; Hamilton et al., 2019). Direct transmission of DFTD among devils means that its spatial spread is inextricably tied to the movements of devils – a relationship which leads to the assumption of genetic co-structuring among host and pathogen (Criscione, 2008; Jarne & Théron, 2001; Mazé-Guilmo et al., 2016). Yet, for co-structuring to occur, pathogen dispersal must be synchronized with host dispersal and subsequent reproduction. In other words, individuals must disperse while infected and reproduce thereafter. This requirement has been identified previously but is often overlooked in studies that use host movements to predict disease spread. In devils, gene flow typically occurs through individuals that dispersed away from their natal sites as juveniles, whereas DFTD transmission occurs primarily during the adult life stage. Juvenile dispersal is likely to take place over greater distances than the typical movements of adult devils because adults maintain high fidelity to their established home ranges, which are typically 5–30 km2 (Lachish, Miller, Storfer, Goldizen, & Jones, 2011; Pemberton, 1990). Yet, genetic spatial autocorrelation distances are up to 100 km in eastern Tasmania (Lachish et al., 2011) and 60 km in western Tasmania (Storfer et al., 2017). On this basis, we would hypothesize that co-structuring among devils and tumors is weak and that devil gene flow should be less geographically constrained than the spread of DTFD.
An alternative hypothesis is that DFTD disperses more rapidly and shows less genetic structure than devils because opportunities for transmission occur more frequently than devil reproduction. That is, whereas the biting contacts required for DFTD transmission are a common social behavior occurring throughout the year (albeit more frequently during the mating season), devils generally mate between February and May (Hamede et al., 2009, 2013; Hamilton et al., 2019). Furthermore, the potential effect of a single dispersing individual on genetic structure is less in devils than for tumors. This is because a single tumor may proliferate into a large, clonal lineage that dramatically shifts the overall genetic structure of tumors in its new population. High mobility of DFTD tumors is supported by the fact that DFTD has spread from the northeastern corner of Tasmania to the west coast of Tasmania in just over 20 years (Epstein et al., 2016; Storfer et al., 2017) (Figure 1). It is unclear which of these competing hypotheses is best supported, exemplifying the need to understand the extent to which host and pathogen movements are linked and whether they are subject to the same environmental constraints.
Herein, we employ a comparative landscape genetics framework to test these competing hypotheses. Specifically, we test whether Tasmanian devil population structure predicts DFTD tumor population structure and whether host gene flow and pathogen spread are dictated by distinct environmental factors. We use 6,478 SNPs in devils and 1,595 SNPs in tumors genotyped using RAD-capture (Ali et al., 2016; Margres et al., 2018) to reveal broad-scale population structure as well as fine-scale patterns of genetic variation. Individual-level estimates of genetic variation were analyzed using complementary landscape genetic approaches to investigate the relative roles of isolation-by-environment (IBE) and isolation-by-resistance (IBR) in influencing genetic structure in both devils and DFTD. In short, IBE occurs due to the environment at sample locations, whereas IBR occurs due to the environment intervening sample locations. IBR approaches allow us to quantify how environmental heterogeneity across entire landscapes can affect functional connectivity (McRae, 2006), and distinguish these effects from the classical isolation-by-distance model (IBD; Wright, 1943). In contrast, IBE describes the effect of divergent environments on genetic differentiation (Wang & Bradburd, 2014) and can occur for various reasons, including population-specific adaptation to local environmental conditions (and thus maladaptation of and selection against migrants) or natal habitat preference induction leading to habitat-biased dispersal (Wang & Bradburd, 2014).
Methods
Study system
Tasmanian devils are carnivorous marsupials endemic to the island of Tasmania, Australia, where they are apex predators. Tasmania comprises a total land mass of 68,401 km2 and encompasses a dramatic east-to-west climatic gradient and a high degree of topographic variability. Devils prefer eucalypt and sclerophyll forests and coastal scrub lands, but they can also be found near to human developments and agricultural land (Guiler, 1970; Hawkins et al., 2006; James et al., 2019). Previous work indicates up to six genetic populations island-wide, including a clear distinction between individuals sampled from northwestern Tasmania and those from elsewhere on the island (Brüniche-Olsen, Jones, Austin, Burridge, & Holland, 2014; Fraik et al., 2020; Hendricks et al., 2017; Miller et al., 2011; Storfer et al., 2017). The cause of this east-to-west spatial genetic heterogeneity remains unclear, with previous landscape genetics work implementing least-cost path modelling and microsatellite loci unable to identify any landscape factors driving this variation (Storfer et al., 2017).
The transmissible tumor first identified in 1996 is now present across nearly the entire devil geographic range, with all extant cases having a common origin. However, in 2014, a second transmissible cancer of devils, devil facial tumor disease 2 (DFT2), was discovered in southern Tasmania, independent in origin from the first (Pye et al., 2016). DFT2 remains geographically restricted; yet, insights gained into the transmission of the first tumor may help inform the management of DFT2 and any subsequent transmissible tumors, as well as other directly transmitted diseases. Herein, we focus on the first tumor, to which we refer exclusively in this study as “DFTD” or “tumors”, with any references to the second tumor, DFT2, specified as such. No cases of DFT2 were included in this study.
DFTD infection is typically observed in adult devils, most likely due to limited injurious biting contact until adulthood (Hamede et al., 2013) and changes in immune system function at sexual maturity (Cheng et al., 2017). Nonetheless, tumors are occasionally observed in juveniles, with a long latent period likely biasing detectability toward adults (Hamede et al., 2013, 2015; Lazenby et al., 2018). DFTD replicates clonally, with no evidence of recombination among tumors. However, cancer lineages accumulate somatic mutations over time, thus generating genetic differences among locations that reflect how a given lineage has spread spatially (Murchison et al., 2012; Schwartz & Schäffer, 2017; Stammnitz et al., 2018). Therefore, characterization of DFTD genetic structure enables us to infer how it has spread among devil populations with respect to geographic and environmental factors.
Sample collection
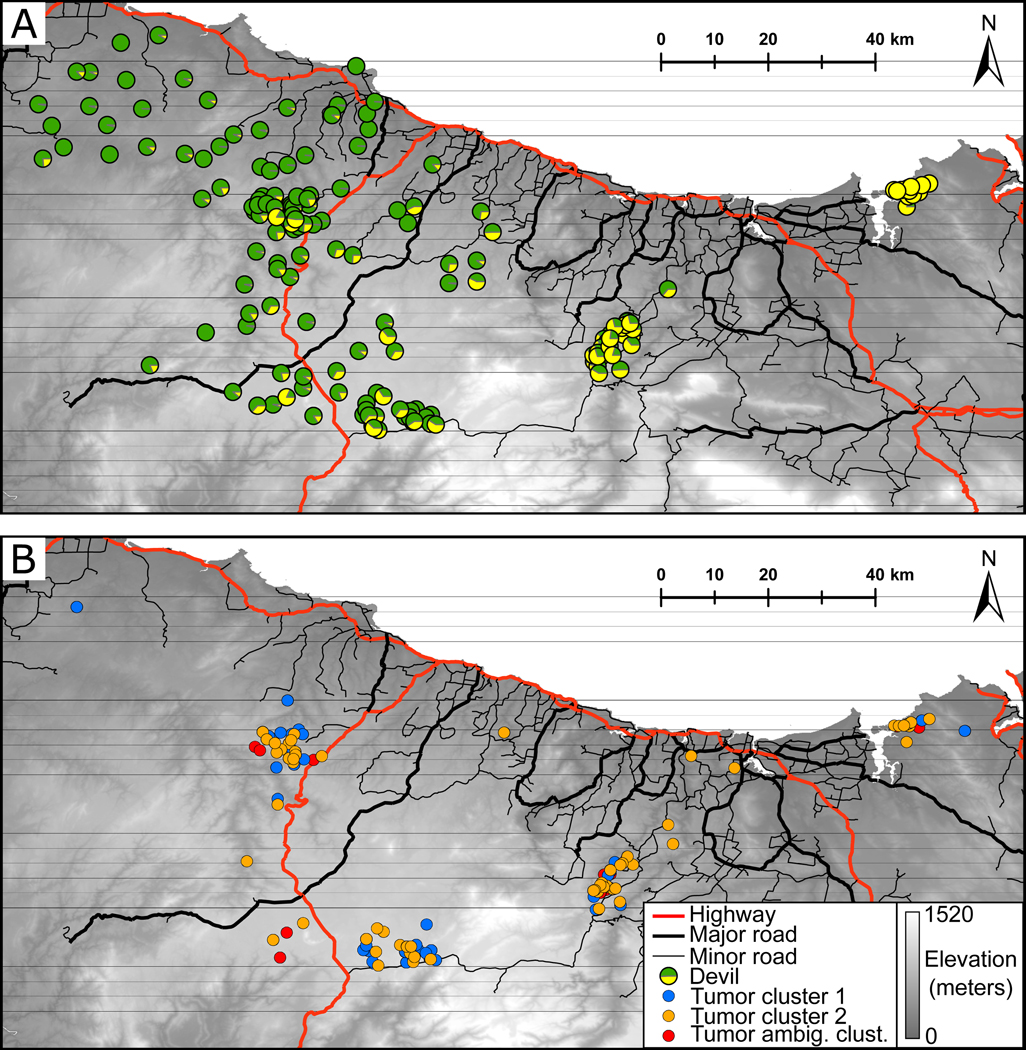
We collected georeferenced Tasmanian devil ear and tumor tissue samples using a 3 mm biopsy punch from wild devils over a 12-year period. A detailed description of field trapping protocols can be found in Hawkins et al. (2006) and Hamede et al. (2015). Two hundred and seventeen devil samples and 177 tumor samples, of which 87 were paired samples with both tumor and host tissue taken from the same individual, were collected from an approximately 12,000 km2 area in northwest Tasmania between 2004 and 2016 (Figures 1 and 2). We focused on this area because it contains a high degree of environmental and topographic variation and overlaps with a broad-scale genetic discontinuity among devil populations identified in previous studies (Brüniche-Olsen et al., 2014; Hendricks et al., 2017; Miller et al., 2011; Storfer et al., 2017), suggesting potential environmental/landscape constraints on devil movements. Sampling across this region was relatively consistent throughout the sample period and coincided with the arrival and spread of DFTD in this region (Figure 1).
Figure 2.
Spatial distribution of population genetic structure in (A) Tasmanian devils and (B) DFTD tumors. For devils, relative STRUCTURE assignment probabilities for K = 2 genetic clusters are depicted as pie charts. For tumors, genetic clusters as determined by combined STRUCTURE and DAPC analyses are depicted, with samples for which analyses were incongruent shown as being of ambiguous cluster assignment.
RAD-capture array
We used a Restriction site Associated DNA (RAD) capture (i.e., “Rapture”) array (Ali et al., 2016) to target loci across the devil and tumor genome. The capture array was developed from RAD sequencing of 360 devils (Epstein et al., 2016); 15,898 of the 90,000 RAD loci from this earlier study were used to make a targeted array using the myBaits for high throughput population genomics studies kit (Arbor Biosciences, Ann Arbor, MI) as described in Margres et al. (2018). Targeted loci met one or more of the following criteria: 1) genotyped in ≥ 50% of individuals, contained ≤ 3 non-singleton SNPs with a minor allele frequency (MAF) ≥ 0.05, and was ≥ 20 kb away from other targeted loci to increase genome coverage (7,108 loci); 2) located within 50 kb of an immune related gene, with ≤ 4 non-singleton SNPs, and genotyped in ≥ 67% of the individuals (6,315 loci); and, 3) showing some preliminary evidence of association with DFTD susceptibility and having ≤ 5 non-singleton SNPs (3,316 loci).
Because the myBaits array was developed for devils and not DFTD, we tested whether the array could successfully capture RAD loci from tumor samples by aligning whole genome tumor samples (sequenced at 90x coverage; from Margres et al., 2020) to the devil reference genome (downloaded from Ensembl June 2014; Murchison et al., 2012) using Burrows-Wheeler Aligner v0.7.12 (option MEM; Li & Durbin, 2009). We measured tumor coverage across each Rapture region using Bedtools v2.27.0 (Quinlan & Hall, 2010). Only 10 genomic regions covered on the capture array showed low coverage (< 10x), illustrating that 99.9% of the baits should capture tumor DNA.
Sequencing and data processing
We extracted DNA from tissue biopsies using the Qiagen DNeasy Blood & Tissue Kit, doubling the recommended amount of proteinase K to maximize lysis efficiency. DNA was digested using the Pst1 restriction enzyme and the RAD-capture libraries were sequenced on an Illumina HiSeq 4000 at the Genomics Sequencing Laboratory at the University of California, Berkeley. We processed the raw data as previously described (Margres et al., 2018). Briefly, reads were de-multiplexed and low-quality reads as well as potential PCR duplicates were removed using Stacks v1.21 (Catchen, Hohenlohe, Bassham, Amores, & Cresko, 2013). Reads were then aligned to the reference genome using bowtie2 v2.3.4 (Langmead & Salzberg, 2012) with the --sensitive, --end-to-end, and -X 900 settings.
Variant calling
To identify variants, we used HaplotypeCaller in GATK v3.8 (DePristo et al., 2011; McKenna et al., 2010), with devils and tumors genotyped separately. For each, we removed SNPs and indels matching any of the following criteria: quality by depth < 2.0, strand bias Phred-scaled p-value > 60.0, root mean square of the mapping quality < 40.0, mapping quality rank sum test approximation of 12.5, and a read position rank sum test approximation of eight.
We removed non-targeted regions from the dataset using Bcftools isec (Li, 2011), followed by removal of SNPs with a minimum depth < 5, minimum genotype quality < 25, missing data > 50%, and MAF < 0.01 using VCFtools v0.1.15 (Danecek et al., 2011). Then, to identify tumor-specific somatic SNPs and account for possible host contamination during tumor biopsy, we again used Bcftools isec to remove any SNP in the tumor dataset that was also identified in the host samples. Following filtering, we retained 6,478 devil and 1,595 tumor SNPs for analysis.
Population structure
We investigated both host and tumor population genetic structure using two complementary approaches, following best practices recommended by (Janes et al., 2017). First, we performed a discriminant analysis of principal components (DAPC) using adegenet (Jombart, 2008) in R version 3.6.3 (R Development Core Team, 2013). Briefly, we used the find.clusters function to perform k-means estimation of the best-fit number of genetic clusters (K) as determined by the Bayesian Information Criterion (BIC), followed by the DAPC function to estimate probabilities of membership to each cluster for each tumor sample. Second, we evaluated population structure using STRUCTURE v2.3.4 (Pritchard, Stephens, & Donnelly, 2000). We tested all values of K between 1 and 5, performing ten replicate runs per K. Each run comprised 1,000,000 Markov chain Monte Carlo iterations following a burn-in of 50,000 iterations. Although STRUCTURE is inappropriate for clonal populations, we performed this analysis for tumors to maintain consistency with the host analysis and to complement the more suitable DAPC analysis. Because there are no recorded observations of recombination among tumors, we specified the admixture-free model in STRUCTURE. The most likely K was determined using ΔK according to the Evanno method (Evanno, Regnaut, & Goudet, 2005), implemented in STRUCTURE HARVESTER (Earl & VonHoldt, 2012; Van Rossum & Drake Jr, 1995), and assessment of mean estimated natural logarithm of the probability of the data [LnPr(X|K)] values. To identify possible hierarchical population structure, we repeated analyses of population structure on individual genetic clusters identified in initial runs until no further additional genetic clusters were identified.
Due to lack of recombination among tumors, we interpreted genetically distinct clusters of tumor samples as discrete, non-recombining groups. To ensure confidence in the identified clusters, we assigned tumors to a genetic cluster only where DAPC and STRUCTURE assignments were concordant. We excluded tumor samples with ambiguous assignment from any analysis pertaining to a specific cluster. Once tumor clusters had been identified, we performed an Analysis of Molecular Variance (AMOVA; Excoffier, Smouse, & Quattro, 1992) to quantify the proportion of overall genetic variance explained by differentiation between clusters relative to that explained by variation among and within individual tumors. AMOVA was performed using the poppr package in R (Kamvar, Tabima, & Grünwald, 2014) and significance determined using a randomization test with 100 permutations, which was performed using ade4 (Dray & Dufour, 2007).
We tested for genetic co-structuring among paired devil-tumor samples using two approaches. Firstly, we conducted a Mantel test comparing host genetic distances and tumor genetic distances. Individual genetic distances were calculated as 1 – Dps, where Dps is the proportion of shared alleles between paired samples, using adegenet. Secondly, we fitted a logistic regression to determine if STRUCTURE assignment probabilities for hosts were predictive of the genetic cluster to which a given host’s tumor was assigned. We also used a logistic regression to determine whether sample date was predictive of the genetic cluster of each tumor.
Landscape genetics
We conducted landscape genetic analyses to identify how environmental factors influence patterns of devil and tumor genetic structure within both IBR and IBE frameworks. All landscape genetic analyses were conducted separately for host and tumor. In addition to analyzing all tumors together, we also conducted landscape genetic analyses separately for each of the identified tumor clusters (as identified by the above described population genetic approaches) to account for differences in environmental associations among clusters.
We selected six continuous and two categorical variables to test in our landscape genetic analyses based on habitat preferences observed through prior devil mark-recapture studies (Guiler, 1970; Hawkins et al., 2006), radio collaring studies (M.E. Jones, unpublished data), and a previous landscape genetic study of Tasmanian devils (Storfer et al., 2017). The continuous variables comprised elevation, elevation relief ratio (a measure of relative altitudinal relief between two points; Pike & Wilson, 1971), annual mean temperature, temperature annual range (the difference between the average 24-hour maximum temperature of the hottest month and the average 24-hour minimum temperature of the coldest month), annual precipitation, and precipitation seasonality (the coefficient of precipitation variation; Feng, Porporato, & Rodriguez-Iturbe, 2013). Categorical variables were land cover type and roads. Land cover types were derived from the TASVEG 3.0 vegetation communities dataset (DPIPWE, 2013) and partitioned according to the ten broad vegetation categories defined by TASVEG 3.0, with agriculture and urban areas/exotic vegetation forming a further two categories. Roads data were downloaded from Geoscience Australia (data.gov.au) and classified as principal, secondary, and minor roads, to which we refer as highways, major roads, and minor roads, respectively. Elevation data were downloaded from Geoscience Australia and elevation relief ratio was calculated from the elevation data using the raster calculator in ArcGIS v10.7 (ESRI, 2011). Climatic data were downloaded from WorldClim v2 (Fick & Hijmans, 2017). We assessed multicollinearity among environmental rasters using Variance Inflation Factors (VIF), retaining only variables with VIF < 10 (Table S1). Annual mean temperature had a VIF score exceeding this threshold and was subsequently removed from all analyses.
Pairwise individual genetic distances were interpreted for devils and tumors as a relative proxy for genetic connectivity and used as a response variable for landscape genetic analyses.
Isolation-by-resistance: effects of landscape heterogeneity intervening sites
We tested for effects of landscape variables on genetic connectivity in an IBR framework using the R package ResistanceGA (Peterman, 2018). ResistanceGA optimizes the correlation between genetic distances and resistance surface cost values by using a genetic algorithm to explore potential resistance surface parameterizations for each landscape variable. Resistance surface optimization approaches avoid the need to a priori assign costs to environmental variables through expert opinion or species distribution and habitat suitability models, which can be difficult to translate to numerical values of resistance to movement (Elliot, Cushman, Macdonald, & Loveridge, 2014; Spear, Balkenhol, Fortin, McRae, & Scribner, 2010). In contrast to least-cost path modelling, which considers only a single optimal dispersal pathway with respect to a heterogeneous landscape factor of interest (thus assuming that individuals have complete knowledge of the landscape), IBR analytical frameworks that implement circuit theory can account for all possible dispersal pathways in predicting rates of gene flow (McRae, 2006).
We optimized resistance surfaces singly for each environmental variable based on random-walk commute time between locations (van Etten, 2017). In brief, the genetic algorithm used for optimization comprised a randomly generated population of individuals possessing parameters with randomly chosen values that determine which of a variety of transformations is applied to the resistance surface, the shape of the transformation, and the maximum resistance value (Peterman, 2018). Thus, each simulated individual represents a uniquely parameterized resistance surface. Across each resistance surface (i.e., per simulated individual), pairwise commute times are calculated and evaluated against the true pairwise genetic distances using a linear mixed effect model with maximum likelihood population effects (MLPE), which accounts for nonindependence among pairwise samples (Clarke, Rothery, & Raybould, 2002; Van Strien, Keller, & Holderegger, 2012). Model support, or “fitness” of each simulated individual is determined using log-likelihood, with those achieving the highest log-likelihood allowed to “reproduce” to form a population comprising the next generation of the algorithm. This new population inherits the parameters from the previous generation (while allowing for random mutation and recombination of the parameters), and the process repeats itself through a number of subsequent generations. For each landscape variable, we specified that 25 generations must pass with no improvement to the MLPE model log-likelihood for a resistance surface to be identified as optimal. Following optimization, to test the relative support of each environmental variable as a predictor of genetic distance, we used the final optimized surfaces to again generate commute times and fit MLPE models, calculated without restricted maximum likelihood (REML) and bootstrapped for 1,000 iterations with 90% subsampling. We ranked environmental variables by average AICC scores across all bootstrap iterations.
Isolation-by-environment: effects of environmental differentiation on genetic differentiation
To investigate the extent to which genetic differentiation in hosts and tumors is influenced by patterns of IBE, we used generalized dissimilarity modelling (GDM) as implemented in the R package gdm (Fitzpatrick & Keller, 2015). Originally designed for community-level modelling of species turnover, GDM performs linear regressions to test associations between dissimilarity and distance matrices, but fits i-spline functions to allow for non-linear responses and controls for geographic distance among sample locations (Ferrier, Manion, Elith, & Richardson, 2007). GDM assumes ordered categorical or continuous predictor variables (Ferrier et al., 2007), so we included only elevation, elevation relief ratio, and our climatic variables in this analysis. Environmental variables were measured as the mean value within a 15 km2 buffer around each sample location, approximating a typical devil home range (M.E. Jones, unpublished data). We used matrix permutation (500 permutations with 90% subsampling of both sites and site-pairs) with backward elimination to evaluate model and variable significance and estimate variable importance (Fitzpatrick & Keller, 2015). During each iteration of the backward elimination procedure, the least important variable was removed, and variable importance and significance re-calculated for the new model. As non-explanatory (i.e., the least important) variables were removed, the percent deviance explained by each successive model relative to the null did not change. Only as explanatory variables were removed did the percent deviance explained drop. Thus, the top model was identified as the model with the highest deviance explained and containing the fewest variables. Variable importance was calculated as the percent change in model deviance upon permutation of the given variable. Geographic distance was included as a control in all models and was not subject to backward elimination.
In addition to the host, all-tumor, and tumor cluster-specific tumor analyses, to compare the relative effects of host genetic variation and environmental variables on tumor genetic differentiation, we performed a separate GDM analysis of tumors for which the corresponding host devils were genotyped. For this analysis, the same environmental variables were included as above, with the addition of host genetic distances.
Results
Host and pathogen population structure
Analysis of devil population genetic structure using DAPC suggested the most likely number of genetic clusters was K = 2, according to BIC support. However, ΔBIC did not exceed 2 for either K = 1 or K = 2 (Figure S1), suggesting that patterns of population structure were difficult to resolve with our data (Burnham & Anderson, 2002). Similarly, STRUCTURE provided the most support for K = 2 as determined by ΔK calculated using the Evanno method. Although the Evanno method is unable to evaluate K = 1 and thus cannot exclude it as a potential solution (Janes et al., 2017), K = 1 was the least supported solution according to mean LnPr(X|K), supporting the existence of multiple genetic clusters. Further, mean LnPr(X|K) values supported successively higher values of K (Table 1), indicating a potential genetic cline. However, there was also greater variation in LnPr(X|K) among iterations at higher values of K (Table 1), suggesting some uncertainty. Further analysis of hierarchical structure within the initial K = 2 clusters did not provide clear evidence for any further genetic clusters for DAPC, yet STRUCTURE again supported successively higher values of K according to LnPr(X|K). Thus, for devils, we settled on K = 2 as representing opposite ends of a genetic cline. Accordingly, these clusters were not geographically discrete, with individual assignment probabilities indicating a continuous longitudinal admixture gradient (Figures 2 and 3).
Table 1.
Results from the Evanno method showing relative support for STRUCTURE models of varying numbers of genetic clusters (K) in Tasmanian devils and DFTD. Optimal K was determined according to the model with the highest ΔK, together with assessment of mean natural logarithm of the probability of the data (Ln Pr(X|K), and is shown in bold typeface.
| K | Reps | Mean Ln Pr(X|K) | Stdev LnP(K) | ΔK | |
|---|---|---|---|---|---|
|
| |||||
| Devil | |||||
| 1 | 10 | −1025607.12 | 4.90 | - | |
| 2 | 10 | −1005918.67 | 4.55 | 3339.52 | |
| 3 | 10 | −1001419.28 | 9.87 | 180.47 | |
| 4 | 10 | −998701.25 | 37.17 | 30.84 | |
| 5 | 10 | −997129.52 | 2514.96 | - | |
| Tumor | |||||
| 1 | 10 | −93561.09 | 0.31 | - | |
| 2 | 10 | −91383.05 | 22.36 | 271.29 | |
| 3 | 10 | −95270.47 | 6058.33 | 1.40 | |
| 4 | 10 | −90660.12 | 503.25 | 24.24 | |
| 5 | 10 | −98251.00 | 23635.46 | - | |
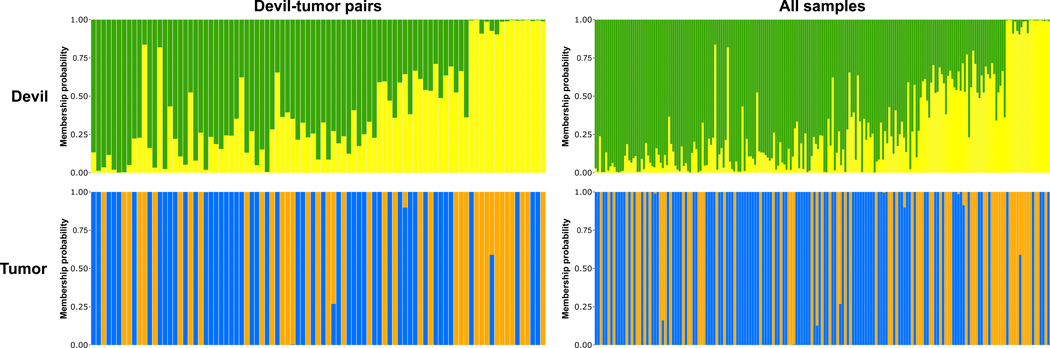
Figure 3.
Population structure is evident in both Tasmanian devils (top) and DFTD (bottom). STRUCTURE genetic assignment probabilities are shown for K = 2, showing both full (right) and paired host-tumor (left) sets. Each column represents an individual devil or tumor sample, with genetic clusters indicated by color and the relative proportions of each color representing a sample’s relative probability of membership of each genetic cluster. Tumor cluster 1 is indicated in blue and tumor cluster 2 is indicated in orange. Samples are arranged along the x-axis from west-to-east.
In tumors, DAPC and STRUCTURE both supported two genetic clusters (Table 1, Figure S1). However, LnPr(X|K) was higher for STRUCTURE runs at K = 4 but, similarly to devils, with greater variation among iterations. Subsequent DAPC and STRUCTURE runs showed no evidence of hierarchical population structure in tumors. Of the 177 tumors, 147 had cluster assignments that were supported by both DAPC and STRUCTURE at K = 2, with 30 tumors ambiguously assigned. Hereafter, we refer to the two identified tumor clusters as tumor cluster 1 (n = 74) and tumor cluster 2 (n = 73). There was no clear geographic structure among these clusters, with almost complete spatial overlap. However, we did observe a slight predominance of tumor cluster 2 towards the eastern end of the study area (Figures 2, 3). AMOVA revealed significant genetic variance attributable to the identified tumor clusters, which explained 6.48% of variation (P = 0.01) compared to minimal (1.58%; P = 0.23) variation attributable to among-tumor variation within clusters (Table S2). Variation within individual tumors comprised 91.94% of overall genetic variation (P = 0.04). This is due to somatic mutation in cancers producing high rates of heterozygosity.
Tasmanian devils and DFTD are weakly co-structured
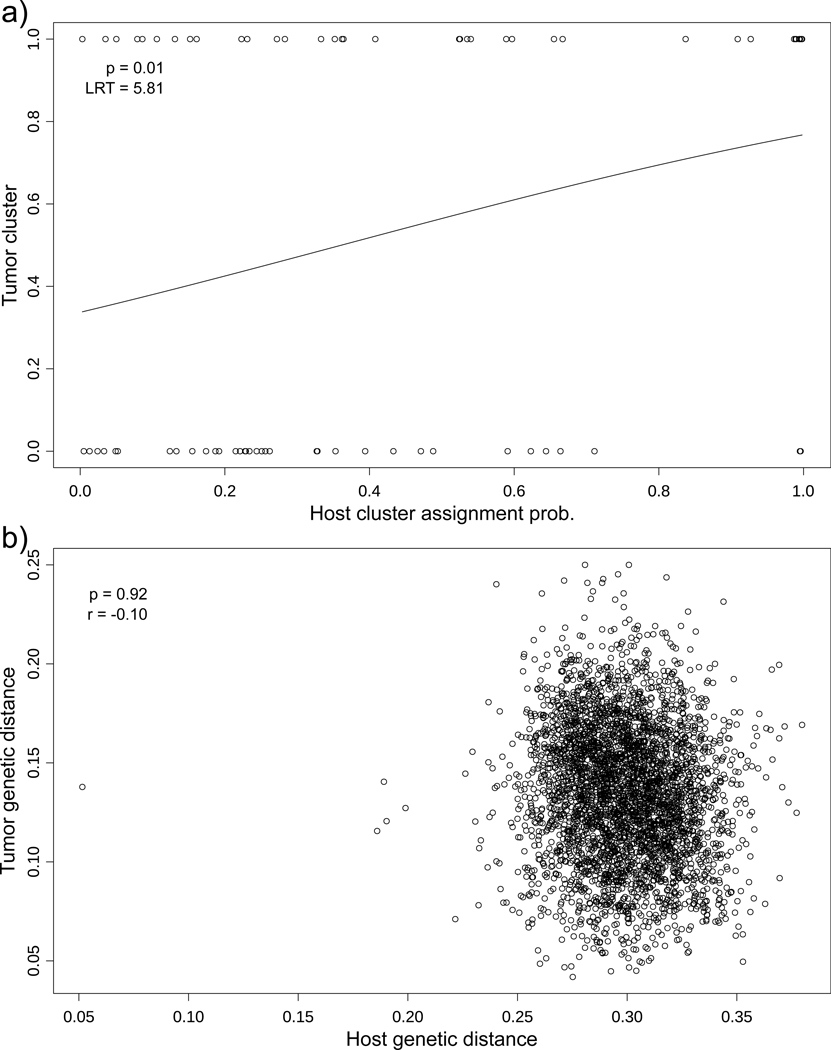
Our STRUCTURE results provide some evidence for host-tumor co-structuring along a longitudinal gradient (Figures 2, 3). Logistic regression revealed that tumor cluster identity was predicted by devil population structure (LRT = 5.81; P = 0.016; Figure 4a) but not sampling date (LRT = 1.74; P = 0.19), suggesting co-circulating tumor clusters that broadly co-structure with host populations. However, when comparing host and tumor genetic distances directly, we found no correlation (Mantel r = −0.10, P = 0.92; Figure 4b). Further, host genetic distances performed worse than environmental differences in predicting tumor genetic differentiation (see below landscape genetic analyses). Mean genetic distances were greater among devils (0.30, SD = 0.025) than among tumors (0.14, SD = 0.035).
Figure 4.
Tests of Tasmanian devil and DFTD tumor co-structuring, with logistic regression (A) suggesting that host genetic cluster assignment broadly predicts tumor genetic cluster, but with a Mantel test (B) showing no correlation between devil and tumor individual genetic distances (1 – DPS). Removal of left-tail outlier in panel B Mantel test produced negligible change in result.
Landscape factors more strongly affect spatial genetic variation in devils than DFTD
Isolation-by-resistance: effects of landscape heterogeneity intervening sites
In devils, landscape heterogeneity intervening sites explained substantial variation in gene flow. Although geographic distance was most frequently the top model (52.7% of bootstrap iterations) and explained 24.9% of genetic variation among devils, it had relatively low mean AICc support across bootstraps (mean ΔAICc = 5.97; Table 2). Roads as a barrier to gene flow had the highest average support of all models and was the top model in 38.4% of bootstrap iterations, explaining 37.9% of genetic variation among devils. Optimization of the roads resistance surface assigned the greatest costs to devil movement to highways and major roads, with minor roads and non-road cells having relatively low costs to devil movement. Although two other variables – precipitation seasonality and elevation relief ratio – had greater mean AICc support than geographic distance, they were poorly supported overall, being the top models in less than 7% of bootstrap iterations and having a mean ΔAICc > 2. No other landscape resistance model had mean ΔAICc < 2.
Table 2.
Linear mixed effect models with maximum likelihood population effects testing the influence of landscape resistance variables on genetic differentiation in devils, tumors, and tumor clusters 1 and 2. Model performance was evaluated by AICc averaged over 1,000 bootstrap iterations, with models with ΔAICc < 2 highlighted. Marginal R2 (mR2) is the proportion of overall variation explained by the model fixed effects and % Top Model is the percentage of times the model was the top performing model over 1,000 bootstraps, as determined by AICc support.
| Variable | K | AICc | ΔAICc | mR2 | % Top Model | |
|---|---|---|---|---|---|---|
|
| ||||||
| Devils | Roads | 5 | −7364.67 | 0.00 | 0.379 | 38.4 |
| Precip. seasonality | 4 | −7359.56 | 4.66 | 0.269 | 1.7 | |
| Elevation relief ratio | 4 | −7358.72 | 5.49 | 0.253 | 6.8 | |
| Temp. annual range | 4 | −7357.35 | 6.87 | 0.255 | 0.0 | |
| Distance | 2 | −7357.64 | 5.97 | 0.249 | 52.7 | |
| Elevation | 4 | −7357.35 | 6.86 | 0.253 | 0.1 | |
| Annual precip. | 4 | −7355.11 | 9.11 | 0.255 | 0.0 | |
| Land cover | 13 | −7322.04 | 50.90 | 0.319 | 0.3 | |
|
| ||||||
| All tumors | Elevation | 4 | −7083.89 | 0.00 | 0.015 | 67.7 |
| Precip. seasonality | 4 | −7082.19 | 1.70 | 0.030 | 30.5 | |
| Annual precip. | 4 | −7080.23 | 3.67 | 0.020 | 1.4 | |
| Elevation relief ratio | 4 | −7072.25 | 11.64 | 0.012 | 0.3 | |
| Distance | 2 | −7070.41 | 13.48 | 0.009 | 0.1 | |
| Temp. annual range | 4 | −7069.27 | 14.62 | 0.006 | 0.0 | |
| Land cover | 13 | −7067.75 | 16.14 | 0.024 | 0.0 | |
| Roads | 5 | −7065.33 | 18.57 | 0.009 | 0.0 | |
|
| ||||||
| Tumor cluster 1 | Elevation relief ratio | 4 | −7627.07 | 0.00 | 0.026 | 77.2 |
| Annual precip. | 4 | −7625.59 | 1.48 | 0.019 | 11.5 | |
| Precip. seasonality | 4 | −7624.56 | 2.51 | 0.016 | 4.6 | |
| Distance | 2 | −7624.19 | 2.88 | 0.009 | 6.4 | |
| Elevation | 4 | −7623.73 | 3.35 | 0.021 | 0.2 | |
| Temp. annual range | 4 | −7623.67 | 3.40 | 0.009 | 0.0 | |
| Roads | 5 | −7622.07 | 5.01 | 0.020 | 0.1 | |
| Land cover | 13 | −7616.24 | 10.83 | 0.016 | 0.0 | |
|
| ||||||
| Tumor cluster 2 | Elevation | 4 | −7972.78 | 0.00 | 0.025 | 77.6 |
| Annual precip. | 4 | −7969.02 | 3.76 | 0.043 | 2.1 | |
| Elevation relief ratio | 4 | −7967.41 | 5.37 | 0.044 | 10.3 | |
| Precip. seasonality | 4 | −7965.74 | 7.04 | 0.024 | 8.6 | |
| Distance | 2 | −7959.39 | 13.39 | 0.007 | 0.5 | |
| Roads | 5 | −7958.98 | 13.80 | 0.047 | 0.9 | |
| Land cover | 13 | −7957.66 | 15.12 | 0.053 | 0.0 | |
| Temp. annual range | 4 | −7958.77 | 14.01 | 0.006 | 0.0 | |
Among DFTD tumors, genetic variation was poorly explained by between-site landscape variables. Elevation and precipitation seasonality both had mean ΔAIC < 2 and were the most frequent top models among bootstrap iterations. However, these models explained minimal genetic variation among tumors. Elevation was most the supported model (mean ΔAICc = 0; top model in 67.7% of bootstrap iterations) but explained only 1.5% of genetic variation among tumors. Precipitation seasonality was less supported (mean ΔAICc = 1.70; top model in 30.5% of bootstrap iterations) but explained slightly more genetic variation among tumors (mean mR2 = 0.03).
When analyzing each tumor cluster separately, the top landscape resistance models differed among clusters but still explained relatively little genetic variation for each. For tumor cluster 1, elevation relief ratio was the top model in 77.2% of bootstrap iterations, with annual precipitation being the top model in 11.5% of bootstrap iterations (mean ΔAICc = 1.48). However, all but two of the models for cluster 1 had a mean ΔAICc < 4, suggesting relatively weak support for the top models over the others. For tumor cluster 2, elevation was the top model in 77.6% of bootstrap iterations (mean ΔAICc = 0), with all other models poorly supported.
Isolation-by-environment: effects of environmental differentiation on genetic differentiation
Analysis of isolation-by-environment patterns using GDM did not identify any environmental differences among sample locations that were explanatory of genetic differentiation among devils (Table 3). The top model explained a reduction in deviance relative to the null model of 11.87%, but contained only a significant effect of geographic distance, which explained just 1.84% of this reduction in model deviance. This suggests a weak effect of isolation-by-distance among devils.
Table 3.
Summary of top generalized dissimilarity models explaining genetic distances in devils, all DFTD tumors, and DFTD clusters separately. % deviance explained refers to the reduction in model deviance relative to the null. % model deviance explained refers to the percent change in model deviance upon permutation of a given variable.
| % deviance explained | Variable | Variable significance (P) | % model deviance explained | ||
|---|---|---|---|---|---|
|
| |||||
| Devils | 11.87 | Geographic distance | 0.00 | 1.84 | |
| Elevation relief ratio | - | - | |||
| Elevation | - | - | |||
| Precip. seasonality | 0.47 | 0.90 | |||
| Annual precip. | 0.08 | 7.64 | |||
| Temp. annual range | 0.25 | 3.17 | |||
|
| |||||
| All tumors | 6.67 | Geographic distance | 0.00 | 0.00 | |
| Elevation relief ratio | 0.99 | 0.00 | |||
| Elevation | 0.00 | 99.95 | |||
| Precip. seasonality | - | - | |||
| Annual precip. | - | - | |||
| Temp. annual range | - | - | |||
|
| |||||
| Tumors with matched host samples | 5.50 | Geographic distance | 0.01 | 0.00 | |
| Elevation relief ratio | 0.07 | 38.96 | |||
| Elevation | 0.03 | 44.81 | |||
| Precip. seasonality | - | - | |||
| Annual precip. | - | - | |||
| Temp. annual range | - | - | |||
| Host genetic distance | - | - | |||
|
| |||||
| Tumor cluster 1 | No significant model | ||||
|
| |||||
| Tumor cluster 2 | 4.66 | Geographic distance | 0.11 | 0.00 | |
| Elevation relief ratio | 0.47 | 7.07 | |||
| Elevation | 0.02 | 93.36 | |||
| Precip. seasonality | - | - | |||
| Annual precip. | - | - | |||
| Temp. annual range | - | - | |||
Among all tumors, the top model explained a reduction in model deviance relative to the null model of 6.67% and contained significant effects of geographic distance and differences in elevation. Elevation predominated, explaining 99.95% of this reduction in model deviance, while the effect of geographic distance was nonexistent. This lack of an effect of geographic distance despite statistical significance was likely due to geographically distant animals being located in areas that differ in elevation, resulting in elevation explaining a high proportion of model deviance that would otherwise be partly explained by geographic distance.
When analyzing tumor clusters separately, the effect of elevation differences on genetic differentiation among tumors persisted only for tumor cluster 2, whose top model explained a 4.66% reduction in deviance relative to the null model. Elevation explained 93.36% of this reduction in model deviance, whereas the effect of geographic distance was non-significant. None of the models for tumor cluster 1 were significant upon permutation of environmental dissimilarity matrices, suggesting that none of the tested landscape variables, nor geographic distance, were influencing genetic differentiation among tumors within this cluster.
Host genetic distances did not perform better than environmental differences in explaining tumor genetic differentiation. In tumors for which the host devil was genotyped, host genetic distance was absent from the top model, which explained a reduction in model deviance relative to the top model of 5.50%. Elevation was the most important variable, explaining 44.81% of this reduction in model deviance, consistent with the all-tumor analysis.
Discussion
We conducted a comparative landscape genetic study of Tasmanian devils and DFTD to identify environmental factors driving IBR and IBE patterns in both host and pathogen. Our results warrant caution when inferring pathogen spread using host population genetic structure. Although we found evidence for broad-scale co-structuring between devils and tumors, the primary landscape processes influencing genetic variation appeared to differ between host and pathogen. In devils, we found two genetic clusters, consistent with previous studies (Storfer et al., 2017). Further, a relatively strong IBR pattern was present, whereby genetic variation was driven largely by major roads and highways acting as barriers to gene flow. However, evidence of IBE was absent in devils. Surprisingly, we found no geographic or temporal structure among two identified tumor clusters, suggesting coexistence of distinct tumor lineages throughout the study area for the entire sampling period. IBE in tumor cluster 2, although not particularly strong, was largely attributable to differences in elevation. Despite almost complete spatial overlap with cluster 2, tumor cluster 1 exhibited no evidence of IBE.
Co-structuring among Tasmanian devils and DFTD
In devils, we observed a clinal pattern of admixture between two genetic clusters from east-to-west across our study area. Previous broader-scale studies of devils have identified relatively discrete genetic clusters, with a genetic discontinuity approximately overlapping our study area that distinguishes northwest Tasmanian devils from other populations (Brüniche-Olsen et al., 2014; Hendricks et al., 2017; Jones, Paetkau, Geffen, & Moritz, 2004; Miller et al., 2011). Our study encompasses a relatively smaller geographical area at a higher sampling density than previous studies, and it is likely that the observed clinal pattern reflects admixture between the previously identified northwestern population and those further to the east.
We observed broad-scale genetic co-structuring between infected devils and their tumors, whereby devil genetic cluster assignment probabilities were predictive of the tumor cluster to which a given individual was host. However, there was no correlation between host and tumor genetic distances, suggesting that individual-level tumor variation (i.e., within clusters) is not influenced by host gene flow and a lack of co-structuring at a fine scale. Our inferred DFTD clusters had almost complete spatial overlap with one another, but we observed a higher prevalence of cluster 2 within Narawntapu National Park, our eastern-most collection site. Devils from this area showed almost complete assignment to a genetic cluster that was only present at admixture levels among other samples in this study (Figure 2), suggesting at least partial isolation of the Narawntapu population. Geographic isolation of Narawntapu, a coastal site surrounded by large water bodies and mountains, is further supported by documentation of a genetic distinct group of bare-nosed wombats (Vombatus ursinus) in this area (Martin et al., 2019a). Thus, we believe the observed broad-scale co-structuring is driven predominantly by geographic isolation of Narawntapu from the rest of our study area, rather than concordant patterns of gene flow.
Previous work has shown evidence of DFTD lineage replacement based on karyotype (Hamede et al., 2015), which may affect the spatial structuring of tumors. For example, a tetraploid DFTD strain first arrived at West Pencil Pine (a portion of our study area) in 2006, and initially resulted in lower than typical prevalence and higher than typical survival rates among infected individuals (Hamede et al., 2012, 2015). Devil populations subsequently began to decline with the arrival of a diploid tumor strain, which out-competed and replaced the tetraploid strain (Hamede et al., 2015). In contrast, we did not observe lineage replacement but rather co-circulation. However, we had insufficient data to test for differences in karyotype or virulence among our observed tumor strains, and the spatial scale of our study was considerably broader than that at which karyotypic partitioning was observed by Hamede et al. (2015) (within a 25km2 area). As such, our results do not preclude the occurrence of lineage replacement at highly localized spatial scales.
Isolation-by-resistance affects devils but not DFTD
Overall, IBR had a strong influence on genetic structure of devils but not tumors, supporting our hypothesis that tumor transmission among adult devils is less constrained by landscape than gene flow among juvenile dispersers. A significant negative effect of roads (predominantly highways and major roads) on gene flow was observed in devils, explaining 38% of genetic variation among our samples, compared to 25% of variation attributable to isolation-by-distance alone. Roads are a source of wildlife mortality due to vehicle collision, including in devils (Grueber et al., 2017; Jones, 2000). Coupled with the loss of habitat associated with road construction as well as fences and other structures, roads reduce structural and functional landscape connectivity and often lead to decreased gene flow. Such responses to roads are well-documented, and have been observed in both small, sedentary species (Arens et al., 2007; Holzman et al., 2009) as well as large, wide-ranging species (Coulon et al., 2006; Epps et al., 2005), including carnivores (Kozakiewicz et al., 2019; Riley et al., 2006). However, use of minor roads as movement corridors has been observed in devils, likely due to greater ease of movement through cleared vegetation and an abundance of roadkilled carcasses for scavenging (Andersen, Johnson, Barmuta, & Jones, 2017). We found neither a positive nor a negative effect of minor roads on devil gene flow. However, our study was conducted over a much larger area than Andersen et al. (2017), with road use potentially occurring over only small distances without a significant effect on longer distance dispersal events.
Roads that form barriers to wildlife do not necessarily act similarly as barriers to their pathogens – even those relying on direct transmission. For example, a major highway was found to produce strong population genetic structure in bobcats (Lynx rufus) but not in their directly-transmitted viruses (Lee et al., 2012). Similarly, our results suggest that roads do not significantly influence DFTD transmission. Roads are known to disproportionately affect juvenile devils, which exhibit higher mortality rates from vehicle collision than adults (Jones, 2000). Thus, roads likely present a greater barrier to dispersing juveniles, via which devil gene flow is primarily mediated, than to adults, via which DFTD transmission predominantly occurs. Overall, differentiation among tumors was not governed by any variation in connectivity due to landscape or environmental heterogeneity, with IBR patterns explaining barely more than 3% of tumor genetic variation. DFTD has spread across Tasmania very rapidly (Lazenby et al., 2018; McCallum et al., 2007), so it is not surprising that tumor movement has been largely unconstrained by geography. Tumors can proliferate rapidly if even a single infected individual reaches a naive population after crossing a challenging landscape. By contrast, the same challenging landscape may facilitate only occasional dispersal by juveniles, which may not even reproduce subsequently. Thus, although major roads constrain devil movements to the extent that devil population genetic structure is increased, even infrequent crossing of roads by DFTD-infected individuals is sufficient to sustain rapid DFTD spread.
Isolation-by-environment affects DFTD but not devils
Despite substantial topographic variation and a large rainfall gradient from east-to-west that produces dramatic variation in vegetation types and structure across Tasmania, we found no detectable IBE effect. This result is somewhat surprising because devil population densities vary throughout Tasmania concordant with habitat preference for low-elevation dry eucalypt forest, with lower densities at high elevations and in areas of cool temperate rainforest (Jones & Barmuta, 2000). However, the relatively narrow geographic focus of our study likely did not capture a sufficient proportion of these environmental gradients (relative to range-wide variation) for IBE patterns to be evident, with devils throughout our study area occupying (and preferring) relatively similar habitats.
In contrast to devils, we did detect evidence of IBE in tumors. Specifically, we found a significant positive correlation between elevation difference and genetic distance of tumors. When analyzing tumor clusters separately, we found that this effect was entirely driven by cluster 2, with genetic differentiation among cluster 1 lacking any significant association with any tested environmental factor, including geographic distance. We believe this effect of elevation on genetic differentiation among cluster 2 is most likely a result of population structure that is coincident with an elevation gradient. As we discussed above, a large proportion of cluster 2 tumors were sampled from Narawntapu National Park. Narawntapu is effectively at sea level, whereas the majority of tumors were sampled from devil populations in higher elevation areas. Thus, genetic differentiation among these groups owing to geographic isolation of Narawntapu tumors would be expected to produce an isolation-by-elevation effect. Although it is possible that some innate biological characteristic of the tumor may instead be driving this effect, the mechanism by which this would occur is unclear. Potentially, climatic differences (e.g., temperature, moisture) among high and low elevation areas could influence the ability of tumor cells to successfully implant in uninfected devils, driving local adaptation of tumors in these regions, although this has yet to be demonstrated. Alternatively, differences in local landscape characteristics and thus devil densities may change the frequency of biting interactions among devils that in turn alters the DFTD transmission rate. However, existing studies of devil interactions provide no support for this explanation, with biting behaviors tied to interactions that devils seek out regardless of landscape structure (Hamede et al., 2009, 2013; Hamilton et al., 2019).
Conclusions
Comparative landscape genetic studies facilitate identification of patterns of connectivity that are common to multiple species. However, use of host gene flow estimates as a proxy for pathogen transmission and spread can lead to erroneous conclusions in cases of incongruent host and pathogen genetic structure (Kozakiewicz et al., 2018; Mazé-Guilmo et al., 2016). We have shown that host population structure, and the landscape features that influence it, is decoupled from that of their pathogens. Roads, which were found to constrain devil gene flow significantly, were not associated with DFTD transmission, suggesting that genetic studies of devils are insufficient to infer or predict the spatial spread of tumors. This decoupling of host and pathogen likely occurred due to a mismatch between dispersal life stage and the stage at which devils typically carry and transmit DFTD. In other systems, external ecological factors such as multiple host/vector species or transmission via the environment are also known to mediate host-pathogen interactions (Näpflin et al., 2019; Witsenburg et al., 2015). Such ecological factors are amenable to inclusion in a comparative landscape genetic framework, emphasizing the value of comparative landscape genetics studies in host-pathogen systems where the dynamics of host dispersal and pathogen transmission may differ. Examples include sarcoptic mange, which infects various mammal species and can be transmitted environmentally (Martin et al., 2019b; Niedringhaus, Brown, Sweeley, & Yabsley, 2019), or pathogens requiring arthropod vectors, such as Plasmodium spp. (malaria; Lo et al., 2017), whereby disease spread relies on multiple species and is strongly mediated by the environment (Hemming-Schroeder et al., 2018; Schwabl et al., 2017).
Despite the apparent de-coupling of host and pathogen gene flow herein, host connectivity generally plays a significant role in wildlife disease dynamics. Higher connectivity among habitat patches and increased host movements increase rates of pathogen spread, prevalence, and persistence in the landscape (Becker, Snedden, Altizer, & Hall, 2018; Wilber, Johnson, & Briggs, 2020). However, wildlife populations themselves benefit similarly from increased connectivity, which is critical for maintaining genetic diversity and facilitating demographic rescue (Brown & Kodric-Brown, 1977; Keyghobadi, 2007; Whiteley, Fitzpatrick, Funk, & Tallmon, 2015). Thus, management of the landscape to isolate and constrain the spread of disease must be balanced against the need to maintain genetic and demographic exchange among wildlife populations (McCallum & Dobson, 2002). In light of increasing threats owing to habitat loss and wildlife disease globally (Haddad et al., 2015; Jones et al., 2008), this trade-off has become a major conundrum for wildlife managers. Any interventions should therefore proceed with caution and can benefit from comparative landscape genetic studies to help consider the impact of alternative management strategies.
Supplementary Material
Acknowledgements
We thank Matthew Lawrance, Rachael Kane, Marc Beer, and three anonymous reviewers for their helpful critique of this manuscript. This work was funded by the National Science Foundation (DEB 1316549) and the National Institutes of Health (R01-GM126563-01) as part of the joint NSF-NIH-USDA Ecology and Evolution of Infectious Diseases program (AS, PAH, MEJ and HM).
Data Availability
Devil and tumor sequence data have been deposited under NCBI BioProjects PRJNA306495, PRJNA634071, and PRJNA641648. Sample accession numbers and sample locations are provided in Supporting Information.
References
- Ali OA, O’Rourke SM, Amish SJ, Meek MH, Luikart G, Jeffres C, & Miller MR (2016). RAD Capture (Rapture): flexible and efficient sequence-based genotyping. Genetics, 202(2), 389–400. doi: 10.1534/genetics.115.183665 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andersen GE, Johnson CN, Barmuta LA, & Jones ME (2017). Use of anthropogenic linear features by two medium-sized carnivores in reserved and agricultural landscapes. Scientific Reports, 7(1), 1–11. doi: 10.1038/s41598-017-11454-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- Archie EA, Luikart G, & Ezenwa VO (2009). Infecting epidemiology with genetics: a new frontier in disease ecology. Trends in Ecology and Evolution, 24(1), 21–30. doi: 10.1016/j.tree.2008.08.008 [DOI] [PubMed] [Google Scholar]
- Arens P, Van Der Sluis T, Van’t Westende WPC, Vosman B, Vos CC, & Smulders MJM (2007). Genetic population differentiation and connectivity among fragmented Moor frog (Rana arvalis) populations in The Netherlands. Landscape Ecology, 22(10), 1489–1500. doi: 10.1007/s10980-007-9132-4 [DOI] [Google Scholar]
- Becker DJ, Snedden CE, Altizer S, & Hall RJ (2018). Host dispersal responses to resource supplementation determine pathogen spread in wildlife metapopulations. The American Naturalist, 192(4), 503–517. doi: 10.1086/699477 [DOI] [PubMed] [Google Scholar]
- Biek R, & Real LA (2010). The landscape genetics of infectious disease emergence and spread. Molecular Ecology, 19(17), 3515–3531. doi: 10.1111/j.1365-294X.2010.04679.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blanchong JA, Robinson SJ, Samuel MD, & Foster JT (2016). Application of genetics and genomics to wildlife epidemiology. Journal of Wildlife Management, Vol. 80, pp. 593–608. doi: 10.1002/jwmg.1064 [DOI] [Google Scholar]
- Blanchong JA, Samuel MD, Scribner KT, Weckworth BV, Langenberg JA, & Filcek KB (2008). Landscape genetics and the spatial distribution of chronic wasting disease. Biology Letters, 4(1), 130–133. doi: 10.1098/rsbl.2007.0523 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown JH, & Kodric-Brown A.(1977). Turnover rates in insular biogeography: effect of immigration on extinction. Ecology, 58(2), 445–449. doi: 10.2307/1935620 [DOI] [Google Scholar]
- Brüniche-Olsen A, Jones ME, Austin JJ, Burridge CP, & Holland BR (2014). Extensive population decline in the Tasmanian devil predates European settlement and devil facial tumour disease. Biology Letters, 10(11), 20140619. doi: 10.1098/rsbl.2014.0619 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burnham KP, & Anderson DR (2002). Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach (2nd ed.). New York, NY, USA: Springer-Verlag. [Google Scholar]
- Catchen J, Hohenlohe PA, Bassham S, Amores A, & Cresko WA (2013). Stacks: an analysis tool set for population genomics. Molecular Ecology, 22(11), 3124–3140. doi: 10.1111/mec.12354 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng Y, Heasman K, Peck S, Peel E, Gooley RM, Papenfuss AT, … Belov K.(2017). Significant decline in anticancer immune capacity during puberty in the Tasmanian devil. Scientific Reports, 7(1), 44716. doi: 10.1038/srep44716 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clarke RT, Rothery P, & Raybould AF (2002). Confidence limits for regression relationships between distance matrices: estimating gene flow with distance. Journal of Agricultural, Biological, and Environmental Statistics, 7(3), 361–372. doi: 10.1198/108571102320 [DOI] [Google Scholar]
- Cleary KA, Waits LP, & Finegan B.(2017). Comparative landscape genetics of two frugivorous bats in a biological corridor undergoing agricultural intensification. Molecular Ecology, 26(18), 4603–4617. doi: 10.1111/mec.14230 [DOI] [PubMed] [Google Scholar]
- Cote H, Garant D, Robert K, Mainguy J, & Pelletier F.(2012). Genetic structure and rabies spread potential in raccoons: the role of landscape barriers and sex-biased dispersal. Evolutionary Applications, 5(4), 393–404. doi: 10.1111/j.1752-4571.2012.00238.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coulon A, Guillot G, Cosson JF, Angibault JM, Aulagnier S, Cargnelutti B, … Hewison AJ (2006). Genetic structure is influenced by landscape features: empirical evidence from a roe deer population. Mol Ecol, 15(6), 1669–79. doi: 10.1111/j.1365-294X.2006.02861.x [DOI] [PubMed] [Google Scholar]
- Craft ME (2015). Infectious disease transmission and contact networks in wildlife and livestock. Philosophical Transactions of the Royal Society B: Biological Sciences, 370(1669), 20140107. doi: 10.1098/rstb.2014.0107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Craft ME, Volz E, Packer C, & Meyers LA (2009). Distinguishing epidemic waves from disease spillover in a wildlife population. Proceedings of the Royal Society B: Biological Sciences, 276(1663), 1777–1785. doi: 10.1098/rspb.2008.1636 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Criscione CD (2008). Parasite co-structure: broad and local scale approaches. Parasite, 15(3), 439–443. doi: 10.1051/parasite/2008153439 [DOI] [PubMed] [Google Scholar]
- Danecek P, Auton A, Abecasis G, Albers CA, Banks E, DePristo MA, … Durbin R.(2011). The variant call format and VCFtools. Bioinformatics, 27(15), 2156–2158. doi: 10.1093/bioinformatics/btr330 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davy CM, Martinez-Nunez F, Willis CKR, & Good SV (2015). Spatial genetic structure among bat hibernacula along the leading edge of a rapidly spreading pathogen. Conservation Genetics, 16(5), 1013–1024. doi: 10.1007/s10592-015-0719-z [DOI] [Google Scholar]
- De Castro F, & Bolker B.(2005). Mechanisms of disease-induced extinction. Ecology Letters, 8(1), 117–126. doi: 10.1111/j.1461-0248.2004.00693.x [DOI] [Google Scholar]
- DePristo MA, Banks E, Poplin R, Garimella KV, Maguire JR, Hartl C, … Daly MJ (2011). A framework for variation discovery and genotyping using next-generation DNA sequencing data. Nature Genetics, 43(5), 491–501. doi: 10.1038/ng.806 [DOI] [PMC free article] [PubMed] [Google Scholar]
- DPIPWE. (2013). TASVEG 3.0. Tasmanian Vegetation Monitoring and Mapping Program. Resource Management and Conservation Division, Department of Primary Industries, Parks, Water and Environment. [Google Scholar]
- Dray S, & Dufour A-B (2007). The ade4 Package: implementing the duality diagram for ecologists. Journal of Statistical Software, 1(4), 1–20. Retrieved from https://www.jstatsoft.org/v022/i04 [Google Scholar]
- Earl DA, & VonHoldt BM (2012). STRUCTURE HARVESTER: a website and program for visualizing STRUCTURE output and implementing the Evanno method. Conservation Genetics Resources, 4(2), 359–361. [Google Scholar]
- Elliot NB, Cushman SA, Macdonald DW, & Loveridge AJ (2014). The devil is in the dispersers: predictions of landscape connectivity change with demography. Journal of Applied Ecology, 51(5), 1169–1178. doi: 10.1111/1365-2664.12282 [DOI] [Google Scholar]
- Epps CW, Palsbøll PJ, Wehausen JD, Roderick GK, Ramey RR, & McCullough DR (2005). Highways block gene flow and cause a rapid decline in genetic diversity of desert bighorn sheep. Ecol Lett, 8(10), 1029–1038. doi: 10.1111/j.1461-0248.2005.00804.x [DOI] [Google Scholar]
- Epstein B, Jones M, Hamede R, Hendricks S, McCallum H, Murchison EP, … Storfer A.(2016). Rapid evolutionary response to a transmissible cancer in Tasmanian devils. Nature Communications, 7, 12684. doi: 10.1038/ncomms12684 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evanno G, Regnaut S, & Goudet J.(2005). Detecting the number of clusters of individuals using the software STRUCTURE: a simulation study. Molecular Ecology, 14(8), 2611–2620. doi: 10.1111/j.1365-294X.2005.02553.x [DOI] [PubMed] [Google Scholar]
- Excoffier L, Smouse PE, & Quattro JM (1992). Analysis of molecular variance inferred from metric distances among DNA haplotypes: application to human mitochondrial DNA restriction data. Genetics, 131(2), 479 LP – 491. Retrieved from http://www.genetics.org/content/131/2/479.abstract [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feng X, Porporato A, & Rodriguez-Iturbe I.(2013). Changes in rainfall seasonality in the tropics. Nature Climate Change, 3(9), 811. [Google Scholar]
- Ferrier S, Manion G, Elith J, & Richardson K.(2007). Using generalized dissimilarity modelling to analyse and predict patterns of beta diversity in regional biodiversity assessment. Diversity and Distributions, 13(3), 252–264. doi: 10.1111/j.1472-4642.2007.00341.x [DOI] [Google Scholar]
- Fick SE, & Hijmans RJ (2017). WorldClim 2: new 1‐km spatial resolution climate surfaces for global land areas. International Journal of Climatology, 37(12), 4302–4315. [Google Scholar]
- Fitzpatrick MC, & Keller SR (2015). Ecological genomics meets community-level modelling of biodiversity: mapping the genomic landscape of current and future environmental adaptation. Ecology Letters, 18(1), 1–16. doi: 10.1111/ele.12376 [DOI] [PubMed] [Google Scholar]
- Fraik AK, Margres MJ, Epstein B, Barbosa S, Jones M, Hendricks S, … Storfer A.(2020). Disease swamps molecular signatures of genetic-environmental associations to abiotic factors in Tasmanian devil (Sarcophilus harrisii) populations. Evolution. doi: 10.1111/evo.14023 [DOI] [PMC free article] [PubMed]
- Goldberg CS, & Waits LP (2010). Comparative landscape genetics of two pond-breeding amphibian species in a highly modified agricultural landscape. Molecular Ecology, 19(17), 3650–3663. doi: 10.1111/j.1365-294X.2010.04673.x [DOI] [PubMed] [Google Scholar]
- Grueber CE, Reid-Wainscoat EE, Fox S, Belov K, Shier DM, Hogg CJ, & Pemberton D.(2017). Increasing generations in captivity is associated with increased vulnerability of Tasmanian devils to vehicle strike following release to the wild. Scientific Reports, 7(1), 2161. doi: 10.1038/s41598-017-02273-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guiler ER (1970). Observations on the Tasmanian devil, Sarcophilus harrisii (Marsupialia: Dasyuridae) II. Reproduction, breeding and growth of pouch young. Australian Journal of Zoology, 18(1), 63–70. Retrieved from 10.1071/ZO9700063 [DOI] [Google Scholar]
- Guivier E, Galan M, Chaval Y, Xuereb A, Ribas Salvador A, Poulle ML, … Cosson JF (2011). Landscape genetics highlights the role of bank vole metapopulation dynamics in the epidemiology of Puumala hantavirus. Mol Ecol, 20(17), 3569–3583. doi: 10.1111/j.1365-294X.2011.05199.x [DOI] [PubMed] [Google Scholar]
- Haddad NM, Brudvig LA, Clobert J, Davies KF, Gonzalez A, Holt RD, … Townshend JR (2015). Habitat fragmentation and its lasting impact on Earth’s ecosystems. Science Advances, 1(2), e1500052. doi: 10.1126/sciadv.1500052 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamede RK, Bashford J, McCallum H, & Jones M.(2009). Contact networks in a wild Tasmanian devil (Sarcophilus harrisii) population: using social network analysis to reveal seasonal variability in social behaviour and its implications for transmission of devil facial tumour disease. Ecology Letters, 12(11), 1147–1157. doi: 10.1111/j.1461-0248.2009.01370.x [DOI] [PubMed] [Google Scholar]
- Hamede RK, Lachish S, Belov K, Woods G, Kreiss A, Pearse AM, … Mccallum H.(2012). Reduced effect of Tasmanian devil facial tumor disease at the disease front. Conservation Biology, 26(1), 124–134. doi: 10.1111/j.1523-1739.2011.01747.x [DOI] [PubMed] [Google Scholar]
- Hamede RK, Mccallum H, & Jones M.(2013). Biting injuries and transmission of Tasmanian devil facial tumour disease. Journal of Animal Ecology, 82(1), 182–190. doi: 10.1111/j.1365-2656.2012.02025.x [DOI] [PubMed] [Google Scholar]
- Hamede RK, Pearse AM, Swift K, Barmuta LA, Murchison EP, & Jones ME (2015). Transmissible cancer in Tasmanian devils: localized lineage replacement and host population response. Proceedings of the Royal Society B: Biological Sciences, 282(1814), 20151468. doi: 10.1098/rspb.2015.1468 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamilton DG, Jones ME, Cameron EZ, McCallum H, Storfer A, Hohenlohe PA, & Hamede RK (2019). Rate of intersexual interactions affects injury likelihood in Tasmanian devil contact networks. Behavioral Ecology, 30, 1087–1095. doi: 10.1093/beheco/arz054 [DOI] [Google Scholar]
- Hawkins CE, Baars C, Hesterman H, Hocking GJ, Jones ME, Lazenby B, … Wiersma J.(2006). Emerging disease and population decline of an island endemic, the Tasmanian devil Sarcophilus harrisii. Biological Conservation, 131(2), 307–324. doi: 10.1016/j.biocon.2006.04.010 [DOI] [Google Scholar]
- Hemming-Schroeder E, Lo E, Salazar C, Puente S, & Yan G.(2018). Landscape genetics: a toolbox for studying vector-borne diseases. Frontiers in Ecology and Evolution, 6(March), 1–11. doi: 10.3389/fevo.2018.00021 [DOI] [Google Scholar]
- Hendricks S, Epstein B, Schönfeld B, Wiench C, Hamede R, Jones M, … Hohenlohe P.(2017). Conservation implications of limited genetic diversity and population structure in Tasmanian devils (Sarcophilus harrisii). Conservation Genetics, 18(4), 977–982. doi: 10.1007/s10592-017-0939-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holzman JP, Bohonak AJ, Kirkendall LR, Gottlieb D, Harari AR, & Kelley ST (2009). Inbreeding variability and population structure in the invasive haplodiploid palm-seed borer (Coccotrypes dactyliperda). Journal of Evolutionary Biology, 22(5), 1076–1087. doi: 10.1111/j.1420-9101.2009.01722.x [DOI] [PubMed] [Google Scholar]
- James S, Jennings G, Kwon YM, Stammnitz M, Fraik A, Storfer A, … Hamede R.(2019). Tracing the rise of malignant cell lines: Distribution, epidemiology and evolutionary interactions of two transmissible cancers in Tasmanian devils. Evolutionary Applications, 12(9), 1772–1780. doi: 10.1111/eva.12831 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Janes JK, Miller JM, Dupuis JR, Malenfant RM, Gorrell JC, Cullingham CI, & Andrew RL (2017). The K = 2 conundrum. Molecular Ecology, 26(14), 3594–3602. doi: 10.1111/mec.14187 [DOI] [PubMed] [Google Scholar]
- Jarne P, & Théron A.(2001). Genetic structure in natural populations of flukes and snails: a practical approach and review. Parasitology, 123(7), 27–40. doi: 10.1017/S0031182001007715 [DOI] [PubMed] [Google Scholar]
- Jombart T.(2008). adegenet: a R package for the multivariate analysis of genetic markers. Bioinformatics, 24(11), 1403–5. doi: 10.1093/bioinformatics/btn129 [DOI] [PubMed] [Google Scholar]
- Jones KE, Patel NG, Levy MA, Storeygard A, Balk D, Gittleman JL, & Daszak P.(2008). Global trends in emerging infectious diseases. Nature, 451(7181), 990–993. doi: 10.1038/nature06536 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones ME (2000). Road upgrade, road mortality and remedial measures: impacts on a population of eastern quolls and Tasmanian devils. Wildlife Research, 27(3), 289–296. Retrieved from 10.1071/WR98069 [DOI] [Google Scholar]
- Jones ME, & Barmuta LA (2000). Niche Differentiation Among Sympatric Australian Dasyurid Carnivores. Journal of Mammalogy, 81(2), 434–447. doi: [DOI] [Google Scholar]
- Jones ME, Paetkau D, Geffen E, & Moritz C.(2004). Genetic diversity and population structure of Tasmanian devils, the largest marsupial carnivore. Molecular Ecology, 13(8), 2197–2209. doi: 10.1111/j.1365-294X.2004.02239.x [DOI] [PubMed] [Google Scholar]
- Kamvar ZN, Tabima JF, & Grünwald NJ (2014). Poppr: an R package for genetic analysis of populations with clonal, partially clonal, and/or sexual reproduction. PeerJ, 2, e281. doi: 10.7717/peerj.281 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keyghobadi N.(2007). The genetic implications of habitat fragmentation for animals. Canadian Journal of Zoology-Revue Canadienne De Zoologie, 85(10), 1049–1064. doi: 10.1139/z07-095 [DOI] [Google Scholar]
- Kozakiewicz CP, Burridge CP, Funk WC, Salerno PE, Trumbo DR, Gagne RB, … Carver S.(2019). Urbanization reduces genetic connectivity in bobcats (Lynx rufus) at both intra– and interpopulation spatial scales. Molecular Ecology, 28(23), 5068–5085. doi: 10.1111/mec.15274 [DOI] [PubMed] [Google Scholar]
- Kozakiewicz CP, Burridge CP, Funk WC, Vandewoude S, Craft ME, Crooks KR, … Carver S.(2018). Pathogens in space: advancing understanding of pathogen dynamics and disease ecology through landscape genetics. Evolutionary Applications, 11(10), 1763–1778. doi: 10.1111/eva.12678 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lachish S, Miller KJ, Storfer A, Goldizen AW, & Jones ME (2011). Evidence that disease-induced population decline changes genetic structure and alters dispersal patterns in the Tasmanian devil. Heredity, 106(1), 172–182. doi: 10.1038/hdy.2010.17 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langmead B, & Salzberg SL (2012). Fast gapped-read alignment with Bowtie 2. Nature Methods, 9(4), 357–359. doi: 10.1038/nmeth.1923 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lazenby BT, Tobler MW, Brown WE, Hawkins CE, Hocking GJ, Hume F, … Pemberton D.(2018). Density trends and demographic signals uncover the long-term impact of transmissible cancer in Tasmanian devils. Journal of Applied Ecology, 55(3), 1368–1379. doi: 10.1111/1365-2664.13088 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee JS, Ruell EW, Boydston EE, Lyren LM, Alonso RS, Troyer JL, … Vandewoude S.(2012). Gene flow and pathogen transmission among bobcats (Lynx rufus) in a fragmented urban landscape. Molecular Ecology, 21(7), 1617–1631. doi: 10.1111/j.1365-294X.2012.05493.x [DOI] [PubMed] [Google Scholar]
- Leo SST, Gonzalez A, Millien V, & Cristescu ME (2016). Multi-taxa integrated landscape genetics for zoonotic infectious diseases: deciphering variables influencing disease emergence. Genome, 59(5), 349–361. doi: 10.1139/gen-2016-0039 [DOI] [PubMed] [Google Scholar]
- Li H.(2011). A statistical framework for SNP calling, mutation discovery, association mapping and population genetical parameter estimation from sequencing data. Bioinformatics, 27(21), 2987–2993. doi: 10.1093/bioinformatics/btr509 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H, & Durbin R.(2009). Fast and accurate short read alignment with Burrows-Wheeler transform. Bioinformatics, 25(14), 1754–1760. doi: 10.1093/bioinformatics/btp324 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lo E, Hemming-Schroeder E, Yewhalaw D, Nguyen J, Kebede E, Zemene E, … Yan G.(2017). Transmission dynamics of co-endemic Plasmodium vivax and P. falciparum in Ethiopia and prevalence of antimalarial resistant genotypes. PLoS Neglected Tropical Diseases, 11(7), 1–25. doi: 10.1371/journal.pntd.0005806 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manel S, & Holderegger R.(2013). Ten years of landscape genetics. Trends in Ecology and Evolution, 28(10), 614–621. doi: 10.1016/j.tree.2013.05.012 [DOI] [PubMed] [Google Scholar]
- Manel S, Schwartz MK, Luikart G, & Taberlet P.(2003). Landscape genetics: combining landscape ecology and population genetics. Trends in Ecology and Evolution, 18(4), 189–197. doi: 10.1016/s0169-5347(03)00008-9 [DOI] [Google Scholar]
- Margres MJ, Jones ME, Epstein B, Kerlin DH, Comte S, Fox S, … Storfer A.(2018). Large-effect loci affect survival in Tasmanian devils (Sarcophilus harrisii) infected with a transmissible cancer. Molecular Ecology, 27(21), 4189–4199. doi: 10.1111/mec.14853 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Margres MJ, Ruiz-Aravena M, Hamede R, Chawla K, Patton AH, Lawrance MF, … Storfer A.(2020). Spontaneous tumor regression in Tasmanian devils associated with RASL11A activation. Genetics, genetics.303428.2020. doi: 10.1534/genetics.120.303428 [DOI] [PMC free article] [PubMed]
- Martin A, Carver S, Proft K, Fraser TA, Polkinghorne A, Banks S, & Burridge CP (2019a). Isolation, marine transgression and translocation of the bare-nosed wombat (Vombatus ursinus). Evolutionary Applications, 12(6), 1114–1123. doi: 10.1111/eva.12785 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin AM, Ricardo H, Tompros A, Fraser TA, Polkinghorne A, & Carver S.(2019b). Burrows with resources have greater visitation and may enhance mange transmission among wombats. Australian Mammalogy, 41(2), 287–290. Retrieved from 10.1071/AM18013 [DOI] [Google Scholar]
- Mazé-Guilmo E, Blanchet S, Mccoy KD, & Loot G.(2016). Host dispersal as the driver of parasite genetic structure: A paradigm lost? Ecology Letters, 19(3), 336–347. doi: 10.1111/ele.12564 [DOI] [PubMed] [Google Scholar]
- McCallum H, & Dobson A.(2002). Disease, habitat fragmentation and conservation. Proceedings of the Royal Society B: Biological Sciences, 269(1504), 2041–2049. doi: 10.1098/rspb.2002.2079 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCallum H, Tompkins DM, Jones M, Lachish S, Marvanek S, Lazenby B, … Hawkins CE (2007). Distribution and impacts of Tasmanian devil facial tumor disease. EcoHealth, 4(3), 318–325. doi: 10.1007/s10393-007-0118-0 [DOI] [Google Scholar]
- McKenna A, Hanna M, Banks E, Sivachenko A, Cibulskis K, Kernytsky A, … DePristo MA (2010). The Genome Analysis Toolkit: a MapReduce framework for analyzing next-generation DNA sequencing data. Genome Research, 20(9), 254–260. doi: 10.1101/gr.107524.110.20 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McRae BH (2006). Isolation by resistance. Evolution, 60(8), 1551–1561. [PubMed] [Google Scholar]
- Metzger MJ, & Goff SP (2016). A sixth modality of infectious disease: contagious cancer from devils to clams and beyond. PLoS Pathogens, 12(10), 1–7. doi: 10.1371/journal.ppat.1005904 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller W, Hayes VM, Ratan A, Petersen DC, Wittekindt NE, Miller J, … Schuster SC (2011). Genetic diversity and population structure of the endangered marsupial Sarcophilus harrisii (Tasmanian devil). Proceedings of the National Academy of Sciences, 108(30), 12348–12353. doi: 10.1073/pnas.1217345109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murchison EP, Schulz-Trieglaff OB, Ning Z, Alexandrov LB, Bauer MJ, Fu B, … Stratton MR (2012). Genome sequencing and analysis of the Tasmanian devil and its transmissible cancer. Cell, 148(4), 780–791. doi: 10.1016/j.cell.2011.11.065 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Näpflin K, O’Connor EA, Becks L, Bensch S, Ellis VA, Hafer-Hahmann N, … Edwards SV (2019). Genomics of host-pathogen interactions: challenges and opportunities across ecological and spatiotemporal scales. PeerJ, 7, e8013. doi: 10.7717/peerj.8013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niedringhaus KD, Brown JD, Sweeley KM, & Yabsley MJ (2019). A review of sarcoptic mange in North American wildlife. International Journal for Parasitology: Parasites and Wildlife, 9, 285–297. doi: 10.1016/j.ijppaw.2019.06.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ostrander EA, Davis BW, & Ostrander GK (2016). Transmissible tumors: breaking the cancer paradigm. Trends in Genetics, 32(1), 1–15. doi: 10.1016/j.tig.2015.10.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paquette SR, Talbot B, Garant D, Mainguy J, & Pelletier F.(2014). Modelling the dispersal of the two main hosts of the raccoon rabies variant in heterogeneous environments with landscape genetics. Evolutionary Applications, 7(7), 734–749. doi: 10.1111/eva.12161 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pemberton D.(1990). Social organisation and behaviour of the Tasmanian devil, Sarcophilus harrisii. PhD Thesis, University of Tasmania. [Google Scholar]
- Peterman WE (2018). ResistanceGA: an R package for the optimization of resistance surfaces using genetic algorithms. Methods in Ecology and Evolution, 9(6), 1638–1647. doi: 10.1111/2041-210X.12984 [DOI] [Google Scholar]
- Petren K, Grant PR, Grant BR, & Keller LF (2005). Comparative landscape genetics and the adaptive radiation of Darwin’s finches: the role of peripheral isolation. Mol Ecol, 14(10), 2943–57. doi: 10.1111/j.1365-294X.2005.02632.x [DOI] [PubMed] [Google Scholar]
- Pike RJ, & Wilson SE (1971). Elevation-relief ratio, hypsometric integral, and geomorphic area-altitude analysis. Geological Society of America Bulletin, 82(4), 1079–1084. [Google Scholar]
- Pritchard JK, Stephens M, & Donnelly P.(2000). Inference of population structure using multilocus genotype data. Genetics, 155(2), 945–959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pye RJ, Pemberton D, Tovar C, Tubio JMC, Dun KA, Fox S, … Woods GM (2016). A second transmissible cancer in Tasmanian devils. Proceedings of the National Academy of Sciences, 113(2), 374–379. doi: 10.1073/pnas.1519691113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quinlan AR, & Hall IM (2010). BEDTools: a flexible suite of utilities for comparing genomic features. Bioinformatics, 26(6), 841–842. doi: 10.1093/bioinformatics/btq033 [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Development Core Team. (2013). R: A language and environment for statistical computing. R Foundation for Statistical Computing. [Google Scholar]
- Riley SPD, Pollinger JP, Sauvajot RM, York EC, Bromley C, Fuller TK, & Wayne RK (2006). A southern California freeway is a physical and social barrier to gene flow in carnivores. Molecular Ecology, 15(7), 1733–1741. doi: 10.1111/j.1365-294X.2006.02907.x [DOI] [PubMed] [Google Scholar]
- Robinson SJ, Samuel MD, Rolley RE, & Shelton P.(2013). Using landscape epidemiological models to understand the distribution of chronic wasting disease in the Midwestern USA. Landscape Ecology, 28(10), 1923–1935. doi: 10.1007/s10980-013-9919-4 [DOI] [Google Scholar]
- Save the Tasmanian Devil Programme. (2019). About DFTD. Retrieved November 8, 2019, from https://dpipwe.tas.gov.au/wildlife-management/save-the-tasmanian-devil-program/about-dftd
- Schwabl P, Llewellyn MS, Landguth EL, Andersson B, Kitron U, Costales JA, … Grijalva MJ (2017). Prediction and prevention of parasitic diseases using a landscape genomics framework. Trends in Parasitology, 33(4), 264–275. doi: 10.1016/j.pt.2016.10.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartz R, & Schäffer AA (2017). The evolution of tumour phylogenetics: principles and practice. Nature Reviews Genetics, 18(4), 213–229. doi: 10.1038/nrg.2016.170 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spear SF, Balkenhol N, Fortin M-J, McRae BH, & Scribner K.(2010). Use of resistance surfaces for landscape genetic studies: considerations for parameterization and analysis. Mol Ecol, 19(17), 3576–3591. doi: 10.1111/j.1365-294X.2010.04657.x [DOI] [PubMed] [Google Scholar]
- Stammnitz MR, Coorens THH, Gori KC, Hayes D, Fu B, Wang J, … Murchison EP (2018). The origins and vulnerabilities of two transmissible cancers in Tasmanian devils. Cancer Cell, 33(4), 607–619.e15. doi: 10.1016/j.ccell.2018.03.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Storfer A, Epstein B, Jones M, Micheletti S, Spear SF, Lachish S, & Fox S.(2017). Landscape genetics of the Tasmanian devil: implications for spread of an infectious cancer. Conservation Genetics, 18(6), 1287–1297. doi: 10.1007/s10592-017-0980-4 [DOI] [Google Scholar]
- Storfer A, Murphy MA, Evans JS, Goldberg CS, Robinson S, Spear SF, … Waits LP (2007). Putting the “landscape” in landscape genetics. Heredity, 98(3), 128–142. doi: 10.1038/sj.hdy.6800917 [DOI] [PubMed] [Google Scholar]
- Talbot B, Garant D, Paquette SR, Mainguy J, & Pelletier F.(2012). Lack of genetic structure and female-specific effect of dispersal barriers in a rabies vector, the striped skunk (Mephitis mephitis). PLoS One, 7(11), e49736. doi: 10.1371/journal.pone.0049736 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Talbot B, Vonhof MJ, Broders HG, Fenton B, & Keyghobadi N.(2017). Comparative analysis of landscape effects on spatial genetic structure of the big brown bat and one of its cimicid ectoparasites. Ecology and Evolution, 7(20), 8210–8219. doi: 10.1002/ece3.3329 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trumbo DR, Spear SF, Baumsteiger J, & Storfer A.(2013). Rangewide landscape genetics of an endemic Pacific northwestern salamander. Molecular Ecology, 22(5), 1250–1266. doi: 10.1111/mec.12168 [DOI] [PubMed] [Google Scholar]
- van Etten J.(2017). R Package gdistance: distances and routes on geographical grids. Journal of Statistical Software, 76(13). doi: 10.18637/jss.v076.i13 [DOI] [Google Scholar]
- Van Rossum G, & Drake FL Jr (1995). Python reference manual. Centrum voor Wiskunde en Informatica Amsterdam.
- Van Strien MJ, Keller D, & Holderegger R.(2012). A new analytical approach to landscape genetic modelling: least-cost transect analysis and linear mixed models. Molecular Ecology, 21(16), 4010–4023. doi: 10.1111/j.1365-294X.2012.05687.x [DOI] [PubMed] [Google Scholar]
- Vander Wal E, Edye I, Paquet PC, Coltman DW, Bayne E, Brook RK, & Andres JA (2013). Juxtaposition between host population structures: implications for disease transmission in a sympatric cervid community. Evolutionary Applications, 6(7), 1001–1011. doi: 10.1111/eva.12065 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang IJ, & Bradburd GS (2014). Isolation by environment. Molecular Ecology, 23(23), 5649–5662. doi: 10.1111/mec.12938 [DOI] [PubMed] [Google Scholar]
- Whiteley AR, Fitzpatrick SW, Funk WC, & Tallmon DA (2015). Genetic rescue to the rescue. Trends in Ecology & Evolution, 30(1), 42–49. doi: 10.1016/j.tree.2014.10.009 [DOI] [PubMed] [Google Scholar]
- Wilber MQ, Johnson PTJ, & Briggs CJ (2020). Disease hotspots or hot species? Infection dynamics in multi-host metacommunities controlled by species identity, not source location. Ecology Letters. doi: 10.1111/ele.13518 [DOI] [PMC free article] [PubMed]
- Wilder AP, Kunz TH, & Sorenson MD (2015). Population genetic structure of a common host predicts the spread of white-nose syndrome, an emerging infectious disease in bats. Molecular Ecology, 24(22), 5495–5506. doi: 10.1111/mec.13396 [DOI] [PubMed] [Google Scholar]
- Witsenburg F, Clément L, López-Baucells A, Palmeirim J, Pavlinić I, Scaravelli D, … Christe P.(2015). How a haemosporidian parasite of bats gets around: the genetic structure of a parasite, vector and host compared. Molecular Ecology, 24(4), 926–940. doi: 10.1111/mec.13071 [DOI] [PubMed] [Google Scholar]
- Wright S.(1943). Isolation by distance. Genetics, 28, 114–138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zancolli G, Rödel MO, Steffan-Dewenter I, & Storfer A.(2014). Comparative landscape genetics of two river frog species occurring at different elevations on Mount Kilimanjaro. Molecular Ecology, 23(20), 4989–5002. doi: 10.1111/mec.12921 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Devil and tumor sequence data have been deposited under NCBI BioProjects PRJNA306495, PRJNA634071, and PRJNA641648. Sample accession numbers and sample locations are provided in Supporting Information.