Abstract
Computational, in silico prediction of resistance-conferring escape mutations could accelerate the design of therapeutics less prone to resistance. This article describes how to use the Resistor algorithm to predict escape mutations. Resistor employs Pareto optimization on four resistance-conferring criteria—positive and negative design, mutational probability, and hotspot cardinality—to assign a Pareto rank to each prospective mutant. It also predicts the mechanism of resistance, that is, whether a mutant ablates binding to a drug, strengthens binding to the endogenous ligand, or a combination of these two factors, and provides structural models of the mutants. Resistor is part of the free and open-source computational protein design software OSPREY.
Keywords: cancer, mutation, OSPREY, Pareto, resistance, RESISTOR
1. INTRODUCTION
Resistance to drugs is a major public health challenge affecting antibiotic (Centers for Disease Control and Prevention, 2020; Pang et al, 2019), antiviral (Bar-On et al, 2018; Lampejo, 2020; Li and Chung, 2019), antifungal (Du et al, 2020; Hendrickson et al, 2019), and antineoplastic therapies (Assaraf et al, 2019; Hanna and Balko, 2021; Housman et al, 2014). Algorithms that accurately predict, early in the challenging drug development and approval process, the kinds of resistance that will occur could aid medicinal chemists in developing more durable therapies with longer effective lifespans (Frey et al, 2010; Kaserer and Blagg, 2018; Reeve et al, 2015). To that end, we have developed a new algorithm named Resistor to predict resistance mutations (Guerin et al, 2022a).
2. METHODS
Resistor combines structural and genomic data to predict which protein residues, when mutated, may confer resistance. The structural component consists of positive and negative affinity designs. Positive design refers to optimizing an amino acid sequence to improve binding between a protein and its ligand, and conversely, negative design to optimizing a sequence to ablate binding. Resistor models both positive and negative design because resistance can occur when a mutation increases binding between a protein and its endogenous ligand or ablates binding between a protein and its drug (or a combination of these two factors). The algorithms for positive and negative design, and their implementations, are discussed in Frey et al (2010), Reeve et al (2015), Ojewole et al (2018), Jou et al (2016, 2020), Hallen and Donald (2016), Lilien et al (2005), Hallen et al (2018), and Donald (2011). Resistor computes how mutations affect binding affinity using the algorithm.
is an -accurate algorithm implemented in OSPREY for computing a provable approximation to the affinity constant Ka (Hallen et al, 2018; Lilien et al, 2005). is defined as the quotient of the bound over unbound partition functions of a protein:ligand system for a given amino acid sequence. calculates an -accurate prediction for the Ka quotient and the partition functions of three structural states: the bound protein:ligand complex (denoted PL), the unbound protein (denoted P), and the unbound ligand (denoted L). Let X be a state, . The partition function is a sum of the Boltzmann-weighted energies for all conformations in the thermodynamic ensemble of X. Let s denote an amino acid sequence, then the partition function of s in state X (which we donate as ) is:

where is the entire conformational ensemble of sequence s in state X, and c is a single conformation in that ensemble. is the energy of conformation c as computed by an energy function (Hallen et al, 2018). R is the ideal gas constant and T is the temperature in absolute Kelvin. By using search with iMinDEE over to enumerate an ordered gap-free sequence of lower bounds on conformational energies (Georgiev et al, 2008), the algorithm generates an -approximation of the partition function . This allows the score for a sequence s to approximate Ka:
| (2) |
There are a number of algorithms that implement the computation of the score in OSPREY, including iMinDEE (Georgiev et al, 2008), (Ojewole et al, 2018), and (Jou et al, 2020). These three aforementioned algorithms all employ continuous minimized rotamers.
The genomic component of Resistor exploits mutational signatures derived from whole genome and whole exome sequencing of cancers (Alexandrov et al, 2020, 2013). A mutational signature is a distribution representing the probability that one nucleotide will mutate to another nucleotide in a given codon context and particular cancer type (Alexandrov et al, 2013). The different signatures are a result of diverse mutational processes (Alexandrov et al, 2013), and different cancer types are associated with one or more mutational signatures. And although a cancer type is associated with a set of signatures, not every associated signature is found in all tumor samples of a particular cancer type. We use these empirical mutational signature data to calculate the probability that an amino acid's codon mutates to another amino acid.
Specifically, let C be the set of cancers and S the set of mutational signatures, with and . We denote the set of signatures operative in a particular cancer c as Sc, and the proportion of tumor samples in c exhibiting signature s as . Let D be the set of amino acid-encoding codons and A the set of amino acids, with and . We denote the set of codons encoding amino acid a as Da. Last, we denote Z as the set of ways that d can mutate to any within two single mutational events. Then to calculate the probability that codon d mutates to amino acid a we compute:
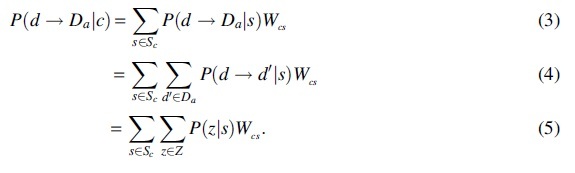
We determine Z for all amino acids and compute the values using a recursive graph algorithm. For this, we construct a directed graph for each mutational signature where the vertices v are codons and edges e connect codons that differ by their center base. The weight assigned to each edge e is the probability of one codon mutating to another codon, as provided in Alexandrov et al (2013). The input codon d must contain two flanking bases to lookup the probability of the first or last base of the codon mutating. Inputs to the algorithm are G, d, the path probability , and the max number of mutational steps (n). The algorithm enumerates all possible single point mutations in d in a function called step_codon. It looks up the probability of mutating from the current codon to the next codon using G and recursively calls itself n times. When the terminating condition is met the algorithm returns the set of codons it reached in steps and their probabilities. See Algorithm 1 for pseudocode of the algorithm.
3. HOW TO USE RESISTOR TO PREDICT RESISTANCE MUTATIONS
In this section, we describe how a medicinal chemist could use Resistor in OSPREY to predict resistance mutations.
Algorithm 1: calc_probs computes the complete set of paths that can be reached within n mutational steps from codon. The parameter path_prob is the probability of reaching the current codon via a particular path. After calc_probs is executed, the codons reached by all paths and their associated probabilities are in the paths variable. The codons in this variable are then grouped and summed by the amino acid they encode (omitted below). The initial invocation of calc_probs initializes path_prob to 1. The step_codon function produces all 9 variants of a codon with a single mutated base. paths def cal_probs (codon, path_prob, G, n): if n = 0: return for next_codon in step_codon(codon): mutational_prob G [codon, next_codon] next_prob path_prob * mutational_prob push(paths, (next_codon, next_prob)) calc_probs(next_codon, next_prob, G, n − 1)
3.1. Inputs to RESISTOR
There are a number of requisite inputs to running Resistor. First, two structural models of a protein must be obtained, one with the protein binding the endogenous ligand (for the positive design) and one with the drug (for the negative design), preferably from the Protein Databank (Berman et al, 2003) if experimentally determined models are available. If models are lacking, it is possible to use docking, homology modeling, or other computational modeling techniques to generate structures (Frey et al, 2010; Guerin et al, 2022a; Reeve et al, 2015; Roberts et al, 2012; Wang et al, 2022). The structures must be protonated, and if small molecules are used, their connectivity templates and forcefield parameters must be generated using Ambertools (Case et al, 2021). A detailed instructional example is included in the Supplementary Information from Guerin et al (2022b).
We have added a new YAML-based design specification file format to OSPREY to simplify the process of performing a computational mutational scan and computing scores. In searching for resistance mutations, we are often interested in interrogating all residues within a certain radius (called the mutational radius) from the drug or endogenous ligand. A mutational scan allows one to specify a target molecule or residue, a mutational radius, and a flexibility radius. Executing the scan generates a set of complete, ready-to-run OSPREY design files.
These design specification files are also in YAML format, and a separate file is generated per residue within the mutational radius. The mutational scan automatically sets all residues within the flexibility radius of the mutable residue as continuously flexible [see Gainza et al (2012) for background on the importance of continuous flexibility]. The scan can be used to generate a design file for each residue of interest for both the positive and negative design states. These design files are used as input to the affinity command in OSPREY to compute the score.
3.2. Running RESISTOR
This section describes how to create the design template, do the mutational scan, and then run the individual OSPREY designs. All of the following code snippets are typed into a Unix shell.
3.2.1. Create the design template
First create the design template file. This file is a simplified version of the affinity design file type omitting the specification of flexibility or mutability in the protein or ligand. In other words, the residue_configurations properties of the protein and ligand objects in the design file must be empty lists. Copy the protein and ligand coordinates into the template file. Then add a new top-level property called scan. Under the scan property add a target property, and set that property to the ligand. Then the following command creates the set of designs (substitute your template file for template.yaml):
| osprey affinity –do-scan –design |
You need to do this for two structures: the protein interacting with its endogenous ligand (the positive design) and the protein with its drug (the negative design).
3.2.2. Compute the positive and negative scores
After the mutational scan has created the positive and negative design files, run the OSPREY algorithm on each. There are a number of different options you can select, such as the –cuda flag to accelerate the energy function calculations if your computer has CUDA-capable GPUs, and the –epsilon flag to specify the accuracy of the approximation [we showed in Ojewole et al (2018) that of 0.683 guarantees that the approximated score is within one order of magnitude of the score without approximation]. The following is just an example; run osprey affinity–help for the full list of options.
| osprey affinity \ |
| –design |
| –epsilon 0.683 |
| –cuda |
3.2.3. Compute the mutational probabilities
Create a CSV file with three columns: the residue number, the wild-type amino acid, and the mutant amino acid. Do this for each of the wild-type+mutant pairs. Assuming you have downloaded the OSPREY source code, run the following command to add a mutational probabilities column:
| julia –project = . main.jl \ |
| –mut-prob |
| –fasta |
| –identifier |
| –csv |
The –mut-prob argument should be a path to a JSON file. This JSON file contains a JSON object with the per-cancer type codon-to-codon mutational probabilities [see the Supplementary Information from Guerin et al (2022b) for the precise form]. The –fasta argument should be provided a path to a FASTA file with the coding DNA for the protein. Since FASTA files can contain multiple sequences, the –identifier argument must contain the sequence identifier of the sequence of interest (viz. the text following the “>” from the header/description line). The –csv argument should be the path to the 3-column CSV file created earlier. This program outputs a new CSV file with the added mutational probability column.
3.2.4. Run pareto optimization
The last step is to run Pareto optimization on the four axes. Append the scores associated with the positive and negative design results to the spreadsheet produced in Section 3.2.3. Create a JSON file with the names of the column headings and whether a column must be maximized or minimized [see the Supplementary Information from Guerin et al (2022b) for the precise form]. The following command will append a column with the Pareto rank of each sequence:
| julia –project = . main.jl |
where the first argument CSV-file refers to the input CSV file and the second argument pareto-settings refers to the JSON settings file you created earlier.
3.3. Interpreting the results to predict resistance mutants
The results of Resistor are in tabular form. Table 1 is excerpted from a result set from Guerin et al (2022a). The results are listed in order of the Pareto Rank, with those with rank 1 being on the Pareto frontier. The Sig Prob, Lig WT, Lig Mut, Drug WT, Drug Mut, and count columns can be used to interpret the different contributions to a mutant's Pareto rank.
Table 1.
Example Resistor Resistance Mutation Predictions
| Pos | WT AA | Mut AA | Sig Prob | Lig WT | Lig Mut | Drug WT | Drug Mut | Count | Rank |
|---|---|---|---|---|---|---|---|---|---|
| 593 | GLY | ILE | 4.55E-05 | 18.66 | 19.8 | 37.17 | 30.24 | 16 | 1 |
| 593 | GLY | SER | 6.09E-02 | 18.66 | 18.83 | 37.17 | 34.27 | 16 | 1 |
| 466 | GLY | GLN | 7.24E-05 | 18.80 | 12.55 | 37.16 | 11.37 | 11 | 2 |
| 593 | GLY | THR | 2.67E-05 | 18.66 | 19.06 | 37.17 | 27.33 | 16 | 2 |
| 464 | GLY | GLN | 7.24E-05 | 18.58 | 2.95 | 37.09 | 11.05 | 1 | 3 |
“Pos” is the position of the residue. “WT AA” is the wild-type identity of the amino acid. “Mut AA” is the resistance mutation. “Sig Prob” is the mutational signature probability for the mutation from “WT AA” to “Mut AA.” “Lig WT” and “Lig Mut” are the scores of the endogenous ligand with the wild-type and mutant residues, respectively. “Drug WT” and “Drug Mut” are the scores of the drug with the wild-type and mutant residues, respectively. “Count” is number of resistance mutations at the position. “Rank” is the Pareto rank of the mutation. Note: scores are in units.
4. SUMMARY
We provide Resistor to predict and prioritize resistance mutations for therapeutic design. Although we have incorporated four resistance-causing criteria, Resistor's use of Pareto optimization as a general method for ranking prospective mutants allows the incorporation of additional criteria. As free and open-source software, we encourage others investigating therapeutic resistance to incorporate and contribute additional objective functions into Resistor. Potential future applications include predicting resistance to antimicrobials (Frey et al, 2010; Reeve et al, 2015), antivirals, antifungals, and other antineoplastic therapies.
A comprehensive tutorial demonstrating an application of Resistor to predict resistance mutations in the epidermal growth factor receptor to the tyrosine kinase inhibitor erlotinib is provided in the Supplementary Information in Guerin et al (2022b). OSPREY with Resistor, installation instructions, additional documentation, and tutorials are available on the OSPREY software suite's website,* and further discussions on OSPREY and structure-based computational protein design can be found in Hallen et al (2018) and Donald (2011).
ACKNOWLEDGMENTS
We thank all members of the Donald Lab for helpful discussions. This article was not previously submitted to a preprint server.
AUTHORs' CONTRIBUTIONS
NG: Conceptualization, Methodology, Software, Validation, Writing: Original Draft. TK: Conceptualization, Methodology, Validation, Writing: Review and Editing, Funding Acquisition. BRD: Conceptualization, Methodology, Writing: Review and Editing, Supervision, Project Administration, Funding Acquisition.
AUTHOR DISCLOSURE STATEMENT
B.R.D. is a founder of Ten63 Therapeutics, Inc.
FUNDING INFORMATION
B.R.D. and N.G.'s contributions to this study were funded by the NIH (Grant Nos. R01-GM078031, R01-GM118543, and R35-GM144042 to B.R.D.). T.K. was funded in whole, or in part, by the Austrian Science Fund (FWF) P34376. For the purpose of open access, the authors have applied a CC-BY public copyright license to any Author Accepted Manuscript version arising from this submission.
REFERENCES
- Alexandrov LB, Kim J, Haradhvala NJ, et al. The repertoire of mutational signatures in human cancer. Nature 2020;578(7793):94–101; doi: 10.1038/s41586-020-1943-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alexandrov LB, Nik-Zainal S, Wedge DC, et al. Signatures of mutational processes in human cancer. Nature 2013;500(7463):415–421; doi: 10.1038/nature12477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Assaraf YG, Brozovic A, Goncalves AC, et al. The multi-factorial nature of clinical multidrug resistance in cancer. Drug Resist Updates 2019;46:100645; doi: 10.1016/j.drup.2019.100645. [DOI] [PubMed] [Google Scholar]
- Bar-On Y, Gruell H, Schoofs T, et al. Safety and antiviral activity of combination hiv-1 broadly neutralizing antibodies in viremic individuals. Nat Med 2018;24(11):1701–1707; doi: 10.1038/s41591-018-0186-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berman H, Henrick K, Nakamura H.. Announcing the worldwide protein data bank. Nat Struct Mol Biol 2003;10(12):980; doi: 10.1038/nsb1203-980. [DOI] [PubMed] [Google Scholar]
- Case DA, Belfon K, Ben-Shalom I, et al. Amber 2021, University of California, San Francisco. 2021. [Google Scholar]
- Centers for Disease Control and Prevention. Antibiotic/antimicrobial resistance. Available from: https://www.cdc.gov/drugresistance/index.html Last viewed July 2020. [Google Scholar]
- Donald BR. Algorithms in Structural Molecular Biology. MIT Press, Cambridge, Massachusetts and London, England; 2011. [Google Scholar]
- Du H, Bing J, Hu T, et al. Candida auris: Epidemiology, biology, antifungal resistance, and virulence. PLoS Pathogens 2020;16(10):e1008921; doi: 10.1371/journal.ppat.1008921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frey KM, Georgiev I, Donald BR, et al. Predicting resistance mutations using protein design algorithms. Proc Natl Acad Sci 2010;107(31):13707–13712; doi: 10.1073/pnas.1002162107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gainza P, Roberts KE, Donald BR. Protein design using continuous rotamers. PLoS Comput Biol 2012;8(1):e1002335; doi: 10.1371/journal.pcbi.1002335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Georgiev I, Lilien RH, Donald BR. The minimized dead-end elimination criterion and its application to protein redesign in a hybrid scoring and search algorithm for computing partition functions over molecular ensembles. J Comput Chem 2008;29(10):1527–1542; doi: 10.1002/jcc.20909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guerin N, Feichtner A, Stefan E, et al. Resistor: An algorithm for predicting resistance mutations using pareto optimization over multistate protein design and mutational signatures. Cold Spring Harbor; 2022a; doi: 10.1101/2022.01.18.476733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guerin N, Kaserer T, Donald BR. Supplementary Information: Resistor: An Algorithm for Predicting Resistance Mutations Using Pareto Optimization Over Multistate Protein Design and Mutational Signatures; 2022b. Available from: www.cs.duke.edu/donaldlab/Supplementary/jcb22/ [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hallen MA, Donald BR. Comets (constrained optimization of multistate energies by tree search): A provable and efficient protein design algorithm to optimize binding affinity and specificity with respect to sequence. J Comput Biol 2016;23(5):311–321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hallen MA, Martin JW, Ojewole A, et al. Osprey 3.0: Open-source protein redesign for you, with powerful new features. J Comput Chem 2018;39(30):2494–2507; doi: 10.1002/jcc.25522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanna A, Balko JM. Breast cancer resistance mechanisms: Challenges to immunotherapy. Breast Cancer Res Treat 2021;190(1):5–17; doi: 10.1007/s10549-021-06337-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hendrickson JA, Hu C, Aitken SL, et al. Antifungal resistance: A concerning trend for the present and future. Curr Infect Dis Rep 2019;21(12):1–8; doi: 10.1007/s11908-019-0702-9. [DOI] [PubMed] [Google Scholar]
- Housman G, Byler S, Heerboth S, et al. Drug resistance in cancer: An overview. Cancers 2014;6(3):1769–1792; doi: 10.3390/cancers6031769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jou JD, Holt GT, Lowegard AU, et al. Minimization-aware recursive k*: A novel, provable algorithm that accelerates ensemble-based protein design and provably approximates the energy landscape. J Comput Biol 2020;27(4):550–564; doi: 10.1089/cmb.2019.0315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jou JD, Jain S, Georgiev IS, et al. Bwm*: A novel, provable, ensemble-based dynamic programming algorithm for sparse approximations of computational protein design. J Comput Biol 2016;23(6):413–424; doi: 10.1089/cmb.2015.0194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaserer T, Blagg J.. Combining mutational signatures, clonal fitness, and drug affinity to define drug-specific resistance mutations in cancer. Cell Chem Biol 2018;25(11):1359–1371; doi: 10.1016/j.chembiol.2018.07.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lampejo T. Influenza and antiviral resistance: An overview. Eur J Clin Microbiol Infect Dis 2020;39(7):1201–1208 doi: 10.1007/s10096-020-03840-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li DK, Chung RT. Overview of direct-acting antiviral drugs and drug resistance of hepatitis c virus. Humana Press, New York, NY. Hepatitis C Virus Protoc 2019;1911:3–32; doi: 10.1007/978-1-4939-8976-8_1. [DOI] [PubMed] [Google Scholar]
- Lilien RH, Stevens BW, Anderson AC, et al. A novel ensemble-based scoring and search algorithm for protein redesign and its application to modify the substrate specificity of the gramicidin synthetase a phenylalanine adenylation enzyme. J Comput Biol 2005;12(6):740–761; doi: 10.1089/cmb.2005.12.740. [DOI] [PubMed] [Google Scholar]
- Ojewole AA, Jou JD, Fowler VG, et al. Bbk*(branch and bound over k*): A provable and efficient ensemble-based protein design algorithm to optimize stability and binding affinity over large sequence spaces. J Comput Biol 2018;25(7):726–739; doi: 10.1089/cmb.2017.0267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pang Z, Raudonis R, Glick BR, et al. Antibiotic resistance in pseudomonas aeruginosa: Mechanisms and alternative therapeutic strategies. Biotechnol Adv 2019;37(1):177–192; doi: 10.1016/j.biotechadv.2018.11.013. [DOI] [PubMed] [Google Scholar]
- Reeve SM, Gainza P, Frey KM, et al. Protein design algorithms predict viable resistance to an experimental antifolate. Proc Natl Acad Sci 2015;112(3):749–754; doi: 10.1073/pnas.1411548112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roberts KE, Cushing PR, Boisguerin P, et al. Computational design of a pdz domain peptide inhibitor that rescues cftr activity. PLoS Comput Biol 2012;8(4):e1002477; doi: 10.1371/journal.pcbi.1002477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang S, Reeve SM, Holt GT, et al. Chiral evasion and stereospecific antifolate resistance in staphylococcus aureus. PLoS Comput Biol 2022;18(2):e1009855; doi: 10.1371/journal.pcbi.1009855. [DOI] [PMC free article] [PubMed] [Google Scholar]


