Abstract
We developed a novel method for efficiently estimating time-varying selection coefficients from genome-wide ancient DNA data. In simulations, our method accurately recovers selective trajectories and is robust to misspecification of population size. We applied it to a large data set of ancient and present-day human genomes from Britain and identified seven loci with genome-wide significant evidence of selection in the past 4500 yr. Almost all of them can be related to increased vitamin D or calcium levels, suggesting strong selective pressure on these or related phenotypes. However, the strength of selection on individual loci varied substantially over time, suggesting that cultural or environmental factors moderated the genetic response. Of 28 complex anthropometric and metabolic traits, skin pigmentation was the only one with significant evidence of polygenic selection, further underscoring the importance of phenotypes related to vitamin D. Our approach illustrates the power of ancient DNA to characterize selection in human populations and illuminates the recent evolutionary history of Britain.
Ancient DNA (aDNA) provides direct insight into human evolutionary history. So far, this information has mainly been used to study demographic history—the migrations, splits, and admixtures that humans experienced in the recent past (Skoglund and Mathieson 2018). But, in principle, aDNA can also tell us about phenotypic evolution and, in particular, about the contribution of natural selection to phenotypic and genomic variation. Compared with demographic inference, this is more challenging, because studies of natural selection typically require larger sample sizes than studies of population history, which can integrate information from across the genome.
Although some recent studies have used aDNA to study selection and phenotypic evolution, they have mostly focused on a relatively small number of loci (e.g., Wilde et al. 2014; Mathieson and Mathieson 2018; Kerner et al. 2021). Studies that performed genome-wide scans for selection using aDNA (Mathieson et al. 2015; Skoglund et al. 2017; Margaryan et al. 2020) have compared allele frequencies across populations but have not made use of the precise temporal information available from direct dating of ancient samples. For example, the approach of Mathieson et al. (2015) was able to detect selection that happened some time in the past 8000 yr, somewhere in Western Eurasia, but could not be more specific.
With the recent publication of large aDNA data sets (e.g., Olalde et al. 2019; Margaryan et al. 2020; Patterson et al. 2022), sample sizes for some regions are now in the hundreds of individuals, large enough to study selection with good spatial and temporal resolution. However, there is a lack of suitable methods to analyze these data. There are many published methods for estimating selection coefficients from time series data (e.g., Bollback et al. 2008; Malaspinas et al. 2012; Mathieson and McVean 2013; Feder et al. 2014; Lacerda and Seoighe 2014; Steinrücken et al. 2014; Terhorst et al. 2015; Tataru et al. 2017), but all of them unrealistically assume that selective pressures are constant over time, and most are too slow to run on millions of markers at once. We therefore developed a novel statistical approach that is able to estimate arbitrary time-varying selection coefficients while being fast enough to run genome-wide.
The population of Britain, from 4500 yr before present (BP; i.e., the start of the Bronze Age) to the present day is ideal to show this approach for several reasons. First, it is relatively homogeneous in terms of both genetics and environment. Second, it is the population with the largest aDNA sample size. Third, there is a large amount of data about the genetic basis of complex traits in this population owing to analysis of the UK Biobank. Finally, one of the few studies that attempted to detect selection over this time period (based on data from present-day individuals) was performed in this population (Field et al. 2016), giving us a point of comparison for our aDNA-based approach.
Methods
We begin by formally defining the data, the inference problem, and the model we used to solve it. Our model is a generalization of the one used by Mathieson and McVean (2013). We assume a haploid Wright–Fisher (WF) population model whose size t generations before present was 2Nt. Time runs backward, so that t = 0 is the present, and t = T is the earliest point where we have data. We are interested in the frequency of a single allele with two types A and a. In generation t, the a allele has relative fitness 1 + st/2 relative to A. Our inferential target is the vector of selection coefficients over time. The population size history (N0, …, NT) is also allowed to vary with time, but we assume that it is known and do not attempt to jointly estimate it with .
The data consist of pairs of counts . Each pair represents the number at of a alleles observed out of nt samples collected t generations ago. Missing data or generations where no sampling occurred are indicated by setting nt = 0. Our model conditions on the sample sizes nt, and we suppress notational dependence on them going forward.
The data-generating model is as follows. At time t, let the (unobserved) population frequency of the a allele be ft ∈ [0, 1]. Given ft, the data in generation t are binomially distributed with success probability ft:
| (1) |
The latent allele frequency trajectory evolves according to a WF model with genic selection and no mutation (e.g., Ewens 2004). Given ft and st, the number of individuals Ft−1 ∈ [0, 2Nt−1] possessing the a allele in next generation has distribution
| (2) |
and then we set ft−1 = Ft−1/(2Nt−1).
Let denote the data. The complete likelihood is
| (3) |
where πT(fT) is a prior distribution on the initial allele frequency (described in more detail below), and the probabilities and p(at|ft) are specified by Equations 1 and 2. (Throughout this section, we use the notation to denote probability distributions that depend on the selection parameters .) The likelihood of the observed data is obtained by marginalizing Equation 3 over :
| (4) |
By exploiting the Markov structure of Equation 3, the integral (4) can be efficiently evaluated using the forward algorithm. Each step of the forward algorithm costs owing to the need to evaluate the transition probability (2) for all possible values of ft−1 and ft. When the effective population size is large (greater than 103, say), this quadratic scaling causes computation to become slow, and it is advantageous to model the latent allele trajectory ft using a continuous approximation. Several have been proposed, including using the WF diffusion (Bollback et al. 2008; Malaspinas et al. 2012; Lacerda and Seoighe 2014; Steinrücken et al. 2014; Ferrer-Admetlla et al. 2016), Gaussian approximations to the WF model (Mathieson and McVean 2013; Feder et al. 2014; Lacerda and Seoighe 2014; Terhorst et al. 2015), and approximations based on the beta distribution (Tataru et al. 2015, 2017; Gompert 2016; see also Malaspinas 2016 and references therein). A recent review (Paris et al. 2019) found the beta-with-spikes (hereafter, bws) approximation of Tataru et al. (2017) to perform consistently better than other approaches, so we use it as our starting point.
In this model, the latent frequency ft ∈ [0, 1] of the selected allele is modeled as a mixture distribution with three components. There are two atoms at ft = 0 and ft = 1 to allow for the possibility of allele loss or fixation, and the third component is a beta density characterizing the intermediate frequencies, ft ∈ (0, 1). The form of this model is motivated by the fact that, in the original WF process, the probability of loss or fixation is positive, whereas it is zero if ft possesses an absolutely continuous density.
Although the bws model is state of the art, room for improvement remains. Paris et al. (2019) found that, although generally accurate, the bws approximation degrades when selection is strong and the effective population size is small. Crucially, we cannot necessarily rule such a regime out when analyzing aDNA data. Another potential shortcoming, not reported by Paris et al. (2019) but encountered when we implemented the bws model, concerns the method used to approximate the transition probability
| (5) |
We found that errors in the moment recursions used to compute these probabilities (Equations 6 onward of Paris et al. 2019) tended to accumulate, leading to numerical instability and situations in which the variance of the resulting beta approximation, or the spike probabilities, were sometimes computed to be negative (Python code illustrating this phenomenon is included as Supplemental Code S1). This led us to consider refinements of the bws model.
Beta mixture model
Breakdown of the moment-based approximation can be explained by insufficient degrees of freedom. The two-parameter beta distribution is not flexible enough to accurately approximate the density (5) in all cases. A potential solution is to enrich the approximating class of distributions, by modeling the continuous component of Equation 5 as a mixture of beta distributions. This solution is intuitive and also has theoretical justification: By a famous result of Bernstein (e.g., Feller 2008), it holds for any continuous function that
| (6) |
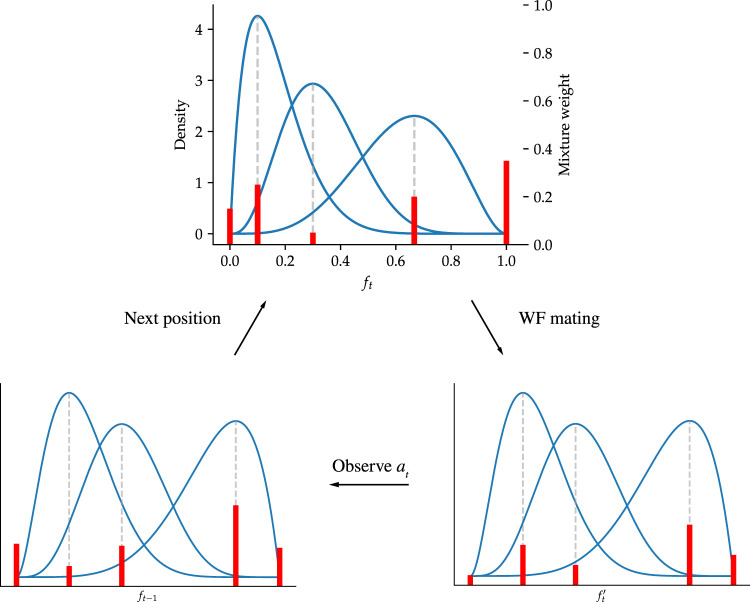
where bm,M is proportional to the Beta(m + 1, M − m + 1) density. Hence, by taking M on the right-hand side of Equation 6 to be large but finite, we can accurately approximate any absolutely continuous density on the unit interval. We refer to this model as the beta-mixture-with-spikes (bmws). A schematic of our model, which accompanies the discussion in the next few subsections, is shown in Figure 1.
Figure 1.
The bmws model. At each time step t, the latent allele frequency ft is modeled as a mixture of beta distributions, plus spikes at zero and one. In this diagram, there are M = 3 mixture components (blue lines). Mixture weights are indicated as red bars, including the spike weights p0 and p1 at ft = 0 and ft = 1, respectively. After Wright–Fisher (WF) mating, the shape of each beta mixture component, as well as the mixture weights, is updated according to Equation 15. After observing the data at, the mixture weights are again updated according to Bayes’ rule (Equation 16). The process then iterates.
Under bmws, the (posterior) density of ft is modeled as a mixture of M beta densities, plus two atoms at ft = 0 and ft = 1. We abuse notation slightly and write this as
| (7) |
where δx denotes a point mass at x, and M is a user-specified parameter that trades approximation accuracy for speed. To model allele frequency trajectories, we need to characterize the distribution of ft−1 when ft has the distribution (7). We follow earlier work in using a moment-based approximation; however, the form of approximation is new. Previously (e.g., Lacerda and Seoighe 2014; Terhorst et al. 2015; Tataru et al. 2017; Paris et al. 2019), the mean and variance of ft−1 were obtained by Taylor expansion about the infinite-population (zero variance) allele frequency trajectory, and then a moment-matched Gaussian or beta distribution was used to approximate the distribution of ft−1. Here we proceed differently, by directly modeling the action of the WF transition kernel on a beta-distributed random variable.
Assume first that , and let and ft−1 be as in Equation 2. Using a computer algebra system, we determined that
| (8) |
| (9) |
| (10) |
(A Mathematica notebook verifying these computations is included as Supplemental Code S2.) These approximations are obtained by Taylor expansion of about s = 0, followed by substituting in moments of the beta distribution. It would be easy to extend them to higher powers of s, but we did not find it necessary because |s| = 0.1 is already at the extreme end of what we expect to find in natural data. Note that for |s| < 1 (at least), the above equations imply , so this approximation is robust to the pathology described above.
Using Equations 8 through 10, we can find α′, β′ such that ft−1 has approximately a Beta(α′, β′) distribution:
| (11) |
| (12) |
| (13) |
The other components of the bmws model are the “spikes” at ft = 0 and ft = 1. They are handled similarly to the original bws model: At each mating event ft → ft−1, some amount of probability mass is leaked from the beta (mixture) component to atomic components, corresponding to the events Ft−1 = 0 and Ft−1 = 2Nt−1 in Equation 2 (see the next section for a precise statement).
More generally, suppose the continuous component of ft is a mixture, as in Equation 7. We make the following approximation in order to cheaply compute the conditional density of ft−1. Let Ct have the categorical distribution , and interpret Equation 7 hierarchically as
| (14) |
We assume that the continuous component of ft−1 is again a mixture of beta densities, with parameters obtained by applying Equations 11 through 13 with (specified by Equation 14) in place of . That is, we separately compute the effect of Equation 2 on each mixture component in Equation 7 and average the results together using the mixing weights . This “linear” approximation requires only computations and is much more efficient and easier to implement compared to modeling the effect of applying Equation 2 to the overall mixture shown in Equation 7. Although a closer approximation could be obtained by optimizing over the mixture weights , it would introduce additional computational expense and did not seem necessary in the examples we considered.
The astute reader will have noticed that, in contrast to some earlier works, we did not properly condition on nonfixation when constructing this approximation. That is, instead of, for example, in Equation 8, we should instead have considered
However, the resulting expressions are very complex because they involve taking expectation over terms of the form for k as high as 2Nt−1. We opted for the simpler and more numerically stable Equations 8 through 10 and confirmed in simulations that the model is still accurate across a range of parameter settings.
Likelihood
The likelihood (4) is calculated using a variant of the usual forward algorithm for hidden Markov models. We explain this computation in greater detail here because the approach is nonstandard.
The forward algorithm recursively updates the so-called filtering density p(ft|at, …, aT), which takes the form shown in Equation 7 under our model. Given the filtering density and the observation at−1, we need to extend the filtering density one step toward the present to obtain p(ft−1|at−1, …, aT). This is accomplished in stages:
- We use Equations 8 through 12 to compute and , as well as
and similarly for . This yields the predictive density
| (15) |
where we define .
- 2. We compute the probability
noting that the integral can be evaluated analytically using Equations 1 and 15 and conjugacy.
where the right-hand side is the p.m.f. The posterior weight on the atom at ft−1 = 1 is , and similarly for pt−1,0. The constant of proportionality in these equations is , calculated in step 2.
4. The filtering distribution takes the same form as Equation 7, with mixture weights as defined in the preceding step, and .
Recalling Equation 4, the log-likelihood of the data is then
| (17) |
The running time of this algorithm is , as opposed to the standard forward algorithm, which scales quadratically in M if it were to denote the number of hidden states in an HMM. This enables us to set M fairly large, ensuring that our model can flexibly approximate differently shaped filtering distributions.
Prior distribution
The filtering recursion is initialized by setting p(fT) = πT(fT), where πT is a prior on the ancestral allele frequency. When developing our method, we observed that the choice of prior affected the accuracy of inferences in the ancient past when analyzing aDNA data. This is because when the data are sparsely observed and allele counts are low, there is not enough data to overwhelm the prior in the early stages of the Markov chain. An uninformative choice of πT can falsely suggest that the selected allele experienced a large change in frequency, potentially generating a spurious signal of selection. To mitigate this effect, we adopted a coordinate-ascent approach in which we alternatively maximized the log-likelihood (17) with respect to (1) the selective trajectory and (2) the prior πT.
For the prior distribution, we assumed that and optimized over αT, βT. Although this choice of prior is not necessarily in the family of Beta(i + 1, n − i + 1) mixture densities that comprise the interpolation scheme (6), we can accurately approximate it (or any other choice of prior) by setting M large, setting , where is the prior's density function, and invoking the aforementioned Bernstein approximation theorem.
Inference
Given the probability model and approximations described in the preceding section, inference is now straightforward. Parameter estimation is performed as described in the previous section, with one additional modification. Depending on the quality and density of the data, many entries of may only be weakly resolved, and we also found it advantageous to add a regularization term. The objective function for all the analyses reported below was
| (18) |
where λ > 0 is a tuning parameter. The regularizer penalizes variation in , with larger values of λ shrinking all entries toward a single common value, s0 = · · · = sT. The number of mixture components for the bmws model was fixed to M = 100, and we performed three rounds of coordinate ascent. For all the examples in this paper, we assumed that the size history (N0, …, NT) is known, but coestimation of selection and size history is also possible using our method and could be an avenue for future research. Finally, our method is implemented using a JIT-compiled, differentiable programming language (https://github.com/google/jax) to allow for efficient, gradient-based fitting.
We use a parametric bootstrap to estimate the uncertainty in our inference. Specifically, after fitting the model, we sample allele frequency trajectories from the posterior distribution (Equation 7). We then sample observations conditional on the trajectory and the original sample sizes and times, and refit the model to those observations. We repeat this 1000 times and use the central 95% of results (based on the mean value of ) as an estimate of the 95% credible interval for , taking into account the uncertainty in the allele frequency trajectory and the sampling of observations.
Simulations
We evaluated the performance of the estimator under three different types of selection, each lasting for T = 100 generations:
Constant selection with s = 0.01 and initial frequency of 0.1;
Selection that decreases sinusoidally from s = +0.02 to s = −0.02 and initial frequency of 0.1; and
Selection that alternates between +0.02 and −0.02 every 20 generations and initial frequency of 0.5.
In each case, we simulated allele frequency trajectories in a WF population with N = 104 and then sampled 100 haploid individuals every 10 generations. We also simulated the same selective models under two scenarios of variable effective population size:
Exponential growth from N = 104 to N = 105; and
N = 104 with a bottleneck of N = 103 lasting 10 generations.
For these scenarios, we ran the estimator both with the correct effective population size and incorrectly, assuming a constant N = 104 to evaluate its robustness to misspecification of N. We varied the smoothing parameter λ from log10(λ) = 1 to 6 and report the root mean squared (RMS) bias, variance, and total error of the estimator. Finally, we evaluated the error of the estimator as the sample size and frequency vary.
These simulations explore the effects of relatively strong selection with human-like demographic parameters (N = 104, 100 generations of observations, bottlenecks, and exponential growth; selection coefficients of )). However, other species may have very different sets of parameters. We therefore recommend that for any particular application, users should run simulations based on their prior parameter values in order to understand the behavior of the estimator in their specific case and to determine the appropriate smoothing parameter. We provide functions to easily implement simulations under arbitrary selective and population size scenarios. To illustrate this approach, we also ran the simulations described above using the sampling distribution of the British aDNA data used in the rest of paper.
aDNA data
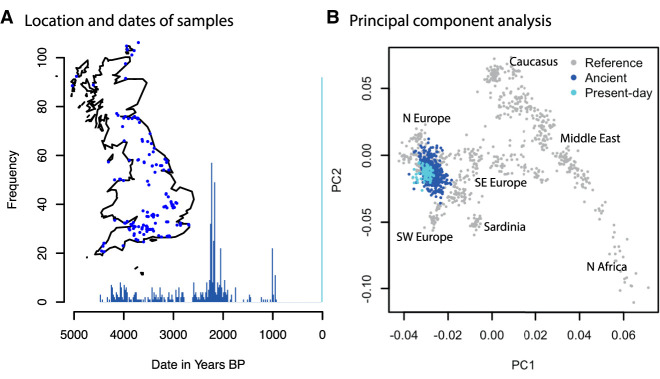
We collected data from ancient British individuals dated to the past 4500 yr from the Allen Ancient DNA Resource (AADR version 44.3, https://reich.hms.harvard.edu/allen-ancient-dna-resource-aadr-downloadable-genotypes-present-day-and-ancient-dna-data) and from original sources (Martiniano et al. 2016; Schiffels et al. 2016; Olalde et al. 2018; Brace et al. 2019; Margaryan et al. 2020; Patterson et al. 2022). Most samples had been sequenced at sites targeted using the 1240k in-solution capture reagent, and the small number of shotgun samples had been genotyped at the 1240k SNPs so we therefore restricted our analysis to this set of SNPs. All data were pseudohaploid. After removing 22 PCA outliers, we were left with 529 ancient individuals and 98 present-day individuals from the GBR population of the 1000 Genomes Project (The 1000 Genomes Project Consortium 2015), processed into pseudohaploid data as part of the AADR (Fig. 2A).
Figure 2.
Ancient British data. (A) Histogram of dates of ancient individuals. Inset map shows locations of sites. (B) Principal components of ancient and present-day samples projected onto axes defined by 777 West Eurasian individuals (for details of these individuals, see Lazaridis et al. 2014).
Our method assumes that samples are drawn from a closed, randomly mating population in which every individual experiences the same selective pressures. Although no natural population satisfies these conditions, we chose to restrict to Britain dated in the period 4500 BP to present because it is the largest aDNA sample from a time and region that comes close to satisfying the assumptions of the model for the following reasons. First, Britain is a relatively small region (compared with previous Europe-wide studies), meaning that selective pressures are more likely to be shared. Second, we know from previous aDNA studies that the last major change in ancestry in Britain occurred around 4500 BP (Olalde et al. 2018). Although recent work has shown more recent Bronze Age migrations into Britain (Patterson et al. 2022), these involved populations that were genetically similar and inhabited geographically adjacent regions. Third, we confirmed using principal component analysis (PCA) that all the ancient samples in our analysis clustered with the present-day British individuals from the 1000 Genomes Project and, more broadly, with other Northwestern European individuals in the context of present-day West Eurasia (Fig. 2B).
aDNA analysis
Starting with 1,150,639 autosomal SNPs, we removed 428,624 with a minor allele frequency (MAF) < 0.1 in the full data set on the grounds that any SNP with a significant frequency shift in this time period would have intermediate MAF. We also removed 101,967 SNPs with >90% missingness and 210,725 SNPs with MAF = 0 in the ancient data to leave 409,232 SNPs genome-wide. We inferred selection coefficients at generation t for every SNP in the filtered data using a smoothing parameter of λ = 104.5 and an effective population size of N = 104. For each SNP, we summarize this estimate by the mean selection coefficient and the RMS selection coefficient . We then computed the mean value of in 20-SNP sliding windows, sliding in 10-SNP increments, so each SNP contributes to two windows. We denote these window statistics as 20. Finally, we fit a gamma distribution using the method of moments to the values of 20 and used this fitted distribution to compute P-values for each window. We therefore calibrate the test statistics to the genome-wide background, analogous to the use of genomic control to account for genetic drift in association studies. We confirmed that this procedure leads to well-calibrated P-values when there is no temporal change in allele frequencies by repeating the analysis with the dates of each sample randomized.
We compared our results with two previous genome-wide selection scans. The first—an aDNA-based scan (Mathieson et al. 2015)—is an allele frequency scan to detect selection in approximately the past 8000 yr in Western Eurasia. The second, the SDS test (Field et al. 2016), is a scan based on haplotype lengths in the present-day United Kingdom population and is most sensitive to selection in the past few 1000 yr. First, we restricted the previous scans to the same set of SNPs used in the present scan. Next, for each window in the present scan, we computed the mean test statistics (chi-squared statistic for the aDNA scan and squared Z-score for the SDS) in each window and compared them with the test statistics generated by our method.
Polygenic selection test
We obtained summary statistics from genome-wide association studies (GWAS) for 28 quantitative traits (Taal et al. 2012; Wood et al. 2014; Horikoshi et al. 2016; Chen et al. 2021; http://www.nealelab.is/uk-biobank). We took the intersection of GWAS SNPs with the 1240k SNPs, restricted to P-values < 10−4, and pruned to an independent set of SNPs by iteratively taking the SNP with the smallest P-value and removing all other SNPs within 250 kb. For each trait, we calculated the correlation between effect size and estimated selection coefficient for each independent SNP.
Results
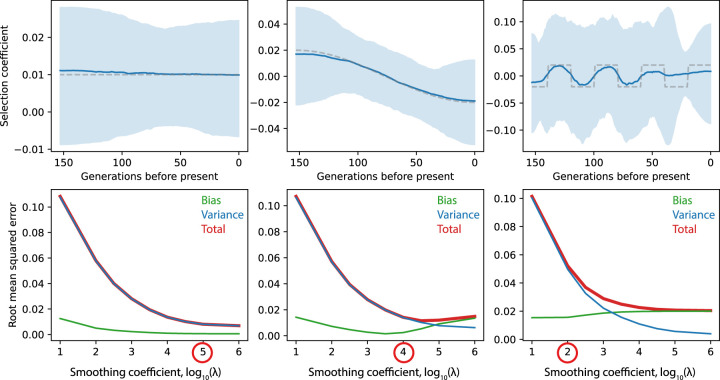
Our estimator successfully recovers complex selection trajectories from simulated data (Fig. 3), with total sample sizes and times equal to the ancient sample, although individual selection coefficient estimates can have considerable uncertainty—on the order of ±0.01 − 0.02 with these parameter values. This suggests that with the data available we should be able to reliably detect selection coefficients around 0.02, similar to the SDS and aDNA allele frequency approaches that we compare to our method (Mathieson et al. 2015; Field et al. 2016). The absolute error of the estimate does not depend on the selection coefficient, meaning that, at least in this parameter range, we cannot reliably distinguish smaller selection coefficients from zero. As expected, the optimal smoothing parameter depends on the true selective trajectory: the smoother the trajectory, the higher the optimal λ (Supplemental Fig. S1). We therefore recommend choosing λ based on simulations, with parameters that are informed by the specific application.
Figure 3.
Simulation results for the sampling distribution of the ancient British data. Each column shows a different selection coefficient trajectory. (Top) Estimated selection coefficients. Dashed line indicates simulated selection coefficient; solid blue line, mean selection coefficient from 1000 simulations; and light blue shaded area, region containing point estimates from 950/1000 simulations. (Bottom) Square root of squared bias, variance, and total squared error as a function of log10(λ). The circled value is the one used for the estimates in the top row.
The estimator performs similarly in the presence of population size bottlenecks or exponential growth, although it tends to slightly oversmooth changes in s in these cases (Supplemental Fig. S2). It is relatively robust to misspecification of effective population size: If we input constant N to the estimator, results are not noticeably different than if we specify the correct population size history (Supplemental Fig. S3). Increasing the size and frequency of sampling reduces error (Supplemental Fig. S4), although, in general, sample size is more important than sampling frequency; all else being equal, it is better to have infrequent samples of large sizes than frequent small samples.
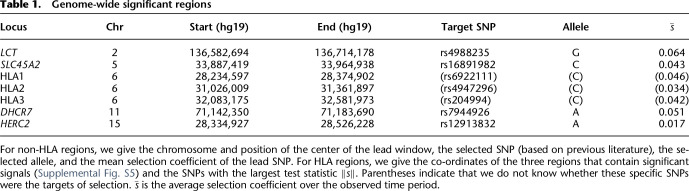
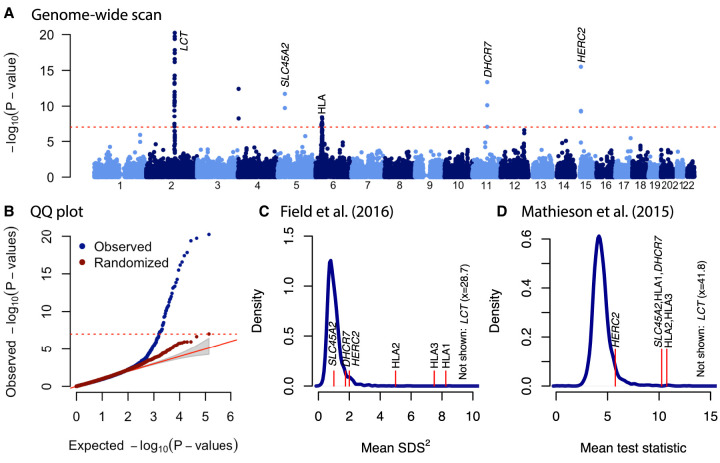
In the ancient British data, we identified seven regions with genome-wide significant evidence of selection (Table 1; Fig. 4A; Supplemental Table S2). We used a P-value cutoff of 10−7 as a genome-wide significant cutoff. Although conservative for the 68,061 overlapping windows in our analysis, we used this value because when we reran the analysis with randomized sample dates, no window had a smaller P-value (Fig. 4B). Three of these regions, which we denote HLA1, HLA2, and HLA3, are in the HLA region on Chromosome 6 (Supplemental Fig. S5), although these themselves may contain multiple signals. An eighth apparent signal on Chromosome 4 containing the gene LINC00955 is likely artifactual. The lead SNP rs4690044 has a MAF of zero in present-day samples but is around 0.5 in ancient samples. In gnomAD (Karczewski et al. 2020), rs4690044 has a MAF of 0.48 but no homozygotes, suggesting an artifactual call caused by a duplication. An additional locus on Chromosome 12 (P = 2.5 × 10−7), which contains the gene OAS1 and is known to be a target of adaptive Neanderthal introgression (Sams et al. 2016), was significant at a Bonferroni-corrected significance threshold (P = 7.3 × 10−7).
Table 1.
Genome-wide significant regions
Figure 4.
Genome-wide scan for selection in Britain. (A) P-values for selection in 20-SNP sliding windows. Genome-wide significant (P < 10−7) windows are labeled with the closest gene or known target of selection. (B) QQ plot for observations in A (blue) and after randomizing the dates of each sample (red). (C) Comparison with results of Field et al. (2016). Blue solid line shows the density of mean SDS2 in 20-SNP windows. Labeled red lines indicate windows that are genome-wide significant in our analysis. (D) Comparison with results of Mathieson et al. (2015). Blue solid line shows the density of mean statistic in 20-SNP windows. Labeled red lines indicate windows that are genome-wide significant in our analysis. In both C and D, HERC2 is approximately at the upper fifth percentile of the distribution.
All seven of these regions were identified by a previous allele frequency-based selection scan using aDNA to detect selection in West Eurasia over the past 8000 yr (Fig. 4D; Mathieson et al. 2015). Only LCT and the HLA region show significant evidence of selection in a haplotype-based scan using present-day sequence data that aimed to detect selection in Britain in the past few 1000 yr (Fig. 4C; Field et al. 2016) or in a scan based on identifying very recent coalescence times (about 50 generations) in the UK Biobank (Nait Saada et al. 2020).
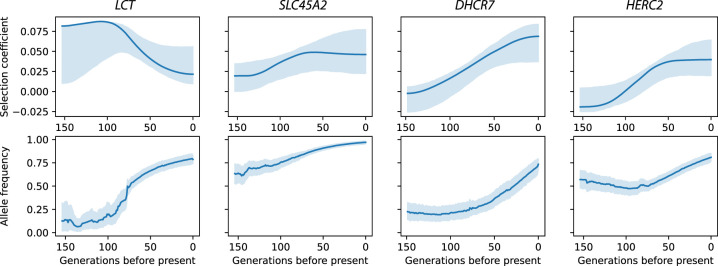
For the non-HLA signals for which we have a strong candidate for the causal variant based on previous literature, we examined the precise timing and trajectory of selection estimates from our model (Fig. 5). The most significant signal was the well-known LCT locus on Chromosome 2, where the selected allele is associated with lactase persistence (Enattah et al. 2002; Bersaglieri et al. 2004). We find that selection for the persistence allele was strongest (s ≈ 0.08) from 150 to 100 generations before the present (roughly 4500–3000 BP) before decreasing to around 0.02 in the past 50 generations. This large change in strength of selection might explain the wide range of estimates from models that assume a constant value (Bersaglieri et al. 2004; Peter et al. 2012; Mathieson and Mathieson 2018). At DHCR7, the haplotype tagged by the SNP in our analysis, rs7944926, is associated with protection against vitamin D insufficiency (Wang et al. 2010) and has been shown to have been under recent selection in both Europe (Mathieson et al. 2015) and East Asia (Kuan et al. 2013). We infer that, in Britain, the selection coefficient increased over the past 150 generations, from around zero to 0.06, leading to an increase in frequency from ∼20% to 60% over the past 3000 yr (Fig. 5).
Figure 5.
Trajectories of genome-wide significant non-HLA loci. Solid lines show the inferred selection coefficient and trajectory of the lead SNP given in Table 1. Shaded areas show 95% credible intervals based on resampling of the allele frequency trajectories and observations. (Top) Estimated selection coefficients. (Bottom) Estimated allele frequency trajectories.
Derived alleles at SLC45A2 and HERC2 are associated with light skin, hair, and eye pigmentation (Norton et al. 2007; Eiberg et al. 2008; Canela-Xandri et al. 2018; Hysi et al. 2018; Simcoe et al. 2021). Both these alleles have been shown to have been under selection broadly in Europe (Lao et al. 2007; Norton et al. 2007; Donnelly et al. 2012) and specifically during the Holocene (Wilde et al. 2014; Mathieson et al. 2015). Time series of aDNA have shown that both alleles were under selection in the past 5000 yr in Eastern Europe (Wilde et al. 2014). There, the derived SLC45A2 allele increased in frequency from 40% to 90% over the past 5000 yr, suggesting a selection coefficient of around 0.03, very similar to our estimate of selection in Britain during the same time (Fig. 5). For the derived HERC2 allele, we estimate a selection coefficient of 0.02–0.04, similar to that estimated in Eastern Europe, although we find that in Britain, selection was largely restricted to approximately the past 2000 yr. Wilde et al. (2014) also found a derived allele of TYR to be under strong selection in Eastern Europe, but we find little evidence that it was under selection in Britain, except possibly before 3000 BP (window P-value = 0.03) (Supplemental Fig. S6).
At the HLA, we find three regions with genome-wide significant evidence of selection, which we denote HLA1-3 (Supplemental Fig. S5). All three correspond to regions identified by Mathieson et al. (2015) and also have strong evidence of selection in the Field et al. (2016) scan (Fig. 4C). Because of high gene density and complex patterns of linkage disequilibrium in the region, we did not attempt to identify causal genes or variants. However, we note that the lead SNP at HLA1 is strongly associated with a decreased risk of celiac disease in the UK Biobank (Canela-Xandri et al. 2018). The lead HLA2 SNP is associated with an increased risk of ankylosing spondylitis (Canela-Xandri et al. 2018), but the region contains the gene HLA-C, a variant of which is the strongest known risk factor for psoriasis (Yin et al. 2015). Finally, the lead SNP at HLA3 is strongly associated with a decreased risk of celiac disease and psoriasis (Canela-Xandri et al. 2018). These associations suggest that risk of these diseases has been affected by selection, even if they themselves are not the direct targets.
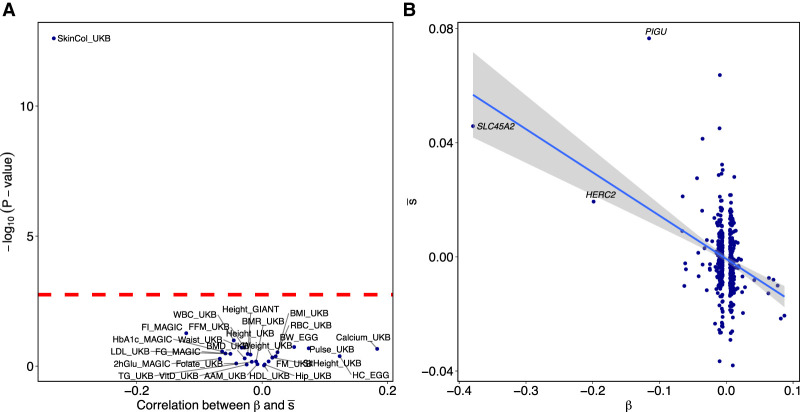
Finally, we searched for evidence of polygenic selection by testing for a correlation between GWAS effect size and selection coefficient for 28 anthropometric and morphological traits (Fig. 6A; Supplemental Table S1; Supplemental Fig. S7). We find significant evidence of polygenic selection for reduced skin pigmentation (P = 3.6 × 10−16) (Fig. 6B) but none of the other 27 traits (P > 0.04). Although not statistically significant, the largest absolute correlation apart from skin pigmentation is for increased calcium. We do not detect evidence of selection on any of the phenotypes identified by Field et al. (2016) as under selection in Britain in the past 2000 yr, including height, infant head circumference, and fasting insulin.
Figure 6.
Evidence of polygenic selection. (A) Each point represents a single GWAS. The x-axis gives the (Pearson) correlation between effect size estimates, β, and selection coefficient estimates, , for independent SNPs with GWAS P-value < 10−4 and minor allele frequency (MAF) > 5%. The y-axis gives the log10 (P-value) for null hypothesis of no correlation. Abbreviations, exact values, and sources are given in Supplemental Table S1. (B) Effect sizes and selection coefficient estimates for independent skin color–associated SNPs in the UK Biobank with GWAS P-value < 10−4 and MAF > 5%. If the three labeled large-effect SNPs are removed, the correlation is weaker but still significant (ρ = −0.20, P = 1.5 × 10−5).
Discussion
Our fast and flexible estimator allowed us to perform a direct genome-wide scan for selection based on allele frequency trajectories. On our standard compute cluster, average run-time for each SNP was 41 sec, requiring 220 Mb of RAM, so analyzing all 1.15 million loci took around 13,000 CPU h in total. All of the significant loci we identified have been identified by a previous allele frequency-based scan using aDNA (Mathieson et al. 2015). However, that approach scanned for selection broadly in Holocene Europe and was unable to localize selection further in either space or time. Here, we are able to localize selection to Britain in the past 4500 yr and, even further, to identify changes in the strength of selection over that time period (Fig. 5). We are also able to identify selected loci that were not identified in studies of much larger samples of present-day individuals (Field et al. 2016; Nait Saada et al. 2020).
On the other hand, when we search for polygenic selection, the only trait for which we find significant evidence is skin pigmentation, which is known to have been under selection in Europe more broadly into this time period (Wilde et al. 2014; Mathieson et al. 2015; Field et al. 2016; Ju and Mathieson 2021). Although many previous studies (Turchin et al. 2012; Berg and Coop 2014; Mathieson et al. 2015; Robinson et al. 2015; Field et al. 2016) reported evidence for recent selection on height, this has been shown to be largely driven by residual stratification in the GIANT Consortium GWAS (Berg et al. 2019; Sohail et al. 2019). Evidence of recent polygenic selection for other traits (e.g., Field et al. 2016) may suffer from the same issue, although findings based on the UK Biobank GWAS results may be more reliable. It is also possible that our negative findings reflect a lack of power. Even though our approach is relatively well-powered to detect strong selection compared with other selection scans, it may be less able to detect the weak selection that contributes to polygenic adaptation even in aggregate. A more complete investigation of the way in which the time series analysis in this study could be used to detect polygenic selection is a question for future work.
Although there may have been multiple environmental drivers of selection, taken together, our results strongly suggest that a major selective pressure at this time was for increased calcium largely moderated through increased vitamin D levels. Vitamin D is required for the absorption of calcium, and deficiency leads to bone deformities with potentially major effects on fitness. Because a major source of vitamin D is synthesis in the skin in the presence of UV radiation, the cloudy skies of Britain are likely to have limited this synthesis. The Mesolithic inhabitants of Britain may have avoided this problem through consumption of vitamin D–rich marine resources, but later Neolithic and Bronze Age populations, including those in our study, relied on agricultural products for their subsistence (Richards et al. 2003), leading to a need for genetic adaptation.
In fact, almost all of our signals of selection can be related to selection for increased vitamin D or directly for increased calcium. Selection at SLC45A2 and HERC2, as well as selection for lighter skin pigmentation more generally, naturally leads to increased penetration of UV into the skin and therefore higher levels of vitamin D (Murray 1934; Jablonski and Chaplin 2010). Lactase persistence allows the consumption of milk, which contains both calcium and a small amount of vitamin D. This “calcium absorption” hypothesis has long been suggested to explain the high frequency of the persistence phenotype in Northern Europe (Flatz and Rotthauwe 1973; Gerbault et al. 2011). DHCR7 is directly involved in vitamin D metabolism, and the selected allele protects against insufficiency (Wang et al. 2010). Although the HLA associations are more difficult to specifically identify, two of the selected alleles are protective against celiac disease, which itself is a risk factor for malabsorption of calcium and vitamin D and consequent osteoporosis (Meyer et al. 2001). Strong selective pressure for increased vitamin D and calcium levels is therefore a plausible and parsimonious explanation for the patterns of selection that we observe in this data set.
The main limitation of our approach is the assumption of population continuity. Although there is evidence of external migration into Britain during the time period we investigated (Patterson et al. 2022), there is relatively little change in genetic ancestry because the sources of that migration are genetically similar populations from other nearby parts of Northern Europe. If this affects our results, it would likely mean that some of the selection we detected actually occurred in those neighboring populations, somewhat earlier than the dates we find here. However, given that the selection pressures we detect are likely to be shared with these similar populations anyway, we do not think this possibility has a major impact on the interpretation of our results. This limitation is more serious if we want to extend the temporal and geographic range of our analysis. In particular, both ancient and present-day individuals from the Iberian and Italian peninsulas are much more genetically diverse than those from Britain (Supplemental Fig. S8). Because of this, and the much smaller ancient sample sizes, we did not analyze selection in these Southern European populations, although identifying differences in selective pressures between Northern and Southern Europe is an important direction for future analysis.
Although we have identified the loci under the strongest selection in recent British history, there is evidence in our data of additional selected loci. For example, several known loci, including OAS1 (P = 2.5 × 10−7) (Sams et al. 2016) and FADS1 (P = 1.5 × 10−5) (Mathieson et al. 2015), have evidence of selection, although below genome-wide significance. With larger sample sizes, we can expect that these and other, potentially novel, loci would be identified. An alternative way to increase sample size would be to modify our method to analyze genotype likelihoods rather than pseudohaploid calls. We estimate that this could increase effective sample size by up to 22%. An even bigger increase could be gained by using genotype imputation, although with the caveat that imputation may be less reliable in strongly selected regions. There are also several technical limitations that may affect interpretations of our results. For example, we identified at least one locus where systematic differences between ancient and present-day samples created a spurious signal of selection. Other systematic differences related to mapping errors, or aDNA damage, might create similar effects. It is important therefore to check that results based on the comparison of ancient and present-day samples are robust by verifying that they are consistent when present-day samples are excluded or, as we have performed here, that they are consistent with signals derived from present-day data alone. Another limitation is that we rely on sites included in the 1240k capture reagent and therefore cannot detect selection on rare SNPs or structural variants that are not tagged by such SNPs. Imputation or large data sets of shotgun sequence data might extend the range of variation on which selection can be detected.
Our study shows the power of aDNA to robustly detect and precisely characterize the timing of natural selection in humans. We appear to have similar power to detect selection as previously published methods based on present-day and ancient data. On the other hand, present-day sample sizes will always be much larger, and approaches that can scale to hundreds of thousands or millions of genomes (Nait Saada et al. 2020) will probably be more powerful. The major advantage of aDNA is the ability to precisely estimate the timing of selection, suggesting a potential hybrid approach using very large present-day data sets to identify nonneutral regions of the genome and then use aDNA time series to characterize the timing and nature of selection at those loci. Indeed, several of the loci that we identify have evidence of substantial change in the strength of selection over the past 4500 yr, suggesting that modeling this variability may be an important addition to previous approaches that assume constant selective pressure. One caveat is that in order to do this, we need to be able to identify the selected variant at a locus, which is not always possible (e.g., in the case of HLA). Indeed, imperfect tagging of the causal variant could lead to spurious signals of time-varying selection, as could dominance coefficients different from 0.5 or spatially structured selection. In particular, lactase persistence is dominant, although enzymatic activity is not (Ségurel and Bon 2017). Therefore, selection on LCT could act in a dominant fashion, which could give the appearance of decreasing the selective coefficient over time. If the selective pressure on LCT did decrease over time, perhaps owing to cultural changes, it may have contributed to an increase in selective pressures related to other sources (e.g., pigmentation and metabolism). In this way, culture could have determined the genetic response to a constant environmental selective pressure. The prospect of exploring this and similar interactions is an exciting future direction for aDNA research.
Software availability
Source codes to run the estimator and reproduce the analyses in this paper are available at GitHub (https://github.com/jthlab/bmws) and as Supplemental Codes S1–S3.
Supplementary Material
Acknowledgments
We thank Pontus Skoglund for helpful comments. This research was funded by the National Institute of General Medical Sciences (R35GM133708 to I.M.) and the National Science Foundation (DMS-2052653 to J.T.). The content is solely the responsibility of the authors and does not necessarily represent the official views of the funding agencies.
Author contributions: I.M. and J.T. conceived and designed the study, wrote the code, analyzed the data, and wrote the manuscript.
Footnotes
[Supplemental material is available for this article.]
Article published online before print. Article, supplemental material, and publication date are at https://www.genome.org/cgi/doi/10.1101/gr.276862.122.
Competing interest statement
The authors declare no competing interests.
References
- The 1000 Genomes Project Consortium. 2015. A global reference for human genetic variation. Nature 526: 68–74. 10.1038/nature15393 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berg JJ, Coop G. 2014. A population genetic signal of polygenic adaptation. PLoS Genet 10: e1004412. 10.1371/journal.pgen.1004412 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berg JJ, Harpak A, Sinnott-Armstrong N, Joergensen AM, Mostafavi H, Field Y, Boyle EA, Zhang X, Racimo F, Pritchard JK, et al. 2019. Reduced signal for polygenic adaptation of height in UK Biobank. eLife 8: e39725. 10.7554/eLife.39725 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bersaglieri T, Sabeti PC, Patterson N, Vanderploeg T, Schaffner SF, Drake JA, Rhodes M, Reich DE, Hirschhorn JN. 2004. Genetic signatures of strong recent positive selection at the lactase gene. Am J Hum Genet 74: 1111–1120. 10.1086/421051 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bollback JP, York TL, Nielsen R. 2008. Estimation of 2Nes from temporal allele frequency data. Genetics 179: 497–502. 10.1534/genetics.107.085019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brace S, Diekmann Y, Booth TJ, van Dorp L, Faltyskova Z, Rohland N, Mallick S, Olalde I, Ferry M, Michel M, et al. 2019. Ancient genomes indicate population replacement in Early Neolithic Britain. Nat Ecol Evol 3: 765–771. 10.1038/s41559-019-0871-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Can O, Rawlik K, Tenesa A. 2018. An atlas of genetic associations in UK Biobank. Nat Genet 50: 1593–1599. 10.1038/s41588-018-0248-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen J, Spracklen CN, Marenne G, Varshney A, Corbin LJ, Luan J, Willems SM, Wu Y, Zhang X, Horikoshi M, et al. 2021. The trans-ancestral genomic architecture of glycemic traits. Nat Genet 53: 840–860. 10.1038/s41588-021-00852-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donnelly MP, Paschou P, Grigorenko E, Gurwitz D, Barta C, Lu RB, Zhukova OV, Kim JJ, Siniscalco M, New M, et al. 2012. A global view of the OCA2-HERC2 region and pigmentation. Hum Genet 131: 683–696. 10.1007/s00439-011-1110-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eiberg H, Troelsen J, Nielsen M, Mikkelsen A, Mengel-From J, Kjaer KW, Hansen L. 2008. Blue eye color in humans may be caused by a perfectly associated founder mutation in a regulatory element located within the HERC2 gene inhibiting OCA2 expression. Hum Genet 123: 177–187. 10.1007/s00439-007-0460-x [DOI] [PubMed] [Google Scholar]
- Enattah NS, Sahi T, Savilahti E, Terwilliger JD, Peltonen L, Järvelä I. 2002. Identification of a variant associated with adult-type hypolactasia. Nat Genet 30: 233–237. 10.1038/ng826 [DOI] [PubMed] [Google Scholar]
- Ewens WJ. 2004. Mathematical population genetics: theoretical introduction, Vol. 1. Springer, New York. [Google Scholar]
- Feder AF, Kryazhimskiy S, Plotkin JB. 2014. Identifying signatures of selection in genetic time series. Genetics 196: 509–522. 10.1534/genetics.113.158220 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feller W. 2008. An introduction to probability theory and its applications, Vol. 2. John Wiley & Sons, New York. [Google Scholar]
- Ferrer-Admetlla A, Leuenberger C, Jensen JD, Wegmann D. 2016. An approximate Markov model for the Wright–Fisher diffusion and its application to time series data. Genetics 203: 831–846. 10.1534/genetics.115.184598 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Field Y, Boyle EA, Telis N, Gao Z, Gaulton KJ, Golan D, Yengo L, Rocheleau G, Froguel P, McCarthy MI, et al. 2016. Detection of human adaptation during the past 2000 years. Science 354: 760–764. 10.1126/science.aag0776 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flatz G, Rotthauwe HW. 1973. Lactose nutrition and natural selection. Lancet 302: 76–77. 10.1016/S0140-6736(73)93267-4 [DOI] [PubMed] [Google Scholar]
- Gerbault P, Liebert A, Itan Y, Powell A, Currat M, Burger J, Swallow DM, Thomas MG. 2011. Evolution of lactase persistence: an example of human niche construction. Philos Trans R Soc Lond B Biol Sci 366: 863–877. 10.1098/rstb.2010.0268 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gompert Z. 2016. Bayesian inference of selection in a heterogeneous environment from genetic time-series data. Mol Ecol 25: 121–134. 10.1111/mec.13323 [DOI] [PubMed] [Google Scholar]
- Horikoshi M, Beaumont RN, Day FR, Warrington NM, Kooijman MN, Fernandez-Tajes J, Feenstra B, van Zuydam NR, Gaulton KJ, Grarup N, et al. 2016. Genome-wide associations for birth weight and correlations with adult disease. Nature 538: 248–252. 10.1038/nature19806 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hysi PG, Valdes AM, Liu F, Furlotte NA, Evans DM, Bataille V, Visconti A, Hemani G, McMahon G, Ring SM, et al. 2018. Genome-wide association meta-analysis of individuals of European ancestry identifies new loci explaining a substantial fraction of hair color variation and heritability. Nat Genet 50: 652–656. 10.1038/s41588-018-0100-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jablonski NG, Chaplin G. 2010. Human skin pigmentation as an adaptation to UV radiation. Proc Natl Acad Sci 107 (Suppl 2): 8962–8968. 10.1073/pnas.0914628107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ju D, Mathieson I. 2021. The evolution of skin pigmentation-associated variation in West Eurasia. Proc Natl Acad Sci 118: e2009227118. 10.1073/pnas.2009227118 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karczewski KJ, Francioli LC, Tiao G, Cummings BB, Alföldi J, Wang Q, Collins RL, Laricchia KM, Ganna A, Birnbaum DP, et al. 2020. The mutational constraint spectrum quantified from variation in 141,456 humans. Nature 581: 434–443. 10.1038/s41586-020-2308-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kerner G, Laval G, Patin E, Boisson-Dupuis S, Abel L, Casanova JL, Quintana-Murci L. 2021. Human ancient DNA analyses reveal the high burden of tuberculosis in Europeans over the last 2,000 years. Am J Hum Genet 108: 517–524. 10.1016/j.ajhg.2021.02.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuan V, Martineau AR, Griffiths CJ, Hyppönen E, Walton R. 2013. DHCR7 mutations linked to higher vitamin D status allowed early human migration to northern latitudes. BMC Evol Biol 13: 144. 10.1186/1471-2148-13-144 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lacerda M, Seoighe C. 2014. Population genetics inference for longitudinally-sampled mutants under strong selection. Genetics 198: 1237–1250. 10.1534/genetics.114.167957 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lao O, de Gruijter JM, van Duijn K, Navarro A, Kayser M. 2007. Signatures of positive selection in genes associated with human skin pigmentation as revealed from analyses of single nucleotide polymorphisms. Ann Hum Genet 71: 354–369. 10.1111/j.1469-1809.2006.00341.x [DOI] [PubMed] [Google Scholar]
- Lazaridis I, Patterson N, Mittnik A, Renaud G, Mallick S, Kirsanow K, Sudmant PH, Schraiber JG, Castellano S, Lipson M, et al. 2014. Ancient human genomes suggest three ancestral populations for present-day Europeans. Nature 513: 409–413. 10.1038/nature13673 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malaspinas A-S. 2016. Methods to characterize selective sweeps using time serial samples: an ancient DNA perspective. Mol Ecol 25: 24–41. 10.1111/mec.13492 [DOI] [PubMed] [Google Scholar]
- Malaspinas A-S, Malaspinas O, Evans SN, Slatkin M. 2012. Estimating allele age and selection coefficient from time-serial data. Genetics 192: 599–607. 10.1534/genetics.112.140939 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Margaryan A, Lawson DJ, Sikora M, Racimo F, Rasmussen S, Moltke I, Cassidy LM, Jørsboe E, Ingason A, Pedersen MW, et al. 2020. Population genomics of the Viking world. Nature 585: 390–396. 10.1038/s41586-020-2688-8 [DOI] [PubMed] [Google Scholar]
- Martiniano R, Caffell A, Holst M, Hunter-Mann K, Montgomery J, Müldner G, McLaughlin RL, Teasdale MD, Van Rheenen W, Veldink JH, et al. 2016. Genomic signals of migration and continuity in Britain before the Anglo-Saxons. Nat Commun 7: 10326. 10.1038/ncomms10326 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mathieson S, Mathieson I. 2018. FADS1 and the timing of human adaptation to agriculture. Mol Biol Evol 35: 2957–2970. 10.1093/molbev/msy180 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mathieson I, McVean G. 2013. Estimating selection coefficients in spatially structured populations from time series data of allele frequencies. Genetics 193: 973–984. 10.1534/genetics.112.147611 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mathieson I, Lazaridis I, Rohland N, Mallick S, Patterson N, Roodenberg SA, Harney E, Stewardson K, Fernandes D, Novak M, et al. 2015. Genome-wide patterns of selection in 230 ancient Eurasians. Nature 528: 499–503. 10.1038/nature16152 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer D, Stavropolous S, Diamond B, Shane E, Green PH. 2001. Osteoporosis in a North American adult population with celiac disease. Am J Gastroenterol 96: 112–119. 10.1111/j.1572-0241.2001.03507.x [DOI] [PubMed] [Google Scholar]
- Murray FG. 1934. Pigmentation, sunlight, and nutritional disease. Am Anthropol 36: 438–445. 10.1525/aa.1934.36.3.02a00100 [DOI] [Google Scholar]
- Nait Saada J, Kalantzis G, Shyr D, Cooper F, Robinson M, Gusev A, Palamara PF. 2020. Identity-by-descent detection across 487,409 British samples reveals fine scale population structure and ultra-rare variant associations. Nat Commun 11: 6130. 10.1038/s41467-020-19588-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Norton HL, Kittles RA, Parra E, McKeigue P, Mao X, Cheng K, Canfield VA, Bradley DG, McEvoy B, Shriver MD, et al. 2007. Genetic evidence for the convergent evolution of light skin in Europeans and East Asians. Mol Biol Evol 24: 710–722. 10.1093/molbev/msl203 [DOI] [PubMed] [Google Scholar]
- Olalde I, Brace S, Allentoft ME, Armit I, Kristiansen K, Booth T, Rohland N, Mallick S, Szécsényi-Nagy A, Mittnik A, et al. 2018. The Beaker phenomenon and the genomic transformation of northwest Europe. Nature 555: 190–196. 10.1038/nature25738 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olalde I, Mallick S, Patterson N, Rohland N, Villalba-Mouco V, Silva M, Dulias K, Edwards CJ, Gandini F, Pala M, et al. 2019. The genomic history of the Iberian Peninsula over the past 8000 years. Science 363: 1230–1234. 10.1126/science.aav4040 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paris C, Servin B, Boitard S. 2019. Inference of selection from genetic time series using various parametric approximations to the Wright-Fisher model. G3 (Bethesda) 9: 4073–4086. 10.1534/g3.119.400778 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patterson N, Isakov M, Booth T, Büster L, Fischer CE, Olalde I, Ringbauer H, Akbari A, Cheronet O, Bleasdale M, et al. 2022. Large-scale migration into Britain during the Middle to Late Bronze Age. Nature 601: 588–594. 10.1038/s41586-021-04287-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peter BM, Huerta-Sanchez E, Nielsen R. 2012. Distinguishing between selective sweeps from standing variation and from a de novo mutation. PLoS Genet 8: e1003011. 10.1371/journal.pgen.1003011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richards MP, Schulting RJ, Hedges RE. 2003. Archaeology: sharp shift in diet at onset of neolithic. Nature 425: 366. 10.1038/425366a [DOI] [PubMed] [Google Scholar]
- Robinson MR, Hemani G, Medina-Gomez C, Mezzavilla M, Esko T, Shakhbazov K, Powell JE, Vinkhuyzen A, Berndt SI, Gustafsson S, et al. 2015. Population genetic differentiation of height and body mass index across Europe. Nat Genet 47: 1357–1362. 10.1038/ng.3401 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sams AJ, Dumaine A, Nédélec Y, Yotova V, Alfieri C, Tanner JE, Messer PW, Barreiro LB. 2016. Adaptively introgressed Neandertal haplotype at the OAS locus functionally impacts innate immune responses in humans. Genome Biol 17: 246. 10.1186/s13059-016-1098-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schiffels S, Haak W, Paajanen P, Llamas B, Popescu E, Loe L, Clarke R, Lyons A, Mortimer R, Sayer D, et al. 2016. Iron Age and Anglo-Saxon genomes from east England reveal British migration history. Nat Commun 7: 10408. 10.1038/ncomms10408 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ségurel L, Bon C. 2017. On the evolution of lactase persistence in humans. Annu Rev Genomics Hum Genet 18: 297–319. 10.1146/annurev-genom-091416-035340 [DOI] [PubMed] [Google Scholar]
- Simcoe M, Valdes A, Liu F, Furlotte NA, Evans DM, Hemani G, Ring SM, Smith GD, Duffy DL, Zhu G, et al. 2021. Genome-wide association study in almost 195,000 individuals identifies 50 previously unidentified genetic loci for eye color. Sci Adv 7: eabd1239. 10.1126/sciadv.abd1239 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skoglund P, Mathieson I. 2018. Ancient genomics of modern humans: the first decade. Annu Rev Genomics Hum Genet 19: 381–404. 10.1146/annurev-genom-083117-021749 [DOI] [PubMed] [Google Scholar]
- Skoglund P, Thompson JC, Prendergast ME, Mittnik A, Sirak K, Hajdinjak M, Salie T, Rohland N, Mallick S, Peltzer A, et al. 2017. Reconstructing prehistoric African population structure. Cell 171: 59–71.e21. 10.1016/j.cell.2017.08.049 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sohail M, Maier RM, Ganna A, Bloemendal A, Martin AR, Turchin MC, Chiang CW, Hirschhorn J, Daly MJ, Patterson N, et al. 2019. Polygenic adaptation on height is overestimated due to uncorrected stratification in genome-wide association studies. eLife 8: e39702. 10.7554/eLife.39702 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steinrücken M, Bhaskar A, Song YS. 2014. A novel spectral method for inferring general diploid selection from time series genetic data. Ann Appl Stat 8: 2203–2222. 10.1214/14-AOAS764 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taal HR, Pourcain BS, Thiering E, Das S, Mook-Kanamori DO, Warrington NM, Kaakinen M, Kreiner-Møller E, Bradfield JP, Freathy RM, et al. 2012. Common variants at 12q15 and 12q24 are associated with infant head circumference. Nat Genet 44: 532–538. 10.1038/ng.2238 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tataru P, Bataillon T, Hobolth A. 2015. Inference under a Wright–Fisher model using an accurate beta approximation. Genetics 201: 1133–1141. 10.1534/genetics.115.179606 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tataru P, Simonsen M, Bataillon T, Hobolth A. 2017. Statistical inference in the Wright–Fisher model using allele frequency data. Syst Biol 66: e30–e46. 10.1093/sysbio/syw056 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Terhorst J, Schlötterer C, Song YS. 2015. Multi-locus analysis of genomic time series data from experimental evolution. PLoS Genet 11: e1005069. 10.1371/journal.pgen.1005069 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turchin MC, Chiang CW, Palmer CD, Sankararaman S, Reich D, Genetic Investigation of ANthropometric Traits (GIANT) Consortium, Hirschhorn JN. 2012. Evidence of widespread selection on standing variation in Europe at height-associated SNPs. Nat Genet 44: 1015–1019. 10.1038/ng.2368 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang TJ, Zhang F, Richards JB, Kestenbaum B, van Meurs JB, Berry D, Kiel DP, Streeten EA, Ohlsson C, Koller DL, et al. 2010. Common genetic determinants of vitamin D insufficiency: a genome-wide association study. Lancet 376: 180–188. 10.1016/S0140-6736(10)60588-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilde S, Timpson A, Kirsanow K, Kaiser E, Kayser M, Unterländer M, Hollfelder N, Potekhina ID, Schier W, Thomas MG, et al. 2014. Direct evidence for positive selection of skin, hair, and eye pigmentation in Europeans during the last 5,000 y. Proc Natl Acad Sci 111: 4832–4837. 10.1073/pnas.1316513111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wood AR, Esko T, Yang J, Vedantam S, Pers TH, Gustafsson S, Chu AY, Estrada K, Luan J, Kutalik Z, et al. 2014. Defining the role of common variation in the genomic and biological architecture of adult human height. Nat Genet 46: 1173–1186. 10.1038/ng.3097 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yin X, Low HQ, Wang L, Li Y, Ellinghaus E, Han J, Estivill X, Sun L, Zuo X, Shen C, et al. 2015. Genome-wide meta-analysis identifies multiple novel associations and ethnic heterogeneity of psoriasis susceptibility. Nat Commun 6: 6916. 10.1038/ncomms7916 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.