Fast and accurate mapping of long reads to complete genome assemblies with VerityMap

Abstract

Recent advancements in long-read sequencing have enabled the telomere-to-telomere (complete) assembly of a human genome and are now contributing to the haplotype-resolved complete assemblies of multiple human genomes. Because the accuracy of read mapping tools deteriorates in highly repetitive regions, there is a need to develop accurate, error-exposing (detecting potential assembly errors), and diploid-aware (distinguishing different haplotypes) tools for read mapping in complete assemblies. We describe the first accurate, error-exposing, and partially diploid-aware VerityMap tool for long-read mapping to complete assemblies.

The initial draft sequence of the human genome contained thousands of gaps and scaffolds (International Human Genome Sequencing Consortium 2001; Venter et al. 2001). Even nowadays, the up-to-date human reference genome (GRCh38.p13) still contains 349 gaps and 472 scaffolds (Miga et al. 2014). These gaps contain regions that include large and biomedically important multimegabase arrays of tandem satellite repeats that orchestrate chromosome segregation during cell division (Miga 2019, 2020). For two decades, centromeric and pericentromeric satellite arrays evaded all assembly efforts, resulting in a limited understanding of their sequence organization. Recently, the Telomere-to-Telomere (T2T) Consortium generated the first nearly complete assembly of an effectively haploid human cell line, CHM13, that, in particular, includes assemblies of all satellite repeats (Jain et al. 2018; Miga et al. 2020; Logsdon et al. 2021; Nurk et al. 2022).

Long-read technologies, such as the ones developed by Pacific Biosciences (PacBio) and Oxford Nanopore Technologies (ONT), have changed the landscape of computational methods for genome assembly and opened a possibility to generate haplotype-resolved complete assemblies (Chin et al. 2016; Li 2016; Lin et al. 2016; Koren et al. 2017; Wick et al. 2017; Kolmogorov et al. 2019, 2020; Nurk et al. 2020; Ruan and Li 2020; Cheng et al. 2021). Some of these assemblers use ultralong error-prone reads in order to assemble the most repetitive genomic regions, such as satellite arrays (Bzikadze and Pevzner 2020; Miga et al. 2020; Shafin et al. 2020). The emergence of long high-fidelity (HiFi) PacBio reads has, once again, revolutionized the field of genome assembly (Wenger et al. 2019; Logsdon et al. 2021) and resulted in some of the most contiguous assemblies to date (Nurk et al. 2020, 2022; Cheng et al. 2021).

The emergence of “complete genomics” (Nurk et al. 2020, 2022; Cheng et al. 2021) and “complete metagenomics” (Bickhart et al. 2022) is shifting the focus of read mapping from detecting mutations to detecting errors in the newly generated assemblies (see Supplemental Note 1, “Similarities and differences between detecting mutations and detecting misassemblies”; Supplemental Fig. 1). Although most previous read mapping efforts were aimed at detecting mutations by aligning reads against the reference genome instead of assembling them (because genome assemblers typically fail to assemble highly repetitive regions), HiFi assemblers accurately assemble even the most complex genomic regions, and although a limited number of misassemblies persist, these assemblies provide a path to potentially eliminate the need for mapping reads against a reference. They also result in extremely low rates of single-nucleotide errors in nonrepetitive regions (Nurk et al. 2020, 2022; Cheng et al. 2021), largely eliminating the need for the follow-up read mapping to these regions: instead of mapping reads using external tools, existing HiFi assemblers automatically provide highly accurate alignments of reads to the assemblies they generate. However, HiFi assemblers still make assembly errors in highly repetitive regions and thus necessitate the development of new mapping tools for detecting these errors by identifying discordant reads.

The need for evaluation of the complete genome assemblies and the absence of ground truth data sets has resulted in the development of specialized pipelines for assembly validation (Mc Cartney et al. 2022). Even though the QUAST tools represent the state-of-the-art framework for quality assessment of genome assemblies (Gurevich et al. 2013; Bushmanova et al. 2016; Mikheenko et al. 2016, 2018), these tools mostly rely on the availability of a reference genome and are thus inapplicable for evaluating complete assemblies that include megabases of novel sequence. In particular, QUAST uses BUSCO (Simão et al. 2015) to evaluate the gene content of assemblies and assess completeness of an assembly without a reference genome. However, BUSCO only analyzes conserved single-copy genes and is inapplicable for gene-poor regions such as centromeres. Moreover, QUAST identifies assembly errors only in comparison with a reference genome. Alternative reference-free methods can be divided into alignment-free methods that compare k-mer spectra between reads and an assembly (Mapleson et al. 2017; Rhie et al. 2020) and alignment-based methods that use the read mapping tools (Li and Durbin 2009; Langmead and Salzberg 2012; Li 2016, 2018; Jain et al. 2020) to generate read alignments, use them for assessing the quality of an assembly, and correct the assembly based on the identified discordant reads. However, although alignment-free methods can estimate assembly quality and completeness, they do not output information about the positions of assembly errors.

Mikheenko et al. (2020) showed that the performance of existing read mapping tools deteriorates in complex regions, especially in the presence of assembly errors, and developed the TandemMapper tool for mapping long reads to extra-long tandem repeats (ETRs) in the constructed assemblies. Even though TandemMapper accurately maps reads to centromeric regions and enables evaluations of their assemblies (Bzikadze and Pevzner 2020; Miga et al. 2020; Logsdon et al. 2021), it falls short of mapping reads in even more challenging megabase-long genomic regions like HSAT2,3. Moreover, TandemMapper, designed specifically for ETRs, becomes prohibitively slow for evaluating complete genome assemblies.

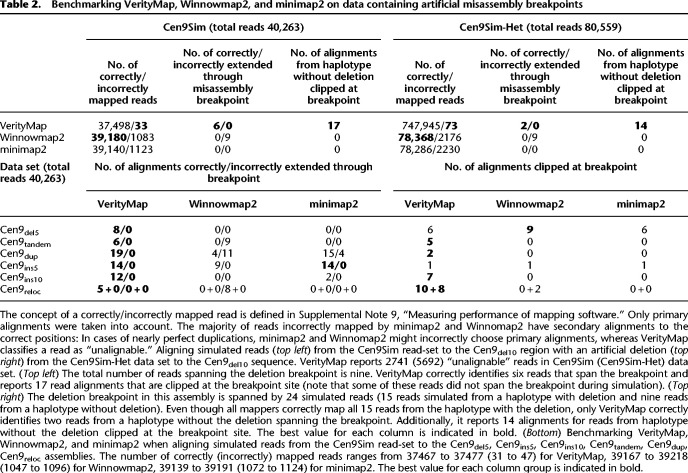
Generating a complete assembly for a single haploid human genome represents a landmark achievement (Nurk et al. 2022). However, because a single genome does not represent the genomic diversity of the human population, the Human Pangenome Reference (HPR) Consortium is now generating high-quality diploid assemblies for hundreds of humans. This ambitious goal raises the bar for scalable diploid-aware quality assessment tools that can evaluate entire diploid assemblies rather than certain selected (albeit complex) loci and identify errors in these assemblies. To the best of our knowledge, no error-exposing tool for reference-free benchmarking of complete haplotype-resolved assemblies or even individual loci is currently available. Although Winnowmap2 (Jain et al. 2020, 2022) maps reads to complex repetitive regions of the error-free assemblies, it is neither error-exposing nor diploid-aware because its performance deteriorates in the case of error-prone assemblies and heterozygous sites (Table 2; Mikheenko et al. 2020).

Table 2.

Benchmarking VerityMap, Winnowmap2, and minimap2 on data containing artificial misassembly breakpoints

We present VerityMap, a fast, accurate, and error-exposing aligner for mapping long reads to the complete assemblies (for an informal comparison of various long-read aligners, see Table 1). VerityMap also represents the first step toward diploid-aware alignment by mapping reads to haplotype-resolved assemblies of individual loci (see Supplemental Note 2, “The challenge of diploid-aware read mapping”). It was used for detecting and correcting misassemblies in the intermediate assemblies of the first complete human genome assembled by the T2T Consortium (Miga et al. 2020; Mc Cartney et al. 2022; Nurk et al. 2022). The Supplemental section “Alpha-satellite and human satellite 1,2,3 validation” in the work by Nurk et al. (2022) illustrates how VerityMap contributed to verifying the complete human genome assembly generated by the T2T Consortium.

Table 1.

Benchmarking VerityMap, TandemMapper, Winnowmap2, and minimap2 with reads simulated from Chromosomes 1 and 9

All state-of-the-art long-read aligners are based on finding some shared k-mers between a read and an assembly, followed by sparse dynamic programming in a graph in which each vertex represents a pair of the starting positions of a shared k-mer. Ideally, the parameter k (k-mer size) should be selected to be as large as possible (e.g., slightly below the read length) for accurate mapping of error-free reads. In practice, it is selected to be rather small to ensure that an error-prone read has some shared k-mer with an assembly. This condition dictates selecting a rather small k in the case of long error-prone reads (minimap2 v2.24 uses default k = 15 for mapping ONT reads, and k = 19 for mapping PacBio CLR reads; https://lh3.github.io/minimap2/minimap2.html) and makes it difficult to map reads in highly repetitive regions. Accurate HiFi reads allow one to increase k by an order of magnitude, thus facilitating read mapping in complex regions.

Although an increased k-mer size looks like a rather minor parameter change in read mapping tools, it actually represents a new challenge. We show that developing a fast, accurate, error-exposing, and diploid-aware long read mapping tool requires new algorithmic ideas, not unlike constructing the de Bruijn graph of large genomes for large k-mer sizes (Bankevich et al. 2022). To achieve this goal, VerityMap first identifies all rare k-mers in the assembly, carefully selects a small subset of rare k-mers (solid k-mers), finds locations of solid k-mers in each read, constructs a compatibility graph with the vertex-set formed by all matches between the selected solid k-mers shared by a read and the assembly, finds an optimal path in this graph using sparse dynamic programming, and uses this path for read mapping. Because HiFi reads are accurate, VerityMap uses large k-mer sizes (e.g., k = 300) for constructing the compatibility graph to achieve accurate read mapping. It thus faces the algorithmic challenge of identifying rare k-mers in a large genome for a large k.

Although efficient indexing (finding locations) of all k-mers in the genome (and thus identifying rare k-mers) represents a backbone of many bioinformatics algorithms (Marçais and Kingsford 2011), it remains an open problem in the case of large genomes and large k-mer sizes. Indeed, a naive indexing algorithm with the running time O(|Genome|*k) becomes prohibitively slow in the case of accurate HiFi reads because mapping these reads is based on large k-mer sizes (e.g., k = 300). Jellyfish (Marçais and Kingsford 2011), KMC3 (Kokot et al. 2017), and more scalable GPU–based k-mer counting approaches (Nisa et al. 2021) generate a database of counts that allows a constant-time count query for any k-mer. However, even though one can rapidly generate a counting database, existing implementations for indexing all rare k-mers still require O(|Genome|*k) time. On the other hand, the Meryl k-mer counting algorithm (Rhie et al. 2020) only works with k ≤ 64, which is substantially lower than what is needed for accurate mapping of HiFi reads (e.g., k = 300). Inspired by Jellyfish, VerityMap overcomes limitations of existing approaches for rapid indexing of rare k-mers in the case of large genomes and large k-mer sizes by using multiple Bloom filters (Bloom 1970) and the count-min sketches (Cormode and Muthukrishnan 2005).

VerityMap also addresses the challenge of identifying errors in genome assemblies in a reference-free mode. Even though the CHM13 cell line is effectively haploid, it features genomic instabilities between two haplotypes typically represented by insertions in one of the homologous chromosomes that are referred to as Het sites (Nurk et al. 2022). The ratio of two haplotypes in a Het site is not necessarily 1:1, suggesting that one of the haplotypes might be more prevalent. Automatic detection of Het sites in a haploid assembly and distinguishing them from misassemblies are important prerequisites for validating diploid assemblies. In addition to its read-mapping module, VerityMap includes a misassembly detection module for identifying misassemblies, Het sites, collapsed haplotypes, and haplotype-switch errors. The T2T Consortium applied this module to verify and correct intermediate assemblies of the CHM13 cell line (Nurk et al. 2022).

Results

Limitations of existing read mapping approaches

Because all existing assemblers generate some misassembled contigs, accurate mapping of reads that span the misassembly breakpoints is a critically important assembly validation step. Although minimap2 (Li 2018, 2021) and Winnowmap2 (Jain et al. 2020, 2022) accurately map reads to an error-free assembly (even in repetitive regions), their accuracy deteriorates in the case of error-prone assemblies or haplotype-resolved assemblies (because reads from highly similar regions often map to incorrect instances of these regions, albeit with several mismatches). Moreover, the dynamic programming algorithm for sequence alignment (with standard scoring) often fails to correctly align reads in highly repetitive regions, motivating the need for a new scoring (Supplemental Note 3, “Frequency-aware sequence alignment scoring”; Supplemental Figs. 2, 3).

Currently, TandemMapper is the only error-exposing aligner that accurately maps long reads to ETR assemblies that potentially contain misassemblies (Mikheenko et al. 2020). However, even though TandemMapper was used to validate the first centromere assemblies (Bzikadze and Pevzner 2020; Miga et al. 2020; Logsdon et al. 2021), it has limitations that prevent its applications to more complex regions of the genome; for example, it is designed for analyzing various higher-order repeats (HORs) such as human centromeres and is not applicable to repeats without HORs or for analyzing nonrepetitive parts of the genome.

Rare and solid k-mers

To speed-up the standard (time-consuming) dynamic programming algorithm for aligning long reads, many mappers (Li 2018; Jain et al. 2020; Mikheenko et al. 2020), as well as fast algorithms for detecting overlapping reads in genome assemblers (Chin et al. 2016; Li 2016; Lin et al. 2016; Koren et al. 2017; Wick et al. 2017; Kolmogorov et al. 2019, 2020; Nurk et al. 2020; Ruan and Li 2020; Cheng et al. 2021) construct a compatibility graph on a carefully selected small subset of k-mers in each read. The key differences between these tools are reflected in algorithms for selecting these k-mers and weighting the edges of the compatibility graph (rather than constructing the compatibility graph). VerityMap uses a new approach for selecting k-mers and weighting edges in the compatibility graph that addresses limitations of the previously developed long-read mappers and enables error-exposing and partially diploid-aware read mapping. VerityMap further finds a longest path in this graph using sparse dynamic programming and uses this path for read mapping.

A k-mer from an assembly is rare if it appears at most MaxRareOccurrences times in this assembly (otherwise a k-mer is called frequent). A rare k-mer is solid if it appears in a single contig, and its reverse-complementary k-mer does not appear in any contig. Note that this definition of a solid k-mer differs from the one used by TandemMapper (Mikheenko et al. 2020). Although the highly repetitive regions in the newly assembled complete genome constitute the biggest challenge for read mapping, they form <8% of the human genome (Nurk et al. 2022). Because nearly all k-mers in other regions are solid, VerityMap downsamples them to reduce the running time and memory footprint (Supplemental Note 5, “Downsampling solid k-mers in nonrepetitive regions”).

VerityMap pipeline

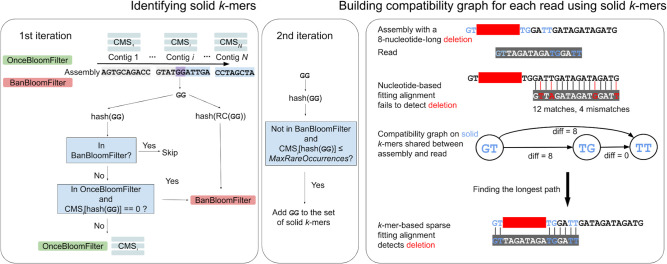
Figure 1 illustrates the VerityMap pipeline. First, VerityMap stores all k-mers from the assembly in two Bloom filters (Bloom 1970) and count–min sketch (CMS) data structures (Cormode and Muthukrishnan 2005) for estimating the count of each k-mer in the assembly and generating the set of solid k-mers that are later used for read mapping (see Methods subsection “Bloom filter and count-min sketch”).

Figure 1.

VerityMap pipeline. (Left) The input of VerityMap is an assembly (a set of contigs) and a set of reads that contributed to this assembly. VerityMap iterates through each contig twice in order to identify solid k-mers. At the first iteration, VerityMap stores k-mers that appear in multiple contigs and all reverse-complementary k-mers within the BanBloomFilter. For each contig, VerityMap constructs a CMS that counts occurrences of k-mers within this contig. Finally, VerityMap uses OnceBloomFilter (and BanBloomFilter) to distinguish between rare k-mers that appear within a single and multiple contigs. Both Bloom filters and the CMS corresponding to the current contig are being modified simultaneously during the first iteration through the assembly. At the second iteration, VerityMap queries the constructed data structures to identify the set of solid k-mers. (Right) Aligning a read GTTAGATAGATGGATT against a misassembled contig GTTGGATTGATAGATAGATG with an 8-nucleotide-long deletion TAGATAGA (solid k-mers are shown in blue). The solid k-mer GT (TG) precedes (follows) the deletion breakpoint. The nucleotide-based fitting alignment fails to identify this deletion owing to limitations of the standard scoring approaches in highly repetitive regions. In contrast, VerityMap identifies this deletion using the k-mer-based sparse fitting alignment and a new scoring approach. To achieve this goal, it constructs a compatibility graph on all pairs of solid k-mers shared between a read and the assembly and finds a longest path in this graph. The new scoring reflects the discrepancies in distances between solid k-mers in the assembly (distance 2 between GT and TG in the assembly) and solid k-mers in the read (distance 10 between GT and TG in the read), resulting in diff(GT,TG) = 8. VerityMap incorporates these discrepancies into the edge-weights of the compatibility graph and outputs a longest path in this graph as the primary read alignment.

For each read, VerityMap finds all solid k-mers in this read and builds a compatibility graph with the vertex-set formed by pairs of all solid k-mers shared between a read and the assembly. Because the downsampled set of solid k-mers is small, the compatibility graph is typically small; the longest path in this graph can be rapidly found using sparse dynamic programming. The careful definition of edge-weights in the compatibility graph helps to select the correct path (that represents the primary read alignment), even in the presence of assembly errors. Moreover, because the graph stores information about discrepancies in distances between solid k-mers occurring in a read and solid k-mers occurring in the assembly, it can be used to detect approximate locations of misassembly breakpoints without a base-level alignment that might be quite unreliable in highly repetitive regions. VerityMap first attempts to align the read to the forward strand and then to the reverse strand. Defaults for all parameters of VerityMap were selected based on performance analysis (Supplemental Figs. 5, 6; Supplemental Note 6, “VerityMap parameters”). The output of VerityMap is in the standard SAM format.

Data sets

Recently, the T2T Consortium generated the first complete assembly of a human genome represented by the CHM13 cell line (referred to as CHM13 assembly [Nurk et al. 2022]; Chr Y in this assembly is from a male sample HG002). In addition to analyzing the entire assembly using VerityMap, we focused on a particularly complex centromeric satellite region in Chromosome 9. Supplemental Table 2 in Supplemental Note 4, “Extended benchmarking of long-read mapping tools,” describes benchmarking results on a multitude of even more challenging data sets. Below we focus on one of these data sets that was generated by extracting the centromeric region from Chromosome 9 of the CHM13 assembly (referred to as Cen9). This region contains a human satellite 3 (HSat3) array that represented some of the most difficult challenges for the assembly effort of the T2T Consortium (Supplemental Note, “Resolution of Chr 6 and Chr 9,” of Nurk et al. 2022). To analyze how VerityMap handles assembly errors, we introduced an artificial deletion of length 10 kbp into the Cen9 region at position 20 Mbp (referred to as Cen9_del10). We further introduce a series of assemblies with various artificial misassemblies including a deletion, insertions, duplications, and a relocation in the Cen9 region: Cen9_del5, Cen9_ins5, Cen9_ins10, Cen9_tandem, Cen9_dup, Cen9_reloc (for a detailed description of all data sets, see Supplemental Table 1; Supplemental Note 4, “Extended benchmarking of long-read mapping tools”).

It remains unclear how to benchmark VerityMap on haplotype-resolved diploid assemblies because the Human Pangenome Reference (HPR) Consortium is still validating these assemblies. We thus used the assembled centromere of Chromosome X (CenX) from the HG002 HiFi read-set (from a male) generated by the HPR Consortium and the assembled CenX from the haploid CHM13 HiFi read-set generated by the T2T Consortium to mimic a diploid assembly of CenX. To analyze how VerityMap handles diploid assemblies we took alpha-satellite regions from Chromosome X of CHM13 and HG002 assemblies (combined, we refer to these chromosomes as ChrXDiploid, a synthetic diploid chromosome) and merged them into one file (referred to as CenX-Diploid). Then we cut each assembly at one of the canonical HOR units and concatenated them to mimic a haplotype-switch error (referred to as CenX-Diploid-Switch). Afterward, we simulated reads from both HG002 and CHM13 assemblies of Chr X to check whether VerityMap can detect the haplotype-switch error. We refer to alpha satellite arrays in Chromosome X in CHM13 (HG002) genome as ASat-X (ASat-X-HG002).

To illustrate that VerityMap identifies errors in real assemblies, we consider Cen10 in the interim version of CHM13 that predates the earliest publicly released version v0.9 (referred to as CHM13-Cen10-interim). CHM13-Cen10-interim contains a structural error that was detected by VerityMap and was later corrected by the T2T Consortium (Cen10 in current CHM13 assembly does not contain this error).

Below we list some benchmarking data sets (for the list of all benchmarking data sets, see Supplemental Table 1 in Supplemental Note 4, “Extended benchmarking of long-read mapping tools”). All simulated data sets are generated with pbsim2 (Ono et al. 2021).

• The CHM13-SimHiFi data set contains HiFi reads simulated from the CHM13 assembly.

• The Cen9Sim data set contains HiFi reads simulated from Cen9, whereas the Cen9Sim-Het data set contains HiFi reads simulated from both Cen9 and Cen9_del10 (1:1 ratio).

• The CenXDiploid-Sim data set contains HiFi reads simulated from ASat-X and ASat-X-HG002.

• The CHM13-RealHiFi data set contains real HiFi reads for the CHM13 sample generated by the T2T Consortium (20-kbp library; accession numbers SRX7897685-8). This data set is extended by reads originating from the Chr Y of HG002 sample.

• The ChrXDiploid-RealHiFi data set contains HiFi reads from CHM13-RealHiFi recruited to ChrXDiploid using Winnowmap2.

VerityMap maps nearly all reads with an extremely low number of incorrectly mapped reads

Analysis of the CHM13-SimHiFi data set (Supplemental Table 2) illustrates that VerityMap mapped >97% of reads in all chromosomes (except for Chr 21, where it mapped 94.25% of reads) with a low number of incorrectly mapped reads (76 out of 1.7 million reads for the entire genome). Mapped reads cover 99.5% of the entire genome (only 14 million uncovered bases).

VerityMap identifies assembly errors and heterozygous sites even in highly repetitive genomic regions

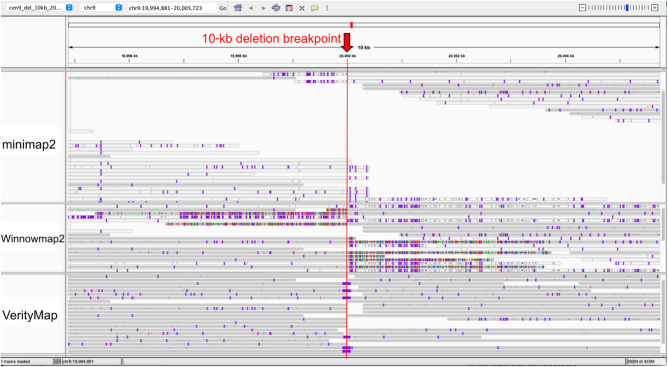
Table 1 illustrates that VerityMap, Winnowmap2, and minimap2 accurately map long and accurate reads to error-free assemblies (for description of all data sets and detailed benchmarking, section “Data sets” and Supplemental Table 1 in Supplemental Note 4, “Extended benchmarking of long-read mapping tools”). However, assembly errors and Het variants often trigger incorrect alignments, especially in highly repetitive regions. To benchmark the ability to map reads in a vicinity of the misassembly breakpoint, we aligned reads from the Cen9Sim data set to the Cen9_del10 assembly containing an artificial deletion of length 10 kbp (Table 2, top left). Although minimap2 and Winnomap2 map more reads than VerityMap, they have a high rate of incorrectly mapped reads, whereas VerityMap yields few incorrectly mapped reads. Because incorrect read alignments may prevent the detection of errors and heterozygous sites in downstream analysis, it is preferable to classify some reads as “unalignable” instead of generating erroneous alignments. Both minimap2 and Winnowmap2 failed to detect this deletion: minimap2 did not report any primary alignment in a 1-kb region before the breakpoint (all reads were incorrectly mapped somewhere else), whereas Winnowmap2 incorrectly extended alignments through the deletion breakpoint in the Cen9_del10 region (Fig. 2). In addition, to reproduce a scenario of a heterozygous deletion (Table 2, top right), we aligned reads from the Cen9Sim-Het data set containing HiFi reads simulated from both Cen9 and Cen9_del10 to the Cen9_del10 assembly. Table 2 (top right) illustrates that both minimap2 and Winnowmap2 incorrectly mapped reads simulated from Cen9 near the deletion breakpoint. VerityMap either reports reads that are correctly spanning the deletion breakpoint or clips read alignments from Cen9Sim data set at the breakpoint and thus indicates a putative heterozygous deletion. Table 2, bottom, provides further benchmark of VerityMap, Winnowmap2, and minimap2 of aligning simulated reads from the Cen9Sim read-set to the Cen9_del5, Cen9_ins5, Cen9_ins10, Cen9_tandem, Cen9_dup, and Cen9_reloc assemblies (for a detailed description of these data sets and for benchmarking on more data sets, see Supplemental Tables 1–4; Supplemental Note 4, “Extended benchmarking of long-read mapping tools”). In all cases, VerityMap has the minimal number of incorrectly mapped reads and either reports reads that are correctly spanning the breakpoint or clips read alignments at the breakpoint.

Figure 2.

Alignments of reads from the Cen9Sim data set to Cen9_del10 generated by minimap2, Winnowmap2, and VerityMap shown using the Integrative Genomics Viewer (IGV) browser (Robinson et al. 2011). minimap2 does not report any primary alignments (shown in gray) spanning the deletion breakpoint, and all secondary alignments (shown in white) indicate systematic mismatches mapping to an incorrect copy of the repeat. Winnowmap2 reports mappings that are incorrectly spanning the breakpoint. VerityMap either reports an alignment correctly spanning the deletion breakpoint (indicates a 10-kb deletion) or clips read alignment at the breakpoint.

Supplemental Note 7, “Validation of fragmented haploid and diploid assemblies,” shows how VerityMap can be applied to fragmented rather than complete assemblies. Supplemental Note 4, “Extended benchmarking of long-read mapping tools” (Supplemental Fig. 4), applies VerityMap to the assembly of the CHM13 cell line generated by LJA (Bankevich et al. 2022) and identifies putative misassemblies and heterozygous sites.

VerityMap correctly distinguishes haplotypes in diploid assemblies and identifies haplotype-switch errors

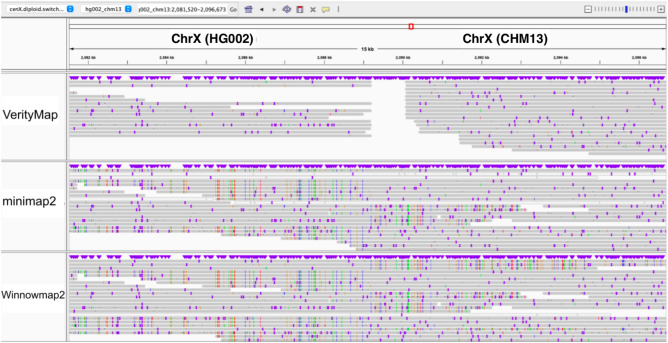
We aligned reads from the CenXDiploid-Sim data set to CenXDiploid-Switch assembly containing a haplotype-switch error. We launched VerityMap in the special DiploidVerityMap mode that uses a more permissive strategy for selecting solid k-mers. Figure 3 illustrates that VerityMap does not incorrectly extend alignments of any reads through the haplotype-switch breakpoint (and thus detects this haplotype-switch error), whereas Winnowmap2 and minimap2 extend them through it.

Figure 3.

Visualization of VerityMap, Winnowmap2, and minimap2 alignments of simulated reads from the CenX-Diploid data set to the CenX-Diploid-Switch sequence using the IGV browser (Robinson et al. 2011). VerityMap, in difference from Winnowmap2 and minimap2, reveals the haplotype-switch breakpoint.

We also aligned reads from the ChrX-RealHiFi data set (total number of reads 621,522) to ChrXDiploid assembly. VerityMap (Winnowmap2, minimap2) mapped 4474 (10,190, 10,255) reads to the incorrect haplotype and 493,012 (553,953, 552,051) to the correct haplotype. Here, we filtered all secondary alignments, as well as all alignments with mapping quality zero. VerityMap uses a more conservative strategy for mapping reads to the diploid reference to achieve higher accuracy (that is critically important for detecting misassemblies) at the cost of mapping fewer reads. Even though VerityMap presents an advancement in accurate mapping of reads to diploid assemblies, this problem remains a difficult challenge.

VerityMap identifies assembly errors and Het sites using real HiFi data sets

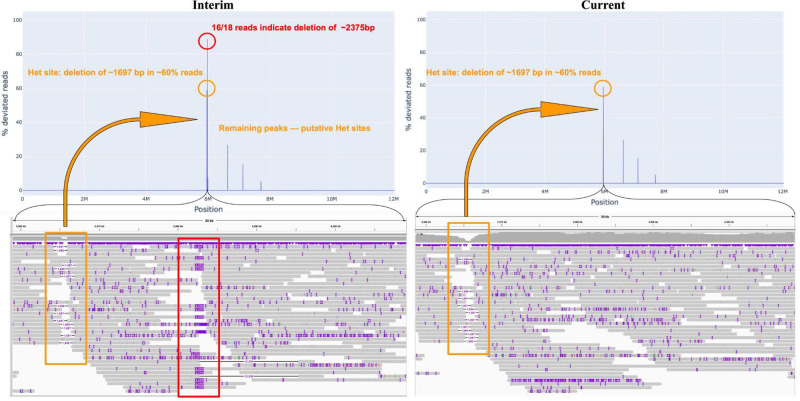
The CHM13-Cen10-interim data set contains an interim version of Cen10 in CHM13 that predates the earliest publicly released CHM13 assembly by the T2T Consortium. VerityMap was used to detect a deletion of length ∼2.4 kbp in this version, an error that was later corrected by the T2T Consortium and is fixed in the current version of Cen10 in the CHM13 assembly (Fig. 4).

Figure 4.

VerityMap detects a deletion in CHM13-Cen10-interim that is absent from the publicly released CHM13 assembly. The top panel shows the distance concordance test applied to CHM13-Cen10-interim (left) and Cen10 in CHM13 assembly (right). The bottom panel shows read alignments ∼6 Mbp in two versions of the assembly. (Bottom left) VerityMap reveals a deletion of length ∼2.4 kbp in CHM13-Cen10-interim. The remaining peaks correspond to the Het sites with various multiplicities in the assembly. In particular, one heterozygous deletion of ∼1.7 kbp that is supported by ∼60% of reads is only 20 kbp upstream of the misassembly site. (Bottom right) The misassembly is corrected in the current version of Cen10 assembly, whereas the putative Het sites remain.

We also aligned the CHM13-RealHiFi data set to CHM13 assembly to reveal possible assembly errors and Het sites (Supplemental Table 4). Overall, we found 86 heterozygous sites with Concordance = 0.2–0.8 and one site with Concordance = 1. The manual validation of this site confirmed a likely 2.4-kbp insertion in the Chr 19 (Fig. 5, right; Nurk et al. 2022). Importantly, this site was not detected by the state-of-the-art methods for detecting structural variations (SVs) (Mc Cartney et al. 2022).

Figure 5.

Distance concordance test applied to simulated and real read-sets. (Left) Mapping reads from the data set Cen9Sim reveals an artificial deletion at location 20 Mbp. Concordance(a_A, b_A) = 1 and TopDiff(a_A, b_A) = 10,003 for solid k-mer a_A at position 19,999,691 and b_A at position 20,000,001, revealing the approximate location of the deletion of size 10 kbp. (Middle) Mapping reads from the data set Cen9Sim-Het reveals an artificial Het site at position 20 Mbp with Concordance(a_A, b_A) = 0.33 for the same solid k-mers a_A and b_A and TopDiff(a_A, b_A) = 10,005 pointing at insertion in Cen9_del10 of size 10 kbp existing in one of the artificial haplotypes. (Right) Mapping HiFi reads reveals several Het variants and a likely assembly error (with Concordance = 1 at 28.5 Mbp) in the centromere of Chromosome 19 (for description of all data sets, see Supplemental Table 1; Supplemental Note 4, “Extended benchmarking of long-read mapping tools”).

Discussion

We presented the VerityMap tool, the first accurate, error-exposing and partially diploid-aware tool for long-read mapping to complete assemblies. We used it to validate and improve the recently published complete human assembly during several rounds of its evaluations (Mc Cartney et al. 2022; Nurk et al. 2022). Even though Mc Cartney et al. (2022) used VerityMap for validating this assembly, they refer to TandemMapper because VerityMap was still in development and did not have a name at the time when this paper was submitted.

Below we discuss some limitations of VerityMap that we plan to address. All state-of-the-art read-mappers use multiple (often poorly justified) parameters for selecting a small set of k-mers in each read, weighting edges in the compatibility graph, etc. For example, minimap2, the workhorse of long-read mapping, has many parameters (including some hidden parameters), and it remains unclear how they were optimized (no description in Li 2018). Even though we used the default parameters for Winnowmap2 and minimap2, we do not rule out that other parameter values could improve the performance of these tools. VerityMap also suffers from the “curse of multiparameters”: Even though we carefully selected its parameters using alignments of reads to the human genome, a systematic approach using diverse organisms for learning these parameters is needed. In particular, scoring of the edges in the compatibility graph might overfit to the human genome k-mer distribution.

The output of VerityMap is in standard SAM/BAM format and is, in principle, compatible with downstream variant calling tools for detection of Het variants or misassembles. However, VerityMap detects approximate locations of a structural event rather than its exact coordinates, which may present a challenge for variant calling tools especially in highly repetitive regions such as centromeres.

The definition of a solid k-mer requires that it appears in a single contig of the assembly. Even though solid k-mers are not uniformly distributed over the human genome, our benchmarking revealed that VerityMap detected many true-positive and never-reported false-positive misassemblies. However, this definition might be too restrictive for a highly inbred organism with long stretches of homologous chromosomes sharing the same sequence. A highly fragmented assembly presents a similar challenge because rare k-mers within a single chromosome might be shared between several contigs, rendering them nonsolid. As a result, few to no solid k-mers will be selected in such regions of the genome, leading to gaps in read coverage. Allowing a solid k-mer to be shared by multiple contigs, albeit potentially more error-prone, might mitigate this issue. Similarly, the requirement that the reverse-complement of a solid k-mer does not appear in any contig needs to be relaxed. We selected a conservative strategy for the initial VerityMap development because our primary goal was to evaluate the complete haploid assembly. Our next goal is to overcome these limitations and apply VerityMap for validating haplotype-resolved assemblies generated by the HPR Consortium. The described benchmarking suggests that VerityMap has a potential for effective evaluation of complete haplotype-resolved assemblies. Supplemental Note 7, “Validation of fragmented haploid and diploid assemblies,” introduces a more general k-mer indexing scheme as well as modifications to the compatibility graph that allow validation of more general fragmented haploid or diploid assemblies (rather than limited to only complete haploid assemblies). Supplemental Note 4, “Extended benchmarking of long-read mapping tools,” presents an example of the application of VerityMap to a fragmented assembly. Accurate estimation of VerityMap's statistical power for detecting misassemblies in fragmented assemblies remains an open problem.

Even though HiFi reads allow validation of the most regions of the CHM13 assembly, ONT reads provide important complementary quality assessment (Bzikadze and Pevzner 2020; Nurk et al. 2022). Even though this paper focuses on HiFi reads, VerityMap has an ONT mode for ONT reads. We have chosen to focus on HiFi reads because ONT reads currently represent a moving target: Over the past year, the error-profile of ONT reads has been rapidly improving, with the latest chemistry approaching error-rate as low as 1% (Sereika et al. 2022). Although HiFi reads are more accurate (hence they allow selection of longer solid k-mers), they are shorter than ONT reads. As a result, the length of the longest paths in the compatibility graph for ONT reads can exceed those lengths for HiFi reads and thus connect solid k-mers surrounding “solid k-mer deserts”—long stretches of DNA without any solid k-mers. Together with rapidly improving chemistry, ONT reads might become a self-sufficient alternative for quality assessment of genome assembly.

VerityMap has been designed primarily to detect errors in the assemblies rather than identify SVs in genomes. Even though, many misassemblies and SVs can be represented as indels, the distribution of misassemblies and SVs over the universe of all possible indels is substantially different. First, a prominent source of genomic diversity is presented by short SVs and copy number variants (CNVs) in short tandem repeats (STRs). Such differences are rarely observed as misassemblies because they do not present a challenge for long-read assemblers. Previous studies showed that HiFi assemblers are very accurate with respect to single-nucleotide substitutions and short indels (Nurk et al. 2020; Cheng et al. 2021; Bankevich et al. 2022), and these inaccuracies in assemblies typically present polishing artifacts rather than imperfections of an assembly algorithm itself. Second, misassemblies typically involve large (multikilobasepair) long indels (or inversions) that correspond to the incorrect traversal of the assembly graph (or, worse, its faulty topology). Although it is possible that an alternative (and incorrect) traversal of the graph might result in a haplotype that is present in the population (we are aware of a single case that involves a large 600-kbp inversion on Chr Y recently assembled by the T2T Consortium), it remains unclear whether this is a widespread phenomenon. Finally, some of the variations in the genome (e.g., in human centromeres) are much more complex than simple CNVs of the tandem repeat units, and it seems infeasible that an assembly algorithm might produce such a complicated misassembly as a result of an incorrect graph traversal.

When developing VerityMap, we have concentrated on simulated examples that resemble misassemblies that we have observed in practice of developing assembly algorithms: specifically, (1) the indels that were introduced in the early versions of centromere assemblies (Miga et al. 2020) that were subsequently detected by an early version of TandemMapper (Mikheenko et al. 2020) and were later corrected in Bzikadze and Pevzner (2020), (2) misassemblies that were present in interim versions of CHM13 assemblies generated by the T2T Consortium, and (3) misassemblies generated by LJA assembler (Bankevich et al. 2022). Supplemental Note 1, “Similarities and differences between detecting mutations and detecting misassemblies,” shows that VerityMap can be used as an input to various SV detection tools, and VerityMap's own DistanceDiscordant test can complement these tools.

Methods

Selecting solid k-mers

Similar to TandemMapper (Mikheenko et al. 2020), VerityMap uses rare k-mers as anchors for the read mapping. Selection of the k-mer size is dictated by the error rate in long reads. Because long error-prone reads have a high error rate, long genomic k-mers rarely “survive” without errors in such reads. For example, the probability that a 19-mer “survives” in an error-prone ONT read (generated with basecaller Guppy flip-flop 2.3.1) is only 0.34 (Bzikadze and Pevzner 2020). However, because long and accurate reads have much smaller error rates (0.7% for ONT reads generated with flow cell R10.4 and 0.2% for HiFi reads) (Nurk et al. 2020; https://nanoporetech.com/accuracy), one can set the large default k-mer size to accurately map such reads even in highly repetitive regions such as Cen9 (see Supplemental Note 10, “The choice of k-mer size and the shortest unique substrings”; Supplemental Fig. 7). VerityMap sets the default value k = 301 and MaxRareOccurrences = 10 (see Supplemental Note 6, “VerityMap parameters”).

HSAT2,3 array in the Cen9 region is an ETR containing long inverted repeats. Importantly, for 6344 out of ≅22 million rare k-mers (k = 301) in this region, their reverse-complementary k-mer is frequent in the genome. Because the strandedness information is not available, using such k-mers for read mapping might reduce the mapping accuracy. Similarly, using a rare k-mer that is shared between two contigs (e.g., two homologous or nonhomologous chromosomes) might also lead to incorrect read mapping. Because VerityMap aims primarily to reduce the number of incorrect alignments, it implements a rather conservative strategy and uses solid rather than rare k-mers for read mapping to complete assemblies.

Sparse dynamic programming for read mapping

A standard dynamic programming approach for computing the fitting alignment of a query onto a target finds a longest path in the grid-like directed acyclic graph (DAG), where vertices correspond to all pairs of positions (one in the target and one in the query). Analysis of the CHM13 assembly by the T2T Consortium revealed that although the fitting alignment of a read usually finds its correct position in the assembly, it may misplace the reads that originated from highly repetitive regions (e.g., centromeres and other ETRs), particularly in regions with assembly errors (see Supplemental Note 3, “Frequency-aware sequence alignment scoring”; Supplemental Figs. 2, 3). Thus, mapping reads to ETRs requires a new algorithm and a new scoring approach.

Sparse dynamic programming (Gusfield 1997) is a common way to speed-up sequence alignment by selecting a small subset of points in a grid that are likely traversed by an optimal path, constructing an edge-weighted DAG on these points (rather than on all points in the entire grid), and finding a longest path in the resulting smaller graph. We note that although sparse dynamic programming approximates rather than reconstructs the optimal sequence alignment, this approximation is usually sufficient for read mapping. However, to achieve an accurate approximation, one has to (1) carefully select a vertex-set of the DAG and (2) carefully define the edge-weights in the sparse DAG to address the ETR mapping challenge. For example, a k-mer-based sparse fitting alignment amounts to finding a longest path in the DAG where vertices correspond to all pairs of k-mer-matching positions from the target and the query (positions are k-mer-matching if k-mers starting at these positions are identical) and directed edges connect all pairs of vertices (i,j) and (i′,j′) with i < i′ and j < j′. However, the standard scoring approach for the sparse fitting alignment, which scores all edges with unit weights, fails to address the ETR mapping challenge because it does not account for greatly varying frequencies of k-mers in some targets.

Although the sparse fitting alignment is faster than the standard fitting alignment, it still may be computationally infeasible in long highly repetitive regions owing to a quadratic running time in the number of matching positions. Below we describe how VerityMap addresses the mapping challenge by considering matches of (undersampled) solid k-mers rather than all k-mers.

Compatible k-mers

As solid k-mers are not necessarily unique in the assembly, we consider each occurrence of each solid k-mer separately. Let a_R and b_R (a_A and b_A) be occurrences of solid k-mers a and b in the read R (contig A) such as a_R precedes b_R (a_A precedes b_A). To make a_R and b_R uniquely defined for each read, we limit attention to solid k-mers that appear exactly once in this read. We define d(a_R, b_R) (d(a_A, b_A)) as the distance between a_R and b_R in R (a_A and b_A in A). We refer to the pair of a_A and a_R (b_A and b_R) as a match a_M (b_M) and write a_M < b_M if a_A precedes b_A and a_R precedes b_R. We define distance(a_M, b_M) = min{d(a_R,b_R), d(a_A,b_A)}, diff(a_M, b_M) = |d(a_R,b_R)−d(a_A,b_A)|, and bias(a_M, b_M) = ln(diff(a_M, b_M)) (Supplemental Note 3, “Frequency-aware sequence alignment scoring”; Supplemental Figs. 2, 3).

We call matches a_M and b_M close if distance(a_M, b_M) < MaxJump (the default value MaxJump = 100,000) to exclude k-mers locating far apart from each other but preserve consecutive rare k-mers even if they are separated by a long stretch of frequent k-mers. Matches a_M and b_M are overlapping if distance(a_M,b_M) < k. Close matches a_M and b_M are synced if either (1) a_M and b_M are overlapping with diff(a_M, b_M) = 0 or (2) they are not overlapping. Finally, we call a_M and b_M compatible if (1) a_M < b_M and (2) a_M and b_M are synced (see Supplemental Note 3, “Frequency-aware sequence alignment scoring”; Supplemental Figs. 2, 3). Note that VerityMap modifies the notion of compatible k-mers introduced by Mikheenko et al. (2020) to detect assembly errors that evade detection by TandemMapper.

Compatibility graph

Given a read R, an assembly A, and a set S of solid k-mers, VerityMap constructs a weighted compatibility graph G(R, A, S) on the vertex-set of all pairs of identical solid k-mers from R and A. Vertices a_M = (a_A,a_R) and b_M = (b_A,b_R) are connected by an edge if a_M and b_M are compatible. Edge-weights in this graph should be carefully chosen because a match of a unique solid k-mer is more valuable than a match of a nonunique solid k-mer and because nonoverlapping matches are more valuable than overlapping matches. VerityMap thus defines weight(a_M, b_M) = premium(a_M, b_M)−penalty(a_M, b_M) in such a way that (1) premium(a_M, b_M) is larger in the case when b_M represents a unique k-mer as compared to the case when it represents a nonunique k-mer; (2) premium(a_M, b_M) is larger for nonoverlapping matches a_M and b_M as compared to overlapping matches; and (3) if a_M and b_M represent a pair of k-mers that flank misassembly breakpoints, penalty(a_M, b_M) should not be too large, thus allowing VerityMap to detect a misassembly.

To address goal 1, VerityMap assigns the score UniqueScore to all unique k-mers and the smaller score RareScore to all nonunique solid k-mers in the assembly (default values UniqueScore = 3 and RareScore = 0.1). The score Score(b_M) of a match b_M is defined as the score of the k-mer it represents.

To address goal 2, VerityMap defines the score EdgeScore(a_M, b_M) of the edge (a_M,b_M) in the compatibility graph as one for nonoverlapping matches and as a smaller distance(a_M,b_M)/k for overlapping matches. Finally, it defines premium(a_M, b_M) = Score(b_M) * EdgeScore(a_M,b_M).

To ensure that the longest path in the compatibility graph correctly aligns a read against the assembly, it is important to penalize edges with large bias, for example, to define penalty(a_M, b_M) = bias(a_M, b_M). However, to address goal 3 and to design an error-exposing read-mapper, it is important that the penalties of edges connecting k-mers that represent misassembly breakpoints are not excessive, even in the case when these edges have a large bias. VerityMap thus limits the maximum possible penalty using the MisassemblyPenalty threshold (default value is five) and defines penalty(a_M, b_M) = min[MisassemblyPenalty, bias(a_M, b_M)]. Supplemental Note 11, “Finding a longest path in the compatibility graph,” describes how VerityMap finds a longest path in the compatibility graph.

The challenge of finding positions of all solid k-mers in a large genome

TandemMapper uses a naive strategy of indexing solid k-mers in a genome, Genome (finding a list of positions for each solid k-mer), by traversing Genome twice. During the first traversal, it counts all k-mers by storing them in a hash-table. During the second traversal, it checks if a k-mer is solid using the constructed hash-table and records positions of all solid k-mers (total time and memory is O(|Genome|*k)). This strategy becomes prohibitively time-consuming unless mapping reads against relatively short regions (e.g., several Mbp) using short k-mers (e.g., with k < 30). VerityMap uses a different strategy that enables mapping reads against the entire human genome using long k-mers (e.g., with k > 300).

The complexity of pattern matching can be reduced by indexing rolling hashes of k-mers rather than the k-mers themselves (Karp and Rabin 1987). Given a rolling hash function and a hash value for a k-mer a_i…a_{i + k−1} in a genome …a_i…a_{i + k−1} a_{i + k}…, one can compute the hash value of the next k-mer a_{i + 1}…a_{i + k−1} a_{i + k} in O(1) time, thus, improving the run-time complexity from O(|Genome|*k) to O(|Genome|). Note that a hash collision will lead to an overestimated frequency for k-mers with collided hashes. This might lead to misclassification of some solid k-mers as nonsolid but never leads to recruiting nonsolid k-mers. Unfortunately, the existing k-mer counting tools do not allow querying a count of a rolling hash instead of a k-mer and thus do not immediately lead to a fast-indexing algorithm with O(|Genome|) running time. Moreover, because most of the k-mers in the nonrepetitive parts of the genome are solid, we aim to select only their small subset for constructing the (small) compatibility graph (see Supplemental Note 5, “Downsampling solid k-mers in nonrepetitive regions”). Unfortunately, the existing k-mer counting tools do not produce a downsampled database of k-mer counts, which leads to an unnecessary computational burden. To overcome the limitations of existing approaches, VerityMap uses a probabilistic procedure for indexing solid k-mers inspired by the Jellyfish algorithm (Marçais and Kingsford 2011). Below we briefly describe the Bloom filter and the CMS data structures that VerityMap uses for indexing solid k-mers.

Bloom filter and count-min sketch

The Bloom filter (Bloom 1970) is a space-efficient probabilistic data structure that is used to test whether an element is a member of a set and that may report false positives (with a small false-positive probability) but never false negatives. Given a genome, Genome (or its assembly), its Bloom filter is formed by BloomNumber independent hash functions, each mapping a k-mer from Genome into a bit array of size BloomSize. Storing all k-mers in a Bloom filter allows one to quickly query whether an arbitrary k-mer occurs in the genome. Given hash functions h₁,h₂,…,h_BloomNumber and a k-mer a, one can quickly check whether all bits h₁(a), h₂(a),…, h_BloomNumber(a) of the Bloom filter are equal to one, an indication that the k-mer a may occur in the genome. Thus, a Bloom filter allows one to efficiently query whether an arbitrary k-mer occurs in the genome (with a small false-positive probability).

Bloom filter allows one to check whether an element belongs to a multiset but does not evaluate how frequent it is in this multiset. The CMS is a space-efficient probabilistic data structure that provides an upper bound on the count of an element in a multiset (Cormode and Muthukrishnan 2005). CMS is a modification of a single-bit Bloom filter array that uses a counter array of size CMSNumber * CMSSize with cells containing several bits. This property allows it to count repeatedly inserted elements: When an element is inserted, the values of all CMSNumber hash functions are computed and the corresponding cells in the counter arrays are incremented by one (in case an increment leads to an overflow, the corresponding cell gets frozen). To provide an upper bound for the count of a given element, CMS computes the values of all CMSNumber hash functions and reports the minimum of the corresponding cells in the counter arrays (a frozen cell votes for the infinity count). Thus, CMS sometimes overestimates the count of an element but never underestimates it. VerityMap uses CMS to distinguish unique, rare, and frequent k-mers and with a controlled probability misclassifies a rare (unique) k-mer as frequent (rare).

Identification of rare k-mers using CMS

For each Contig in genome, Genome, VerityMap counts all k-mers in this contig by storing them in the count-min-sketch CMS(Contig) = CMS(Contig, k, Bits, CMSNumber, CMSSize) formed by CMSNumber hash functions, each mapping a k-mer into a counter array of size CMSSize, where each counter takes Bits bits. The memory footprint of CMS is CMSNumber*Bits*CMSSize bits. The total run-time for inserting all k-mers from Contig into this CMS is O(|Contig|*CMSNumber*Bits*k). Storing rolling hashes instead of k-mers further reduces the complexity to O(|Genome|*CMSNumber*Bits). Supplemental Note 6, “VerityMap parameters,” describes how VerityMap sets the parameters of the CMS and the Bloom filters.

Identification of solid k-mers using the bloom filter

To verify whether a rare k-mer is solid, VerityMap checks that (1) its reverse-complement does not appear in the genome, and (2) it appears only in a single contig. Storing all k-mers from the genome, Genome, in a Bloom filter allows VerityMap to efficiently query whether an arbitrary k-mer is present in Genome. To check conditions 1 and 2 for identifying solid k-mers, VerityMap constructs two Bloom filters: BanBloomFilter(Genome) and OnceBloomFilter(Genome) of an optimal size (Bloom 1970) for the expected number of k-mers (|Genome| is an upper bound) and for the target false-positive probability BloomFPP (default value BloomFPP = 0.00001).

For every rare k-mer a, we ensure that its reverse complement a* does not appear in the Genome by inserting a* in the BanBloomFilter and, in the end, checking that a is not present in BanBloomFilter. To check if a k-mer a appears in a single contig, VerityMap scans all contigs and synchronously inserts a k-mer a from a contig Contig in both OnceBloomFilter(Genome) and CMS(Contig). This synchronous construction of both OnceBloomFilter(Genome) and CMS(Contig) allows one to check whether the k-mer a occurs in a single contig, albeit with a small probability of error. Indeed, if it is already present in OnceBloomFilter(Genome) but missing in CMS(Contig), it likely appeared in a previously scanned contig. In this case, VerityMap filters out the k-mer a by inserting it into BanBloomFilter(Genome). However, if it is present in both OnceBloomFilter(Genome) and CMS(Contig), the k-mer a is retained because it may occur in a single contig.

To reduce the complexity, instead of inserting k-mers in the Bloom filter, we store their rolling hashes. The total running time of finding all solid k-mers and determining their genomic positions is O(|Genome|*(BloomHashNumber + CMSNumber)). The total memory footprint is O(|Genome|+(CMSNumber*CMSSize*Bits + BloomHashNumber*BloomSize)).

Because the Bloom filter is a probabilistic data structure, some solid k-mers might be falsely removed as breaking either condition 1 or 2. In practice, very few solid k-mers are filtered out (as controlled by the parameter BloomFPP), and that does not lead to deterioration of read mapping. Importantly, no true nonsolid k-mer might be misclassified as solid. For example, a naive implementation of an “exact” strategy (that uses deterministic albeit more memory consuming data structures) extracts 149,548,373 solid k-mers from Chr X in CHM13 assembly, whereas the “approximate” strategy described above (based on Bloom filters and CMSs) extracts 147,105,002 solid k-mers from the same data set (>98% of truly solid k-mers). For the sake of easy comparison, we did not downsample solid k-mers in this example as described in Supplemental Note 5, “Downsampling solid k-mers in nonrepetitive regions.”

Distance concordance test

VerityMap detects approximate locations of misassembly breakpoints without requiring a time-consuming nucleotide-level alignment. Indeed, if a read, R, spans a misassembly breakpoint, a longest path in the compatibility graph G(R,A,S) often provides a hint for finding this breakpoint. For example, a deletion of length L in an assembly typically triggers an edge (a_M, b_M) with a large difference diff(a_M, b_M)≅L, where a_M and b_M represent solid k-mers flanking the deletion breakpoint in such a way that a_M (b_M) precedes (follows) the deletion breakpoint as illustrated in Figure 1.

However, a single read may have nonzero values of diff(a_M, b_M) even in the case of error-free assembly, especially when d(a_R,b_R) is high. However, this difference is usually low for accurate HiFi reads and error-free assemblies, suggesting that large differences can be used for detecting misassemblies. To show that it is indeed the case, we considered 18 million of unique k-mers (k = 301) in Cen9 and selected 100,000 pairs of unique k-mers such that k-mers in each pair are 10,000 bp apart in the assembly. The mean distance between the same pairs of k-mers in reads was 10,002 ± 3.4 bp. Thus, diff(a_M, b_M) usually does not exceed 3 * 3.4 = 10.2 bp if d(a_A,b_A) = 10,000 bp. Given our upper limit for a distance between two consecutive k-mers equal to 100,000 bp, we set a lower threshold for an indel size MinIndelSize to 100 bp. Thus, if nearly all longest paths containing k-mers a and b show a systematic bias in values of diff(a_M, b_M) and diff(a_M, b_M) > MinIndelSize, then an indel of approximate size diff(a_M, b_M) is likely contained between a_A and b_A. We classify each read that shows systematic bias in values of diff(a_M, b_M) as a discordant read and report the fraction of discordant reads connecting each pair of solid k-mers in the assembly.

Formally, for each read R and for each pair a_M and b_M of consecutive matches in a longest path in compatibility graph, we add the number diff(a_M, b_M) to a set Diffs(a_A, b_A). We test the hypothesis that the mean of Diffs(a_A, b_A) is zero and refer to the pair a_A and b_A as significant if this hypothesis is rejected (two-sided one-sample t-test). We use Bonferroni family-wise error rate correction and set up significance level α_DC (the default value α_DC = 0.05). For each significant pair a_A and b_A of consecutive k-mers in a contig A, we compute the proportion Concordance(a_A, b_A) of the most frequent difference TopDiff(a_A, b_A) in Diffs(a_A, b_A). Figure 5 (left and middle) shows the Concordance(a_A, b_A) across the Cen9_del10 region when aligning simulated reads from the data set Cen9Sim (Cen9Sim-Het) and reveals the artificial deletion (Het site) of length 10 kbp at position 20 Mbp. Figure 5 (right) shows the Concordance(a_A, b_A) across Cen19 when aligning real HiFi reads and reveals the likely assembly error and several Het sites (see Results).

Software availability

The codebase of VerityMap version 2.1.2 generated in this study has been submitted to GitHub (https://github.com/ablab/VerityMap), to Zenodo (https://zenodo.org/record/6469695#.Y5O5w33MI5s), and is available as Supplemental Code.

Competing interest statement

The authors declare no competing interests.