MR Fingerprinting for Semisolid Magnetization Transfer and Chemical Exchange Saturation Transfer Quantification

Abstract

Chemical exchange saturation transfer (CEST) MRI has positioned itself as a promising contrast mechanism, capable of providing molecular information at sufficient resolution and amplified sensitivity. However, it has not yet become a routinely employed clinical technique, due to a variety of confounding factors affecting its contrast-weighted image interpretation and the inherently long scan time. CEST MR fingerprinting (MRF), is a novel approach for addressing these challenges, allowing simultaneous quantitation of several proton exchange parameters using rapid acquisition schemes. Recently, a number of deep-learning algorithms were developed to further boost the performance and speed of CEST and semi-solid macro-molecule magnetization transfer (MT) MRF. This review article describes the fundamental theory behind semisolid MT/CEST-MRF and its main applications. It then details supervised and unsupervised learning approaches for MRF image reconstruction and describes artificial intelligent (AI)-based pipelines for protocol optimization. Finally, practical considerations are discussed, and future perspectives are given, accompanied by basic demonstration code and data.

1. Introduction

Semisolid magnetization transfer (MT) and chemical exchange saturation transfer (CEST) MRI have proven to be powerful tools for detecting changes in semisolid macromolecular components (e.g., myelin sheets or membranes and lipids) and solute molecules (e.g., mobile proteins, peptides, and metabolites) in numerous disease pathologies.^1-7 However, most currently used imaging protocols are not able to provide quantitative measurement of tissue parameters and acquire semisolid MT and CEST weighted images only. In addition, the observed CEST contrast is a complex overlay of contributions from different proton pools, including amide, amine, semisolid MT, and/or relayed nuclear Overhauser enhancement (rNOE), which can sometimes bias the biological interpretation of the observed signal changes. For instance, amide proton transfer (APT) imaging, a variant of CEST MRI, has shown promise in brain cancer detection, diagnosis, and treatment-response assessment.^8-11 These studies have established that increased cytosolic protein content in gliomas can cause an APT hyperintensity, as revealed by proteomics and in-vivo MR spectroscopy.^12,13 However, some recent preclinical,^14,15 and clinical studies of brain tumors,^16,17 which observed a hyperintense tumor APT signal, demonstrated a decreased tumor amide CEST contrast after separating out the contributions to the APT signal from the semisolid MT and rNOE proton pools. This decreased tumor amide CEST signal may be due to the significant tumor edema or due to differences in the RF saturation parameter or analysis method used. Thus, the complex nature of the CEST contrast can challenge the interpretation of the underlying disease pathology in some cases.¹⁸

Similarly, the MT ratio (MTR) metric conventionally used in semisolid MT imaging is influenced by relaxation effects, thus limiting the detection of the specific tissue composition.^4,19 Even worse, the weighted signals or image contrasts are highly dependent on the image acquisition parameters (e.g., TR, RF saturation powers, durations, frequency offsets, and saturation labeling strategies, etc.) and data analysis methods.²⁰ These differences presumably contribute in part to the inconsistencies observed across studies. Consequently, the development of quantitative semisolid MT and CEST imaging methodologies could provide correct proton-exchange-parameter estimates, independent of the above-mentioned confounds, experimental settings, and data analysis approaches, and improve the repeatability and reproducibility of the measurements across different imaging platforms.

Currently, the semisolid MT and CEST communities have a great interest in quantifying exchangeable proton concentrations and exchange rates as surrogate biomarkers of protein/metabolite/lipid composition and intracellular pH, respectively. One of the most promising exchange quantification methods, fits the CEST signals using the steady-state analytical solution of the Bloch McConnell (BM) equations.²¹ However, it requires long scan and computation times. Over the past decade, although many quantification methodologies have been developed to address the challenges discussed above, a tremendous leap in acquisition and reconstruction times was only recently made by integrating semisolid MT and CEST with MR fingerprinting (MRF). Furthermore, recent advances in deep-learning provide a new paradigm for solving ill-posed inverse problems in MRF reconstruction. Herein, we provide readers with an overview of semisolid MT and CEST-MRF acquisition, reconstruction, optimization, and inter-pretation strategies. The scope and organization of this review are described in Supporting Information Figure S1.

2. CEST MRI Background

2.1. CEST-Weighted Imaging

CEST-weighted signals are usually obtained from the Z-spectrum using an MTR asymmetry analysis at certain frequency offsets, where the MTR_asym is given by:³

$$MT{R}_{asym}=\frac{S(-\Delta \omega )-S(+\Delta \omega )}{S_0}=Z(-\Delta \omega )-Z(+\Delta \omega )$$ (1)

where S(±Δω) is the signal measured with saturation at offset ±Δω, and S₀ is a reference signal acquired without saturation. In the case of APT imaging, the MTR_asym is evaluated at the amide chemical shift of 3.5 ppm from the water resonance. However, due to the contribution to the MTR_asym from the nuclear Overhauser enhancement (NOE) effect of aliphatic protons of mobile cellular macromolecules with a chemical shift of around −3.5 ppm, including the inherent semisolid MT asymmetry, the APT signals are reduced and do not provide a clean quantification of the amide proton signal.

In addition, the fast-exchanging amine protons of glutamate, at a chemical shift of around 3 ppm, and guanidinium protons in proteins and creatine, resonating at around 2 ppm, can make contributions to the APT signal, particularly for high RF saturation power levels. Various methods were developed for separating the desired APT effects from the background semisolid MT and NOE signals. These include the three-offset approach, which estimates the MT and direct water saturation contribution using a linear approximation,²² and its later refinement using relaxation-based direct saturation correction (DISC).²³ In a different work, a two-pool BM equation-based fitting with super-Lorentzian line shape, called extrapolated semisolid MT reference (EMR)^24,25 has been proposed, which subtracts the fitted semisolid MT signal from the acquired Z-spectrum. Furthermore, a multi-pool Lorentzian fitting analysis of the Z-spectrum can also be used to better separate the different spectral components.^26,27 Nevertheless, dilution effects from direct water and semisolid MT saturations still remain on the measured APT signal due to the non-linear contributions from the different proton pool components (water, semisolid MT, APT, and other CEST components) of the Z-spectrum, which changes with the RF saturation parameters. In addition, these approaches cannot completely disentangle the coupled parameters of exchange rate and concentration. All of the above challenges have motivated a considerable effort to develop truly quantitative CEST imaging techniques, as described below.

2.2. Non-MRF Quantitative CEST Imaging

In light of the detailed review papers for CEST quantification,^28-32 this section aims to briefly describe the general concept underlying previous quantitative approaches and highlight the motivation to develop CEST-MRF methodology.

One of the first in-vivo measurements of chemical exchange rate was performed using the water exchange spectroscopy (WEX) method for the quantification of the amide proton exchange rate from endogenous mobile proteins.³³ An exchange rate of ~30 Hz was estimated from the mixing-time evolution of the amide signal in the WEX spectrum using a simple two-pool exchange model (free bulk water and amide proton pools). Relatively long mixing times for the water labeling preparation were used in the study, limiting the detection of fast-exchanging amide protons. The amide proton concentration of ~72 mM was calculated by solving the two-pool-based amide proton transfer ratio (APTR) equation with the exchange rate estimated from the WEX spectrum. Moreover, the use of a high saturation power in the WEX experiment would increase spillover effect of direct water saturation and semisolid MT. Therefore, the amide exchange rate and concentration reported from the WEX experiment may not necessarily be accurate for all amide protons.

Quantification of exchange rate using varying saturation power (QUESP) or saturation time (QUEST) methods were proposed to estimate the exchange rate using a simplified analytical solution of the two-pool BM equations.³⁴ The methods estimate and correct spillover water saturation by applying a saturation pulse on the opposite side of water from the exchangeable protons to calculate the proton transfer ratio (PTR). However, the result may be corrupted by upfield NOE as well as semisolid MT signals for in-vivo applications. In addition, the analytical solution used in QUESP/QUEST assumes complete saturation under a strong B₁ saturation power which can significantly increase direct water saturation and semisolid MT signal contributions, and thus, is less accurate for measuring fast exchange rates. Recently, refined QUESP/QUEST analytical equations were introduced for inefficient saturation conditions.³⁵ In addition, an empirical solution, which also considers the direct water saturation (spillover) effect was derived.^36,37 However, this approach is sensitive to water relaxation, and requires voxel-wise mapping of the T₁ and T₂ relaxation times.²⁹ Finally, the acquisition of multiple Z-spectra with various saturation pulse powers and durations requires very long acquisition times, although an acceleration is feasible using a multi-echo length and offset varied saturation (MeLOVARS),³⁸ a progressive saturation for quantifying exchange rates using saturation times (PRO-UEST),³⁹ and a post-processing solution for quasi–steady-state (QUASS) saturation time and relaxation delays.⁴⁰

The apparent exchange-dependent relaxation (AREX) method⁴¹ was demonstrated for measuring an inverse exchange rate (from a free bulk water proton pool to a labile proton pool) using an inverse Z-spectrum metric with known water T₁ relaxation time. Using this metric, an in-vivo quantification of solute concentrations can be further estimated, following the use of a phantom calibration study and by acquiring multiple Z-spectra,⁴² or assuming a fixed volume fraction of the solute pool.⁴¹ However, the simple analytical solution used for AREX method could be a poor approximation of the full BM-equation solution at strong RF saturation and low spectral resolution (clinical field strength) conditions.^31,43

Additional prominent CEST quantification methods include omega-plots,^44,45 full BM equation fitting,²¹ ratiometric analysis,^46,47 and frequency labeled exchange (FLEX).^48,49 However, these approaches are either challenging to be applied in-vivo,⁵⁰ require a long processing time,⁵¹ involve exogeneous media injection,⁵²or are mostly appropriate for saturating fast exchanging protons.⁴⁹

3. Semisolid MT/CEST Magnetic Resonance Fingerprinting

The differential Bloch equation is complex, and its inverse can have multiple solutions for an observed MR signal. In a multiple-pool exchange model, finding a unique solution to the inverse problem of the Bloch equation coupled by exchange terms is even more challenging. Recently, a novel, quantitative MR-fingerprinting (MRF)⁵³ paradigm was introduced with a completely different approach to image acquisition and reconstruction. Instead of exploiting steady-state signals for the characterization of individual parameters of interest, as in conventional quantitative MRI, MRF uses a pseudorandomized acquisition that causes MR signals from different tissue properties to have unique signal trajectories (so-called fingerprints). For reconstruction, a pattern-matching algorithm is used to find different tissue-type parameters against a pre-calculated dictionary (or database) from Bloch simulations with a wide range of tissue parameter combinations. The best-match is then used for practically solving the inverse problem of the Bloch equations.

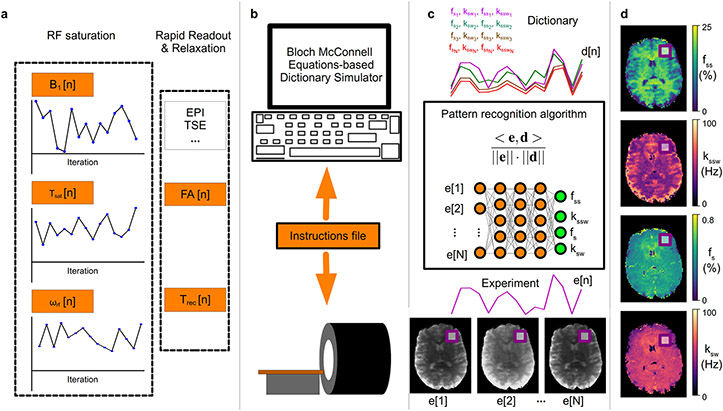
Originally introduced for water T₁ and T₂ relaxation, B₀ shift, and proton density quantification, MRF has gradually expanded for the quantification of additional tissue parameters,⁵⁴ such as blood flow velocity,⁵⁵ perfusion,⁵⁶ and ${\mathrm{B}}_1^{+}$.⁵⁷ Importantly, the MRF framework can be adapted to estimate multiple proton-exchange components such as semisolid MT and CEST parameters. A significant effort is currently ongoing to develop a robust, quantitative semisolid MT and CEST MRF imaging framework using pseudorandomized RF saturation and acquisition schedules, and database matching process for reconstruction. Figure 1 shows the primary components of the semisolid MT/CEST-MRF: image acquisition, dictionary generation, reconstruction, and visualization.

Figure 1. General pipeline of a semisolid MT/CEST MRF experiment.

a. Initially, a pseudo-random imaging protocol is designed, where at least one acquisition parameter is being varied, to produce a set of N images. Importantly, a pre-saturation block needs to be implemented, where at least the saturation pulse power (B₁), duration (T_sat), or frequency offset (ω_rf) should vary, for sufficient encoding of the chemical exchange parameters. The protocol typically includes a rapid readout, e.g., using EPI or turbo spin echo, with either a fixed or varied flip angle (FA) and recovery time (T_rec). b. The designed protocol is then loaded into a computerized Bloch-McConnell equations-based signal simulator, which produces the signal trajectories expected for a large number of tissue parameter combinations. The same CEST-MRF acquisition protocol is fed as an instruction file to the MRI scanner, allowing the acquisition of N molecular information encoding images, where each pixel series comprises an experimentally acquired trajectory (e[1] – e[N]). c. Each trajectory (e[n]) is then compared to all dictionary entries (d[n]), via a pattern recognition algorithm (such as the dot-product metric) for the determination of the best match. Importantly, this step can be accelerated and improved using a deep neural-network. d. Finally, simultaneous pixel-wise quantification of the proton exchange rates (k), and volume fractions (f) for a single or several metabolite/protein/lipid pools of interest can be made, based on the neural network output, or the best-matched dictionary entry.

3.1. Dictionary Matching for Semisolid MT/CEST-MRF Reconstruction

A preliminary CEST “fingerprinting-like” experiment was performed by Geades et al.,⁵⁸ where a numerically simulated look up table was used to extract the NOE, amide, and semisolid MT quantitative proton volume fractions from Z-spectra acquired with three different saturation powers. However, the simulations were performed for a very restrictive parameter space, with only eight different proton concentration values considered for each pool, a fixed proton exchange rate, and a total acquisition time of 24 min.

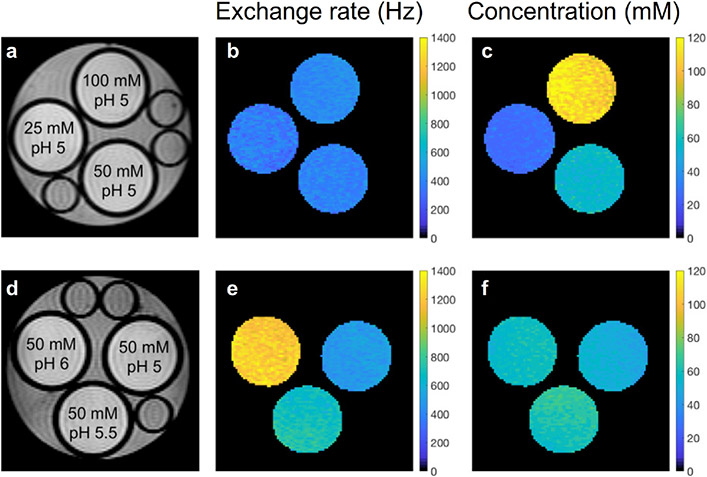
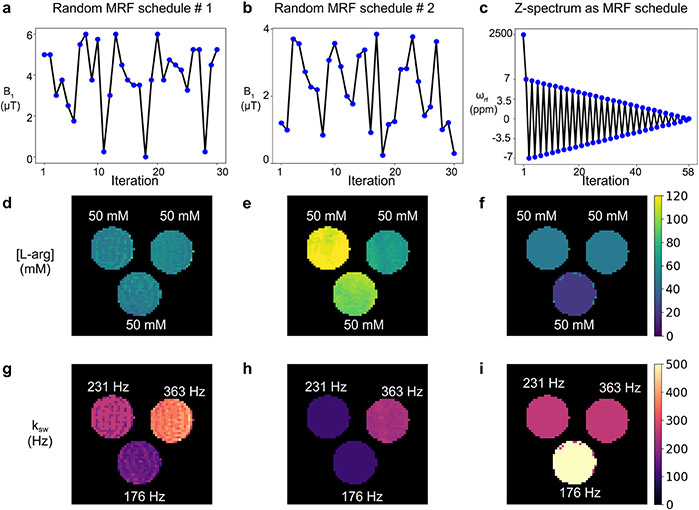
The first CEST-MRF experiments with rapid fingerprinting acquisition schedules and densely simulated dictionaries were demonstrated by Cohen et al.⁵⁹ and Zhou et al.⁶⁰ using CEST phantoms and/or in-vivo rat brain. For the study of Cohen et al.,⁵⁹ a pseudorandom acquisition schedule of 30 saturation-pulse powers was used while other scan parameters such as the RF saturation time, frequency offset, and TR, were kept fixed. For reconstruction of the concentration and exchange rate maps of the exchangeable proton, the experimental signal trajectories were matched to a simulated dictionary using a correlation-based metric (dot product). The estimated exchange parameters for the L-Arg phantom (Figure 2) were shown to be in good agreement with results from the QUESP method. Although reasonable in-vivo semisolid MT and amide parameter maps were obtained from a wild-type in-vivo rat, this approach is limited by the use of a single acquisition schedule with a fixed frequency offset (3.5 ppm), which is sub-optimal for assessing the semisolid MT exchange parameters and separating it out from the amide-related signal contribution.¹⁵ In addition, the B₀ field inhomogeneity was not considered.

Figure 2. Disentangling proton exchange rate and concentration using CEST-MRF.

(a and d) Proton density images of L-arginine phantoms with varying concentrations (top row) and pH (bottom row) along with the associated quantitative chemical exchange rate (b and e) and L-arginine concentration (c and f) maps generated from MRF dot-product matching. The CEST-MRF reconstruction was able to correctly detect and quantify the different proton exchange rates and concentrations. Reproduced and modified with permission from Cohen et al., Magn Reson Med. 2018;80:2449-2463.⁵⁹

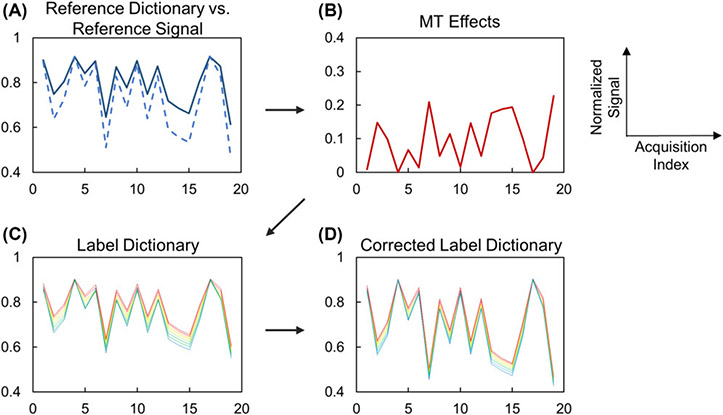
The study of Zhou, et al.⁶⁰ reported a CEST-MRF sequence for the quantification of creatine amine proton exchange rates in a 3-pool creatine/agarose phantom, which explored methods for removing the semisolid component from the amine CEST signal at 2 ppm and correcting for B₀ inhomogeneity. Prior to the dictionary matching, the semisolid MT effects were estimated by measuring saturated signals at the opposite frequency offset (−2 ppm), upfield from the water resonance, and removed using a pre-calculated dictionary (Figure 3). However, the estimation of semisolid MT signals from the opposite frequency offset might be biased, particularly for in-vivo tissue, due to asymmetric semisolid MT and NOE contributions. To allow for retrospective correction of B₀ field inhomogeneities, the CEST-MRF image acquisition was also repeated at multiple frequency offsets. However, this prolonged the total scan time to approximately 10 minutes.

Figure 3. Semisolid MT correction for CEST-MRF.

(A) Reference dictionary (solid) and reference signal (dashed) are different in the presence of the semisolid MT effect. (B) Signal attenuation due to the semisolid MT effect can be estimated by comparing the reference dictionary and reference signal. (C) The label dictionary is generated by simulating 2-pool Bloch-McConnell equations with known T₁ and T₂ values. (D) The corrected label dictionary can be generated by adding the semisolid MT effect (B) to the dictionary (C). Reproduced with permission from Zhou et al., Magn Reson Med. 2018;80(4):1352-1363.⁶⁰

Conventional dictionary matching based MRF reconstruction methods, however, have certain challenges and limitations. First, the dictionary generation time, which is built on the numerical solution of the BM equations, is exceedingly long and may take hours, or even days, depending on the available hardware and complexity of the CEST imaging scenario.¹⁵ Second, the reconstructed parameters are discrete, and their resolution is limited by the size of the dictionary. Third, large dictionaries with millions of entries are needed for complicated multi-pool CEST scenarios requiring expansive computational storage. Finally, the quantitative image reconstruction may take many hours, making it infeasible for use in clinical settings, where rapid clinical decisions, must sometimes be made.

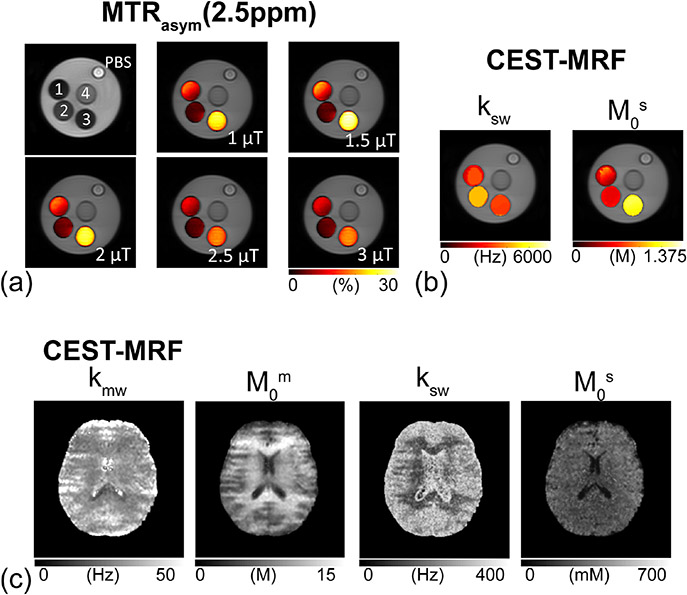
The first attempt to overcome the limitations of dictionary matching methods was demonstrated by Heo, et al.⁶¹ where the acquired MRF trajectories were fit to a multiple-pool exchange model using a nonlinear least-square procedure. The dictionary-free reconstruction method was demonstrated on CEST phantoms and healthy volunteer human brains at 3T (Figure 4). Although the model-based fitting approach has almost unlimited tissue parameter range and precision for estimating semisolid MT and CEST parameters, it may be affected by the parameter initialization conditions and prone to local minima errors. Moreover, it still suffers from a long reconstruction time.⁶¹ This important consideration has therefore motivated the exploration of alternative, deep-learning-based MRF reconstruction methods for fast tissue parameter quantification.

Figure 4. Quantitative proton exchange parameter maps of ammonium chloride (NH₄Cl) phantoms and a healthy human volunteer obtained using dictionary-free CEST-MRF..⁶¹.

a. CEST phantom validation experiments. MTR_asym (2.5 ppm) maps with RF saturation powers of 1, 1.5, 2, 2.5, and 3 μT. A phantom with four compartments: (1) pH 4.5, 0.5M NH₄Cl + 1% agarose + PBS, (2) pH 5.0, 0.5 M NH₄Cl + 1% agarose + PBS, (3) pH 4.6, 1 M NH₄Cl +1% agarose + PBS, and (4) pH 7.0, 1% agarose + PBS. RF saturation power dependencies of the direct water saturation, semisolid MTC, and CEST signals can be seen clearly in the MTR_asym (2.5 ppm) maps. b. CEST exchange rate (k_sw) and concentration (M0_s) maps of the phantom from the dictionary-free CEST-MRF. c. Quantitative semisolid MT exchange rate (k_mw) and concentration (M0_m), and amide proton exchange rate (k_sw) and concentration (M0_s) maps of a healthy volunteer human brain. Reproduced and modified with permission from Heo et al. Neuroimage. 2019;189:202-213.⁶¹

3.2. Deep Learning for Semisolid MT/CEST-MRF Reconstruction

The recent improvements in deep learning capabilities have created unique opportunities for medical imaging. While the most familiar examples include accurate pathology detection,⁶² segmentation,⁶³ and classification,⁶⁴ at the post-processing stage, an evident benefit lies in utilizing deep learning for improving image reconstruction. In addition to being able to approximate and represent complex non-linear relations,⁶⁵ a significant advantage of using deep learning compared to earlier machine learning approaches is its ability to automatically learn and optimize the classification features, thereby reducing the need for domain expertise and manual feature selection/design.^66,67 However, the main practical limitation for using deep learning in medical imaging is the need to acquire large quantities of training data for high performance. While big databases are available for natural scene images,⁶⁸ only a few, much smaller MRI data repositories were made publicly available (e.g., ref.⁶⁹). Luckily, the MRF reconstruction approach is based on artificially synthesized data, allowing the generation of data sets of any desired size. This characteristic has rendered the combination of deep learning and MRF an attractive means for rapid reconstruction of MR images, as demonstrated for water T₁ and T₂. By voxel-wise feeding a fully connected neural network (NN) with MRF trajectories (acquired using a pseudorandom sequence with varied flip angles and repetition times), Cohen et al.⁶⁷ were able to reconstruct water relaxation times in less than 100 ms. Can deep learning be similarly applied in the molecular imaging and semisolid MT/CEST realm?

As mentioned in section 2.1, CEST-related signals are commonly measured from the Z-spectrum. It is therefore not surprising that the first reported combination of NN and CEST data for quantitative exchange parameter mapping has used this intuitive signal as the input source for an artificial neural network (dubbed ANNCEST).⁷⁰ By training four ANNCESTs (Figure 5a) with the BM equation generated Z-spectra, the phosphocreatine (pCr) exchange parameters of the human skeletal muscle (Figure 6b) and the B₀/B₁ field inhomogeneities were successfully quantified in-vivo. Although this approach was not originally reported as an MRF experiment,⁷⁰ the use of a simulated dictionary for the neural-network training, together with an input signal that encodes for CEST changes, allow this approach to be considered as a CEST-MRF variant.

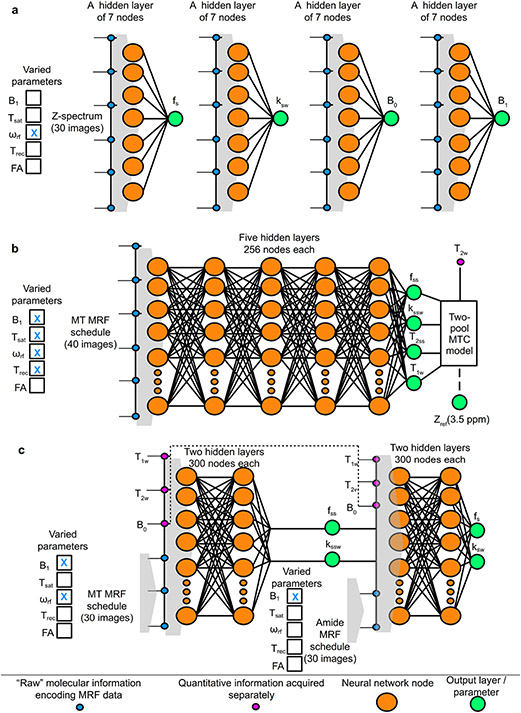
Figure 5. Supervised machine learning architectures for semisolid MT/CEST MRF.

a. Quantification of phosphocreatine (pCr) exchange parameters using an artificial NN composed of a single hidden layer.⁷⁰ The input layer was fed with Z-spectrum measurements (analogous to a CEST-MRF schedule where the varied parameter is the saturation pulse frequency offset (ω_rf), and the output was either the pCr proton volume fraction (f_s), exchange rate (k_sw), (B₀), or transmit field (B₁). The NN had 4 variants that were fed with the same input but trained to output each of the 4 different sought-after parameters, using a simulated dictionary. b. Brain semisolid MT exchange parameter quantification and background semisolid MT (Z_ref) contrast image synthesis,⁷³ using a fully connected neural network. The input MRF schedule varied the saturation pulse power (B₁), duration (T_sat), ω_rf, and the recovery time (T_rec). The output included the semisolid MT parameters, and a synthesized MT reference image at 3.5 ppm, calculated by plugging in the resulting parameters and the water T₂-values obtained from a separate protocol in the two-pool BM equations solution. c. Sequential and deep CEST and semisolid MT quantification in the brain.¹⁵ A semisolid MT-oriented MRF acquisition schedule, which varies ω_rf and B₁, yields 30 images that are fed volxelwise into the first NN, together with the quantitative water pool and field homogeneity maps (T₁, T₂, B₀). This NN map the semisolid MT pool exchange parameters, which are then fed, together with the previously obtained quantitative data into the second NN, ultimately yielding the amide proton f_s and k_sw.

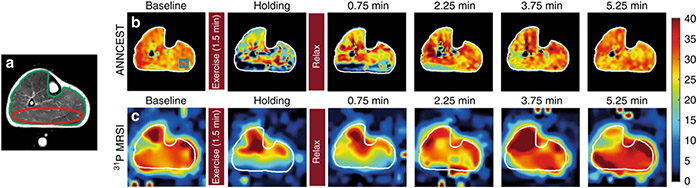
Figure 6. Phosphocreatine concentration mapping in the exercised human leg muscle.

a. T₂-weighted anatomy image. b. Phosphocreatine concentration maps obtained by ANNCEST are in good agreement with the dynamics observed using ³¹P 2D MRS (c). Reproduced and modified from Chen et al., Nat Commun 2020;11:1-10.⁷⁰

While the semisolid MT pool can be treated as a spatially homogeneous proton pool in the leg muscle (as performed in the ANNCEST approach), its properties vary markedly across the brain.⁷¹ Given that changes in semisolid MT exchange parameter values are useful for the diagnosis of several diseases (the most well-known example is multiple sclerosis),⁷² there is a clear motivation for developing rapid semisolid MT quantification methods. Accordingly, Kim et al.⁷³ developed a deep learning approach for simultaneously quantifying semisolid MT proton exchange rate, volume fraction, and transverse relaxation, as well as the water longitudinal relaxation, demonstrated in the brain of healthy volunteers at 3T. A dynamic MRF schedule that varied the saturation pulse power, duration, frequency offset, and relaxation recovery-time was used to train deep neural networks (Figure 5b). Furthermore, using the tissue parameters estimated from MRF and the acquired water T2 relaxation, accurate semisolid MT signal intensities were able to be estimated at certain CEST frequency offsets (e.g., 3.5 ppm and −3.5 ppm for APT and NOE imaging, respectively), allowing for a clean separation of the semisolid MT and CEST signals.

There is a clear value in the ability to accurately de-bias CEST-weighted brain images from the semisolid MT and water contribution. Nevertheless, a fully quantitative and rapid estimation of the amide proton volume fraction and exchange rate, would provide an ideal means for assessing the underlying molecular phenomena and pathology, as discussed in section 2. However, for this application, there are at least three prominent compound pools involved (amide, semisolid MT, and water), whose parameters are all varying simultaneously with disease progression. This complex and highly multi-dimensional parameter-space imposes a considerable challenge. Accordingly, trying to employ a single NN with a single parameter encoding acquisition schedule in tumor bearing mice has resulted in very noisy and poorly discriminating parameter maps.⁷⁴ The first deep learning based CEST-MRF method that fully quantified these parameters in the brain disease environment was recently reported by Perlman et al.¹⁵ The key element responsible for this progress was a sequential deep-learning pipeline (Figure 5c), aimed to obtain both semisolid MT and amide quantitative information, while reducing the complexity of each quantification step, by relying on the results of the former. The method was explored in the context of neuro-oncology applications and was used for monitoring the treatment response of glioblastoma multiforme (GBM) bearing mice to oncolytic virotherapy (Figure 7). The translation of this method to a 3T clinical scanner has demonstrated good agreement with previous literature reports in a healthy human volunteer (Table 1).

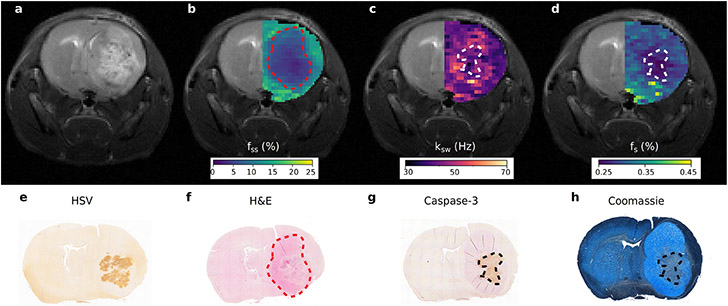
Figure 7. Quantitative imaging of apoptosis following oncolytic virotherapy using sequential and deep semisolid MT/CEST MRF.

a. Conventional T₂-weighted image of an oncolytic virotherapy treated mouse, 72 hours post virus inoculation, is incapable of detecting treatment responsive apoptotic regions. b. Semisolid macro-molecules proton volume fraction (f_ss) map, where a decreased volume-fraction represents tumor-related edema and a change in the lipid composition of tumor tissue relative to normal brain tissue. c. Amide proton exchange-rate (k_sw) and d. volume fraction (f_s) maps. Regions of decreased intracellular pH and mobile protein concentration, respectively, are indicative of apoptosis. e-h. Histology and immunohistochemistry images validate the MR findings with cleaved caspase-3 positive tumor regions and decreased Coomassie blue protein staining, indicative of apoptosis, colocalizing with the regions of decreased exchange rate and mobile protein concentration. Reproduced with permission from Perlman et al. Nat Biomed Eng. 2021;1-10. https://doi.org/10.1038/s41551-021-00809-7.¹⁵

Table 1.

Literature values of the brain white/gray matter semisolid MT and amide proton volume fractions (f_ss / f_s) and exchange rates (k_ssw / k_sw).

Brain tissue	fss (%)	kssw (Hz)	fs (%)	ksw (Hz)	Method
WM	12.2 ± 1.7	48.6 ± 2.4	0.76 ± 0.09	47.9 ± 11.6	Dictionary-correlation matched CEST MRF59
GM	8.1 ± 1.1	47.1 ± 4.0	0.61 ± 0.13	34.8 ± 11.7	(rat at 4.7T)
WM	11.2 ± 0.7	29 ± 4	0.19 ± 0.02	162 ± 16	Sub-grouping proton exchange models61
GM	6.3 ± 0.7	40 ± 5	0.24 ± 0.02	365 ± 19	(human at 3T)
WM	16.9 ± 1.3	10.3 ± 0.9	—	—	Deep semisolid MT MRF with synthetic signal validation73
GM	10.6 ± 1.5	12.5 ± 2.0	—	—	(human at 3T)
WM	15.2 ± 2.0	14.0 ± 2.4	—	—	Unsupervised semisolid MT MRF75
GM	10.2 ± 1.1	16.3 ± 1.6	—	—	(human at 3T)
WM	9.4 ± 3.0	14.0 ± 6.9	0.31 ± 0.02	42.3 ± 2.9	Sequential and deep semisolid MT/CEST MRF15
GM	4.2 ± 4.4	35.1 ± 15.4	0.32 ± 0.07	34.6 ± 9.5	(human at 3T)
WM	19.8 ± 0.5	43.9 ± 2.4	0.40 ± 0.27	73.0 ± 51.1	AutoCEST82
GM	12.8 ± 0.8	56.5 ± 3.1	0.29 ± 0.16	61.0 ± 29.3	(mouse at 9.4T)
WM	13.9 ± 2.8	23 ± 4	—	—	Two pool model fitting of semisolid MT71
GM	5.0 ± 0.5	40 ± 1	—	—	(bovine at 3T)
WM	8.9 ± 0.3	—	0.21 ± 0.03	—	Numerically simulated look up table with three Z-spectra58
GM	4.4 ± 0.4	—	0.20 ± 0.02	—	(human at 7T)
WM	6.2 ± 0.4	67.5 ± 7.0	0.22 ± 0.04	281.2 ± 0.6	Four pool model fitting109
GM	3.4 ± 0.4	63.5 ± 4.5	0.25 ± 0.05	281.9 ± 0.9	(human at 7T)
WM	13.48 ± 0.37	—	—	—	Semisolid MT proton fraction mapping110
GM	5.77 ± 0.34	—	—	—	(human at 3T)
WM	—	—	—	—	Water exchange spectroscopy (WEX)33
GM	—	—	—	28.6 ± 7.4	(rat at 4.7T)
WM	11.4 ± 1.2	11 ± 2	—	—	Selective inversion recovery based quantitative semisolid MT111
GM	7.5 ± 0.7	15 ± 6	—	—	(human at 3T)
WM	17.6 ± 1.3	14.5 ± 1.5	—	—	Selective inversion recovery based quantitative semisolid MT112
GM	10.3 ± 1.6	24.4 ± 4.4	—	—	(human at 7T)
WM/GM	—	—	—	350-400	Frequency labeled exchange transfer (FLEX) imaging49 (human at 3T)

All the NN strategies discussed so far, can be associated with the machine learning branch of supervised learning, where labeled ground-truth information is paired to each input signal during the system’s training. In the context of MRF, these data pairs are obtained via an extensive numerical dictionary generation step, which may take hours, depending on the complexity and number of pools involved in the simulated scenario and the availability of computational resources (number of CPUs/GPUs, RAM, etc.). In addition, the accuracy of the quantification is highly dependent on the model used for dictionary simulation, which is not guaranteed to accurately reflect the experimentally measured data. To address these challenges, Kang et al.⁷⁵ have recently proposed an unsupervised learning approach for quantifying the semisolid MT exchange parameters (Figure 8). Instead of presenting the NN with pairs of simulated MRF trajectories and the corresponding ground truth tissue parameters, the convolutional neural network (CNN) architecture was trained to minimize the different between ‘real’ experimentally acquired MRF trajectories (input) and synthesized MRF trajectories (output) by solving the BM equations. By defining the loss as the L₂ distance between the ‘real’ MRF trajectories and the simulated counterparts, the CNN iteratively optimizes its quantification ability. The convolutional neural network in the unsupervised fashion outperformed supervised NN at lower SNRs, in terms of robustness to noise, which could be beneficial to estimate low-concentration CEST parameters. However, the unsupervised learning has limited generalization ability because the deep-learning framework was trained with a limited range of tissue parameter in healthy volunteers. In particular, pathological cases that include a distinctly different combination of tissue (and exchange) parameters are not expected to be accurately mapped, unless sufficiently represented in the CNN parameter optimization. While the dictionary generation, required for training the NN in the supervised approach is time-consuming, it could, in principle, take place only once and include a huge number of parameter combinations, potentially sufficient for many different pathologies (e.g. brain cancer, stroke, etc.).

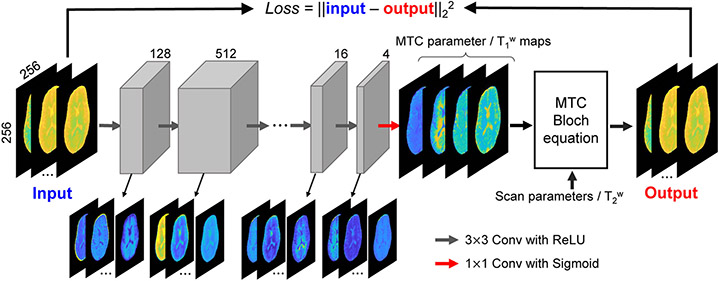
Figure 8. Unsupervised machine learning approach for semisolid MT/CEST MRF.

The raw MRF images are given as input to an 8-layer CNN, yielding quantitative semisolid MT exchange parameter and water T₁ maps. Gray boxes represent feature spaces with the depth of the spaces indicated above each box. Colored arrows show the receptive field size of the kernel and the activation function. The estimated quantitative maps, the MRF schedule parameters, and a separately acquired water T₂ map are plugged into the BM equations analytical solution, generating an estimation of the original semisolid MT MRF raw images. These output images are compared to the experimentally acquired raw MRF data (using the L₂ loss function), allowing for the optimization of the semisolid MT parameter maps. Reproduced and modified with permission from Kang et al. Magn Reson Med. 2021;85:2040-2054.⁷⁵

3.3. Optimization of MRF Acquisition Schedules

The ability to discriminate different exchange parameters is sensitive to the acquisition schedule used (Figure 9). Thus, it is crucial to tailor and optimize the properties of the imaging protocol for the biological imaging scenario of interest.

Figure 9. Comparing different CEST-MRF acquisition schedules.

A phantom containing three vials of 50 mM L-arginine at pH 4, 4.5, and 5 was imaged using a 9.4T scanner. The dot-product matched L-arg concentration (d-f) and amine proton exchange rate (g-i) are shown for three different acquisition schedules, including the random acquisition schedule used in Coehn et al.⁵⁹ (left column); a different random acquisition schedule of similar length (center column), which also varied the saturation pulse duration, the repetition time, and the readout flip angle; and a schedule based on a z-spectrum obtained using a fixed saturation power of 2uT, at 7 to −7 ppm with 0.25 increments (right column).

A basic means for understanding the influence of the acquisition parameters on the discrimination ability of CEST-MRF and for comparing different schedules is to employ a similarity-based loss metric, such as the dictionary Frobenius norm dot-product loss.^59,76,77 Intuitively, such metrics compare the correlation between different pairs of simulated signal trajectories, associated with a given MRF dictionary, assuming that minimal correlation is a predictor for improved parameter discrimination ability. Using this metric, it was demonstrated that different molecular scenarios, such as endogenous amide imaging, and exogenous fast exchanging CEST agents imaging require a distinctly different MRF schedule (Figure 10).⁷⁷ While similarity metrics, such as the dot-product and Euclidean-distance can also serve as predictors of the encoding capability of CEST-MRF acquisition schedules, it was recently shown that an improved pH quantification prediction could be obtained by using the Cramer-Rao bound.⁷⁸

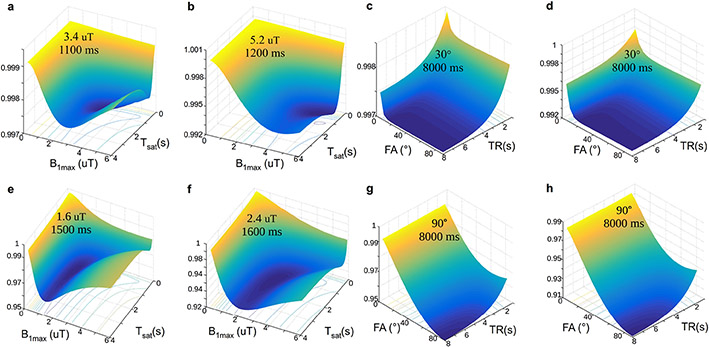
Figure 10. Dependence of the discrimination loss on the acquisition parameters used in CEST-MRF.

The surface plots with projected loss iso-contours describe the effect of the maximal saturation power (B_1max) and the saturation time (T_sat) (a-b) or the flip angle (FA) and TR (c-d) on the loss, for a 3-pool water/amide/semisolid MT imaging scenario (a, c) and a 2-pool scenario with a dilute solute in the medium to fast exchange rate regime (b, d). In all images, the z-axis represents the loss (lower values indicate improved parameter discrimination ability), which is also color coded from blue to yellow. The optimal combination for each examined parameter pair is given in the surface plot. (e-h). A similar analysis was performed using the Euclidean distance instead of the dot-product reconstruction metric with an Euclidean distance based loss function. Note the different optimal parameters obtained. Reproduced and modified with permission from Perlman et al. Magn Reson Med. 2020;83:462-478.⁷⁷

Another approach for acquisition protocol optimization is Monte Carlo simulations of noise propagation.⁷⁹ Here, a dictionary with a particular imaging protocol is repeatedly generated with random noise perturbations. As the noisy trajectories are matched to the original ‘clean’ dictionary, the proton exchange rate and volume fraction quantification error can be calculated. Based on this strategy, a numerical evaluation predicted that a CEST-MRF schedule could be shortened by more than 60%, with only a minor decrease in reconstruction accuracy. The finding was then successfully confirmed using an experimental phantom study.⁷⁷

The main limitations of the numerical optimization strategies mentioned above, is the need to calculate a particular loss (or quantification error) for each acquisition-schedule candidate. Given the very large parameter space involved in CEST-MRF, where at least 5 scan parameters (saturation pulse power, duration, frequency offset, readout flip angle, and repetition time) could be varied, and a huge dictionary of biophysical parameter combinations must be synthesized for each schedule, it is virtually impossible to explore all (or most) of the acquisition parameter space.

In an attempt to bypass the time-consuming dictionary generation requirement, and improve the chances of finding a global solution, a preliminary work by Cohen et al.⁸⁰ has developed a schedule optimization network, aimed to learn the direct functional mapping between the acquisition schedule and the corresponding reconstruction error. In the first step, a mapping between the raw dictionary signals, associated with an MRF protocol to the corresponding quantitative parameters is performed, using a supervised-learning approach, similar to that described in section 3.2. The process is repeated for a few thousand random schedules, creating pairs of scan parameter combinations and their associated reconstruction errors. These pairs are then used as the input and output data for training a second neural network. This schedule optimization network (SCONE) could predict the performance of unseen acquisition schedules in less than a second, allowing a drastic expansion of the evaluated acquisition parameter space. In addition, SCONE can be used in combination with computational optimization solvers. Although the combined T₁/T₂/CEST/semisolid MT reconstruction using the SCONE-optimized schedule was able to improve the tumor contrast in a mouse GBM model,⁸¹ there were some deviations in the quantitative parameter values compared to the literature, warranting additional optimization and validation.

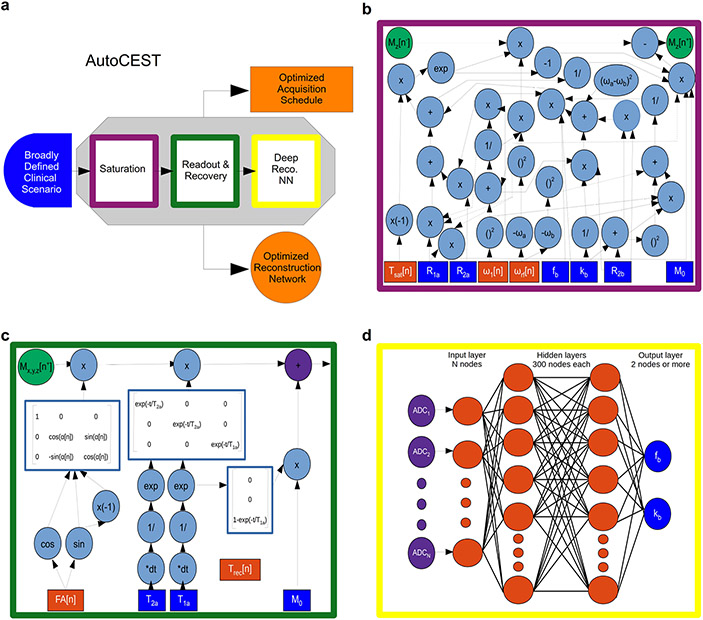
Recently, a more unified framework termed AutoCEST was developed, allowing an end-to-end automated discovery of semisolid MT/CEST MRF acquisition protocols and quantitative deep reconstruction (Figure 11).⁸² Its key component was treating each acquisition schedule parameter similarly to a neural network node weight, thereby allowing its efficient optimization. To enable such optimization, the CEST saturation block was represented as a computational graph (Figure 11b), based on the analytical solution of the two⁸³ or three⁸⁴ proton pool BM equations. Next, the readout and relaxation blocks were similarly represented using the Bloch equations with a discrete-time state-space model in the rotating frame (Figure 11c), allowing for the calculation of the expected MR signal for a randomly initialized set of acquisition parameters. These signals are then directly fed into a quantitative reconstruction network (Figure 11d), trained to output the desired semisolid MT/CEST exchange parameters. To obtain efficient and simultaneous optimization of the acquisition and reconstruction parameters involved in deep CEST-MRF, all computational graphs were serially connected. This enables a ‘single-click’ optimization using automatic differentiation and stochastic gradient descent. AutoCEST was used for discovering optimized amide and semisolid MT acquisition schedules and yielded amide and semisolid MT exchange parameters in good agreement with previous reports (Table 1).

Figure 11. An end-to-end AI-based framework for automatic optimization of semisolid MT/CEST MRF acquisition protocols and quantitative deep reconstruction (AutoCEST).

a. Schematic representation of the optimization pipeline. A broadly defined tissue-parameter scenario serves as input to the pipeline which consists of sequential simulations of the CEST saturation (purple), readout and recovery (green), and deep reconstruction (yellow). AutoCEST outputs an optimized acquisition schedule and a reconstruction network (orange). b. CEST saturation block as a computational graph. The blue rectangles represent the input tissue parameters: initial magnetization (M₀), water relaxation rates (R_1a, R_2a), solute transverse relaxation (R_2b), exchange-rate (k_b), and volume fraction (f_b). The orange rectangles represent the dynamically updated protocol parameters: saturation time (T_sat), saturation power (ω₁), and saturation frequency offset (ω_rf). The graph calculates the magnetization at the end of the saturation block M_z[n⁺]. c. Bloch equation-based image readout as a computational graph. The blue rectangles represent the water-pool parameters, while the orange rectangles represent the dynamically updated protocol parameters: flip angle (FA) and recovery time (T_rec), which is embedded in the appropriate relaxation step. Note that this is a partial display due to space limitations. d. Deep reconstruction network for decoding the “ADC” MR signals (purple circles), obtained at c into CEST quantitative parameters (f_b and k_b, blue circles). Reproduced from Perlman et al. Magn. Reson. Med. 2022.⁸²

The potential and strength of using a supervised deep-learning strategy, combined with a loss function that directly evaluates tissue quantification error for MRF schedule optimization, was recently further substantiated by Kang et al.⁸⁵ A framework for learning-based optimization of the acquisition schedule (LOAS) was developed to optimize RF saturation-encoded MRF acquisition with a minimal number of scan parameters for tissue parameter quantification (Figure 12). The BM-based numerical phantom and in-vivo studies showed that the LOAS outperforms existing indirect optimization methods, such as the Cramer-Rao lower bound (CRLB)⁸⁶ and interior-point (IP),⁷⁶ in terms of quantification accuracy and acquisition efficiency.

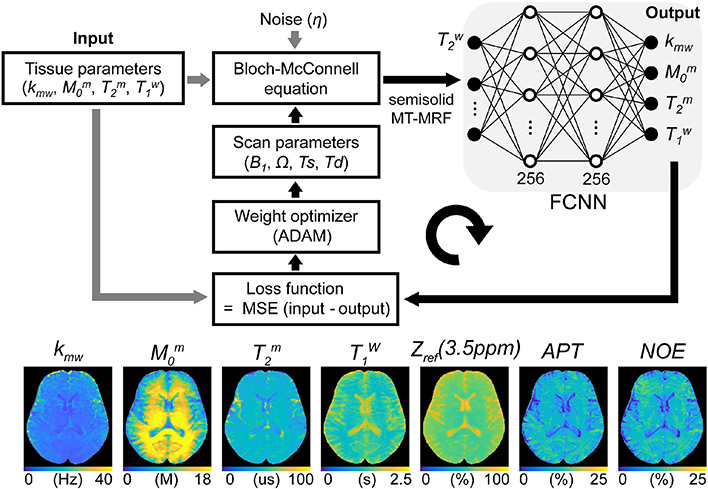
Figure 12. A schematic of the learning-based optimization of the acquisition schedule (LOAS).

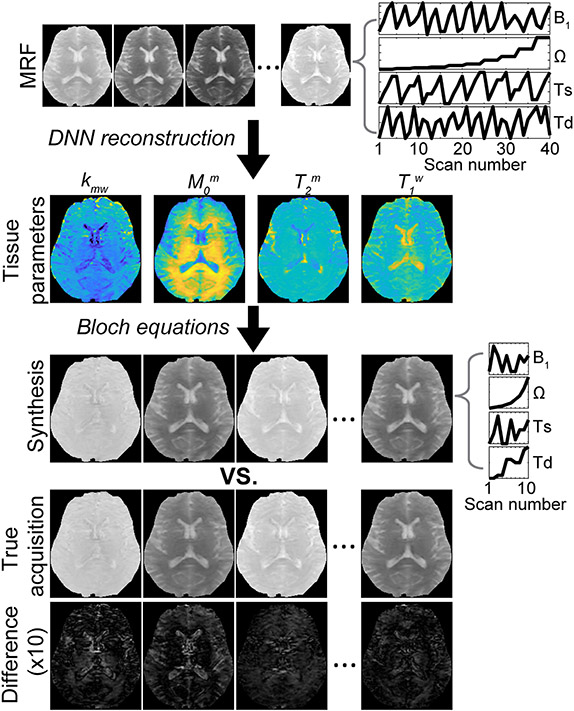
Semisolid MT-MRF signals are synthesized using initialized scan parameters (RF saturation power, B₁, frequency offset, Ω, saturation time, T_s, relaxation delay time, T_d), noise, and tissue parameters (Input) are fed to the fully connected neural network (FCNN). The FCNN outputs tissue parameter estimates (Output). The loss function is defined as the mean square error between the ground-truths and estimated tissue parameters. The calculated loss was back-propagated with an ADAM optimizer to update the scan parameters. APT and NOE images were calculated by subtracting the synthesized semisolid MT image at 3.5 ppm from the acquired saturated image at ±3.5 ppm. Reproduced and modified with permission from Kang et al., NMR Biomed 2021:e4662.⁸⁵

3.4. Practical Considerations in Semisolid MT/CEST-MRF Studies

There are several practical issues to consider in the development of the semisolid MT/CEST-MRF methodologies. The performance of the MRF methods must be rigorously evaluated in terms of their accuracy, repeatability, and reproducibility across subject, vendors, and imaging sites, and assessed with the certainty of the estimated tissue parameters.

3.4.1. Accuracy

For the MRF reconstruction (or tissue parameter quantification), deep-learning neural networks can be trained with a huge dataset that covers all possible combinations of tissue properties. Then, the reconstruction accuracy of the deep-learning neural networks can be evaluated on a never-before-seen test dataset. Furthermore, the semisolid MT/CEST-MRF method can be demonstrated using well-controlled phantoms with known proton concentration and pH. For instance, the amide proton exchange rate has a one-to-one correspondence to pH because the exchange rate of −NH groups is base-catalyzed and decreases with decreasing pH.³ Thus, an estimated proton exchange rate can be indirectly evaluated by observing signal changes at different pH and deriving empirical calibration formulas to relate exchange rate to pH. Several important NMR and MRI methods have been developed to directly estimate proton exchange rates by measuring the temperature-dependent linewidth, fitting of Z-spectrum with the BM equations,²¹ QUESP,³⁴ WEX,³³ or Omega-plot.^44,45 The estimation of semisolid MT and CEST parameters reported in the literature is shown in Table 1. Although the methods are promising as a reference standard, the measurement of the absolute in-vivo exchange rate remains challenging and there is no widely accepted “gold standard” method regarding the measurement. To enable effective validation, previous studies performed synthetic MRI analysis (Figure 13) to evaluate the reconstruction accuracy. Various contrast-weighted images were synthesized with the tissue parameters estimated by deep-learning semisolid MT-MRF by solving the BM equations with new RF saturation parameters and relaxation delay time (T_d). Good agreement between the synthetic and actually acquired images was found, which may guarantee stable solutions (tissue parameters) of the inverse problem of semisolid MT-MRF. In the absence of a ground truth, synthetic MRI could be useful for validation of in-vivo tissue parameters and applied to CEST-MRF or other quantification methods. In addition, histology and immunohistochemistry images can be used to confirm any assumptions made based on proton exchange parameters (e.g. apoptosis, tumor/healthy tissue, total protein content, etc.). Notably, such measurements should be carefully analyzed, as they do not directly reflect the exchangeable proton volume fraction and exchange rate.

Figure 13. Synthetic MRI analysis for validation of the semisolid MT-MRF method.

Synthetic contrast-weighted images are generated using all the tissue parameters obtained from the deep neural network (DNN), which can then be compared with the experimentally acquired images as the standard of reference. Tissue parameters are quantified from an acquisition schedule consisting of 40 dynamic MRF images (a corresponding MRF schedule is shown in top right) using the DNN, and then a new acquisition schedule (middle right) is used for synthesizing 10 dynamic MRF images by inserting the tissue parameters obtained from DNN into the forward BM transform. The synthesized images showed a high degree of agreement with the experimentally acquired images as shown in the difference image. Reproduced and modified with permission from Kim et al., Neuroimage 2020:117165.⁷³

3.4.2. Repeatability and Reproducibility

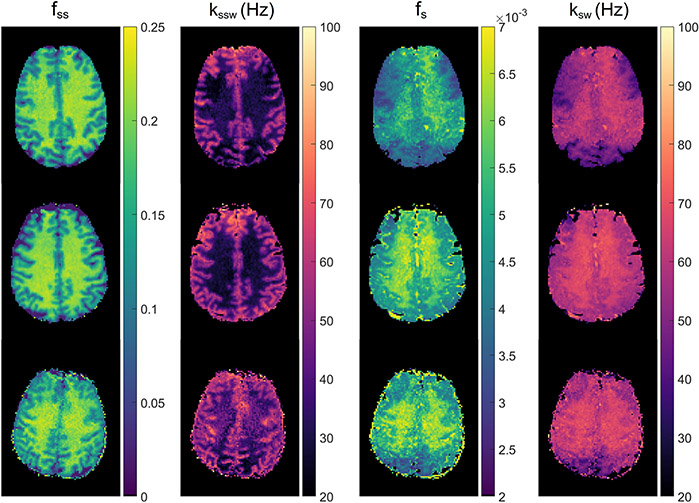
As in any other quantitative MR imaging, it is important to ensure that tissue parameters estimated from semisolid MT/CEST-MRF methods are repeatable and reproducible.⁸⁷ While a conventional MRF method has demonstrated high repeatability and reproducibility of water T₁ and T₂ relaxation times, there is unfortunately sparse literature studying the repeatability and reproducibility of semisolid MT/CEST-MRF measurements due to their relative novelty. A standardized phantom must be used to determine the repeatability for each scanner and between-scanner reproducibility. For human studies, an interesting approach called “the traveling heads”⁸⁸ was recently introduced to improve the reproducibility of quantitative MRI.⁸⁹ The same two subjects were imaged on different scanners at multiple sites, comprising multiple repetitions at each scanner to assess inter-site and intra-site reproducibility. This approach could be adapted to the semisolid MT/CEST-MRF experiments for longitudinal or multicenter studies. A recent study⁹⁰ evaluated the reproducibility of sequential and deep¹⁵ amide and semisolid MT in the healthy brain across three sites with different scanner platforms, but the same vendor. Although quantitative reproducibility metrics (e.g., intra-class correlation coefficient and coefficient of variation) were not reported, the study demonstrated the feasibility of reproducibility assessment across multiple sites for semisolid MT/CEST-MRF as shown in Figure 14.

Figure 14. Reproducibility study of deep CEST-MRF in healthy human volunteers.

Semisolid MT proton volume fraction (f_ss, first column) and exchange rate (k_ssw, second column), amide proton volume fraction (f_s, third column), and exchange rate (k_sw, fourth column) for measurements at a 3T Prisma in Tübingen (first row), 3T Prisma in Boston (second row), and 3T Trio in Erlangen (third row). Reproduced and modified from Herz et al. Magn Reson Med. 2021;86:1845– 1858.⁹⁰

3.4.3. Uncertainty

In deep-learning semisolid MT/CEST-MRF, uncertainty must be considered in the error analysis, which is a quantitative metric of variability in the tissue estimates. There are possible sources of uncertainty in the estimation of tissue parameters, including variance in the noise level and tissue parameter coverage in the training dataset, and size of training dataset. In particular, quantifying semisolid MT exchange rate is very challenging due to insignificant MRF signal discrimination between different exchange rates.⁷⁵ Such a poor signal discrimination is even worse in the estimation of CEST exchange rate due to the lower concentrations of solute molecules and lower signal intensity levels (vulnerable to noise) around the water resonance. Therefore, uncertainty quantification could provide surrogate estimates of the errors from deep-learning models and confidence measures for tissue estimates. Recently, Glang et al.⁹¹ have proposed a deep-learning framework for incorporating an uncertainty measure in multiple-pool Lorentzian fitting of CEST-MRI. A probabilistic output layer in the neural network was used to represent the “trustworthiness” of each estimated Lorentzian parameter, learned without the use of additional certainty targets (or ground truth) but by using a modified Gaussian likelihood function. Even though the approach was used to demonstrate the uncertainty in the quantification of multiple-pool Lorentzian model parameters (amplitude, linewidth, and peak position), it could be incorporated for semisolid MT/CEST-MRF framework to provide an estimation of the uncertainty of the tissue exchange parameters.

3.4.4. Open Source for Semisolid MT/CEST-MRF

One of the main drivers for widespread implementation of a new MR imaging technique is the availability of open-source tools.⁹² Publicly available data and processing codes will facilitate reproducibility and allow research groups to quickly build upon the project, and further advance the research field. For instance, aligned with that principle, Chen et al.⁷⁰ have linked the ANNCEST code to their manuscript, as well as human leg and phantom data. Perlman et al.⁸² have made the raw and analyzed AutoCEST data publicly available.⁹³ For comparison and validation of CEST acquisition and processing techniques across scanners and sites, Yao et al.⁹⁴ have designed a physical phantom, validated its temporal stability, and made the computer automated design (CAD) files for creating the physical phantom available online. For improving the ability to reproduce acquisition protocol across different sites and vendors, Herz et al.⁹⁰ have developed a CEST definition standard using an open format, which allows a complete description and reproduction of the acquisition schedule used in previous CEST-based literature including MRF.^15,59,61 Lastly, to support the readers in implementing the basic steps of semisolid MT/CEST-MRF reconstruction, demonstration code and sample data are provided at: https://github.com/operlman/cest-mrf.

4. Conclusions and Future Perspectives

The limited availability of expert-labeled clinical data and the recent developments in deep learning methodologies have motivated the use of synthetic data for augmenting and improving the training of machine learning models for medical imaging.⁹⁵ Within this approach, MRF lies on the extreme edge of the spectrum, as it builds solely on synthetic, physical-model-based generated signals. Therefore, the success of MRF is heavily dependent on the ability of the physical model to accurately depict the real-world measured signals. Although both the classical Bloch equations⁹⁶, used for “conventional” water T₁/T₂ MRF, and the Bloch McConnell (BM) equations,⁹⁷ used for semisolid MT/CEST MRF, were intensively investigated in the past decades, the latter contains a considerably larger number of parameters, as each of the proton pools involved contains its own transverse and longitudinal relaxation times, concentration, and exchange rates with the other pools. Therefore, as semisolid MT-MRF, and especially CEST-MRF contain a large number of ‘moving parts’, they are more prone to inaccuracies caused by model imperfections. An exception to the general MRF concept, is the use of unsupervised learning (section 3.2.2), which does not involve synthesized dictionaries at all. Instead, the training is performed using ‘real’ experimentally acquired images. However, a model is still an integral part of this approach and considered as the ground truth reference.⁷⁵ We postulate that in the future, a hybrid deep-learning method, trained using both experimental and synthesized data could harvest the benefits of both worlds.

The performance of semisolid MT/CEST MRF is also expected to further improve due to “third-party” developments, stemming from each of the 3 parents of this technique: water T₁/T₂ MRF; deep learning algorithms; and classical CEST theory. Particularly, water T₁/T₂ MRF is an increasingly investigated field,^54,98 where new acquisition schemes and novel reconstruction approaches are continuously suggested and evaluated.^99-101 However, the unique attributes of the CEST-MRF contrast mechanism will mandate careful adaptations to any conventional MRF inspired approach and will require additional and separate research efforts.

The exponential growth in deep learning applications and methods, and the vast international resources allocated for AI research are expected to keep expanding the capabilities of deep learning-based parameter estimation. In the context of the future translation of CEST-MRF for routine clinical care, the topic of explainable AI, which is aimed at uncovering what happens “under the hood” in a deep learning system is of particular importance.^102-104

Last but not least, new investigations into the exact biophysical properties of various CEST compounds are routinely conducted,^105-107 and are expected to improve the accuracy of the semisolid MT/CEST MRF models. Such studies might also assist in clearing the fog of uncertainty concerning the semisolid MT/CEST quantitative ground truth. As demonstrated in Table 1, although some similarities exist between the exchange parameters obtained by various groups, there is a substantial variance for some of the exchange parameters (most strikingly seen for the amide proton exchange rate), for both MRF-based and non-MRF quantitative evaluations. This variability is likely rooted in the different model variants used by different methods (e.g., the use of the analytical or the numerical solution of the BM equations), the assumptions made regarding the biophysical environment (e.g., the number of simulated proton pools and the values of the fixed parameters), the sensitivity and discrimination ability of the particular acquisition schedule used (as discussed in section 3.3), and the resolution/size of the dictionary/data used for image reconstruction and NN training. A related summary of the key concepts and pros and cons of each semisolid MT/CEST MRF method described throughout this review is available in Table 2.

Table 2.

A summary of semisolid MT/CEST MRF methods

Method	Advantages	Limitations
Dictionary-correlation matched CEST MRF59	Rapid acquisition	Prolonged reconstruction for big dictionaries, discrete output parameters
CEST-MRF for exchange rate quantification60	Removal of MT effects prior to dictionary matching	Potential bias from NOE effects in-vivo due to the use of the upfield spectrum signal, discrete output parameters
Sub-grouping proton exchange models61	Least-square fitting is used instead of dot-product matching for continous quantification of amide and MT parameters, circumvents the need for lengthy dictionary generation	Long reconstruction time
Quantitative CEST using artificial NN and partial Z-spectrum acquisition (ANNCEST)70	Rapid CEST acquisition and reconstruction, B0 and B1 mapping	Unsuitable for brain applications where the MT parameters vary
Deep semisolid MT MRF with synthetic signal validation73	Quantification of MT parameters and water T1, allows the removal of MT effects from CEST signals	Amide and NOE reconstruction is semi-quantitative and requires separate water T2 mapping
Sequential and deep semisolid MT/CEST MRF15	Quantitation of both MT and amide parameters, rapid reconstruction	Two acquisition schedules required as well as T1, T2, and B0 mapping
Unsupervised semisolid MT MRF75	No need for dictionary generation, noise robustness	limited generalization ability for unseen pathologies
Acquisition schedule optimization using discrimination ability / SNR efficiency based metrics77,78	Faster than Monte Carlo simulations, enables predicting the encoding capability of different schedules	Time consuming for complicated in-vivo scenarios
Learning-based optimization of acquisition schedule (LOAS) for semisolid MT MRF85	Directly computs quantitative tissue parameter errors, outperforms Cramer–Rao lower bound based optimization, quantitate MT parameters and water T1	Based on the analytical solution of the BM equations, which might be less accurate than the numerical solution
Semisolid MT/CEST MRF acquisition protocols discovery and deep parameter quantification (AutoCEST)82	An end-to-end fully automatic procedure, yiedling short acuisition schedules and trained NNs for quantitative semisolid MT and CEST reconstruction	Based on the analytical solution of the BM equations, which might be less accurate than the numerical solution

An additional open subject in quantitative semisolid MT/CEST is the required performance. Is it sufficient to obtain a 10 mM mean squared error in estimating the compound concentration? A 20 Hz resolution for proton exchange rate estimation? A 10% mean absolute error for any parameter? Arguably, the minimal performance should allow the reasonable detection of disease and its classification into various stages/treatment response.

The clinical imaging field is slowly but steadily transitioning to rely on quantitative instead of qualitative measures.¹⁰⁸ The effort in converting CEST and semisolid MT to become fully quantitative methods for obtaining molecular information could constitute an important component in this transition to quantitative MRI. Given that deep semisolid MT/CEST-MRF provides a drastically shorter scan time, a simultaneous estimation of quantitative biophysical parameters, and a simplified and objective means of analysis, we anticipate that it could play a substantial role in the efforts to make semisolid MT and CEST-MRI an integral part of the clinical imaging routine.

Abbreviations:

ANNCEST

artificial neural network-based chemical exchange saturation transfer

APT

amide proton transfer

APTR

amide proton transfer ratio

AREX

apparent exchange-dependent relaxation

BM

Bloch-McConnell

BSA

bovine serum albumin

CAD

computer automated design

CEST

chemical exchange saturation transfer

CNN

convolutional neural network

CPU

central processing unit

CRLB

Cramer-Rao lower bound

DISC

direct saturation correction

EPI

echo planar imaging

GBM

glioblastoma multiforme

GPU

graphics processing unit

IP

interior-point

LOAS

learning-based optimization of acquisition schedule

MeLOVARS

multi-echo length and offset varied saturation

MRF

magnetic resonance fingerprinting

MRI

magnetic resonance imaging

MRS

magnetic resonance spectroscopy

MS

multiple sclerosis

MTR_asym

magnetization transfer ratio asymmetry

MT

magnetization transfer

NN

Neural network

pCr

phosphocreatine

PRO-QUEST

progressive saturation for quantifying exchange rates using saturation times

QUASS

quasi-steady--state

QUESP

quantifying exchange using saturation power

QUEST

quantifying exchange using saturation time

RAM

random access memory

rNOE

relayed nuclear Overhauser effect

SCONE

schedule optimization network

SNR

signal to noise ratio

TSE

turbo spin echo

WEX

water exchange