Dynamic Self-Organization and Early Lexical Development in Children

Abstract

In this study we present a self-organizing connectionist model of early lexical development. We call this model DevLex-II, based on the earlier DevLex model. DevLex-II can simulate a variety of empirical patterns in children’s acquisition of words. These include a clear vocabulary spurt, effects of word frequency and length on age of acquisition, and individual differences as a function of phonological short-term memory and associative capacity. Further results from lesioned models indicate developmental plasticity in the network’s recovery from damage, in a non-monotonic fashion. We attribute the network’s abilities in accounting for lexical development to interactive dynamics in the learning process. In particular, variations displayed by the model in the rate and size of early vocabulary development are modulated by (a) input characteristics, such as word frequency and word length, (b) consolidation of lexical-semantic representation, meaning-form association, and phonological short-term memory, and (c) delayed processes due to interactions among timing, severity, and recoverability of lesion. Together, DevLex and DevLex-II provide an accurate computational account of early lexical development.

1. Introduction

Early childhood is a remarkable period for language learning and development. By age 6, most children have acquired the major components of their native language and have amassed a vocabulary approaching 14,000 words (Templin, 1957). Although the timetable of these developments is well understood, the details of the computational and neural mechanisms supporting this achievement are not yet very clear. While some scholars think that significant aspects of language are innately coded in the human genome (Chomsky, 1968; Pinker, 1994), others believe that internal linguistic representations emerge from the processing of linguistic input (Elman, Bates, Johnson, Karmiloff-Smith, Parisi, & Plunkett, 1996; Tomasello & Slobin, 2005) in ways that can be modeled by principles and mechanisms in neural networks (Rumelhart & McClelland, 1986; Plunkett, 1997; Rohde & Plaut, 2003).

In this study, we present a self-organizing neural network model that relies on realistic parental input sampled from actual parent-child interactions. We use this model to account for four important developmental patterns: (1) the spurt in vocabulary growth, (2) word-length and word-frequency effects, (3) individual differences in lexical development, and (4) word learning after early brain injury.¹ Our goal is to construct a model that is based on realistic developmental and neurological assumptions and that can adequately account for each of these four developmental patterns.

1.1. Vocabulary spurt

First, let us consider the growth pattern known as the “vocabulary spurt.” As we noted above, by age 6, children have learned nearly 14,000 words. This means that, on average, the child must learn nine new words each day or nearly one new word during each waking hour. In reality, this rapid increase in vocabulary is not spread out evenly across the first six years. Normally, at the age of 18 months, children can produce no more than about 50 words; after this point, vocabulary learning accelerates. Over the next months their vocabulary size increases first to 100, then to 200 and 300, and by 30 months it has reached more than 500 words. This period of rapid growth is referred to as the ‘vocabulary spurt’ or ‘naming explosion’ by developmental psycholinguists (Dromi, 1987; McCarthy, 1946; Nelson, 1973; Goldfield & Reznick, 1990; Van Geert, 1991; Bates & Carnevale, 1993; Elman et al., 1996). Although the exact shape of this spurt varies across children (Ganger & Brent, 2004), word types (Goldfield & Reznick, 1990), and language modality (comprehension versus production, Reznick & Goldfield, 1992),² all normal children demonstrate an initial slow pace of learning followed by a period of more rapid word production.

Results from previous empirical research have served to document the outcome and timing of vocabulary learning under various conditions, but have not clearly elucidated the underlying mechanisms responsible for the alleged vocabulary spurt. A number of factors have been proposed to account for why vocabulary spurt occurs. Researchers have considered the role of phonological ability (Menn & Stoel-Gammon, 1993), overlapping contexts (Siskind, 1996), word retrieval ability (Gerskoff-Stowe & Smith, 1997), social-communicative ‘awakening’ (Tomasello, 1999), or the “naming insight” (McShane, 1979). However, none of these factors seems to be sufficiently clear or constraining in describing the precise shape of change leading to vocabulary spurt (see Bates, Thal, Finlay & Clancy, 2003, for discussion). To overcome some of the empirical limitations associated with studying developmental changes in young children, researchers have made attempts to account for lexical development through computational modeling (see e.g., Plunkett, Sinha, Moller, & Strandsby, 1992; Siskind, 1996; Regier, 2005; Yu, Ballard & Aslin, 2005). These models have been important in informing us of early form-meaning mappings in word learning and the relationships between comprehension and production. However, aspects of these models are often simplified on important dimensions (e.g., lack of realistic form/meaning representations, lack of scalable vocabulary size, or lack of neural plausibility), to which we will turn in later discussion. In this paper, we review the limitations of previous modeling efforts and propose a new computational account of the vocabulary spurt.

1.2. Frequency and length effects

Given the high ecological importance and empirical relevance of word frequency and word length to vocabulary development, we also plan to simulate these effects on lexical learning in our model, with particular reference to vocabulary spurt. Indeed, any model of early lexical acquisition must provide an accurate account of word frequency and length effects. Previous psycholinguistic research has shown that: (1) pictures associated with high frequency words are named faster than pictures associated with low frequency words (e.g., Oldfield & Wingfield, 1965; Seidenberg, 1989; Jescheniak & Levelt, 1994); (2) high frequency makes a word less susceptible to phonological errors (e.g., Stemberger & MacWhinney, 1986; Dell, 1990); and (3) children’s first words are often the most frequently used words in their language input (e.g., Harris, Barrett, Jones & Brookes, 1988; Naigles & Hoff-Ginsberg, 1998; but see Goodman, Dale, & Li, 2006, for a recent analysis). With regards to word length, research has shown that: (1) in picture-naming experiments, longer words are slower to name (e.g., Roelofs, 2002); and (2) pronunciation patterns are often more accurate for shorter words than for longer words during children’s early phonological development (e.g., Menn & Stoel-Gammon, 1993). Both empirical research and modeling studies of adult lexical processing have devoted extensive attention to the effects of word frequency and length. Given this emphasis in the adult work, it is surprising to note that few computational models have considered the role of these factors on early word learning.

1.3. Individual differences in word learning

Individual differences play an important role in language acquisition: children often differ widely in rate, style, and outcome with respect to lexical, grammatical, and phonological development (see a review in Shore, 1995; Bates, Dale & Thal, 1995). With respect to the vocabulary spurt, empirical studies have shown that children vary in the extent to which they demonstrate a pronounced spurt pattern (Goldfield & Reznick, 1990; Bates et al., 1994; Mervis & Bertrand, 1995; Thal et al., 1997; Bates et al., 2003). It is likely that these variations stem, at least in part, from individual differences in the capacity of phonological memory (Gupta & MacWhinney, 1997; Gathercole & Baddeley, 1993). Variations in the pattern of the vocabulary spurt may also depend on underlying differences in general associative ability for word learning: by 14 months, some children can already learn arbitrary word-object associations from single brief exposures (Werker et al. 1998), and some researchers argue that this rapid associative ability may be related to cognitive factors such as object categorization and increased selective attention abilities (Bates et al., 1995; 2003; Milostan, 1995; Regier, 2003, 2005). An important goal of the current study is to investigate the mechanisms underlying individual differences in early vocabulary development through connectionist modeling.

1.4. Recovery from early brain injury

Significant progresses have been made in the understanding of language development and its neurological underpinnings through research with children who suffer from brain injuries that differ in size, location, etiology, and age of onset (e.g., Vargha-Khadem, Isaacs, & Muter 1994; Bates, 1999; MacWhinney et al., 2000; Anderson et al., 2001; Bates & Roe, 2001). Empirical studies show that children with early brain injury can go on to acquire linguistic abilities within the normal range, whereas similar lesions in adults produce dramatic patterns of aphasia (e.g., Bates & Roe, 2001; Bates et al., 2003). These data provide evidence of extensive cortical plasticity across a wide age range, particularly in the early lifespan (e.g., Schneider, 1979; Thomas, 2003). In this study, we hope to highlight the issue of learning plasticity by observing how our neural network model recovers from lesions induced at various points in lexical development.

1.5. Overview of previous computational models

Over the last 15 years a number of computational models of lexical acquisition have been proposed, and several of them attempted to account for aspects of the developmental phenomena discussed above. Here, we will review the assumptions, mechanisms, and achievements of these models.

Plunkett et al. (1992) presented a multilayer connectionist network model of lexical acquisition based on the back-propagation learning algorithm. During training, their model received as input an artificial image (distributed representations), its corresponding label (localist representations), or both, and the network’s task was to associate the label with its corresponding image (comprehension) or to associate the image with its label (production). This auto-association model showed vocabulary spurts in both comprehension and production, along with a general relative advantage for comprehension over production. The authors attributed the vocabulary spurt behavior to the emergent systematization of the conceptual basis of word meanings.

Siskind (1996), using a series of inference rules, tested a computational model that displayed early slow learning and later fast mapping during lexical acquisition. The core of Siskind’s model is the idea of “cross-situational learning” (i.e., learning of the mapping of forms to meanings and their statistical associations in overlapping contexts). In Siskind’s model, the system needs to identify words in utterances and their likely interpretations based on context. As learning progressed, the system gained more knowledge about the meanings of some words, which in turn constrained the possible interpretations of other words in the utterance, resulting in faster learning. However, word forms were not represented or considered in Siskind’s learning model, as pointed out by Regier (2005).

Regier et al. (2001) and Regier (2005) proposed to account for the vocabulary spurt in terms of a process of increased selective attention by which the model develops increasingly accurate expectations about the lexical structure through attention to communicatively relevant dimensions of meaning and form (see also Colunga and Smith’s (2005) detailed exposition of this idea in the learning of the solid-nonsolid distinction and the development of shape bias in early lexicon). Regier (2005) introduced the LEX (lexicon as exemplars) model, in which either word form or word meaning can be sent to the network as input, and then retrieved as output (similar to the auto-association model of Plunkett et al., 1992). The task of the network was to associate the word form-meaning pairs through the gradient descent algorithm. LEX displays many characteristics in children’s language development including fast mapping. The chief mechanism underlying LEX’s learning ability is selective attention, which increases as learning progresses, and reduces memory interference during lexical competition. Thus, words that are similar in phonology or semantics are more likely to be confused with one another early on, but as the child gets older, increased selective attention highlights relevant dimensions that are predictive of form from meaning or predictive of meaning from form. The result of this dimensional focusing is thus reduced memory interference and accelerated lexical growth.

Recently, Yu et al. (2005) proposed a computational model of early lexical acquisition based on word-meaning associations from raw multi-sensory signals to simulate the natural language environment of infants. In their system, real sound patterns of individual words and real image of objects can be transformed into digital representations and input to the network. The authors discussed the model’s potential for explaining fast-mapping as a result of reducing the set of possible candidates in the models’ form and meaning space in a given context, but no direct test was conducted on vocabulary growth profiles.

Although there are several models that have examined the cause of the vocabulary spurt, as discussed above, there are no models of early lexical development that have directly investigated the effects of word frequency and length, individual differences in lexical learning, or lesioned lexicon in acquisition. For example, although type-token frequency information is often considered in connectionist models of the English past tense (Plunkett & Marchman, 1991, 1993; Plunkett & Juola, 1999), it has not been considered in models of early lexical development. With regard to individual difference, Juola and Plunkett (1998) showed how such differences could emerge by starting models with different initial random weights. Also, Plaut (1997) simulated differences in normal and impaired lexical processing as a function of variations in the learning environment. However, no previous computational model has systemically evaluated individual differences in early lexical development. Finally, attempts have also been made to simulate developmental language disorders using connectionist networks, but most of this literature has focused on later language development or impaired reading acquisition (e.g., acquisition of grammatical morphology, particularly past tense; see Joanisse & Seidenberg, 1999; Thomas & Karmiloff-Smith, 2002, 2003).

Our brief review here shows that previous modeling work has produced a continuing accumulation of insights into early lexical learning, but it has also become clear that this work relies on a set of three simplified assumptions that must be eventually corrected in a fuller and more accurate account.

First, many previous models have used artificially generated input representations, rather than training sets derived from actual speech input to children. The use of these synthetic or highly simplified vocabularies provides certain modeling conveniences in terms of analysis of the linkage between input and output. However, inputs of this type fail to make direct contact with the detailed statistical properties and word forms of the naturalist input that children receive. To the degree that we replace actual input with highly idealized constructions, we run the risk of modeling developmental patterns that have no relation to the actual learning task. Realizing this limitation, some researchers (e.g., Roy & Pentland, 2002; Yu et al., 2005) have started to use realistic input in their models, for example, by incorporating perceptual cues grounded in the learning environment. However, these models focused on the role of multi-sensory signals on word learning and paid little attention to the system’s lexical growth over time. In addition, they represented word meanings as visual scenes and thus could learn only concrete nouns that denote objects, whereas the model we propose here is intended to handle a variety of lexical categories in children’s early acquisition.

Second, most previous models have failed to extend the size of the input corpus to a level that adequately simulates the actual growth of the lexicon. Consider the evidence from Gershkoff-Stowe and Smith (1997) that, by the age of 2;6, children begin to suffer from interference between related words in the semantic space of their growing lexicon. Models designed to account for the learning of only the first 50–100 words will fail to detect the emergence of this theoretically important period of between-word competition. The effects of small lexicon size can be further exacerbated in models that rely on either localist representation for word units or a distributed representation that fails to faithfully portray the unevenness of the actual semantic and phonological space of words.

Third, many previous models have relied on supervised learning within the back-propagation framework (e.g., Plunkett et al., 1992; Gasser & Smith, 1998). The core of the back-propagation algorithm is a set of input-output exemplars, which the network learns to associate (e.g., auto-association, in the case of identical inputs and outputs). Models based on this algorithm assume that the learner receives continual and consistent feedback from the environment regarding the correct target on every learning trial. Such an assumption is obviously unrealistic (see discussions in MacWhinney, 2001, 2004; Li, 2003, 2006). It is true that parents will occasionally correct children’s naming errors. If a child calls a cat a dog, parents will correct this. However, MacWhinney (2004) showed that such re-castings are best understood as new competing correct inputs, rather than as feedback linked to the original retrieval trial. Recastings of this type are neither consistent nor diagnostic for the child—they could also be absent in some cultures altogether (see Schieffelin, 1985). In general, models that rely on the continual availability of corrective feedback are developmentally implausible (Shultz, 2003). This may be especially true for a model like ours that examines mental representations of lexical structure—in realistic learning, much of the mental organization and reorganization of the lexicon as a system takes place without explicit teaching or direct feedback, and perhaps largely off-line (see discussion in Bowerman, 1988).

The model we present below addresses each of these three limitations. By modeling actual lexical forms from the parental speech in the CHILDES database (MacWhinney, 2000), we are able to achieve developmental and lexical realism. By constructing data compression methods to deal with the continually expanding nature of children’s lexicon, we are able to model lexical growth up to the level of 591 actual words, and the method could be extended well beyond this level (see Zhao & Li, 2007, in which the model dealt with 1000 words). By using a more neurally plausible model, a self-organizing feature map, we are able to avoid reliance on consistent error feedback. In what follows, we first examine the computational details of our model, and then discuss the simulation results with respect to the properties of realistic input and unsupervised self-organizing processes in the network.

2. Method

2.1. Description of the model

2.1.1. Overview

The DevLex-II model is a multiple layer self-organizing neural network of early lexical development. It is based on the DevLex (Li, Farkas, & MacWhinney, 2004) and DISLEX (Miikkulainen, 1997) models. Fig. 1 presents a diagrammatic sketch of DevLex-II. The model has three basic levels of linguistic information: phonological content, semantic content, and output sequence. At the center of the model is a self-organizing, topography-preserving, feature map (Kohonen, 1982, 2001), which processes semantic content. This central feature map is connected to two other feature maps, one for input (auditory) phonology, and another for articulatory sequence of output phonology.

Fig. 1.

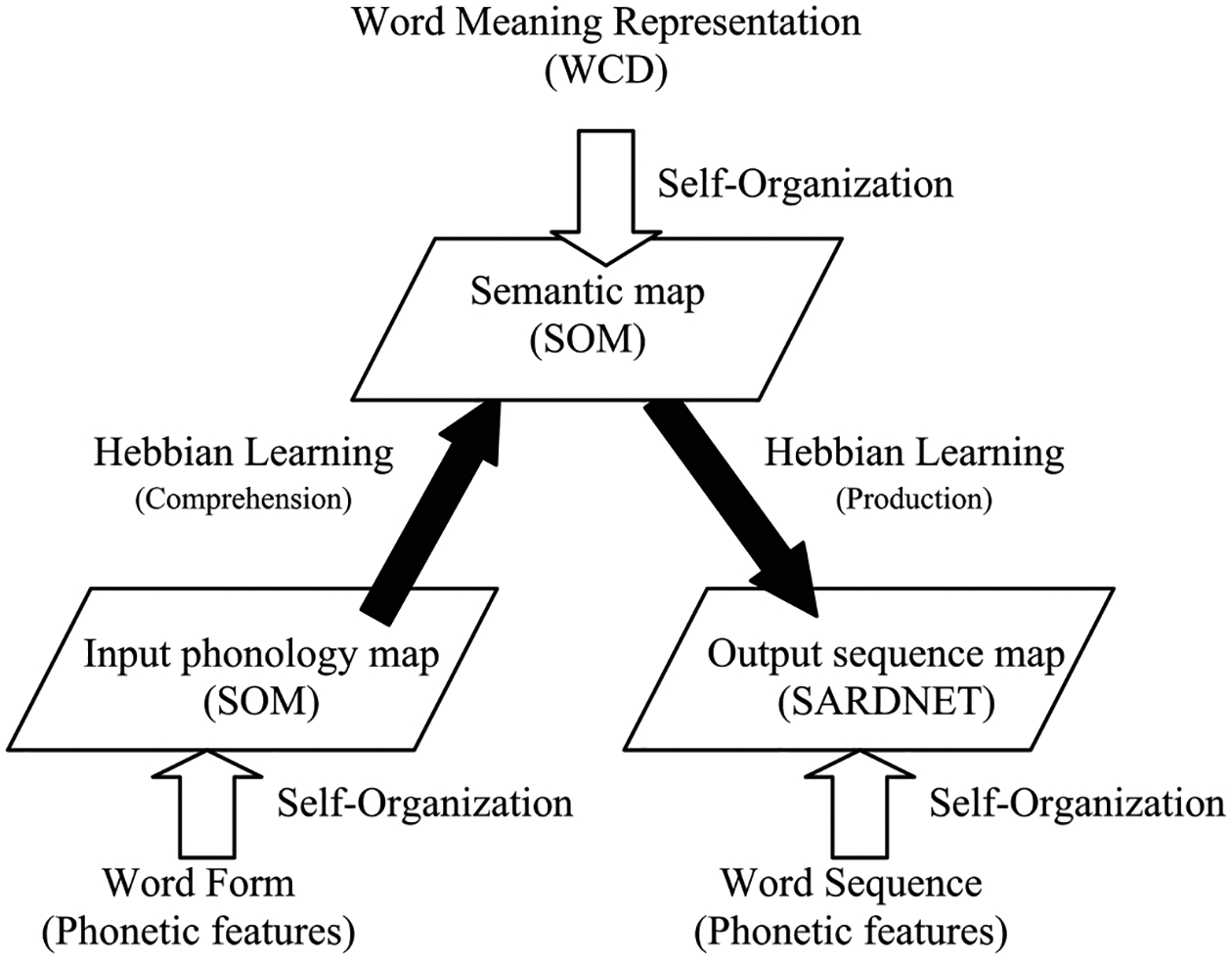
The DevLex-II model of lexical development. Each of the three self-organizing maps (SOM) takes input from the lexicon and organizes phonology, semantics, and phonemic sequence information of the vocabulary, respectively. The maps are connected via associative links updated by Hebbian learning.

On both the semantic and phonological maps, the network forms patterns of activation according to the standard self-organizing map (SOM) algorithm of Kohonen (2001). Here, a SOM is a two-dimensional square lattice with a set of neurons, and every neuron has the same number of input connections to receive external stimulus patterns. So a neuron k has a vector m_k associated with it to represent the weights of the input connections to it. Given a stimulus x (the phonological or semantic information of a word), the localized output response α of neuron k is computed as

$${\alpha }_k=\{\begin{array}{ll}1-\frac{\Vert x-m_k\Vert -d_{\text{min}}}{d_{\text{max}}-d_{\text{min}}},\hfill & \text{ if }k\in N_c\hfill \\ 0,\hfill & \text{ otherwise }\hfill \end{array}$$ (1)

where N_c is the set of neighbors of the winner c (for which α_c = max_kα_k), and d_min and d_max are the smallest and the largest Euclidean distances of x to neuron k’s weight vectors within N_c. In SOM, the winners are depicted as BMUs (best matching units). At each training step as BMUs are picked up, the map also self-organizes to maximally preserve the topography of the input space (for a recent exposition of the role of SOMs in cognitive science, see Silberman, Bentin, & Miikkulainen, in press).

2.1.2. The output sequence map

The output sequence level works in a slightly different way from the other two levels. The addition of this level in the model represents a step forward from the original DevLex model, and is inspired by models of word learning based on temporal sequence acquisition (e.g., Houghton, 1990; Gupta & MacWhinney 1997). It is designed to simulate the challenge that children face during the second year, when they need to develop better articulatory control of the phonemic sequences of words. Just as the learning of auditory sequences requires the mediation of memory systems, the learning of articulatory sequences requires support from phonological rehearsal in working memory (Gathercole & Baddeley, 1993; Gupta & MacWhinney, 1997). Here, the activation pattern corresponding to the phonemic sequence of a word is formed according to the algorithm of SARDNET, a self-organizing sequence map that establishes an activation gradient for representing letter sequences over time (James & Miikkulainen, 1995).

At each training step, phonemes are input into the sequence map one by one, according to their order of occurrence in the word. The winning unit of a phoneme is found and the responses of nodes in its neighborhood are adjusted as shown in Equation 1. Once a unit is designated as the winner, it becomes ineligible to respond to subsequent inputs in the sequence. In this way, the same phoneme in different syllabic locations will be mapped to different (but adjacent) nodes on the map as a result of the network’s topography-preserving ability. Thus, for each phoneme, there might be a cluster of neighboring units responding to it, reflecting the fact that positional variants of a phoneme still share similar segmental content, despite minor allophonic variation (Ladefoged, 1982). When the output status of the current winner and its neighbors is adjusted according to Equation 1, the activation levels of the winners responding to phonemes before the current phoneme will be adjusted by a number γ ^d, where γ is a constant and d is the distance between the location of the current phoneme and the previous phoneme that occurred in the word. This adjustment is intended to model the effect of phonological short-term memory during the learning of articulatory sequences; the activation of the current phoneme could be accompanied by some rehearsal of previous phonemes due to phonological memory, which deepens the network’s or the child’s impression of previous phonemes. The γ here is chosen to be less than 1 (0.8 in our case), in order to model the fact that phonological memory tends to decay with time.

For a word with n phonemes, the output of the winner responding to the j^th phoneme will be 1 + γ + γ ² + ··· + γ ^n–j, which is a geometric progression, and can be written as:

$${\alpha }_{\mathit{\text{winner}}}(j)=\frac{\left(1-{\gamma }^{n-j+1}\right)}{1-\gamma }$$ (2)

According to Equation (3), when all phonemes’ representations of a word are sent to the output sequence map, the activation of some nodes (e.g., the first winner) will be larger than 1, so they need to be normalized to the range between 0 and 1. Thus, the node in response to the first phoneme of the word will have the largest activation, followed by sequentially decaying activations of other phonemes in the sequence. After winners are identified, the weights of the nodes surrounding these winners are updated (self-organized) according to

$$m_{kj}(t+1)=m_{kj}(t)+\alpha (t)\cdot \left[x_j-m_{kj}(t)\right]forallk\in N_c$$ (3)

where α(t) is the learning rate, which changes with time.

In DevLex-II, the activation of a word form can evoke the activation of a word meaning via form-to-meaning links (to model word comprehension) and the activation of a word meaning can trigger the activation of an output sequence via meaning-to-sequence links (to model word production).³ In parallel with the training of three maps, the associative connections between maps are trained via Hebbian learning (Hebb, 1949) in accord with Equation (4):

$$\Delta w_{kl}=\beta \cdot {\alpha }_k^S\cdot {\alpha }_l^D$$ (4)

Here, w_kl is the unidirectional associative weight going from node k in the source map to node l in the destination map, ${\alpha }_k^S$ and ${\alpha }_k^S$ are the associated node activations, and β is a constant learning rate. The associative weight vectors are then normalized and normalization is carried out over all associative links of the source neuron according to Equation (5):

$$w_{kl}(t+1)=\frac{w_{kl}(t)+\Delta w_{kl}}{{\left\{{\sum }_l{\left[w_{kl}(t)+\Delta w_{kl}\right]}^2\right\}}^{1/2}}$$ (5)

2.1.3. Neighborhood function

An important concept of the standard SOM algorithm is the so-called neighborhood function. When a node becomes the BMU, both the node itself and its neighboring nodes undergo weight updating. The size or radius of the neighborhood usually decreases as a function of training time, such that SOM organizes information early on in large areas (establishing basic topography) and later on in small areas (fine-tuning). This scenario thus gives the network greater plasticity at the beginning but decreased ability to reorganize at later stages of learning. This pattern of development in the network, though intuitively clear and practically useful, is subject to the criticism that learning is tied directly to time (amount) of learning, and is rather independent of the input-driven self-organizing process. In this study, we attempt to correct this by using a learning process in which the neighborhood size is not locked with time, but adjusted according to the network’s learning outcome. In particular, neighborhood function will depend on the network’s average quantization error on each layer or map, with quantization errors defined as the Euclidean distances in the input space between an input pattern and the input weight vector of its BMU (Kohonen, 2001). We implement this process as follows: (1) at periodic intervals (e.g., every 5 epochs), the network checks the quantization errors on each layer responding to input patterns; (2) average quantization errors for each layer are calculated; (3) average quantization errors from the current epoch are compared with those from previous epochs, and neighborhood sizes on each layer are adjusted accordingly (either remain unchanged, or decrease by 1 if the current error is smaller than a given amount of the previous average error, which is 75% here); (4) once neighborhood size of any layer decreases to zero, the procedure terminates, so that no negative values of neighborhood size will result.

Our new approach to neighborhood size adaptation is consistent with recent efforts in finding more adaptive SOM algorithms (Schyns, 1991; Iglesias & Barro, 1999; Berglund & Sitte, 2006)⁴ and is meaningful and plausible on neurobiological grounds (cf. Miikkulainen, Bednar, Choe, & Sirosh, 2005). The new approach relates more closely to learner-environment interactions, while the standard SOM approach is more reminiscent of a fixed internal timetable.

2.1.4. Summary of the model

The process of word learning in DevLex-II can be summarized as follows. In comprehension, a winner is first activated on the phonological map, and this activation propagates to the semantic map via associative links. On the semantic map, the node with the strongest associative link with the winner on the phonological map is then activated. This node becomes the winner on the semantic map. The network performs a self-check to see if this unit is the BMU of the meaning of a unique word in the semantic space. If it is, this means that the correct word was retrieved and that comprehension was successful. If the self-check fails, then comprehension has failed, as the meaning of the target word is being confused with that of other words or no word meaning is being retrieved.

The production process is similar to the comprehension process, with a slight modification. This time, the winner on the semantic map propagates its activation to the output sequence map, and several nodes in the sequence map become activated sequentially as winners that represent the word’s phonemes. Then the network checks to see if every node is the BMU of a unique phoneme, according to the Euclidean distance between its input weight vector and the feature representation of every phoneme. If it is, the phoneme closest in Euclidean distance to the current winner becomes its retrieved phoneme; if it is not, the pronunciation of this phoneme has failed. Finally, the pattern of the retrieved phonemes in the sequence is treated as the output of word production. When the retrieved phonemic sequence matches up with the actual word’s phonemic sequence, we say that the word has been correctly produced.

Our discussion above shows that our model (DevLex and DevLex-II) differs from previous connectionist models of language acquisition in fundamental ways, and that it is based on simple but powerful computational principles of self-organization and Hebbian learning. Such principles allow us to address problems in previous models, avoiding the need of consistent corrective feedback and obtaining a level of neural and cognitive plausibility. SOM-based self-organization has been motivated by topography-ordering features which can be found in many parts of the brain (Kohonen, 2001; Miikkulainen et al., 2005)—in a sense the human cortex can be considered as consisting of multiple feature maps that handle auditory, visual, and other sensorimotor information, topographically ordered as a result of responding to input characteristics in the learning environment (Spitzer, 1999). Moreover, SOMs can implement the neurocomputational principle that favors preservation of short local connections over long-distance connections (Shrager & Johnson, 1996). In particular, Moll and Miikkulainen (1997) have shown that connections between non-neighboring units can be pruned gradually through learning to minimize excessive neural connectivity, and such pruning may lead to improvements in retrieval capacity. Our model, in addition to drawing on properties of self-organization in SOMs, further relies on the training of Hebbian connections. Work in neuroscience (Kandel, Schwartz, & Jessell, 2000) has demonstrated the reality and fundamental importance of Hebbian learning on the level of the synapse. Our model relies on SOM-based computation for within-modality self-organization and on Hebbian learning for between-modality interaction. In doing so, it also achieves developmental realism with respect to the structure and characteristics of the input lexicon.

2.2. The CDI vocabulary

To model early lexical acquisition by children, we created an input corpus based on the vocabulary from the MacArthur-Bates Communicative Development Inventories (CDI; Fenson, et al., 1994; Dale & Fenson, 1996). From the 680 words in the Toddler’s List, we extracted 591 words, after excluding homographs and homophones, word phrases, game words, and onomatopoeias. Our list includes verbs, adjectives, 12 categories of nouns (animals, body parts, clothing, food, household, outside things, people, rooms, toys, time, place, and vehicles), and 6 categories of closed-class words (auxiliary verbs, connecting words, prepositions, pronouns, quantifiers, and question words). This lexicon includes 345 nouns, 103 verbs, 61 adjectives, and 82 closed-class words. The preponderance of nouns in our input corpus is in accord with the noun bias found in the early vocabulary of young English-speaking children (see Bates et al., 1994).

2.3. Input representations

To represent the 591 words as input to our network, we first generated the input phonological forms of the words using the PatPho generator, in a left-justified template with binary coding (Li & MacWhinney, 2002). PatPho is a generic phonological pattern generator for neural networks that fits every word (up to trisyllables) onto a template according to its vowel-consonant structure. It uses the concept of syllabic template: a word’s representation is made up by combinations of syllables in a metrical grid, and the slots in each grid are made up by bundles of features that correspond to phonemes, consonants (C) and vowels (V). For example, a full trisyllabic template would be CCCVVCCCVVCCCVVCCC, with each CCCVV representing one syllable and the last CCC representing the final consonant clusters. This template has 18 C and V units. In this representation, the sequential temporal structure of the input phonology is characterized by the position of segmental information in the 18 slots of the template. Compared to traditional phonemic representations (e.g., Miikkulainen, 1997), PatPho is more capable of representing the phonological similarities of multi-syllabic words, because similar words with differing numbers of phonemes can be aligned across similar positions in the grid.

PatPho uses phonetic features based on Ladefoged (1982) to represent the C and V phonemes. A phoneme-to-feature conversion process produces either real-value or binary feature vectors for any word up to three syllables in length. In this study, we decided to use the binary vectors with 114 dimensions, as the binary coding provided better discrimination of words’ phonological information (although with longer training time).

Next, word meaning representations for the 591 words were computed using the parental input from the CHILDES corpus (Li, Burgess, & Lund, 2000). The parental CHILDES corpus contains the speech transcripts from child-directed adult speech in the CHILDES database (MacWhinney, 2000). Representations were created using WCD, a special recurrent neural network that learns the lexical co-occurrence constraints of words (see Farkas & Li, 2001, 2002; Li et al., 2004, for details). WCD reads a stream of input sentences one word at a time, and learns the adjacent transitional probabilities between words which it represents as a matrix of weights. Given a total lexicon sized N, all word co-occurrences can be represented by an N × N contingency table, where the representation for the i-th word is formed by concatenation of i-th column vector and i-th row vector in the table.⁵ WCD computes two vectors that correspond to the left and the right context, respectively; it then transforms these probabilities into normalized vector representations for word meanings. This procedure is similar to the method used within the HAL model of Burgess & Lund (1997). One can consider WCD as a dynamic HAL system, in which lexical representations gradually enrich over time as a function of learning the number of co-occurring words in the input sentences: the more co-occurrences it incorporates, the richer the representation becomes. Metaphorically, this learning scenario can be compared to filling the holes in a Swiss cheese: initially there may be more holes than cheese (shallow representations) but the holes get filled up quickly as the co-occurrence context expands with more words being acquired (rich representations).

Finally, using the method of PatPho, we represented the 38 English phonemes by three-dimensional real-value vectors, which served as inputs to the output sequence map for phonemes. Here, for the representation of a phoneme, different values in each dimension have different meanings, which represent the particular features of that phoneme. In particular, in the vector, the first dimension indicates whether the phoneme is a vowel or a consonant, and in the case of a consonant, whether it is voiced or voiceless. The second dimension indicates the position for vowels and the manner of articulation for consonants, and the third dimension indicates the sonority for vowels and the place of articulation for consonants. We decided to use the real-value representations for phonemes since they have a constant vector dimension, whereas other types of representation (e.g., binary representation) may not; see Li and MacWhinney (2002).

2.4. Simulation parameters

In DevLex-II, the phonological map and the semantic map each consisted of 60 × 50 nodes, and the output sequence map consisted of 15 × 10 nodes. These numbers were chosen to be large enough to discriminate the words and phonemes in the lexicon, while keeping the computation of the network tractable.

The same initial neighborhood radius was used for all feature maps at the beginning of the training (we set it to be 4), and on each map, it gradually reduced to zero according to decreasing average quantization errors described earlier (section 2.1.3). In addition, the same learning rate α(t) was also used for all feature maps simultaneously, and it changed with time as in standard SOM learning. Learning rate α(t) was initially set to 0.4, then linearly decreased to 0.05 during the first 50 epochs. In the next 50 epochs, it remained at 0.05. Learning rate β for associative links between levels was kept constant (0.1) during the entire training process.

At each epoch, words from the training lexicon were presented to the network one by one. To simulate the effect of word frequency in early child language, the network selected a word each time according to its frequency of occurrence in the parental CHILDES corpus. However, since different words in the corpus often differ greatly in their frequency of occurrence, we would need a large amount of training to cover all the 591 words in our simulation. To avoid this problem, we decided to use the logarithms (base 10) of these occurrence frequencies to force a more even distribution of words in the input. Such a setup has been widely used in other computational simulations based on real corpora (e.g., Harm & Seidenberg, 1999), given that word frequency distributions follow the famous Zipf’s law (Zipf, 1932).

Additional parameters are introduced to the model to simulate particular developmental phenomena. For example, in modeling vocabulary spurt, we can introduce a ‘connection probability’ parameter to simulate individual differences in the development of children’s ability to form associations between linguistic levels. Werker et al.’s (1998) study showed clear individual differences in young children’s ability to form associations between a word’s form and its meaning; some children are able to map novel forms to meanings around 14 months, while others take an additional 4–6 months to do so. In our simulations, initially, two feature maps are only partially connected by associative links. Specifically, the ratio of the number of connected links to the number of all possible links between two maps is defined as the connection probability. This probability can be set to linearly increase with time from a low threshold (θ < 1.0) to full interaction (θ = 1.0), as opposed to full interaction throughout in the unmodified model. We tested three connection probabilities, with θ at 0.0, 0.5, and 1.0, respectively (the model becomes the unmodified version when θ equals 1.0).

We also used a ‘memory gating’ parameter τ to simulate individual differences in the development of phonological short-term memory abilities during articulation. This parameter affects learning in the output sequence map. Larger τ means stronger serial-recall ability in phonological short-term memory in this model. Although there has been no empirical study of the development of phonological memory in very young children aged 1–3 (for obvious reasons, as one cannot run the standard memory tests with children of this age; Gathercole, personal communication), we believe that the development of such memory abilities may play an important role in children’s early word production.

In our simulations, the activation of the winner (α_winner) responding to a phoneme in a word receives certain probabilities (determined by τ) to be affected by the short-term memory of the phonemic sequence. Thus, α_winner—the activation of the winning node corresponding to a phoneme—either could be calculated according to Equation 2 (which means that the current phoneme will be more strongly activated than the ones following it due to rehearsal effects), or could be 1 (which means that the following phonemes do not help with the recall of the current phoneme). In the former case, the probability with which the following phoneme will affect the current phoneme depends on the memory gating parameter τ: when τ = 1, every phoneme in a word will be affected by the following phonemes in the sequence according to Equation 2; when τ = 0, all phonemes are independent, and the current phoneme is not affected by following phonemes. Thus, the larger the τ is, the stronger the sequence memory, and the greater the available memory resources. To model the development of this ability in children, the parameter τ is set to linearly increase with time from 0.0 (weakest phonological memory) to 1.0 (strongest phonological memory). As in the model in which α_winner is not affected by τ, the output nodes in the map will be normalized to the range between 0 and 1 when the whole phonemic sequence is input to the network. Here, Equation 2 could be modified as:

$${\alpha }_{\mathit{\text{winner}}}(j)=\{\begin{array}{ll}\frac{\left(1-{\gamma }^{n-j+1}\right)}{(1-\gamma )},\hfill & \mathit{\text{ with probability }}\tau \hfill \\ 1,\hfill & \mathit{\text{ with probability }}1-\tau \hfill \end{array}$$ (6)

Each model is simulated with ten simulation runs (unless otherwise specified), and the reported results in Section 3 are based on the averaged performance from the ten runs that have the same simulation parameters.

2.5. Assumptions

The DevLex-II model makes a few simple assumptions based on the early lexical acquisition literature to date: (a) the child has the ability to learn sequences of phonemes for articulation (Locke, 1983; Menn & Stoel-Gammon, 1995); (b) the child has the ability to hold the phonological representations of words in phonological short-term memory (Gupta & MacWhinney, 1997); and (c) the child has the ability to extract co-occurrence statistics from running speech and that such statistics can be used as the basis for mental representation of lexical-semantic knowledge (Saffran et al., 1996, 1997; Burgess & Lund, 2000; Li et al,, 2000; Li et al., 2004; Li, 2006; Li et al., 2006). The task for our model is to show how the interaction of these abilities yields the developmental patterns we discussed earlier.

3. Simulation results

3.1. The vocabulary spurt

Fig. 2 presents our simulation results with the 591 words from the CDI vocabulary. The figure shows the average receptive and productive vocabulary sizes across the course of training. One can observe a clear vocabulary spurt, preceded by a stage of slow learning and followed by performance on a plateau. On the average, the model’s productive vocabulary did not accelerate until about 35–40 epochs, one third into the total training time, reflecting the model’s early protracted learning of the representations of word forms, meanings, and sequences, and their associative connections. Although the figure shows only the results of the associative connections (form-to-meaning for comprehension, and meaning-to-sequence for production), the hit rates for these connections depend directly on the precision of self-organization in the separate feature maps (Miikkulainen, 1997; Li et al., 2004). In other words, the period of rapid increase in vocabulary size has been prepared by the network’s slow learning of the structured representation of phonemic sequence, word phonology, and word semantics, as well as its learning of the mappings between these characteristics of the lexicon. Once the basic structures are established on the corresponding maps, the associative connections between maps can be reliably strengthened to reach a critical threshold through Hebbian learning.

Fig. 2.

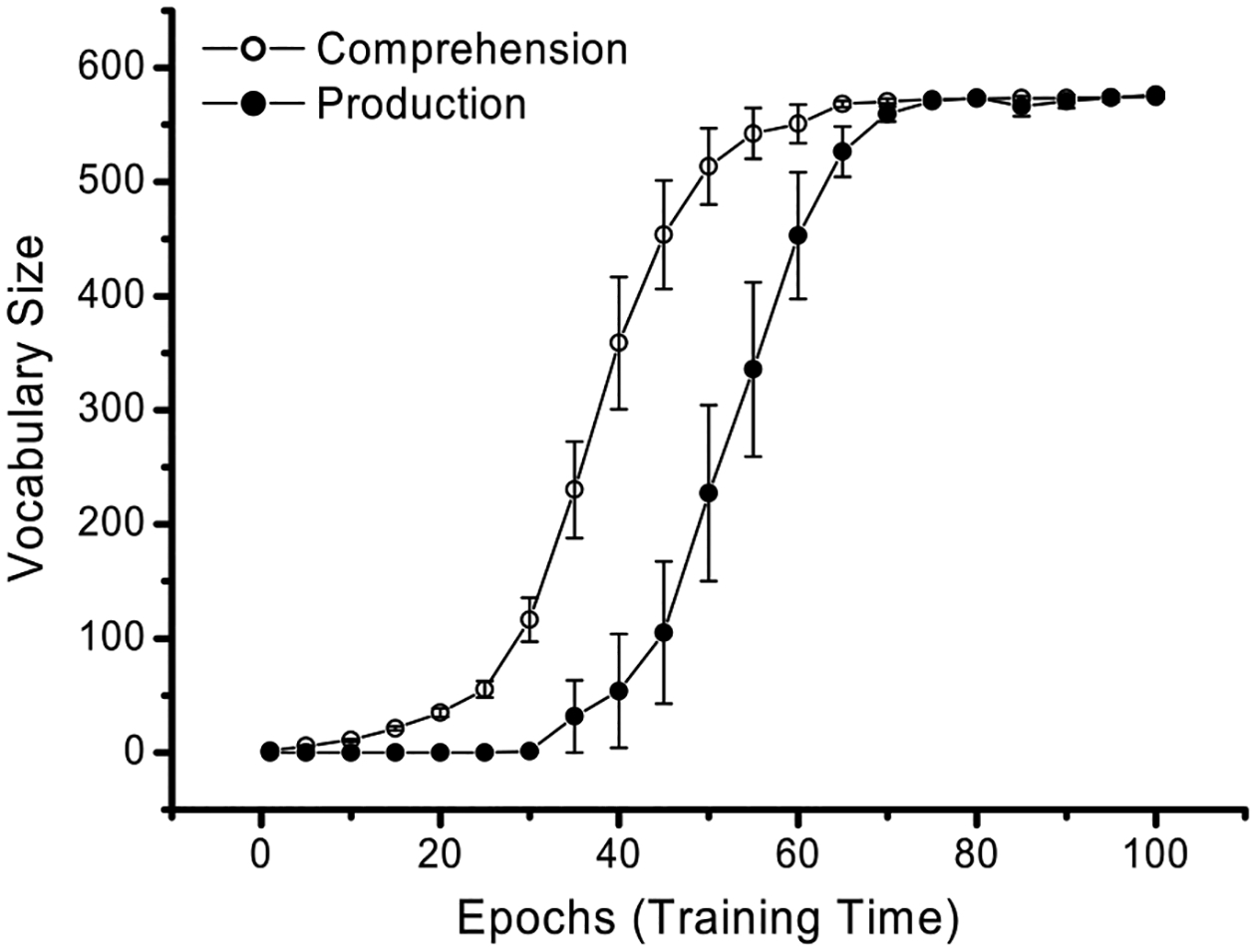
Vocabulary spurt in the learning of the 591 CDI words by DevLex-II. Results are averaged across ten simulation trials (error bars indicate standard errors of the mean); same with other figures.

The second pattern displayed in Fig. 2 is that the vocabulary spurt occurs for both production and comprehension, rather than being restricted to only one modality, consistent with empirical studies and connectionist modeling. Previous empirical studies have largely focused on children’s word production, but a few researchers have also questioned whether a comprehension vocabulary spurt could exist (Reznick & Goldfield, 1992; Werker et al., 1998). Reznick and Goldfield found a clear spurt in children’s receptive vocabulary, and concluded that the presence of a comprehension spurt is associated with that of a production spurt. Although both types of spurt were present in our simulations, the comprehension spurt occurred earlier than the production spurt, which accords with repeated empirical evidence that comprehension generally precedes production (Clark & Hecht, 1983) and in the case of lexical acquisition, a spurt in the receptive vocabulary could start from 14 months of age (Benedict, 1979; Werker et al., 1998).

A third finding is that although the average comprehension and production rates showed a clear vocabulary spurt, as shown in Fig. 2, there were significant individual differences between different simulation trials (all having the same modeling parameters). To see this, we plotted the standard errors of the mean for trials at different epochs in the figure. Most interestingly, the largest variations tended to coincide with the rapid growth or spurt period. Examining the individual trials in detail, we found that different simulated networks could differ dramatically in the onset time of their vocabulary spurt. In our ten simulations, the rapid increase of vocabulary size in production could begin from as early as epoch 30, or from as late as epoch 60, but in each case there was a clear spurt process. Such variations are random effects, due primarily to the network’s random initial states (weight configurations before training) and analogous to the child’s different initial learning states. The random effect may partly explain the individual differences across children’s early language development; we will further discuss other possible factors for individual differences in section 3.3.

To further verify our argument that vocabulary spurt emerges as a result of the system’s structured representation in word form and word meaning, we examined how the confusion rates for each of the three maps changed with time, as shown in Fig. 3. Confusion rate is defined here as the percent of input patterns confused with other input patterns on each layer. Early in training, the confusion rates for each map were relatively high, which means that the maps were not yet capable of classifying different input entries (word forms, word meanings, or phonemes). As training progressed, the confusion rates gradually dropped. Comparing Figs. 2 and 3, we observed the interesting pattern that the onset time of vocabulary acceleration coincided with the time when confusion rates dropped to a given low level. For example, around Epoch 25, the confusion rates for both the phonological and semantic maps reached a level below 35% (which means about two thirds of the target words were correctly represented on the two maps); around the same time, word comprehension also started to accelerate. Around Epoch 40, the confusion rate for the output sequence map also reached the level below 35%, and at about the same time, word production started to accelerate. In addition, the further the confusion rates decreased, the more rapid the acceleration. When confusion rates reached the lowest level and started to level off, vocabulary spurt also reached its peak level.⁶ We interpret this relation as indicating that the solidification of local representations of words provided a crucial support for the onset of the vocabulary spurt.

Fig. 3.

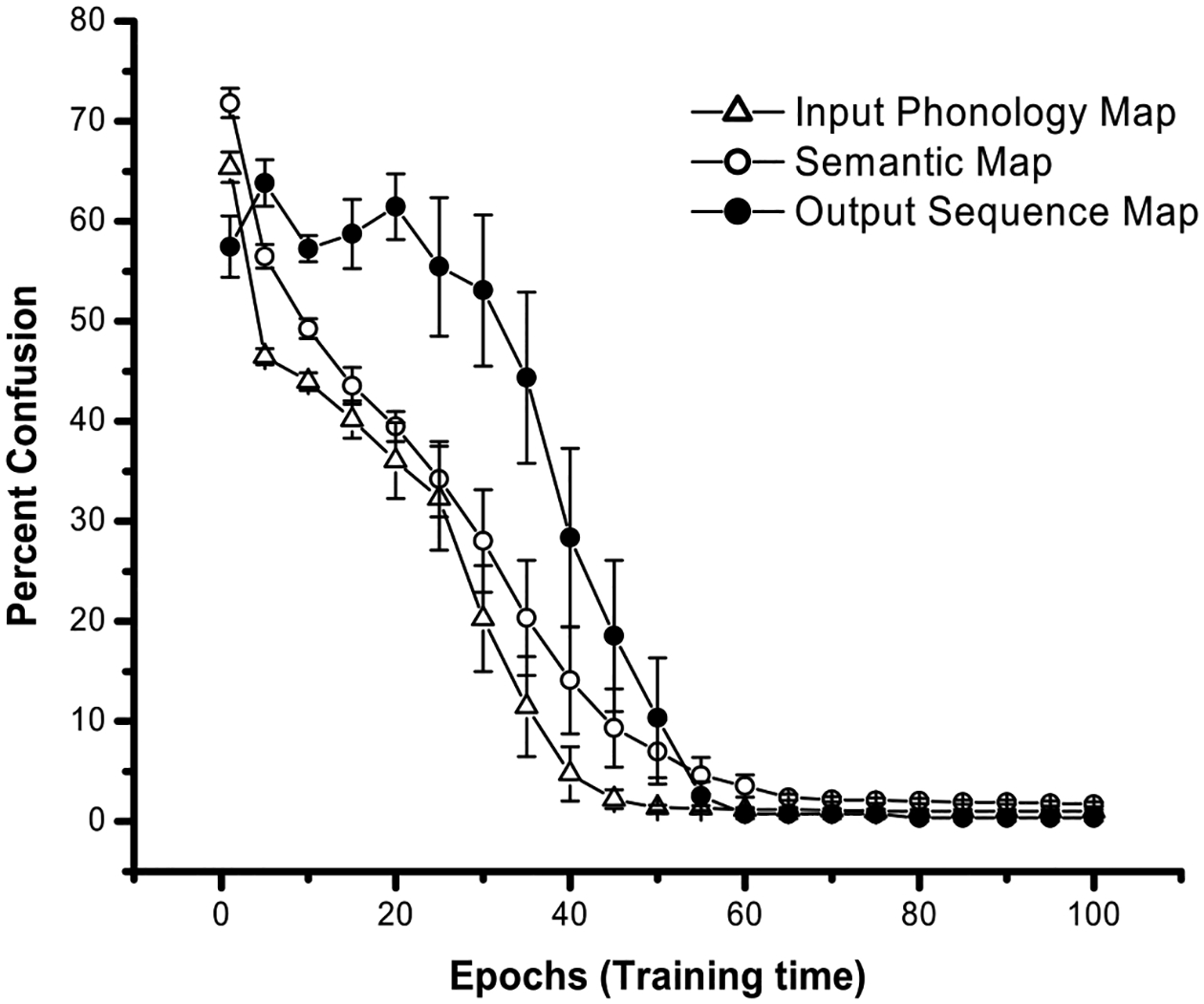
Confusion rates of words and phonemes for input phonological, semantic, and output sequence maps of the model.

3.2. Word-frequency and word-length effects

As discussed earlier, although word frequency and word length have been shown to be critical in language processing, few studies have examined frequency and length effects in early vocabulary learning. In our simulations the frequency of words was determined by the occurrence of words in the CHILDES transcripts (see section 2.4 for detail). We divided frequency into three ranges, low (<10 times in the 2.7 million parental word corpus), medium (10–10000 times), and high (>10,000 times), and word length into short (≤3 phonemes), medium (4–6 phonemes), and long (≥7 phonemes). The short words included mainly monosyllabic words (203 words), while the medium and long words were made up of two to three syllables (333 words within the 4–6 phoneme range, and 55 within the 7–11 phoneme range).

We also defined Age of Acquisition (AoA) as the training epoch at which a word is learned. We say that a word is learned in production, when a node in the semantic map can consistently activate a set of phonemes in sequence as winners of the input word in the output map via the meaning-to-phoneme associative links (see 2.1 for details). Fig. 4 displays the percentage of words acquired for each frequency or length level at each given epoch of training. We can see, in this figure, that the acceleration of the vocabulary spurt was dampened for low-frequency and long-phoneme words, especially toward the mid-to-late stages of training. This shows that, in our network, short and high-frequency words were learned more easily than long and low-frequency words.

Fig. 4.

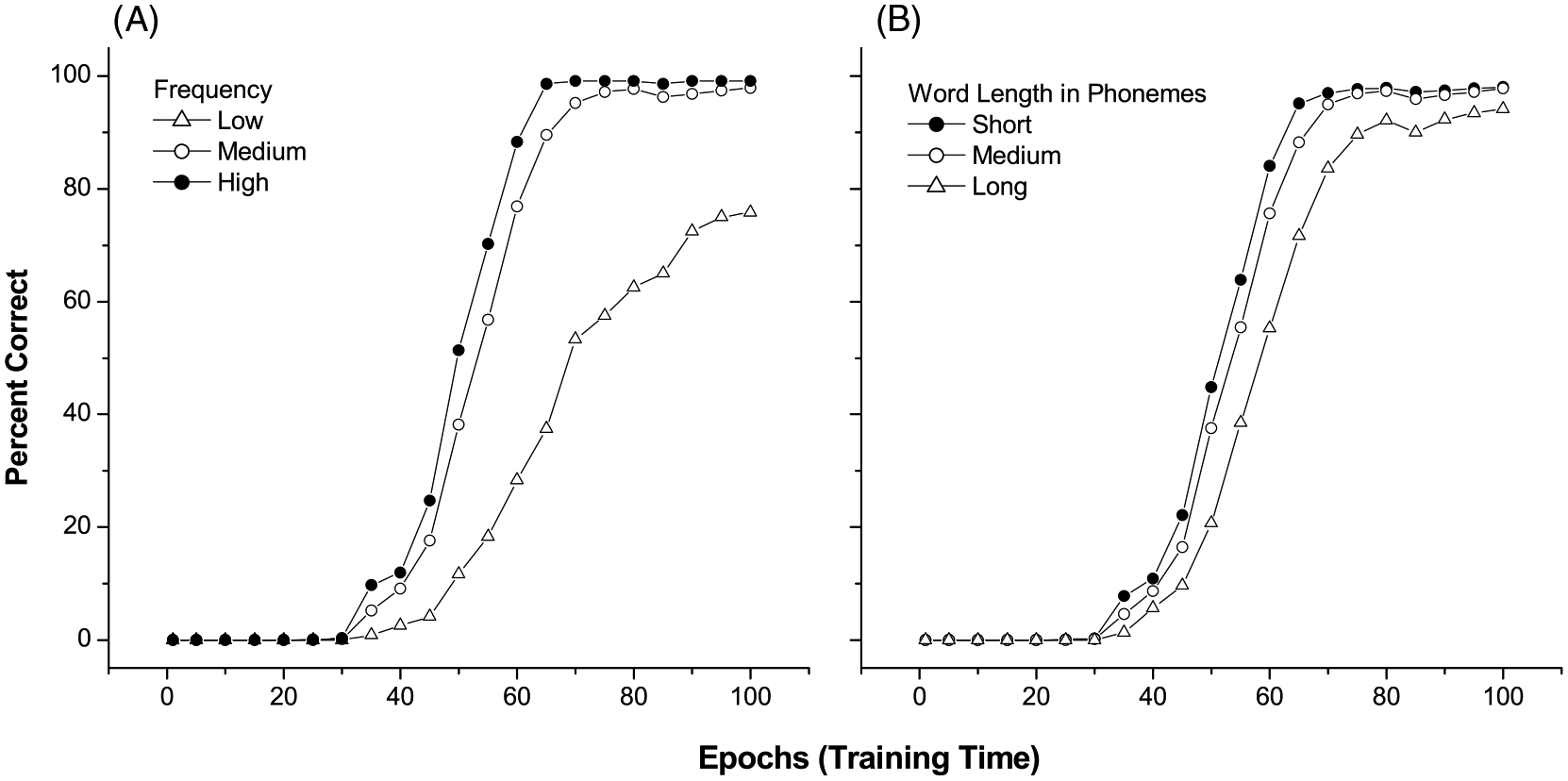
Effects of word frequency (A) and word length (B) in vocabulary spurt.

These findings suggest that in children’s early productive vocabulary, short, and high-frequency words will tend to experience earlier and more rapid spurt patterns than long and low-frequency words. Although there has not been much empirical work on word frequency, length, and AoA in young children (in contrast to adult psycholinguistics work), a recent analysis by Storkel (2004) provided some empirical support for the prediction of our model. Storkel analyzed the nouns in the CDI vocabulary with respect to their AoA according to parental report and adult self-ratings. Using word frequency and word length as predictors in a linear regression analysis, she found that the AoA of the words were negatively correlated with word frequency, but positively correlated with word length, such that early acquired words were higher in frequency but shorter in length than late acquired words. In another detailed analysis of the CDI, Goodman, Dale, and Li (2006) examined further the role of frequency in early vocabulary acquisition. They found that word frequency based on child-directed parental speech (from CHILDES) can significantly predict AoA for the CDI vocabulary. However, this frequency effect was highly dependent on the type of words being acquired (e.g., stronger effect for nouns than verbs), the modality of acquisition (clearer effect for production than comprehension), and the time line of acquisition (earlier vs. later role of the effect). Although we did not analyze these complex interactions between frequency and other variables in our model, we believe that such patterns can emerge naturally from learning in a network like DevLex that incorporates input characteristics of a realistic lexicon.

3.3. Individual differences in early lexical development

Empirical studies have shown individual differences not only in the onset time of vocabulary spurt, but also in the shape and function of the growth curves that young children display across early lexical development: some children show accelerated vocabulary spurt, others a smooth rate of growth, still others a late spurt or no apparent spurt (Reznick & Goldfield, 1991; Bates & Carnevale, 1993; Bates, Dale & Thal, 1995). The random effects in our network discussed earlier represent only one source of the variation and cannot explain individual differences completely.

In Section 2.4 we introduced two other parameters, connection probability and memory gating, and these parameters can be used to simulate individual differences in the development of associative abilities for meaning-to-sound links and the development of short-term verbal memory abilities, respectively (see section 2.4 for details and rationale). Fig. 5A shows how word production rates are modulated by the connection probability θ in different simulations. When θ was 1, the model produced the standard vocabulary spurt profile. However, when θ was less than .5, vocabulary grew at a much slower pace with no obvious spurt, the pattern of which matches with Ganger & Brent’s (2004) reanalyses of empirical data. These growth curves can also be readily mapped to empirical findings regarding the differences between early and late talkers (Thal et al., 1997; Bates et al., 2003), as shown in Fig. 5B.

Fig. 5.

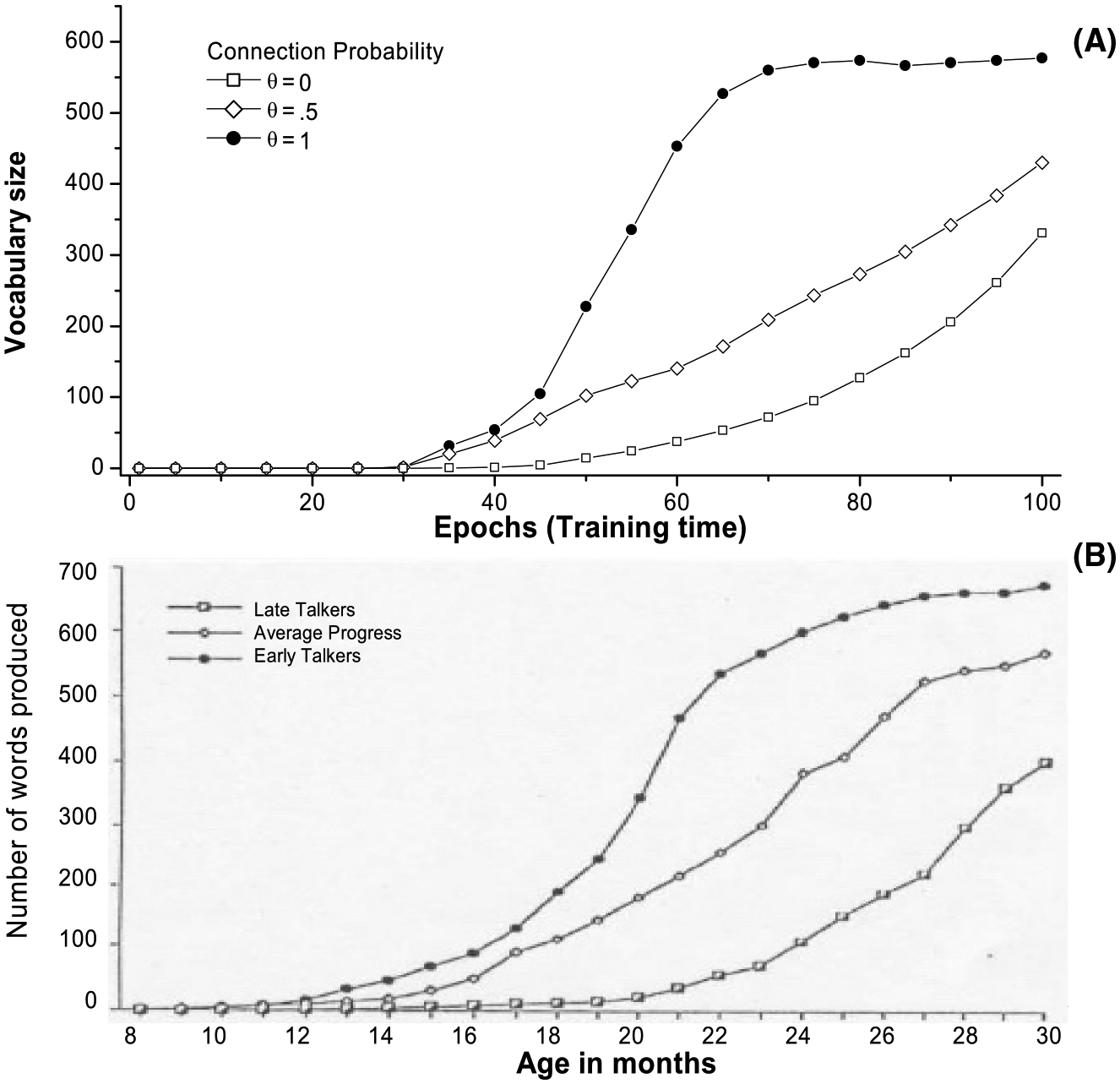
(A) The effect of probability of connection (meaning-to-phonemes) on vocabulary spurt in DevLex-II. (B) Mean number of words produced by children classified as early, late, and average rate talkers (reproduction from Thal et al., 1997; reproduced with permission by authors).

Similar effects were found for word comprehension (Fig. 6), but the individual differences here were not as pronounced as in production. This might be because correct word production requires the formation of correct one-to-many associative links (both in number and in order) from the semantic level to the output sequence level, whereas comprehension requires only correct one-to-one links from the phonological map to the semantic map. Thus, production is more likely to be affected than comprehension by deficient associative links between maps. This discrepancy between comprehension and production in our model might also reflect the different processes involved in language learning and use: production requires more effortful execution of the articulatory organs, which consists of multiple sequential motor events, while comprehension requires the mapping from auditory signals to the existing lexical representations, which involves less of a coordinated sequential response.

Fig. 6.

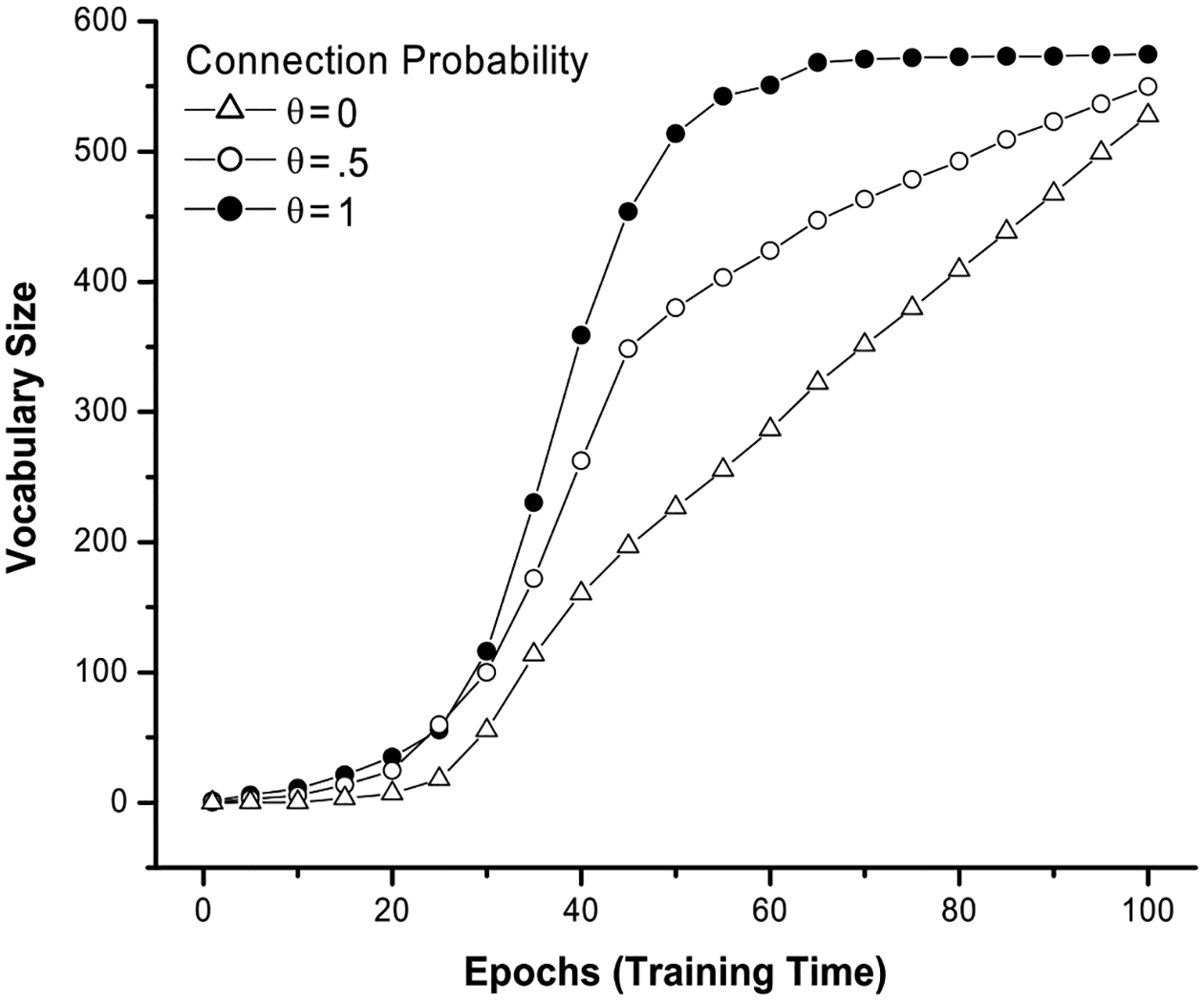
The effect of probability of connection (phonology-to-meaning) on word comprehension in DevLex-II.

Variations in the memory gating parameter provided a second way of characterizing individual differences in learning. Fig. 7 shows that, when the output sequence map was given less memory resources (i.e., τ was set to increase from 0.5 or 0.0, likened to lower ability in serial recall in short-term memory), the network’s performances on word production were not as successful as for the “high-memory” model (i.e., τ = 1). However, in contrast to the connection probability parameter, the modulation of the memory gating parameter has little effect on the early stages of vocabulary learning; rather, it significantly dampened the growth curve only at the mid-to-late stages of the training history. Why should this be so? We think that it might be due to interactions among the memory gating parameter, word frequency, and word length.

Fig. 7.

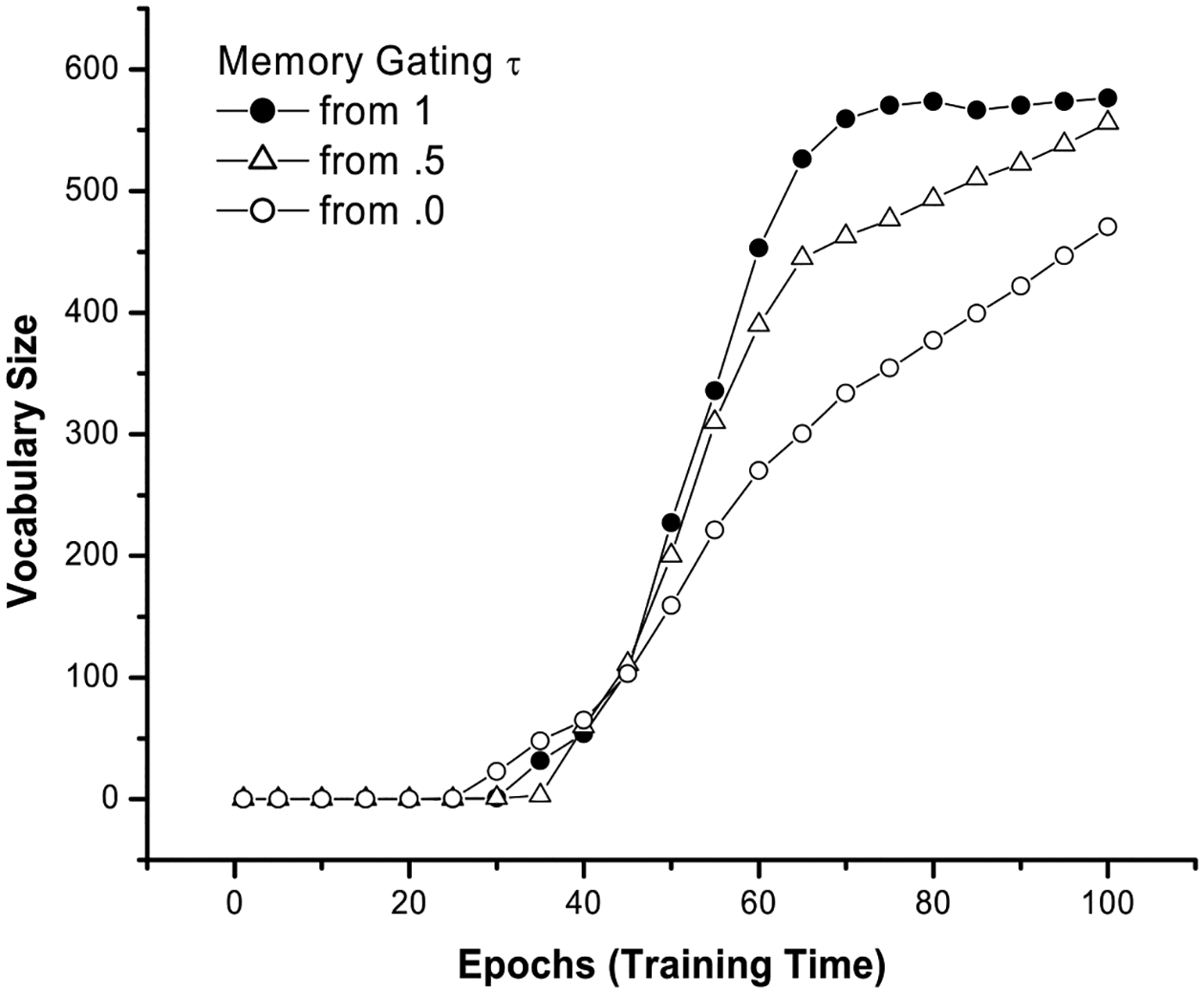
The effect of the memory gating parameter (τ) on word production.

As discussed in section 3.2, our model, like the child, learned short and high-frequency words more readily than long and low-frequency words, and as such most of the early acquired words were the short and high-frequency words. Because the production of short words does not require a large phonological memory, the memory gating parameter should have less of an effect on short words than on long words in our model at the earlier stages. To examine this hypothesis, we looked specifically at the simulations in which the parameter τ started from 0.0. Figs. 8A and 8B present the results for frequency and length effects, respectively. It can be seen that, compared with the original model (Fig. 7, τ = 1), the production performance of the words with short length and high frequency was not greatly affected by the memory gating parameter, but that the words with long length and low frequency were. This type of poor performance with longer words resembles the patterns found with children who show lower short-term verbal memory, accompanied by delays in early vocabulary development (Thal et al., 1997).

Fig. 8.

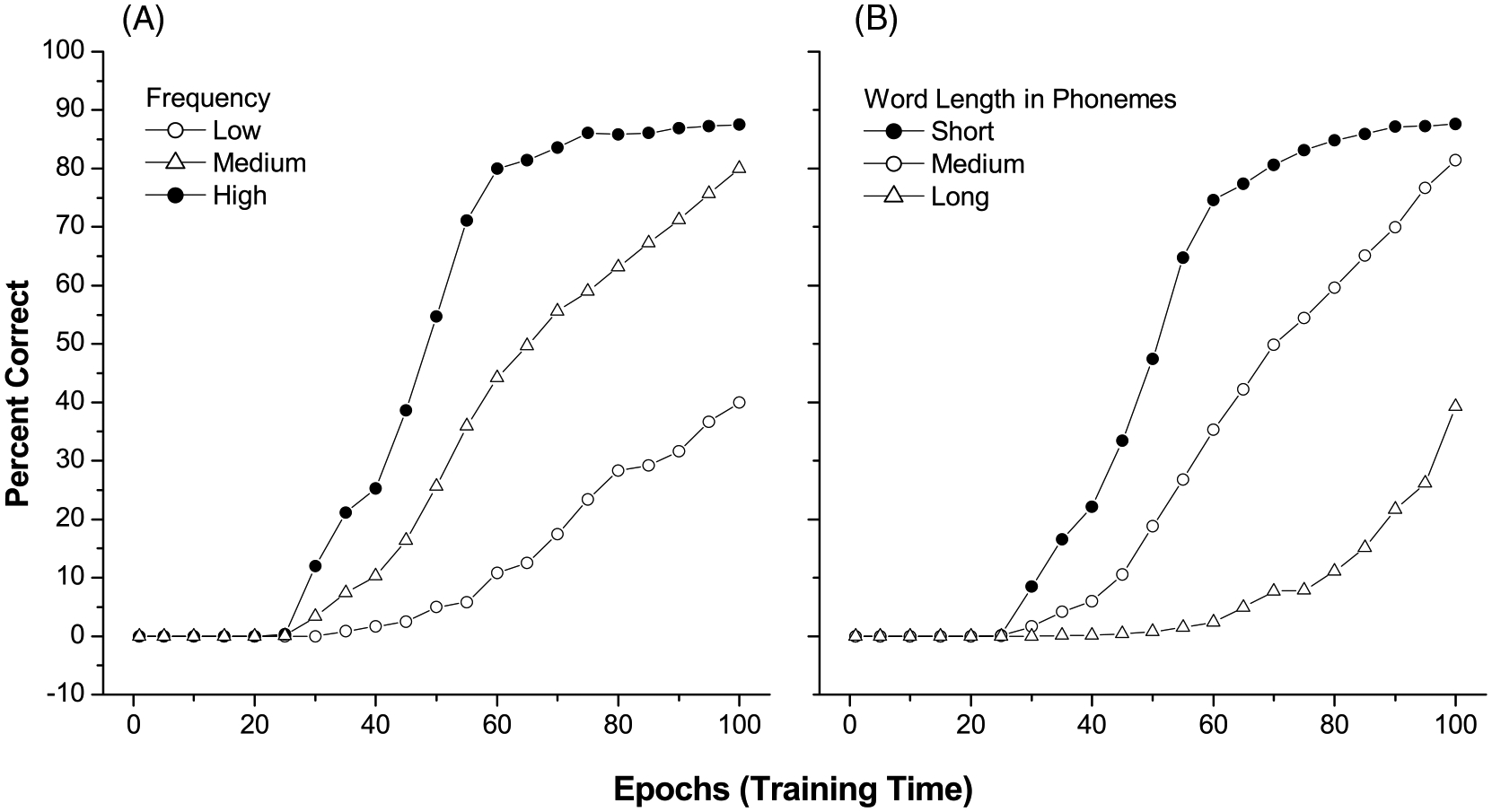
Effects of word frequency (A) and word length (B) on production (τ = 0.0).

3.4. Effects of lesion and developmental plasticity

Previous connectionist studies have modeled simulated lesions in various ways, such as lesion of network structure, alteration of the discriminability of neurons, and addition of noises to nodes and connections (e.g., Marchman, 1993; Thomas & Karmiloff-Smith, 2002). Here we used the lesion method to further identify mechanisms of learning in lexical acquisition. In particular, to lesion the network we added stochastic noise to the input connections to a particular layer of the network (phonological, semantic, or phonemic sequence map) at a given training epoch. In our simulations, we varied the possible size of lesion (lesion severity) such that damage to input connections occurred at different levels. For example, 25% to 100% of the afferent connections of the semantic map can be randomly scrambled, which means that the weights of affected connections each should be multiplied by a random number between 0 and 1 (a noise), and hence the injured connections will randomly deviate from their original weight values. In general, there was a linear relationship between lesion severity and final vocabulary size in the model: the larger the lesion, the smaller the final vocabulary size. To simplify discussion, here we focus on results from a lesion level at which all of the connections were damaged (weights distorted by random noise) but none were broken (weights still eligible for adjustment by future trainings).

Fig. 9 presents the course of vocabulary development with input to the semantic layer lesioned at epoch 35 (early-stage) and 55 (mid-stage), respectively. Both word comprehension and production rates decreased when lesion was introduced to the semantic layer. Although some recovery occurred, the final vocabulary size did not reach a normal level within the learning window. Compared to the final vocabulary size of about 580 words in the simulation without lesion (see Fig. 2), the final vocabulary size in the lesioned model was around 560 (Fig. 9A) or 290 (Fig. 9B), depending on the lesion onset time. These results, on top of the findings from the unlesioned model, indicate further the overarching role that lexical organization plays in comprehension and production. When the well-structured semantic representation of the lexicon is disrupted, the perceived phonological information of a word cannot be correctly projected to its semantic target. Moreover, a jumbled semantic representation also cannot trigger proper word production. Similar results were obtained with other damaged layers, but only comprehension was affected when the phonological layer was lesioned, and only production was affected when the phonemic sequence layer was lesioned. For both word comprehension and production, the network recovered more easily from early damage than from late lesion. Together, these results are consistent with empirical studies that show that linguistic abilities may be delayed following brain injury, and that early injury is associated with more plasticity in recovery (Schneider, 1979; Goodman, 1991; Dawson & Fischer, 1994; Bates & Roe, 2001; Bates et al., 2003).

Fig. 9.

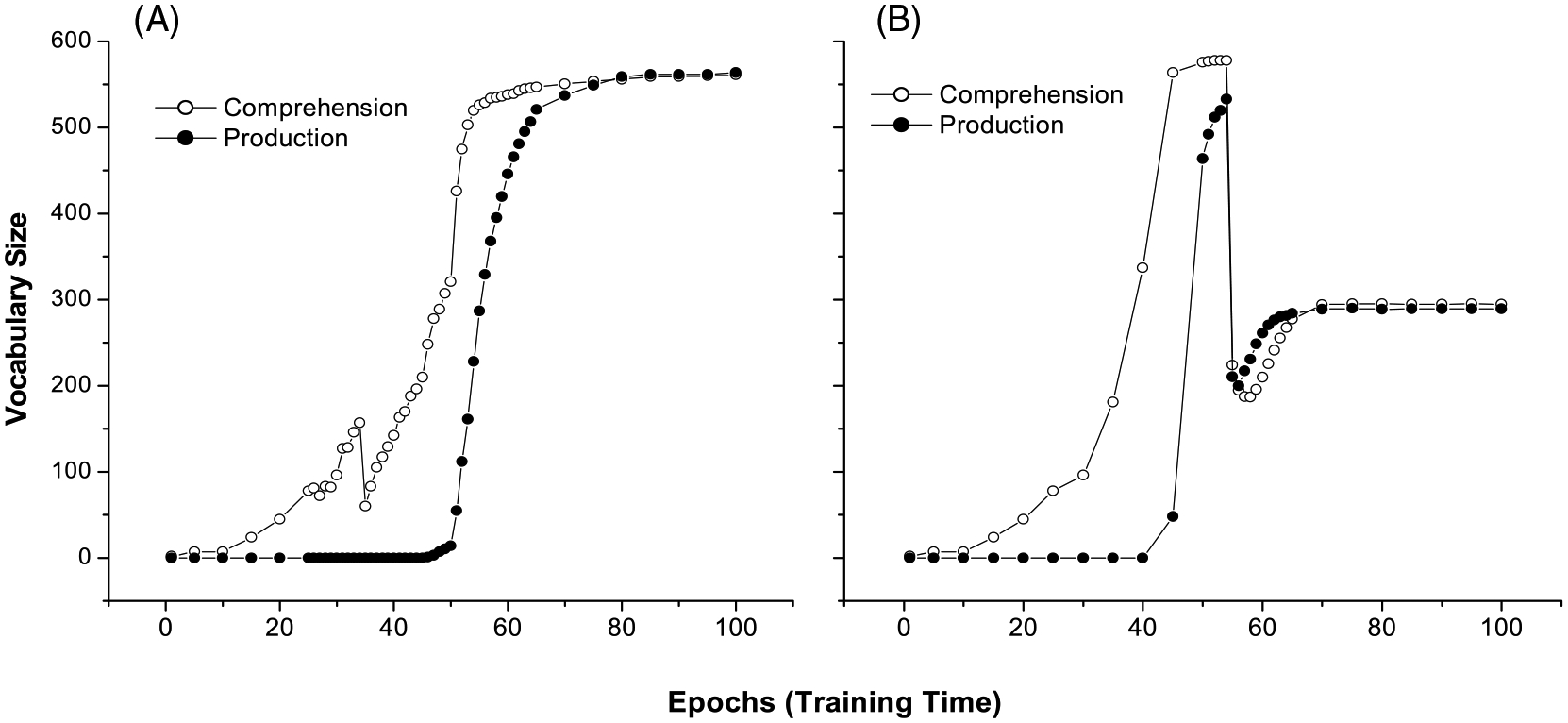
Final vocabulary size as a result of lesion to semantic representations at Epoch 35 (A) and Epoch 55 (B).

However, our modeling results also indicate that the network’s plasticity does not decrease monotonically, as shown in Fig. 10. The worst outcome for the final vocabulary size was not when damage occurred near the end of training (epoch = 80), but when it occurred midway (epoch = 45). More important, this coincided with a point at which the network was establishing its representational structure in both meaning and form, preparing the system for vocabulary spurt (see Fig. 2). After that point, the network showed some more recovery (although not a lot). This pattern resembles a kind of U-shaped change and is consistent with empirical evidence on children’s recovery from focal brain injury. As Bates (1999) has shown, the effect of the onset of injury on cognitive and language development is often non-monotonic. In general, Bates argued against a stringent, “critical period” style of development. She reviewed evidence from large cross-sectional studies that compared cognitive and language outcomes in children who acquired their lesions at different ages: congenital (at or before birth), 1–4 years of age, and 5–12 years of age. The worst outcomes were observed in children who suffered from injuries between 1 to 4 years of age, rather than the later ages. Although this developmental profile pertains to a much larger time scale than the early lexical development we study here, the non-monotonic patterns in the recovery of linguistic functions following lesion appear similar across cases.

Fig. 10.

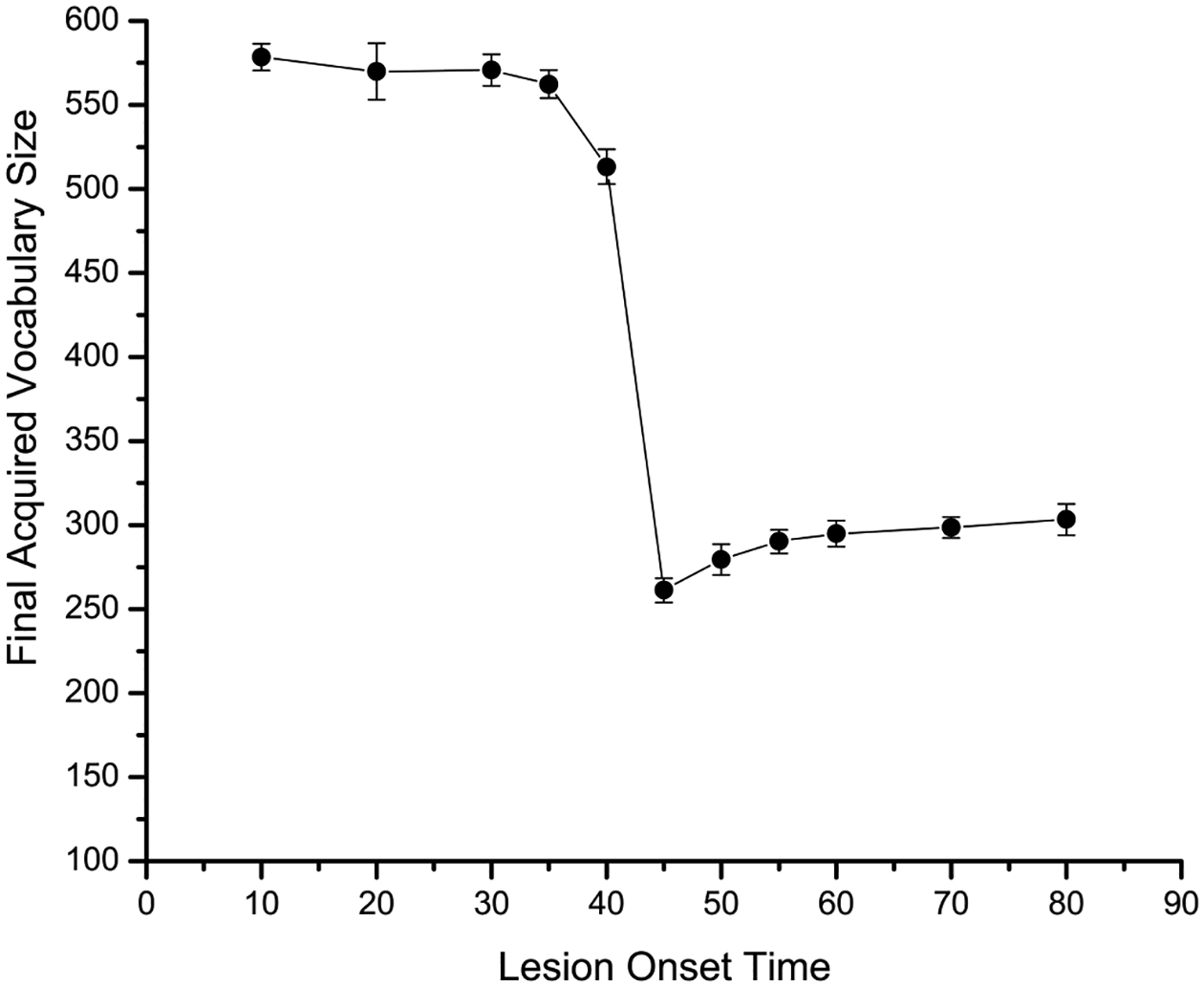
Mean size of final vocabulary as a function of lesion onset time.

4. General discussion

DevLex and DevLex-II are full-scale SOM-based developmental models of language acquisition. Our goal has been to use these cognitively plausible, linguistically realistic, and computationally scalable models to account for dynamic self-organization in children’s lexical learning and representation. The DevLex model (Li et al., 2004) was able to account for a variety of phenomena in early lexical development, including category formation (how categorical representations gradually evolve as a function of learning), lexical confusion (how a rapid increase in the lexicon causes competition in lexical retrieval and production), and effects of age of acquisition (how order of learning in the vocabulary naturally yields age of acquisition patterns). We have here shown that DevLex-II can simulate a variety of additional patterns in lexical development. These effects include a clear vocabulary spurt, effects of word frequency and length on age of acquisition, and individual differences as a function of phonological short-term memory and associative capacity. Finally, the model simulates patterns of recovery from lesion comparable to those found in children with focal brain injury. Together, DevLex and DevLex-II provide a detailed computational account of early lexical development.

The most salient developmental phenomenon that our model captures is the vocabulary spurt. As discussed earlier, several computational models have offered to account for the vocabulary spurt process (e.g., Plunkett et al., 1992; Siskind, 1996; Regier, 2005). In contrast to the perspectives taken in those studies, our model focuses on how word meanings and word forms interact in a lexical system as a whole, in particular, how such interactions can yield structural pre-requisites for the vocabulary spurt. In DevLex-II, developmental changes such as the vocabulary spurt are modulated by lexical organization along with input characteristics. Our results show that the onset of the vocabulary spurt is triggered by structured representations in the semantic, phonological, and phonemic organizations. Once these patterns have consolidated, the associative connections between maps can be reliably strengthened through Hebbian learning to capture the systematic structural relationships between forms and meanings. In other words, earlier learned words help to form the initial links within and across the phonological and semantic levels so that future learning can more readily use the existing patterns and associations. At this point, word learning is no longer hampered by uncertainty and confusion on the maps, and the vocabulary spurt occurs.

By contrast, if the processes of self-organization do not lead to the development of structured representations, or if additional factors (e.g., phonological memory) prevent the system from developing relevant associations or abilities for articulation, the vocabulary spurt will be delayed or minimized. The analyses of confusion rates (section 3.1) and the simulations of individual differences (section 3.3) and lesion effects (section 3.4) further support this overall characterization and interpretation of the networks’ dynamics. We saw that limitations on phonological short-term memory and associative learning could serve to modulate the curve of development and to delay or blunt the vocabulary spurt. In addition, effects of simulated lesions showed that the network’s recovery ability decreases over time, and lesioning that occurs during the crucial period of structural consolidation has the most adverse effects on vocabulary acquisition.

We argue here that structural organization in the lexicon prepares for the vocabulary spurt. This argument receives support from previous computational models as well. To the extent that better and stronger structure emerges from enriched lexical-semantic representations, our model is in accord with Siskind’s (1996) proposal that cross-situational learning results in increased accuracy in identifying the meaning of words, which in turn increases the efficiency of later word learning, leading to the vocabulary spurt. Plunkett et al. (1992) had also hypothesized that the vocabulary spurt could be related to the systematization of the conceptual basis of word meanings. However, due to the limited size of their artificial vocabulary and the nature of their model, Plunkett et al. did not show exactly how the conceptual systematization was instantiated in their model. In contrast, the self-organizing processes of DevLex-II provide concrete examples of how structural representation and organization emerge as a result of learning word-form and word-meaning features with SOM-based topographical maps. The dynamic self-organization displayed in the model is most clearly reflected in the establishment, consolidation, and fine-tuning of the “mental representation” of the lexicon over the course of development (see Fig. 1 in Hernandez, Li, & MacWhinney, 2005, for a graphical illustration of how the model acquires and represents lexical structure over time).

In Regier’s (2005) LEX model, reduced memory interference among word forms or meanings (due to increased selective attention) is believed to be crucial for vocabulary spurt. Increased selective attention allows the system to highlight relevant features for particular words while suppress irrelevant features. The net effect of this process is finer distinction among word forms and meanings. We can draw clear parallels between Regier’s model and our model. Early on in learning, confusion rates are high in our model for word forms and meanings, but as learning progresses, confusion rates drop and the vocabulary spurt begins. What differs between the two models is that while selective attention is required to drive successful learning in Regier’s model, only more word learning itself is required for better representation in our model. This is because the self-organizing process continuously extracts more features for discrimination from the input space—this may be especially true in an incremental learning scenario, in which the lexical representation becomes enriched by incorporating more co-occurrence information over the course of learning (see Li et al., 2004). Thus, analysis of more phonemic features allows the system to further discriminate phonologically related forms such as put, push, and pull that have been originally confused, while learning of semantic information allows the system to pull apart dog, cat, and zebra that may have been originally mapped to the same units. While both Regier’s model and our model make no recourse to factors external to learning, such as ‘naming insight’ (McShane, 1979) or “communicative awakening” (Tomasello, 1999), our model differs from Regier’s by relying only on input characteristics and self-organization to trigger the vocabulary spurt. In short, in our model, the word-learning process itself leads to better and more efficient word learning at a later stage.

McLeod, Plunkett, and Rolls (1998) identified several variables that could lead to individual differences in performance by connectionist networks, including random initial weights, learning rate, number of internal nodes, and the learning environment. Such variables are no doubt important in accounting for developmental variations. In our model, however, we have held these variables constant for the training of individual networks within a given simulation (except random initial weights). We simulated individual differences through the control of two learning parameters, connection probability and memory gating, which are used to simulate associative capacity and phonological short-term memory, respectively. Our results indicate that variables of this type must also additionally influence children’s lexical development, especially in the processes leading to the vocabulary spurt (or no spurt).

In a recent study Ganger and Brent (2004) argued against the generality of vocabulary spurt largely based on considerations of individual differences in young children. Their primary argument was due to their analyses of previously published studies on this topic, which indicates, according to the authors, that only a small portion of the children (5 out of 20) showed vocabulary spurt. Two points are worth noting here. First, Ganger and Brent only analyzed children’s productive speech up to 20 months (within about the 100 word-boundary) while most vocabulary spurt studies (those that did show vocabulary spurt) looked well beyond this age and beyond this vocabulary size (see Bates & Carnevale, 1993, for a summary). Second, even if we grant validity to the Ganger-Brent analysis, our model is able to account for the individual variations in the extent and the timing of the vocabulary spurt in terms of variations in general associative capacity and phonological short-term memory.

Our study has also shown how word frequency and word length effects modulate the developmental profiles of vocabulary spurt (e.g., how they either magnify or dampen the curves of the spurt). Moreover, DevLex-II also provides a mechanistic realization of the effects of frequency and length in early lexical development. When a word occurs frequently in the input, the input weights of neurons responding to this word on each map will undergo frequent adjustments, increasing the stability of representations and associative links. Thus, high frequency words are likely to be uniquely differentiated and thus acquired earlier. The late acquisition of long words, on the other hand, results primarily from effects within the output sequence map. For that map, consolidation of output patterns for long words involves more links and more training. As a result, these forms will not be open as early as the short words to the formation of associative links between maps.

Our account emphasizes the role of self-organizing processes in shaping the developmental course of plasticity and entrenchment. Plasticity arises from the operation of self-organizing learning at early stages. Lesioning to the self-organizing processes will delay the early formation of stable associations between maps (for comprehension and production, see previous discussion about vocabulary spurt). However, the system has greater ability to recover from lesions since the disordered representations can be reorganized very quickly. In particular, early on, on each layer, structures of different linguistic information have not been organized completely. Thus, each map is sensitive to small changes and can reorganize its structure more easily, hence its ability to recover from damage. At later stages, the system reaches a dynamical stable state because clear patterns have formed on each layer and for associations between layers. Each layer is now robust to small changes and becomes harder to reorganize its representations for linguistic inputs. This feature is useful for quick formation of between-layer associations (and in turn for vocabulary spurt), but if a lesion occurs, complete recovery is more unlikely (see also Elman et al., 1996). In addition, our model displays a U-shape pattern for recovery from lesion: late-occurring lesions (e.g., epoch 80) and early-occurring lesions (e.g., epoch 10) result in better recovery than lesions occurring midway (e.g., epoch 45). This is, again, an effect of the relative timing of the formation of within-map and between-map connections. When lesions occur mid-course, it coincides with a time when the network is setting up its “basic frame” for structured representation of the lexicon, while at the same time the system’s intrinsic ability to recover from large changes has dropped significantly (e.g., the weight space becomes more committed or entrenched, neighborhood size and learning rate are both reduced). Thus, lesion at a point such as Epoch 45 (as shown in Fig. 10) has a more devastating effect as the network transitions from an unstable state to a stable state in the dynamical space.

The DevLex and DevLex-II models are grounded on computational and developmental realism by making direct contact with input characteristics of the child lexicon, and they rely on simple principles of self-organization within and between varieties of linguistic information. These models provide us with detailed and interpretable accounts of a wide variety of patterns in early lexical development. In particular, they help us to understand individual variations in the rate and size of early vocabulary development with respect to (a) input characteristics, such as the structure of lexical composition across time, and word frequency and word length effects, (b) consolidation of lexical-semantic structures in representation, meaning-form associations, and phonological short-term memory, and (c) delayed processes in word learning, which by itself is a joint function of the nonlinear dynamic interactions among timing, severity, and recoverability of lesion. In contrast to the empirical focus on how children acquire lexical form-meaning mappings at the individual word level (e.g., on initial fast-mapping; see Bloom, 2000; Regier, 2003, for review), our model projects lexical development at a dynamical systems level, in which words not as individualized items, but as a system, are acquired and organized and their phonological and semantic representations continuously interact, compete, and evolve. This approach is highly consistent with recent perspectives in developmental psychology and cognitive neuroscience, according to which early learning has a cascading effect on later development and learning itself shapes the cognitive and neural structures (Kuhl, 2004; Smith & Thelen, 1994; Elman et al., 1996; Elman, 2005; Hernandez & Li, 2007).