Evaluation of the Potential of Single Particle ICP-MS for the Accurate Measurement of the Number Concentration of AuNPs of Different Sizes and Coatings

Abstract

Single particle inductively coupled plasma-mass spectrometry (spICP-MS) is an emerging technique that is capable of simultaneous measurement of the size and number concentration of metal-containing nanoparticles (NPs) at environmentally relevant levels. Although spICP-MS is widely applied to different fields, challenges remain in obtaining accurate and consistent particle number concentration (PNC) measurements. This paper presents, for the first time, a rigorous assessment of spICP-MS capabilities for measuring the PNC of gold NP (AuNP) suspensions of different sizes and coatings. The calibration of spICP-MS was accomplished with the National Institute of Standards and Technology (NIST) AuNP reference material (RM) 8013. The comparability of both spICP-MS direct and derived determination of PNC and reference PNC derived based on the mean particle size or the particle size distribution obtained by different reference sizing techniques was first assessed for NIST AuNP RM 8012, nominal diameter 30 nm. To enable a proper assessment of the accuracy of the spICP-MS results, a comprehensive estimation of the expanded uncertainty for PNC determination was carried out. Regardless of NP size or coating, a good agreement (90–110%) between spICP-MS direct determination of PNC and reported PNCs was obtained for all of the suspensions studied only when reliable in-house Au mass fractions and thorough mean particle size determinations were included in the calculation of the derived PNCs. The use of the particle size distribution over the mean size to derive PNCs resulted in larger differences for materials with a low contribution (<2%) of smaller NPs (30 nm), materials with a higher polydispersity (100 nm), or materials with two distinct subpopulations of particles (60 nm), regardless of NP coating.

Graphical Abstract

The outstanding physical and chemical properties exhibited by nanoparticles (NPs) are related to many factors, including their chemical compositions and surface structural characteristics. The fate, transport, stability, and potential risks of NPs are directly related to their physicochemical properties, including composition, particle size, shape, and surface coating. Among the most important properties to characterize colloidal suspensions, particle number concentration (PNC) has long been recognized as an important metric to evaluate the risk of exposure and the dose in nanotoxicological research. PNC is of critical importance to assess product stability, lifetime, and variability across different material synthesis batches or production sites and can also provide insight into reaction yield, amount, and hazard potential. Considering that a number-based definition of nanomaterials adopted by the European Commission in 2011 has been proposed for determining if a substance is labeled as containing NPs,¹ and due to the extremely low environmental concentrations (on the order of ng L⁻¹),² innovative and reliable analytical methods are currently needed for in situ NP characterization and quantification. Unlike other properties, accurate measurement of PNC is particularly challenging because validated techniques that span the full nanoscale are not available and there is a lack of certified nanoparticulate reference materials (RMs) with a known PNC for the evaluation of accuracy. The existing methodologies for the determination of PNC are described in detail in other publications,^3–6 so they will not be discussed here.

Recently, single particle inductively coupled plasma-mass spectrometry (spICP-MS) has emerged as a promising technique for sizing and counting individual metal-containing NPs. spICP-MS can simultaneously provide the mean size, size distribution, NP number and mass concentration, and the dissolved fraction at an environmentally relevant number concentration.^7–10 However, the influence of particle size and surface coating on the determination of spICP-MS of PNC at environmentally relevant levels has not been thoroughly explored to date.

While spICP-MS is widely applied to the characterization of NPs in different fields,^11–15 important challenges remain in obtaining accurate and consistent PNC measurements. Out of the several hundred studies published in the last 5 years,¹⁵ the vast majority did not include an assessment of the accuracy of the reported PNC results. In fact, the limited amount of studies fully devoted to PNC measurements typically reported non-quantitative PNC recoveries in a variety of sample introduction systems including total consumption nebulizers,¹⁶ pneumatic nebulizers and microdroplet generators,¹⁷ millisecond and microsecond dwell times,¹⁸ hyphenation with separations techniques,¹⁹ and also different commercially available ICP-MS platforms.^20,21 So far, limited attempts comparing spICP-MS PNC measurements across laboratories have been carried out, indicating a greater variability in the number quantification than in the size characterization, typically yielding non-quantitative PNC recoveries.^22–25 Recently, two multitechnique round robin studies that were aimed at evaluating the measurements of particle size and PNC of AuNPs by multiple analytical techniques indicated that spICP-MS was capable of providing robust PNC results.^26,27

While considerable efforts have been made,^28–30 the metrological quality of spICP-MS PNC measurements must be thoroughly proven before it can be considered an established methodology. This study presents, for the first time, a rigorous assessment of spICP-MS capabilities for measuring PNC of AuNP suspensions. The calibration of spICP-MS was accomplished with the monodispersed National Institute of Standards and Technology (NIST) AuNP RM 8013 (citrate-stabilized, nominal diameter 60 nm).³¹ The comparability of both spICP-MS direct and derived determination of PNC and reported PNC derived based on the mean particle size or the particle size distribution (PSD) reported in our previous study by transmission electron microscopy (TEM), high-resolution scanning electron microscopy (HR-SEM), and spICP-MS³² was first assessed using the monodispersed NIST AuNP RM 8012 (citrate-stabilized, nominal diameter 30 nm).³³ To evaluate if the counting results are truly representative of the population of NPs in the working suspensions, the direct determination of PNC was also compared with derived PNC based on the mean particle size and particle size distribution simultaneously obtained in the same spICP-MS analysis. To enable a proper assessment of the accuracy of the spICP-MS results, a comprehensive estimation of the expanded uncertainty for the determination of PNC by spICP-MS including the main sources of error was carried out. Following this, the influence of particle size and coating on the quantification capabilities of spICP-MS was evaluated for different commercially available AuNP suspensions with three different sizes (30, 60, and 100 nm) and four different coatings: citrate, polyvinylpyrrolidone (PVP), polyethylene glycol (PEG), and branched polyethylenimine (bPEI).

EXPERIMENTAL SECTION

Chemicals.

High-purity water (≥18 MΩ·cm resistivity, Millipore), nitric (HNO₃) acid, and hydrochloric (HCl) acid were used in all ICP-MS experiments. Both acids were Optima grade (Thermo Fisher Scientific). NIST SRM 3121 was used to prepare dissolved gold calibration solutions. Aqueous suspensions of 14 different AuNP samples with approximately spherical shape were analyzed in this study. NIST RM 8013³¹ was used to calibrate spICP-MS, NIST RM 8012³³ was selected as a method validation sample, and the remaining samples were citrate, PVP, bPEI, and PEG-coated AuNP commercial suspensions with nominal diameters of 30 nm, 60 nm, and 100 nm³⁴ (Table S1).

Instrumentation.

A Thermo Electron X Series X7 quadrupole ICP-MS was used for spICP-MS measurements. Samples were introduced into the ICP torch using a quartz C-type nebulizer (Elemental Scientific) and impact bead spray chamber cooled to 2 °C. Instrument operating and data acquisition parameters are listed in Table S2. The sample flow rate was set to approximately 0.5 mL min⁻¹ and measured daily in triplicate by weighing the water uptake after 5 min. Daily tuning of the ICP-MS was accomplished for maximum sensitivity for ¹⁹⁷Au. The dwell time for all spICP-MS experiments was 10 ms, and the acquisition time was 360 s. ¹⁹⁷Au intensity was recorded in TRA mode using Thermo Fisher PlasmaLab software.

Procedure.

spICP-MS for the PNC Quantification of AuNPs.

All AuNP working suspensions were prepared daily by gravimetric serial dilution of stock suspensions with high-purity water to an approximate PNC of 1.5 × 10⁷ L⁻¹ (equivalent to Au mass fractions of 3–180 pg g⁻¹, depending on the diameter). This PNC was selected to mitigate undesired particle coincidence while maintaining adequate particle flow (at least 700 particles per 360 s acquisition time were registered). AuNP working suspensions were bath-sonicated for 4 min before spICP-MS measurement. Longer sonication times were not used to avoid excessive heating of suspensions.

Data Processing and Calibration of spICP-MS.

A total of 36 000 collected readings per acquisition time in units of counts per second were exported to Microsoft Excel for data processing. The signal associated with the particle was discriminated from the background signal using a 5σ criterion³⁵ and corrected for false positive and split-particle events.^36,37 For the size determination of AuNP samples, a response factor, expressed in counts per ng of Au, was established from the signal intensities measured for RM 8013, used as calibration standard (eq S1).³² Note that for the determination of the particle size and PNC of RM 8013, RM 8012 was used as calibration standard. For the direct determination of PNC, the calibration strategy was based on the measurement of transport efficiency via the particle frequency method⁸ using RM 8013 (eq S2). Detailed information for the size calibration of spICP-MS and for the determination of transport efficiency is provided in the Supporting Information (SI).

Direct PNC Quantification and Derivation of PNC.

The direct quantification of PNC (PNC_direct) for all AuNP samples was achieved by counting the number of acquired particle events per volume of solution introduced into the ICP-MS by eq 1

$${\text{PNC}}_{\text{direct}}=\frac{N_{\text{NP}}}{q_{\text{liq}}\times t_{\text{aq}}\times {\eta }_{\text{n}}}\times \text{Dil}.\mathrm{F}$$ (1)

where PNC_direct (L⁻¹) is the target particle number concentration in the working suspension, N_NP is the number of observed particle events, q_liq (g min⁻¹) is the sample uptake rate, t_aq (min) is the time of acquisition, η_n is the transport efficiency, and Dil.F is the dilution factor of stock suspensions. The measurement of the frequency-based transport efficiency requires analysis of a standard NP suspension of known PNC. However, due to the lack of certified nanoparticulate RMs with a known PNC, it is possible to derive or calculate the expected PNC of a NP suspension with the knowledge of the total mass fraction (assuming that all analyte is present in the NP form), the average particle size of the sample (assuming that NPs are spherical and solid), and the density of the particle (assuming bulk material density). Thus, the expected PNC can be derived by eq 2

$${\text{PNC}}_{\text{mean}}=\frac{6\times C_{\text{S}}}{1\times {10}^{-18}\times {d_{\mathrm{NP}}}^3\times \pi \times \rho }$$ (2)

where PNC_mean is the derived target particle number concentration (L⁻¹) in the stock suspension, C_S is the mass fraction of the analyte in the sample (μg g⁻¹), d_NP is the average particle diameter (nm), and ρ is the density of the particle (g cm⁻³). In fact, an expected PNC_mean of (2.99 ± 0.09) × 10¹³ L⁻¹ (for d_NP of 55.6 ± 0.50 nm, ρ of 19.3 ± 0.01 g cm⁻³, and C_S of 51.86 ± 0.64 μg g⁻¹; all expanded uncertainties, U, correspond to an approximate level of confidence of 95% (U95% C.I.))³¹ for the stock suspension of NIST RM 8013 has been consistently used as the reference PNC standard for spICP-MS research over the past decade.^{8,17,18,28,36,38–41} For the stock suspension of NIST RM 8012, an expected PNC_mean of (2.48 ± 0.28) × 10¹⁴ L⁻¹ (for d_NP of 26.8 ± 0.51 nm, ρ of 19.3 ± 0.01 g cm⁻³, and C_S of 48.17 ± 0.33 μg g⁻¹; all expanded uncertainties as U95% C.I.)³³ has used for the similar purpose. For NIST RMs, the values provided for d_NP correspond to the consensus mean of the seven sizing methods listed on each NIST Report of Investigation (ROI).^31,33 Detailed information for the consensus value for particle size for both RMs is provided in the Supporting Information. In this study, this stock PNC_mean value was used as the reference to establish a multiple-point calibration that enabled the evaluation of the analytical performance of spICP-MS, and to calculate frequency-based transport efficiency throughout all of the experiments.

It has been recently reported that due to the intrinsic dispersity of NP populations, manifested by the width of the size distribution, PNC_mean may not be a very good approximation of PNC.²⁷ Thus, instead of using the central tendency for particle diameter, the use of measurement techniques based on the analysis of N individual particles, where the data are in the form of d_NP1, ..., d_NPN, enables the derivation of PNC using the full particle size distribution (PNC_distribution) by eq 3

$${\text{PNC}}_{\text{distribution}}=\frac{1}{N}\sum _{i=1}^N\frac{6\times C_{\text{S}}}{1\times {10}^{-18}\times \rho \times \pi \times {\left(d_{\text{NP}i}\right)}^3}$$ (3)

where N is the total number of analyzed particles and d_NPi is the diameter of the ith particle; see eq 2 for the definition of remaining parameters. Thus, PNC_distribution represents an average estimate of PNC over the individual particle sizes and 1/N is the probability associated with the size.

RESULTS AND DISCUSSION

Evaluation of spICP-MS Capabilities for the Accurate Determination of PNC of NIST RMs 8012 and 8013.

The capabilities of spICP-MS for the PNC_direct quantification were initially evaluated for the analysis of the monodispersed NIST RM 8012 and RM 8013 with well-defined mean size, size distribution, and Au mass fraction.^31,33 The analytical performance of spICP-MS including linearity, limit of detection, and precision for the determination of PNC was assessed through a multiple-point calibration (Figure S1) that was compared with analyte transport efficiency determined via the particle frequency method.⁸ Considering the linear range, excellent long-term intermediate precision,⁴² together with an effective mitigation of undesired particle coincidence while maintaining adequate particle flow, a nominal PNC of 1.5 × 10⁷ L⁻¹ was selected as the target concentration for the remainder of this study. Detailed information on the evaluation of the analytical performance of spICP-MS is provided in the SI.

More than 50 000 individual NPs from different ampoules of both RMs were recorded in 15 independent experiments conducted more than 4 years apart. Application of eq 1, considering the dilution factor of stock suspensions, resulted in PNC_direct values of (2.38 ± 0.07) × 10¹⁴ and (3.16 ± 0.08) × 10¹³ L⁻¹ for RM 8012, and RM 8013, respectively (Figure 1). These results represent the means of the measurement results and U95% C.I. computed based on combined standard uncertainties estimated from the average standard error of the 15 experiments. The small expanded uncertainty (<3% relative) demonstrates the stability and reliability of both RMs and indicates excellent robustness and reproducibility of spICP-MS protocol and calibration approach employed here for the direct determination of PNC. To enable a proper assessment of the accuracy of the spICP-MS results, a comprehensive estimation of the expanded uncertainty including the main sources of error was carried out using the NIST “Uncertainty Machine” (https://uncertainty.nist.gov ).⁴³ The application combines estimated uncertainties for each component of the measurement model. The input quantities involved in the PNC computation were modeled as random variables, and their probability distributions were used to characterize measurement uncertainty for the relative contribution of each component to the total uncertainty, calculated as its variance relative to the total variance. Gaussian distributions were assigned to the input quantities, with means equal to estimates of their values, and standard deviations equal to their standard uncertainties. Equation S3 was used to compute the combined uncertainty of PNC_direct. A breakdown of the uncertainty analysis for a representative spICP-MS determination of PNC_direct for RM 8012 is provided in Table S4. As can be seen in Table 1, variability in the number of observed particle events for the sample and the NP standard was the major component (combined uncertainties of 84 and 49% of the total expanded uncertainty for RM 8012 and RM 8013, respectively).

Figure 1.

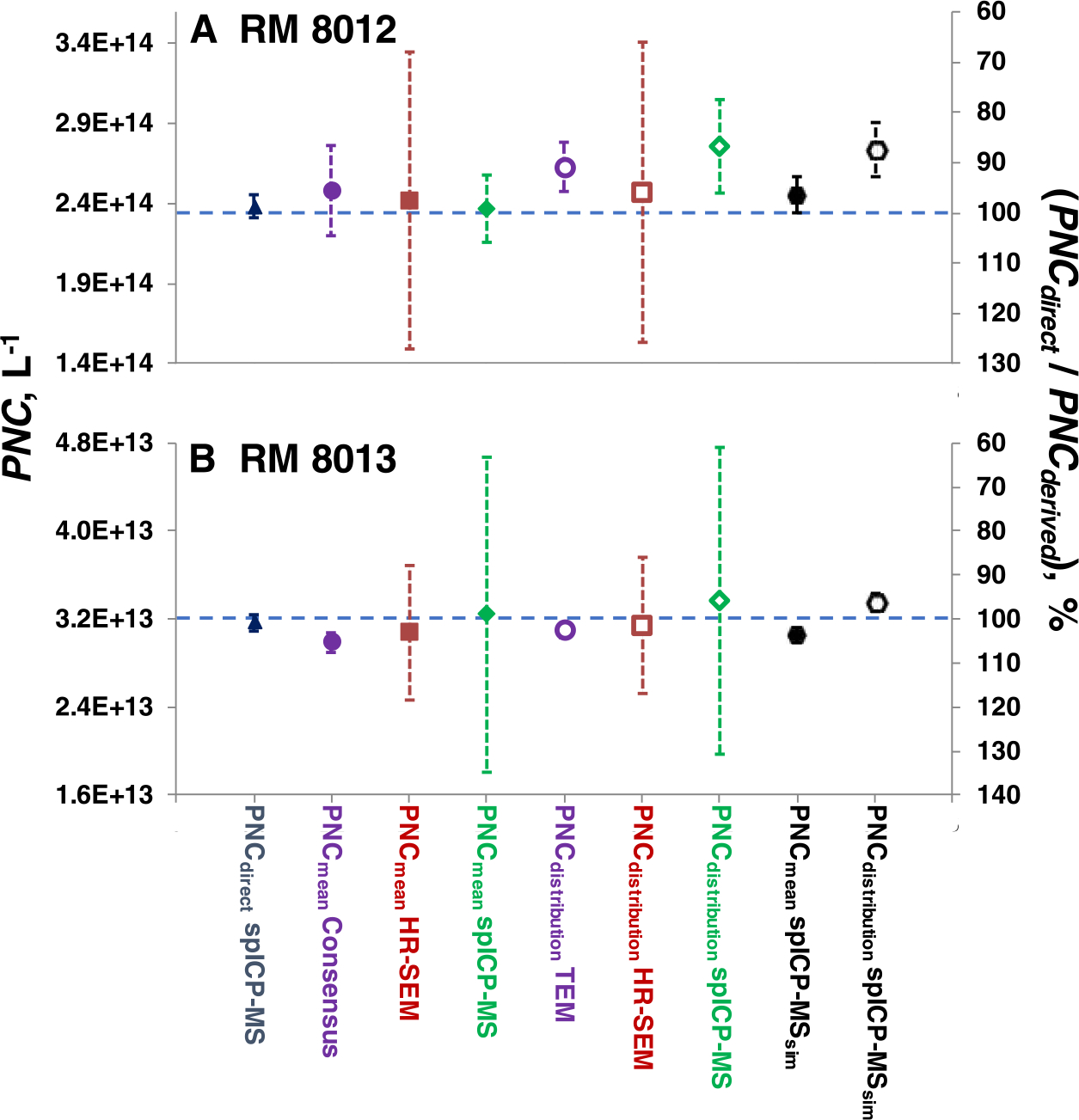
Comparison for the PNC results (left axis) (PNC_direct (blue triangles), PNC_mean (solid symbols), or PNC_distribution (open symbols)) and the ratio between PNC_direct and derived PNCs, expressed in percentage, (right axis) for RM 8012 (A) and RM 8013 (B). Values are provided for spICP-MS (blue triangles for direct PNC measurements, and black hexagons for derived PNC using simultaneous size determinations), consensus particle size or TEM PSD reported in the ROIs (purple circles),^31,33 and previously reported HR-SEM (dark red squares)³² and spICP-MS (green diamonds).³² The vertical bars indicate U95% C.I. for the measured and derived PNC values. Error bars that are not visible are smaller than data points. The horizontal blue lines represent the same value for PNC_direct and derived PNC.

Table 1.

Uncertainty Budget for spICP-MS Determination of PNC_direct of NIST RM 8012 and RM 8013, Respectively

	RM 8012 (PNCdirect 2.38 × 1014 L−1)	RM 8013 (PNCdirect 3.16 × 1013 L−1)
source of uncertainty	relative contribution (%)	relative contribution (%)
particle size consensus value for standard (dNP RM)	4.2	44.3
dilution factor of stock suspension for the sample (Dil.F)	1.8	0.6
measurement repeatability (Rep)	6.6	3.8
number of observed events for the sample (NNP)	54.9	16.7
Au mass fraction of the standard (CS)	0.9	0.2
sample uptake rate for the standard (qliq RM)	0.6	0.3
time of acquisition for the standard (taq RM)	<0.0	<0.0
number of observed events for the standard (NNP RM)	29.1	32.3
sample uptake rate for the sample (qliq)	0.6	0.3
time of acquisition for the sample (taq)	<0.0	<0.0
dilution factor of stock suspension for the standard (Dil.FRM)	1.1	1.0
density of the particles (ρ)	<0.0	<0.0
residual	0.2	0.5
combined standard uncertainty (L−1)	0.4 × 1013	0.4 × 1012
expanded k =2 uncertainty (L−1)	0.7 × 1013	0.7 × 1012

Comparability of PNC_direct and PNC_mean for NIST RMs 8012 and 8013.

Two key parameters used in the derivation of PNC are the Au mass fraction (C_S) and the particle diameter (d_NP), as can be noted from eqs 2 and 3. Statistical modeling for a rigorous evaluation of the impact of bias in both parameters on the calculation of PNC_mean or PNC_distribution has been reported.²⁷ Briefly, a bias in Au mass fraction was shown to have a linear impact on the derived PNC, while the impact of a bias in particle size was asymmetric considering that the derived PNC is based on the size to the inverse third power. Quantification of total Au in stored stock suspensions after aqua regia digestion by conventional ICP-MS showed that measured Au mass fractions were consistent with the informational values provided in the ROIs^31,33 for both RMs. Dissolved Au was not measured during spICP-MS analysis of both RM working suspensions, as expected.^17,31,33 Detailed information for the determination of Au mass fraction is provided in the SI.

For a comparison to PNC_direct, PNC_mean was derived using the Au mass fraction reported on the ROI and various methods to estimate the particle mean size (expressed as Huber estimates): the consensus mean of the seven sizing methods listed on each ROI, the HR-SEM mean,³² and spICP-MS mean³² (Table S3), using eq 2. The various derived PNC_mean values (Figure 1 and Table S5) were statistically similar, with a relative difference of <5% for RM 8012 and <9% for RM 8013, respectively. For the uncertainty budget of PNC_mean a breakdown of the uncertainty analysis for RM 8012 is provided in Table S6. The major component originated in the determination of the particle size, which represented more than 95% on average of the total, regardless of the sizing technique (Table S7).

The evaluation of the potential of spICP-MS for the accurate measurement of PNC_direct was established through comparison with the various derived PNC_mean or PNC_distribution described above; results are reported in Table 2 and the right axis of Figure 1. Results are expressed as the ratio of PNC_direct to PNC_mean or PNC_direct to PNC_distribution multiplied by 100 to express as a percentage. Throughout this study, percentages within 90–110% were considered in good agreement. The combined standard uncertainty (u_c) for the ratio between PNC_direct and derived PNCs, expressed in percentage, corresponds to the square root of the relative standard uncertainties associated with PNC_direct and the derived PNC added in quadrature. Relative to the various derived PNC_mean (Table 2 and right axis of Figure 1), PNC_direct represented on average 98 ± 2% for RM 8012 and 102 ± 4% for RM 8013 (uncertainty indicates 1 standard deviation). The relative expanded uncertainties for the comparison of PNC_direct with PNC_mean varied with the sizing technique. In all cases, particle size of the sample constituted the major component of uncertainty, representing on average >92 and >81% of the total uncertainty for RM 8012 and RM 8013, respectively (Table S8). In general, the very good agreement between PNC_direct and the various reported PNC_mean indicates that for both RMs, the PNC_mean derived based on robust estimators of the central tendency of the PSD faithfully represents the existing PNC in the stock suspensions and demonstrates that a reliable physical transport of NPs from stock suspensions to the working suspensions and to the plasma was achieved under the experimental conditions.

Table 2.

Comparison between Average PNC_direct Obtained across 15 Independent spICP-MS Experiments for RM 8012 and RM 8013 and Various Derived PNCs^a,b

	RM 8012	RM 8013
n	62	66
reported diameter (ROI)c	95.9 ± 5.7 (11.5)d	106.0 ± 2.0 (4.0)d
HR-SEM diameterc	98.4 ± 19.3 (38.7)d	102.7 ± 10.5 (21.0)d
spICP-MS diameterc	100.4 ± 4.7 (9.4)d	97.7 ± 22.2 (44.4)d
TEM (ROI) full PSD	90.4 ± 5.5	102.1 ± 2.5
HR-SEM full PSD	96.5 ± 18.5 (37.0)d	100.8 ± 10.1 (20.1)d
spICP-MS full PSD	86.1 ± 4.7 (9.4)d	93.9 ± 20.8 (41.5)d
spICP-MS simultaneous diameterc	96.9 ± 1.7 (3.3)d	103.9 ± 1.5 (3.1)d
spICP-MS simultaneous full PSD	87.0 ± 2.3 (4.6)d	94.4 ± 1.5 (3.0)d

^aResults are expressed as a ratio of PNC_direct to PNC_mean or PNC_distribution multiplied by 100, where PNC_mean or PNC_distribution was derived based on the combination of Au mass fraction with the mean particle diameter or PSD reported by TEM,^31,33 HR-SEM,³² spICP-MS,³² and the particle size results simultaneously obtained by spICP-MS in this study as specified in each column heading.

^bValues indicate the ratio between PNC_direct and various derived PNCs, expressed in percentage, and the combined standard uncertainty (u_c) associated.

^cAssumes all analyte is present as spherical NPs of the central tendency diameter.

^dAll recognized and evaluated sources of bias affecting PNC determinations were included in the parenthetical expanded uncertainty computation that corresponds to the expanded uncertainty for 95% coverage.

Particle Size Distribution to Derive PNC for NIST RMs 8012 and 8013.

The use of sizing techniques based on the analysis of individual particles enabled the derivation of PNC using the full PSD, PNC_distribution. Considering the intrinsic dispersity of NP populations, the suitability of PNC_distribution to represent the true value of PNC, the difference between PNC_distribution and PNC_mean, and the comparability with PNC_direct were evaluated for both RMs. In this regard, statistical modeling showed that the magnitude of the difference between PNC_distribution and PNC_mean increased with a greater breadth of the distribution and for distributions with a larger proportion of the distribution skewed toward smaller particles.²⁷

For this purpose, PNC_distribution was derived based on the combination of Au mass fraction with the PSD, reported by TEM,^31,33 HR-SEM,³² and spICP-MS³² for both RMs (Figures S2 and S3), using eq 3. For both RMs, the three different PNC_distribution values (Figure 1 and Table S5) were systematically larger than PNC_mean, <6% on average, which is consistent with Jensen’s inequality since PNC_distribution is a convex function of size (eq 3).²⁷ While a good agreement between the three different PSDs was found (Figures S2 and S3), showing a monodispersed population with similar central values around 27 and 55 nm for RM 8012 and RM 8013, respectively, the dispersion and the tails of the distributions varied with sizing technique. For both RMs, HR-SEM presented the closest agreement between PNC_distribution and PNC_mean because of the narrower PSDs and the absence of a tail toward smaller particles, a result in agreement with the reported statistical modeling.²⁷ Interestingly, for RM 8012, the largest difference between PNC_distribution and PNC_mean was observed for reported spICP-MS PSD (Figure S2C). The presence of 1.3% of NPs smaller than 15 nm, which was unobserved in the number size histograms generated by electron microscopy, resulted in an overestimation of PNC_distribution by 11%. The differences in the smaller NPs only observed by spICP-MS may be ascribed to the presence of non-spherical shapes that are included in the spICP-MS results but are minimized for microscopy techniques by the application of a circularity constraint.³² Note that HR-SEM images are essentially two-dimensional projections of AuNPs on the substrate, while spICP-MS measures the mass of Au per particle and calculates a diameter based on the assumption of spherical shape. In fact, the spherical geometry assumption may introduce a significant bias toward lower diameters since non-spherical shapes take up only a certain fraction of the volume of the sphere they are inscribed in. For example, the particle diameter would be underestimated by 17, 28, and 38% if the spherical shape assumption is applied to rods, cubes, and equilateral triangular prisms, respectively. Also, the signal associated with the smaller particles is much closer to the spICP-MS detection limit, increasing the associated uncertainty due to ion counting errors. The conservative false positive criterion^36,37 contributed to minimize measurement artifacts in the lower region of the PSD, as no particle events within one or two counts over the 5σ threshold were considered. In fact, no significant differences in the number of smaller NPs present were observed between 3σ to 8σ threshold criteria. Considering that millisecond time resolution is more prone to split events and coincident particle events that can artificially increase the contribution of tails of particle oligomers in spICP-MS PSD, millisecond spICP-MS PNC_distribution obtained in this study was compared with the recently reported microsecond time-resolved spICP-MS.⁴⁴ PSD reported in the latter study can be considered virtually free of measurement artifacts because it was acquired using a dwell time of 5 μs, under high sensitivity conditions, and by applying a dead time correction. Analysis of both spICP-MS approaches yielded comparable PNC_distribution, which rules out any significant measurement artifacts associated with millisecond time-resolved analysis under the present experimental conditions. Unlike tails toward smaller NP sizes, the presence of a small percentage of larger NPs has a significantly lower impact on PNC_distribution due to the inverse cubic relationship between PNC and size (eq 3). For example, the presence of 4.6% of NPs larger than 67 nm observed in spICP-MS PSD for RM 8013 (Figure S2) resulted only in an underestimation of PNC_distribution by 3%.

Regardless of the sizing technique, the finite width of the distribution, represented by the relative standard error for PNC associated with each individual NP over the entire distribution, did not contribute significantly to the total expanded uncertainty of PNC_distribution, except for TEM PSD for RM 8013. However, the major uncertainty component in the PNC_distribution was still attributable to the determination of the mean particle size, which represented more than 85% on average of the total, regardless of the sizing technique.

The comparison between PNC_direct and PNC_distribution, reported as the ratio of PNC_direct to PNC_distribution, expressed as a percentage, revealed that a good agreement was obtained for all cases (Table 2 and right axis of Figure 1), except for spICP-MS PSD of RM 8012, due to the overestimation of PNC caused by the significant tail toward smaller particles. The particle size of the sample constituted the major component of uncertainty, representing on average 91 and 79% of the total uncertainty for RM 8012, and RM 8013, respectively (Table S10).

Derived PNC Based on Simultaneous spICP-MS Size Determination for NIST RMs 8012 and 8013.

The outstanding capacity of spICP-MS for the simultaneous quantification of PNC and the determination of the size and size distribution of NP populations allowed the comparison between PNC_direct, PNC_mean, and PNC_distribution simultaneously obtained by spICP-MS (Figure 1). Results are the ratio of PNC_direct to PNC_mean or PNC_distribution, expressed as a percentage. Therefore, it was possible to evaluate if the counting results were truly representative of the population of NPs in the working suspensions, which would help to identify loss of NPs to sample containers across the serial dilution as well as within the sample introduction system of the ICP-MS. It is important to note that the PNC derived based on the accurate determination of particle size would not provide an accurate measurement of the true value of PNC if loss of NPs from the stock suspensions occurred in the samples. It should be emphasized that the simultaneous determination of PNC and NP sizes relies on different measurement mechanisms: counting events that translated into PNC through the frequency-based transport efficiency (eq 1) versus converting signal intensity into NP diameter using the response factor, respectively (eq S1). Also, the internal validation of the determination of PNC_direct was established through the comparison with derived PNC based on the mean particle size and PSD obtained for both RMs in the same 15 independent experiments. Global mean particle size (vertical black dashed lines in Figure 2, and Table S11) differed less than 2% from the previously published spICP-MS results,³² which, despite the significant experimental differences, verified the simultaneous size determination of spICP-MS achieved in this study. The comparison between derived PNC_mean using simultaneous spICP-MS measurements for both RMs (Table S12) with the reported PNC_mean (Table S3) showed a relative average difference of ≤3%. Just like for the reported PNC_mean, the determination of the particle size was the major component of the uncertainty budget for PNC_mean using simultaneous spICP-MS size determination (Table S13).

Figure 2.

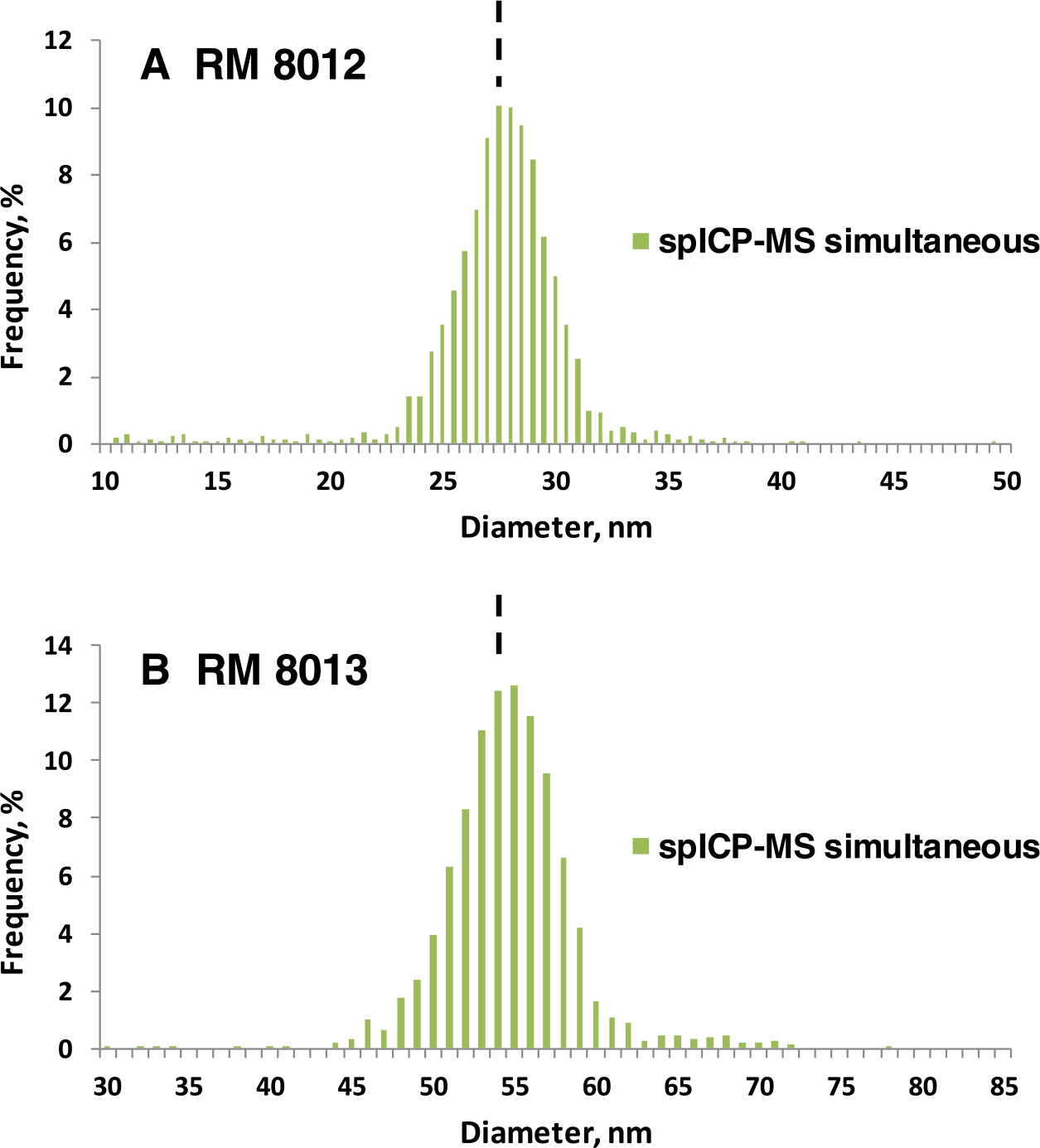
Representative number size distribution histograms for RM 8012 (A) and RM 8013 (B) simultaneously obtained with PNC_direct determinations by spICP-MS in this study. The bin size is 0.5 nm for RM 8012 and 1 nm for RM 8013, respectively. Vertical black dashed lines indicate mean particle diameters.

PNC_mean derived using the obtained global particle size represented 96.9 and 103.9% of PNC_direct for RM 8012 and RM 8013, respectively as can be seen in Table 2 and the right axis of Figure 1. In both cases, the number of observed particle events for the sample and the standard constituted the major component of uncertainty associated with the ratio between PNC_direct and PNC_mean (Table S14).

A representative spICP-MS PSD of the 15 experiments displayed in Figure 2 was selected to derive PNC_distribution for both RMs (Figure 1 and Table S12). For RM 8012, the use of PSD simultaneously obtained by spICP-MS to derive PNC_distribution led to a large percent difference with PNC_direct (13.0%, Table 2, and right axis of Figure 1) due to the presence of 1.2% of NPs smaller than 15 nm (Figure 2A) that increased the derived PNC_distribution by 12%. However, simultaneous PSD by spICP-MS for RM 8013 resulted in a good agreement with PNC_direct (94.4%), indicating that the presence of 1.0% of NPs smaller than 45 nm (Figure 2B) exhibited a much lower impact on the derived PNC_distribution. The excellent agreement between simultaneously obtained and reported PNC_distribution suggest that the small percentage of particles in the low size range is characteristic of spICP-MS analysis for the materials, which rules out any sample preparation or measurement artifacts. For both RMs, the major uncertainty component affecting PNC_distribution and the ratio between PNC_direct and PNC_distribution corresponded to the uncertainty of the diameter of the materials (Tables S15 and S16).

spICP-MS and HR-SEM Size Characterization of Four Different Coated Commercial AuNPs.

Considering that spICP-MS analysis requires a high dilution of the samples (1–10 million, depending on particle size) to reach target working concentrations, the nature of the surface chemistry of the particles may be differently altered depending on their coating. However, the influence of particle size and coating on the spICP-MS determination of PNC of AuNPs at environmentally relevant levels has not been thoroughly explored to date. For these reasons, the study was further extended to the analysis of commercial AuNP suspensions of three different sizes (30, 60, and 100 nm) with four different coatings and surface charge at pH 7: citrate (negatively charged), PVP (negatively charged), bPEI (positively charged), and PEG (neutral). Thus, the potential of spICP-MS for the accurate measurement of PNC_direct was evaluated through the analysis of more than 3000 NPs of 12 commercial AuNPs of different sizes and coatings at environmentally relevant concentrations.

Comparability of PNC_direct and PNC_mean for Commercial AuNPs.

The results for the determination of PNC_direct, through the application of eq 1, measured by spICP-MS in different experiments for all of the commercial AuNPs are provided in the first column of Table 3. The number of events recorded for the sample and the standard constituted the major component of uncertainty associated with PNC_direct, representing on average 70% of the total uncertainty across the particle size range (Table S17). Surprisingly, PNC_direct and PNC_mean (second column of Table 3) were in good agreement only for two materials (PVP-coated and bPEI-coated 100 nm AuNPs) when the Au mass fractions and TEM mean particle diameters provided by the vendor³⁴ (Tables S3 and S18) were used to derive PNC_mean (Tables S19 and S20). To gain a deeper insight into the discrepancy between PNC_direct and PNC_mean, in-house determination of the Au mass fraction for all of the commercial materials was carried out by conventional ICP-MS (Table S18). The relevance of the evaluation of this parameter relies on the linear impact of its bias on PNC_mean (eqs 2 and 3) and on the fact that substantial differences between the nominal value listed on the vendor-supplied documentation and experimental mass fraction have been reported recently for 30 nm PVP-coated AuNPs (~20%)²⁷ and 60 nm AgNPs (~40%).⁴⁵ Regardless of NP size or coating, the amount of ionic Au background measured during spICP-MS analysis was below the limit of detection, 0.020 ng g⁻¹, for all working suspensions. It is expected that as the case for both RMs, the Au ionic fraction of the stock suspensions for the commercial materials is negligible. Despite a bias of up to 20% was obtained between nominal and in-house Au mass fractions (Table S18), the correction of this parameter on the derived PNC_mean (Tables S19 and S20), resulted in a good agreement with PNC_direct for only four of the commercial AuNPs (third column of Table 3, and Table S19). However, when the Au mass fraction measured by conventional ICP-MS was used in conjunction with the HR-SEM mean particle size (Table S3) to derive PNC_mean (Tables S19 and S20), a good agreement with PNC_direct was found for all of the commercial AuNP suspensions under study, regardless of size or coating (fourth column of Table 3, and Table S21). This finding reveals the pivotal role of accurate and reliable average particle size determinations on the computation of PNC_mean. Additionally, larger differences previously obtained for TEM PNC_mean for the commercial suspensions were attributed to inadequate manufacturer characterizations, typically limited to the analysis of only 100 NPs (Table S3), leading to undersampled data that is insufficient to define the mean diameter accurately. For this reason, it was not possible to compute the expanded uncertainty associated with the PNC determinations based on the vendor reported TEM size (third and fourth columns of Table 3, and first column of Table 4). Finally, the fifth column of Table 3 displays the ratio between PNC_direct and PNC_mean calculated using solely ICP-MS measurements of Au mass fraction, mean NP size (third column of Table S3), and PNC. In this case, a good agreement between PNC_direct and PNC_mean was also found for all AuNP suspensions demonstrating the utility of spICP-MS for the thorough characterization of NP suspensions without resorting to other analytical techniques, provided well-characterized and monodispersed calibration materials similar to RM 8013 are available. In general, for commercial AuNPs, the major component contributing to the uncertainty of the ratio between PNC_direct and PNC_mean was particle size of the materials followed by the number of events for the sample and the standard, and, to a lesser extent, Au mass fraction (Table S21). Overall, regardless of NP size or coating, a good agreement (90–110%) between PNC_direct and derived PNC_mean was obtained for all of the AuNP suspensions studied only when reliable in-house Au mass fractions and thorough mean particle size determinations were included in the calculation of PNC_mean.

Table 3.

spICP-MS Determination of PNC_direct and Ratio between PNC_direct and PNC_mean, Expressed in Percentage, for Different Commercial AuNPs^a

	measured PNCdirect (L−1)b	supplier diameter + supplier Au mass fractionc (%)	supplier diameter + in-house Au mass fractionc (%)	HR-SEM diameter + in-house Au mass fractionc (%)	spICP-MS diameter + in-house Au mass fractionc (%)
30 nm PVP	(2.19 ± 0.20) × 1014	117.4 ± 7.6	95.0 ± 6.9	92.2 ± 16.7 (33.4)d	97.0 ± 6.6 (13.1)d
30 nm bPEI	(2.03 ± 0.36 )X 1014	115.1 ± 12.8	96.4 ± 9.8	102.8 ± 18.5 (37.0)d	98.3 ± 8.8 (17.7)d
30 nm PEG	(2.16 ± 0.30) × 1014	148.4 ± 13.6	131.6 ± 10.6	101.4 ± 17.0 (34.1)d	108.9 ± 7.4 (14.7)d
60 nm PVP	(2.69 ± 0.24) × 1013	89.9 ± 9.1	81.2 ± 8.9	96.4 ± 11.1 (22.2)d	91.7 ± 6.3 (12.7)d
60 nm bPEI first lot	(2.46 ± 0.28) × 1013	127.5 ± 12.2	111.3 ± 14.7	91.4 ± 13.1 (26.1)d	90.8 ± 10.3 (20.6)d
60 nm bPEI second lot	(2.80 ± 0.37) × 1013	125.0 ± 12.3	103.9 ± 9.0	90.9 ± 9.7 (19.4)d	90.3 ± 5.6 (11.1)d
60 nm PEG first lot	(2.99 ± 0.41) × 1013	160.0 ± 14.6	148.4 ± 11.1	101.8 ± 9.4 (18.7)d	96.3 ± 2.3 (4.5)d
60 nm PEG second lot	(2.65 ± 0.45) × 1013	144.1 ± 13.9	126.8 ± 10.6	100.1 ± 10.4 (20.8)d	93.2 ± 8.2 (16.5)d
100 nm citrate	(5.75 ± 0.73) × 1012	129.4 ± 13.8	130.6 ± 14.0	108.8 ± 11.2 (22.3)d	91.4 ± 7.6 (15.2)d
100 nm PVP	(4.68 ± 0.74) × 1012	91.6 ± 7.8	107.4 ± 8.4	93.0 ± 8.9 (17.8)d	93.0 ± 8.0 (16.0)d
100 nm bPEI	(4.93 ± 0.59) × 1012	93.4 ± 8.4	115.8 ± 12.9	104.7 ± 11.9 (23.8)d	99.9 ± 9.8 (19.7)d
100 nm PEG	(6.33 ± 0.59) × 1012	139.2 ± 13.3	126.9 ± 10.3	90.9 ± 6.6 (13.3)d	104.3 ± 6.3 (12.7)d

^aPNC_mean values reported for comparison to PNC_direct were derived based on the combination of Au mass fraction and the mean particle size reported by TEM,³⁴ HR-SEM,³² and spICP-MS.³² With regard to Au mass fraction, values provided by the supplier were used in the first column while in-house determinations were used for the remainder columns.

^bValues indicate the direct measurement of PNC_direct and U95% C.I. that includes all recognized and evaluated sources of bias affecting PNC_direct determinations.

^cValues indicate the ratio between PNC_direct and PNC_mean, expressed in percentage, and the combined standard uncertainty (u_c) associated.

^dAll recognized and evaluated sources of bias affecting PNC determinations were included in the parenthetical expanded uncertainty computation that corresponds to U95% C.I.

Table 4.

Ratio between PNC_direct Obtained by spICP-MS and PNC_distribution, Expressed in Percentage, for Different Commercial AuNPs^ab

	TEM (supplier) full PSD	HR-SEM Full PSD	spICP-MS full PSD
30 nm PVP	88.8 ± 7.2	81.6 ± 14.4 (28.9)c	79.8 ± 6.0 (11.9)c
30 nm bPEI	92.4 ± 9.9	81.8 ± 14.9 (29.9)c	79.6 ± 7.6 (15.3)c
30 nm PEG	123.3 ± 10.6	87.7 ± 15.4 (30.7)c	86.7 ± 6.3 (12.5)c
60 nm PVP	68.8 ± 8.3	81.4 ± 9.3 (18.5)c	76.3 ± 5.4 (10.8)c
60 nm bPEI first lot	97.6 ± 13.5	82.9 ± 8.7 (17.5)c	81.0 ± 9.1 (18.3)c
60 nm bPEI second lot	94.5 ± 8.7	82.9 ± 4.0 (18.9)c	77.9 ± 4.8 (9.5)c
60 nm PEG first lot	132.6 ± 11.5	78.1 ± 8.3 (16.7)c	81.7 ± 2.1 (4.2)c
60 nm PEG second lot	113.9 ± 10.5	86.6 ± 8.9 (17.8)c	81.5 ± 7.1 (14.2)c
100 nm Citrate	114.1 ± 13.3	92.1 ± 9.5 (18.9)c	77.1 ± 6.5 (12.9)c
100 nm PVP	103.0 ± 8.4	85.0 ± 8.1 (16.1)c	73.9 ± 6.5 (13.0)c
100 nm bPEI	103.7 ± 12.2	90.2 ± 9.9 (19.8)c	87.4 ± 8.6 (17.1)c
100 nm PEG	104.9 ± 11.1	80.5 ± 5.8 (11.6)c	87.7 ± 5.4 (10.1)c

^aPNC_distribution values reported for comparison to PNC_direct were derived based on the combination of in-house Au mass fraction determination and PSD reported by TEM,³³ HR-SEM,³⁷ and spICP-MS.³⁷

^bValues indicate the ratio between PNC_direct and PNC_distribution, expressed in percentage, and the combined standard uncertainty (u_c) associated.

^cAll recognized and evaluated sources of bias affecting PNC determinations were included in the parenthetical expanded uncertainty computation that corresponds to U95% C.I.

Particle Size Distribution to Derive PNC for Commercial AuNPs.

Despite the claim by the supplier that the commercial suspensions were monodispersed,³⁴ previously reported HR-SEM and spICP-MS analyses showed a higher polydispersity in PSDs for all of the materials regardless of their coating.³² The influence of the dispersion of the size distribution on the derivation of PNC_distribution was evaluated for three representative materials of different nominal particle sizes and different coatings with increasing degree of polydispersity (Figure 3). Relative differences between PNC_distribution and PNC_mean, provided in Table S19, are shown in parentheses in the table inserted at the bottom of Figure 3.

Figure 3.

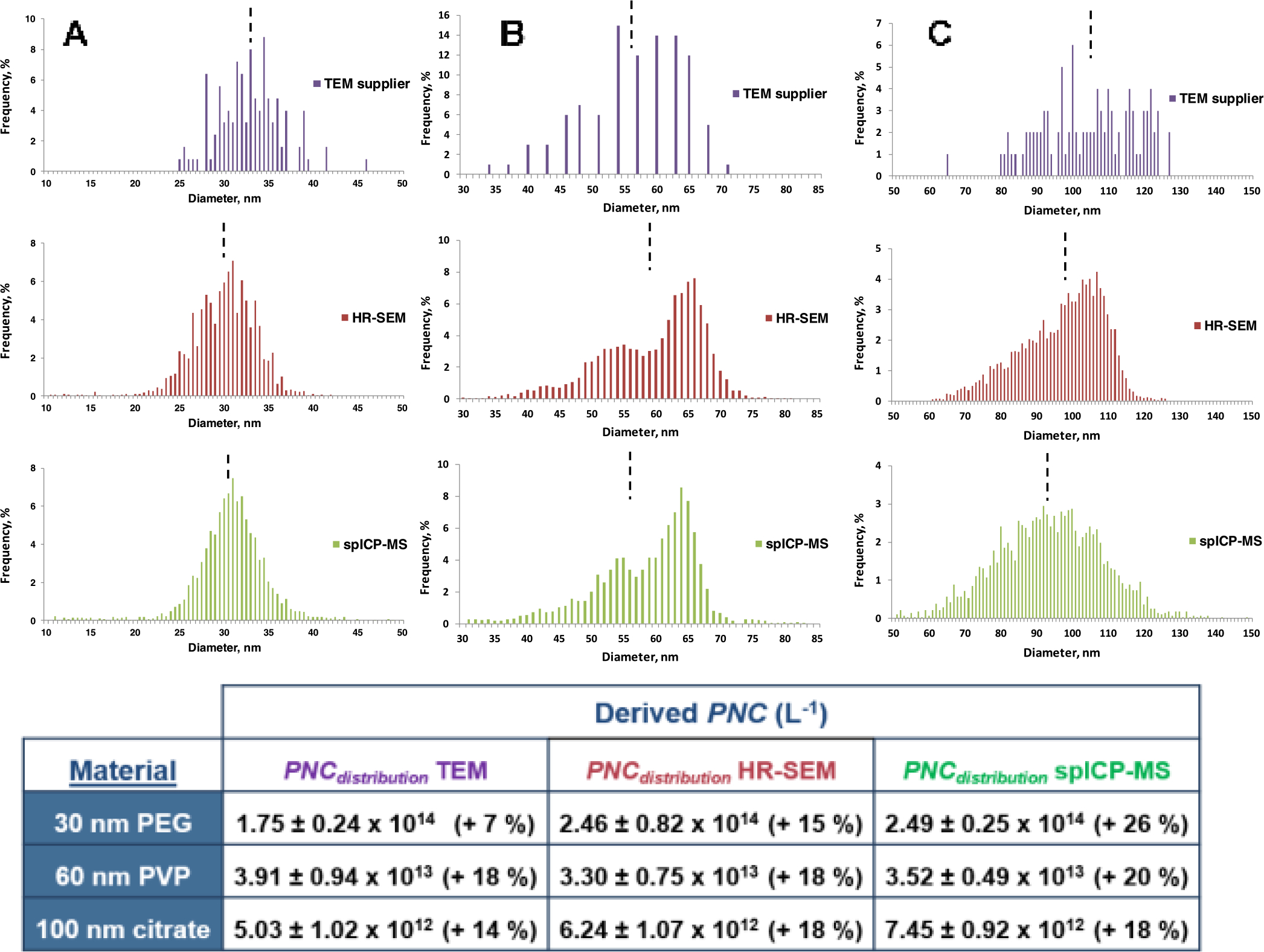
Number size distribution histograms for commercial PEG-coated 30 nm AuNPs (A), PVP-coated 60 nm AuNPs (B), and citrate-coated 100 nm AuNPs (C) measured by TEM (provided by the manufacturer) (purple),³⁴ HR-SEM (dark red),³² and spICP-MS (green).³² Vertical black dashed lines indicate mean particle diameters. Adapted from ref 32. PNC_distribution values calculated using in-house Au mass fractions and PSD reported by TEM,³⁴ HR-SEM,³² and spICP-MS³² are depicted in the table. Listed uncertainties correspond to U95% C.I. Relative differences between PNC_distribution and PNC_mean are shown in parentheses.

The three sizing techniques reported a monodispersed PSD for commercial PEG-coated 30 nm AuNPs (Figure 3A) but significantly broader than that for RM 8012 (Figure S2). The higher dispersion of the PSD of this material was also evidenced by the 4% of NPs in the 10–24 nm size range showed by both HR-SEM and spICP-MS,³² for which the very limited vendor-supplied TEM data failed to provide refined details. For that reason, TEM PNC_distribution was significantly lower than the corresponding for HR-SEM and spICP-MS, both in excellent agreement (Figures 3A and S4A). Unlike RM 8012, the use of PNC_distribution over PNC_mean resulted in a significant impact on the comparability with PNC_direct for PEG-coated 30 nm AuNPs. Thus, a comparison between HR-SEM and spICP-MS size characterizations revealed the presence of a very small population of spherical NPs (0.7% of total) as well as the potential contribution of non-spherical shapes smaller than 15 nm, which significantly increased PNC_distribution relative to PNC_mean, leading to a larger difference compared to PNC_direct (Table 4 and Figure S4A). Similar differences between PNC_direct and PNC_distribution were observed for PVP and bPEI-coated 30 nm AuNPs.

HR-SEM and spICP-MS analyses of the commercial PVP-coated 60 nm AuNPs unexpectedly revealed the existence of two subpopulations of particles in the PSD (Figure 3B).³² In this case, a closer PNC_distribution was found between spICP-MS and HR-SEM than for the vendor-supplied TEM data that failed to adequately define the polydispersity of the PSD of this material (Figures 3B and S4B and Table S19). This unexpected high polydispersity of the PSD was also consistently observed for two different lots of bPEI, and PEG-coated 60 nm AuNPs. The contribution of non-spherical shapes and the presence of a very small population of spherical NPs smaller than 38 nm were reflected in the comparison of the details of the PSDs of both sizing techniques. Thus, unlike RM 8013, HR-SEM and spICP-MS PNC_distribution were 16% on average larger than PNC_mean, which resulted in a significant impact on the comparability with PNC_direct leading to large differences (~20%, Table 4 and Figure S4B) for commercial 60 nm AuNPs regardless of their coating.

All commercial 100 AuNP suspensions showed a higher degree of polydispersity than for RM 8013 regardless of coating, which importantly impacted on the derived PNC_distribution, but was not appropriately defined by the too limited TEM supplied data. The differences in the profile of both spICP-MS and HR-SEM histograms, as exemplarily displayed for citrate-coated AuNPs in Figure 3C, were explained by the higher presence of non-spherical shapes observed in representative HR-SEM images of these materials.³² This observation is consistent with the increasing polydispersity and non-sphericity exhibited by AuNPs produced by the citrate method for particle diameters larger than 50 nm.⁴⁶ Differences perceived in the 120–130 nm range were attributed to particle coincidence yet did not contribute significantly to PNC_distribution. Thus, due to the higher percentage of NPs smaller than 60 nm in spICP-MS PSD, the 100 nm commercial materials exhibited, on average, the largest difference between HR-SEM and spICP-MS PNC_distribution (Figure S4C and Table S19) as well as with PNC_direct (Table 4). In general, for commercial AuNPs, the major component contributing to the uncertainty associated with the ratio between PNC_direct and PNC_distribution was particle size of the materials followed by the number of events for the sample and the standard (Tables S22 and S23).

For all materials, regardless of particle size, coating, and dispersion of PSD, PNC_distribution (Table S19) and the ratio between PNC_direct and PNC_distribution (Table 4) based on reported HR-SEM and spICP-MS PSDs were statistically comparable at one combined standard uncertainty level. This agreement also indicates that large differences between PNC_direct and PNC_distribution can be attributed to the substantial impact of the presence of a very small percentage (<1%) of smaller spherical particles associated with the high polydispersity in the PSD of commercial materials. In fact, a good agreement with PNC_direct was obtained when a reliable robust indicator of the central tendency of the PSD was used to derive PNC_mean because the Huber estimate of location, or typical diameter,⁴⁷ minimized the sensitivity to the tails of the corresponding PSDs.

Derived PNC Based on Simultaneous spICP-MS Size Determination for Commercial AuNPs.

The internal validation of PNC_direct determination through the comparison with PNC_mean and PNC_distribution obtained by spICP-MS in the same experiment was also carried out for the commercial AuNPs. Results are the ratio of PNC_direct to PNC_mean or PNC_distribution, expressed as a percentage. For all of the materials, a very good agreement between measured and previously reported spICP-MS mean particle diameter was found, with a difference less than 1.5% on average (Table S11). Similar to the results from both RMs, the derived determination of PNC using the mean particle size simultaneously obtained by spICP-MS, in general, provided comparable results for the measurements of PNC of varying AuNP size, surface charge, and dispersion of PSD. Thus, PNC_mean results (Table S24) differed by 6% on average from the PNC_direct values (Table 3), resulting in a good agreement for 11 out of 12 commercial materials (Table 5 and Figure S4). Simultaneously obtained PNC_distribution (Table S24) were again significantly higher than PNC_mean because of Jensen’s inequality and the contribution of smaller particles, which also resulted in larger differences with PNC_direct for 60 and 100 nm AuNPs (Table 5). However, despite the results described in Table 4, when the reported PNC_distribution were used, comparable PNC_direct and simultaneous PNC_distribution were obtained for 30 nm AuNPs regardless of their coating, for which a lower contribution of NPs smaller than 15 nm was found. This result likely stems from the natural variability of particle size in the materials and the challenges related to the accurate measurement of the signal associated with the smaller particles, much closer to the spICP-MS detection limit. In any case, the differences observed between simultaneously obtained and reported PNC_distribution were within one combined standard uncertainty level for all materials (Tables S19 and S24). For all commercial AuNPs, the determination of the particle size was the major component of the uncertainty budget for PNC_mean and PNC_distribution followed by Au mass fraction (Tables S25 and S26), while the number of observed particle events for the sample and the standard constituted, in general, the major component of uncertainty associated with the ratio between PNC_direct and simultaneously obtained PNC_mean and PNC_distribution (Tables S27 and S28).

Table 5.

Comparison between PNC_direct and Derived PNC_mean and PNC_distribution Based on the Combination of In-House Au Mass Fraction with the Mean Particle Size or PSD Simultaneously Obtained in This Study by spICP-MS for Different Commercial AuNPs^a

	central tendency (PNCmeanb	full PSD (PNCdistribution)
30 nm PVP	106.5 ± 7.0 (14.1)c	92.6 ± 6.4 (12.9)c
30 nm bPEI	102.8 ± 10.8 (21.8)c	90.9 ± 9.8 (19.6)c
30 nm PEG	114.7 ± 8.2 (16.4)c	93.4 ± 7.0 (13.9)c
60 nm PVP	102.1 ± 7.4 (14.7)c	83.1 ± 6.1 (12.3)c
60 nm bPEI first lot	92.8 ± 10.5 (20.9)c	77.3 ± 8.6 (17.2)c
60 nm bPEI second lot	97.4 ± 5.7 (11.4)c	83.3 ± 4.9 (9.8)c
60 nm PEG first lot	87.5 ± 2.4 (4.9)c	80.9 ± 2.3 (4.6)c
60 nm PEG second lot	103.7 ± 9.1 (18.3)c	92.2 ± 8.0 (16.0)c
100 nm Citrate	92.0 ± 7.9 (15.8)c	77.1 ± 6.6 (13.2)c
100 nm PVP	96.2 ± 8.1 (16.2)c	84.0 ± 7.1 (14.2)c
100 nm bPEI	101.5 ± 9.7 (19.5)c	91.4 ± 8.7 (17.3)c
100 nm PEG	107.4 ± 10.1 (20.1)c	92.4 ± 8.5 (17.1)c

^aValues indicate the ratio between PNC_direct and derived PNCs, expressed in percentage, and the combined standard uncertainty (u_c) associated.

^bAssumes all analyte is present as spherical NPs of the central tendency diameter.

^cAll recognized and evaluated sources of bias affecting PNC determinations were included in the parenthetical expanded uncertainty computation that corresponds to U95% C.I.

CONCLUSIONS

This paper presents, for the first time, a rigorous assessment of spICP-MS capabilities for measuring PNC in suspensions of varying AuNP size and surface charge at environmentally relevant concentrations. Accurate and consistent quantification of PNC was achieved for both monodispersed NIST AuNP RMs in 15 independent experiments conducted more than 4 years apart. spICP-MS provided comparable results for PNC_direct and PNC_mean derived based on the mean particle size obtained by different established sizing techniques, which is considered a reliable representation of the existing PNC in the stock suspensions. This agreement indicates unbiased spICP-MS results and demonstrates a reliable physical transport of NPs from both RM stock suspensions to the plasma.

The analysis of 12 commercially available AuNP suspensions with three different sizes and four different surface coatings revealed that the potential of spICP-MS for the accurate measurement of PNC_direct was not affected by selected particle size or coating. Overall, regardless of NP size or coating, a good agreement between PNC_direct and reported PNCs was obtained for all of the AuNPs analyzed only when reliable in-house Au mass fractions and thorough mean particle size determinations were included in the calculation of PNC_mean.

Alternatively, the outstanding capacity of spICP-MS for the simultaneous measurement of NP size, PSD, and PNC demonstrated that counting results were truly representative of NP population in the working suspensions, evidencing the utility of the ICP-MS technology for the thorough characterization of NP suspensions without resorting to other analytical techniques. Another great benefit of spICP-MS lies in combining an efficient and accurate measurement of a large number of particles in a very short analysis time (a few minutes) with minimal sample perturbation at extremely low number concentrations often found in real-world environmental samples that competing techniques cannot easily target. Thus, it is expected that, following the described strategy, spICP-MS can be applied for the straightforward assessment of the quality of NP suspensions for their potential use as calibration standards to enable both accurate size and PNC determinations.

Furthermore, a comprehensive evaluation of the expanded uncertainty for PNC_direct revealed that variability in the number of observed particle events for the sample and the calibration standard was the major component. In contrast, regardless of the sizing technique, the uncertainty associated with the determination of the particle size was the main factor contributing to the uncertainty budget associated with the ratio between PNC_direct and PNC_mean.

While PSD can be generally considered a more appropriate representation of the material size variability, since an error in the particle diameter leads to a cubic error in its volume, the PNC_distribution estimates are challenged by high polydispersity from the PSD, shape heterogeneity of quasi-spherical NPs, being particularly impacted by the presence of tails toward smaller particles. Thus, a good agreement between PNC_direct and PNC_distribution was generally found only for monodispersed NIST RMs with a well-defined and relatively narrow PSD. In contrast, the use of full PSD over the mean size to derive PNC resulted in larger differences between PNC_direct and PNC_distribution for all commercial suspensions regardless of particle size, surface coating, or dispersion of the PSD. These results emphasize the necessity for accurate characterization of the size distribution of polydispersed materials particularly at the low range of the nanoscale. Additional work is needed on the development of three-dimensional NP characterization techniques (e.g., multiangle electron microscopy) to provide a true particle volume distribution, on a particle by particle basis that would account for the shape dimension significantly improving the accuracy of measurements of the PSD and the comparability of results among analytical methods.