Abstract
Two-dimensional (2D) van-der-Waals (vdW) layered ferroelectric semiconductors are highly desired for in-memory computing and ferroelectric photovoltaics or detectors. Beneficial from the weak interlayer vdW-force, controlling the structure by interlayer twist/translation or doping is an effective strategy to manipulate the fundamental properties of 2D-vdW semiconductors, which has contributed to the newly-emerging sliding ferroelectricity. Here, we report unconventional room-temperature ferroelectricity, both out-of-plane and in-plane, in vdW-layered γ-InSe semiconductor triggered by yttrium-doping (InSe:Y). We determine an effective piezoelectric constant of ∼7.5 pm/V for InSe:Y flakes with thickness of ∼50 nm, about one order of magnitude larger than earlier reports. We directly visualize the enhanced sliding switchable polarization originating from the fantastic microstructure modifications including the stacking-faults elimination and a subtle rhombohedral distortion due to the intralayer compression and continuous interlayer pre-sliding. Our investigations provide new freedom degrees of structure manipulation for intrinsic properties in 2D-vdW-layered semiconductors to expand ferroelectric candidates for next-generation nanoelectronics.
Subject terms: Ferroelectrics and multiferroics, Two-dimensional materials
Exploring two-dimensional layered ferroelectric semiconductors is highly desired for ferroelectric-based devices. Here, the authors realize the room-temperature ferroelectricity in layered Y-doped γ-InSe due to the microstructure modifications.
Introduction
2D vdW-layered ferroelectric semiconductors1, with combinations of electric-field switchable polarization and distinctive electronic band structure, offer a wide range of physical opportunities and technological applications in nanoelectronics in the era of information technology, such as in-memory computing and efficient ferroelectric photovotaics2. Also, new-principle devices were theoretically predicted in 2D vdW ferroelectric semiconductors, involving the quantum spin Hall effect and even the abnormal valley-related (spin) Hall effect when the valley polarization is further considered (or ferrovalley semiconductors)3,4. However, limited to the extremely rare 2D layered parent crystals that belong to the noncentrosymmetric polar space group, only a constrained number of 2D intrinsic ferroelectrics have been successfully demonstrated so far, such as distorted 1 T transition-metal dichalcogenides (TMDs)5, In2Se36, CuInP2S67 and MX (e.g., GeS)8. Continuous efforts have been devoted to exploring for new 2D ferroelectric semiconductors. Owing to the weak interlayer vdW-force in 2D-layered materials, structural control by interlayer twist/translation has successfully enabled the realization of the unexpected interlayer sliding ferroelectricity in Moiré superlattices and TMD heterostructures with artificially-tuned broken inversion symmetry via much more complex fabrication procedures9–18. On the other hand, doping, especially with rare-earth elements19, which can change the lattice structure (such as bond distance and angle, and atom position) of materials, e.g., via microstrain/structure constrain, has also been employed as an effective strategy to tune ferroelectric properties not only in traditional perovskite-based ferroelectrics20 but also in newly-emerging HfO2-based ferroelectrics21,22, showing great potential for manipulating the fundamental properties of 2D vdW semiconductors.
The 2D vdW-layered InSe semiconductor with suitable bandgap (Eg = 1.0~1.6 eV) and high mobility (~103 cm2·V−1·S−1) has demonstrated intriguing physical and optoelectrical properties23. It is theoretically predicted that γ-InSe with R3m symmetry may exhibit sliding ferroelectricity2; however, no experimental studies on the ferroelectricity, either intrinsic or doping-induced, are available, except for a few reports about the piezoelectricity24. This definitely impedes its practical application in nanoferroelectrics. Here, with Y, a member of rare-earth elements that can be considered as “vitamin” dopants, we fantastically improve the crystal quality of vdW-layered γ-InSe prepared by Bridgman method, and realize both robust out-of-plane (OOP) and in-plane (IP) ferroelectricity in InSe:Y at room-temperature. Our atomic imaging results show that Y plays an important role in introducing anisotropic stress/strain in InSe and results in the corresponding microstructure modifications including the stacking-faults elimination and a subtle rhombohedral distortion with intralayer compression along the c-direction (i.e., the thickness direction of the 2D layered InSe) and continuous interlayer pre-sliding, which is supposed to enhance both OOP and IP spontaneous polarizations in InSe. Our optical characterizations together with first-principles calculations indicate that the doping-induced structural perturbations slightly broaden the bandgap of intrinsically-direct InSe and significantly optimize the interlayer transport and distribution of intralayer carriers, which reflects the increase of the interlayer stacking order that are likewise beneficial to the enhancement of OOP and IP spontaneous polarizations. Our work provides a strategy to expand the family member of 2D vdW-layered ferroelectric semiconductors.
Results
Characterization of structures
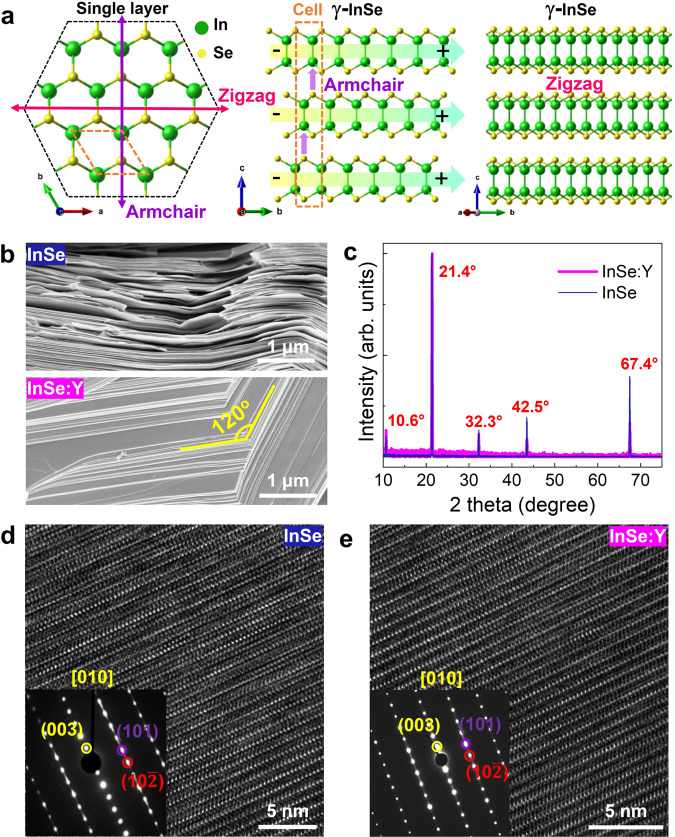
The polymorphic phases of InSe are schematically illustrated in Supplementary Fig. 1, in which γ-InSe is rhombohedral with lattice parameters a = b = 4.00 Å and c = 25.32 Å, and belongs to the R3m (C53 v) noncentrosymmetric space group with ABC-style stacking, possessing three armchair (AC) and three zigzag (ZZ) directions (Fig. 1a)25, exhibiting IP and OOP polarizations. Scanning electron microscopy (SEM) gives the morphology of the as-grown InSe and InSe:Y crystals (Fig. 1b and Supplementary Fig. 2a, b). It is worth noting that the undoped InSe presents a soft and plastic lamellar morphology, due to its superplastic nature induced by interlayer gliding and cross-layer dislocation slip26, while InSe:Y exhibits a well-defined layer structure with a straight and wrinkle-free surface, indicating the fantastical reversion of the natural plasticity of InSe. Both X-ray diffraction (XRD) patterns of InSe and InSe:Y (Fig. 1c) show obvious {00l} reflections without peak shifts between them, indicating that Y-doping has not changed the single-crystal structure of InSe. Additionally, the Raman spectra of both samples (Supplementary Fig. 2e) display three InSe-related characteristic vibrational modes of A11g, E12g and A21g. Notice that the actual phase structure of InSe cannot be precisely elucidated based on XRD and Raman characterizations, since all three polytypes of InSe possess similar diffraction peaks and vibrational modes (Supplementary Note 1)27. Thus, we employ transmission electron microscopy (TEM) to explore the actual InSe phase. As shown in the cross-section TEM images (Fig. 1d, e and Supplementary Fig. 2c, d) and the corresponding selected area electron diffraction (SAED) patterns (insets in Fig. 1d, e) projected along the [010] zone axis, both samples present a 2D layered structure with obvious electron diffraction features of γ-InSe (Supplementary Fig. 1e), implying that Y-doping does not change the phase of InSe28. Energy dispersive spectrometer (EDS) results (both SEM‒EDS and TEM‒EDS; Supplementary Fig. 2f) show the chemical composition of In:Se ≈ 1:1 in InSe and InSe:Y. Due to the high impurity segregation coefficient of InSe29 and the low Y-doping level (only 1 at% in the raw material), the actual Y-content is extremely low, which cannot be detected by EDS. We then performed time-of-flight secondary ion mass spectrometry (TOF-SIMS) analysis, proving the uniform distribution of doped-Y with a truly low concentration and a positive valence state (Supplementary Fig. 3). Interestingly, many natural stacking-faults are observed in undoped InSe (Fig. 1d, and Supplementary Fig. 2c) because of the very low formation energy (almost zero) that is responsible for the interlayer glide-induced superplasticity30, but are significantly reduced in InSe:Y (Fig. 1e and Supplementary Fig. 2d and Note 1). Based on these TEM results, it can be speculated that trace-Y can effectively inhibit stacking-faults formation, and thus has a striking influence on the crystal microstructure and plasticity of InSe, which may give rise to new physical properties.
Fig. 1. Structural characterization of InSe and InSe:Y.
a Schematics of InSe single layer and the atomic arrangement of γ-InSe, demonstrating the IP polarization along the AC direction and the OOP polarization along the thickness-direction (see arrows in the middle panel). b SEM images of InSe and InSe:Y. c XRD patterns of single crystalline InSe and InSe:Y. HRTEM images and the corresponding SAED patterns (inset) of InSe (d) and InSe:Y (e) projected along the [010] zone axis.
Band structure and carrier transport
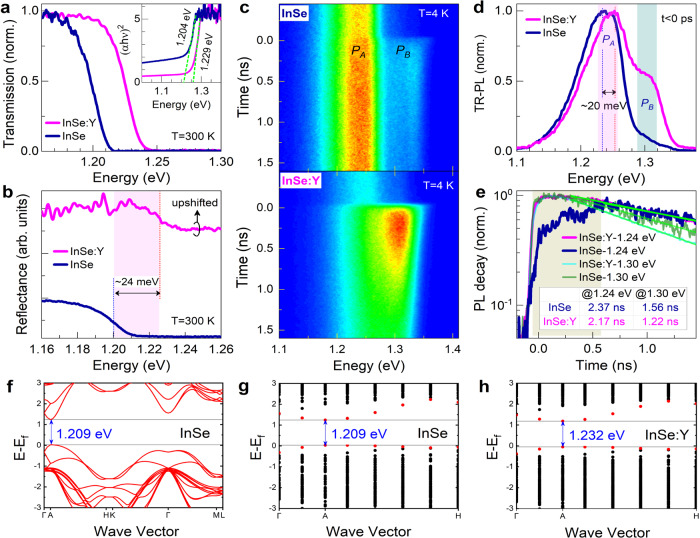
We perform optical characterizations to investigate the influence of Y-doping-induced microstructure perturbations on the optical properties of InSe. The room temperature transmission spectra (Fig. 2a) of both flakes (InSe and InSe:Y) show a direct transition feature, and the intrinsic absorption edge of InSe:Y has a visible blueshift. Tauc-plots31 (inset in Fig. 2a) give Eg ~ 1204 meV for InSe and ~1229 meV for InSe:Y, consistent with the result from the reflectance spectra (Fig. 2b). We perform time-resolved photoluminescence (TR-PL) measurements (Fig. 2c) to further visualize the carrier transition and recombination dynamics. Both crystals present a double-peak structure, of which the low-energy peak (PA) is related to the intralayer exciton recombination (i.e., the conventional Eg) while the high-energy peak (PB) can be ascribed to the interlayer exciton recombination by considering the slight energy separation of ~60 meV from PA and a close lifetime to that of PA (Supplementary Note 2)32,33. Similarly, PA in InSe:Y shows a blueshift of ~20 meV (at 4 K), as observed in transmission and reflectance spectra. More importantly, we should emphasize that i) the intensity of PB (interlayer) is largely enhanced by Y-doping as compared to that of PA (intralayer) (Fig. 2c, d); ii) the intralayer nonequilibrium carriers (PA) in InSe:Y have a sharp rise, but are substantially delayed by ~630 ps in InSe, although the lifetime constant of both crystals is subequal within 1 − 3 ns (Fig. 2e); and iii) the spatially-dependent TR-PL results give uniform peak energy and lifetime for InSe:Y, but relatively broad distributions of lifetime for InSe (Supplementary Fig. 4). From the point of view of the carrier transport and recombination, these results suggest that Y-doping can optimize the crystal quality of InSe and, in particular, the c-direction transport of intralayer carriers that enhanced the density and distribution of interlayer carriers, possibly due to the previously-confirmed (interlayer) stacking-faults elimination and the extremely-low carrier mass along the c-direction in InSe34. This subsequently results in the stronger interlayer exciton recombination (PB) in InSe:Y (Fig. 2c, d). Thus, we can infer that Y-doping-induced microstructure perturbations play a critical role in the Eg blueshift and carrier redistribution in vdW-layered InSe, which can also be confirmed by our first-principles calculations. As shown in our density function theory (DFT) calculation results (Fig. 2f–h and Supplementary Fig. 5), both the pristine and Y-doped InSe are indeed direct with the conduction and valence band maximums situating at the high-symmetric A point, which gives Eg–values of 1.209 eV and 1.232 eV, respectively, totally consistent with the experimental data.
Fig. 2. Optical characterizations of InSe and InSe:Y.
a Transmission spectra at room temperature. The inset gives the corresponding Tauc-plots. b Reflectance spectra at room temperature. c TR-PL images with peaks PA and PB of InSe (upper) and InSe:Y (lower) at 4 K. d Transient-PL curves at t < 0 ps (i.e., before the next pulse). e PL decay curves at ~1240 meV and 1300 meV for both samples. The inset gives the corresponding lifetimes from the fit procedure with a single-exponential decay function. The calculated band structure of InSe (f) and the energy eigenvalues for selected k-points near valence band maximum (VBM) based on the supercell of InSe (g) and InSe:Y (h) (Methods, Supplementary Fig. 5). The bandgap widens with Y-doping, and the VBM stays at the A point. No defect level is introduced in the bandgap by Y-doping.
Structural symmetry and PFM results
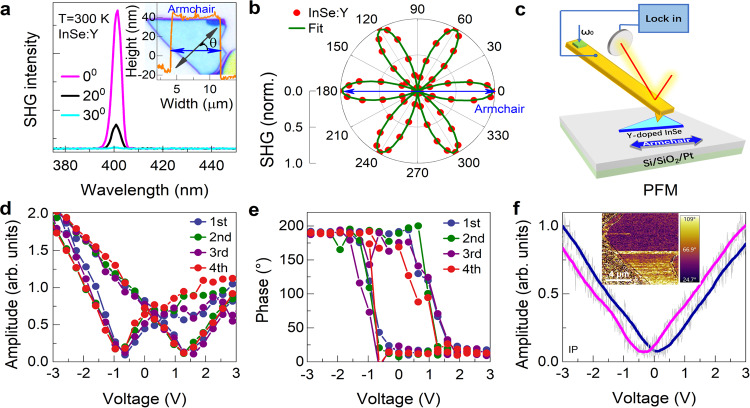
2D γ-InSe belongs to the C53 v point group with noncentrosymmetry, possessing a strong second harmonic generation (SHG) effect24, and was theoretically predicted to exhibit sliding ferroelectricity2. Since we have optimized the crystal quality and the carrier transport, especially the intralayer carriers transport along OOP direction in γ-InSe by Y-doping, we further verify the symmetry and the piezo/ferroelectric properties in InSe:Y. A polarization-dependent SHG signal at 400 nm (an 800 nm laser source) is detected on a ~50 nm (about 20 unit cells) thick InSe:Y flake (inset in Fig. 3a) when rotating the angle (θ) of the sample (Fig. 3a), where θ = 0° means the incident polarized light is parallel to the AC direction of InSe. The θ-dependent SHG intensity (Fig. 3b) indicates an obvious 6-lobe structure, pointing to the R3m space group for InSe:Y, the same as the original InSe. In addition, the AC and ZZ directions can be easily distinguished, indicating the anisotropy of InSe (and InSe:Y) with broken inversion symmetry and directional selectivity. A similar SHG result can be observed in different InSe:Y samples (Supplementary Fig. 6), which should exclude the coincidence of the positive and negative charge centers that break the spatial inversion symmetry1. Next, piezoresponse force microscopy (PFM) is employed to explore both the piezoelectric and ferroelectric properties in InSe:Y. As schematically shown in Fig. 3c, a voltage-dependent PFM hysteresis loop is obtained at individual points on the same InSe:Y flake (inset in Fig. 3a) with the direct voltage swept from −3 V to +3 V and an alternating voltage of 0.5 V with a resonant frequency of ~350-kHz at the needle tip. Surprisingly, the vertical electric field applied between the probe and sample surface causes the ferroelectric-like amplitude response to show a butterfly loop with an opening of ~2 V, while the phase switches 180° at the same turning point (Fig. 3d, e). After cycling the test four times, the amplitude hysteresis loop remains in a butterfly shape and the phase transition remains at 180°. Additionally, the polarization switch on a clean surface is able to write reverse polarity domains at different voltages using the tip as the polarization electrode, further confirming the ferroelectricity in bulk-like InSe:Y (Supplementary Fig. 7). To exclude the random phenomena or experimental errors35, the OOP polarization is verified for InSe:Y flakes with different thicknesses (Supplementary Fig. 8 and Note 3) or at the low frequency (23-kHz) mode (Supplementary Fig. 9 and Note 3). Then, we determine the OOP effective-d33 piezoelectric constant (d) of uniform ∼7.5 pm/V for ∼50 nm thick InSe:Y flakes. Notice that with the thickness decrease from ~120 nm (about 48 unit cells) to ~14 nm (about 5 unit cells), the d-value experimentally demonstrates a monotonous increase from ~4.0 pm/V to 14.1 pm/V (Methods, Supplementary Note 3 and Table S1), suggesting that the thinner of the InSe:Y flakes, the stronger of the piezo/ferroelectricity. This d-value is remarkably larger than earlier reports including the new 3R-like MoS2/WS2 heterobilayers by a factor of ∼716, the monolayer α-In2Se3 by ∼44 times36, and the bulk γ-InSe by ∼10 times13,37 (Methods, Supplementary Table 1), implying new piezo/ferroelectric enhancement mechanism in our InSe:Y material system. Simultaneously, at low frequency, the IP PFM (Fig. 3f) also shows a typical amplitude response as a butterfly loop with an opening voltage of ∼0.4 V and two distinct regions with an ~60° phase difference in the corresponding IP phase image (inset), demonstrating the simultaneous presence of IP ferroelectricity in InSe:Y. No similar phenomena can be observed in ordinary γ-InSe (Supplementary Fig. 10). Thereafter, the OOP and IP ferroelectricity raises an interesting possibility to trigger and enhance the spontaneous polarization of γ-InSe via Y-doping.
Fig. 3. SHG and PFM of InSe:Y.
a SHG intensity at angles of 00, 200, and 300. The inset gives the exfoliated InSe:Y morphology with the thickness of ~50 nm measured by atomic force microscopy (AFM). b Polar plots of SHG intensities collected by rotating the polarizer as a function of the detection angle. c Schemes of the InSe:Y film structure and the setup for the PFM measurement. The local PFM amplitude (d) and phase (e) loops during the switching process of the InSe:Y flake with thickness of ~50 nm (results of four cycles). f IP PFM amplitude at low frequencies together with the IP phase image as inset.
Origin of FE in InSe:Y
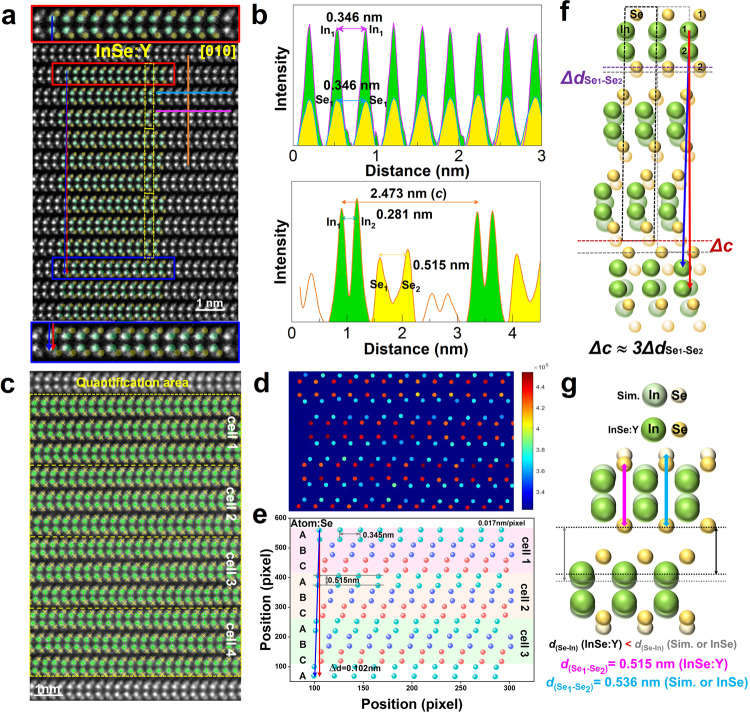
To get deep insight into the interplay of Y-doping-induced structural modifications and the intriguing ferroelectric property in InSe, we perform comprehensive scanning TEM-high angle annular dark field (STEM-HAADF) analyses to directly investigate the atomic configuration. As shown in STEM-HAADF images of InSe (Supplementary Fig. 11) and InSe:Y (Fig. 4a and Supplementary Fig. 12), both crystals indeed belong to the γ-phase with an ABC-stacking sequence (inset in Supplementary Fig. 11a). In sharp contrast, there is a high density of stacking-faults in InSe, but only a few in InSe:Y, in line with the previous TEM/SAED results. The top and bottom insets in Fig. 4a amplify the regions marked by red and blue rectangles, respectively, where the atomic arrangements of In and Se are overlaid on the HAADF image (green/yellow points for In/Se), demonstrating the doping-induced continuous sliding behavior along the AC direction, layer-by-layer with a relatively long periodicity (approximately 30 layers; Fig. 4a, e). Moreover, a localized inward compression of the lattice structure is also observed in InSe:Y. Indexing from the corresponding fast Fourier transform pattern (Supplementary Fig. 12b) of the HAADF image (Fig. 4a), the lattice distance of the (003) planes in InSe:Y is ~0.824 nm, i.e., smaller than that of the undoped (0.843 nm; Supplementary Fig. 11), or the simulated atomic structure (0.844 nm; Supplementary Fig. 1d). This gives a reduced lattice parameter c = 2.473 nm (~2.33%) for InSe:Y in contrast to the theoretical value (2.532 nm). Furthermore, the intensity line profiles (Fig. 4b) along the purple, sky-blue and orange lines in Fig. 4a show that the projected atomic distances of In1-In2, In1-In1, and Se1-Se1 (i.e., dIn1-In2 = 0.281 nm, dIn1-In1 = dSe1-Se1 = 0.346 nm) remain unchanged, but that of Se1-Se2 (dSe1-Se2 = 0.515 nm) is evidently smaller than the theoretical value (0.536 nm in Supplementary Fig. 1d). Detailed atomic arrangement analyses for different STEM samples combined with atomic quantification via Calatom38 based on custom MATLAB scripts also demonstrate the same results (Fig. 4c–e and Supplementary Fig. 14 and Note 4). It can then be concluded that Y plays a critical role in introducing anisotropic stress/strain along the c-axis in InSe during the crystal growth, which leads to a subtle rhombohedral distortion including intralayer compression along the c-axis and continuous interlayer pre-sliding at atomic scale (Fig. 4f) due to the low intralayer rigidity of In-Se bonding and the weak interlayer vdW-force. It is worth noting that the decrease in the intralayer Se-Se vertical distance shortens the bond length between anion (Se) and cation (In or trace-Y) atoms, definitely broadening the optical gap and increasing the binding energy in InSe:Y, which is consistent with the observed blueshift of Eg in optical characterization and is also proven by our first-principles calculations (Methods, Fig. 3f–h) and the X-ray photoelectron spectral results (Supplementary Fig. 15 and Note 5). More significantly, the offset of the atomic position of Se-Se along the c-direction and the interlayer pre-sliding along the AC direction with a long periodicity can induce the redistribution of charges, as discussed in the TR-PL results, and simultaneously decrease the vertical interlayer spacing between the bottom In atoms in the upper layer and the corresponding top Se atoms in the adjacent lower layer (Fig. 4g). This should enhance the interlayer net polarization in the vertical direction14 and also introduce an additional polarization vector along the AC direction to strengthen the IP polarization, resulting in robust OOP and IP ferroelectricity, as observed by PFM.
Fig. 4. Microstructure analysis InSe:Y.
a STEM-HAADF image of InSe:Y with magnified images at the top (bottom) for the red (blue) rectangles. The simulated γ-InSe atomic arrangements with green (yellow) dots representing In (Se) atoms are overlaid on the HAADF image, which demonstrates the continuous slip behavior layer-by-layer, as traced by the red (blue) arrows. b Intensity line profiles extracted from a with the upper along the horizontal purple (In1–In1) and sky-blue (Se1–Se1) lines and the lower along the vertical orange line. c Atomic positions of In (green stars) and Se (yellow crosses) identified by Calatom software. d Normalized intensities of the bright dots in a, with red (blue) points representing for In (Se). e The corresponding atomic positions of Se in c, showing the layer-by-layer sliding (Δd) along the AC direction, well consistent with the results in a. f Schematic diagram of Y-doping-induced microstructural changes of the subtle rhombohedral distortion including intralayer compression along the c-axis (Δd) and continuous interlayer pre-sliding (Δc) in γ-InSe unit cell. g Schematic of Y-doping-induced compressions of Se1-Se2 spacing (d(Se1-Se2)) in Se-In-In-Se intralayer and Se-In dipole spacing (d(Se-In)) in vdW interlayer gap.
It has been theoretically predicted that a small twist or strain difference can give rise to Moiré pattern in the graphitic bilayer of BN, AlN, ZnO, MoS2, GaSe, etc, or in bulk vdW InSe with R3m symmetry14 due to the relatively low sliding potential. And certain stacking in those bilayers that breaks the symmetry and makes two layers unequivalent may lead to net polarizations. For instance, Fei et al.39 reported an interlayer sliding potential (~meV) several orders of magnitude lower in WTe2 than that of conventional ferroelectrics. Accordingly, interlayer sliding ferroelectricity was experimentally demonstrated in BN9,15, graphene10 and TMDs16. Undoubtedly, in the case of InSe:Y, the sliding potential along the continuous interlayer pre-sliding direction should further decrease. It can then be inferred that, although ordinary γ-InSe theoretically possesses spontaneous polarization that can be reversed by external electric fields, and Wu et al.13 even predicted a weak OOP polarization of ~0.08 µC/cm2 for vdW bulk γ-InSe, the abundant naturally-existing planar stacking-faults weakened the probability for an experimental observation of the really weak intrinsic ferroelectricity. In contrast, our structure control approach fantastically stabilizes a subtle distorted rhombohedral configuration with strengthened OOP and IP spontaneous polarizations, thus arousing the robust OOP and IP ferroelectricity in InSe:Y. Our observations provide a strategy to tune and optimize the piezo/ferroelectric property in 2D vdW-layered semiconductors.
Discussion
So far with the help of trace Y dopant, we realized unconventionally robust OOP and IP ferroelectricity in the high crystal quality vdW-layered γ-InSe semiconductor due to the natural stacking-faults elimination and a subtle distorted rhombohedral configuration, underlining the striking role of doping-induced stress/strain in the manipulation of the fundamental properties of condensed matter. This investigation opens up a pathway to tuning the ferroelectric properties for expanding the member of 2D vdW-layered ferroelectric semiconductors and also gives new insight into the interplay of the microstructure and physical properties in 2D layered semiconductors. The high and uniform effective piezoelectric constant covering a wide thickness range suggests the promising application in ferroelectric information storage/processing and self-driving high-speed photonic devices made of InSe narrow-gap semiconductor with a thickness from bilayer to bulk-like states.
Methods
Sample growth and transfer
Samples involved in this work are pure InSe and InSe:Y. The growth environment and process of both single crystals are the same with the Bridgman method26,28. The small particles of high-purity In (99.999%) and Se (99.999%) are mixed in a closed quartz ampoule with a non-stoichiometric ratio In:Se = 0.52:0.48, and the vacuum degree is 10−3 Torr. The material is melted in the high temperature zone (~700 °C), single crystals are grown in the temperature gradient zone (10–15 °C/cm), and crystal annealing is mainly carried out in the low temperature zone (300–550 °C). For the preparation of InSe:Y, 1 at% Y is mixed with In to form In:Y alloy first. The rest of the synthesis steps is the same.
InSe and InSe:Y flakes for SHG and PFM analyses are prepared by employing a scotch-tape mechanical exfoliation method. The thickness and surface morphology of the flakes are characterized by AFM (Multimode 8, Bruker, USA).
Structural characterization
The morphology and composition measurements are performed on the Zeiss Gemini 450 equipped with an EDS (Ultim Extreme, Oxford, UK). XRD patterns are obtained on the Bruker D8 Discover (Germany) with a monochromatic Cu Kα radiation source (λ = 0.15406 nm). The X-ray profiles are recorded in θ–2θ scan mode with 2θ∈(10°, 80°). Cross-section TEM specimens are prepared by dual-beam FIB system (Helios G4 UX, FEI, USA) using Ga-ion accelerating voltage ranging from 2 to 30 kV, followed by ion-milling (Gatan 691, Gatan, USA) operated at 2 kV to remove the residual amorphous layer. TEM images and EDS analysis are acquired at 200 kV using a JEM-2100F JEOL equipped with an Oxford EDS detector (X-Max 80 T, Oxford, UK). Atomic-resolution imaging measurements are performed on an aberration-corrected HAADF STEM (AC-HAADF-STEM) (JEOL Grand ARM300, Japan) equipped with JEOL dual 158 mm2 SDD detectors for atomic level EDS analysis. To improve the signal-to-noise ratio and minimize the drift or distortion of AC-HAADF-STEM images, six serial frames are acquired with a short dwell time (2 μs·pixel−1). The image series are aligned and superimposed.
Chemical composition analysis
TOF-SIMS analysis is carried out on ION-TOF GmbH TOF SIMS 5 (Germany) with detection limit at ppm ~ ppb level, lateral resolution <70 nm, depth resolution <1 nm. The AXIS Ultra DLD (Shimadzu Kratos, Japan) multifunctional X-ray photoelectron spectroscopy provides the chemical information of InSe:Y.
PFM measurement
PFM measurements at the dual amplitude resonance tracking (DART) mode are performed on a commercial scanning probe microscopy (SPM) system (Asylum Research Cypher, Oxford, UK) with conductive Pt-coated silicon cantilevers. A soft tip with a spring constant of 2.8 N m−1 was driven with an AC voltage (Vac = 0.5 V) under the tip-sample contact resonant frequency (~350 kHz). PFM analysis at low frequency under non-resonant mode for the same typical flakes were carried out on Multimode 8 AFM (Bruker, USA).
The LithoPFM mode of the Asylum Research software is used for permanent domain writing of InSe:Y flake’s surface, where the PFM tip carries reverse DC biases (Vdc = ±5 V) when moving in contact mode across the surface.
Derivation of the effective piezoelectric constant d
To quantitatively obtain the piezoelectric information, the contact resonance of the probe can be reduced to a Simple Harmonic Oscillator (SHO) model using IGOR Pro (Asylum Research). The inverse of the optical lever sensitivity (InvOLS) of the probe is calibrated before the experiment to convert the voltage to displacement. During PFM measurements, the experimental parameters used for InSe:Y were Vac = 0.5 V, and the range interval of Vdc is continuously increased from –3~3 V to –7~7 V. The effective piezoelectric constant d in the weak-indentation limit satisfies the relation with d33, d = 0.5d33.
In PFM experiments, the amplitude of the probe can be expressed as below if the sample is polarized in the vertical direction,
| 1 |
where Atip is the vertical amplitude of the probe, As is the vertical amplitude of the sample surface due to the piezoelectric effect, Vac is the amplitude of the AC voltage applied on the probe (Drive Amplitude), C is a factor related to the drive frequency, and is the effective piezoelectric coefficient related to the polarization state of the material.
The spatially-resolved piezoelectric coefficient is found to be stable with a uniform value of ~14.1 pm/V for the thickness of 14 nm (~5 unit cells) InSe:Y, and slightly decreased to ~4.04 pm/V as the thickness increases to 120 nm (~48 unit cells); see Supplementary Table S1. Notice that the flakes are easy to be destroyed under the role of voltage when the thickness is further decreased, possibly due to the voltage-induced thermal effect.
Optical characterization
Raman spectra are recorded on a Renishaw inVia confocal Raman microscope equipped an excitation wavelength of 532 nm and a ×100 objective (NA = 0.85), which provides a spectral resolution of higher than 0.5 cm−1 and a spatial resolution of less than 0.5 μm. Parallel and perpendicular polarization geometries are configured, and the polarization angle can be controlled continuously by rotating either the polarizer or the sample. The laser intensity is set at ~1 mW/cm2 order of magnitude to avoid the excitation-induced thermal effect.
SHG measurements are performed at room temperature using a confocal microscope setup in reflection geometry. A mode locked Ti: sapphire laser (Tsunami) at 800 nm (pulse width 100 fs, repetition frequency 80 MHz) is used as the excitation source. The collimated laser beam is passed through a Glan Thompson polarizer (GTH10M-AM-A, Thorlabs) followed by a wave plate (AQWP05M-600, Thorlabs), which is focused by a ×50 objective lens (Zeiss, 0.75 NA) onto the sample after passing through a beam splitter (CCM1-BS013/M, Thorlabs). The SHG signal is collected by the same objective and directed through a dichroic beam splitter to a spectrometer equipped with a 300 grooves/mm grating and a nitrogen-cooled silicon charge-coupled device.
A Fourier transform infrared spectrometer (Vertex 80 v, Bruker) covering a wavelength range of ~0.4 − 15 µm is employed for optical transmission and reflectance measurements. TR-PL measurements are implemented with a reflectance geometric configuration. The Tsunami Ti: sapphire laser described in SHG measurements is used as the excitation source. The signal is recorded by a Hamamatsu synchroscan streak camera with an S1 photocathode (temporal resolution better than 10 ps). Low pulsed excitation densities of ∼μJ/cm−2 are ensured to avoid the excitation-induced thermal or extrinsic effects. For temperature-dependent measurements, the sample is mounted on the cold head of a circling cryogenerator, which allows for the temperature changing from 4 K to ambient temperature.
DFT calculations
The first-principles calculations of structural optimization and electronic structure are performed using the DFT as implemented in the Vienna ab initio simulation package (VASP) code. The projector augmented-wave (PAW) pseudopotentials with an energy cutoff of 450 eV for the planewave basis set are employed. For the structural optimization, the Perdew–Burkes–Ernzerhof (PBE) form of the generalized gradient approximation (GGA) to the exchange-correlation functional is used. All lattice vectors and atomic positions are relaxed until the total force on each atom is lower than 0.01 eV Å−1. The electronic structures are determined using the HSE06 hybrid exchange-correlation functional so that the Eg matches the experimental value. A 12-atom primitive cell together with 7 × 7 × 1 k-point mesh is employed for band structure of the pure crystal, whereas a 144-atom supercell and 3 × 3 × 1 k-point mesh were used for the Y-doped system. Using HSE06, γ-InSe is determined to have a 1.209 eV direct Eg located at the high symmetric A point (Fig. 2f). To study the effect of Y-doping, we construct a supercell containing 144 atoms, and replace one In atom with Y. The ratio is 1/144, which is close to the experimental doping concentration. We comparatively calculate the electronic band structures of the Y-doped and pristine supercell. Due to the large computational cost, we only calculate the band along Γ-A-H (Fig. 2g, h). While keeping the direct Eg at A, the Y-doping makes the Eg blueshift to 1.232 eV.
Supplementary information
Acknowledgements
We thank Dr. Jens W. Tomm from Max-Born-Institut für Nichtlineare Optik und Kurzzeitspektroskopie, Berlin for the fruitful discussions regarding the TR-PL results, and Prof. Xiao Wang from Hunan University, China for SHG measurements. F.Y. acknowledges partial support from the National Key Research Project (grant 2022YFA1402902), the National Natural Science Foundation of China (NSFC) (grants 12134003, 62274061, 61874043, 61790583), and the Innovation Foundation of Central University. R.Q. and R.H. acknowledge support from the NSFC (grant 61974042). M.J. acknowledges supports from the NSFC (grant 52272006) and the Shuguang Program by the Shanghai Education Development Foundation and Shanghai Municipal Education Commission. Y.W. acknowledges the Program for Professor of Special Appointment (Eastern Scholar) grant TP2019019 and the NSFC (grant 12204170).
Author contributions
R.Q. and F.Y. conceived this project. M.J. and F.S. prepared the samples. F.S., Y.Z., R.Q. and R.H. conducted the investigations and characterizations. Y.W. performed the DFT calculations. F.S., R.Q. and F.Y. analyzed the data. F.S. and R.Q. drafted the original manuscript. R.Q., F.Y. and J.C. reviewed and edited the manuscript with contributions from all authors.
Peer review
Peer review information
Nature Communications thanks Shunbo Hu, Menghao Wu and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Data availability
The data supporting the findings of this work are included within the paper and its Supplementary Information files. Extra data are available from the corresponding authors upon reasonable request.
Code availability
The codes used to process and analyze the data presented in this work are available from the corresponding author upon request.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Ruijuan Qi, Email: rjqi@ee.ecnu.edu.cn.
Fangyu Yue, Email: fyyue@ee.ecnu.edu.cn.
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-022-35490-0.
References
- 1.Qi L, Ruan S, Zeng YJ. Review on recent developments in 2D ferroelectrics: theories and applications. Adv. Mater. 2021;33:e2005098. doi: 10.1002/adma.202005098. [DOI] [PubMed] [Google Scholar]
- 2.Wu M. Two-dimensional van der Waals ferroelectrics: scientific and technological opportunities. ACS Nano. 2021;15:9229–9237. doi: 10.1021/acsnano.0c08483. [DOI] [PubMed] [Google Scholar]
- 3.Huang J, et al. On-demand quantum spin Hall insulators controlled by two-dimensional ferroelectricity. Mater. Horiz. 2022;9:1440–1447. doi: 10.1039/D2MH00334A. [DOI] [PubMed] [Google Scholar]
- 4.Tong WY, Gong SJ, Wan X, Duan CG. Concepts of ferrovalley material and anomalous valley Hall effect. Nat. Commun. 2016;7:13612. doi: 10.1038/ncomms13612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Shirodkar SN, Waghmare UV. Emergence of ferroelectricity at a metal-semiconductor transition in a 1T monolayer of MoS2. Phys. Rev. Lett. 2014;112:157601. doi: 10.1103/PhysRevLett.112.157601. [DOI] [PubMed] [Google Scholar]
- 6.Ding W, et al. Prediction of intrinsic two-dimensional ferroelectrics in In2Se3 and other III2-VI3 van der Waals materials. Nat. Commun. 2017;8:14956. doi: 10.1038/ncomms14956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Liu F, et al. Room-temperature ferroelectricity in CuInP2S6 ultrathin flakes. Nat. Commun. 2016;7:12357. doi: 10.1038/ncomms12357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Fei R, Kang W, Yang L. Ferroelectricity and phase transitions in monolayer group-IV monochalcogenides. Phys. Rev. Lett. 2016;117:097601. doi: 10.1103/PhysRevLett.117.097601. [DOI] [PubMed] [Google Scholar]
- 9.Vizner Stern M, et al. Interfacial ferroelectricity by van der Waals sliding. Science. 2021;372:1462–1466. doi: 10.1126/science.abe8177. [DOI] [PubMed] [Google Scholar]
- 10.Zheng Z, et al. Unconventional ferroelectricity in moire heterostructures. Nature. 2020;588:71–76. doi: 10.1038/s41586-020-2970-9. [DOI] [PubMed] [Google Scholar]
- 11.Miao LP, et al. Direct observation of geometric and sliding ferroelectricity in an amphidynamic crystal. Nat. Mater. 2022;21:1158–1164. doi: 10.1038/s41563-022-01322-1. [DOI] [PubMed] [Google Scholar]
- 12.Xu B, Deng J, Ding X, Sun J, Liu JZ. Van der Waals force-induced intralayer ferroelectric-to-antiferroelectric transition via interlayer sliding in bilayer group-IV monochalcogenides. npj Comput. Mater. 2022;8:47. doi: 10.1038/s41524-022-00724-8. [DOI] [Google Scholar]
- 13.Wu M, Li J. Sliding ferroelectricity in 2D van der Waals materials: Related physics and future opportunities. Proc. Natl Acad. Sci. USA. 2021;118:e2115703118. doi: 10.1073/pnas.2115703118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Li L, Wu M. Binary compound bilayer and multilayer with vertical polarizations: two-dimensional ferroelectrics, multiferroics, and nanogenerators. ACS Nano. 2017;11:6382–6388. doi: 10.1021/acsnano.7b02756. [DOI] [PubMed] [Google Scholar]
- 15.Yasuda K, Wang X, Watanabe K, Taniguchi T, Jarillo-Herrero P. Stacking-engineered ferroelectricity in bilayer boron nitride. Science. 2021;372:1458–1462. doi: 10.1126/science.abd3230. [DOI] [PubMed] [Google Scholar]
- 16.Rogée L, et al. Ferroelectricity in untwisted heterobilayers of transition metal dichalcogenides. Science. 2022;376:973–978. doi: 10.1126/science.abm5734. [DOI] [PubMed] [Google Scholar]
- 17.Wang X, et al. Interfacial ferroelectricity in rhombohedral-stacked bilayer transition metal dichalcogenides. Nat. Nanotech. 2022;17:367–371. doi: 10.1038/s41565-021-01059-z. [DOI] [PubMed] [Google Scholar]
- 18.Weston A, et al. Interfacial ferroelectricity in marginally twisted 2D semiconductors. Nat. Nanotech. 2022;17:390–395. doi: 10.1038/s41565-022-01072-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Zheng B, et al. Rare-earth doping in nanostructured inorganic materials. Chem. Rev. 2022;122:5519–5603. doi: 10.1021/acs.chemrev.1c00644. [DOI] [PubMed] [Google Scholar]
- 20.Bousquet E, et al. Improper ferroelectricity in perovskite oxide artificial superlattices. Nature. 2008;452:732–736. doi: 10.1038/nature06817. [DOI] [PubMed] [Google Scholar]
- 21.Xu X, et al. Kinetically stabilized ferroelectricity in bulk single-crystalline HfO2:Y. Nat. Mater. 2021;20:826–832. doi: 10.1038/s41563-020-00897-x. [DOI] [PubMed] [Google Scholar]
- 22.Yun Y, et al. Intrinsic ferroelectricity in Y-doped HfO2 thin films. Nat. Mater. 2022;21:903–909. doi: 10.1038/s41563-022-01282-6. [DOI] [PubMed] [Google Scholar]
- 23.Bandurin DA, et al. High electron mobility, quantum Hall effect and anomalous optical response in atomically thin InSe. Nat. Nanotech. 2017;12:223–227. doi: 10.1038/nnano.2016.242. [DOI] [PubMed] [Google Scholar]
- 24.Dai M, et al. Robust piezo-phototronic effect in multilayer γ-InSe for high-performance self-powered flexible photodetectors. ACS Nano. 2019;13:7291–7299. doi: 10.1021/acsnano.9b03278. [DOI] [PubMed] [Google Scholar]
- 25.Hopkinson DG, et al. Formation and healing of defects in atomically thin GaSe and InSe. ACS Nano. 2019;13:5112–5123. doi: 10.1021/acsnano.8b08253. [DOI] [PubMed] [Google Scholar]
- 26.Wei TR, et al. Exceptional plasticity in the bulk single-crystalline van der Waals semiconductor InSe. Science. 2020;369:542–545. doi: 10.1126/science.aba9778. [DOI] [PubMed] [Google Scholar]
- 27.Molas MR, et al. Raman spectroscopy of GaSe and InSe post-transition metal chalcogenides layers. Faraday Discuss. 2021;227:163–170. doi: 10.1039/D0FD00007H. [DOI] [PubMed] [Google Scholar]
- 28.Zhang B, et al. Super deformability and thermalelectricity of bulk γ-InSe single crystals. Chin. Phys. B. 2021;30:078101. doi: 10.1088/1674-1056/abf133. [DOI] [Google Scholar]
- 29.Segura A, Pomer F, Cantarero A, Krause W, Chevy A. Electron scattering mechanisms in n-type indium selenide. Phys. Rev. B. 1984;29:5708–5717. doi: 10.1103/PhysRevB.29.5708. [DOI] [Google Scholar]
- 30.Rudenko AN, Katsnelson MI, Gornostyrev YN. Dislocation structure and mobility in the layered semiconductor InSe: a first-principles study. 2D Mater. 2021;8:045028. doi: 10.1088/2053-1583/ac207b. [DOI] [Google Scholar]
- 31.Tauc J, Grigorovici R, Vancu A. Optical properties and electronic structure of amorphous germanium. phys. stat. sol. 1966;15:627. doi: 10.1002/pssb.19660150224. [DOI] [Google Scholar]
- 32.Andersen TI, et al. Excitons in a reconstructed moiré potential in twisted WSe2/WSe2 homobilayers. Nat. Mater. 2021;20:480–487. doi: 10.1038/s41563-020-00873-5. [DOI] [PubMed] [Google Scholar]
- 33.Sung J, et al. Broken mirror symmetry in excitonic response of reconstructed domains in twisted MoSe2/MoSe2 bilayers. Nat. Nanotech. 2020;15:750–754. doi: 10.1038/s41565-020-0728-z. [DOI] [PubMed] [Google Scholar]
- 34.Gomes da Costa P, Dandrea RG, Wallis RF, Balkanski M. First-principles study of the electronic structure of γ-InSe and β-InSe. Phys. Rev. B. 1993;48:14135–14141. doi: 10.1103/PhysRevB.48.14135. [DOI] [PubMed] [Google Scholar]
- 35.Kim B, Seol D, Lee S, Lee HN, Kim Y. Ferroelectric-like hysteresis loop originated from non-ferroelectric effects. Appl. Phys. Lett. 2016;109:102901. doi: 10.1063/1.4962387. [DOI] [Google Scholar]
- 36.Xue F, et al. Multidirection piezoelectricity in mono- and multilayered hexagonal α-In2Se3. ACS Nano. 2018;12:4976–4983. doi: 10.1021/acsnano.8b02152. [DOI] [PubMed] [Google Scholar]
- 37.Wang X, et al. Probing effective out-of-plane piezoelectricity in van der Waals layered materials induced by flexoelectricity. Small. 2019;15:e1904116. doi: 10.1002/smll.201903106. [DOI] [PubMed] [Google Scholar]
- 38.Zhang Q, Zhang LY, Jin CH, Wang YM, Lin F. CalAtom: A software for quantitatively analysing atomic columns in a transmission electron microscope image. Ultramicroscopy. 2019;202:114–120. doi: 10.1016/j.ultramic.2019.04.007. [DOI] [PubMed] [Google Scholar]
- 39.Fei Z, et al. Ferroelectric switching of a two-dimensional metal. Nature. 2018;560:336–339. doi: 10.1038/s41586-018-0336-3. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data supporting the findings of this work are included within the paper and its Supplementary Information files. Extra data are available from the corresponding authors upon reasonable request.
The codes used to process and analyze the data presented in this work are available from the corresponding author upon request.