Abstract
Background:
Positively charged drug carriers are rapidly emerging as a viable solution for long-standing challenges in delivery to dense, avascular, negatively charged tissues. These cationic carriers have demonstrated especially strong promise in targeting drugs to articular cartilage for osteoarthritis (OA) treatment. It is critical to evaluate the dose-dependent effects of their high intratissue uptake levels on charge-shielding of anionic matrix constituents, and the resulting changes in tissue osmotic swelling and mechanical integrity.
Materials and Methods:
We use the ideal Donnan osmotic theory to derive a model for predicting intracartilage swelling pressures as a function of net charge (z) and equilibrium uptake of short-length, arginine-rich, multivalent, cationic peptide carriers (cationic peptide carriers [CPCs], z varied from +8 to +20) in cartilage samples with varying arthritic severities and fixed charge density (FCD). We use this model to determine the dose-dependent influence of CPCs on both physiological osmotic swelling pressures and compressive electrostatic moduli of cartilage in healthy and arthritic states.
Results:
Under physiological conditions, the Donnan model predicted carrier-induced reductions in free swelling pressure between 8 and 29 kPa, and diminished compressive modulus by 20–68 kPa, both dependent on the net charge and uptake of CPCs. The magnitudes of deswelling and stiffness reduction increased monotonically with carrier uptake and net charge. Furthermore, predicted levels of deswelling by CPC charge shielding were amplified in tissues with reduced FCD (which model OA). Finally, the Donnan model predicted markedly higher reductions in tissue compressive modulus in hypotonic bathing salinity compared with physiological and hypertonic conditions.
Conclusion:
This analysis demonstrates the importance of considering charge shielding as a likely adverse effect associated with uptake of cationic drug carriers into negatively charged tissues, especially in the case of damaged tissue. The simple modeling approach and principles described herein can inform the design of cationic drug delivery carriers and their clinical treatment regimens.
Keywords: Donnan osmotic modeling, charge-based delivery, cationic carriers, articular cartilage, tissue swelling, osteoarthritis
Introduction
Many tissues in the human body that are sites of common diseases are composed of negatively charged matrix entities, which renders drug delivery to cellular targets deep within these tissues extremely challenging.1 Examples include musculoskeletal tissues in joints, the intervertebral disc of the spine, and the vitreous humor of the eye, which are all sites of painful, debilitating degenerative diseases that affect millions of people worldwide. As a promising solution, recent advancements have harnessed the intrinsic bioelectrical activity of these tissues for drug delivery by using rationally designed cationic drug carriers, which can passively target the negatively charged matrix barrier.2,3 These carriers rely on Coulombic attractions with matrix constituents, which drive high upward Donnan partitioning at the tissue interface, setting up a steep inward concentration gradient that enhances intratissue transport.4 Carriers designed with optimal charge can facilitate the weak, reversible, electrostatic binding interactions necessary to enable rapid, full-thickness penetration through the tissue to reach deep zone cellular targets, with retention times on the order of days to weeks.5–7 A multitude of positively charged delivery systems have proven successful in targeting a variety of charged tissues such as cartilage,3,8–10 gastrointestinal mucus,1,11,12 the intervertebral disc,7 the tumor microenvironment,13 and the eye,14,15 and there is significant interest in their preclinical development and clinical translation.1–3 As the application of cationic macromolecules gains traction, it is also important to evaluate the effects of their net charge and dosing on the target tissue's electromechanochemical and biological properties,2 which can have strong implications for the design of future modalities.
Recent efforts have addressed the long-standing challenge of delivering drugs into cartilage tissue in articulating joints by designing cationic delivery systems for osteoarthritis (OA) treatments.3,4,16 Promising disease-modifying therapies for OA such as glucocorticoids,17 small-molecule glycation inhibitors,18 and proanabolic growth factors19 have been successful in preclinical trials. However, their clinical translation has been limited because of the difficulty for drugs to diffuse through the full thickness of cartilage and reach cellular targets following an intra-articular (IA) injection. Cartilage comprises a low density of chondrocytes surrounded by a dense, avascular, and aneural meshwork of collagen II and aggrecan proteoglycans, which contain negatively charged glycosaminoglycan (GAG) side chains.1,20 Cartilage GAGs have an abundance of ionizable chondroitin sulfate and keratan sulfate groups that are deprotonated at physiological pH, which impart the tissue with a high negative fixed charge density (FCD). Importantly, not only do the small (∼10 nm) effective pore size and negative FCD of the extracellular matrix (ECM) present significant steric and Coulombic resistance to drug or drug carrier diffusion, but therapeutics are also susceptible to rapid clearance from the joint space by the synovial fluid following IA injection.4
In light of these challenges, the highly anionic FCD of cartilage is becoming increasingly recognized as an opportunity for drug delivery rather than a barrier, which has been leveraged by rationally designing cationic drug carriers that electrostatically target matrix GAGs. A variety of cartilage-targeting cationic carriers have been proposed including protein-,8,21,22 peptide-,5,23 polymer-,9,24 and antibody-25 based modalities, which have exhibited excellent ability to penetrate the full thickness of cartilage in vitro and in vivo.26 Such delivery systems have enabled intratissue uptake concentrations up to two orders of magnitude higher than the surrounding fluid.5,6
Although studies in cartilage have given attention to off-target27,28 and cytotoxic29 side effects of cationic carriers, the effect of high intratissue concentrations of polyvalent cationic molecules on tissue mechanical properties has received little consideration.30 A core function of cartilage in joints is to withstand compressive loads as a shock absorber between bones, and a significant component of the tissue's compressive strength derives directly from its negative FCD.31 In fact, experimental evidence suggests that 62% of the tissue's compressive modulus arises from like-charge repulsions between neighboring GAGs.32 Moreover, the fluid-withdrawing properties of proteoglycans generate a high Donnan osmotic swelling pressure within the tissue; even at rest, the tissue is prestressed as proteoglycan swelling forces exist in equilibrium with tensile resistance from collagen fibers.33 Intracartilage charge shielding is a well-studied phenomenon by which high interstitial concentrations of small counterions (Na+) mask the negative FCD of the tissue when immersed in a hypertonic environment, which can cause significant deswelling.34 We hypothesize that a similar effect may occur in cartilage (and other negatively charged tissues) treated with high concentrations of cationic drug carriers, which could affect the tissue's ability to withstand physiological loads.30 This effect could be particularly severe in mid- to late-stage arthritic cartilage, in which the mechanical integrity of the tissue is already diminished due to proteoglycan loss.35
The goal of this study was to apply Donnan osmotic theory to predict the effects of charge shielding by multivalent cationic macromolecules on the equilibrium swelling properties and mechanical stiffness of cartilage tissue. Using previously published uptake data on short-length, arginine-rich cationic peptide carriers (CPCs) of varying net charges (as an example multivalent, macromolecular drug carrier),5 we describe a modeling approach that incorporates the cationic charge of CPCs into the electroneutrality of the tissue FCD and mobile counterions. We implement this classical ideal Donnan model to predict CPC-induced deswelling, and report estimates for the magnitudes of swelling pressure expected from empirically observed levels of CPC uptake into cartilage. Furthermore, we use this model to investigate the dependence of osmotic swelling on intratissue CPC concentration and net charge, and to predict swelling and stiffness following CPC uptake into GAG-depleted cartilage mimicking mid- and late-stage OA. Finally, we apply the model to estimate the change in the electrostatic contribution to the tissue's compressive bulk modulus expected to result from CPC charge shielding. The results demonstrate the necessity for considering potential adverse effects to tissue electromechanochemical homeostasis when designing cationic drug carriers. We expect that this simple modeling approach may be used by future investigators in conjunction with empirical mechanical measurements to inform design and clinical recommendations for cationic drug carriers targeting a variety of anionic tissues.
Materials and Methods
Defining carrier-induced charge shielding in cartilage
Charge shielding by counterions within cartilage is a well-characterized phenomenon that underlies the dependence of the tissue's osmotic swelling pressure on its ionic environment.34,36 At the nanoscale under the Poisson–Boltzmann (PB) framework, swelling pressure results from like-charge repulsions between neighboring GAG chains: since the inter-GAG distance is on the order of the estimated Debye length (∼0.8 nm) of the polyelectrolyte chain, there is a steep drop in electric potential between neighboring molecules, causing coulombic repulsive forces.37,38 As an alternative view at the macroscale, an imbalance in mobile ion (i.e., NaCl) concentrations arises between the tissue and the surrounding bath due to Donnan partitioning, in which Na+ counterions enter the tissue to maintain electroneutrality against the negative FCD; a higher ionic concentration within the tissue compared with the surrounding bath induces fluid absorption and tissue swelling. With higher surrounding ionic strengths, an increased concentration of counterions within the tissue masks Coulombic repulsive forces between GAG chains, causing lower swelling pressure. This effect of charge shielding has been extensively observed in articular cartilage in hypertonic salt environments.34,39–41 All research presented herein was conducted in accordance with the Declaration of Helsinki as revised in 2013.
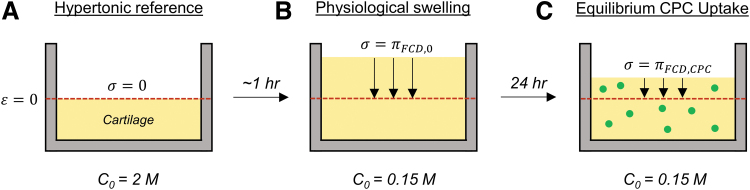
We hypothesize that a similar charge shielding effect may occur in cartilage and other negative tissues following absorption of cationic drug carriers. Intuitively, the phenomenon modeled herein can be best described using the concept of concentration-dependent chemical stress,34 first defined by Eisenberg and Grodzinsky as follows. When a tissue sample is equilibrated in a hypertonic bath with sufficient ionic strength to entirely shield the FCD, the Donnan osmotic pressure within the tissue reduces to zero, and the sample deswells to a zero-strain reference thickness supported only by the solid matrix (Fig. 1A). Subsequently, if this tissue were then equilibrated in a more hypotonic solution (e.g., physiological salinity), it would freely swell to a new thickness by purely charged-based osmotic forces (Fig. 1B). The physiological chemical stress is then defined as the compressive stress required to return the tissue back to the hypertonic reference thickness of zero solid matrix strain. This stress thus represents the free osmotic swelling pressure within the tissue under physiological salinity, which we refer to herein as the baseline swelling stress . Now, if this process were repeated with the same tissue except that it has been pre-equilibrated with high interstitial concentrations of a multivalent cationic macromolecule, such as a CPC (Fig. 1C), we expect the tissue's chemical stress under the same physiological conditions to be less than baseline (). This is because the capacity for the tissue to swell under physiological conditions has been diminished by cationic charge shielding. The magnitude of this change in chemical stress is precisely what this study aims to theoretically predict.
FIG. 1.
Illustration of charge shielding by multivalent CPCs, defined as a reduction in the physiological chemical stress of the tissue. (A) Cartilage immersed in a hypertonic bath will deswell to a zero-strain reference thickness, representing zero osmotic pressure within the tissue. (B) Moving the tissue to physiological salinity will result in tissue swelling, and the force required to compress the tissue back to the hypertonic reference thickness is the tissue's free osmotic swelling pressure. (C) The same tissue pre-equilibrated in CPC will require less force to compress back to reference thickness, representing a reduced capacity for physiological swelling due to charge shielding by the cationic carrier. Red dashed line is the hypertonic reference thickness; black downward arrows represent compressive force; green circles are CPCs. CPCs, cationic peptide carriers.
Modeling assumptions
Here we modeled deswelling induced by CPCs as a representative class of multivalent, cationic drug carrier molecules, which consist of a 3 kDa, ∼20 amino acid sequence of arginine and alanine residues.5 The uptake and transport properties of CPCs in bovine cartilage have been studied previously by our group, and we have chosen these macromolecules for this study because of their high intracartilage uptake and suitability for independently investigating effects of net charge. As shown in Table 1, CPC variants have been designed to be similar in size with positively charged groups distributed symmetrically along the peptide length, such that effects of net charge can be studied separately from other confounding variables such as size and spatial charge distribution. As such, this study exclusively considered the effects of the cationic carrier's charge on cartilage mechanics. Polypeptides and other carriers with polyvalent cationic charge distributed along their length are expected to interact extensively with macromolecular constituents of the solid matrix of cartilage.42 In the case of arginine-rich CPCs, long-range Coulombic interactions as well as short-range hydrogen bonding by guanidinium groups and hydrophobic attractions (due to the presence of alanine spacers) all are likely to facilitate binding to the solid matrix,5 which could alter matrix mechanical properties and interstitial fluid dynamics. In light of these complicating effects, we sought to independently model charge shielding by disregarding the spatial charge distribution and polyelectrolyte character of CPC molecules, the effects of which were assumed to be equal for each CPC variant. Thus, this study only considered the amount of counter-charge introduced into the tissue by different CPCs.
Table 1.
Cationic Peptide Carrier Net Charge, Sequence, and Size
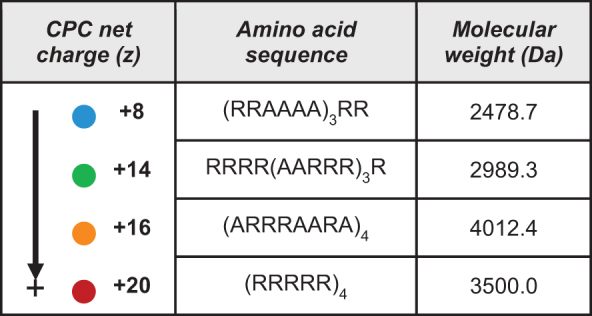
|
CPC, cationic peptide carrier.
Given the lack of experimental data characterizing the microscale interactions of CPC macromolecules with GAGs and their spatial orientation in the brush network, we chose to use a macroscale Donnan model under the fundamental assumption of a uniformly charged polyelectrolyte phase with no molecular-level variation in electrostatic potential.37 The cartilage tissue was assumed to be an isotropic, triphasic mixture comprising a charged solid matrix, a neutral fluid, and monovalent mobile Na+ and Cl− ions.43 Importantly, CPC peptides were assumed to be homogenously distributed throughout the tissue GAG network, such that there is no spatial inhomogeneity in the amount of charge shielding each CPC molecule induces. Only equilibrium uptake conditions (for both CPC and Na+/Cl− ions) were considered; transient solute diffusivities and fluid flow dynamics were omitted. Furthermore, once bound at equilibrium, CPC was considered static, and transient, intratissue CPC mobility was neglected (i.e., the intratissue concentration was assumed to be constant regardless of the surrounding [NaCl]). Thus, we have effectively modeled direct charge shielding of the proteoglycan FCD as resulting from an equivalent amount of moles-charge introduced by the valency of the intratissue CPCs.
Derivation of the Donnan osmotic model
In applying the macroscale Donnan osmotic theory,37 we first define the intratissue electroneutrality condition, incorporating the cationic charge of CPC:
| (1) |
where is defined as the moles of ECM-associated charge normalized to interstitial fluid volume (mEq/L), which is a negative value, z is the net charge of a CPC molecule, and is the intratissue concentration of species X. Furthermore, assuming negligible change in the surrounding bath ion concentrations after ion redistribution, the classical Donnan condition for mobile ion partitioning44 can be defined as follows:
| (2) |
where C0 is the concentration of NaCl in the bulk external fluid. In this system, can be measured using standard biochemical assays (see the Experimental Model Parameters section below); the net charge and uptake of the CPC molecule of interest can be measured experimentally5,45; and the external bath concentration is assumed to be physiological (150 mM). Given constraints (1) and (2) with and being the only two unknowns, the system may be solved to obtain expressions for the intratissue Na+ and Cl− ion concentrations as a function of CPC charge/concentration and tissue FCD. A general expression for the intratissue osmotic swelling pressure relative to the surrounding bath, , can then be obtained using the van't Hoff relation, simplified to the following:
| (3) |
where R is the universal gas constant, T is absolute temperature (310.15 K), and is the osmotic coefficient for mobile ions within the tissue. Importantly, in accordance with previous studies,37,40 we have applied the simplifying assumption that the osmotic and activity coefficients of mobile ions inside and outside of the tissue are effectively equal. By assuming ideal osmotic behavior, in Equation (3) and the ideal Donnan osmotic model is obtained.
Estimating the electrostatic contribution to bulk compressive modulus
The compressive modulus of cartilage can be expressed as the sum of the contributions arising from (1) electrostatic repulsive forces between GAG chains () and (2) nonelectrostatic mechanical integrity and configurational entropy of the solid matrix components ()32:
| (4) |
Here, can be interpreted as the compressive modulus of the tissue in hypertonic conditions ( = 0). In addition to free swelling stress, the electrostatic modulus component can also be estimated using the Donnan osmotic model as previously described.37 The FCD of the tissue and CPC concentration can be expressed as a function of tissue strain according to testing geometry. Assuming confined compression:
| (5) |
The swelling pressure can then be evaluated at multiple strain levels (here, 0.1 and 0.2) using Equation (3), and the relationship between incremental stress and strain yields the electrostatic modulus component:
| (6) |
Experimental model parameters
The FCD of the modeled cartilage tissue was calculated from previous measurements of sulfated GAG in the bovine cartilage explants used in CPC uptake experiments.45 An average value of 280.5 μg of sulfated GAG was observed for 3-mm-diameter, full-thickness cartilage plugs from young bovine femoral grooves, as measured by dimethylmethylene blue (DMMB) biochemical assay.5,46 This was used as a representative value to estimate the FCD of healthy cartilage, using the following relation31:
| (7) |
where is the measured mass of GAG, which is multiplied by −2 mol-charge for chondroitin sulfate, is the molecular weight of the chondroitin sulfate standard from DMMB (458 g/mol), and Vf is the intratissue fluid volume, calculated as 6.6 μL for an explant with 8.2 μg wet weight (assuming a fluid volume fraction of 0.8). The FCD for 50% and 90% enzymatically GAG-depleted tissues was also calculated using Equation (7), except was scaled according to GAG loss (measured by DMMB) assuming a GAG content of 280.5 μg before trypsin digestion. Representative average wet weights of 9.1 and 9.3 μg were used for 50% and 90% tissues, respectively, to account for altered fluid retention in these tissues.
Previously reported equilibrium uptake ratios (RU) for CPC variants into healthy and GAG-depleted tissues were used to calculate intratissue CPC concentrations using the following relation:
| (8) |
where C0 is the initial bath CPC concentration (30 μM for these experiments), 0.8 is the fluid volume fraction of the tissue, and RV is the volume ratio between the bath and the tissue, which was set to ∼45 in accordance with the experimental uptake setup (300 μL bath). Equation (8) is derived from the definition .5
Results
The goal of this study was to model the effect of charge shielding by a representative cationic drug carrier, CPCs, on the swelling properties and stiffness of articular cartilage. By applying the macroscale Donnan osmotic theory and incorporating the intratissue cationic charge introduced by CPCs into the electroneutrality condition, we derived a simple expression relating physiological swelling pressure to CPC uptake, net charge, and the FCD of the tissue [Eq. (3)]. This model allowed us to explore the magnitudes of deswelling and reduction in compressive modulus that may be expected from CPC charge shielding, as well as how these magnitudes differ with the carrier's net charge and the FCD of the tissue (as in the case of matrix degeneration with OA).
The ideal Donnan model predicts CPC-induced reductions in free swelling pressure that depend on carrier net charge and uptake concentration
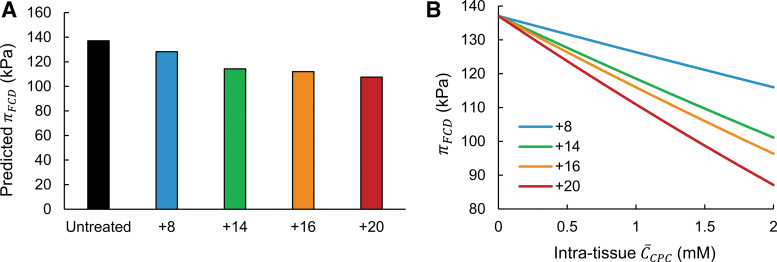
Shown in Figure 2A are the magnitudes of free swelling pressure () in cartilage tissue following an equal 30 μM dose of each CPC net-charge variant, predicted using the ideal Donnan model. Note that weak, reversible electrostatic interactions between CPC molecules and the tissue ECM drive high upward partitioning of the carrier inside the tissue, enabling intratissue CPC concentrations [ in Eq. (3)] several orders of magnitude higher than the external bath treatment dose (e.g., millimolar uptake from a 30 μM bath). In addition, the equilibrium level of intratissue uptake of CPC depends directly on its net charge, so an equal 30 μM external dose of CPCs of different net charge will result in different intratissue uptake concentrations between variants. Here, to calculate , we utilized prior experimental data measuring uptake of CPC variants into bovine articular cartilage explants following 30 μM treatment (uptake ratios provided in Table 2).
FIG. 2.
Magnitudes of articular cartilage swelling following CPC uptake, predicted by the ideal Donnan model. (A) Swelling pressures in tissues equilibrated with CPC net-charge variants, calculated using experimentally observed uptake concentrations in bovine cartilage explants following treatment with an equal 30 μM dose of each variant in the surrounding bath. (B) Predicted swelling pressures for CPC-equilibrated tissues across a range of intratissue concentrations, calculated for each net-charge variant.
Table 2.
Empirical Uptake Ratios (RU) of Cationic Peptide Carriers in Tissue Explants of Varying Fixed Charge Density
| Healthy (100% GAGs) FCD = −0.186 M | Midstage OA (50% GAG-depleted) FCD = −0.084 M | Late-stage OA (90% GAG-depleted) FCD = −0.016 M | |
|---|---|---|---|
| CPC +8 | 55.6 ± 6.8 | 34.8 ± 2.7 | 33.1 ± 0.7 |
| CPC +14 | 366.5 ± 30.3 | 192.3 ± 23.9 | 148.3 ± 18.8 |
| CPC +16 | 258.0 ± 50.8 | 122.4 ± 21.4 | 119.1 ± 4.6 |
| CPC +20 | 181.8 ± 14.2 | 216.7 ± 16.0 | 151.7 ± 21.2 |
Data from Vedadghavami et al.,5 presented as mean ± standard deviation.
FCD, fixed charge density; GAG, glycosaminoglycan; OA, osteoarthritis.
In general, the ideal model predicted swelling pressures on the order of ∼100 kPa, which is in agreement with previously reported calculations with an ideal Donnan model for biomolecular FCD osmotic swelling pressures.47 Notably, these results suggest observable deswelling induced by CPCs: compared with baseline was between −8.8 and −29.6 kPa in healthy tissues, with CPC +20 exhibiting the highest magnitude of deswelling. According to the Donnan model, swelling pressure depends on both CPC net charge and intratissue concentration; as such, CPCs of higher net charge did not necessarily induce substantially higher reductions in swelling pressure. This effect is illustrated by the similar levels of deswelling induced by CPC +14 and +16 despite their difference in net charge (−22.8 and −25.1 kPa, respectively). CPC +14 exhibited the highest uptake out of all the CPC variants (Table 2) due to its optimal charge, which allows weak, reversible binding to matrix GAGs.5 Thus, the relatively low net charge of CPC +14 was balanced by its higher uptake concentration to induce similar predicted deswelling as CPC +16, which has lower uptake.
Next, we used the Donnan model to investigate how cartilage swelling pressure varies in relation to CPC net charge and intratissue concentration. Figure 2B depicts calculated for each CPC variant across a range of theoretical intratissue concentrations (); this range was chosen to be representative of experimentally observed intracartilage molar concentrations of various cationic carriers.5,6 All CPC variants exhibited a monotonic decrease in with increased , as expected, as higher amounts of cationic charged are introduced into the tissue. Also as expected, at comparable , lower swelling pressures were predicted with CPCs of higher net charge, attributable to higher charge shielding per mol-CPC.
The relative effect of deswelling induced by CPC charge shielding is amplified in tissues with reduced FCD
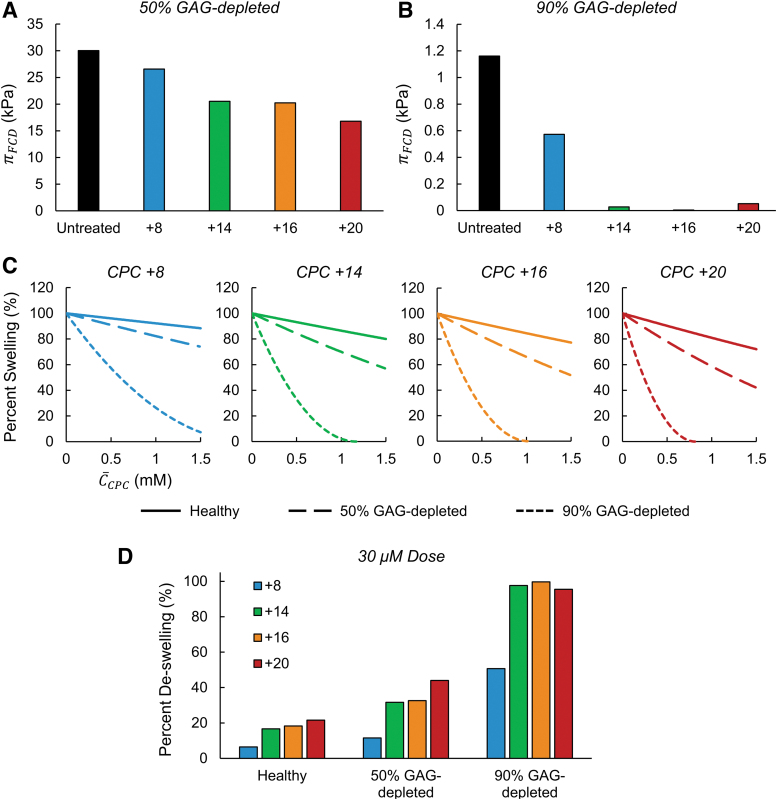
We next considered differences in swelling between cartilage samples with varying levels of FCD. Previous studies have demonstrated that despite severely diminished electrostatic driving forces, CPCs can still penetrate tissues with depleted FCD and bind within due to the synergistic effects of short-range H-bonding (from guanidinium cations of arginine) and hydrophobic interactions (due to the presence of alanine in the sequence).5 For instance, in tissues modeling mid- and late-stage OA (enzymatically GAG-depleted by 50% and 90%, respectively), uptake ratios of CPC +14 were only reduced by half (Table 2). Therefore, we investigated relative between healthy and OA-mimetic tissues, both at baseline and after equilibration with CPCs. Similar to Figure 2A, we used previously measured uptake concentrations of CPC variants in GAG-depleted tissues to calculate swelling pressures with Equation (3) (Fig. 3A, B). The Donnan model predicted significantly lower baseline swelling in GAG-depleted tissues compared with healthy tissues—compared with healthy control, in untreated tissues was diminished by 78.1% and 99.1% for mid- and late-stage OA tissues, respectively. Importantly, the relative deswelling induced by all CPCs in GAG-depleted tissues was considerably amplified, as is evident by CPC +14 through +20 inducing nearly total deswelling in 90% GAG-depleted tissues (Fig. 3B).
FIG. 3.
Relative effects of charge shielding by CPCs in healthy and GAG-depleted (OA model) cartilage. (A, B) Predicted swelling pressures for tissues equilibrated with CPC variants, calculated using experimentally observed uptake concentrations in 50% (A) and 90% (B) GAG-depleted bovine articular cartilage explants. (C) Deswelling induced by CPC variants in healthy and GAG-depleted cartilage over a range of intratissue concentrations. To allow for direct comparison of relative deswelling in tissues of different FCD, values were normalized to the swelling pressure of an untreated sample at the respective FCD level (defined as 100% swelling, with intratissue = 0). (D) Normalized deswelling induced by CPC variants following treatment with an equal 30 μM dose, relative to untreated baseline at the respective FCD level (100% swelling or, alternatively, 0% deswelling). FCD, fixed charge density; GAG, glycosaminoglycan; OA, osteoarthritis.
To directly compare relative deswelling induced by each CPC in tissues of different FCD, we calculated deswelling over a range of intratissue CPC concentrations for each variant (Fig. 3C), in which swelling pressures were normalized using predictions calculated with = 0 for respective FCD levels (i.e., 100% swelling). Figure 3C depicts a clear amplification of the charge shielding effect by equivalent amounts of CPCs in tissues of reduced FCD compared with healthy tissues. For example, whereas CPC +20 induced only up to 28% deswelling in healthy tissues over the concentration range considered, the same concentrations of CPC +20 induced up to 58% deswelling in 50% GAG-depleted tissues, and complete deswelling was predicted at only 0.82 mM in 90% GAG-depleted tissues. Moreover, consistent with the results in healthy tissues (Fig. 2B), deswelling per mol-CPC was higher with increased CPC net charge in GAG-depleted tissues, as shown by curves that drop more rapidly with increased concentration for higher charge CPC variants. The same analysis was performed to compare deswelling between FCD levels based on the in vitro experimental data from a 30 μM external CPC dose, as shown in Figure 3D; these data are expressed as normalized deswelling, with untreated control representing 0% deswelling. Importantly, uptake concentrations resulting from this external dose induced markedly higher deswelling in OA-model tissues: the Donnan model predicted 11.5–44.0% deswelling in 50% GAG-depleted tissues and 50.7–99.7% deswelling in 90% GAG-depleted tissues, compared with <22% deswelling predicted for all CPC variants in healthy cartilage. Overall, these results suggest that charge-shielding by CPC uptake may be amplified in damaged tissue due to a higher relative reduction in effective FCD per mol-CPC, since high levels of uptake are still achieved in GAG-depleted tissues despite their lack of charged matrix macromolecules.
Reductions in the predicted bulk compressive modulus of cartilage caused by CPC charge shielding are magnified at hypotonic salinity
Repulsive forces between neighboring GAG chains increase as they are forced into close proximity due to compressive loads, and thus, electrostatic repulsion contributes to the compressive stiffness of cartilage in addition to affecting the free swelling stress.37 We examined how charge shielding in healthy cartilage might attenuate the tissue's compressive modulus.
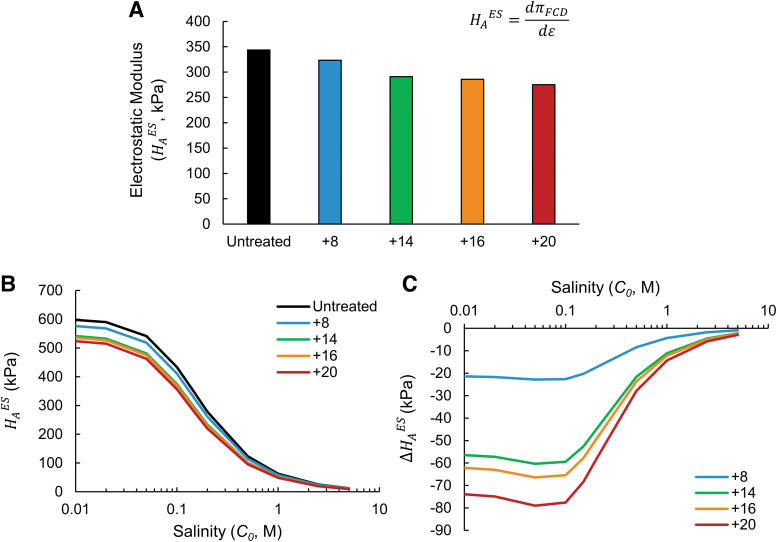
Figure 4 shows estimates for the electrostatic component of the compressive bulk modulus, , following uptake of CPC variants in healthy tissues. As shown in Figure 4A, the Donnan model predicted on the order of ∼300 kPa under physiological salinity, which is consistent with previously estimated magnitudes of the electrostatic modulus component of cartilage using a Donnan model.37 Similar to the trends observed for reductions in free swelling pressure (Fig. 2A), CPC variants were predicted to reduce dependent on both their net charge and uptake concentration, with CPC +20 exhibiting the largest (−68.3 kPa) and CPC's +14 and +16 each inducing similar reductions (−52.6 and −57.8 kPa, respectively). Generally, the magnitudes of predicted reductions in electrostatic compressive modulus were considerable (up to 20% lower following CPC +20 treatment), suggesting that reduced stiffness following CPC uptake due to charge shielding may be an observable effect following intra-articular injection in vivo.
FIG. 4.
Predicted effect of CPCs on the bulk compressive modulus of cartilage tissue and its dependence on bath salinity. (A) Electrostatic component of the compressive modulus () of healthy cartilage following CPC equilibration at physiological salinity. Values were calculated using experimentally observed equilibrium uptake of each CPC variant. (B) Dependence of on surrounding salinity C0, calculated for healthy cartilage holding the intratissue CPC concentration constant. (C) Predicted reduction in induced by CPC variants across a range of bath salt concentrations, compared with of an untreated control tissue at each salinity level.
The dependence of free osmotic swelling and electrostatic modulus on the tissue's surrounding salinity has been studied and characterized extensively.34,44 Given that the response of a tissue's mechanical properties to perturbations in external salinity depends directly on its FCD, we next considered whether cartilage equilibrated with CPCs may exhibit mechanical properties with a different salinity dependence than native tissues. Using constant values for (same uptake concentrations as used for Fig. 4A), we varied C0 in Equation (3) to evaluate the predicted electrostatic modulus component as a function of external bath salinity. As shown in Figure 4B, decreased monotonically with higher salinity under all CPC treatment conditions, approaching 0 kPa at hypertonic salinity (full charge shielding). Consistent with trends at observed physiological salinity (Fig. 4A), CPC +20 exhibited the lowest predicted moduli over this concentration range, indicating the largest effect of charge shielding among the CPC variants. Notably, the absolute magnitude of , calculated compared with untreated control at each respective salinity level, increased dramatically at lower salinities (Fig. 4C): CPCs +14 to +20 exhibited reductions in modulus between −56.5 and −73.9 kPa at 0.01 M NaCl, compared with less than −15 kPa for all CPCs at 1.0 M. This reflects that charge shielding induced by mobile counterions (NaCl) is minimal at lower salinity, in which case electrostatic contributions to swelling and modulus are maximized. Therefore, these results suggest that attenuation of the tissue's compressive modulus by CPC charge shielding may be amplified when stiffness is measured at low salinity.
Discussion
Charge-based delivery is a promising strategy to enable clinical translation of disease-modifying treatments for degenerative conditions of connective tissues, such as OA in articular cartilage.1,4 However, the effect of high-molecular-weight cationic nanocarriers5,8,21,22,25,48 on the electromechanochemical homeostasis of cartilage has received little attention in the development of cationic drug delivery systems.30 In vivo, perturbations to this balance could compromise the tissue's ability to withstand physiological loads, which is crucial to the natural function of cartilage as a shock absorber at joint surfaces. Thus, mechanistic knowledge of the mechanical changes associated with cationic carrier treatment is valuable to inform the design of future carriers.
Here we have performed a theoretical evaluation of the effect of charge shielding by multivalent cationic drug carriers on the mechanical properties of articular cartilage tissue. Using the classical ideal Donnan osmotic theory,37 we have derived a simple expression for estimating the tissue's swelling pressure () as a function of the intratissue concentration and net charge of CPCs. Furthermore, we have extended this model to estimate the changes in the electrostatic component of the tissue's compressive modulus following CPC treatment. Arginine-based CPCs were chosen for this study as a representative drug delivery system for which intracartilage uptake has been characterized before5; however, the deswelling properties of CPCs predicted herein and their dependence on carrier charge and uptake are expected to be reflective of any drug delivery system possessing cationic charge.
The results of this study predict that experimentally observed concentrations of CPC are capable of inducing reductions in the free swelling pressure of healthy cartilage on the order of 10–30 kPa (Fig. 2). Direct precise measurements of free swelling pressures in cartilage have remained elusive due to the presence of restraining collagen fibers in situ; as such, previous studies have relied on proteoglycan solutions or the ideal Donnan theory for estimating swelling pressure magnitudes.49 However, a recent study previously reported directly measured physiological swelling pressures of healthy bovine articular cartilage of ∼70 kPa,40 about half the pressure estimated by the Donnan model here (Fig. 2A; an observation consistent with previous studies40). Using this point of comparison for physiological swelling in cartilage, the results presented here suggest that cationic carriers may induce observable deswelling in comparison with physiological values that could potentially hinder mechanophysiological functionality or disturb chondrocyte physiology.50,51 In addition, a key finding from this study was the increased relative magnitude of deswelling in GAG-depleted cartilage tissues mimicking OA (Fig. 3C). Given that CPCs and other drug delivery modalities are intended for administration to OA patients for which mechanical side effects may be amplified, the results herein strongly indicate that full experimental characterization of charge shielding effects by future cationic carriers of interest is a necessary consideration in their development.
This model can be useful for drug carrier design as a tool to define constraints on carrier uptake properties and net charge on the basis of induced deswelling. By rearranging the Donnan model [Eq. (3)] and inputting tolerable limits for deswelling or modulus reduction, it can be implemented to assess safe uptake limits for cationic carriers of a given net charge. As an example, we performed such a sensitivity analysis for the case of CPCs. To induce a 36.7% reduction in compressive modulus () in healthy cartilage, which was previously reported as the difference in shear modulus between Grade 0 and Grade 1 OA in human articular cartilage,52 the uptake of CPC +20 would have to be 2.1 mM. This level of uptake is approximately twice as high as experimentally observed levels and thus is not practically achievable by CPCs with a therapeutic intra-articular dose. Nevertheless, this representative analysis demonstrates how the Donnan model can be used to define the upper limits of uptake for future cationic drug carriers that may possess higher net charge (such as nanoparticles).
Other effects of cationic carriers on tissue mechanical properties besides charge shielding may arise that have not been considered here, such as changes in modulus due to physical interactions between carrier molecules and the solid matrix. For instance, intratissue macromolecular cationic carriers may be expected to exhibit an ionic crosslinking effect, since their macrosize allows them to span and simultaneously interact with multiple GAG chains.* In designing cationic drug carriers, it is important to characterize changes in tissue mechanical properties that arise from such interactions, since the downstream mechanical changes likely depend on tunable parameters such as net charge and spatial charge distribution, which can be integral design considerations. We envision that the Donnan model presented herein can be leveraged to investigate these nonelectrostatic effects in conjunction with experimental bulk modulus measurements. Since the modulus of cartilage tissue can be expressed as the linear sum of electrostatic and nonelectrostatic components [e.g., Eq. (4)], the Donnan model described here can be used to deconvolute measurements into components arising from charge shielding (predicted by the model) and interactions between a carrier and the solid matrix [extrapolated with Eq. (4)].
Importantly, the relative changes of modulus components resulting from treatment with a cationic drug carrier can provide mechanistic insight into how the structural features of the carrier influence mechanical and swelling properties. For instance, the magnitude of nonelectrostatic changes may depend on the external salinity, since binding interactions between carriers and matrix proteins are likely facilitated by electrostatic attractive forces.5 Therefore, the relationship between the nonelectrostatic modulus component and external salinity (if any) following carrier uptake could provide insight into the dependence of carrier/matrix interactions on electrostatic attractions. Here, we have demonstrated the utility of the Donnan model in characterizing these interactions, as our results predict that electrostatic charge shielding effects may dominate modulus measurements when performed at low salinity (Fig. 4C).
There are multiple notable limitations inherent in the use of an ideal Donnan model for estimating swelling pressures in cartilage tissue. First, it was recently shown that swelling pressures in cartilage exhibit considerable nonideality when measured at hypotonic salinity,40 which was corrected by modifying the Donnan model to include a constitutive parameter based on counterion condensation theory.53 Such a model more accurately predicted absolute magnitudes of swelling pressures compared with overestimated pressures from the ideal Donnan model and thus represents a possible extension to the modeling approach presented herein. This method of incorporating nonideality was omitted from the analysis here because it relies on fitting the constitutive Manning parameter to experimental mechanical data. Future studies measuring mechanical changes following CPC uptake should be conducted to allow for implementation of the nonideal Donnan model in this context for more accurate estimations of absolute swelling pressures and electrostatic compressive moduli.
Second, models based on the Donnan osmotic theory are generally inferior to swelling pressure models that incorporate microscale variations in electrostatic potential within the tissue, such as the PB cell.37 As such, the magnitudes of swelling pressure and electrostatic modulus obtained by the macroscale Donnan model used here are likely higher than what would be predicted by the PB cell model. Importantly, a macroscale model was chosen here because the use of PB cell and other microscale models requires knowledge of the spatial orientation of the drug carrier in relation to single GAG chains in the brush network. Furthermore, the sizes of CPC polypeptides are on the order of the Debye length of GAGs in the PB cell model (∼1 nm) and may be large enough to span multiple GAGs (PB cells). Therefore, experimental characterization of physical interactions between CPCs and GAG chains in the ECM network is necessary before microscale models can be reliably used to obtain more accurate swelling pressure predictions when cationic carriers are present in the system. Finally, since the ideal Donnan model is applied at the macroscale, spatial variations in CPC uptake and FCD are ignored. Since CPCs exhibit variable penetrations through the tissue based on their net charge (some being hindered in the superficial zone),5 CPC-induced deswelling may exhibit significant local variations between the superficial and deep zones of cartilage following physiological uptake.
Conclusion
In summary, we have implemented the ideal Donnan osmotic theory to evaluate the charge shielding effects of cationic drug delivery systems in articular cartilage. While this study has focused on delivery systems for articular cartilage, the predicted effects of cationic carriers described here may be extended to a variety of anionic tissues for which cationic delivery systems are being evaluated, such as the vitreous humor of the eye1 and the intervertebral disc.7 The modeling approach described here may therefore be an integral tool in the design and evaluation of future cationic delivery systems for treatment of a variety of diseases.
Acknowledgments
We would like to thank Armin Vedadghavami and Dr. Shikhar Mehta for their expertise, guidance, and advice pertaining to polyarginine CPCs.
Authors' Contributions
M.R.W. and A.G.B. designed the study, developed the model, performed data analysis, created figures, and wrote and edited the article. A.G.B. conceived the study and obtained funding. All coauthors have reviewed and approved the article before submission. This article has been submitted solely to Bioelectricity: Science, Engineering and Medicine and is not published, in press, or submitted elsewhere.
Author Disclosure Statement
No competing financial interests exist.
Funding Information
This study was supported by the National Institute of Health (NIH) Trailblazer R21 Grant EB028385 and NIH R01 Grant AR075121.
In the context of tissue mechanics, this effect is considered “nonelectrostatic,” since it would alter the component of the bulk modulus in Equation (4).
References
- 1. Vedadghavami A, Zhang C, Bajpayee AG. Overcoming negatively charged tissue barriers: Drug delivery using cationic peptides and proteins. Nano Today 2020;34:100898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Young CC, Vedadghavami A, Bajpayee AG. Bioelectricity for drug delivery: The promise of cationic therapeutics. Bioelectricity 2020;2:68–81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Kumar S, Sharma B. Leveraging electrostatic interactions for drug delivery to the joint. Bioelectricity 2020;2:82–100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Bajpayee AG, Grodzinsky AJ. Cartilage-targeting drug delivery: Can electrostatic interactions help? Nat Rev Rheumatol 2017;13:183–193. [DOI] [PubMed] [Google Scholar]
- 5. Vedadghavami A, Wagner EK, Mehta S, et al. Cartilage penetrating cationic peptide carriers for applications in drug delivery to avascular negatively charged tissues. Acta Biomater 2019;93:258–269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Bajpayee AG, Wong CR, Bawendi MG, et al. Avidin as a model for charge driven transport into cartilage and drug delivery for treating early stage post-traumatic osteoarthritis. Biomaterials 2014;35:538–549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Wagner EK, Vedadghavami A, Jacobsen TD, et al. Avidin grafted dextran nanostructure enables a month-long intra-discal retention. Sci Rep 2020;10:12017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. He T, Zhang C, Vedadghavami A, et al. Multi-arm Avidin nano-construct for intra-cartilage delivery of small molecule drugs. J Control Release 2020;318:109–123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Geiger BC, Wang S, Padera Jr. RF, et al. Cartilage-penetrating nanocarriers improve delivery and efficacy of growth factor treatment of osteoarthritis. Sci Transl Med 2018;10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Zhang C, He T, Vedadghavami A, et al. Avidin-biotin technology to synthesize multi-arm nano-construct for drug delivery. MethodsX 2020;7:100882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Warren MR, Zhang C, Vedadghavami A, et al. Milk exosomes with enhanced mucus penetrability for oral delivery of siRNA. Biomater Sci 2021;9:4260–4277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Liu Y, Yang T, Wei S, et al. Mucus adhesion- and penetration-enhanced liposomes for paclitaxel oral delivery. Int J Pharm 2018;537:245–256. [DOI] [PubMed] [Google Scholar]
- 13. Mohanty RP, Liu X, Ghosh D. Electrostatic driven transport enhances penetration of positively charged peptide surfaces through tumor extracellular matrix. Acta Biomater 2020;113:240–251. [DOI] [PubMed] [Google Scholar]
- 14. Sasaki H, Karasawa K, Hironaka K, et al. Retinal drug delivery using eyedrop preparations of poly-L-lysine-modified liposomes. Eur J Pharm Biopharm 2013;83:364–369. [DOI] [PubMed] [Google Scholar]
- 15. Melgar-Asensio I, Kandela I, Aird F, et al. Extended intravitreal rabbit eye residence of nanoparticles conjugated with cationic arginine peptides for intraocular drug delivery: In vivo imaging. Invest Ophthalmol Vis Sci 2018;59:4071–4081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Mehta S, He T, Bajpayee AG. Recent advances in targeted drug delivery for treatment of osteoarthritis. Curr Opin Rheumatol 2021;33:94–109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Huebner KD, Shrive NG, Frank CB. Dexamethasone inhibits inflammation and cartilage damage in a new model of post-traumatic osteoarthritis. J Orthop Res 2014;32:566–572. [DOI] [PubMed] [Google Scholar]
- 18. Mehta S, Young CC, Warren MR, et al. Resveratrol and curcumin attenuate ex vivo sugar-induced cartilage glycation, stiffening, senescence, and degeneration. Cartilage 2021:1947603520988768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Hunter DJ, Pike MC, Jonas BL, et al. Phase 1 safety and tolerability study of BMP-7 in symptomatic knee osteoarthritis. BMC Musculoskelet Disord 2010;11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Bhosale AM, Richardson JB. Articular cartilage: Structure, injuries and review of management. Br Med Bull 2008;87:77–95. [DOI] [PubMed] [Google Scholar]
- 21. Bajpayee AG, De la Vega RE, Scheu M, et al. Sustained intra-cartilage delivery of low dose dexamethasone using a cationic carrier for treatment of post traumatic osteoarthritis. Eur Cell Mater 2017;34:341–364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Krishnan Y, Rees HA, Rossitto CP, et al. Green fluorescent proteins engineered for cartilage-targeted drug delivery: Insights for transport into highly charged avascular tissues. Biomaterials 2018;183:218–233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Cook Sangar ML, Girard EJ, Hopping G, et al. A potent peptide-steroid conjugate accumulates in cartilage and reverses arthritis without evidence of systemic corticosteroid exposure. Sci Transl Med 2020;12:eaay1041. [DOI] [PubMed] [Google Scholar]
- 24. Perni S, Prokopovich P. Poly-beta-amino-esters nano-vehicles based drug delivery system for cartilage. Nanomedicine 2017;13:539–548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. DiDomenico C, Bonassar LJ. The effect of charge and mechanical loading on antibody diffusion through the articular surface of cartilage. J Biomech Eng 2019;141:014502. [DOI] [PubMed] [Google Scholar]
- 26. Bajpayee AG, Scheu M, Grodzinsky AJ, et al. A rabbit model demonstrates the influence of cartilage thickness on intra-articular drug delivery and retention within cartilage. J Orthop Res 2015;33:660–667. [DOI] [PubMed] [Google Scholar]
- 27. Verdurmen WP, Brock R. Biological responses towards cationic peptides and drug carriers. Trends Pharmacol Sci 2011;32:116–124. [DOI] [PubMed] [Google Scholar]
- 28. Brown S, Pistiner J, Adjei IM, et al. Nanoparticle properties for delivery to cartilage: The implications of disease state, synovial fluid, and off-target uptake. Mol Pharm 2019;16:469–479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Kilk K, Mahlapuu R, Soomets U, et al. Analysis of in vitro toxicity of five cell-penetrating peptides by metabolic profiling. Toxicology 2009;265:87–95. [DOI] [PubMed] [Google Scholar]
- 30. Young WT. Cartilage stress relaxation induced by intra-tissue transport of cationic nanoparticles: implications for post-traumatic osteoarthritis drug delivery. Massachusetts Institute of Technology Department of Mechanical Engineering. 2016. Available at: http://hdl.handle.net/1721.1/104138 (accessed November 1, 2021).
- 31. Han EH, Chen SS, Klisch SM, et al. Contribution of proteoglycan osmotic swelling pressure to the compressive properties of articular cartilage. Biophys J 2011;101:916–924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Canal Guterl C, Hung CT, Ateshian GA. Electrostatic and non-electrostatic contributions of proteoglycans to the compressive equilibrium modulus of bovine articular cartilage. J Biomech 2010;43:1343–1350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Maroudas A. Balance between swelling pressure and collagen tension in normal and degenerate cartilage. Nature 1976;260. [DOI] [PubMed] [Google Scholar]
- 34. Eisenberg SR, Grodzinsky AJ. Swelling of articular cartilage and other connective tissues: Electrornechanochemical forces. J Orthop Res 1985;3:148–159. [DOI] [PubMed] [Google Scholar]
- 35. Poulet B. Models to define the stages of articular cartilage degradation in osteoarthritis development. Int J Exp Pathol 2017;98:120–126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Grodzinsky AJ. Fields, Forces, and Flows in Biological System. London, New York: Garland Science, 2011. [Google Scholar]
- 37. Buschmann MD, Grodzinsky A.J. A molecular model of proteoglycan-associated electrostatic forces in cartilage mechanics. J Biomech Eng 1995;117:179–192. [DOI] [PubMed] [Google Scholar]
- 38. Basser PJ, Grodzinsky AJ. The Donnan model derived from microstructure. Biophys Chem 1993;46:57–68. [DOI] [PubMed] [Google Scholar]
- 39. Parsons JR, Black J. Mechanical behavior of articular cartilage: quantitative changes with alteration of ionic environment. J Biomech 1979;12:765–773. [DOI] [PubMed] [Google Scholar]
- 40. Zimmerman B, Nims R, Chen A, et al. Direct osmotic pressure measurements in articular cartilage demonstrate non-ideal and concentration-dependent phenomena. J Biomech Eng 2021;143:041007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Grodzinsky AJ, Roth V, Myers E, et al. The significance of electromechanical and osmotic forces in the nonequilibrium swelling behavior of articular cartilage in tension. J Biomech Eng 1981;103:221–231. [DOI] [PubMed] [Google Scholar]
- 42. Naik RJ, Sharma R, Nisakar D, et al. Exogenous chondroitin sulfate glycosaminoglycan associate with arginine-rich peptide-DNA complexes to alter their intracellular processing and gene delivery efficiency. Biochim Biophys Acta 2015;1848:1053–1064. [DOI] [PubMed] [Google Scholar]
- 43. Lai WM, Hou JS, Mow VC. A triphasic theory for the swelling and deformation behaviors of articular cartilage. J Biomech Eng 1991;113:245–258. [DOI] [PubMed] [Google Scholar]
- 44. Maroudas A. Physiochemical properties of cartilage in the light of ion exchange theory. Biophys J 1968;8:575–595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Vedadghavami A, Mehta S, Bajpayee AG. Characterization of intra-cartilage transport properties of cationic peptide carriers. J Vis Exp 2020;162:e61340. [DOI] [PubMed] [Google Scholar]
- 46. Farndale RW, Sayers CA, Barrett AJ. A direct spectrophotometric microassay for sulfated glycosaminoglycans in cartilage cultures. Connect Tissue Res 1982;9:247–248. [DOI] [PubMed] [Google Scholar]
- 47. Lu XL, Sun DDN, Guo E, et al. Indentation determined mechanoelectrochemical properties and fixed charge density of articular cartilage. Ann Biomed Eng 2004;32:370–379. [DOI] [PubMed] [Google Scholar]
- 48. Bajpayee AG, Scheu M, Grodzinsky AJ, et al. Electrostatic interactions enable rapid penetration, enhanced uptake and retention of intra-articular injected avidin in rat knee joints. J Orthop Res 2014;32:1044–1051. [DOI] [PubMed] [Google Scholar]
- 49. Ehrlich S, Wolff N, Schneiderman R, et al. The osmotic pressure of chondroitin sulphate solutions: Experimental measurements and theoretical analysis. Biorheology 1998;35:383–397. [DOI] [PubMed] [Google Scholar]
- 50. Amin AK, Huntley JS, Bush PG, et al. Osmolarity influences chondrocyte death in wounded articular cartilage. J Bone Joint Surg Am 2008;90:1531–1542. [DOI] [PubMed] [Google Scholar]
- 51. Bush PG, Hall AC. Passive osmotic properties of in situ human articular chondrocytes within non-degenerate and degenerate cartilage. J Cell Physiol 2005;204:309–319. [DOI] [PubMed] [Google Scholar]
- 52. Peters AE, Akhtar R, Comerford EJ, et al. The effect of ageing and osteoarthritis on the mechanical properties of cartilage and bone in the human knee joint. Sci Rep 2018;8:5931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Manning GS. Limiting laws and counterion condensation in polyelectrolyte solutions i. colligative properties. J Chem Phys 1969;51:924–933. [Google Scholar]