Cerebral cortex layer segmentation using diffusion magnetic resonance imaging in vivo with applications to laminar connections and working memory analysis

Abstract

Understanding the laminar brain structure is of great help in further developing our knowledge of the functions of the brain. However, since most layer segmentation methods are invasive, it is difficult to apply them to the human brain in vivo. To systematically explore the human brain's laminar structure noninvasively, the K‐means clustering algorithm was used to automatically segment the left hemisphere into two layers, the superficial and deep layers, using a 7 Tesla (T) diffusion magnetic resonance imaging (dMRI)open dataset. The obtained layer thickness was then compared with the layer thickness of the BigBrain reference dataset, which segmented the neocortex into six layers based on the von Economo atlas. The results show a significant correlation not only between our automatically segmented superficial layer thickness and the thickness of layers 1–3 from the reference histological data, but also between our automatically segmented deep layer thickness and the thickness of layers 4–6 from the reference histological data. Second, we constructed the laminar connections between two pairs of unidirectional connected regions, which is consistent with prior research. Finally, we conducted the laminar analysis of the working memory, which was challenging to do in the past, and explained the conclusions of the functional analysis. Our work successfully demonstrates that it is possible to segment the human cortex noninvasively into layers using dMRI data and further explores the mechanisms of the human brain.

This manuscript contains two main results: (a) First, it proposes a K‐means clustering algorithm to automatically segment the left hemisphere into two layers, on a 7 Tesla diffusion magnetic resonance imaging (MRI) data. The results demonstrate that the cerebral cortex can be successfully divided into the superficial and deep layers, corresponding to layers 1–3 and 4–6 of the Brodmann atlas, respectively. (b) Second, two pairs of unidirectional connected regions were selected to validate the laminar connections. The results show that estimating laminar connections using diffusion MRI (dMRI) is valuable and it indicates that dMRI has the potential to estimate laminar connections. The method was used to analyse the working memory, which was challenging to do in the past.

1. INTRODUCTION

According to cytoarchitecture, the cerebral cortex can be segmented into different layers. The Brodmann atlas (Brodmann, 1909) divides the isocortex into six layers. From the outermost to the innermost layer, these include: the molecular layer, the external granular layer, the external pyramidal layer, the internal granular layer, the internal pyramidal layer and the polymorphic layer. The allocortex does not have six layers, and the limbic cortex either lacks or has an incipient layer IV (Ángel García‐Cabezas et al., 2019). Recently, some researchers used high‐resolution functional magnetic resonance imaging (fMRI) to detect the laminar specificity of the neural activity and thus explore cognitive processing in the human brain noninvasively (Finn et al., 2019). It was found that different layers are active in different time periods. This suggests that the functions of the different layers are different even though the layers belong to the same region, and that noninvasive approaches can detect differences between layers. Thus, this leads to the need to study layer‐specific structure in living humans, which will help to understand the human brain structure on a deeper level. Diffusion magnetic resonance imaging (dMRI) can noninvasively detect the brain tissue structure in vivo and is sensitive to the brain myeloarchitecture. In previous studies, dMRI has been mainly used for constructing fiber connections in white matter (Donahue et al., 2016) and for studying brain diseases (Aganj et al., 2020). Some studies (Assaf, 2018; Dhital et al., 2014; Kleinnijenhuis et al., 2013; Trong‐Kha et al., 2014) have shown that dMRI parameters vary with grey matter depth and show significant differences among layers, which makes it possible to segment the cerebral cortex into layers based on the myeloarchitecture. A recent study (Bastiani et al., 2016) shows that high‐resolution ex vivo dMRI can be used to segment the cerebral cortex into layers. These studies encouraged us to segment cerebral layers and study layer specificity using dMRI acquired in vivo.

On the other hand, depending on different cytoarchitectures and functions, the cerebral cortex can be divided into different regions that communicate with each other through nerve fibers. The study of fiber connections, the "connectome," between different regions plays an important role in understanding how the brain works (Sporns et al., 2005). To study brain connections in more detail, it is very important to take cortical layers into account. Tracer injections (Majka et al., 2016), including anterograde and retrograde tracing, are often used to study laminar connections in animals (Butler et al., 2016; Gattass et al., 2014; Sakata et al., 2019). Recently, viral‐genetic tracing (Beier et al., 2019; Schwarz et al., 2015; Wood et al., 2019) has also been used to explore laminar connections. However, since these methods are invasive, their application on human brains is limited. On the other hand, dMRI is very sensitive to the diffusion of water molecules, and their diffusion along the fiber direction is apparent. In contrast, the diffusion perpendicular to the fiber direction is relatively small. Based on this principle, tractography algorithms can use dMRI data to estimate the three‐dimensional trajectory of fibers within the brain (Bastiani et al., 2012; Tournier et al., 2004). Due to its reliability and noninvasiveness, dMRI technology is favoured by researchers devoted to exploring brain structures. However, when constructing brain connections using dMRI in previous studies, only the connections between different regions were investigated; meanwhile, the connections between the regions' layers were not well‐revealed. If dMRI could be used to estimate the laminar connections, it would be beneficial to further understand the brain connection structure, diagnose brain‐related diseases and simulate the human brain.

Past research has shown that working memory is linked to the dorsolateral prefrontal cortex (dlPFC) (Courtney et al., 1997; Courtney et al., 1998; D'Esposito et al., 1995; Goldman‐Rakic, 1995). Moreover, recent works have shown that the superficial and deep layers of the dlPFC of monkeys are responsible for different modes of the working memory (Bastos et al., 2018; Markowitz et al., 2015). For humans, a recent study on fMRI suggested that the superficial layer is mainly responsible for the maintenance and manipulation of the working memory, while the deep layer is mainly responsible for task response (Finn et al., 2019). Therefore, it is necessary to study the laminar structure of working memory‐related regions.

In order to explore the living human brain deeply, dMRI of the human brain acquired in vivo was used in this study to segment the cortex into different laminar layers. We estimated the laminar connections between regions and analyzed the laminar structure of working memory‐related regions. First, the cortex was segmented using K‐means clustering in the space of the dMRI parameters, and was validated using histological data. Our analysis shows that segmenting the cortex into the so‐called superficial and deep layers worked best. Then, the laminar connections between different human cerebral regions were estimated using tractography, and the results were compared with hierarchical laminar connection patterns found in a histological dataset. It turns out that using dMRI to estimate laminar connections is valuable, and it provides an effective way to study laminar connections in the human brain. Finally, the relationship between working memory and layer thickness was analyzed, further enhancing our understanding of the working memory‐related brain structure.

2. MATERIAL AND METHODS

Our method consists of the following steps: (1) Based on dMRI data, 31‐dimensional features derived from the apparent diffusion coefficient (ADC) were extracted (Bastiani et al., 2016), and several cortical regions were automatically segmented into layers using K‐means clustering. After that, the clustering results were evaluated. (2) The layer thickness was calculated, and it was then compared with the layer thickness acquired from the reference dataset (Wagstyl et al., 2020). (3) Generalized fractional anisotropy (GFA) (Tuch, 2004) was added to the features. Then, the new features were reclustered, and the result was evaluated using the same method. Segmentation results before and after adding GFA were compared, and the influence of GFA on the clustering results was analyzed. (4) Two pairs of unidirectionally connected regions were chosen; that is, those where only connections from one region to the other were found. Then, the laminar connections were estimated using tractography. The proportion of laminar connections per unit volume was calculated and evaluated using hierarchical laminar connection patterns. (5) Layer thickness was used to analyze the relationship between laminar structure and working memory. The framework of this work is shown in Figure 1.

FIGURE 1.

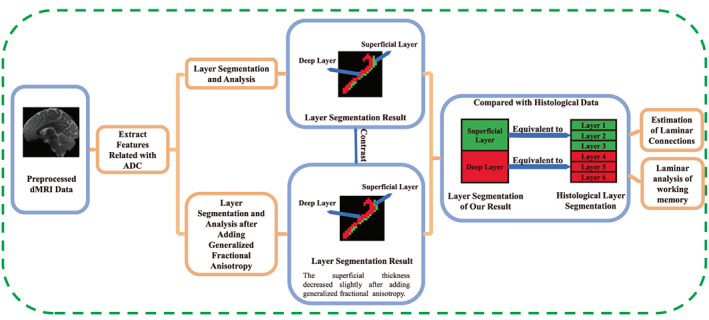
Flow chart of the method used. First, we used preprocessed diffusion magnetic resonance imaging (dMRI) data to extract features for segmenting the cortex into layers. Then, we added generalized fractional anisotropy to the features and segmented again. The results obtained before and after adding generalized fractional anisotropy were compared and analyzed. Furthermore, the results were compared with histological data, with the superficial layer corresponding to Brodmann's layers 1–3 and the deep layer corresponding to layers 4–6. Finally, the results were used for the estimation of laminar connections and for laminar analysis of the working memory.

2.1. dMRI dataset

We used the pre‐processed 7T dMRI open dataset of 30 subjects randomly selected from the WU‐Minn Human Connectome Project (HCP) (Essen et al., 2013). We have accepted the HCP Open Access Data Use Terms. The subjects were all healthy adults, and included 15 females and 15 males aged from 26 to 35 years old. The data were collected using spin‐echo echo‐planar imaging sequences. The data resolution is 1.05 mm × 1.05 mm × 1.05 mm. The measurement parameters were: field of view 210 × 210mm², repetition time 700 ms, echo time 71.2 ms and flip angle 90°. Each gradient table includes 65 diffusion weighting directions plus 6 b = 0 acquisitions interspersed throughout each run. Diffusion weighting consisted of two shells: b = 1000 s/mm² and 2000 s/mm². In our experiments, we used dMRI data with b = 2000 s/mm².

2.2. Automatic layer segmentation

Grey matter regions and their perpendicular vectors were extracted using FreeSurfer (Fischl, 2012). The ADC is a dMRI parameter reflecting the diffusion of water molecules in the gradient field direction. For every voxel, the ADC of the gradient field's direction is calculated through the following formula:

$${\psi }_j=-\frac{1}{b}\ln \left(\frac{S_j}{S_0}\right)$$ (1)

where 𝑆₀ is the signal when the gradient field is not applied; b is the diffusion weighted factor, whose magnitude is related to the gradient field; and 𝑆_𝑗 is the attenuated signal in the direction of the gradient field 𝑗. After the calculation, each voxel's ADC profile is fitted by spherical harmonics. According to previous works (Bastiani et al., 2016; Nagy et al., 2013), the number of parameters used for clustering and the data‐fit rate are most appropriate when the spherical harmonic order is six. Therefore, sixth order spherical harmonics were chosen for the task. Because the ADC profile is real and antipodally symmetric, only the real even elements are computed. A total of 28 spherical harmonic coefficients are required to fit the ADC. To make later calculations easier, we need to rotate the spherical harmonics so that the Z‐axis coincides with the cortical surface's normal direction.Following previous works (Bastiani et al., 2016; Nagy et al., 2013), four derived ADC features of each voxel were extracted:

(1) the mean ADC value (1 feature), (2) the ADC value of the cortical normal direction (1 feature), (3) the mean ADC value in the cortical tangential plane (1 feature), (4) the even spherical harmonic coefficients used to fit the ADC (28 features). These sets of features form a 31‐dimensional vector. ADC spherical harmonic coefficients were calculated using MRtrix v3.0‐RC3 (Tournier et al., 2019), and the rotation and feature extraction were performed using MATLAB 2021a (Politis, 2016). After that, Z‐score was used to standardize the features. Using the statistics tools in MATLAB, features were fed into an unsupervised K‐means clustering algorithm (Jain, 2010) with the maximum number of iterations and with replicates equal to 100 to cluster cortex voxels into different cortical layers.

Many studies have shown that in grey matter, the fiber orientation distribution (FOD) is mostly in the radial and tangential directions (Dhital et al., 2014; Trong‐Kha et al., 2014). Furthermore, the FOD reveals significant differences in different layers (Assaf, 2018). A study (Kleinnijenhuis et al., 2013) even manually segmented the cortex into layers according to the FOD. These works provide an important basis for selecting the above 31 features.

The Calinski‐Harabaz Index (CH) (Lukasik et al., 2016; Wang & Xu, 2019) was used to decide the number of clusters. CH is a commonly used index to judge the number of clusters, and combines the aggregation and separation degree of the clustering results. The number of clusters is taken into account in the evaluation. 𝐶𝐻 is calculated as follows:

$$\mathit{CH}\left(k\right)=\frac{\mathit{\text{BGSS}}}{\mathit{\text{WGSS}}}\times \frac{n-k}{k-1},\mathit{\text{with}}$$ (2)

$$\begin{array}{l}\mathit{\text{BGSS}}=\frac{1}{2}\left[\left(k-1\right){\overline{d}}^2+\sum _{i=1}^k\left(n_i-1\right)\left({\overline{d}}^2-{\overline{d}}_i^2\right)\right],\\ \mathit{\text{WGSS}}=\frac{1}{2}\sum _{i=1}^k\left(n_i-1\right){\overline{d}}_i^2,\end{array}$$

where 𝑛 represents the number of samples; 𝑛_𝑖 is the number of samples in cluster 𝑖; k represents the number of clusters; ⁻𝑑² is the mean squared distance of all 𝑛(𝑛 − 1)/2 pairs samples; ⁻𝑑_𝑖 ²is the mean square distance of all 𝑛_𝑖(𝑛_𝑖 − 1)/2 pairs samples in cluster 𝑖; between‐groups sum of squared error (BGSS) is used to measure the degree of separation between clusters; finally, within‐groups sum of squared error (W𝐺𝑆𝑆) is used to measure the degree of aggregation within the clusters. The larger the 𝐶𝐻 value is, the better the clustering effect will be.

To check the stability of the clustering results, 10% of the samples were randomly removed and the clustering process was repeated. Then, the clustering results of the remaining samples were compared with the original results. The larger the ratio of samples with the same clustering result, the more stable the clustering will be. The above steps were repeated 100 times, and the average ratio value was taken as the evaluation index of the clustering stability.

The t‐Distributed Stochastic Neighbor Embedding (t‐SNE) (Pezzotti et al., 2017) and the Uniform Manifold Approximation and Projection (UMAP) (McInnes & Healy, 2018) algorithms are nonlinear techniques for dimensionality reduction. They are particularly well‐suited for the visualization of high‐dimensional datasets. As such, to visually evaluate the clustering results, t‐SNE and UMAP were used for dimensionality reduction and visualization of high‐dimensional features.

Statistical methods were used to analyze the differences of the parameters between different clusters' voxels. First, the one‐sample Kolmogorov‐Smirnov test was used to determine whether the samples in a cluster after the z‐score came from a standard normal distribution. Then, for those samples which did come from normal distributions, the Welch's t‐test with a significance level α equal to .05 was used to analyze the clusters' differences. Otherwise, the Wilcoxon rank sum test with a significance level α equal to .05 was used. In addition to analyzing the parameters in the clustering features, the commonly‐used dMRI parameter, fractional anisotropy, which is used to characterize the degree of anisotropy, was also added. However, in our study, GFA was used to replace fractional anisotropy, as discussed below.

2.2.1. Adding GFA to the clustering features

Fractional anisotropy (Basser & Pierpaoli, 1996) is an essential dMRI parameter. It was shown that in grey matter, fractional anisotropy is correlated with fiber complexity (Assaf, 2018). Some studies (Kleinnijenhuis et al., 2013; Trong‐Kha et al., 2014) have also demonstrated that fractional anisotropy varies with cortex depth. As a result, we tried to add fractional anisotropy to the features.

Since spherical harmonics had been used to fit ADC, we decided to use GFA (Tuch, 2004), which considers diffusion in all orientations compared to fractional anisotropy. GFA is calculated as follows:

$$\mathit{GFA}=\frac{\mathit{std}\left(\psi \right)}{\mathit{rms}\left(\psi \right)}=\sqrt{\frac{m{\sum }_{j=1}^m{\left({\psi }_j-⟨\psi ⟩\right)}^2}{\left(m-1\right){\sum }_{j=1}^m{\psi }_j^2}}$$ (3)

where 𝜓_𝑗 is the diffusion at orientation 𝑗, and $⟨\psi ⟩=\left(1/m\right){\sum }_{j=1}^m{\psi }_j$ is the diffusion mean. The greater the GFA, the greater the degree of anisotropy.

The same methods described above were used to segment and analyze the cortex layer after adding the GFA feature.

2.3. Histological verification of clustering

FreeSurfer v6.0.0 (Fischl, 2012) was used to calculate the thickness of the regions (Tustison et al., 2014), while LAYNII v2.2.1 (Huber et al., 2021) was used to calculate the thickness proportion of each segmented layer. To verify the calculated thickness, we calculated correlations with BigBrain (Wagstyl et al., 2020), von Economo (v. Economo & Koskinas, 1925) and HCP's MRI cortical thickness (Glasser et al., 2016). To verify the segmentation results, we compared our results to the histological dataset layer thickness: BigBrain (Wagstyl et al., 2020), which was derived from a 3D histological atlas of the human brain at 20‐micrometer isotropic resolution, and von Economo (v. Economo & Koskinas, 1925). The allocortex was excluded from the layer thickness analysis.

2.4. Laminar connections between regions

After segmenting the grey matter into layers, laminar connections of the brain regions were created using MRtrix v3.0‐RC3 (Tournier et al., 2019). First, the Tournier iterative algorithm (Tournier et al., 2013) was used to estimate the response function. Then, the constrained spherical deconvolution algorithm (Tournier et al., 2007) was used to estimate the FOD. The maximum harmonic degree was 8, which is commonly used to estimate the FOD (Tournier et al., 2004). It is more accurate than lower degrees and is less affected by noise than higher degrees. Finally, based on the FOD, the improved probabilistic streamlines tractography approach (iFOD2) (Tournier et al., 2010) was used to reconstruct streamlines. The desired number of streamlines was set to 10,000,000 and the step size was 0.5 times the voxel size. The maximum angle in degrees between successive steps was set to 45°. The minimum length of any track was two times the voxel size, while the maximum length was 100 times the voxel size. The FOD amplitude cutoff for terminating tracks was set to 0.1. The maximum number of sampling trials at each point was set to 1000. Using the above method, whole‐brain connections were estimated, and the laminar connections were then extracted from the overall connections. The number of streamlines per unit volume were used to calculate the average laminar connections of all subjects. Finally, the laminar connection proportion in the two regions was calculated.

2.5. Laminar analysis of working memory

The HCP dataset used visual N‐back tasks to assess the working memory, including 2‐back and 0‐back tasks. The 2‐back task is used to determine whether the current image is the same as the one presented two images prior, while the 0‐back task is used to determine whether the current image is the same as the original cue image. The reaction time and accuracy were used to evaluate the working memory. For a specific task flow, the reader may refer to the paper (Barch et al., 2013). Past research (Krogsrud et al., 2021; Metzler‐Baddeley et al., 2016; Østby et al., 2011) has shown that the working memory performance is correlated with the cortical thickness. Therefore, we first analyzed the correlation between the cortical thickness and the performance in working memory tasks using the Pearson correlation coefficient (Schober et al., 2018). Furthermore, previous works (Bastos et al., 2018; Finn et al., 2019; Markowitz et al., 2015) have shown that the superficial and deep layers of the cortex are responsible for different patterns in working memory tasks. Therefore, to explore the laminar brain structure of the working memory, the correlation between different layers and the working memory performance was also analysed. One of the subjects in the dataset did not do the task, so we only used twenty‐nine subjects in this analysis.

3. RESULTS

3.1. Layer clustering and analysis

The von Economo atlas (v. Economo & Koskinas, 1925; Scholtens, d. Reus, d. Lange, Scholtens et al., 2018) is one of the most commonly used in academia. The recently published BigBrain histological dataset (Wagstyl et al., 2020) calculated the six layers' thickness of each region based on the von Economo atlas. We divided the grey matter of the left hemisphere of 30 subjects into 43 regions based on the von Economo atlas by using FreeSurfer v6.0.0 (Scholtens et al., 2018; Fischl, 2012). Then, we separately applied clustering to every subject's regions. Figure 2 shows the four commonly used regions' segmentation results of a subject when the number of clusters ranges from 2 to 6. These four regions are the Area praecentralis (FA), Area parastriata (OB), Area striata (OC) and Area postcentralis intermedia (PC), which approximately represent the primary motor cortex, the second visual cortex, the primary visual cortex and the primary sensory cortex, respectively. Although the resolution is limited, the layer structure is still seen in each clustering result.

FIGURE 2.

Clustering results of some axial sections of a subject. The results of a section of regions FA, OB, OC, and PC are presented, from top to bottom. The results when the number of clusters is 2–6 are shown from left to right. Different colours represent different categories obtained by clustering. It can be seen that the clustering results have the effect of stratification

Figure 3 shows the mean 𝐶𝐻 curves when the number of clusters is from 2 to 15 of the four regions. Except for a few subjects' regions, usually when the number of clusters is equal to two, the 𝐶𝐻 is much higher than that of the other number of clusters. This may be because the cortex's total thickness is only about 2–3 times the resolution. Thus, when the number of clusters is too large, the results are not ideal. Considering the CH indexes and the image resolution, two was chosen as the optimal number of clusters. When that is the case, the cortex can be segmented into two layers: the superficial and deep layers.

FIGURE 3.

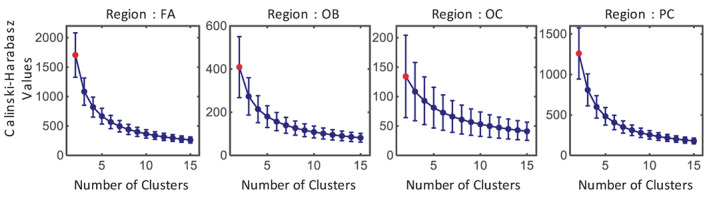
Mean 𝐶𝐻 values of the 30 subjects when the number of clusters is from 2 to 15. The vertical bar at each data point represents the standard deviation of the values. Results for regions FA, OB, OC, and PC are presented, from left to right. The CH value is largest when the number of clusters is 2

Some subjects' regions were visually poorly segmented. Supplementary Figure S1 shows some poor clustering examples where we cannot distinguish the layer structure from the results. Most poorly segmented regions are primarily located on the Limbic lobe, the orbital frontal cortex, the insula and the anterior tip of the temporal lobe. For Area parolfactoria + Area geniculata + Area praecommissuralis (FLMN) and for area cingularis limitans posterior (LC3), all 30 subjects had poor segmentation results. FLMN is located on the most caudoinferior edge of the frontal cortex and belongs to the allocortex. LC3 occupies a portion of the gyrus intralimbicus and a small edge of the limbic gyrus. Because these regions' layer structures are incomplete and not obvious (Ángel García‐Cabezas et al., 2019), it is challenging to segment them accurately.

Figure 4 shows the boxplot of the stability of all the subjects for all regions. For most regions, the stability was above 90% or even close to 100%, and there was little variation among the different subjects. However, for a few regions the stability was relatively low and varied significantly from subject to subject. These regions were also poorly segmented in some subjects. In the subsequent analysis, we will remove these poorly segmented results.

FIGURE 4.

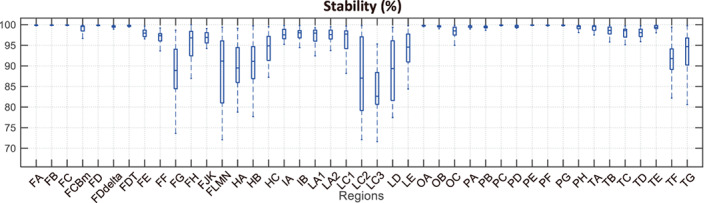
The stability of all the subjects for all regions. On each box, the central mark indicates the median, and the bottom and top edges of the box indicate the 25% and 75%, respectively. The whiskers extend to the most extreme data points which are not considered to be outliers. The x‐coordinate represents the abbreviated region names. The full region name can be found in Table S2. For some regions, the clustering stability was close to 100 percent, and the stability was similar across subjects. However, some regions show a relatively small stability, and it varies greatly among different subjects. At the same time, in some subject the segmentation results of these regions were poor

Figure 5 shows the results of the t‐SNE and UMAP algorithms for a subject's four regions. It can be seen that after dimensionality reduction using both algorithms, the features of the two layers overlap to some extent but can be roughly distinguished.

FIGURE 5.

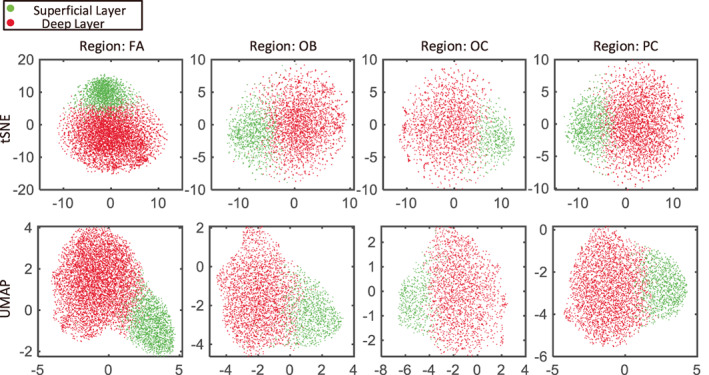
t‐SNE and UMAP results of a subject when the number of clusters is two. Red represents the deep layer, while green corresponds to the superficial layer. The two layers can be roughly distinguished

Figure 6 shows the boxplot of the dMRI parameters for all regions within each cluster after removing poorly segmented results. Data from all 30 subjects was put together. It can be seen that for most regions, the ADC‐related coefficient decreases from the superficial layer to the deep layer, which is consistent with previous studies (Bastiani et al., 2016; Trong‐Kha et al., 2014). Similarly, GFA decreases from the superficial layer to the deep layer due to the larger ADC in the superficial layer. The significance of the Welch's t‐test or the Wilcoxon rank‐sum test, which is used to analyze the differences between the two layers, was labeled before every region's name. For most regions and parameters, the differences between layers are strongly significant.

FIGURE 6.

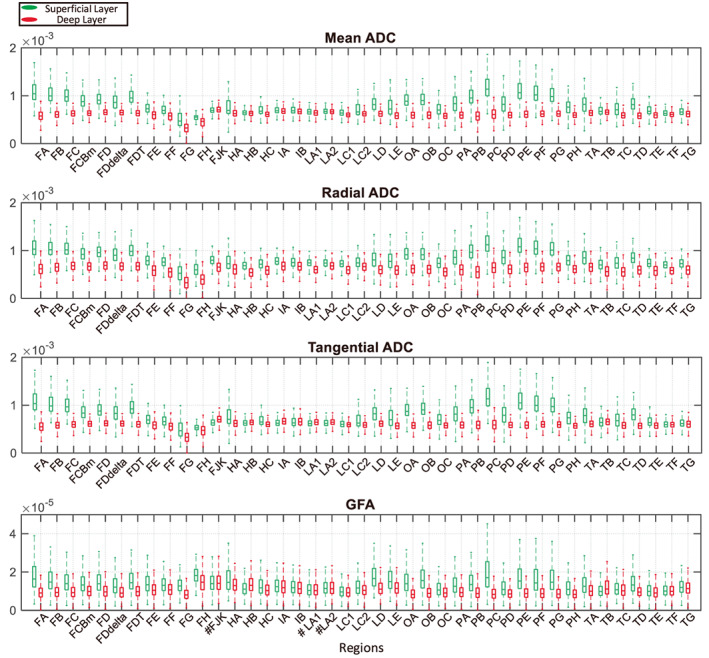
Analysis of the clustering results. Boxplots of the distribution of the voxel's parameters for all subjects are shown. From top to bottom, they correspond to parameters mean ADC, radial ADC, tangential ADC and GFA, respectively. The x‐coordinate represents the region name. Green represents the superficial layer, and red corresponds to the deep layer. On the whole, the superficial value is larger than the deep value for these four parameters. To analyze the differences between the voxel's parameters of two layers, the one‐sample Kolmogorov–Smirnov test was first used to determine whether the data came from a normal distribution. Then, the Welch's t‐test was used for samples from normal distributions to analyze the differences between the two layers. Otherwise, the Wilcoxon rank sum test was used. Additionally, the significance is labeled before each region name on the x‐coordinate. No label indicates p < .001; # indicates no significant difference between the two layers' parameters (three cases for the GFA).

3.2. Validation of layer clustering

Figure 7 shows the correlation between our average thickness and the thickness of the reference data, and the correlation between the average layer thickness and the layer thickness of the reference data. These reference data have all been used in (Wagstyl et al., 2020). The mean thickness and the layer thickness of all the subjects are included in the supplementary materials. We first divided the left cerebral cortex into 180 regions based on the HCP atlas (Glasser et al., 2016). We compared the calculated thickness with HCP's MRI cortical thickness (r = 0.8174, p < .001) and BigBrain's thickness (r = 0.5578, p < .001) of the left hemisphere. We then divided the left cortex according to the von Economo atlas (v. Economo & Koskinas, 1925) and compared the thickness with the BigBrian thickness (r = 0.6561, p < .001) and the von Economo and Koskinas thickness (r = 0.6683, p < .001). The thickness is significantly correlated with the reference data, which proves the effectiveness of the obtained results. The layer thickness was compared with BigBrain data (Wagstyl et al., 2020) and von Economo data. The allocortex was excluded. The superficial thickness was positively correlated with the thickness of layers 1–3 in the reference data (BigBrain: r = 0.4826, p = .0025; von Economo: r = 0.4216, p = 0.0093), while the deep thickness was positively correlated with the thickness of layers 4–6 in the reference data (BigBrain: r = 0.7959, p < .001; von Economo: r = 0.5466, p < .001). The thickness of layers two and four in some regions may equal zero in the von Economo data. The correlation between deep thickness and the reference data is stronger, which may be because the superficial thickness is relatively small on the whole and the data resolution used is large. As a result, the superficial layer is more difficult to segment accurately and the thickness error is larger.

FIGURE 7.

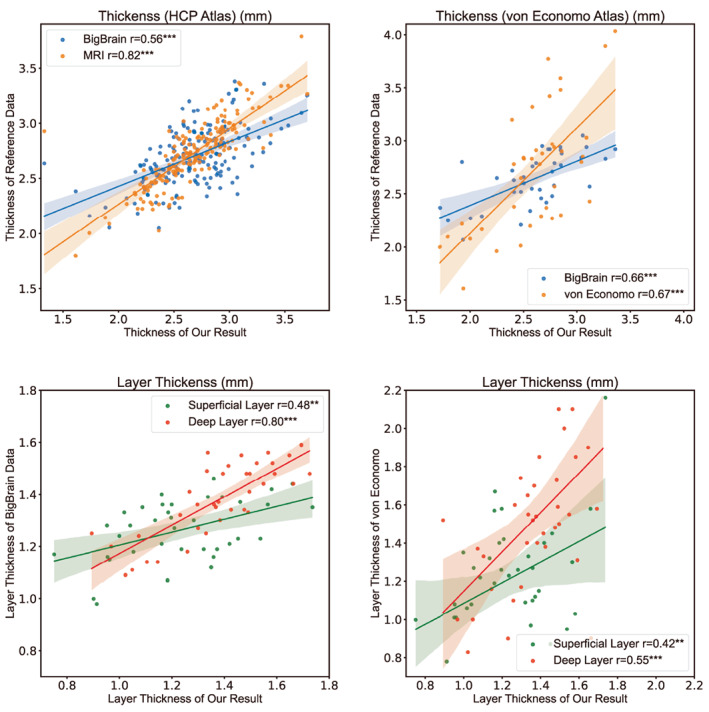
The left cortex was divided into regions based on the HCP and the von Economo atlas, and the calculated cortical thickness was compared to the reference data, which showed a significant correlation. The thickness of the superficial and deep layers was also significantly correlated with BigBrain and Von Economo's layers 1–3 and 4–6, respectively. The deep layer thickness correlation between our result and BigBrain's data is nearly 0.8

3.3. Reclustering and analysis after adding GFA as a feature

Figure 8 shows a comparison of a subject's clustering results before and after adding the GFA feature. It can be seen that the clustering results are very similar both before and after its addition. Figure 9 shows the difference between the mean superficial thickness before and after adding the feature. Once again, there is little thickness difference before and after the addition of the feature. In most subjects and regions, the superficial thickness decreased slightly after adding GFA, but the decrease was not significant. The superficial thickness of the region HA increased by nearly 0.04 mm after adding GFA, which is due to the region having been poorly segmented in most subjects. Before adding GFA, only subjects 9,14, and 15 had a good segmentation result, so only three subjects were used for thickness calculation. After adding the feature, subjects 6 and 16 were also used to calculate the thickness in addition to these three subjects. Due to the large superficial thickness of subject 6, the result of the average thickness is also large. However, the superficial thickness of subjects 9 and 14 did in fact decrease after adding the feature. Finally, the superficial thickness of subject 15 increased slightly. The analysis results are similar to those above, and they are available in the supplementary Figures S4–S6.

FIGURE 8.

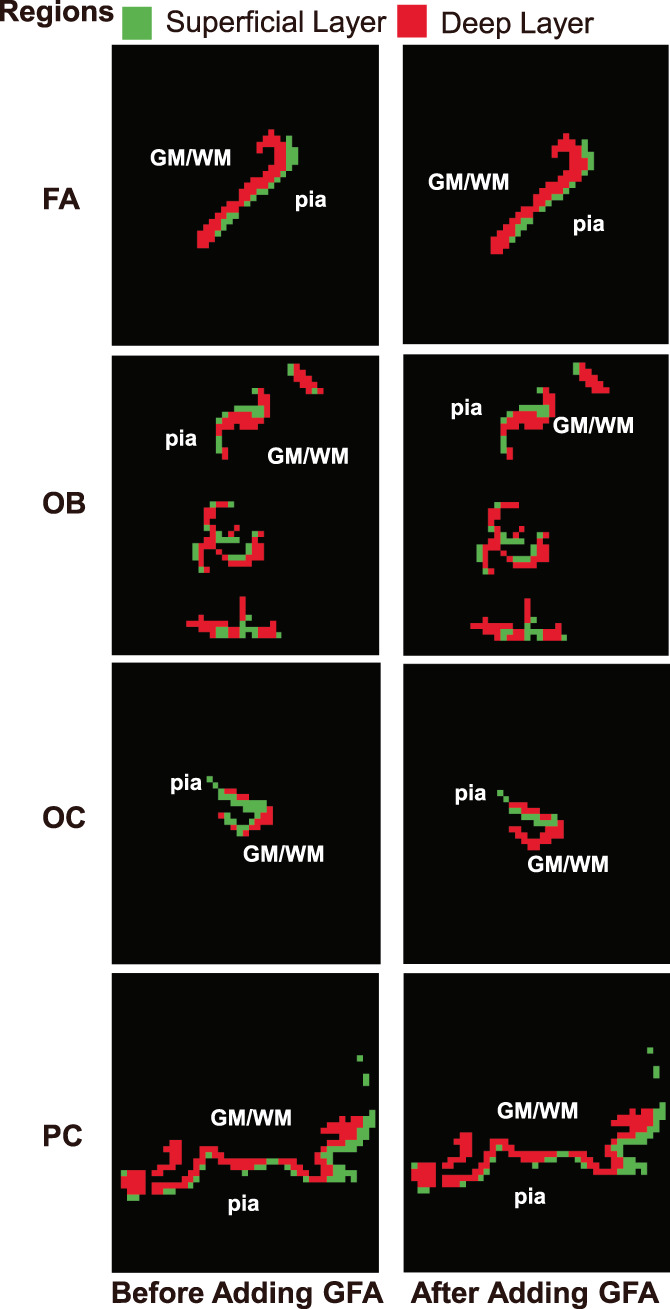
Reclustering results of a subject before and after adding the generalized fractional anisotropy feature for some axial section when the number of clusters is 2. From top to bottom, the results correspond to regions FA, OB, OC, and PC. Green represents the superficial layer, while red corresponds to the deep layer

FIGURE 9.

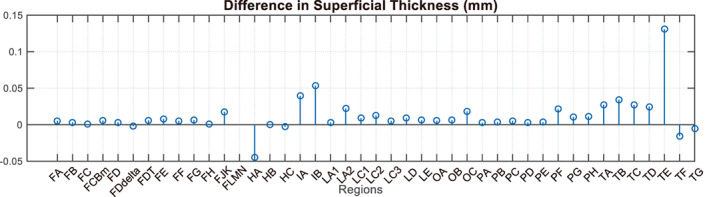
Difference in superficial thickness before and after adding the GFA feature. In most subjects and regions, the superficial thickness decreased slightly after adding GFA

Figure 10 shows the correlation between the average layer thickness after adding the GFA feature and the layer thickness of the reference data. The layer thickness after adding the GFA feature was in the supplementary Table S2. The layer thickness was compared with BigBrain and von Economo data. The allocortex was excluded. The superficial thickness was positively correlated with the thickness of layers 1–3 in the reference data (BigBrain: r = 0.4748, p = .0030; von Economo: r = 0.4219, p = .0093), while the deep thickness was positively correlated with the thickness of layers 4–6 in the reference data (BigBrain: r = 0.8063, p < .001; von Economo: r = 0.5679, p < .001). After adding GFA, the correlation between the superficial thickness and Bigbrain data decreased slightly. All other correlations increased.

FIGURE 10.

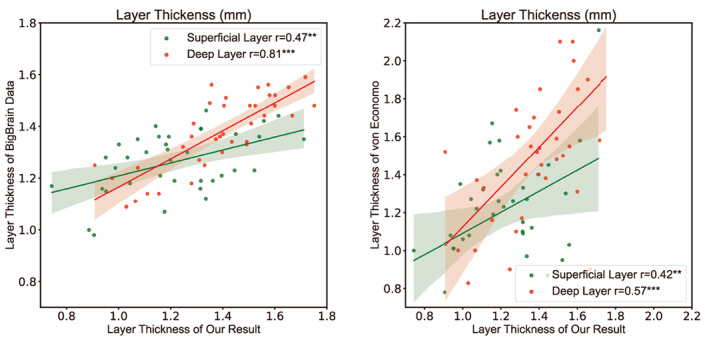
Correlation between layer thickness and reference data after adding GFA. After this addition, the thickness of the superficial and deep layers was significantly correlated with BigBrain and Von Economo's layers 1–3 and 4–6, respectively. Correlations with BigBrain's deep thickness as well as von Economo's superficial and deep thickness increased

3.4. Laminar connections of brain regions

In previous works on laminar connections of macaque monkeys, connections between most regions were found to be bidirectional. However, there was a reported lack of reciprocity in the projections from V4t to the primary visual cortex (V1) and from the second visual area (V2) to the FST (Felleman & Essen, 1991). That is to say, the connections between regions V4t and V1 only existed going from region V4t to V1, whereas there was no connection going from region V1 to V4T. Similarly, the connections between regions V2 and FST only went from region V2 to FST. Hierarchical laminar connections showed that the connection from V4t to V1 went from the deep layer of V4t to region V1, while the connection from V2 to FST went from the superficial layer of V2 to region FST. We suppose that the same holds true for the human brain due to the similarities between human and macaque brains. Because the connections obtained from the dMRI data do not have directional information, these two pairs of regions were selected as the experimental regions for the convenience of verification. Regions V1, V2, V4t and FST in the left hemisphere were segmented using the HCP MMP 1.0 atlas (Glasser et al., 2016) in FreeSurfer v6.0.0. Figure 11 shows the location of regions V1, V2, V4t and FST. Table. 1 shows the proportion of the average laminar connections per unit volume between V4t and V1 as well as V2 and FST for all 30 subjects.

FIGURE 11.

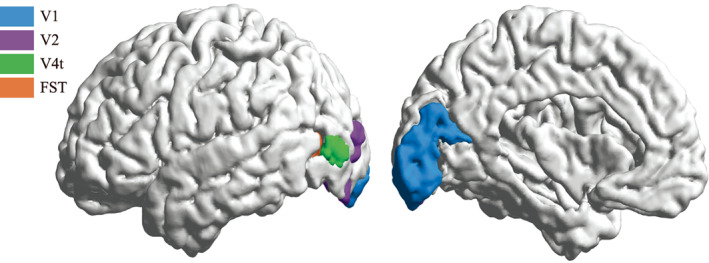
The location of brain regions V1, V2, V4t, and FST in a subject

TABLE 1.

Proportion of the average laminar connections per unit volume of the 30 subjects

Laminar connections between V4t and V1
Regions	V1 superficial layer	V1 deep layer
V4t superficial layer	8.65%	9.61%
V4t deep layer	42.80%	38.94%

Laminar connections between V2 and FST
Regions	FST superficial layer	FST deep layer
V2 superficial layer	7.41%	47.12%
V2 deep layer	4.35%	41.12%

Note: The connections with the largest proportion are in bold.

As can be observed in Table 1, although the result is not so obvious, the proportion of connections from the deep layer of V4t to the superficial layer of V1 is the largest, along with the proportion of connections from the superficial layer of V2 to the deep layer of FST. This result is consistent with previous research on hierarchical laminar connections (Felleman & Essen, 1991). For the dMRI data obtained in vivo, these results are already promising. Connections between deep layers are also large, while other laminar connections are less than 10%.

3.5. Laminar analysis of working memory

We divided the left hemisphere into 180 regions based on the HCP atlas. For several regions, it was found that the accuracy or reaction time of the working memory was correlated with their thickness. Some regions are concentrated in the DorsoLateral Prefrontal Cortex (dlPFC), which was found to be associated with working memory in a previous study (Bastos et al., 2018; Finn et al., 2019). The HCP Atlas divides the dlPFC into 13 regions, of which three regions' thickness was correlated with the reaction time. Nevertheless, the surprise was that the thickness of the dlPFC was positively correlated with the reaction time. The three regions are 8Ad, 9p and 9a. Table 2 shows the values of the correlation coefficient.

TABLE 2.

Correlation coefficient between region thickness and reaction time of the working memory

Correlation coefficient(thickness)
Regions	Median_RT	2bk_Median_RT	0bk_Median_RT
8Ad	0.546 b	0.5565 b	0.4772 b
9p	0.3933 a	0.3564	0.3839 a
9a	0.4187 a	0.4813 b	0.3276

Note: Median_RT indicates average of median reaction time for all conditions in the task; nbk indicates n‐back task.

^a Indicates p < .05.

^b Indicates p < .01.

Finally, the correlation coefficient between the layer thickness and the reaction time in the dlPFC region was calculated. Table 3 shows the correlation coefficient between the layer thickness and the reaction time. It can be seen that the superficial thickness is mainly related to the reaction time of the 2‐back task, while the deep thickness is related to the 0‐back task.

TABLE 3.

Correlation coefficient between layer thickness and reaction time of the working memory

Correlation coefficient of superficial thickness
Regions	Median_RT	2bk_Median_RT	0bk_Median_RT
8Ad	0.3374	0.441 a	0.2191
9p	0.4215 a	0.4879 b	0.3291
9‐46d	0.375 a	0.4992 b	0.2393
9a	0.3718 a	0.5031 b	0.2336

Correlation coefficient of deep thickness
Regions	Median_RT	2bk_Median_RT	0bk_Median_RT
8Ad	0.3696 a	0.3155	0.371 a

Note: Median_RT indicates average of median reaction time for all conditions in the task; nbk indicates n‐back task.

^a Indicates p < .05.

^b Indicates p < .01.

4. DISCUSSION

In order to segment the human cerebral cortex into layers using a noninvasive method, we segmented the left hemisphere into two layers using dMRI and proved the reliability of our results. Furthermore, the results were then applied to construct laminar connections and to analyze the laminar structure of the working memory.

The segmentation results of some regions were generally unsatisfactory in multiple subjects. These regions were mainly concentrated in the Limbic lobe, the orbital frontal cortex, the insula and the anterior tip of the temporal lobe. Their clustering stability results are also relatively poor. It is probably because these regions belong to or are close to the limbic cortex, which has an incomplete or not obvious layer structure (Ángel García‐Cabezas et al., 2019). More detailed analysis and results are presented in the supplementary material, in particular in Figures 1, 2, 3.

Figure 6 shows that ADC‐related parameters in the superficial layer are larger than those in the deep layer in most regions, which is consistent with previous studies (Assaf, 2018; Kleinnijenhuis et al., 2013; Trong‐Kha et al., 2014). These studies have also shown that the fractional anisotropy dMRI parameter varies with the cortical depth and that its value is related to the complexity of the myeloarchitecture. When we segment the cortex into layers, regardless of whether GFA is present in the clustering features, either the t‐test or the Wilcoxon rank sum test results show that the GFA parameter is significantly different in the superficial layer compared to the deep layer for most regions. In Figure 6 and in supplementary Figure S6, the boxplot of the GFA parameter also shows the differences between the two layers. We think a possible explanation for the fact that layer segmentation does not change much after adding GFA could be that the previously used features already encode the information of the GFA; that is, GFA is not an independent feature from these ADC‐derived features. Therefore, the multiple linear regression model was applied, and ADC‐derived 31‐dimensional features were used to fit the GFA feature. We then used the F‐test with a significance level α equal to .05 to test the regression equation's significance, with all 𝑝 values being less than .001, that is, 𝑝 < .001. This result also proves what was suspected. However, after adding GFA into the features, the superficial thickness decreased slightly for most regions. Furthermore, in addition to the slight decrease in the correlation with the BigBrain superficial thickness, the correlation with the von Economo layer thickness and the one with the BigBrain deep thickness have increased. Although the difference is slight compared with the previous results, we think that adding GFA into the features will make the results more accurate when using dMRI to segment the cerebral cortex into layers.

The connections estimated using dMRI have no directional information. That is, the origin and the end of each connection are unknown. Therefore, two pairs of regions with known unidirectional connections were selected for verification purposes. Referring to the hierarchical laminar connection data from (Felleman & Essen, 1991), the connections between regions V4t and V1 only originate from V4t's deep layer to V1. In contrast, the connections between regions V2 and FST only originate from V2's superficial layer to FST. However, it is unknown which specific layer the connections terminate at. In hierarchical laminar connection patterns, projections that originate primarily from the superficial layer and terminate in layer four are classified as “forward.” In contrast, projections that originate mainly from the deep layer and terminate outside layer four, particularly in the superficial layers, are classified as “backward.” Thus, the connections from V4t to V1 are regarded as backward projections, while the connections from V2 to FST are considered to be forward projections. In our results, the connections between V4t's deep layer and V1's superficial layer, as well as the connections between V2's superficial layer and FST's deep layer, are the strongest. The results fit the “forward” and “backward” projection patterns.

In addition, these conclusions on laminar connection patterns come from experiments carried out on macaque monkey brains. Because of their invasive nature, applying some histological experiments to the human brain is challenging. In previous studies (Mackey & Petrides, 2010; Petrides et al., 2012), some experiments on the human brain have been based on conclusions from experiments on the macaque monkey brain while achieving good results due to the similarities between the human and macaque brains. Therefore, we think applying these conclusions to the human brain makes sense.

A recent study (Donahue et al., 2016) quantitatively compared the dMRI tractography data with the tracer data. A correlation was found between these two data, though the correlation was small. This suggests that the dMRI tractography data is valuable yet far from perfect. In our study, the proportion of laminar connections per unit volume between V4t's deep layer and V1's superficial layer, as well as between V2's superficial layer and FST's deep layer, are the strongest. In addition, the laminar connections between deep layers are also strong. It is probably because the deep layers are close to white matter, which is full of regularly distributed fibers. Moreover, using dMRI to estimate the fibers in grey matter is not easy. Therefore, many connections estimated by dMRI between deep layers should end at superficial layers, and the connections between the deep layers should have been overestimated. Thus, this result is good enough for the dMRI. Considering the noninvasive nature of dMRI data, this approach is still a good choice for studying laminar connections, especially for the human brain.

Our study on the correlation between the working memory and the cortical thickness shows that dlPFC's thickness is positively correlated with the reaction time. The median reaction time was negatively correlated with the accuracy (r = −0.5932, p < .001). This suggests a negative correlation between cortical thickness and working memory performance, which may differ from popular perception. Nevertheless, some previous studies have found a negative correlation between cortical thickness and working memory performance (Krogsrud et al., 2021; Metzler‐Baddeley et al., 2016; Østby et al., 2011). This negative correlation also is found in other cognitive tasks (Boen et al., 2021). Studies (Whitaker et al., 2016) have shown that cortical thickness during adolescence is negatively correlated with myelination, and more rapidly shrinking cortical thickness had faster rates of myelination. Therefore, a better working memory performance is probably associated with more myelination.

In dlPFC, the superficial thickness was only significantly correlated with the 2‐back task but not with the 0‐back task. The deep thickness, however, was correlated with the 0‐back task. Past research (Bastos et al., 2018; Markowitz et al., 2015) has shown that the prefrontal cortex's different layers are responsible for different patterns of the working memory. Furthermore, recent studies (Finn et al., 2019) on fMRI have demonstrated that during maintenance in the dlPFC, superficial layers are preferentially active, especially when the task requires much more manipulation. On the other hand, during the response, deep layers are preferentially active. Compared with the 0‐back task, the 2‐back task requires more maintenance and manipulation, which explains the correlation between superficial thickness and the 2‐back task but not the 0‐back task. However, both the 2‐back and 0‐back tasks require responses, and 0‐back tasks are more affected by the response, which may explain why the deep layer is mainly correlated with these tasks. Since the subjects were all adults between 26 and 35 years old and there was little age difference, the age influence was not considered.

In the future, we will try to combine structural MRI and dMRI with higher resolution to investigate the cortical laminar structure. Meanwhile, the functional MRI will be used to further validate the laminar structure and to explain the relationship between laminar structure and function.

5. CONCLUSIONS

Most methods used to study the cortex laminar structure are invasive, so it is not easy to experiment on living humans. Therefore, finding a noninvasive way to learn more about the laminar structure is vital to understanding the human brain. Our research provides a noninvasive method to segment the whole left human hemisphere into layers. This provides a basis for further exploring and simulating the human brain in the future. Additionally, it offers new ideas for further understanding and treating brain‐related diseases. In the future, we hope to segment the brain with higher resolution data to improve the accuracy of the results. Furthermore, we hope to use a more accurate method to construct laminar connections and further analyze the relationship between laminar structure and human cognition.

FUNDING INFORMATION

The National Natural Science Foundation of China (61673224, 11932013), Tianjin Natural Science Foundation for Distin‐guished Young Scholars (No. 18JCJQJC46100), PICT 2017–3208, PICT2020‐SERIEA‐00457, UBACYT20020190200305BA and UBACYT20020170100192BA (Argentina). J.S‐C. work is also based upon work from COST Action CA18106, supported by COST (European Cooperation in Science and Technology). Y. Z. is supported by Lehigh University Accelerator, FIG, and CORE Grants.

CONFLICT OF INTEREST

None of the authors has any conflict of interest to disclose.

Supporting information

Appendix S1 Supporting information

Zhang, J. , Sun, Z. , Duan, F. , Shi, L. , Zhang, Y. , Solé‐Casals, J. , & Caiafa, C. F. (2022). Cerebral cortex layer segmentation using diffusion magnetic resonance imaging in vivo with applications to laminar connections and working memory analysis. Human Brain Mapping, 43(17), 5220–5234. 10.1002/hbm.25998

DATA AVAILABILITY STATEMENT

Diffusion MRI data were obtained from the open dataset, the WU‐Minn Human Connectome Project (Essen et al., 2013), which is freely available at https://db.humanconnectome.org/. The thickness and layer thickness data are in the supplementary material. The code used to segment the cerebral cortex is available at https://github.com/JieZhang11/LayerdMRI.