Analytical solution of non-Fourier heat conduction in a 3-D hollow sphere under time-space varying boundary conditions

Abstract

In the current research, a comprehensive analytical technique is presented to evaluate the non-Fourier thermal behavior of a 3-D hollow sphere subjected to arbitrarily-chosen space and time dependent boundary conditions. The transient hyperbolic thermal diffusion equation is driven based upon the Cattaneo-Vernotte (C-V) model and nondimensionalized using proper dimensionless parameters. The conventional procedure of separation of variables is applied for solving the 3-D hyperbolic heat conduction equation with general boundary conditions. In order to handle the time dependency of the boundary conditions, Duhamel's theorem is employed. Furthermore, for the purpose of demonstrating the applicability of the obtained general solution, two particular cases with different time-space varying boundary conditions are considered. Subsequently, their respective non-Fourier thermal characteristics are elaborately discussed and compared with the Fourier case. The quantitative analysis is carried out, including the profiles of the time-dependent temperature and 3-D distributions of temperature at different time frames. Eventually, the influences of the controlling factors such as Fourier number and Vernotte number on the temperature field distributions within a hollow sphere for both cases are assessed. The findings reveal that the lag time in the hyperbolic thermal propagation diminishes with a decrement of Vernotte number, and it asymptotically vanishes for the Fourier case. Also, the number and severity of the jump points that occurred in the non-Fourier cases decrease by increasing the Fourier number, and these points finally vanish at particular Fourier numbers.

Mathematical solution; Non-Fourier heat conduction; 3D modeling; Time-space dependent boundary conditions

1. Introduction

The traditional Fourier law implies an unbounded pace for thermal disturbance propagation [1], [2], which disagrees with some experimental observations [3], [4], [5]. In this model, any thermal disturbance imposed on a medium is instantly perceived through the entire body [6], [7]. It is now approved that in specific scientific cases, including the heat transfer phenomena at the nanoscale [8], extremely great thermal energy flux for annealing of semiconductors [9], [10], laser-material interactions with concise duration [11], a low-temperature application like cryogenics [12], [13], laser surgery in biomedical engineering, and impulse drying [14], [15], Fourier's thermal conduction theory gets physically unreasonable. During the last few decades, multiple endeavors have done to postulate a novel heat conduction formulation to substitute Fourier's law and propose accurate evaluations for thermal investigation in pragmatic applications. The most well-known model is the hyperbolic heat conduction represented by Cattaneo [16] and Verenotte [17], which becomes more authentic in characterizing the diffusion procedure and assessing the temperature profile, especially in the biological tissues. This model is accepted due to its plainness and usefulness [18]. In order to rectify the contradiction of the unlimited speed of thermal propagation, they improved Fourier's equation by considering a relaxation time. Accordingly, the thermal conduction equation was modified to a hyperbolic wave equation. This model describes the thermal wave to the lagging impact between heat flux and temperature gradient.

In an attempt to analyze the thermal characteristics of materials with non-Fourier behavior, various researchers have contributed to solving the problem of non-Fourier thermal diffusion in different geometries and with several choices of material properties. Baharmi et al. [19] analytically investigated the axisymmetric 2-D non-Fourier temperature field in a hollow sphere subjected to a transient boundary heat flux. Moosaie [20] employed an analytical approach to solve the two-dimensional Cattaneo–Vernotte hyperbolic heat conduction equation in the spherical coordinate system. The treatment of the proposed solution is evaluated under various types of boundary conditions. Talaee and Atefi [21] performed an analytical study to determine the non-Fourier temperature field within a finite hollow cylinder subjected to a periodic wall heat flux. They employed the separation of variables method combined with Duhamel's principle to deal with the problem containing time-varying boundary conditions. Shirmohammadi and Moosaie [22] generated an exact mathematical expression for the temperature distribution in a hollow sphere with the non-uniform heat flux applied to its outer surface. They also assessed the switching procedure from Fourier to non-Fourier thermal treatment by evaluating the results obtained by parabolic and hyperbolic models. Luo et al. [23] conducted a mathematical procedure to inspect the transient heat transfer response of a one-dimensional finite medium under prescribed fixed heat flux at the one side and isothermal boundary at the other side with several relaxation times. Then, they modified the initial condition to achieve precise solutions for the cases of suddenly applied wall heat flux. Wankhade et al. [24] analyzed wet fins' temperature response by employing both Fourier and non-Fourier thermal conduction theories. Two types of boundary conditions, namely isothermal and convective base conditions, were considered to study the non-Fourier impact on the wet fin's temperature profile and heat transfer behavior. Ahmadikia et al. [25] presented a theoretical solution of the thermal wave model to describe the bioheat transfer in a skin tissue with uniform and time-dependent heat flux conditions. They applied the Laplace transform method for semi-infinite and finite regions. The skin's thermal damage is investigated by using both the Fourier and non-Fourier heat transfer equations.

Based on the current literature review, almost all of the studies carried out in the context of non-Fourier thermal conduction are limited to 1-D and 2-D problems under the effect of specific types of boundary conditions. In addition, although analytical method has a great ability in evaluating the problems of science and engineering [26], to the best of the authors' knowledge, there is not any comprehensive analytical research on the temperature response in a spherical body under the general space-time dependent boundary conditions. Also, the classical thermal conduction theory based on Fourier's law considers an unlimited thermal disturbance propagation rate, which is physically impractical. In an attempt to fill these gaps, the current work aims to analyze the non-Fourier thermal treatment of a hollow sphere subjected to the arbitrarily-chosen space and time-dependent boundary conditions using the three-dimensional hyperbolic thermal diffusion equation. The main objective of this study is to present a general analytical solution which can be used for different practical applications. The well-known method of separation of variables is employed for handling the problem with time-independent boundary conditions. Then, the obtained result is generalized using Duhamel's Theorem to cope with the time dependency of the boundary conditions. In order to prove the acceptability of the proposed model, the solution is applied for the special cases of boundary conditions, and their corresponding non-Fourier thermal characteristics are elaborately discussed and compared with Fourier ones. Finally, the impacts of the key factors, namely, Fourier number and Vernotte number a hollow sphere's temperature field distributions are scrutinized.

2. Description and geometry of the problem

In the current work, it is presumed that a hollow sphere with inner radius $r_i$ and outer radius $r_o$ is subjected to the arbitrary space-time dependent boundary condition. The sphere is considered to be composed of a homogeneous and isotropic heat conducting material with constant thermal features and non-Fourier behavior. The spherical polar coordinate (r, θ, φ) system is used in order to analyze the system's heat transfer behavior, where r, θ, and φ are the radial distance, polar angle, and azimuthal angle, orderly. The schematic diagram of the sphere and the coordinates are demonstrated in Fig. 1.

Figure 1.

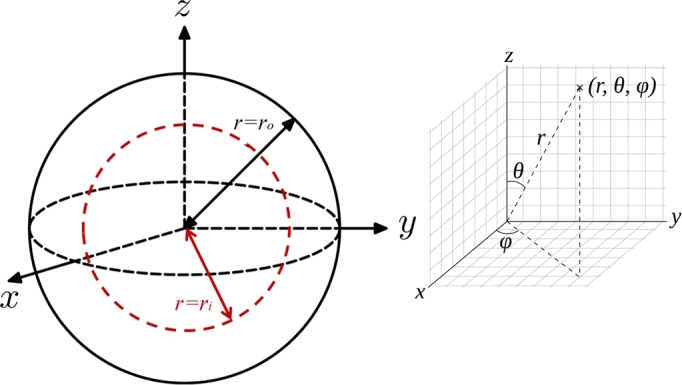
The sphere configuration.

3. Mathematical analysis

3.1. Heat transfer model

The following assumptions are adopted in the current study.

• •Only conductive heat transfer mode is taken into account within the material.
• •Heat conduction in the sphere is three-dimensional and transient.
• •The medium is considered homogeneous and isotropic.
• •The surroundings temperature is uniform.
• •The thermal properties of material are assumed to be constant.
• •Since boundary conditions involve thermal interaction with the medium, convection mode of surface heat transfer is considered.

In this study, the Cattaneo-Vernotte (C-V) model is applied to scrutinize the heat transfer behavior of the considered system. Cattaneo [16] and Vernotte [17] proposed a modified type of Fourier's theory by considering a relaxation time of heat flux. In this respect, the conventional thermal conduction equation is transferred into a hyperbolic wave equation [27]. The C-V constitutive equation for heat conduction is expressed in the form of

$$-k\mathrm{\nabla }T={\tau }_q\frac{\partial q}{\partial t}+q$$ (1)

where q and k are the heat flux and thermal conductivity, respectively. ${\tau }_q$ is relaxation time and describes the time lag required for the heat flux to initiate with the temperature gradient exerted on the element [28]. For thermal diffusion procedures unaccompanied by an internal heat source or sink, the conservation of internal energy yields [29]

$$\frac{\partial \rho C_{v}T}{\partial t}+\mathrm{\nabla }.q=0$$ (2)

where ρ is the density of material, $C_v$ is the volumetric specific heat. Consequently, a combination of Eqs. (1), (2) give the hyperbolic temperature evolution equation

$$\alpha {\mathrm{\nabla }}^{2}T={\tau }_q\frac{{\partial }^{2}T}{\partial t^2}+\frac{\partial T}{\partial t}$$ (3)

where $\alpha =\frac{k}{\rho C_v}$ is the thermal diffusivity. Eq. (3) describes that the heat propagates as a weakening wave with a finite pace of ${(\alpha /{\tau }_q)}^{1/2}$.

3.2. Analytical solution

The three-dimensional, differential equation of hyperbolic heat diffusion in the spherical coordinate system can be given as

$$\frac{{\partial }^{2}T}{\partial r^2}+\frac{2}{r}\frac{\partial T}{\partial r}+\frac{1}{r^2\sin \theta }\frac{\partial }{\partial \theta }(\sin \theta \frac{\partial T}{\partial \theta })+\frac{1}{r^2{\sin }^2\theta }\frac{{\partial }^{2}T}{\partial {\phi }^2}=\frac{1}{\alpha }[{\tau }_q\frac{{\partial }^{2}T}{\partial t^2}+\frac{\partial T}{\partial t}]$$ (4)

To aid our solution of Eq. (4), it is convenient to define a new independent variable μ as

$$\mu =\cos \theta$$ (5)

Substituting Eq. (5) into Eq. (4) gives

$$\frac{{\partial }^{2}T}{\partial r^2}+\frac{2}{r}\frac{\partial T}{\partial r}+\frac{1}{r^2}\frac{\partial }{\partial \mu }\left((1-{\mu }^2)\frac{\partial T}{\partial \mu }\right)+\frac{1}{r^2(1-{\mu }^2)}\frac{{\partial }^{2}T}{\partial {\phi }^2}=\frac{1}{\alpha }[{\tau }_q\frac{{\partial }^{2}T}{\partial t^2}+\frac{\partial T}{\partial t}]$$ (6)

Eq. (6) can be handled subject to the boundary conditions

$$-k_1{\frac{\partial T}{\partial r}|}_{r=r_i}+h_1({T|}_{r=r_i}-T_{\infty })=F_i(\mu ,\phi ,t)$$ (7a)

$$k_2{\frac{\partial T}{\partial r}|}_{r=r_o}+h_2({T|}_{r=r_o}-T_{\infty })=F_o(\mu ,\phi ,t)$$ (7b)

$$T(\mu \to \pm 1)=finite$$ (7c)

$$T\left(\phi \right)=T(\phi +2\pi )$$ (7d)

$${\frac{\partial T}{\partial \phi }|}_{\phi }={\frac{\partial T}{\partial \phi }|}_{\phi +2\pi }$$ (7e)

In Eqs. (7a) and (7b), $F_i(\mu ,\phi ,t)$ and $F_o(\mu ,\phi ,t)$ are arbitrary functions. The initial conditions are considered to be as Eqs. (8a) and (8b).

$$T(t=0)=T_0$$ (8a)

$${\frac{\partial T}{\partial t}|}_{t=0}=0$$ (8b)

To evaluate the influences of crucial factors on the thermal treatment of the sphere, the following dimensionless variables are introduced as Eq. (9).

$$\overline{r}=\frac{r}{r_o},\overline{t}=\frac{\alpha t}{r_o^2},{\gamma }_e=\sqrt{\frac{\alpha {\tau }_q}{r_o^2}},\epsilon =\frac{r_i}{r_o}$$ (9)

where $\overline{t}$ is the Fourier number and ${\gamma }_e$ is the Vernotte number. Defining a new temperature variable $\overline{T}=T-T_{\infty }$ and applying the aforementioned non-dimensional variables to Eq. (4) gives

$$\frac{{\partial }^2\overline{T}}{\partial {\overline{r}}^2}+\frac{2}{\overline{r}}\frac{\partial \overline{T}}{\partial \overline{r}}+\frac{1}{{\overline{r}}^2}\frac{\partial }{\partial \mu }\left((1-{\mu }^2)\frac{\partial \overline{T}}{\partial \mu }\right)+\frac{1}{{\overline{r}}^2(1-{\mu }^2)}\frac{{\partial }^2\overline{T}}{\partial {\phi }^2}={\gamma }_e^2\frac{{\partial }^2\overline{T}}{\partial {\overline{t}}^2}+\frac{\partial \overline{T}}{\partial \overline{t}}$$ (10)

with the boundary conditions

$${-\frac{k_1}{r_o}\frac{\partial \overline{T}}{\partial \overline{r}}|}_{\overline{r}=\epsilon }+h_1{\overline{T}|}_{\overline{r}=\epsilon }=F_i(\mu ,\phi ,\overline{t})=f_i(\mu ,\phi )[g_i\left(\overline{t}\right)+{\gamma }_e^2\frac{d{g}_i\left(\overline{t}\right)}{d\overline{t}}]$$ (11a)

$$\frac{k_2}{r_o}{\frac{\partial \overline{T}}{\partial \overline{r}}|}_{\overline{r}=1}+h_2{\overline{T}|}_{\overline{r}=1}=F_o(\mu ,\phi ,\overline{t})=f_o(\mu ,\phi )[g_o\left(\overline{t}\right)+{\gamma }_e^2\frac{d{g}_o\left(\overline{t}\right)}{d\overline{t}}]$$ (11b)

$$\overline{T}(\mu \to \pm 1)=finite$$ (11c)

$$\overline{T}\left(\phi \right)=\overline{T}(\phi +2\pi )$$ (11d)

$${\frac{\partial \overline{T}}{\partial \phi }|}_{\phi }={\frac{\partial \overline{T}}{\partial \phi }|}_{\phi +2\pi }$$ (11e)

Eqs. (11a) and (11b) can be rewritten as

$${-\frac{\partial \overline{T}}{\partial \overline{r}}|}_{\overline{r}=\epsilon }+H_1{\overline{T}|}_{\overline{r}=\epsilon }={\overline{F}}_i(\mu ,\phi ,\overline{t})={\overline{f}}_i(\mu ,\phi )[g_i\left(\overline{t}\right)+{\gamma }_e^2\frac{d{g}_i\left(\overline{t}\right)}{d\overline{t}}]$$ (12a)

$${\frac{\partial \overline{T}}{\partial \overline{r}}|}_{\overline{r}=1}+H_2{\overline{T}|}_{\overline{r}=1}={\overline{F}}_o(\mu ,\phi ,\overline{t})={\overline{f}}_o(\mu ,\phi )[g_o\left(\overline{t}\right)+{\gamma }_e^2\frac{d{g}_o\left(\overline{t}\right)}{d\overline{t}}]$$ (12b)

The unknown variables in Eqs. (12a) and (12b) are defined by Eq. (13).

$$\begin{array}{c}{H}_1=\frac{h_1{r}_o}{k_1},H_2=\frac{h_2{r}_o}{k_2},{\overline{F}}_i(\mu ,\phi ,\overline{t})=\frac{r_o{F}_i(\mu ,\phi ,\overline{t})}{k_1},{\overline{F}}_o(\mu ,\phi ,\overline{t})=\frac{r_o{F}_o(\mu ,\phi ,\overline{t})}{k_2}\hfill \\ {\overline{f}}_i(\mu ,\phi ,\overline{t})=\frac{r_o{f}_i(\mu ,\phi )}{k_1},{\overline{f}}_o(\mu ,\phi ,\overline{t})=\frac{r_o{f}_o(\mu ,\phi )}{k_2}\hfill \end{array}$$ (13)

The initial conditions become as Eqs. (14a) and (14b).

$$\overline{T}(\overline{t}=0)={\overline{T}}_0$$ (14a)

$${\frac{\partial \overline{T}}{\partial \overline{t}}|}_{\overline{t}=0}=0$$ (14b)

Since the boundary and initial conditions are non-homogeneous, Duhamel's theorem cannot be utilized straightly [30]. We represent a solution of the form

$$\overline{T}(\overline{r},\mu ,\phi ,\overline{t})={\overline{T}}_1(\overline{r},\mu ,\phi ,\overline{t})+{\overline{T}}_2(\overline{r},\mu ,\phi ,\overline{t})$$ (15)

where, ${\overline{T}}_1(\overline{r},\mu ,\phi ,\overline{t})$ is introduced to satisfy the homogeneous boundary conditions and non-homogeneous initial conditions, while ${\overline{T}}_2(\overline{r},\mu ,\phi ,\overline{t})$ takes the non-homogeneous boundary conditions and homogeneous initial conditions. Substituting Eq. (15) into Eq. (10) and splitting it into two parts yields

$$\frac{{\partial }^2{\overline{T}}_1}{\partial {\overline{r}}^2}+\frac{2}{\overline{r}}\frac{\partial {\overline{T}}_1}{\partial \overline{r}}+\frac{1}{{\overline{r}}^2}\frac{\partial }{\partial \mu }\left((1-{\mu }^2)\frac{\partial {\overline{T}}_1}{\partial \mu }\right)+\frac{1}{{\overline{r}}^2(1-{\mu }^2)}\frac{{\partial }^2{\overline{T}}_1}{\partial {\phi }^2}={\gamma }_e^2\frac{{\partial }^2{\overline{T}}_1}{\partial {\overline{t}}^2}+\frac{\partial {\overline{T}}_1}{\partial \overline{t}}$$ (16)

The boundary and initial conditions are

$$-{\frac{\partial {\overline{T}}_1}{\partial \overline{r}}|}_{\overline{r}=\epsilon }+H_1{{\overline{T}}_1|}_{\overline{r}=\epsilon }=0$$ (17a)

$${\frac{\partial {\overline{T}}_1}{\partial \overline{r}}|}_{\overline{r}=1}+H_2{{\overline{T}}_1|}_{\overline{r}=1}=0$$ (17b)

$${\overline{T}}_1(\mu \to \pm 1)=finite$$ (17c)

$${\overline{T}}_1\left(\phi \right)={\overline{T}}_1(\phi +2\pi )$$ (17d)

$${\frac{\partial {\overline{T}}_1}{\partial \phi }|}_{\phi }={\frac{\partial {\overline{T}}_1}{\partial \phi }|}_{\phi +2\pi }$$ (17e)

$${\overline{T}}_1(\overline{t}=0)={\overline{T}}_0$$ (18a)

$${\frac{\partial {\overline{T}}_1}{\partial \overline{t}}|}_{\overline{t}=0}=0$$ (18b)

We now introduce a new dependent variable $V_1(\overline{r},\mu ,\phi ,\overline{t})$, using the transform

$$V_1(\overline{r},\mu ,\phi ,\overline{t})={\overline{r}}^{\frac{1}{2}}{\overline{T}}_1(\overline{r},\mu ,\phi ,\overline{t})$$ (19)

which upon substitution Eq. (19) into Eq. (16) yields Eq. (20).

$$\frac{{\partial }^2{V}_1}{\partial {\overline{r}}^2}+\frac{2}{\overline{r}}\frac{\partial V_1}{\partial \overline{r}}-\frac{1}{4}\frac{V_1}{{\overline{r}}^2}+\frac{1}{{\overline{r}}^2}\frac{\partial }{\partial \mu }\left((1-{\mu }^2)\frac{\partial V_1}{\partial \mu }\right)+\frac{1}{{\overline{r}}^2(1-{\mu }^2)}\frac{{\partial }^2{V}_1}{\partial {\phi }^2}={\gamma }_e^2\frac{{\partial }^2{V}_1}{\partial {\overline{t}}^2}+\frac{\partial V_1}{\partial \overline{t}}$$ (20)

Using such a transformation, the boundary and initial conditions (Eqs. (17a)–(17e) and Eqs. (18a), (18b)) become Eqs. (21a)–(21e) and Eqs. (22a), (22b), respectively.

$$-{\frac{\partial V_1}{\partial \overline{r}}|}_{\overline{r}=\epsilon }+(H_1+\frac{1}{2\epsilon }){V_1|}_{\overline{r}=\epsilon }=0$$ (21a)

$${\frac{\partial V_1}{\partial \overline{r}}|}_{\overline{r}=1}+(H_2-\frac{1}{2}){V_1|}_{\overline{r}=1}=0$$ (21b)

$$V_1(\mu \to \pm 1)=finite$$ (21c)

$$V_1\left(\phi \right)=V_1(\phi +2\pi )$$ (21d)

$${\frac{\partial V_1}{\partial \phi }|}_{\phi }={\frac{\partial V_1}{\partial \phi }|}_{\phi +2\pi }$$ (21e)

$$V_1(\overline{t}=0)={\overline{T}}_0{\overline{r}}^{\frac{1}{2}}$$ (22a)

$${\frac{\partial V_1}{\partial \overline{t}}|}_{\overline{t}=0}=0$$ (22b)

Taking into account a product solution of the form

$$V_1(\overline{r},\mu ,\phi ,\overline{t})=R\left(\overline{r}\right)M\left(\mu \right)\mathrm{\Phi }\left(\phi \right)\mathrm{\Gamma }\left(\overline{t}\right)$$ (23)

Substituting Eq. (23) into the PDE, separating variables, and setting the acquired equation equal to a constant yields the following four ordinary differential equations.

$${\gamma }_e^2\frac{d^2\mathrm{\Gamma }}{d{\overline{t}}^2}+\frac{d\mathrm{\Gamma }}{d\overline{t}}+{\lambda }^2\mathrm{\Gamma }=0$$ (24)

$$\frac{d^2\mathrm{\Phi }}{d{\phi }^2}+m^2\mathrm{\Phi }=0$$ (25)

$$\frac{d}{d\mu }\left[(1-{\mu }^2)\frac{dM}{d\mu }\right]+[n(n+1)-\frac{m^2}{1-{\mu }^2}]M=0$$ (26)

$$\frac{d^{2}R}{d{\overline{r}}^2}+\frac{1}{\overline{r}}\frac{dR}{d\overline{r}}+[{\lambda }^2-\frac{{(n+\frac{1}{2})}^2}{{\overline{r}}^2}]R=0$$ (27)

The solution of Eq. (24) imposed to the initial condition (Eq. (22b)) is obtained by Eqs. (28a), (28b).

$$\mathrm{\Gamma }\left(\overline{t}\right)=c_2{e}^{\frac{-\overline{t}}{2{\gamma }_e^2}}[2{\gamma }_e^2\eta \cosh \left(\eta \overline{t}\right)+\sinh \left(\eta \overline{t}\right)]\text{if}1\ge 4{\gamma }_e^2{\lambda }^2$$ (28a)

$$\mathrm{\Gamma }\left(\overline{t}\right)=c_2{e}^{\frac{-\overline{t}}{2{\gamma }_e^2}}[2{\gamma }_e^2{\eta }_i\cos \left({\eta }_i\overline{t}\right)+\sin \left({\eta }_i\overline{t}\right)]\text{if}1<4{\gamma }_e^2{\lambda }^2$$ (28b)

where η and ${\eta }_i$ can be calculated by Eq. (29).

$$\eta =i{\eta }_i=\frac{\sqrt{1-4{\gamma }_e^2{\lambda }^2}}{2{\gamma }_e^2}$$ (29)

The solutions of the Eqs. (25)–(27) with the help of the associated boundary conditions can be given as Eqs. (30)–(32), respectively,

$$\mathrm{\Phi }\left(\phi \right)=a_m\cos \left(m\phi \right)+b_m\sin \left(m\phi \right),m=0,1,2,3,...$$ (30)

$$M\left(\mu \right)=c_{nm}{P}_n^m\left(\mu \right),n=0,1,2,3,...,m=0,1,2,3,...$$ (31)

$$\begin{array}{c}{R}_{n+\frac{1}{2}}({\lambda }_{np},\overline{r})=c_{np}[\frac{{\lambda }_{np}{Y}_{n-\frac{1}{2}}\left(\epsilon {\lambda }_{np}\right)-2(H_1+\frac{1}{2\epsilon })Y_{n+\frac{1}{2}}\left(\epsilon {\lambda }_{np}\right)-{\lambda }_{np}{Y}_{n+\frac{3}{2}}\left(\epsilon {\lambda }_{np}\right)}{-{\lambda }_{np}{J}_{n-\frac{1}{2}}\left(\epsilon {\lambda }_{np}\right)+2(H_1+\frac{1}{2\epsilon })J_{n+\frac{1}{2}}\left(\epsilon {\lambda }_{np}\right)+{\lambda }_{np}{J}_{n+\frac{3}{2}}\left(\epsilon {\lambda }_{np}\right)}{J}_{n+\frac{1}{2}}\left({\lambda }_{np}\overline{r}\right)+Y_{n+\frac{1}{2}}\left({\lambda }_{np}\overline{r}\right)],\hfill \\ n=0,1,2,...,p=1,2,3,...\hfill \end{array}$$ (32)

where eigenfunctions ${\lambda }_{np}$ are the roots of the transcendental Eq. (33).

$$\frac{{\lambda }_{np}}{2}[\frac{{\lambda }_{np}{Y}_{n-\frac{1}{2}}\left(\epsilon {\lambda }_{np}\right)-2(H_1+\frac{1}{2\epsilon })Y_{n+\frac{1}{2}}\left(\epsilon {\lambda }_{np}\right)-{\lambda }_{np}{Y}_{n+\frac{3}{2}}\left(\epsilon {\lambda }_{np}\right)}{-{\lambda }_{np}{J}_{n-\frac{1}{2}}\left(\epsilon {\lambda }_{np}\right)+2(H_1+\frac{1}{2\epsilon })J_{n+\frac{1}{2}}\left(\epsilon {\lambda }_{np}\right)+{\lambda }_{np}{J}_{n+\frac{3}{2}}\left(\epsilon {\lambda }_{np}\right)}{J}_{n-\frac{1}{2}}\left({\lambda }_{np}\right)+Y_{n-\frac{1}{2}}\left({\lambda }_{np}\right)]-\frac{{\lambda }_{np}}{2}[\frac{{\lambda }_{np}{Y}_{n-\frac{1}{2}}\left(\epsilon {\lambda }_{np}\right)-2(H_1+\frac{1}{2\epsilon })Y_{n+\frac{1}{2}}\left(\epsilon {\lambda }_{np}\right)-{\lambda }_{np}{Y}_{n+\frac{3}{2}}\left(\epsilon {\lambda }_{np}\right)}{-{\lambda }_{np}{J}_{n-\frac{1}{2}}\left(\epsilon {\lambda }_{np}\right)+2(H_1+\frac{1}{2\epsilon })J_{n+\frac{1}{2}}\left(\epsilon {\lambda }_{np}\right)+{\lambda }_{np}{J}_{n+\frac{3}{2}}\left(\epsilon {\lambda }_{np}\right)}{J}_{n+\frac{3}{2}}\left({\lambda }_{np}\right)+Y_{n+\frac{3}{2}}\left({\lambda }_{np}\right)]+(H_2-\frac{1}{2})[\frac{{\lambda }_{np}{Y}_{n-\frac{1}{2}}\left(\epsilon {\lambda }_{np}\right)-2(H_1+\frac{1}{2\epsilon })Y_{n+\frac{1}{2}}\left(\epsilon {\lambda }_{np}\right)-{\lambda }_{np}{Y}_{n+\frac{3}{2}}\left(\epsilon {\lambda }_{np}\right)}{-{\lambda }_{np}{J}_{n-\frac{1}{2}}\left(\epsilon {\lambda }_{np}\right)+2(H_1+\frac{1}{2\epsilon })J_{n+\frac{1}{2}}\left(\epsilon {\lambda }_{np}\right)+{\lambda }_{np}{J}_{n+\frac{3}{2}}\left(\epsilon {\lambda }_{np}\right)}{J}_{n+\frac{1}{2}}\left({\lambda }_{np}\right)+Y_{n+\frac{1}{2}}\left({\lambda }_{np}\right)]=0$$ (33)

We now form the general solution by summing over all possible product solutions, yielding Eq. (34).

$$V_1(\overline{r},\mu ,\phi ,\overline{t})=\sum _{p=1}^P\sum _{n=0}^N\sum _{m=0}^n{e}^{\frac{-\overline{t}}{2{\gamma }_e^2}}[2{\gamma }_e^2\eta \cosh \left(\eta \overline{t}\right)+\sinh \left(\eta \overline{t}\right)][a_{nmp}\cos \left(m\phi \right)+b_{nmp}\sin \left(m\phi \right)]R_{n+\frac{1}{2}}({\lambda }_{np},\overline{r})P_n^m\left(\mu \right)+\sum _{p=P+1}^{\infty }\sum _{n=N+1}^{\infty }\sum _{m=0}^n{e}^{\frac{-\overline{t}}{2{\gamma }_e^2}}[2{\gamma }_e^2{\eta }_i\cos \left({\eta }_i\overline{t}\right)+\sin \left({\eta }_i\overline{t}\right)][a_{nmp}\cos \left(m\phi \right)+b_{nmp}\sin \left(m\phi \right)]R_{n+\frac{1}{2}}({\lambda }_{np},\overline{r})P_n^m\left(\mu \right)$$ (34)

Where P and N are maximum magnitude of p and n, respectively, when the η is real for each loop.

Applying the initial condition and invoking orthogonality results in Eqs. (35a), (35b).

$$a_{nmp}=\frac{\frac{{\overline{T}}_0}{\pi }{\int }_{{\overline{r}}^{\prime }=\epsilon }^1{\int }_{{\mu }^{\prime }=-1}^1{\int }_{{\phi }^{\prime }=0}^{2\pi }{\overline{r}}^{\prime \frac{3}{2}}{R}_{n+\frac{1}{2}}({\lambda }_{np},{\overline{r}}^{\prime })P_n^m\left({\mu }^{\prime }\right)\cos \left(m{\phi }^{\prime }\right)d{\phi }^{\prime }d{\mu }^{\prime }d{\overline{r}}^{\prime }}{2{\gamma }_e^2\left|\eta \right|N(n,m)N\left({\lambda }_{np}\right)}$$ (35a)

$$b_{nmp}=\frac{\frac{{\overline{T}}_0}{\pi }{\int }_{{\overline{r}}^{\prime }=\epsilon }^1{\int }_{{\mu }^{\prime }=-1}^1{\int }_{{\phi }^{\prime }=0}^{2\pi }{\overline{r}}^{\prime \frac{3}{2}}{R}_{n+\frac{1}{2}}({\lambda }_{np},{\overline{r}}^{\prime })P_n^m\left({\mu }^{\prime }\right)\sin \left(m{\phi }^{\prime }\right)d{\phi }^{\prime }d{\mu }^{\prime }d{\overline{r}}^{\prime }}{2{\gamma }_e^2\left|\eta \right|N(n,m)N\left({\lambda }_{np}\right)}$$ (35b)

where $N(n,m)$ norm of the associated Legendre polynomials and $N\left({\lambda }_{np}\right)$ norm of the Bessel function can be determined by Eqs. (36a), (36b).

$$N(n,m)=\underset{-1}{\overset{1}{\int }}{\left[P_n^m\left({\mu }^{\prime }\right)\right]}^{2}d{\mu }^{\prime }=\frac{2}{2n+1}\frac{(n+m)!}{(n-m)!}$$ (36a)

$$N\left({\lambda }_{np}\right)=\underset{{\overline{r}}^{\prime }=\epsilon }{\overset{1}{\int }}{\overline{r}}^{\prime }{R}_{n+\frac{1}{2}}^2({\lambda }_{np},{\overline{r}}^{\prime })d{\overline{r}}^{\prime }$$ (36b)

Finally, we shift the problem back to ${\overline{T}}_1(\overline{r},\mu ,\phi ,\overline{t})$, yielding

$${\overline{T}}_1(\overline{r},\mu ,\phi ,\overline{t})=\frac{{\overline{T}}_0}{\pi {\overline{r}}^{\frac{1}{2}}}\{\sum _{p=1}^P\sum _{n=0}^N\sum _{m=0}^n\frac{(2n+1)}{2}\frac{(n-m)!}{(n+m)!}{e}^{\frac{-\overline{t}}{2{\gamma }_e^2}}[\cosh \left(\eta \overline{t}\right)+\frac{\sinh \left(\eta \overline{t}\right)}{2{\gamma }_e^2\eta }]\frac{R_{n+\frac{1}{2}}({\lambda }_{np},\overline{r})}{N\left({\lambda }_{np}\right)}{P}_n^m\left(\mu \right)+\sum _{p=P+1}^{\infty }\sum _{n=N+1}^{\infty }\sum _{m=0}^n\frac{(2n+1)}{2}\frac{(n-m)!}{(n+m)!}{e}^{\frac{-\overline{t}}{2{\gamma }_e^2}}[\cosh \left({\eta }_i\overline{t}\right)+\frac{\sinh \left({\eta }_i\overline{t}\right)}{2{\gamma }_e^2{\eta }_i}]\frac{R_{n+\frac{1}{2}}({\lambda }_{np},\overline{r})}{N\left({\lambda }_{np}\right)}{P}_n^m\left(\mu \right)\}\underset{{\overline{r}}^{\prime }=\epsilon }{\overset{1}{\int }}\underset{{\mu }^{\prime }=-1}{\overset{1}{\int }}\underset{{\phi }^{\prime }=0}{\overset{2\pi }{\int }}{\overline{r}}^{\prime \frac{3}{2}}{R}_{n+\frac{1}{2}}({\lambda }_{np},{\overline{r}}^{\prime })P_n^m\left({\mu }^{\prime }\right)\cos \left(m(\phi -{\phi }^{\prime })\right)d{\phi }^{\prime }d{\mu }^{\prime }d{\overline{r}}^{\prime }$$ (37)

Note that π should be replaced by 2π for the case of $m=0$.

The formulation for ${\overline{T}}_2(\overline{r},\mu ,\phi ,\overline{t})$ becomes

$$\frac{{\partial }^2{\overline{T}}_2}{\partial {\overline{r}}^2}+\frac{2}{\overline{r}}\frac{\partial {\overline{T}}_2}{\partial \overline{r}}+\frac{1}{{\overline{r}}^2}\frac{\partial }{\partial \mu }\left((1-{\mu }^2)\frac{\partial {\overline{T}}_2}{\partial \mu }\right)+\frac{1}{{\overline{r}}^2(1-{\mu }^2)}\frac{{\partial }^2{\overline{T}}_2}{\partial {\phi }^2}={\gamma }_e^2\frac{{\partial }^2{\overline{T}}_2}{\partial {\overline{t}}^2}+\frac{\partial {\overline{T}}_2}{\partial \overline{t}}$$ (38)

subject to the boundary and initial conditions

$$-{\frac{\partial {\overline{T}}_2}{\partial \overline{r}}|}_{\overline{r}=\epsilon }+H_1{{\overline{T}}_2|}_{\overline{r}=\epsilon }=f_i(\mu ,\phi )[g_i\left(\overline{t}\right)+{\gamma }_e^2\frac{d{g}_i\left(\overline{t}\right)}{d\overline{t}}]$$ (39a)

$${\frac{\partial {\overline{T}}_2}{\partial \overline{r}}|}_{\overline{r}=1}+H_2{{\overline{T}}_2|}_{\overline{r}=1}=f_o(\mu ,\phi )[{\mathrm{g}}_o\left(\overline{t}\right)+{\gamma }_e^2\frac{d{\mathrm{g}}_o\left(\overline{t}\right)}{d\overline{t}}]$$ (39b)

$${\overline{T}}_2(\mu \to \pm 1)=finite$$ (39c)

$${\overline{T}}_2\left(\phi \right)={\overline{T}}_2(\phi +2\pi )$$ (39d)

$${\frac{\partial {\overline{T}}_2}{\partial \phi }|}_{\phi }={\frac{\partial {\overline{T}}_2}{\partial \phi }|}_{\phi +2\pi }$$ (39e)

$${\overline{T}}_2(\overline{t}=0)=0$$ (40a)

$${\frac{\partial {\overline{T}}_2}{\partial \overline{t}}|}_{\overline{t}=0}=0$$ (40b)

The partial differential equation (Eq. (38)) subjected to Eqs. (39a)–(39e) and Eqs. (40a), (40b) cannot be solved by the method of separation of variables because of having two non-homogeneous conditions in the r-variable. Hence, Eq. (38) should be solved twice for two different sorts of boundary conditions. Problem 1 is introduced as Eqs. (41a), (41b).

$$-{\frac{\partial {\overline{T}}_{2,1}}{\partial \overline{r}}|}_{\overline{r}=\epsilon }+H_1{{\overline{T}}_{2,1}|}_{\overline{r}=\epsilon }=f_i(\mu ,\phi )[g_i\left(\overline{t}\right)+{\gamma }_e^2\frac{d{g}_i\left(\overline{t}\right)}{d\overline{t}}]$$ (41a)

$${\frac{\partial {\overline{T}}_{2,1}}{\partial \overline{r}}|}_{\overline{r}=1}+H_2{{\overline{T}}_{2,1}|}_{\overline{r}=1}=0$$ (41b)

The boundary conditions in r direction for problem 2 are as Eqs. (42a), (42b).

$$-{\frac{\partial {\overline{T}}_{2,2}}{\partial \overline{r}}|}_{\overline{r}=\epsilon }+H_1{{\overline{T}}_{2,2}|}_{\overline{r}=\epsilon }=0$$ (42a)

$${\frac{\partial {\overline{T}}_{2,2}}{\partial \overline{r}}|}_{\overline{r}=1}+H_2{{\overline{T}}_{2,2}|}_{\overline{r}=1}=f_o(\mu ,\phi )[{\mathrm{g}}_o\left(\overline{t}\right)+{\gamma }_e^2\frac{d{\mathrm{g}}_o\left(\overline{t}\right)}{d\overline{t}}]$$ (42b)

Problems 1 and 2 cannot be solved by the separation of variables technique because the nonhomogeneous boundary conditions are time-dependent. Hence, the two auxiliary problems regarding problems 1 and 2 are defined as follows.

• •Auxiliary problem 1

$$\frac{{\partial }^2{\psi }_1}{\partial {\overline{r}}^2}+\frac{2}{\overline{r}}\frac{\partial {\psi }_1}{\partial \overline{r}}+\frac{1}{{\overline{r}}^2}\frac{\partial }{\partial \mu }\left((1-{\mu }^2)\frac{\partial {\psi }_1}{\partial \mu }\right)+\frac{1}{{\overline{r}}^2(1-{\mu }^2)}\frac{{\partial }^2{\psi }_1}{\partial {\phi }^2}={\gamma }_e^2\frac{{\partial }^2{\psi }_1}{\partial {\overline{t}}^2}+\frac{\partial {\psi }_1}{\partial \overline{t}}$$ (43)

Eq. (43) is imposed to the appropriate boundary and initial conditions (Eqs. (44a)–(44e) and Eqs. (45a), (45b)).

$$-{\frac{\partial {\psi }_1}{\partial \overline{r}}|}_{\overline{r}=\epsilon }+H_1{{\psi }_1|}_{\overline{r}=\epsilon }=f_i(\mu ,\phi )$$ (44a)

$${\frac{\partial {\psi }_1}{\partial \overline{r}}|}_{\overline{r}=1}+H_2{{\psi }_1|}_{\overline{r}=1}=0$$ (44b)

$${\psi }_1(\mu \to \pm 1)=finite$$ (44c)

$${\psi }_1\left(\phi \right)={\psi }_1(\phi +2\pi )$$ (44d)

$${\frac{\partial {\psi }_1}{\partial \phi }|}_{\phi }={\frac{\partial {\psi }_1}{\partial \phi }|}_{\phi +2\pi }$$ (44e)

$${\psi }_1(\overline{t}=0)=0$$ (45a)

$${\frac{\partial {\psi }_1}{\partial \overline{t}}|}_{\overline{t}=0}=0$$ (45b)

Because all boundary conditions must be homogeneous for a transient problem, we use superposition of the form

$${\psi }_1(\overline{r},\mu ,\phi ,\overline{t})={\psi }_{1,ss}(\overline{r},\mu ,\phi )+{\psi }_{1,Tr}(\overline{r},\mu ,\phi ,\overline{t})$$ (46)

In Eq. (46), ${\psi }_{1,Tr}(\overline{r},\mu ,\phi ,\overline{t})$ takes the homogeneous version of the boundary conditions and ${\psi }_{1,ss}(\overline{r},\mu ,\phi )$ satisfies the nonhomogeneous boundary conditions.

The steady-state solution for the auxiliary problem is given by Eq. (47).

$${\psi }_{1,ss}=\frac{1}{\pi }\sum _{n=0}^{\infty }\sum _{m=0}^n\frac{(2n+1)}{2}\frac{(n-m)!}{(n+m)!}\frac{(\frac{1-H_2+n}{H_2+n}{\overline{r}}^n+{\overline{r}}^{-n-1})}{(1+n){\epsilon }^{-2-n}+H_1{\epsilon }^{-1-n}+\frac{1-H_2+n}{H_2+n}(-n{\epsilon }^{-1-n}+H_1{\epsilon }^n)}\times P_n^m\left(\mu \right)\underset{{\mu }^{\prime }=-1}{\overset{1}{\int }}\underset{{\phi }^{\prime }=0}{\overset{2\pi }{\int }}{P}_n^m\left({\mu }^{\prime }\right)\cos \left(m(\phi -{\phi }^{\prime })\right)f_i({\mu }^{\prime },{\phi }^{\prime })d{\phi }^{\prime }d{\mu }^{\prime }$$ (47)

By setting ${\psi }_{1,Tr}(\overline{t}=0)=-{\psi }_{1,ss}$, as the initial condition, to the transient solution resulting from the method of separation of variables, we have Eq. (48).

$${\psi }_{1,Tr}=-\frac{{\overline{r}}^{-\frac{1}{2}}}{\pi }\{\sum _{p=1}^P\sum _{n=0}^N\sum _{m=0}^n\frac{(2n+1)}{2}\frac{(n-m)!}{(n+m)!}\frac{R_{n+\frac{1}{2}}({\lambda }_{np},\overline{r})}{N\left({\lambda }_{np}\right)}{P}_n^m\left(\mu \right)e^{\frac{-\overline{t}}{2{\gamma }_e^2}}[\cosh \left(\eta \overline{t}\right)+\frac{\sinh \left(\eta \overline{t}\right)}{2{\gamma }_e^2\eta }]+\sum _{p=p+1}^{\infty }\sum _{n=N+1}^{\infty }\sum _{m=0}^n\frac{(2n+1)}{2}\frac{(n-m)!}{(n+m)!}\frac{R_{n+\frac{1}{2}}({\lambda }_{np},\overline{r})}{N\left({\lambda }_{np}\right)}{P}_n^m\left(\mu \right)e^{\frac{-\overline{t}}{2{\gamma }_e^2}}[\cosh \left({\eta }_i\overline{t}\right)+\frac{\sinh \left({\eta }_i\overline{t}\right)}{2{\gamma }_e^2{\eta }_i}]\}\times \underset{{\overline{r}}^{\prime }=\epsilon }{\overset{1}{\int }}\underset{{\mu }^{\prime }=-1}{\overset{1}{\int }}\underset{{\phi }^{\prime }=0}{\overset{2\pi }{\int }}{R}_{n+\frac{1}{2}}({\lambda }_{np},{\overline{r}}^{\prime })P_n^m\left({\mu }^{\prime }\right)\cos \left(m(\phi -{\phi }^{\prime })\right){\overline{r}}^{\prime \frac{3}{2}}{\psi }_{2,1,ss}({\overline{r}}^{\prime },{\mu }^{\prime },{\phi }^{\prime })d{\phi }^{\prime }d{\mu }^{\prime }d{\overline{r}}^{\prime }$$ (48)

• •Auxiliary problem 2

$$\frac{{\partial }^2{\psi }_2}{\partial {\overline{r}}^2}+\frac{2}{\overline{r}}\frac{\partial {\psi }_2}{\partial \overline{r}}+\frac{1}{{\overline{r}}^2}\frac{\partial }{\partial \mu }\left((1-{\mu }^2)\frac{\partial {\psi }_2}{\partial \mu }\right)+\frac{1}{{\overline{r}}^2(1-{\mu }^2)}\frac{{\partial }^2{\psi }_2}{\partial {\phi }^2}={\gamma }_e^2\frac{{\partial }^2{\psi }_2}{\partial {\overline{t}}^2}+\frac{\partial {\psi }_2}{\partial \overline{t}}$$ (49)

Eq. (49) is subjected to the boundary and initial conditions (Eqs. (50a)–(50e) and Eqs. (51a), (51b)).

$$-{\frac{\partial {\psi }_2}{\partial \overline{r}}|}_{\overline{r}=\epsilon }+H_1{{\psi }_2|}_{\overline{r}=\epsilon }=0$$ (50a)

$${\frac{\partial {\psi }_2}{\partial \overline{r}}|}_{\overline{r}=1}+H_2{{\psi }_2|}_{\overline{r}=1}=f_o(\mu ,\phi )$$ (50b)

$${\psi }_2(\mu \to \pm 1)=finite$$ (50c)

$${\psi }_2\left(\phi \right)={\psi }_2(\phi +2\pi )$$ (50d)

$${\frac{\partial {\psi }_2}{\partial \phi }|}_{\phi }={\frac{\partial {\psi }_2}{\partial \phi }|}_{\phi +2\pi }$$ (50e)

$${\psi }_2(\overline{t}=0)=0$$ (51a)

$${\frac{\partial {\psi }_2}{\partial \overline{t}}|}_{\overline{t}=0}=0$$ (51b)

The BC of Eq. (50b) is nonhomogeneous; hence we must seek the superposition of the form

$${\psi }_2(\overline{r},\mu ,\phi ,\overline{t})={\psi }_{2,ss}(\overline{r},\mu ,\phi )+{\psi }_{2,Tr}(\overline{r},\mu ,\phi ,\overline{t})$$ (52)

In Eq. (52), ${\psi }_{2,Tr}(\overline{r},\mu ,\phi ,\overline{t})$ takes the homogeneous form of the boundary conditions, while ${\psi }_{2,ss}(\overline{r},\mu ,\phi )$ will take the nonhomogeneous boundary condition.

After some straightforward mathematical manipulations, the solution for the auxiliary problem can be obtained by Eqs. (53), (54).

$$\begin{gathered} {\psi }_{1,ss}=\frac{1}{\pi }\sum _{n=0}^{\infty }\sum _{m=0}^n\frac{(2n+1)}{2}\frac{(n-m)!}{(n+m)!}\frac{(\frac{{\epsilon }^{-1-2n}(1+H_1\epsilon +n)}{n-H_1\epsilon }{\overline{r}}^n+{\overline{r}}^{-n-1})}{-(1+n)+H_2+\frac{1+H_1\epsilon +n}{n-H_1\epsilon }(n+H_2){\epsilon }^{-1-2n}} \\ \times P_n^m\left(\mu \right)\underset{{\mu }^{\prime }=-1}{\overset{1}{\int }}\underset{{\phi }^{\prime }=0}{\overset{2\pi }{\int }}{P}_n^m\left({\mu }^{\prime }\right)\cos \left(m(\phi -{\phi }^{\prime })\right)f_o({\mu }^{\prime },{\phi }^{\prime })d{\phi }^{\prime }d{\mu }^{\prime } \end{gathered}$$ (53)

$${\psi }_{2,2,Tr}=-\frac{{\overline{r}}^{-\frac{1}{2}}}{\pi }\{\sum _{p=1}^P\sum _{n=0}^N\sum _{m=0}^n\frac{(2n+1)}{2}\frac{(n-m)!}{(n+m)!}\frac{R_{n+\frac{1}{2}}({\lambda }_{np},\overline{r})}{N\left({\lambda }_{np}\right)}{P}_n^m\left(\mu \right)e^{\frac{-\overline{t}}{2{\gamma }_e^2}}[\cosh \left(\eta \overline{t}\right)+\frac{\sinh \left(\eta \overline{t}\right)}{2{\gamma }_e^2\eta }]+\sum _{p=p+1}^{\infty }\sum _{n=N+1}^{\infty }\sum _{m=0}^n\frac{(2n+1)}{2}\frac{(n-m)!}{(n+m)!}\frac{R_{n+\frac{1}{2}}({\lambda }_{np},\overline{r})}{N\left({\lambda }_{np}\right)}{P}_n^m\left(\mu \right)e^{\frac{-\overline{t}}{2{\gamma }_e^2}}[\cosh \left({\eta }_i\overline{t}\right)+\frac{\sinh \left({\eta }_i\overline{t}\right)}{2{\gamma }_e^2{\eta }_i}]\}\times \underset{{\overline{r}}^{\prime }=\epsilon }{\overset{1}{\int }}\underset{{\mu }^{\prime }=-1}{\overset{1}{\int }}\underset{{\phi }^{\prime }=0}{\overset{2\pi }{\int }}{R}_{n+\frac{1}{2}}({\lambda }_{np},{\overline{r}}^{\prime })P_n^m\left({\mu }^{\prime }\right)\cos \left(m(\phi -{\phi }^{\prime })\right){\overline{r}}^{\prime \frac{3}{2}}{\psi }_{2,2,ss}({\overline{r}}^{\prime },{\mu }^{\prime },{\phi }^{\prime })d{\phi }^{\prime }d{\mu }^{\prime }d{\overline{r}}^{\prime }$$ (54)

Duhamel's integral [22], [31] is applied so as to yield the solution for ${\overline{T}}_2(\overline{r},\mu ,\phi ,\overline{t})$.

$${\overline{T}}_2(\overline{r},\mu ,\phi ,\overline{t})=\underset{\tau =0}{\overset{\overline{t}}{\int }}(\frac{\partial {\psi }_1(\overline{r},\mu ,\phi ,\tau )}{\partial \tau }+{\gamma }_e^2\frac{{\partial }^2{\psi }_1(\overline{r},\mu ,\phi ,\tau )}{\partial {\tau }^2})g_i(\overline{t}-\tau )d\tau +\underset{\tau =0}{\overset{\overline{t}}{\int }}(\frac{\partial {\psi }_2(\overline{r},\mu ,\phi ,\tau )}{\partial \tau }+{\gamma }_e^2\frac{{\partial }^2{\psi }_2(\overline{r},\mu ,\phi ,\tau )}{\partial {\tau }^2})g_o(\overline{t}-\tau )d\tau$$ (55)

Finally, we can superimpose the two solutions (i.e., Eqs. (37), (55)) to generate the desired solution:

$$\overline{T}(\overline{r},\mu ,\phi ,\overline{t})=\frac{{\overline{r}}^{-\frac{1}{2}}}{\pi }\sum _{p=1}^{\infty }\sum _{n=0}^{\infty }\sum _{m=0}^n{G}_{pnm}\left(\overline{t}\right)\frac{(2n+1)}{2}\frac{(n-m)!}{(n+m)!}\frac{R_{n+\frac{1}{2}}({\lambda }_{np},\overline{r})}{N\left({\lambda }_{np}\right)}{P}_n^m\left(\mu \right)\times \underset{{\overline{r}}^{\prime }=\epsilon }{\overset{1}{\int }}\underset{{\mu }^{\prime }=-1}{\overset{1}{\int }}\underset{{\phi }^{\prime }=0}{\overset{2\pi }{\int }}{\overline{T}}_0{R}_{n+\frac{1}{2}}({\lambda }_{np},{\overline{r}}^{\prime })P_n^m\left({\mu }^{\prime }\right)\cos \left(m(\phi -{\phi }^{\prime })\right){\overline{r}}^{\prime \frac{3}{2}}d{\phi }^{\prime }d{\mu }^{\prime }d{\overline{r}}^{\prime }+\frac{{\overline{r}}^{-\frac{1}{2}}}{\pi }\sum _{p=1}^{\infty }\sum _{n=0}^{\infty }\sum _{m=0}^n\frac{(2n+1)}{2}\frac{(n-m)!}{(n+m)!}\frac{R_{n+\frac{1}{2}}({\lambda }_{np},\overline{r})}{N\left({\lambda }_{np}\right)}{P}_n^m\left(\mu \right)\times [-K_{pnm,1}\left(\overline{t}\right)\underset{{\overline{r}}^{\prime }=\epsilon }{\overset{1}{\int }}\underset{{\mu }^{\prime }=-1}{\overset{1}{\int }}\underset{{\phi }^{\prime }=0}{\overset{2\pi }{\int }}{R}_{n+\frac{1}{2}}({\lambda }_{np},{\overline{r}}^{\prime })P_n^m\left({\mu }^{\prime }\right)\cos \left(m(\phi -{\phi }^{\prime })\right){\overline{r}}^{\prime \frac{3}{2}}{\psi }_{1,ss}({\overline{r}}^{\prime },{\mu }^{\prime },{\phi }^{\prime })d{\phi }^{\prime }d{\mu }^{\prime }d{\overline{r}}^{\prime }-K_{pnm,2}\underset{{\overline{r}}^{\prime }=\epsilon }{\overset{1}{\int }}\underset{{\mu }^{\prime }=-1}{\overset{1}{\int }}\underset{{\phi }^{\prime }=0}{\overset{2\pi }{\int }}{R}_{n+\frac{1}{2}}({\lambda }_{np},{\overline{r}}^{\prime })P_n^m\left({\mu }^{\prime }\right)\cos \left(m(\phi -{\phi }^{\prime })\right){\overline{r}}^{\prime \frac{3}{2}}{\psi }_{2,ss}({\overline{r}}^{\prime },{\mu }^{\prime },{\phi }^{\prime })d{\phi }^{\prime }d{\mu }^{\prime }d{\overline{r}}^{\prime }]$$ (56)

where $G_{pnm}\left(\overline{t}\right)$, $K_{pnm,1}\left(\overline{t}\right)$, and $K_{pnm,2}\left(\overline{t}\right)$ can be determined by Eqs. (57)-(59).

$$G_{pnm}\left(\overline{t}\right)=\{\begin{array}{c}\hfill e^{\frac{-\overline{t}}{2{\gamma }_e^2}}[\cosh \left(\eta \overline{t}\right)+\frac{1}{2{\gamma }_e^2\eta }\sinh \left(\eta \overline{t}\right)]\eta =real\hfill \\ \hfill e^{\frac{-\overline{t}}{2{\gamma }_e^2}}[\cos \left({\eta }_i\overline{t}\right)+\frac{1}{2{\gamma }_e^2{\eta }_i}\sin \left({\eta }_i\overline{t}\right)]\eta =i{\eta }_i\hfill \end{array}$$ (57)

$$K_{pnm,1}\left(\overline{t}\right)=\{\begin{array}{c}\hfill \frac{-1+4{\gamma }_e^4{\eta }^2}{8{\gamma }_e^4\eta }\underset{\tau =0}{\overset{\overline{t}}{\int }}{e}^{\frac{-\tau }{2{\gamma }_e^2}}[\sinh \left(\eta \tau \right)+2{\gamma }_e^2\eta \cosh \left(\eta \tau \right)]g_i(\overline{t}-\tau )d\tau \eta =\mathrm{real}\hfill \\ \hfill -\frac{(1+4{\gamma }_e^4{\eta }_i^2)}{8{\gamma }_e^4{\eta }_i}\underset{\tau =0}{\overset{\overline{t}}{\int }}{e}^{\frac{-\tau }{2{\gamma }_e^2}}[\sin \left({\eta }_i\tau \right)+2{\gamma }_e^2{\eta }_i\cos \left({\eta }_i\tau \right)]g_i(\overline{t}-\tau )d\tau \eta =i{\eta }_i\hfill \end{array}$$ (58)

$$K_{pnm,2}\left(\overline{t}\right)=\{\begin{array}{c}\hfill \frac{-1+4{\gamma }_e^4{\eta }^2}{8{\gamma }_e^4\eta }\underset{\tau =0}{\overset{\overline{t}}{\int }}{e}^{\frac{-\tau }{2{\gamma }_e^2}}[\sinh \left(\eta \tau \right)+2{\gamma }_e^2\eta \cosh \left(\eta \tau \right)]g_o(\overline{t}-\tau )d\tau \eta =\mathrm{real}\hfill \\ \hfill -\frac{(1+4{\gamma }_e^4{\eta }_i^2)}{8{\gamma }_e^4{\eta }_i}\underset{\tau =0}{\overset{\overline{t}}{\int }}{e}^{\frac{-\tau }{2{\gamma }_e^2}}[\sin \left({\eta }_i\tau \right)+2{\gamma }_e^2{\eta }_i\cos \left({\eta }_i\tau \right)]g_o(\overline{t}-\tau )d\tau \eta =i{\eta }_i\hfill \end{array}$$ (59)

4. Demonstration and results

Aiming to illustrate the usefulness of the achieved general solution, two particular cases with different boundary conditions are presented.

• •Case 1

As a first instance, a 3-D non-Fourier heat diffusion problem in a hollow sphere with an inner and outer radius of $r_i$ and $r_o$ respectively, is investigated. It is assumed that the non-uniform heat flux is imposed on the outer surface while the inner surface is maintained at the initial temperature.

Therefore, the coefficients of Eqs. (11a), (11b) can be considered as Eq. (60).

$$\begin{array}{c}{k}_1=0,k_2=k,h_2=0,T_{\infty }=T_0,f_i(\mu ,\phi )=0,g_i\left(\overline{t}\right)=0,\hfill \\ f_o(\mu ,\phi )=q_w\mu \exp [-\frac{{(\phi -\pi )}^2}{2{\phi }_0^2}],g_o(\mu ,\phi ,\overline{t})=\cos \left(\frac{\overline{t}}{{\overline{t}}_1}\right)\hfill \end{array}$$ (60)

where ${\overline{t}}_1$ can be defined as Eq. (61).

$${\overline{t}}_1=\frac{\alpha }{a{r}_0^2}$$ (61)

It should be noted that the harmonic heat flux is exerted on the sphere's outer surface. A dimensionless temperature is introduced as Eq. (62).

$$\mathrm{\Theta }=\frac{T-T_0}{\frac{q_w{r}_o}{k}}$$ (62)

Boundary and initial conditions are defined as Eqs. (63a)–(63e) and Eqs. (64a), (64b), respectively.

$${\mathrm{\Theta }|}_{\overline{r}=\epsilon }=0$$ (63a)

$${\frac{\partial \mathrm{\Theta }}{\partial \overline{r}}|}_{\overline{r}=1}=\mu [\cos \left(\frac{\overline{t}}{{\overline{t}}_0}\right)+{\gamma }_e^2\frac{\mathrm{d}\cos \left(\frac{\overline{t}}{{\overline{t}}_1}\right)}{\mathrm{d}\overline{t}}]\exp [-\frac{{(\phi -\pi )}^2}{2{\phi }_0^2}]$$ (63b)

$$\mathrm{\Theta }(\mu \to \pm 1)=finite$$ (63c)

$$\mathrm{\Theta }\left(\phi \right)=\mathrm{\Theta }(\phi +2\pi )$$ (63d)

$${\frac{\partial \mathrm{\Theta }}{\partial \phi }|}_{\phi }={\frac{\partial \mathrm{\Theta }}{\partial \phi }|}_{\phi +2\pi }$$ (63e)

$$\mathrm{\Theta }(\overline{t}=0)=0$$ (64a)

$${\frac{\partial \mathrm{\Theta }}{\partial \overline{t}}|}_{\overline{t}=0}=0$$ (64b)

respecting the above boundary and initial conditions, the general solution (Eq. (56)) is modified to yield the solution for this specific case as Eq. (65).

$$\mathrm{\Theta }(\overline{r},\mu ,\phi ,\overline{t})=\frac{-{\overline{r}}^{-\frac{1}{2}}}{{\pi }^2}\sum _{p=1}^{\infty }\sum _{n=0}^{\infty }\sum _{m=0}^n{K}_{pnm}^{\prime }\left(\overline{t}\right)\frac{(2n+1)}{2}\frac{(n-m)!}{(n+m)!}\frac{R_{n+\frac{1}{2}}({\lambda }_{np},\overline{r})}{N\left({\lambda }_{np}\right)}{P}_n^m\left(\mu \right)\frac{e^{-\frac{m^2{\phi }_0^2}{2}}\sqrt{\frac{\pi }{2}}{\phi }_0}{[-1+n(-1-{\epsilon }^{-1-2n})]}[erf\left(\frac{\pi -im{\phi }_0^2}{\sqrt{2}{\phi }_0}\right)+erf\left(\frac{\pi +im{\phi }_0^2}{\sqrt{2}{\phi }_0}\right)]\left[\underset{{\mu }^{\prime }=-1}{\overset{1}{\int }}{\mu }^{\prime }{P}_n^m\left({\mu }^{\prime }\right)d{\mu }^{\prime }\right]\left[\frac{4m\pi \cos \left(m(\pi -\phi )\right)-\sin \left(m(-3\pi +\phi )\right)+\sin \left(m(\pi +\phi )\right)}{4m}\right]\left[\underset{{\overline{r}}^{\prime }=\epsilon }{\overset{1}{\int }}[-{\epsilon }^{-1-2n}{\overline{r}}^{\prime n}+{\overline{r}}^{\prime -n-1}]R_{n+\frac{1}{2}}({\lambda }_{np},{\overline{r}}^{\prime }){\overline{r}}^{\prime \frac{3}{2}}d{\overline{r}}^{\prime }\right]$$ (65)

where $K_{pnm}^{″}\left(\overline{t}\right)$ can be calculated by Eq. (66).

$$K_{pnm}^{\prime }\left(\overline{t}\right)=\{\begin{array}{cc}\frac{-1+4{\gamma }_e^4{\eta }^2}{8{\gamma }_e^4\eta }\underset{\tau =0}{\overset{\overline{t}}{\int }}{e}^{\frac{-\tau }{2{\gamma }_e^2}}[\sinh \left(\eta \tau \right)+2{\gamma }_e^2\eta \cosh \left(\eta \tau \right)]\cos \left(\frac{\overline{t}-\tau }{{\overline{t}}_1}\right)d\tau \hfill & \eta =\mathrm{real}\hfill \\ -\frac{(1+4{\gamma }_e^4{\eta }_i^2)}{8{\gamma }_e^4{\eta }_i}\underset{\tau =0}{\overset{\overline{t}}{\int }}{e}^{\frac{-\tau }{2{\gamma }_e^2}}[\sin \left({\eta }_i\tau \right)++2{\gamma }_e^2{\eta }_i\cosh \left({\eta }_i\tau \right)]\cos \left(\frac{\overline{t}-\tau }{{\overline{t}}_1}\right)d\tau \hfill & \eta =\mathrm{i}{\eta }_i\hfill \end{array}$$ (66)

Furthermore, $R_{n+\frac{1}{2}}({\lambda }_{np},\overline{r})$, known as eigenfunctions, are formulated as Eq. (67).

$$R_{n+\frac{1}{2}}({\lambda }_{np},\overline{r})=[-\frac{Y_{n+\frac{1}{2}}\left(\epsilon {\lambda }_{np}\right)}{J_{n+\frac{1}{2}}\left(\epsilon {\lambda }_{np}\right)}{J}_{n+\frac{1}{2}}\left({\lambda }_{np}\overline{r}\right)+Y_{n+\frac{1}{2}}\left(\epsilon {\lambda }_{np}\overline{r}\right)]$$ (67)

where eigenvalues ${\lambda }_{np}$ can be determined employing the transcendental Eq. (68).

$$\frac{{\lambda }_{np}}{2}[-\frac{Y_{n+\frac{1}{2}}\left(\epsilon {\lambda }_{np}\right)}{J_{n+\frac{1}{2}}\left(\epsilon {\lambda }_{np}\right)}{J}_{n-\frac{1}{2}}\left({\lambda }_{np}\right)+Y_{n-\frac{1}{2}}\left({\lambda }_{np}\right)]-\frac{{\lambda }_{np}}{2}[-\frac{Y_{n+\frac{1}{2}}\left(\epsilon {\lambda }_{np}\right)}{J_{n+\frac{1}{2}}\left(\epsilon {\lambda }_{np}\right)}{J}_{n+\frac{3}{2}}\left({\lambda }_{np}\right)+Y_{n+\frac{3}{2}}\left({\lambda }_{np}\right)]-\frac{1}{2}[-\frac{Y_{n+\frac{1}{2}}\left(\epsilon {\lambda }_{np}\right)}{J_{n+\frac{1}{2}}\left(\epsilon {\lambda }_{np}\right)}{J}_{n+\frac{1}{2}}\left({\lambda }_{np}\right)+Y_{n+\frac{1}{2}}\left({\lambda }_{np}\right)]=0$$ (68)

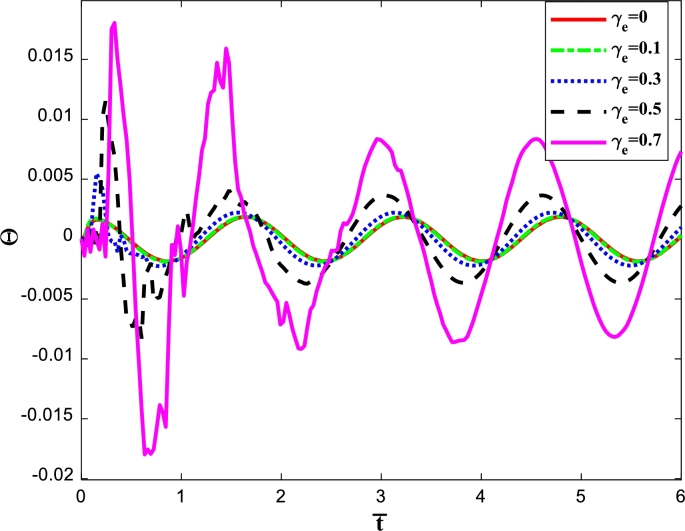
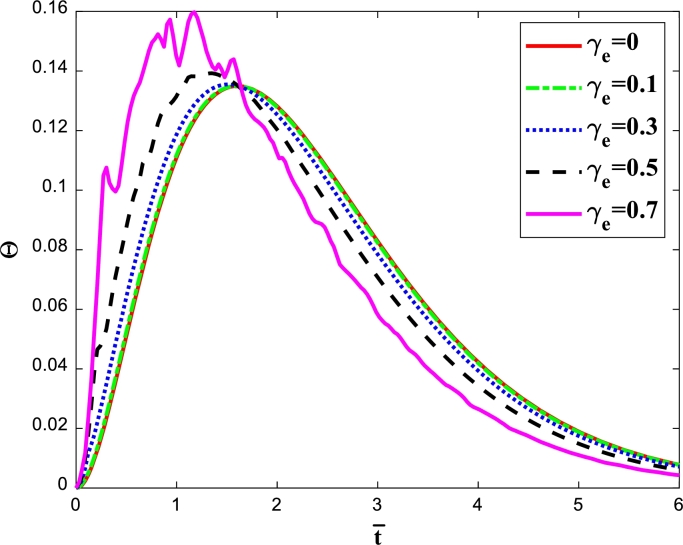
Fig. 2 illustrates the change of dimensionless temperature in terms of time for various magnitudes of Vernotte number ${\gamma }_e$. The time-dependent temperature at $\overline{r}=0.6$, $\mu =0.5$, and $\phi =\pi /2$ predicted by both parabolic and hyperbolic heat diffusion equations are depicted. The switching procedure between the Fourier and non-Fourier treatments can be obviously seen. The comparison indicates that, in contrast to the parabolic one (${\gamma }_e=0$), there is a time delay in the hyperbolic heat propagation. This lag time gets smaller with a decrement in the values of Vernotte number ${\gamma }_e$, and it asymptotically vanishes for the Fourier case. Also, the time-varying temperature profile in the Fourier case is smooth, while in the non-Fourier case, the temperature distribution over time has a sequence of jump points, which corresponds to the moment when the propagating thermal wave approaches the investigated location after propagation through the body and reflection at the boundaries. Nevertheless, the number of jump points diminishes with increasing time, and finally, these points fade away with time, leading the time-dependent temperature profile to undergo a smooth periodic oscillation. Furthermore, it can be observable that elevating the Vernotte number improves the amplitude of the harmonic curves. As a matter of fact, by enhancing the Vernotte number ${\gamma }_e$ (i.e., increasing relaxation time ${\tau }_q$), the propagation rate of the heat wave declines, resulting in an increment in the amplitude of the oscillations. According to Fig. 2, for the Vernotte numbers of 0, 0.3, and 0.7, the dimensionless temperature of the sphere at the considered position is found to be about 0.0007632, 0.0014394, and 0.0081454, respectively, when $\overline{t}=4.5$. Furthermore, the maximum difference with the value of 1.71% between non-Fourier one with ${\gamma }_e=0.7$ and Fourier one occurs when Fourier number equals 0.33.

Figure 2.

Dimensionless temperature as a function of time considering Vernotte number effect for case 1.

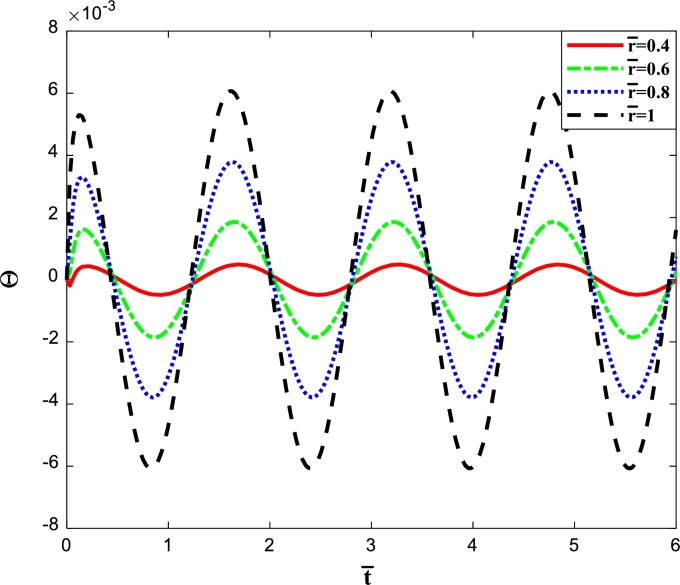
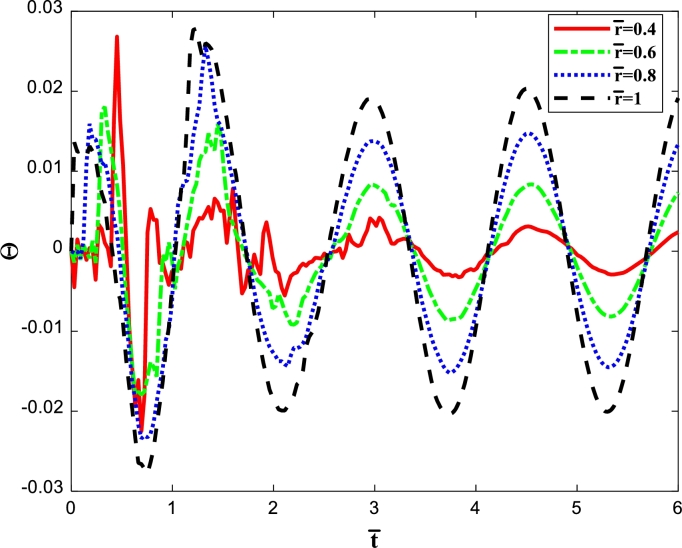
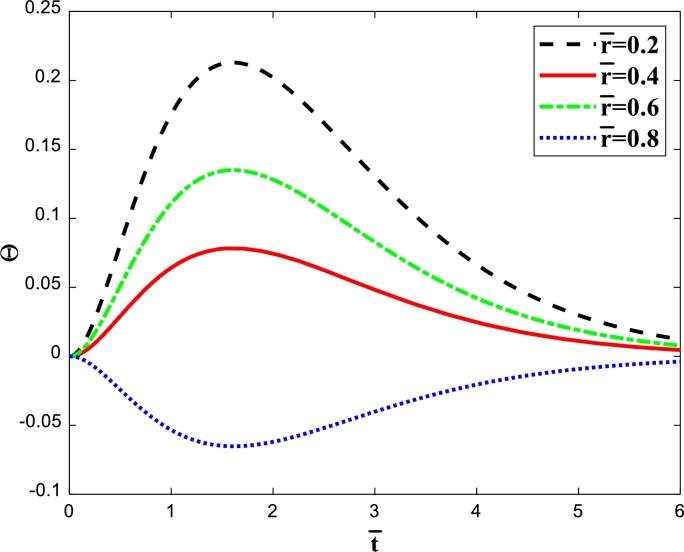
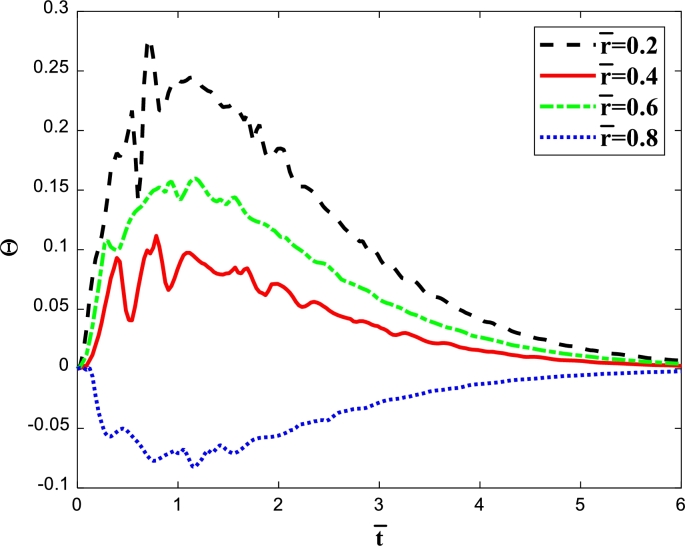
Figure 3a, Figure 3b demonstrate time-dependent dimensionless temperature profiles at different radial positions for ${\gamma }_e=0$ and ${\gamma }_e=0.7$, respectively. As shown, the main characteristic of the non-Fourier temperature distributions compared to Fourier one is the lag time in establishing the temperature gradient induced by the applied boundary heat flux. In point of fact, for the Fourier case, any heat disturbance exerted on the sphere is immediately felt through the whole body due to the infinite pace of heat wave propagation, which is physically unrealistic. While, for the non-Fourier case, since the speed of the hyperbolic heat propagation is finite, the inner layers stay at their initial temperature for a moment, and it takes some time for the heat wave to transfer from the outer surface, subjected to the time-space varying heat flux, into the inner layers. With respect to Fig. 3b, the jump points continuously lessen by marching through the radial direction of the sphere from the inner surface to the outer one. Due to the fact that the surface of the sphere is convex, as the thermal wave transmits toward the center, the value of the wavefront grows, leading the jump points of the inner layers to get more significant than those of the outer surface. Also, when time passes, the jump points of each curve decay and finally vanish completely at particular times. Subsequently, temperature smoothly varies periodically. Regarding these figures, when the time-dependent temperatures reach their respective periodic state with a constant amplitude, the maximum value of dimensionless temperature at $\overline{r}=0.8$ for ${\gamma }_e=0.7$ and ${\gamma }_e=0$ are approximately 0.013702 and 0.0027741 respectively.

Figure 3a.

Dimensionless temperature against time for several radial distances for case 1, γ_e = 0.

Figure 3b.

Dimensionless temperature against time for several radial distances for case 1, γ_e = 0.7.

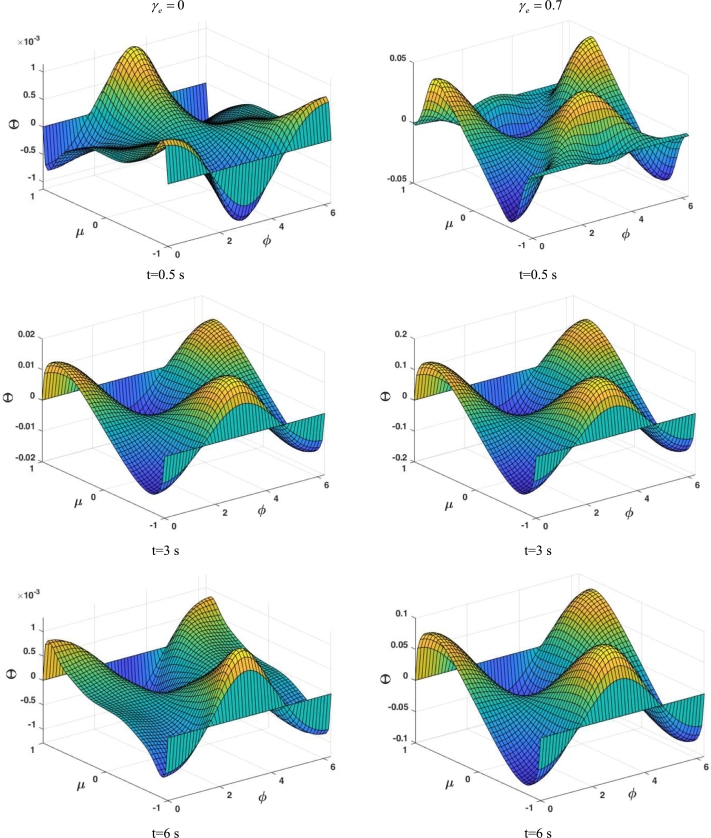
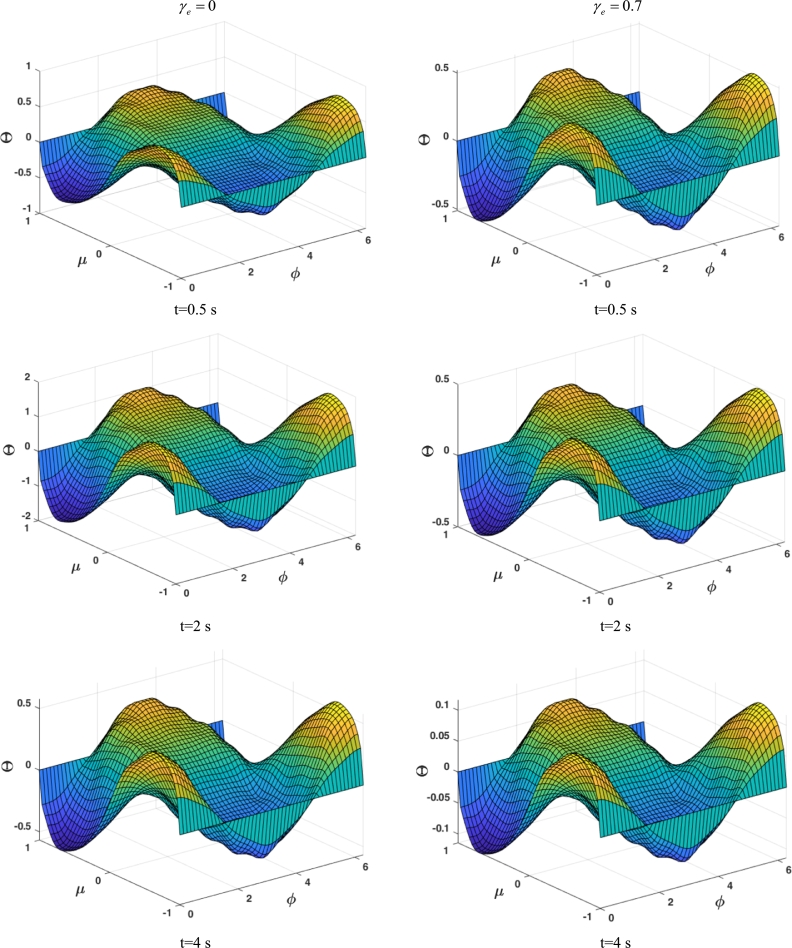
In order to evaluate the thermal characteristics of Fourier and non-Fourier with one another, the temperature changes with respect to polar and azimuthal angles at various times for ${\gamma }_e=0$ and ${\gamma }_e=0.7$ are indicated in Figs. 4 (a) and (b), respectively. As shown from these figures, the maximum temperature under the non-Fourier case is much greater than that under the Fourier case at certain times. This phenomenon can be explained as follows: enhancing the Vernotte number ${\gamma }_e$ means that the propagation rate of the heat wave declines, which will cause to improvement in the amplitude of the oscillations. In other words, the maximum temperature increases with augmenting the Vernotte number due to the thermal inertial impact.

• •Case 2

For the second example, it is assumed that the temperature of the outer surface depends on both time and space while the inner wall is insulated. Based on the assumptions, the coefficients of Eqs. (11a), (11b) can be rewritten as Eq. (69).

$$\begin{gathered} k_1=k,k_2=0,h_1=0,h_2=1,T_0=0,f_i(\mu ,\phi )=0,g_i\left(\overline{t}\right)=0 \\ {f}_o(\mu ,\phi )=T_{\infty }\mu {(\phi -\pi )}^2,g_o\left(\overline{t}\right)={\left(\frac{\overline{t}}{{\overline{t}}_p}\right)}^2{e}^{(-\frac{\overline{t}}{{\overline{t}}_p})} \end{gathered}$$ (69)

where the dimensionless variable ${\overline{t}}_p$ denotes pulse width and can be defined as Eq. (70).

$${\overline{t}}_p=\frac{\alpha t_p}{r_o^2}$$ (70)

Noting that the temperature of the outer surface exponentially decays with time. Also, a non-dimensional temperature adopted here is described as Eq. (71).

$$\mathrm{\Theta }=\frac{T}{T_{\infty }}$$ (71)

The boundary and initial conditions for this case can be written as Eqs. (72a)–(72e) and Eqs. (73a), (73b), respectively.

$${\frac{\partial \mathrm{\Theta }}{\partial \overline{r}}|}_{\overline{r}=\epsilon }=0$$ (72a)

$$\mathrm{\Theta }(\overline{r}=1)=\mu \{{\left(\frac{\overline{t}}{{\overline{t}}_p}\right)}^2{e}^{(-\frac{\overline{t}}{{\overline{t}}_p})}+{\gamma }_e^2\frac{\mathrm{d}}{\mathrm{d}\overline{t}}\left[{\left(\frac{\overline{t}}{{\overline{t}}_p}\right)}^2{e}^{(-\frac{\overline{t}}{{\overline{t}}_p})}\right]\}{(\phi -\pi )}^2$$ (72b)

$$\mathrm{\Theta }(\mu \to \pm 1)=finite$$ (72c)

$$\mathrm{\Theta }\left(\phi \right)=\mathrm{\Theta }(\phi +2\pi )$$ (72d)

$${\frac{\partial \mathrm{\Theta }}{\partial \phi }|}_{\phi }={\frac{\partial \mathrm{\Theta }}{\partial \phi }|}_{\phi +2\pi }$$ (72e)

$$\mathrm{\Theta }(\overline{t}=0)=0$$ (73a)

$${\frac{\partial \mathrm{\Theta }}{\partial \overline{t}}|}_{\overline{t}=0}=0$$ (73b)

Regarding the presented boundary and initial conditions, the general solution (Eq. (56)) is manipulated to give the solution for this particular case as Eq. (74).

$$\mathrm{\Theta }(\overline{r},\mu ,\phi ,\overline{t})=-\frac{{\overline{r}}^{-\frac{1}{2}}}{{\pi }^2}\sum _{p=1}^{\infty }\sum _{n=0}^{\infty }\sum _{m=0}^n{K}_{pnm}^{″}\left(\overline{t}\right)\frac{(2n+1)}{2}\frac{(n-m)!}{(n+m)!}\frac{R_{n+\frac{1}{2}}({\lambda }_{np},\overline{r})}{N\left({\lambda }_{np}\right)}\frac{P_n^m\left(\mu \right)}{[\frac{1+n}{n}\frac{1}{{\epsilon }^{1+2n}}+1]}\left\{\frac{\pi \cos (m\pi )[4m\pi \cos \left(m(\pi -\phi )\right)-\sin \left(m(-3\pi +\phi )\right)+\sin \left(m(\pi +\phi )\right)]}{m^3}\right\}\left[\underset{{\mu }^{\prime }=-1}{\overset{1}{\int }}{\mu }^{\prime }{P}_n^m\left({\mu }^{\prime }\right)d{\mu }^{\prime }\right]\left[\underset{{\overline{r}}^{\prime }=\epsilon }{\overset{1}{\int }}(\frac{1+n}{n}\frac{{\overline{r}}^{\prime n}}{{\epsilon }^{1+2n}}+{\overline{r^{\prime }}}^{-n-1})R_{n+\frac{1}{2}}({\lambda }_{np},\overline{r}){\overline{r}}^{\prime \frac{3}{2}}d{\overline{r}}^{\prime }\right]$$ (74)

where $K_{pnm}^{″}\left(\overline{t}\right)$ can be calculated by Eq. (75).

$$K_{pnm}^{″}\left(\overline{t}\right)=\{\begin{array}{cc}\frac{-1+4{\gamma }_e^4{\eta }^2}{4{\gamma }_e^4\eta }\underset{\tau =0}{\overset{\overline{t}}{\int }}{e}^{\frac{-\tau }{2{\gamma }_e^2}}[\sinh \left(\eta \tau \right)+2{\gamma }_e^2\eta \cosh \left(\eta \tau \right)]{\left(\frac{\overline{t}-\tau }{{\overline{t}}_p}\right)}^2{e}^{-\left(\frac{\overline{t}-\tau }{{\overline{t}}_p}\right)}d\tau \hfill & \eta =\mathrm{real}\hfill \\ -\frac{(1+4{\gamma }_e^4{\eta }_i^2)}{4{\gamma }_e^4{\eta }_i}\underset{\tau =0}{\overset{\overline{t}}{\int }}{e}^{\frac{-\tau }{2{\gamma }_e^2}}[\sin \left({\eta }_i\tau \right)+2{\gamma }_e^2{\eta }_i\cos \left({\eta }_i\tau \right)]{\left(\frac{\overline{t}-\tau }{{\overline{t}}_p}\right)}^2{e}^{-\left(\frac{\overline{t}-\tau }{{\overline{t}}_p}\right)}d\tau \hfill & \eta =\mathrm{i}{\eta }_i\hfill \end{array}$$ (75)

Moreover, eigenfunctions $R_{n+\frac{1}{2}}({\lambda }_{np},\overline{r})$ are expressed as Eq. (76).

$$R_{n+\frac{1}{2}}({\lambda }_{np},\overline{r})=[-\frac{Y_{n+\frac{1}{2}}\left({\lambda }_{np}\right)}{J_{n+\frac{1}{2}}\left({\lambda }_{np}\right)}{J}_{n+\frac{1}{2}}\left({\lambda }_{np}\overline{r}\right)+Y_{n+\frac{1}{2}}\left({\lambda }_{np}\overline{r}\right)]$$ (76)

in which eigenvalues ${\lambda }_{np}$ can be calculated from the transcendental Eq. (77).

$$\frac{{\lambda }_{np}}{2}[-\frac{Y_{n+\frac{1}{2}}\left({\lambda }_{np}\right)}{J_{n+\frac{1}{2}}\left({\lambda }_{np}\right)}{J}_{n-\frac{1}{2}}\left(\epsilon {\lambda }_{np}\right)+Y_{n-\frac{1}{2}}\left(\epsilon {\lambda }_{np}\right)]-\frac{{\lambda }_{np}}{2}[-\frac{Y_{n+\frac{1}{2}}\left({\lambda }_{np}\right)}{J_{n+\frac{1}{2}}\left({\lambda }_{np}\right)}{J}_{n+\frac{3}{2}}\left(\epsilon {\lambda }_{np}\right)+Y_{n+\frac{3}{2}}\left(\epsilon {\lambda }_{np}\right)]-\frac{1}{2\epsilon }[-\frac{Y_{n+\frac{1}{2}}\left({\lambda }_{np}\right)}{J_{n+\frac{1}{2}}\left({\lambda }_{np}\right)}{J}_{n+\frac{1}{2}}\left(\epsilon {\lambda }_{np}\right)+Y_{n+\frac{1}{2}}\left(\epsilon {\lambda }_{np}\right)]=0$$ (77)

Fig. 5 displays the time-varying dimensionless temperature for different magnitudes of Vernotte number ${\gamma }_e$ at $\overline{r}=0.6$, $\mu =0.5$, and $\phi =\pi /2$. Scrutiny of this figure leads one to observe the shifting procedure between the Fourier and non-Fourier treatments. However, the behavior of temperature distributions with low magnitudes of ${\gamma }_e$ like ${\gamma }_e=0.1$ is similar to the Fourier case. Furthermore, there is a time delay between heat flux and temperature gradient for all cases, except for the parabolic one (${\gamma }_e=0$). This lag time becomes more prominent with a growth in the values of the Vernotte number ${\gamma }_e$. Additionally, the transient temperature distribution in the non-Fourier case has a series of jump points due to the reflection of the heat wave at the boundaries of the sphere. The intensity of the irregularities is substantially attenuated with increasing time, and ultimately vanishes with time, causing the transient temperature distribution to experience a smooth periodic fluctuation. Regarding this figure, one can conclude that enhancing the Vernotte number escalates the harmonic curves' amplitude due to increasing the thermal inertial impact. As explained before (see Fig. 2), the propagation speed of the heat wave decreases by extending relaxation time ${\tau }_q$ in the form of the Vernotte number ${\gamma }_e$, leading to an augment in the amplitude of the oscillations. With respect to Fig. 5, for the Vernotte numbers of 0, 0.3, and 0.7, the dimensionless temperature of the sphere at the prescribed position is found to be approximately 0.028558, 0.026697, and 0.017582 orderly, when $\overline{t}=4.5$. Moreover, the maximum difference with the value of 8.30% between non-Fourier with ${\gamma }_e=0.7$ and Fourier one occurs when Fourier number equals 0.30.

Figure 4.

The variation of dimensionless temperature as a function of polar and azimuthal angles at different time frames for case 1, a) γ_e = 0 and b) γ_e = 0.7.

Figure 5.

Dimensionless temperature as a function of time considering Vernotte number effect for case 2.

The transient dimensionless temperature profiles at different radial locations for ${\gamma }_e=0$ and ${\gamma }_e=0.7$ are depicted in Figure 6a, Figure 6b, respectively, in order to compare the thermal characteristics of Fourier and non-Fourier with one another. These figures clearly indicate that the primary specification of the non-Fourier temperature distribution in comparison to Fourier one is the lag time in the inception of temperature gradient induced by the considered boundary conditions in both inner and outer walls. In point of fact, for the Fourier case, any thermal disturbance imposed on the sphere is instantly felt through the whole medium due to the unbounded pace of heat wave propagation, which is physically impossible. While, for the non-Fourier case, since the speed of the hyperbolic heat propagation is finite, the inner layers stay at their initial temperature for a moment, and it takes some time for the heat wave to transfer from the outer surface into the inner layers. With respect to Fig. 6b, by marching through the radial direction of the sphere from the inner surface to the outer one, the jump points continuously lessen. Due to the convex geometry of the sphere surface, as the thermal wave transmits toward the center, the value of the wavefront grows, leading the jump points of the inner layers to get more significant than those of the outer surface. Also, when time passes, the jump points of each curve decay and finally fade away thoroughly at the particular times. Consequently, temperature smoothly varies periodically. As shown, when the transient temperatures reach their respective periodic state with a constant amplitude, the maximum value of dimensionless temperature at $\overline{r}=0.8$ for ${\gamma }_e=0.7$ and ${\gamma }_e=0$ are about −0.082109 and −0.065186, orderly.

Figure 6a.

Dimensionless temperature against time for several radial distances for case 2, γ_e = 0.

Figure 6b.

Dimensionless temperature against time for several radial distances for case 2, γ_e = 0.7.

Figs. 7 (a) and (b) indicate temperature changes with respect to polar and azimuthal angles at various times for ${\gamma }_e=0$ and ${\gamma }_e=0.7$, respectively. As observable, the maximum temperature of the non-Fourier case is considerably higher than that of the Fourier case at certain times. The primary reason for this phenomenon is that elevating the Vernotte number ${\gamma }_e$ decline the propagation rate of the heat wave, leading the amplitude of the oscillations to improve. In other words, the greater the Vernotte number, the higher the maximum temperature.

Figure 7.

The variation of dimensionless temperature as a function of polar and azimuthal angles at different time frames for case 2, a) γ_e = 0 and b) γ_e = 0.7.

5. Conclusion

The present work conducted a detailed mathematical method to determine a general solution for 3-D non-Fourier thermal conduction in spherical geometry. It was considered that a hollow sphere is imposed on the arbitrarily chosen space and time-dependent boundary conditions. The non-Fourier behavior of the system was characterized by the Cattaneo-Vernotte model. To obtain a general solution of the non-Fourier temperature field, the method of separation of variables along with Duhamel's theorem is used. Subsequently, two special cases with different time-space varying boundary conditions are taken into account to validate the application of the obtained general solution and demonstrate the physical behavior of the system more precisely. The time-dependent temperature distributions of the body are obtained for both cases and are compared with Fourier one. Finally, the effect of the crucial parameters, including Fourier number and Vernotte number on the temperature field profiles within a hollow sphere for the considered cases are elaborately evaluated. It is revealed that the main specification of the non-Fourier temperature distributions in comparison to Fourier one is the time delay. However, this lag time gets smaller with a decrement in the values of the Vernotte number ${\gamma }_e$, and it asymptotically vanishes for the Fourier case. It is also found that increasing relaxation time ${\tau }_q$ in the form of the Vernotte number improves the amplitude of the harmonic fluctuations. The results show that the time-varying temperature profile in the Fourier case is smooth while that in the non-Fourier case has a sequence of jump points, which corresponds to the instant when the propagating thermal wave approaches the investigated location after propagation through the sphere and reflection at the boundaries. The number and severity of the jump points are significantly attenuated with increasing time; Consequently, these points fade away with time, leading the time-dependent temperature profile to undergo a smooth periodic oscillation. Based on the results, for cases 1 and 2, the dimensionless temperature of the sphere at the considered position is found to be about 0.0081454 and 0.017582, respectively, when ${\gamma }_e=0.7$, $\overline{r}=0.6$, and $\overline{t}=4.5$. Also, the maximum difference between non-Fourier one with ${\gamma }_e=0.7$ and Fourier one is 1.71% and 8.30% for case 1 and case 2, respectively.

Overall, this study presents an exact analytical solution for a hollow sphere subjected to the general space and time-varying boundary conditions, which can be used for different special cases. It is noteworthy that the transient behavior of non-Fourier heat conduction in a hollow spherical material with temperature-dependent thermophysical properties considering the thermal radiation mode of surface heat transfer can be investigated in future works.

Declarations

Author contribution statement

Shahin Akbari, Shahin Faghiri, Parham Poureslami, Khashayar Hosseinzadeh, Mohammad Behshad Shafii: Conceived and designed the analysis; Analyzed and interpreted the data; Contributed analysis tools or data; Wrote the paper.

Funding statement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Data availability statement

Data will be made available on request.

Declaration of interest's statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.