Active Control of Plasmonic–Photonic Interactions in a Microbubble Cavity

Abstract

Active control of light–matter interactions using nanophotonic structures is critical for new modalities for solar energy production, cavity quantum electrodynamics (QED), and sensing, particularly at the single-particle level, where it underpins the creation of tunable nanophotonic networks. Coupled plasmonic–photonic systems show great promise toward these goals because of their subwavelength spatial confinement and ultrahigh-quality factors inherited from their respective components. Here, we present a microfluidic approach using microbubble whispering-gallery mode cavities to actively control plasmonic–photonic interactions at the single-particle level. By changing the solvent in the interior of the microbubble, control can be exerted on the interior dielectric constant and, thus, on the spatial overlap between the photonic and plasmonic modes. Qualitative agreement between experiment and simulation reveals the competing roles mode overlap and mode volume play in altering coupling strengths.

Introduction

Tailoring light–matter interactions in resonant nanophotonic structures is central to applications in energy,¹ photonics-altered chemistry,²⁻⁵ quantum information science (QIS),⁶⁻⁹ and sensing and imaging.¹⁰⁻¹⁷ Multiple ways exist to achieve this control, including altering how the photonic structure localizes light in time or energy (as reflected in the quality factor, Q), altering how the photonic structure localizes light in space (as reflected in the mode volume, V), or altering the spatial overlap between the light and matter systems, thus altering the magnitude of the light–matter coupling (typically denoted g). For example, operating at low temperatures may substantially reduce the matter’s damping rate by reducing dephasing until it is lower than the coupling strength, resulting in an effective increase in coherent interactions per lifetime and increased interactions.¹⁸ An ultrasmall mode volume in a plasmonic dimer nanocavity can lead to extremely strong light–matter interactions,¹⁹ and inhomogeneous field distribution in this nanocavity results in multiple possible coupling regimes in a plasmon-emitter coupled system, from weak-coupling to intermediate-strong-coupling to strong-coupling.²⁰ The coupling energy itself can be altered in exciton-polariton,²¹ molecular vibration-polariton,³ and plasmon-polariton systems,²² by controlling the number of contributing molecular or excitonic modes. However, there is a need for new strategies for controlling coupling strengths that can operate at room temperature, are conveniently externally controlled, and can allow operation on a single nano-object. Tailoring interactions at the single-particle level is particularly important for QIS applications^23,24 and for photonics-based single-particle and single-molecule detection strategies.^{10,12,15−17,25,26}

Recently, coupled plasmonic–photonic systems^{7,22,25,27−36} have emerged as rich platforms for control of light–matter interactions because they may inherit the ultrasmall mode volumes and ultrahigh Q-factors from their respective plasmonic and photonic components, leading to strong Purcell enhancement. We have recently demonstrated new ways to control detuning through controlled nanorod melting²⁷ and quantitatively determine all system parameters that govern energy dissipation pathways in a coupled plasmonic–photonic cavity through simultaneous measurement of photothermal absorption and two-sided transmission.³⁶ The ability to tailor these system parameters, particularly the coupling between the photonic and plasmonic constituents, is needed to create a tunable multi-component photonic network for applications in photonic sensing¹⁰ and QIS.⁸ Further, coupled plasmonic–photonic cavities with high Q-factors and low mode volumes may allow stronger interactions between the mixed photonic structure and a two-level system, potentially opening an avenue for attaining strong-coupling in polariton chemistry when molecules or other two-level systems are coupled to the coupled plasmonic–photonic cavity. The mode overlap, the spatial overlap of field profiles of the plasmonic and photonic modes in the two constituents, influences the coupling strength. Increasing the mode overlap by directly embedding plasmonic nanoparticles into an optical microcavity may entail difficult fabrication (though this strategy is more easily used for rare-earth dopants^37,38) or the need for additional polymer layers.^39,40 Precisely tuning the cavity diameter, as demonstrated in hybrid plasmonic-microfiber systems,^13,41,42 can also alter the coupling strength. However, these strategies lack the capability for active modulation of mode overlap.

In this work, we present a solvent-embedding approach to actively modulate plasmonic–photonic interactions between a microfluidics-integrated whispering-gallery mode (WGM) microbubble cavity and single gold nanorods (AuNRs) deposited on the inner wall (Figure 1). The alteration in interior dielectric environment exerts an effect upon the distribution of plasmonic–photonic coupling strengths, which is highly dependent on both spatial locations and orientations of the AuNRs relative to the WGMs in the microbubble cavity. As shown below, optical simulations qualitatively agree with the experimentally determined distribution in coupling strengths, showing that both mode volume and mode overlap play important roles in shaping the distributions of coupling strengths. For some WGMs, the coupling strength is seen to increase, while for others, the contribution from an increase in mode overlap is largely counteracted by an increase in mode volume, rendering minimal change in coupling strength.

Figure 1.

Schematic of active control via modifying the interior dielectric environment in a microbubble cavity via solvent. The microbubble is either filled with air (A) or chloroform (B) in this work. The zoomed-in field intensity profile for a fundamental mode shows a pronounced difference when the solvent dielectric constant matches that of the SiO₂ wall. The white scale bar: 1 μm. Note that the dimension of the AuNRs used in this work is 25 × 137.5 nm².

Methods

Sample Preparation

Microbubble cavities were fabricated as described previously.⁷⁵ The procedure for AuNRs deposition (see Figure S1) on the interior surface of a microbubble was adapted from refs (17) and (48). First, a diluted HCl solution (pH ∼ 1.3) prepared from concentrated HCl (Sigma-Aldrich, ACS Grade) was flowed from one end of the microbubble using a Luer Lock syringe assembly until about 10 drops came out from the other end. Subsequently, a diluted cetyltrimethylammonium bromide (CTAB) (Sigma-Aldrich, SKU: M6880-25G) solution prepared in HCl (100 μM, pH ∼ 1.3) was flowed in a similar way. The two steps readied the interior surface of the microbubble for binding AuNRs. Afterward, a 250× diluted AuNR solution was prepared from a stock AuNR solution (25 × 137.5 nm², Nanopartz A12-25-1064) by serial dilution using diluted CTAB solution. This diluted AuNR solution was flowed through the microbubble until about 12 big drops came out. The microbubble was flushed by the diluted CTAB solution (100 μM, pH ∼ 1.3), diluted HCl (pH ∼ 1.3), and Milli-Q water to remove extra unbound AuNRs and excess CTAB. Finally, Milli-Q water was pushed out from the microbubble and taken away by flushing the microbubble with methanol (high-performance liquid chromatography (HPLC) grade) for several minutes. The remaining methanol was removed, and then the microbubble was allowed to dry overnight under ambient conditions. Chloroform (Sigma-Aldrich, HPLC grade) was then flowed through the microbubble for several minutes, after which the two capillary ends of the microbubble were sealed to retain chloroform inside by dipping them in a degassed aqueous solution of sodium silicate (J.T. Baker) and then taking the capillary out for drying for a few seconds; this step was repeated three times.

Spectroscopic Measurements

The previously described experimental setup (see Figure S2) was used to carry out spectroscopic and polarization characterization.^25,36 A free-space pump beam is amplitude-modulated at 510 Hz for all of the measurements. The resulting photothermal signal is demodulated by a lock-in amplifier (Ametek, Signal Recovery 7265). Note that the uncertainty of mode identity prevents quantitative determination of absorption cross section, unlike in previous microresonator experiments.^25,36

Optical Simulations

All electromagnetic simulations were run in COMSOL Multiphysics using Oxborrow’s method.⁷² First, the diameter and length of the microbubble used in experiments were determined from an optical image. Then, the wall thickness was estimated, as described previously.^76,77 These geometric parameters were used to create a model to solve for mode eigenvalues and eigenfunctions. The domain designated for the air or chloroform medium has a refractive index of 1.0 or 1.43, respectively. For a given azimuthal mode number, a set of eigen solutions were obtained and then exported along with field intensity data to compute g. Note that only transverse electric (TE) polarization modes were kept for further analysis.

Embedding Method

Optical microbubble cavities^43,44 have been used for a variety of applications in (bio)sensing,⁴⁵⁻⁴⁷ spectroscopy,^48,49 lasing,^38,50 and frequency comb generation⁵¹ because of their attractive properties that include ultrahigh Q-factors (∼10⁷) (see Figure S3), hollow structure that can be integrated with microfluidics, and subwavelength wall thickness.⁵² Recently, this photonic structure has enabled photothermal monitoring of chemical reaction dynamics of gold AuNRs exposed to aqueous solution at the single-particle level.⁴⁸ An intriguing feature in this cavity is the tunability in mode properties, which are highly dependent on the refractive index of the interior (air, solvent, etc.) and can be easily controlled. This tunability may lead to a very high thermo-optic coefficient, a figure of merit for applications in photothermal measurement⁴⁶ and microscopy⁵³⁻⁵⁶ due to the large negative thermo-optic response in liquids (e.g., water and organic solvents) while introducing minimal absorption loss to the cavity in visible or telecommunication bands.

In this study, we perform single-particle photothermal spectroscopy (see below) on AuNRs coupled to microbubble WGMs. Chloroform is chosen to fill the microbubble cavity because it has a very similar refractive index (n = 1.43) to the silica comprising the microbubbles (see Methods), and therefore a chloroform-filled microbubble may provide the maximum mode overlap in a plasmonic–photonic coupled system, as illustrated in Figure 1. Embedding the AuNRs in a solid polymer matrix may also allow tuning of the mode overlap but not in an easily adjustable manner that also allows before-and-after characterization.^39,40 Another consideration is that chloroform absorbs less light than other solvents (water, toluene, etc.) at both the pump (1275–1355 nm) and probe (1550–1570 nm) wavelengths³⁶ of our experiment, resulting in very small losses to the Q-factors (see Figure S3). These characteristics, combined with chloroform’s large thermo-optic coefficient, may render the chloroform-filled microbubble an excellent single-particle absorption spectrometer for nonaqueous analytes. Spectroscopy in other wavelength regions could make optimal use of different solvents. After AuNRs were deposited as described previously (see Methods),⁴⁸ the remaining aqueous solution was removed, and the cavity was flushed by flowing Milli-Q water, then methanol, and finally drying the cavity (Methods). This treatment leaves AuNRs exposed to the air inside the cavity (see Figure S4). Single AuNRs were identified using photothermal imaging and polarization measurements (see Methods), where a high depth of modulation strongly suggests a single AuNR.^25,57 A photothermal map in Figure 2A shows several individual AuNR particles sparsely distributed on the interior surface of the microbubble cavity. Subsequently, single-particle photothermal absorption spectroscopy was conducted, where each particle acts as an individual coupled plasmonic–photonic system independent from all other AuNRs due to their sparse distribution. Upon the introduction of chloroform (Methods), photothermal imaging (Figure 2) determines that the spatial location of individual AuNRs under study does not change, suggesting that chloroform neither washes away nor translates the particles. At the same time, polarization dependence measurements (bottom panel of Figure 2 and Table S1) demonstrate that the AuNR orientations also do not change. Taken together, these results indicate that introducing chloroform does not impact the geometry of our coupled systems, rendering the change in spectral behavior solely attributable to shifted environmental refractive index and downstream consequences, including altered optical modes and therefore different coupling strengths.

Figure 2.

Fixation of single AuNRs on the interior surface of the microbubble. Both spatial locations and orientations are not perturbed by filling the microbubble with chloroform, as evidenced by photothermal coarse (top) and fine (bottom) maps and polarization plots (objects i and ii) under air-filled (A) and chloroform-filled (B) conditions. The polar plots are fitted to cos²(θ) (red dashed line) for determination of the depth of modulation (M) and peak angle (θ_max). Each dashed square indicates a single AuNR, while other unlabeled objects seen in the coarse map are not single AuNRs. The red dashed line shows where the fiber taper is and resides at slightly different locations relative to those of the AuNRs in panels (A) and (B). The scale bars in coarse (fine) maps are 10 μm (2 μm). Though only two particles are highlighted here, all seven detected particles are included in the following analysis.

Single-Particle Spectroscopy

We have recently demonstrated a single-particle photothermal absorption technique that takes advantage of the combination of ultrahigh sensitivity of whispering-gallery mode microcavities along with sophisticated locking and modulation schemes. This technique enables the measurement of resonance shifts induced by thermal dissipation from an excited nano-object by a pump laser, with a limit of detection down to under 1 attometer.²⁵ Leveraging this ultrahigh sensitivity, we have interrogated properties of conductive polymers,^58,59 examined plasmonic–photonic interactions,^25,27,36 introduced transparent substrates compatible with visible spectroscopy,^60,61 and shown the capability of real-time monitoring and control of nanoparticle properties⁴⁸ at the single-particle level. Photothermal absorption spectra at various spectral resolutions (low, intermediate, and high) were taken for each single AuNR, as described previously,³⁶ to determine how altering the medium refractive index influences the light–matter interaction as inferred from spectral signatures. The low-resolution (32 μeV per point) spectra, with the broadest spectral window, show that the peaks of the broad plasmonic absorption of most of the single AuNRs under study are beyond our pump spectral range for all but one of the AuNRs (Figure S5). Fitting of these low-resolution spectra in isolation does not allow precise determination of the spectral center or width. However, simultaneous fitting of the high- and low-resolution spectra (see below and Supporting Information) largely mitigates this issue. Intermediate-resolution (3.2 μeV per point) spectra, Figure 3, contain rich information about the plasmonic–photonic couplings, with the Fano antiresonance a signature of the light–matter interaction between the spectrally broad plasmonic mode and comparatively narrow photonic mode.^{25,27,62−68} The relative difference in spectral density of Fano antiresonances between air and chloroform samples is highly variable, suggesting that the specific details of each coupled system exert an effect on the spectral density of Fano antiresonances. For example, Figure 3 shows that in one of the AuNR-microcavity coupled systems, the Fano spectral density barely changes (Figure 3A,C) upon the introduction of chloroform, whereas a drastic increase in Fano spectral density is observed in the other coupled system (Figure 3B,D). The scarcity of Fano antiresonances seen in this particular system under the air-filled condition is attributed to the fact that this AuNR is approximately 30 μm away from the center of the microcavity along the z-axis (see Figures S6 and S7A). At this large shift, the only WGMs available to interact with the localized surface plasmon (LSP) are high-order polar WGMs with large mode volumes (∼3000 μm³), and their coupling strength is consequently weak. When AuNRs are located closer to the center of the microcavity where the tapered optical fiber resides (Figures 2 and S6), the LSP interacts with fundamental or low-order polar WGMs, and Fano antiresonances are more likely to be seen assuming nonorthogonal polarization of the LSP and the transverse electric (TE) polarization of the WGMs. The increasing number of WGMs in the radial direction (see Figure S7B) upon the introduction of chloroform suggests the possibility that a better mode overlap outcompetes the effect due to the increase in mode volume. In contrast, the drastic difference in Fano spectral density is not seen for those AuNR-microcavity systems where AuNRs are located close to the center of the microcavity.

Figure 3.

Intermediate-resolution and high-resolution photothermal absorption spectra of two single AuNRs in the air-filled (A, B) and chloroform-filled (C, D) microbubble. The spectra are normalized to their own maximum absorbance. The two AuNRs are objects i and ii in Figure 2. Fits (cyan and blue solid curves) to high-resolution spectra (black and red dots) are presented at different spectral locations. The dips at the pump energy of ∼0.952 eV shown in the intermediate-resolution spectra are artifacts due to imperfect power spectrum correction.

High-resolution (0.8 μeV per point) spectra of the Fano antiresonances are critical to extract the system parameters of the coupled photonic–plasmonic system. Representative spectra are shown as insets in Figure 3A,C, where minor differences in spectral lineshapes are observed between air-filled and chloroform-filled cases. Because these system parameters extend over many energy scales, quantitative fitting of the spectra must be carried out simultaneously over multiple spectral resolutions. To accomplish this fitting, we developed a fitting protocol that treats high-resolution and low-resolution absorption spectra simultaneously. Here, a 0 (1) subscript denotes a LSP (WGM) property. A low-resolution spectrum carrying information about LSP parameters, i.e., plasmon resonant frequency (ω₀), nonradiative damping rate (γ_0,NR), and radiative damping rate (γ_0,Rad), and a high-resolution spectrum, containing information about WGM parameters, i.e., WGM’s resonant frequency (ω₁), nonradiative decay rate (γ_1,NR) and radiative decay rate (γ_1,Rad), and couplings (g), in addition to LSP parameters, are simultaneously fitted to a phenomenological composite function (G). Here, G is a linear combination of the normalized LSP absorption cross section (f₁) scaled by a weighting factor (χ) and reduced absorption cross section (f₂), as shown below

1

where 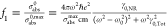, , 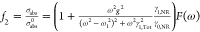F(ω) is the familiar Fano line shape function described previously (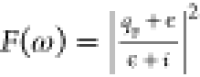, ϵ is the scaled and shifted pump frequency, and q_F is a complex-valued asymmetry parameter, both of which are given in the Supporting Information)³⁶ showing an antiresonance in pump-tuning frequency (ω) near ω₁, σ_abs⁰ is the bare LSP absorption cross section,³⁶ σ_abs is the maximum cross section of the unperturbed LSP absorption, σ_abs is the WGM-dressed absorption cross section, γ_0,Tot = γ_0,NR + γ_0,Rad, γ_1,Tot = γ_1,NR + γ_1,Rad, e is the elementary charge, and m is the effective mass that describes the inertial response of the LSP to external fields (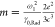, see Supporting Information).⁶⁹ An optimal value of χ is chosen such that fitting errors in both high-resolution and low-resolution spectra remain low and do not fluctuate appreciably through fit iterations (Figure S8). A global optimization algorithm (MultiStart, MathWorks Inc.) is utilized to avoid convergence to local minima of G (Supporting Information).

The first results of the parameter extraction are shown in Figure 4, which presents bar plots of plasmon natural frequency (ω₀) and plasmon total damping rate (γ_0,Tot) for different AuNRs under air- and chloroform-filled conditions. Determination of ω₀ is consistent with the spectral location of the longitudinal LSP resonance (∼1.16 eV) reported by the manufacturer (Nanopartz Inc., see Figure S10). ω₀ decreases upon introduction of chloroform in all of the coupled systems under study with a difference of up to 70 meV, showing that an increase in the interior dielectric constant induces a red shift in the LSP resonance, which is consistent with previous literature studies on LSP environmental effects.^70,71 This relatively small shift is likely due to substrate effects⁷⁰ as AuNRs in the air-filled microbubble experience a highly asymmetric dielectric environment, while shifting to chloroform results in a nearly symmetric dielectric environment. Values of γ_0,Tot are observed to decrease as well on average (see the Supporting Information and Figure S9), although the effect is usually modest and within measurement uncertainty.

Figure 4.

LSP parameters determined via simultaneous fits to high-resolution and low-resolution spectra. NR1-7 are single AuNRs studied on one microbubble, and NR8 is a single AuNR on a different microbubble. The error bar for NR3, chloroform-filled, is too small to be observable.

Determining Couplings and Optical Simulations

Of key interest is how the coupling strength (g) for the interaction between a single LSP and a set of WGMs in each AuNR-microcavity coupled system is influenced by the solvent-induced shifting spatial overlap of the photonic and plasmonic modes. Due to the absence of a direct method of mode identification in our coupled system, our experimental method is unable to interrogate the exact same coupled WGM while altering the interior dielectric environment. Instead, the statistical analysis of the WGMs’ response to this alteration is discussed. By fitting to each Fano antiresonance in the high-resolution spectra, our analysis gives rise to a statistical distribution of experimental coupling strengths, with ℏg reaching up to 7.5 × 10^–4 eV in one of our studied coupled systems (Figure S11), which is comparable to our estimated maximum value (6.7 × 10^–4 eV, see below) for a fundamental WGM when the maximum mode overlap is achieved under chloroform-filled conditions. This value is less than γ_0,Tot by about 2 orders of magnitude, confirming that our system still operates in the weak-coupling regime even if the maximum mode overlap is achieved. The lowest determined coupling strength is approximately 1.0 × 10^–4 eV, at which point our experimental signal-to-noise ratio (SNR) in high-resolution spectra precludes observation of weaker Fano antiresonances due to their smaller magnitude.

Figure 5A shows that the distribution profile of g values shifts to smaller values under chloroform-filled condition relative to that under air-filled condition in one coupled system (panel i, mean value decrease of 1.3×), whereas in another system (panel ii), larger g values are seen (mean value increase of 1.4×). Further examination of other AuNR-microcavity coupled systems (panels iii and iv in Figures 5A and S11) shows that the distribution profile can upshift, downshift, or barely change when chloroform fills the microbubble. Overall, the mean of g across all of the experimental data sets is not seen to change significantly, though specific nanorods may exhibit an increase in g due to the location of the specific nanorod relative to the WGMs. Simply analyzing the influence of the chloroform on the mean of g and its distribution profile is insufficient for deciphering the roles mode volume and mode overlap play in affecting g and its statistical distribution.

Figure 5.

Distributions of g determined in experiments for four single AuNRs (i–iv) (A) and comparison of changing distributions for g between experiments and simulations for four AuNRs under air-filled (black) and chloroform-filled (red) conditions (B–E), which are also presented in Figure S13. The values of g are scaled by an implicit factor of ℏ.

Optical simulations via a finite element method provide eigen solutions for WGM optical modes from which the mode volume and mode spatial distribution can be derived to compute theoretical estimates of g, which can be compared with experimental values obtained through fits. Furthermore, these theoretical estimates can be used to quantify the interplay between changes in mode volume and mode overlap. Thus, optical simulations were conducted to reveal the contributions of mode volume and mode overlap to g. The simulations take into consideration all of the WGM eigenfunctions, regardless of mode volume, in a frequency range that matches our pump range in experiments. These simulations are then filtered to include only the specific frequency ranges of the high-resolution spectra. In addition, our finite SNR only allows fitting of Fano signatures with the coupling strength above an experimentally determined minimum value (∼1.0 × 10^–4 eV), so simulations were post-processed to only include those that are likely experimentally observable (Supporting Information).

The expression for g is adapted from our previous work³⁶ and shown in eq 2

2

where , , 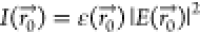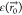is the permittivity, and 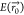is the electric field strength at the location of an examined AuNR calculated by solving Maxwell’s equations, and cos(θ) determines the AuNR’s orientation relative to the TE polarization of the WGM with field vectors parallel to the interior surface of a microbubble. Note that V is obtained using the equation (V = ∫ε(r)|E(r)|² d³r/max[ε(r)|E(r)|²]) according to ref (72). In addition to mode volume (V) and mode overlap (J), factors specific to a particular WGM in the weak coupling regime, the expression also contains the effective mass (m). Using the relationship⁶⁹ between the effective mass and the ideal radiative damping rate for a point dipole 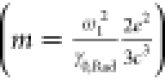results in an underestimation of the simulated g by over 2× (Supporting Information). However, this calculation suffers from several non-idealities, including imprecise experimental determination of γ_0,Rad³⁶ and an assumption of perfect harmonic behavior⁶⁹ despite considerable damping. This issue was resolved instead by employing a prolate spheroid model to analytically determine the effective mass.^73,74 This method is further corroborated in a different recently examined coupled plasmonic–photonic cavity,³⁶ where a microtoroid allows more accurate determination of key system parameters due to the less densely packed mode structure (see the Supporting Information and Figure S12). J is spatially dependent on where single AuNRs are deposited on the interior surface relative to the equator of the microbubble along the z-axis and is thus a function of polar mode number (Figure S7). Since the mode volume in the AuNRs is substantially smaller as compared to that of WGMs in the microbubble, the LSP is treated as a point dipole. When the AuNR is located in the maximum of the WGM field, J is equal to 1, i.e., maximum mode overlap is achieved, leading to the above calculation for maximum coupling strength. Otherwise, J decreases rapidly and may vanish when the AuNR sits in a WGM node.

Unfortunately, estimating the precise position of the nanoparticle relative to the microbubble waist is challenging due to the difficulty of determining the absolute position of the waist using the photothermal image. Coarsely coaligning the photothermal map and the optical image of the microbubble allows determination of this parameter with an uncertainty of ∼10 μm, which prevents determination of the exact location of individual AuNRs on the interior surface relative to the equator along z-axis (Figure S6). To work around this limitation, multiple spatial locations on the interior surface relative to the equator are sampled for each WGM in our simulations (see the Supporting Information and Figure S11). A distribution of g is obtained at individual discrete spatial locations where a AuNR may reside. As shown in Figure 5B–E, the changing behavior in the simulated distributions of g due to different interior photonic environments qualitatively resembles those in experimentally determined distributions for the AuNRs. When the spatial location of a AuNR moves further away from the center of an air-filled microcavity (i.e., z has a large magnitude), Fano antiresonances with low-valued coupling strength are more common. Our simulations clearly demonstrate this distinct trend (see Figure S13). Fano antiresonances with smaller coupling strengths are less likely to be observed in our measurements (see Figure 3A,B) because the spectral features are less pronounced since there is a finite amount of experimental noise. However, changing the dielectric environment from air to chloroform shmears out this spatial dependence due to a rising number of accessible WGMs (see Figure 3C,D), leading to a weaker dependence of Fano antiresonance density on nanoparticle position and higher overall density.

Importantly, simulations only include as inputs the LSP resonant energy (ℏω₀), which is extracted from the course spectra, and the physical dimensions of the AuNR and microbubble. The simulations do not include inputs from the fine spectra, which are used to determine the experimental values of g and are thus an independent estimation. In general, simulations are able to approximate the magnitude of the g values Figure 5B–E), as well as situations where higher g values are observed in chloroform (Figure 5C), seen in air (Figure 5E), or situations where the magnitudes are largely similar (Figure 5B,D). Simulations for other AuNRs deposited onto the same interior surface of the microbubble also qualitatively agree with experimental results at particular AuNR locations (Figure S11).

We further investigate the distribution of possible V, J, and J/√V values. Here, we perform this analysis on the full set of WGM eigenmodes over the pump wavelength window rather than limiting to specific high-resolution windows and high SNR values. The probability density distribution profiles of V for air-filled and chloroform-filled microbubbles are shown in Figure 6A. V in a chloroform-filled microbubble shows a bimodal distribution, with peaks at 4500 and 5800 μm³. Only the fundamental and a few low-order modes in the chloroform-filled microbubble extend to the low-V regime, where they are comparable to the mode volumes in the air-filled microbubbles. Overall, the mean of V increases by a factor of ∼2 when chloroform is added. On the other hand, the distribution of J spreads out relatively evenly in the chloroform-filled microbubble (Figure 6B), whereas J exhibits a bimodal distribution in the air-filled microbubble due to alternating even and odd nodes. These two peaks will gradually merge as the spatial location of the nanoparticle moves away from the equator, and the values of J pile up at the lower bound, suggesting very weak coupling strengths for nanoparticles far from the equator (Figure S14). Such peaks are not initially visible in the chloroform distribution because of the contributions of high-order radial modes. Figure 6C shows the probability density distribution of J/√V (∝g), where the profile of the air-filled microbubble is also bimodal like J, whereas the distribution profile is relatively narrow compared to the distributions of both J and V in the chloroform-filled microbubble. Thus, the diluting effect of the large mode volumes in the chloroform-filled microbubble sometimes offsets the contribution of the stronger mode overlap to the overall interaction, particularly for higher-order modes. On the other hand, in low-order modes, particularly fundamental modes, this diluting effect is weaker, and overall, a stronger interaction is seen. For example, when the fundamental modes in both air and chloroform are coupled to a AuNR at z = 0, the mode overlap increases from 0.1 to 1, whereas the mode volume increases from ∼1100 from ∼2000 μm³. Taken together, g is expected to increase by a factor of ∼7 for the fundamental modes.

Figure 6.

Kernel density distributions of V (A), J (B), and J/√V (C) under air-filled (black curve) and chloroform-filled (red curve) conditions. Distributions of J and J/√V are presented at the spatial location of z = 0 μm projected along the microbubble z-axis (see Figures S6 and S7). The values of J/√V are scaled by an implicit factor of 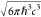. cos(θ) is assumed to be 1 in J.

Alternative geometries can be pursued to decouple the degrees to which J and V rise together when the AuNRs are embedded in chloroform. If a single AuNR is embedded in a thin layer of chloroform less than or comparable to the thickness of the glass wall (∼608 nm) instead of a bulk chloroform medium, then V does not increase significantly while a stronger mode overlap is still preserved. Alternatively, a smaller microbubble (diameter: ∼50 μm) provides a relatively small V to begin with, which may decrease the degree to which V increases when the microbubble is filled with chloroform.⁴⁵ Another alternative strategy focuses on the use of water. If the microbubble cavity operates at 780 nm, the interfacial mode in a water-filled microbubble⁴⁵ may provide the maximum mode overlap with only a modest increase in mode volume, leading to the maximum coupling strength.

Conclusions

We present a solvent-embedding method to influence plasmonic–photonic interactions in a microbubble cavity. We find that changing the dielectric environment by filling the microbubble cavity with chloroform alters the system parameters (g in particular), resulting in an increased interaction for low-order WGM modes and a decreased or minimally changed interaction for high-order WGM modes. Our combined experimental and numerical approach reveals that both V and J increase as the dielectric contrast decreases, influencing the change in g in a competing manner. Our simulated results qualitatively agree with the experimentally determined distribution of g. This agreement implies that the spatial locations of AuNRs relative to mode profiles of WGMs may result in distinct distributions of g as the LSP interacts with fundamental or low-order WGMs more strongly in the chloroform-filled microbubble.²⁸ The active control of the interaction provides a new experimental handle for the design of plasmonic–photonic microsensors for sensing of biomolecules and for other applications which rely on control of light–matter interactions.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcc.2c05733.

• Transmission electron microscopy (TEM) image of AuNRs, experimental setup diagram, polarization dependence of single AuNRs, the effect of changing dielectric on mode spectrum, optical images for air-filled and chloroform-filled microbubbles, low-resolution spectra under air-filled and chloroform-filled conditions, fitting method, Fano line shape function (F(ω)), decrease of γ_0,Tot, distribution of experimentally determined coupling strength, optical simulations, determining the effective mass (m) using a prolate spheroid model, and resolving the discrepancy between experimentally determined and simulated values of g, Kernel density plots (PDF)

Author Present Address

^# Department of Materials Science and Engineering, Stanford University, Stanford, California 94305, United States

The authors declare no competing financial interest.