New achievement of the global sheath-bulk model for the collisionless radio-frequency using in scale industries

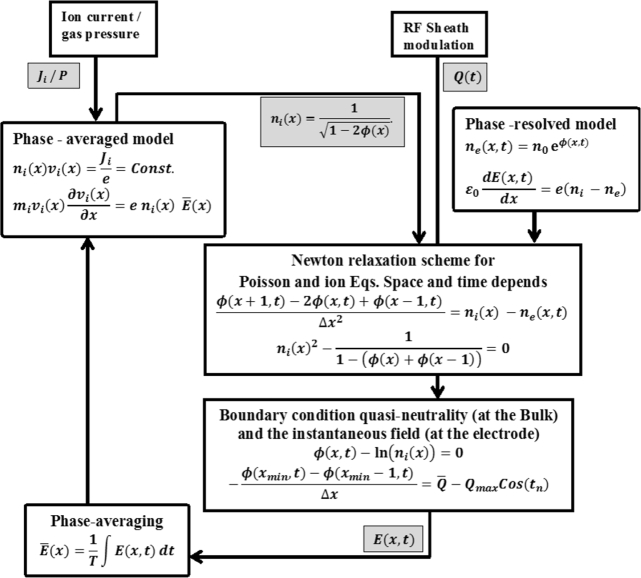
Abstract

Plasma processing is extensively utilized in enormous industries products like semiconductor devices, textile fabrics, modifying polymers, and seed treatments. One of the most significant enhancements to this technology is the low pressure of capacitively coupled plasma (CCPs). Contrary to other plasma processes like atmospheric pressure plasma jet, low-pressure plasma under vacuum is the best choice for scale industrial applications, including etching, semiconductor IC fabrication, and seed processing for agricultural use. This is due to its full soft control and complete ionization chamber. It is quite difficult to analyze the dynamics of the plasma sheath theory. Despite being among the most relevant models, the step approximation model does not fully account for all nonlinear dynamics, particularly high harmonic effects, the particle density singularity between the sheath and bulk regions, and the absence of an ambipolar field in the bulk zone. We provide a significant solution to this issue in this study. The numerical fluid model for collisionless self-consistency is solved. As a result, the sheath charge distribution V(Q), which is considered as the main factor of control all nonlinear dynamics of the sheath, is estimated. Strong agreement between experimental data from the Ziegler et al. [7] study and our cubic fitting formula for the V(Q) distribution. Additionally, by compared the results of step approximation with the non step model, theoretical advancements like handling the particle density singularity and the merging of the sheath-bulk zone are further illustrated. Moreover, the most simple but effective solution at a minimal computing cost, the global model, is solved. By applying accurate sheath charge distribution, which controls all nonlinear dynamics, the global model's accuracy is established. As a result, more nonlinear dynamics are achieved, including distributions of currents, densities, charges, and power. Finally, excellent calculations of average power and sheath distance in case of collisionless region are calculated. Our study can find a more accurate physical and engineering approach which may help in industry applications.

Collisionless; Rf plasma; Capacitive; Sheath; Step model; Cubic fitting

1. Introduction

Although there are many tools for using plasma processes in advanced industry, agriculture, cancer therapy, and biomedical applications such as plasma at low pressure and plasma atmospheric. In general, plasma jets have small and weak effects compared to vacuum plasma at low pressure. As a result, non-thermal plasma in low pressure and temperature is considered more significant than plasma jets in most scale industries applications. Therefore, it is widely used in semiconductor manufacture and recently in the agriculture field of seeds treatment. As an example, one of the most important devices to scale industry fabrication, a capacitively coupled plasma discharge (CCPs) that the apparatus is very simple, full ionized champers, has full control using different applied voltage-driven radio-frequency waveform, and is almost maintenance free. The bulk and the sheath are split theoretically into two regions. The strong electric field at the walls accelerates and controls the energy of the positive ions when the voltage is fully over the sheath. This is crucial for the processing of plasma where the voltage sinks completely over the sheath, creating a strong electric field at the walls that accelerate and controls the energy of positive ions. The bulk plasma occupies the majority of the discharge volume V of size L whereas the sheath only creates a thin layer with an average thickness of s. We adopt length scales with the formula ${\lambda }_D\ll \overline{s}\ll L$. Many mathematical models idealize these phenomena like Godyak's homogeneous model [1], Riemann with consist step model [2], and Lieberman's inhomogeneous model [3], [4]. Riemann's model, however, uses the sheath bulk model of the one dimensional theory [5], [6]. The investigation of the plasma boundary sheath has shown to be the most complicated due to its non-linear dynamics even after having simplified the assumptions and physical approximations. Therefore, one needs to be aware of this significant occurrence and use accurate mathematical modeling and simulation in order to accurately examine the nonlinear dynamics of sheath plasma effects. For theoretical as well as practical purposes, it is consequently of utmost essential to have a complete understanding of its physical behavior of nonlinear dynamics. [7], [8], [9], [10], [11], [12], [13], [14], [15], [16], [17], [18], [19], [20]. One simple but effectively accurate approaches, known as the global model [7], [8]. The use of global models in the study of plasma, which describe the nonlinear dynamics of plasma reactor by a finite number of passive electric elements like resistance, capacitance, and inductance, is related to simple ordinary differential equation (ODE). The accuracy of the global model is justified when the lumped-element equivalent circuits are equivalent to a more significant solution of fluid models. An important step in the validation of global model is to identify the sufficiently accurate sheath charge distribution, which controls this region as a variable capacitor and is in charge of all complex nonlinear dynamics. Accordingly, in this research we will study three important models, self consisting fluid model, step approximation and global sheath. In order to get a solution for global sheath-bulk model we should find the sheath voltage distribution which is unknown in the analysis of ordinary differential equations (ODE). The more getting perfect relationship of the V(Q) distribution, the more accurate study of the nonlinear dynamics of the plasma sheath theory [9]. As a result, we were able to solve the majority of the difficulties with the self-consistent numerical fluid model of the collisionless regime. According to the collected set of equations for this model, there are two reasons that make it difficult to solve this problem. First, the ion equation of motion has also no analytical solution. The second reason is that the Poisson's equation has no analytical solution to get the time-dependent field; hence the average electric field cannot be calculated. In this paper we could find a new achievement of non step model for the collisionless regime. We describe the schematic scheme of solving non step model covering step approximation in the Appendix (Fig. 18). For the purpose of solving the continuity equation for the ion model, we adopt the collisionless regime. After that, we solve the Poisson equation using an appropriate Newton relaxation scheme for spatio-temporal discretization in order to determine the instantaneous electric field and its average [10], [11]. Once the instantaneous electric field and its average are obtained, the solutions of the Poisson equation for different modulation amplitudes of the applied current are obtained then all nonlinear sheath dynamics were calculated. Additionally, the non step model provides a higher level of physical analysis, allowing for the verification of the merging of the sheath and bulk regions such as instantaneous electron, average ion density, instantaneous electric field, and average of electric field distributions. These results lead to find more accurate sheath voltage distribution with cubic fitting formula of the plasma boundary sheath. In contrast, the results of step approximation failed to correctly merge into the ambipolar field of the bulk in compared with our non step model. Consequently, the experimental data in the reference [7] have been validated with our cubic sheath voltage formula, and there is good agreement. The cubic relation of $V(Q)$ distribution, which is the key factor for global model, is calculated to get the values of the exact nonlinear elements in the sheath. Also, the significant nonlinear dynamics in the bulk like current, charge, power distributions and the exact average power is achieved. The results have a good response to the experimental data. The higher harmonic effect in the bulk which does not exist in the step approximation is obtained and higher average power is calculating. At least, the sheath distance of the collisionless sheath regime with simple approach in case of modulated current is computed. The paper give a new achievement to the study of the global sheath - bulk model and find a correct path of merging between them. The study was matching with growing rate needs of market requirements for low-pressure plasma devices.

Figure 18.

Schematic depiction of the problem posed by the step model and self-consistent numerical solution.

2. Global sheath model of CCPs

The global behavior of the sheath can be represented by a diode, a current, and a nonlinear capacitor in parallel:

• •The diode model of the sheath

Fig. 1 depicts the distributions $n_{\mathrm{i}}(x)$ and $n_{\mathrm{e}}(x,t)$ of the ions and the electrons respectively in an RF-modulated sheath in more detail. It is represented by a lumped element equivalent circuit shown on the right. The diode represents the highly nonlinear flux of the electrons to the electrode:

$$J_e=\mathrm{e}\sqrt{\frac{{\mathrm{T}}_{\mathrm{e}}}{\mathrm{2}\mathit{\pi }{\mathrm{m}}_{\mathrm{e}}}}{\mathrm{n}}_{\mathrm{B}}\exp (\frac{\mathrm{e}\left(\mathit{\varphi }{(\mathrm{x})}_{{\mathrm{x}}_{\mathrm{E}}}-\mathit{\varphi }(\mathrm{s}(\mathrm{t}))\right)}{{\mathrm{T}}_{\mathrm{e}}})$$ (1)

The current source represents the temporally constant ion flux

$$J_i=e{\psi }_i$$ (2)

The nonlinear capacitor represents the displacement current to the electrode center

$$J_D={ϵ}_0\frac{dE}{dt}$$ (3)

The total current will equal to

$$J_{total}={ϵ}_0\frac{dE}{dt}+j_{\mathrm{i}}+j_{\mathrm{e}}$$ (4)

The phase average of the electron current $j_e(t)$ is equal to the ion current density with different sign. Assuming that electrons which reach the electrode are absorbed. The net electric field at $(E_{\infty }\to 0)$ is $E_{x_E}=-\frac{Q(t)}{{ϵ}_0}$ [10]. The total current of lumped model circuits can be written as;

$$J_{total}=-\frac{dQ}{dt}-e{\psi }_i+\mathrm{e}\sqrt{\frac{{\mathrm{T}}_{\mathrm{e}}}{\mathrm{2}\mathit{\pi }{\mathrm{m}}_{\mathrm{e}}}}{\mathrm{n}}_{\mathrm{B}}\exp (-\frac{\mathrm{e}{\mathrm{V}}_{\mathrm{sh}}(\mathrm{Q})}{{\mathrm{T}}_{\mathrm{e}}})$$ (5)

Figure 1.

Schematic sketch of the particle densities in an RF-driven plasma boundary sheath (left), and lumped element equivalent (right).

3. Global bulk model of CCPs

We could analyze Fig. 2, by using Kirchhoff's voltage law, which state their total sum vanishes,

$$V_{\mathrm{r}f}-V_{\mathrm{S}B}+V_{\mathrm{s}h}-V_{\mathrm{P}}-V_{\mathrm{G}}=0$$ (6)

Figure 2.

Schematic sketch of global model of bulk model (Ziegler et al. [7]).

The total rf current conduction in the plasma bulk which carried by electrons is,

$$\frac{\partial J_{\mathrm{t}otal}}{\partial t}+{\nu }_{\mathrm{eff}}{J}_{\mathrm{t}otal}=L_{\mathrm{P}}^{-1}{V}_{\mathrm{P}}$$ (7)

Here, ${\nu }_{\mathrm{e}ff}={\nu }_m+{\overline{v}}_e/L$ is the effective collision frequency, the constant $L_P^{-1}$ may be called the effective inverse inductance of the plasma column (it is not a result of a magnetic effect but reflects the inertia of the electrons), it can be expressed as $L_P^{-1}=\frac{e^2}{m_e}\frac{A_E}{L}{\overline{n}}_e$, where L stands for “effective extension” of the plasma bulk and ${\overline{n}}_e$ denotes an “effective plasma density”. The ground potential, floating potential can be represented by

$$V_G=V_{fl}=\ln \left(\frac{m_{\mathrm{i}}}{2\pi m_{\mathrm{e}}}\right)\frac{T_e}{2e}$$ (8)

From above global model equations we can obtain important study for a nonlinear boundary sheath, through collecting, the algebraic relations to eliminate dependent variables, and obtain closed system for the current density $J=I/A_E$, the sheath voltage ${\mathbf{\text{V}}}_{\mathrm{sh}}(\mathbf{\text{Q}})$, the self-bias $V_{\mathrm{SB}}$, and the discharge current density, which can be introduced.

$$\frac{d\mathbf{\text{Q}}}{dt}=-I(t)-e{\psi }_i+e\sqrt{\frac{T_{\mathrm{e}}}{2\pi m_{\mathrm{e}}}}{n}_{\mathrm{B}}\exp (-\frac{e{\mathbf{\text{V}}}_{\mathrm{sh}}(\mathbf{\text{Q}})}{T_{\mathrm{e}}})$$ (9)

$$\frac{\partial I(t)}{\partial t}=L_{\mathrm{P}}^{-1}(V_{\mathrm{r}f}+{\mathbf{\text{V}}}_{\mathrm{sh}}(\mathbf{\text{Q}})-V_{\mathrm{S}B}-V_G)-{\nu }_{\mathrm{eff}}I(t)$$ (10)

$$\frac{\partial V_{\mathrm{S}B}}{\partial t}=\frac{{\mathrm{L}}_p}{A{ϵ}_0}I(t)$$ (11)

In our study we will calculate a more elaborate and significant relationship between the sheath charge and voltage sheath distributions, which is missing in this study where,

$$V_{\mathrm{sh}}=V_{\mathrm{sh}}(Q)=?$$ (12)

Summing up, the current density J through the sheath can be described as a sum of three terms with quite different characteristics. In addition, equations of bulk model are itself related to $V_{\mathrm{sh}}(Q)$. The important formula of the collisionless sheath voltage $V_{\mathrm{sh}}(Q)$ will obtain by study the exact semi analytical solution of fluid model. Finally, the missing part in the lumped element equivalent circuits is achieved and establishes perfect results of nonlinear dynamics of CCP.

4. Self-consistent collisionless fluid model

In the plasma boundary sheath region at low pressure discharge and high frequency RF-regime, there is a depletion of electrons within a much larger electric field which confines the electrons to the discharge and extracts more massive ions. There is an ambipolar field in the bulk, which is a result of the coupled diffusion of the negative and positive charge carriers. The fluid descriptions of the high RF regime are assumed to be ${\omega }_{\mathrm{pi}}\ll {\omega }_{\mathrm{rf}}\ll {\omega }_{\mathrm{pe}}$, where the electrons are in equilibrium with the time-varying field, and the ions react only in phase average field. The model of the RF-plasma boundary sheath can be expressed using the following: electron model dynamics, ion model dynamics, field model Maxwell's equation, and one dimensional geometry. In this approach we will use a scale length of Debye length ${\lambda }_D$, mean free path λ, reactor length R, sheath plasma s, scale time of electrons plasma frequency ${\omega }_{\mathrm{pe}}$, ion plasma frequency ${\omega }_{\mathrm{pe}}$, high frequency ${\omega }_{\mathrm{rf}}$, collision frequency ν. Through the fluid model, specialized for an RF sheath this assumption of non-collisional model the ion model states [3] at gas pressure $<5\text{ Pa}$. An improved on the basis of a scale analysis of Boltzmann-Poisson equation [10] is calculated. The set equations set can be represented as follows (see Fig. 3):

• •Ion model

$$n_{\mathrm{i}}{v}_{\mathrm{i}}=-{\mathrm{\Psi }}_{\mathrm{i}}$$ (13)

$$m_{\mathrm{i}}{n}_{\mathrm{i}}{v}_{\mathrm{i}}\frac{\partial v_{\mathrm{i}}}{\partial x}=-e{n}_{\mathrm{i}}\overline{E}$$ (14)

$$\frac{1}{2}{m}_{\mathrm{i}}{v}_{\mathrm{i}}^2+\frac{1}{2}e\varphi =\frac{1}{2}{T}_{\mathrm{e}}$$ (15)

Figure 3.

Schematic sketch of the plasma reactor in case of collisionless regime.

Stationary ion dynamics is connected to the phase averaged electric field $\overline{E}$ which is related to the instantaneous field $E(x,t)$ when we apply a high RF, where (${\omega }_{\mathrm{rf}}\gg {\omega }_{\mathrm{pi}}$), via ($T_{\mathrm{rf}}=2\pi /{\omega }_{\mathrm{rf}}$) is calculated as

$$\overline{E}(x)=\frac{1}{T_{\mathrm{rf}}}\underset{0}{\overset{T_{\mathrm{rf}}}{\int }}E(x,t)dt$$ (16)

• •Electron model

The electrons follow the electric field instantaneously. It can be assumed in the Boltzmann equilibrium, i.e., that their diffusion pressure $p_{\mathrm{e}}=n_{\mathrm{e}}{T}_{\mathrm{e}}$ balances within the electric force $-e{n}_{\mathrm{e}}E$. For a constant electron temperature,

$$T_{\mathrm{e}}\frac{\partial n_{\mathrm{e}}}{\partial x}=-eE{n}_{\mathrm{e}}$$ (17)

$$n_{\mathrm{e}}={\hat{n}}_{\mathrm{e}}\exp \left(\frac{\mathrm{e}\mathit{\varphi }}{{\mathrm{T}}_{\mathrm{e}}}\right)$$ (18)

• •Maxwell equation

The instantaneous electric field which is parametrically RF-modulate via Poisson's equation:

$${ϵ}_0\frac{\partial E}{\partial x}=e(n_{\mathrm{i}}-n_{\mathrm{e}})$$ (19)

The instantaneous sheath charge can be determined through the RF modulation ($j,{\omega }_{\mathrm{rf}}$) and it can be introduced as follows:

$$Q(t)=\underset{x_E}{\overset{\infty }{\int }}e(n_{\mathrm{i}}-n_{\mathrm{e}})dx=\underset{0}{\overset{s(t)}{\int }}e{n}_{\mathrm{i}}dx$$ (20)

By integrating instantaneous sheath charge

$$Q(t)=-\frac{{ϵ}_0}{e}E{|}_0$$ (21)

Through the above equation we can determine the instantaneous sheath charge. The current balance equation is derived as:

$$\frac{dQ(t)}{dt}=\frac{J_{\mathrm{rf}}}{e}\sin ({\omega }_{\mathrm{rf}}t)-{\psi }_{\mathrm{i}}+\frac{1}{e}{j}_{\mathrm{e}}{|}_0$$ (22)

$$\frac{1}{2\pi }\underset{0}{\overset{2\pi }{\int }}\exp (\mathit{\varphi })\mathrm{dt}{|}_{\mathrm{0}}=\mathit{\mu }$$ (23)

From the non dimensional equations, of Poisson's and fluid equation of electrons and ions, the electron loss ratio μ and the dimensionless RF current J can be determined as

$$\mu =\frac{\hat{v}}{\sqrt{T_{\mathrm{e}}/(2\pi m_{\mathrm{e}})}}\equiv 0.00706781$$ (24)

$$J=\frac{J_{\mathrm{rf}}}{e\hat{n}{\lambda }_{\mathrm{D}}{\omega }_{\mathrm{rf}}}\equiv 3.9.$$ (25)

The normalization of the dynamical quantities is carried out by $x\to {\hat{\lambda }}_{\mathrm{D}}x$, $t\to t/{\omega }_{\mathrm{rf}}$, $n_{\mathrm{i}}\to \hat{n}{n}_{\mathrm{i}}$, $n_{\mathrm{e}}\to \hat{n}{n}_{\mathrm{e}}$, $v_{\mathrm{B}}\to {\hat{v}}_{\mathrm{B}}\sqrt{\frac{T_{\mathrm{e}}}{m_{\mathrm{i}}}}$, $\varphi \to (T_{\mathrm{e}}/e)\overline{\varphi }$, $E\to (T_{\mathrm{e}}/e{\hat{\lambda }}_{\mathrm{D}})\hat{E}$, $Q\to {\hat{\lambda }}_{\mathrm{D}}\hat{n}Q$, and ${\psi }_{\mathrm{i}}\to v_{\mathrm{B}}\hat{n}$, $v_{\mathrm{B}}\to 1$ (from Bohm criterion), $J_{\mathrm{e}}\to e\hat{n}{\hat{\lambda }}_{\mathrm{D}}{\omega }_{\mathrm{rf}}{\hat{J}}_e$, $J_{\mathrm{rf}}\to e\hat{n}{\hat{\lambda }}_{\mathrm{D}}{\omega }_{\mathrm{rf}}{\hat{J}}_{\mathrm{rf}}$ (see Fig. 4). The dimensionless system of fluid equations for ion, electron and electric densities can be obtained by: The ion and electron densities in terms of the average potential

$$\widehat{n_{\mathrm{i}}}=\frac{1}{\sqrt{1-2\overline{\varphi }}}$$ (26)

$$\widehat{n_{\mathrm{e}}}={\mathrm{e}}^{\overline{\varphi }}$$ (27)

Normalized Poisson equation can be represented as follows:

$$-\frac{{\partial }^2\varphi }{\partial x^2}=\frac{1}{\sqrt{1-2\overline{\varphi }}}-\exp (\mathit{\varphi })$$ (28)

The last differential equation could be decreased to the first order by integrating the equation and multiplying by $\partial \varphi /\partial x$:

$$\frac{\partial \varphi }{\partial x}=\sqrt{2}\sqrt{-2+\sqrt{1-2\varphi }+\exp (\mathit{\varphi })}.$$ (29)

Figure 4.

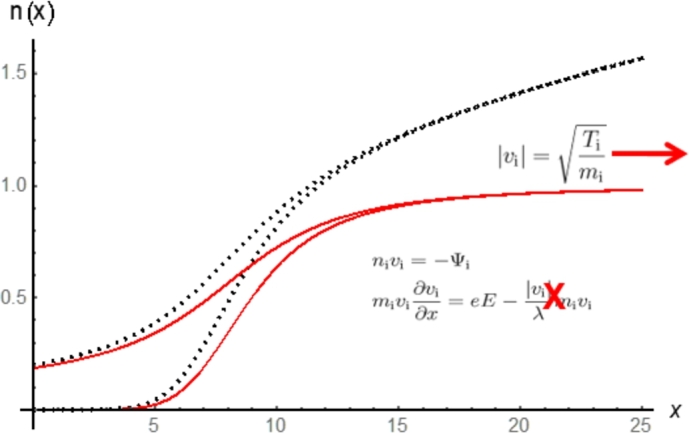
In the collisionless limit sheath approximation has a Bohm criterion at infinity and appears as asymptotic condition. In other hand, collision regime sheath approximation has no Bohm criterion where no mathematical structure that may be identified.

Within the boundary conditions

$$\frac{\partial \varphi }{\partial x}{|}_0=Q(t)=\overline{Q}-Q\cos \left(\mathrm{t}\right)$$ (30)

$$\varphi -\ln \left({\mathrm{n}}_{\mathrm{i}}\right)=0.$$ (31)

5. V(Q) solution for collisionless non step model

To solve the nonlinear differential Poisson's equation and find $\varphi (x,t)$ [10]. We apply the model at space-time dependent function $\varphi (x,t)$, where the normalized displacement current is not equal zero $j\ne 0$. A relaxation time scheme was taken between 0 and, 2π and numerical spatial scheme $[x_{\min }=0,x_{\max }=100]$. The boundary condition of $\frac{\partial \varphi }{\partial x}{|}_{x_{\min }}=\overline{Q}-Q\cos (t)$, where $\overline{Q}$ was suitable arbitrary positive number. The interval was applied for size $\mathrm{\Delta }x=1/3$. The relaxation scheme is applied for our experimental reference $J=2$ [7]. See the self consisting fluid model at the scheme of Figure 18, Figure 19 in the appendix.

Figure 19.

Schematic of self consistency collisionless fluid model using Newton relaxation scheme.

5.1. The charge - voltage distribution cubic approximation

The $V(Q)$ distributions of the sheath vary with different modulation amplitude of J can approximate in the form of a nonlinear polynomial series such as linear, quadratic, and cubic fits (see Fig. 5). We find cubic fit is the less relative error to the exact model distribution in our case 0.16%. A cubic polynomial can approximate the $V(Q)$ characteristics more sufficiently with higher accurate than the approach of quadratic [15], [16] and standard cubic fit [9]:

$$V(Q)=\sum _{k=0}^3{C}_k(J)Q^k,$$ (32)

$$V(Q)=C_0+C_{1}Q+C_2{Q}^2+C_3{Q}^3.$$ (33)

Figure 5.

Different accuracy of the charge-voltage distribution is calculated. The standard line (red) and quadratic (blue) curve is less fitting than the cubic approximation (Dotted) with respect to the exact solution of VQ (black). Exact solution of VQ curve (black) is more conceded with cubic approximation (dotted).

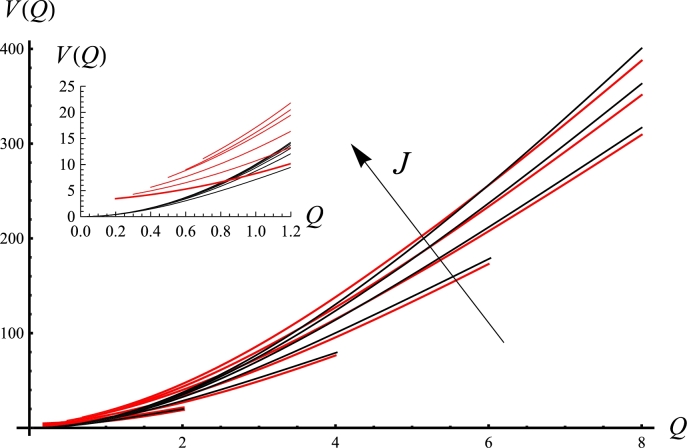
The total relation of applied voltage on the sheath $V(Q)$ and the charge $Q(t)$ varies with different modulated current density $J=1-6$ are obtained. Fig. 6 shows the comparison of the $V(Q)$ distributions of collisionless fluid model with results of the step model approximations.

Figure 6.

Charge voltage distributions of collisionless fluid model employing exact solutions to step approximation. The results are calculated for different amplitude of RF modulation J = 1 − 6. The value of current amplitude J increasing from 1 to 6 in the direction of arrow.

6. Comparison of theoretical V(Q) distribution via experimental data

One of the significant methods to investigate the dynamics of dual frequency capacitively coupled plasmas 2f-CCPs is the use of empirical approximations of charge voltage distributions with higher order of sensor charge that is related to the experimental results. This method is capable of achieving accurate physical investigations using the global formula of nonlinear representation of 2f-CCPs, where, the electrical equivalent circuit provides the following equation to describe the dynamics of high-frequency plasma

$$\sum _{\mathrm{k}=2}^M{V}_{\mathrm{k}}^Q+L_{\mathrm{p}}[\frac{{\partial }^{2}Q}{\partial t^2}+{\nu }_{\mathrm{p}}\frac{\partial Q}{\partial t}]-V_{\mathrm{SB}}-V_{\mathrm{G}}+V_{\mathrm{LF}}\cos ({\omega }_{\mathrm{LF}}t+{\varphi }_{\mathrm{LF}})+V_{\mathrm{HF}}\cos ({\omega }_{\mathrm{HF}}t+{\varphi }_{\mathrm{HF}})=0.$$ (34)

with in the physical parameters of experimental model of Argon that evaluated in the reference [7], where, $p=5.4$ Pa $L_{\mathrm{p}}=3.1\times {10}^{-8}\text{V}\text{s}{\text{A}}^{-1}$, ${\nu }_{\mathrm{p}}=1.17\times {10}^8{\text{s}}^{-1}$, $V_{\mathrm{LF}}=299.4\text{V}$, $V_{\mathrm{HF}}=260.1\text{V}$, ${\varphi }_{\mathrm{LF}}=0.547\text{rad}$, ${\varphi }_{\mathrm{HF}}=1.313\text{rad}$, $M=4$, $V_2=6.73\times {10}^{26}\text{V}{\text{A}}^{-1}{\text{s}}^{-2}$, $V_3=-3.1\times {10}^{38}\text{V}{\text{A}}^{-1}{\text{s}}^{-3}$, $V_4=4.7\times {10}^{42}\text{V}{\text{A}}^{-1}{\text{s}}^{-3}$, $V_{\mathrm{SB}}=550\text{V}$, $V_{\mathrm{G}}=20\text{V}$, ${\omega }_{\mathrm{LF}}=2\pi \times 13.56\text{MHz}$, and ${\omega }_{\mathrm{HF}}=2\pi \times 67.8\text{MHz}$. From the global model, the input parameters of the sheath model were determined. The electron temperature was estimated as $T_{\mathrm{e}}=3.2\text{eV}$, the ion current can be obtained also. Furthermore, the temporal development of the charge per area was obtained. The temporal development of the sheath charge of fluid model can be represented as follows.

The sheath charge distribution of the self-consistent numerical solution of the fluid model has the same accuracy of the experimental results. Finally, it is observed that the sheath charge characteristics can be calculated as cubic fitting which is more accurate for the global model than the step model [7]. The cubic fitting of our solution $J=3.9$ can be expressed as follows:

$$V(Q)=-1.31+2.1Q+0.178Q^2-0.00073Q^3.$$

The model is valid only for higher radio frequencies. In other hand, the V(Q) relation may be a hysteresis loop as a signification publication at lower radio frequencies - Shihab et al. [21].

6.1. Collisionless sheath dynamics via step model

To get a significant comparison we will study the most famous model that is general used in case of studying plasma sheath theory and we will compare the results to our work. In case of sheath width flow step model is subjected to a purely sinusoidal variation of amplitude like

$$s(t)=s_0(1-\cos \left({\omega }_{\mathrm{rf}}t\right)),$$ (35)

where $s_0=\frac{J_{\mathrm{rf}}}{n_{0}e{\omega }_{\mathrm{rf}}}$. The sheath charge can be calculated in terms of step model by integrated the ion flux reaches the electrode where electrons sheath is neglected and the equivalent electron edge $s(t)$, as follows:

$$Q(t)=e\underset{0}{\overset{s(t)}{\int }}{n}_{\mathrm{i}}(x)dx=eA{n}_{\mathrm{i}}s(t).$$ (36)

Hence,

$$V_{\mathrm{sh}}(Q)=\frac{e}{{ϵ}_0}\underset{x_{\mathrm{E}}=0}{\overset{s(t)}{\int }}(s-x_{\mathrm{E}})n_{\mathrm{i}}(x)dx=\left(\frac{1}{2e{n}_{\mathrm{i}}{ϵ}_0}\right){(Q(t)/A)}^2.$$ (37)

6.2. Comparison of collisionless sheath dynamics: non step model versus step model

In this section we will cover the most important physical behavior of the complex dynamic of plasma boundary sheath. Displayed in figures, the comparison of particle densities, instantaneous electric field and the average of it and the charge voltage distributions between the step model and the non step model as shown in Figure 6, Figure 7, Figure 8. The result shows different significant results of the solution of time dependent Poisson equation such as all nonlinear dynamics are merging between the sheath and the bulk model, all harmonic oscillation can be valid for our solutions and more accuracy for global model.

• •Nonlinear dynamics of instantaneous and phase averaged electric fields distributions of collisionless plasma boundary sheath at normalized current density $J=3.9$.

Figure 7.

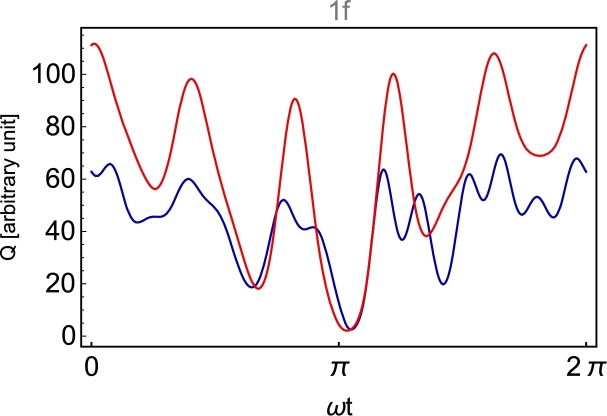
The temporal development of the sheath charge of the dynamical model as a function of the phase angle ω_LFt (red).

Figure 8.

Comparison between charge-voltage distributions of the collisionless fluid model employing exact solutions (black) to the experimental result (red).

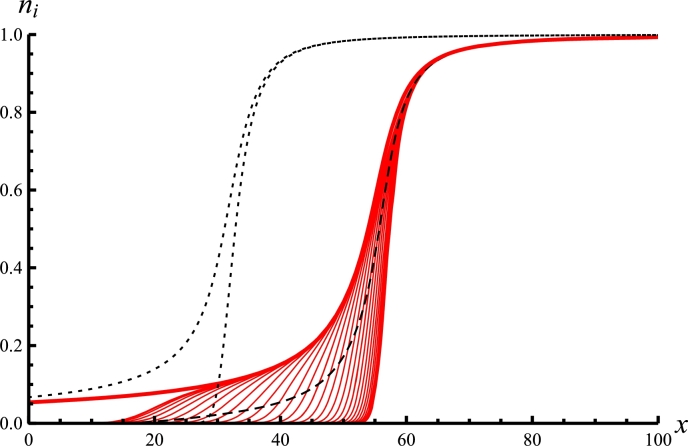
Figs. Figure 9, Figure 10, Figure 11, Figure 12 show several significant physical parameters difference of non step model such as merging between the sheath and bulk region in case of density and electric distributions, covering the singularity of electron ion density and significant increasing of current in the sheath. The results show more accurate results than the step approximation inside a CCPs.

Figure 9.

Density distributions of the RF driven collisionless fluid model at modulation value of J = 3.9. The ion density n(x) (red) and the instantaneous electron densities n(x,t) (red) at various phases t from 0 − 2π. The average electron density $\overline{ne}(x)$ is (Black). The dashed curves are the electron and ion densities of the unmodulated sheath.

Figure 10.

Density distributions of the RF driven collisionless capacitive sheath under the step approximation for J=3.9. The thick solid line represents the ion density n(x), the thin solid lines are the instantaneous electron densities n(x,t) for different phases t from 0 − 2π. The gray lines in the background show, for comparison, the corresponding densities n(x), n(x,t) and $\overline{ne}(x)$ of the non step model. As a result we can see that the fluid model covers the divergence of step model.

Figure 11.

Electric field of the RF driven collisionless capacitive sheath under the step approximation for J=3.9. Shown is the field strength E(x,t) (solid) at various phases t between 0 and 2π, together with its phase average $\overline{E}(x)$ (dashed). For comparison, the gray curves in the background show the corresponding fields E(x,t) and $\overline{E}(x)$ of the non step model.

Figure 12.

Comparison between the current distribution inside the sheath in case of step approximation (red) and exact solution (blue): ion current as average constant value and electron current as diode physical character of lumped element circuits approach. The result shows significant increasing in its value which match with experimental results.

6.3. Collisionless bulk dynamics between non step model via step model

Our model verifies the most significant physical and engineering approach that is needed for the nonlinear bulk study of low pressure plasma at low computational effort using the global model. One path to find all these important complex solutions is the evaluation of high accuracy sheath voltage distribution with cubic fitting. Several nonlinear complex dynamics such as nonlinear current behavior, charge distribution, power distribution and average power is achieved at low computational effort.

As shown in the Fig. 12 the cubic fitting represents the phenomena of nonlinear current distribution more precisely which is missing in case of step approximation inside the bulk region.

It is determined that no more than 50% of the dissipation power in the analyzed CCPs can be explained by the conventional scenario. A more accurate numerical solution than a step approximation can be used to identify nonlinear electron resonance heating and locate any missing dissipation power [7] see Figure 12, Figure 13, Figure 14, Figure 15, Figure 16.

Figure 13.

Difference between nonlinear current distribution inside the bulk of quadratic and cubic sheath charge solution: cubic V(Q) of non step model give more nonlinear behavior (red) than the step approximation (blue).

Figure 14.

A significant difference between the nonlinear characteristic of charge distribution for self non step model (red) and step model (blue). The non step model is more compatible with experimental result.

Figure 15.

A significant higher difference at power distribution in case of apply cubic sheath voltage distribution (red) to global model than the step approximation (blue).

Figure 16.

Evaluation of the average power distribution: The non step model is higher value than the step approximation.

7. Sheath thickness (engineering approach) in case of non step model

In the non step model show smooth transition between sheath and bulk plasma. Therefore, the sheath distance could be obtained with a more accurate calculation as follows. The plasma boundary sheath thickness $S_{max}$, in case of DC-Child-Langmuir collisionless model is determined as:

$$S_{max}=\sqrt{C}(\frac{2^{4/5}}{3})\frac{V_{sh}^{3/4}\sqrt{{\epsilon }_0}}{{\left(m_{\mathrm{i}}e\right)}^{3/4}\sqrt{{\psi }_{\mathrm{i}}}},$$ (38)

where, ${\psi }_{\mathrm{i}}=n_{\mathrm{i}}{v}_{\mathrm{i}}=0.61n_0\sqrt{T_{\mathrm{e}}/m_{\mathrm{i}}}$, C is a numerical factor of DC sheath equal to 0.44. To get a more accurate sheath distance for a collisionless regime based on our results of the non step model. We get the ratio of the extension sheath in the case of modulated current to the dc current which is approximately constant at 1.5. In our case of Fig. 17 and Fig. 9, the distance sheath is around $s_{max}=60$ of RF modulation current at $J=4$ and 3.7 with the corresponding maximum dc sheath distance $s_{max}=40$. The same expecting ratio of collisionless RF sheath to DC sheath for $J=1,2,3$, and 4 is around ≈1.5. Therefore, the expecting equation for the sheath distance of RF modulated can be represented as:

$$S_{max}=1.5\sqrt{C}(\frac{2^{4/5}}{3})\frac{V_{sh}^{3/4}\sqrt{{\epsilon }_0}}{{\left(m_{\mathrm{i}}e\right)}^{3/4}\sqrt{{\psi }_{\mathrm{i}}}}.$$ (39)

Figure 17.

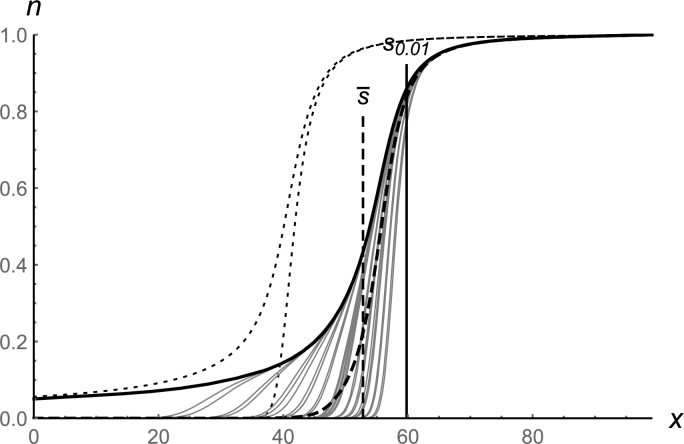
Electron and ion distribution of non step model in case of modulated density at j = 4 (black (ion distribution) and gray (electron distribution)) and the density at non modulated current (dotted). The expectation ratio of the sheath distance of maximum RF collisionless modulation current s_max = 60 at j = 4 to the dc sheath s_max = 40 is 1.5.

8. Conclusion

The new numerical exact solution merging between the sheath and bulk region is obtained. Results mostly fill the nonlinear dynamics shortage of the well-known step approximation such as singularity of the electron and ion density, and present an electric field distribution with $E=0$ at maximum sheath distance rather than taking into account the ambipolar field. The significant numerical cubic formula of non step model which is identical with experimental data is achieved [7]. The global model uses cubic fitting have shown the higher harmonic effects inside the bulk such as current distribution, charge distribution, and power distribution. In addition, more significant results to total current of the sheath matching with the experimental results. Obtain higher average power than the step approximation which is identified to the phoneme of the nonlinear electron resonance heating. Finally, simple formula of sheath thickness in case of collisionless regime is achieved. The paper may be given a precise analysis of the most applicable uses in industrial and agriculture applications of low-pressure plasma. The result of the research may also come to the requirement of needed market.

Declarations

Author contribution statement

Abdelfattah T. Elgendy: Conceived and designed the experiments; Performed the experiments; Contributed reagents, materials, analysis tools, or data; Wrote the paper.

Haifa A. Alyousef: Performed the experiments, Contributed reagents, materials, analysis tools or data.

Kamal M. Ahmed: Performed the experiments; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Funding statement

Haifa A. Alyousef was supported by Princess Nourah Bint Abdulrahman University [PNURSP2022R17].

Data availability statement

Data will be made available on request.

Declaration of interests statement

The authors declare no competing interests.

Additional information

No additional information is available for this paper.

Appendix A.

The final collected set of equations of the sheath model is still very difficult to solve. If one makes the assumption that the ion density depends only on the average electric field, can the ion equation of motion be calculated? There are two general reasons for the difficulty of solving this equation. First, Poisson's equation has no analytical solution to get the time-dependent field, hence the average electric field can not be calculated. The second reason is that the ion equation of motion has also no analytical solution. The collection of equations is illustrated in the Figs. Figure 17, Figure 18, Figure 19, Figure 20. If two different regimes of collision and collisionless for the ion equation of motion is applied and the Poisson's equation is solved, the time-dependent electric field and its average can be calculated. Consequently, electron and ion densities can also be calculated and the self-consistent fluid model can be verified. Finally, the self-consistent closed model is the important path to merge between the sheath and the bulk model. A double frequency bias generator is more used in the etching process of semiconductor industries than the single-frequency plasma generation (see Fig. 20). Due to full separate control of high plasma density, high ion flux, and large ion energy.

Figure 20.

Sheath plasma application of semiconductor fabrication.