Abstract
Internal states such as arousal, attention and motivation modulate brain-wide neural activity, but how these processes interact with learning is not well understood. During learning, the brain modifies its neural activity to improve behavior. How do internal states affect this process? Using a brain–computer interface learning paradigm in monkeys, we identified large, abrupt fluctuations in neural population activity in motor cortex indicative of arousal-like internal state changes, which we term ‘neural engagement.’ In a brain–computer interface, the causal relationship between neural activity and behavior is known, allowing us to understand how neural engagement impacted behavioral performance for different task goals. We observed stereotyped changes in neural engagement that occurred regardless of how they impacted performance. This allowed us to predict how quickly different task goals were learned. These results suggest that changes in internal states, even those seemingly unrelated to goal-seeking behavior, can systematically influence how behavior improves with learning.
As we move about the world, we experience fluctuations in internal states such as arousal, motivation and engagement. Such fluctuations, which do not directly reflect sensory stimuli or intended movements, are governed by the modulation of neural activity throughout the brain1–5. The manner in which these modulations relate to the ongoing computations performed by the cerebral cortex is not well understood. In predominantly sensory areas of cortex, changes in an animal’s internal state are known to affect neural response magnitude, signal-to-noise ratio, timing and variability2,6–8. Depending on how these changes align with respect to neural encoding of stimulus information or downstream readout, changes in an animal’s internal state can impact perceptual processing and decision-making9–12. Changes in internal state are also known to impact motor control and behavior, as the speed and latency of both eye movements and arm reaches are known to be modulated by signals such as motivation, intrinsic value and reward expectation13–16. These studies and others illustrate the importance of understanding the influence of internal states on sensory processing and behavior.
What has been less well studied is the impact of internal state changes on learning (Fig. 1a). When we learn to perform a task, such as shooting a basketball, the firing activity of populations of neurons in the brain (Fig. 1a) is modified in a particular manner to drive improved behavior17–29. We also know that while animals perform a task, neural activity undergoes internal state fluctuations that are not directly related to task performance4,12,30–34. Depending on the task goals, changes in internal state have the potential to make some learning-related neural changes easier to achieve, while other changes may be made more difficult (Fig. 1a). When changes due to internal state are incongruous with learning, how do neural populations modify their activity to drive improved behavior? One possibility is that the internal state fluctuations that make learning more difficult might be suppressed. Alternatively, the impact of internal state fluctuations on learning may be unavoidable, such that some task goals are harder to achieve than others.
Fig. 1 |. Studying how changes in neural activity during learning relate to changes in internal state.
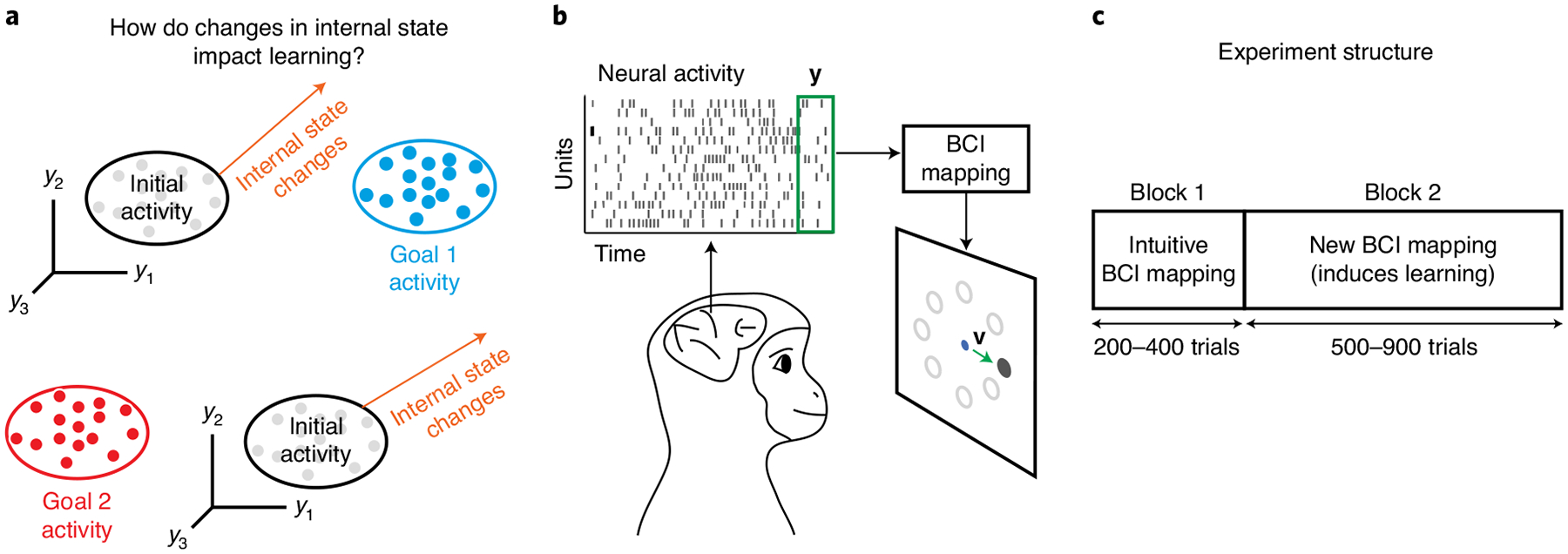
a, Here we asked whether changes in internal state relate to how neural population activity is modified during learning. Before learning, neural activity resides in some region (‘initial activity’) of population activity space, depicted here by the spiking activity of three neurons (y1, y2 and y3). During learning, the neural activity needs to migrate to a different region of population activity space to achieve a particular task goal (‘Goal 1 activity’ and ‘Goal 2 activity’). Changes in the animal’s internal state can push the neural activity closer to (top orange arrow) or further from (bottom orange arrow) the region appropriate for achieving a given task goal. b, Monkeys performed an eight-target center-out task using a BCI. Neural activity was recorded using a multi-electrode array implanted in M1. Spike counts (y) were taken in 45-ms bins (green box). The BCI mapping converted the neural activity into a cursor velocity (v) at each 45-ms timestep, updating the position of a visual cursor on a screen. Monkeys were rewarded for successfully guiding the cursor to hit the visually instructed target. c, Each experiment consisted of two blocks of trials. In block 1, a monkey completed 200–400 trials using an intuitive BCI mapping. In block 2, the monkey completed 500–900 trials with a new BCI mapping that the monkey had not used before.
Answering this question is challenging because the causal relationship between neural activity and behavior is not known in general. This makes it difficult to understand which changes to neural activity would yield improved performance, as well as how fluctuations in internal state would either interfere or augment that performance. To address this difficulty, we can leverage a brain–computer interface (BCI)35–38, where the causal relationship, or ‘mapping,’ between neural activity and behavior is known exactly and determined by the experimenter.
We trained three rhesus monkeys to modulate the activity of ~90 units in primary motor cortex (M1) to move a computer cursor on a screen using a BCI23. In previous work, we compared the neural population activity before versus after monkeys learned to use a new BCI mapping26,39. Here we study how neural activity changes throughout learning, and the degree to which these changes are influenced by fluctuations in the monkey’s internal state.
We first identified the dimensions of the largest fluctuations in M1 population activity. Surprisingly, abrupt changes in population activity along these dimensions were triggered by changes in various aspects of the task, ranging from brief pauses in the task to perturbations of the BCI mapping. Furthermore, trial-to-trial changes in population activity along these dimensions were correlated with changes in the monkey’s pupil size. These observations suggested that changes in population activity along these dimensions could be related to the monkey’s arousal, engagement with the task or motivation throughout the experiment. For this reason, we termed these dimensions ‘neural engagement’ axes.
To induce learning, we perturbed the mapping between neural activity and cursor movements, requiring monkeys to modify the neural activity they produced, so as to restore proficient control of the cursor toward each target23. This allowed us to study how changes in activity along neural engagement axes interacted with learning. We found that neural population activity did not take a direct path from the activity produced before learning to the activity produced at the end of learning. In particular, neural activity changed abruptly along the neural engagement axes at the start of learning. This change occurred regardless of the relationship between neural engagement axes and cursor movements, which led to an immediate improvement in behavioral performance for some targets and impaired performance for others. Following the abrupt change, neural activity retreated along neural engagement axes, which impacted performance differently for different targets. These findings enabled us to predict which targets would be learned more quickly than others, based on how neural engagement interacted with the demands of the learning task. Our results suggest that changes in internal states, even those seemingly unrelated to goal-seeking behavior, can influence how behavior improves with learning.
Results
To understand how changes in internal state might interact with learning (Fig. 1a), we studied three monkeys performing an eight-target center-out task using a BCI (Fig. 1b and Methods). On each trial, monkeys controlled a computer cursor by modulating neural activity recorded from primary motor cortex (M1). The relationship between the recorded neural activity and cursor velocity was specified by the BCI mapping. In each experimental session, monkeys used two different BCI mappings (Fig. 1c). During the first block of trials, monkeys used an ‘intuitive’ BCI mapping, calibrated so as to provide the monkey with proficient control of the cursor. After monkeys performed the task for a few hundred trials using the intuitive mapping, we changed the mapping between neural activity and cursor movement to a new BCI mapping that the monkey had not used before. This new BCI mapping (a ‘within-manifold’ perturbation (WMP)23) was typically learned within 1–2 h.
Before each experiment, we applied factor analysis to identify the top ten dimensions, or factors, capturing the most covariability of the neural population activity. The BCI mappings presented during each experiment were chosen such that the cursor velocity was determined by only these top ten factors. To ensure that our results captured changes in neural activity describing substantial covariance in the population, we analyzed neural activity only in these factors.
Internal state fluctuations in primary motor cortex.
We first show that the neural population activity shifted abruptly in response to salient, experimenter-controlled events. We observed that, while monkeys used the intuitive mapping, the neural activity produced for a given target showed substantial trial-to-trial variability (Fig. 2a). We found the direction of greatest variance of the neural activity for each target (Fig. 2a). Surprisingly, later in the session when the new BCI mapping was introduced, neural activity on the first trial to a given target showed an abrupt change from the neural activity produced during block 1, with this change occurring almost directly along the axis identified earlier (Fig. 2b). Interestingly, on subsequent trials, neural activity gradually retreated down this same axis (Fig. 2b).
Fig. 2 |. Neural activity increased abruptly along a neural engagement axis following experimental events.
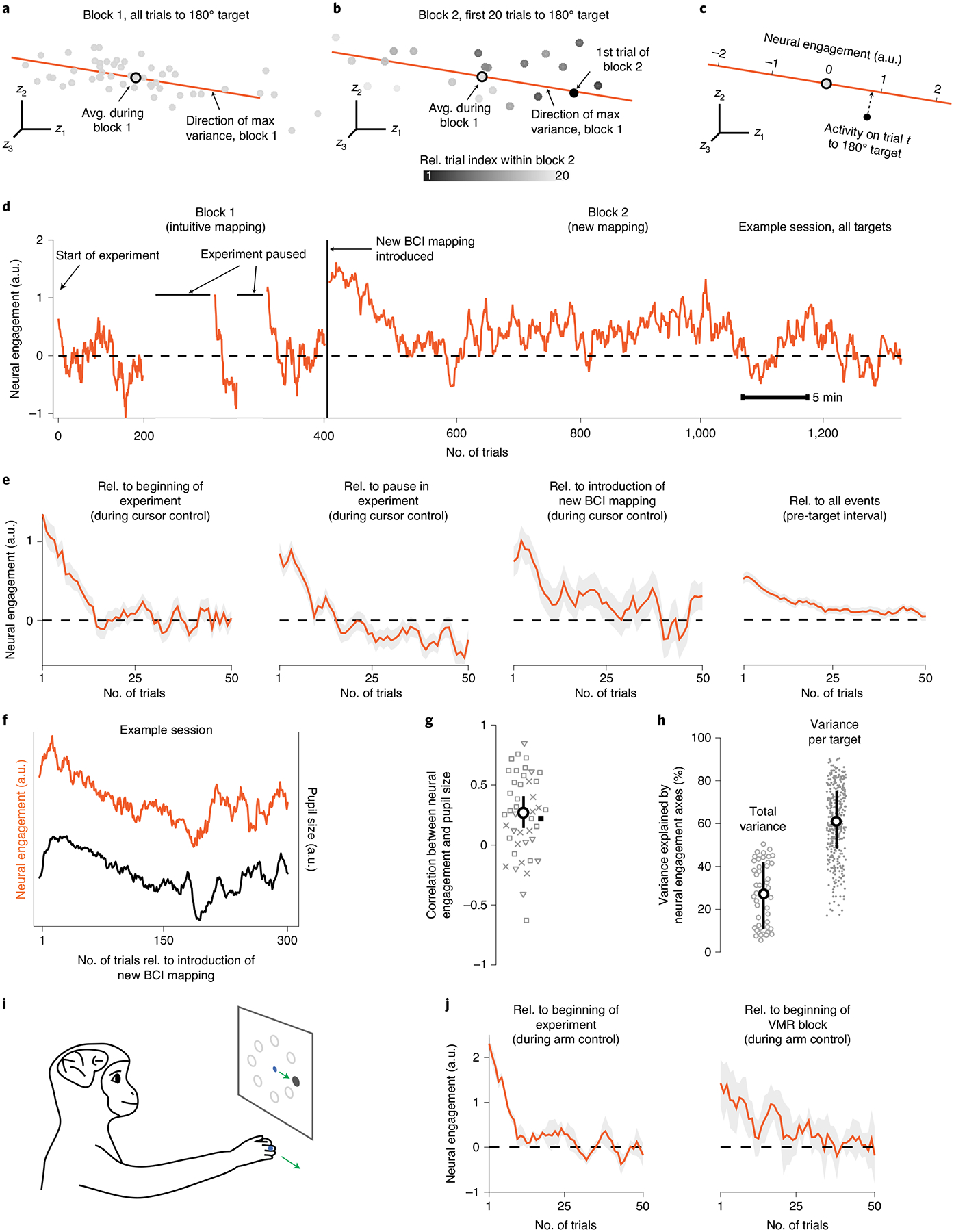
a, Neural activity in the top three factor dimensions of highest covariance (z1, z2 and z3) for trials to the same target from block 1 of session J20120528. Each gray point is the average neural activity recorded within a single trial. The orange axis depicts the direction of maximum variance of all gray points. The axis was defined in the ten-dimensional (10D) factor space, although only the top three dimensions are depicted here. b, Same as a, but for the first 20 trials to the same target during block 2 (color indicates trial index). The orange axis from a is shown for reference. Neural engagement for each trial is the projection of neural activity onto the axis identified during block 1 for trials to the same target. c, The value of neural engagement is given by the projection (dashed arrow) of the recorded neural activity (black circle) onto the neural engagement axis (orange) corresponding to the current target. Projections were normalized relative to the mean and standard deviation across trials to the same target during block 1 (Methods). a.u., arbitrary units. d, Neural engagement overtime from session J20120528, with annotations indicating timing of various events controlled by the experimenter. Position along horizontal axis indicates clock time, with trial indices marked for reference. The horizontal dashed line indicates average neural engagement across all trials during block 1. e, Neural engagement averaged across sessions from all monkeys (n = 46 sessions) during cursor control relative to the start of the experiment, the longest pause during block 1 and the start of block 2. Neural engagement during the interval of each trial before the monkey had seen the target (Methods), averaged across all three experimental events. Shading indicates mean ± s.e. across sessions. f, Neural engagement during block 2 from the example session shown in d, alongside the monkey’s average pupil size during the same trials. g, Pearson’s correlation between neural engagement and pupil size during block 2 for each session, with sessions from monkeys J, L and N indicated by squares, triangles and crosses, respectively. Example session from f indicated as a black square. The white circle and black lines depict the bootstrapped median and 95% CI of the correlations across sessions, respectively. h, Percentage of shared covariance of neural population activity explained by neural engagement axes during block 1, across trials to all targets (‘total variance’; n = 46 sessions), or across trials to a single target (‘variance per target’; n = 368 targets). The white circle depicts the median; error bars represent the median ± 25th percentile of correlations across sessions/targets. i, A monkey performed a center-out task by moving its hand to control the cursor’s position (Methods). j, Neural engagement averaged across sessions from hand control experiments (n = 3 sessions), relative to the beginning of the experiment and relative to the introduction of a visuomotor rotation (VMR). Same conventions as e. Rel., relative.
To quantify how these trial-to-trial changes in neural activity progressed throughout the experiment (Fig. 2c), we identified the axis of greatest variability during block 1 for each target separately (for example, the orange axis in Fig. 2a,b), and projected the neural activity for each trial along the appropriate target-specific axis. To compare these values across trials to different targets, we normalized the projected values for each target separately (Methods). This yielded a trial-by-trial measure we call neural engagement, for reasons we discuss below.
Neural engagement abruptly increased and gradually decreased following various experimental events, beyond just the introduction of the new BCI mapping (Fig. 2d). For example, neural engagement was initially elevated on the first trials of the experiment, and then gradually decreased on later trials (Fig. 2d). Next, near the middle of block 1, the experimenter would pause the experiment for a few minutes to choose the BCI mapping that would be introduced in the upcoming block 2. Following these pauses (Fig. 2d), neural engagement increased, and then gradually subsided. Finally, a few minutes later when the experimenter seamlessly introduced the new BCI mapping (without pausing the experiment), neural engagement again abruptly increased and gradually subsided on subsequent trials (Fig. 2d). The ensuing time course of neural engagement was similar following all three of these experimenter-controlled events, indicating that the changes in neural engagement during block 2 were not due simply to the monkey trying to learn the new BCI mapping. These changes were not specific to the particular BCI mappings used during a given session, as we observed similar neural changes across multiple sessions from all three monkeys (Extended Data Fig. 1). Nor could the abrupt increases in neural engagement be explained by hand movements, as monkeys showed little to no hand movements during these experiments, and no increase in hand speeds when the new BCI mapping was introduced (Extended Data Fig. 2). Rather, these changes in neural activity appeared to reflect stereotyped changes in the monkey’s internal state during the experiment, and could reflect changes in arousal8, engagement with the task5 or motivation14. While the specific source of these changes is as yet unknown (Discussion), these changes have important consequences for learning, as we discuss below.
Two additional aspects of neural engagement were consistent with it reflecting variations in the monkey’s internal state. First, when averaged across trials from all sessions, neural engagement showed a consistent time course following each experimental event (Fig. 2e). These changes in neural engagement appeared not only while the monkeys controlled the cursor, but also during the beginning of each trial before the monkey had seen the visual target (Fig. 2e). Thus, neural engagement remained elevated even when the monkey was not actively performing the task, consistent with this signal reflecting a slowly varying change in the monkey’s internal state. Second, changes in an organism’s internal state are typically correlated with changes in its pupil size2. On trials with elevated levels of neural engagement, the pupil was typically more dilated (Extended Data Fig. 3), suggesting that neural engagement may be correlated with an arousal-like state. In agreement with this, we found that trial-to-trial fluctuations in neural engagement were often strikingly positively correlated with the monkey’s pupil size (Fig. 2f). For the majority of sessions from all three monkeys, trial-to-trial changes in neural engagement and pupil size were positively correlated (Fig. 2g), with a median Pearson’s correlation across sessions of ρ = 0.27 (bootstrapped 95% confidence interval (CI; 0.15, 0.40), n = 44 sessions), similar to levels observed in other work12.
Changes in activity along the neural engagement axes accounted for a substantial amount of the covariance of the population activity. When considering population activity during block 1 across trials to all eight targets—and thus also including the across-target variance in neural activity due to the monkey aiming toward different targets—changes in neural engagement explained ~30% of the total trial-to-trial variance of the factor activity (Fig. 2h). Within trials to the same target, changes along the neural engagement axis explained ~60% of the trial-to-trial variance (Fig. 2h). These results indicate that the trial-to-trial changes in population activity along the neural engagement axes were substantial.
To assess whether similar changes in neural engagement were present during arm movements (as opposed to BCI control), we analyzed data from a fourth monkey who performed an eight-target center-out task using hand control of a computer cursor (Fig. 2i and Methods). As with the BCI experiments, we identified a set of neural engagement axes in the population activity after applying factor analysis. We found that neural engagement was elevated both at the beginning of each experiment, and following the introduction of a visuomotor rotation (Fig. 2j), with a time course that was strikingly similar to that of BCI control (Fig. 2e). Taken together, we found that neural population activity in M1 during both BCI and hand control showed large, trial-to-trial variations with a consistent time course relative to experimental events. Next, we focused on BCI control, where we know the causal relationship between neural activity and behavior. This enabled us to directly assess how changes in neural engagement relate to behavior (that is, cursor velocities).
Studying the impact of changes in neural engagement on behavior using a BCI paradigm.
Having established the presence of large fluctuations in neural engagement in M1, we next sought to understand how these fluctuations might interact with learning. Specifically, we asked whether the monkey’s ability to learn to move the cursor in a given direction with the new BCI mapping could be understood in terms of the relationship between the neural engagement axes and the new mapping.
First, we explain how a BCI paradigm allows us to quantify the interaction between neural engagement and behavior (that is, cursor velocities). Consider a schematic of the neural activity produced by the monkey during block 1 (Fig. 3a). For a given target, we can summarize the monkey’s trial-averaged neural activity as a point in neural space (z), where here we depict the neural activity in the three factor dimensions of highest variance. The cursor velocity under the intuitive BCI mapping (v) is given by projecting the neural activity onto the intuitive BCI mapping (v = M1z). During block 1, the monkey’s trial-averaged cursor velocities were near the target direction (Fig. 3b), indicating the monkey’s ability to produce cursor movements that moved the cursor toward the target on average. We can also characterize the effect of an increase in neural engagement on cursor velocities by projecting the neural engagement axis (Fig. 3a) onto the intuitive BCI mapping (Fig. 3b). For this target, increasing neural engagement increases cursor speeds toward the target.
Fig. 3 |. Understanding the impact of neural engagement on behavior during a BCI learning task.
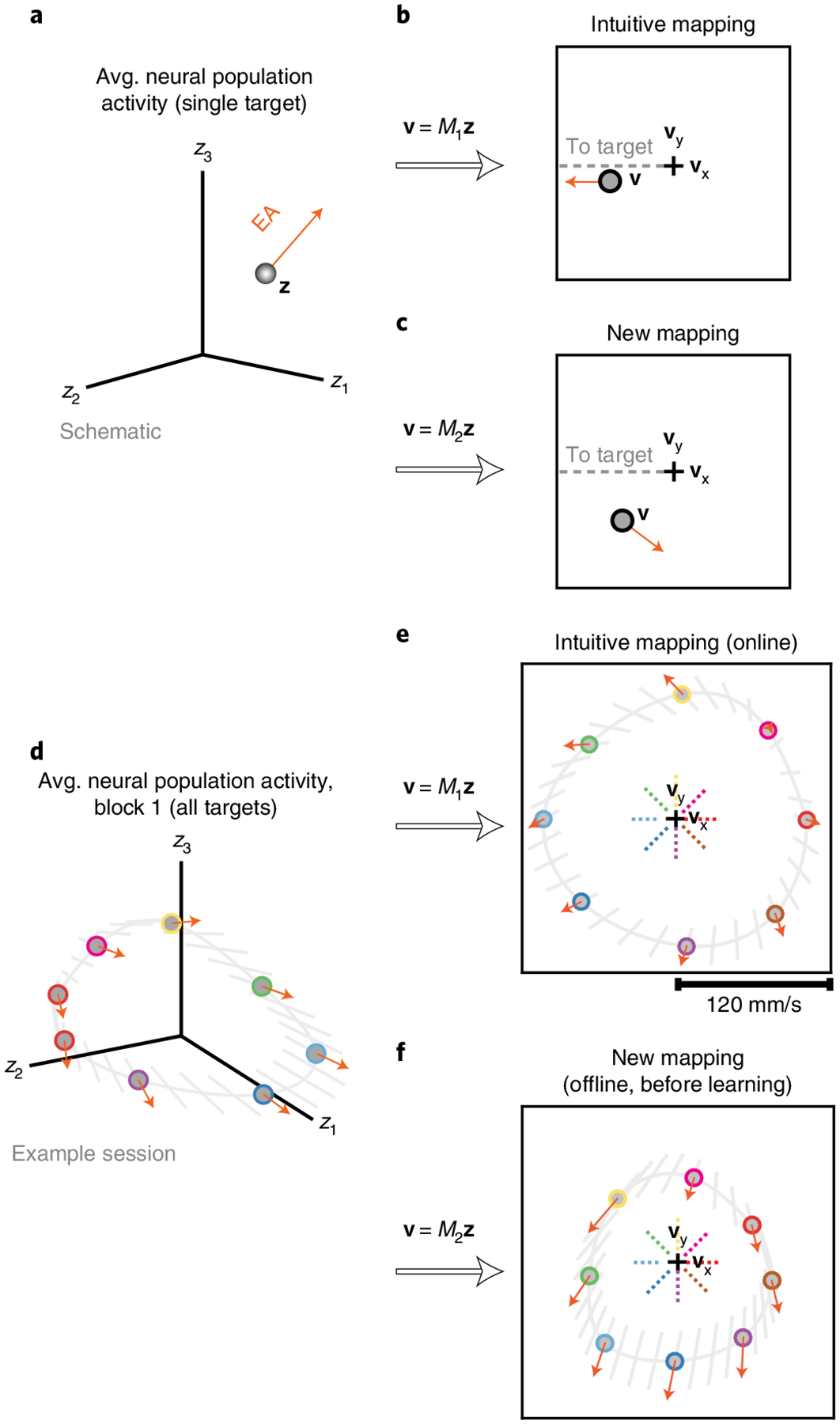
a, Schematic of the average neural activity (z) recorded across all trials to the same target during block 1, along with the direction in which this activity is expected to move following an increase in neural engagement (EA, engagement axis). b, Using the intuitive BCI mapping (M1), we can inspect the intuitive cursor velocity (v, gray circle) corresponding to z, as well as how this velocity will change if neural engagement increases. In this case, increased neural engagement will result in faster cursor movements toward the target (gray dashed line). Zero velocity is indicated by the black cross. c, We can repeat the same procedure using the new BCI mapping (M2) with the same neural activity z and neural engagement axis. d–f, In an example session, the trial-averaged neural activity (gray circles with colored outlines) and engagement axes for all eight targets is visualized. Target directions are indicated with dashed colored lines. Gray lines indicate interpolations between the neural engagement axes for each target. Avg., average.
Next, consider the first trial of block 2, when the monkey first encounters the new BCI mapping. If the monkey were to continue to produce the same average neural activity as in block 1 (Fig. 3a), this would no longer result in cursor movements straight to the target (Fig. 3c). Thus, the monkey must learn how to modify the neural activity produced in order to make faster cursor speeds in the target direction. Importantly, the new BCI mapping also changes the manner in which neural engagement relates to cursor velocity. For this target, increasing neural engagement would move the cursor velocities even further from the target direction (Fig. 3c). In this manner, changes in neural engagement can interact with the monkey’s attempts to move the cursor toward the target.
We can gain a more holistic picture of the interaction between neural engagement and cursor velocities by visualizing the neural activity produced for all eight targets together (Fig. 3d). We observed that, when visualized in factor space (Fig. 3d), the neural engagement axes identified for different targets often appeared quite similar. In fact, neural engagement axes were almost always consistent with the firing rates of all neural units changing in the same direction (Extended Data Fig. 4). Increases in neural engagement corresponded to increased average firing rates in nearly all units, in a gain-like manner (Extended Data Fig. 5). However, while the neural engagement axes for different targets were similar in terms of how they related to single-unit firing rates, these axes also showed behaviorally relevant differences. For example, under the intuitive BCI mapping, increases in neural engagement typically led to faster speeds toward each target (Fig. 3e), which could not happen if the neural engagement axes were identical for all targets. A similar feature was also present during arm movements: By identifying the linear mapping of neural population activity most predictive of ensuing hand velocities, we found that increases in neural engagement typically predicted faster hand speeds toward each target (Extended Data Fig. 6). Thus, the orientation of the neural engagement axis in population activity space depends on the monkey’s intended movement direction.
Finally, focus on the velocities under the new BCI mapping (Fig. 3f), as this indicates the initial cursor velocities the monkey would expect to produce during block 2, were the monkey to continue producing the same activity as during block 1. As discussed above, neural engagement can have different effects on cursor velocities depending on the monkey’s intended movement direction. For example, increased neural engagement may increase cursor speeds toward some targets (for example, the purple target in Fig. 3f) and decrease speeds toward other targets (for example, the pink target in Fig. 3b). Additionally, increased neural engagement can affect not just the speed but also the angular error of the velocity relative to the target direction (for example, the red and yellow targets in Fig. 3f). Overall, we observed that the new BCI mappings induced a variety of different relationships between neural engagement and cursor velocity, both across sessions and within targets of the same session (Extended Data Fig. 7). Thus, these experiments provided us with the means to assess how different relationships between neural engagement and cursor velocity related to how each target was learned.
Neural engagement increased initially regardless of its impact on performance.
To study how changes in neural engagement might interact with learning, we first characterized the level of neural engagement on the first trial to each target using the new BCI mapping. As shown earlier, the monkeys’ initial reaction to the introduction of the new mapping was, on average, to increase neural activity along the neural engagement axis (Fig. 2e). However, as we have also shown, there are a variety of ways in which the neural engagement axes affected velocities under the second mapping (Extended Data Fig. 7). This raises the possibility that neural engagement might have increased by different amounts depending on whether increasing neural engagement was expected to increase (Fig. 4a) or decrease (Fig. 4b) the speed of the cursor toward the target under the new mapping.
Fig. 4 |. Neural engagement increased on the first trial of a learning task regardless of its impact on task performance.
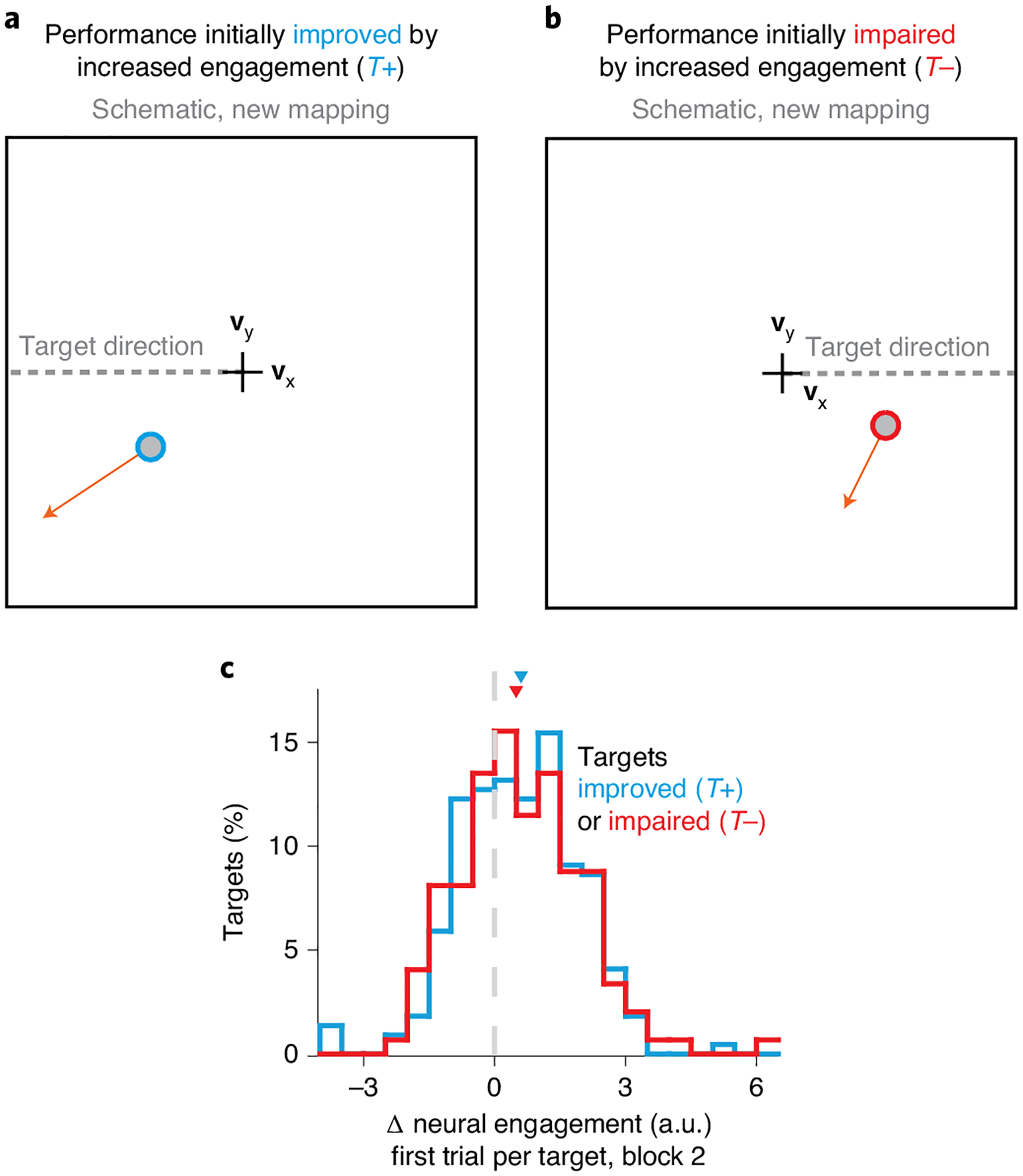
a,b, Schematics depicting how increased neural engagement can lead to either faster (a) or slower (b) cursor speeds toward the target direction under the new BCI mapping. Same conventions as Fig. 3c. c, Distribution of the increase in neural engagement on the first trial to each target during block 2, as a function of whether performance under the new mapping was expected to be improved or impaired by an increase in neural engagement (as in a and b). Triangles depict the median of each distribution.
We anticipated that neural engagement might increase more for targets where doing so would increase cursor speeds toward the target. To assess whether this was the case, for each target, we used the trial-averaged activity from block 1 to estimate the expected velocity under the new mapping, as well as the expected impact on that velocity if neural engagement increased (Fig. 4a,b). We then classified each target as belonging to one of two groups, based on whether an increase in neural engagement was expected to increase (T +; Fig. 4a) or decrease (T −; Fig. 4b) the speed of the cursor toward the target direction. We next assessed the levels of neural engagement on the first trial to each target in block 2. Across targets from all sessions, the distribution of neural engagement on the first trial using the new mapping did not differ as a function of how performance for that target was impacted (Fig. 4c; p = 0.954, two-sample Kolmogorov–Smirnov test, n1 = 220 and n2 = 148 targets). This indicates that initially, neural activity increased along the neural engagement axes even when doing so negatively impacted task performance. As a result, the initial increase in neural engagement made T− targets more difficult than they would have been otherwise (relative to the average neural activity produced during block 1), while T+ targets were made easier.
Differences in learning across targets can be explained by changes in neural engagement.
We saw that changes in neural engagement on the first trials using the new BCI mapping occurred regardless of the impact on performance. We wondered whether, given repeated practice with the new mapping over subsequent trials, changes in neural engagement might interact with learning-driven changes for each type of target.
We visualized how cursor velocities under the second mapping changed throughout learning, as a function of whether the initial increase in neural engagement increased (T+) or decreased (T−) the speed of the cursor toward the target (Fig. 5a,b). For both types of targets, neural activity on the first trial jumped out abruptly along the neural engagement axis (Fig. 5a,b). Then, over tens of trials, velocities gradually aligned with the target direction, leading to increased speeds toward the target (Fig. 5a,b). Were these behaviorally beneficial changes to velocity driven by target-specific changes in neural engagement? We measured the levels of neural engagement for each target during block 2 after accounting for any changes due to learning by neural reassociation26 (Methods). In agreement with what we observed earlier (Fig. 2e), we found that neural engagement gradually decreased throughout block 2 (Fig. 5c). Importantly, this decrease in neural engagement was likely beneficial to T− targets, the ones initially impaired by the increase in neural engagement. In fact, neural engagement decreased more for T− targets than for T+ targets (Fig. 5c). These target-specific differences in neural engagement could not be explained by differences in the animal’s arousal, as the average time course of pupil size did not differ between T+ and T− targets (Fig. 5d). These results suggest that, as learning proceeded, changes along the neural engagement axis were driven by two components: one target-invariant (because neural engagement decreased throughout learning for both target types), and one target-specific (because neural engagement decreased by different amounts depending on the target type). This led us to ask whether these differential changes in neural engagement might explain how quickly the two types of targets were learned.
Fig. 5 |. Relationship between neural engagement axes and task performance predicted which targets were learned more quickly.
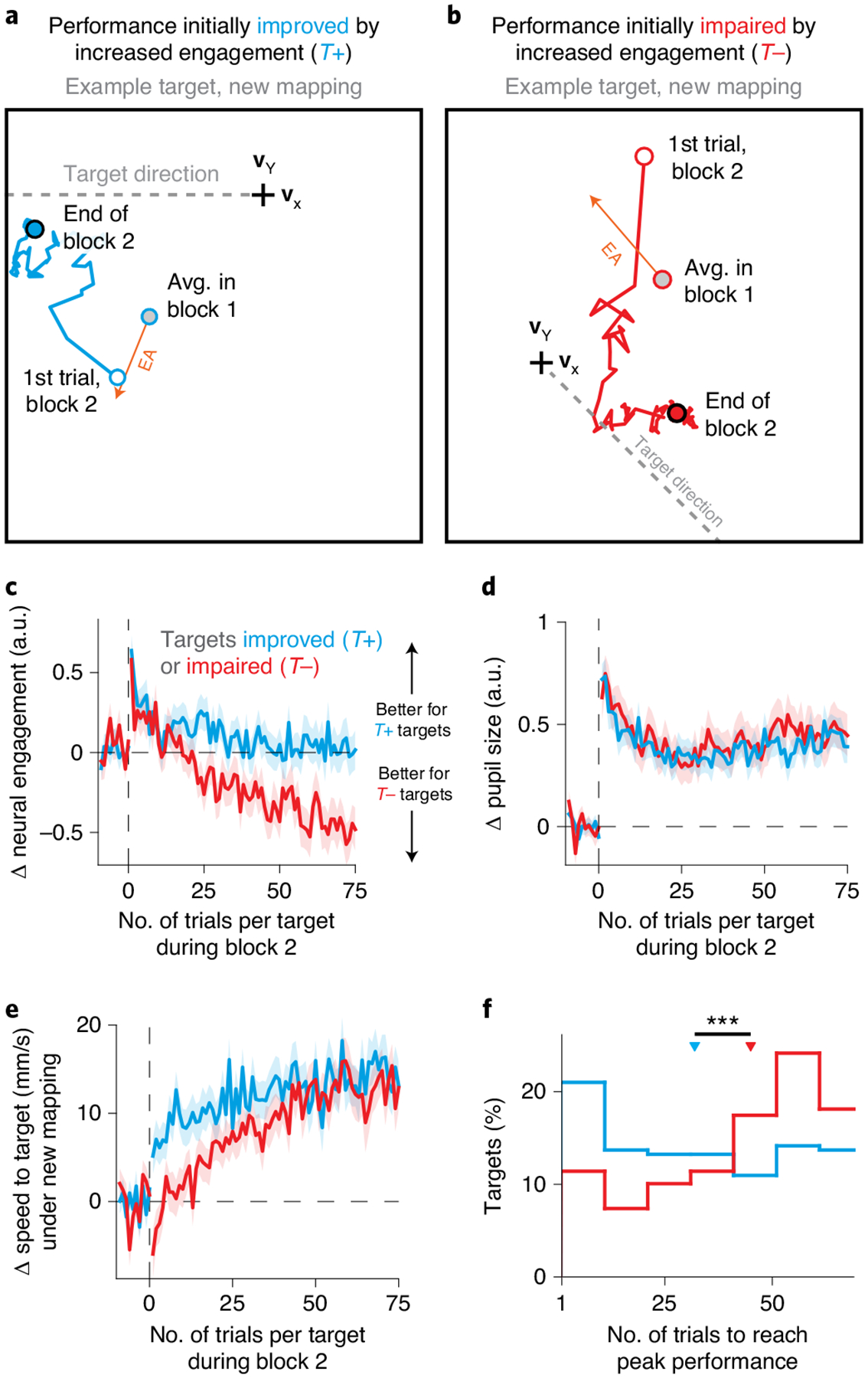
a, Average cursor velocities under the new mapping across trials during block 2, for an example T+ target (180°; session J20120528) where an increase in neural engagement initially improved performance relative to the average activity produced during block 1 (gray circle). Same conventions as Fig. 4a. The blue line depicts how the trial-averaged velocity evolved throughout block 2, starting with the first trial to that target (white circle) and ending with the average during the last trials (blue circle). Velocities gradually moved toward the target direction, both decreasing angular error and increasing the speed in the target direction, indicating learning. b, Same as a, but for an example T− target (315°; J20120601) where an increase in neural engagement was initially expected to impair performance under the new mapping. c, Changes in neural engagement during block 2, averaged across T+ (n = 220) and T− (n = 148) targets (mean ± s.e.). Trial index is relative to the start of block 2 for each target. d, Changes in pupil size during block 2. Same conventions and sample sizes as in c. e, Changes in cursor speed toward the target under the new mapping during block 2, relative to the expected speed under the new mapping based on the neural activity produced during block 1. Same conventions and sample sizes as in c. f, Distribution of the number of trials at which each target attained its peak level of performance (Methods), for all T+ and T− targets. Triangles depict the median of each distribution; asterisks indicate that the medians were significantly different (p = 1.259 × 10−4, two-sided Wilcoxon rank-sum test, n1 = 220 and n2 = 148 targets).
To quantify the amount of learning for each target, we measured cursor speeds toward the target relative to the speeds that the monkeys would experience if they continued to use the neural activity they produced before the introduction of the new BCI mapping (Fig. 5e and Methods). On the first trial of block 2, the cursor speed toward the target increased for T+ targets and decreased for T− targets (Fig. 5e; trial 1). This is in agreement with monkeys immediately increasing neural engagement at the start of block 2, regardless of its impact on performance (Fig. 4c). As block 2 continued, performance for both target types gradually improved (Fig. 5e; trials 1–75), indicating learning.
Interestingly, the monkeys reached peak performance more quickly for T+ targets than for T− targets (p = 1.259 × 10−4, two-sided Wilcoxon rank-sum test, n1 = 220 and n2 = 148 targets; Fig. 5f and Extended Data Fig. 8). This was not due to a difference in learning rate, as the learning rates for the two target types were not statistically different (p = 0.202, two-sided Wilcoxon rank-sum test, n1 = 220 and n2 = 148 targets; Methods). Additionally, performance levels at the end of block 2 for the two target types were not statistically different (p = 0.884, two-sided Wilcoxon rank-sum test, n1 = 220 and n2 = 148 targets). Other groupings of targets agnostic to neural engagement did not predict differences in how quickly targets reached peak performance (Extended Data Fig. 9). Overall, these results suggest that, although performance at the end of learning was similar for T+ and T− targets, the initial increase in neural engagement gave performance for T+ targets a head start, allowing the monkeys to reach peak performance levels for these targets more quickly. This explanation is at apparent odds with the fact that neural engagement decreased throughout learning for both target types (Fig. 5c), which should have led to slower cursor speeds for the T+ targets. Next, we explore how the initial performance improvements for T+ targets were maintained even as neural engagement decreased throughout learning.
Neural engagement changed differently in neural dimensions aligned with the new BCI mapping.
Based on the relationship between neural engagement and cursor speed, one might expect that the gradual decrease in neural engagement (Fig. 5c) should have resulted in gradually slower cursor speeds for T+ targets. But in Fig. 5e, one can see that performance for T+ targets actually increased over time. How is this possible? Crucially, our measurement of neural engagement did not account for which changes in neural engagement affect cursor movements, and which changes do not affect cursor movements. We therefore decomposed each neural engagement axis into two components (Fig. 6a and Methods), where the first component was output-null to the new BCI mapping (that is, changes in this direction would not impact cursor velocities under the new mapping), and the other component was output-potent39–41. This resulted in measures of output-null and output-potent neural engagement, which allowed us to look specifically at whether neural engagement changed differently depending on whether it impacted cursor movements. Changes along the output-null component of the neural engagement axis had no impact on cursor velocities (Fig. 6b), and followed the same pattern as the total neural engagement (Fig. 5c). By contrast, changes along the output-potent component of the neural engagement axis moved in the directions necessary to yield performance improvements for each target type (Fig. 6c). In particular, neural population activity for T+ targets remained elevated along the output-potent component of the neural engagement axis, where performance was initially improved by the increase in neural engagement (Fig. 6c). This indicates that the net decrease in total neural engagement throughout learning was not entirely agnostic to task performance, as neural activity remained elevated specifically in the neural dimensions that were relevant to controlling the cursor.
Fig. 6 |. Neural engagement changed differently in output-potent versus output-null dimensions of the new BCI mapping.
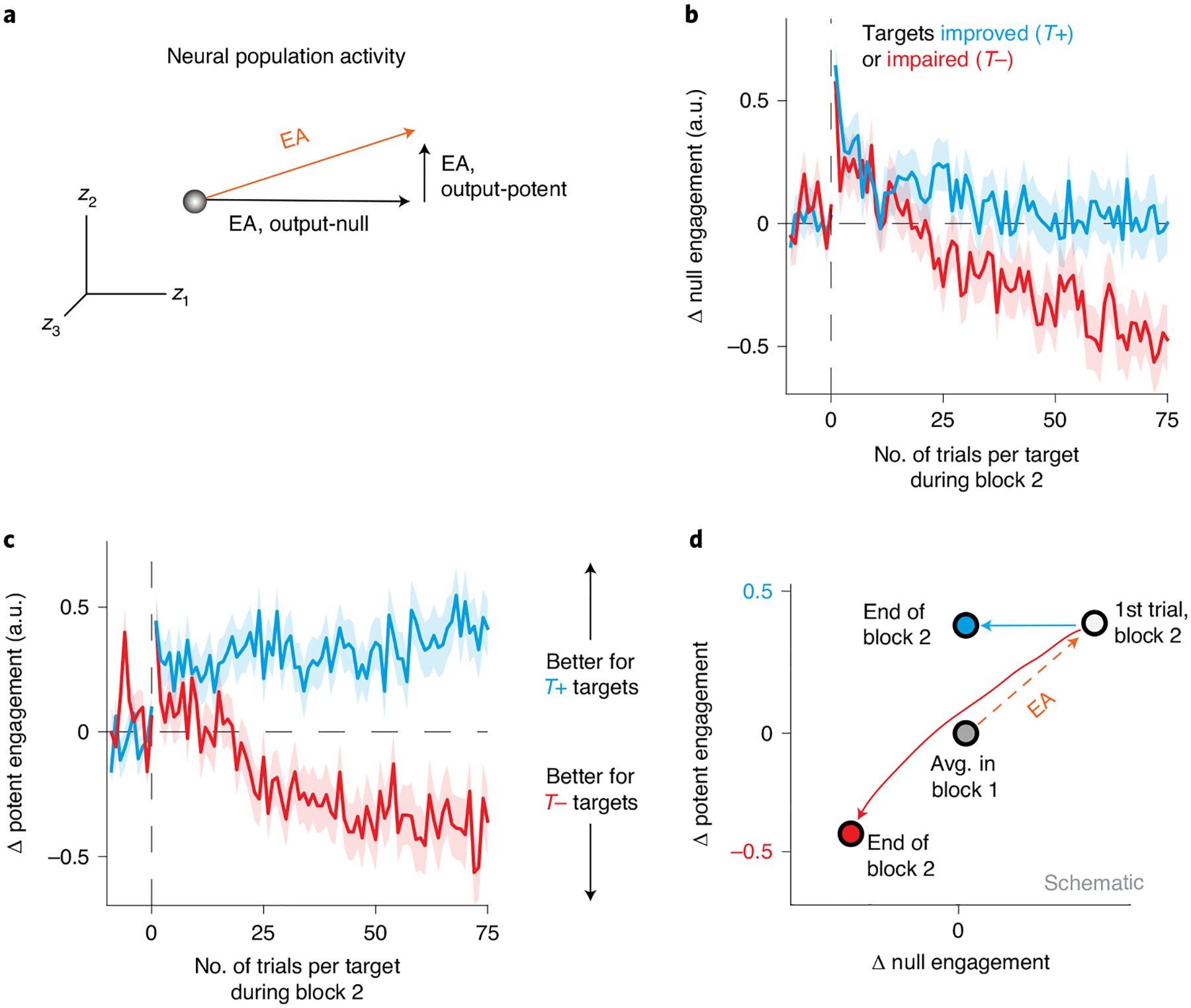
a, Schematic of decomposing a neural engagement axis into output-null and output-potent components. Given the new BCI mapping, this axis can be decomposed into output-null and output-potent axes, such that only changes in neural activity along the output-potent axis will affect cursor velocities under the new mapping. b,c, Changes in neural activity along the output-null (b) and output-potent (c) neural engagement axes during learning, averaged across T+ (n = 220) and T− (n = 148) targets (mean ± s.e.). Same conventions as Fig. 5c. Changes in output-null neural engagement did not affect cursor movements, while changes in output-potent neural engagement did. d, Schematic summarizing how the evolution of neural activity during learning differed based on whether a neural engagement increase was predicted to initially improve (T+) or impair (T−) performance to a given target. The average neural activity for each target type was similar on the first trial of block 2 (white circle), relative to where activity was before the introduction of the new BCI mapping (gray circle), but gradually diverged during learning (blue and red arrows).
Taken together, these results explain how the monkeys reached peak performance more quickly for some targets than for others, based on the relationship between neural engagement and cursor movements (Fig. 6d). On the first trial of block 2, neural activity increased along the neural engagement axis, regardless of its impact on performance (Fig. 6d). This led to immediate performance improvements for T+ targets and decrements for T− targets (Fig. 5e; trial 1). As the trials continued, neural activity gradually decreased along the neural engagement axis for both target types (Fig. 6d). For T− targets, this decrease in neural engagement was beneficial to performance, yielding progressively faster cursor speeds toward the target. For these targets, neural activity decreased similarly along the components of the neural engagement axis that were output-potent and output-null to cursor velocities under the new BCI mapping (Fig. 6d). By contrast, for T+ targets, neural activity decreased along the output-null components of the neural engagement axis, but maintained the initial increase in the output-potent components (Fig. 6d). This allowed the immediate performance improvements from the increase in neural engagement on trial 1 to be maintained, even as total neural engagement decreased. As a result, the monkeys reached peak performance more quickly for T+ targets than for T− targets.
These results indicate that during learning, neural population activity did not change gradually from the activity observed before learning to the activity at the end of learning (Fig. 6d). Rather, neural population activity underwent an abrupt change at the start of learning, improving performance for some targets and impairing performance for others. While the performance levels at the end of learning were similar for both target types (Fig. 5e), the path along which neural population activity changed to achieve this performance was quite different (Fig. 6d). These findings help to explain why some targets were learned more quickly than others.
Discussion
We have shown that large, trial-to-trial fluctuations in M1 population activity along neural engagement axes exhibit hallmarks of an arousal- or motivation-like process. On the first trials that monkeys used a new BCI mapping, neural activity increased abruptly along neural engagement axes, regardless of the effect on behavioral performance. On subsequent trials, neural activity retreated along neural engagement axes, impacting monkeys’ performance using the new BCI mapping. The way that neural engagement axes related to behavior allowed us to predict which targets would be learned more quickly than others. Our findings indicate that (1) changes in neural activity during learning need not be a gradual transition between the activity produced before learning and the activity produced at the end of learning, and (2) changes in internal states seemingly unrelated to goal-seeking behavior can systematically influence how behavioral performance improves with learning.
In this study, we found that trial-to-trial changes in neural engagement were positively correlated with changes in the monkey’s pupil size, a common psychophysical index for an animal’s internal state2. The term ‘internal state’ is used broadly, but typically refers to any neural signal that does not directly reflect, but may interact with, sensory encoding or behavior generation2. This includes internal states related to computation (for example, internal models42, reward prediction43 and working memory44), as well as those reflective of more autonomic processes (for example, arousal8, motivation14 and task engagement5). We have termed the internal state identified in the present work ‘neural engagement’ because its stereotyped time course was suggestive of changes in the monkey’s engagement with the task throughout the experiment (for example, increases in neural engagement following pauses in the experiment and the introduction of a new BCI mapping). This is likely distinct from the concept of task engagement5, which refers to the difference between an animal actively performing a task versus passive sensory stimulation. Our results add to a growing line of work finding that there are large, systematic changes in M1 activity that are not related on a moment-by-moment basis to movement kinematics45,46.
While our current study design does not allow us to identify the exact source of changes in neural engagement, here we briefly consider multiple possibilities and how they might explain (or fail to explain) the results in the present work. First, we observed that increased neural engagement predicted increased hand speed toward the target (Extended Data Fig. 6), suggesting that neural engagement may simply reflect the monkey’s intended movement speed. However, this seems unlikely given that neural engagement decreased over time even for T+ targets, which would decrease reward rate. Thus, neural engagement is likely not directly related to the monkey’s intended movement speed. Second, neural engagement may reflect a default motor response such as muscle co-contraction. Co-contraction is thought to be a default strategy for reducing kinematic errors early in learning47. However, we also observed an increase in neural engagement following pauses during block 1 (Fig. 2e), when there were no unexpected kinematic errors to correct. Thus, if neural engagement does reflect a default motor response such as co-contraction, this response may be the manifestation in motor cortex of an uncertainty- or arousal-driven response, rather than a response to kinematic errors. Finally, neural engagement may reflect changes in animals’ arousal, as indicated by its correlation with pupil diameter. We speculate that neural engagement may have a similar origin as the ‘neural drift’ identified in V4 and prefrontal cortex12.
How might neural engagement impact learning? We found that neural engagement increased abruptly early in learning, and then gradually decreased on subsequent trials, regardless of its impact on behavior. We can imagine two mechanisms by which these stereotyped changes in neural engagement might impact the learning process. First, modifying one’s future behavior to improve performance requires feedback. Thus, whenever changes in neural engagement directly impact behavior (that is, BCI cursor movements), this will also impact the monkeys’ feedback about their performance, which will necessarily influence the learning process. This is likely to be the case during arm movements as well, as we found that changes in neural engagement were related to hand speeds during hand control experiments (Extended Data Fig. 6). A second, not mutually exclusive possibility is that neural engagement may influence which neural activity patterns the monkey returns to on later trials via a reinforcement-like process25. For example, early in learning when levels of neural engagement were higher, animals produced neural activity patterns with an increased likelihood of reward for T+ (as compared to T−) targets. If neural activity patterns are more likely to be revisited when they lead to higher rewards, then the animals may revisit these same neural activity patterns on later trials for T+ targets. This could explain why T+ targets were learned more quickly than T− targets.
Previous work has observed an increase in neural variability early in learning48. It was proposed that this increased variability may allow the brain to improve behavior by exploring new neural activity patterns. Our results confirm this observation, and may offer a new interpretation. We found that increased neural engagement corresponded with increased modulation depths and neural variability in most individual neural units (Extended Data Fig. 5), consistent with findings of increased neural variability at the beginning of learning in previous studies48. If changes in neural activity at the beginning of learning are indeed related to an exploratory drive, our results suggest that this process may not be a general exploratory process (that is, an increase in variability without changing the mean), but rather a stereotyped exploration process (that is, neural activity moves in a particular direction along neural engagement dimensions, which also results in more variability). Importantly, we found that neural engagement (and thus, neural variability) also increased even in the absence of learning (that is, following pauses in block 1). This raises the possibility that the changes in neural variability observed during learning in previous work may be driven by different internal states—not only by an exploratory drive, but also by internal states that reflect the animal’s arousal or uncertainty about its environment. Future work is needed to disentangle the effects of these diverse sources of variability in neural population activity, all of which may impact behavior, and thus learning.
Overall, our results add to a growing body of work finding population-level signatures of internal state fluctuations3,4,12,33,34,49,50. Changes in internal state can influence on a moment-by-moment basis how we perceive a sensory stimulus (for example, through attention), or how we execute a movement (for example, through vigor). Building upon these previous studies, we found that changes in internal state can influence how behavior evolves during learning. Thus, internal state fluctuations can influence not only concurrent behavior, but also future behavior through their interaction with the learning process.
Methods
Experimental details.
Experimental methods are described in detail in previous work23,26. Briefly, we recorded from the proximal arm region of primary motor cortex (M1) in three male rhesus macaques (Maccaca mulatta; ages: monkey J, 7 years; monkey L, 8 years; monkey N, 7 years) using implanted 96-electrode arrays (Blackrock Microsystems). Data collection was performed using LabVIEW (2012–2014) and MATLAB (2011b–2015a). All animal care and handling procedures conformed to the National Institutes of Health (NIH) Guidelines for the Care and Use of Laboratory Animals and were approved by the University of Pittsburgh’s Institutional Animal Care and Use Committee. We recorded from 85 to 94 neural units in each session. The activity of each neural unit is defined as the number of threshold crossings recorded by an electrode in nonoverlapping 45-ms bins. The average firing rate of the neural units across sessions was 46 ± 7, 38 ± 8 and 56 ± 13 spikes per second (mean ± s.d.) for monkeys J, L and N, respectively.
During each experimental session, monkeys performed an eight-target center-out task by modulating their recorded neural activity to control the velocity of a computer cursor on a screen. Each session involved two different BCI mappings. The first ‘intuitive’ mapping was chosen to provide the monkey with proficient control of the cursor. The animal used the intuitive mapping for 321 ± 96 trials (mean ± s.d.), after which the mapping was switched abruptly to a second, new BCI mapping that the monkey had never controlled before. This new mapping was chosen so as to be initially difficult for the monkey to use, and the monkey was given 698 ± 227 trials (mean ± s.d.) to learn the new mapping. Both BCI mappings were chosen so that they were controlled exclusively by the neural activity within the monkey’s intrinsic manifold (defined below). During the BCI task, each animal’s arms were loosely restrained. We monitored hand movements using an LED marker (PhaseSpace) on the hand contralateral to the recording array. During BCI control, animals showed little to no arm movements23 (Extended Data Fig. 2).
At the beginning of each trial, a cursor appeared in the center of the workspace, followed by the appearance of one of eight possible peripheral targets (chosen pseudorandomly among θ ∈ {0°, 45°, 90°, 135°, 180°, 225°, 270° and 315°}). For the first 300 ms of the trial, the velocity of the cursor was fixed at zero. After this, the velocity of the cursor was controlled by the animal through the BCI mapping. If the animals acquired the peripheral target with the cursor within 7.5 s, they received a water reward, and the next trial began 200 ms after target acquisition. Otherwise, the trial ended, and animals were given a 1.5-s time-out before the start of the next trial.
During all experiments, we monitored the monkey’s pupil diameter (a.u.) using an infrared eye tracking system (EyeLink 1000; SR Research). The eye tracker was first turned on while monkeys used the intuitive mapping, but this time varied from session to session. Pupil diameter was always measured while monkeys controlled the new BCI mapping.
Defining the BCI mappings.
Each session began with the monkey performing a block of calibration trials, as described in previous work23. Using these calibration trials, we z-scored the spike counts separately for each neural unit. We then applied factor analysis (FA) to the z-scored spike counts to identify the 10D linear subspace (that is, the ‘intrinsic manifold’) that captured dominant patterns of co-modulation across neural units31,48,51–54. We used ten factors (that is, dimensions), as this was the average dimensionality identified by cross-validation across experiments from monkeys J and L23. In fact, we used exactly the same FA model and 10D latent factors that were found during the experiment to drive the BCI cursor (see below).
The factor activity, , was estimated as the posterior expectation given the z-scored spike counts, , where q is the number of neural units, as given by equation (1):
| (1) |
Above, L, Ψ and d are FA parameters estimated using the expectation–maximization algorithm, where L is termed the loading matrix, and Ψ is constrained to be a diagonal matrix. The factor activity, zt, can be interpreted as a weighted combination of the activity of different neural units. Before analysis, we orthonormalized zt so that it had units of spike counts per time bin39,55. We refer to zt as a ‘population activity pattern.’
As discussed above, each experiment consisted of animals using two different BCI mappings. Each BCI mapping translated the resulting moment-by-moment factor activity (zt) into a two-dimensional (2D) cursor velocity (vt) using a Kalman filter represented by equation (2):
| (2) |
For the intuitive BCI mapping, , and were computed from the Kalman filter parameters, estimated using the calibration trials. For the second, new BCI mapping, we changed the relationship between population activity and cursor movement by randomly permuting the elements of zt before applying equation (2). This permutation procedure can be formulated so that equation (2) still applies to the second BCI mapping, but for a new matrix used in place of M1 (ref.23).
Hand control experiments.
Data were collected from a fourth monkey (monkey G) for three sessions. During these experiments, the monkey performed an eight-target center-out task using hand movement to control a computer cursor. An infrared marker was taped to the back of the monkey’s hand and tracked optically using an Optotrak 3020 system. The marker position was used to update the position of the cursor in real time on a stereoscopic computer monitor. During these experiments, we recorded from the proximal arm region of M1 using an implanted 96-electrode array (Blackrock Microsystems).
Similarly to the BCI control experiments, the targets shown on each trial were chosen pseudorandomly. At the beginning of each trial, a target (sphere; radius of 6 mm) was presented in the center of the reaching workspace. The animal was trained to move the cursor (sphere; radius of 6 mm) to this start target and hold for 0–100 ms. A peripheral target (sphere; radius of 6 mm) was presented at the end of this hold period. Water reward was delivered if the target was acquired within 1.5 s and the cursor was held on the target for a random hold period drawn uniformly from 150–550 ms. The next trial was initiated 200 ms after the trial ended, regardless of success or failure. The data analyzed included 160 trials of baseline center-out trials, where the marker position was directly mapped to the cursor position, followed by 320 trials where a visuomotor rotation was applied to all reaches (40° CW, 40° CCW and 30° CW for the three sessions, respectively).
To match the analysis procedure used in the BCI experiments, we took spike counts in nonoverlapping 50-ms bins, and z-scored the spike counts using the mean and standard deviation of each neural unit during baseline reaches. We then applied FA to the z-scored spike counts recorded during all baseline reaches to identify a 12D linear subspace, where 12 was the number of dimensions that maximized the cross-validated log likelihood. We then orthonormalized the resulting 12D factor activity. All analyses of population activity considered only these top 12 factors.
Data analysis.
Session and trial selection.
The data analyzed in this study were part of a larger study involving learning two different types of BCI mapping changes: WMPs, described above, and outside-manifold perturbations (OMPs)23. We found that animals learned WMPs better than OMPs, and so we only considered WMP sessions in this study. We analyzed all sessions regardless of whether animals showed learning. For consistency, we excluded two sessions where the WMP was not the first perturbation shown during that experiment. In total, we analyzed 46 WMP sessions (monkey J: 25 sessions; monkey L: 10 sessions; monkey N: 11 sessions). No statistical method was used to predetermine sample sizes but our sample sizes are similar to those reported in previous publications12,26,29,39.
In the BCI experiments, spike counts were taken in nonoverlapping 45-ms bins (‘timesteps’), indexed here by j = 1, …, J, where J is the number of timesteps in a given trial, and j = 1 is the timestep where the target first appeared. Each trial consisted of three intervals of interest: (1) the pre-target interval (j ≤ 2, or 90 ms), during which the monkey had not yet perceived the target due to sensory processing delays; (2) the freeze interval (j ≤ 6), during which the cursor was frozen in place at the center of the workspace; and (3) the cursor control interval (j ≥ 7), where the cursor velocity was determined by equation (2). Unless otherwise noted, all analyses used data only during the cursor control interval.
We noted that when the cursor was near the target, or at the end of long trials, cursor movements were often idiosyncratic (for example, reflecting small corrective movements), and so we discarded from our analyses any timesteps where the cursor was more than 65% of the way to the target, and any timesteps j > 20. To report trial-averaged quantities, we aimed to ensure that all neural activity within the same trial came from timesteps where the monkey attempted to push the cursor in the same direction. This was especially important given that we compared the time course of neural engagement during learning on a target-by-target basis (Figs. 4–6). We therefore analyzed only the timesteps where the angle between the cursor and target was within 22.5° of the target direction on that trial. Performing our analyses without this exclusion criterion did not change our results.
We analyzed both correct and incorrect trials in this study. We reasoned that sufficiently large increases in neural engagement (for example, on the first trial using the new BCI mapping) may slow down the cursor’s speed to the extent that the monkey is unable to obtain the target. Removing incorrect trials would then bias any analyses that compare levels of neural engagement between targets whose performance was improved versus impaired by neural engagement (Figs. 4–6). We did, however, remove trials where the monkey appeared to quit the task, by removing any sequence of more than five consecutive incorrect trials that occurred following at least one correct trial during block 2. This occurred in only 11 of 46 sessions, resulting in the removal of 0.71% of trials. All results were qualitatively similar without this exclusion criterion.
For the hand control experiments, we analyzed data from the 15 timesteps of each trial immediately following the appearance of the target (which cued the monkey to begin hand movement toward the target).
Quantifying behavioral performance.
To quantify the monkey’s moment-by-moment performance, we calculated the speed of the cursor in the target direction (that is, cursor progress26). To do this, we first calculated the ‘single timestep’ cursor velocity according to equation (3):
| (3) |
where zj is the neural activity produced at timestep j, and M2 and c are the new BCI mapping parameters (equation (2)). The cursor’s speed toward the target, sj, is then given by equation (4):
| (4) |
where pj is a unit vector pointing from the cursor position at timestep j to the target position. Assessing performance in this manner ensured that our measures of neural engagement and performance (Fig. 5) were both assessed using precisely the same neural activity, and at the same resolution (that is, every timestep).
Changes in performance during block 2 (Fig. 5e) were calculated as follows. Let sθ(t) be the average of sj for all timesteps j from the tth trial to target θ. Let sθ(0) be the expected speed to the target under the new BCI mapping before learning begins, given by projecting the monkey’s trial-averaged neural activity to the same target during block 1 into the new BCI mapping (that is, using equations (3) and (4)). For each t, Fig. 5e depicts Δsθ(t) = sθ(t) − sθ(0) averaged across all targets in the same group (for example, all T+ targets).
To find the trial at which performance for each target θ reached its peak (Fig. 5f), we first found the running mean of Δsθ(t) in a sliding eight-trial window. Let be the resulting running mean. The trial at which performance for each target θ reached its peak was then arg max .
To test whether performance levels at the end of block 2 differed between T+ and T− targets, let be the performance level of target θ at the end of block 2. To assess whether learning rates differed between T+ and T− targets, for each θ we fit a saturating exponential to sθ(t) with free parameter τ > 0, according to equation (5):
| (5) |
where τ is the learning rate, governing how quickly sθ(t) transitions from initial performance, sθ(1) (unsmoothed because s changed more quickly early in learning), to performance at the end of block 2, . For each target, τ was chosen so as to minimize the mean squared error between and sθ(t) for all t.
Identifying neural engagement axes.
For each experimental session (for either BCI or hand control), we identified a set of neural engagement axes, capturing the dimension along which neural activity varied in the absence of learning pressure (that is, while monkeys used the intuitive BCI mapping, or during baseline reaches, respectively) for each target θ ∈ {0°, 45°, 90°, 135°, 180°, 225°, 270° and 315°}. Let , with ∥aθ∥ = 1 be the neural engagement axis for target θ. We defined aθ as the direction of greatest variance in the factor activity recorded during all trials to that target. Identifying this direction in the factor activity rather than in the spiking activity ensured that we focused on the shared covariance among neural units rather than variance that is independent to each unit.
We observed that the neural engagement axes involved the activity of nearly all neural units changing in the same direction (Extended Data Fig. 4). We therefore chose the sign of aθ so that positive values of neural engagement corresponded to increases in the firing rate for the majority of units. This allowed us to average across values of neural engagement across targets and sessions.
Quantifying neural engagement.
During block 1, we defined the value of neural engagement, , for each timestep j to target θ, as given by equation (6):
| (6) |
where is the mean neural activity produced to target θ during block 1. The level of neural engagement on trial t was then defined as the average of ej for all timesteps j from trial t.
To compute neural engagement during block 2, we cannot simply use equation (6), because some of the changes in neural activity across trials will also be due to learning (for example, by neural reassociation26). According to neural reassociation26, to move the cursor in a particular direction θ ∈ [0, 2π) during block 2, the monkeys sample the neural population activity they used for movements in a potentially different direction θ′ ∈ [0, 2π) during block 1. Thus, to estimate neural engagement during block 2 (Figs. 5 and 6), we used the following equation (7):
| (7) |
where is no longer necessarily equal to the target direction, θ. We estimated from the neural activity, zj, which is reasonable provided that changes in neural activity due to θj and ej are not entirely overlapping. Specifically, was defined as the direction that the cursor would have moved if zj were produced under the intuitive mapping, as changes in neural engagement tended to have less effect on the cursor’s movement direction using the intuitive mapping. This procedure allowed our estimate of to vary as the monkey learned to control the new BCI mapping, thus accounting for any changes in neural activity due to neural reassociation. To compute and for any continuous value of , we used a cubic spline to interpolate between the values measured for each θ ∈ {0°, 45°, 90°, 135°, 180°, 225°, 270° and 315°}.
In the above procedure, the neural engagement axes corresponding to a given θ are assumed to be the same during both block 1 and block 2. We confirmed that the neural engagement axes estimated before learning (during block 1) and after learning (at the end of block 2) were similar (Extended Data Fig. 10), indicating that the largest fluctuations in neural activity occurred along similar dimensions throughout the experiment.
To compare values of neural engagement across trials to different targets in Fig. 2 and Extended Data Fig. 1, we z-scored the neural engagement for each target separately using the mean and standard deviation across all trials to each target during block 1. In all other figures, neural engagement was z-scored using the mean of the last ten trials to each target during block 1. This was done so that the level of neural engagement on the first trial of block 2 was relative to the average level at the end of block 1 (for example, Figs. 4c and 5c).
Comparing neural engagement to pupil size.
For each session, we estimated the trial-by-trial correlation between neural engagement and the monkey’s pupil size (Fig. 2f,g). To do this, we first found the average pupil size and neural engagement during the control interval of each trial. Similar to previous work correlating population activity and pupil size12, we applied boxcar smoothing to the trial-averaged measurements of each quantity with a sliding window of 30 trials, and then computed the Pearson’s correlation between the resulting time series. Pupil recordings began partway into block 1 and continued throughout block 2 (‘Experimental details’). Thus, the analysis shown in Fig. 2g used trials throughout block 2, for all sessions where block 2 consisted of at least 200 trials (44 of 46 sessions). During the 13 sessions where pupil size was measured during block 1for at least 200 trials (all sessions were from monkey J), the median correlation between neural engagement and pupil size was ρ = 0.67 (bootstrapped 95% CI (0.41, 0.79), n = 13 sessions).
Variance explained by changes in neural engagement.
We sought to estimate the amount of variance in the neural population activity due to changes in neural engagement during block 1 (Fig. 2h). To estimate the variance for trials to a given target, we first found the average neural activity zt during each trial to that target, along with the corresponding neural engagement, et. The measure of the variance explained by changes in engagement for that target was then . To calculate the total amount of variance explained by changes in engagement, we computed the same metric above, but used the activity from all trials combined rather than just the trials to a particular target.
Predicting the impact of neural engagement on performance under the new mapping.
We labeled a target as T+ or T− based on whether an initial increasein neural engagement would increase (T+) or decrease (T−) the cursor’s speed toward the target under the new mapping (for example, Figs. 4–6). Specifically, let be the average neural activity recorded during block 1 for target θ, and let aθ be the corresponding neural engagement axis. Then we labeled that target as T+ if an increase in neural engagement led to an increase in the cursor’s speed to the target (see equations (3) and (4)) according to equation (8):
| (8) |
where M2 and c are the parameters of the new BCI mapping, p is a unit vector corresponding to the target direction and ϵ > 0 is a small constant. Otherwise, the target was labeled as T−.
Identifying output-potent and output-null-engagement axes.
Given a neural engagement axis, , not all changes in neural activity along this axis will lead to changes in cursor velocity through the new BCI mapping, M2. This is because the mapping between neural activity and cursor velocity, given by equation (2), is a linear mapping from 10D to 2D, implying that M2 has a nontrivial null space, Nul(M2). To identify which components of a will result in changes in cursor velocity, we can find bases for the null space, Nul(M2), and the row (or potent) space, Row(M2)39. To do so, we took a singular value decomposition of M2 = USVT, with , , and , where the columns of S were ordered so that only the first two columns had nonzero elements. Then, we let be the first two columns of V, and be the remaining eight columns. The columns of N and R are mutually orthonormal and together form an orthonormal basis for the 10D space of factor activity. This allowed us to rewrite the neural engagement axis for each target θ as the sum of a null-engagement axis, , and a potent-engagement axis, , given by equations (9), (10) and (11):
| (9) |
| (10) |
| (11) |
We then normalized and to be unit vectors. Finally, we used these axes in equation (7) to compute values of null and potent engagement (Fig. 6).
Statistics and research design.
Data collection and analyses were not performed blind to the conditions of the experiments. Experiments were not grouped, and thus no group randomization procedures were performed. Statistical analyses were conducted in MATLAB (2015a). To test whether the distributions of neural engagement were different for T+ and T− targets at the start of block 2, we used a two-sample Kolmogorov–Smirnov test. To compare the medians of two distributions we used a two-sided Wilcoxon rank-sum test (unpaired) or a two-sided sign test (paired). Statistical tests were non-parametric and so did not assume normality.
Extended Data
Extended Data Fig. 1 |. Neural engagement showed stereotyped changes relative to experimental events, in multiple example sessions.
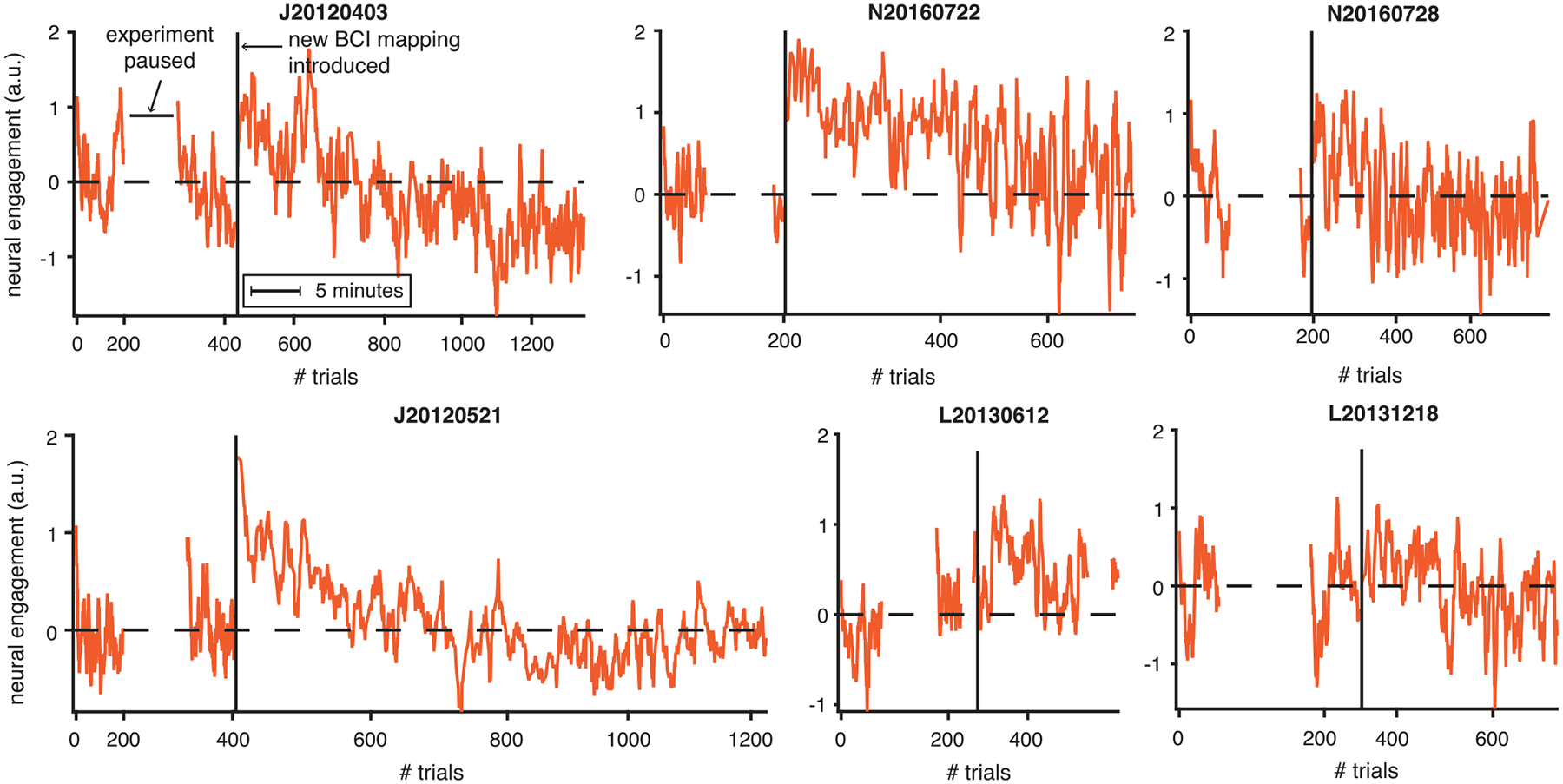
Same conventions as Fig. 2d. Note that in contrast to other figures (for example, Fig. 5c), here neural engagement is shown across trials to all eight instructed targets, where trials to different targets were interleaved. As a result, each time course shown here includes variability due to the target-specific differences in neural engagement during learning (for example, see Fig. 5c). Position along the horizontal axis indicates clock time (see legend indicating ‘5 minutes’), so that pauses in the experiment are more visible. All sessions are plotted with the same time scale, and trial indices are marked for reference.
Extended Data Fig. 2 |. Changes in neural engagement during BCI control could not be explained by hand movements.
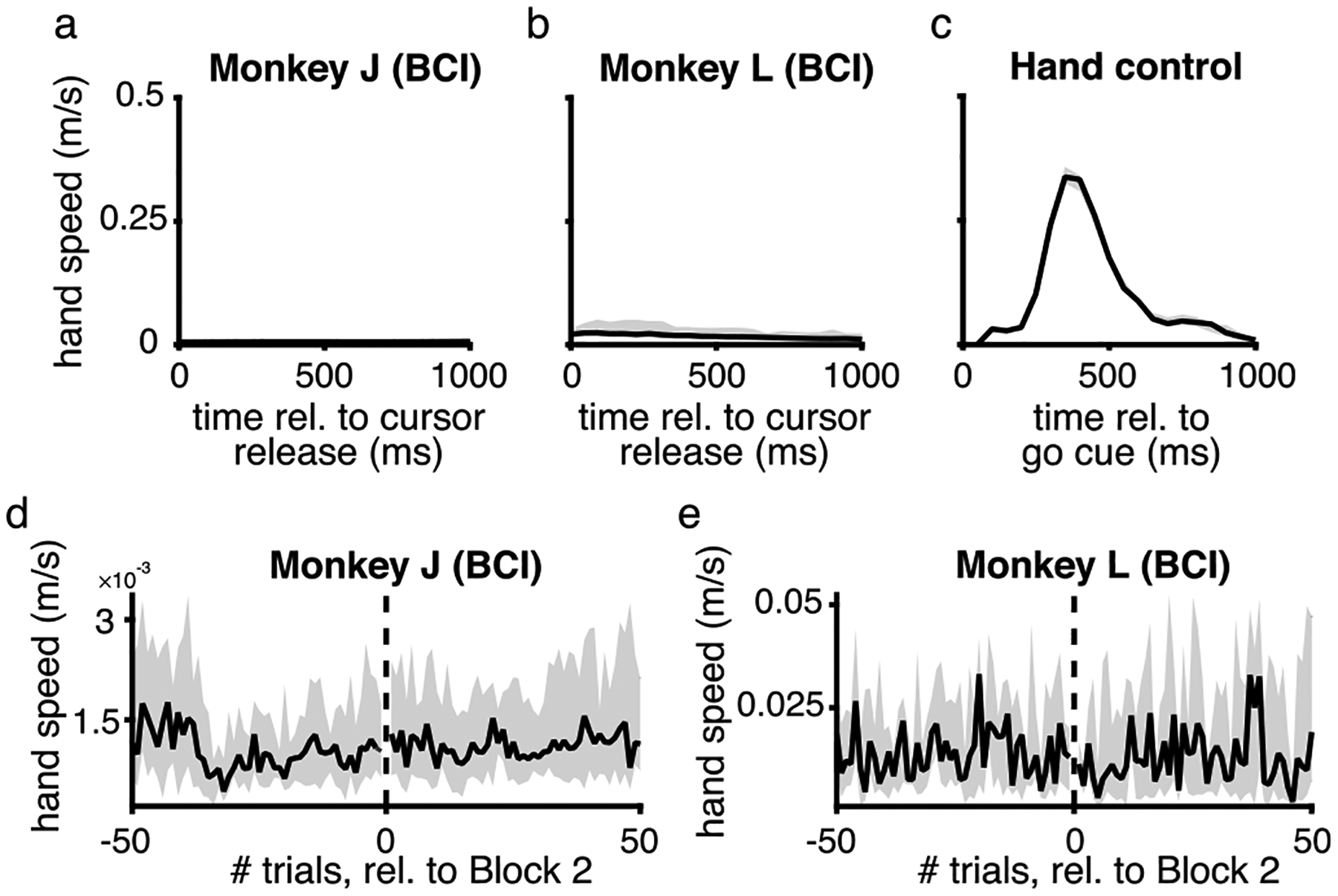
a-c. During the BCI experiments, we recorded the hand speed of two animals (monkey J, shown in panel a; and monkey L, shown in panel b), for the hand contralateral to the recording array (the other hand was restrained). Monkey N’s hand speed was not recorded because his hand was restrained in a tube, and the reflection of the light on the tube made his hand difficult to track. We also recorded the hand speed of monkey G (shown in panel c), who performed a center-out arm reaching task (as shown in Fig. 2i–j). This allowed us to compare hand speeds across both types of experiments. We found that the arm movements during the BCI task (panels a and b) were substantially smaller than during the center-out arm reaching task. Black line indicates median across trials to all sessions, while shading indicates median ± 25th percentile (a, n = 25 sessions; b, n = 10 sessions; c, n = 3 sessions). d-e. Even if animals showed little to no arm movements (as shown in panels a and b), might it be the case that the increase in neural engagement at the start of block 2 (Fig. 4c) can be explainedby animals moving their hands more than they did on previous trials? We found no substantial increase in hand speed at the start of Block 2 for either monkey. Black line indicates median across sessions, while shading indicates median ± 25th percentile (d, n = 25 sessions; e, n = 10 sessions). Thus, the increase in neural engagement we observe at the start of Block 2 cannot be explained by animals suddenly moving their hands more than during Block 1.
Extended Data Fig. 3 |. Trials with elevated levels of neural engagement also showed increased pupil size.
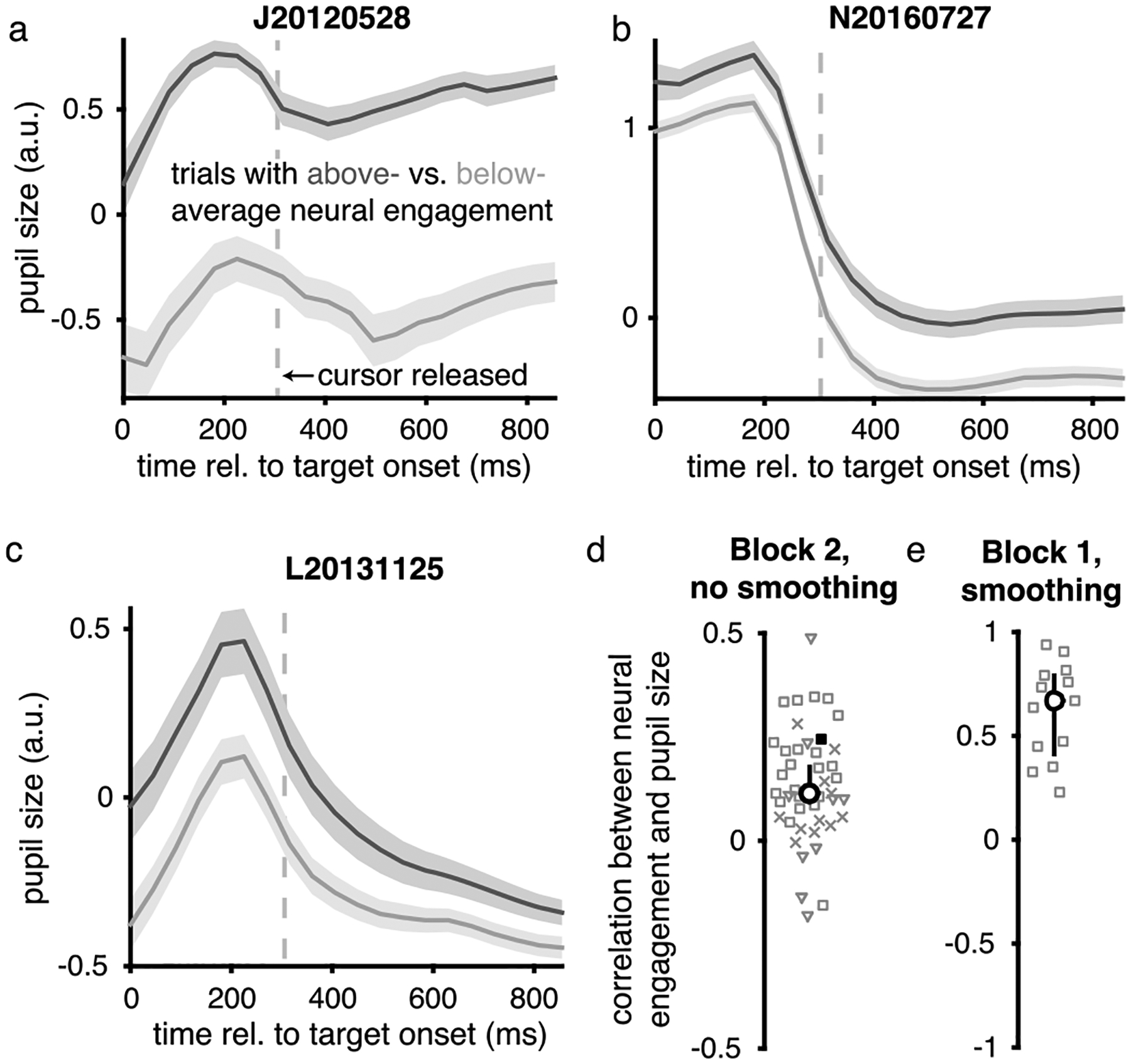
a-c. In Fig. 2g, we related neural engagement and pupil size by first averaging the pupil size across time points within a trial. To further explore this relationship, here we consider the time course of pupil size within a trial. Trial-averaged pupil sizes are shown for three example sessions after grouping trials separately based on whether neural engagement during the control interval of each trial during Block 2 was above- (dark gray) or below- (light gray) the median across trials during Block 2. Vertical dashed line indicates the time within each trial when the cursor was released (300 ms; see Methods), that is, the beginning of the control interval. Shading indicates mean ± SE across trials (a, n = 456 trials; b, n = 296 trials; c, n = 202 trials). Within each example session, the time course of pupil size was similar for trials with above- versus below-average levels of neural engagement, but with a larger overall pupil size on trials with above-average neural engagement. d. Prior to computing the correlations between neural engagement and pupil size shown in Fig. 2g (and in the previous panel), we first smoothed the trial-by-trial time courses of pupil size and neural engagement with a 30-trial boxcar filter, similar to previous work correlating population activity and pupil size12. Here we show that neural engagement and pupil size were typically positively correlated even without smoothing. Without smoothing, the median Pearson’s correlation across sessions was ρ = 0.12 (bootstrapped 95% C.I. [0.09, 0.18], n = 44 sessions). Same conventions as Fig. 2g. e. Although the recording of pupil size began part way into Block 1 due to experimental constraints, we computed the trial-by-trial correlation between pupil size and neural engagement during Block 1 for the 13 sessions with a sufficient number of trials (all from monkey J). The median Pearson’s correlation during these sessions was ρ = 0.67 (bootstrapped 95% C.I. [0.41, 0.79], n = 13 sessions). Thus, a positive correlation between neural engagement and pupil size was also present before learning. Same conventions as Fig. 2g.
Extended Data Fig. 4 |. Changes in neural engagement corresponded to nearly all neural units increasing or decreasing their activity together.
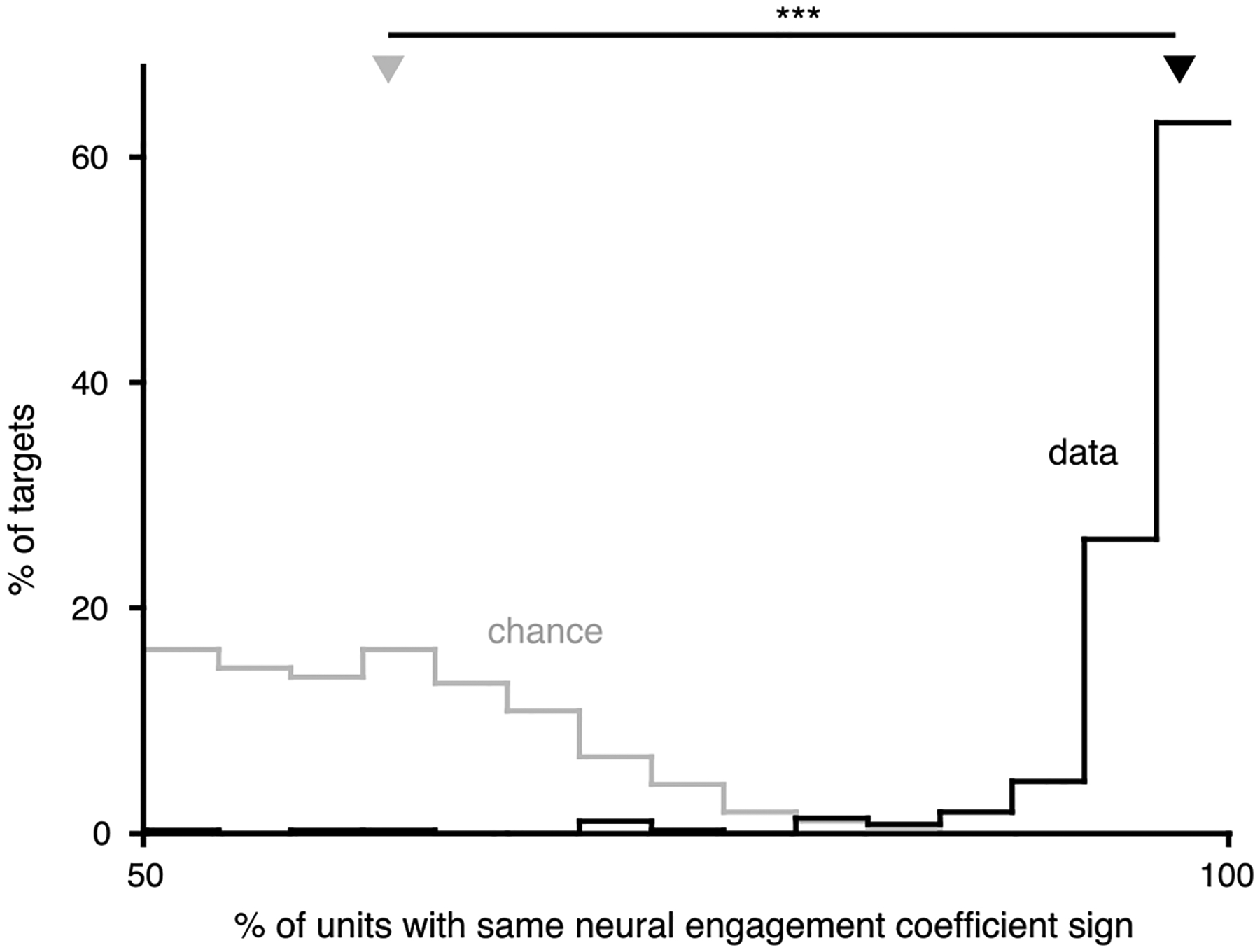
We wanted to understand how changes in neural engagement were represented by the activity of individual units. For each target, a neural engagement axis was defined in 10-dimensional factor space. We used the q × 10 loading matrix from factor analysis (see Methods) to define the neural engagement axis in the q-dimensional population activity space of the q recorded units. For example, if there were 90 units, the neural engagement axis would have 90 coefficients, describing how changes in neural engagement for a given target would be represented by the activity of each of the 90 units. For each target, we computed the percentage of units whose coefficients had the same sign (for whichever sign was in the majority, so that percentages could never be below 50%). Shown in black is the distribution of these percentages across the neural engagement axes for all targets across all sessions (bootstrapped 95% C.I. [97.6%, 97.7%], n = 368 axes (one per target)). This relationship means that an increase in neural engagement corresponds to an increase in the firing rate of most units (by an amount that is unit- and target-dependent). For reference, in gray, is the distribution after sampling random dimensions in factor space, and computing the corresponding effects on individual neural units (bootstrapped 95% C.I. [59.7%, 62.5%], n = 368 random axes). Triangles depict the medians of the ‘data’ and ‘chance’ distributions, which were significantly different (p < 10−10, paired, two-sided sign test, n = 368 axes).
Extended Data Fig. 5 |. Increased neural engagement corresponded with increased baseline firing rate, modulation depth, and spiking variance in single units.
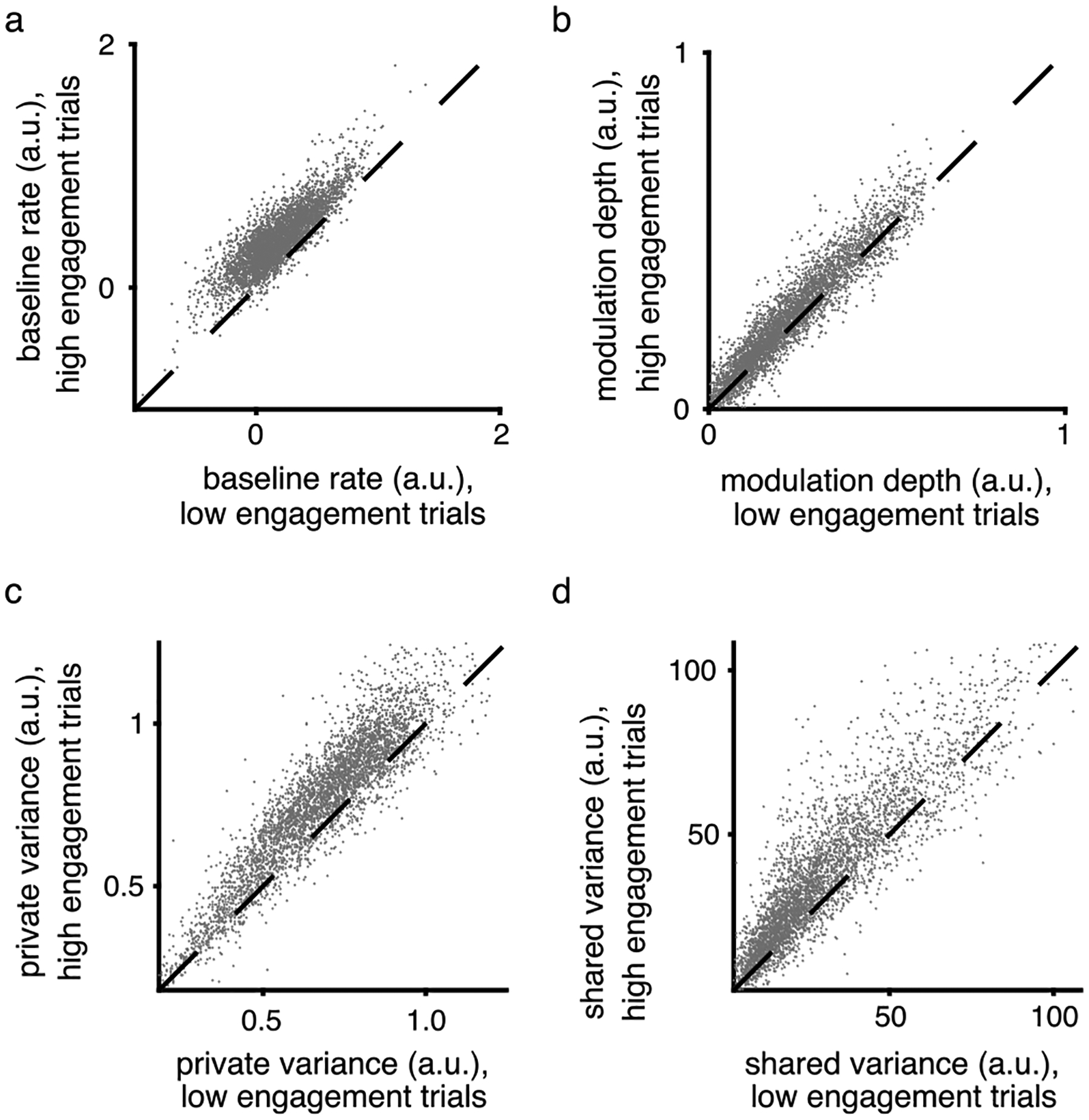
To understand the relationship between neural engagement and the firing properties of individual units, for each experiment we grouped trials during Block 1 based on whether they had above- versus below-average levels of neural engagement (similar to Extended Data Fig. 3). a-b. For each individual unit from all sessions, we fit two cosine tuning models to each unit’s z-scored spike counts: one model was fit to the average spike counts on trials with above-average levels of neural engagement (‘high engagement trials’), while the other model fit to the spike counts on trials with below-average levels of neural engagement (‘low engagement trials’). The cosine model was of the form y = b + m cos(θ − θpref), where y is the unit’s expected firing rate on a trial to target θ, b is the unit’s baseline (average) firing rate, m is the unit’s modulation depth, and θpref is the unit’s preferred direction. We estimated b, m, and θpref using linear regression. Each dot corresponds to one unit. For most units, both the baseline firing rate (b; panel a) and the modulation depth (m; panel b) were higher on high engagement trials than on low engagement trials (in both cases: p < 10−10, paired, two-sided sign test, n = 4074 units). c-d. For each session, we fit a factor analysis (FA) model to the z-scored spike counts of all units during low engagement trials, and then fit a separate FA model to the z-scored spike counts during high engagement trials. Each model had the same form as equation (1), resulting in parameter estimates of L and Ψ. The estimated private variance of unit i is given by Ψii, while the shared variance is given by (LL⊤)ii, where the ii subscript indicates the ith diagonal element. Each dot corresponds to one unit. We found that both the private variance (panel c) and shared variance (panel d) of most units was higher on high engagement trials than on low engagement trials (in both cases: p < 10−10, paired, two-sided sign test, n = 4074 units). This result is expected from Extended Data Fig. 4 because the sum of a unit’s shared and private variances equals its spike count variance. Because a unit’s spike count variance tends to increase with its mean spike count, a higher firing rate will typically correspond with a higher shared and/or private variance.
Extended Data Fig. 6 |. Increased neural engagement during arm movements predicted faster hand speeds towards most targets.
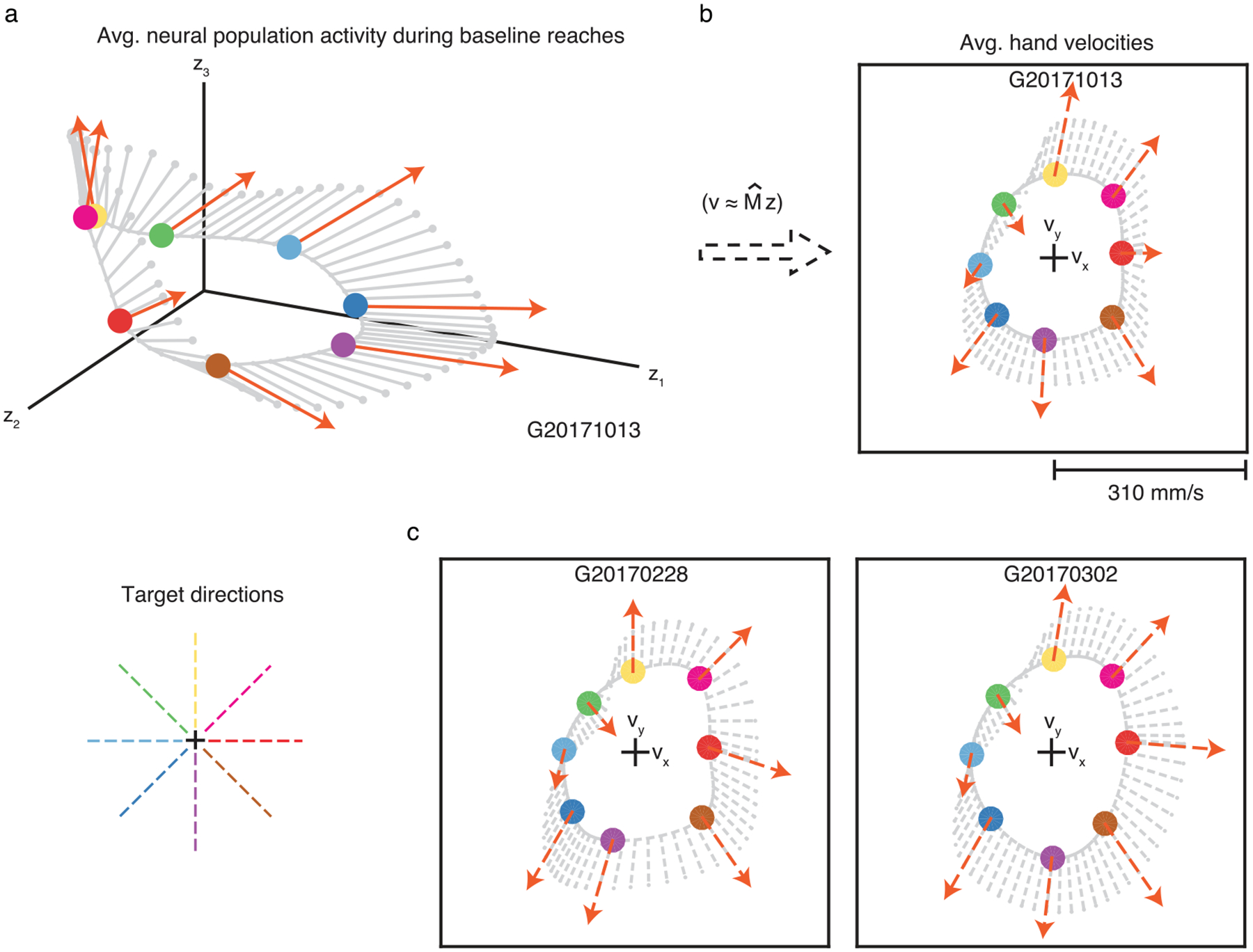
a. For the experiments involving arm movements (see Methods), we visualized the average neural population activity (circles) and neural engagement axes (orange arrows) during baseline reaches to each of eight targets. Same conventions as Fig. 3d. ‘Target directions’ panel is a legend depicting the color corresponding to each target direction. b. We also visualized the monkey’s average hand velocity during reaches to each target (circles), similar to Fig. 3e. Unlike during BCI control, we do not know the causal relationship between neural population activity and hand velocity. To understand how changes in neural engagement related to hand velocity, we used linear regression to predict the monkey’s hand velocity during baseline reaches at each 50 ms timestep during the movement epoch of every trial, using the neural population activity recorded 100 ms prior. Cross-validated r2 for the x- and y- components of hand velocity were 67% and 77%, respectively. The linear regression model () allowed us to estimate how increases in the neural engagement related to the monkey’s average hand velocity towards each target (orange dashed arrows), and to intermediate target directions (gray dashed lines). In this session, an increase in neural engagement predicted an increase in the monkey’s hand speed towards all but the 135° target. This suggests that differences in the neural engagement axes across targets may have behavioral relevance. c. We repeated the procedure in panel b during the other two arm movement sessions. Across sessions, increased neural engagement during arm movements predicted faster hand speeds towards most targets.
Extended Data Fig. 7 |. New BCI mappings induced a variety of relationships between neural engagement and cursor velocity, across targets and sessions.
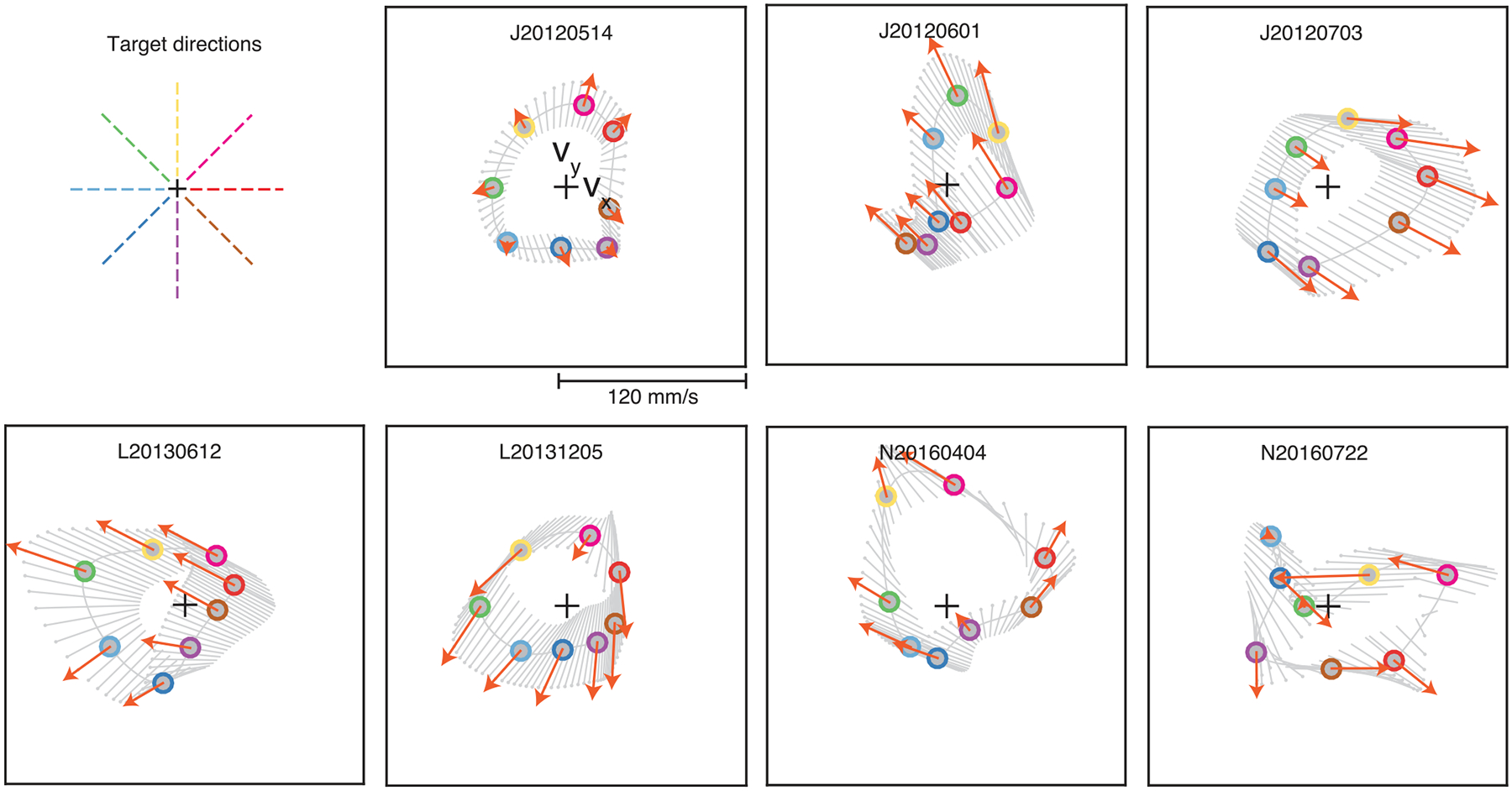
Same conventions as Fig. 3f, for multiple example sessions (all with the same scale). ‘Target directions’ panel is a legend depicting the color corresponding to each target direction.
Extended Data Fig. 8 |. Changes in neural engagement and performance per monkey.
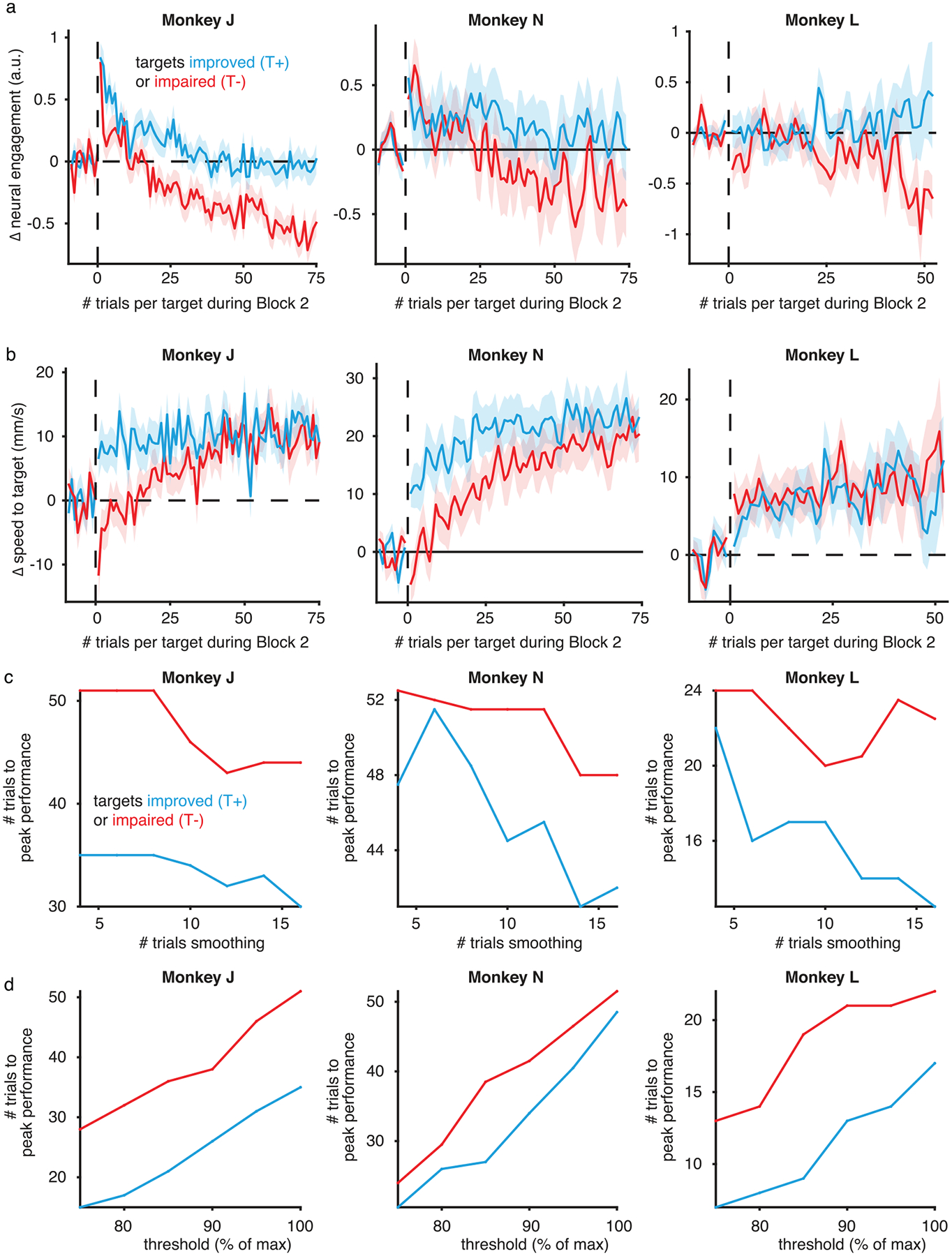
a-b. Changes in neural engagement (a) and performance (b) during Block 2, averaged across T + and T − targets for each monkey separately (J: nT+ = 119, nT− = 81 targets; N: nT+ = 50, nT− = 38; L: nT+ = 51, nT− = 29). Same conventions as Fig. 5c (a) and Fig. 5e (b). c-d. Difference in learning speed between T + and T − targets is robust to amount of smoothing (c) and how the peak performance was determined (d). We found the number of trials at which performance for a given target reached x% of its maximum, after first smoothing the performance for each target with a k-trial boxcar filter (see Methods), where in Fig. 5f, k = 8 and x = 100. Here we sweep the amount of smoothing (k; panel c) while holding x = 100 constant, and sweep the threshold percentage (x; panel d) while holding k = 8 constant. Across all monkeys, the blue line was always below the red line, indicating that our result that T + targets reached peak performance more quickly than T − targets was robust to different parameter settings.
Extended Data Fig. 9 |. Non-uniform task performance did not predict how quickly different targets reached peak performance.
a-b. In BCI tasks, performance across targets is often non-uniform. Can differences in the animal’s pre-learning performance across targets predict how quickly different targets were learned? We defined pre-learning performance in two ways: using the performance under the intuitive BCI mapping during Block 1 (panel a), and using the predicted initial performance under the new BCI mapping (panel b). For the latter quantity, we projected the trial-averaged neural activity for each target during Block 1 onto the new BCI mapping. For each definition of pre-learning performance, we divided all targets from each monkey into two groups based on whether pre-learning performance was above (green, ‘easier’) or below (gray, ‘harder’) the median performance level across all targets. We then found the number of trials needed for each group of targets to reach peak performance during Block 2, similar to Fig. 5f. The median number of trials needed to reach peak performance was not different for targets that were initially harder (gray triangle) versus easier (green triangle) during Block1 using the intuitive BCI mapping (p = 0.91, two-sided Wilcoxon rank-sum test, n1 = 184 and n2 = 184 targets; panel a). Nor was there a difference in the median number of trials needed to reach peak performance for the targets that were predicted to be initially harder (gray triangle) versus easier (green triangle) under the new BCI mapping (p = 0.06, two-sided Wilcoxon rank-sum test, n1 = 184 and n2 = 184 targets; panel b).
Extended Data Fig. 10 |. Neural engagement axes were largely unchanged after learning.
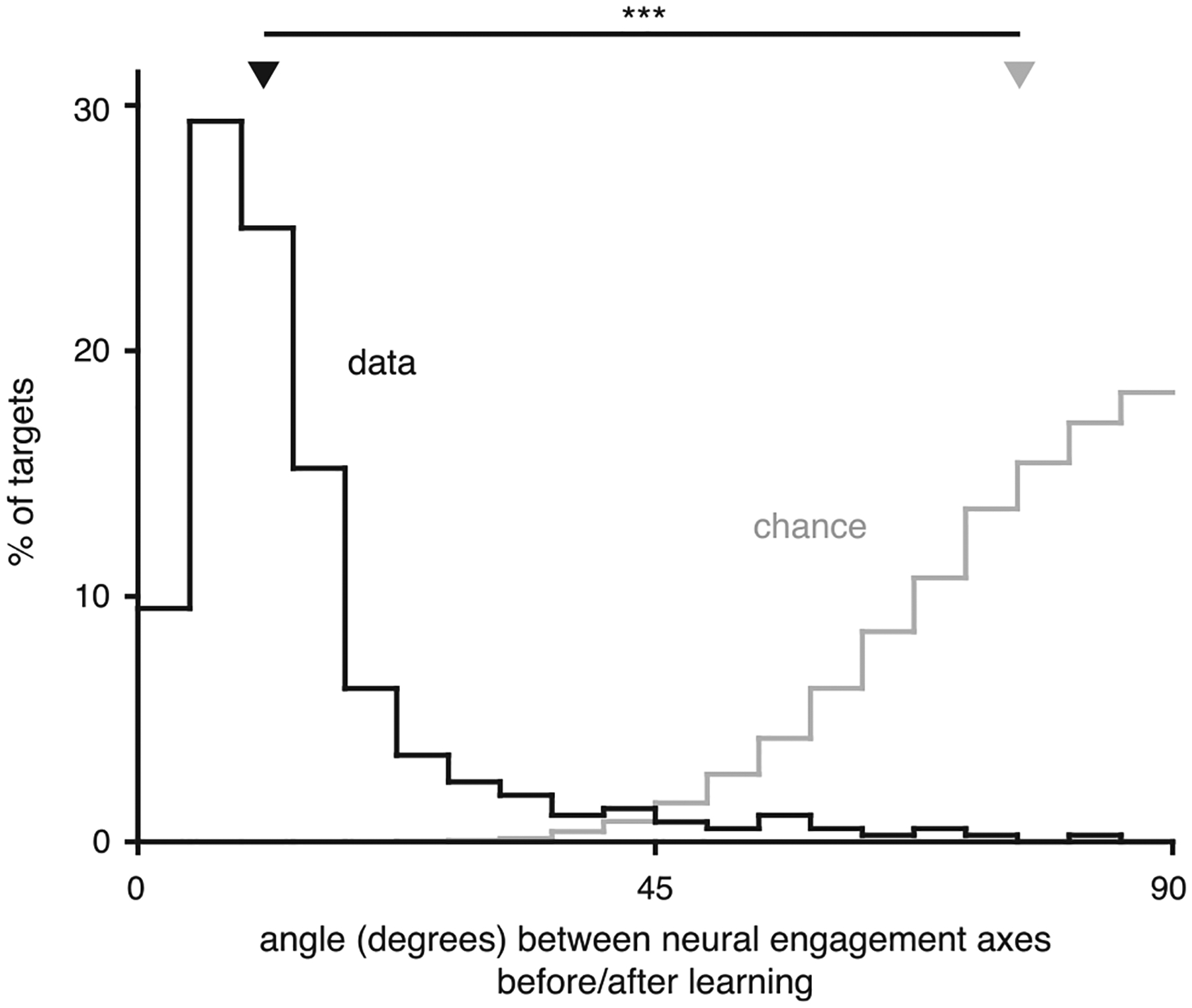
Distribution of the angle (‘data’, in black) between the neural engagement axis identified for each target during Block 1 (‘before learning’) vs. during the last 50 trials of Block 2 (‘after learning’). To identify neural engagement axes during the last 50 trials of Block 2, we used the same procedure as used during Block 1 (that is, the procedure used in the main text; see Methods), but applied to the last 50 trials of Block 2. ‘Chance’ (in gray) indicates the distribution of the angle between random directions in ten-dimensional space. Triangles depict the medians of the ‘data’ and ‘chance’ distributions, which were significantly different (p < 10−10, two-sided Wilcoxon rank-sum test, n1 = 368 (data) and n2 = 50, 000 (chance) axes).
Supplementary Material
Acknowledgements
The authors thank J. Graves, B. Cowley, M. Smith and E. Yttri for helpful discussions. This work was supported by the Richard King Mellon Presidential Fellowship (to J.A.H.), the Carnegie Prize Fellowship in Mind and Brain Sciences (to J.A.H.), NIH R01 HD071686 (to A.P.B., B.M.Y. and S.M.C.), NSF NCS BCS1533672 (to S.M.C., B.M.Y. and A.P.B.), NSF CAREER award IOS1553252 (to S.M.C.), NIH CRCNS R01 NS105318 (to B.M.Y. and A.P.B.), NSF NCS BCS1734916 (to B.M.Y.), NIH CRCNS R01 MH118929 (to B.M.Y.), NIH R01 EB026953 (to B.M.Y.) and Simons Foundation 543065 (to B.M.Y.).
Footnotes
Online content
Any methods, additional references, Nature Research reporting summaries, source data, extended data, supplementary information, acknowledgements, peer review information; details of author contributions and competing interests; and statements of data and code availability are available at https://doi.org/10.1038/s41593-021-00822-8.
Reporting Summary. Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Code availability
The code used in this study for performing analyses and generating figures can be found at https://github.com/mobeets/neural-engagement/.
Competing interests
The authors declare no competing interests.
Extended data is available for this paper at https://doi.org/10.1038/s41593-021-00822-8.
Supplementary information The online version contains supplementary material available at https://doi.org/10.1038/s41593-021-00822-8.
Data availability
The data that support the findings of this study are available from the authors upon reasonable request.
References
- 1.Aston-Jones G & Cohen JD An integrative theory of locus coeruleus–norepinephrine function: adaptive gain and optimal performance. Annu. Rev. Neurosci 28, 403–450 (2005). [DOI] [PubMed] [Google Scholar]
- 2.McGinley MJ et al. Waking state: rapid variations modulate neural and behavioral responses. Neuron 87, 1143–1161 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Allen WE et al. Thirst regulates motivated behavior through modulation of brain-wide neural population dynamics. Science 364, 253–253 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Stringer C et al. Spontaneous behaviors drive multidimensional, brain-wide activity. Science 364, 255 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Steinmetz NA, Zatka-Haas P, Carandini M & Harris KD Distributed coding of choice, action and engagement across the mouse brain. Nature 576, 266–273 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Mitchell JF, Sundberg KA & Reynolds JH Spatial attention decorrelates intrinsic activity fluctuations in macaque area V4. Neuron 63, 879–888 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Cohen MR & Maunsell JH Attention improves performance primarily by reducing interneuronal correlations. Nat. Neurosci 12, 1594 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Vinck M, Batista-Brito R, Knoblich U & Cardin JA Arousal and locomotion make distinct contributions to cortical activity patterns and visual encoding. Neuron 86, 740–754 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Averbeck BB, Latham PE & Pouget A Neural correlations, population coding and computation. Nat. Rev. Neurosci 7, 358–366 (2006). [DOI] [PubMed] [Google Scholar]
- 10.Moreno-Bote R et al. Information-limiting correlations. Nat. Neurosci 17, 1410–1417 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ruff DA & Cohen MR Simultaneous multi-area recordings suggest that attention improves performance by reshaping stimulus representations. Nat. Neurosci 22, 1669–1676 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Cowley BR et al. Slow drift of neural activity as a signature of impulsivity in macaque visual and prefrontal cortex. Neuron 108, 551–567 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Sugrue LP, Corrado GS & Newsome WT Matching behavior and the representation of value in the parietal cortex. science 304, 1782–1787 (2004). [DOI] [PubMed] [Google Scholar]
- 14.Mazzoni P, Hristova A & Krakauer JW Why don’t we move faster? Parkinson’s disease, movement vigor and implicit motivation. J. Neurosci 27, 7105–7116 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Xu-Wilson M, Zee DS & Shadmehr R The intrinsic value of visual information affects saccade velocities. Exp. Brain Res 196, 475–481 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Leathers ML & Olson CR In monkeys making value-based decisions, lip neurons encode cue salience and not action value. Science 338, 132–135 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Li C-SR, Padoa-Schioppa C & Bizzi E Neuronal correlates of motor performance and motor learning in the primary motor cortex of monkeys adapting to an external force field. Neuron 30, 593–607 (2001). [DOI] [PubMed] [Google Scholar]
- 18.Andalman AS & Fee MS A basal ganglia–forebrain circuit in the songbird biases motor output to avoid vocal errors. Proc. Natl Acad. Sci. USA 106, 12518–12523 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ganguly K & Carmena JM Emergence of a stable cortical map for neuroprosthetic control. PLoS Biol 7, e1000153 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Hwang EJ, Bailey PM & Andersen RA Volitional control of neural activity relies on the natural motor repertoire. Curr. Biol 23, 353–361 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Jeanne JM, Sharpee TO & Gentner TQ Associative learning enhances population coding by inverting interneuronal correlation patterns. Neuron 78, 352–363 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Law AJ, Rivlis G & Schieber MH Rapid acquisition of novel interface control by small ensembles of arbitrarily selected primary motor cortex neurons. J. Neurophysiol 112, 1528–1548 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Sadtler PT et al. Neural constraints on learning. Nature 512, 423–426 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Poort J et al. Learning enhances sensory and multiple non-sensory representations in primary visual cortex. Neuron 86, 1478–1490 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Athalye VR, Santos FJ, Carmena JM & Costa RM Evidence for a neural law of effect. Science 359, 1024–1029 (2018). [DOI] [PubMed] [Google Scholar]
- 26.Golub MD et al. Learning by neural reassociation. Nat. Neurosci 21, 1546–1726 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Vyas S et al. Neural population dynamics underlying motor learning transfer. Neuron 97, 1177–1186 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Perich MG, Gallego JA & Miller LE A neural population mechanism for rapid learning. Neuron 100, 964–976 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Oby ER et al. New neural activity patterns emerge with long-term learning. Proc. Natl Acad. Sci. USA 116, 15210–15215 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Arieli A, Sterkin A, Grinvald A & Aertsen A Dynamics of ongoing activity: explanation of the large variability in evoked cortical responses. Science 273, 1868–1871 (1996). [DOI] [PubMed] [Google Scholar]
- 31.Churchland MM et al. Stimulus onset quenches neural variability: a widespread cortical phenomenon. Nat. Neurosci 13, 369–378 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Gu Y et al. Perceptual learning reduces interneuronal correlations in macaque visual cortex. Neuron 71, 750–761 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ecker AS et al. State dependence of noise correlations in macaque primary visual cortex. Neuron 82, 235–248 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Lin I-C, Okun M, Carandini M & Harris KD The nature of shared cortical variability. Neuron 87, 644–656 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Shenoy KV & Carmena JM Combining decoder design and neural adaptation in brain–machine interfaces. Neuron 84, 665–680 (2014). [DOI] [PubMed] [Google Scholar]
- 36.Moxon KA & Foffani G Brain–machine interfaces beyond neuroprosthetics. Neuron 86, 55–67 (2015). [DOI] [PubMed] [Google Scholar]
- 37.Golub MD, Chase SM, Batista AP & Yu BM Brain-computer interfaces for dissecting cognitive processes underlying sensorimotor control. Curr. Opin. Neurobiol 37, 53–58 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Orsborn AL & Pesaran B Parsing learning in networks using brain–machine interfaces. Curr. Opin. Neurobiol 46, 76–83 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Hennig JA et al. Constraints on neural redundancy. Elife 7, e36774 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Kaufman MT, Churchland MM, Ryu SI & Shenoy KV Cortical activity in the null space: permitting preparation without movement. Nat. Neurosci 17, 440–448 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Stavisky SD, Kao JC, Ryu SI & Shenoy KV Motor cortical visuomotor feedback activity is initially isolated from downstream targets in output-null neural state space dimensions. Neuron 95, 195–208 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Shadmehr R & Holcomb HH Neural correlates of motor memory consolidation. Science 277, 821–825 (1997). [DOI] [PubMed] [Google Scholar]
- 43.Schultz W, Dayan P & Montague PR A neural substrate of prediction and reward. Science 275, 1593–1599 (1997). [DOI] [PubMed] [Google Scholar]
- 44.Constantinidis C & Klingberg T The neuroscience of working memory capacity and training. Nat. Rev. Neurosci 17, 438–439 (2016). [DOI] [PubMed] [Google Scholar]
- 45.Kaufman MT et al. The largest response component in the motor cortex reflects movement timing but not movement type. eNeuro 3, ENEURO.0085–16.2016 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Russo AA et al. Motor cortex embeds muscle-like commands in an untangled population response. Neuron 97, 953–966 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Osu R et al. Short- and long-term changes in joint co-contraction associated with motor learning as revealed from surface EMG. J. Neurophysiol 88, 991–1004 (2002). [DOI] [PubMed] [Google Scholar]
- 48.Athalye VR, Ganguly K, Costa RM & Carmena JM Emergence of coordinated neural dynamics underlies neuroprosthetic learning and skillful control. Neuron 93, 955–970 (2017). [DOI] [PubMed] [Google Scholar]
- 49.Rabinowitz NC, Goris RL, Cohen M & Simoncelli EP Attention stabilizes the shared gain of V4 populations. Elife 4, e08998 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Ni AM, Ruff DA, Alberts JJ, Symmonds J & Cohen MR Learning and attention reveal a general relationship between population activity and behavior. Science 359, 463–465 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Santhanam G et al. Factor-analysis methods for higher-performance neural prostheses. J. Neurophysiol 102, 1315–1330 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Harvey CD, Coen P & Tank DW Choice-specific sequences in parietal cortex during a virtual-navigation decision task. Nature 484, 62–68 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Williamson RC et al. Scaling properties of dimensionality reduction for neural populations and network models. PLoS Comput. Biol 12, e1005141 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Huang C et al. Circuit models of low-dimensional shared variability in cortical networks. Neuron 101, 337–348 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Yu BM et al. Gaussian-process factor analysis for low-dimensional single-trial analysis of neural population activity. J. Neurophysiol 102, 614–635 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data that support the findings of this study are available from the authors upon reasonable request.


