Abstract
Here, it is shown that the M3B12 (M = Cu-Au) clusters’ global minima consist of an elongated planar B12 fragment connected by an in-plane linear M3 fragment. This result is striking since this B12 planar structure is not favored in the bare cluster, nor when one or two metals are added. The minimum energy structures were revealed by screening the potential energy surface using genetic algorithms and density functional theory calculations. Chemical bonding analysis shows that the strong electrostatic interactions with the metal compensate for the high energy spent in the M3 and B12 fragment distortion. Furthermore, metals participate in the delocalized π-bonds, which infers an aromatic character to these species.
Keywords: boron clusters, group 11 metals, potential energy surface, DFT computations, chemical bonding, aromaticity
1. Introduction
Boron’s electronic deficiency allows it to assemble into diverse architectures to form systems with unusual electronic properties, making it promising for applications in diverse technologies. For instance, in super hard materials, semiconductors, nanomaterials, and compounds with potential biological applications [1,2,3,4,5,6,7,8,9,10].
However, this structural versatility makes it challenging to establish chemical bonding patterns that facilitate these systems’ structural rationalization. In contrast to its carbon neighbor in the periodic table, there are very limited models for predicting the structures of boron-based molecular systems. Boron hydrides, for instance, are characterized using electron counting-based rules [11,12,13,14,15,16,17,18].
Structures of bare Bn clusters have been thoroughly analyzed in recent years. These studies show that small clusters prefer planar structures up to a maximum size depending on the charge of the system. Cationic, neutral, and anionic clusters prefer planar structures up to 15, 20, and 40 atoms, respectively [19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42]. This demonstrates the significant effect that even one electron has on the structural preference of boron clusters.
In recent years, it has been shown that adding alkali metals to the B12 structure induces fascinating structural changes. For instance, in the LiB12 global minimum (GM) structure, the naked cluster B12 structure remains almost unchanged [43], but LiB12– and NaB12– GMs prefer a conical shape with an inner B4 ring and a higher concavity than the quasi-planar B12 cluster [44]. More noticeable is the D6d-Li2B12 GM, a tubular structure consisting of two stacked B6 rings capped with Li’s along the main axis [43]. Interestingly, the other alkali metals (Na-Cs) do not induce relevant B12 structural changes, highlighting the Li role [44]. An additional Li, in Li3B12, favors a cage-like B12 structure [43]. The isomerization energy decomposition analysis (IEDA) [45] has proven to be an appropriate theoretical method that provides an insightful explanation for these structural preferences; an enhanced stabilizing electrostatic interaction between the Li cations and the 3D-B12 moiety counterbalances the energetic cost of distorting the B12 fragment. A systematic review of metal-doped boron clusters is reported elsewhere [46].
What about the group 11 elements (Cu, Ag, Au)? Since they form compounds with oxidation states of +1, they could transfer one electron to B12, in analogy with the alkali metals. Our group has recently reported the minimum energy structures of CuB12 and CuB12–. In CuB12, Cu is placed capping the B9 ring of the B12-nacked cluster. In the anion, there are significant structural changes, with Cu participating in the electronic delocalization responsible for the doubly aromatic character of this species [47]. In AuB12 and AuB12, Au is bonded to one of the B’s of the B12 peripheral ring without inducing significant changes in the B12 structure [48]. All these results are consistent with the vast structural opportunities feasible by doping boron clusters with different metals [49,50,51,52,53,54,55,56], demanding systematic studies of the structural preferences for different combinations. This becomes a challenge from computational chemistry as the number and kind of atoms conforming to the study system increase since it demands the help of algorithms that facilitate the potential energy surface (PES) exploration [57,58].
Here, we show that doping B12 with three Cu, Ag, or Au atoms favors an elongated planar structure not preferred in the B12 bare cluster. Our study involves the PES exploration, employing genetic algorithms in conjunction with density functional theory (DFT) calculations, of the MnB12 combinations (M = Cu-Au, n = 1–3). Analysis of the chemical bonding and magnetic behavior shows that M3B12 are local and global aromatic species. The structural analogs to the LinB12 global minima (n = 1–3) were also analyzed, showing that for n = 2 and 3, the structural preferences are drastically different. This highlights the importance of appropriate methods to provide reliable information on the energetically preferred structures of metal-doped boron clusters.
2. Results and Discussion
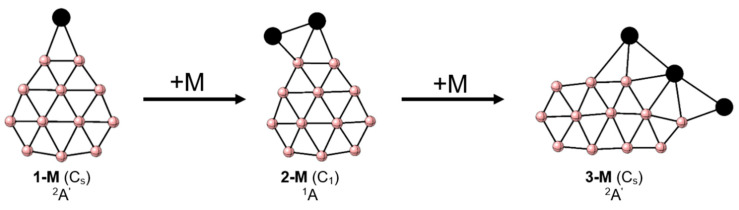
The putative GM structures of MnB12 (M = Cu-Au and n = 1–3) clusters are depicted in Figure 1, and relevant lowest energy isomers are depicted in Figures S1–S9. Figure 1 shows that the B12 structure of the bare cluster is retained at the GM by adding one and two metal atoms. The first metal atom forms a bridged-like B-M-B bond with two boron atoms of the peripheral B9 ring (1-M), while the second one is placed on one of the edges of the MB2 triangle (2-M). Note that in previous reports the effect of doping B12 with other transition metals was evaluated, revealing that metal is placed on the main axis, above the peripheral B9 ring on the concave side of the B12 structure [49,50,51,52,53,54], which in the present work has been identified as an isomer close in energy to the putative global minimum of CuB12 (structure 1b, Figure S1). In the case of AgB12 and AuB12, this structure does not correspond to a local minimum since it has an imaginary frequency, and therefore is not reported. Furthermore, the analogous to the GM structures reported for the ZrB12 and AlB12 combinations [55,56] have relative energies higher than 20.0 kcal mol–1, thus lying above the relative energy range considered in our report. For the MnB12 (M = Cu-Au and n = 1–3) clusters, there are marginal changes in the B-B bond distances due to the addition of metals, more significant in the fragment where the metal is bonded. This agrees with the bond orders according to the WBIB-B values, which are in the range of 0.4–1.3 in both the B12 and the MnB12 clusters (M = Cu-Au, n = 1, 2), where values close to or greater than 1.0 are among the peripheral atoms, as can be seen in Figure S10.
Figure 1.
Lowest energy structures for MnB12 clusters (M = Cu-Au and n = 1–3) at the PBE0-D3/def2-TZVP level. M: black spheres, B: pink spheres.
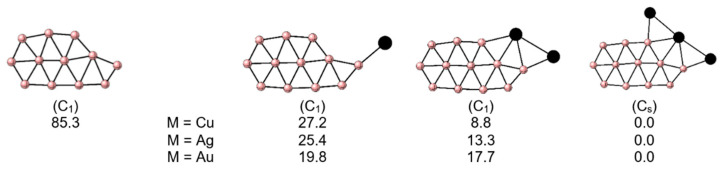
The WBIM-B values are less than 1.0 for the bridged metal and close to 1.0 for the metal bonded to one boron at the periphery, while the WBIM-M value in 2-M is less than 0.1, showing that metals lack a significant covalent bonding character. When one more metal is added, in M3B12, the minimum energy structure has a significantly different B12 fragment than that of the B12 GM. An elongated planar structure is now favored, 3-M (Figure 1). The stabilizing role of M to tend planar elongated structure is significant, as evidenced in Figure 2, which shows how the relative energy of this motif decreases as M atoms are added to become the GM in M3B12. WBIB-B values range from 0.4 to 1.4, with values near or above 1.0 among the outer borons. One of the M atoms closes the elongated ring, while the other two are linked at the periphery in bridged positions with the M-B edges, the three metal atoms forming a linear M3 structure. The WBIM-B values between the extreme M and B are the highest, more significant than 0.5, while the WBIM-B values involving the central M are lower (see Figures S11 and S12). The charges from the natural population analysis (NPA) indicate a charge transfer from the M to the B12 fragment (qM = 0.2–0.7 |e|); however, it does not reach the magnitude of the alkali atoms, where almost one electron per metal atom is transferred (Figures S10–S12). Additionally, the natural electron configurations of the Cu, Ag, and Au atoms in these systems are reported in Table S1. The charge transfer occurs mainly from the 4s and 5s orbitals of Cu and Ag, respectively. While for systems with Au, this transfer, to a lesser extent, occurs from the 5d orbitals.
Figure 2.
Stabilization of the elongated planar B12 fragment as it is doped with M atoms in MnB12 clusters (M = Cu-Au and n = 1–3). Structures were optimized at the PBE0-D3/def2-TZVP level. The relative energies are also reported in kcal mol–1 (regarding GM for each combination). M: black spheres, B: pink spheres.
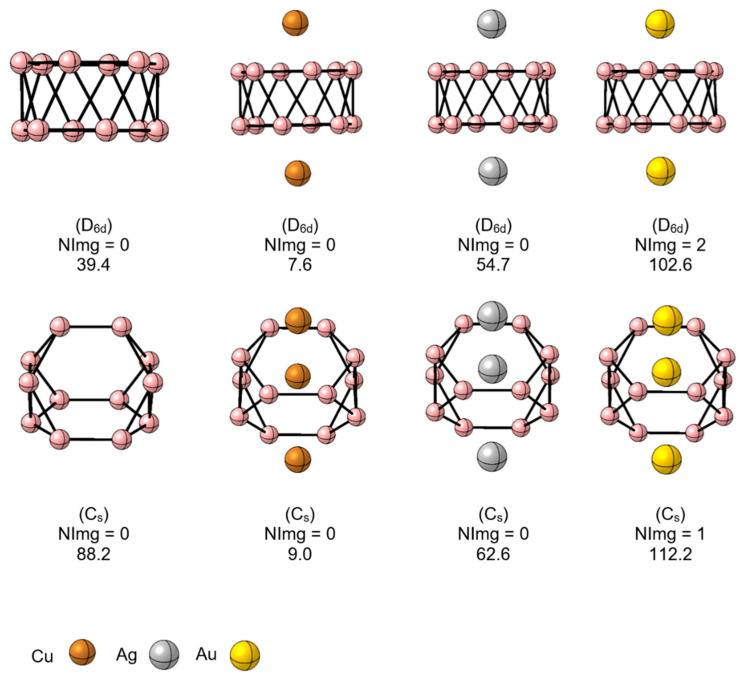
After reviewing the identified structures, we realized that the counterpart structures of the LinB12 (n = 2, 3) GMs were missing. This prompted us to evaluate these geometries, and as shown in Figure 3, the relative energies when Li is replaced by group 11 metals change significantly. This underlines the importance of using suitable algorithms to explore the PES since it is unreliable to use structural knowledge of related systems, which could lead to entirely wrong conclusions. The structural counterparts are local minima, except for Au2B12 and Au3B12, with two and one imaginary frequencies. Remarkably, for M = Ag and Au, the relative energies are at least 50.0 kcal mol–1 above the GM identified by PES exploration.
Figure 3.
Optimized structures for MnB12 (M = Cu-Au and n = 2, 3) in analogous geometries to the global minima of Li2B12 and Li3B12 clusters, and their relative energies (kcal mol–1) concerning the corresponding GMs, at the PBE0-D3/def2-TZVP level.
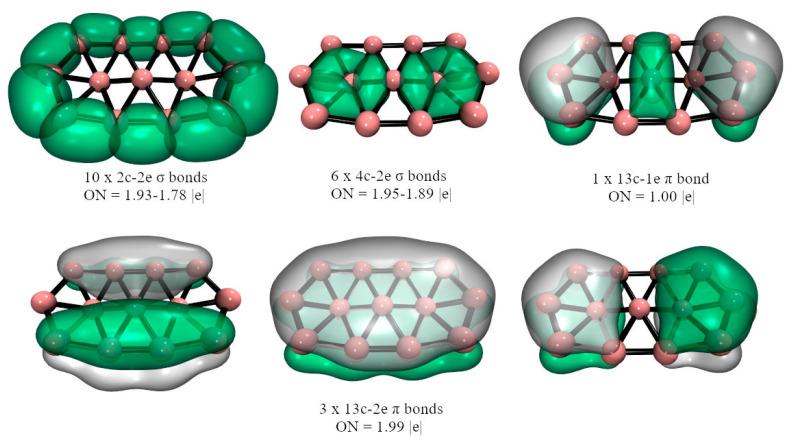
To gain further insights into the chemical bonding, we performed an AdNDP analysis. Orbital localization methods proved insightful in understanding chemical bonding in boron clusters [59,60]. The results of the AdNDP analysis for all systems are reported in Figures S13–S15. In the three systems 1-M, 2-M, and 3-M, five, ten, and fifteen 1c-2e lone pairs are identified, corresponding to the d orbitals of the metals of each system. For 1-M and 2-M, the bonding picture of the B12 fragment remains identical to that of the bare B12 cluster (see Figures S13 and S14). In 1-M, the metal connects to the B12 fragment through a three-center one-electron (3c-1e) B-M-B σ-bond, as shown in Figure S13.
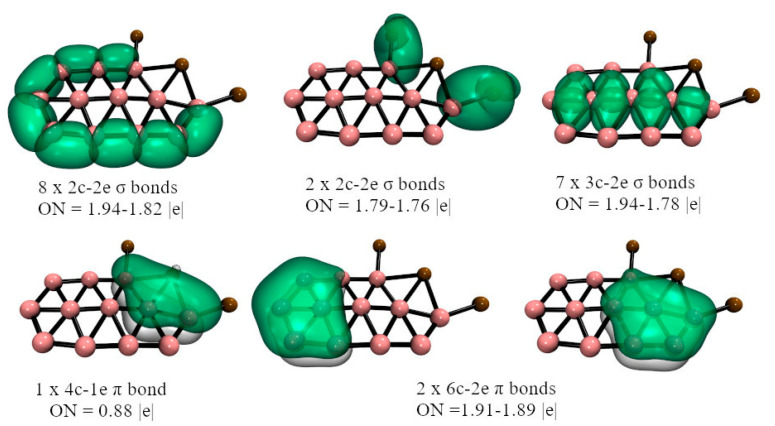
In the case of 2-M, the bonding situation is very similar, only now the second M atom is attached to one of the periphery B’s by one M-B 2c-2e σ-bond. Furthermore, the bridged M is now linked via a B-M-B 3c-2e σ-bond at the cost of delocalization of the periphery B-B bond. The 3-M bonding will be discussed in more detail. For 3-Cu, the localized orbitals, excluding the lone pairs, recovered by AdNDP are reported in Figure 4. The other systems show similar bonding patterns (see the full bonding picture in Figure S15). Eight B-B 2c-2e σ-bonds link the nine periphery borons. Seven 3c-2e σ-bonds are also detected between each triangular fragment that forms the three internal boron with those of the periphery. The M extremes of the M3 fragment are linked to borons by M-B 2c-2e σ-bonds. The central M does not participate in any bonds, according to AdNDP. The remaining electrons, AdNDP locates in three π-orbitals, two of 6c-2e, and one of 4c-1e, for a total of five π-electrons. These results suggest the possibility of (anti)aromaticity, local or global, given both σ- and π-delocalized bonds. We will discuss below this possibility by analyzing the 3-M magnetic behavior.
Figure 4.
Chemical bonding representation according to the AdNDP method of 3-Cu, at the PBE0-D3/Def2-TZVP level. Cu: brown spheres, B: pink spheres.
The shape of the 3-M structure evokes the geometry of an isomer of its valence isoelectronic B13 cluster, which is 3.7 kcal mol–1 above the GM (at the PW91/TZ2P level) [61]. The AdNDP analysis of this system is shown in Figure 5, where it is seen that there are significant differences with 3-M, the B9 contour is closed by 10 B-B 2c-2e σ-bonds, there are six delocalized 4c-2e σ-bonds connecting the internal B3 fragment to the B9 contour, and AdNDP places seven electrons forming π-bonds. These bonding differences, i.e., having 4n delocalized σ-bonds, could be responsible for the non-planarity of B13.
Figure 5.
Chemical bonding representation according to the AdNDP method of B13, at the PBE0-D3/Def2-TZVP level.
The isomerization energy decomposition analysis (IEDA) allows us to analyze quantitatively the structural preference between two isomers in terms of energy components [45]. A hypothetical thermodynamic cycle used to perform the IEDA in the M3B12 systems is shown in Figure S16. Thus, we compare 3-Cu vs. the first Cu3B12 isomer that preserves the B12 fragment of the naked cluster (ΔEiso = 13.0 kcal mol−1); the relative energy is slightly different from that reported in Figure S7 since the IEDA calculations were performed at the PBE0-D3-BJ/ZORA/TZ2P level. The values summarized in Table 1 show that interactions favor GM in the orbital (ΔΔEorb = 115.3 kcal mol–1) contribution, compensating for the electrostatic (ΔΔVelstat = –7.9 kcal mol–1) and Pauli repulsion (ΔΔEPauli = –19.5 kcal mol–1) terms which favor the higher energy isomer; the difference in the dispersion interaction is negligible. These results show that the covalent interactions between M3 and the B12 are enhanced and are more important in terms of magnitude than ionic interactions in the GM, thus accounting for its preference. However, ΔEiso also depends on the distortion energy of each fragment, favoring, in this case, the higher energy isomer (ΔΔEdist (total) = –74.5 kcal mol–1). Note that the major contribution of this term comes from the distortion of the M3 fragment, while the B12 fragment slightly prefers the geometry it has in the GM. Therefore, Cu3B12 prefers the planar elongated shape granted by better orbital interactions between the Cu3 and B12 fragment, compensating for the energy cost to distort its M3 moiety, and to a lesser extent, the unfavorable electrostatic interaction and Pauli repulsion terms. IEDA predicts a similar trend for Ag3B12 with the difference that the Pauli repulsion term, in this case, also favors GM. Finally, for Au3B12, the results are slightly different. The distortion energies follow the same trends and magnitudes as for its lighter analogs, and the orbital interaction remains the most important term; however, the electrostatic interaction, which, as in Cu3B12 and Ag3B12, favors the second isomer, is now comparable in magnitude to the orbital term, so that the balance of all the terms that make up ΔEiso leaves both isomers virtually isoenergetic at the PBE0-D3-BJ/ZORA/TZ2P level. Note that although at the PBE0-D3/def2-TZVP level, the planar elongated system is still predicted to be the global minimum of Au3B12, the difference in energy between it and the highest energy isomer is much smaller (2.1 kcal mol–1) than for Cu3B12 and Ag3B12.
Table 1.
IEDA results (kcal mol–1) at the PBE0-D3-BJ/ZORA/TZ2P level for the M3B12 clusters with M33+ + B123– as fragments.
| System | Cu3B12 | Ag3B12 | Au3B12 |
|---|---|---|---|
| ΔEiso | 13.0 | 9.8 | −0.2 |
| ΔEdist (M33+) | −82.1 | −75.7 | −73.2 |
| ΔEdist (B123−) | 7.6 | 6.7 | 8.2 |
| ΔΔEint | 87.5 | 78.9 | 64.8 |
| ΔΔEorb | 115.3 | 85.2 | 86.8 |
| ΔΔVelstat | −7.9 | −22.5 | −70.6 |
| ΔΔEPauli | −19.9 | 16.4 | 49.0 |
| ΔΔEdisp | 0.0 | −0.2 | −0.4 |
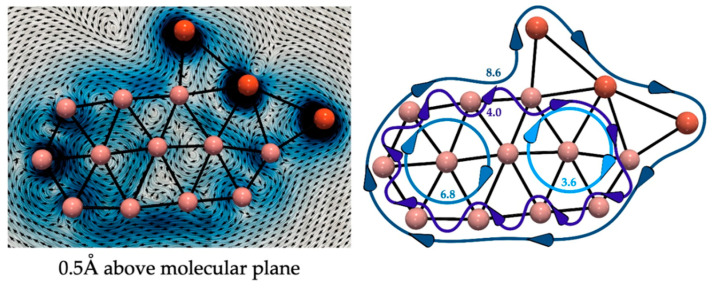
AdNDP analysis reveals the presence of delocalized π-bonds, which could be associated with a possible (anti)aromatic character. To investigate this possibility, we have evaluated the current densities induced by an external magnetic field (perpendicular to the molecular plane). According to the magnetic criteria, an (anti)aromatic system is characterized by the presence of (diatropic) paratropic ring currents circuits. Figure 6 shows that 3-Cu exhibits both local and global diatropic ring currents circuits. The local circuits are internal and around the inner B atoms. At the same time, the global ring current surrounds the cluster decorating the external M3B9 chain. By analyzing the integrated current profiles (Figures S17–S19), it has been possible to estimate the ring current strength (RCS) of each circuit (see Figure 6). RCS values are significant, considering benzene has a net RCS of 11.8 nA T–1 at the same level. The magnetic behavior of 3-Ag and 3-Au are similar, as shown in Figures S17–S19. Therefore, the 3-M are classified as local and global aromatic species according to the magnetic criterion.
Figure 6.
On the left, the magnetically induced current density of Cu3B12 in a plane placed 0.5 A above the molecular plane. Diatropic currents are assumed to circle clockwise, and paratropic ones circle anticlockwise. On the right are the detected currents’ paths and their strength (in nA T–1).
3. Materials and Methods
We systematically explored the potential energy surfaces employing the AUTOMATON program [57,62], with an initial screening (in the singlet states) at the PBE0 [63]/SDDALL [64] level. The low-lying energy isomers (<20.0 kcal mol–1 above the putative global minimum) were re-minimized at the PBE0-D3 [65]/def2-TZVP [66] level. The top isomers were optimized in the triplet state at the PBE0-D3/def2-TZVP level to test the relative energies at this multiplicity. To provide more reliability in our energetic analysis, relative energies were computed using the domain-based local pair-natural orbital-based single-, double-, and perturbative triple excitations coupled cluster DLPNO-CCSD(T) method [67] as implemented in ORCA-4.2.1 [68,69] in conjunction with extrapolation to the complete basis set limit via the def2-SVP and def2-TZVP basis sets [70,71] (labeled as DLPNO-CCSD(T)/CBS). This refinement was performed for isomers up to 10.0 kcal mol–1 above the putative global minimum. The chemical bonding was analyzed (at the PBE0-D3/def2-TZVP level) using the Wiberg bond index (WBI) and natural population analysis (NPA), as implemented in the NBO 6.0 program [72]. Furthermore, the adaptive natural density partitioning (AdNDP) method [73,74] was performed with the Multiwfn program [75]. AdNDP represents the electronic structure in n-center-two-electron (nc-2e) bonds, with n ranging from one to the total number of atoms in the molecule, recovering the Lewis’ electron pair concept as the fundamental chemical bonding component complemented with delocalized bonds, when they are present. Isomerization energy decomposition analysis (IEDA) [45] was computed. IEDA allows the decomposition of the isomerization energy (ΔEiso) in terms of the distortion energy of the fragments (ΔEdist) and the change in the interaction energies between the fragments of each isomer (ΔΔEint). The latter term, in turn, is decomposed as the sum of the changes in the orbital (ΔΔEorb) and electrostatic (ΔΔVelstat) interaction, the Pauli repulsion (ΔΔEPauli), and the dispersion energy (ΔΔEdisp). This analysis was performed at the PBE0-D3-BJ [76]/ZORA [77]/TZ2P [78] level using ADF2012 [79].
To assess aromaticity, we have analyzed the current densities induced by an external magnetic field applied perpendicularly to the molecular plane (at the PBE0-D3/def2-TZVP level) using the GIMIC program [80,81], which employs the gauge-included atomic orbitals (GIAO) method [82]. For vector plots, we used the Paraview 5.10.0 software [83,84]. The ring current strengths (RCS), a quantitative descriptor of aromaticity, were obtained by integrating the ring current flow in a perpendicular plane using the two-dimensional Gauss–Lobatto algorithm [80,85] as implemented in GIMIC. The integration planes correspond to cut-off planes perpendicular to the chosen bonds of the interest annular moiety and extend horizontally for 3.6 Å along the ring’s plane, with 2.6 Å above and below the bond. Positive (diatropic), negative (paratropic), and near-zero RCS values indicate aromaticity, antiaromaticity, and non-aromaticity. The bisected current densities (sigma and pi) were calculated using AIMAll software [86] at the PBE0-D3/def2-TZVP level. As previously established in other studies, the different ring current circuits have been identified by analyzing the RCS profiles in appropriate planes [87,88].
4. Conclusions
The effect of doping the B12 cluster with group 11 metals, in M3B12 (M = Cu-Au) clusters is evaluated to compare with the impact of alkali metals, especially Li, where the minimum energy structures of Li2B12 and Li3B12 consist of B12 arrays quite different from those of the bare B12 cluster. Exploration of the potential energy surface, using genetic algorithms and DFT calculations, reveals that adding one or two metal atoms induces substantial changes in the B12 fragment, with minor modifications in bond distances, especially of the fragments in contact with the metals. However, when the third M atom is added, in M3B12, a structure containing a planar elongated B12 fragment (3-M), whose shape is high-energy in the bare cluster, is favored. This is evidence of the wealth of structural possibilities by doping boron clusters with metals, where the nature of the metal may have unexpected effects. The latter also evidences the need for adequate methods to identify minimum energy structures since no structural preferences can be assumed based on similar systems. For example, the GM analogous structures of Li2B12 are less stable by at least 7 kcal mol–1, while the Li3B12 analogs are not even all local minima and are more than 50 kcal mol–1 away from the most stable one. Bonding analysis evidences the presence of delocalized σ- and π-bonds in 3-M. Furthermore, magnetically induced current density analysis evidences the existence of local and global diatropic ring currents, characterizing them as aromatic.
Acknowledgments
We thank the financial support of the National Agency for Research and Development (ANID) through FONDECYT projects 1211128 (W.T.) 1221019 (A. V-E.). National Agency for Research and Development (ANID)/Scholarship Program/BECAS DOCTORADO NACIONAL/2019-21190427 (D.I.). National Agency for Research and Development (ANID)/Scholarship Program/BECAS DOCTORADO NACIONAL/2020-21201177 (L.L-P.). Scholarship Program/BECAS DOCTORADO UNAB (J.S.-E). Powered@NLHPC: This research was partially supported by the supercomputing infrastructure of the NLHPC (ECM-02).
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/molecules28010236/s1, Figures S1–S9: Global minimum and low-lying isomers of MnB12 (M = Cu-Au; n = 1–3), their point group symmetries and spectroscopic states. Relative energies are shown in kcal·mol–1 at PBE0-D3/def2-TZVP (in bold) level including zero-point energy (ZPE) corrections and DLPNO-CCSD(T)/CBS (red parenthesis). A number-letter label identifies structure to facilitate their connection with their Cartesian coordinates (at the end of the ESI); Figures S10–S12: Bond lengths (r, Å), natural charges (q, |e|), and Wiberg bond indices (WBI) of the MnB12 (M = Cu-Au; n = 1–3) GMs at the PBE0-D3/def2-TZVP level; Figures S13–S15: The AdNDP bonding pattern of the MnB12 (M = Cu-Au; n = 1–3) GMs at the PBE0-D3/def2-TZVP level; Figure S16: Energy cycle for the isomerization between the GM (top) and the higher energy isomer (bottom) of M3B12 (M = Cu, Ag, Au) used in IEDA computations; Figures S17–S19: The susceptibility of density current for M3B12 (M = Cu-Au) in a plane 0.5 Å above the molecular plane (vector plot). The scheme for identifying different ring current circuits through a computed profile of the ring current strength (RCS) passing selected planes. The RCS profiles and the identified ring current circuits with their respective RCS value in nA.T–1; Table S1: Computed natural electron configurations of the Cu, Ag and Au atoms in the putative global minima of MB12, M2B12 and M3B12 systems; Cartesian Coordinates of isomers of the MnB12 (M = Cu, Ag, Au) (n = 1–3) clusters at the PBE0-D3/def2-TZVP level.
Author Contributions
Conceptualization, W.T., J.S.-E. and W.O.; methodology, J.S.-E., L.L.-P., A.V.-E., W.O., M.L.V. and O.Y.; software, D.I., O.Y. and W.O.; validation, W.T., J.S.-E., M.L.V., W.O. and A.V.-E.; formal analysis, W.T. and A.V.-E.; investigation, W.T., W.O. and O.Y.; resources, W.T. and M.L.V.; data curation, J.S.-E., L.L.-P., D.I. and O.Y.; writing—original draft preparation, W.T., J.S.-E. and A.V.-E.; writing—review and editing, all authors; visualization, J.S.-E., D.I. and O.Y.; supervision, W.T. and W.O.; project administration, W.T.; funding acquisition, W.T. and M.L.V. All authors have read and agreed to the published version of the manuscript.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Sample Availability
Not applicable.
Funding Statement
This research was funded by FONDECYT grants number 1211128 and 1221019.
Footnotes
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
References
- 1.Akopov G., Yeung M.T., Kaner R.B. Rediscovering the Crystal Chemistry of Borides. Adv. Mater. 2017;29:1604506. doi: 10.1002/adma.201604506. [DOI] [PubMed] [Google Scholar]
- 2.Scheifers J.P., Zhang Y., Fokwa B.P.T. Boron: Enabling Exciting Metal-Rich Structures and Magnetic Properties. Acc. Chem. Res. 2017;50:2317–2325. doi: 10.1021/acs.accounts.7b00268. [DOI] [PubMed] [Google Scholar]
- 3.An Q., Goddard W.A. Improved Ductility of B12 Icosahedra-Based Superhard Materials through Icosahedral Slip. J. Phys. Chem. C. 2017;121:11831–11838. doi: 10.1021/acs.jpcc.7b01761. [DOI] [Google Scholar]
- 4.Robinson P.J., Liu G., Ciborowski S., Martinez-Martinez C., Chamorro J.R., Zhang X., McQueen T.M., Bowen K.H., Alexandrova A.N. Mystery of Three Borides: Differential Metal-Boron Bonding Governing Superhard Structures. Chem. Mater. 2017;29:9892–9896. doi: 10.1021/acs.chemmater.7b04378. [DOI] [Google Scholar]
- 5.Chen W., Li Y., Yu G., Li C.Z., Zhang S.B., Zhou Z., Chen Z. Hydrogenation: A Simple Approach to Realize Semiconductor-Half-Metal-Metal Transition in Boron Nitride Nanoribbons. J. Am. Chem. Soc. 2010;132:1699–1705. doi: 10.1021/ja908475v. [DOI] [PubMed] [Google Scholar]
- 6.Dai X., Zhang L., Li J., Li H. Metal-Semiconductor Transition of Single-Wall Armchair Boron Nanotubes Induced by Atomic Depression. J. Phys. Chem. C. 2017;121:26096–26101. doi: 10.1021/acs.jpcc.7b08309. [DOI] [Google Scholar]
- 7.Bud’ko S.L., Lapertot G., Petrovic C., Cunningham C.E., Anderson N., Canfield P.C. Boron Isotope Effect in Superconducting MgB2. Phys. Rev. Lett. 2001;86:1877–1880. doi: 10.1103/PhysRevLett.86.1877. [DOI] [PubMed] [Google Scholar]
- 8.Kazakov S.M., Puzniak R., Rogacki K., Mironov A.V., Zhigadlo N.D., Jun J., Soltmann C., Batlogg B., Karpinski J. Carbon Substitution in MgB2 Single Crystals: Structural and Superconducting Properties. Phys. Rev. B Condens. Matter. Mater. Phys. 2005;71:024533. doi: 10.1103/PhysRevB.71.024533. [DOI] [Google Scholar]
- 9.Nakamura H. Development of High Boron Content Liposomes and Their Promising Antitumor Effect for Neutron Capture Therapy. Yakugaku Zasshi. 2013;133:1297–1306. doi: 10.1248/yakushi.13-00222-5. [DOI] [PubMed] [Google Scholar]
- 10.Leśnikowski Z.J. Challenges and Opportunities for the Application of Boron Clusters in Drug Design. J. Med. Chem. 2016;59:7738–7758. doi: 10.1021/acs.jmedchem.5b01932. [DOI] [PubMed] [Google Scholar]
- 11.Ohishi Y., Kimura K., Yamaguchi M., Uchida N., Kanayama T. Formation of Hydrogenated Boron Clusters in an External Quadrupole Static Attraction Ion Trap. J. Chem. Phys. 2008;128:124304. doi: 10.1063/1.2894864. [DOI] [PubMed] [Google Scholar]
- 12.Szwacki N.G., Weber V., Tymczak C.J. Aromatic Borozene. Nanoscale Res. Lett. 2009;4:1085–1089. doi: 10.1007/s11671-009-9362-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Sahu S., Shukla A. Probing Aromaticity of Borozene through Optical and Dielectric Response: A Theoretical Study. Nanoscale Res. Lett. 2010;5:714–719. doi: 10.1007/s11671-010-9536-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Forte G., La Magna A., Deretzis I., Pucci R. Ab Initio Prediction of Boron Compounds Arising from Borozene: Structural and Electronic Properties. Nanoscale Res. Lett. 2010;5:158–163. doi: 10.1007/s11671-009-9458-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bai H., Li S.D. Hydrogenation of B120/−: A Planar-to-Icosahedral Structural Transition in B12Hn0/− (n = 1–6) Boron Hydride Clusters. J. Clust. Sci. 2011;22:525–535. doi: 10.1007/s10876-011-0408-0. [DOI] [Google Scholar]
- 16.Ohishi Y., Kimura K., Yamaguchi M., Uchida N., Kanayama T. Hydrogen Detachment from B12Hn+ Clusters by Kinetic Energy. Trans. Mater. Res. Soc. Jpn. 2010;35:533–536. doi: 10.14723/tmrsj.35.533. [DOI] [Google Scholar]
- 17.Ohishi Y., Kimura K., Yamaguchi M., Uchida N., Kanayama T. Synthesis and Formation Mechanism of Hydrogenated Boron Clusters B12Hn with Controlled Hydrogen Content. J. Chem. Phys. 2010;133:074305. doi: 10.1063/1.3474996. [DOI] [PubMed] [Google Scholar]
- 18.Gonzalez Szwacki N., Tymczak C.J. B12H n and B12F N: Planar vs. Icosahedral Structures. Nanoscale Res. Lett. 2012;7:236. doi: 10.1186/1556-276X-7-236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Zhai H.J., Wang L.S., Alexandrova A.N., Boldyrev A.I., Zakrzewski V.G. Photoelectron Spectroscopy and Ab Initio Study of B3− and B4− Anions and Their Neutrals. J. Phys. Chem. A. 2003;107:9319–9328. doi: 10.1021/jp0357119. [DOI] [Google Scholar]
- 20.Alexandrova A.N., Boldyrev A.I., Zhai H.J., Wang L.S., Steiner E., Fowler P.W. Structure and Bonding in B6− and B6: Planarity and Antiaromaticity. J. Phys. Chem. A. 2003;107:1359–1369. doi: 10.1021/jp0268866. [DOI] [Google Scholar]
- 21.Alexandrova A.N., Boldyrev A.I., Zhai H.J., Wang L.S. Electronic Structure, Isomerism, and Chemical Bonding in B7− and B7. J. Phys. Chem. A. 2004;108:3509–3517. doi: 10.1021/jp037341u. [DOI] [Google Scholar]
- 22.Pan L.L., Li J., Wang L.S. Low-Lying Isomers of the B9− Boron Cluster: The Planar Molecular Wheel versus Three-Dimensional Structures. J. Chem. Phys. 2008;129:024302. doi: 10.1063/1.2948405. [DOI] [PubMed] [Google Scholar]
- 23.Martínez-Guajardo G., Sergeeva A.P., Boldyrev A.I., Heine T., Ugalde J.M., Merino G. Unravelling Phenomenon of Internal Rotation in B13+ through Chemical Bonding Analysis. Chem. Comm. 2011;47:6242–6244. doi: 10.1039/c1cc10821b. [DOI] [PubMed] [Google Scholar]
- 24.Sergeeva A.P., Zubarev D.Y., Zhai H.J., Boldyrev A.I., Wang L.S. A Photoelectron Spectroscopic and Theoretical Study of B16 and B162−: An All-Boron Naphthalene. J. Am. Chem. Soc. 2008;130:7244–7246. doi: 10.1021/ja802494z. [DOI] [PubMed] [Google Scholar]
- 25.Sergeeva A.P., Averkiev B.B., Zhai H.J., Boldyrev A.I., Wang L.S. All-Boron Analogues of Aromatic Hydrocarbons: B17− and B18−. J. Chem. Phys. 2011;134:224304. doi: 10.1063/1.3599452. [DOI] [PubMed] [Google Scholar]
- 26.Huang W., Sergeeva A.P., Zhai H.J., Averkiev B.B., Wang L.S., Boldyrev A.I. A Concentric Planar Doubly π-Aromatic B19 Cluster. Nat. Chem. 2010;2:202–206. doi: 10.1038/nchem.534. [DOI] [PubMed] [Google Scholar]
- 27.Kiran B., Bulusu S., Zhai H.J., Yoo S., Zeng X.C., Wang L.S. Planar-to-Tubular Structural Transition in Boron Clusters: B20 as the Embryo of Single-Walled Boron Nanotubes. Proc. Natl. Acad. Sci. USA. 2005;102:961–964. doi: 10.1073/pnas.0408132102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Piazza Z.A., Li W.L., Romanescu C., Sergeeva A.P., Wang L.S., Boldyrev A.I. A Photoelectron Spectroscopy and Ab Initio Study of B21−: Negatively Charged Boron Clusters Continue to Be Planar at 21. J. Chem. Phys. 2012;136:104310. doi: 10.1063/1.3692967. [DOI] [PubMed] [Google Scholar]
- 29.Sergeeva A.P., Piazza Z.A., Romanescu C., Li W.L., Boldyrev A.I., Wang L.S. B22− and B23−: All-Boron Analogues of Anthracene and Phenanthrene. J. Am. Chem. Soc. 2012;134:18065–18073. doi: 10.1021/ja307605t. [DOI] [PubMed] [Google Scholar]
- 30.Popov I.A., Piazza Z.A., Li W.L., Wang L.S., Boldyrev A.I. A Combined Photoelectron Spectroscopy and Ab Initio Study of the Quasi-Planar B24− Cluster. J. Chem. Phys. 2013;139:144307. doi: 10.1063/1.4824156. [DOI] [PubMed] [Google Scholar]
- 31.Piazza Z.A., Popov I.A., Li W.L., Pal R., Cheng Zeng X., Boldyrev A.I., Wang L.S. A Photoelectron Spectroscopy and Ab Initio Study of the Structures and Chemical Bonding of the B25− Cluster. J. Chem. Phys. 2014;141:034303. doi: 10.1063/1.4879551. [DOI] [PubMed] [Google Scholar]
- 32.Luo X.M., Jian T., Cheng L.J., Li W.L., Chen Q., Li R., Zhai H.J., Li S.D., Boldyrev A.I., Li J., et al. B26−: The Smallest Planar Boron Cluster with a Hexagonal Vacancy and a Complicated Potential Landscape. Chem. Phys. Lett. 2017;683:336–341. doi: 10.1016/j.cplett.2016.12.051. [DOI] [Google Scholar]
- 33.Li W.L., Pal R., Piazza Z.A., Zeng X.C., Wang L.S. B27−: Appearance of the Smallest Planar Boron Cluster Containing a Hexagonal Vacancy. J. Chem. Phys. 2015;142:204305. doi: 10.1063/1.4921732. [DOI] [PubMed] [Google Scholar]
- 34.Li H.R., Jian T., Li W.L., Miao C.Q., Wang Y.J., Chen Q., Luo X.M., Wang K., Zhai H.J., Li S.D., et al. Competition between Quasi-Planar and Cage-like Structures in the B29− Cluster: Photoelectron Spectroscopy and: Ab Initio Calculations. Phys. Chem. Chem. Phys. 2016;18:29147–29155. doi: 10.1039/C6CP05420J. [DOI] [PubMed] [Google Scholar]
- 35.Wang Y.J., Zhao Y.F., Li W.L., Jian T., Chen Q., You X.R., Ou T., Zhao X.Y., Zhai H.J., Li S.D., et al. Observation and Characterization of the Smallest Borospherene, B28− and B28. J. Chem. Phys. 2016;144:064307. doi: 10.1063/1.4941380. [DOI] [PubMed] [Google Scholar]
- 36.Li W.L., Zhao Y.F., Hu H.S., Li J., Wang L.S. [B30]−: A Quasiplanar Chiral Boron Cluster. Angew. Chem. Int. Ed. 2014;53:5540–5545. doi: 10.1002/anie.201402488. [DOI] [PubMed] [Google Scholar]
- 37.Chen Q., Li W.L., Zhao X.Y., Li H.R., Feng L.Y., Zhai H.J., Li S.D., Wang L.S. B33− and B34−: Aromatic Planar Boron Clusters with a Hexagonal Vacancy. Eur. J. Inorg. Chem. 2017;2017:4546–4551. doi: 10.1002/ejic.201700573. [DOI] [Google Scholar]
- 38.Li W.L., Chen Q., Tian W.J., Bai H., Zhao Y.F., Hu H.S., Li J., Zhai H.J., Li S.D., Wang L.S. The B35 Cluster with a Double-Hexagonal Vacancy: A New and More Flexible Structural Motif for Borophene. J. Am. Chem. Soc. 2014;136:12257–12260. doi: 10.1021/ja507235s. [DOI] [PubMed] [Google Scholar]
- 39.Piazza Z.A., Hu H.S., Li W.L., Zhao Y.F., Li J., Wang L.S. Planar Hexagonal B36 as a Potential Basis for Extended Single-Atom Layer Boron Sheets. Nat. Commun. 2014;5:3113. doi: 10.1038/ncomms4113. [DOI] [PubMed] [Google Scholar]
- 40.Chen Q., Tian W.J., Feng L.Y., Lu H.G., Mu Y.W., Zhai H.J., Li S.D., Wang L.S. Planar B38− and B37− Clusters with a Double-Hexagonal Vacancy: Molecular Motifs for Borophenes. Nanoscale. 2017;9:4550–4557. doi: 10.1039/C7NR00641A. [DOI] [PubMed] [Google Scholar]
- 41.Oger E., Crawford N.R.M., Kelting R., Weis P., Kappes M.M., Ahlrichs R. Boron Cluster Cations: Transition from Planar to Cylindrical Structures. Angew. Chem. Int. Ed. 2007;46:8503–8506. doi: 10.1002/anie.200701915. [DOI] [PubMed] [Google Scholar]
- 42.Tai T.B., Tam N.M., Nguyen M.T. The Boron Conundrum: The Case of Cationic Clusters Bn+ with n = 2–20. Theor Chem Acc. 2012;131:1241. doi: 10.1007/s00214-012-1241-8. [DOI] [Google Scholar]
- 43.Dong X., Jalife S., Vásquez-Espinal A., Ravell E., Pan S., Cabellos J.L., Liang W.Y., Cui Z.H., Merino G. Li2B12 and Li3B12: Prediction of the Smallest Tubular and Cage-like Boron Structures. Angew. Chem. Int. Ed. 2018;57:4627–4631. doi: 10.1002/anie.201800976. [DOI] [PubMed] [Google Scholar]
- 44.Hernández-Juárez G., Ravell E., Arcudia J., Zarate X., Cui Z., Merino G., Barroso J. Structural Effects of Alkali-Metals on the B12 Skeleton. Phys. Chem. Chem. Phys. 2020;22:17344–17350. doi: 10.1039/D0CP02750B. [DOI] [PubMed] [Google Scholar]
- 45.Contreras M., Osorio E., Ferraro F., Puga G., Donald K.J., Harrison J.G., Merino G., Tiznado W. Isomerization Energy Decomposition Analysis for Highly Ionic Systems: Case Study of Starlike E5Li7+ Clusters. Chem. Eur. J. 2013;19:2305–2310. doi: 10.1002/chem.201203329. [DOI] [PubMed] [Google Scholar]
- 46.Barroso J., Pan S., Merino G. Structural Transformations in Boron Clusters Induced by Metal Doping. Chem. Soc. Rev. 2022;51:1098–1123. doi: 10.1039/D1CS00747E. [DOI] [PubMed] [Google Scholar]
- 47.Solar-Encinas J., Leyva-Parra L., Yáñez O., Inostroza D., Barrios-Llacuachaqui J.R., Vásquez-Espinal A., Orellana W., Tiznado W. Bowl-Shaped CuB12− Cluster. A Viable Global Minimum with Twofold Aromaticity. ChemPhysChem. 2022;23:e202200366. doi: 10.1002/cphc.202200366. [DOI] [PubMed] [Google Scholar]
- 48.Bai H., Zhai H.-J., Li S.-D., Wang L.-S. Photoelectron Spectroscopy of Aromatic Compound Clusters of the B12 All-Boron Benzene: B12Au− and B12(BO)−. Phys. Chem. Chem. Phys. 2013;15:9646–9653. doi: 10.1039/c3cp50167a. [DOI] [PubMed] [Google Scholar]
- 49.Liu L., Moreno D., Osorio E., Castro A.C., Pan S., Chattaraj P.K., Heine T., Merino G. Structure and Bonding of IrB12−: Converting a Rigid Boron B12 Platelet to a Wankel Motor. RSC Adv. 2016;6:27177–27182. doi: 10.1039/C6RA02992B. [DOI] [Google Scholar]
- 50.Shao X., Qu X., Liu S., Yang L., Yang J., Liu X., Zhong X., Sun S., Vaitheeswaran G., Lv J. Structure Evolution of Chromium-Doped Boron Clusters: Toward the Formation of Endohedral Boron Cages. RSC Adv. 2019;9:2870–2876. doi: 10.1039/C8RA09143A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Li S.X., Zhang Z.P., Long Z.W., Chen D.L. Structures, Electronic, and Spectral Properties of Doped Boron Clusters MB120/− (M = Li, Na, and K) ACS Omega. 2020;5:20525–20534. doi: 10.1021/acsomega.0c02693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Popov I.A., Li W.L., Piazza Z.A., Boldyrev A.I., Wang L.S. Complexes between Planar Boron Clusters and Transition Metals: A Photoelectron Spectroscopy and Ab Initio Study of CoB12− and RhB12−. J. Phys. Chem. A. 2014;118:8098–8105. doi: 10.1021/jp411867q. [DOI] [PubMed] [Google Scholar]
- 53.Xiang Z., Luo Z., Bi J., Jin S., Zhang Z., Lu C. Structural Evolution and Relative Stability of Vanadium-Doped Boron Clusters. J. Phys. Condens. Matter. 2022;34:445302. doi: 10.1088/1361-648X/ac8b4f. [DOI] [PubMed] [Google Scholar]
- 54.le Chen B., Sun W.G., Kuang X.Y., Lu C., Xia X.X., Shi H.X., Maroulis G. Structural Stability and Evolution of Medium-Sized Tantalum-Doped Boron Clusters: A Half-Sandwich-Structured TaB12− Cluster. Inorg. Chem. 2018;57:343–350. doi: 10.1021/acs.inorgchem.7b02585. [DOI] [PubMed] [Google Scholar]
- 55.Sun W., Xia X., Lu C., Kuang X., Hermann A. Probing the Structural and Electronic Properties of Zirconium Doped Boron Clusters: Zr Distorted B12 Ligand Framework. Phys. Chem. Chem. Phys. 2018;20:23740–23746. doi: 10.1039/C8CP03384F. [DOI] [PubMed] [Google Scholar]
- 56.Jin S., Chen B., Kuang X., Lu C., Sun W., Xia X., Gutsev G.L. Structural and Electronic Properties of Medium-Sized Aluminum-Doped Boron Clusters AlBn and Their Anions. J. Phys. Chem. C. 2019;123:6276–6283. doi: 10.1021/acs.jpcc.9b00291. [DOI] [Google Scholar]
- 57.Yañez O., Inostroza D., Usuga-Acevedo B., Vásquez-Espinal A., Pino-Rios R., Tabilo-Sepulveda M., Garza J., Barroso J., Merino G., Tiznado W. Evaluation of Restricted Probabilistic Cellular Automata on the Exploration of the Potential Energy Surface of Be6B11−. Theor. Chem. Acc. 2020;139:41. doi: 10.1007/s00214-020-2548-5. [DOI] [Google Scholar]
- 58.Thimmakondu V.S., Sinjari A., Inostroza D., Vairaprakash P., Thirumoorthy K., Roy S., Anoop A., Tiznado W. Why an Integrated Approach between Search Algorithms and Chemical Intuition Is Necessary? Phys. Chem. Chem. Phys. 2022;24:11680–11686. doi: 10.1039/D2CP00315E. [DOI] [PubMed] [Google Scholar]
- 59.Oña O.B., Alcoba D.R., Torre A., Lain L., Torres-Vega J.J., Tiznado W. Orbital Localization Criterion as a Complementary Tool in the Bonding Analysis by Means of Electron Localization Function: Study of the Sin(BH)5 -N2− (n = 0–5) Clusters. J. Phys. Chem. A. 2013;117:12953–12958. doi: 10.1021/jp4081228. [DOI] [PubMed] [Google Scholar]
- 60.Oña O.B., Torres-Vega J.J., Torre A., Lain L., Alcoba D.R., Vásquez-Espinal A., Tiznado W. Chemical Bonding Analysis in Boron Clusters by Means of Localized Orbitals According to the Electron Localization Function Topology. Theor. Chem. Acc. 2015;134:28. doi: 10.1007/s00214-015-1627-5. [DOI] [Google Scholar]
- 61.Zhai H.-J., Kiran B., Li J., Wang L.-S. Hydrocarbon Analogues of Boron Clusters—Planarity, Aromaticity and Antiaromaticity. Nat. Mater. 2003;2:827–833. doi: 10.1038/nmat1012. [DOI] [PubMed] [Google Scholar]
- 62.Yañez O., Báez-Grez R., Inostroza D., Rabanal-León W.A., Pino-Rios R., Garza J., Tiznado W. AUTOMATON: A Program That Combines a Probabilistic Cellular Automata and a Genetic Algorithm for Global Minimum Search of Clusters and Molecules. J. Chem. Theory Comput. 2019;15:1463–1475. doi: 10.1021/acs.jctc.8b00772. [DOI] [PubMed] [Google Scholar]
- 63.Adamo C., Barone V. Toward Reliable Density Functional Methods without Adjustable Parameters: The PBE0 Model. J. Chem. Phys. 1999;110:6158–6170. doi: 10.1063/1.478522. [DOI] [Google Scholar]
- 64.Fuentealba P., Von Szentpaly L., Preuss H., Stoll H. Pseudopotential Calculations for Alkaline-Earth Atoms. J. Phys. B At. Mol.Opt. 1985;18:1287–1296. doi: 10.1088/0022-3700/18/7/010. [DOI] [Google Scholar]
- 65.Grimme S., Antony J., Ehrlich S., Krieg H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010;132:154104. doi: 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
- 66.Weigend F., Ahlrichs R. Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy. Phys. Chem. Chem. Phys. 2005;7:3297. doi: 10.1039/b508541a. [DOI] [PubMed] [Google Scholar]
- 67.Riplinger C., Pinski P., Becker U., Valeev E.F., Neese F. Sparse Maps—A Systematic Infrastructure for Reduced-Scaling Electronic Structure Methods. II. Linear Scaling Domain Based Pair Natural Orbital Coupled Cluster Theory. J. Chem. Phys. 2016;144:024109. doi: 10.1063/1.4939030. [DOI] [PubMed] [Google Scholar]
- 68.Neese F. The ORCA Program System. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012;2:73–78. doi: 10.1002/wcms.81. [DOI] [Google Scholar]
- 69.Neese F. Software Update: The ORCA Program System, Version 4.0. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2018;8:73–78. doi: 10.1002/wcms.1327. [DOI] [Google Scholar]
- 70.Truhlar D.G. Basis-Set Extrapolation. Chem. Phys. Lett. 1998;294:45–48. doi: 10.1016/S0009-2614(98)00866-5. [DOI] [Google Scholar]
- 71.Neese F., Hansen A., Liakos D.G. Efficient and Accurate Approximations to the Local Coupled Cluster Singles Doubles Method Using a Truncated Pair Natural Orbital Basis. J. Chem. Phys. 2009;131:064103. doi: 10.1063/1.3173827. [DOI] [PubMed] [Google Scholar]
- 72.Glendening E.D., Badenhoop J.K., Reed A.E., Carpenter J.E., Bohmann J.A., Morales C.M., Landis C.R., Weinhold F. Natural Bond Orbital Analysis Program: NBO 6.0. Theoretical Chemistry Institute, University of Wisconsin; Madison, WI, USA: 2013. [Google Scholar]
- 73.Zubarev D.Y., Boldyrev A.I. Developing Paradigms of Chemical Bonding: Adaptive Natural Density Partitioning. Phys. Chem. Chem. Phys. 2008;10:5207–5217. doi: 10.1039/b804083d. [DOI] [PubMed] [Google Scholar]
- 74.Zubarev D.Y., Boldyrev A.I. Revealing Intuitively Assessable Chemical Bonding Patterns in Organic Aromatic Molecules via Adaptive Natural Density Partitioning. J. Org. Chem. 2008;73:9251–9258. doi: 10.1021/jo801407e. [DOI] [PubMed] [Google Scholar]
- 75.Lu T., Chen F. Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 2012;33:580–592. doi: 10.1002/jcc.22885. [DOI] [PubMed] [Google Scholar]
- 76.Grimme S., Ehrlich S., Goerigk L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011;32:1456–1465. doi: 10.1002/jcc.21759. [DOI] [PubMed] [Google Scholar]
- 77.Van Lenthe E., Baerends E.J., Snijders J.G. Relativistic Total Energy Using Regular Approximations. J. Chem. Phys. 1994;101:9783–9792. doi: 10.1063/1.467943. [DOI] [Google Scholar]
- 78.Van Lenthe E., Baerends E.J. Optimized Slater-Type Basis Sets for the Elements 1–118. J. Comput. Chem. 2003;24:1142–1156. doi: 10.1002/jcc.10255. [DOI] [PubMed] [Google Scholar]
- 79.Baerends E.J., Ziegler T., Atkins A.J., Autschbach J., Baseggio O., Bashford D., Bérces A., Bickelhaupt F.M., Bo C., Boerritger P.M., et al. ADF2012. 01; SCM, Theoretical Chemistry. Vrije Universiteit; Armsterdam, The Netherland: 2012. [Google Scholar]
- 80.Jusélius J., Sundholm D., Gauss J. Calculation of Current Densities Using Gauge-Including Atomic Orbitals. J. Chem. Phys. 2004;121:3952–3963. doi: 10.1063/1.1773136. [DOI] [PubMed] [Google Scholar]
- 81.Fliegl H., Taubert S., Lehtonen O., Sundholm D. The Gauge Including Magnetically Induced Current Method. J. Chem. Phys. 2011;13:20500–20518. doi: 10.1039/c1cp21812c. [DOI] [PubMed] [Google Scholar]
- 82.Wolinski K., Hinton J.F., Pulay P. Efficient Implementation of the Gauge-Independent Atomic Orbital Method for NMR Chemical Shift Calculations. J. Am. Chem. Soc. 1990;112:8251–8260. doi: 10.1021/ja00179a005. [DOI] [Google Scholar]
- 83.Ayachit U., Geveci B., Moreland K., Patchett J., Ahrens J. The ParaView visualization application. In: Bethel E.W., Childs H., Hansen C., editors. High Performance Visualization—Enabling Extreme-Scale Scientific Insight. Taylor & Francis; Abingdon, UK: 2012. pp. 383–400. [Google Scholar]
- 84.Ahrens J., Geveci B., Law C. The Visualization Handbook. Volume 717 Elsevier Academic Press Cambridge; Cambridge, MA, USA: 2005. Paraview: An End-User Tool for Large Data Visualization. [Google Scholar]
- 85.Abramowitz M. Handbook of Mathematical Functions, with Formulas, Graphs, and Mathematical Tables. Dover Publications, Inc.; New York, NY, USA: 1974. [Google Scholar]
- 86.Keith T.A. AIMAll. TK Gristmill Software; Overland Park, KS, USA: 2019. Version 19.10. 12. [Google Scholar]
- 87.Sundholm D., Berger R.J.F., Fliegl H. Analysis of the Magnetically Induced Current Density of Molecules Consisting of Annelated Aromatic and Antiaromatic Hydrocarbon Rings. Phys. Chem. Chem. Phys. 2016;18:15934–15942. doi: 10.1039/C6CP01968D. [DOI] [PubMed] [Google Scholar]
- 88.Inostroza D., García V., Yañez O., Torres-Vega J.J., Vásquez-Espinal A., Pino-Rios R., Báez-Grez R., Tiznado W. On the NICS Limitations to Predict Local and Global Current Pathways in Polycyclic Systems. New J. Chem. 2021;45:8345–8351. doi: 10.1039/D1NJ01510A. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Not applicable.