Abstract
Introduction:
Many multi-genic systemic diseases such as neurological disorders, inflammatory diseases, and the majority of cancers do not have effective treatments yet. Reinforcement learning powered systems pharmacology is a potentially effective approach to designing personalized therapies for untreatable complex diseases.
Areas covered:
In this survey, state-of-the-art reinforcement learning methods and their latest applications to drug design are reviewed. The challenges on harnessing reinforcement learning for systems pharmacology and personalized medicine are discussed. Potential solutions to overcome the challenges are proposed.
Expert opinion:
In spite of successful application of advanced reinforcement learning techniques to target-based drug discovery, new reinforcement learning strategies are needed to address systems pharmacology-oriented personalized de novo drug design.
1. Introduction
Drug discovery and development is a costly and heavily time-consuming process. Despite massive investment of time and money, it is infeasible to explore the whole chemical space of drug-like compounds, which is composed of around 1033 small molecules [1], by using conventional technologies. Owing to the improvement of computer power, tremendous progress in deep learning (DL) and the emergence of quantum computing, computer-aided drug design has the potential to dramatically speed up the drug discovery process. With a reasonably reliable and accurate computational model, it is possible to synthesize and test a small number of compounds precisely interacting with expected drug target(s) and achieve desirable clinical outcomes. Recently, researchers have introduced various methods to generate novel molecules or optimize existing molecules towards designed properties. The mostly used methods include generative adversarial network (GAN) [2], variational autoencoder (VAE) [3], normalizing flow [4, 5], and reinforcement learning (RL) [6]. The molecules generated by GAN, VAE, and normalizing flow are biased to specific data distributions. They generally lack the ability to explore the unknown space that has a distribution shift or directly optimize molecules toward specific targets. RL, on the other hand, is able to learn or tune a generative model specifically toward the properties of interest and enable the model to generate molecules that have a different distribution from the training data. However, RL is usually less efficient compared with other methods. Training a model with RL from scratch will either cost a long time or lead to a model that is hard to converge. Thus, recent studies tend to combine pre-training or adversarial training with RL to take the advantage of the exploitation ability of transfer or adversarial learning [7–9] and the exploration power of RL.
Existing efforts in applying RL to drug discovery mainly follow the conventional one-drug-one-gene target-based paradigm. Although target-based drug discovery is mostly successful in tackling mono-genic diseases whose etiologies are driven by a single gene, it suffers from high failure rate especially for multi-genic, multi-factorial, heterogeneous diseases. Moreover, a drug rarely interacts only with its primary target in human bodies. Off-target effects are common, and may contribute to therapeutic effects or side effects [10]. Therefore, systems pharmacology that targets a gene-gene interaction network instead of a single gene and is tailored to individual patients has emerged as a new drug discovery paradigm for complex diseases. However, unlike target-based compound screening that can be easily measured by drug-target binding affinities, advances of systems pharmacology are hindered by the lack of effective read-outs for high-throughput compound screening. Powered by the development of many high-throughput cell-based phenotypic detection methods, phenotype-based drug discovery starts to gain an increasing attention in recent years due to its ability to identify drug lead compounds in a physiologically relevant condition [11]. Phenotype-based drug discovery is a target agnostic and empirical approach to exploit new drugs with no prior knowledge about the drug target or mechanism of action in a disease [12]. The use of molecular signatures as phenotype read-outs makes it possible to not only establish robust drug-disease associations but also deconvolute drug targets from the unbiased phenotype screening. Additionally, phenotype-based drug discovery has the power to exploit drugs for rare or poorly understood diseases such as neurological disorders and many types of cancers. Recently, several computational methods have been developed for high-throughput phenotype compound screening using chemical-induced gene expressions [13] and images [14] as read-outs. Tremendous progress in protein structure predictions [15, 16] and development of new methods for exploring dark chemical genomics space [17] significantly enhance our ability to deconvolute genome-wide target profiles for dark proteins that are not readily accessible by experimental methods. Another fundamental challenge in systems pharmacology-oriented precision drug design is to transfer compound activity in cell-line and animal models into therapeutic efficacy in an individual patient. Although human tissue-based organoid and ex vivo models have been developed for anti-cancer drug testing, they are expensive and often infeasible and even unethical in many disease areas. Thus, computational approaches such as transfer learning which can predict new target variables (e.g., tumor growth) of unseen samples (e.g., patients) from a model trained by an existing data set with different distributions (e.g., cell line screens) and targets (e.g., IC50 of cell viability) can be an indispensable tool to fill in the knowledge gap between in vitro bioassays and in vivo clinical endpoints of drug candidates. These computational tools pave the way for systems pharmacology-oriented high-throughput compound screening for personalized drug discovery.
This review will be organized as follows. We will first give a brief overview of RL, including definitions of some key concepts, problem setting and formulation of leading methods. Then we will survey the recent developments of applying deep RL to drug discovery. Finally, we will highlight the challenges and opportunities of RL in systems pharmacology and personalized medicine.
2. Overview of reinforcement learning
In reinforcement learning, there are usually two main characters -- an agent and an environment. The agent is the key component of RL that makes sequential decisions, and the environment is the world that the agent lives in. A typical RL problem can be considered as training an agent to interact with an environment that follows a Markov Decision Process (MDP) [18].
In each interaction (with the environment), the agent receives the information of the current state st ∈ 𝒮 and performs an action at ∈ 𝒜 accordingly, where 𝒮 and 𝒜 are state and action spaces and t is used to track the time-step, e.g., st is the state at time t. After performing an action at, the agent will transition to a new state st+1 and receive a reward rt. These are characterized by underlying state transition dynamics P: 𝒮 × 𝒜 → Δ(𝒮) and the reward function r: 𝒮 × 𝒜 → , i.e., P(st+1| st, at) and r(st, at) are the probability and reward of taking action at in state st and then transitioning into state st+1. This process repeats indefinitely or until a predefined termination condition is met. The sequence of states and actions followed in this process constitutes a so-called trajectory τ, e.g., at time t, τt = {s1, a1, s2, a2, …, st, at}. Moreover, with a discount factor γ ∈ (0, 1], we can define the discounted cumulative reward under a trajectory τ as . An MDP ℳ can be represented as a tuple of all components mentioned above along with an initial state distribution μ, i.e., ℳ = {μ, 𝒮, 𝒜, P, r, γ}.
In the typical setting of MDP, agent behaves by following a (stationary) policy π, which specifies a decision-making strategy in which the agent chooses an action at adaptively only based on its current state st. Precisely, a stochastic policy is specified as π : 𝒮 → Δ(𝒜) while a deterministic policy is of the form π : 𝒮 → 𝒜.
Given an MDP ℳ and a policy π, we can define some functions that measures the quality of being in a state s or taking an action a upon s in the long run. Specifically, we can define the value function that gives discounted sum of future rewards at a state s following an arbitrary policy π:
| (1) |
where
Similarly, the action-value function (or Q-function) can be defined as:
| (2) |
With and , we can also define another value function, the advantage function , which measures the relative reward that the agent could obtain by taking a particular step a upon s (compared to an average action).
The objective of RL is to learn a policy π that optimizes the expectation of accumulated reward under a particular initial state distribution μ:
| (3) |
| (4) |
where
With the basics of RL terminology and notation, we will review several leading RL algorithms in this section, with the focus on the mathematical formulation and foundational design. We will start with the model-free RL including value-based methods, policy gradient and actor-critic, and then briefly introduce model-based RL. A non-exhaustive taxonomy of RL algorithms can be found in Figure 1.
Figure 1.
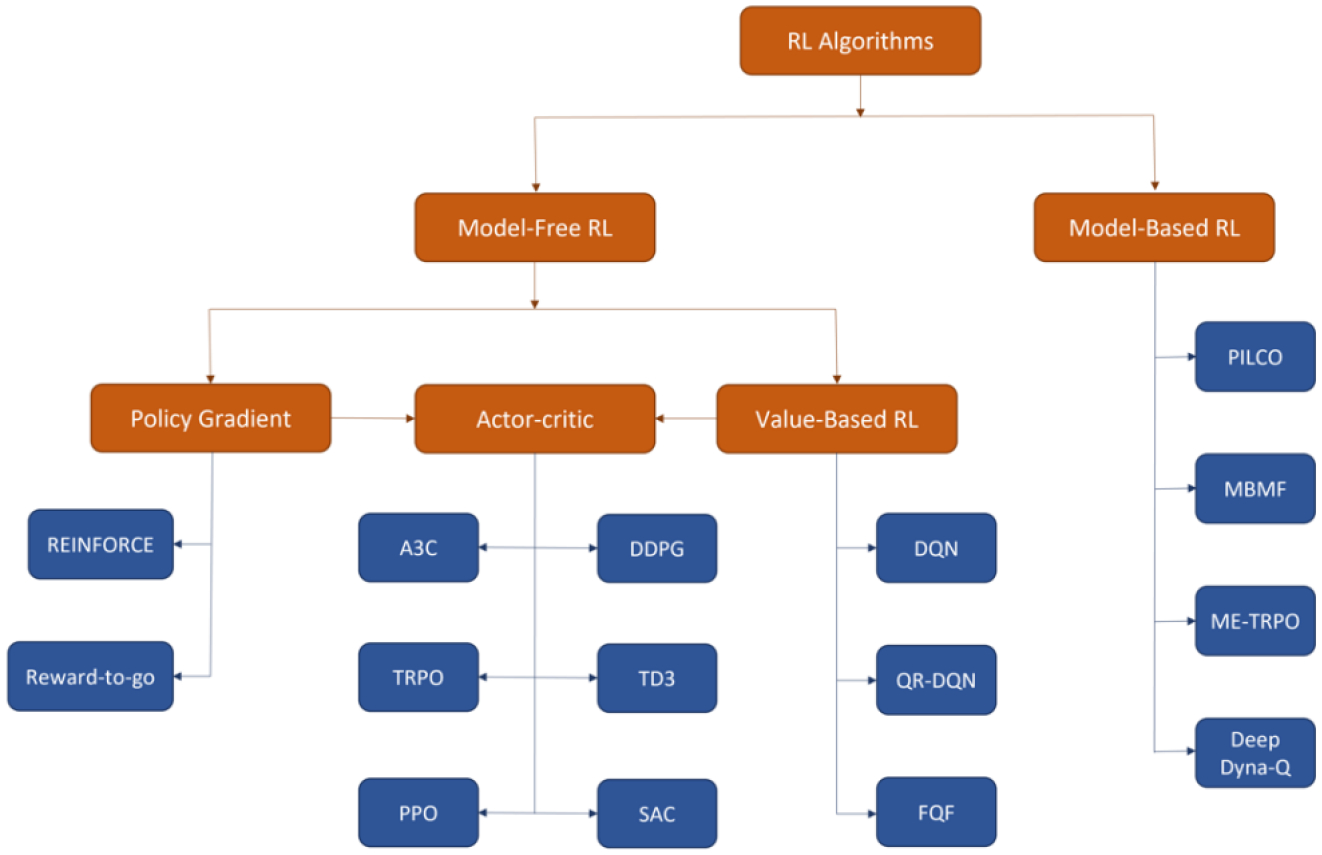
A taxonomy of RL algorithms
In the following subsections, we will drop the subscripts of ℳ and μ from value functions and the objective function Jμ (π) respectively assuming working under the same MDP ℳ.
Value-based Methods
A common way to optimize the RL objective J(π) is by the observation that if the optimal value function or Q-function could be accurately estimated, we can easily recover an optimal policy. For instance, given the optimal Q-function Q*(s, a), an optimal policy π* (s) could be obtained by
| (5) |
Dynamic Programming (DP) is a classical approach to approximate these desired value functions assuming a perfect model of the environment is given, and the number of states and actions is small so that value functions can be represented in some lookup tables [18]. The foundation of DP is centered on bellman optimality equation and bellman expectation equation, and they can be defined as follows with respect to Q-function:
| (6) |
| (7) |
Where s′ is the successor state and a′ is the action performed at s′.
According to these equations, two important mathematical operations, bellman optimality operator and bellman evaluation operator can be defined as follows:
| (8) |
| (9) |
These operators map any Q-function from to another Q-function in the same space. It’s helpful to consider the Q-function as a vector of length |𝒮||𝒜| and the operators are some transformations that take the vector and output another vector with the same dimensions. More specifically, considering 𝒯 and a state-action value Q(s, a), 𝒯 can be viewed as an assignment statement that updates the original value of Q(s, a) with the one computed from the RHS of (8). There are two pleasant properties of these operators, related to contraction mapping, which help the design of the classical DP algorithms. First, given any arbitrary Q-function Q, repeatedly applying 𝒯π or 𝒯 on Q yields Qπ or Q* respectively. This property can directly turn Bellman operators into update rules, providing iterative algorithms for approximating the optimal Q-function Q*(s, a). Moreover, 𝒯π and 𝒯 have unique fixed points Qπ and Q* such that 𝒯πQπ = Qπ and 𝒯Q* = Q*. This second property serves as the termination condition of many classical DP algorithms and the building blocks of some advanced RL algorithms, such as actor-critic.
Since, in practice, the complete knowledge of the environment is usually unknown, and the number of states and actions can be arbitrarily large, dynamic programming is thus limited to some restricted problems by its assumptions and function representation. The value-based RL, sometimes known as approximate dynamic programming, provides a class of algorithms that overcome these problems, extending the framework of iterative dynamic programming with modified bellman operators and/or function approximation. The essence of this approach is to modify the update rule by approximating the bellman operators with some empirical estimators, i.e., estimating the RHS of equations (8) and (9) with sampling [19]. In the simplest form of using a single sampled successor state s′ ~ P(·|s, a) for estimation, the empirical bellman operators and can be defined as [20–22]:
| (10) |
| (11) |
It is worth noting that (10) and (11) are analogous to the update rules of Q-learning [23] and Sarsa [24], two classical value-based RL algorithms, respectively (with the learning rate α = 1). Theoretically, if we want to turn or directly into an update rule, a modification is required to guarantee convergence by replacing the single successor state s′ with n successor states , e.g., , where n needs to satisfy a mild condition [20, 21]. Otherwise, an algorithm with a customized learning strategy needs to be proposed [22–24].
Unlike Q-learning and Sarsa that are tabular solution methods, Fitted Q-Iteration (FQI) is a more advanced classical value-based RL algorithm which uses function approximation rather than tables for representing value functions and this allows FQI to be applied to problems with arbitrarily large state and/or action spaces [25]. In FQI, the algorithm first gathers a dataset where state si and action ai are drawn from a pre-defined distribution ν, and the next state and the reward ri are obtained from the unknown state transition probability function P and reward function r of the environment. With the initialization of a parameterized Q-function Qθ, the Q-values Qθ(si, ai) are updated towards their target and the update rule can be formulated as:
| (12) |
Where
Equation (12) can be interpreted as applying Monte-Carlo approximation of Bellman optimality to Q-function Qθ through minimizing the square loss over θ. And since the Q-values in FQI are estimated by a parameterized function rather than a lookup table, they are closely correlated to each other, implying that a small update of θ may benefit some Q-values but push others away from their targets. Therefore, unlike supervised learning where the ground truth labels are stationary, the targets in FQI may vary every time when the parameter changes, which introduces instability in training. Consequently, without knowing the generalization and extrapolation ability of the function approximator, the contraction mapping property of Bellman operators cannot guarantee convergence for RL algorithms with function approximation, especially for those using advanced parameterized function approximators, such as neural networks, that lack theoretical understanding. [26]. On the other hand, there exist other variants of FQI using non-parametric approximation architecture, such as k-nearest-neighbor and totally randomized trees, showing strong theoretical guarantees under some designed learning strategies [27–30].
Regarding the value-based methods using neural networks, Deep Q-Network (DQN) algorithm, showing strong performance in a variety of ATARI games, can be viewed as an instantiation of FQI in online settings [31]. The Q-function approximator of DQN can be any typical neural network, referred to as Q-network. The framework of DQN uses two heuristics to limit the instability inherited from FQI with neural networks. First, a separated network called target network is introduced solely for computing the targets (interpreted as the ground truth) due to their inconsistency. Compared to Q-network, the target network is updated less frequently to keep the targets fixed for some amount of time. With this strategy, DQN prevents the instability from propagating too quickly and thus reduces the risk of divergence.
Moreover, DQN is an online learning algorithm which follows its current (behavior) policy for exploring and data sampling. Without proper care, this may deliver a policy that has inferior performance since previously visited state-action pairs with high rewards may not guarantee to be revisited due to the stochasticity of the system. Experience Replay (ER), a replay buffer, is introduced to solve this issue by storing all samples < s, a, r, s′ > from the last N steps in the memory where N is usually very large. Besides, ER selects samples from the memory following the uniform distribution for every mini-batch update. This sampling method, though simple, effectively breaks the temporal correlation between samples in the same trajectory, which helps reduce bias. With large memory and uniform sampling, mini-batch samples constructed under ER are more representative than those from alternative methods such as Q-learning [23] which uses only one sample for an update. Additionally, a large buffer provides good coverage of the state-action space, which makes the policy training more exploratory and consistent, thus increasing the efficiency of searching for a desirable policy.
In addition to target network and ER, there are other advanced approaches that could help improve the stability and efficiency of policy learning including Double DQN [32] for overestimation reduction, Multi-step learning for accurate target estimation [26], Dueling Networks [33] for enhanced Q-function representation and Prioritized ER (PER) for efficient TD-error minimization [34], along with other extensions such as Distributional DQN [35], Quantile Regression DQN (QR-DQN) [36], and Fully parameterized Quantile Function (FQF) [37].
Policy gradient
Unlike the value-based approach that approximates the optimal policy by estimating the optimal value functions, the Policy Gradient (PG) methods work directly on the objective function defined in (4) or some equivalent ones. In the setting of this review, we limit our focus on (4). Specifically, with a policy π parameterized by θ ∈ Θ ⊂ , the goal of PG is to find a θ that maximizes J(πθ):
| (13) |
Since the search space has now shifted from the policy space Π in (4) to Θ which is continuous and has fixed dimensions, various numerical optimization methods could be utilized to solve (13). Gradient ascent is one direct approach to this, which iteratively moves in the direction of steepest ascent as defined by the gradient for maximizing J(πθ). Following is the expression of the gradient for J(πθ):
| (14) |
Where .
At each update iteration k, gradient ascent, with a fixed step size α, follows the update rule:
| (15) |
Since the policy gradient ∇θJ(πθ) is an expectation over all possible trajectories, it can be directly estimated by a set of samples where each is a trajectory collected by the agent interacting with the environment while following policy πθ. With the set of samples denoted as D and the length of each trajectory assumed to be H, we can estimate ∇θJ(θ) by:
| (16) |
| (17) |
Where .
With equation (17), we have derived our first policy gradient method, commonly known as REINFORCE [38], which serves as the foundation of PG-based methods.
Because ∇θJ(πθ) is an expectation, a long-standing issue centered on PG-based methods is to derive an unbiased estimator of ∇θJ(πθ) with possibly low variance. For instance, R(τ) in (17) can be replaced by a smaller term thanks to causality that the policy at time t′ cannot affect the reward at time t when t < t′. This gives us a new unbiased estimator of ∇θJ(πθ) with reduced variance called Reward-to-go [39]:
| (18) |
Regarding the policy gradient ∇θJ(πθ), it can be viewed as an analogue of the gradient in maximum likelihood where the term log πθ (ai,t | si,t) in equations (17) and (18) is the log likelihood of the policy πθ given data <si,t, ai,t>. Unlike maximum likelihood, the log likelihood in PG is now weighted by some discounted cumulative rewards, such as R(τ) or . Thus, updating the parameter θ with ∇θJ(πθ) would change the policy according to the sign of R(τ) or , e.g., the chance of selecting ai,t given si,t increases if R(τ) is positive or decreases otherwise.
On the other hand, if the reward function only outputs positive values and some mediocre actions are selected stochastically for parameter updates, the agent may tend to choose these inferior actions even their absolute values of log πθ (ai,t | si,t) are small. A popular strategy to address this unstable issue is to introduce an extra term, called baseline b, which can be shown to always keep the estimator of ∇θJ(θ) unbiased while reducing its variance if selected properly [40]. For instance, by simply choosing an average reward over sampled trajectories as baseline, the term in (19) is (approximately) centered around 0, which improves the sampling efficiency by distinguishing actions with their relative rewards.
| (19) |
Where b can be
Thus, with proper care of designing the baseline, the policy πθ could eliminate the inferior actions and choose more desirable ones with higher probability. In the next subsection, a learnable baseline will be introduced, which is more stable and significantly reduces the variance of the classical policy gradient estimators.
Actor-Critic
Actor-critic algorithms can be viewed as an approach that combines policy gradients with value-based methods to optimize J(θ). Generally, it takes a policy πθ as an actor to interact with the environment, while maintaining a learnable value function as the critic to evaluate the actor’s actions [26, 41]. The simplest form of actor-critic called Q actor-critic [41] can be derived directly from the reward-to-go and we denote below as the estimator of ∇θJ(θ) from (18):
| (20) |
Where
A direct advantage of this new estimator, the one inside the expectation of (20), is that it has less variance than the reward-to-go. This can be shown following the tower property of conditional probability and the definition of variance. The intuition is that is indeed the cumulative reward of a single sample trajectory that estimates , which inevitably has larger variance and so does the reward-to-go. In practice, we usually estimate by a parameterized Q-function and update ω following a similar procedure as described in FQI.
Similar to (19), a baseline can be incorporated into Q actor-critic to further reduce its variance. A favorable choice is using a value function parameterized by φ where ∇θJ(πθ) can be further reduced to a form of advantage function:
| (21) |
Where
The derived PG estimator in (21) is the naïve advantage actor-critic [26, 42, 43]. As the advantage function measures the performance difference between a specific action and the average action in a given state, it’s usually considered as a favorable critic to evaluate the actor and determine which action should be chosen more often.
Moreover, ∇θJ(πθ) can be approximated in another way as specified below by the observation that given a sample < s, a, r, s′ >, the sum of r and γVπ(s′) is a sample estimate of Qπ (s, a):
| (22) |
Where
The unbiased estimator of ∇θJ(πθ) derived in (22) is called TD-error actor-critic [42, 44, 45]. Theoretically, it has a higher variance than the naïve advantage actor-critic in (21) as we replace with a single sample estimate . But in practice the estimator of ∇θJ(πθ) in (22) is more stable for policy training and has less bias as it only requires a function estimator for the value function while the naïve advantage actor-critic requires an extra function estimator for Q-function other than , which inevitably needs more samples to achieve a comparable performance. Owing to the favorable property of TD-error actor-critic, precisely the term of , it has been widely adapted to many advanced actor-critic algorithms such as Asynchronous Advantage Actor Critic (A3C) [43], Trust Region Policy Optimization (TRPO) [46] and Proximal Policy Optimization (PPO) [47].
The methods discussed so far in this subsection, as well as the ones mentioned in PG, are generally on-policy methods where the target policy being learned (i.e., evaluated and improved) is used as the one to interact with the environment and generate samples, which is commonly referred to as behavior policy [26]. On the other hand, in an off-policy setting, an agent usually learns a policy that is different from the one being executing. Some typical examples are the methods introduced in the value-based RL, such as FQI, Q-learning and DQN, where the samples used for training are not exactly generated by the current learning policy, the target policy. There is a class of off-policy actor-critic methods, such as Deep Deterministic Policy Gradient (DDPG) [48], Twin Delayed DDPG (TD3) [49] and Soft Actor-Critic (SAC) [50], that adopt the replay buffer and heavily depend on Q-function estimator for approximating desired policy. These methods, in practice, are usually more sample efficient yet less robust to hyperparameter settings than their on-policy counterparts, which is mainly due to the incorporation of off-policy samples and sometimes convoluted tricks for stabilizing training.
Model-based RL
Model-based RL is a general term that refers to a broad class of algorithms, which is widely seen as a potential approach to improve the sample efficiency of model-free RL [51–53]. Unlike model-free RL which learns a policy πθ and/or a value function without modeling the environment, model-based RL explicitly estimates the transition dynamics P(st+1 | st, at), which we denote Pψ (st+1 | st, at) parameterized by ψ, and uses it for planning [54] or policy learning. Since model-based RL has not been well standardized and there exist many variants, we will briefly summarize three important types of algorithms. A common class of model-based RL algorithms, related to shooting methods [55], learns the dynamics model Pψ, and uses it to derive a local planning strategy for action selection. This is typically achieved by formulating and solving receding horizon problems posed in model-predictive control [56] using various trajectory optimization methods [57, 58]. Other model-based RL methods, such as PILCO, learn a policy πθ in addition to the dynamics model Pψ, and employ backpropagation through time with respect to the expected future reward for policy search and improvement [59–61]. Dyna-style algorithms, another set of model-based methods, incorporate the dynamic model Pψ to the general model-free framework for augmenting samples and accelerating policy learning [62–66]. Specifically, training under this category usually iterates between two steps: first, the agent learns Pψ and πθ with a set of real experiences gathered from interacting with the environment. Second, a number of ‘synthetic’ samples are generated using the current policy πθ under the learned dynamic model Pψ and another round of policy update is performed with these ‘synthetic’ samples. Such an iterative process can significantly boost the sample efficiency of pure model-free learning once Pψ precisely estimates the environmental dynamics.
3. State-of-the-arts in applying reinforcement learning to drug discovery
There are different approaches in applying reinforcement learning to drug discovery depending on the objectives [67–69]. Distributional learning, a common task of computational drug design, is to generate a set of molecules distributed differently from an existing dataset, which satisfy one or more predefined requirements. One typical approach is to pretrain a generative model with some well-established dataset and incorporate it into a RL framework for optimization. In this case, the generative model is trained as learning a policy that maximizes a RL loss function as defined in (3), where the reward is customized for the objective(s). Another set of problems, usually referred to as goal-directed learning, requires searching for the exact molecule with specific properties. These tasks are usually formulated as solving a combinatorial optimization problem [70, 71], which falls exactly into the region that could be potentially solved by RL [72, 73]. In this section, we will briefly review different adaptations of RL algorithms, as described in section 2, to drug discovery, with a focus on the practical strategy and design of RL-based generative models. A taxonomy of RL-based methods for drug design can be found in Figure 2.
Figure 2.
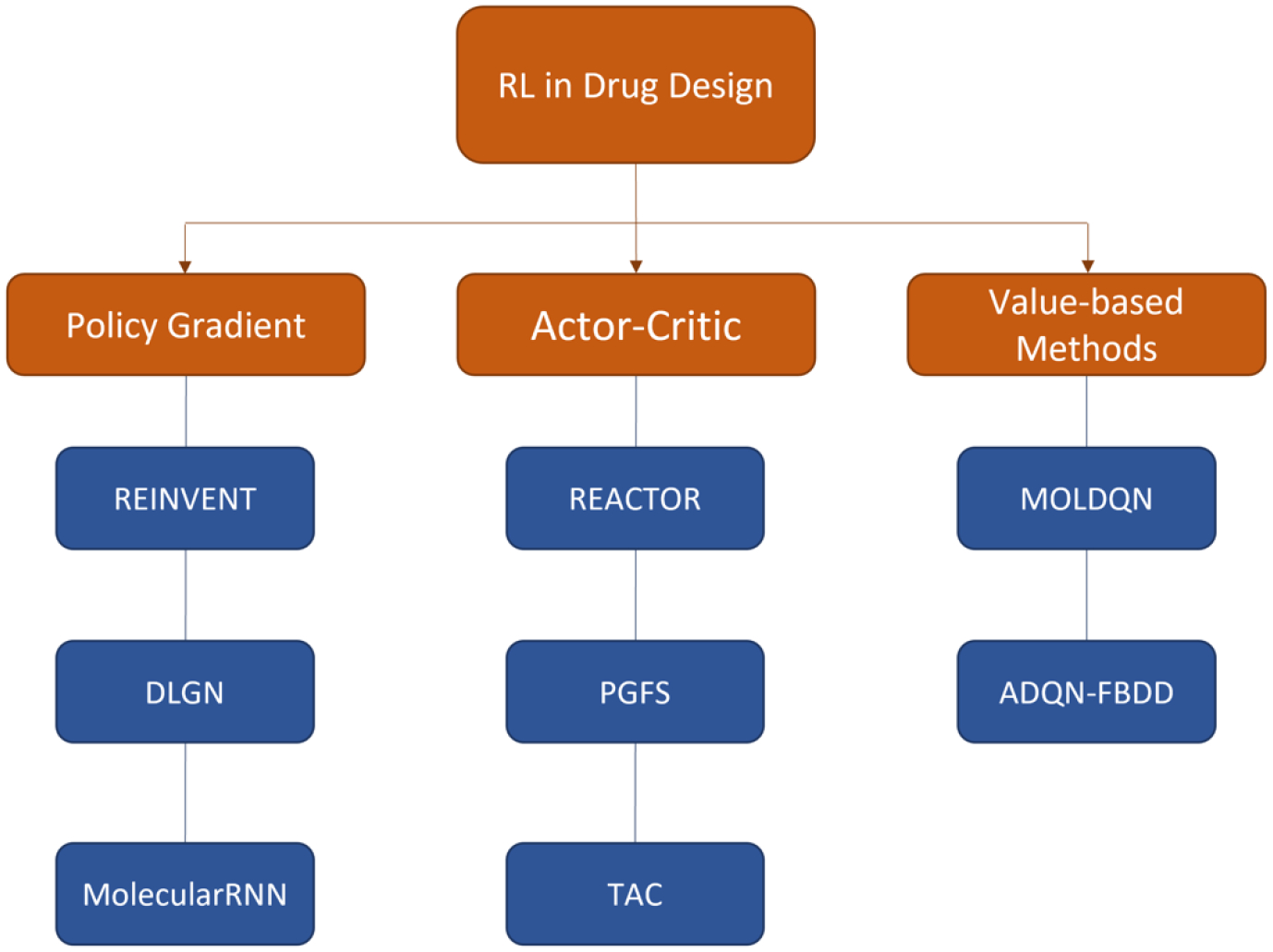
RL-based methods for drug design
Models with policy gradient
Policy gradient method has been adapted to a variety of RL-based generative models for distributional learning owing to its policy stochasticity and learning capability for high-dimensional state and/or action spaces. Olivercrona et al. developed an approach REINVENT for distributional learning based on REINFORCE algorithm, in which they first pre-trained a recurrent neural network (RNN) known as prior policy that could generate a set of samples with a similar structural distribution as ChEMBL [7]. The agent RNN for learning target policy was then initialized with the same architecture and parameters as the pre-trained RNN and tuned with RL to achieve higher expected score while keeping the target policy close to the prior policy. The generated molecules thus have a similar structural distribution as the ChEMBL dataset while being optimized towards the target properties. Since the agent RNN is pre-trained, the RL searching efficiency has been increased whereas the exploration capability of this model is somewhat limited.
Recently, the attention to polypharmacology is constantly increasing owing to its therapeutic potential in some complex pathologies. Dual-target ligand generative network (DLGN), leveraging RL and adversarial training, was developed to generate molecules that have bioactivities toward two targets [74]. With SMILES string as input, DLGN uses an RNN-based generator to produce novel molecules that satisfy the predefined constraints. To make generated molecules dual-targeted, DLGN utilizes two discriminators to monitor the generative process and encourages the generated molecules lying in the intersection of the two bioactive-compound distributions. The drawback of this model is that, although the generator does not need to be trained with labeled data, the discriminators require reliable labeled data to control the qualities of generated molecules.
As graph is a more natural way to represent a molecule, graph neural networks (GNNs) are widely used in computational drug discovery. You et al. developed a graph convolutional policy network (GCPN) that generates molecules under some guidance towards desired objectives while restricting the output molecules to some specific chemical rules [8]. To achieve this goal, they leveraged RL for molecule generation and optimization under a customized environment with a designed reward function, and used expert pre-training and adversarial training to incorporate prior knowledge for guidance. In another work, Atance et al. extended REINVENT with gated graph neural networks to generate molecules with desired properties [75]. To overcome the difficulty of RL training, they introduced a best agent reminder (BAR) loss, which is calculated based on the actions given by the current agent and the best agent and shown to significantly improve the speed of convergence and the final performance. MolecularRNN is another interesting work based on the REINFORCE algorithm that utilizes graph data structure to represent molecules while exploiting RNN as the generator. It employs a dual network model, consisting of both node-level and edge-level RNNs, to predict the next atom and bond given an intermediate generated molecular graph [76]. With valency-based rejection sampling constraints, MolecularRNN achieves 100% validity of the generated molecules in the experiments.
To balance the exploration and exploitation, Liu et al. employed two pretrained RNNs in DrugEx to generate novel molecules [77]. The two RNNs share the same architecture while having different internal parameters. One of the RNN, which serves as the exploration network, is pretrained on the ZINC database and then fine-tuned with desired molecules to memorize the distribution of the potential drug space. This exploration network will not be updated during training. The other RNN, performing as exploitation network, is only pretrained on ZINC database, followed by policy gradient update to generate molecules with high pIC50 values for properties of interests. During the training phase, the exploration and the exploitation networks are randomly assigned to generate the next token based on a predefined ‘exploring rate’. This helps the generated molecules to be well diverse while maintaining high pIC50 value for target proteins. To improve the balance of exploration and exploitation, Pereira et al. extended DrugEx by introducing a dynamically adaptive ‘exploring rate’ which is determined by the property of two latest batches of generated molecules [78]. Additionally, they added a penalty in reward for improving novelty when the diversity of the latest generated molecules decreases.
Models with Deep Q-networks (DQNs)
Value-based RL methods are usually more stable and sample efficient than those using policy gradient [26]. In addition, as the policy learned by value-based approach is deterministic, it’s more natural to choose these methods for solving the goal-directed problems. Molecule Deep Q-Network (MolDQN) based on bootstrapped-DQN is a leading method for goal-directed learning [79]. By allowing only valid actions, MolDQN guarantees that the generated molecules are 100 % valid. The molecule generation or optimization starts from an empty or a seed molecule in the form of Morgan fingerprint. In the constrained optimization task, MolDQN optimizes a seed molecule toward the target property while maintaining its similarity to the original molecule above a specified threshold. The advantage of MolDQN is that it does not depend on a pre-trained model for molecule generation, and thus it is not biased to any observed chemical space. Therefore, MolDQN can in principle generate novel chemical structures or molecules with desired properties but may require considerable time for exploring to achieve favorable performance.
Tang et al. developed an advanced deep Q-learning network with the fragment-based drug design (ADQN-FBDD) to generate molecules specifically targeting a protein with known 3D structure [80]. They designed a practical reward by considering drug-likeness, as well as specific fragments and pharmacophores which are protein-structure dependent. Although this approach has an obvious limitation, which is the high dependency of 3D structures of target proteins, a recent breakthrough in protein structure prediction [15] may provide it with a wide range of application scenarios.
Models with actor-critic
As mentioned in section 2, the actor-critic methods improve the sampling efficiency of policy gradient by learning a parameterized value function (critic). It usually consists of two networks, a policy network and a variance-reduced value network. Intuitively, the actor, the policy network, decides what action to take based on the current policy and state whereas the critic, value network, evaluates the action and informs the actor how the policy should be adjusted. With the guidance from the critic, the policy training process usually becomes more stable and efficient [81].
Simm et al. developed a novel actor-critic architecture for 3D molecule generation that exploits the symmetries of the design process [82]. Specifically, it employs a state embedding network to obtain rotation-covariant and -invariant state representations of 3D molecular graphs, which improves the generalization of the policy network and enables it to generate more complex 3D structure than previous approaches. Ståhl et al. introduced a fragment-based RL framework based on actor-critic where both actor and critic are modeled with bidirectional long short-term memory (LSTM) networks [83]. As the research is focused more on the constrained optimization task and the molecular fragments are utilized as atomic actions, a novel encoding approach using a balanced binary tree was developed to represent the fragments. With the help of this design, the RL agent is more capable of distinguishing promising steps from those mediocre ones.
Generating molecules in silicon is far from the final goal of developing drugs. The first step after molecular design is to synthesize designed compounds and test their effects with wet experiments. However, not all computational designed molecules are synthesizable. This seriously affects the practical value of computational drug design. Some studies try to resolve this by taking synthesizability into consideration while generating molecules. Reaction-driven objective reinforcement (REACTOR) empowered by actor-critic method, for example, defines the state-action trajectory in RL as a sequence of chemical reactions, and thus not only improves the synthesizability of the generated molecules, but also speeds up the exploration rate of the model in the chemical space [84]. Additionally, REACTOR employs a synchronous version of A3C which can perform parallelized policy search and thus tremendously improves the efficiency of the policy training. In addition to REACTOR, there are other works that leverage actor-critic methods for synthesis-oriented molecule generation, such as Towered Actor-Critic (TAC) [85] and Policy Gradient for Forward Synthesis (PGFS) [86].
Remarks on RL algorithms
With the jumbo chemical searching space and limited pretraining samples, machine learning algorithms like GAN and VAE have difficulties to generate a set of molecules distributing differently from the training dataset. Moreover, such methods are inherently hard to be adapted for goal-directed tasks, especially for those related to exhaustive search. Under such circumstances, RL, which does not rely on training data and can be adopted to skew the underlying distribution of the (pretrained) generative model or directly learn a policy to optimize a seed molecule, is a promising approach to tackle various drug discovery problems. However, the current RL methods applied for molecule generation are generally sample inefficient especially in high-dimensional search space under multiple constraints, which is usually the case for drug-like molecule space. Recent studies tend to incorporate expert pretraining and adversarial training into conventional RL framework to overcome this difficulty. Moreover, the quality of the molecules generated by RL-based generative model highly relies on the reward function. Thus, in future studies, improving the sample efficiency of RL and the accuracy of the property predicting model is the key to bring computational drug design to practical production.
4. Challenges and opportunities of reinforcement learning in systems pharmacology and personalized medicine
Figure 3 illustrates a RL framework for systems pharmacology-oriented personalized lead optimization and drug design. The molecule and the in vivo state together constitute an agent state. A molecule generator (agent) will first take an action based on the current state and policy to generate a new molecule or modify a seed molecule (e.g., replacing a hydrogen atom with a methyl group). Then, multiplex phenotypic responses (cell viability, drug-target profile, chemical-induced gene expression, pharmacokinetics etc.) in an individual patient (environment) will be predicted for the newly generated molecule by machine learning, biophysics, systems biology, or other methods, and these responses are used as the reward for policy training. A new policy will be learned based on observed actions, states, and rewards by performing an optimization with a multi-objective RL (MORL) algorithm, and a new molecule will be generated again from the updated policy. Unlike target-based compound screening where only chemical space is needed to be explored, systems pharmacology-oriented personalized drug discovery needs to optimize the interplay of chemicals, the druggable genome, and high-dimensional omics characterizations of disease models or patients. Several barriers need to be overcome when applying RL to systems pharmacology and precision medicine. These include the exploration of out-of-distribution samples, generalization power of RL, adaptive multi-objective optimization [87–89], and activity cliffs of quantitative structure-activity relationship (QSAR) space [90].
Figure 3.
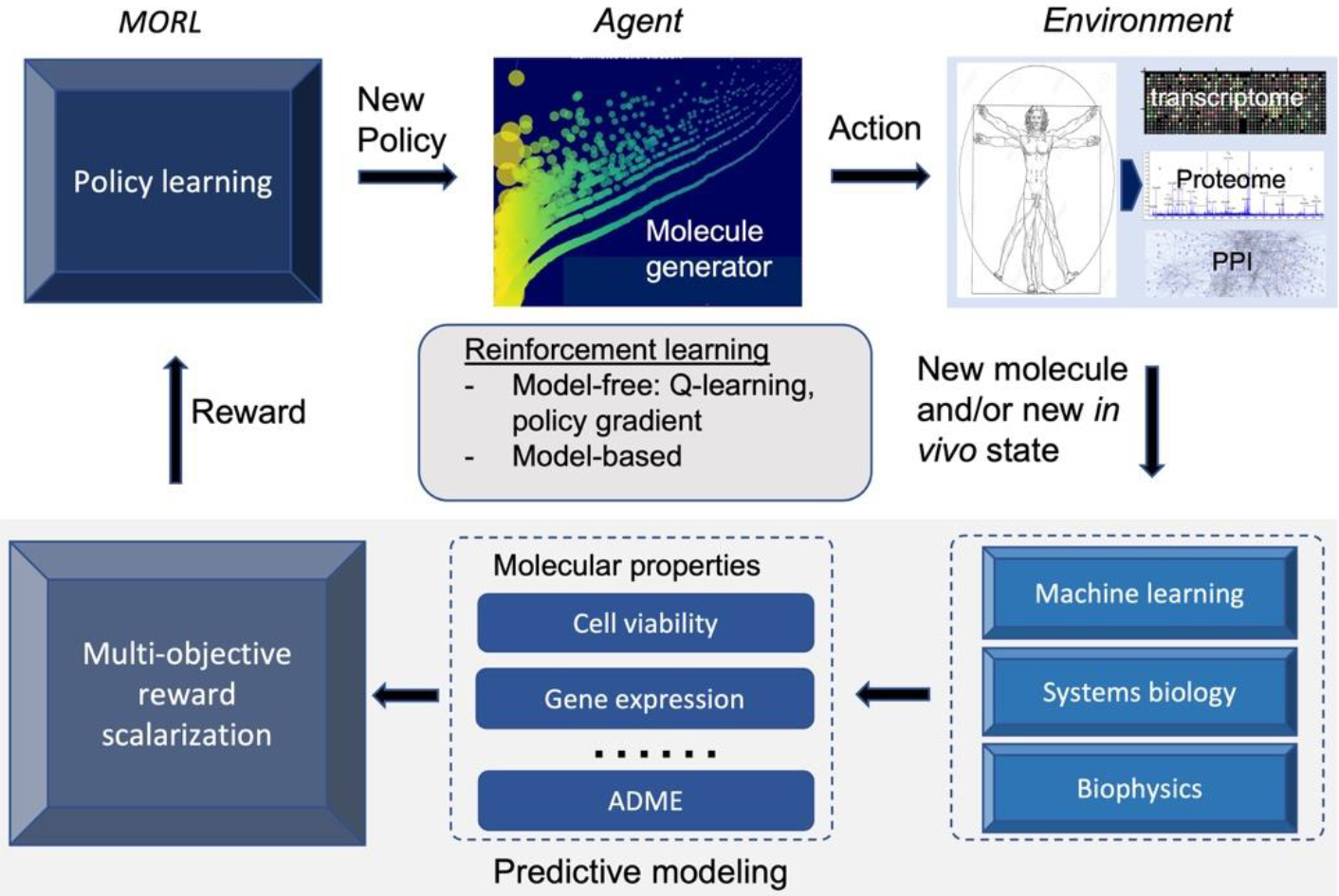
Illustration of a RL framework for systems pharmacology-oriented lead optimization.
Out-of-distribution reward function.
Although rewards for several molecular properties (e.g., logP and druglikeness) can be directly calculated from a given molecular structure, reward functions that are the most important for drug actions such as binding affinity and chemical-induced gene expression need to be obtained from a predictive model that is dependent on machine learning, mathematical or physics-based modeling. In spite of tremendous advances in deep learning and availability of diverse omics data sets, robust and accurate predictions of genome-wide drug-target interactions and molecular phenotypic read-outs in a physiological relevant condition remain as an unsolved challenging problem. The problem is rooted in biased, noisy, and incomplete omics data and inherited from the limitation of machine learning. In the case of genome-wide drug-target prediction, only less than 10% of gene families have known small molecule ligands. The remaining 90% gene families are dark matters in the chemical genomics space [17]. Even for mostly studied G-protein coupled receptors (GPCRs), more than 99% receptors are orphans, i.e., their endogenous or exogenous ligands are unknown. Similarly, only a small number of cell lines have annotated drug response data. It is a fundamental challenge to generalize a “well-trained” machine learning model to unseen data (e.g., patients), which lie out-of-the-distribution (OOD) of the training data (e.g., cell lines), so as to successfully predict outcomes from conditions that the model has never before encountered. While deep learning is capable, in theory, of simulating any functional mapping, its generalization power is notoriously limited in the case of distribution shifts [91].
Generalization power of RL.
The conventional MDP defined in section 2 is assumed that the problem setting is stationary, i.e., the transition dynamics and the reward function do not change over time, and the agent fully observes the underlying state, i.e., the observation received by the agent includes perfect information of the current state. Thus, the conventional RL methods, especially those falling into the model-free RL, may perform poorly in an environment that is non-stationary (e.g., from one patient to another) with partially observed states though they perform well in the conventional setting [92, 93]. Additionally, directly employing conventional RL methods to solve an MDP with corrupted reward, where the observed reward may not be an unbiased estimate of the true reward, or sparse reward, in which rewards are not available for most of the state-action pairs, could fail catastrophically [94, 95]. The partially observed, non-stationary or corrupted sparse-reward environment is the exact situation in systems pharmacology. Due to observed chemical activity and omics data highly biased and incomplete, it is likely that a novel molecule is an OOD sample. Thus, no reliable reward can be assigned to this molecule as mentioned above. Additionally, drug response data mainly comes from cell lines or disease models. The environment in a cell line or animal model could be dramatically different from human bodies. A naïve adaptation of standard RL systems is not sufficient for systems pharmacology. New methods are needed to improve the robustness, generalizability and transferability of RL.
Adaptive multi-objective optimization.
To design drugs that optimize the system-level responses to maximize therapeutic effects and minimize side effects, it is needed for a RL algorithm to optimize multiple (sometimes conflict) objectives such as pharmacokinetics, blood-brain barrier permeation, drug binding affinities to multiple targets, or chemical-induced gene expression profiles. Although RL methods have been developed for multiple objectives [79], the final reward function in these methods is a linear combination of the reward functions of individual objectives with a priori defined weights. It is often difficult to define such weights. Moreover, the weight may be altered when an environment changes. For example, gene expression profiles can be dramatically different for different patients and in different disease states. Thus, for conventional RL, typically with fixed weight, a generative model (the policy) needs to be trained for different conditions. In addition, it is more computationally challenging to find optimal solutions in the framework of Pareto optimization for the multi-objective drug design due to the high dimensionality and uncertainty of omics and bioassay data. It has been suggested that Pareto optimization should be integrated with evolutionary algorithms or other complexity reduction methods [87, 96].
Activity cliff of QSAR.
Reward drop is a phenomenon that the reward rt received from a trajectory {s1, a1, s2, a2, …} suddenly drops or oscillates dramatically within certain range due to the nonsmoothness of the reward function, and many advanced RL algorithms have suffered from this problem [97]. Unfortunately, in computational molecule design, a well-known phenomenon in QSAR is activity cliff, in which a slight modification of chemical structure may lead to a dramatic activity change. The activity cliff is more complicated in systems pharmacology than single-targeted drug discovery. For example, the replace of a methyl group with an ethyl group for a chemical compound that has moderate binding affinities to two targets may increase the binding affinity to one of targets, but completely destroy the binding to another target due to steric clash. As a result, the phenotype response modulated by this compound could be changed significantly. Such unpleasant property (of QSAR landscape) thus increases the difficulty of policy learning for RL-based drug design.
To address aforementioned challenges in adapting RL to systems pharmacology and precision medicine, a synergistic integration of latest advances in RL with new development in machine learning and other related fields is needed.
Improving robustness, generalizability, and transferability of RL algorithms.
Recently, Ghosh et al, showed that optimal generalization of RL at test-time corresponds to solving a partially-observed Markov decision process (POMDP) that is induced by the agent’s epistemic uncertainty about the test environment [93]. They proposed an algorithm, LEEP, which uses an ensemble of policies to approximately learn the Bayes-optimal policy for maximizing test-time performance. In another study, Agarwal et al. proposed meta-reward learning to achieve the generalizability of RL in a sparse-reward environment [98]. In principle, these techniques can be adapted for systems pharmacology.
The majority of existing work in RL for drug design is based on the model-free approach. Model-based RL [6] may provide new opportunities for addressing the challenges in systems pharmacology-oriented drug discovery for precision medicine. Different from model-free approach, model-based method typically employs a learned dynamics model to facilitate policy training. It is more powerful in predicting future reward, has higher sample efficiency, and bears stronger transferability and generality than the model-free approach. The ability of predicting future reward may help to avoid activity cliffs. Sample efficiency will be helpful to alleviate issues in data sparsity, biasness, and noisiness. Transferability and generalizability are critical to address the OOD problem.
Several algorithms have been developed to solve multi-objective optimization problems in RL. Yang et al. introduced an envelope Q-learning method that can quickly adapt and solve new tasks with different preferences [99]. The capability of learning a single Q function over all preferences is important for personalized drug discovery. In another study, Chen et al. proposed a two-stage model [100] for multi-objective deep RL. At the first stage, a multi-policy soft actor-critic algorithm is applied to collaboratively learn multiple policies with different targets, in which each policy targets on a specific scalarized objective. At the second stage, a multi-objective covariance matrix adaptation evolution strategy is applied to fine-tune the policy-independent parameters.
New methods to improve reward functions for OOD data.
A plethora of machine learning approaches including self-supervised learning, transfer learning, semi-supervised learning, meta-learning and their combinations have been recently developed to address out-of-distribution problems in compound screening in terms of chemicals, proteins and cell lines. Self-supervised learning has enjoyed a great success in Natural Language Processing, image recognition, and protein sequences modeling. Cai et al. have proposed a DIstilled Sequence Alignment Embedding (DISAE) transformer for predicting ligand binding to orphan receptors [101]. DISAE has been further extended to out-of-distribution prediction of receptor activities of ligand binding, specifically, agonist vs antagonist [102]. An out-of-cluster meta-learning algorithm has been proposed to explore dark chemical genomics space that includes all Pfam families [103]. Self-supervised learning and semi-supervised learning have also been applied to explore chemical space [104]. Transfer learning is particularly useful in predicting drug responses (both cell viability and gene expressions) for novel cell lines [105] or translating in vitro compound screens to clinical outcomes in patients [106]. These methods, when applied to reward functions, could improve the performance of RL in systems pharmacology.
Biophysics-based methods such as molecular dynamics (MD) simulation, quantum chemistry, and protein-ligand docking (PLD), can be directly applied to evaluate the chemical properties, and thus can be used as reward functions. MD simulation and quantum chemistry calculation are computationally expensive. Emergence of quantum computing may make it feasible to incorporate them directly into RL as reward functions [107]. With the advent of high-accuracy protein structural models, such as AlphaFold2 [15], it now becomes feasible to use PLD to predict ligand-binding sites and poses on dark proteins, on a genome-wide scale. However, PLD suffers from a high false-positive rate due to poor modeling of protein dynamics, solvation effects, crystallized waters, and other challenges [108]; often, small-molecule ligands will indiscriminately ‘stick’ to concave, pocket-like patches on protein surfaces. For these reasons, although AlphaFold2 can accurately predict many protein structures, the relatively low reliability of PLD still poses a significant limitation, even with a limitless supply of predicted structures [109]. Thus, the direct application of PLD remains a challenge for predicting ligand binding to dark proteins. Recently, Cai et al. have proposed an end-to-end sequence-structure-function learning framework PortalCG [17]: protein structure information is not used as a fixed input, but rather as an intermediate layer that can be tuned using various structural and functional information. PortalCG significantly outperforms the direct use of PLD for predicting ligand binding to dark proteins. Thus, it could be an effective strategy to incorporate biophysics domain-knowledge into deep learning frameworks as constraints or regularizations.
Expert opinions
In spite of the great success of RL in GO board game, computer games, and other settings with well-defined environments, its application to drug discovery is still in its infancy. Current efforts in RL mainly focus on target-based drug design. Although RL is a promising technique, its actual value in the target-based drug discovery is overestimated in the current stage. The major hurdle comes from the reward function that is based on predicted binding affinities and needs to be obtained from either a machine learning approach or a physics-based scoring. Both of them are not reliable and accurate enough when applied to chemical compounds with novel structures. For a machine learning approach, it remains a great challenge to predict an OOD sample, i.e., a generated molecule that falls outside the distribution of chemicals in the training data for activity predictions. As a result, the structure of active compounds inferred from RL may not be significantly different from those in the training data. In terms of physical-based scoring, there is a lack of computationally efficient and accurate methods to model multiple factors including conformational dynamics, solvent effects, hydrogen bonding, entropies, crystallized waters, etc., which contribute to the protein-ligand binding affinity. Consequently, the scoring function is still suboptimal and unreliable. In the authors’ humble opinion, existing RL approaches to de novo drug design are scarcely fruitful in regard to the structural novelty of chemical compounds without the significant improvement of efficiency and accuracy of binding affinity predictions.
Although current efforts in RL mainly center around the target-based drug design, systems pharmacology and personalized medicine have emerged as new paradigms in drug discovery. They have advantages over the conventional “one-drug-one-gene” approach when tackling multi-genic, heterogeneous diseases. On the other hand, systems pharmacology-oriented and personalized drug design imposes new challenges on RL-based drug design. Conceptually, systems pharmacology has not been fully appreciated by the pharmaceutical and biotechnology industry. Technically, there are few high-quality labeled data available for training a generalizable machine learning model to predict molecular phenotypic readouts suitable for systems pharmacology-oriented and personalized drug design. Thus, the OOD problem in systems pharmacology is more serious than the target-based drug design. Besides the OOD issue that incapacitates the reward function, the success of RL in systems pharmacology-oriented and personalized drug design needs to overcome additional roadblocks. Firstly, the generalizability and transferability are the central challenges for the deployment of RL in systems pharmacology as the environments are partially observable or changed dramatically (e.g., from cell lines to human tissues). Secondly, RL needs to optimize multiple dynamic and often conflict rewards in a non-stationary environment while the dynamic multi-objective optimization still remains as an unsolved research problem. Finally, it is necessary to integrate multiple heterogeneous, noisy, and high-dimensional omics data for successful systems pharmacology modeling, which is a challenging task under intensive investigations. Thus, the realization of the full potential of RL in drug discovery relies on not only new developments in RL but also advances in other fields that are beyond RL. Specifically, RL needs to be synergistically integrated with unsupervised/supervised machine learning, biophysics, systems biology, multi-omics technology, quantum computing, and beyond.
Article highlights.
Systems pharmacology-oriented personalized drug design is critical to discover effective and safe therapies for untreatable complexed diseases
Reinforcement learning is a potentially powerful technique to enable systems medicine by bridging gaps between target-based and phenotype-based drug discovery
Reinforcement learning has achieved remarkable success in target-based drug design, but is not sufficient to address the challenges in systems pharmacology and personalized medicine
New reinforcement learning techniques are needed to boost the generalizability and transferability of reinforcement learning in partially observed and non-stationary environments, optimize multi-objective reward functions for system-level molecular phenotype readouts and generalize predictive models for out-of-distribution data.
A synergistic integration of reinforcement learning with other machine learning techniques and related fields such as biophysics and quantum computing is needed to achieve the ultimate goal of systems pharmacology-oriented de novo drug design for personalized medicine.
Funding:
The authors are supported by the National Institute of General Medical Sciences (via grant no. R01GM122845) and the National Institute of Aging (via grant no. R01AG057555) of the National Institutes of Health, USA.
Footnotes
Declaration of Interest:
The authors have no other relevant affiliations or financial involvement with any organization or entity with a financial interest in or financial conflict with the subject matter or materials discussed in the manuscript apart from those disclosed.
References
- 1.Polishchuk PG, Madzhidov TI, Varnek A. Estimation of the Size of Drug-like Chemical Space Based on GDB-17 Data. J Comput Aided Mol Des. 2013;27(8):675–679. [DOI] [PubMed] [Google Scholar]
- 2.Goodfellow I, Pouget-Abadie J, Mirza M, Xu B, Warde-Farley D, Ozair S, Courville A, Bengio Y. Generative Adversarial Networks. Commun ACM. 2014;63(11):139–144. [Google Scholar]
- 3.Kingma DP, Welling M. Auto-Encoding Variational Bayes. 2nd Int Conf Learn Represent ICLR 2014 - Conf Track Proc. 2013. [Google Scholar]
- 4.Rezende DJ, Mohamed S. Variational Inference with Normalizing Flows. 32nd Int Conf Mach Learn ICML 2015. 2015;2:1530–1538. [Google Scholar]
- 5.Madhawa K, Ishiguro K, Nakago K, Abe M. GraphNVP: An Invertible Flow Model for Generating Molecular Graphs. 2019.
- 6.Pack Kaelbling L, Littman ML, Moore AW, Hall S. Reinforcement Learning: A Survey. J Artiicial Intell Res. 1996;4:237–285. [Google Scholar]
- 7.Olivecrona M, Blaschke T, Engkvist O, Chen H. Molecular De-Novo Design through Deep Reinforcement Learning. J Cheminform. 2017;9(1):48. [DOI] [PMC free article] [PubMed] [Google Scholar]; * A pioneering work for RL-based molecule generation that uses SMILES strings as state representation and a policy gradient method for policy learning as well as a pretrained prior policy for guidance.
- 8.You J, Liu B, Ying R, Pande V, Leskovec J. Graph Convolutional Policy Network for Goal-Directed Molecular Graph Generation. Adv Neural Inf Process Syst. 2018;2018-Decem:6410–6421. [Google Scholar]; * A leading RL-based method for drug design that introduces molecular graphs as the state representation in MDP rather than SMILES strings and leverages both expert pretraining and adversarial training to guide the policy learning.
- 9.Guimaraes G, Sanchez-Lengeling B, Outeiral C, Luis P, Farias C, Aspuru-Guzik A. Objective-Reinforced Generative Adversarial Networks (ORGAN) for Sequence Generation Models.
- 10.Xie L, Xie L, Kinnings SL, Bourne PE. Novel Computational Approaches to Polypharmacology as a Means to Define Responses to Individual Drugs. Annu Rev Pharmacol Toxicol. 2012;52:361–379. [DOI] [PubMed] [Google Scholar]
- 11.Swinney DC, Lee JA. Recent Advances in Phenotypic Drug Discovery. F1000Research. 2020;9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Moffat JG, Vincent F, Lee JA, Eder J, Prunotto M. Opportunities and Challenges in Phenotypic Drug Discovery: An Industry Perspective. Nat Rev Drug Discov 2017 168. 2017;16(8):531–543. [DOI] [PubMed] [Google Scholar]
- 13.Pham TH, Qiu Y, Zeng J, Xie L, Zhang P. A Deep Learning Framework for High-Throughput Mechanism-Driven Phenotype Compound Screening and Its Application to COVID-19 Drug Repurposing. Nat Mach Intell. 2021;3(3):247–257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Méndez-Lucio O, Zapata PAM, Wichard J, Rouquié D, Clevert D-A. Cell Morphology-Guided De Novo Hit Design by Conditioning Generative Adversarial Networks on Phenotypic Image Features. 2020.
- 15.Jumper J, Evans R, Pritzel A, Green T, Figurnov M, Ronneberger O, et al. Highly Accurate Protein Structure Prediction with AlphaFold. Nature. 2021;596(7873):583–589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Baek M, DiMaio F, Anishchenko I, Dauparas J, Ovchinnikov S, Lee GR, et al. Accurate Prediction of Protein Structures and Interactions Using a Three-Track Neural Network. Science. 2021;373(6557):871–876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Cai T, Xie L, Chen M, Liu Y, He D, Zhang S, Mura C, Bourne PE, Xie L. Exploration of Dark Chemical Genomics Space via Portal Learning: Applied to Targeting the Undruggable Genome and COVID-19 Anti-Infective Polypharmacology. arXiv Prepr arXiv211114283. 2021. [Google Scholar]
- 18.BELLMAN R A Markovian Decision Process. J Math Mech. 1957;6(5):679–684. [Google Scholar]
- 19.Munos R Error Bounds for Approximate Value Iteration. In Proceedings of the 20th National Conference on Artificial Intelligence - Volume 2; AAAI’05; AAAI Press, 2005; pp 1006–1011. [Google Scholar]
- 20.Haskell WB, Jain R, Kalathil D. Empirical Dynamic Programming. Math Oper Res. 2013;41(2):402–429. [Google Scholar]
- 21.Szepesvári C, Munos R. Finite Time Bounds for Sampling Based Fitted Value Iteration. ICML 2005 - Proc 22nd Int Conf Mach Learn. 2005881–888. [Google Scholar]
- 22.Ghavamzadeh M, Kappen H, Azar M, Munos R. Speedy Q-Learning. In Advances in Neural Information Processing Systems; Shawe-Taylor J, Zemel R, Bartlett P, Pereira F, Weinberger KQ, Eds.; Curran Associates, Inc., 2011; Vol. 24. [Google Scholar]
- 23.Watkins CJCH, Dayan P. Q-Learning. Mach Learn. 1992;8(3–4):279–292. [Google Scholar]
- 24.Rummery GA, Niranjan M. On-Line Q-Learning Using Connectionist Systems; 1994.
- 25.Gordon GJ. Approximate Solutions to Markov Decision Processes; Carnegie Mellon University, 1999. [Google Scholar]
- 26.Sutton RS, Barto AG. Reinforcement Learning: An Introduction; MIT press, 2018. [Google Scholar]
- 27.Ormoneit D, Glynn P. Kernel-Based Reinforcement Learning in Average-Cost Problems. IEEE Trans Automat Contr. 2002;47(10):1624–1636. [Google Scholar]
- 28.Ormoneit D, Sen Ś. Kernel-Based Reinforcement Learning. Mach Learn. 2002;49(2):161–178. [Google Scholar]
- 29.Shen J, Yang LF. Theoretically Principled Deep RL Acceleration via Nearest Neighbor Function Approximation. In Proceedings of the AAAI Conference on Artificial Intelligence; 2021; Vol. 35, pp 9558–9566. [Google Scholar]
- 30.Ernst D, Geurts P, Wehenkel L. Tree-Based Batch Mode Reinforcement Learning. J Mach Learn Res. 2005;6:503–556. [Google Scholar]
- 31.Mnih V, Kavukcuoglu K, Silver D, Rusu AA, Veness J, Bellemare MG, et al. Human-Level Control through Deep Reinforcement Learning. Nat 2015 5187540. 2015;518(7540):529–533. [DOI] [PubMed] [Google Scholar]; * A pioneering work of extending approximate dynamic programming to complex problems with large-scale state and/or action spaces, serving as the foundational work for deep reinforcement learning.
- 32.Hasselt H Double Q-Learning. Adv Neural Inf Process Syst. 2010;23:2613–2621. [Google Scholar]
- 33.Wang Z, Schaul T, Hessel M, Hasselt H, Lanctot M, Freitas N. Dueling Network Architectures for Deep Reinforcement Learning. In International conference on machine learning; 2016; pp 1995–2003. [Google Scholar]
- 34.Schaul T, Quan J, Antonoglou I, Silver D. Prioritized Experience Replay. arXiv Prepr arXiv151105952. 2015. [Google Scholar]
- 35.Bellemare MG, Dabney W, Munos R. A Distributional Perspective on Reinforcement Learning. 34th Int Conf Mach Learn ICML 2017. 2017;1:693–711. [Google Scholar]
- 36.Dabney W, Rowland M, Bellemare MG, Munos R. Distributional Reinforcement Learning with Quantile Regression. 32nd AAAI Conf Artif Intell AAAI 2018. 20172892–2901. [Google Scholar]
- 37.Yang D, Zhao L, Lin Z, Qin T, Bian J, Liu T. Fully Parameterized Quantile Function for Distributional Reinforcement Learning. Adv Neural Inf Process Syst. 2019;32. [Google Scholar]
- 38.Williams RJ. Simple Statistical Gradient-Following Algorithms for Connectionist Reinforcement Learning. Mach Learn. 1992;8(3):229–256. [Google Scholar]
- 39.Ghavamzadeh M, Mahadevan S. Hierarchical Policy Gradient Algorithms. Comput Sci Dep Fac Publ Ser. 2003173. [Google Scholar]
- 40.Greensmith E, Bartlett PL, Baxter J. Variance Reduction Techniques for Gradient Estimates in Reinforcement Learning. J Mach Learn Res. 2004;5(9). [Google Scholar]
- 41.Konda VR, Tsitsiklis JN. Actor-Critic Algorithms. In Advances in neural information processing systems; 2000; pp 1008–1014. [Google Scholar]
- 42.Degris T, Pilarski PM, Sutton RS. Model-Free Reinforcement Learning with Continuous Action in Practice. In 2012 American Control Conference (ACC); 2012; pp 2177–2182. [Google Scholar]
- 43.Mnih V, Badia AP, Mirza M, Graves A, Lillicrap T, Harley T, Silver D, Kavukcuoglu K. Asynchronous Methods for Deep Reinforcement Learning. In International conference on machine learning; 2016; pp 1928–1937. [Google Scholar]
- 44.Schulman J, Moritz P, Levine S, Jordan M, Abbeel P. High-Dimensional Continuous Control Using Generalized Advantage Estimation. arXiv Prepr arXiv150602438. 2015. [Google Scholar]
- 45.Kimura H, Kobayashi S. An Analysis of Actor/Critic Algorithms Using Eligibility Traces: Reinforcement Learning with Imperfect Value Function. In ICML; 1998. [Google Scholar]
- 46.Schulman J, Levine S, Abbeel P, Jordan MI, Moritz P. Trust Region Policy Optimization. ArXiv. 2015;abs/1502.0. [Google Scholar]
- 47.Schulman J, Wolski F, Dhariwal P, Radford A, Klimov O. Proximal Policy Optimization Algorithms. ArXiv. 2017;abs/1707.0. [Google Scholar]; * An on-policy SOTA RL method for large-scale state-action space, which has been adopted in various RL-based molecule generation frameworks and is relatively simple to implement.
- 48.Lillicrap TP, Hunt JJ, Pritzel A, Heess NMO, Erez T, Tassa Y, Silver D, Wierstra D. Continuous Control with Deep Reinforcement Learning. CoRR. 2016;abs/1509.0. [Google Scholar]
- 49.Fujimoto S, van Hoof H, Meger D. Addressing Function Approximation Error in Actor-Critic Methods. ArXiv. 2018;abs/1802.0. [Google Scholar]; *An off-policy SOTA RL method that extends conventional deep Q-learning to continuous problems with PG, which is suitable for high-dimensional space and usually very stable for training. This method has been used in TAC and PGFS for synthesis-oriented molecule generation due to the extremely large action space at each time step.
- 50.Haarnoja T, Zhou A, Abbeel P, Levine S. Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor. In ICML; 2018. [Google Scholar]
- 51.Kaiser Ł, Babaeizadeh M, Miłos P, Zej Osí Nski B, Campbell RH, Czechowski K, et al. Model-Based Reinforcement Learning for Atari. 2019.
- 52.Atkeson CG, Santamaria JC. A Comparison of Direct and Model-Based Reinforcement Learning. In Proceedings of International Conference on Robotics and Automation; 1997; Vol. 4, pp 3557–3564 vol.4. [Google Scholar]
- 53.Berkenkamp F, Turchetta M, Schoellig A, Krause A. Safe Model-Based Reinforcement Learning with Stability Guarantees. In Advances in Neural Information Processing Systems; Guyon I, Luxburg UV, Bengio S, Wallach H, Fergus R, Vishwanathan S, Garnett R, Eds.; Curran Associates, Inc., 2017; Vol. 30. [Google Scholar]
- 54.LaValle SM. Planning Algorithms; Cambridge University Press, 2006. [Google Scholar]
- 55.Rao AV A Survey of Numerical Methods for Optimal Control. Adv Astronaut Sci. 2009;135(1):497–528. [Google Scholar]
- 56.Qin SJ, Badgwell TA. A Survey of Industrial Model Predictive Control Technology. Control Eng Pract. 2003;11(7):733–764. [Google Scholar]
- 57.Chua K, Calandra R, McAllister R, Levine S. Deep Reinforcement Learning in a Handful of Trials Using Probabilistic Dynamics Models. Adv Neural Inf Process Syst. 2018;2018-December:4754–4765. [Google Scholar]
- 58.Nagabandi A, Kahn G, Fearing RS, Levine S. Neural Network Dynamics for Model-Based Deep Reinforcement Learning with Model-Free Fine-Tuning. Proc - IEEE Int Conf Robot Autom. 20177579–7586. [Google Scholar]
- 59.Deisenroth M, Rasmussen C. PILCO: A Model-Based and Data-Efficient Approach to Policy Search.; 2011.
- 60.Levine S, Koltun V. Guided Policy Search. In International conference on machine learning; PMLR, 2013; pp 1–9. [Google Scholar]
- 61.Heess N, Wayne G, Silver D, Lillicrap T, Tassa Y, Erez T. Learning Continuous Control Policies by Stochastic Value Gradients. Adv Neural Inf Process Syst. 2015;2015-January:2944–2952. [Google Scholar]
- 62.Sutton RS. Integrated Architectures for Learning, Planning, and Reacting Based on Approximating Dynamic Programming. In In Proceedings of the Seventh International Conference on Machine Learning; Morgan Kaufmann, 1990; pp 216–224. [Google Scholar]
- 63.Kurutach T, Clavera I, Duan Y, Tamar A, Abbeel P. Model-Ensemble Trust-Region Policy Optimization. 6th Int Conf Learn Represent ICLR 2018 - Conf Track Proc. 2018. [Google Scholar]
- 64.Parmas P, Rasmussen CE, Peters J, Doya K. PIPPS: Flexible Model-Based Policy Search Robust to the Curse of Chaos. 35th Int Conf Mach Learn ICML 2018. 2019;9:6463–6472. [Google Scholar]
- 65.Janner M, Fu J, Zhang M, Levine S. When to Trust Your Model: Model-Based Policy Optimization. Adv Neural Inf Process Syst. 2019;32. [Google Scholar]; * A SOTA model-based RL that achieves favorable performances in various complex tasks by combining model ensembles and short model rollouts.
- 66.Peng B, Li X, Gao J, Liu J, Wong KF. Deep Dyna-Q: Integrating Planning for Task-Completion Dialogue Policy Learning. ACL 2018 – 56th Annu Meet Assoc Comput Linguist Proc Conf (Long Pap. 2018;1:2182–2192. [Google Scholar]
- 67.Polykovskiy D, Zhebrak A, Sanchez-Lengeling B, Golovanov S, Tatanov O, Belyaev S, et al. Molecular Sets (MOSES): A Benchmarking Platform for Molecular Generation Models. Front Pharmacol. 2020;11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Brown N, Fiscato M, Segler MHS, Vaucher AC. GuacaMol: Benchmarking Models for de Novo Molecular Design. J Chem Inf Model. 2019;59(3):1096–1108. [DOI] [PubMed] [Google Scholar]
- 69.Neil D, Segler MHS, Guasch L, Ahmed M, Plumbley D, Sellwood M, Brown N. Exploring Deep Recurrent Models with Reinforcement Learning for Molecule Design. In ICLR; 2018. [Google Scholar]
- 70.Yang X, Aasawat TK, Yoshizoe K. Practical Massively Parallel Monte-Carlo Tree Search Applied to Molecular Design. 2020. [Google Scholar]
- 71.Ahn S, Kim J, Lee H, Shin J. Guiding Deep Molecular Optimization with Genetic Exploration. Adv Neural Inf Process Syst. 2020;2020-December. [Google Scholar]
- 72.Bengio Y, Lodi A, Prouvost A. Machine Learning for Combinatorial Optimization: A Methodological Tour d’horizon. Eur J Oper Res. 2021;290(2):405–421. [Google Scholar]
- 73.Bello I, Pham H, Le QV., Norouzi M, Bengio S. Neural Combinatorial Optimization with Reinforcement Learning. 5th Int Conf Learn Represent ICLR 2017 - Work Track Proc. 2016. [Google Scholar]
- 74.Lu F, Li M, Min X, Li C, Zeng X. De Novo Generation of Dual-Target Ligands Using Adversarial Training and Reinforcement Learning. Brief Bioinform. 2021;22(6). [DOI] [PubMed] [Google Scholar]
- 75.Atance SR, Diez JV, Engkvist O, Olsson S, Mercado R. De Novo Drug Design Using Reinforcement Learning with Graph-Based Deep Generative Models. 2021. [DOI] [PubMed]
- 76.Popova M, Shvets M, Oliva J, Isayev O. MolecularRNN: Generating Realistic Molecular Graphs with Optimized Properties. arXiv Prepr arXiv190513372. 2019. [Google Scholar]
- 77.Liu X, Ye K, van Vlijmen HWT, IJzerman AP, van Westen GJP. An Exploration Strategy Improves the Diversity of de Novo Ligands Using Deep Reinforcement Learning: A Case for the Adenosine A2A Receptor. J Cheminform. 2019;11(1):1–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Pereira T, Abbasi M, Ribeiro B, Arrais JP. Diversity Oriented Deep Reinforcement Learning for Targeted Molecule Generation. J Cheminform. 2021;13(1). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Zhou Z, Kearnes S, Li L, Zare RN, Riley P. Optimization of Molecules via Deep Reinforcement Learning. Sci Rep. 2019;9(1):1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Tang B, He F, Liu D, Fang M, Wu Z, Xu D. AI-Aided Design of Novel Targeted Covalent Inhibitors against SARS-CoV-2. bioRxiv Prepr Serv Biol. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Wen J, Kumar S, Gummadi R, Schuurmans D. Characterizing the Gap Between Actor-Critic and Policy Gradient. arXiv Prepr arXiv210606932. 2021. [Google Scholar]
- 82.Simm GNC, Pinsler R, Csányi G, Hernández-Lobato JM. Symmetry-Aware Actor-Critic for 3D Molecular Design. ArXiv. 2021;abs/2011.1. [Google Scholar]
- 83.Ståhl N, Falkman G, Karlsson A, Mathiason G, Boström J. Deep Reinforcement Learning for Multiparameter Optimization in de Novo Drug Design. 2019. [DOI] [PubMed]
- 84.Horwood J, Noutahi E. Molecular Design in Synthetically Accessible Chemical Space via Deep Reinforcement Learning. ACS Omega. 2020;5(51):32984–32994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Gottipati SK, Pathak Y, Sattarov B, Sahir, Nuttall R, Amini M, Taylor ME, Chandar APS. Towered Actor Critic For Handling Multiple Action Types In Reinforcement Learning For Drug Discovery. In AAAI; 2021. [Google Scholar]
- 86.Gottipati SK, Sattarov B, Niu S, Pathak Y, Wei H, Liu S, et al. Learning To Navigate The Synthetically Accessible Chemical Space Using Reinforcement Learning. In ICML; 2020. [Google Scholar]; * A novel RL framework for synthesis-oriented molecule generation includes a designed environment using reactants and reaction templates as hierarchical actions, which guarantees the molecule generated are synthesizable along providing a recipe for synthesis, and a proposed agent that leverages TD3 and KNN algorithm for stable policy learning and efficient action selection in a large action space (at every time-step).
- 87.Lambrinidis G, Tsantili-Kakoulidou A. Challenges with Multi-Objective QSAR in Drug Discovery. Expert Opin Drug Discov. 2018;13(9):851–859. [DOI] [PubMed] [Google Scholar]
- 88.Li Z, Cho BR, Melloy BJ. Quality by Design Studies on Multi-Response Pharmaceutical Formulation Modeling and Optimization. J Pharm Innov. 2013;8(1):28–44. [Google Scholar]
- 89.Cruz-Monteagudo M, Schürer S, Tejera E, Pérez-Castillo Y, Medina-Franco JL, Sánchez-Rodríguez A, Borges F. Systemic QSAR and Phenotypic Virtual Screening: Chasing Butterflies in Drug Discovery. Drug Discov Today. 2017;22(7):994–1007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Cruz-Monteagudo M, Medina-Franco JL, Pérez-Castillo Y, Nicolotti O, Cordeiro MNDS, Borges F. Activity Cliffs in Drug Discovery: Dr Jekyll or Mr Hyde? Drug Discov Today. 2014;19(8):1069–1080. [DOI] [PubMed] [Google Scholar]
- 91.Scholkopf B, Locatello F, Bauer S, Ke NR, Kalchbrenner N, Goyal A, Bengio Y. Towards Causal Representation Learning. Proc IEEE. 2021;109(5):612–634. [Google Scholar]; * A prominent work tackling model generalization problems, such as in the settings of limited i.i.d data or distribution shift, using causal representation learning, which could be useful to address the OOD problem of reward functions and generalization issues of deep reinforcement learning.
- 92.Chandak Y, Theocharous G, Shankar S, White M, Mahadevan S, Thomas PS. Optimizing for the Future in Non-Stationary MDPs. 37th Int Conf Mach Learn ICML 2020. 2020;PartF168147–2:1391–1402. [Google Scholar]
- 93.Ghosh D, Rahme J, Kumar A, Zhang A, Adams RP, Levine S. Why Generalization in RL Is Difficult: Epistemic POMDPs and Implicit Partial Observability. Adv Neural Inf Process Syst. 2021;34. [Google Scholar]; * A potential approach to improve the generalization of RL through introducing a new formulation of MDP, epistemic POMDP, that accounts for partial observability and proposing a policy gradient method with bootstrap sampling technique to solve the epistemic POMDP.
- 94.Everitt T, Krakovna V, Orseau L, Legg S. Reinforcement Learning with a Corrupted Reward Channel. IJCAI Int Jt Conf Artif Intell. 2017;0:4705–4713. [Google Scholar]
- 95.Riedmiller M, Hafner R, Lampe T, Neunert M, Degrave J, Van De Wiele T, Mnih V, Heess N, Springenberg T. Learning by Playing - Solving Sparse Reward Tasks from Scratch. 35th Int Conf Mach Learn ICML 2018. 2018;10:6910–6919. [Google Scholar]
- 96.Sánchez-Rodríguez A, Pérez-Castillo Y, Schürer SC, Nicolotti O, Mangiatordi GF, Borges F, Cordeiro MNDS, Tejera E, Medina-Franco JL, Cruz-Monteagudo M. From Flamingo Dance to (Desirable) Drug Discovery: A Nature-Inspired Approach. Drug Discov Today. 2017;22(10):1489–1502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Dong Y, Zhang S, Liu X, Zhang Y, Shen T. Variance Aware Reward Smoothing for Deep Reinforcement Learning. Neurocomputing. 2021;458:327–335. [Google Scholar]
- 98.Agarwal R, Liang C, Schuurmans D, Norouzi M. Learning to Generalize from Sparse and Underspecified Rewards. 36th Int Conf Mach Learn ICML 2019. 2019;2019-June:184–194. [Google Scholar]; * A promising RL method for tackling sparse reward problem with a design of a mode covering exploration using KL divergence and an auxiliary reward function using meta-learning.
- 99.Yang R, Sun X, Narasimhan K. A Generalized Algorithm for Multi-Objective Reinforcement Learning and Policy Adaptation. Adv Neural Inf Process Syst. 2019;32. [Google Scholar]; * A potential approach to approximately retrieve the pareto front for MORL by leveraging a designed bellman operator and integrating homotopy optimization into the framework.
- 100.Chen D, Wang Y, Gao W. A Two-Stage Multi-Objective Deep Reinforcement Learning Framework. Front Artif Intell Appl. 2020;325:1063–1070. [Google Scholar]
- 101.Cai T, Lim H, Abbu KA, Qiu Y, Nussinov R, Xie L. MSA-Regularized Protein Sequence Transformer toward Predicting Genome-Wide Chemical-Protein Interactions: Application to GPCRome Deorphanization. J Chem Inf Model. 2021;61(4):1570–1582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Cai T, Abbu KA, Liu Y, Xie L. DeepREAL: A Deep Learning Powered Multi-Scale Modeling Framework Towards Predicting Out-of-Distribution Receptor Activity of Ligand Binding. bioRxiv. 20212021.09.12.460001. [Google Scholar]
- 103.Mistry J, Chuguransky S, Williams L, Qureshi M, Salazar GA, Sonnhammer ELL, et al. Pfam: The Protein Families Database in 2021. Nucleic Acids Res. 2021;49(D1):D412–D419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Liu Y, Wu Y, Shen X, Xie L. COVID-19 Multi-Targeted Drug Repurposing Using Few-Shot Learning. Front Bioinforma. 2021;0:18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Liu Q, Qiu Y, Xie L. Predictive Modeling of Multiplex Chemical Phenomics for Novel Cells and Patients: Applied to Personalized Alzheimer’s Disease Drug Repurposing. bioRxiv. 20212021.08.09.455708. [Google Scholar]
- 106.He D, Liu Q, Xie L. Robust Prediction of Patient-Specific Clinical Response to Unseen Drugs From in Vitro Screens Using Context-Aware Deconfounding Autoencoder. bioRxiv. 2021. [Google Scholar]
- 107.Marx V Biology Begins to Tangle with Quantum Computing. Nat Methods 2021 187. 2021;18(7):715–719. [DOI] [PubMed] [Google Scholar]
- 108.Grinter SZ, Zou X. Challenges, Applications, and Recent Advances of Protein-Ligand Docking in Structure-Based Drug Design. Molecules. 2014;19(7):10150–10176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Jaiteh M, Rodríguez-Espigares I, Selent J, Carlsson J. Performance of Virtual Screening against GPCR Homology Models: Impact of Template Selection and Treatment of Binding Site Plasticity. PLOS Comput Biol. 2020;16(3):e1007680. [DOI] [PMC free article] [PubMed] [Google Scholar]


