Control of Ca²⁺ signals by astrocyte nanoscale morphology at tripartite synapses

Abstract

Much of the Ca²⁺ activity in astrocytes is spatially restricted to microdomains and occurs in fine processes that form a complex anatomical meshwork, the so‐called spongiform domain. A growing body of literature indicates that those astrocytic Ca²⁺ signals can influence the activity of neuronal synapses and thus tune the flow of information through neuronal circuits. Because of technical difficulties in accessing the small spatial scale involved, the role of astrocyte morphology on Ca²⁺ microdomain activity remains poorly understood. Here, we use computational tools and idealized 3D geometries of fine processes based on recent super‐resolution microscopy data to investigate the mechanistic link between astrocytic nanoscale morphology and local Ca²⁺ activity. Simulations demonstrate that the nano‐morphology of astrocytic processes powerfully shapes the spatio‐temporal properties of Ca²⁺ signals and promotes local Ca²⁺ activity. The model predicts that this effect is attenuated upon astrocytic swelling, hallmark of brain diseases, which we confirm experimentally in hypo‐osmotic conditions. Upon repeated neurotransmitter release events, the model predicts that swelling hinders astrocytic signal propagation. Overall, this study highlights the influence of the complex morphology of astrocytes at the nanoscale and its remodeling in pathological conditions on neuron‐astrocyte communication at so‐called tripartite synapses, where astrocytic processes come into close contact with pre‐ and postsynaptic structures.

Main Points

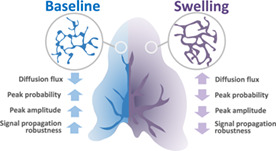
• Astrocyte nano‐morphology favors the compartmentalization of biochemical signals.

• This compartmentalization promotes local Ca²⁺ activity and signal propagation robustness.

• In contrast, its pathological remodeling upon swelling attenuates Ca²⁺ activity.

1. INTRODUCTION

Astrocytes are glial cells of the central nervous system that are essential for brain development and function (Verkhratsky and Nedergaard 2018). They notably modulate neuronal communication at synapses. Astrocytic Ca²⁺ signals are triggered by neurotransmitters released by active neurons, which can trigger the release of neuroactive molecules by the astrocyte, referred to as gliotransmitters. The first type of astrocytic Ca²⁺ signals that has been observed was Ca²⁺ waves that propagate through gap junctions in astrocyte networks (Giaume and Venance 1998). Ca²⁺ waves have also been observed in the branches of single astrocytes, sporadically propagating to the soma (Haustein et al. 2014; Bindocci et al. 2017). The recent development of Ca²⁺ imaging techniques with improved spatial and temporal resolution has revealed the existence of spatially‐restricted Ca²⁺ signals in astrocytes, referred to as microdomains or hotspots (Di Castro et al. 2011; Panatier et al. 2011; Stobart, Ferrari, Barrett, Glück, et al. 2018; Srinivasan et al. 2015; Shigetomi et al. 2013; Sherwood et al. 2017; Otsu et al. 2015; Lind et al. 2013; Bindocci et al. 2017; Agarwal et al. 2017; Arizono et al. 2020; Otsu et al. 2015; Grosche et al. 1999). These local Ca²⁺ signals account for the vast majority ($\approx$ 80%) of astrocytic Ca²⁺ activity and occur in fine processes, which occupy 75% of the astrocytic volume (Bindocci et al. 2017), forming the spongiform domain, also referred to as the gliapil. Given that one astrocyte may contact tens of thousands of synapses simultaneously (Bushong et al. 2002) via these fine processes, local and fast Ca²⁺ signals might enable the astrocyte to powerfully yet precisely control the flow of information through synaptic circuits. Importantly, reactive astrocytes, hallmark of brain diseases, display aberrant amplitude, duration, frequency and spatial spread of Ca²⁺ signals (Shigetomi et al. 2019; Nedergaard et al. 2010; Lee et al. 2022).

Cellular micro‐morphology lends itself to the compartmentalization of biochemical signals. For example, the anatomical design of dendritic spines restricts the diffusion of Ca²⁺ to the activated synapse, which reduces cross‐talk between nearby synapses (Santamaria et al. 2011; Tonnesen et al. 2014; Yuste et al. 2000; Noguchi et al. 2005; Yasuda 2017; Holcman and Schuss 2011). The complex shapes of Bergmann glia (Grosche et al. 1999) and perisynaptic “astrocytic compartments” along major branches (Panatier et al. 2011) have been proposed to restrict Ca²⁺ signals to the vicinity of synapses. Fine processes of the spongiform domain, however, cannot be resolved by diffraction‐limited light microscopy (Rusakov 2015), so that the contribution of their morphology to shaping local Ca²⁺ signals is poorly understood. Our recent 3D STED study (Arizono et al. 2020) revealed the structural basis of compartmentalized spontaneous Ca²⁺ signals in fine astrocytic processes. Importantly, pathological changes in astrocytic morphology (Lafrenaye and Simard 2019), such as “astrocytic swelling,” are paired with aberrant Ca²⁺ signals (Shigetomi et al. 2019). We have recently reported that swelling can also occur at the level of fine astrocytic processes (Arizono, Bancelin, et al. 2021). The effect of such a remodeling of astrocytic nano‐morphology on the local Ca²⁺ signals involved in regulating synapses remains yet unclear. Together, there is a great interest in understanding the mechanistic link between the nano‐morphology of astrocytic processes and Ca²⁺ profiles in health and disease. Computational approaches make it possible to simulate different geometrical scenarios, in a much more systematic and controlled way than what could be done experimentally. Computational models can thus help us gain insights into the impact of morphological parameters on Ca²⁺ activity.

Here, we use computational tools to explore the role of the anatomical design of the gliapil. To do so, we perform simulations in branchlet geometries that we designed based on super‐resolution microscopy data reported in live tissue (Arizono et al. 2020), consisting of nodes, which host Ca²⁺ microdomains, and their intervening shafts of variable widths. Our simulation results suggest that the nanoscale design of the spongiform domain effectively decreases diffusion flux, which increases Ca²⁺ peak probability, duration and amplitude in the stimulated and neighboring nodes. To test those predictions, we performed Ca²⁺ recordings in organotypic hipppocampal cultures in hypo‐osmotic conditions, where the normal node‐shaft arrangement is altered. In line with our model predictions, Ca²⁺ activity in hypo‐osmotic conditions was decreased compared to Ca²⁺ activity in normal tissue. We further found that, upon repeated neuronal stimulation, thin shafts allow signal propagation even if some stimuli are omitted, thus allowing for a more robust signal propagation.

Overall, our study sheds light on the influence of the nanoscale morphology of the complex spongiform domain of astrocytes on Ca²⁺ microdomain activity and indicates that pathological morphological changes may substantially affect their Ca²⁺ activity.

2. METHODS

2.1. Stochastic spatially‐explicit voxel‐based simulations

In order to model astrocyte Ca²⁺ signals in astrocyte branchlets, we have used the voxel‐based “GCaMP” implementation of the Inositol 3‐Phosphate (IP₃) receptor‐dependent Ca²⁺ signaling model from Denizot et al. (2019), using the same reaction scheme and parameter values (Figure 1b). Briefly, we model Ca²⁺ fluxes in and out of the cytosol, mediated by ${\mathrm{Ca}}^{2+}$ channels and pumps on the endoplasmic reticulum (ER) and on the plasma membrane. ${\mathrm{Ca}}^{2+}$ signals occur when some IP₃R channels are in the open state. IP₃ can be synthesized by the Ca²⁺‐dependent activity of phospholipase Cδ (PLCδ) and the removal of IP₃ molecules from the cytosol is expressed as a single decay rate. IP₃R kinetics is described by a Markov model, derived from De Young & Keizer's model (De Young and Keizer 1992). Each IP₃R molecule contains one IP₃ binding site and two ${\mathrm{Ca}}^{2+}$ binding sites. An IP₃R is in the open state when in state $\left\{110\right\}$ (first Ca site and IP₃ bound, second Ca site free). Depending on the simulation, other diffusing molecules were added to the model, such as the fluorescent molecule ZsGreen and fluorescent ${\mathrm{Ca}}^{2+}$ indicators, here 10 μM of GCaMP6s. GCaMPs are genetically‐encoded ${\mathrm{Ca}}^{2+}$ indicators (GECIs) that are derived from the fluorescent protein GFP and the ${\mathrm{Ca}}^{2+}$ buffer calmodulin (see Shigetomi et al. (2016) for a review on GECIs). Unless specified otherwise, simulation time T was 50 s. Data collection interval was 1 ms. For further details on the kinetic scheme and model assumptions, please refer to Denizot et al. (2019).

FIGURE 1.

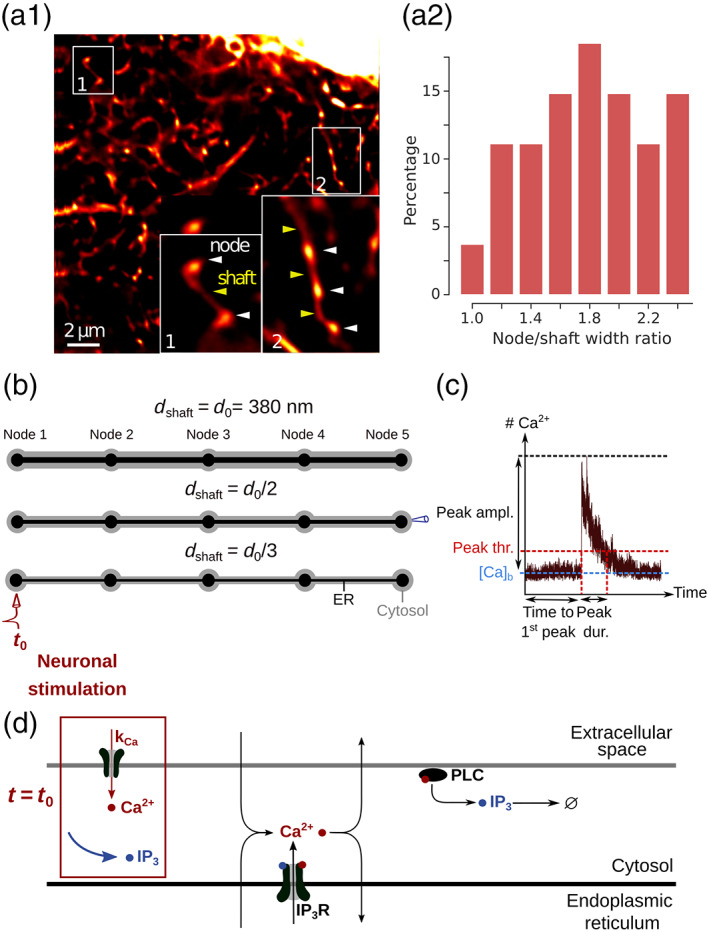
Geometries and kinetic scheme used for simulating ${\mathrm{Ca}}^{2+}$ dynamics in node/shaft structures of the gliapil. (a1) Representative STED image showing the astrocytic spongiform domain. Zoom‐in images show its anatomical units: Nodes and shafts. (a2) Distribution of the ratio between node width and the width of its neighboring shaft, measured using STED microscopy, n = 28. (b) Idealized geometries designed to reproduce the node/shaft ultrastructure of the spongiform domain. Nodes are approximated as spheres of diameter 380 nm and shafts as 1 μm‐long cylinders, based on their recent characterization in live tissue by Arizono et al. (2020) (Figure 1i–k. Shaft width varied based on experimentally‐observed node‐shaft width ratios reported in panel b: $d_{\text{shaft}}={\mathrm{d}}_0=380$ nm, $d_{\text{shaft}}=\frac{{\mathrm{d}}_0}{2}$ and $d_{\text{shaft}}=\frac{{\mathrm{d}}_0}{3}$. The geometries designed in this study, referred to as “5 nodes,” contain 5 identical nodes and 4 identical shafts. Unless specified otherwise, ER geometry (black) also consists in node/shaft successions (see Methods). The associated cytosolic volume, plasma and ER membrane areas are presented in Table 1. (c) Example of a ${\mathrm{Ca}}^{2+}$ trace of the model, recorded in one node. ${\mathrm{Ca}}^{2+}$ activity is quantified by measuring time to 1^st peak, peak probability, amplitude, duration and frequency. A peak is detected when the number of ${\mathrm{Ca}}^{2+}$ ions in the recorded node increases above peak threshold ${\left[\mathit{Ca}\right]}_{\mathrm{b}}+n{\sigma }_{\mathrm{Ca}}$ (see Methods). (d) Biochemical processes included in the model. ${\mathrm{Ca}}^{2+}$ can enter/exit the cytosol from/to the extracellular space or the endoplasmic reticulum (ER), resulting from the activity of ${\mathrm{Ca}}^{2+}$ channels/pumps. ${\mathrm{Ca}}^{2+}$ and IP₃ diffuse in the cytosol following Brownian motion. The kinetics of ${\mathit{IP}}_{3}R$ channels corresponds to the 8‐state Markov model from Denizot et al. (2019), adapted from De Young and Keizer (1992); Bezprozvanny et al. (1991). When both IP₃ and ${\mathrm{Ca}}^{2+}$ are bound to IP₃R activating binding sites, the IP₃R is in open state and ${\mathrm{Ca}}^{2+}$ enters the cytosol. ${\mathrm{Ca}}^{2+}$ can activate phospholipase C δ (PLCδ), which results in the production of IP₃. For more details, please refer to Denizot et al. (2019). Neuronal stimulation is simulated as an infusion of IP₃ in the cytosol and the opening of ${\mathrm{Ca}}^{2+}$ channels at the plasma membrane with an influx rate ${\mathrm{k}}_{\mathrm{Ca}}$ (see Methods).

The model was implemented using the STochastic Engine for Pathway Simulation (STEPS, http://steps.sourceforge.net/), a python package performing exact stochastic simulation of reaction–diffusion systems (Hepburn et al. 2012). More precisely, simulations were performed using the spatial stochastic “Tetexact” solver, based on Gillespie's Stochastic Simulation Algorithm (SSA) (Gillespie 1977), extended for diffusive fluxes across voxels in tetrahedral meshes (Hepburn et al. 2012). Diffusion is treated as a first order reaction in the SSA system, whose rate is determined by the diffusion coefficient of the diffusing species.

Simulations in STEPS can be performed in complex geometries in three spatial dimensions. Space is divided into well‐mixed tetrahedral compartments, referred to as voxels. Reactions between two molecules can only occur if they are located within the same voxel. Diffusion events are modeled as a decrease of the number of molecules in the original voxel and an increase in the number of molecules in its neighboring voxel. Boundary conditions, except when specified otherwise, were reflective. In other words, mobile molecules could not diffuse away from the geometry, as if they were “bouncing” onto the plasma membrane. STEPS enables to compute, in complex 3D geometries, reactions and diffusion in the cytosol as well as reactions between cytosolic molecules and molecules located at the plasma or ER membrane.

2.2. Geometries

Typical astrocyte branchlet geometries were designed from their recent experimental characterization in live tissue at high spatial resolution (50 nm in x–y) (Arizono et al. 2020). Those geometries consist in alternations of bulbous structures, nodes, connected to each other with cylindrical structures, shafts. Geometries with different shaft widths ${\mathrm{d}}_{\text{shaft}}$ were designed using Trelis software (https://www.csimsoft.com/trelis, Figure 1a). The geometry of a node was approximated as being a sphere of diameter 380 nm. Shaft geometry consisted in a 1 μm long cylinder. Shaft diameter was defined relative to node diameter. For example, shaft diameter was the same as node diameter, that is, ${\mathrm{d}}_{\text{shaft}}$ = $d_0$ = 380 nm. Similarly, shaft diameter was 190 nm and 127 nm for ${\mathrm{d}}_{\text{shaft}}$ = $\frac{{\mathrm{d}}_0}{2}$ and $\frac{{\mathrm{d}}_0}{3}$, respectively. Cones were positioned between spheres and cylinders in order to create a smoother transition between nodes and shafts, better approximating the geometry observed experimentally. Cytosolic volume was thus V ₁ = 0.620 μm³, V ₂ = 0.263 μm³, and V ₃ = 0.195 μm³, for ${\mathrm{d}}_{\text{shaft}}$ = $d_0$, $\frac{{\mathrm{d}}_0}{2}$ and $\frac{{\mathrm{d}}_0}{3}$, respectively. Please note that molecular concentrations were the same in all simulations, so that the total number of molecules in basal conditions in shafts varied depending on shaft width. A subset of simulations was performed in a geometry with V ₁ = 0.258 μm³. This geometry is characterized, similarly to geometries with ${\mathrm{d}}_{\text{shaft}}$ = $d_0$, by a node/shaft width ratio of 1. It contains cylinders of length 750 nm, diameter 285 nm and spheres of diameter 285 nm. As a first approximation, ER geometry was considered to be similar to the geometry of the astrocyte branchlet: node/shaft successions. ER nodes were aligned with cytosolic nodes. As no quantification of the ratio between astrocytic ER volume and cellular volume was found in the literature, ER volume was 10% of the total branchlet volume, based on available data in neurons (Spacek and Harris 1997). As the shape and distribution of the ER in fine processes have not been characterized in live tissue but are likely highly variable, additional simulations were performed in meshes with various ER shapes: “No ER,” “Node ER,” and “Cyl ER,” in which there was no ER, discontinuous ER in nodes or cylindrical ER, respectively (Figures S7–S9). The cytosolic volume, plasma and ER membrane surface areas of those 3D geometries are presented in Table 1.

TABLE 1.

Characteristics of the geometries of astrocyte branchlets used in this study. $V_{\mathrm{cyt}}$ is the cytosolic volume, $S_{\mathrm{PM}}$ is the area of the plasma membrane and $S_{\mathrm{ER}}$ is the area of the ER membrane. Volumes are expressed in nm³ and areas in nm². Meshes are available at http://modeldb.yale.edu/266928.

Geometry	$V_{\mathrm{cyt}}$ (nm3)	$S_{\mathrm{PM}}$ (nm2)	$S_{\mathrm{ER}}$ (nm2)
“5nodes” $d_{\text{shaft}}={\mathrm{d}}_0$	$6.20\times {10}^8$	$7.73\times {10}^6$	$2.19\times {10}^6$
“5nodes” $d_{\text{shaft}}={\mathrm{d}}_0/2$	$2.63\times {10}^8$	$4.95\times {10}^6$	$1.28\times {10}^6$
“5nodes” $d_{\text{shaft}}={\mathrm{d}}_0/3$	$1.95\times {10}^8$	$4.10\times {10}^6$	$9.99\times {10}^5$
“No ER” $d_{\text{shaft}}={\mathrm{d}}_0$	$6.73\times {10}^8$	$7.73\times {10}^6$	0.00
“No ER” $d_{\text{shaft}}={\mathrm{d}}_0/2$	$2.83\times {10}^8$	$4.95\times {10}^6$	0.00
“No ER” $d_{\text{shaft}}={\mathrm{d}}_0/3$	$2.10\times {10}^8$	$4.09\times {10}^6$	0.00
“Node ER” $d_{\text{shaft}}={\mathrm{d}}_0$	$6.67\times {10}^8$	$7.75\times {10}^6$	$4.17\times {10}^5$
“Node ER” $d_{\text{shaft}}={\mathrm{d}}_0/2$	$2.74\times {10}^8$	$4.96\times {10}^6$	$4.37\times {10}^5$
“Node ER” $d_{\text{shaft}}={\mathrm{d}}_0/3$	$2.00\times {10}^8$	$4.11\times {10}^6$	$4.41\times {10}^5$
“Cyl ER” $d_{\text{shaft}}={\mathrm{d}}_0$	$6.27\times {10}^8$	$7.74\times {10}^6$	$2.03\times {10}^6$
“Cyl ER” $d_{\text{shaft}}={\mathrm{d}}_0/2$	$2.77\times {10}^8$	$4.95\times {10}^6$	$8.78\times {10}^5$
“Cyl ER” $d_{\text{shaft}}={\mathrm{d}}_0/3$	$2.07\times {10}^8$	$4.09\times {10}^6$	$5.86\times {10}^5$

A sensitivity study was performed to investigate the effect of voxel size on the kinetics of the molecular interactions modeled. Information on the voxel sizes of the different meshes used is presented in Table S1. Results are presented in Figure S1. Meshes that contained voxels that were <50 nm³ were characterized by aberrant kinetics, resulting in aberrant average numbers of molecules in a given state. Those results thus suggest that to prevent errors due to voxel size, meshes should not display voxel sizes that are <50 nm³. We have thus made sure, while meshing the geometries in which simulations were ran, that no voxels were <50 nm³. Minimum voxel size was 443, 1100, and 447 nm³, for ${\mathrm{d}}_{\text{shaft}}$ = ${\mathrm{d}}_0$, $\frac{{\mathrm{d}}_0}{2}$ and $\frac{{\mathrm{d}}_0}{3}$ geometries, respectively.

In a subset of simulations, ER geometry varied. The shape of the cell was the same as in “5nodes” geometries (Figure 1). ER geometry consisting of node/shaft alternations, described above, is referred to as “Node/shaft ER.” “No ER” geometry contains no ER. “Node ER” is characterized by a discontinuous ER geometry, consisting in spheres of diameter 54 nm, located in cellular nodes. “Cyl ER” corresponds to a cylindrical ER, of length $l_{\mathrm{ER}}$ = 6274 nm and a diameter of 108, 54, and 36 nm, for ${\mathrm{d}}_{\text{shaft}}$ = $d_0$, $\frac{{\mathrm{d}}_0}{2}$ and $\frac{{\mathrm{d}}_0}{3}$, respectively. The associated cytosolic volume, ER and plasma membrane area are presented in Table 1.

2.3. Protocol for simulating bleaching experiments

In order to test whether the idealized geometries presented in Figure 1 are a good approximation of the spongiform ultrastructure of astrocyte branchlets, we have simulated their fluorescence recovery after photobleaching (FRAP) experiments. Briefly, laser pulses are simulated on a node (region of interest) while the fluorescence level is being recorded. At bleaching time, the fluorescence level in the region of interest decreases to $I_0$. Then, because of the diffusion of fluorescent molecules into the region of interest, fluorescence increases until it reaches a new steady state, $I_{\inf }$. We characterize node compartmentalization by measuring the time $\tau$ taken by fluorescing molecules to diffuse into the node to reach $I_{\inf }$. In other words, a high node compartmentalization will be associated with a high value of $\tau$. Thus, three main parameters characterize bleaching traces: $I_0$, $\tau$ and $I_{\inf }$.

To mimic bleaching experiments in fine branchlets performed by (Arizono et al. 2020), ZsGreen molecules were added to simulation space. After 2 s of simulation, providing the basal level of fluorescence, 60% of ZsGreen molecules were bleached. In order to fit $I_0$ and $I_{\inf }$ that were measured experimentally, and as bleaching time lasted 10 ms in experiments and 1 ms in simulations, the bleached volume in simulations was adjusted depending on the geometry (see Figure 2a). Bleaching was simulated as a transition from ZsGreen molecules to ZsGreen‐bleached molecules, the latter being considered as non‐fluorescing molecules. Screenshots of simulations, illustrating the diffusion of ZsGreen and ZsGreen‐bleached molecules, are presented in Figure S2b. The number of ZsGreen molecules in the central node was recorded over simulation time and a fit was performed following Equation (1) to determine the values of $I_0$, $I_{\inf }$ and $\tau$.

$$I\left(t\right)=I_0-\left(I_0-I_{\inf }\right)e^{-\mathrm{t}/\tau },$$ (1)

where I(t) is the level of fluorescence measured at time t. The coefficient of diffusion, $D_{\text{ZsGreen}}$, and the concentration, [ZsGreen], of ZsGreen were adjusted to fit experimental data. Indeed, the amplitude of [ZsGreen] fluctuations at steady state is inversely proportional to the number of ZsGreen molecules in the geometry. In other words, fluorescence signals are more noisy when [ZsGreen] is low. Moreover, the autocorrelation of those fluctuations depends on the coefficient of diffusion of ZsGreen, $D_{\text{ZsGreen}}$. If $D_{\text{ZsGreen}}$ increases, the autocorrelation of Lag, where Lag is the autocorrelation delay, will decrease faster as Lag increases. Comparing the fluctuations of [ZsGreen] and its autocorrelation in experiments and in simulations thus enabled to find the values of $D_{\text{ZsGreen}}$ and of [ZsGreen] that allowed for the best fit to experimental data. In the simulations presented here, $D_{\text{ZsGreen}}$ = 90 $\mu m^2.s^{-1}$ and [ZsGreen] = 25 μM.

FIGURE 2.

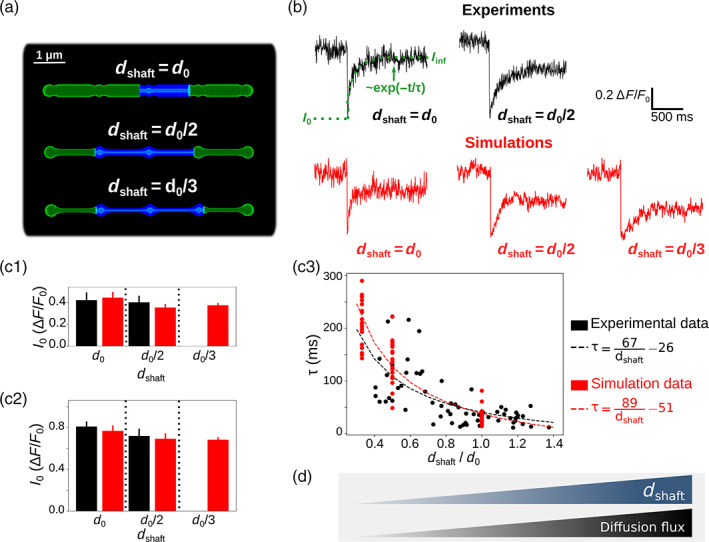
Simulations confirm that thin shafts favor node compartmentalization. (a) Geometries of different shaft widths ${\mathrm{d}}_{\text{shaft}}$, $d_{\text{shaft}}={\mathrm{d}}_0$, $\frac{{\mathrm{d}}_0}{2}$ and $\frac{{\mathrm{d}}_0}{3}$, used in the bleaching simulations. Blue color represents the bleached volume, which varied depending on the value of ${\mathrm{d}}_{\text{shaft}}$ in order to fit experimental values of $I_0$ and $I_{\mathit{inf}}$. (b) Representative experimental (top) and simulation (bottom) traces for different shaft width values. $I_0$, $I_{\mathit{inf}}$ and $\tau$ were calculated using Equation (1). Note that simulations were also performed for $d_{\text{shaft}}=\frac{{\mathrm{d}}_0}{3}$. (c) Quantification of $I_0$ (c1), $I_{\mathit{inf}}$ (c2), and $\tau$ (c3) values in simulations (red) compared to experiments (black). Note that no experimental data was available for $d_{\text{shaft}}=\frac{{\mathrm{d}}_0}{3}$. In c1 and c2, n = 5 × 2 and 20 × 3 for experiments and simulations, respectively. Data are presented as mean ± STD. In c3, n = 66 and n = 20 × 3 for experiments and simulations, respectively. $\tau$ is negatively correlated to ${\mathrm{d}}_{\text{shaft}}$ in experiments (n = 66 from 7 slices; Spearman r = −0.72, p < 0.001***) and simulations (n = 60; Spearman r = −0.89, p < 0.001***). Black and red lines represent curve fit of $\tau$ as a function of ${\mathrm{d}}_{\text{shaft}}$ of the form $\tau =a^{*}\frac{1}{d_{\text{shaft}}}+b$ for experiments and simulations, respectively. (d) Schematic summarizing the conclusion of this figure: Diffusion flux increases with ${\mathrm{d}}_{\text{shaft}}$. In that sense, thin shafts favor node compartmentalization. Data in panels c1 and c2 are represented as mean ± STD, n = 20 for each geometry.

2.4. Protocols for simulating neuronal stimulation

In order to investigate the propagation of ${\mathrm{Ca}}^{2+}$ signals from nodes that contact neuronal spines, we have developed two different protocols for our simulations, performed in the geometries presented in Figure 1. As nodes were the site of ${\mathrm{Ca}}^{2+}$ signal initiation (Arizono et al. 2020) and as most spines contacted nodes rather than shafts, we have simulated neuronal stimulation in nodes. To simulate neuronal stimulation, IP₃ and ${\mathrm{Ca}}^{2+}$ were infused in the cytosol at stimulation time. IP₃ infusion reflects the production of IP₃ by phospholipase C that results from the activation of G _q‐G‐protein‐coupled receptors (GPCRs). ${\mathrm{Ca}}^{2+}$ infusion mimics the influx of ${\mathrm{Ca}}^{2+}$ in the cytosol through ${\mathrm{Ca}}^{2+}$ channels at the plasma membrane. The rate of this neuronal activity‐induced ${\mathrm{Ca}}^{2+}$ influx, ${\mathrm{k}}_{\mathrm{Ca}}$, varied within a physiological range of values, from 0 to 1000 s⁻¹ (Wu et al. 2018; Brazhe et al. 2018). Signals were recorded both in the stimulated node, Node 1, and in the neighboring node, Node 2.

• In the first protocol, 100 IP₃ molecules were infused in Node 1, at t = t ₀ = 1 s, while ${\mathrm{Ca}}^{2+}$ activity was monitored in Node 1 and in the neighboring node, Node 2 (see e.g., Figure 3a). Neuronal activity‐induced ${\mathrm{Ca}}^{2+}$ influx was mediated by generic ${\mathrm{Ca}}^{2+}$ channels at the plasma membrane. Twenty‐five of those ${\mathrm{Ca}}^{2+}$ channels were placed on the plasma membrane of Node 1, corresponding to a similar density to the IP₃R density on the ER membrane, and were set to an inactive state. At stimulation time t = t ₀, ${\mathrm{Ca}}^{2+}$ channels were set to an active state, resulting in an influx of ${\mathrm{Ca}}^{2+}$ within the cytosol at rate ${\mathrm{k}}_{\mathrm{Ca}}$ = 0–1000 s⁻¹. At t = t ₀ + 1, ${\mathrm{Ca}}^{2+}$ channels were set back to their initial inactive state. Simulations were performed in geometries with varying shaft width ${\mathrm{d}}_{\text{shaft}}$.

• In the second protocol, we have investigated signal propagation in the node/shaft geometry depending on shaft width ${\mathrm{d}}_{\text{shaft}}$ when several nodes were successively stimulated. In “5 nodes” geometries, 50 IP₃ molecules were infused at t ₀ = 5 s, $t_0+{\tau }_{\mathrm{IP}3}$, $t_0+2{\tau }_{\mathrm{IP}3}$, $t_0+3{\tau }_{\mathrm{IP}3}$ in Nodes 1, 2, 3, and 4, respectively. During the whole simulation time, ${\mathrm{Ca}}^{2+}$ activity was recorded in Node 5 (see Figure 5). In a subset of simulations, stimulation of Nodes 2, 3 and 4 occurred with a probability $1-p_{\text{fail}}$, with $p_{\text{fail}}\in \left[0,1\right]$.

FIGURE 3.

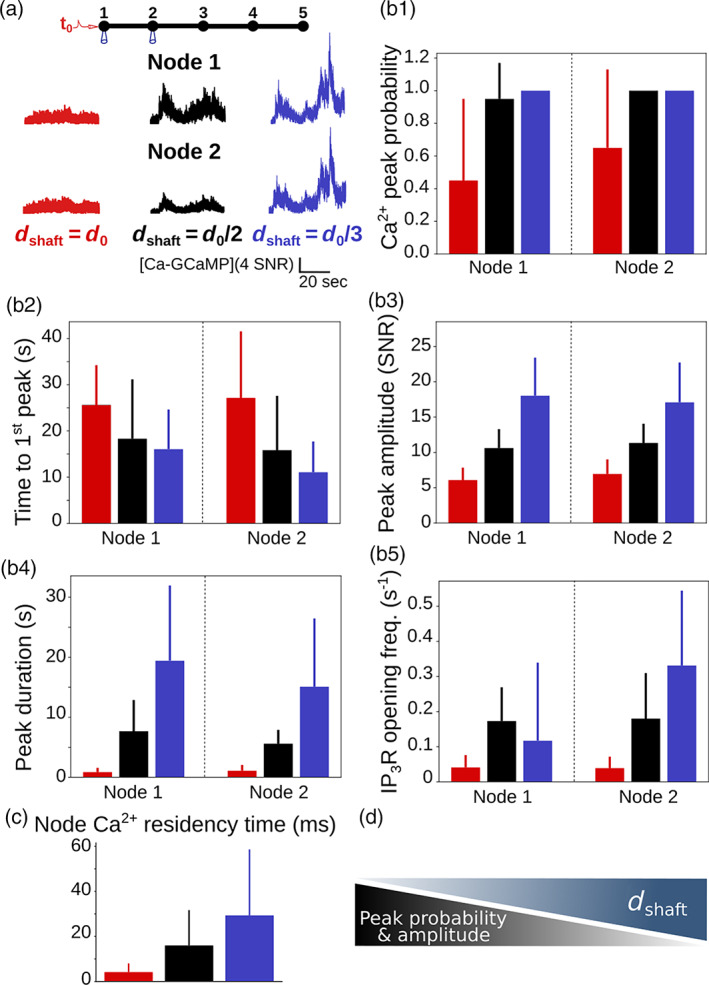
${\mathrm{Ca}}^{2+}$ peak probability, amplitude and duration increase when shaft width decreases. (a) (top) Neuronal stimulation protocol simulated for each geometry: Node 1 was stimulated at t = t ₀ = 1 s, while ${\mathrm{Ca}}^{2+}$ activity was monitored in node 2. Representative ${\mathrm{Ca}}^{2+}$ traces for shaft width $d_{\text{shaft}}={\mathrm{d}}_0$ (red), $\frac{{\mathrm{d}}_0}{2}$ (black) and $\frac{{\mathrm{d}}_0}{3}$ (blue), expressed as SNR (see Methods). (b) Quantification of the effect of ${\mathrm{d}}_{\text{shaft}}$ on ${\mathrm{Ca}}^{2+}$ signal characteristics data are represented as mean ± STD, n = 20. ${\mathrm{Ca}}^{2+}$ peak probability increases (***, b1), time to 1^st peak decreases (***, b2), peak amplitude (***, b3) and duration (***, b4) increase when ${\mathrm{d}}_{\text{shaft}}$ decreases. (c) ${\mathrm{Ca}}^{2+}$ residency time in node 1 increases when ${\mathrm{d}}_{\text{shaft}}$ decreases (***, n = 300). (d) Schematic summarizing the main result from this figure: ${\mathrm{Ca}}^{2+}$ peak probability and amplitude increase when shaft width decreases.

FIGURE 5.

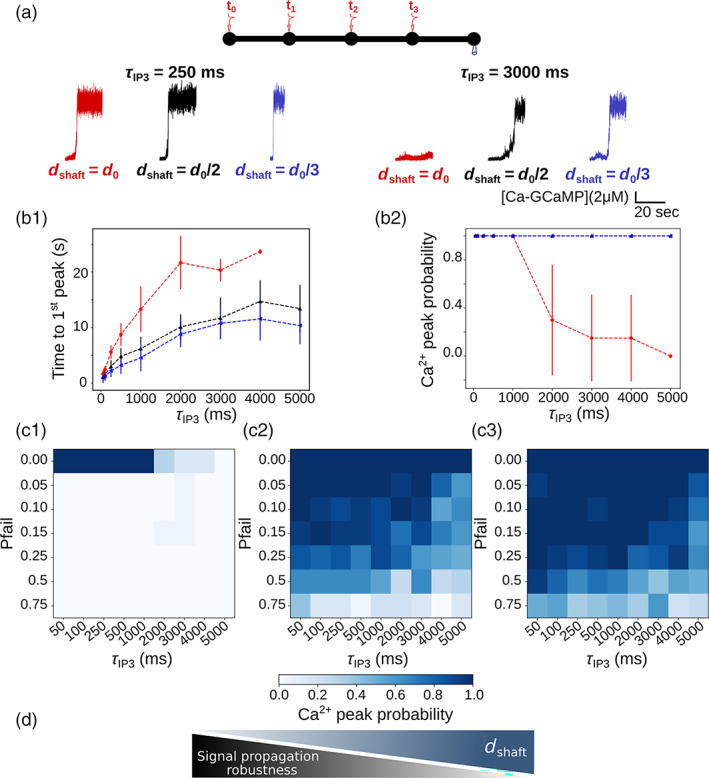
Thin shafts favor a more robust signal propagation upon repeated neurotransmitter release events. (a) (top) Neuronal stimulation protocol: Node 1 is stimulated at t = t ₀ = 5 s, node 2 at $t_0+{\tau }_{\mathrm{IP}3}$, node 3 at $t_0+2{\tau }_{\mathrm{IP}3}$ and node 4 at $t_0+3{\tau }_{\mathrm{IP}3}$, ${\mathrm{k}}_{\mathrm{Ca}}$ = 0 $s^{-1}$. ${\mathrm{Ca}}^{2+}$ activity is recorded in node 5. (bottom) representative ${\mathrm{Ca}}^{2+}$ traces in node 5 for shaft width $d_{\text{shaft}}={\mathrm{d}}_0$ (red), $\frac{{\mathrm{d}}_0}{2}$ (black) and $\frac{{\mathrm{d}}_0}{3}$ (blue), with ${\tau }_{\mathrm{IP}3}$ = 250 ms (left) and 3000 ms (right), expressed as SNR (see Methods). For all values of ${\tau }_{\mathrm{IP}3}$ tested, simulation time was 25 s. (b1) Time to 1^st peak increases with ${\tau }_{\mathrm{IP}3}$ for ${\mathrm{d}}_{\text{shaft}}$ =$d_0$ (***), $\frac{{\mathrm{d}}_0}{2}$ (***) and $\frac{{\mathrm{d}}_0}{3}$ (***). T‐tests revealed that for any value of ${\tau }_{\mathrm{IP}3}$, time to 1^st peak is higher for ${\mathrm{d}}_{\text{shaft}}$ = $d_0$ compared to ${\mathrm{d}}_{\text{shaft}}$ = $\frac{{\mathrm{d}}_0}{2}$ and $\frac{{\mathrm{d}}_0}{3}$. Time to 1^st peak is significantly higher when ${\mathrm{d}}_{\text{shaft}}$ = $\frac{{\mathrm{d}}_0}{2}$ compared to ${\mathrm{d}}_{\text{shaft}}$ = $\frac{{\mathrm{d}}_0}{3}$, for most values of ${\tau }_{\mathrm{IP}3}$ (p = 0.032*, 0.0025**, 0.034*, 0.016*, and 0.019* for ${\tau }_{\mathrm{IP}3}$ = 250, 500, 1000, 4000, and 5000 ms, respectively). (b2) ${\mathrm{Ca}}^{2+}$ peak probability in node 5 is lower for ${\mathrm{d}}_{\text{shaft}}$ = $d_0$ compared to ${\mathrm{d}}_{\text{shaft}}$ = $\frac{{\mathrm{d}}_0}{2}$ and $\frac{{\mathrm{d}}_0}{3}$. ${\mathrm{Ca}}^{2+}$ peak probability decreases as ${\tau }_{\mathrm{IP}3}$ increases for ${\mathrm{d}}_{\text{shaft}}$ = $d_0$ (***). (c) ${\mathrm{Ca}}^{2+}$ peak probability in node 5 (colorbar) as a function of ${\tau }_{\mathrm{IP}3}$ and of the probability of failure of node stimulation $p_{\text{fail}}$, for ${\mathrm{d}}_{\text{shaft}}$ =$d_0$ (c1), ${\mathrm{d}}_{\text{shaft}}$ =$\frac{{\mathrm{d}}_0}{2}$ (c2) and ${\mathrm{d}}_{\text{shaft}}$ =$\frac{{\mathrm{d}}_0}{3}$ (c3), with $p_{\text{fail}}\in \left[0,1\right]$. (d) Schematic summarizing the main conclusion of this figure: Decreased shaft width allows signal propagation despite omitted node stimulation, thus favoring more robust signal propagation. Data are represented as mean ± STD, n = 20 for each value of ${\mathrm{d}}_{\text{shaft}}$ and of ${\tau }_{\mathrm{IP}3}$. Lines in panel B are guides for the eyes.

2.5. Code accessibility

The simulation code, implemented with STEPS 3.5.0, and the meshes are available on ModelDB (McDougal et al. 2017) at http://modeldb.yale.edu/266928. The original model from Denizot et al. (2019) is available at http://modeldb.yale.edu/247694.

2.6. Peak detection and analysis

The same strategy as developed by Denizot et al. (2019) was used for detecting and analyzing ${\mathrm{Ca}}^{2+}$ signals. Briefly, basal concentration of ${\mathrm{Ca}}^{2+}$, ${\left[\mathit{Ca}\right]}_{\mathrm{b}}$, was defined based on a histogram of the number of ${\mathrm{Ca}}^{2+}$ ions in the absence of neuronal stimulation. Peak initiation corresponded to the time when [Ca²⁺] was higher than the following threshold: ${\left[\mathit{Ca}\right]}_{\mathrm{b}}+n{\sigma }_{\mathrm{Ca}}$, where ${\sigma }_{\mathrm{Ca}}$ is the standard deviation of [Ca²⁺] histogram in the absence of neuronal stimulation. The value of n was set by hand depending on signal/noise ratio of the simulation of interest. Peak termination corresponded to the time when [Ca²⁺] decreased below the peak threshold.

Several parameters were analyzed to characterize ${\mathrm{Ca}}^{2+}$ signals. Peak duration corresponds to the time between peak initiation and peak termination. Peak amplitude corresponds to the maximum number of ${\mathrm{Ca}}^{2+}$ ions recorded in the studied node during peak duration. It is expressed as signal to noise ratio $\mathit{SNR}=\frac{A-{\left[\mathit{Ca}\right]}_{\mathrm{b}}}{{\left[\mathit{Ca}\right]}_{\mathrm{b}}}$. Time to 1^st peak corresponds to the delay between the beginning of the simulation and the first peak detection, measured in the cellular compartment of interest. Peak probability corresponds to the fraction of simulations in which at least one peak was detected during simulation time in the region of interest. ${\mathrm{Ca}}^{2+}$ residency time was measured by performing n = 300 simulations for each value of ${\mathrm{d}}_{\text{shaft}}$, in which only 1 ${\mathrm{Ca}}^{2+}$ ion was added to node 1, without other molecular species. ${\mathrm{Ca}}^{2+}$ residency time corresponds to the time taken by the ion to diffuse away from node 1.

2.7. Organotypic hippocampal slice cultures

All experiments were conducted as described in Arizono et al. (2020) and were in accordance with the European Union and CNRS UMR5297 institutional guidelines for the care and use of laboratory animals (Council directive 2010/63/EU). Organotypic hippocampal slices (Gähwiler type) were dissected from 5 to 7‐d‐old wild‐type mice and cultured 5 to 8 week in a roller drum at 35°C, as previously described (Gähwiler 1981).

2.8. Viral infection

AAV9‐GFAP‐GCaMP6s (Stobart, Ferrari, Barrett, Stobart, et al. 2018) was injected by brief pressure pulses (40 ms; 15 psi) into the stratum radiatum of 2–3‐week old slices from Thy1‐YFP‐H (JAX:003782) mice 4–6 weeks prior to the experiment.

2.9. Image acquisition

For Ca²⁺ imaging, we used a custom‐built setup based on an inverted microscope body (Leica DMI6000), as previously described in Tonnesen et al. (2011). We used a 1.3 NA glycerol immersion objective equipped with a correction collar to reduce spherical aberrations and thereby allow imaging deeper inside brain tissue (Urban et al. 2011). The excitation light was provided by a pulsed diode laser (l = 485 nm, PicoQuant, Berlin, Germany). The fluorescence signal was confocally detected by an avalanche photodiode (APD; SPCM‐AQRH‐14‐FC; PerkinElmer). The spatial resolution of the setup was around 200 nm (in x–y) and 600 nm (z). Confocal time‐lapse imaging (12.5 × 25 μm, pixel size 100 nm) was performed at 2 Hz for 2.5 min in artificial cerebrospinal fluid containing 125 mM NaCl, 2.5 mM KCl, 1.3 mM MgCl₂, 2 mM CaCl₂, 26 mM NaHCO₃, 1.25 mM NaH₂PO₄, 20 mM D‐glucose, 1 mM Trolox; 300 mOsm; pH 7.4. Perfusion rate was 2 ml/min and the temperature 32°C. Hypo‐osmotic stress (300–200 mOsm) was applied by perfusing ACSF with reduced NaCl concentration (119–69 mM NaCl).

2.10. Image analysis

Image analysis was performed as described in Arizono et al. (2020). ${\mathrm{Ca}}^{2+}$ events in the spongiform structure were detected and analyzed using the ImageJ LC_Pro plugin (Francis et al. 2012), which allows automatic and unbiased detection of ${\mathrm{Ca}}^{2+}$ events.

2.11. Experimental design and statistical analysis

For each parameter set, 20 simulations, with different seed values, were generated to get a large enough sample size for statistical analysis while keeping the computational cost of the work to a minimum. Each parameter describing ${\mathrm{Ca}}^{2+}$ dynamics was expressed as mean ± standard deviation. The effect of ${\mathrm{d}}_{\text{shaft}}$ on each ${\mathrm{Ca}}^{2+}$ signal characteristic was tested using one‐way ANOVA. Comparison between two different conditions was performed using unpaired Student T‐test if values followed a Gaussian distribution, Mann–Whitney test otherwise. Significance is assigned by * for $p\le 0.05$, ** for $p\le 0.01$, *** for $p\le 0.001$.

3. RESULTS

3.1. Geometrical representation of typical astrocyte processes

In order to investigate the role of the nano‐morphology of astrocytic processes on the spatio‐temporal properties of ${\mathrm{Ca}}^{2+}$ microdomains, we have designed geometries of typical astrocyte processes, derived from our recent characterization of their ultrastructure at a high spatial resolution (50 nm in x–y) in organotypic hippocampal culture as well as in acute slices and in vivo (Arizono et al. 2020) (Figure 1a). Geometries consist of alternations of bulbous structures, nodes, connected to each other via cylindrical structures, referred to as shafts. At this spatial scale, cell swelling resulting from hypo‐osmotic conditions is not homogeneous: node width is constant while shaft width increases (Figure 3 in Arizono, Inavalli, et al. 2021). To test the effect of such morphological changes of node‐shaft structures on astrocytic activity, we designed idealized node‐shaft geometries in three spatial dimensions in which we could perform reaction–diffusion simulations of astrocytic calcium signaling. In those geometries, node width was d ₀ = 380 nm, consistent with median values of node width reported previously (Arizono et al. 2020). The range of shaft width tested was based on node‐shaft width ratios that we measured in organotypic hippocampal culture using STED microscopy (Figure 1a2). The resulting 3D geometries are presented in Figure 1b. To model astrocytic ${\mathrm{Ca}}^{2+}$ activity with a high spatial resolution while taking into account the randomness of reactions in small volumes, we used the stochastic voxel‐based model from Denizot et al. (2019). The reactions included in the model are presented in Figure 1d and in the Methods section. As the majority of ${\mathrm{Ca}}^{2+}$ signals in astrocytes result from the opening of Inositol 3‐Phosphate receptors (IP₃Rs), located at the membrane of the endoplasmic reticulum (ER) (Srinivasan et al. 2015), signals in the model result from the opening of IP₃ 3Rs, while IP₃ 3R‐independent ${\mathrm{Ca}}^{2+}$ fluxes into the cytosol are lumped into a single rate $\gamma$ (see Denizot et al. (2019) for more details on the model's assumptions). Neuronal stimulation was simulated as an injection of IP₃ molecules in the cytosol and a ${\mathrm{Ca}}^{2+}$ influx at ${\mathrm{Ca}}^{2+}$ channels at the plasma membrane at a rate ${\mathrm{k}}_{\mathrm{Ca}}$ = 0–1000 s⁻¹. Astrocytic activity was quantified by measuring ${\mathrm{Ca}}^{2+}$ peak probability, frequency, amplitude, duration and time to 1^st peak (see Figure 1 and Methods).

3.2. Validation of the geometrical model of astrocyte processes

In order to test whether the geometries designed in this study are a good approximation of the ultrastructure of the gliapil, we have compared molecular diffusion flux in those geometries with those reported experimentally. To do so, we simulated photobleaching experiments and compared our results to experimental results from Arizono et al. (2020). The principle of bleaching simulations is presented in the Methods section and in Movie S1. Here, we refer to an increased node compartmentalization when the time to recovery after bleaching, $\tau$, increases (see Figure 2b).

Bleaching traces in simulations are both qualitatively (Figure 2b) and quantitatively (Figure 2c) similar to experimental bleaching traces, for shaft width $d_{\text{shaft}}={\mathrm{d}}_0$ and $d_{\text{shaft}}=\frac{{\mathrm{d}}_0}{2}$. Indeed, no significant difference of $I_0$ (Figure 2c1), $I_{\mathit{inf}}$ (Figure 2c2) and $\tau$ (Figure 2c3) was observed between simulations and experimental traces. Simulations were also performed with $d_{\text{shaft}}=\frac{{\mathrm{d}}_0}{3}$. Our simulations successfully reproduce experimental bleaching experiments and suggest that $\tau$, and thus node compartmentalization, increases when shaft width decreases (Figure 2c3). This result is not surprising as a decreased shaft width results in a smaller size of the exit point for diffusing molecules from the node. This is similar to, for example, dendritic spines, which compartmentalization is increased for thinner spine necks (Santamaria et al. 2011; Tonnesen et al. 2014). The geometries that we have designed can thus be considered as a reasonable approximation of the ultrastructure of the gliapil observed experimentally in live tissue.

3.3. Thin shafts enhance ${\mathrm{Ca}}^{2+}$ activity in nodes

About 80% of astrocyte ${\mathrm{Ca}}^{2+}$ activity occurs in the gliapil (Bindocci et al. 2017), which suggests that most neuron‐astrocyte communication occurs at fine astrocytic processes. As we observed that a decreased shaft width is associated with a decreased diffusion flux, that is, an increased compartmentalization of nodes, we have tested whether this effect influences ${\mathrm{Ca}}^{2+}$ activity upon neuronal stimulation. To do so, we have first analyzed ${\mathrm{Ca}}^{2+}$ signals resulting from a single neuronal stimulation, which was simulated as an infusion of IP₃ and ${\mathrm{Ca}}^{2+}$ in the stimulated node, node 1 (see Methods). Those parameters encompass the IP₃ production by phospholipase C following the activation of G _q‐G‐protein‐coupled receptors (GPCRs) resulting from the binding of neuronal glutamate, ATP and noradrenaline to $G_q$ proteins, and ${\mathrm{Ca}}^{2+}$ entry at the plasma membrane through ${\mathrm{Ca}}^{2+}$ channels, ionotropic receptors or the sodium/calcium exchanger (NCX) functioning in reverse mode (Ahmadpour et al. 2021; Semyanov et al. 2020). Signals were recorded both in the stimulated node, node 1, and in the neighboring node, node 2 (Movie S2). Representative ${\mathrm{Ca}}^{2+}$ traces in node 2 for $d_{\text{shaft}}={\mathrm{d}}_0$, $\frac{{\mathrm{d}}_0}{2}$ and $\frac{{\mathrm{d}}_0}{3}$ are displayed in Figure 3a. Our first result is that ${\mathrm{Ca}}^{2+}$ peak probability increases when ${\mathrm{d}}_{\text{shaft}}$ decreases (Figure 3b1). The time to 1^st peak increases with ${\mathrm{d}}_{\text{shaft}}$ (Figure 3b2). By contrast, peak amplitude (Figure 3b3) and duration (Figure 3b4) increase when ${\mathrm{d}}_{\text{shaft}}$ decreases. Interestingly, time to 1^st peak was similar in the stimulated and neighboring node, which probably results from the homogenization of IP₃ concentration throughout the branchlet by diffusion prior to peak detection. To better understand the mechanisms responsible for the increased ${\mathrm{Ca}}^{2+}$ peak probability, amplitude and duration when ${\mathrm{d}}_{\text{shaft}}$ decreases, we measured the frequency of ${\mathit{IP}}_{3}R$ opening in nodes 1 and 2. The frequency of ${\mathit{IP}}_{3}R$ opening increases when ${\mathrm{d}}_{\text{shaft}}$ decreases (Figure 3b5). Note that the duration of ${\mathit{IP}}_{3}R$ opening and the number of ${\mathit{IP}}_{3}R$ s open per ${\mathrm{Ca}}^{2+}$ peak did not vary with ${\mathrm{d}}_{\text{shaft}}$. The increased ${\mathit{IP}}_{3}R$ opening frequency associated with small values of ${\mathrm{d}}_{\text{shaft}}$ probably results from the increased residency time of molecules in nodes connected to thin shafts (Figure 3c). Indeed, a thin shaft can “trap” ${\mathrm{Ca}}^{2+}$ and ${\mathit{IP}}_3$ longer in the node, thus locally increasing the probability of IP ₃ Rs to open, resulting in larger ${\mathrm{Ca}}^{2+}$ peaks. For more details, the reader can refer to the theoretical work investigating the narrow escape problem for diffusion in microdomains (Schuss et al. 2007). Nodes connected to thinner shafts, despite being characterized by a lower diffusion flux (Figure 2), could thus consist of signal amplification units, favoring the generation of larger signals, therefore increasing ${\mathrm{Ca}}^{2+}$ peak probability, amplitude and duration both in the stimulated and in neighboring nodes.

To identify the cause of the increased ${\mathrm{Ca}}^{2+}$ activity when shaft width decreases (Figure 3), we performed simulations in which we altered the stimulated node (Figure 3S2D‐E), ${\mathrm{Ca}}^{2+}$ influx at the plasma membrane (Figure S3) and boundary conditions (Figure S4). Those parameters did not affect the observed effects of ${\mathrm{d}}_{\text{shaft}}$ on ${\mathrm{Ca}}^{2+}$ dynamics. Furthermore, we repeated simulations of Figure 3 with constant cytosolic volume and constant number of IP₃Rs, irrespective of the value of ${\mathrm{d}}_{\text{shaft}}$ (Figure S5). Our results highlight that the relevant parameter responsible for the observed effects of ${\mathrm{d}}_{\text{shaft}}$ on ${\mathrm{Ca}}^{2+}$ signal characteristics is the node/shaft width ratio or the cytosolic volume rather than ${\mathrm{d}}_{\text{shaft}}$ itself. Spontaneous ${\mathrm{Ca}}^{2+}$ signals were affected by shaft width in the same way as neuronal‐induced ${\mathrm{Ca}}^{2+}$ signals (Figure S6) and, in particular, reproduced the increase of the amplitude ratio of spontaneous ${\mathrm{Ca}}^{2+}$ signals between node 2 and node 1 with shaft width observed in hippocampal organotypic cultures (Arizono et al. 2020). Note that ER morphology, in particular ER surface area (Figures S7, S8 and S9), and ${\mathrm{Ca}}^{2+}$ buffering by ${\mathrm{Ca}}^{2+}$ indicators (Figure S10), consistent with previous reports (Denizot et al. 2019; Bartol et al. 2015; Majewska et al. 2000), also altered local ${\mathrm{Ca}}^{2+}$ activity. Overall, our results suggest that a decreased shaft width, resulting in a decreased diffusion efflux from nodes, increases ${\mathrm{Ca}}^{2+}$ peak probability, amplitude and duration. Conversely, the swelling of fine processes, resulting in an increase of shaft width, attenuates local ${\mathrm{Ca}}^{2+}$ peak probability, amplitude, and duration.

3.4. ${\mathrm{Ca}}^{2+}$ imaging confirms that swelling attenuates local spontaneous ${\mathrm{Ca}}^{2+}$ activity

To validate the role of thin shafts suggested by our model's predictions, we tried to recreate the widening of shaft width in experimental conditions. Coincidentally, our recent super‐resolution study revealed that the nano‐architecture of fine processes is remodeled in hypo‐osmotic conditions, where shaft width increased while node width remained unaltered (see Figure 3 in Arizono, Inavalli, et al. (2021)). While hypo‐osmotic conditions undoubtedly cause many physiological changes to astrocytes, it is the closest experimentally available model to test our model predictions. We thus performed experimental measurements of ${\mathrm{Ca}}^{2+}$ activity in fine astrocytic processes under basal and hypo‐osmotic conditions. To record ${\mathrm{Ca}}^{2+}$ signals in fine branchlets, we used confocal microscopy in organotypic cultures, which provide a high level of optical access and sample stability in live tissue (resolution $\approx$ 200 nm in x–y versus $\approx$ 500 nm for two‐photon microscopy). In accordance with our model's predictions, ${\mathrm{Ca}}^{2+}$ peak amplitude and duration were lower in hypo‐osmotic compared to basal conditions (Figure 4a–d). Such differences were not observed in the absence of HOC (Figure 4e, f). Overall, our experimental results confirm that the complex nano‐architecture of fine astrocytic processes and its alteration, such as cell swelling, shapes local ${\mathrm{Ca}}^{2+}$ activity.

FIGURE 4.

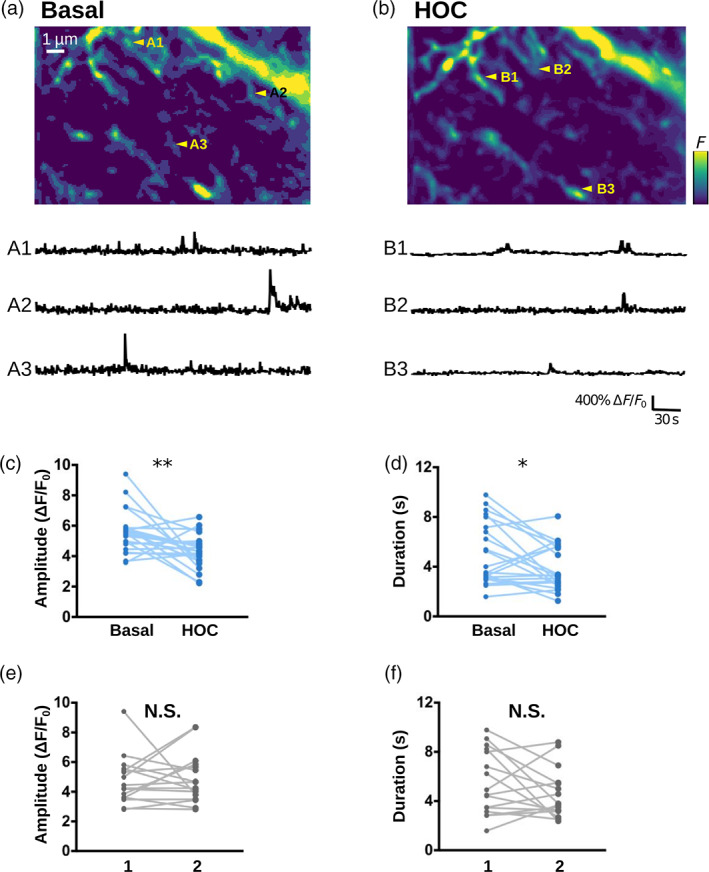
${\mathrm{Ca}}^{2+}$ imaging confirms that swelling attenuates local spontaneous ${\mathrm{Ca}}^{2+}$ activity. (a, b) (top) Confocal images of the astrocytic spongiform domain expressing GCaMP6s at baseline (basal, a) and in hypo‐osmotic condition (HOC, b), measured in organotypic hippocampal cultures (resolution: 200 nm in x–y, 600 nm in z). (bottom) representative traces of spontaneous ${\mathrm{Ca}}^{2+}$ events from ROIs indicated in (a) (a1–a3) and (b) (b1–b3). (c, d) ${\mathrm{Ca}}^{2+}$ peak amplitude (c) and duration (d) of spontaneous ${\mathrm{Ca}}^{2+}$ events are significantly smaller in hypo‐osmotic conditions (HOC) compared to basal conditions (Basal). (e, f) Amplitude (e) and duration (f) of spontaneous ${\mathrm{Ca}}^{2+}$ events do not significantly vary when measured twice in a row (1, 2) in the absence of HOC. Lines represent measurements in the same cell, before and after applying hypo‐osmotic stress.

3.5. Thin shafts favor more robust signal propagation

As a single branchlet communicates with multiple dendritic spines, which can function independently or belong to a cluster of co‐active synapses (Arizono et al. 2020; Reichenbach et al. 2010; Witcher et al. 2007; Cali et al. 2019; Semyanov et al. 2020), the frequency of node stimulation within the branchlet can vary drastically. Thus, we have tested how node stimulation frequency affects ${\mathrm{Ca}}^{2+}$ activity in the branchlet. To do so, we have performed simulations in which neighboring nodes were repeatedly stimulated after a time period ${\tau }_{\mathrm{IP}3}$, that varied from 50 ms to 5 s, while ${\mathrm{Ca}}^{2+}$ signals were recorded in a remote node, node 5 (Figure 5a). In this stimulation protocol, node 1 is stimulated at t = t ₀ = 5 s, node 2 at $t_0+{\tau }_{\mathrm{IP}3}$, node 3 at $t_0+2{\tau }_{\mathrm{IP}3}$ and node 4 at $t_0+3{\tau }_{\mathrm{IP}3}$. Neuronal stimulation is simulated as an infusion of 50 IP₃ molecules in the stimulated node. Representative ${\mathrm{Ca}}^{2+}$ traces in node 5 in branchlets with various shaft widths ${\mathrm{d}}_{\text{shaft}}$ are presented in Figure 5a for ${\tau }_{\mathrm{IP}3}$ = 250 and 3000 ms. Our first notable result is that the time to 1^st peak in node 5 decreases with ${\mathrm{d}}_{\text{shaft}}$, whatever the value of ${\tau }_{\mathrm{IP}3}$ (Figure 5b1). More specifically, time to 1^st peak is higher for ${\mathrm{d}}_{\text{shaft}}$ = $d_0$ compared to both ${\mathrm{d}}_{\text{shaft}}$ = $\frac{{\mathrm{d}}_0}{2}$ and $\frac{{\mathrm{d}}_0}{3}$, while differences between ${\mathrm{d}}_{\text{shaft}}$ = $\frac{{\mathrm{d}}_0}{2}$ and $\frac{{\mathrm{d}}_0}{3}$ are not as striking. Moreover, the difference between ${\mathrm{d}}_{\text{shaft}}$ = $d_0$, $\frac{{\mathrm{d}}_0}{2}$ and $\frac{{\mathrm{d}}_0}{3}$ increases with ${\tau }_{\mathrm{IP}3}$. This suggests that geometries with ${\mathrm{d}}_{\text{shaft}}$ = $d_0$ better discriminate slow from fast frequency of node stimulation compared to geometries with thinner shafts. Geometries with ${\mathrm{d}}_{\text{shaft}}$ = $d_0$ are further characterized by a lower ${\mathrm{Ca}}^{2+}$ peak probability in node 5 compared to geometries with ${\mathrm{d}}_{\text{shaft}}$ = $\frac{{\mathrm{d}}_0}{2}$ and $\frac{{\mathrm{d}}_0}{3}$ (Figure 5b2). More precisely, ${\mathrm{Ca}}^{2+}$ peak probability decreases as ${\tau }_{\mathrm{IP}3}$ increases for ${\mathrm{d}}_{\text{shaft}}$ = $d_0$, which was observed independently of our boundary conditions (Figure S11, see Methods). Interestingly, the same effect was observed with various node stimulation patterns, where nodes were stimulated in a different order (Figure S12a) or where a single node was repeatedly stimulated (Figure S12b, c). This suggests that geometries with larger shafts could be associated with decreased signal propagation to remote nodes in case of repeated node stimulation at low frequency (${\tau }_{\mathrm{IP}3}$ > 2 s).

For ${\tau }_{\mathrm{IP}3}$ = 4 s and ${\mathrm{d}}_{\text{shaft}}$ = $\frac{{\mathrm{d}}_0}{3}$, signals were detected in node 5 11.55 ± 3.89 s after the stimulation of node 1, which means that they occurred before the stimulation of node 4 (t = $t_0$ + 12 s for ${\tau }_{\mathrm{IP}3}$ = 4 s). This phenomenon was not observed for ${\mathrm{d}}_{\text{shaft}}$ = $d_0$, for which time to 1^st peak when ${\tau }_{\mathrm{IP}3}$ = 4 s was 23.67 ± 0.47 s. This suggests that for ${\mathrm{d}}_{\text{shaft}}$ = $\frac{{\mathrm{d}}_0}{3}$, contrary to ${\mathrm{d}}_{\text{shaft}}$ = $d_0$, one node stimulation could be omitted without having any consequence on ${\mathrm{Ca}}^{2+}$ peak probability in node 5. In order to test this hypothesis, we have performed simulations in which the stimulation of nodes 2, 3 and 4 occurred with a given probability of failure $p_{\text{fail}}$. Simulations were performed for $p_{\text{fail}}$ = 0, 0.05, 0.1, 0.15, 0.25 and 0.75. ${\mathrm{Ca}}^{2+}$ peak probability in node 5, depending on $p_{\text{fail}}$ and on ${\tau }_{\mathrm{IP}3}$ is presented in Figure 5c, for ${\mathrm{d}}_{\text{shaft}}$ = $d_0$ (Figure 5c1), ${\mathrm{d}}_{\text{shaft}}$ = $\frac{{\mathrm{d}}_0}{2}$ (Figure 5c2) and ${\mathrm{d}}_{\text{shaft}}$ = $\frac{{\mathrm{d}}_0}{3}$ (Figure 5c3). As expected, ${\mathrm{Ca}}^{2+}$ peak probability, despite high values of $p_{\text{fail}}$, increases when ${\mathrm{d}}_{\text{shaft}}$ decreases. Thus, thin shafts can favor signal propagation by allowing the omission of a node stimulation. In that sense, geometries displaying thin shafts are characterized by a more robust signal propagation (Figure 5d).

Together, our results suggest that, in the context of repeated node stimulation, thin shafts are associated with an increase of ${\mathrm{Ca}}^{2+}$ peak probability in more remote nodes, with an earlier signal onset, suggesting increased signal propagation. Astrocytic processes with thicker shafts (here ${\mathrm{d}}_{\text{shaft}}$ = $d_0$), such as observed in hypo‐osmotic conditions (Arizono, Inavalli, et al. 2021), are associated with lower signal propagation in case of low stimulation frequency (time period >2 s), potentially favoring the formation of local ${\mathrm{Ca}}^{2+}$ hotspots. Our results suggest that geometries with thick shafts could impair signal propagation when a branchlet is stimulated at a low frequency. In that sense, astrocyte branchlets with thicker shafts would be better detectors of the surrounding level of neuronal activity. By contrast, branchlets with thin shafts would be less discriminating and provide more robust signal propagation.

4. DISCUSSION

Fine astrocytic processes are responsible for most astrocytic ${\mathrm{Ca}}^{2+}$ signals (Bindocci et al. 2017) and are preferential sites of neuron‐astrocyte communication (Arizono et al. 2020). A better understanding of the mechanistic link between their morphology and the spatio‐temporal properties of local ${\mathrm{Ca}}^{2+}$ signals is crucial, yet hard to test experimentally. Here, we perform reaction–diffusion simulations in idealized morphologies of astrocytic processes derived from 3D super‐resolution microscopy to investigate the effect of astrocyte nanoscale morphology on ${\mathrm{Ca}}^{2+}$ activity in the gliapil. Our simulation results indicate that the nanoscale morphological features of astrocytic processes effectively increase the peak probability, duration, amplitude and propagation of ${\mathrm{Ca}}^{2+}$ signals. Conversely, the alteration of the node‐shaft arrangement of the spongiform domain associated with astrocyte swelling attenuates local ${\mathrm{Ca}}^{2+}$ activity and signal propagation. Our simulation results, in accordance with experimental data, suggest that thin shafts effectively decrease diffusion flux, resulting in an increased compartmentalization of biochemical signals in nodes. Thus, nodes, similarly to dendritic spines (Santamaria et al. 2011), act as diffusion traps when shaft width is low. Note that, more than the value of shaft width itself, our results emphasize the effect of the ratio between node and shaft diameter on ${\mathrm{Ca}}^{2+}$ activity. The simple geometries that we have evaluated in this study could be used to build a more comprehensive model of the spongiform structure to simulate ${\mathrm{Ca}}^{2+}$ activity in the entire astrocyte. By recording the molecular interactions resulting in ${\mathrm{Ca}}^{2+}$ signals upon neuronal stimulation in small cellular compartments of the gliapil, which cannot be performed experimentally, our simulation results shed light on the mechanisms by which the nano‐architecture of astrocytic processes influences the frequency, amplitude and propagation of local ${\mathrm{Ca}}^{2+}$ signals at tripartite synapses in health and disease.

Experimental ${\mathrm{Ca}}^{2+}$ recordings of astrocyte activity have established that astrocyte processes display both highly localized microdomain signals and propagating ${\mathrm{Ca}}^{2+}$ waves (Srinivasan et al. 2015; Bindocci et al. 2017). Our simulations suggest that the morphology of the cell and of its organelles can strongly influence the formation of these patterns of astrocytic ${\mathrm{Ca}}^{2+}$ signaling. Notably, thinner shafts allow less discriminating and more robust signal propagation upon repeated stimuli compared to larger shafts. On the contrary, geometries with thick shafts seem to be more discriminating, potentially favoring the propagation of signals resulting from repeated stimuli from co‐active synapses. Cellular morphology thus emerges as a key parameter that regulates the active propagation of ${\mathrm{Ca}}^{2+}$ signals. The ultrastructure of the spongiform domain of astrocytes is very complex, characterized by abundant branching points, conferring a reticular morphology (Arizono et al. 2020). Those branching points are reportedly sometimes arranged into ring‐like structures, although their occurrence and shape are still debated and could differ depending on the brain region under study (Arizono et al. 2020; Panatier et al. 2014; Kiyoshi et al. 2020; Salmon et al. 2021; Arizono and Nägerl 2021). The effect of this reticular ultrastructure on the propagation of ${\mathrm{Ca}}^{2+}$ signals remains to be uncovered. Further characterization of the shape of fine astrocytic processes of the spongiform domain, their variability as well as their connectivity to the neighboring synapses are thus required. Pairing those observations with biophysically‐detailed models such as the one presented in this study stands to deepen our understanding of the roles of astrocytic and neuronal morphology at tripartite synapses on neuron‐astrocyte communication.

In neurons, both experimental (Yuste et al. 2000; Noguchi et al. 2005; Tonnesen et al. 2014) and modeling (Schmidt and Eilers 2009; Biess et al. 2007; Simon et al. 2014; Bell et al. 2019; Holcman and Schuss 2005, 2011; Santamaria et al. 2011; Cugno et al. 2019) studies have suggested that thin spine necks favor the compartmentalization of ${\mathrm{Ca}}^{2+}$ signals within the spine head. This compartmentalization of synapses allows neurons to discriminate various inputs and to process information locally (Wybo et al. 2019, Poirazi and Papoutsi 2020), increasing the computational power of the neuronal circuits. According to our simulation results, nodes connected to thin shafts could favor the emergence of large signals at the site of neuron‐astrocyte communication. Interestingly, we further propose that those amplified signals in nodes, instead of resulting in ${\mathrm{Ca}}^{2+}$ hotspots, favor active signal propagation. Fine astrocytic processes encounter morphological rearrangements that are activity‐dependent, which notably influence synaptic maturation, efficacy and spine stability (Theodosis et al. 2008; Zhou et al. 2019; Henneberger et al. 2020). Our study sheds light on the influence of rearrangements of the reticular morphology of fine processes on signal computation by astrocytes. Further investigation manipulating astrocyte morphology in situ as well as in vivo is required to better characterize the variability of astrocyte ultrastructure and the associated integration of ${\mathrm{Ca}}^{2+}$ signals.

The morphology of the complex spongiform domain of astrocytes is highly dynamic, subject to activity‐dependent as well as pathological remodeling. Our study, providing mechanisms by which an altered astrocyte morphology influences neuron‐astrocyte communication at the nanoscale, gives new insights into the involvement of astrocytes in brain function in health and disease.

AUTHOR CONTRIBUTION

AD, HB and EDS designed the study. UVN, EDS and HB supervised the work. AD implemented the code, conducted the simulations, and analyzed the computational data. Calcium imaging and analysis was performed by MA. AD wrote the first draft of the manuscript, which was revised and approved by all authors.

CONFLICT OF INTEREST

The authors declare no competing financial interests.

Supporting information

Appendix S1 Supporting Information

Movie S1 

Movie S2 

Denizot, A. , Arizono, M. , Nägerl, U. V. , Berry, H. , & De Schutter, E. (2022). Control of Ca²⁺ signals by astrocyte nanoscale morphology at tripartite synapses. Glia, 70(12), 2378–2391. 10.1002/glia.24258

DATA AVAILABILITY STATEMENT

The simulation code and meshes used in this study are available at http://modeldb.yale.edu/266928.