Highlights
-
•
Combining morphological measures provides unique perspective on neurodegeneration.
-
•
Cortical curvature-thickness interplay is associated with age and sex.
-
•
Motor symptoms in Parkinson’s disease are related to curvature-thickness interplay.
-
•
Motor effects on curvature-thickness interplay mainly found in older patients.
Keywords: Cortical brain morphology, Structural MRI, Parkinson’s disease, Motor symptoms, Cognitive performance
Abstract
Introduction
Brain atrophy in Parkinson’s disease occurs to varying degrees in different brain regions, even at the early stage of the disease. While cortical morphological features are often considered independently in structural brain imaging studies, research on the co-progression of different cortical morphological measurements could provide new insights regarding the progression of PD. This study’s aim was to examine the interplay between cortical curvature and thickness as a function of PD diagnosis, motor symptoms, and cognitive performance.
Methods
A total of 359 de novo PD patients and 159 healthy controls (HC) from the Parkinson’s Progression Markers Initiative (PPMI) database were included in this study. Additionally, an independent cohort from four databases (182 PD, 132 HC) with longer disease durations was included to assess the effects of PD diagnosis in more advanced cases. Pearson correlation was used to determine subject-specific associations between cortical curvature and thickness estimated from T1-weighted MRI images. General linear modeling (GLM) was then used to assess the effect of PD diagnosis, motor symptoms, and cognitive performance on the curvature-thickness association. Next, longitudinal changes in the curvature-thickness correlation as well as the predictive effect of the cortical curvature-thickness association on changes in motor symptoms and cognitive performance across four years were investigated. Finally, Akaike information criterion (AIC) was used to build a GLM to model PD motor symptom severity cross-sectionally.
Results
A significant interaction effect between PD motor symptoms and age on the curvature-thickness correlation was found (βstandardized = 0.11; t(350) = 2.12; p = 0.03). This interaction effect showed that motor symptoms in older patients were related to an attenuated curvature-thickness association. No significant effect of PD diagnosis was observed for the PPMI database (β = 0.03; t(510) = 0.35; p = 0.72). However, in patients with a longer disease duration, a significant effect of diagnosis on the curvature-thickness association was found (βstandardized = 0.31; t(306.7) = 3.49; p = 0.0006). Moreover, rigidity, but not tremor, in PD was significantly related to the curvature-thickness correlation (βstandardized = 0.11, t(350) = 2.24, p = 0.03; βstandardized = -0.03, t(350) = -0.58, p = 0.56, respectively). The curvature-thickness association was attenuated over time in both PD and HC, but the two groups did not show a significantly different effect (βstandardized = 0.03, t(184.7) = 0.78, p = 0.44). No predictive effects of the CC-CT correlation on longitudinal changes in cognitive performance or motor symptoms were observed (all p-values > 0.05). The best cross-sectional model for PD motor symptoms included the curvature-thickness correlation, cognitive performance, and putamen dopamine transporter (DAT) binding, which together explained 14 % of variance.
Conclusion
The association between cortical curvature and thickness is related to PD motor symptoms and age. This research shows the potential of modeling the curvature-thickness interplay in PD.
1. Introduction
Parkinson’s disease (PD) involves the progressive degeneration of the brain’s neurons associated with accumulation of Lewy bodies (Braak et al., 2003). Over time, this degeneration can lead to macroscopically detectable changes in the brain’s cortical and subcortical morphology (Sarasso et al., 2021). Laansma et al. (2021) analyzed anatomical MRI images from 2357 PD patients and 1182 healthy controls and found that PD patients showed widespread cortical thinning as well as smaller volumes of specific subcortical regions including the bilateral putamen. The same study also showed that increased Hoehn and Yahr staging was related to more widespread cortical thinning, with the frontal cortex remaining relatively spared in earlier stages, as well as decreased subcortical volumes. Cognitive performance was mainly related to cortical thickness in temporal, frontal, and parietal regions, as well as to volumes of the amygdala and hippocampus. Other studies found reduced cortical gyrification of PD patients in specific brain areas compared to healthy controls (Tang et al., 2021, Zhang et al., 2014), which has also been found to decrease with PD disease duration (Sterling et al., 2016). Tang et al. (2021) showed that specifically the akinetic-rigid subtype of PD is associated with decreased gyrification across the cortex.
The morphology of the cortex is determined by a complex interplay between genetic, biochemical, and physical factors (Ronan & Fletcher, 2015), with cortical morphological characteristics such as thickness and curvature showing local variations (Demirci & Holland, 2022). Individual brain morphological measures such as cortical thickness or brain volumes are likely not able to efficiently capture these systematically varying properties. The interplay between different morphological measures across the cortex, however, could reflect aspects of these systematically varying morphological patterns (Demirci & Holland, 2022). Therefore, associations between cortical morphological characteristics could provide a unique perspective on neurodegeneration in PD that would not be apparent if morphological features are considered independently. Such research could give new insights into the progression of PD and could help identify new biologically meaningful biomarkers for disease severity and progress. Some previous research in healthy subjects indeed suggests that cortical morphological features exhibit specific associations with each other (Chaudhary et al., 2021, Gautam et al., 2015, Hogstrom et al., 2013). Negative relationships between cortical thickness and gyrification, as well as positive associations between gyrification and surface area, have been observed in healthy adults and have been argued to be partly caused by mechanical tension and cortical expansion during development (Gautam et al., 2015, Hogstrom et al., 2013). Chaudhary et al. (2021) observed negative correlations between cortical thickness and gyrification across subjects in PD patients with and without cognitive impairment in the left frontal pole and right entorhinal cortex, respectively. However, little is known about whether and how this association is related to PD diagnosis and symptom severity.
The aims of this study were fourfold. First, we aimed to assess whether the association between cortical curvature and thickness is related to PD diagnosis, motor symptoms, and cognitive performance cross-sectionally. Our second aim was to assess region-specific interaction effects of cortical curvature and thickness on motor and cognitive symptoms. Third, we aimed to investigate whether the curvature-thickness association changes over time in PD patients and controls, and whether it is related to longitudinal changes in motor and cognitive symptoms. Our final aim was to assess the utility of the curvature-thickness association as part of a set of features to model motor symptom severity by comparing different models using Akaike’s information criterion (AIC).
2. Material and methods
2.1. Dataset and subjects
Data were obtained from the original cohort of the Parkinson’s Progression Markers Initiative database (PPMI; https://www.ppmi-info.org/). This cohort includes data of de novo (untreated) PD patients without dementia, and healthy controls (HC) without first-degree relatives with PD (Marek et al., 2018). Inclusion criteria for the present study were as follows: (1) a T1-weighted MRI scan at baseline, (2) availability of demographic data and scores for all tests used in this study (for all participants: age, sex, years of education, and scores for Montreal Cognitive Assessment; for the PD group specifically: additional scores for MDS-UPDRS part III). To assess the effects of PD diagnosis in a cohort with a longer disease duration, we combined four different databases that had both PD patients and healthy controls, which included a dataset acquired at the Movement Disorders Clinic of the University of Alberta (Acharya et al., 2007), a dataset acquired at the Unité de Neuroimagie Fonctionnelle of the Centre de Recherche de l’Institut Universitaire de Gériatrie de Montréal (Hanganu et al., 2013), a dataset acquired at the Seaman Family Imaging Centre at the University of Calgary (Ramezani et al., 2021), and the Tao Wu dataset (Badea et al., 2017; https://fcon_1000.projects.nitrc.org/indi/retro/parkinsons.html). Inclusion criteria for this database were as follows: (1) a T1-weighted MRI scan, (2) availability of the following variables: disease duration (for PD only), age, and sex.
For all datasets, subjects were excluded if (1) the FreeSurfer processing failed, or (2) atlas-based mis-registration occurred for that subject. Supplementary Fig. 1 shows a detailed flowchart of inclusion and exclusion criteria for the PPMI dataset. For the other datasets, a total of four subjects (three healthy controls and one PD patient) were excluded because of artifacts in the raw data or misregistration of the atlas.
Each PPMI recruiting center and each acquisition center for the other datasets included in this study received ethics approval from their local ethics board and received written informed consent from all participants in accordance with the declaration of Helsinki. In addition, the present study was approved by the Conjoint Health Research Ethics Board at the University of Calgary.
2.2. MRI acquisition and processing
2.2.1. MRI acquisition
MRI scanner vendors and scan sequences differed between the 24 PPMI acquisition sites. T1-weighted magnetic resonance images were acquired with Phillips (21 HC; PD: 36), GE (37 HC; PD: 90), and Siemens (101 HC; PD: 233) scanners, with a magnetic field strength of 0.7 T (HC: 0; PD: 2), 1.5 T (HC: 47; PD: 123), or 3.0 T (HC: 112; PD: 234). Most images were acquired in the sagittal plane (HC: 95 %; PD: 95 %). Slice thickness varied between 1 mm and 2 mm. In-slice spatial resolution varied between 0.5 and 1.25 mm isotropic (HC: 10 subjects between 0.4 and 0.5 mm, 144 subjects between 0.9 and 1 mm, and 5 subjects approximately 1.25 mm; PD: 20 subjects between 0.4 and 0.5 mm, 3 subjects between 0.7 and 0.9 mm, 327 subjects between 0.9 and 1 mm, and 9 subjects approximately 1.25 mm). For the four other datasets, T1-weighted MRI was acquired with Siemens (103 PD; 90 HC) and GE scanners (79 PD; 42 HC), with a magnetic field strength of 1.5 T (45 PD; 49 HC) or 3.0 T (137 PD; 83 HC). The scan sequence for each site was as follows: A coronal 3D magnetization prepared rapid gradient echo (MPRAGE) sequence was used for the dataset acquired at the University of Alberta (TR = 1800 ms, TE = 3.82 ms, inversion time (TI) = 1100 ms, flip angle = 15 degrees, FOV = 256 mm, resolution = 256 × 256, 128 slices, 1.5 mm slice thickness), a 3D T1-weighted MPRAGE sequence was used for the dataset acquired at l’Institut Universitaire de Gériatrie in Montréal (TR = 2300 ms; TE = 2.91 ms; TI = 900 ms; flip angle = 9 degrees; 160 slices; field of view = 256 × 240 mm; voxel size = 1 × 1 × 1 mm3), a 3D inversion recovery prepared fast spoiled gradient recalled (IR-FSPGR) sequence was used for the dataset acquired at the University of Calgary (TR = 7.176 ms, TE = 2.252 ms, flip angle = 10 degrees, acquisition matrix = 256 × 256 mm, voxel size = 1 × 1 × 1 mm3, 172 slices), and a 3D MPRAGE sequence was used for the Tao Wu dataset (TR = 2530 ms; TE = 3.39 ms; TI = 1100 ms; voxel size = 1 × 1 × 1 mm3).
2.2.2. FreeSurfer processing
Cortical curvature and thickness were estimated from T1-weighted structural MRI images using FreeSurfer (version 7.1.1). Image preprocessing was performed using standard automated procedures, which included intensity non-uniformity correction, brain extraction, tessellation of the grey and white matter boundaries, and cortical parcellation, amongst others (for details see, https://surfer.nmr.mgh.harvard.edu/fswiki/recon-all) (Dale et al., 1999, Fischl, 2012, Fischl and Dale, 2000, Fischl et al., 1999). Cortical parcellations were visually checked for correct registration of pial and white matter surfaces on an individual basis, as well as for correct parcellation of the cortex. Participants with mis-registration or mis-parcellation were excluded from further analyses, which included ten healthy controls and 17 subjects with Parkinson’s disease in the PPMI dataset (for details see Supplementary Fig. 1), and three healthy controls and one PD patient for the other datasets. Cortical thickness was computed as the average of (1) the distance from each white surface vertex to their corresponding closest point on the pial surface, and (2) the distance from the corresponding pial vertex to the closest point on the white surface (Fischl & Dale, 2000). Cortical (extrinsic) curvature was calculated as the mean of the principal curvatures of the cortical surface. Both curvature and thickness were estimated for each of the 62 cortical regions (31 per hemisphere) that are part of the Desikan–Killiany–Tourville (DKT) brain region atlas (Klein & Tourville, 2012).
2.3. Assessments
2.3.1. Motor assessment
Motor symptoms were assessed in the PPMI dataset using part III of the MDS-UPDRS (Movement Disorder Society-Sponsored Revision of the Unified Parkinson’s Disease Rating Scale; Goetz et al., 2007), which includes 33 scores on 18 items rated from 0 to 4 (total scores range from 0 to 132), with higher scores indicating greater motor impairment (Goetz et al., 2007, Goetz et al., 2008). Total part III scores off medication were used for the present study.
Additionally, subscores for tremor and rigidity were calculated based on part III of the MDS-UPDRS in the PPMI dataset. Tremor scores were calculated as the sum of all ten individual tremor items, including postural tremor for both hands, kinetic tremor for both hands, rest tremor for left and right upper extremities, rest tremor for left and right lower extremities, rest tremor of the lips or jaw, and constancy of rest tremor. Scores for rigidity were calculated as the sum of all five individual rigidity items, including rigidity of left and right upper extremities, left and right lower extremities, and the neck.
Motor assessment with MDS-UPDRS was repeated approximately every year in the PPMI dataset. For our longitudinal analyses concerning the prediction of cognitive and motor changes (see section 2.4.6), we selected the follow-up score after four years (more specifically between 3.5 and 4.5 years) because that interval had most data available and was sufficiently long to reasonably expect a measurable decline in symptoms.
2.3.2. Cognitive assessment
Cognitive performance was assessed in the PPMI dataset using Montreal Cognitive Assessment (MoCA), which ranges in score between 0 and 30 with higher scores indicating better cognitive function (Nasreddine et al., 2005). This test measures multiple cognitive domains, including visuospatial processing, executive functions, verbal memory, language, attention, and others. Cognitive assessment with MoCA was repeated approximately every year. For our longitudinal analyses (see section 2.4.6), we selected the follow-up score after four years (more specifically between 3.5 and 4.5 years) for reasons outlined in paragraph 2.3.1.
Additionally, we examined several cognitive subdomains in the PPMI dataset. This included visuospatial perception, subdomains of verbal memory (namely immediate, delayed recall, and recognition discrimination), working memory capacity, and attention. Visuospatial perception was calculated as the sum of all correct items in the Benton Judgement of Line Orientation test (BJLOT). Results were z-scores based on population data with similar age and education. Immediate recall was calculated as the sum of the first three parts of the Hopkins Verbal Learning Test Revised (HVLT-R). Delayed recall was calculated as the score on the delayed memory part of the HVLT-R. Recognition discrimination was computed as the number of true positives minus the number of false positives on the HVLT-R. Working memory capacity was calculated as the maximum number of correct responses on the letter-number sequencing (LNS) test. Finally, attention was calculated as the total number of correctly completed items on the symbol digit modalities (SDM) test.
2.4. Statistical analyses
2.4.1. Participant characteristics
To compare demographic characteristics, clinical data (i.e., cognitive performance and motor symptoms), and brain morphological measures between HC and PD, we used conventional two-sided two-sample t-tests for normally distributed continuous data, permutation-based two-sided tests for non-normally distributed continuous data (using 10,000 permutations), and chi-square tests for categorical data. For the conventional t-test, a two-sample F-test for equality of variances was used to decide on the assumption of (un)equal variances.
2.4.2. The interplay between cortical curvature and thickness
To compute a subject-specific brain-wide measure for the interplay between cortical curvature and thickness, Pearson correlation was calculated between cortical curvature and cortical thickness across all regions of the DKT atlas (across hemispheres) for each subject. This correlation is henceforth referred to as the CC-CT correlation. This brain-wide CC-CT correlation was used in the models described in sections 2.4.3, 2.4.5, 2.4.6, and 2.4.7, and was Fisher z-transformed to achieve normality of the residuals in all models in which it was used as outcome.
2.4.3. The effect of PD diagnosis, motor symptoms, and cognitive performance on the CC-CT correlation
We first tested the effect of PD diagnosis on the CC-CT correlation in the PPMI dataset using a general linear model (GLM). Co-variates in this model included age, sex, years of education, MoCA score, brain volume, and average cortical thickness. Given that the PPMI dataset includes mainly de novo PD patients, we also tested the effects of diagnosis in a sample with a longer disease duration. Therefore, we additionally analyzed data from four datasets that included PD patients with longer disease durations (and healthy controls). The median disease duration across these datasets was 5.25 years. Years of education and MoCA scores were not included as independent variables because those values were not available for all subjects. A linear mixed effect model with random intercepts for each dataset was estimated. Degrees of freedom were approximated using Satterthwaite’s method.
Next, we studied the effect of motor and cognitive symptoms in PD on the CC-CT correlation in the PPMI dataset. We estimated a model with MDS-UPDRS part III and MoCA scores as variables of interest and the CC-CT correlation as outcome. Covariates included age, sex, years of education, brain volume, and average cortical thickness. In the next step, we tested the interaction effect between MDS-UPDRS part III and age on the CC-CT correlation by adding it as an interaction term to the existing model. Finally, to test whether the interaction between age and UPDRS part III is still significant after taking into account disease duration, we estimated the same model with PD disease duration as additional variable.
We also tested the effect of motor subscores, namely tremor and rigidity scores, on the CC-CT correlation in the PPMI dataset. Therefore, we built a model with rigidity and tremor scores as independent variables of interest, using the same covariates as in the previous models. Finally, we tested for the effects of the cognitive subdomain scores (outlined in section 2.3.2) on the CC-CT correlation. Because of considerable collinearity between cognitive subscores, we tested each cognitive subdomain in a separate model using the same covariates used in our previous models. Because of missing cognitive test scores for one subject, the total number of subjects was 358 for this analysis.
2.4.4. Region-specific interaction effects of cortical thickness and curvature on motor and cognitive symptoms
Next, we investigated region-specific interaction effects between cortical thickness and curvature on PD motor and cognitive symptoms in the PPMI dataset. For these analyses, we used cortical thickness and curvature estimates for each region in the DKT atlas as variables in separate models with motor and cognitive symptoms as outcomes. No confounders were included in these exploratory analyses. To normalize residuals, a Box-Cox transformation was performed on both the MDS-UPDRS part III and MoCA scores (lambda = 0.46 and lambda = 5.24, respectively, based on maximum likelihood estimation). All together, we estimated 31 models for each hemisphere for both motor and cognitive outcomes (124 models in total). Bonferroni’s correction for family-wise error rate (FWER) was applied across tests within each hemisphere and for each outcome separately using a significance threshold of 0.05.
2.4.5. Longitudinal changes in the CC-CT correlation
We assessed the longitudinal changes in the CC-CT correlation in both PD and HC groups, as well as the interaction effect between longitudinal changes and PD diagnosis on the CC-CT correlation. Therefore, we calculated the CC-CT correlation for each follow-up session in the PPMI dataset with a T1-weighted image. For sessions in which multiple T1-weighted scans were acquired at the same day, we only kept the earliest scan. Subjects with only a baseline scan were discarded from these analyses. Two additional scans were excluded because of insufficient registration of the atlas to the T1-weighted image. Our final sample for these analyses included 153 PD patients with a total of 537 scan sessions and 68 HC with a total of 160 scan sessions. The median number of sessions per subject for PD and HC was four and two, respectively, with an average maximum span of 3.40 and 1.90 years, respectively.
Linear mixed models were used to determine the effect of time on the CC-CT correlation for the PD and HC group separately, and an overarching linear mixed model was computed to estimate the differential longitudinal change in CC-CT correlation between the PD and HC group. In all models the dependent variable was the CC-CT correlation. Time since baseline was used as independent variable. Each subject was allowed to have a different intercept (i.e., we included random intercepts), and the effect of time was also allowed to differ between subjects (i.e., we included random slopes for the effect of time). In the model that included both PD and HC, we added the interaction between diagnosis and time, as well as the main effect of diagnosis (which was included as a fixed effect). The degrees of freedom of these linear mixed models were approximated using Satterthwaite’s method.
2.4.6. The effect of the CC-CT correlation on longitudinal changes in motor and cognitive scores
Next, we assessed the effect of CC-CT correlation on longitudinal changes in motor and cognitive scores in PD in the PPMI dataset. Our variable of interested was the CC-CT correlation, and covariates included age, sex, years of education, and brain volume. The outcomes were changes in MDS-UPDRS part III scores and change in MoCA scores, both across a period of four years (more specifically between 3.5 and 4.5 years). To normalize residuals, longitudinal changes in MoCA scores were transformed using a Yeo-Johnson transformation (lambda = 1.19 based on maximum likelihood estimation). For the same reason, two outliers were discarded from the change in MDS-UPDRS part III scores. Because of missing test scores at follow-up, 286 subjects were included for the model with change in MoCA scores as outcome (73 subjects were excluded) and 224 subjects were included for the model with change in MDS-UPDRS part III scores as outcome (133 subjects were excluded).
2.4.7. Modeling PD motor symptom severity
To model PD motor severity, we considered the CC-CT correlation, age, sex, years of education, MoCA, brain volume, average cortical curvature, and average cortical thickness as potential features. Additionally, we considered cerebrospinal fluid (CSF) alpha-synuclein and amyloid-beta1-42 levels, as well as SPECT-based dopamine transporter (DAT) binding measured in the caudate nucleus and putamen, as potential features (all available in the PPMI dataset). These features have been shown to be related to motor symptom progression in PD (Kägi et al., 2010, Kang et al., 2013). The outcome of the GLM was MDS-UPDRS part III score, which reflects PD motor symptom severity. A Box-Cox transformation was performed on MDS-UPDRS part III scores to achieve normality of the residuals (lambda = 0.46, based on maximum likelihood estimation). All combinations of regressors were compared using Akaike’s information criterion (AIC). Thirteen additional subjects were excluded for this analysis because of missing data for at least one CSF or SPECT-based feature. The final sample for these analyses included 346 subjects.
2.4.8. Assumptions of linear models
Assumptions of all reported linear models were assessed using normal quantile–quantile plots and residual scatter plots (both raw and squared values). In case of violations, the appropriate transformation (e.g., Box-Cox) was performed and is reported in the methods or results section. Datapoints were excluded from the outcome if they deviated more than three standard deviations from the mean. In case a transformation was performed, outliers were only assessed and excluded after the transformation. Multicollinearity was checked using correlation matrices and variance inflation factors.
3. Results
3.1. Participants characteristics
After applying the study exclusion and inclusion criteria for the PPMI dataset, our final sample included 359 PD patients and 159 healthy controls from a total of 24 sites (see Supplementary Fig. 1 for details on subject exclusion). Table 1 shows the subject characteristics for each group. Participants with PD were found to score significantly lower on MoCA (difference in median = -1.00; p < 0.0001), and significantly higher on MDS-UPDRS part III (difference in median = 20; p < 0.0001), compared to healthy controls (based on permutation tests with 10,000 permutations).
Table 1.
Demographic and clinical data for the PD and HC group in the PPMI database. Abbreviations: Δ = difference; std = standard deviation; IQR = interquartile range. NA = not applicable/available. 1Based on a permutation test for differences in medians with 10,000 permutations.
| Variable | PD group | HC group | Statistical comparison |
|---|---|---|---|
| Number of subjects | 359 | 159 | |
|
Age (Years) Mean (std; min–max) |
61.7 (9.75; 33.7–84.9) |
60.2 (11.6; 30.6–82.7) |
Δ(mean) = 1.50; t(216) = 1.42; p = 0.16 |
|
Sex Total Female Total Male |
132 (36.8 %) 227 (63.2 %) |
57 (35.8 %) 102 (64.2 %) |
Δ(proportion) = 0.01; χ(1) = 0.04; p = 0.84 |
|
Years of education Median (IQR; min–max) |
16 (4; 5–26) |
16 (4; 8–24) |
Δ(median) = 0; p1 = 1.00 |
|
MoCA score Median (IQR; min–max) |
27 (3; 17–30) |
28 (2; 26–30) |
Δ(median) = -1; p1 < 0.0001 |
|
MDS-UPDRS Part III score off medication Median (IQR; min–max) |
20 (11; 4–51) |
0 (1; 0–10) |
Δ(median) = 20; p1 < 0.0001 |
|
Duration of disease (months) Median (IQR; min–max) |
4.2 (5.8; 0.4–35.8) (months) |
NA |
|
|
Hoehn and Yahr staging Total Stage 1 Total Stage 2 Total stage 3 |
155 (43.2 %) 202 (56.3 %) 2 (0.5 %) |
NA |
Sample characteristics of our combination of four datasets can be found in Supplementary Table 1. After exclusion of four subjects (three healthy controls and one PD patients) because of misregistration of the atlas, our final sample included 182 PD patients and 132 healthy controls. This included 45PD/49HC from the dataset acquired at the University of Alberta, 41PD/21HC from the dataset acquired at l’Institut Universitaire de Geriatrie in Montréal, 79PD/42HC from the dataset acquired at the University of Calgary, and 17PD/20HC from the Tao Wu dataset.
3.2. Cortical curvature, thickness, and the CC-CT correlation
The median cortical thickness was 2.38 mm for the PD group and 2.37 mm for the healthy controls in the PPMI dataset, while the median extrinsic cortical curvature was 0.13 mm−1 for both groups. No cortical morphological measure differed significantly between both groups (see Table 2). Fig. 1 shows scatter plots and correlations between cortical curvature and thickness for some exemplar subjects (upper panel) and the distribution of the CC-CT correlation for healthy controls and PD (lower panel). The median CC-CT correlation was −0.27 for controls and −0.24 for PD patients, which was not significantly different between both groups (see Table 2).
Table 2.
Brain morphological features for each group. Abbreviations: Δ = difference; IQR = interquartile range. NA = not applicable. 1Based on permutation tests with 10,000 permutations.
| Feature | PD group | HC group | Statistical comparison |
|---|---|---|---|
|
Average cortical thickness (mm) Median (IQR; min–max) |
2.38 (0.13; 1.52–2.66) |
2.37 (0.13; 1.51–2.62) |
Δ(median) = 0.01; p1 = 0.68 |
|
Average extrinsic curvature (mm−1) Median (IQR; min–max) |
0.13 (0.01; 0.11–0.16) |
0.13 (0.01; 0.11–0.16) |
Δ(median) = 0.00; p1 = 0.95 |
|
CC-CT correlation Median (IQR; min–max) |
−0.24 (0.26; −0.73–0.41) p1 < 0.0001 |
−0.27 (0.23; −0.63–0.45) p1 < 0.0001 |
Δ(median) = 0.03; p1 = 0.20 |
Fig. 1.
Upper panel: Scatter plots and corresponding correlations between cortical (extrinsic) curvature and thickness across all regions in the DKT atlas for selected subjects. Blue dots depict individual brain regions and black lines depict regression lines. Lower panel: violin plots and boxplots of the CC-CT correlation for both controls (red, left) and PD (cyan, right) in the PPMI dataset. The difference in median CC-CT correlation between both groups was not statistically significant (see, Table 2). Abbreviations: r = Pearson correlation coefficient, HC = healthy controls, PD = Parkinson’s disease, CC-CT correlation = correlation between cortical curvature and thickness.
3.3. The effect of PD diagnosis, motor symptoms, and cognitive performance on the CC-CT correlation
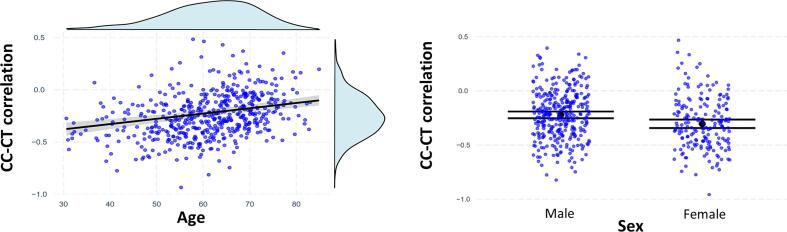
We did not observe a statistically significant effect of diagnosis on the CC-CT correlation in our model for the PPMI dataset (β = 0.03; t(510) = 0.35; p = 0.72). However, we found a statistically significant effect of age (βstand = 0.25; t(510) = 5.88; p < 0.00001), sex (β = -0.40; t(510) = -4.19; p < 0.0001), brain volume (βstand = -0.12; t(510) = -2.5; p = 0.01), and average cortical thickness (βstand = -0.32; t(510) = -7.49; p < 0.00001). Specifically, older age was associated with a less negative CC-CT correlation, while females and subjects with a thicker cortex and larger brain showed a more negative CC-CT correlation. Fig. 2 shows the influence of age and sex on the CC-CT correlation. The total model explained about 23 % of variance in the CC-CT correlation (adjusted R2 = 22 %). Details of the estimated model are shown in Table 3. No multicollinearity among regressors was observed (see Supplementary Fig. 2). The effect of diagnosis across the four datasets with a longer disease duration was statistically significant (βstand = 0.31; t(306.7) = 3.49; p = 0.0006). In these datasets, PD patients showed a (raw) CC-CT correlation that was on average 0.08 higher (i.e., closer to zero) compared to the CC-CT correlation of the HC group (average r = -0.10 and average r = -0.18 for PD and HC, respectively).
Fig. 2.
The effect of age and sex on the correlation between cortical curvature and thickness. Left panel: The effect of age on the CC-CT correlation. Blue circles depict the observed datapoints, the black line depicts the regression line, and the grey area depicts the 95% confidence interval. Light blue graphs show densities for both variables. Right panel: The effect of sex on the CC-CT correlation. Blue circles depict the observed datapoints, black circles depict the expected value for each category, and horizontal black lines show the corresponding 95% confidence interval. In both panels, CC-CT correlations were Fisher z-transformed. Plots were made using R libraries jtools, ggplot2, and ggExtra.
Table 3.
Details of the model in the total group. All continuous variables were standardized, and the CC-CT correlation was Fisher z-transformed. 1Coding: 0 = controls; 1 = PD. 2Coding: 0 = male; 1 = female. *p < 0.05.
| Variable | Coefficient estimates (standard error) | t-statistic | p-value |
|---|---|---|---|
| Diagnosis1 | 0.03 (0.09) | 0.4 | 0.72 |
| Age | 0.25 (0.04) | 5.9 | < 0.00001* |
| Sex2 | −0.40 (0.10) | −4.2 | < 0.0001* |
| Years of Education | −0.04 (0.04) | −0.9 | 0.35 |
| MoCA score | 0.01 (0.04) | −0.2 | 0.88 |
| Brain volume | −0.12 (0.05) | −2.5 | 0.01* |
| Average cortical thickness | −0.32 (0.04) | −7.5 | < 0.00001* |
Next, we assessed the effect of motor symptoms and cognitive performance on the CC-CT correlation in the PPMI dataset. We found that the interaction between age and MDS-UPDRS part III was significant and positive (βstand = 0.11; t(350) = 2.12; p = 0.03), indicating that older age enhances the effect of motor symptoms on the CC-CT correlation (see, Fig. 3). For younger adults, the effect of motor symptoms on the CC-CT correlation was negligible. This interaction remained statistically significant, even after taking into account disease duration in our model (βstand = 0.11; t(349) = 2.12; p = 0.03). In contrast, MoCA score was not associated with the CC-CT correlation (βstand = 0.00; t(351) = 0.09; p = 0.92). The complete model explained 23 % of variance (adjusted R2 = 21 %). We did not observe any issues with multicollinearity among regressors (see Supplementary Fig. 3). Bivariate associations between independent variables and outcomes without accounting for confounders are shown in Supplementary Table 2. These results showed that MDS-UPDRSIII scores and age were positively related to the CC-CT correlation (r = 0.19, p = 0.0042; r = 0.36, p < 0.0001, respectively), reflecting an attenuated (i.e., less negative) CC-CT correlation with increasing motor symptom severity and age. MoCA scores and average cortical thickness were negatively related to the CC-CT correlation (r = -0.12, p = 0.037; r = -0.29, p = 0.007), reflecting a more negative correlation with increased cognitive performance and cortical thickness.
Fig. 3.
The interaction effect between age and MDS-UPDRS part III scores on the correlation between cortical curvature and thickness in the PD group. Circles depict the observed datapoints, blue lines depict the regression lines for different ages (+/- 1SD), and the light blue areas depict the 95% confidence interval. Grey graphs show densities for both variables. CC-CT correlations were Fisher z-transformed. This plot was made using R libraries ‘interactions’, and ggExtra.
In the next step, we assessed the effects of motor and cognitive subdomains on the CC-CT correlation. We found that rigidity, but not tremor, was significantly related to the CC-CT correlation in the PD group (βstand = 0.11, t(350) = 2.24, p = 0.03; βstand = -0.03, t(350) = -0.58, p = 0.56, respectively). No multicollinearity among regressors was present (see Supplementary Fig. 4). We did not observe an effect of any of the cognitive subdomains on the CC-CT correlation in any of our models (all p-values > 0.05). No multicollinearity among regressors was found in these models (see Supplementary Fig. 5). Exploratory analyses showed that MoCA scores and the recognition discrimination index were significantly related to the CC-CT correlation when they were considered in models without other covariates (βstand = -0.12, t(357) = -2.32, p = 0.02; βstand = -0.12, t(356) = -2.38, p = 0.02).
3.4. Region-specific interaction effects of cortical thickness and curvature on motor and cognitive symptoms
There was a statistically significant interaction effect of cortical thickness and curvature on motor scores in the isthmus of the left cingulate cortex of PD patients (βstand = -0.10; t(356) = -3.31; p (Bonferroni-corrected) = 0.03). The interaction effect showed a larger (i.e., more beneficial) effect of increased cortical thickness on PD motor symptoms with higher levels of cortical curvature (see Supplementary Fig. 6). No significant interaction effects on cognitive scores surviving Bonferroni correction were found.
3.5. Longitudinal changes in the CC-CT correlation
To assess the longitudinal changes in the CC-CT correlation, we estimated mixed effects models for PD and HC separately. In both the PD and HC group, we found a statistically significant effect of follow-up time on the CC-CT correlation (βstand = 0.04, t(122.3) = 2.56, p = 0.01; βstand = 0.08, t(63.6) = 2.18, p = 0.03, respectively), indicating that over time the CC-CT correlation is attenuated (i.e., becomes less negative). In the model including both PD and HC, we did not observe a statistically significant interaction effect between diagnosis and time (βstand = 0.03, t(184.7) = 0.78, p = 0.44).
3.6. The effect of the CC-CT correlation on longitudinal changes in motor and cognitive scores
To assess the effect of the CC-CT interplay on longitudinal changes in motor and cognitive scores in the PPMI dataset, we estimated models with age, sex, years of education, brain volume, and the CC-CT correlation as predictors. Changes in MDS-UPDRS part III and MoCA scores across four years (i.e., follow-up scores minus baseline scores) were used as outcomes. We did not observe significant effects (all p-values > 0.05) of the CC-CT correlation in either model (βstand = -0.08; t(218) = -1.04; p = 0.30 in the model for longitudinal change in motor scores; βstand = -0.47; t(280) = -0.50; p = 0.62 in the model for longitudinal cognitive change). Age and brain volume were marginally related to a change in MoCA scores in this model (βstand = -0.37, t(280) = -1.96, p = 0.05; βstand = 0.35, t(280) = 1.66, p = 0.10, respectively). No multicollinearity among regressors was observed in any of the models (see Supplementary Fig. 7).
3.7. Modeling PD motor symptom severity
Next, we built a model for PD motor symptom severity. We used AIC scoring to identify the most generalizable model by comparing all possible combinations of features and selecting the model with the lowest AIC value. The model with the lowest AIC score included MoCA, mean putamen DAT binding, and the CC-CT correlation as features (βstand = -0.11, t(342) = -2.2, p = 0.03; βstand = -0.3, t(342) = -6.1, p < 0.00001; βstand = 0.15, t(342) = 2.9, p = 0.004; respectively). This model did not include any other global brain morphological features such as brain size and explained about 14% of variance in MDS-UPDRS III scores (adjusted R2 = 13 %). The same model without CC-CT correlation had an AIC value of 5 units higher than the model with CC-CT correlation, indicating lower generalizability.
4. Discussion
In this study, we investigated whether the relationship between cortical curvature and cortical thickness (CC-CT correlation) is associated with PD diagnosis, motor symptoms and cognitive impairment, both cross-sectionally as well as longitudinally. We also aimed to build a model of PD motor symptom severity cross-sectionally. Across the healthy control and PD groups, we found a negative curvature-thickness correlation that was attenuated (i.e., less negative) in older subjects and males. This relationship was not significantly different between PD and healthy controls in the PPMI dataset. However, the effect of diagnosis was found to be statistically significant in a combination of datasets that included PD patients with a longer disease duration. Additionally, we observed an interaction effect between motor symptoms and age on the curvature-thickness association in the PD group in the PPMI dataset. Specifically, older patients demonstrated a positive relationship between motor symptoms and the curvature-thickness relationship, meaning that greater motor symptoms are related to an attenuated CC-CT correlation. Younger PD patients did not show such relationship. We also found that rigidity, but not tremor, in PD was related to the curvature-thickness relationship. Additionally, we tested for region-specific interaction effects across subjects between thickness and curvature on motor symptoms and found a significant interaction in the isthmus of the left cingulate cortex. Cognitive symptoms were not significantly related to the curvature-thickness relationship when considered in a full model. However, global cognitive scores and the recognition discrimination index were related to the CC-CT correlation when considered alone. The CC-CT correlation significantly increased (i.e., became less negative) over time in both the PD and HC group, with no significantly different longitudinal effects between both. There were no effects of the CC-CT correlation on longitudinal changes in cognitive performance and motor symptoms. Finally, we found that the most generalizable model for motor symptoms in PD included the curvature-thickness relationship as well as cognitive performance and mean putamen DAT binding, while it did not include total brain size nor average cortical thickness.
Generally, the average correlation between extrinsic curvature and cortical thickness was negative. This is in line with previous studies using empirical data (Gautam et al., 2015, Hogstrom et al., 2013) as well as simulations (Toro & Burnod, 2005). Gautam et al. (2015), for instance, found that healthy middle-aged adults show a negative relationship between cortical thickness and the local gyrification index (LGI) in many brain regions in the cortex. Similar results were reported by Hogstrom et al. (2013) in healthy adults with ages ranging from 20 to 85 years. Chaudhary et al. (2021) showed that this negative relationship is also present in PD patients with and without cognitive impairment in the left frontal pole and right entorhinal cortex respectively. The negative correlation can be explained mechanically: more force is needed to bend a thicker as opposed to a thinner cortex (Toro & Burnod, 2005), leading to less curvature in thicker cortices. Additionally, the negative correlation could also be explained by space constraints: brain regions with more constraints caused by the presence of the skull could be more likely to show a higher curvature but a thinner cortex (i.e., more tangential but less radial expansion; Gautam et al., 2015). This may also partly explain our observation that females show a more negative correlation than males given their difference in intracranial volume. In post-hoc analyses (not reported), we indeed observed that intracranial volume showed some association with CC-CT correlation when added to our model. However, the effect of sex only decreased slightly, indicating that it is not fully explained by smaller intracranial space.
We also found that older adults showed, on average, a correlation between curvature and thickness that is close to zero. A likely explanation for this finding is that widespread age-related cortical atrophy attenuates the association between cortical curvature and thickness. It has been shown that the effect of age on cortical thickness differs between brain regions, but that cortical curvature is relatively spared across the brain (Long et al., 2012). In post-hoc analyses (not reported), we found that some regions were affected more by cortical thinning but less by changes in curvature (e.g., bilateral superior temporal cortex), while other regions were affected more by changes in curvature than changes in cortical thickness (e.g., right lateral orbitofrontal cortex). Such regionally different atrophy effects could explain why older adults showed a smaller association between curvature and thickness. In general, our observation that age attenuates the negative relationship between cortical curvature and thickness could mean that a more negative curvature-thickness relationship reflects an optimal brain structure. The observed effect of sex (i.e., a more negative curvature-thickness association in females) suggests different levels of what defines optimal for males and females.
The observed effects of age seem to be in contrast to the findings reported by Hogstrom et al. (2013) who found highly similar spatial patterns of negative correlations between cortical thickness and local gyrification index between age bins. However, there are several differences between their study and the present study. First, Hogstrom et al. (2013) assessed the curvature-thickness relationship across subjects, while our study focused on the subject-specific curvature-thickness relationship (across brain regions), which could lead to different results. Second, our analyses included an explicit statistical test in a model with age as a continuous variable, rather than comparison of curvature-thickness relationships between age-bins.
Our main result showed that the effect of motor symptoms on the curvature-thickness association interacted with age. Specifically, the effect of motor symptoms on the CC-CT correlation was negligible for younger adults with PD, while its effect was positive for older adults. This effect is probably related to general cortical degeneration: both age and motor symptoms in PD patients have been related to widespread cortical degeneration including cortical thinning, reduction of cortical volumes, and changes in gyral curvature. Motor symptoms in PD patients have been shown to be associated with decreased cortical thickness of bilateral fusiform gyrus and temporal pole (Gao et al., 2018), and to decreased gyrification in inferior parietal, post and precentral, super frontal and supramarginal areas (Sterling et al., 2016). Age in PD patients has been shown to have a more negative impact on cortical thickness than in healthy controls (Pereira et al., 2012). A possible explanation for the observed effect in older adults could be that Lewy body pathology interacts with age-related accumulation of amyloid-beta pathology (Lim et al., 2019). This would imply that Lewy body pathology only has a profound effect on the curvature-thickness association in de novo PD patients once age-related amyloid-beta accumulation is present. We also found a specific association of rigidity with the curvature-thickness association, showing that the observed relationship between motor symptoms and the curvature-thickness interplay may be driven by rigidity rather than tremor symptoms.
We also observed that the curvature-thickness association attenuates (i.e., became less negative) over time in both PD patients and healthy controls. However, no significant differences between PD patients and healthy controls were observed regarding these longitudinal effects. It is therefore possible that the observed increases in the curvature-thickness correlation over time could be an effect of aging rather than PD pathology. However, an effect of PD pathology cannot completely be excluded since it is confounded with time.
Regarding region-specific effects, cortical curvature and thickness showed an interaction effect on motor symptoms across subjects specifically in the isthmus of the left cingulate cortex. The isthmus of the cingulate cortex has been shown to be degenerated in Parkinson’s disease compared to healthy controls (Laansma et al., 2021). Moreover, atrophy of this region has also been shown to be predictive of clinical outcomes after focused ultrasound subthalamotomy in PD (Lin et al., 2022). We specifically found that a higher curvature in the isthmus of the cingulate cortex is related to more beneficial effects of the cortical thickness on motor symptoms. Possibly, a thicker cortex in the isthmus cingulate helps to compensate for increased gyral curvature, which reflects neurodegeneration (Lin et al., 2021). Our results are seemingly in contradiction to the results in Chaudhary et al. (2021), who did not find a significant correlation between cortical thickness and curvature in the isthmus of the cingulate cortex. However, our study focused on the interaction effect between curvature and thickness on motor symptoms in PD rather than the existence of a region-specific correlation. Additionally, our sample was much larger allowing us to detect smaller effects.
The lack of an effect of diagnosis in the PPMI dataset could be related to the early disease stage for most subjects: almost all subjects were in Hoehn and Yahr stages 1 or 2, and the median duration of the disease was only 4.2 months. Therefore, it is possible that the effect of diagnosis was not yet observable on a T1-weighted MRI scan with the spatial resolutions used. This agrees with the observation that the direction of the effect of motor symptoms and diagnosis was the same. More precisely, subjects with PD showed a slightly less negative CC-CT correlation than healthy controls. Moreover, post-hoc analyses (not reported) showed that the difference in CC-CT correlation and PD patients with above-median motor symptoms approached significance. However, the effect did not reach statistical significance, possibly because of a low effect size in combination with some estimation error and measurement noise. Indeed, we found an effect of diagnosis in a population with a longer disease duration for which a larger effect is expected.
In our full model, there was no significant effect of global cognitive performance, as assessed with MoCA, nor any other cognitive subdomain on the curvature-thickness association. However, when cognitive scores were considered alone in models without confounding variables, the effect of global cognition and the recognition discrimination index on the curvature-thickness interplay was significant. This discrepancy shows that a combination of demographics, general brain morphology, and motor symptoms explained the observed bivariate relationships between cognitive performance and the curvature-thickness interplay.
The best model for motor symptoms (cross-sectionally) in PD included MoCA scores, mean putamen DAT binding, and the correlation between cortical curvature and thickness. The association between cognitive and motor symptoms in PD patients has been reported in previous studies and has been argued to be related to vascular burden and widespread brain atrophy (Laansma et al., 2021, Stojkovic et al., 2018). Reduced striatal DAT binding in PD has been observed in previous studies and has been shown to be a potential biomarker of disease progression (Kägi et al., 2010). Importantly, our model included the curvature-thickness association, but no other global brain features such as brain size or average cortical thickness. This finding suggests that the curvature-thickness association captures a unique property of neurodegeneration. We did not find any effects of the curvature-thickness interplay on longitudinal changes in motor and cognitive scores, showing that the CC-CT correlation did not have a longitudinal predictive effect in our sample. Possibly, the effects of the curvature-thickness relationship on longitudinal changes in motor symptoms were too subtle to detect.
The association between cortical curvature and thickness likely reflects a systematically and spatially varying pattern of thickness and curvature, which both show subtle local variations when considered independently (Demirci & Holland, 2022). However, the exact neurobiological basis of the cortical curvature-thickness interplay in neurodegeneration is currently unknown. It likely involves a complex interplay between genetics, neuroinflammation, environmental factors, neurovascular damage, and metabolic stress (Wareham et al., 2022). Future research could help elucidate the contribution of each of these neurobiological determinants to changes in the interplay between cortical metrics.
5. Conclusion
Our results show that the relationship between cortical curvature and cortical thickness is related to motor symptoms and age in PD patients, even after accounting for brain size and average cortical thickness. Our best model for motor symptoms in PD included the cortical curvature-thickness association. This research shows the potential of modeling the curvature-thickness interplay in PD.
CRediT authorship contribution statement
Hannes Almgren: Conceptualization, Methodology, Visualization, Software, Validation, Formal analysis, Writing – original draft. Alexandru Hanganu: Conceptualization, Writing – review & editing, Conceptualization, Methodology, Writing – review & editing. Milton Camacho: Conceptualization, Methodology, Writing – review & editing. Mekale Kibreab: Data curation, Writing – review & editing. Richard Camicioli: Conceptualization, Methodology, Writing – review & editing. Zahinoor Ismail: Conceptualization, Methodology, Writing – review & editing. Nils D. Forkert: Conceptualization, Methodology, Writing – review & editing. Oury Monchi: Conceptualization, Methodology, Writing – review & editing, Supervision.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
Acknowledgements
This study was funded by a project grant from the Canadian Institutes of Health Research project grant (PJT-1661232) to OM, ZI and NF, the Tourmaline Oil Chair in Parkinson’s Disease to OM and an operating grant from l’Institut de valorisation des données (IVADO) to OM.
ZI is funded by the Canadian Institutes of Health Research (CIHR). RC is funded by the Canadian Consortium on Neurodegeneration in Aging (CCNA) and Canadian Institutes of Health Research (CIHR). NF and MC are funded by Canada Research Chairs program, the River Fund at Calgary Foundation, and the Canadian Consortium on Neurodegeneration in Aging (CCNA).
Data used in the preparation of this article were obtained from the Parkinson’s Progression Markers Initiative (PPMI) database (https://www.ppmi-info.org/access- data-specimens/download-data). For up-to-date information on the study, visit www.ppmi-info.org. PPMI – a public-private partnership – is funded by The Michael J. Fox Foundation for Parkinson’s Research and funding partners (https://www.ppmi-info.org/about-ppmi/who-we-are/study-sponsors).
The authors would like to thank the reviewers for their help in improving this study.
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.nicl.2022.103300.
Contributor Information
Hannes Almgren, Email: Hannes.Almgren@ucalgary.ca.
Oury Monchi, Email: oury.monchi@umontreal.ca.
Appendix A. Supplementary data
The following are the Supplementary data to this article:
Data availability
The data that support the findings of this study are available from the Parkinson's Progression Markers Initiative. Restrictions apply to the availability of these data, which were used under license for this study. Data are available at https://www.ppmi-info.org/access-data-specimens/download-data with the permission of the Parkinson's Progression Markers Initiative. The data used in this study that was acquired at the Movement Disorders Clinic of the University of Alberta are available on reasonable request to Dr. Richard Camicioli (rcamicio@ualberta.ca). Data used in this study that was acquired at the Unité de Neuroimagie Fonctionnelle of the Centre de Recherche de l’Institut Universitaire de Gériatrie de Montréal and the Seaman Family Imaging Centre at the University of Calgary are available on request to Dr. Oury Monchi (oury.monchi@umontreal.ca). The Tao Wu dataset is available from http://fcon_1000.projects.nitrc.org/indi/retro/parkinsons.html.
References
- Acharya H.J., Bouchard T.P., Emery D.J., Camicioli R.M. Axial Signs and Magnetic Resonance Imaging Correlates in Parkinson’s Disease. Can. J. Neurol. Sci. 2007;34(1):56–61. doi: 10.1017/S0317167100005795. [DOI] [PubMed] [Google Scholar]
- Badea L., Onu M., Wu T., Roceanu A., Bajenaru O. Exploring the reproducibility of functional connectivity alterations in Parkinson’s disease. PLoS One. 2017;12(11) doi: 10.1371/journal.pone.0188196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Braak H., Tredici K.D., Rüb U., de Vos R.A.I., Jansen Steur E.N.H., Braak E. Staging of brain pathology related to sporadic Parkinson’s disease. Neurobiol. Aging. 2003;24(2):197–211. doi: 10.1016/S0197-4580(02)00065-9. [DOI] [PubMed] [Google Scholar]
- Chaudhary S., Kumaran S.S., Goyal V., Kaloiya G.S., Kalaivani M., Jagannathan N.R., Sagar R., Mehta N., Srivastava A.K. Cortical thickness and gyrification index measuring cognition in Parkinson’s disease. Int. J. Neurosci. 2021;131(10):984–993. doi: 10.1080/00207454.2020.1766459. [DOI] [PubMed] [Google Scholar]
- Dale A.M., Fischl B., Sereno M.I. Cortical surface-based analysis. I. Segmentation and surface reconstruction. NeuroImage. 1999;9(2):179–194. doi: 10.1006/nimg.1998.0395. [DOI] [PubMed] [Google Scholar]
- Demirci N., Holland M.A. Cortical thickness systematically varies with curvature and depth in healthy human brains. Hum. Brain Mapp. 2022;43(6):2064–2084. doi: 10.1002/hbm.25776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B. FreeSurfer. NeuroImage. 2012;62(2):774–781. doi: 10.1016/j.neuroimage.2012.01.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B., Dale A.M. Measuring the thickness of the human cerebral cortex from mag-netic resonance images. Proceedings of the National Academy of Sciences of the United States of America. 2000;97(20):11050–11055. doi: 10.1073/pnas.200033797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B., Sereno M.I., Dale A.M. Cortical Surface-Based Analysis: II: Inflation, Flatten-ing, and a Surface-Based Coordinate System. Neuroimage. 1999;9(2):195–207. doi: 10.1006/nimg.1998.0396. [DOI] [PubMed] [Google Scholar]
- Gao Y., Nie K., Mei M., Guo M., Huang Z., Wang L., Zhao J., Huang B., Zhang Y., Wang L. Changes in Cortical Thickness in Patients With Early Parkinson’s Disease at Different Hoehn and Yahr Stages. Front. Hum. Neurosci. 2018;12 doi: 10.3389/fnhum.2018.00469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gautam P., Anstey K.J., Wen W., Sachdev P.S., Cherbuin N. Cortical gyrification and its relationships with cortical volume, cortical thickness, and cognitive performance in healthy mid-life adults. Behav. Brain Res. 2015;287:331–339. doi: 10.1016/j.bbr.2015.03.018. [DOI] [PubMed] [Google Scholar]
- Goetz C.G., Fahn S., Martinez-Martin P., Poewe W., Sampaio C., Stebbins G.T., Stern M.B., Til-ley B.C., Dodel R., Dubois B., Holloway R., Jankovic J., Kulisevsky J., Lang A.E., Lees A., Leurgans S., LeWitt P.A., Nyenhuis D., Olanow C.W., LaPelle N. Movement Disorder Society-sponsored revision of the Unified Parkinson’s Disease Rating Scale (MDS-UPDRS): Process, format, and clinimetric testing plan. Mov. Disord. 2007;22(1):41–47. doi: 10.1002/mds.21198. [DOI] [PubMed] [Google Scholar]
- Goetz C.G., Tilley B.C., Shaftman S.R., Stebbins G.T., Fahn S., Martinez-Martin P., Poewe W., Sampaio C., Stern M.B., Dodel R., Dubois B., Holloway R., Jankovic J., Kulisevsky J., Lang A.E., Lees A., Leurgans S., LeWitt P.A., Nyenhuis D., LaPelle N. Movement Disorder Society-sponsored revision of the Unified Parkinson’s Disease Rating Scale (MDS-UPDRS): Scale presentation and clinimetric testing results. Mov. Disord. 2008;23(15):2129–2170. doi: 10.1002/mds.22340. [DOI] [PubMed] [Google Scholar]
- Hanganu A., Bedetti C., Jubault T., Gagnon J.-F., Mejia-Constain B., Degroot C., Lafontaine A.-L., Chouinard S., Monchi O. Mild cognitive impairment in patients with Parkinson’s disease is associated with increased cortical degeneration. Mov. Disord. 2013;28(10), Article 10 doi: 10.1002/mds.25541. [DOI] [PubMed] [Google Scholar]
- Hogstrom L.J., Westlye L.T., Walhovd K.B., Fjell A.M. The Structure of the Cerebral Cortex Across Adult Life: Age-Related Patterns of Surface Area, Thickness, and Gyrification. Cereb. Cortex. 2013;23(11):2521–2530. doi: 10.1093/cercor/bhs231. [DOI] [PubMed] [Google Scholar]
- Kägi G., Bhatia K.P., Tolosa E. The role of DAT-SPECT in movement disorders. J. Neurol. Neurosurg. Psychiatry. 2010;81(1):5–12. doi: 10.1136/jnnp.2008.157370. [DOI] [PubMed] [Google Scholar]
- Kang J.-H., Irwin D.J., Chen-Plotkin A.S., Siderowf A., Caspell C., Coffey C.S., Waligórska T., Tay-lor P., Pan S., Frasier M., Marek K., Kieburtz K., Jennings D., Simuni T., Tanner C.M., Singleton A., Toga A.W., Chowdhury S., Mollenhauer B., Parkinson’s Progression Markers Initiative. As-sociation of cerebrospinal fluid β-amyloid 1–42, T-tau, P-tau181, and α-synuclein levels with clinical features of drug-naive patients with early Parkinson disease. JAMA Neurology. 2013;70(10):1277–1287. doi: 10.1001/jamaneurol.2013.3861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klein A., Tourville J. 101 Labeled Brain Images and a Consistent Human Cortical Labeling Protocol. Front. Neurosci. 2012;6:171. doi: 10.3389/fnins.2012.00171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laansma M.A., Bright J.K., Al-Bachari S., Anderson T.J., Ard T., Assogna F., Baquero K.A., Ber-endse H.W., Blair J., Cendes F., Dalrymple-Alford J.C., de Bie, Debove I., Dirkx M.F., Druzgal J., Emsley H.C.A., Garraux G., Guimarães R.P.…Gutman B.A. International Multicenter Analysis of Brain Structure Across Clinical Stages of Parkinson’s Dis-ease. Movement Disord. 2021;36(11):2583–2594. doi: 10.1002/mds.28706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lim E.W., Aarsland D., Ffytche D., Taddei R.N., van Wamelen D.J., Wan Y.-M., Tan E.K., Ray Chaudhuri K., Parcog K., groupMDS Nonmotor study group. Amyloid-β and Parkinson’s disease. J. Neurol. 2019;266(11):2605–2619. doi: 10.1007/s00415-018-9100-8. [DOI] [PubMed] [Google Scholar]
- Lin H.-Y., Huang C.-C., Chou K.-H., Yang A.C., Lo C.-Y.-Z., Tsai S.-J., Lin C.-P. Differential Patterns of Gyral and Sulcal Morphological Changes During Normal Aging Process. Front. Aging Neurosci. 2021;13 doi: 10.3389/fnagi.2021.625931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin S.-J., Rodriguez-Rojas R., Baumeister T.R., Lenglos C., Pineda-Pardo J.A., Máñez-Miró J.U., del Alamo M., Martinez-Fernandez R., Obeso J.A., Iturria-Medina Y. Neuroimaging signa-tures predicting motor improvement to focused ultrasound subthalamotomy in Parkinson’s disease. Npj Parkinson’s Disease. 2022;8(1):1–9. doi: 10.1038/s41531-022-00332-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long X., Liao W., Jiang C., Liang D., Qiu B., Zhang L. Healthy Aging: An Automatic Anal-ysis of Global and Regional Morphological Alterations of Human Brain. Acad. Radiol. 2012;19(7):785–793. doi: 10.1016/j.acra.2012.03.006. [DOI] [PubMed] [Google Scholar]
- Marek K., Chowdhury S., Siderowf A., Lasch S., Coffey C.S., Caspell-Garcia C., Simuni T., Jen-nings D., Tanner C.M., Trojanowski J.Q., Shaw L.M., Seibyl J., Schuff N., Singleton A., Kieburtz K., Toga A.W., Mollenhauer B., Galasko D., Chahine L.M., Sherer T. The Parkinson’s progres-sion markers initiative (PPMI) – establishing a PD biomarker cohort. Ann. Clin. Transl. Neurol. 2018;5(12):1460–1477. doi: 10.1002/acn3.644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nasreddine Z.S., Phillips N.A., Bédirian V., Charbonneau S., Whitehead V., Collin I., Cummings J.L., Chertkow H. The Montreal Cognitive Assessment, MoCA: A Brief Screening Tool For Mild Cognitive Impairment. J. Am. Geriatr. Soc. 2005;53(4):695–699. doi: 10.1111/j.1532-5415.2005.53221.x. [DOI] [PubMed] [Google Scholar]
- Pereira J.B., Ibarretxe-Bilbao N., Marti M.-J., Compta Y., Junqué C., Bargallo N., Tolosa E. Assessment of cortical degeneration in patients with Parkinson’s disease by voxel-based mor-phometry, cortical folding, and cortical thickness. Hum. Brain Mapp. 2012;33(11):2521–2534. doi: 10.1002/hbm.21378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramezani M., Mouches P., Yoon E., Rajashekar D., Ruskey J.A., Leveille E., Martens K., Kibreab M., Hammer T., Kathol I., Maarouf N., Sarna J., Martino D., Pfeffer G., Gan-Or Z., Forkert N.D., Monchi O. Investigating the relationship between the SNCA gene and cognitive abilities in idiopathic Parkinson’s disease using machine learning. Sci. Rep. 2021;11:4917. doi: 10.1038/s41598-021-84316-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ronan L., Fletcher P.C. From genes to folds: A review of cortical gyrification theory. Brain Struct. Funct. 2015;220(5):2475–2483. doi: 10.1007/s00429-014-0961-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sarasso E., Agosta F., Piramide N., Filippi M. Progression of grey and white matter brain damage in Parkinson’s disease: A critical review of structural MRI literature. J. Neurol. 2021;268(9):3144–3179. doi: 10.1007/s00415-020-09863-8. [DOI] [PubMed] [Google Scholar]
- Sterling N.W., Wang M., Zhang L., Lee E.-Y., Du G., Lewis M.M., Styner M., Huang X. Stage-dependent loss of cortical gyrification as Parkinson disease “unfolds”. Neurology. 2016;86(12):1143–1151. doi: 10.1212/WNL.0000000000002492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stojkovic T., Stefanova E., Soldatovic I., Markovic V., Stankovic I., Petrovic I., Agosta F., Galan-tucci S., Filippi M., Kostic V. Exploring the relationship between motor impairment, vascular burden and cognition in Parkinson’s disease. J. Neurol. 2018;265(6):1320–1327. doi: 10.1007/s00415-018-8838-3. [DOI] [PubMed] [Google Scholar]
- Tang X., Zhang Y., Liu D., Hu Y., Jiang L., Zhang J. Association of Gyrification Pattern, White Matter Changes, and Phenotypic Profile in Patients With Parkinson Disease. Neurology. 2021;96(19):e2387–e2394. doi: 10.1212/WNL.0000000000011894. [DOI] [PubMed] [Google Scholar]
- Toro R., Burnod Y. A Morphogenetic Model for the Development of Cortical Convolutions. Cereb. Cortex. 2005;15(12):1900–1913. doi: 10.1093/cercor/bhi068. [DOI] [PubMed] [Google Scholar]
- Wareham L.K., Liddelow S.A., Temple S., Benowitz L.I., Di Polo A., Wellington C., Goldberg J.L., He Z., Duan X., Bu G., Davis A.A., Shekhar K., Torre A.L., Chan D.C., Canto-Soler M.V., Flanagan J.G., Subramanian P., Rossi S., Brunner T., Calkins D.J. Solving neurodegeneration: Common mechanisms and strategies for new treatments. Mol. Neurodegener. 2022;17(1):23. doi: 10.1186/s13024-022-00524-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y., Zhang J., Xu J., Wu X., Zhang Y., Feng H., Wang J., Jiang T. Cortical gyrification reductions and subcortical atrophy in Parkinson’s disease. Mov. Disord. 2014;29(1):122–126. doi: 10.1002/mds.25680. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data that support the findings of this study are available from the Parkinson's Progression Markers Initiative. Restrictions apply to the availability of these data, which were used under license for this study. Data are available at https://www.ppmi-info.org/access-data-specimens/download-data with the permission of the Parkinson's Progression Markers Initiative. The data used in this study that was acquired at the Movement Disorders Clinic of the University of Alberta are available on reasonable request to Dr. Richard Camicioli (rcamicio@ualberta.ca). Data used in this study that was acquired at the Unité de Neuroimagie Fonctionnelle of the Centre de Recherche de l’Institut Universitaire de Gériatrie de Montréal and the Seaman Family Imaging Centre at the University of Calgary are available on request to Dr. Oury Monchi (oury.monchi@umontreal.ca). The Tao Wu dataset is available from http://fcon_1000.projects.nitrc.org/indi/retro/parkinsons.html.