Luciferase‐free Luciferin Electrochemiluminescence

Abstract

Luciferin is one of Nature's most widespread luminophores, and enzymes that catalyze luciferin luminescence are the basis of successful commercial “glow” assays for gene expression and metabolic ATP formation. Herein we report an electrochemical method to promote firefly's luciferin luminescence in the absence of its natural biocatalyst—luciferase. We have gained experimental and computational insights on the mechanism of the enzyme‐free luciferin electrochemiluminescence, demonstrated its spectral tuning from green to red by means of electrolyte engineering, proven that the colour change does not require, as still debated, a keto/enol isomerization of the light emitter, and gained evidence of the electrostatic‐assisted stabilization of the charge‐transfer excited state by double layer electric fields. Luciferin's electrochemiluminescence, as well as the in situ generation of fluorescent oxyluciferin, are applied towards an optical measurement of diffusion coefficients.

The spectral tuning—from green to red—of luciferase‐free luciferin's electrochemiluminescence (ECL) was demonstrated by means of electrolyte engineering. The color change does not require, as still debated, a keto/enol isomerization of the light emitter, and brings evidence of the electrostatic‐assisted stabilization of the charge‐transfer (CT) excited state by double layer electric fields. Visual mapping of ECL and fluorescence fronts enables the optical quantitation of superoxide and oxyluciferin diffusivities.

Introduction

Light‐emitting chemical reactions have wide‐ranging ramifications across Nature, and are broadly exploited in technology. ^[1] Light emission accompanying luciferin oxidation—a widespread natural luminophore—covers most of the visible spectrum, ^[2] and for example while American railroad worms emit red light, African fireflies’ bioluminescence is green. ^[3] From a technological standpoint, light emission upon the enzyme‐assisted (luciferase) conversion of luciferin into oxyluciferin (ox‐luc hereafter, Scheme 1) is the basis of methodologies for the optical detection of ATP formation, ^[4] bio‐sensing of pollutants,[ ^2b , ⁵ ] and gene expression bioassays. ^[6]

Scheme 1.

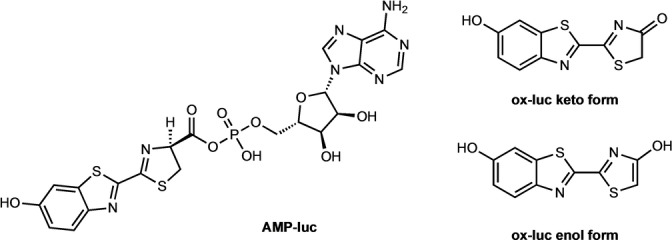
Structures of AMP‐luc and the keto and enol forms of ox‐luc.

The first study on fireflies’ bioluminescence was published in the late 1940s by McElroy, ^[7] who some years later also succeeded in isolating the light‐emitting molecule. ^[8] The reaction begins with the luciferase‐catalyzed formation of the adenosine monophosphate ester of luciferin (AMP‐luc hereafter, Scheme 1), followed by an oxidative decarboxylation that leads to the excited ox‐luc, which in turn relaxes emitting light. ^[9] In 1971 White and co‐workers, in a first attempt to explain the aforementioned broad spectral distribution, advanced the hypothesis of it being the result of a keto‐enol tautomerization of the excited state, with its keto‐form leading to red emission, while the enol decay being responsible for a yellow‐green emission. ^[9a] In the following decades several other mechanisms were proposed to account for the color range of natural luciferin luminescence, from changes in polarity of the light reaction micro‐environment, ^[10] to electrostatic interactions. ^[11] Both the origin of luciferin spectral tuning and the chemical details of the adenylate firefly luciferin light‐emitting path remain however poorly understood, ^[12] largely because the lack of a laboratory model system capable of triggering this luminescent reaction in a simplified experimental environment, ideally without enzymes. ^[13]

One such laboratory systems could take the form of an electrical trigger of the luciferin light path, a method capable of the selective generation of the excited state light‐emitter near an electrified surface. Demonstrating such an electrochemical path remains an unmet challenge. Besides removing the complexity of the protein environment, realizing an on/off switch of luciferin chemiluminescence is important as the environment sensed by the light‐emitting excited state affects the energy of its radiative decay. ^[14] The development of luciferin electrochemiluminescence, therefore, offers the possibility of validating (or falsifying) the hypothesis of electric fields stabilizing/destabilizing the charge‐transfer character of the emitting excited state, accounting for the natural luciferin spectral tuning.[ ¹¹ , ¹⁵ ] Such new methodology, alongside its validation via theoretical models, would also enable a systematic screen of the microenvironment (solvent and electrolyte) role on this widespread, yet actively debated,[ ^3c , ¹⁶ ] luminescent reaction.

Results and Discussion

As discussed above, luciferin light emission is catalyzed in vivo by an oxidoreductase, luciferase. The activity of this enzyme is known to be pH‐dependent, and for luciferase immobilized on an electrode surface, the electrochemically induced depletion of protons has been previously shown to alter its activity. ^[13a] Our broad goal is, however, to remove altogether the need of an enzyme, and to simply rely on an external bias to trigger the luciferin light path at an electrified solid–liquid electrolyte interface. Several reports detail luciferin chemiluminescence in water,[ ^9a , ¹⁷ ] hence water was the first solvent choice to begin exploring an electrochemical path to luciferin's light emission.

However, despite our efforts, neither anodic nor cathodic voltage pulses applied to aqueous solutions (0.1 M KCl) of AMP‐luc led to a light emission above the dark background (≈500 cps) of a single‐photon counter. There is a known correlation between oxygen concentration and luciferin's emission,[ ^16a , ¹⁸ ] and once a dioxetane intermediate is formed, basic conditions can trigger the light path of AMP‐luc.[ ^9a , ^16a , ¹⁹ ] Hence, we decided to attempt triggering the luciferin light path by electrochemical generation of superoxide radical anion (superoxide hereafter), a basic oxidizing agent capable of also mediating radical chemistry that could lead to the dioxetane intermediate. DMSO was chosen as the solubility of AMP‐luc is greater in DMSO than in water,[ ^9a , ^9b , ²⁰ ] and because—unlike in water—the one‐electron reduction of oxygen in DMSO leads to superoxide. ^[21]

Simultaneous photon counting and cyclic voltammetry data (Figure 1a) show a steep rise in the cathodic current at ≈−0.8 V (blue trace), slightly preceding the appearance of a light output (black trace). The cathodic current rise corresponds to the onset of oxygen reduction, and control experiments with deoxygenated solutions showed no measurable luminescence (Figure S1). The point where the photon counts peak, on average (10±1.7)×10⁴ photon/s, is reached with a small delay relative to the cathodic flow peak of (12±4.4)×10¹⁴ electron/s. We believe this delay is explained by the relatively high energy barrier of the first step of the light path (vide infra). Further, a significant portion of the experiments showed a shoulder on the cathodic wave at ≈−0.7 V (Figure S2). The origin of this parasitic signal is unclear, but its presence was generally associated with an even larger delay between current rise and light emission onset. This shoulder was absent in voltammograms performed without AMP‐luc (Figure S3). Further, photon counts traces as that of Figure 1a are qualitatively similar to data recorded with a conventional spectrometer monitoring emission at 626 nm (Figure S4).

Figure 1.

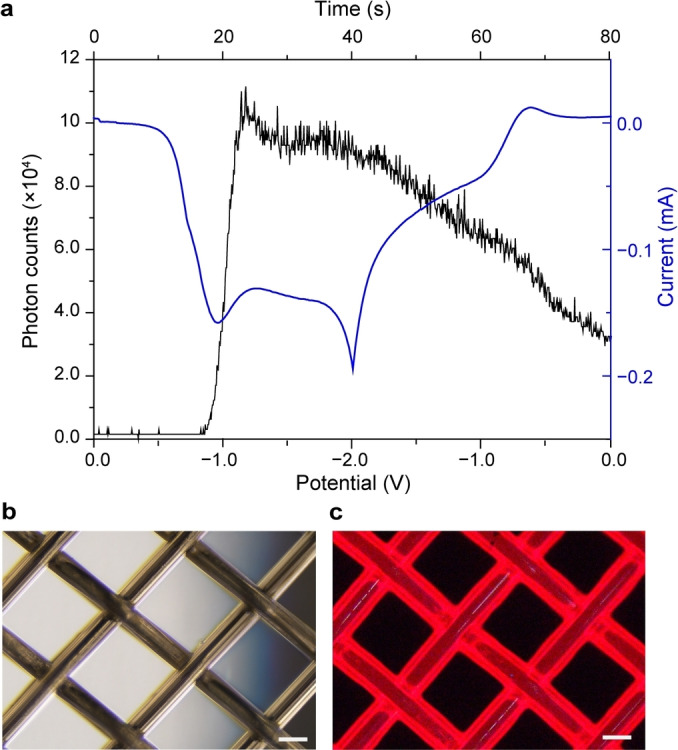
a) Representative simultaneous photon counting and current recording for the electrochemically generated light emission of AMP‐luc (0.43×10⁻³ M in oxygen‐saturated 0.2 M Bu₄NClO₄/DMSO) at a platinum mesh electrode. The electrode potential was swept cyclically between 0.0 V and −2.0 V at a rate of 0.05 V s⁻¹ (Figure S6). The emission peak corresponds to ≈11.3×10⁴ photon/s. b) Bright field image (4× magnification) of the platinum electrode under ambient light, and c) electrochemiluminescence image (4× magnification) captured in a dark room ≈0.5 s after the onset of the cathodic voltage bias (−2.0 V, Video S1). Scale bars in (b, c) are 100 μm.

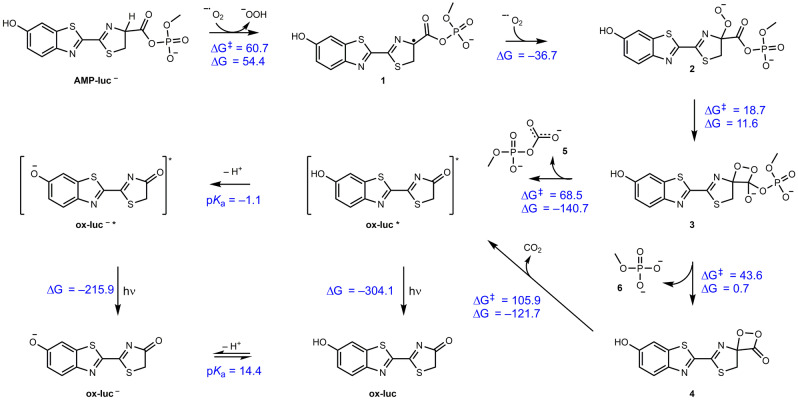
The cyclic voltammetry of AMP‐luc in Bu₄NClO₄/DMSO results in a red glow easily visible to the naked eye around the platinum‐mesh electrode (Figure 1c). Similar experiments with an alkyl ester of luciferin (D‐luciferin ethyl ester, Figure S5) replacing the adenosine monophosphate ester (AMP‐luc) resulted in a significantly lower emission, and consequently the latter was used to perform all experiments in this work. Considering the novelty of the above electrochemical trigger of luciferin luminescence, we carried out a computational study to investigate its reaction mechanism. We first established the protonation state of a model of the starting material in DMSO by evaluating pK _a values for the first, second, and third deprotonation steps (Scheme 2). Under the reaction conditions, we expect the phosphate to be deprotonated (pK _a1=3.5) but not the phenol (pK _a2=17.3) or CH (pK _a3=27.7).

Scheme 2.

Predicted pK _a values for the 1^st, 2^nd and 3^rd deprotonations of a model of AMP‐luc. All pK _a values (298 K, DMSO) were computed via an isodesmic method using 4‐hydroxydinaphtho[2,1‐d : 1′,2′‐f][1,3,2]dioxaphosphepine 4‐oxide (experimental pK _a=3.37) ^[22] as a reference, and performed at the wB97XD/Def2‐TZVP//M062X/6–31+G(d,p) level of theory using the SMD solvent model.

Using the singly deprotonated species, we next considered its reaction with superoxide (Scheme 3). Superoxide initially abstracts a hydrogen atom of the alpha carbon of the AMP ester, yielding the radical species 1 which is then kinetically trapped by a barrierless radical combination with a second superoxide. The resulting intermediate (2) undergoes a mildly endergonic rearrangement to form an unstable dioxetanone (3). This intermediate is kinetically trapped by a rapid exergonic decarboxylation to the excited state of ox‐luc (ox‐luc*), which then releases light upon relaxation. The pathway in which the phosphate (6) and CO₂ are lost sequentially was found to be less kinetically favourable than the concerted loss of 5 (Scheme 3). Interestingly, the computed pK _a of ox‐luc* in the S₁ excited state is −1.1, whereas in the ground state it is 14.4. Thus, if deprotonation kinetically competes with ox‐luc* radiative decay, the emitting species would be the phenoxide (ox‐luc⁻*), though once in the ground state the neutral form would be reformed and dominate. We believe this is the case since ox‐luc* deprotonation should be faster than its radiative decay lifetime that typically falls in the nanosecond timescale. This is also supported by the computational study presented afterwards (see Table 1 and the corresponding discussion).

Scheme 3.

Proposed mechanism of the AMP‐luc electrochemically generated light path, supported by first principles calculated Gibbs free reaction energies and barriers (298 K, kJ mol⁻¹) as obtained with wB97XD/Def2‐TZVP//M062X/6–31+G(d,p) using SMD to model the DMSO solvent environment. Electrochemically generated superoxide abstracts a hydrogen atom to generate a radical intermediate (1) that is kinetically trapped by a barrierless radical combination with a second superoxide molecule. This undergoes a mildly endergonic rearrangement to yield an endoperoxide intermediate (3), which is kinetically trapped by a highly exergonic oxidative decarboxylation to yield the excited state of ox‐luc (ox‐luc*), which in turn emits light upon relaxation to the product ox‐luc. Sequential loss of the phosphate to yield 4 followed by decarboxylation to yield the excited state of ox‐luc* was also considered but is less kinetically feasible. The excited state has a pK _a of −1.1 and thus in principle could deprotonate if the reaction is kinetically competitive with relaxation to the ground state. In the ground state the pK _a is 14.4 and the neutral form is preferred.

Table 1.

Calculated QM (XMS‐PT2)/MM emission energies for the excited state light emitter (ox‐luc⁻ *) at full and partial solvation.

				Emission maximum [nm], (oscillator strength)				Charge‐transfer (CT)[a]				Relative energy [kJ mol−1]
Environment		Electric field [V nm−1]		Enol		Keto		Enol		Keto		Enol		Keto
Vacuum		−1		572 (0.65)		622 (0.73)		−0.28		−0.23		48.5		−11.3
		0		611 (0.69)		660 (0.76)		−0.27		−0.18		67.4		0.0
		+1		652 (0.73)		695 (0.76)		−0.25		−0.11		84.9		10.9
DMSO (complete solvation)		−1		537 (0.62)		596 (0.75)		−0.26		−0.24		31.0		−12.1
		0		574 (0.66)		633 (0.77)		−0.26		−0.20		56.5		0.0
		+1		614 (0.70)		671 (0.78)		−0.25		−0.14		77.8		13.0
DMSO (half‐solvated)		−1		570 (0.67)		627 (0.78)		0.27		−0.20		58.2		−4.2
		0		610 (0.70)		660 (0.79)		−0.26		−0.16		74.5		0.0
		+1		649 (0.74)		696 (0.79)		−0.23		−0.07		86.2		10.5
THF (complete solvation)		−1		546 (0.61)		602 (0.71)		−0.26		−0.24		37.7		−10.5
		0		584 (0.65)		639 (0.74)		−0.27		−0.21		60.7		0.0
		+1		623 (0.69)		677 (0.76)		−0.26		−0.15		76.6		12.6
THF (half‐solvated)		−1		566 (0.61)		630 (0.68)		−0.27		−0.23		39.7		−7.9
		0		606 (0.65)		661 (0.73)		−0.27		−0.19		52.3		0.0
		+1		643 (0.69)		698 (0.74)		−0.25		−0.13		67.4		20.5

[a] The CT index is calculated as the difference between the electron densities on the benzothiazole side of the final (S₀) and starting (S₁) states.

In order to experimentally validate the role played by the superoxide anion we have performed control experiments where the AMP‐luc solution was added to a cuvette containing a small amount (0.02 g) of KO₂, but with no electrodes present. The results of these experiments (Figure S7) indicate that there is sizable chemiluminescence even in an oxygen‐free environment (argon atmosphere), provided superoxide radical anions are present, validating the light path discussed above and presented in Scheme 3.

Next, we tested experimentally whether this enzyme‐free and electrode‐triggered path to luciferin emission could be used to tune the luminescence color, either by changing the electrolyte and/or the magnitude of the external voltage bias. The design of these experiments is based on theoretical models that suggest a link between the electrostatic forces sensed by the light‐emitting excited state and the energy (color) of the emitted light. ^[23] Large electric fields exist at an electrode‐electrolyte interface,[ ¹⁵ , ²⁴ ] where the electro‐neutrality of an electrolytic solution is lost. The voltage–distance profile—electric field—of the interface depends on the nature of the electrolyte, ^[25] and stronger near‐surface double‐layer fields are obtained by increasing the electrolytic support.[ ¹⁵ , ²⁶ ]

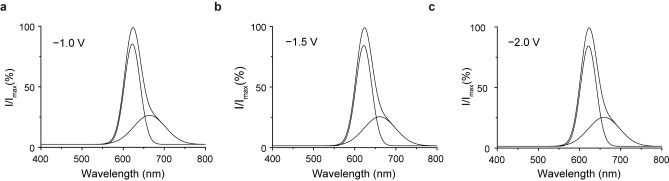
In DMSO all attempts to tune the AMP‐luc electrochemically generated emission from red to yellow‐green by means of changes to the electrolyte and its concentration were at a first inspection unsuccessful (Figures S8–S10). However, while the position of the main band centered at 626 nm did not shift appreciably, the low‐energy shoulder present in all the spectra showed a ≈10 nm blueshift in response to an external bias increase: from 674 nm at −1.0 V to 664 nm at −1.5 V (Figure 2a, b). A further cathodic increase of the applied potential didn't lead to a further shift in the shoulder's position (Figure 2c). To explain this shift, the nature of the light emitter, and the origin of the solvent dependent (vide infra) luminescence shift, we developed a theoretical model of the system. Several theories had been proposed to explain the different colors of the luciferin emission. ^[16a] Color changes may be caused by the light path proceeding through chemically different light emitters, and/or by changes to the nature of the reaction environment.

Figure 2.

Deconvoluted emission spectra of AMP‐luc (0.43×10⁻³ M) electrochemiluminescence in Bu₄NClO₄/DMSO (2.0×10⁻¹ M) on platinum mesh electrodes under negative voltage pulses of different magnitude [−1.0 V, (a); −1.5 V, (b); −2.0 V, (c)]. At a more negative voltage bias, the low energy shoulder shifts progressively towards shorter wavelengths (10 nm blueshift from −1.0 V to −1.5 V, while from −1.5 V to −2.0 V there is not any additional spectral shift). All potential biases are versus Ag/AgCl. The emission spectra recording takes 2.0 s and was started simultaneously with the cathodic pulse.

We theoretically studied in vacuum, in THF and in DMSO (that were both treated explicitly employing a hybrid quantum mechanics/molecular mechanics (QM/MM) approach) ^[27] with and without exogenous electric fields, the emission spectra of the two most plausible luciferin light‐emitters:[ ^9a , ²⁸ ] the keto and enol form of deprotonated ox‐luc* (ox‐luc⁻*) (see Scheme 3 and Figure S11). The other possible chemical forms of oxyluciferin are excluded as possible light emitters since they either emits out the visible range or they display very low oscillator strengths. ^[29] Electric fields were aligned along the main molecular axes (z‐direction, Figure S11). Calculated emission maxima are collected in Table 1 and Table S1 and show that the enol‐form emission is systematically blue‐shifted compared to the keto form by approximately 49 nm (vacuum), 55 nm (THF), and 59 nm (DMSO). A previous study in which the DMSO solvent was treated implicitly, reached an opposite conclusion, suggesting the enol‐form to be more stable. ^[30] Hence the importance of modelling explicit solvent molecules that accounts for local, directional, and anisotropic interactions. A similar blueshift is also found for both tautomers by changing the environment from gas to a polar solvent, with enol being more influenced than the keto form. At low concentrations of the counter ion, the negatively charged light emitting molecule is expected to be fully solvated by the high polar solvent, hence reducing the probability of ion‐pair formation.

Remarkably, the calculated emission wavelength of the keto‐form (ox‐luc⁻*) in pure DMSO matches closely the experimental value recorded at low electrolytic support (633 nm versus 626 nm), in agreement with it being the thermodynamically stable species in the excited state. The enol‐form would have an emission maximum at 574 nm, which rules out the possibility of this species being the prevalent light emitter in the experiments. On the other hand, direct light excitation of ground state ox‐luc results into green fluorescence (peaking at ≈560 nm) in DMSO. ^[31] Interestingly, both experimental[ ³¹ , ³² ] and theoretical ^[28] studies confirm that it is the neutral and deprotonated enol form of ox‐luc to dominate the ground state in solvents such as DMSO. It is thus apparent that it is this form responsible for the photoluminescence spectrum and green emission observed for oxyluciferin as it is the species that absorbs light. Due to the change in the pK _a of the phenol group upon excitation (see Scheme 3), the neutral enol form gets quickly deprotonated in the excited state, eventually leading to green emission as observed experimentally and in match with our predictions (574 nm, see Table 1), while excitation of the already deprotonated (anionic) ground state enol form directly leads to the green emitting species.

The emission in luciferin is attributed to the S₁→S₀ (first singlet excited state→singlet ground state) radiative transition, which is accompanied with an internal negative charge transfer (CT hereafter) from the thiazolone to the benzothiazole moiety (see Table 1). Stabilization of the CT state in DMSO upon the formation of contact ion‐pairs (with Li⁺ binding the negative oxygen of the benzothiazole moiety) is expected to blueshift the emission of both keto‐form and enol‐form. Very notably, such a shift is indeed predicted by the calculated emission energies in DMSO in the presence of contact ion‐pairs with Li⁺ and K⁺ (see Table S1) and it is indeed experimentally observed (10–15 nm) at higher concentrations of Li⁺ (Figure S8) where contact ion‐pairs are expected.

Finally, it is worth noting that the higher CT character for the enol‐form compared to the keto‐form is reflected in a larger energy difference between the S₀ and S₁ states, and therefore in a blueshift. By reducing the solvent polarity, moving for example from DMSO to THF‐based electrolytes, contact ion‐pairs are more likely to occur (Table S1), which explains the mismatch between the predicted emission energy from the keto‐form computed in neat THF (639 nm) and the experimental blue‐shifted value measured in LiClO₄/THF (575 nm, Table S1). Accordingly, the emission maximum is tuned by the nature of the cation, with ion‐pairs with Li⁺ causing a more pronounced blueshift than for K⁺ due to an enhanced stabilization of the S₀ CT state (Table 1), as already pointed out above. An electrolyte is necessary to couple electronic conduction in the solid electrode with ionic conduction in the electrolyte, which is required to trigger a redox change at the electrode, and it has therefore not been possible to test experimentally AMP‐luc electrochemiluminescence in non‐supported (electrolyte‐free) THF. When trying to reach a conclusion on the prevalent form of the light emitter in THF we note that the S₁ keto‐form is more stable than the enol S₁ state by 55.5–67.4 kJ mol⁻¹, both in vacuum as well as in solution (see Table 1). Moreover, the reaction pathway forming the S₁ excited state ends with the keto‐form. Consequently, the enol‐form could only originate by tautomerization of the keto isomer. Such tautomerization is unlikely to occur as it is both kinetically and thermodynamically disfavoured (see Scheme 3). ^[29]

A good agreement between theory and experiments is eventually found for the emission in THF when considering keto‐form/Li⁺ contact ion‐pairs (578 nm vs 573 nm for the computational and experimental results, respectively: see Figure S12), a scenario which is likely to occur in the less polar THF solvent (as mentioned above and also proposed by Hirano et al.), ^[30] thus calling for the S₁ keto‐form as the light emitter in THF and, in conclusion, in whatever environment.

We have validated experimentally such environmental shifts (Figure 3) by demonstrating that for the smallest cation, lithium, and in low dielectric solvents, the emission undergoes a significant blueshift (from 626 nm in 0.2 M Bu₄NClO₄/DMSO to 605 nm in 0.2 M LiClO₄/THF). Furthermore, the lithium concentration has a clear energetic impact on the radiative decay of the light emitter, with lower concentrations showing a green instead of the red luminescence (573 nm in THF with 5.0×10⁻³ M LiClO₄). This suggests that, at high concentrations, Li⁺ binds both oxygens at the two opposite sides of the luminophore, thus balancing (and quenching) the blueshifting effect due to the single oxygen complexation at the benzothiazole side found at lower lithium concentrations. Interestingly there may be a parallel between the blueshift in THF and similar shifts observed in vivo which are ascribed to the luciferase's active site hydrophobicity.[ ²⁸ , ³³ ] Moreover, even though different perchlorate‐based salts were tried in THF (Bu₄NClO₄ and NaClO₄), spectral tuning of the AMP‐luc towards the blue remains larger with LiClO₄ (Figure S13–S14). It needs also to be highlighted that achieving a blueshift was always at the expenses of the emission intensity. Photon‐counting experiments indicate ≈900 photon/s for the electrolysis of AMP‐luc in 5.0×10⁻³ M LiClO₄/THF, and ≈3200 photon/s in 0.2 M LiClO₄/THF, both being considerably less than the ≈10⁵ photon/s obtained for 0.2 M Bu₄NClO₄/DMSO. This drop is partly caused by a lower current density as the electrolyte resistance increases, and partly by the quenching effect of small cations on superoxide. ^[34] Furthermore, changes to the nature of anion did not have any measurable effect on the energy of the AMP‐luc emission, not even with a completely non‐coordinating anion such as BARF (Figure S15). In DMSO, neither varying the type, nor the concentration of electrolyte had any effect on the emission wavelength, and only LiClO₄ at concentrations close to saturation (2.0 M) caused a very small blueshift (Figure S8). Solvents with a dielectric constant similar to DMSO, such as DMF, resulted in a similar (hard to tune) red light emission (Figure S16).

Figure 3.

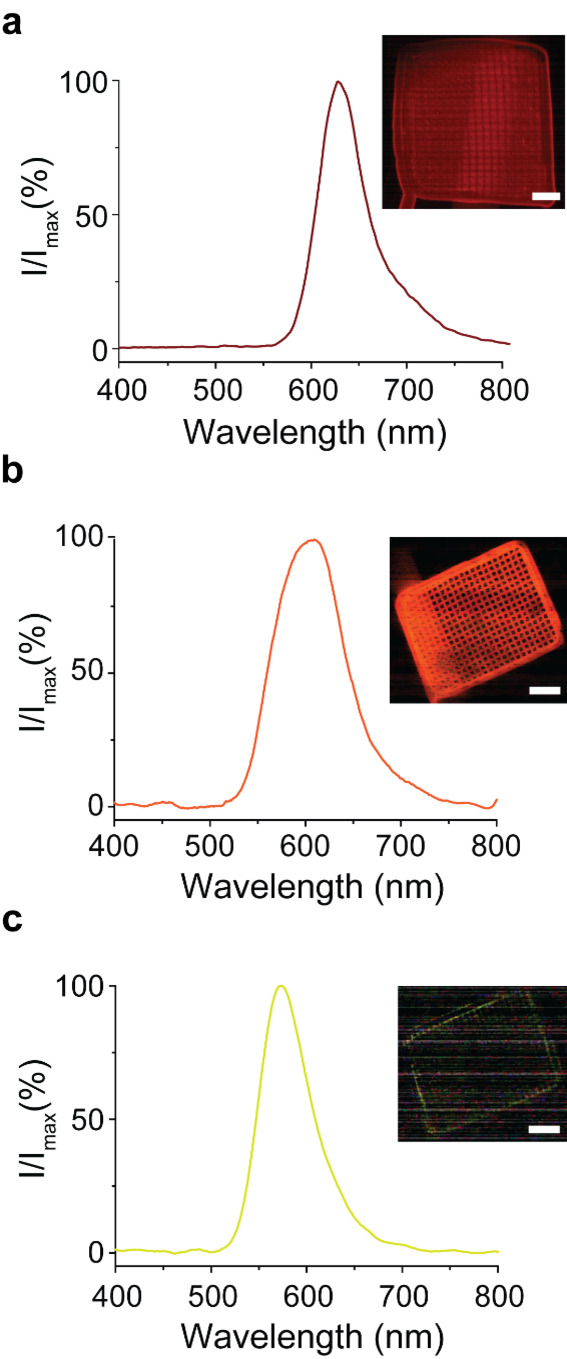
Spectral tuning of the electrochemically induced AMP‐luc luminescence. Normalized emission spectra acquired by applying a constant negative bias (−2.0 V vs Ag/AgCl) to a platinum mesh working electrode (pictured in figure) in contact with a 0.43×10⁻³ M solution of AMP‐luc. The electrolyte was a) 2.0×10⁻¹ M Bu₄NClO₄ in DMSO, b) 2.0×10⁻¹ M LiClO₄ in THF, and c) 5.0×10⁻³ M LiClO₄ in THF. The peaks maximums are progressively blue‐shifted [626 nm (a), 605 nm (b), and 573 nm (c)]. Scale bars in the optical image insets are 1.0 mm.

We now focus on finding a theoretical explanation for the asymmetric shape of the emission spectra of Figure 2 and Figure 3. The low‐energy shoulder that, as discussed above, shifts with changes to the magnitude of the exogenous electric field, is probably the radiative decay of half‐solvated ox‐luc⁻* molecules. Molecules of AMP‐luc adsorbed on the electrode's surface, a not unlikely scenario, can be roughly considered as half‐solvated and half facing a vacuum‐like environment (the electrode's surface). The observed redshift (relative to the main band, Figure 2) is in agreement with our theoretical predictions for the emission of a half‐solvated molecule (Table 1). An oriented exogenous electric field will stabilize or destabilize ox‐luc⁻* depending on the relative dipole‐field orientation. The energies of both the keto and enol isomers have a high sensitivity to changes in the electric field magnitude and direction. Table 1 reports the calculated emission spectral tuning in response to an electric field (±1 V nm⁻¹, Table 1) aligned along the z‐direction, which is the direction of the S₁→S₀ dipole moment change (Figure S11), and therefore giving maximum field sensitivity. The field‐dependent shifts for the half‐solvated molecule are as high as 35–40 nm, and are due to changes in CT character, with a high CT resulting in a blueshift, while a CT reduction causing a redshift.

The experimental blueshift of the emission shoulder possibly indicates that the exogenous field is stabilizing S₀ more than S₁, owning to the CT character of the ground state that is also increasing upon the effect of the electric field: more electrons are pushed from the thiazolone towards the benzothiazole ring of ox‐luc⁻* (see Table 1). As summarized in Table 1, such emission shift is predicted both for vacuum and solvated molecules, as well as for half‐solvated systems. The main emission band did not shift in the experiments, possibly because in our freely diffusive solution system the majority of the emission occurs at some distance from the electrode. As discussed above, voltage‐dependent shifts towards higher energy were however observed for the emission shoulder, which is therefore tentatively attributed to adsorbed (half‐solvated) molecules. The experimental shifts (≈10 nm, Figure 2) are significantly lower than those theoretically expected for a 1 V nm⁻¹ field. Such lower than predicted shifts are probably an indirect indication of only a fraction of the external voltage bias dropping across the light emitter, or in other words, indicating that the Debye length is for instance 3–4 times greater than the molecular dimension. It can be envisioned that analogous optical “spectral tuning” measurements may become a viable alternative to a direct probing of the double potential profile, as such direct electrical measurements have serious intrinsic limitations, most notably that any electrified probe will carry its own double layer of charges which will add up to the one under investigation. ^[35]

Beyond the value and scope of an electrochemical trigger of luciferin luminescence (and of other CT light emitters, such as luminol) to probe near surface electric fields, time‐resolved microscopy of the AMP‐luc electrochemiluminescence can enable a simple and direct optical measurement of diffusion coefficients. Analogous “imaging” of electrochemiluminescent reactions and of electrochemically modulated fluorescence, to study electrode heterogeneity and mass transport, have been reported for luminol, rubrene and tris(2,2′‐bipyridyl)ruthenium(II). ^[36] Selected time‐stamped micrographs in Figure 4a–c track the diffusion of the red glowing front away from the platinum surface after the electrolysis of AMP‐luc. Due to the complexity of the light path, which involves several steps, chemical and electrochemical, it is hard to separate from a single optical readout individual diffusivity (D) values, but since D scale roughly with the inverse of size, the species more likely to govern the movement of the electrochemiluminescent front is superoxide. Analysis of the distance (r) travelled over time by the front, away from the electrode surface and along the A–B line marked in Figure 4, and by modelling diffusivity as an Einstein's random walk (r²=2 D  t), we were able to estimate D for superoxide in DMSO to (2.45±0.18)×10⁻⁶ cm² s⁻¹. This “optical” D value is marginally lower, but of the same order of magnitude, as that obtained for superoxide in DMSO through more established electrochemical methods. ^[37] We also remark that AMP‐luc is profluorescent, as its electrolysis yields fluorescent ox‐luc. Optical mapping of the diffusion of electrogenerated ox‐luc is shown Figure S17. We believe that this method will complement diffusivity measurements based on electrochemical techniques, such as hydrodynamic methods with rotating disk electrodes. Especially in viscous solvents, such as ionic liquids, ^[38] adventitious evolution of gas bubbles often leads to mass transport complications, such as convection upon the detachment of surface pinned bubbles. ^[39] Convection issues are hard to detect and account for in electrochemistry. Through an optical method as the one shown in Figure 4 and Figure S17, it is possible to gauge the severity of convection events, or even to bypass them by mapping local diffusivities instead of relying, as is typically done, on an average measurement of the entire electrode area.

Figure 4.

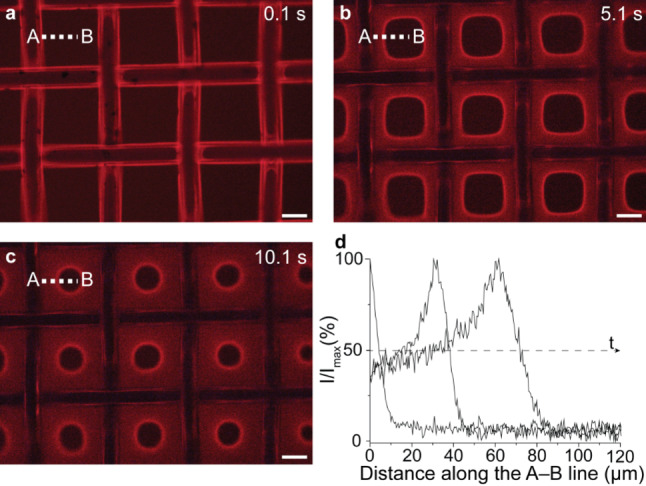
a)–c) Selected time‐stamped micrographs (10× magnification) mapping the in situ generated AMP‐luc electrochemiluminescence upon the cathodic electrolysis of an oxygen‐saturated AMP‐luc solution (0.43×10⁻³ M in 2.0×10⁻¹ M Bu₄NClO₄/DMSO, Video S2) on a platinum mesh electrode. The images were captured in a dark room at 0.1 s (a), 5.1 s (b) and 10.1 s (c) after the onset of the cathodic bias voltage (−2.0 V). Scale bars in (a)–(c) are 100 μm. d) Electrochemiluminescence profiles sampled along the A–B line marked in (a)–(c), capturing the expansion of the diffusion front, away from the electrode's surface, at electrolysis times (t) of 0.1, 5.1 and 10.1 s. Point A is placed approximately on the edge (top view) of the platinum surface.

Conclusion

We have reported for the first time the enzyme‐free, electrochemically triggered luciferin light emission. Such a laboratory model allows one to trigger this luminescent reaction in a controlled environment, removing ambiguity introduced by the complexity of the protein environment of luciferase.

The excited state of the light‐emitter was generated near an electrified surface, allowing us to control simultaneously exogenous electric fields, solvation and ion pairs. Using quantum chemistry, we have shown that the light path is initiated by radical chemistry mediated by electrogenerated superoxide, we have clarified the nature of the light emitter and explained the debated spectral tuning of luciferin as field effects and ion pairing, rejecting the keto‐enol tautomerization hypothesis. We believe that this or similar CT electrochemiluminescent systems will find use in clarifying debated topics in surface science, such as the existence of a density‐depleted solvent region near hydrophobic surfaces. ^[40] Spectral tuning of the partially solvated luciferin light emitter by the electrode generated exogenous electric field, as was observed in this study, could be adapted to verify or falsify the existence of such depletion layer even on rough surfaces, on samples with surface impurities, or in samples with unknown chemical features, where X‐ray or neutron‐based methods would not be applicable.[ ^40d , ⁴¹ ]

Finally, we have demonstrated that the electrochemiluminescence of AMP‐luc can be used to map optically the diffusivity of superoxide away from its generation site (the electrode) towards the bulk of the electrolyte. This optical mapping of electro‐generated diffusion fronts can measure diffusivity in viscous solvents, in systems where mass transport by convection is likely to interfere with diffusion, as for electrodes evolving gaseous products, ^[39a] or can be applied to electrode geometries where hydrodynamic electrochemical measurements, such as rotating disk techniques, are not viable.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

M. Belotti, M. M. T. El-Tahawy, L.-J. Yu, I. C. Russell, N. Darwish, M. L. Coote, M. Garavelli, S. Ciampi, Angew. Chem. Int. Ed. 2022, 61, e202209670; Angew. Chem. 2022, 134, e202209670.

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.