New indexes for myofibril linearity in muscle image analysis

Abstract

The endeavor to evaluate the linearity of myofibrillar structures and their potential deviation from a straight line is a fascinating problem in muscle tissue image analysis. In this Letter, we suggest two different strategies for solving the same challenge. The first strategy is based on an alignment index, which could be derived by comparing the sum of the lengths of the individual sarcomeres with the distance between the "head" of the first and the "tail" of the last sarcomere. The second strategy relies on circular statistics, which takes a cue from an already suggested method. Our proposed methods are alternatives: the former has the advantage of simplicity; the latter is certainly more elegant and gives greater substance to statistical analysis, but in contrast, it also has greater computational complexity.

Ethical Publication Statement

We confirm that we have read the Journal’s position on issues involved in ethical publication and affirm that this report is consistent with those guidelines.

An intriguing problem in analysing the image of muscle tissue is represented by the attempt to evaluate the linearity of myofibrillar structures and their possible deviation from a straight line. By indicating with αi the angles between two successive sarcomeres along the same myofibril, Cisterna et al.¹ proposed an index that can formally be described as follows:

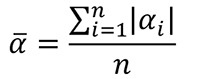where n is the number of angles (i.e., the number of sarcomeres minus 1); the absolute value was introduced to avoid that random fluctuations around a hypothetical central axis could lead to an average equal to zero (i.e., the same result we would obtain in case of perfect alignment).

In this paper, we propose two alternative approaches to the same problem. An alignment index could be obtained by comparing the sum of the lengths of the individual sarcomeres (ls_i) with the distance between the "head" of the first sarcomere (indicated by h) and the "tail" of the last sarcomere (indicated by t) (we will call this distance lh_t), so that if the sarcomeres are perfectly aligned, the two quantities coincide, and their ratio is therefore 1; on the contrary, the more the behaviour is "zigzag", the more this ratio increases (> 1):

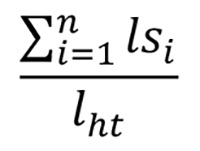The second proposal is based on circular statistics, taking a cue from the same α_i proposed by Cisterna et al.;¹ circular statistics has been used earlier to study muscle cell alignment.² Ideally, for each angle α_i, it is possible to construct a unit vector having the base at the centre of a goniometric circumference and the vertex on the circumference from which to calculate the resulting vector, which, divided by n (that is the number of angles or the number of sarcomeres minus 1), gives the resulting mean vector. From here, two parameters can be obtained

(a) The direction of the mean vector α* (if it is equal to 0, it means that the displacements to the right balance those to the left; or, as an extreme case, that the sarcomeres are perfectly aligned):

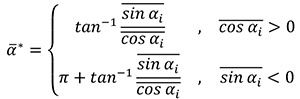where sin α_i and cas α_i are respectively the mean of the sine and cosine components of the n α_i angles.

(b) Much more important would be the length of the mean vector r:

the mean vector length r can range between 0 (representing perfect isotropy – or a circular uniform distribution – i.e., the maximum possible misalignment) and 1 (representing perfect anisotropy, i.e., the maximum possible alignment). This approach, as opposed to the one proposed by Cisterna et al.,¹ is based on the hypothesis of circularity (and non-linearity of the angles). It is also possible to perform a statistical test using the mean vector length r as test statistics: Rayleigh test (1919)³ is the best known in circular statistics; its null hypothesis is the uniform circular distribution of the angles, and the alternative hypothesis is a generic anisotropy. Likewise, the V-test is also based on the mean vector length r, which uses the projection V of the mean vector over an a priori direction (in our case, we can think of it as the direction of the muscle fibre) as test statistics:

V=r cosφ,

where φ, is the angle between the mean vector and the a priori direction. Both the Rayleigh test and the V-test have appropriate tables of critical values (see Batschelet 1981).⁴ Moreover, a concentration parameter k can be estimated [using the Maximum Likelihood approach (ML)] starting from the mean vector length r, under the hypothesis of a Von Mises distribution (an analogue of Normal distribution for angular data); the following approximated formula was proposed by Best and Fisher (1981)⁵:

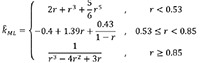Nevertheless, for n . 15 or r < 0.45, this estimation would be corrected as follows:

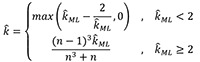In this way, the concentration parameter k should also be used as a linearity index, useful for our purposes: the higher the k value, the higher the alignment.

In conclusion, our first method represents an alternative to the one previously proposed by Cisterna et al. (2021),¹ equivalent in terms of potential but with the practical advantage of not having to measure angles, but only lengths, which makes it much more "convenient”. The second method we propose, on the other hand, uses angles but uses circular analysis techniques instead of linear analysis methods, which makes it more elegant and gives greater substance to statistical analysis, but in contrast, it also has greater computational complexity. Our methods have potential use in several sarcomere-related conditions by providing a quantitative definition of myofibril linearity in skeletal muscle.^6,7

List of acronyms

ls_i

lengths of the individual sarcomeres

ML

Maximum Likelihood approach

Funding Statement

Funding: The authors received no specific funding for this work.