A new DelPhi feature for modeling electrostatic potential around proteins: Role of bound ions and implications for Zeta-potential

Abstract

A new feature of the popular software DelPhi is developed and reported, allowing for computing the surface averaged electrostatic potential (SAEP) of macromolecules. The user is given the option to specify the distance from the van der Waals surface where the electrostatic potential will be outputted. In conjunction with DelPhiPKa and the BION server, the user can adjust the charges of titratable groups according to specific pH values, and add explicit ions bound to the macromolecular surface. This approach is applied to a set of four proteins with “experimentally” delivered zeta-potentials at different pH values and salt concentrations. It has been demonstrated that the protocol is capable of predicting zeta-potentials in the case of proteins with relatively large net charges. This protocol has been less successful for proteins with low net charges. The work demonstrates that in the case of proteins with large net charges, the electrostatic potential should be collected at distances about 4 Å away from the vdW surface and explicit ions should be added at a binding energy cut-off larger than 1–2 kT, in order to accurately predict zeta (ζ)-potentials. The low salt conditions substantiate this effect of ions on SAEP.

Graphical Abstract

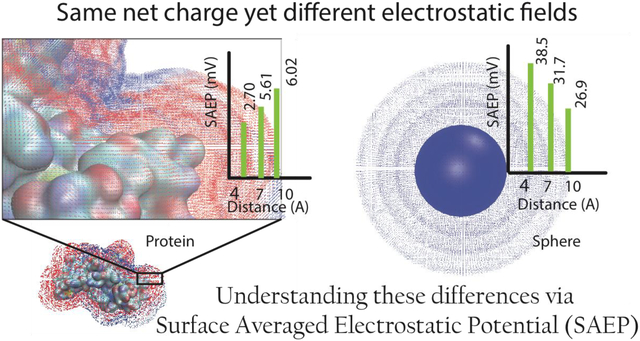
Introduction

Electrostatics plays an important role in molecular biology, as all macromolecules carry atoms with partial changes situated at Angstrom distances^{1, 2, 3}. Typically, the focus is on revealing electrostatic interactions within the macromolecules^{4, 5}, computing solvation energy⁶, investigating pH-dependent properties^{7, 8} and predicting other properties inside the biomolecules or across their interfaces (protein-protein; protein-nucleic acids)^{9, 10}. While the knowledge of the electrostatic potential inside a macromolecule is crucial for understanding its role in protein stability, dynamics, and reactions, the ability to model electrostatic potential outside of the macromolecule is equally important¹⁰. In the past, modeling of the electrostatic potential around a macromolecule was implicated in protein-protein recognition², substrate guiding to active site¹¹, ligand docking¹², prediction of binding rate¹³, non-specific ion binding¹⁴, and similar studies related to protein functionalities¹⁵.

The importance of electrostatic potential outside of macromolecules is highlighted by the fact that electrostatic interactions are the only long-range interactions in molecular biology^{1, 2}. If two objects (macromolecules or nano-particles) are situated at distances longer than several Angstroms, then the electrostatics is the only force acting between them and guiding their association/disassociation. It was recently demonstrated that electrostatic potential and forces guide kinesin-microtubule¹⁶ and dynein-microtubule¹⁷ binding, even at distances larger than 20 A. Dimerization, or in general, oligomerization or aggregation, is frequently driven by electrostatic interactions as well^{18, 19}. Similarly, amyloid formation could be also electrostatically controlled^{20, 21}. While in many cases dimerization^{10, 11} and in general molecular complexes formation^{22, 23} are essential and required events for normal function of the cell, non-natural aggregation is typically unwanted phenomena and is frequently associated with diseases^{24, 25}.

In colloid science, aggregation is typically an unwanted effect and care must be taken to prevent that. For this purpose, the electrostatic potential around macromolecules is attributed to two quantities: electrophoretic mobility (μ) and zeta-potential (ζ-potential). The knowledge of these quantities is vital to the elucidation of several fundamental properties of the solution, such as aggregation, filtration, crystallization, and shelf life. These quantities are essentially proxies for the molecular charge of the macromolecules, and are primary indicators of their dispersion stability²⁶. A large magnitude (>±30 mV) of ζ-potential indicates stability²⁷. Emphasis on this aspect of the role of electrostatics is important for the industrial manufacturing of protein-based products, as well as underlying areas of research and development²⁸.

In experiments regarding these colloidal properties, ζ-potential is inferred from the electrophoretic mobility of the solute, with the latter being directly observed. Their relation (mobility-potential relationship, U(ζ)) is interpreted based on a specific model. There are three commonly used models – the Debye-Huckel approximation model (for thick double layer, DL), the Helmholtz-Smoluchowski approximation model (for thin DL), and the Henry’s formula model (for DL of intermediate thickness)²⁹. These formulations are based on classical electrophoresis theory for perfectly spherical solutes endowed with a homogeneous and isotropic ionic double layer. However, biomolecules such as proteins are known to be objects with inhomogeneous charge distribution and have non-spherical shapes. This may cause one to wonder exactly how justified those assumptions are in deducing ζ-potential for proteins and other asymmetrically shaped/charged objects from the experiments of electrophoretic mobility.

In this work, we report a new DelPhi³⁰ feature and use it to model the electrostatic potential outside of proteins at user-specified distances from the van der Waals (vdW) surface. We demonstrate that the electrostatic potential on a probe surface (situated closely to vdW surface), especially in the case of proteins carrying a low net charge, is highly inhomogeneous. Thus, simply reporting the averaged value does not provide robust scientific insights. However, at distances larger than 4 Å, especially in the case of highly charged proteins, the surface averaged electrostatic potential (SAEP) can be considered as a macroscopical quantity, which can be related to ζ-potential. Furthermore, we report a new method for predicting non-specifically bound surface ions, and use it to model the electrostatic potential in the presence of bound ions. It has been shown that the calculated SAEP can be used to predict the corresponding zeta-potential, provided one has knowledge of the 3D structure of the corresponding protein, the pH value of interest, and surface bound ions at cut-off binding energy of about 1kT are added to the protein structure.

Methods

The goal of this work is to elucidate the factors affecting the electrostatic potential generated by proteins, as well as the role of surface bound ions. Furthermore, the calculated surface average electrostatic potential (SAEP) is compared with the quantity termed Zeta-potential (ζ-potential), widely used in colloidal science. Due to this, the modeling work is done on proteins with available 3D structure and experimental data regarding ζ-potential “measured” at different conditions (as pH and salt concentration). In the following paragraphs, we describe dataset selection, the details of computational protocol for assigning protonation states at given pH values and electrostatic potential calculations via DelPhi, the algorithm for predicting explicit ions bound to the protein surface, and the basic formulas used to deliver ζ-potential from measured electrophoretic mobility.

Proteins and their experimental ζ-potential values

Four different proteins are considered in our work. They have both a pH-dependent ζ-potential determined from experiments as well as a 3D structure available in the Protein Data Bank (PDB)³¹. The latter condition is vital for the computational modeling of electrostatic potential distribution at an atomic level of detail. In the choice of protein structures, several considerations were made. Not all the experimental works provide specific information about the structure of the protein being investigated. Since a given protein (for example, lysozyme from a particular source organism) has multiple structures in the PDB, the structure with the best resolution was selected. Many of these proteins have an oligomeric biological assembly. For all of these proteins, a single chain was used in our work (Table 1). Several of these structures contained other ligands (including crystal water molecules and ions), which were all deleted before the modeling. Table 1 lists the proteins considered for this study, the associated experimental conditions, and other relevant information. The experimental ζ-potential values for these proteins at different pH values and salt concentrations are provided as Supporting Information (Table S1). It must be noted that Ref³² does not provide exact numerical values for the ζ-potentials. These values were estimated from the relevant figures in the article.

Table 1:

The list of proteins used in our work and the relevant details

Protein	PDB ID (Chain)	Resolution (Å)	Source of experimental ζ-potential	Approximation used to derive ζ-potential from mobility**
Bovine Serum Albumin (BSA)	4F5S (A)	2.47	32	HF
α-Amylase from Type 2A Bacillus Sp.	1UA7 (A)	2.21	32	HF
Lysozyme from Chicken Egg White	2VB1 (A)	0.65	33	SM
Invertase from Baker’s Yeast	4EQV (A)	3.40	32	HF

^**HF = Henry’s Formula, SM = Smoluchowski’s Formula (see the bottom of method section)

pH-dependent protonation of protein residues

The 3D crystal structure of a protein from PDB was protonated according to the pH value for which the experimental ζ-potential is provided, using the standalone version of DelPhiPKa³⁴. Generalized Amber force-field (GAFF)³⁵ parameters were used. DelPhiPKa outputs protonated files according to the calculated pKa values of ionizable groups and the corresponding pH values. It must be noted that not all of the pH values for which ζ-potential of a protein is experimentally known were used in our study. The reason for this lies in the fact that at very low (< 3) and very high (> 11) pH values, proteins may be very unstable or adopt a 3D structure significantly different from the X-ray structure in PDB^{7, 36}. Therefore, we restricted our protocol to pH values >3 and <11. The net charge for a protein, treated using DelphiPKa, was calculated by adding together the charges on its component atoms. Table S2 lists the calculated net charges for the protein molecules used in our study, at various pH values.

Electrostatic Potential Modeling

All of the electrostatic potential calculations were made using the Poisson-Boltzmann solver DelPhi³⁰. The dielectric constant of the protein region was fixed at low values of 4, however, a sensitivity test was carried out exploring different values from 2 to 20 (in step of 2 as described in the Results section, as well as the Supporting Info). Since the results were found to be largely insensitive to the value of the internal dielectric constant, the results presented in the paper are obtained with a protein dielectric constant of 4. The external dielectric constant was set at 80 (emulating water as the solvent). Similarly, the ion concentration and ionic valences were adjusted to match experimental conditions. The ion-exclusion region was treated as a 2Å wide region around the proteins’ van der Waals (vdW) surface. A scale of 2 grids/Å was used in all cases. The box size was set so that the solute occupied 60% of the box volume. The potential at the boundaries was determined using the ‘dipolar’ method. The protonated structures of the proteins (PQR formatted structure obtained using DelPhiPKa) were provided as inputs.

DelPhi inherently computes the potential distribution in a 3D array of grids inside and outside the macromolecule. A new module has been developed and released in DelPhiv7.0 that identifies the grid-points lying roughly (with a margin of the grid distance) on a surface positioned at a specified distance from the vdW surface of the protein (algorithm depicted in Figure 1). Thus, for an atom with vdW radius ‘R_vdw’, the surface desired at distance ‘d’ from the protein would contain all the grid-points which are ‘R_vdw + d’ away from its 3D Cartesian center. Since each atom is evaluated along these lines, the final surface is a coalescence of the individual surfaces. The module outputs the 3D Cartesian coordinates of the identified surface grid-points (in Å) and the potential there (in kT/e units). Simultaneously, it also outputs the average potential on the surface. This surface average potential depicts the first moment of the potential distribution on a surface. Since the ζ-potential values reported by experiments are in ‘mV’ units, kT/e was converted to ‘mv’ using the conversion formula:

$$1kT/e\approx 25.6mVatT=298K$$

Figure 1:

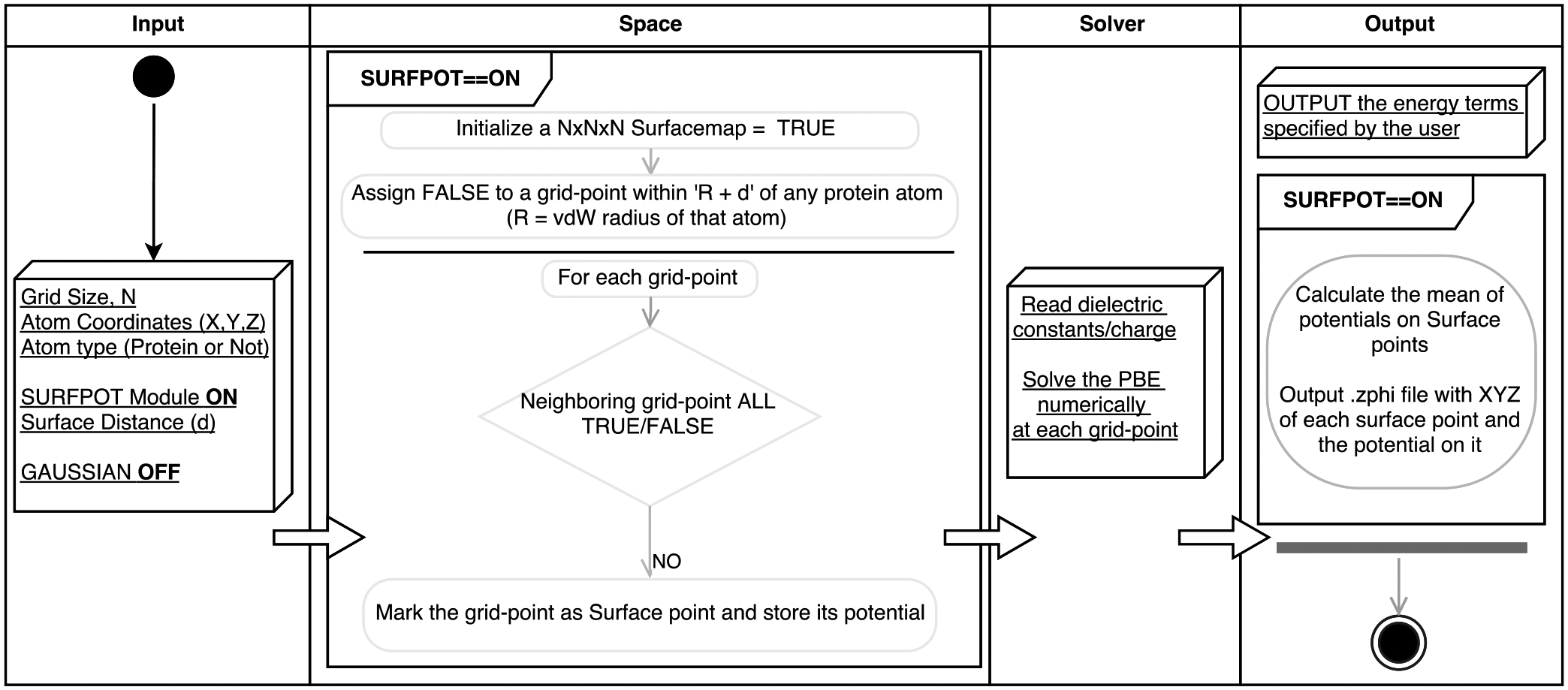
Schematic of the algorithm of surface module (SURFPOT) implemented in DelPhi.

Each protein considered in our study was subjected to these calculations to obtain a profile of SAEP as a function of distance ‘d (4 Å ≤ d ≤ 10 Å)’ from the vdW surface. For a perfect sphere with a homogenous charge distribution, the average potential matches well with the analytical form provided by Coulomb’s law, assuring us of the method’s credibility (comparison shown in Supporting Info., Figure S1).

Addition of Explicit Ions:

It is anticipated that some ions may bind to the protein surface and become part of the protein. However, such ions are typically not seen in PDB structures. In addition, their presence is pH and salt dependent. Thus, the surface bound ions must be predicted. BION³⁷, a web-based tool developed in our lab, was used to add explicit ions to the proteins in the course of this work. As a function of pH value and salt concentration, Na and/or CL ions were added. To allow the usage of DelPhiPKa output PQR files (protonated 3D structures as a function of pH), BION was customized to not only accept PQR files as inputs, but to recognize the presence of non-protein atoms in the structure (HETATM records; e.g. ions). This allowed for further ion additions based on the electrostatic potential generated by protein as well as non-protein atoms. Besides this, BION was enabled to handle user-specified interaction energy cutoffs in order to decide the number of ions to be added to the structure.

It is of primary importance to determine how many ions should be added for a protein at a particular pH and salt concentration, and of which polarity they should be. It is expected that if the protein is highly charged, then ions of the opposite polarity (counter-ions) will be more likely to bind than ions of the same polarity (co-ions). However, if either the net charge is close to zero or the protein charges are very inhomogeneously distributed, ions of both polarities are equally likely to bind. A new approach was developed to overcome such uncertainties – we have termed this approach as the “sequential addition of ions with decision based on their binding energies”.

Sequential addition of ions with decision based on their binding energies:

Calculations of the SAEP with and without ions constitute a major part of this work. However, unlike the original BION algorithm¹⁴ (which adds ions without recognizing the contribution of non-protein atoms), the modified version allows for sequential addition of ions (where each addition is affected by the ions added previously). As a result, an iterative methodology was developed in which Na/Cl ions were tried for their interaction energies (ranking). This method of non-simultaneous addition of explicit ions shares the rationale of the variant Hamiltonian replica exchange method (VHREM) technique of Ye, Xiang et. al.³⁸ Based on ranking, it was decided which of the two ions to add, with rank being defined as the absolute value of the interaction energy. Na/Cl was added if the ranking was above the cut-off value (absolute value of the cut-off interaction energy in kT). The algorithm of iterative addition is depicted in Figure 2.

Figure 2:

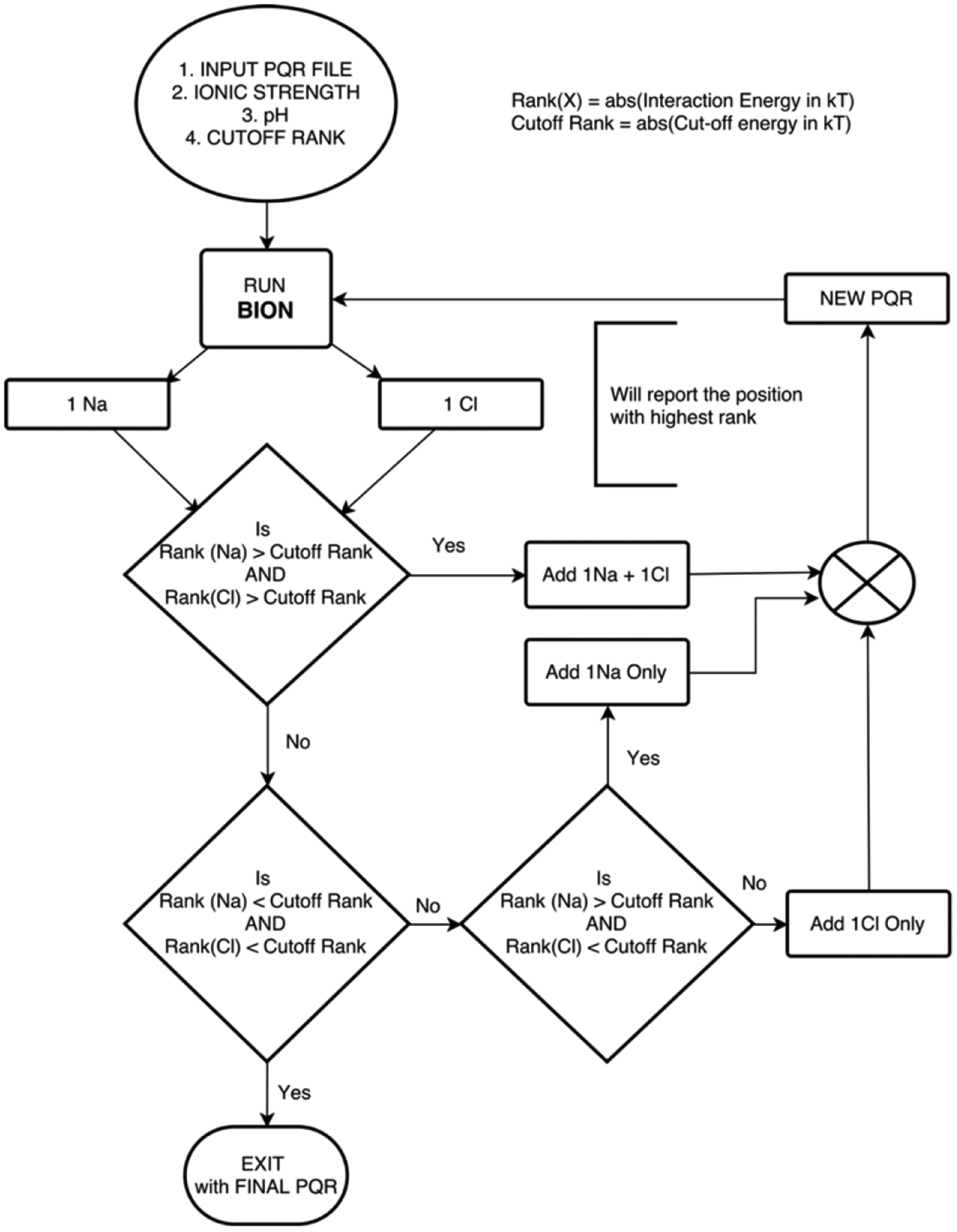
Algorithm flow chart for the sequential addition of explicit ions, using modified BION, with decisions based on the interaction energies.

Unlike original BION (which integrates NACCESS³⁹ for determination of accessible atoms), the ion radii values from Ref.⁴⁰ were used (instead of the default water radius (1.4 Å)) to draw the accessible surface. Furthermore, extra filters were integrated into BION to prevent counter-ions from being positioned unrealistically close to extant ions (with a distance less than the sum of individual vdW radii). We consider this approach to closely mimic the physical reality that underlies the formation of an ionic double layer around a solute (especially solutes with inhomogeneous shape and charge distribution).

Electrophoretic mobility and ζ-potential.

ζ-potential is the electrostatic potential on the surface, enclosing the colloid and the ions that are tightly bound to it (forming a double layer, DL), which moves as a singular unit. This surface is termed as the “surface of shear” or “slipping plane”. It lies in the region between the Stern layer and the Diffuse layer (that separates the bulk from the colloid and the ions that move with it). Refs.^{41, 42} provide some of the best information about these fundamental concepts of electrophoresis. Traditionally, the Helmholtz-Smoluchowski formula published in 1921 (reported in Ref²⁶) is used to obtain ζ-potential from electrophoretic velocity (U) in the presence of an external field E.

$$U=\frac{ϵ\zeta E}{\eta }$$ #(1)

In this expression, ‘η’ and ‘ε’ denote the viscosity and dielectric permittivity of the fluid respectively while ‘ζ’ denotes the surface potential (ζ-potential). This approximation works well when the radius (r) of the solute (or the local radius of curvature) satisfies κr >> 1 where ‘κ⁻¹’ is the Debye Length. This implies a thin DL. Debye-Huckel approximation (1924; reported in Ref²⁶), which on the other hand, works only when κr << 1 (thick DL).

$$U=\frac{2ϵ\zeta }{3\eta }$$ #(2)

The regime that lies at the transition between these extremes of the DL thickness is dealt with Henry’s Formula of 1931(reported in Ref²⁶).

$$U=\frac{ϵ\zeta }{\eta }{f}_1\left(\kappa r\right)$$ #(3)

Function ‘f₁’ is referred to as the Henry function, which increases monotonically with the thickness of the DL (or κ⁻¹). The above U(ζ) relations are the most commonly used methods to interpret the electrophoretic mobility values in terms of ζ-potential. Moreover, they relate the mobility to the first moment (average ζ-potential) and discard the higher moment terms. These relations are based on certain assumptions that are described in the Results and Discussion in connection to the significance of higher moments terms. Additional details are contained in the Supporting Info. with Equations S1–S5.

Results and Discussion

Our work reports a new feature of the popular DelPhi package⁴³, which allows computing the electrostatic potential over a surface positioned at a user-specified distance from the vdW surface of the macromolecule. This feature can be used for variety of investigations regarding the role of electrostatics on receptor-ligand recognition, homo- and hereto-oligomerization, and ζ-potential modeling. In addition, we demonstrate the crucial role of surface bound ions and report a new method for sequential addition of ions of different polarity to the protein surface. This section is organized as follows: (a) we test the sensitivity of the calculated electrostatic potential with respect to the value of the internal dielectric constant and grid spacing (grid resolution), (b) we report the surface averaged electrostatic potential (SAEP) calculated at various distances from the vdW surface and compare it with “experimentally” determined ζ-potentials for four proteins at different pH values, and (c) we report the results on the same dataset but with surface bound ions added in corresponding 3D structures.

Sensitivity of calculated SAEP with respect to internal dielectric constant and grid-spacing.

SAEP’s sensitivity towards different modeling parameters was tested prior to undertaking extensive calculations. The sensitivity of the results was tested on two arbitrarily chosen proteins that are different from the four proteins used in this work (PDB IDs: 2EA3 and 3GUU). The protein dielectric constant was varied from 2 to 20 in steps of 2. Further, the effect was tested in conjunction with grid-spacing of 0.5 Å and 0.25 Å (scale 2 and 4 grids/ Å).

The results are shown in Figure S2 in the Supporting Info. The plots indicate that the SAEP is not sensitive to either the internal dielectric constant or the grid spacing. Indeed, the error bars in Figure S2 are less than 1kT/e. Thus, we chose to employ an interior dielectric constant value of 4 for rest of the cases. Similarly, we chose to use a grid-spacing of 0.5 Å (2 grids/ Å) for rest of the work.

SAEP at different distances from vdW surface: Implication to ζ-potential values.

As has been noted in the Methods section, experimental ζ-potential values published for various proteins were considered in our work. By definition, ζ-potential is the electrostatic potential on a surface termed as the “slipping-plane” which lies between the Stern layer and the diffuse layer created around the solute. However, in the framework of continuum electrostatics, the position of slipping-plane cannot be determined since the water phase is considered as continuum media. Therefore, we adopted a pragmatic approach and sought to find the distance from the vdW surface at which the SAEP, calculated by DelPhi, would match the experimental ζ-potential. This was tried on all four of the proteins under varying pH and salt concentrations. For the sake of convenience, we adopt the following terminologies: (a) the distance at which the computed potential equals the experimental ζ-potential as the ζ-distance and (b) the surface at the distance as the ζ-surface (which, by definition, would be the slipping plane). We first report the results without adding explicit ions to the corresponding proteins, and then report the results obtained with explicit surface bound ions added to the corresponding PDB structures.

SAEP without explicit surface bound ions:

The comparison of calculated SAEP as a function of the distance from the vdW surface and the experimental ζ-potential values are shown in Figures 3–6. The experimental ζ- potential is indicated by the horizontal solid line. The grey band centered at this line depicts a ± 3mV range for the experimental potential. This is to allow for the uncertainties associated with reading the values exactly from the experimental papers considered in this work. We outline several important features of computed SAEP observed across these cases before delving into specific discussion of the results.

Figure 3:

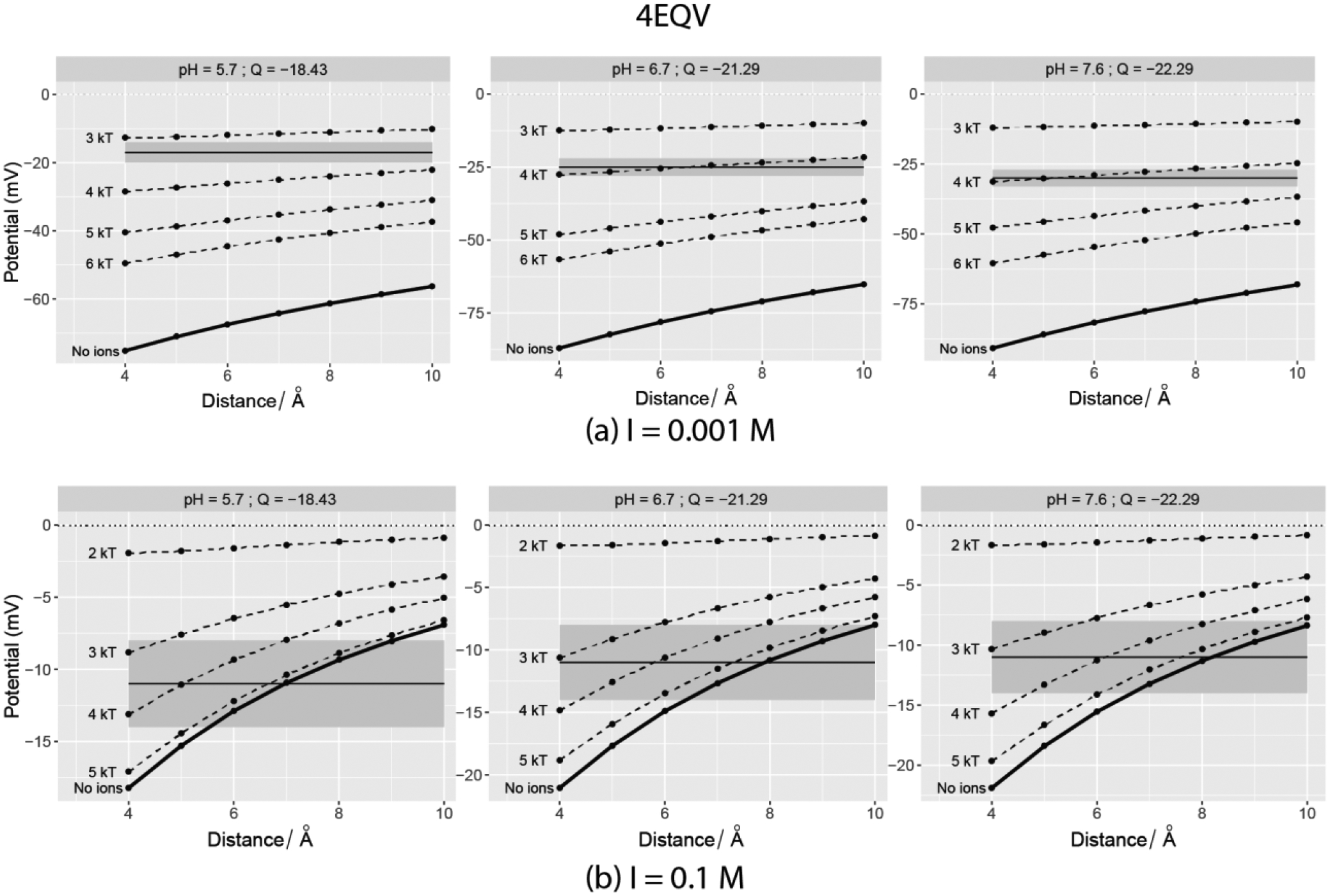
Computed SAEP plotted vs. distance from the vdW surface of Invertase monomer (PDB ID: 4EQV). The horizontal solid line depicts the experimental value at the pH mentioned in the plot facets and it is centered at the grey band that denoted the ±3mV. The dotted lines indicate the potentials when explicit ions with adjacent cut-off interaction energies were added using BION. Left panel – 0.001M salt; Right Panel – 0.1M.

Figure 6:

Computed SAEP plotted vs. distance from the vdW surface of Bovine Serum Albumin (PDB ID: 4F5S). The horizontal solid line depicts the experimental value at the pH mentioned in the plot facets and it is centered at the grey band that denoted the ±3mV. The dotted lines indicate the potentials when explicit ions with adjacent cut-off interaction energies were added using BION. Top panel – 0.001M salt; Bottom Panel – 0.1M.

As expected, the surface potential drops as distance increases. Since we only present a range of distances between 4–10Å we do not see the potential decaying to zero in all the cases. Regardless, the decay follows the e^−κr/r (Yukawa like/Screened Coulomb Potential⁴⁴) form in most of the cases. For a few cases, this was not observed in the 4–10Å range, because the net charge of the corresponding protein was close to zero and the charge distribution of the protein was very inhomogeneous. As expected, an increase in the salt concentration screens the electrostatic potential, resulting in a lowered magnitude with respect to cases with zero or low salt concentration. Though the same lowering of ζ-potential is observed in the experiments, the computational and experimental trends are not the same in all cases. Perhaps this is due to the fact that we did not consider explicit ion binding in the PB modeling^{14, 37}. Authors of Ref⁴⁵ have previously accounted for the effect of ions in deriving relations between electrophoretic mobility, ζ-potential, and DL thickness.

The results presented in Figures 3–6 indicate that experimental ζ-potentials and computed SAEP do not necessarily match at a given distance or a range of distance valid for every case. In some cases, the ζ-surface appears to be within 10 Å of the vdW surface, while in others a definite match never appears. A majority of them feature overestimated values of the computed surface potential, and a few of them exhibit underestimation. For several pH values, even the polarities of the computed potential and experimental ζ-potential values differ in the considered range of distances.

Figure 7 shows the correlation plot of experimental ζ-potentials and the computed SAEP at a certain optimal distance. This optimal distance is the one (within 4 – 10 Å) at which the computed SAEP is closest to the experimental ζ-potential. We consider this computed potential to be the best predicted potential for a given case. For instance, in Fig 3(a; top panel), referring to protein 4EQV, the best predicted potential is −55 mV with an optimal distance of 10 Å from the vdW surface (experimental zeta potential = −17 mV at pH = 7.7). In case of the same protein and pH but I=0.1M, this distance is 7 Å - resulting into an exact match. The best predicted potential is −11mV and the experimental zeta-potential is also −11mV.

Figure 7:

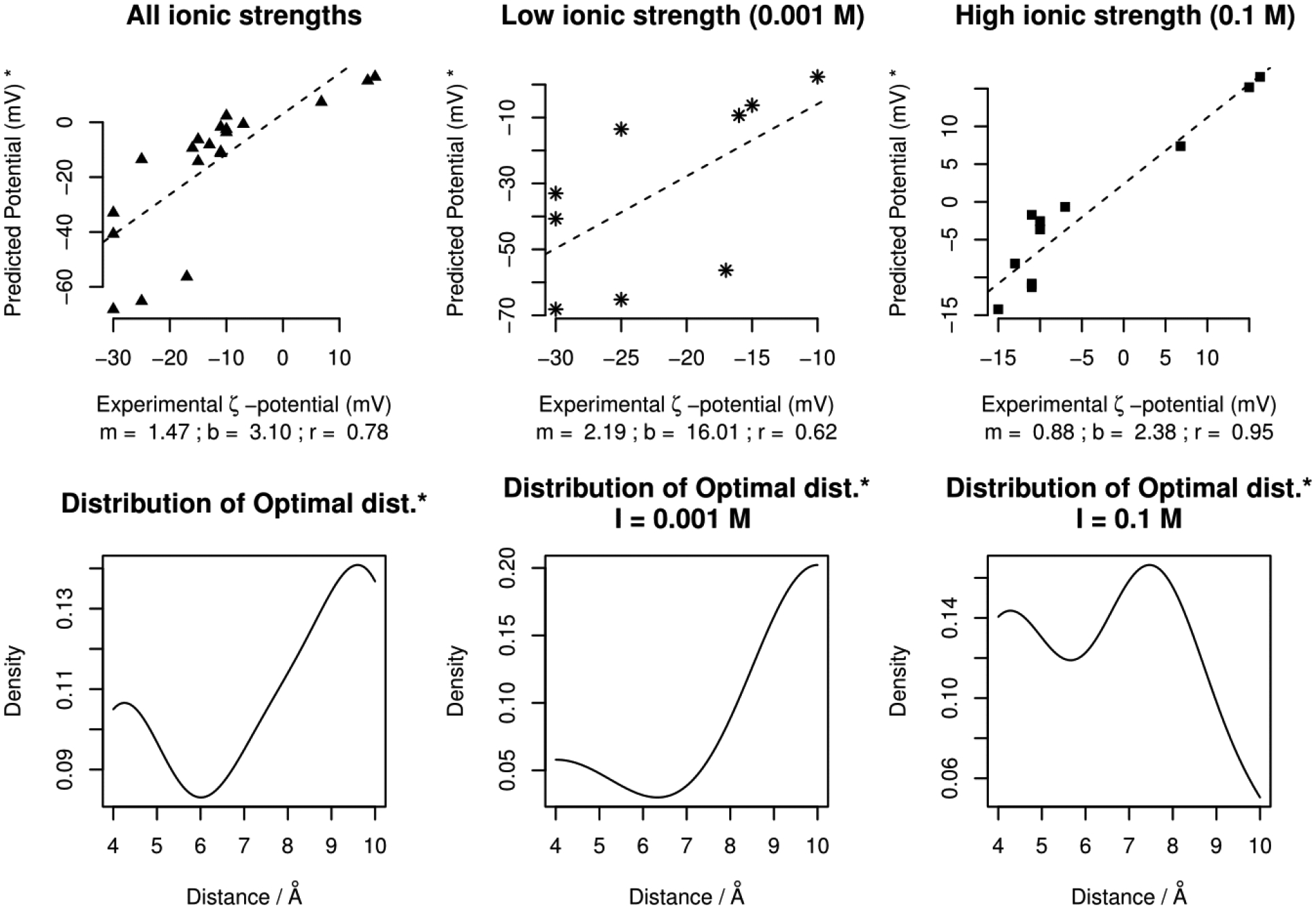
Top Panel – The correlation plots (slope = m, y-intercept = b, correlation = r) for the best predicted potential (* using the definition given in the relevant paragraph). The plots in the center and far right combine to produce the one in the far left. Bottom Panel – the corresponding density distribution of optimal distances.

It can be seen that the best predicted potential correlates reasonably with experimental zeta-potential (Figure 7, top panels), with distinctively better correlation for cases at relatively higher salt concentration (Figure 7, top-right panel). This indicates that ion contribution is an important factor. Taking a look at the distribution of the optimal distances (Figure 7, bottom panels), it can be seen that at low salt concentration, the optimal distance is about 10 Å. In contrast, at higher salt concentration (I=0.1M), the optimal distance is closer to the vdW surface.

SAEP with explicit surface bound ions

To test the role of explicit ions bound to protein surface, the ions were added using BION as described in the Methods section. Furthermore, since there is no data on how many ions should be bound to a particular protein at a particular pH and salt concentration, the number of ions bound was predicted based on their interaction energy. Different cut-offs were explored (cut-offs 0.5 – 6kT). The resulting SAEPs are shown in Figures 3–6. It should be mentioned that Figures 3–6 only show results of the cut-offs which resulted in unique potential vs. distance profiles for a given protein, pH, and salt combination (if the results for cut-offs were identical, only one of them is shown). It must also be noted that although the predicted ions were added to the corresponding PDB structure, only the protein atoms were considered in determining the surface of a protein-ion complex. This ensures that the same surface is probed in the investigations with and without ions (for a given distance).

The effect of explicit ions can be best understood by categorizing the 4 proteins into two groups. The first group (Figures 3,4) pertains to 4EQV and 2VB1. These proteins have a high absolute value of net charge across the corresponding pH values. The second group containing 1UA7 and 4F5S (Figures 5,6) has smaller values of net charge (absolute value). The pure correlation of the calculated surface potential and the experimental ζ-potential (discussed in the previous section) is significantly improved by the presence of explicit ions for proteins from the first group. This is clear from the best predicted potential being identically equal to the corresponding experimental ζ-potential with highly charged proteins (Figures 3,4).

Figure 4:

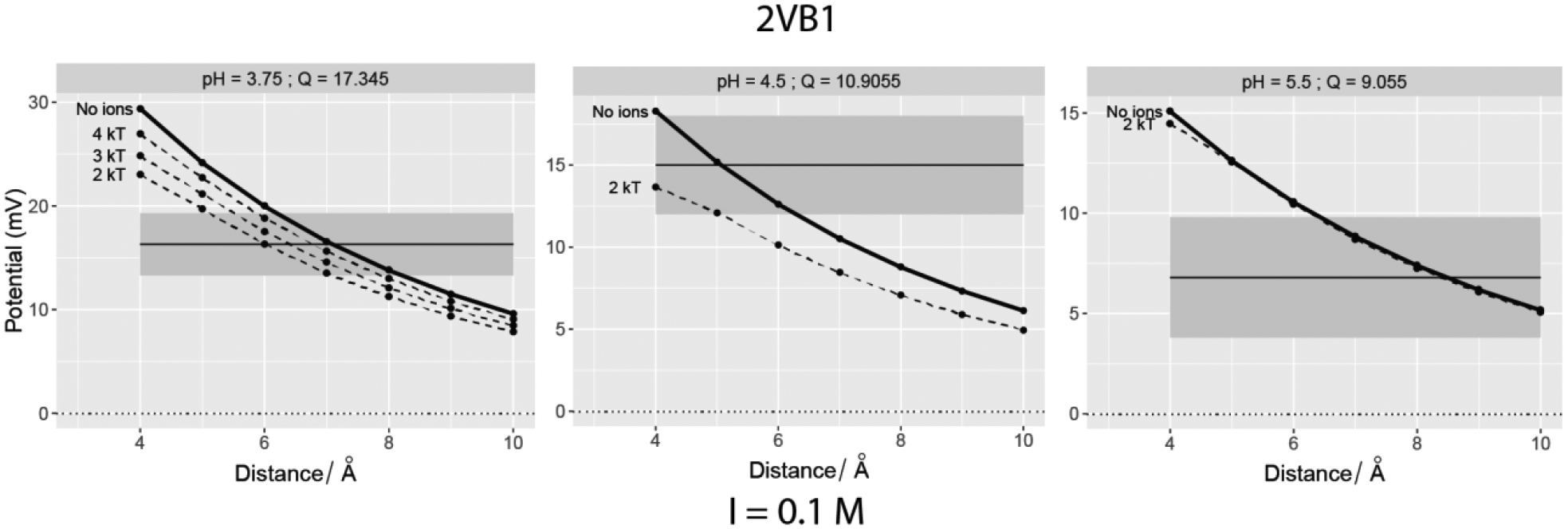
Computed SAEP plotted vs. distance from the vdW surface of Chicken egg Lysosyme (PDB ID: 2VB1). The horizontal solid line depicts the experimental value at the pH mentioned in the plot facets and it is centered at the grey band that denoted the ±3mV. The dotted lines indicate the potentials when explicit ions with adjacent cut-off interaction energies were added using BION.

Figure 5:

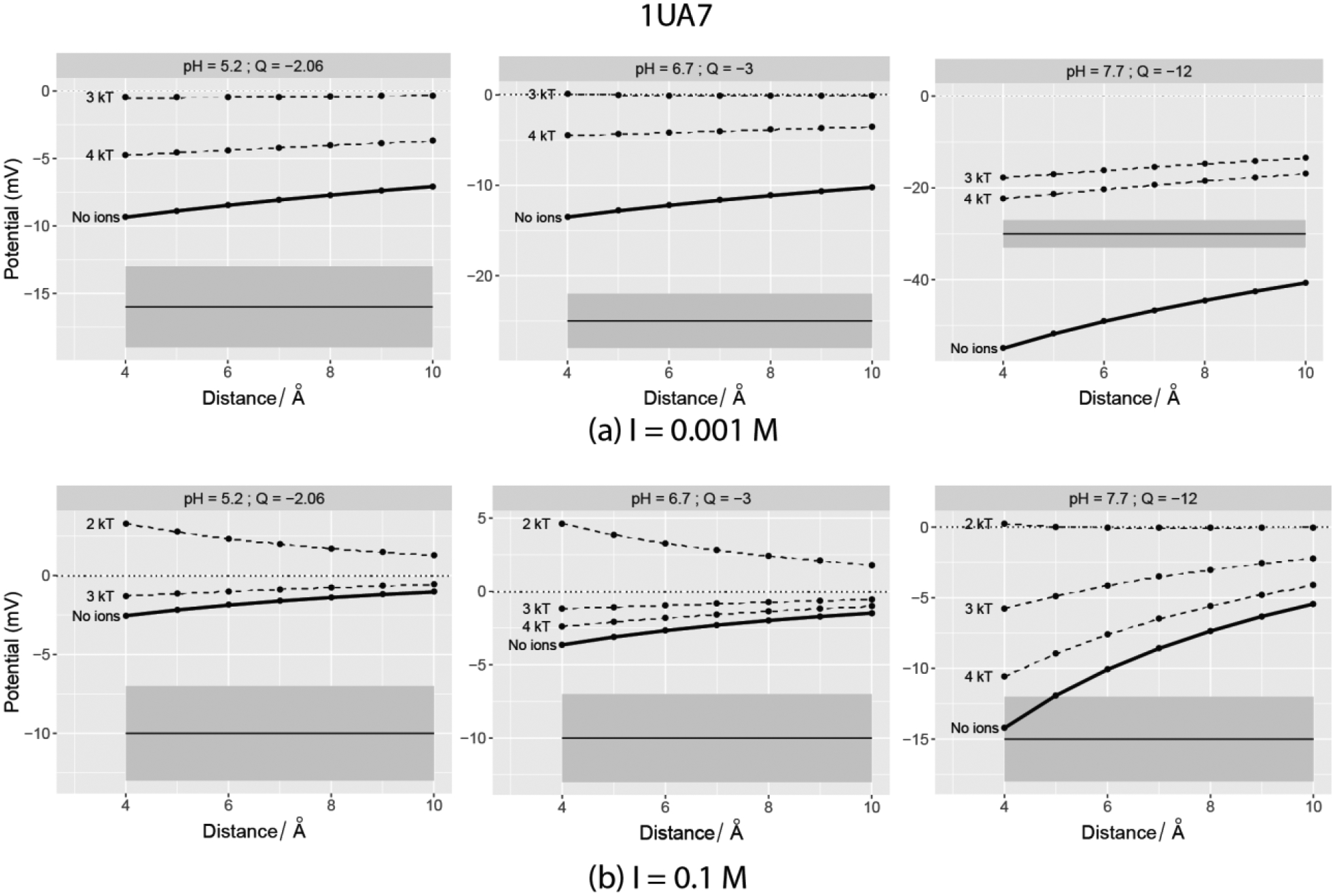
Computed SAEP plotted vs. distance from the vdW surface of Type-2A Bacillus Sp. α-Amylase (PDB ID: 1UA7). The horizontal solid line depicts the experimental value at the pH mentioned in the plot facets and it is centered at the grey band that denoted the ±3mV. The dotted lines indicate the potentials when explicit ions with adjacent cut-off interaction energies were added using BION. Left panel – 0.001M salt; Right Panel – 0.1M.

Let us consider 4EQV first, which is a highly negatively charged protein (Figure 3). At a salt concentration of 0.001 M, ions with interaction energy no less than 4 kT make the surface potential fall in the ± 3 mV range of the ζ-potential (grey band). When the salt is 0.1M, ions with interaction energy no less than 3–4 kT do the same. The match majorly occurs at a distance of < 6Å away.

Let us now consider 2VB1 (Figure 4), which is a highly positively charged protein. At a salt concentration of 0.1 M, the calculated electrostatic potential matches experimental zeta-potential even without explicit ions present. However, in the presence of explicit ions, the surface potentials are not only closer to the experimental ζ-potential but the optimal distances are close to the protein’s vdW surface (< 6Å away). An ion binding energy cut-off of 2 KT provides the best match for all cases of 2VB1.

In the second group of proteins (those with smaller magnitudes of net charge), the addition of explicit ions does not necessarily improve the match between computed electrostatic potential and experimental zeta-potential (Figures 5–6). Though there are a few cases of high negative charge (at pH 7.7 for both 4F5S and 1UA7), not all the observations made for the highly charged proteins are retained. Cases with lower net charges (absolute value < 3) reveal that the addition of ions causes the surface potential to further deviate from the experimental ζ-potential. In addition, some of them exhibit a change in polarity of the computed SAEP after addition of ions. This indicates that the ion binding to the protein surface may involve effects different from electrostatics.

The results obtained in the presence of explicit ions are summarized in Figures 8, where the correlation plots are shown for the best predicted potential with respect to the corresponding experimentally determined zeta-potential at some optimal distance and in addition to optimal cut-off of the ion binding energy. Just like optimal distance, optimal cut-off for ions is the absolute interaction energy cut-off (kT) that corresponds to the best predicted potential (at some pH and salt concentration). A cut-off rank of zero implies presence of no explicit ions.

Figure 8:

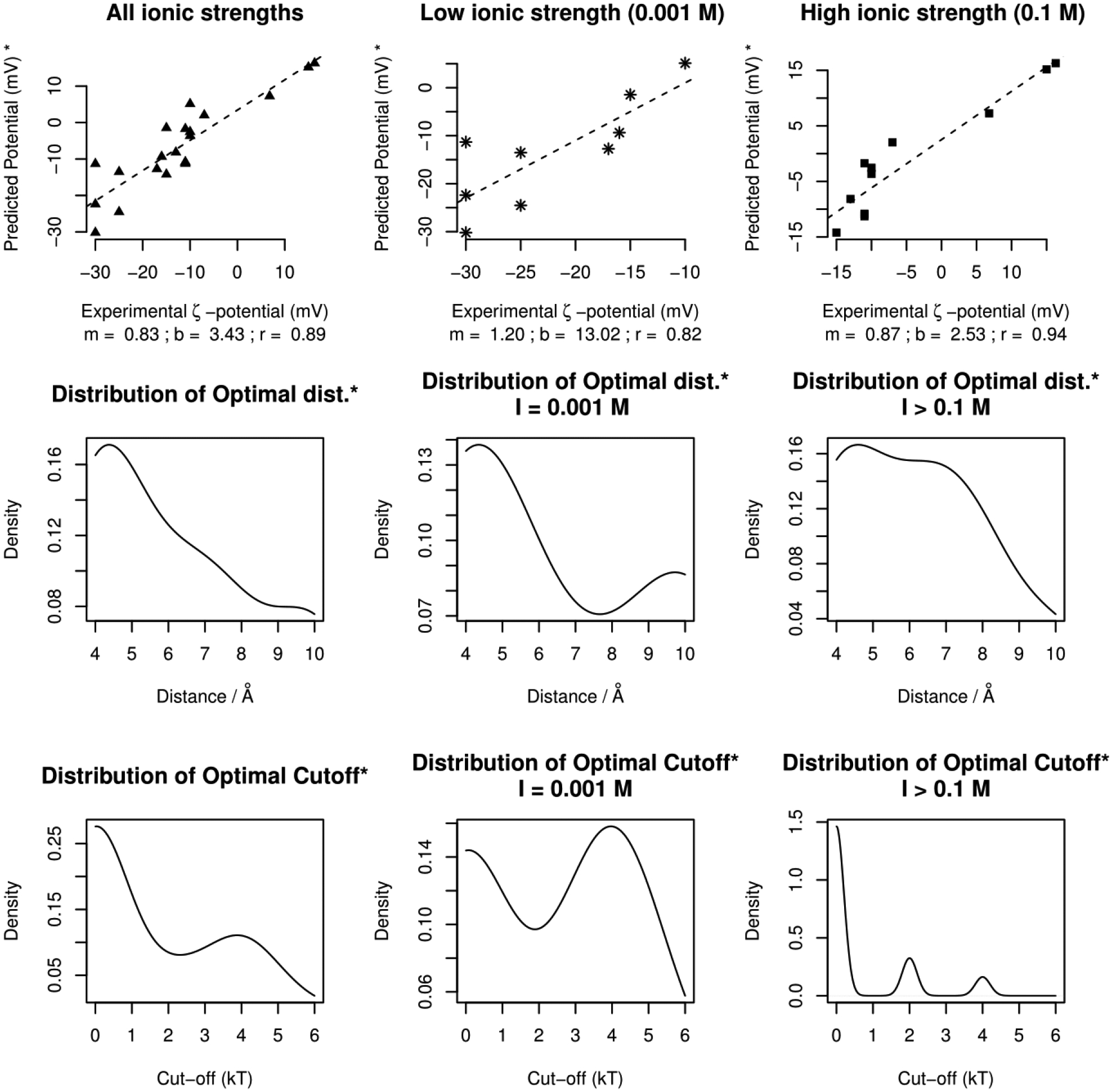
Top Panel – The correlation plots (slope = m, y-intercept = b, correlation = r) for the best predicted potential. The plots in the center and far right combine to produce the one in the far left. Bottom Panel – the corresponding density distribution of optimal cut-offs.

Comparing Figures 7 and 8, it can be seen that the addition of explicit ions does not affect the correlation of calculated and experimental zeta-potentials. However, it improves the match between calculated and experimental values in the case of low salt concentration (Figure 8, top middle panel). The correlation increases to 0.82 (0.62 without explicit Na/Cl ions). The difference of the effect of adding explicit ions at low and high salt concentration reflects the difference between explicit and implicit ion modeling. The screening effect dominates at high salt concentration - while at low salt concentration, individual ions are much more important for modeling electrostatic potential.

Besides the general correlation, one can also notice the shift in the peak of the optimal distance distribution profile from 10 Å (bottom panel in Figure 7) to around 4 Å. This implies that the predicted zeta-plane lies at a reasonable distance from the vdW surface in presence of explicit ions. This is of the same order of magnitude as the thickness of Stern layer or a single Bjerrum length (≈ 7.1 Å in water [BNID 106405]⁴⁶).

Care must be taken in interpreting the implication of these cut-offs. In the bottom panel in Figure 8, a peak at zero kT simply indicates that a close match was obtained in the absence of explicit ions and that the addition of ions exacerbated the difference. This was a common feature of proteins with low net charge, which are equally likely to bind ions of both polarities. However, a second bulge at cut-offs > 2KT reveal that when ions with rank greater than the cut-off rank were present, the predictions came close to the experimental ζ-potentials (in some cases resulting in an exact match). This adds to the information obtained from the optimal distance distribution – the presence of ions with absolute interaction energies > 2kT leads to a likely realistic model of a protein enveloped in an ionic double layer with the SAEP around the Stern layer being close to the ζ-potential⁴⁷.

Overall, the presence of explicit ions makes the computed SAEP close to experimental ζ-potential. This is particularly felt for cases involving proteins with low charge. However, the improvement is not impressive in the case of proteins with high charge. This non-generality indicates uncertainty of ion placement, both in terms of their positions and number of ions. Regarding the number of ions that are predicted to be surface bound, one can validate this via the following considerations. The experimental investigations used in this work report the isoelectric point (IP) for three out of four of the proteins. We calculated the protonation states of these proteins at respective IPs using DelPhiPKa, with the total net charges reported in Table S3. One can find that the predicted net charge at the IP is drastically different from zero. However, addition of explicit ions with a cut-off of 1 kT resulted in a significant decrease in net charge. Further lowering of the cut-off (from 1 kT to 0.5 kT) resulted in a similar net charge, but with a significant increase in the number of ions added. For instance, 27Na + 61Cl were added with a cut-off of 1 kT to 4EQV. At 0.5kT cut-off, this number changed to 282Na + 317Cl. Similar trends were seen for the other two proteins as well. Such low binding energies are comparable to the thermal fluctuation energies, making it possible for the thermal fluctuations to knock these ions out. This is corroborated by the fact that ions with interaction energies below 1 kT were placed at distances more than the Bjerrum length (≈ 7.1 Å). Since these ions would not contribute to the formation of the double layer, it is advisable to use cut-offs > 1kT.

Interpretation of “experimental” ζ-potential and outcomes from computational approach:

An understanding of the underlying theory of the surface phenomena is essential to the interpretation of the experimental ζ-potential. This is primarily due to the fact that ζ-potential is not directly observable. The experimental ζ-potentials, used as benchmarks in our work, are derived from linear mobility-potential relationships, which only consider the first moment (surface average) of the potential distribution at the plane of ζ-potential. The mathematical expressions are mentioned in the Methods section. In our computational approach, we determined the surface average potentials (first moment) at various distances from the vdW surface in order to identify a location where the computed surface average would match the experimental ζ-potential.

Across the results presented in this work, the computed SAEP matches the experimentally obtained zeta-potential at approximately 4 Å away from the vdW surface of protein in most of the cases with presence of explicit ions. However, this is not always the case, especially proteins with a low absolute value of net charge. Furthermore, the majority of the low charge proteins do not exhibit the decay of electrostatic potential with distance (within the range of 4–10 Å). In fact, a protein with a zero net-charge was found to show a non-zero surface average potential at all distances between 4–10 Å. Collectively, these observations indicate that the averaged surface potential should be considered in the context of the protein net charge and shape. In terms of ζ -potential, one must understand the fundamental connection between average surface potentials, ζ-potentials and motion under an applied external electric field.

The commonly-used formulations that help deduce ζ-potential from electrophoretic mobility (U) are based on the following set of assumptions about the geometry and conductivity of the solute: that it is rigid, a charge monopole, non-conducting, and its local mean radius of curvature is much larger than the Debye screening length. These assure that the ζ-potential and electrophoretic mobility have a O(ζ) relationship. None of the above assumptions are mutually true for biological macromolecules like proteins. Yet these assumptions are the basis for all the experimental works reporting ζ-potential. The problem associated with this methodology has previously been highlighted and extensively explained^{48, 49, 50, 51}. Primarily, this stems from assuming that proteins are spherical objects with a uniform charge distribution, which is not true. Due to the presence of non-trivial dipole and quadrupole moments of the protein charge distribution, the linear relationship between the mobility and ζ-potential do not suffice. In fact, a non-zero dipole and quadrupole moments ensue a non-uniform surface potential distribution and non-linear relationship between mobility and the applied external electric field⁵⁰. Therefore, it is vital to consider the higher moment terms of the surface potential integrals when attempting to relate zeta-potential to the electrophoretic mobility for non-spherical and inhomogeniously charged objects like proteins. For the 4 proteins considered in our work, the higher order moments for the surface potential integrals are non-zero owing to their non-zero dipole and quadrupole moments of charge distribution (not shown). This raises a valid question as to how credible these experimental values are.

Previously, the above issue has been discussed and dealt with by Chae and Lenhoff⁵². They demonstrated the drawbacks of assuming that proteins are spherically symmetrical objects. Further, Fair and Anderson⁵⁰ have shown that Smoluchowski’s relation fails to apply to an inhomogeneously charged spheroid/ellipsoid with a thick double layer, despite the fact that these have very few geometric differences. Yoon⁴⁸ has studied the effect of non-uniform charge distribution on spherical objects, showing that for justified use of Henry’s formula, the solute must be a rigid sphere regardless of the uniformity of charge distribution. Anderson⁴⁹ has examined the effect of inhomogeneous surface potential on electrophoretic mobility and underlined the spatial requirements for Smoluchowski’s approximation. Ajdari et. al.⁵³ has demonstrated the challenges of using these simplistic formalisms for interpreting the electrophoretic behavior of DNAs. Similarly, Cleland⁵⁴ has addressed the problems of treating wormlike polymer chains as spheres, and subsequently suggested a cylinder-based model for the same.

On the other hand, several publications have reported the success of their models obtained from treating proteins as spheres of low dielectric constants⁵⁵. Morrison⁵⁶ and Teubner⁵⁷ have demonstrated the validity of Smoluchowski’s formulation for arbitrarily shaped molecules for very thin double layers. Significant contributions from O’Brien and White⁴⁵ have resulted in better methods of relating mobility with ζ-potential when the effects of relaxation and polarization of DL around spherical solutes are taken into account. Overall, it is well understood that the results of electrophoresis experiments cannot be interpreted trivially^{47, 58}.

The above understanding also provides a probable explanation of as to why proteins with higher net charge, after explicit ion addition, appear to feature a match with experimental observations. Consider Figure 9 where 9(a) depicts 4EQV, which is a highly negatively charged protein (used to exemplify high charge proteins in general). Figure 9(b) depicts 4F5S, which is electrically neutral (exemplifying low charge proteins). The pH values are 6.7 and 5.2 respectively. The surface around them is placed at a 7 Å distance from the respective vdW surface, with blue representing positive potential and red representing negative potential, along with the entire set of potential being linearly mapped into colors within this range. As one can see, proteins with higher positive/negative net charge are very likely dominated by the presence of charges of corresponding polarity. This enhances their ability to behave as a monopole and possess a potential distribution with little fluctuation. For instance, the surface potential distribution has a fluctuation of 0.33 (std. deviation/|mean|). The shell of counter ions is subsequently distributed fairly uniformly. As a result, the monopole like behavior is still retained while the potentials are screened. This dominantly monopole like behavior could be instrumental in validating the use of linear U(ζ) relation to deduce ζ-potential from mobility. However, since presence of higher charge or addition of ions does not make the solute charge distribution spherical, we can expect some discrepancies to continually exist. On the other hand, for proteins with low net charge values, charges of both polarities have similar population. This not only creates a dipole and/or quadrupoles, but also allows addition of ions with both polarities, which subsequently results in a protein with no preferred polarity. This is vividly depicted in Figure 9(b), as well as the fact that the surface potential has a fluctuation of 5.33. Therefore, a monopole like behavior is very unlikely. Subsequently, the linear U(ζ) relations are not the best way to interpret their mobility data. The higher order moments must be taken into account. Equations S1–S5 in the Supporting Info. provide the equations that depict, in general, the relationship of mobility (U) to various moments of surface potential distribution. Table S4 therein explicitly shows how the best predicted potentials compare with the experimental ζ-potentials and that the predictions are fairly accurate for cases where the absolute value of the net charge is high.

Figure 9:

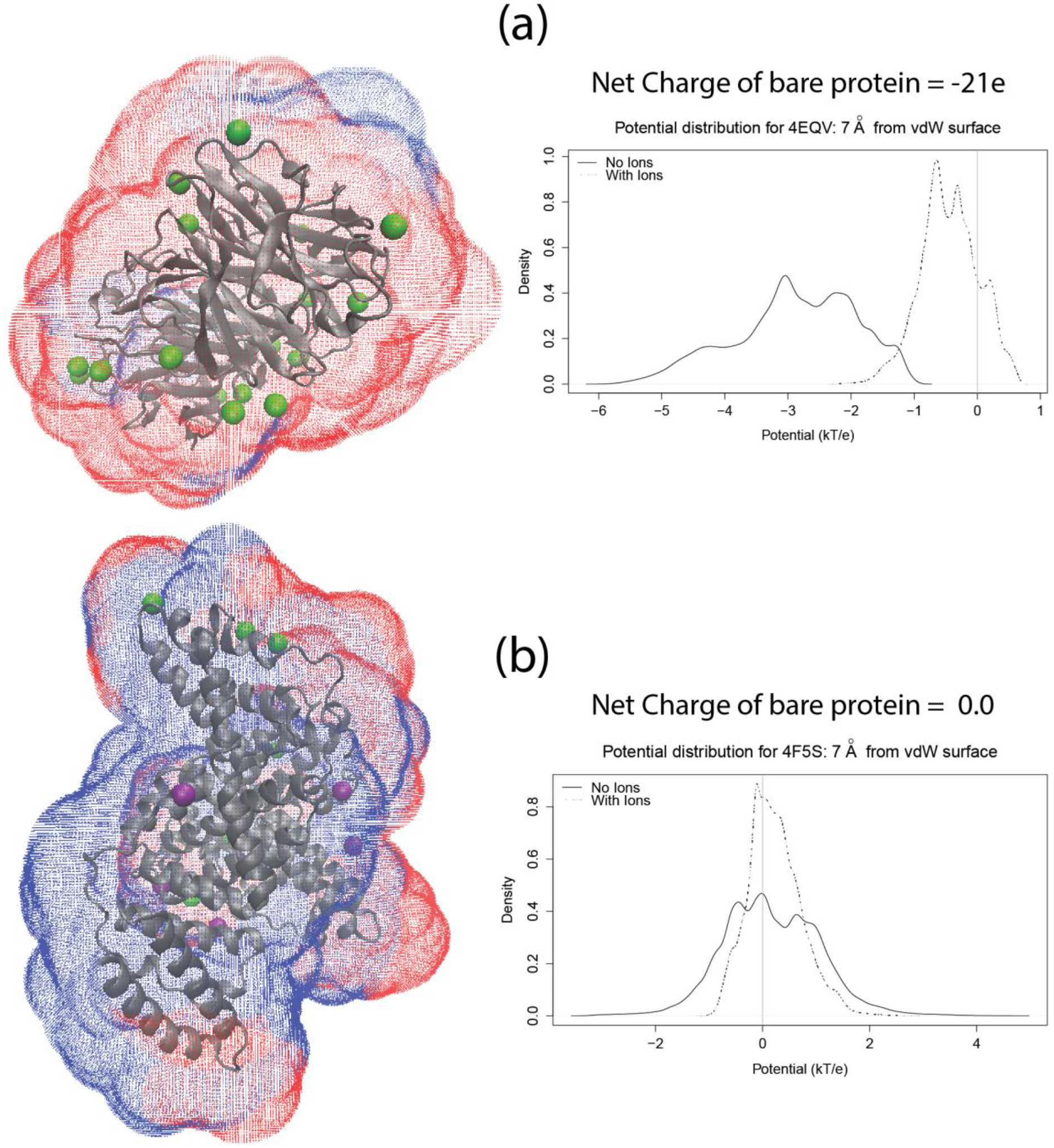
Illustrations of the surface drawn using the new module of DelPhi around (a) 4EQV (highly charged) and (b) 4F5S (net neutral). The color of the points on the surface are a linear function of the potential with the negative potentials being red and the positive ones blue. The proteins are shown in cartoon representation and the ions are shown as colored beads (Na – green; Cl – purple). The right panel plots show the distribution of potential on the respective surfaces. The TCL script to draw these surfaces can be obtained from http://compbio.clemson.edu/downloadDir/seeSurface.tcl.

At the same time, other misconceptions about proteins also need to be addressed. First, protein molecules are not rigid objects. Second, the presence of clefts and cavities can cause ions from the solution to occupy these sites and bind strongly (under steric restrictions). As a result, the width of the layer of ions surrounding them is non-uniform. Third, the inhomogeneous electrostatic potential field around the protein causes an inhomogeneity in the distribution of the polarity and concentration of ions in the Stern layer. This is vividly deviant from the ionic double layer that is known to exist around spherical objects with uniform charge distribution. Though O’Brien and White⁴⁵ suggest a method for inferring ζ-potential from mobility data for non-spherical diffuse ionic double layer, the cases of proteins and other biomolecules are complex having non-uniform local/global curvature.

All of the above factors indicate the necessity of interpreting the experimental mobility data with added considerations, especially in the case of biomolecules that deviate significantly from ideal spheres. Not only do these factors help understand the discrepancies in our work, they can also help understand certain discrepancies in some of the other protein ζ-potential experiments present in the literature. For instance, the ζ-potential for a given protein appears to have different values from different experimental sources for the same pH range and similar experimental conditions. For example, Ref.³² reports a ζ-potential of −25 mV at pH 7.2 in the presence of 0.001M NaCl for BSA. On the other hand, Ref.⁵⁹ reports a value of −51 mV for BSA at the same pH and similar NaCl concentration (the values differ by almost 100 %). Another case is the ζ-potential of Lipase-A from Candida Antarctica (CALA; PDB Id: 3GUU/ not studied here)⁶⁰ and α-amylase (PDB Id. 1UA7)³². Their experimental ζ-potential is reported to become more negative with increase of pH until a certain point. After that, the potential reverses the trend (see Table S1). Such behavior is opposite to standard titration behavior. The reader can find a good deal of information on this topic from the work of Delgado et. al.⁴⁷

There are factors that highlight uncertainties in the computational approach as well. For instance, the experimental sources do not mention the details of the protein oligomerization. A particular protein might have various oligomeric states, which very well might be influenced by the external field, solvent pH, and concentration of protein. An equally important factor is the 3D structure being used. The structures taken from PDB are structures representing the protein at a particular pH. Significant deviation of such pH is expected to cause small or large changes of the 3D structure (including unfolding), which are not considered in our protocol. Even if one models the electrostatic potential at a pH close to the crystallographic conditions, an error could be introduced by incorrect prediction of the protonation states of all titratable residues. Our pKa protocol, DelPhiPKa, was shown to be quite accurate³⁴ - however, even an error of 1/2pH unit in predicting the pKa of a given group may change the net charge of the protein.

Conclusion

A new feature of popular PBE solver DelPhi was reported in this work and used to model the surface averaged electrostatic potential (SAEP) for proteins. Results showed the importance of surface bound ions on the calculated electrostatic potential around the macromolecule, especially in case of low salt concentration. The new feature can be used to investigate charged substrates’ association with macromolecules and oligometization processes. In the absence of experimental data for such processes, we demonstrated that the new feature can be used to predict zeta-potential of proteins, provided that the knowledge of their 3D structure is available and certain criteria are met. It is shown that if one uses BION and places predicted ions explicitly on protein surface, the zeta-potential can be predicted in most cases (not including macromolecules with low net charge) at a distance about 4 Å away from vdW surfaces.