Biomechanical evaluation of bridge span with three implant abutment designs and two connectors for tooth-implant supported prosthesis: A finite element analysis

Abstract

Background/purpose

Bridge stability under loading was influenced by bridge span with the connector and implant abutment design. Thus, the purpose of this study was to evaluate the effects of rigid and non-rigid connector designs and pontic connections of different abutment systems in the tooth-implant supported prosthesis (TISP) at different span distances on the biomechanical stress distribution of the overall system components.

Materials and methods

For comparative analysis, rigid and non-rigid bridge connections were fitted with three implant abutment systems (one-piece, two-piece and three-piece), and five implant-to-natural tooth distance configurations (12 mm, 14 mm, 16 mm, 18 mm, and 20 mm) were provided.

Results

The maximum stress between TISP components occurred at the distal side of crown margin of cement1 in rigid connector with one-piece group and the bottom of the crown3 in non-rigid connector with one-piece group, while the other groups were more concentrated at the junction between the mesial side of the implant collar and the abutment. In addition, neither the rigid nor non-rigid connector model showed that stress distribution increased proportionally with the bridge span distance.

Conclusion

It was clinically recommended that if the implant with a shorter bridge distance of 12 mm from the natural tooth, the rigid connection of the three-piece abutment can be used as the TISP design. If the bridge distance was 18 mm longer, the non-rigid connection of the three-piece abutment could maintain the physiological movement of the natural tooth and avoid the excessive stress on the bone crest around the implant.

Introduction

The application of dental bridges is a prosthetic way to restore oral function when the oral cavity is missing teeth. It consists of three parts: abutment retainer, connector and pontic. The resultant force of this structure on the fixed bridge must be within the acceptable physiological range of the abutment retainer and will not cause any pathological changes. Furthermore, the design of the dental bridge should also minimize or eliminate stress concentration that damages the abutment teeth and supporting tissues, thereby protecting the soft and hard tissues of the oral cavity.^1,2 From a mechanical point of view, the stress describes the mechanical state of various points and directions inside an object. When a dental bridge like a double-ended fixed beam is subjected to occlusal load, two completely opposite compressive and tensile stresses are formed in the internal compression and extension regions of the beam. When the pressure is small, the two bridge abutments show a simple load-bearing response. If the pressure continues to increase, the internal flexural stress of the fixed beam will increase. However, since the two ends of the fixed beam cannot be lifted up and deformed, the abutment bridge foundation not only has a load-bearing action, but also resists or prevents the upward moment action at both ends. The moment response generated in the abutment bridge is called the bending moment response.

Although the basic structure of a fixed dental bridge is similar to that of a general engineering bridge, the stress response of a fixed dental bridge is quite similar to that of a simple fixed beam.³ However, since Branemark proposed the concept of osseointegration in 1952, if the osseointegrated implant retainer in a fixed dental bridge is connected to the abutment teeth with a certain physiological mobility, its mechanical distribution is more complicated. This includes not only the moment response of the original dental bridge, but also the compensated stress distribution. Therefore, many researchers have tried to explain the biomechanical mechanism after the implant is connected to the natural tooth. Weinberg et al.⁴ described the mechanical distribution of the prosthesis after the combination of a single implant and a natural toot, and divided the tooth-implant supported prosthesis (TISP) structure into rigid prosthesis (connection element), rigid vertical element (implant), flexible vertical element (natural tooth) and supporting medium (bone or periodontal ligament). The authors argued that when the vertical element with the supporting medium was rigid, the applied lateral force caused the maximum stress distribution at the load and the minimum stress distribution across multiple other members of the system. As the stiffness of a vertical element was decreased, an increase in bending or motion was distributed more and more stress to other vertical elements and their supporting medium. Therefore, the stress distribution was proportional to the degree of bending of the vertical element or the support medium.⁴ Richter⁵ depicted more detailed analysis of the reaction force and bending momentum forces in the supported alveolar bone due to occlusal loading on a TISP implant or prosthesis.

The researchers were also analyzed the stress distribution of the prosthetic system components through finite element biomechanical analysis to provide clinicians with the design of the prosthesis.6, 7, 8, 9 For example, Koosha et al.⁶ analyzed the stress distribution of rigid and non-rigid connectors in TISP by finite element method. The stress discussion in the study was focused on the comparison of the maximum equivalent stress values on the proximal and distal sides of natural teeth and implants. Kumar et al.⁷ divided natural teeth and peri-implant bone into 12 zones to investigate the stress distribution in 3D finite element analysis of different TISP designs under 300 N occlusal loading. Tsouknidas et al.⁸ used computer simulation to analyze the biomechanical behavior of TISP under different occlusions in different bone types to understand the maximum stress distribution of various implant components and alveolar bone, thus making recommendations for prosthesis design. Lin et al.⁹ analyzed the biomechanical interaction of the span length of the resin-bonded prosthesis through finite element static kinematics, and found that a longer bridge led to high stress on the prosthesis, and the span length was a biomechanical factor in the design of fixed dentures. However, when discussing the mechanical behavior of various prosthetic pontic designs under loading, most researchers mainly used the bone around the implant as the observed stress distribution, and rarely extended to stress distribution of the overall system. Furthermore, in terms of TISP design parameters, in addition to the influence of the stress distribution of the prosthesis caused by the mismatch pillar element between the natural teeth and the implants, the stress analysis of the fixed dental bridge also included the design of the abutment connection for the second-stage implant. And the length of the bridge was also one of the factors affecting the prosthesis strain and bone graft anchoring. If we can understand the influence of dental bridge connector and implant abutment design along with bridge extension span, it will help dental bridge stability under load and the consideration of dental bridge design. Accordingly, the purpose of this study was to evaluate the effects of rigid and non-rigid connector designs and pontic connections of different abutment systems TISP at different span distances on the biomechanical stress distribution of the overall system components in order to suggest prosthetic treatment plans.

Materials and methods

Create three dimensional models

In order to simulate a unilateral mandibular distal extension of the edentulous arch, the alveolar bone with the missing first, second and third molars and the remaining teeth in the dental arch have good periodontal health and ideal bone support. Referring to the modeling method studied by Huang et al.¹⁰ Firstly, a bone block model of 55 mm in length, 25 mm in width and 12 mm in thickness was constructed in the Solidworks 2019 software environment (Dassault systèmes solidworks Corp, Waltham, MA. USA) covered with 2 mm thick cortical bone, and cancellous bone was used for the entire internal structure. Then, the mandibular part of the simulated alveolar bone was combined with the natural tooth of the second premolar and the implant abutment as the fixed prosthesis of the abutment to form a three dimensional finite element model of the three-unit TISP connecting the natural tooth and the implant in the posterior mandibular area. Among them, the second premolar natural tooth referred to Wheeler's measurement parameters to establish a second premolar with a length of 16 mm, a vertebral degree from 5 mm to 0.5 mm in mesio-distal diameter, and a vertebral degree from 6 mm to 1.5 mm in buccolingual diameter.^5,6,11 Model of the premolar root overlaid with a simplified 0.25 mm periodontal ligament (PDL) and 0.4 mm cortical bone. A simulation model of the Biotech KONTACT system with 4.2 mm in diameter and 10 mm in length implant fixture was created at a distance of 12 mm–20 mm from the center point of the second premolar. Its thread was designed with a geometry of pitch distance of 0.6 mm and thread depth of 0.2 mm to simplify the original design. The Implant abutment system was simulated one-piece, two-piece and three-piece abutments based on the original geometry of the standard abutment and its components. The edge of the natural tooth and the implant abutment of the simulated TISP were both 1 mm away from the top of the bone fragment and the thickness of the casting crown was at least 1 mm thick. The contact between the adjacent crowns was set to a 3 mm diameter area. The crown material was set to nickel-chromium alloy. A 0.05 mm thickness space was provided between the abutment and the crown to simulate the space for accommodating the cement. For comparative analysis, rigid and non-rigid bridge connections were fitted with three implant abutment systems, and five implant-to-natural tooth distance configurations (12 mm, 14 mm, 16 mm, 18 mm, and 20 mm) were provided. This was to compare stress analysis of 30 groups of masticatory loads with different distances to different connectors in three implant abutment systems. The non-rigid connectors used in the study referred to the prototype of Beyeler's non-adjustable friction grip dovetail slider attachments (Cendres + Métaux SA, Biel-Bienne, Switzerland). A solid component with a vertical length of 4 mm and a width of 2.5 mm was attached to the proximal side of the implant crown. After the construction of the model, the construction of TISP includes tooth solid, PDL, 0.4 mm cortical bone, crown1+2, crown3, cement1, cement3, cortical bone, sponge bone, implant fixture, implant abutment and fixation screw, a total of 12 entity originals (Fig. 1).

Fig. 1.

TISP structure model.

Set up conditions for simulation

All materials were assumed to be isotropic, homogeneous and linear elastic. The Young's modulus and Poisson's ratio of the materials used in this study were described in Table 1.¹² The boundary constraint of the model was defined in the proximal and distal planes of the bone block, and the movement of the mandible was restricted according to the combination of the mandible and the muscles. The movement of the node was completely restricted in this area. The bone-implant interface has been fully considered to simulate osseointegration, and there were no crater-like defects around the implant neck, so the bone and prosthesis in the implant were assumed a perfect structural fit. In the mathematical model, however, when the implant was in direct contact with the bone, the natural tooth was exhibited its predominant mobility within the boundaries of the periodontal ligament due to the elastic modulus. All TISP structural components were initially set to have an integral bonding contact. When the solid surface was bonded by the integral contact condition, the program will generate a compatible mesh in the contact area, and the merge node becomes a bonded state. It did not allow relative micro-movement, and the displacement between different materials was continuous. In addition, the matrix of the non-rigid connector of the TISP and the parent surface were allowed to be in vertical sliding contact with each other without penetrating. No penetrating contact conditions between implant abutment, fixation screw and implant fixture were set. There are usually three occlusal schemes of implant prosthesis in clinical practice: canine guidance, group function and monoplane occlusion. And occlusal contacts with tripoding contact or cusp-to-fossa contact are found. In addition, clinicians will try to minimize the lateral loading of the implant. Therefore, the occlusal design simulated in this study was based on the static vertical loading of the monoplane occlusion with cusp-to-fossa contact. The crowns of the monoplane were established on the three-unit bridge model, supplemented by six cusp-to-fossa contact points, and the bridge models were applied with a vertical occlusal force of 300 N to simulate the focus of clinical bridge design. The two circular dimples were established on the occlusal table of each crown with a diameter of 2 mm and a depth of 0.25 mm for occlusal contact points. There were six occlusal points in the whole length of the bridge to simulate a static occlusal force of 300 N, and a uniformly distributed load of 50 N perpendicular to the occlusal plane along the axis of the bridge was applied to the vertex of the 6 circular dimples.

Table 1.

Physical properties of the materials.

Material	Modulus of elasticity (MPa)	Poisson's ratio
Tooth solid	18,600	0.31
Ni–Cr alloy	204,000	0.30
Titanium (fixture, abutment, fixation screw)	117,000	0.35
Cement (glass ionomer)	16,900	0.30
Cortical bone	13,700	0.30
Spongy bone	1370	0.30
Periodontal ligament	170	0.45

Simulation

The model was meshed in Solidworks Simulation with a blended curvature-based mesher to generate the mesh structure with the 4-node linear tetrahedral solid elements. The number of elements of the models were described in Table 2. We chose the FFEPlus iterative solver of soliderworks software to solve the equations using an approximate solution method that evaluates the associated error at each iteration. And continue to iterate until an acceptable error was obtained. Then the mesh size of the model was gradually refined from 5.5 mm, 4.5 mm, 3.8 mm, 3.42 mm–3.02 mm, and the maximum equivalent stress was calculated. After five repeated solutions, the maximum stress at 3.8 mm, 3.42 mm and 3.02 mm was appeared to a discrepancy of less than 5% between the meshes, so it could be considered that the maximum stress was converged at the mesh size of 3.8 mm. The model created at the same time was subjected to a linear static analysis in the environment piece. The output of the analysis was done in the post-processing module of the software. The obtained simulation results were calculated according to the Von Mises equivalent stress level at the bone-implant interface as well as the individual components of TISP. The mathematical solution obtained in the results was also converted into a visual result characterized by the degree of color ranging between red and blue. The red represents the highest stress value and the color gradient table was normalized.

Table 2.

Number of elements that the TISP with rigid connector and non-rigid connector in different bridge distances models.

	12 mm	14 mm	16 mm	18 mm	20 mm
R1	480,484	453,991	467,878	502,575	505,577
R2	449,459	458,229	453,962	466,766	471,584
R3	457,232	474,804	469,748	484,845	458,272
NR1	419,735	449,254	552,700	458,415	492,416
NR2	462,997	473,973	481,545	469,071	474,657
NR3	459,086	436,277	462,057	410,136	468,249

R1: Rigid connector with 1-piece abutment; R2: Rigid connector with 2-piece abutment; R3: Rigid connector with 3-piece abutment; NR1: Non-rigid connector with 1-piece abutment; NR2: Non-rigid connector with 2-piece abutment; NR3: Non-rigid connector with 3-piece abutment.

Results

TISP structure components

The maximum equivalent stress values of each component of R1, NR1, R2, NR2, R3 and NR3 TISP models with non-rigid and rigid connectors at different bridge distances (12 mm, 14 mm, 16 mm, 18 mm, and 20 mm) were described in Table 3 and Table 4, respectively. The views captured by the 3D model section (Fig. 2, Fig. 3) showed the stress distribution in the natural tooth and peri-implant area in the TISP and supporting bone tissue models. When analyzing 30 configurations under all loading conditions, the maximum stress between TISP components appeared on the distal side of crown margin of cement1 in the R1 group; at the bottom of the non-rigid connector of crown3 in the NR1 group. The R2, R3, NR2, NR3 groups were more concentrated at the junction between the mesial side of the implant collar and the abutment. In addition, regardless of the rigid or non-rigid connector model, there was no proportional increase in the pattern of stress distribution with the increase in bridge span distance.

Table 3.

The stress values (MPa) of the TISP with a rigid connector in different bridge distances (12 mm, 14 mm, 16 mm, 18 mm, and 20 mm) models.

	TS	PDL	0.4 mm	CM1	CR1+2	CM3	CR3	COR	SPO	IF	IAB	FS
R1 (12)	57.52	27.09	35.30	231.05	163.31	38.67	92.69	47.75	37.67	82.50	NA	NA
R1 (14)	47.80	18.72	25.25	210.11	139.28	28.46	81.22	36.01	24.76	59.42	NA	NA
R1 (16)	44.35	18.42	27.49	214.35	137.86	27.73	70.76	32.61	23.70	57.29	NA	NA
R1 (18)	52.90	31.78	40.28	213.89	142.71	32.95	90.25	41.01	30.84	68.75	NA	NA
R1 (20)	53.17	30.57	39.23	213.66	138.96	30.77	96.88	37.29	28.70	65.03	NA	NA
R2 (12)	50.32	21.61	33.36	220.76	142.00	34.84	38.72	25.22	21.15	419.44	140.68	NA
R2 (14)	49.64	21.99	32.62	216.81	146.15	32.05	36.72	29.95	20.32	388.72	190.16	NA
R2 (16)	46.23	21.62	32.06	208.38	152.06	30.35	34.65	37.43	37.43	398.04	145.76	NA
R2 (18)	48.16	23.77	33.45	218.32	159.30	29.98	33.85	25.16	17.04	356.60	161.26	NA
R2 (20)	52.98	23.82	32.77	234.79	174.39	29.00	74.10	29.99	20.27	355.67	160.97	NA
R3 (12)	57.50	19.73	28.49	228.85	144.25	77.83	35.92	25.29	15.61	314.54	245.09	45.19
R3 (14)	55.52	21.54	30.75	222.48	144.30	72.29	37.11	25.70	20.26	306.27	202.44	38.15
R3 (16)	47.22	25.37	35.38	227.17	149.26	75.41	35.95	25.00	23.12	306.39	176.20	39.87
R3 (18)	51.98	22.17	30.67	219.33	148.59	72.87	34.04	23.88	17.50	293.70	176.19	39.83
R3 (20)	55.92	43.83	57.75	227.12	143.72	85.01	39.17	31.38	16.34	346.57	271.74	54.08

TISP: Tooth-implant supported prosthesis; R1: Rigid connector with 1-piece abutment; R2: Rigid connector with 2-piece abutment; R3: Rigid connector with 3-piece abutment; TS: Tooth solid; PDL: Periodontal ligament; 0.4 mm: 0.4 mm Cortical bone; CM1: Cement1; CR1+2: Crown1+2; CM3: Cement3; CR3: Crown3; COR: Cortical bone; SPO: Spongy bone; IF: Implant fixture; IAB: Implant abutment; FS: Fixture screw.

Table 4.

The stress values (MPa) of the TISP with a non-rigid connector in different bridge distances (12 mm, 14 mm, 16 mm, 18 mm, and 20 mm) models.

	TS	PDL	0.4 mm	CM1	CR1+2	CM3	CR3	COR	SPO	IF	IAB	FS
NR1 (12)	70.85	28.13	42.40	297.83	222.05	37.70	349.51	47.51	41.53	77.44	NA	NA
NR1 (14)	63.35	35.88	42.45	264.11	184.47	34.69	390.69	40.56	28.63	69.12	NA	NA
NR1 (16)	58.70	35.72	47.50	242.72	163.77	33.30	275.32	41.43	27.00	68.99	NA	NA
NR1 (18)	55.81	30.92	44.76	228.69	147.69	30.77	268.94	33.77	24.03	58.76	NA	NA
NR1 (20)	68.56	45.76	64.40	251.02	174.81	33.15	327.93	39.13	28.00	65.28	NA	NA
NR2 (12)	26.10	33.26	41.91	78.67	115.75	40.82	160.08	32.87	24.63	351.67	204.07	NA
NR2 (14)	25.80	32.00	42.33	79.18	117.42	36.98	142.53	33.96	21.63	375.28	237.14	NA
NR2 (16)	25.85	32.26	44.59	81.77	103.85	33.97	143.91	33.06	15.69	273.89	219.88	NA
NR2 (18)	27.95	35.52	43.82	78.16	113.97	34.49	128.07	30.37	20.18	301.23	159.52	NA
NR2 (20)	28.59	36.22	44.92	77.76	113.27	31.74	122.32	30.37	16.81	305.39	188.62	NA
NR3 (12)	21.96	20.74	24.64	60.57	91.09	30.95	123.71	19.27	20.30	256.79	140.48	26.86
NR3 (14)	22.09	25.02	33.31	68.39	132.14	30.54	120.00	25.62	15.74	247.37	237.78	47.11
NR3 (16)	21.83	25.75	30.92	67.39	119.77	30.72	138.78	21.52	15.25	214.26	140.95	70.52
NR3 (18)	23.48	19.70	25.02	78.23	100.39	26.19	111.45	19.95	13.33	231.22	115.39	33.65
NR3 (20)	22.68	26.72	31.47	70.36	114.43	28.73	132.67	18.37	18.68	252.43	134.65	19.43

TISP: Tooth-implant supported prosthesis; NR1: Non-rigid connector with 1-piece abutment; NR2: Non-rigid connector with 2-piece abutment; NR3: Non-rigid connector with 3-piece abutment; TS: Tooth solid; PDL: Periodontal ligament; 0.4 mm: 0.4 mm Cortical bone; CM1: Cement1; CR1+2: Crown1+2; CM3: Cement3; CR3: Crown3; COR: Cortical bone; SPO: Spongy bone; IF: Implant fixture; IAB: Implant abutment; FS: Fixture screw.

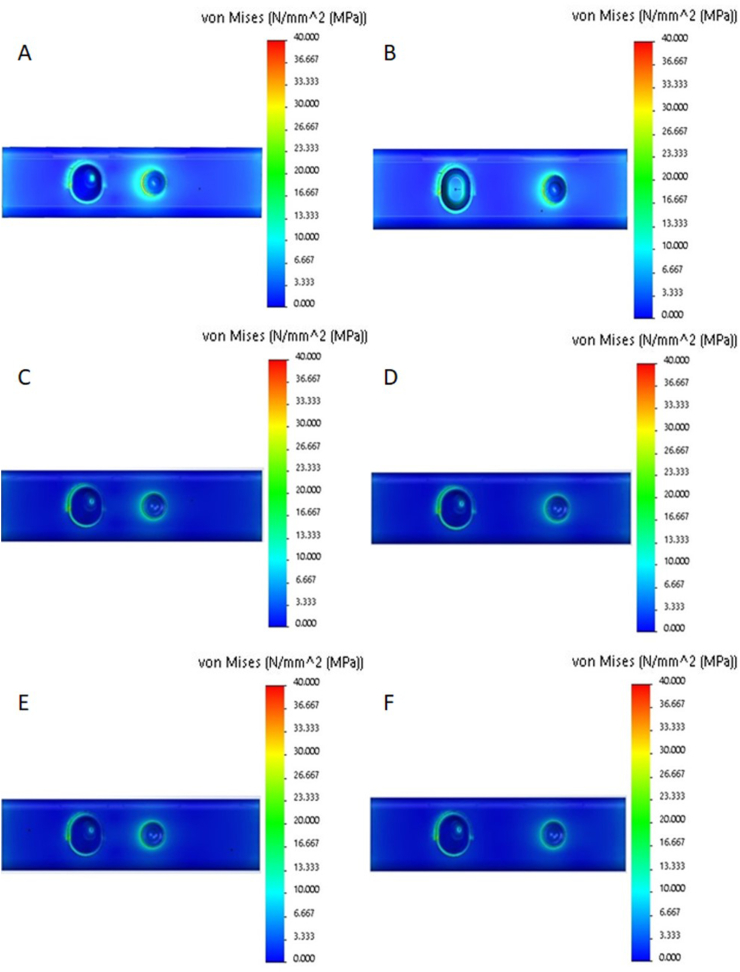
Fig. 2.

Von Mises stress distribution at TISP structure components. (A) R1 (12): 12 mm distance with rigid type and one-piece implant system; (B) R1 (18): 18 mm distance with rigid type and one-piece implant system; (C) R2 (12): 12 mm distance with rigid type and two-piece implant system; (D) R2 (18): 18 mm distance with rigid type and two-piece implant system; (E) R3 (12): 12 mm distance with rigid type and three-piece implant system; (F) R3 (18): 18 mm distance with rigid type and three-piece implant system.

Fig. 3.

Von Mises stress distribution at TISP structure components. (A) NR1 (12): 12 mm distance with non-rigid type and one-piece implant system; (B) NR1 (18): 18 mm distance with non-rigid type and one-piece implant system; (C) NR2 (12): 12 mm distance with non-rigid type and two-piece implant system; (D) NR2 (18): 18 mm distance with non-rigid type and two-piece implant system; (E) NR3 (12): 12 mm distance with non-rigid type and three-piece implant system; (F) NR3 (18): 18 mm distance with non-rigid type and three-piece implant system.

PDL component finding

Regardless of rigid or non-rigid connectors, the maximum stress of PDL appeared in the apical region (Fig. 4, Fig. 5). The minimum stress values were in the rigidly connected one-piece implant abutment system with a bridge span distance of 14 mm (18.72 MPa) and 16 mm (18.42 MPa) (Table 3). Except the bridge span distances of 18 mm and 20 mm, the non-rigid connector groups were all larger than the rigid connector groups (Table 3, Table 4 and Fig. 6).

Fig. 4.

Von Mises stress distribution at support medium (upper view). (A) R1 (12): 12 mm distance with rigid type and one-piece implant system; (B) R1 (18): 18 mm distance with rigid type and one-piece implant system; (C) R2 (12): 12 mm distance with rigid type and two-piece implant system; (D) R2 (18): 18 mm distance with rigid type and two-piece implant system; (E) R3 (12): 12 mm distance with rigid type and three-piece implant system; (F) R3 (18): 18 mm distance with rigid type and three-piece implant system.

Fig. 5.

Von Mises stress distribution at support medium (upper view). (A) NR1 (12): 12 mm distance with non-rigid type and one-piece implant system; (B) NR1 (18): 18 mm distance with non-rigid type and one-piece implant system; (C) NR2 (12): 12 mm distance with non-rigid type and two-piece implant system; (D) NR2 (18): 18 mm distance with non-rigid type and two-piece implant system; (E) NR3 (12): 12 mm distance with non-rigid type and three-piece implant system; (F) NR3 (18): 18 mm distance with non-rigid type and three-piece implant system.

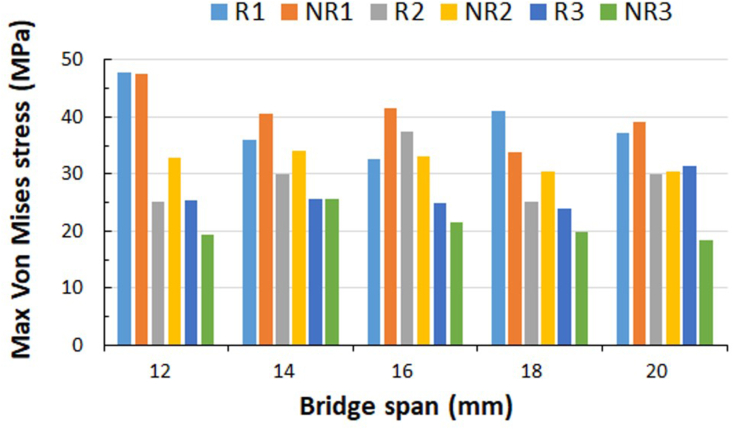
Fig. 6.

The maximum Von Mises stress of PDL.

Cortical bone supported medium finding

The maximum stress of the cortical bone components was concentrated at the interface between the bone crest and the implant collar (Fig. 4, Fig. 5). The maximum stress value between models occurred in the rigidly connected one-piece implant abutment system with a bridge span of 12 mm (47.75 MPa) and the non-rigidly connected one-piece implant abutment system with a bridge span of 12 mm (47.53 MPa). In contrast, the minimum stress value occurred in the bridge non-rigidly connected three-piece implant abutment system (18.37 MPa) at 20 mm (Table 3, Table 4 and Fig. 7).

Fig. 7.

The maximum Von Mises stress of cortical bone.

Implant fixture component finding

In the two-piece implant abutment system with rigid or non-rigid connectors, the highest stress value appeared at the interface between the implant fixture and the implant abutment (Fig. 2, Fig. 3), followed by the three-piece, and the one-piece was the lowest (Table 3, Table 4). Moreover, the pressure pattern of the implant body did not appear to change significantly as the bridge span distance changed (Fig. 8).

Fig. 8.

The maximum Von Mises stress of Implant fixture.

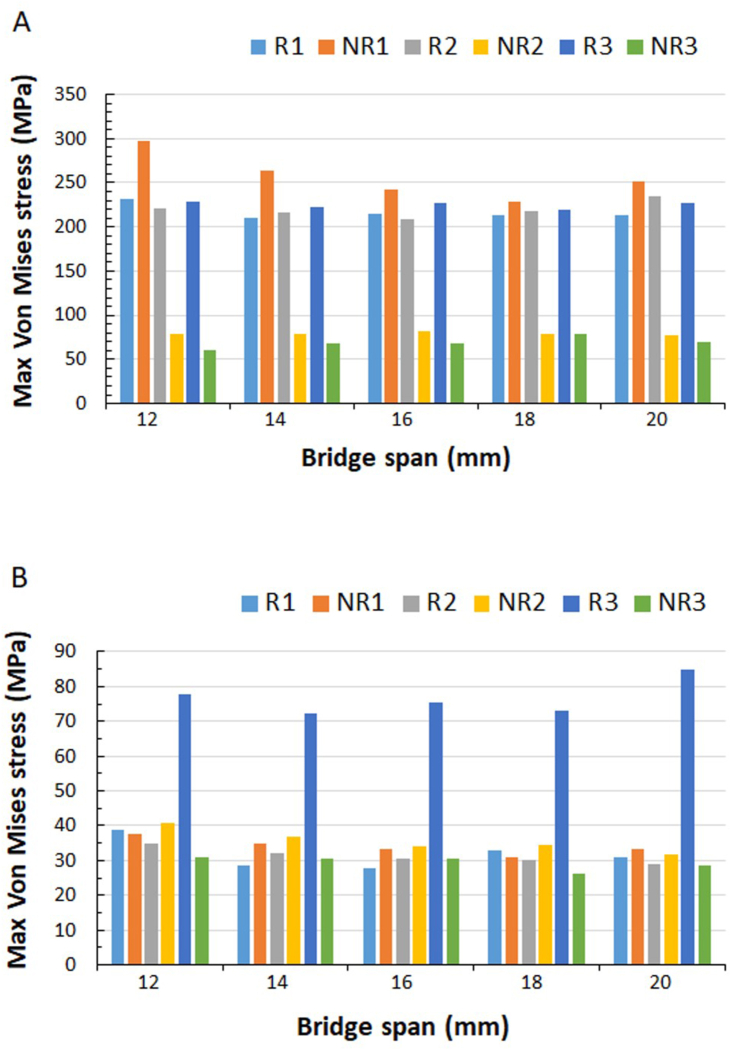
Crown components effect

The crown1+2 combined one-piece abutment system and the rigid connector had lower stress value than the non-rigid connector. On the contrary, rigid connectors containing two- or three-piece abutment systems had higher stress values of crown 1 + 2 than non-rigid connectors (Table 3, Table 4). In addition, the maximum stress area of the rigid connector crown1+2 occurred on the distal side of the crown margin and the natural tooth (Fig. 2), while the maximum stress area of the non-rigid connector crown1+2 was at the bottom of the dovetail interface connected to the crown3 (Fig. 3). Furthermore, with the change of the bridge span distance, the stress value and mode of the crown1+2 did not change significantly (Fig. 9 A).

Fig. 9.

The maximum Von Mises stress of (A) Crown1+2 and (B) Crown3.

The crown 3 stress of the rigid connector was concentrated near the mesial surface of the crown margin, and its stress distribution did not vary greatly with the bridge span (Fig. 2). However, the crown of the non-rigid connector was not only stressed at the mesial proximal margin of the crown, but also at the bottom of the attachment (Fig. 3). And the maximum stress value was the largest in the NR1 group, followed by the NR2 group, and the smallest in the NR3 group (Fig. 9 B).

Cement components effect

Cement1 existed between the natural tooth and the crown, and the stress will be concentrated on the interface between the crown margin and the distal side of the tooth body. As a result, the stress value was twice that of the non-rigid connector TISP. In addition, there was only a small change in the stress value of the rigid or non-rigid connectors with the change of the bridge span distance (Fig. 10 A).

Fig. 10.

The maximum Von Mises stress of (A) Cement1 and (B) Cement3.

The Implant abutment and crown3 were bonded by cement3. Regardless of the rigid or non-rigid connector, the stress values of the models for cement3 did not change much, except for R3. And the change of bridge span distance did not affect the stress value of cement3 (Fig. 10 B).

Discussion

The present study was to evaluate the stress distribution of TISP after vertical occlusal loading when two different connector designs were incorporated into three different abutment implant systems with five different bridge span distances. The results showed that both the connector and the implant abutment system had an effect on the biomechanical behavior of the entire dental bridge system combined with natural teeth and implants. In addition, with the appropriate bridge span length, connector and implant abutment system, suitable prosthetic design suggestions could be obtained.

In this study, the maximum stress map of each component between the TISP models was observed. The natural tooth end of the rigid connector TISP was gradually concentrated from the proximal side of the neck to the apical area. The force at the other end was transmitted to the bone surrounding the implant along the long axis. And it was densely distributed at the interface between the implant collar area and the cortical bone of the proximal bone crest. The maximum stress concentration area of the pontic was appeared at the connection between the natural tooth crown with the distal side of the cement1 crown margin and the pontic body. The natural tooth end of the non-rigid connector TISP was more concentrated in the apical region. The implant end was more concentrated in the junction of the mesial side of the implant collar and the abutment. The pontic stress was concentrated in the natural tooth crown margin with the abutment and the bottom of the connecting area of the dovetail attachment interface between the male buckle and the female buckle. In addition, the stress distribution of rigid or non-rigid connectors with different bridge span distances had no obvious variation. Such stress map behavior may be related to the stress distribution between components induced by rigid or non-rigid connectors. Structural mechanics depicted the rigid connector TISP as a structural diagram of the natural tooth end bearing support and the implant abutment cantilever beam support at the implant end.¹³ When the applied static vertical occlusal load is transmitted by the natural tooth into the alveolar bone, with the stiffness difference between the natural tooth support and the implant abutment cantilever beam support, the increase in the load distributes more stress to the rigid implant support and its supporting medium. Therefore, the system must compensate for the difference in stiffness between natural tooth and implant by bearing load on the tooth and creating flexures on the implant and surrounding bone. This is because the bending moments can force the implant to rotate, and the center of rotation of the implant is at a higher ridge level compared to the natural tooth. As a result, pressure accumulation is occurred in the mesial cervical cortical bone area of the implant, and at the same time the natural pontic connection area will also be subjected to the stress concentration from bending moments. If the dovetail attachment was incorporated into the TISP, since the non-rigid connector could be regarded as a set of pressure breakers,¹⁰ it could construct a stress buffer that converted the cantilever beam to the stress distribution of the composite beam. The combination of simply supported beam and the cantilever beam formed a special structure with continuous support in the middle, which transferred the bending moment stress on both sides, so more stress would be carried by the dovetail attachment and the interface between the implant collar and the implant abutment.

On the other hand, the longer the distance between the bridge body, the greater bending the bridge body will undergo.¹ Rangert et al.¹⁴ assumed that the mechanical properties of the natural tooth-implant connection system were a cantilever unit extending from the implant as the center. The cantilever distance was converted from different force positions to obtain the size of the bridge body deformation, and the correlation between the force and bridge body deformation distance was calculated. The results showed that the longer the cantilever distance, the larger the bridge deformation was. White et al.¹⁵ constructed a photoelastic model of fixed implant-supported prostheses with different cantilever lengths and found that with increasing cantilever length, the increase in distal tipping force resulted in a disproportionate increase in the maximum stress affected by the cantilever. However, although the implant abutment in this study was supported by a cantilever beam, the natural tooth of TISP was partially loaded with occlusal stress, so the stress distribution of rigid or non-rigid connectors with different bridge distances did not change significantly. This result was different from the effect of implant cantilever studied by Rangert et al.¹⁴ and White et al.¹⁵ It may be that the bending amplitude of the TISP cantilever beam after loading and the stiffness of the bridge were not purely based on the bending of the unsupported cantilever beam at the end as suggested by Rangert in 1991. The moment calculation and therefore the difference in the bridge span distance of the bridge body did not have a proportionally significant pattern change in the stress distribution of the TISP.

Regardless of rigid or non-rigid connectors, the maximum stress of PDL appeared at the bottom and gradually concentrated from the neck to the apical region. Except for the bridge span distances of 18 mm and 20 mm, the non-rigid connector groups were all larger than the rigid connector groups. And the 14 mm and 16 mm bridge distances for the rigidly connected one-piece abutment implant system were the minimum values. PDL is a soft, thin layer of connective tissue present between teeth and alveolar bone that exhibits a nonlinear time-dependent viscoelastic behavior under occlusal loading, absorbing forces and reducing thickness, resulting in tooth displacement.16, 17, 18 Therefore, PDL plays a key role in bone remodeling and resorption after tooth loading.¹⁹ Because the stress of PDL was concentrated in the apical region, some scholars believed that it will cause the intrusion of natural teeth in clinical practice. Lang et al.²⁰ reported that a total of 5.2% of natural abutment teeth were affected by intrusion over a 5-year observation period, most of which occurred in the non-rigid connections. In addition, according to Tsaousoglou et al.,²¹ no intrusion of natural teeth was found in the rigid connector group, while 5 natural teeth (8.19%) intrusion were noted in the non-rigid connector group. Therefore, with the more rigidity of the TISP prosthesis, the tooth-implant connection may lead to the transfer of a larger part of the masticatory load to the implant. With the increase of the elasticity of the prosthesis, the limitation of the implant is reduced, so that the PDL of the natural tooth can be freely stretched but the apical region will also experience greater stress.

In this study, the PDL stress distribution of the non-rigid connector and rigid connector did not significantly change when the bridge span was from 12 mm to 16 mm. However, the 18 mm and 20 mm three-piece abutment implant systems had greater the PDL stress distribution in the rigid connectors than non-rigid connectors, which may be due to the longer bridge span distance with the non-rigid connector and the stress buffering mechanism of the three-piece abutment system. The physiological movement of the tooth is not restricted by the implant and the stress is dispersed, thereby reducing the stress concentration of the PDL.

In this study, the stress in the bone was concentrated near the interface between the bone crest and the implant collar, just like the distribution observed in other studies.^6,10,22 However, the maximum stress values between the models appeared in the rigid and non-rigidly connected one-piece abutment implant systems with a bridge span distance of 12 mm, which were 47.75 MPa and 47.51 MPa, respectively. The non-rigidly connected three-piece abutments with bridge span distances of 12 mm and 20 mm had the minimum stress, which were 19.27 MPa and 18.37 MPa, respectively. The stress peak formed in the neck region supported by the implant may be due to the stress shielding phenomenon caused by the different elastic moduli of cortical and spongy bone. This phenomenon relies on the presence of a cortical bone surface with a high elastic modulus. In addition, in this study, the increased stress under vertical occlusal loading occurred on the mesial cervical side of the implant because the design of the TIFP model assumed that the implant was 100% osseointegration and that the movement of the implant in the bone was almost complete bonding. Bone is clinically living tissue, and the long-term durability of osseointegrated implants depends on the adaptation of the bone to the stresses and strains that occur in the vicinity of the prosthesis. Mechanical overload and disuse may cause bone resorption, thereby reducing the implant stability. However, a proper mechanical environment can improve the level of integration, with the help of 3D FE analysis. The results of this study around the peri-implant bone stress between the models implied a longer bridge distance combined with a non-rigidly connected three-piece abutment implant system that can provide a better stress distribution at the peri-implant bone interface.

The connection design of the TISP implant abutment not only considers the stress distribution of the implant itself, but also aims to reduce the stress concentration on the marginal bone, so as to achieve the goal of long-term stability of the implant. For the implant-abutment connection system, the researchers believe that there is a flexible connection between the implants, allowing a certain degree of movement of the natural teeth of the TISP after occlusal loading. For example, Rangert et al.¹⁴ calculated a 10-fold difference between the bridge body deformation of a TISP implant cantilever beam and the actual measured value, which this difference may be due to the flexibility of the screw joints of the implant connecting system. Finite element analysis of Wu et al.²³ showed that although the maximum stress value (250.9 MPa) of the two-piece implant system was higher than that of the one-piece implant system (220.5 MPa), the stress and strain of the overall surrounding bone of the one-piece implant system (151.7 MPa) was higher than the two-piece implant system (115.3 MPa). In addition, their results also revealed that the two-piece implant abutment system with rigid or non-rigid connectors had the highest stress value at the implant-abutment system interface, followed by the three-piece implant abutment system, while the one-piece implant abutment system was the lowest. The stress values of the peri-implant bone interface were the minimum for the three-piece implant abutment system and the maximum for the one-piece implant abutment system. The reason may be that the multi-segment connection system has a larger contact area with the implant abutment, so the stress could be distributed more widely and penetrated into the implant and further away from the marginal bone, thereby reducing bone loss of the bone crest. Therefore, implant-abutment connection design may lead to treatment differences due to pressure distribution. Furthermore, the contact conditions at the implant-abutment interface and the abutment neck create a wedging effect that reduces the effects of bending caused by the horizontal component of the load and improves implant-abutment stability and lateral force distribution. Therefore, implant-abutment connection design may contribute to treatment differences due to pressure distribution.

In the present study, after occlusal loading, the bending momentum of the rigid connector TISP caused the cement1 stress existing between the natural tooth and the crown to concentrate on the distal surface due to the mismatch of the mobility of the natural tooth and the implant. And its stress value was twice that of the non-rigid connector TISP. In addition, for the cement3 bonded between the implant abutment and the crown, because the implant abutment absorbed most of the stress, the stress values of the other models except R3 did not change much whether they were rigid connectors or non-rigid connectors. Although Anusavice et al.²⁴ in an FEA study considered occlusal impact on stress distribution in the cement of full-coverage crowns, it was found that the stress transmitted to the cement by the masticatory load was well below the elastic limit of the cement. However, in the study of Kamposiora et al.,²⁵ it was considered that the distribution of the load magnitude in the stress level and the cement may lead to the microfracture in the cement. Therefore, in view of the uneven stress distribution of the cement after loading in this study, a permanent adhesive with good tensile strength was recommended as the primary choice. Glass ionomer cement chemically bonds with enamel or dentin to release fluoride for the prevention of caries. In addition, glass ionomer cement for implant abutments is a candidate material for clinical cement because of its low coefficient of thermal expansion coefficient, its ability to chemically bond to metal oxides, as well as sufficient compressive strength.²⁶

Finite element analysis is a non-invasive and reliable tool for analyzing biomechanical properties of implants. This research method is limited by theoretical assumptions, including the assumption of specified loading and boundary conditions to simulate the necessary loading conditions and the properties of material homogenization. These assumptions may affect the accuracy of obtaining analytical results for biomechanical stress states. As mentioned previously, occlusal load was clinically expressed as simple occlusal contact. Homogeneous and isotropic linear elastic material properties were adopted for numerical convergence considerations, especially for the characterization of periodontal ligament viscoelasticity. Therefore, FEA results can only provide a relative comparison of the biomechanics of the components of the TISP system under average conditions. Further long-term clinical studies on the outcomes of these TISPs were warranted to examine the correlation between prosthetic systems and stress analysis. With recent advances in digital imaging techniques, more efficient methods are available, including the development of specialized software for the direct transformation of 2- or 3-D information in image data from computed tomography (CT) or magnetic resonance imaging (MRI) into FEA meshes. In addition, the friction between contact surfaces can also be modeled with nonlinear frictional contact elements to provide an excellent simulation of the non-rigid connector, implant-abutment system, and the influence of the periodontal ligament during mastication. This can provide a reference for future research.

Based on the limited linear numerical results of this study, the stress transfer mechanisms of rigid-connected TISP cantilever beams and non-rigid-connected TISP composite beams after loading were different. For rigid connectors, the overall system stress distribution was more concentrated on the distal side where the crown margin engaged with natural tooth and the alveolar bone around the proximal side of the implant than non-rigid connectors. Non-rigid connectors were more concentrated in the apical region of the natural tooth and the bottom of the dovetail interface that was connected to the implant crown. In order to disperse the overall stress more evenly, it was clinically recommended that if the implant was implanted with a shorter bridge distance of 12 mm from the natural tooth, the rigid connection of the three-piece implant abutment system designed by TISP could not only reduce the apical stress of the natural tooth, but also increase more contact area between the implant and the abutment. Thus, the stress could penetrate more widely into the interior of the implant and further away from the marginal bone. If the bridge distance between the implant and the natural tooth was lengthened to 18 mm, the non-rigid connection of the three-piece implant abutment system could better maintain the physiological movement of the natural tooth, thereby reducing the stress on the natural tooth and avoiding the excessive concentrated stress on the bone crest around the implant.

Declaration of competing interest

The authors have no conflicts of interest relevant to this article.