Parameter Space CNN for Cortical Surface Segmentation

Abstract

Spherical coordinate systems have become a standard for analyzing human cortical neuroimaging data. Surface-based signals, such as curvature, folding patterns, functional activations, or estimates of myelination define relevant cortical regions. Surface-based deep learning approaches, however, such as spherical CNNs primarily focus on classification and cannot yet achieve satisfactory accuracy in segmentation tasks. To perform surface-based segmentation of the human cortex, we introduce and evaluate a 2D parameter space approach with view aggregation (p³CNN). We evaluate this network with respect to accuracy and show that it outperforms the spherical CNN by a margin, increasing the average Dice similarity score for cortical segmentation to above 0.9.

1. Introduction

Human cortical neuroimaging signals, such as cortical neuroanatomical regions or thickness are typically associated with the cortical surface. Thus, processing and analyzing these signals on geometric surface representations, rather than in a regular voxel grid, stays true to the underlying anatomy. As an example, smoothing kernels can be applied along the surface without the risk of blurring signal into neighboring structures such as cerebrospinal fluid (CSF), a neighboring gyrus, or the white matter (WM), which frequently occurs in a voxel grid. Here, these structures are in close proximity, while they are quite distant (e.g. neighboring gyrus) or non-existent (CSF, WM) on a cortical surface. Spherical coordinate systems have, therefore, become the standard for analyzing human cortical neuroimaging data [1]. Traditional algorithms are, however, computational expensive due to extensive numerical optimization and suffer from long run-times. This significantly limits their scalability to large-scale data analysis tasks. Therefore, supervised deep learning approaches are an attractive alternative due to their 2-3 orders of magnitude lower run-time. The new field of geometric deep learning offers great promise by providing ways to apply convolutional operations directly on a surface model. A subset of this field focuses on analyzing signals represented on spheres. However, these spherical convolutional neural networks (SCNNs) have mainly been proposed for classification tasks with only one (the ugscnn [2]) being suitable for semantic segmentations. Traditional CNNs for voxel grid based segmentation tasks on the other hand are already well established and have thus been optimized to a great extent over the last few years. Potentially, a spherical signal can be mapped into the image space given an effective parameterization approach such as the mapping of the globe to a world map. A perfect (isometric) mapping between plane and sphere does, however, not exist leading to metric distortions and resulting in a non-uniform distribution of sample points which can affect regional segmentation quality. In this paper, we introduce a deep learning approach called parameter space CNN (p³CNN; Fig. 1) for cortical segmentation. After reducing the problem from the sphere to a flat 2D grid via a latitude/colatitude parameterization a view aggregation scheme is used to alleviate errors introduced by distortion effects of a single parameterization. We finally train the network with multimodal (thickness and curvature) maps and evaluate the results in comparison to a SCNN for segmentation (ugscnn) and the single view (parameterization) approach. We demonstrate that our p³CNN achieves the highest accuracy on a variety of datasets.

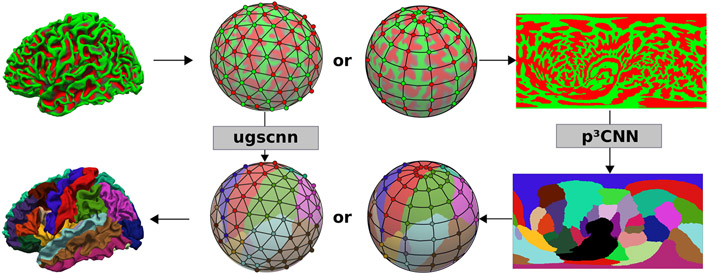
Fig. 1.

Two segmentation networks are compared: a spherical CNN (ugscnn [2]) on the icosahedron (middle left) and our proposed view-aggregation on 2D spherical parameter spaces (p³CNN, right). Both operate on curvature maps (top row) and thickness (not shown) for cortical segmentation of the cortex (bottom row).

2. Methodology

2.1. Network architecture

Within this paper we contrast a latitude/colatitude 2D parameterization (pCNN) and view aggregation scheme (p³CNN) with an SCNN architecture [2] for semantic segmentation. For comparability, all networks are implemented with a consistent architecture, i.e. four encoding-decoding layers, same loss function, and equal number and dimension of convolutional kernels. All architectures are trained with a batch-size of 16 and an initial learning rate of 0.01 which is reduced every 20 epochs (γ = 0.9). After implementation in PyTorch all models are trained until convergence on one (p³CNN) or eight (ugscnn) NVIDIA V100 GPUs to allow the aforementioned batch-size while maintaining comparability.

Longitude/colatitude spherical parameterization

Original signals, such as thickness, curvature and the cortical labels are defined on the left and right WM surfaces of each subject. First these surfaces are mapped to the sphere via a distortion minimizing inflation procedure [1]. We then map the cortical surface signals to a grid (i, j) in a 2D parameter space with 512 × 256 pixels (equal to 131072 vertices on the original sphere). To this end, we employ a longitude/colatitude coordinate system where each vertex position on the sphere (x, y, z) can be described by (i) the azimuthal angle φ ∈ [0, 2π], (ii) the polar angle θ ∈ [0, π] and (iii) the radius r=100 via the spherical parameterization:

$$x=r\sin \phi \cos \theta ,y=r\sin \phi \sin \theta ,z=r\cos \phi$$ (1)

When sampling the (φ, θ) parameter space to the (i, j) grid, to avoid singularity issues at the poles, we shift the corresponding angles θ by half the grid width. After the transformation step, we sample the signal of interest (thickness, curvature or label map) at the given coordinates on the left and right hemisphere and project it onto the 2D parameter grid. The resulting parameter space “images” can then be fed into the multi-modal 2D deep learning segmentation architecture.

Parameter Space CNN (pCNN)

We use a DenseUNet [3] where each dense block consists of a sequence of three convolution layers with 64 kernels of size 3x3. Between the blocks, an index preserving max-pooling operation is used to half the feature map size. To enforce spherical topology while still permitting the use of standard convolution operations without loss of information at the image borders, we use a circular longitude padding. Prior to each convolution the left and right image borders are extended with values from the opposite side to provide a smooth transition. The horizontal borders are padded by splitting them in half and mirroring about the center (sideways) thereby modeling the transition across the poles. All networks are trained with two channels: thickness and curvature maps, which provide a representation of the underlying geometry of the cortex and are useful to e.g. locate region boundaries inside the sulcii.

View-Aggregation (p³CNN)

Due to the unequal distribution of grid points across the sphere in the longitude/colatitude parameterization, cortical regions mapping to the equator are less densely represented as those at the poles. Thus, segmentation accuracy may vary depending on the location of a given structure. To alleviate this problem, we propose to rotate the grid such that the poles are located along the x-, y- and z-axis, respectively. We then train one network per rotation and aggregate the resulting probability maps: (i) First, the label probabilities of each network are mapped to the original WM spherical mesh by computing a distance-weighted average of the three closest vertices on the sphere to each target vertex. (ii) Then, the three probability maps are averaged on a vertex-by-vertex basis to produce the final label map.

Due to the view aggregation across three parameter spaces, we term this approach p³CNN.

Spherical CNN

The ugscnn [2] is selected for comparison with a geometric approach. Therein a linear combination of parameterized differential operators weighted by a learnable parameter represents the convolutional kernel. To allow well-defined coarsening of the grid in the downsampling step, the spherical domain is approximated by an icosahedral spherical mesh. Here, we use an icosahedron of level 7 as the starting point (163842 vertices) to approximate the original FreeSurfer sphere (average number of vertices: 132719) as close as possible.

Mapping

The cortical thickness signal, the curvature maps and class labels defined in the subject’s spherical space need to be mapped to the respective mesh architectures for both networks (i.e. icosahedron or polar grid). This is achieved via a distance weighted k-nearest neighbor regression and classification (i.e. majority voting). Equivalently, the final network predictions are mapped back to the subject’s spherical space using the same technique. All evaluations are then performed in the original subject space, i.e., on the WM surface where the ground truth resides.

2.2. Evaluation

Surface-based Dice Similarity Coefficient

We evaluate the segmentation accuracy of the different models by comparing a surface-based Dice Similarity Coefficient (DSC) in the subject space on the original brain surface. With binary label maps of ground truth G and prediction P (1 at each labeled vertex, 0 outside), we modify the classic DSC as follows:

$$DSC(\mathit{G},\mathit{P})=\frac{2area(\mathit{G}\cap \mathit{P})}{area(\mathit{G})+area(\mathit{P})},area(\mathit{X})=\underset{M}{\int }\mathit{X}{d}_{\sigma }={\mathit{a}}^T\cdot \mathit{X}$$ (2)

where ∩ is the element-wise product, and the area of a binary label X is its integral on the underlying Riemannian manifold M (here triangulated surface) which can be computed by the dot product of X and a where $a_i=\frac{1}{3}\sum T_i$, i.e. a third of the total area of all triangles T_i at vertex i. The DSC ranges from 0 to 1, with 1 indicating perfect overlap and 0 no similarity between the sets.

3. Results

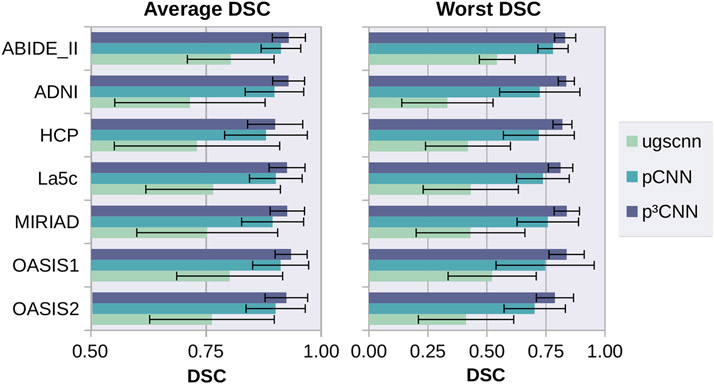
We use five publicly available datasets (La5c [4], ADNI [5], MIRIAD [6], OASIS [7], ABIDE-II [8]) to train and evaluate our models. In total, 160 subjects balanced with regard to gender, age, diagnosis, and MR field-strength are used for training and 100 subjects for validation. Finally, we use 240 subjects from the Human Connectome Project (HCP) [9] as a completely independent testing set to measure segmentation accuracy. In our experiments, we utilize FreeSurfer [1] annotations of the cortical regions according to the ”Desikan–Killiany–Tourville” (DKT) protocol atlas [10] as ground truth (see Fig. 1). Figure 2 represents the average (left) and worst (right) DSC across all 32 cortical regions evaluated on the test and validation set and pooled across hemispheres. The spherical CNN (green) reaches the lowest DSC for all five datasets with an average DSC of 0.76. Introduction of our spherical parameterization approach (light blue, pCNN) already outperforms the spherical CNN (green) with an up to 0.18 DSC point increase. Note, that this improvement is already achieved in spite of the non-linear distortions induced by the latitude/colatitude parameterization. The view aggregation approach (dark blue, p³CNN) further increases the segmentation accuracy and reaches the highest DSC for all six datatsets (all above 0.9). Further, our proposed method improves the consistency of the segmentation accuracy. The p³CNN has the lowest variation in segmentation accuracy across subjects with a standard deviation of below 0.06 for each dataset (0.18 for ugscnn and 0.09 for pCNN). Notably, pCNN enhances the average lowest DSC score observed in the test set by up to 0.4 DSC points (see Figure 2, right side). This indicates that we do not only improve the average performance of the model but also raise the prediction accuracy on error-prone regions and subjects. As for the average DSC, aggregating the different views of the latitude/colatitude parameterization (p³CNN) surpasses the pCNN approach raising the average worst DSC by another 0.1 DSC point. Interestingly, the variation across subjects is much lower when using view aggregation compared to the single view network. Here, p³CNN stays within the same range observed for the average DSC (0.03 to 0.08) whereas the pCNN is less consistent (0.06 to 0.21). Possibly, errors introduced by unequal sampling at the pole and equator regions are compensated by inclusion of information from the other two views in which the structures might be more evenly sampled (different local attention).

Fig. 2.

Average (left) and Worst (right) DSC across the test sets. Highest accuracy is achieved for latitude/colatitude parameterization with view aggregation (p³CNN).

4. Discussion

We introduce a novel method for cortical segmentation of spherical signals and compare it to a spherical-CNN for semantic segmentation. The presented approach is expected to generalize to other surface-based segmentation tasks. We showed that our view aggregation of spherical parameterizations (p³CNN) achieves a high average DSC of 0.92 for cortical segmentation and outperforms spherical CNNs. Geometric deep learning is still in its infancy and holds great potential for further optimizations. Yet, the promise of a non-distorted operating space is counter-balanced by high computational demands and challenging definitions of pooling and convolution operations. Furthermore, network architectures for 2D segmentations have improved significantly in the recent years, while spherical approaches are still lacking many of these innovations. Therefore, we recommend comparing all novel spherical or geometric CNN approaches not only to existing geometric methods but more importantly to view-aggregating 2D segmentation networks in the spherical parameter space as a baseline.