Assessment of the Components of the Electrostatic Potential of Proteins in Solution: Comparing Experiment and Theory

Abstract

In this work, the components of the protein electrostatic potentials in solution are analyzed with NMR paramagnetic relaxation enhancement experiments and compared with continuum solution theory, and multiscale simulations. To determine the contributions of the solution components, we analyze them at different ionic strengths from 0 to 745 mM. A theoretical approximation allows the determination of the electrostatic potential at a given proton without reference to the protein structure given the ratio of paramagnetic relaxation enhancements rates between a cationic and an anionic probe. The results derived from simulations show good agreement with experiment and simple continuum solvent theory for many of the residues. A discrepancy including a switch of sign of the electrostatic potential was observed for particular residues. By considering the components of the potential, we found the discrepancy is mainly caused by angular correlations of the probe molecules with these residues. The correction for the correlations allows a more accurate analysis of the experiments determining the electrostatic potential of proteins in solution.

Graphical Abstract

INTRODUCTION

Experimental determination of the electric potential and field around proteins is an important challenge. Recently, Yu et al.¹ introduced an NMR-based method to measure near-surface electrostatic potentials for individual protein residues without chemically attaching probes or using structural information. In this method, paramagnetic relaxation enhancements (PRE) arising from analogous oppositely charged paramagnetic probes are determined for ¹H nuclei of a protein. The electrostatic potentials near the molecular surface proximal to the observed ¹H nuclei are then determined from the ratio of PRE rates reflecting different spatial distributions of cationic and anionic probes around the biomolecules. The measured potentials at ionic strengths of 30 and 130 mM agree reasonably well with the theoretical predictions of the Poisson−Boltzmann (PB) equation using a standard fixed charge model. The root-mean-square deviation (RMSD) between the experimental and theoretical values was about 6 mV for secondary structure regions.¹ A few discrepancies, including a change of sign, at certain residues existed, which limits the possible uses of the analysis.

The approximations made to allow for a structure-independent analysis of the ratio of paramagnetic relaxation rates1 in principle can be relaxed. The components contributing to the electrostatic fields can be separated theoretically and considered in terms of both chemical components and how they are affected by various approximations. The PRE experiments can be analyzed with preexisting structures to aid in considering the origin of the discrepancies. Questions of whether protein conformational flexibility, the proximity approximation used in the analysis, or even the underlying simulation force field might cause differences between theory and experiment are considered here. The experimental determination of the protein electrostatic field has the potential to validate and ultimately improve theoretical model force fields which are in wide use.^2–5

The electrostatic potential generated by a molecular system can not only be employed to describe many of the molecular properties but also used to interpret intermolecular interactions related to mechanism.^6,7 Once average atomic charges are determined, the application of Coulomb’s law is a straightforward pairwise additive form; the long-ranged nature of the electrostatic field, however, can present a variety of challenges in implementation and interpretation for a given computational method. As a result, many approximations which are computationally convenient exist. One of the most widely used methods for modeling biomolecular electrostatics is the PB method which assumes that the mobile ions in a system follow the Boltzmann distribution in a continuum solvent as point charges.^8,9 However, the PB method has well-known limitations when ion correlations exist and/or highly charged molecules are involved.

Simulation of a polar molecule in explicit water molecules and ions usually relies on approximate methods to ensure or force convergence of the electrostatic properties. Commonly, electrostatic potentials can be derived from reaction fields^10–12 or the Ewald summation method^13,14 using a periodic boundary condition. The Ewald sum decomposes the potential into two parts: a short-ranged real space part (computed in a unit cell) and a long-ranged Fourier space part (computed for image cells). The task of computing the electrostatic potential is still the most time-consuming part of any explicit all-atom simulation. Fortunately, many techniques (e.g., particle mesh Ewald method,¹⁵ the fast multipole method,¹⁶ fast Fourier transforms,¹⁷ etc.) have been applied to accelerate the calculations for particular conditions and size ranges.

Experimentally, the molecular potential can be derived, in principle, from X-ray or electron diffraction by fitting a multipolar density function to the data.¹⁸ The method requires availability of very high-resolution data (as is the possible case with some inorganic materials). As a result, it is not applicable to most chemical compounds and biomolecules. Another experimental method is vibrational spectroscopy,¹⁹ which utilizes the sensitivity of vibrational transitions to electric fields (the Stark effect) to provide a local probe of electrostatic fields in systems such as proteins. However, the approach provides only limited information and requires covalently attached probes, which may perturb the native conformation of some systems. Inferences can also be made from ion counting and similar experimental methods.²⁰ Historically, pK_a data have often been used to examine electrostatic models.^21,22 In the past decade, there was significant progress in experimental pK_a measurements for protein side chains.^23,24 However, pK_a data do not explicitly report electrostatic potentials or fields. Thus, the NMR PRE ratio method has advantages over other experimental methods for biomolecular electrostatics.

Here we apply the PRE ratio method to analyze the components of the electric potential of ubiquitin with and without prior knowledge of a protein structure. In the analysis of the experimental data, we include aspects of the known structure of ubiquitin in a multiscale computational approach and thus eliminate many of the approximations used in the previous analysis. Direct calculations of PREs for a protein are problematic due to the inverse sixth power dependence on the distance between the probe and a hydrogen on the protein. We adopt a multiscale computational strategy combining molecular dynamics (MD) simulations and Brownian dynamics (BD) simulations on the fields from MD calculated with a well-known potential model²⁵ to evaluate terms in the theoretical analysis of the experimental data. We test the effectiveness and accuracy of the approximations and methods of analysis in determination of electrostatic potentials in the near-surface zone of ubiquitin in total ionic strengths up to 745 mM. We explore the discrepancy of the potentials between the experiment and simple model computations by studying possible effects on the interpreted potentials from sources including protein conformational flexibility and correlations with mobile ions, water, and charged probe orientations.

THEORY

The PRE rate arising from paramagnetic cosolutes for a transverse ¹H magnetization (Γ₂) previously derived is^1,26

$${\mathrm{\Gamma }}_2=\xi c_{\text{p}}{\tau }_{\text{c}}\langle r^{-6}\rangle =4\pi \xi c_{\text{p}}{\tau }_{\text{c}}{\int }_0^{\infty }{r}^{-4}\exp \left[-\frac{W(r)}{k_{\text{B}}T}\right]\text{d}r$$ (1)

where ξ is a parameter involving ¹H nuclei of a given protein and electron gyromagnetic ratios (see ref 1 for explicit expression), c_P is the concentration of the paramagnetic probe, τ_c is the effective correlation time for the dipole–dipole interaction between the probe’s unpaired electron and the ¹H nucleus, r is the distance between the paramagnetic center of the cosolute and the ¹H nucleus, ⟨r⁻⁶⟩represents the ensemble average of r⁻⁶, W(r) is the angle-averaged potential of mean force between the probe cosolute and the ¹H nucleus along r, k_B is the Boltzmann constant, and T is the absolute temperature.

The integral in eq 1 may be discretized on a three-dimensional (3D) lattice grid surrounding the macromolecule:¹

$${\mathrm{\Gamma }}_2=\xi c_{\text{p}}{\tau }_{\text{c}}\sum _i{r}_i^{-6}\exp \left[-\frac{W_i}{k_{\text{B}}T}\right]\mathrm{\Delta }\nu$$ (2)

where i indexes the grid points around the solute to be probed and Δv is the volume of the voxels.

Since only the distance between the unpaired electron in the spin probe and the nucleus being excited is required, one could employ a simple spherical model of the probe tuned to obtain the distance dependence.¹ The spin probe usually has nontrivial orientational correlations with the target molecule, which in part affects the potential of mean force or distribution function with respect to distance from the solute. Thus, in some strongly correlated cases, the PRE interpretation may require the potential of mean force, W, with all degrees of freedom between the probe molecules and the target.

A complete model would consider the full complement of intermolecular interactions including the electrostatic interactions, the combination of which causes the correlations between the PRE probe molecule, solvent, and the protein solute. In general, two rigid bodies have six degrees of freedom between them. The full pair intermolecular probability distributions, $g=(\overrightarrow{r_1},\overrightarrow{r_2})$, are related to the potential of mean force W, which includes both the direct potential, U, and the indirect or solvent induced environmental influences, ΔW.

$$\begin{gathered} g(\overrightarrow{r_1},\overrightarrow{r_2})=g\left(r_{12},{\mathrm{\Omega }}_1,{\mathrm{\Omega }}_2\right)=\exp \left(-\beta W\left(r_{12},{\mathrm{\Omega }}_1,{\mathrm{\Omega }}_2\right)\right) \\ W\left(r_{12},{\mathrm{\Omega }}_1,{\mathrm{\Omega }}_2\right)=U\left(r_{12},{\mathrm{\Omega }}_1,{\mathrm{\Omega }}_2\right)+\mathrm{\Delta }W\left(r_{12},{\mathrm{\Omega }}_1,{\mathrm{\Omega }}_2\right) \end{gathered}$$ (3)

in which the subscript “1” denotes the target (here a protein), the subscript “2” denotes other solvent species such as the probe molecules, β is 1/k_BT, and Ω_i represents the orientation of the molecules. We note that while U may be a straightforward pairwise additive form as often found in molecular mechanics intermolecular potentials, the indirect contributions are generally not a simple sum over pairs of molecules.

From eq 1, we write

$$\begin{array}{l}{\mathrm{\Gamma }}_2\propto \int \frac{g\left(r,{\mathrm{\Omega }}_1,{\mathrm{\Omega }}_2\right)}{r_6}\\ \propto \int \frac{\exp \left[-\beta W\left(r,{\mathrm{\Omega }}_1,{\mathrm{\Omega }}_2\right)\right]}{r^6}\text{d}v\\ \cong \sum \frac{\exp \left[-\beta W\left(r,{\mathrm{\Omega }}_1,{\mathrm{\Omega }}_2\right)\right]}{r^6}\mathrm{\Delta }v\end{array}$$ (4)

Integrating over the angles modifies the probability distribution with respect to the distance r versus a system with no angle dependence such as a sphere.

We may convert to a coordinate system which fixes the protein in a specific orientation at the origin. Probe orientations affect the distribution of distances, r, so we require the full six-dimensional distribution for probe molecules around the protein. We use a Cartesian grid around the protein (x, y, z), and at each spatial grid point, we have three Euler angles to fully describe the position and orientation of the molecules in the solvent (water, ions, and probes) with respect to the protein. Thus, eq 4 is reduced to

$${\mathrm{\Gamma }}_2\propto \int \frac{\exp \left[-\beta W\left(x,y,z,{\mathrm{\Omega }}_2\right)\right]}{r^6}\text{d}v$$ (5)

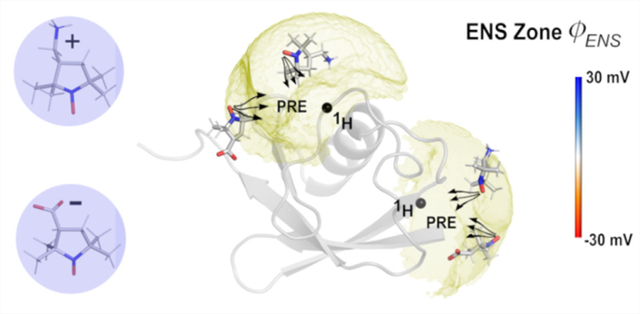
For a probe with nontrivial orientational correlations with the protein, we must sample the angular dependence at each grid point. The value of Γ₂ is proportional to the integral of the inverse sixth power of distance between the probe and the target nucleus, so the Γ₂ rate is dominated by terms in a zone close to the observed ¹H nucleus. We have referred to this as the effective near-surface (ENS) zone.¹ To consider the near-surface electrostatic potential, the experiment is run with two different probes of opposite charge. Then at any grid point surrounding the protein we can compute the ratio of the PRE rates of the cationic (+) and anionic (−) probes

$$\frac{{\mathrm{\Gamma }}_{2,+}}{{\mathrm{\Gamma }}_{2,-}}=\frac{{\sum }_{xyz,{\mathrm{\Omega }}_{+}}\exp \left[-\beta W_{+}\left(x,y,z,{\mathrm{\Omega }}_{+}\right)\right]/r_{+}^6\mathrm{\Delta }v}{{\sum }_{xyz,{\mathrm{\Omega }}_{-}}\exp \left[-\beta W_{-}\left(x,y,z,{\mathrm{\Omega }}_{-}\right)\right]/r_{-}^6\mathrm{\Delta }v}$$ (6)

In the case of assuming spherically shaped probes with a point charge,¹ the excluded volume effects in ΔW between probes and protein cancel by using an identical radius of exclusion in the sum. We define an effective cation potential of mean force, $\overline{W_{+}}$, in the near-surface proximity zone voxels ν_ENS as

$$\overline{-\beta W_{+}\left(r,{\mathrm{\Omega }}_{+}\right)}\equiv \ln C{\mathrm{\Sigma }}^{\prime }\exp \left(-\beta W_{+}\left(r_{+},{\mathrm{\Omega }}_{+}\right)\right)$$ (7)

where C is the normalization for the zone. If the potential of mean force is relatively constant within a given proximity zone (denoted with ′), which assumes that the effects of the averaged angular orientations are equal as well as the indirect potentials for both the cationic and anionic probe, then we obtain a simple approximation for the average electrostatic potential in the near-surface region

$$\begin{gathered} -{kT\ln \frac{{\mathrm{\Gamma }}_{2,+}}{{\mathrm{\Gamma }}_{2,-}}|}_{\text{ENS}}=\overline{W_{+}\left(r,{\mathrm{\Omega }}_{+}\right)}-\overline{W_{-}\left(r,{\mathrm{\Omega }}_{-}\right)} \\ \approx \overline{U_{+}\left(r,{\mathrm{\Omega }}_{+}\right)}-\overline{U_{-}\left(r,{\mathrm{\Omega }}_{-}\right)}=2e{\varphi }_{\text{ENS}} \end{gathered}$$ (8)

where $\overline{U}$ is the effective Coulomb potential energy between the probe and the protein in the effective near-surface zone, e is the elementary charge, and ϕ_ENS is the corresponding effective electrostatic potential. Only if the steric and indirect parts of the potential of mean force between the probes and the protein cancel does this approximation hold and allow a simple structure-free analysis of the underlying macromolecular electrostatics. This also assumes that the probe molecules, cation, or anion correlations with the protein hydrogens of interest are dominated by electrostatics. We can consider the dominant contributions of the indirect potential as the dielectric response of the solvent and ion screening.

Previous analysis of ϕ_ENS potentials showed good agreement for most residues of ubiquitin between the experiment and PB theory using simple spherical models for the probe molecule’s exclusion zone.¹ In this study, we raise the resolution and details of the calculations of electrostatic potential field using a multiscale simulation method. We evaluate the electric fields with MD simulations of ubiquitin in explicit solvent at the specified ionic strengths of the experiment. Then, we improve the calculations of ϕ_ENS potentials by considering the angular correlation between the probe molecule and ubiquitin, which can be accomplished by performing BD simulations on the fields produced in the MD simulations.

METHODS

Protein and Other Materials for NMR Experiments.

Chemical reagents were purchased from Sigma-Aldrich unless indicated otherwise. A pET-50b-derivative plasmid harboring a synthetic gene of human ubiquitin was purchased from GenScript. Escherichia coli BL21(DE3) cells were transformed with this plasmid and were cultured at 37 °C in minimal media containing 1 g/L ¹⁵NH₄Cl (Cambridge Isotope Laboratories) as the sole nitrogen source in the presence of 30 μg/L kanamycin. When the optical density at 600 nm reached 0.8 for the culture, 0.4 mM isopropyl β-d-1-thiogalactopyranoside (IPTG) was added to induce expression of ubiquitin. The culture was continued at 18 °C for 16 h. Ubiquitin (¹⁵N-labeled) was purified through the procedures of Sundd et al.²⁷ and additionally, through size-exclusion chromatography using a Sephacryl S-100 column (GE Healthcare) equilibrated by a buffer of 100 mM ammonium acetate at pH 7.0. The purified ¹⁵N ubiquitin was lyophilized and kept at −20 °C until use.

NMR Samples.

Solutions of 0.4 mM ¹⁵N ubiquitin in a buffer at pH 7.5 containing 20 mM acetate, 28 mM tris, 10 mM DMSO, 5% D₂O, and 0, 100, 300, or 700 mM KCl were prepared for the NMR experiments. Paramagnetic samples contained 10 mM 2,2,5,5-tetramethylpyrrolidine-N-oxyl nitroxide (PROXYL) derivative (either carboxy-PROXYL or amino-methyl-PROXYL) for the 0 and 100 mM KCl samples and 25 mM PROXYL derivative for the 300 and 700 mM KCl samples. The higher PROXYL concentration was chosen for the high ionic strength samples because PRE rates are smaller when electrostatic attraction of charged PROXYL molecules to the protein is weaker (see below). The PROXYL derivatives in stock solutions were quantified as previously described.¹ To ensure the expected concentration of the paramagnetic concentration, the PROXYL derivatives were added to the protein solutions at the final stage of sample preparation. For the NMR samples at 0 and 100 mM KCl, 0.5 mL of solution was sealed in standard 5 mm NMR tubes (Norell). To mitigate the adverse impact of high ionic strength on the sensitivity of NMR detection,²⁸ thinner tubes with an outer diameter of 4 mm (Wilmad; part no. 435-PP-7) together with a 4 mm spinner turbine (Wilmad; part no. B-PEEK-4-NS) were used for the NMR samples at 300 and 700 mM KCl (0.35 mL each).

NMR PRE Measurements.

PRE rates Γ₂ for ¹H transverse magnetizations were measured for protein backbone ¹H_N nuclei of ¹⁵N-labeled ubiquitin. For each molecular system, the PRE experiments were conducted with three samples: one without any paramagnetic cosolute (diamagnetic) and the others with carboxy-(anionic) or aminomethyl-PROXYL (cationic) for each. The two time-point approach²⁹ with a 10 ms difference was used to measure PRE Γ₂ rates. The uncertainty in the Γ₂ rate was estimated using the standard deviations of the noise σ_d and σ_p in the spectra for the diamagnetic and paramagnetic samples, as described.²⁹ All NMR experiments were carried out at 25 °C using a Bruker Avance III spectrometer equipped with a QCI cryogenic probe operated at the ¹H frequency of 600 MHz. The spectra were processed with the NMRPipe software.³⁰ Spectra were analyzed using the NMRFAM-SPARKY software.³¹ PRE rates were calculated using the MATLAB software (Math-Works).

Determination of Effective Near-Surface Electrostatic Potentials.

Effective near-surface electrostatic potentials, ϕ_ENS, for individual ¹H nuclei were determined from Γ_2,+ and Γ_2,− data using eq 8. The uncertainties in ϕ_ENS were estimated through error propagation ³² using

$${\sigma }_{\varphi }=\frac{k_{\text{B}}T}{2e}\sqrt{{\left({\sigma }_{+}/{\mathrm{\Gamma }}_{2,+}\right)}^2+{\left({\sigma }_{-}/{\mathrm{\Gamma }}_{2,-}\right)}^2}$$ (9)

in which Γ_2,+ and Γ_2,− are the experimental PRE rates from aminomethyl-PROXYL and carboxy-PROXYL, respectively; σ₊ and σ₋, the uncertainties in Γ_2,+ and Γ_2,− respectively. PRE rates with statistical significance were selected using the following criteria: Γ_2,+ > 3σ₊, Γ_2,− > 3σ₋, and ${\mathrm{\Gamma }}_{2,+}/{\mathrm{\Gamma }}_{2,-}>3\left({\mathrm{\Gamma }}_{2,+}/{\mathrm{\Gamma }}_{2,-}\right)\sqrt{{\left({\sigma }_{+}/{\mathrm{\Gamma }}_{2,+}\right)}^2+{\left({\sigma }_{-}/{\mathrm{\Gamma }}_{2,-}\right)}^2}$. Only PRE data satisfying these criteria were used for the determination of ϕ_ENS potentials. The ϕ_ENS data were analyzed using MATLAB scripts.

MD Simulations.

To calculate the electrostatic field around ubiquitin, four MD simulations of ubiquitin in 0, 130, 345, and 745 mM KCl salt solutions were carried out using NAMD 2.14 software³³ with the CHARMM36 force field parameter set.² The salt concentrations represent a total salt ionic strength including probes and excess salt in the experiment except for the 0 mM concentration used to check the theoretical limit of the field without salt screening. The probes were not explicitly simulated but simply counted as salt, because it would be computationally inconvenient to obtain sampling convergence of the full angularly dependent spatial correlations by direct MD simulation due to the small number of probe molecules and their slow translational and rotational diffusion combined with the inverse sixth power dependence on the distance.¹ In each simulation, the initial structure of ubiquitin (Protein Data Bank (PDB) code: 1UBQ) was solvated in a box ~58.0 Å on a side containing ~6200 TIP3P³⁴ water molecules. Because ubiquitin itself has no net charge, one simulation was set up in the absence of salt as a control. In the other three simulations, K⁺ and Cl⁻ ions were randomly added to set the expected ionic strength. The resulting systems contain about ~20K atoms. The details of the systems are listed in Table S1.

Particle mesh Ewald¹⁵ was used to calculate the long-range electrostatic interactions, and van der Waals interactions were truncated at 12 Å. All bonds were constrained using the SETTLE algorithm³⁵ with a time step of 2 fs. The temperature was controlled with Langevin dynamics with a damping coefficient of 5 ps⁻¹. The Nosé–Hoover method^36,37 with a Langevin piston was used to maintain a pressure of 1 atm. After energy minimization, the ubiquitin systems were first heated from 0 to 298.15 K, then equilibrated in the NPT (constant pressure) ensemble for 20 ns, from which one snapshot with a temperature close to 298.15 K, and a pressure close to 1 atm was chosen as the starting step for the production run in the NVT ensemble.

In the production runs, we removed the translation and rotation of the protein by introducing two collective variable restraints by means of harmonic potentials with the corresponding force constants for the positional restraint of ubiquitin as k_r = 1000 kcal/(mol·Å²) and orientation of ubiquitin as kΩ = 2000 kcal/(mol·deg²). All the simulations were run for ~1.0 μs, and the trajectories were saved at an interval of 1 ps for analysis.

Electrostatic Potential Calculations.

To obtain the near-surface electrostatic potential for each residue of ubiquitin, we first calculated the electrostatic potentials on 3D grid points with a grid spacing 0.5 Å. From MD simulations, the electrostatic potential at any grid point (grid potential) was calculated using the standard Ewald summation^13,14 (see the details in the Supporting Information). This avoids the problem of cutoffs in the electrostatic potential at the expense of a slight computational complexity. Sampling in the simulation reveals the time scales needed for convergence. Autocorrelation analysis of the time dependence of the backbone RMSDs of the protein from the MD simulations produces a decay time of ~50 ns. Potentials and the protein structure were calculated and averaged in several 50 ns blocks. The final grid potentials were averaged over the simulation production time. For comparisons, grid potentials from the PB theory were obtained by solving the full PB equation using APBS package⁹ on the MD structures on the same resolution grid.

Brownian Dynamic Simulations.

Brownian dynamics simulation was used to sample the correlations of a fully atomistic paramagnetic probe molecule with the protein. With the protein fixed at the origin, we allowed the probe molecule to move relative to the protein in the electrostatic potential field generated from the MD simulation at a given ionic strength. The locations and orientations of the probe molecule were collected from BD trajectories. In this way, the probe molecule spatial and orientational sampling is performed in a preaveraged field of the solvent. This allowed us to calculate the Boltzmann-weighted effective potential energies between the probe molecule and the protein. We note that due to the multidimensional nature of the angular correlations many forms of enhanced sampling would not be as efficient as the multiscale route chosen here using a precomputed solvation field from MD simulations sampled by BD.

For the protein structure in the BD simulations, we used an averaged structure from the MD simulation. The model structures of amino-methyl-PROXYL and carboxy-PROXYL were built and optimized using Avogadro software³⁸ by modifying the structures of reduced analogs (Zinc409214 and Zinc156924, whose chiral carbon atoms are in the S-enantiomeric form, from the Zinc database),^39,40 respectively. The parameters pertaining to the nitroxide moiety were taken from a quantum chemical study of nitroxide systems⁴¹ and CGenFF3.0.1.^42,43 The structures and partial charges of aminomethyl-PROXYL and carboxy-PROXYL are shown in Figure 1.

Figure 1.

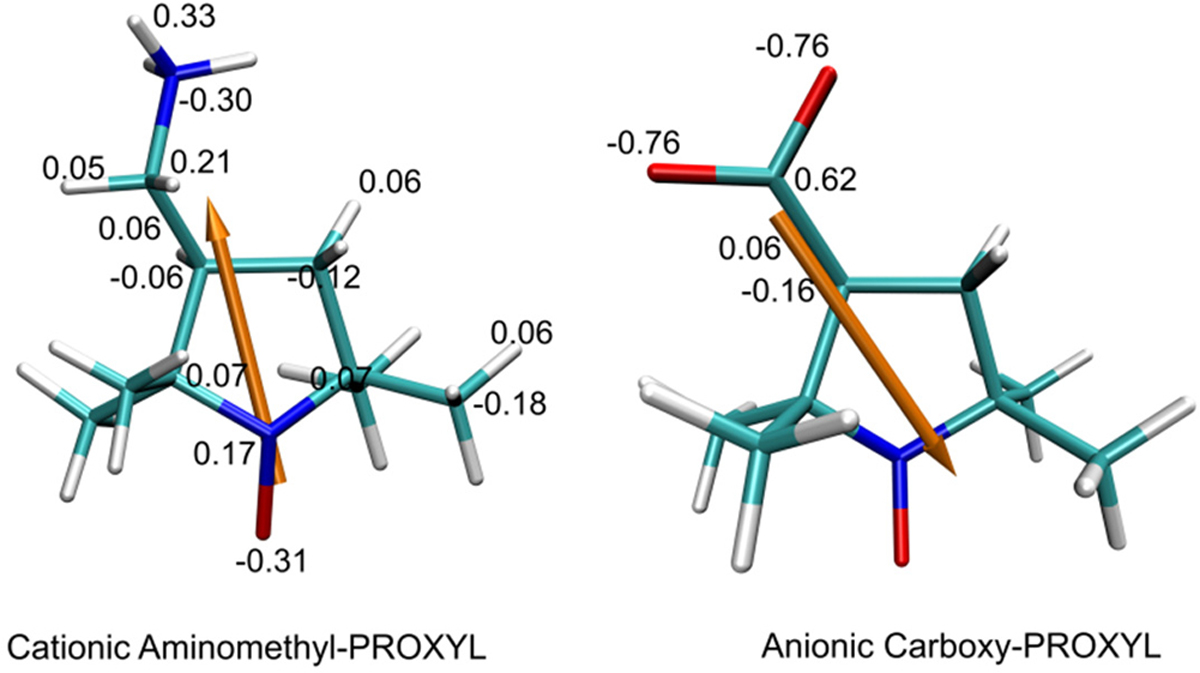
Structures and partial charges of amino-methyl-PROXYL and carboxy-PROXYL, respectively. The atoms are rendered in red for O, blue for N, cyan for C, and white for H. The orange arrow demonstrates the direction of the dipole of each probe molecule with respect to the center of charge.

We modified the software package SDA4.23⁴⁴ to perform BD simulations. Only the electrostatic and repulsive exclusion forces were considered. The translational diffusion coefficient was 1.49 × 10⁻⁶ cm²/s for ubiquitin⁴⁵ and 5.2 × 10⁻⁶ cm²/s for each probe.¹ The rotational diffusion coefficients were estimated to be 4.344 × 10⁻⁵ radian/ps for ubiquitin and 1.850 × 10⁻³ radian/ps for each probe from the Stokes−Einstein relations. Each run of the BD simulations starts with the probe randomly placed and oriented at a center-to-center distance of 40 Å and is terminated when the probe moves outside of a center-to-center distance of 60 Å. The time step was 2.0 ps when the distance is <30 Å and then increased linearly with a slope of 0.45 ps/Å until the probe molecule reached 60 Å. Other details of the BD simulation have been described previously.²⁵ We carried out 20 million such BD runs here to collect averages for our analysis.

RESULTS

ϕ_ENS Potentials Determined from NMR Experiments.

According to eq 8, the ϕ_ENS potentials for the backbone ¹H_N nuclei of ubiquitin at 0, 100, 300, and 700 mM KCl were determined by measuring the Γ_2,+ and Γ_2,− data from NMR experiments for ¹⁵N-labeled ubiquitin. Due to ionic components other than K⁺ and Cl⁻ ions, the overall ionic strengths of the analyzed samples were 30, 130, 345, and 745 mM. The ¹H−¹⁵N HSQC spectra recorded for ubiquitin at different KCl concentrations were similar, though ¹⁵N chemical shifts systematically increased upon an increase in the KCl concentration (Figure S1). In our previous study, PRE rates Γ_2,+ and Γ_2,− for ubiquitin at 0 and 100 mM KCl were measured using 10 mM PROXYL derivatives.¹ In the current study, the Γ_2,+ and Γ_2,− rates at 300 and 700 mM KCl were measured using 25 mM PROXYL derivatives. The higher concentration of paramagnetic probes was chosen for those salt concentrations because the PREs arising from the charged PROXYL derivatives are smaller at higher ionic strength due to weaker electrostatic attraction. The Γ_2,+ and Γ_2,− data are shown in Figure 2A (see also Tables S2 and S3). Differences between Γ_2,+ and Γ_2,− rates (|Γ_2,+ − Γ_2,−|) were generally smaller for 700 mM KCl, suggesting that abundant mobile ions considerably attenuate the electrostatic bias in the spatial distribution of charged probes around the protein.

Figure 2.

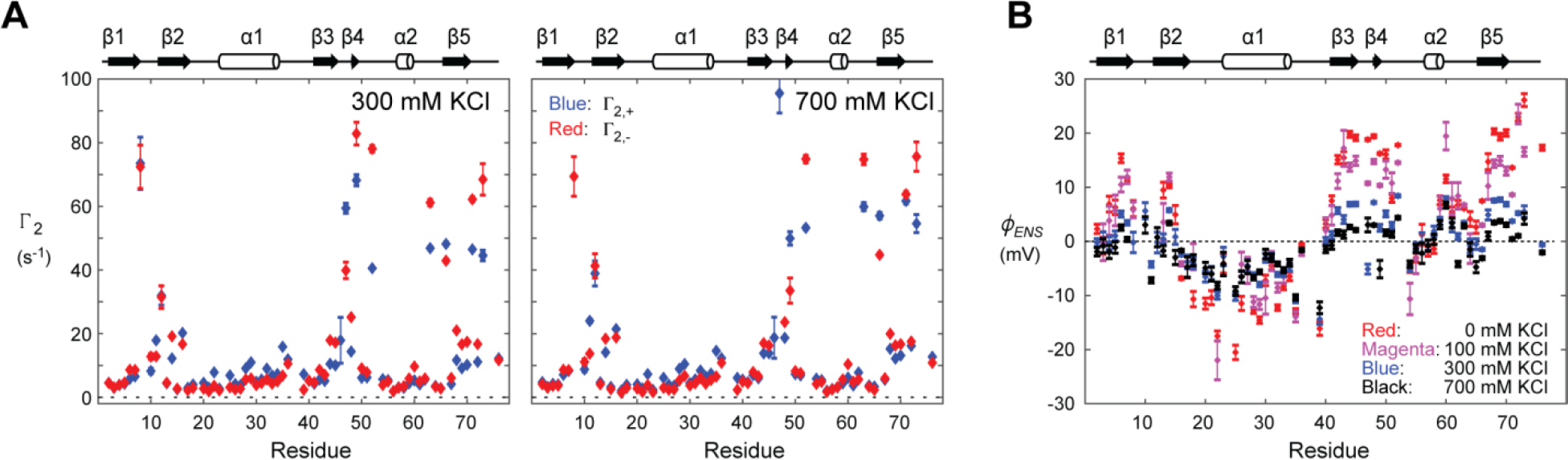
Experimental data of ϕ_ENS potentials measured for ubiquitin at various ionic strengths. (A) PRE rates Γ_2,+ and Γ_2,− for ubiquitin at 300 and 700 mM KCl. (B) ϕ_ENS potentials measured for backbone H_N atoms of ubiquitin at 0, 100, 300, 700 mM KCl.

For the determination of ϕ_ENS potentials, only PRE rates that are statistically significantly larger than zero (i.e., Γ_2,+ > 3σ and Γ_2,− > 3σ) were used. The ratio Γ_2,+/Γ_2,− should also be statistically significant and satisfy the condition indicated in the “Methods” section above. We found that these criteria are more difficult to satisfy at higher ionic strengths because of smaller PRE rates and lower NMR sensitivity at higher ionic strengths. The use of a higher concentration (25 mM) of the PROXYL derivatives was helpful to obtain a larger number of PRE data which satisfy the criteria for the analysis of ϕ_ENS potentials at 300 and 700 mM KCl. As shown in Figure 2B, the NMR-derived data show that the overall magnitude of ϕ_ENS potentials decreases upon an increase in ionic strength, clearly reflecting the electric-field screening effects by mobile ions.⁴⁶

ϕ_ENS Potentials from MD Simulations.

The ϕ_ENS potentials for individual residues were determined for comparison with previous work¹ using a spherical probe model with a radius of 3.5 Å. This optimal probe radius previously gave the least discrepancy between experiment and PB calculations using a crystal structure at low salt concentrations.¹ Generally the structures of ubiquitin are stable and insensitive to the different ionic strengths used here (see details in the Supporting Information).

We wish to probe the electrostatic field of a protein in an aqueous saline solution. The electrostatic potential at a point in space is caused by all charges in the system. We decomposed the ϕ_ENS potentials into two major components: one contributed from the protein itself and another contributed from the mobile ions, as shown in Figure 3A. The results show that the protein components are essentially the same within the statistical errors in different ionic strength solutions, reflecting the structural similarity and stability of the protein backbone structure over a range of solution conditions. In addition, this stability indicates that side-chain movements and low-populated conformational states have little influence on the ϕ_ENS potential. As expected, the ionic components of the ϕ_ENS potentials are anticorrelated with the protein component, reflecting the known screening effects of the ions on the field from the protein. We note that the protein electrostatic potential at 0 mM ionic strength, shown in Figure 3B, reflects the actual potential of our molecular mechanics model of ubiquitin without approximation. The salt screening effect becomes stronger as the ionic strength increases, consistent with the experimental observation. Including the solvent component, the contribution from all charges to the field is small and nearly featureless at this probe size, indicating that the major dielectric effects of water cancel in the ratio of eq 8 (Figure S3).

Figure 3.

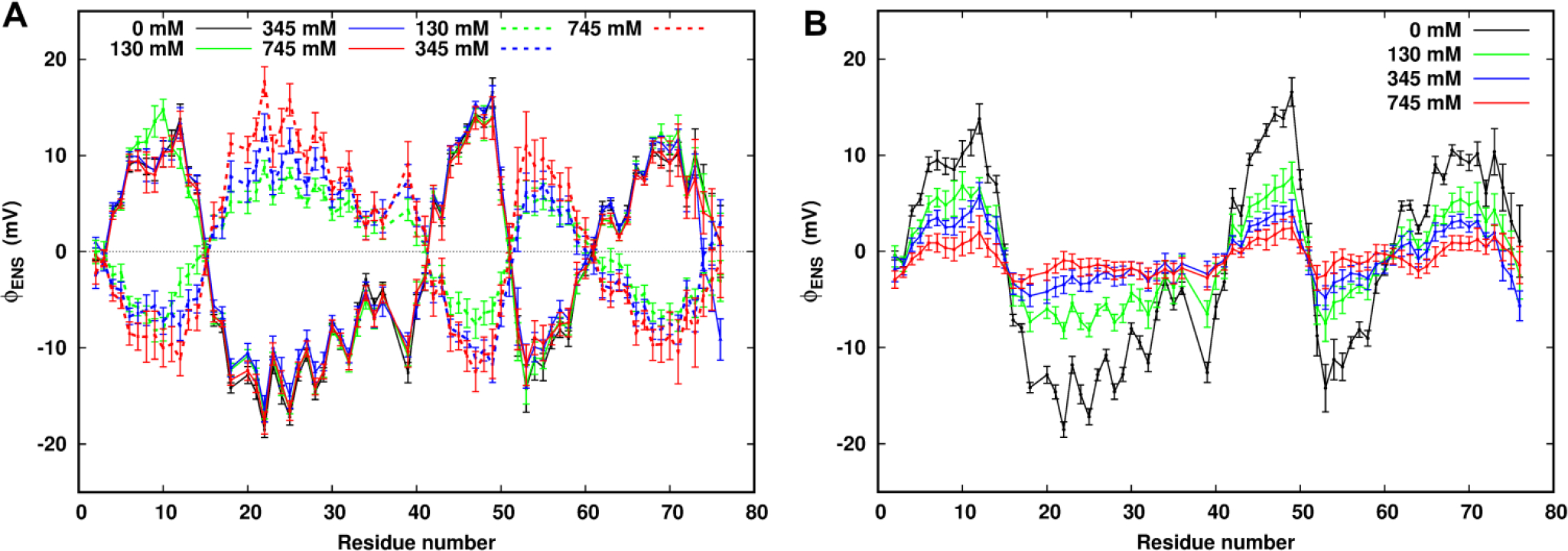
MD-derived ϕ_ENS potentials for individual residues using a spherical probe with a radius of 3.5 Å at different ionic strengths. (A) ϕ_ENS potential components from the charges of the protein (solid line) and from the mobile ions (dash lines). (B) Total ϕ_ENS potentials summed from the ϕ_ENS potential components from the protein and the mobile ions.

Comparison of the MD-derived results with the NMR experimental and the continuum PB potentials at 130 mM ionic strength (Figure 4A) shows that all curves of the total ϕ_ENS potentials follow a similar trend. We found that the MD potentials are somewhat smaller in magnitude by using the PB optimal probe size of 3.5 Å. Examination of the grid potentials around the protein (Figure S4) illustrates that the majority of the places having high magnitude potentials in the neighborhood of the protein atoms are excluded in the calculations of ϕ_ENS potentials with such a large model probe. As a result, only positions having smaller magnitudes of potentials from the MD simulations are summed with the large probe size that best fits the experiment from the PB calculations.

Figure 4.

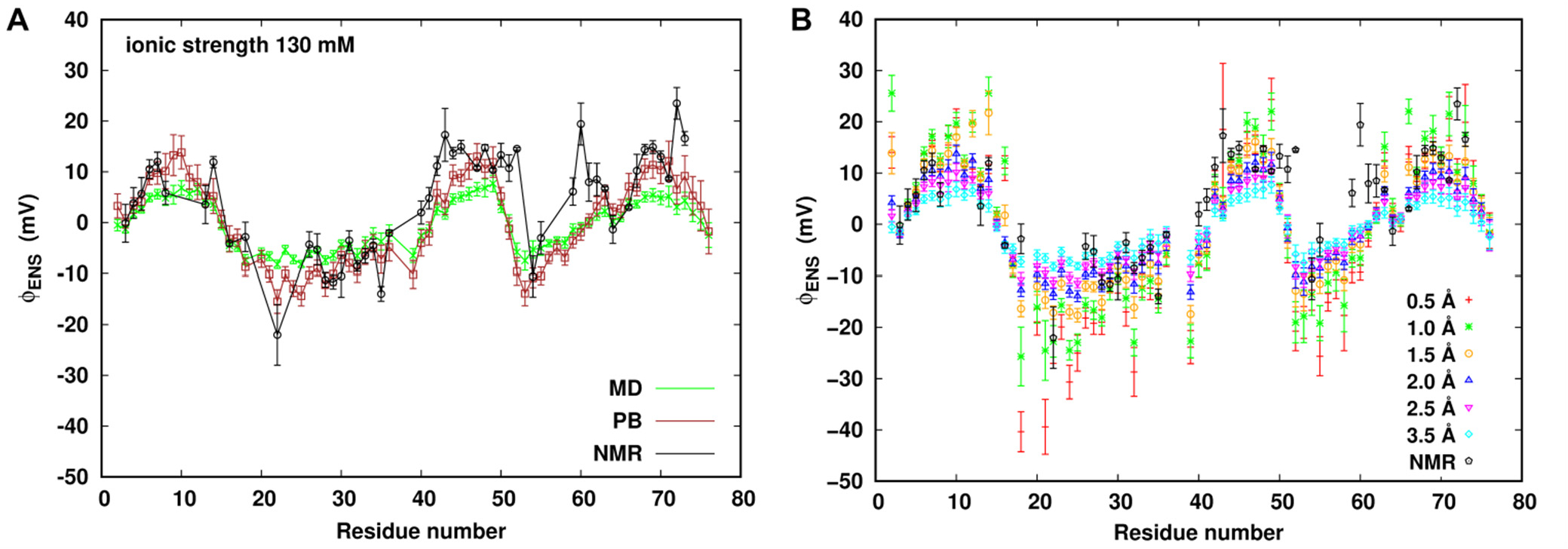
At 130 mM ionic strength, (A) a comparison of NMR-derived ϕ_ENS potentials with MD- and PB-derived ϕ_ENS potentials using the probe radius of 3.5 Å. (B) MD-derived ϕ_ENS potentials dependence on the probe size compared with experiment at 130 mM ionic strength.

To further understand effects of spherical probe size on the calculated ϕ_ENS potentials from explicit MD simulations, we calculated the ϕ_ENS potentials using probes of radius from 0.5 to 3.5 Å, as shown in Figure 4B. We found that the unphysically smaller probe models sense stronger potential fields near the protein especially in crevices. However, in comparison with experiment the electrostatic correlations with the spherical probe model are apparently underestimated at the larger model probe radii for most residues. In addition, probe size adjustment over the range given does not improve the agreement between simulation and experiment with certain outlier residues.

Given the dependence of ϕ_ENS potentials on probe size, we considered the fit of probe radius between simulation with experiment. We found that an effective probe radius between 1.5 and 2.0 Å produces MD potentials in better agreement with the experimental results than the larger probe sizes shown in Figure 4B. The difference in probe size required to fit the data is apparently due to the difference in the potential field produced by correlations in explicit solvent which are averaged or absent in the PB calculations.

Salt Dependence Comparison of ϕ_ENS Potentials.

Figure 5 shows the comparison of the experimental ϕ_ENS potentials with both MD and the PB values at 130 and 745 mM ionic strength. In this comparison, potentials derived from the MD simulation use a probe radius of 2.0 Å, and those from the PB theory use a probe radius of 3.5 Å. The comparison of ϕ_ENS potentials in KCl-free solution and 345 mM ionic strength are displayed in Figure S5.

Figure 5.

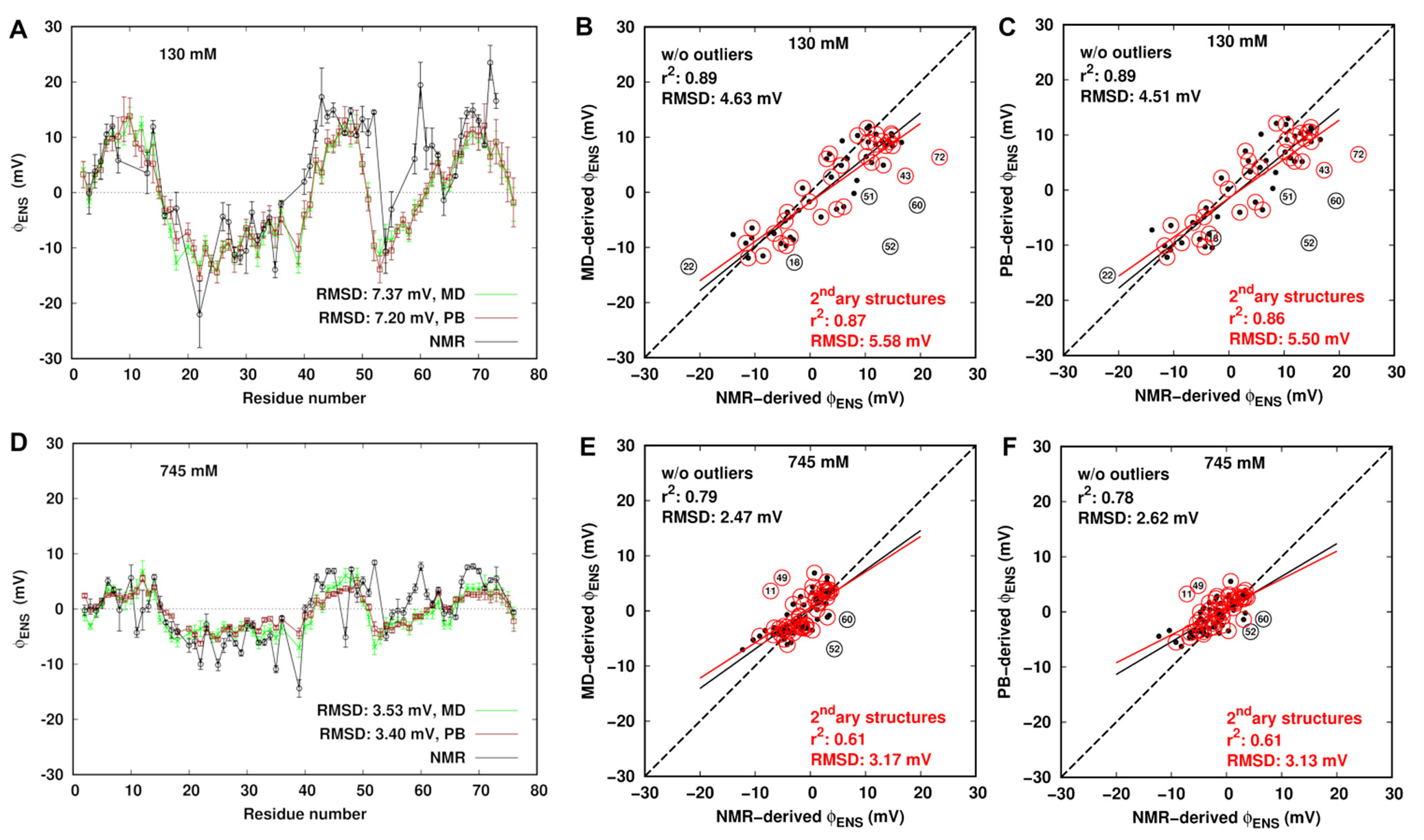
(A, D) Comparison of ϕ_ENS potentials derived from NMR, MD simulation and PB theory at ionic strengths of 130 and 745 mM, respectively. (B, C, E, and F) Correlation plots comparing the NMR-derived ϕ_ENS potentials and the MD- and PB-derived ones at ionic strengths of 130 and 745 mM. The outliers are labeled. The black dots represent ϕ_ENS for the residues excluding the outliers. The red circles represent data for the residues in the secondary (secondary) structure region. The black and red solid lines represent linear regression on data points without outliers and the residues in the secondary structure, respectively. The dash line indicates predicted ϕ_ENS = NMR-derived ϕ_ENS.

Generally, the computed results show the same trends in all ionic strength solutions and are in good agreement (Figure 5A,D). The RMSD in ϕ_ENS potentials between experiment and MD simulation is 7.37 mV with the correlation coefficient of r² = 0.77 at 130 and 3.53 mV with r² = 0.58 at 745 mM. As the ionic strength increases, the correlation diminishes slightly. The correlation plots comparing the NMR- and MD-derived ϕ_ENS data show that the RMSD between them is 5.58 mV with r² = 0.87 for secondary structure regions of ubiquitin at 130 mM (Figure 5B) and 3.17 mV with r² = 0.61 at 745 mM (Figure 5E). Correlations between the NMR-derived ϕ_ENS potentials and the computed ones are improved when only the residues in the secondary structure are considered resulting in smaller RMSD and higher r² than using the entire original data set. Such improvement was also found in comparison between the experiment and PB theory (Figure 5C,F). Moreover, slightly better improvement is obtained if some outliers are removed from the original data points. Among these outliers, there exists a change of a sign between the calculated potentials and the experimental ones for several individual residues. The ϕ_ENS potentials of Asp52 and Asn60 are positive in the experimental structure-free analysis, while they are negative in the MD and PB calculations in all four systems. In addition, the sign switch was also observed for Gln40 in the lowest salt solution and Lys11 at ionic strengths of 345 (Figure S5) and 745 mM.

Ubiquitin is known to have two stable conformations^47–49 (see details in the Supporting Information): State1 is close to the crystal structure, and State2 has some residues shifting from the positions in State1. Such a conformational change is not large enough to give rise to a sign flip in the potentials (Figure S5A), nor did we find evidence for any changes in the pK_a of the residues involved. We also found that trapping of water or mobile ions in cavities does not lead to the sign switch of ϕ_ENS potentials for the affected residues. The protein itself generates a substantial dipolar potential field (Figure 6). Interestingly, we found that the residues having a sign switch are located close to the boundary of the positive and negative potential regions.

Figure 6.

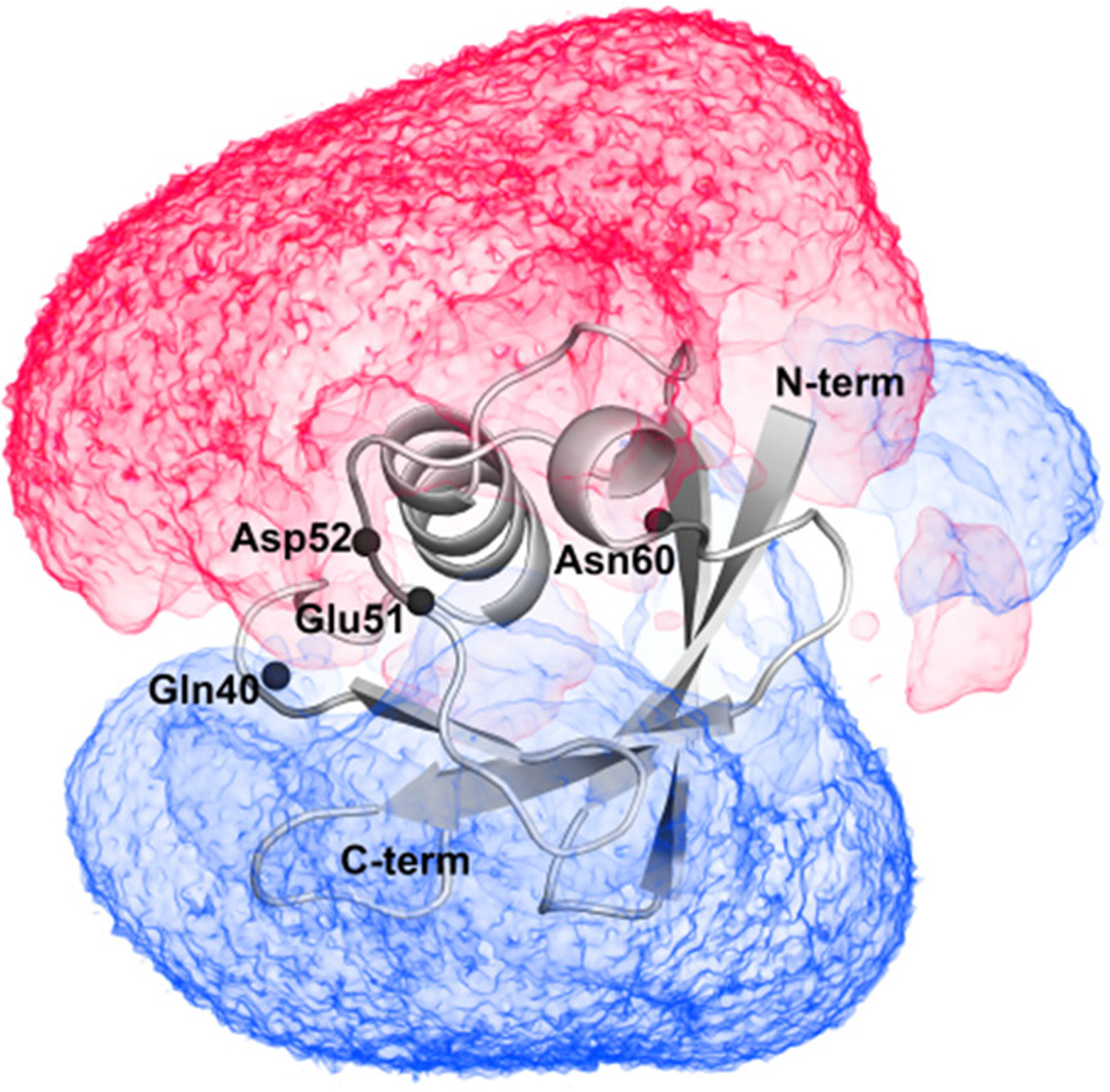
At 0 mM ionic strength, the volume map of electrostatic potentials in a range of −0.5 k_BT/e (red color) and 0.5 k_BT/e (blue color) around ubiquitin. Black spheres represent the backbone N atoms of labeled residues.

We have assumed a spherically averaged probe model for the exclusion zone such that we need only consider the position of the probe with respect to the H_N of any individual residue of the protein. However, the interaction of direct importance to the PRE experiments is that of the unpaired probe electron spin with a given protein ¹H nucleus. As shown in Figure 1, the paramagnetic probe molecule (i.e., aminomethyl-PROXYL and carboxy-PROXYL) is a nonspherical molecule, which have the unpaired electron on a nitroxide group and either a cationic or anionic group tethered to the opposite end of the molecule. The shape and charge distribution of the probe in interaction with the protein electrostatic potential field can result in significant orientational correlations. According to eq 3, the potential energy, potential of mean force, and therefore the pair distribution are six-dimensional properties dependent on not only the probe’s relative position to an H_N atom but also its angular orientation in the electrostatic field. To obtain the required potential of mean force depending only on the distance between the unpaired electron center and a given protein hydrogen, the Boltzmann-weighted angular correlations must be considered. At a position close to the boundary of the positive and negative protein potentials, it can happen that the nitroxide oxygen bearing an unpaired electron and the ionic group of the probe molecule can be located in potential fields having opposite signs.

ϕ_ENS Potentials Using Atomistic Probe Models.

We carried out BD simulations at the ionic strength of 130 mM to calculate the Boltzmann-weighted potential energies of a fully atomistic probe model with the protein in the electrostatic potential field from the MD simulation and thus determined the ϕ_ENS potentials for individual residues. Considering the effective interactions are weak between the probe molecules and ubiquitin, 20 million runs for one BD simulation were carried out to ensure sufficient sampling in the near-surface zone. Ten independent sets of simulations were carried out for statistical error estimates.

The value of ϕENS potential depends on the ratio $\frac{{\mathrm{\Gamma }}_{2,+}}{{\mathrm{\Gamma }}_{2,-}}$, and a relaxation ratio greater than 1 indicates a negative near-surface electrostatic potential. The experimental ratio is measured directly from NMR experiments without further assumptions. A predicted ratio is calculated from eq 6 with the assumption that indirect potential ΔW cancels or is sufficiently small in a voxel volume for both the probes. As shown in Figure 7A, compared to the experiment, the RMSD in the ratio $\frac{{\mathrm{\Gamma }}_{2,+}}{{\mathrm{\Gamma }}_{2,-}}$ by using the atomistic model is 0.74 which is smaller than 0.90 by using a spherical model. The atomistic model, without being a fit to the experimental data, thus provides better agreement in the ratio $\frac{{\mathrm{\Gamma }}_{2,+}}{{\mathrm{\Gamma }}_{2,-}}$ with the experimental results than the spherical model for many residues. The ratio discrepancy observed in the spherical model is corrected by consideration of orientational correlations of the probe in the atomistic model. However, for residues 16, 22, and 53, large uncertainties were found, which could be because aspects of ΔW₊(r, Ω₊) and/or ΔW−(r, Ω₋) cannot be neglected.

Figure 7.

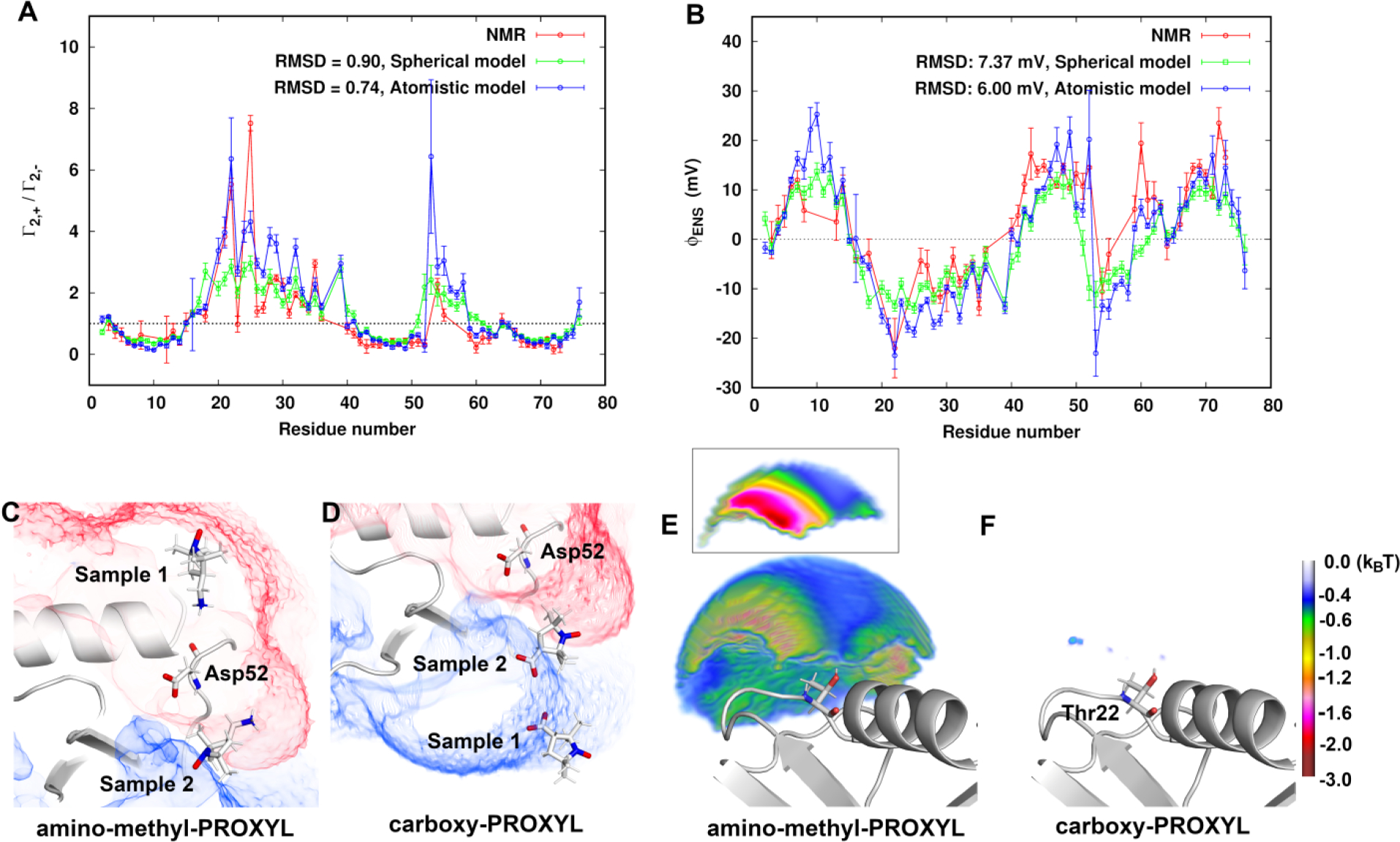
Comparison of (A) the ratio $\frac{{\mathrm{\Gamma }}_{2,+}}{{\mathrm{\Gamma }}_{2,-}}$ and (B) ϕ_ENS potentials for backbone ¹H_N nuclei of ubiquitin using atomistic model and spherical model with the experimental results at 130 mM ionic strength. (C) and (D) display two orientational samples of amino-methyl-PROXYL and carboxy-PROXYL, respectively, at the boundary of the positive (+0.3 k_BT/e in blue) and negative (−0.3 k_BT/e in red) potential field around Asp52. (E) and (F) Favorable potential energies of amino-methyl-PROXYL and carboxy-PROXYL, respectively, in the near-surface zone within 10 Å from the H_N atom of Thr22. The inset in (E) is a cross section showing the energy differences on the same grid points.

Figure 7B compares the predicted ϕ_ENS potentials using the spherical and atomistic model with the NMR-derived ones. The atomistic model improves the agreement with the experiment with a smaller RMSD of 6.00 mV. In particular, for outliers such as Asp52 and Asn60, the calculated ϕ_ENS potentials have the same sign as the experimental ones. The Boltzmann-weighted potential energies for the cationic probe and the anionic probe, show respectively, as expected, that the cationic probe is energetically favorably distributed in the negative potential field, and the anionic probe in the positive potential field (Figure S6C,D). Here we take Asp52 as an example. Far from the boundary between the positive and negative protein potential field, the whole probe is immersed in opposite field as the ionic moiety (Sample 1 around Asp52 in Figure 7C,D). However, for example, when the cationic probe is in proximity to the protein dipolar boundary, it is able to take an orientation in which the ionic end of the molecule stays in the negative potential field and the unpaired electron can report on a proton in the positive field (Sample 2 in Figure 7C). As a result, a sign switch can be observed in the estimated ϕ_ENS potential of Asp52 from a negative value using a spherical probe to a positive value using an atomistic model having the chemical shape of the probe molecule.

Large uncertainties in ϕ_ENS potentials were observed for residues 16, 22, 52, and 53. Similarly, in the NMR experiment, the ϕ_ENS potentials are difficult to obtain for residues 15, 17, 20−25, 53, and 56−58 due to large uncertainties. residues 15−21, 53, and 56−58 are located near a potential boundary (Figures S7A and 6). In these boundary regions the effects of orientational correlations on the potential of mean force for both the probes cannot be exactly canceled, as discussed above. Residues 22−25 are in the deeply negative potential field (Figure S7A). Investigation of the potential energies for the cationic probe molecules in the near-surface zone within 10 Å from the H_N atoms of the residues shows that the minimum potential energies for the above-mentioned residues are about −3 k_BT, at least about 1 k_BT lower than the other residues (Figure S7B). This indicates that the near-surface proximity zone of some residues (Thr22 as an example in Figure 7E) is not well-represented as an electrostatic mean field for the cationic probe. In addition, due to the low population of the anionic probe in the near-surface zone (Figure 7F), $\overline{\mathrm{\Delta }W}$ for both the probes cannot exactly be canceled. Therefore, the assumptions held in eq 8 cannot be properly satisfied in the assessment of ϕ_ENS potentials from both the experiment and the calculations in the case of some residues.

DISCUSSION

In this work, we combined NMR PRE experiments and multiresolution simulations to determine the near-surface electrostatic potentials for the residues of ubiquitin in different salt solutions. Salt dependence of ϕ_ENS potentials was studied at ionic strengths from 0 to 745 mM. The ϕ_ENS potential results from theory and simulation are in good agreement with those from experiment for most of residues using a simple spherical model of the probe and allowing for different effective probe sizes when considering the surface accessible volumes. A discrepancy of the sign of ϕ_ENS potentials was observed for a few particular residues in both continuum and explicit solvent calculations. We found the discrepancy is mainly caused by angular correlations of the probe which are particularly damaging to an interpretation of the electrostatic potential field for residues near the dipolar boundary of the protein. More problematic situations may arise when the proton of interest is surrounded by even more complicated multipolar fields.

While in principle the probe molecules can be included in the MD simulations, the low concentrations used would require considerable computational effort to obtain converged results. The use of Brownian trajectories of an atomistic probe model in a precomputed MD solvent potential field overcomes this limitation and produces the required angular correlation dependence.

Probe Size Dependence in Calculations Using Spherical Model.

In the calculations of ϕ_ENS potentials from experiment, two major assumptions of the analysis are considered. The first assumption is that the correlation times of the dipole−dipole interaction between the macromolecular ¹H nucleus and the unpaired electron of the probe are identical for the cationic and anionic probes. This is confirmed by the nearly identical diffusion constants for both probes.¹ The second assumption is that orientation correlations and the indirect part of the potential of mean force, ΔW, approximately cancel in the near-surface proximity zone of a residue. This allows the probe exclusion volume to be modeled as a sphere with a point charge. We used a best fit radius of 3.5 Å for the probe for predictions with PB theory and a smaller radius of 2.0 Å for the MD simulations which points out differences in modeling the effects of the aqueous solution. The PB predictions used an ionic probe radius of 2.0 Å to determine the ion accessibility function and used a dielectric continuum to represent the solution. Additionally, a spherical exclusion radius of 1.4 Å was used to define the boundary between the low dielectric protein and the high dielectric solvent. All-atom MD simulations with explicit solvent molecules provide access to the detailed correlations in a heterogeneous environment, where correlations produce the charge−charge response. Moreover, accessibility of ions and solvent to the surface of the protein is controlled by nonbonded interactions. In the radial distributions of the K⁺ ions, Cl⁻ ions, and water molecules from the protein vdW surface (Figure S8), the first peak of the distribution is found at 2.6, 3.2, and 2.7 Å for the K⁺ ions, Cl⁻ ions, and water oxygen atoms, respectively, indicating that the mobile ions and solvent have more accessibility to the vdW surface of the protein than with the PB model. Thus, the region near the vdW surface of the protein is influenced more deeply in the MD simulation than in the PB theory. This contributes to the smaller size of the spherical probe needed to best fit the experiment in the MD simulation analyses.

Salt Dependence of ϕ_ENS Potentials.

Experiment (Figure S9A−C) and PB and MD simulations (Figure S9D–F) demonstrate the strong ionic strength dependence of ϕ_ENS. As shown in Figure S9, the NMR-derived ϕ_ENS potentials at 345 and 745 mM ionic strength were on average only 40 and 24%, respectively, of those at 30 mM ionic strength. The decrease in the magnitude of ϕ_ENS potentials upon an increase in ionic strength is also demonstrated in Figure S9C, which shows the ionic strength dependence of ϕ_ENS potentials for selected residues.

Compared to experiment, the PB-calculated ϕ_ENS potentials demonstrate slightly smaller RMSDs with experiment than the MD-derived ones at 130 and 345 mM ionic strengths, but larger RMSDs at 745 mM. Due to the small number of mobile ions in the low-salt solutions in the MD simulations, more sampling is required for convergence of ion distribution, while in the high-salt solution the MD simulations should be converged and demonstrate nontrivial ion−ion correlations. At 745 mM, the ions contribute to a favorable amount of interaction energy of about −1.0 k_BT in the region close to Glu16, Glu18, Asp21, and Lys29 (Figure S10). The ions not only play a role in screening the protein charges but also correlate to form an explicit interaction cluster among the residues. Nevertheless, in this case of ubiquitin, the PB equation with the large spherical probe model still provides a reasonable prediction of most residues near-surface zone potentials in solutions with an ionic strength as high as 745 mM.

Implication of ϕ_ENS Potentials Calculated with BD from Atomistic Models.

Assessment of electrostatic potentials near a residue with this experimental technique relies on the distribution of probe molecules around the protein. The probes are nonspherical molecules each with a full charge and other multipoles dependent on origin. The atomistic models’ dipole moment with respect to the center of the molecule is 19.7 D for amino-methyl-PROXYL and 13.1 D for carboxy-PROXYL. The charge distribution controls the orientation of the probe near a dipolar boundary. Thus, the potential of mean force on the probe is not only a function of the distance of the probe with respect to the H_N atoms but also a function of angular orientation. The probe’s orientational correlation determines whether the nitroxide oxygen stays in a potential field similar or opposite to the ionic moiety of the probe. As a result, far from the dipolar potential boundary the spherical probe model can report a reasonably true field. However, for some residues near the boundary (e.g., amino acids 15−21, 40, and 50−60), the neglect of orientational correlations can lead to the discrepancy of ϕ_ENS potentials between the NMR experiments and the computations with the spherical probe model. The atomistic probe model demonstrates that the unpaired electrons on the probes are able to be in a potential field opposite to the electrostatic field sensed by the other end of the charged probe molecule. Locations of ¹H nuclei that may exhibit such a discrepancy for ubiquitin are predictable to some extent through a relatively simple inspection of dipolar boundaries, as demonstrated above. Such an analysis extends to other protein hydrogens, in particular to those on aliphatic groups.⁵⁰

CONCLUSIONS

In this work, we presented the determination of the ratios of PRE rates and the relation to near-surface electrostatic potentials of ubiquitin by NMR experiment and simulations in different ionic strength solutions. Decomposing contributions to the potential of mean force and the electrostatic potentials in an atomistic detail, we obtained structure-dependent yet more accurate comparisons with the experiment. We found that the angular correlation of the probe molecule with the protein cannot be neglected for ¹H nuclei near the dipolar potential boundary of the protein. If the indirect effects of solvent and the effects of angular correlations are the same for the cationic and anionic probe in the near-surface zone of a residue, then we can accurately obtain a measure of the near-surface electrostatic potential with simple spherical exclusion models. The electrostatic potential is central to many applications like protein folding and molecular recognition. The advantage of the PRE rate experiment is that the method simultaneously provides the near-surface electrostatic potentials for many residues with no prior knowledge of structural information on the protein when spherical probe exclusion models may be used. This PRE rate method may help tune such model potentials in difficult cases, such as pK_a shift due to change of chemical environment and electrostatic properties of intrinsically disordered protein.