Abstract
Diffusion MRI (dMRI) is a unique tool for the study of brain circuitry, as it allows us to image both the macroscopic trajectories and the microstructural properties of axon bundles in vivo. The Human Connectome Project ushered in an era of impressive advances in dMRI acquisition and analysis. As a result of these efforts, the quality of dMRI data that could be acquired in vivo improved substantially, and large collections of such data became widely available. Despite this progress, the main limitation of dMRI remains: it does not image axons directly, but only provides indirect measurements based on the diffusion of water molecules. Thus, it must be validated by methods that allow direct visualization of axons but that can only be performed in post mortem brain tissue. In this review, we discuss methods for validating the various features of connectional anatomy that are extracted from dMRI, both at the macro-scale (trajectories of axon bundles), and at micro-scale (axonal orientations and other microstructural properties). We present a range of validation tools, including anatomic tracer studies, Klingler’s dissection, myelin stains, label-free optical imaging techniques, and others. We provide an overview of the basic principles of each technique, its limitations, and what it has taught us so far about the accuracy of different dMRI acquisition and analysis approaches.
1. Introduction
Diffusion MRI (dMRI) tractography was introduced two decades ago as a technique for reconstructing the trajectories of white-matter axon bundles by exploiting the anisotropy of water diffusion within these bundles (Mori et al., 1999; Jones et al., 1999; Conturo et al., 1999).
Early applications of tractography demonstrated that it was generally able to reconstruct the large highways of the human brain, as they had been identified by prior anatomical studies (Catani et al., 2002; Wakana et al., 2004). However, this was only possible after extensive manual intervention on the paths reconstructed by tractography, which was necessary to select only those that reflected true anatomy. The challenge in this process is that the true anatomy is not fully known. Axon bundles form a highly complex network. The large highways (e.g., corpus callosum, cingulum bundle, etc.) serve as conduits for smaller groups of axons, which merge on and off the highways at different points along their trajectory to project to different cortical and subcortical structures (Lehman et al., 2011; Jbabdi et al., 2013; Haynes and Haber, 2013; Heilbronner and Haber, 2014; Safadi et al., 2018). Although the main highways of the brain are fairly well-known (Schmahmann and Pandya, 2006), the complete trajectories of all the small fiber bundles that travel through them are not.
The fact that tractography is prone to errors is straightforward to establish using either simulated dMRI data (Côté et al., 2013; Daducci et al., 2014; Leemans et al., 2005; Neher et al., 2014; Maier-Hein et al., 2017), or real dMRI data collected from phantoms (Fieremans et al., 2008; Perrin et al., 2005; Poupon et al., 2008). In both of these scenarios, the ground-truth fiber geometry is known. Such studies are valuable for demonstrating the general limitations of tractography, and for comparing different tractography methods with respect to quantitative accuracy metrics. However, simulated and phantom data do not reflect the full complexity of brain circuitry. Thus the performance of a tractography method in such a setting cannot be used to determine which of the fiber bundles that this method reconstructs in a real brain are true and which are artifactual.
The technical advances spearheaded by the Human Connectome Project (Van Essen et al., 2013; Setsompop et al., 2013) led to a dramatic improvement in dMRI data quality. These advances increased the spatial and angular resolution, as well as the contrast-to-noise ratio, of the dMRI data that can be acquired routinely for in vivo studies. One of the main motivations behind this improvement was the expectation that higher quality of dMRI data, and specifically of data acquired with high b-values, would lead to more accurate tractography. The ultra-high b-values that can be achieved with these new technologies have been shown to reduce the uncertainty of probabilistic estimates of diffusion orientations (Setsompop et al., 2013) and to sharpen deterministic estimates of orientation distribution functions (Fan et al., 2014). These findings suggest improved ability to resolve crossing fiber bundles. However, not all fiber configurations in the brain can be modeled as crossings, and dMRI voxel sizes are still at a scale where multiple fiber configurations can lead to indistinguishable diffusion profiles. As a result, tractography is still imperfect. Therefore, the recent improvements in dMRI data quality have not obviated the need for validating the output of tractography algorithms; on the contrary, they have created the need for more sophisticated validation methods, capable of evaluating the fine-grained anatomy that can be captured by state-of-the-art dMRI.
Prior to the introduction of dMRI, all of our knowledge on the circuitry of the brain came from post mortem anatomical studies, using various techniques for dissection, tracing, histology, and microscopy. These are also the tools that we have at our disposal for post mortem validation of dMRI. The main focus of this review is connectional anatomy, hence we discuss techniques for validating the pathways that are output by tractography algorithms, or the local diffusion orientations that are the input to those algorithms. However, in many applications of tractography, the ultimate goal is to extract tract-specific biomarkers. In that sense, tractography is closely intertwined with dMRI microstructural modeling. Thus, we also survey the post mortem validation of microstructural parameters estimated from dMRI data.
For a precise, voxel-by-voxel comparison of white-matter circuitry and microstructure as obtained from dMRI and anatomy, both the dMRI and anatomical validation data should be collected from the same brain. Given the changes that a brain undergoes when it is excised and fixed, the dMRI scan should be collected after these procedures. Therefore, validation studies require expertise in both ex vivo dMRI scanning and anatomy. In Section 2, we review the main methodological considerations for collecting ex vivo dMRI data. In Section 3, we provide a brief overview of the evolution of anatomical studies, and specifically the techniques that can be used to obtain “gold standard” data for comparison to dMRI. We then discuss in more detail the validation of tractography (Section 4), fiber orientations (Section 5), and other microstructural parameters (Section 6). We end with a discussion of open questions and future directions in Section 7.
2. Ex vivo dMRI
Ex vivo dMRI acquisitions can harness the advantages of higher magnetic field and/or gradient strengths, more sensitive radiofrequency (RF) coils, and longer scan times. With tailored acquisition pulse sequences, isotropic spatial resolutions of a few hundred microns can be achieved for the whole brain and smaller specimens. This is almost an order of magnitude higher than typical in vivo resolutions of 1.5-2 mm. In recent years, ex vivo dMRI has emerged as a powerful tool for 3D mapping of human brain circuitry at mesoscopic scales, which is particularly important for comparison and validation of tractography methods using complementary post mortem modalities.
Tissue fixation and preparation procedures must be optimized carefully to ensure high-quality ex vivo dMRI, as discussed extensively elsewhere (D’Arceuil et al., 2007; Dyrby et al., 2011; Miller et al., 2011; Dyrby et al., 2018). In particular, the specimen setup is aimed at minimizing the effects of mechanical vibrations and tissue instability over time. As dMRI experiments are also especially sensitive to temperature variations, temperature monitoring is often used for scans with long durations (Dyrby et al., 2011).
Important considerations for ex vivo dMRI protocol design are the reduced T2 and reduced diffusivity of fixed tissue (D’Arceuil et al., 2007; Pfefferbaum et al., 2004; Roebroeck et al., 2019). While the former leads directly to loss of signal-to-noise ratio (SNR), the latter requires heavier diffusion weighting to offset the loss in contrast-to-noise ratio (CNR), but also contributes to further loss of SNR. Both of these factors need to be taken into account when designing optimal acquisition sequences and sampling schemes for ex vivo imaging. The species and anatomical structures of interest must also be factored in to determine the optimal spatial resolution. For example, brain mass and number of neurons scale by four orders of magnitude as we go from the mouse to the marmoset, to the macaque monkey, and finally to the human brain (Herculano-Houzel, 2009). Below we discuss the main technical considerations for acquiring ex vivo dMRI data in the brain, and highlight the different acquisition sequences that can be used to achieve the high image quality and spatial/angular resolutions needed for tractography and microstructure validation studies.
Acquisition of ex vivo dMRI datasets often requires the use of tailored pulse sequences to combat the loss in SNR and CNR due to reduced T2 and diffusivity of fixed tissue. While 2D single-shot echo planar imaging (ss-EPI) sequences are most widely used for in vivo dMRI of the human brain, these are sub-optimal for ex vivo imaging, as the shorter T2 precludes the use of lengthy echo trains. Moreover, the decrease of diffusivity in fixed tissues must be offset by an increase in b-values (Sun et al., 2005; Roebroeck et al., 2019), achieved with stronger diffusion-weighting gradients and/or longer gradient durations. This can exacerbate eddy-current induced distortions when k-space is traversed in a single shot. Thus, multi-shot acquisition techniques and 3D echo trains are ideal for ex vivo dMRI. These techniques are not widely used in vivo, as they typically suffer from severe artifacts due to motion-induced phase errors across excitations. In ex vivo imaging, however, motion is not an issue, provided the specimen preparation ensures stability over the duration of the scan.
The most common acquisition strategies for ex vivo dMRI are summarized in Table 1. Compared to 2D ss-EPI, 3D multi-shot or segmented EPI sequences allow for shorter effective echo times and thus higher SNR, and have been used for ex vivo dMRI of the whole human brain at 3 T (McNab et al., 2009; Miller et al., 2011; McNab et al., 2013) and the intact human brainstem at preclinical field strengths (Aggarwal et al., 2013). Multi-echo acquisitions involving repetitions of segmented EPI readouts at different echo times can be used to improve SNR (Eichner et al., 2020). On the other end of the spectrum, spin-echo (SE) readouts, which traverse a single line in k-space per excitation, have also been used for ex vivo dMRI (D’Arceuil et al., 2007; Dyrby et al., 2011; Guilfoyle et al., 2003; Modo et al., 2016). While these allow the highest anatomical fidelity with low geometric distortion, depending on the targeted spatial and angular resolution, they require prohibitively long scan times due to the relatively low SNR efficiency. At these lengthy scan times, problems with both magnetic field drift and specimen stability can become significant.
Table 1. Summary of ex vivo dMRI acquisition methods.
The 3D sequences commonly used for ex vivo dMRI are compared in terms of SNR efficiency and factors affecting image quality. The approximate acceleration factors are computed for similar in-plane resolutions and repetition times. Note that, in practice, the echo times and relative T2/T2* weighting also vary across the sequences and can affect the image contrast. (DW: diffusion-weighted; SE: spin-echo; RARE: rapid acquisition with relaxation enhancement; GRASE: gradient and spin echo; EPI: echo planar imaging; ss: single-shot; ms: multi-shot; ETL: echo train length.)
| Acquisition sequence | Acceleration factor |
Pros and cons | |
|---|---|---|---|
| Single line readout | 3D DW-SE | 1 | Lowest scan efficiency Highest anatomic fidelity with minimal distortion Long acquisition times pose limits on spatial and angular resolution |
| Multiple radiofrequency pulse readouts | 3D DW-RARE | RARE factor | Intermediate scan efficiency Phase modulation across k-space can lead to ghosting artifacts |
| 3D DW-GRASE | RARE factor x EPI factor | Correction of phase related artifacts by use of reference scans or twin-navigator echoes | |
| EPI readouts | 3D ss-DW-EPI | ETL | High scan efficiency Susceptibility induced distortion and ghosting artifacts |
| 3D ms-DW-EPI | ETL | ss-EPI readouts generally suboptimal due to low SNR and reduced T2/T2* of fixed tissues | |
Diffusion weighted (DW) sequences with multiple RF-pulse echo trains, such as fast spin echo or gradient and spin echo, enable accelerated 3D imaging by factors of ~4-12x as compared to DW-SE, while minimizing the distortion-related artifacts that DW-EPI sequences are prone to, and can therefore achieve combined high spatial and angular resolutions (Aggarwal et al., 2010; Tyszka and Frank, 2009). These may currently offer the best trade-off between SNR efficiency and image quality for smaller specimens, but require sophisticated schemes to correct for phase error induced artifacts, including but not limited to, the acquisition of navigator echoes or reference phase scans. Using volumetric excitations, the 3D k-space encoding can be further optimized to separate out eddy current and T2-decay effects on different k-space axes for techniques that combine gradient- and spin-echoes, thereby allowing dMRI data to be acquired with high SNR efficiency and reduced artifacts (Aggarwal et al., 2010). Such combined high spatial-angular resolutions are crucial, e.g., for resolving fiber orientation distributions in the cortex (Aggarwal et al., 2015; Leuze et al., 2012).
In addition to optimized readout strategies to combat the effects of reduced T2, depending on the application at hand, modifications to the diffusion encoding may also be necessary. The b-values used for ex vivo dMRI need to be considerably higher than their in vivo counterparts, typically by factors of 2-4x, in order to achieve comparable diffusion contrast (Dyrby et al., 2011; Roebroeck et al., 2019; Schilling et al., 2017a). At such high b-values, eddy-current artifacts are particularly problematic, and can be further exacerbated when moving to higher field strengths. For micro-imaging applications (voxel sizes < 100 μm) at high field, bipolar diffusion-encoding gradients can be combined with multi-echo readouts to reduce the effects of eddy currents (Reese et al., 2003). As another alternative, DW steady-state free precession (SSFP) sequences, which can retain signal over multiple repetition intervals, have been shown to provide improved SNR efficiency with heavy diffusion weighting for whole brain ex vivo dMRI at 3 T and 7 T (Foxley et al., 2014; Miller et al., 2012). The slower T1 decay at higher field strengths can also be harnessed for strong diffusion weighting by employing stimulated-echo preparations, as shown for whole brain ex vivo dMRI at 9.4 T (Fritz et al., 2019).
Ex vivo acquisitions can also benefit from advances in gradient hardware or customized RF coils. Multi-channel coils, custom-built to closely fit the whole brain or smaller specimens, can allow increased reception sensitivity, thereby leading to a boost in the achievable SNR. For whole-brain imaging on human scanners, custom-built coils have been shown to lead to SNR gains of ~1.6-2 fold as compared to standard in vivo head coils (Edlow et al., 2019; Roebroeck et al., 2015; Scholz et al., 2021). When combined with parallel transmit RF pulses for B1 + homogeneity, maximal SNR gain of as much as 5-fold was reported in the peripheral cortex using a custom-built cylindrical phased-array receive coil for the ex vivo occipital lobe at 9.4 T (Sengupta et al., 2018). Customized transmit/receive RF coils can be further combined with optimized acquisition pulse sequences such as DW-SSFP to achieve improved SNR for whole-brain ex vivo dMRI at submillimeter resolutions (Fritz et al., 2016). These advances in RF coils can enable the acquisition of much higher-quality dMRI validation data sets than what would be possible with standard, in vivo coils.
3. Anatomy: the gold standard for dMRI
Here we provide a brief historical overview of techniques that have been used by neuroanatomists to map brain pathways, setting the stage for the methods that are used to validate dMRI and that will be discussed in greater detail in subsequent sections. The development of cellular and axonal markers at the turn of the 20th century began the modern era of neuroanatomy. Two stains (Nissl and Golgi) provided the ability to visualize cell morphology, thus permitting the classification of cell types and the cytoarchitectonic organization of cortex. Degenerative stains made possible the visualization of myelinated axons, leading to a new understanding of connections between brain regions. These two anatomic subfields for understanding brain organization blossomed during the early 20th century: cytoarchitectonics, which segmented the brain based on cortical layer cell morphology, and myeloarchitectonics, which classified cortical areas based on myelin distribution and fiber orientation through cortical layers (Vogt, 1903; Brodmann, 1909; Nieuwenhuys et al., 2015). Prior to the early 1950s, the only available anterograde tracer was the Marchi stain, which specifically marks degenerating myelin sheaths following well-placed lesions (Marchi and Algeri, 1885). However, as this method did not identify unmyelinated, thinly myelinated axons, or terminals, it was quite limited. While a reduced silver method did become available to visualize the axons themselves, shortly after, more sensitive tracing techniques were developed. These newer tracers relied on active neuronal transport, allowed the precise visualization of both axons and terminal fields, and became our most reliable source of information on connectional anatomy. We discuss these tracers as a validation tool for dMRI tractography in Section 4.1.
Although tracing experiments allow us to map axon bundles with high precision, they cannot be conducted on human subjects. The only alternative in the human brain is to perform blunt dissection on fixed ex vivo specimens. The methodology that is used for this purpose to this day was devised by Joseph Klingler in the 1930s. It involves loosening the structure of fixed brain tissue, and particularly fiber bundles, by freezing and thawing the tissue (Klingler, 1935; Ludwig and Klingler, 1956; Klingler and Goor, 1960). We discuss Klingler’s dissection method as a technique for validating dMRI tractography in Section 4.2.
In tracing and blunt dissection studies, the goal is to follow a group of axons from its origin to its terminations. When the goal is to visualize all the axon bundles that intersect in a given brain location, for comparison with a fiber orientation distribution (FOD) computed from dMRI data at a certain voxel, we need other techniques. In neuroanatomy, fiber orientations in a tissue section are usually visualized by processing the section with histological stains for myelin. The precursor to such stains was developed in 1873 by Camillo Golgi, one of the pioneers of modern-day histology, who perfected a silver-staining method that he coined “the black reaction” (Glickstein, 2006). The stain had affinity to only a few neurons, but stained their structure - soma, dendrites and axon - in its entirety. We discuss histological stains as a method for validating fiber orientations in Section 5.1.
In the past decade, novel optical imaging techniques have been adopted to visualize fiber orientations in the brain. These include label-free methods, like polarization microscopy and optical coherence tomography, which rely on intrinsic tissue contrast instead of staining. Another novel approach is clearing, i.e., rendering tissue transparent, after which the tissue is treated with fluorescent dyes and imaged with fluorescence microscopy. These methods have a shorter history than traditional histological techniques, but they hold great promise as the digital neuroanatomy tools of the future. We discuss these methods for validating fiber orientations in Section 5.2.
The post mortem imaging techniques reviewed in this work are summarized in Table 2. Studies that have performed comparisons of dMRI tractography and anatomic tracing are summarized in Table 3. Studies that have compared dMRI orientation estimates and microscopic measurements of fiber orientations in the same sample are summarized in Table 4.
Table 2. Summary of methods for mapping connectional anatomy.
Each method is listed with the section(s) of this review where it is discussed (dMRI: diffusion-weighted magnetic resonance imaging; PLI: polarized light imaging; PS-OCT: polarization-sensitive optical coherence tomography; CLARITY: clear lipid-exchanged acrylamide-hybridized rigid imaging/immunostaining/in situ hybridization-compatible tissue-hydrogel; CT: computed tomography; EM: electron microscopy). *: Needed in the human brain. **: Needed in transmission but not block-face scanning mode.
Table 3. Summary of literature: validation of tractography.
Studies that have performed comparisons of dMRI tractography and anatomic tracing in non-human primates. We list the source of the tracer data (from a previously published database or from the same brain as the dMRI scan), type of comparison (E: endpoints; Q: qualitative; T: trajectory), and dMRI acquisition parameters for each study (“iso” indicates isotropic voxels). †: These b-values were collected in vivo; hence they are not directly comparable to the b-values of the other studies
Table 4. Summary of literature: validation of fiber orientations.
Studies that have compared dMRI orientation estimates in post-mortem brain tissue to independent measurements of fiber orientations from a reference modality in the same sample. We list the reference modality, type of tissue, and dMRI acquisition parameters for each study (“iso” indicates isotropic voxels).
| Reference modality |
Tissue type |
dMRI b-values [s/mm2] |
Gradient directions | Voxel size [mm] | ||
|---|---|---|---|---|---|---|
| Leergaard et al. (2010) | Myelin stain | 2D | Rat | Max 30452 | 514 | .265 iso |
| Choe et al. (2012) | 2D | Owl monkey | 1309 | 21 | .3 iso | |
| Seehaus et al. (2015) | 2D | Human | 3000 | 60 | .34 iso | |
| Schilling et al. (2017a) | 2D | Macaque | 6000 | 101 | .3-.8 iso | |
| Schilling et al. (2016) | DiI | 3D | Squirrel monkey | 3200/6400 | 30/90 | .4 iso |
| Schilling et al. (2018) | 3D | Squirrel monkey | 3000/6000 9000/12000 | 100/100 100/100 | .2 x .2 x .4 | |
| Mollink et al. (2017) | PLI | 2D | Human | 5000 | 120 | .4 iso |
| Henssen et al. (2019) | 2D | Human | 4000 | 256 | .5 iso | |
| Wang et al. (2014b) | PSOCT | 2D | Human | 4032 | 20 | .3 iso |
| Jones et al. (2020) | 2D | Human | Max 40000 | 514 | .25 iso | |
| Jones et al. (2021) | ||||||
| Stolp et al. (2018) | CLARITY | 3D | Mouse | 1500 | 42 | .125 x .125 x .2 |
| Leuze et al. (2021) | 3D | Human | 2000 | 447 | 1.0 iso |
4. Validation of tractography
4.1. Anatomic tracing
4.1.1. Methodology
Anatomic tracing studies in non-human primates (NHPs) allow a direct visualization of the wiring of the brain, including cells of origin, axon trajectories, and terminals. This level of detail allows the appreciation of the full complexity of brain connections, and makes tracer studies an anatomic “gold standard” for interpreting and validating the indirect measurements of the wiring of the brain that we obtain with dMRI tractography.
The first tracers that relied on active neuronal transport were preferentially transported anterogradely (e.g., tritiated amino acids) or retrogradely (e.g., horse radish peroxidase-HPR conjugated to wheat germ agglutin-WGA). Soon other molecules followed with intrinsic fluorescence and with better sensitivity, which could be further increased with immunohistochemical processing. Tracer molecules are microinjected in the brain region of interest, taken up into the cell body, and transported to the terminal fields (anterograde tracers) or taken up by the terminal fields and transported to the cell body (retrograde tracers). Different tissue processing protocols are applied to visualize the labeled axons, terminal fields and cell bodies, depending on the specific molecule injected. Nonetheless, they all provide the ability to directly visualize and quantify the labeled cells, axons, and their pathways through the white matter and terminal fields.
For details on the surgery, perfusion, and histological processing involved in tracer studies, see Haber et al. (2006) and Lehman et al. (2011). Briefly, animals receive an injection of one or more of the following antero-grade/bidirectional tracers: lucifer yellow (LY), fluororuby (FR), or fluorescein (FS) conjugated to dextran amine; phaseolus vulgaris-leucoagglutinin (PHA-L); or tritiated amino acids. Two weeks after surgery, animals are again deeply anesthetized and perfused with saline, followed by a paraformaldehyde/sucrose solution in phosphate buffer. Brains are postfixed overnight and cryoprotected in increasing gradients of sucrose.
Serial sections of 50 μm are cut on a freezing microtome into phosphate buffer or cryoprotectant solution. They are processed free-floating for immunocytochemistry to visualize the tracers. Tissue is incubated in primary anti-LY, anti-FS, anti-FR, or anti-PHA-L for four nights at 4 °C. Immunoreactivity is visualized using standard diaminobenzidine procedures. Sections are mounted onto gel-coated slides, dehydrated, defatted in xylene, and coverslipped. Sections for autoradiography are mounted on chrome alum gelatin-coated slides and defatted in xylene overnight. Slides are dipped in photographic emulsion, exposed for 4 – 6 months at 4 °C in a light-tight box and then developed, fixed, washed, and counterstained with cresyl violet. Each slide that has been processed to visualize a given tracer is annotated under the microscope to outline the fiber bundles as they travel from the injection site. The slides are co-registered and the outlines are concatenated across slices to produce a 3D reconstruction of the bundles.
4.1.2. Comparison to dMRI
We focus here on studies that have compared dMRI tractography to tracers visualized by immunohistochemistry in NHPs. These are the classical tracers that have been used extensively by neuroanatomists, and the NHP brain is the classical model for connectional anatomy due to its similarity to the human brain. Thus there is a large body of work that can be used to confirm the individual injections performed in these validation studies. However, it is worth noting that tracer-based validation of dMRI has also been performed in other species, such as the minipig (Dyrby et al., 2007) and mouse (Chen et al., 2015; Aydogan et al., 2018). Some dMRI validation studies have used manganese, an MR-visible tracer (Lin et al., 2001; Lin et al., 2003; Leergaard et al., 2003; Dyrby et al., 2007; Yamada et al., 2008; Gutman et al., 2013; Knösche et al., 2015). This tracer does not require histological processing, as it can be imaged with MRI. However, the quality of the tracer maps is limited by the resolution and SNR of MRI, and this approach is not guaranteed to visualize all axons labeled by classical tracers. Hence, we focus on studies that used classical anatomic tracing in the following.
There are three main approaches to comparing anatomic tracing to dMRI tractography, and they differ in terms of the information that is extracted from the tracer data. These approaches are: (i) comparing only the areas of origin and termination of the bundles, (ii) comparing the topography of the bundles as they travel through the white matter, and (iii) comparing the exact position of the bundles throughout their trajectory.
(i). Comparison of areas of origin/termination.
This is the approach taken by most prior studies that have compared anatomic tracing to dMRI tractography. Here the information on brain connections is reduced to a “connectivity matrix” that indicates which brain region is connected to which. These general connection patterns are highly reproducible between individual brains, hence it is reasonable to perform such a comparison using dMRI data and tracer experiments from different brains. This approach has been popular because it can take advantage of existing data on the “connectivity matrix” of the brain from prior NHP tracer studies, such as those included in the CoCoMac or other published databases (Felleman and Van Essen, 1991; Stephan et al., 2001; Markov et al., 2014). The accuracy of tractography is evaluated based on the frequency of the following outcomes: dMRI tractography detects a connection between a pair of brain regions that is also shown to be connected based on tracer experiments (true positive); it misses such a connection (false negative); or it detects a connection between a pair of regions that is not shown to be connected based on the tracer data (false positive).
Several studies have generated area-to-area connectivity matrices using tractography in dMRI scans of NHP brains and compared them to existing collections of NHP tracer data (Hagmann et al., 2008; van den Heuvel et al., 2015; Azadbakht et al., 2015; Donahue et al., 2016; Ambrosen et al., 2020). Despite the variety in dMRI acquisition and analysis methods, as well as the tracer databases used by these studies (see Table 3), there is considerable agreement in receiver operating characteristic (ROC) analyses. For the most part, for a specificity around 60%, tractography achieves sensitivity in the 60%-70% range in most studies (Hagmann et al., 2008; Azadbakht et al., 2015; Donahue et al., 2016; Ambrosen et al., 2020). A study that performed this analysis with a variety of more modern tractography algorithms, found that the sensitivity at the same level of specificity edged somewhat higher, in the 60–80% range (Girard et al., 2020). One of the previous studies examined the effect of dMRI acquisition parameters on the accuracy of the connectivity matrix (Ambrosen et al., 2020). A notable finding was that increasing the b-value from 1477 to 8040 s/mm2 led to indistinguishable ROC performance.
Analyses of correlation between the connectivity matrices obtained from dMRI tractography and tracer databases show less agreement than ROC analyses. Reported correlation coefficients range from r = .25 (van den Heuvel et al., 2015) to r = .59 (Donahue et al., 2016). Beyond the NHP literature, one study relied on a database of tracer injections in ferrets (Delettre et al., 2019). After regressing out the distance between cortical areas (to account for path-length dependence, see Morris et al., 2008, Liptrot et al., 2014), correlation between connectivity matrices obtained from dMRI tractography in a ferret scan and from the tracer database was much lower for deterministic tractography (r = .36-.40; not statistically significant) that probabilistic tractography (r = .54-.77; statistically significant). The only study that performed this type of correlation analysis using dMRI and tracer data from the same animal, a squirrel monkey, showed much higher correlation of area-to-area connectivity matrices, which ranged from r = .73 to r = .93, depending on the dMRI analytic approach (Gao et al., 2013). This may suggest that using dMRI and tracer data from different animals underestimates the accuracy of tractography. However, differences in analysis steps between these studies make it difficult to draw a definitive conclusion on this point.
(ii). Comparison of topographies.
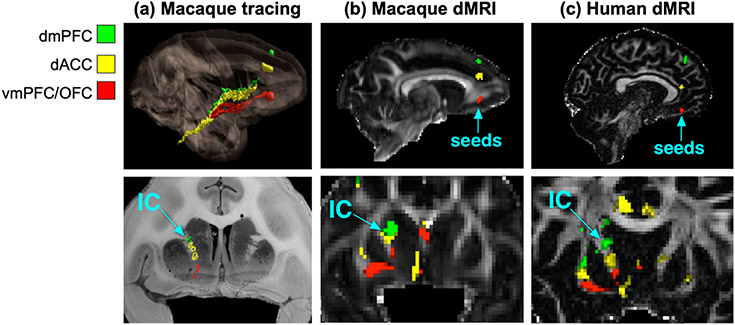
This approach requires tracer data that go beyond those widely available in databases, as it examines the trajectories of the axon bundles through the white matter and not just their areas of origin/termination. In several of the major white-matter pathways (e.g., corpus callosum, internal capsule, etc.), groups of axons that project from different cortical areas are topographically organized. Tracer studies are an excellent source of information on these topographies (Lehman et al., 2011; Jbabdi et al., 2013; Haynes and Haber, 2013; Heilbronner and Haber, 2014; Safadi et al., 2018). Fig. 1 shows an example of axon bundles projecting from three different cortical areas through the internal capsule. The dorsal-to-ventral topography of these cortical areas is preserved by the corresponding bundles as they travel within the internal capsule. This is revealed by NHP tracing experiments and replicated with tractography in both ex vivo NHP dMRI and in vivo human dMRI.
Fig. 1. Topographies of axon bundles shown with anatomic tracing vs. dMRI.
The projections of the dorsomedial prefrontal cortex (dmPFC), dorsal anterior cingulate cortex (dACC), and ventromedial prefrontal cortex (vmPFC) / orbitofrontal cortex (OFC) follow a dorsal-to-ventral topographic organization in the internal capsule (IC). This is shown by placing tracer injections in each of the three areas in NHP (a) and replicated by seeding dMRI probabilistic tractography in the three areas, in both ex vivo NHP data (b) and in vivo human data (c). (Adapted from Safadi et al., 2018.)
While dMRI tractography is known since its inception to reconstruct the large highways of the brain, replicating the fine topographies of smaller axon bundles within them is a far more challenging task, and hence a more rigorous testbed for the accuracy of tractography methods. Comparisons of topographies in NHP tracing, NHP ex vivo dMRI, and human in vivo dMRI show that many of them can be replicated by tractography in both NHPs and humans (Safadi et al., 2018). Importantly, this work demonstrates that, while the absolute coordinates of small axon bundles in template space are inconsistent across individual subjects, the relative positions of these bundles with respect to each other are highly consistent. This finding has two key implications. First, it suggests that validation of dMRI tractography in terms of such organizational rules could reasonably be performed using dMRI and tracer data from different brains. Second, it demonstrates that it is more reliable to define white-matter bundles in terms of their relative positions with respect to each other and to their surrounding anatomy than it is to define them in terms of absolute coordinates in a template space.
(iii). Voxel-by-voxel comparison.
This is a much more detailed level of validation, where the precise route of the axon bundles through the brain is compared between tractography and tracing on a voxel-wise basis. While comparisons of dMRI and tracing at the two previous levels (areas of origin/termination or topographic organization) are valuable for assessing how often tractography errors occur, voxel-wise comparisons are the only way to determine exactly where the errors occur. This is critical for revealing which fiber configurations are the most common failure modes of tractography algorithms, and therefore identifying ways to improve these algorithms. For this type of validation study, tracer and dMRI data must come from the same brain. (See Grisot et al., 2021 for an analysis of intra- vs. inter-individual variability.) Even if the general patterns of connectional anatomy are similar across brains, it is unlikely that image registration will lead to perfect voxel-wise alignment of all bundles, and especially of the small groups of axons that are labeled by a tracer injection.
Some of the early studies that compared tractography to anatomic tracing in terms of the trajectory of the bundles through the white matter did not have dMRI and tracer data from the same animals (Schmahmman et al., 2007; Jbabdi et al., 2013; Calabrese et al., 2014). Hence, the comparisons were performed in a qualitative manner, ensuring that tractography could replicate the route of bundles that had been previously described in the anatomy literature. Another study superimposed a set of illustrations of tracer maps from a previously published collection to a dMRI scan from a different animal (Thomas et al., 2014). The authors evaluated deterministic and probabilistic tractography, but only performed a full ROC analysis on the latter. For data points where the deterministic and probabilistic approaches have approximately the same true or false positives, the latter appears to outperform the former.
An early study that performed anatomic tracing and dMRI scanning in the same NHP brain was able to achieve a Dice coefficient (i.e., overlap) between tracing and tractography as high as 0.75, despite being limited by low spatial and angular resolution (Dauguet et al., 2007). Another dataset that included anatomic tracing and dMRI in the same animals was used to compare a wide range of tractography algorithms, including as part of the VoTEM challenge (Schilling and Gao,2019a; Schilling and Nath 2019b). These data confirm a result from (Thomas et al., 2014), that the default thresholds for probabilistic tractography operate in a regime with higher true and false positives than the default thresholds for deterministic tractography.
A more recent study used dMRI and tracer data from the same animal, collected with a more advanced dMRI acquisition protocol than the previous studies (Grisot et al., 2021). This allowed the comparison of multiple q-space sampling schemes (Cartesian, single-, and multi-shell). A full ROC analysis revealed that probabilistic tractography consistently achieved higher true positive rates than deterministic tractography, when the two were compared at the same false positive rates, for a variety of orientation reconstruction methods and sampling schemes. The maximum b-value had only a modest impact on the accuracy of tractography. Finally, the voxel-wise comparison of tractography and tracer data in the same brain revealed which axonal configurations led to errors consistently, across dMRI acquisition and analysis methods. These common failure modes of tractography involved geometries such as branching or turning, which are not modeled well by conventional crossing-fiber reconstruction methods. The same data were used as the training case for the IronTract challenge, with an additional injection in a different brain serving as the validation case (Maffei et al., 2021). The first round showed that, when tractography pipelines were optimized to achieve maximum accuracy for one injection site, they were generally much less accurate for the other site. Two teams were the exception to this rule, exhibiting robustness across the two seed regions. In the second round, all teams used the pre- and post-processing methods that had been used by these two top teams. This increased both accuracy and robustness between seed areas for most other teams. One of the two post-processing strategies involved a simple Gaussian filter and the other applied a set of a priori anatomical inclusion masks. Remarkably, Gaussian filtering led to similar improvements in the accuracy of tractography methods as the use of a priori anatomical constraints.
4.1.3. Limitations
The first, and perhaps most important, limitation of tracer studies is that they can only be performed in animals. The benefit of performing these studies in NHPs is that holomologies between the monkey and human brain have been studied extensively. Despite the expansion of the frontal lobe in humans, similarities in position, cytoarchitectonics, connections, and behavior indicate that the circuitry is relatively comparable (Uylings and van Eden, 1990; Petrides, 1994; Petrides and Pandya, 1994; Ongür and Price, 2000; Chiavaras and Petrides, 2000; Petrides and Pandya, 2002; Petrides et al., 2012; Innocenti et al., 2017). Thus, a possible route for using the knowledge generated by NHP tracer studies to validate dMRI tractography in humans is via the first two approaches described in the previous section, i.e., validation in terms of end regions or topographies.
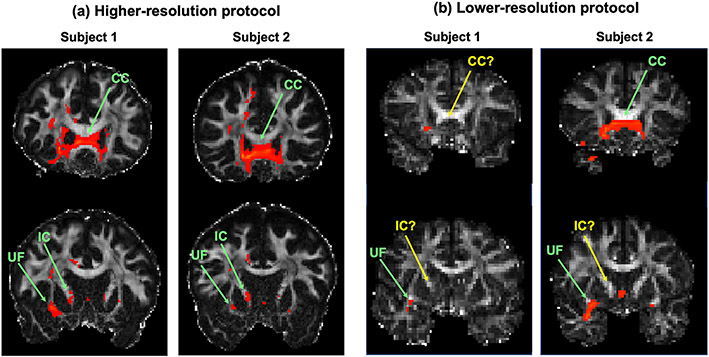
Of course, it is possible that a difference between anatomic tracing in NHPs and dMRI tractography in humans may be due to one of the true inter-species differences that are documented in the references above. This is where dMRI in NHPs can serve as a crucial stepping stone. When the NHP tracing disagrees with dMRI in both NHP and human, this is more likely to be due to an error in dMRI than an inter-species difference (Safadi et al., 2018). Furthermore, if the bundles reconstructed with dMRI tractography in humans become more similar to those seen in the NHP tracing when dMRI data quality improves, we can be more confident about using NHP tracer data and across-species homologies to evaluate tractography in human dMRI. Fig. 2 shows an example of this. Probabilistic tractography is seeded in area 10 (frontal pole) in two in vivo human dMRI datasets collected with higher spatial and angular resolution (bmax = 10 K s/mm2, 384 directions, 1.5mm resolution), and two collected with lower spatial and angular resolution (b = 700 s/mm2, 60 directions, 2mm resolution). Based on both anatomic tracing and ex vivo dMRI in NHPs, we expect area 10 to project through the corpus callosum, internal capsule, and uncinate fasciculus, among other pathways (see Lehman et al., 2011; Safadi et al., 2018; Grisot et al., 2021). These projections are seen reliably in the higher-resolution human dMRI (Fig. 2a) but not in the lower-resolution human dMRI (Fig. 2b). This is an example where across-species differences diminish as dMRI data quality improves.
Fig. 2. Improved in vivo human dMRI shows greater agreement with NHP anatomic studies.
Probabilistic tractography from a seed region in the frontal pole is shown for in vivo human dMRI datasets acquired with (a) a higher-resolution protocol (bmax = 10 K s/mm2, 384 directions, 1.5mm resolution), and (b) a lower-resolution protocol (b = 700 s/mm2, 60 directions, 2mm resolution). Based on both anatomic tracing and ex vivo dMRI tractography in NHPs, we expect frontal pole to project through the corpus callosum (CC), internal capsule (IC), and uncinate fasciculus (UF), among other pathways. These projections are present consistently in the higher-resolution human dMRI tractography, while many are missing in the lower-resolution human dMRI tractography. True positives are marked with green arrows; false negatives with yellow arrows. When discrepancies between human dMRI and NHP tracing disappear as dMRI data quality improves, these discrepancies are likely to be dMRI errors and not true inter-species differences.
Tracers suffer from a variety of other limitations. Care must be taken when extracting inter-areal connectivity matrices from tracer data, as including connections that involve very few labeled neurons can result in a very dense connection matrix (Markov et al., 2014). Conventional tracers can be taken up by fibers of passage and the exact area of axonal uptake at the injection site can be difficult to determine. In addition, inconsistency in uptake and transport can result in variable quality between injections. Conventional tracers have now been largely replaced by viral tracers (Oh et al., 2014; Chen et al., 2015; Aydogan et al., 2018), RNA barcoding (Kebschull et al., 2016; Chen et al., 2019), etc., for rodent work. Unfortunately, some of these more modern anatomic methods that circumvent these issues are difficult and costly to carry out in old-world NHPs.
Finally, as is the case for all methods that rely on histological processing (see Section 5.1 for a detailed discussion), distortions due to sectioning and staining can interfere with the alignment of histological sections. However, tracer studies have the advantage that the same axons are labeled by the tracer across slices, and this provides a visual aid in ascertaining that slices have been aligned correctly. In the future, the acquisition of more data with tracing and dMRI in the same brains, and the development of algorithms for automated annotation and analysis of axon bundles from tracer data will be critical for harnessing the full potential of anatomic tracing as a tool for the validation of dMRI tractography.
4.2. Gross dissection
4.2.1. Methodology
The tracer studies described in the previous section are not applicable to human subjects. Klingler’s dissection technique is the only means available to anatomists for following fiber bundles in ex vivo human brains. Detailed descriptions of this technique are provided in the reviews by Wysiadecki et al. (2019) and Dziedzic et al. (2021). In short, the brain is fixed in a 10% formalin solution. It must remain in fixative for at least 2 months, and suspension prevents it from deforming during the fixation process. The meninges are carefully removed. The brain is frozen at −10 to −15°C for one week and then thawed by washing with running water for one day. The brain is immersed again in new formalin and the freezing-thawing procedure can be performed a second time. Klingler and colleagues recommended freezing the specimens before dissection, because they thought that the formalin solution did not penetrate the myelinated nerve fibers fully, resulting in higher formalin concentrations between the fibers. When the specimens are frozen, formalin ice crystals form between the nerve fibers, expanding and separating them. The freezing process facilitates the dissection of fine fiber bundles in particular (Türe et al., 2000). Soft wooden spatulas are used to peel away the fiber bundles along the anatomic planes. When fibers are too thin for the eye to see, an operating microscope can be used, with a × 6 to × 40 magnification.
Protocols vary among different publications on Klingler’s technique. Differences are found in the perfusion method (whole body perfusion or brain perfusion via the vertebral and carotid arteries), freezing time, frequency of the freezing procedure, temperature and formalin percentage. Türe et al. (2000) and de Castro et al. (2005) provide clear descriptions of Klingler’s method. Best practices from these two reports are combined with our own experience in the detailed protocol of Arnts et al (2013).
Türe et al. (2000) and de Castro et al. (2005) describe the removal of the pia mater, arachnoid membrane, and vessels of the specimens using the operative microscope. However, with some experience it is possible to remove the membranes and vessels without a microscope (Arnts et al., 2013). Both Türe et al. (2000) and de Castro et al. (2005) also recommend that the brains be stored in a refrigerator at −10 to −15 degrees Celsius and placed in fresh 10% formalin solution for 8–10 days. Freezing time differs in Pujari et al. (2008), who report a freezing time of 14 days. Castro et al. (2005) is the only one to repeat the freezing periods and freeze the brains in a formalin solution. For the dissection step itself, all authors use wooden spatulas to tease out the white matter tracts by blunt dissection. Lawes et al. (2008) use spatulas of 3 mm or 6 mm width. Most authors also use an operation microscope. As with brain preparation, the dissection technique differs between publications. Some report on a cortex-sparing dissection technique, where not all cortex is scraped away (Martino et al., 2011). Regardless of the specifics of the technique, however, knowledge of white matter anatomy is crucial for Klingler’s dissection. For a review, see Schmahmann (2008) and Mandonnet (2018).
With the introduction of dMRI and tractography, white matter dissection has regained interest in the neuroimaging and neuroanatomical community. Klingler’s dissection is still practiced to date, not only for research on white-matter anatomy, but also for developing surgical approaches (Türe et al. 2000; Baydin 2016), and for the preparation of educational specimens (Arnts et al. 2013).
4.2.2. Comparison to dMRI
Ideally, when white-matter tracts dissected with Klingler’s method are compared with those reconstructed by dMRI tractography, both dissection and dMRI scanning should be performed in the same brain. Ex vivo dMRI scanning followed by Klingler’s dissection was performed on two vervet monkey brains to investigate the existence of the inferior fronto-occipital fasciculus, and found evidence for it from both techniques (Sarubbo et al., 2019). Dissections of the optic radiations in ex vivo human brain specimens have been compared to dMRI tractography of the same tract in a different set of ex vivo human brains (Nooij et al., 2015).
In most cases, however, the results of Klingler’s dissection have been compared to tractography results from in vivo dMRI scans of a different set of subjects (Lawes et al., 2008; Martino et al., 2011; Martino et al., 2013; Goryainov et al., 2017; Latini et al., 2017; Maffei et al., 2018; Briggs et al., 2019,2020,2021; Flores-Justa et al., 2019; Bernard et al., 2020; Li et al., 2020; Shinohara et al., 2020; Egemen et al., 2021; Weiller et al., 2021). In those cases, only qualitative comparisons between tractography and dissection have been possible. Sometimes, differences in reconstructions of the same tract across different subjects is reported not only with tractography, but also with dissection. For example, Goryainov et al. (2017) performed dissections of the superior longitudinal fasciculus in 12 brain specimens and found it to be subdivided into two components in 10 of the specimens and three components in the remaining two specimens. In some cases, Klingler’s dissection on its own is able to demonstrate shortcomings of tractography. For example, a study that performed dissections on fetal brains revealed that several of the main white-matter pathways were present, at earlier gestational stages than what had been previously shown by dMRI studies (Horgos et al., 2020). This suggests that the inability of tractography to reconstruct these pathways in utero is likely to be due to technical limitations of fetal MRI scanning.
Zemmoura et al. (2014) used a laser scanner to capture the surface and texture of a post mortem brain repeatedly as it underwent Klingler’s dissection. They then used this reconstruction to align ex vivo MRI and dissection results from the same brain. They reported a total accuracy for the method in the order of 1 mm. This included the accuracy of the surface-based, cross-modal registration, the deformation of the specimen during dissection, and the distance between two consecutive surface acquisitions with the laser scanner. Alternatively, De Benedictis et al. (2018) used photogrammetry to collect point clouds of the surface of a human brain at consecutive stages of Klingler’s dissection and registered them to a surface obtained from a structural MRI scan. Techniques such as these may facilitate quantitative comparisons of dMRI tractography and dissections in the future.
4.2.3. Limitations
Although the precision of Klingler’s dissection method is sometimes questioned, an electron microscopy study of fiber microstructure at different stages during the freezing, thawing, and dissection showed that, while the procedure destroyed most extra-axonal structures, it preserved myelin sheaths (Zemmoura et al., 2016).
Nonetheless, Klingler’s technique has several shortcomings as a tool for the validation of dMRI tractography. First, it cannot chart the complete trajectory of fibers, as it cannot follow them into the grey matter. Thus, the exact termination of axon bundles in the cortex or subcortical structures cannot be determined. Furthermore, the technique has difficulty following fibers through areas of dense crossing, as in the centrum semiovale, where commissural, projection, and association fibers intersect. Klingler’s technique is suitable for dissecting large pathways, but not for distinguishing small axon bundles that travel through them or for mapping the topographic organization of smaller axon bundles within the large pathways.
There are several steps in the preparation of the brain that are key for a successful comparison between dissection and dMRI: early extraction of the brain after death, a long fixation time at a low concentration of formalin, and a long period of freezing (Zemmoura et al., 2014). Any deviation from best practices can lead to errors. If the brain is to also undergo MRI scanning, a short post mortem interval (within 24 h of death) is key for obtaining good MR contrast. This limits the availability of suitable specimens. Finally, dissection with Klingler’s technique is time consuming and requires extensive neuroanatomical expertise. As a result, most studies are performed on a small number of specimens. Given the substantial inter-individual variability in the geometry of the human brain, and the fact that the dissection is typically compared to dMRI tractography from a different set of brains, it is difficult to ascertain if any discrepancies between dissection and tractography results are due to errors of tractography or true individual differences.
5. Validation of fiber orientations
5.1. Histological stains
5.1.1. Methodology
Histology is used extensively in research to describe tissue microanatomy and in clinical practice for the diagnosis and staging of disease through tissue biopsies. Excised tissue is sectioned into thin slices and stained chemically. Histology slides can be digitized using high-throughput slide scanners, producing 2D images with micron or sub-micron resolution. In this section, we focus on the histological stains that are most relevant to visualizing fiber orientations. These include myelin stains (Heidenhain-Woelcke, luxol fast blue), silver stains (Bodian, Gallyas), and others. An alternative approach involves lipophilic dyes that act as post mortem tracers. While these techniques have been used mainly to validate fiber configurations locally within a histological section, it is also possible to apply 3D reconstruction to the sections and use them to follow fiber bundles through the brain (Mollink et al., 2016; Alho et al., 2021).
(i). Myelin stains
The modified Heidenhain-Woelcke stain (Bürgel et al., 1997; Holl et al., 2011) was designed to provide contrast to distinguish between densely packed axon bundles, such as the optic radiation in post mortem human brain. Traditional myelin stains do not provide contrast to distinguish between different axon bundles. The modification of this protocol inactivates the chromatogen complexes in the thinnest myelin sheaths. This produces a graded reduction in myelin staining in white matter that appears to be proportional to the amount of myelination (Bürgel et al., 1997, 1999, 2006). This myelin stain is based on the presence of lipoproteins in the neuroceratine skeleton of myelin sheaths (Bürgel et al., 1997).
Luxol fast blue (LFB) stains myelin blue. It is suitable for formalin-fixed and paraffin-embedded tissue. The conventional LFB method is especially useful in the central nervous system, but its weak contrast limits its use in peripheral nerves (Carriel et al., 2017). It stains the whole subcortical white matter blue and is not able to distinguish the various white-matter fasciculi or superficial fibers. However, the stria of Gennari in the primary visual cortex, where myelinated fibers are abundant, can be identified with LFB (Fig. 3; see also Kleinnijenhuis, 2014). Conventional LFB can be modified to improve its contrast. The Klüver-Barrera stain, which combines LFB with cresyl violet, stains cell nuclei pink or purple (Klüver and Barrera, 1953). The LFB MBS salt stains the myelin sheet blue and, in ethanol solution, the anion of the salt binds to the cationic elements of the tissue. Further processing removes weakly bound anions from gray matter, while the stronger ionic bonds with the lipoproteins in the myelin sheet remain intact.
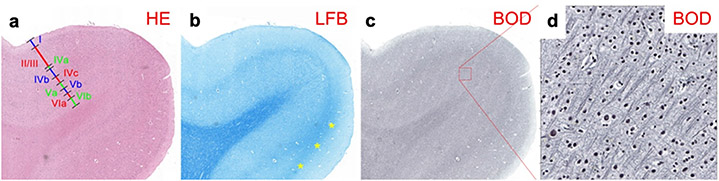
Fig. 3.
Histological sections from paraffin-embedded human brain samples around the calcarine sulcus containing the stria of Gennari, stained with: a: Hematoxylin & Eosin (HE; 5 μm). Cortical layers are identified as I-VIb. b: Luxol Fast Blue (LFB; 5 μm). c: Bodian (BOD; 6 μm). d: Detail of g. (Adapted from Kleinnijenhuis, 2014.)
(ii). Silver stains
Bodian is a silver stain that stains all neurites black (Bodian, 1936). It is argyrophilic, i.e., ions from a silver proteinate solution (combined with metallic copper) bind to neurofilaments in the cytoskeleton (Gambetti et al., 1981). The silver protein oxidizes the metallic copper, and both are reduced onto the section by hydroquinone. During a process known as toning, both silver and copper are replaced by gold, resulting in more intense staining (Uchihara 2007). Bodian stains all axons, dendrites, and cell body.
Bodian is compared to LFB in Fig. 3. The LFB-stained section has a particularly high fiber volume fraction in the white matter and stria of Gennari, where myelinated fibers are abundant. In the infragranular layers, LFB staining is much denser when compared to the supragranular layers. The Bodian stain shows modest contrast between gray and white matter. However, more detail can be seen intracortically with Bodian than with LFB. In the supragranular layers, which appear rich in unmyelinated fibers, Bodian staining is relatively denser than LFB.
Gallyas is another silver stain for myelin (Gallyas, 1979). It labels myelin well and produces clearly interpretable histology images. However, it is less consistent than other protocols, often exhibiting substantial variance within and between tissue probes (Seehaus et al., 2015).
(iii). Other techniques for labeling myelin
The black-gold stain (Schmued and Slikker, 1999) and Heidenhain-Woelcke stain (Romeis, 1989) have also been used to map myeloarchitecture in the human cortex (Eickhoff et al., 2005). Finally, immunohistochemical approaches to the identification of myelin use antibodies against myelin basic-protein (MBP; Kuhlmann et al., 2017) or proteolipid-protein (PLP; Mollink et al., 2017). For PLP staining in Mollink et al (2017), the tissue was paraffin-embedded and sections were counterstained with haematoxylin (HE).
(iv). Lipophilic dyes
Lipophilic carbocyanine dyes, such as DiI and DiO, spread by lateral diffusion within the cell membrane (Honig and Hume 1989a,b). These dyes can be used as post mortem tracers in the human brain, where the use of active-transport tracers (see Section 4.1.1) is not an option. However, tracing with DiI in human post mortem material is challenging. Although the speed of diffusion increases with temperature, the propagation of these dyes in the tissue is very slow. Hence, they can only be used to trace short-range connections, e.g., to follow fibers within a histological section. Tangential spread of about 8 mm was shown with DiI in the hippocampal formation (Tardif and Clarke, 2001). The technique is also appropriate for showing dendritic alterations in cortical neurons (Thal et al., 2008). A recent study described a modification of the method, where ethanol-dissolved DiI was used to achieve much faster diffusion than conventional DiI in fixed human brain (Sivukhina et al., 2021).
5.1.2. Comparison to dMRI
In the following we discuss studies that used histological stains to validate fiber orientation estimates. These studies varied widely in terms of their dMRI acquisition protocols. They ranged from around 20 diffusion-encoding directions with a low b-value, in which case only single-tensor fitting could be performed, to 514 directions with a Cartesian-grid sampling scheme, in which case full orientation distribution functions (ODFs) could be fit to the data.
Most of these studies relied on myelin stains. In-plane (2D) fiber orientations were extracted from the histological sections by manual labeling (Leergaard et al., 2010), Fourier analysis (Choe et al., 2012), or structure tensor analysis (Seehaus et al., 2015; Schilling et al., 2017b). Reported angular errors include 5.7° for ODFs in a two-way fiber crossing area of rat brain (Leergaard et al., 2010) and less than 10° for tensors in a single-fiber area of owl monkey brain (Choe et al., 2012). The angular error of tensors in human M1 was found to increase from 10° to 40° as the fractional anisotropy (FA) decreased from 0.3, indicating more coherent fibers, to 0.05, indicating less coherent fibers due to more fanning or crossing (Seehaus et al., 2015).
A potential complication when evaluating dMRI orientation reconstruction methods in terms of their angular error is that the methods that tend to detect more fiber populations, i.e., produce ODFs with more peaks (some of which may be spurious), also tend to have lower angular errors. Thus it is important to also validate the number of peaks. A study that compared the number of fiber populations extracted from myelin-stained histological sections to that detected by dMRI found that this number increased as the voxel size decreased (Schilling et al., 2017b). This may seem counter-intuitive at first, if one expects that increasing the spatial resolution should lead to more voxels with a single fiber population. However, the multiple, distinct fiber populations found in smaller voxels can merge into single but more dispersed fiber populations as the voxel size increases. This is an example where the ground-truth fiber configurations obtained from post mortem microscopy can challenge the simplistic assumptions that are made in the development of dMRI analysis techniques.
An alternative to myelin staining is to stain sections of white matter with DiI or DiA (fluorescent lipophilic dyes) and subsequently image them with confocal microscopy. In this case, axonal orientations can be obtained with structure tensor analysis (Budde and Frank 2012). A benefit of this approach is that it can be extended to compute not only in-plane but 3D orientations from each histological section (Khan et al. 2015). A study that applied this technique to the squirrel monkey brain reported angular errors of 11.2° for tensors and 6.4° for fiber ODFs in areas with a single fiber population, and 10.4°/11.6° for fiber ODFs in the primary/secondary orientation of crossing-fiber areas (Schilling et al., 2016). Fiber ODFs had less than 20% success rate at resolving fiber populations that crossed at angles smaller than 60°. A follow-up study, which examined a greater variety of single-shell dMRI protocols and reconstruction methods for resolving crossing fibers, reported a median angular error of around 10° in voxels with a single fiber population and 11°/16° in the primary/secondary peak of voxels with multiple fiber populations (Schilling et al., 2018). There was little change in the angular error when the b-value increased from 6,000 to 12,000 s/mm2 or when the number of diffusion-encoding directions increased from 64 to 96.
5.1.3. Limitations
Histological processing involves a laborious sequence of steps, which include embedding, sectioning, mounting on glass slides, staining, and cover-slipping. These procedures require considerable expertise and can be error-prone. Notably, the tissue undergoes non-linear physical deformations (warping and tearing) during sectioning. Such deformations make it difficult to align consecutive histological sections to each other and to the target dMRI volumes. Complex registration frameworks have been proposed to reduce such distortions and improve the alignment of histological and MRI data (Lebenberg et al., 2010; Choe et al., 2011; Adler et al., 2014; Majka and Wójcik 2016; Iglesias et al., 2018). A common approach is to align each distorted histological section to an undistorted blockface photograph taken before the section is cut, and then align the stacked sections from the blockface space to the MRI volume. This involves a series of 2D (slice-to-slice) registrations, followed by a 3D (volume-to-volume) registration. The registration algorithms used in each step involve several free parameters (deformation model, image similarity metric, regularization metrics, multi-resolution scheme, interpolation method, etc.) Each of these has its own trade-offs and can thus introduce subjectivity. At every step of the process, neuroanatomical expertise is key for evaluating the quality of the registration.
In addition to deformations due to sectioning, the dehydration that the tissue undergoes during staining can lead to tissue shrinkage (Wehrl et al., 2015; Williams et al., 1997). This may introduce discrepancies in fiber orientations pre- vs. post-staining, which may compound the estimated angular errors of dMRI orientations. It is important, however, to remember the difference in scale between the two modalities. Errors at the microscopic scale of the histological data may not have a significant impact on computations performed at the mm scale of the dMRI data.
Another possible concern arises when only in-plane fiber orientations are available from the histological data. In this case, the 3D diffusion orientations are projected onto the plane of the histological section and the angular error is computed in 2D. One may question whether such a comparison is as informative as one that uses the full 3D fiber orientations. Encouragingly, 2D and 3D angular errors reported in the literature (see previous section) are comparable. Finally, validation studies that rely on histology require that fiber orientations be computed, e.g., by Fourier or structure tensor analysis, from the stained and scanned sections. These image processing steps can be an additional source of errors. The following section describes optical imaging techniques that can measure fiber orientations directly, as an intrinsic contrast of the tissue.
5.2. Optical imaging
5.2.1. Methodology
The 21st century has seen a renaissance in light microscopy applications in neuroscience, driven by a combination of advances in tissue preparation and labeling methods, automation for faster image acquisition, and increased computational power. Here we focus on the latest optical imaging techniques that are specifically targeted at the visualization of axonal orientations.
Polarization microscopy and polarization-sensitive optical coherence tomography belong to the family of label-free methods. That is, they do not use exogenous contrast agents, such as stains, dyes, or tracers. Instead, they rely exclusively on a contrast mechanism that is intrinsic to the tissue. Specifically, these methods rely on birefringence, a property of anisotropic tissues. The use of polarization microscopy as a tool for visualizing myelinated fibers in both normal and pathological nervous tissue has been described in numerous studies for more than a century (e.g., Ehrenberg 1849, Brodmann 1903, Fraher et al. 1970, Miklossy et al. 1987). The basic principle is to generate polarized light, pass it through a thin brain section, and measure alterations in the polarization state of the light. This generates contrast between structures with different optic axis orientations. In white matter, the optic axis of the tissue is defined by the orientation of myelinated axons. For polarization microscopy, most microscopes operate in transmission mode, with few exceptions working in reflection mode (Takata et al., 2018).
The most prominent method for polarization microscopy is 3D Polarized Light Imaging (3D-PLI), introduced by Axer M et al. (2011a,b). It uses a physical model to estimate the orientation of the optic axis of the underlying tissue directly from the measured sinusoidal signal. Fiber orientations can be not only reconstructed within sections, but also followed across sections. The orientation vectors can then be displayed as color-coded fiber orientation maps (FOMs) or combined over a neighborhood of microscopic-resolution voxels to compute a fiber orientation distribution (FOD) (Axer et al., 2016; Alimi et al., 2020). When the neighborhood over which the FOD is computed represents a mesoscopic-resolution dMRI voxel, this FOD can serve as the ground truth for validating the FOD or ODF obtained from dMRI.
Brain preparation is crucial in polarization microscopy, as the organization of the lipid bilayers composing the myelin sheaths has to be preserved. The tissue is immersed in a buffered solution of formaldehyde (4% in Axer M et al., 2011a,b; 7.7% in Henssen et al., 2019) for several days to months depending on the sample size, and in a cryoprotectant such as glycerin or sucrose. Sectioning is done with a cryostat microtome. In principle, PLI could be performed on sections of any thickness. In practice, however, due to constraints related to cryo-sectioning and handling large-area sections, the typical thickness is 50-100 μm, i.e., 2-5 times thicker than the sections used for conventional histology (e.g., Amunts et al. 2020). Polarizing microscopes can achieve in-plane resolutions ranging from 100 μm (Axer H et al., 2011), 64 μm (Axer M et al., 2011a), 4 μm (Mollink et al., 2017), to 1.3 μm (Reckfort et al., 2015), and fields of view ranging from a few mm2 to a whole human brain section (up to 300 cm2). Large areas of interest are imaged tile-wise and the tiles are assembled by stitching.
The use of PLI to image brain tissue has been demonstrated in human (Axer et al., 2011a,b; Caspers et al., 2015; Mollink et al., 2017; Zeineh et al., 2017; Henssen et al., 2019), seal (Dohmen et al., 2015), rat (Schubert et al., 2016, 2018), pigeon (Herold et al., 2018; Stacho et al., 2020), and vervet monkey (Takemura et al., 2020). Examples of the detailed visualizations of cortical and white-matter fiber architecture that can be achieved by PLI are shown in Fig. 4. Research is ongoing on several extensions to this technology. Transmitted light intensity measurements have recently been shown to differentiate between areas with low fiber density and in-plane crossing fibers vs. areas with out-of-plane fibers, thus removing a potential confound for PLI (Menzel et al., 2020). Finally, scattered light imaging (SLI) is a new, label-free technique that can resolve crossing fibers within a microscopic-scale (6.3 μm) voxel and can be integrated into a polarization microscope (Menzel et al., 2020, 2021).
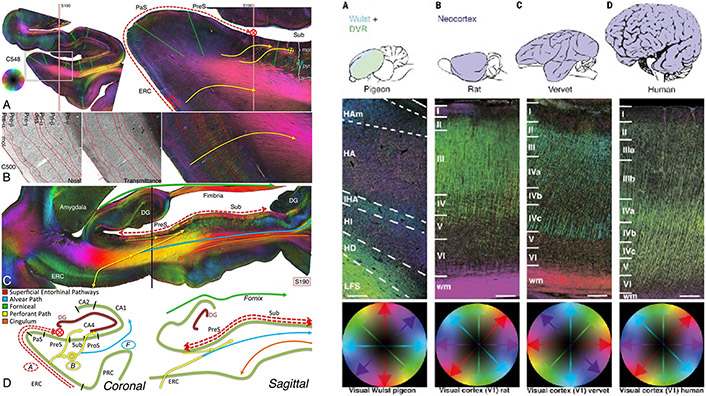
Fig. 4.
Fiber orientation maps acquired with 3D-PLI. Left: Entorhinal pathways and the angular bundle in the human hippocampus (reused from Zeineh et al., 2017). Right: 3D fiber architecture of the avian and mammalian primary visual regions (reused from Stacho et al., 2020). Fiber orientations are encoded in HSV color space.
Optical coherence tomography (OCT) is another approach to label-free imaging. Unlike the polarization microscopy methods described above, OCT does not operate in transmission mode, i.e., the light does not go through a section of tissue. Instead, OCT relies on the back-scattering of light from a block of tissue, analogous to ultrasound technologies. As a result, it does not require the tissue to be sectioned before it is imaged. It uses optical interferometry to image depth-resolved tissue structures at resolutions in the order of 1–20 μm (Huang et al., 1991). After the superficial layer of the tissue block is imaged, it is sectioned to reveal and image the next layer. This technique has been successfully employed in various human brain applications both ex vivo and in vivo (Boppart et al., 1998; Böhringer et al., 2009; Assayag et al., 2013; Magnain et al., 2014, 2015, 2016, 2019).
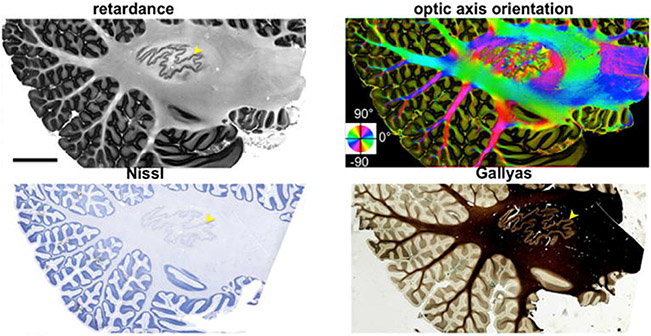
Polarization-sensitive OCT (PSOCT) is a variation of OCT that was introduced by De Boer et al. (1997) to measure fiber orientations. It uses polarized light to probe birefringence. Wang et al. (2018) developed a fully automatic, serial-sectioning PSOCT (as-PSOCT) system for volumetric reconstruction of human brain samples at 3.5 μm in-plane and 50 μm through-plane voxel size. The as-PSOCT system is composed of a spectral domain PSOCT, motorized xyz translational stages enabling tile-wise imaging, and a vibratome to repeatedly remove a superficial layer slice of the formalin fixated tissue block upon completion of the full area scan. The implemented pipeline allows imaging and reconstruction of cm3-sized tissue blocks over multiple hours without the need for human intervention. The contrasts obtained with PSOCT include the light reflectivity provided by classical OCT, as well as additional contrasts derived from the polarization of light. The latter are the retardance, which is associated with myelin content, and the en face optic axis orientation, which is the orientation of fibers within the imaging plane. The use of PSOCT to image intricate fiber architectures in the brain has been demonstrated in mouse (Nakaji et al., 2008; Wang et al., 2011; Wang et al., 2016), rat (Wang et al., 2014a), and human (Wang et al., 2014b; Wang et al., 2018; Jones et al., 2020; Jones et al., 2021). Fig. 5 shows an example of PSOCT contrasts obtained from a human cerebellum
Fig. 5.
Top: PSOCT retardance and optic axis orientation maps of a 15 cm2 parasagittal section of the human cerebellum. Bottom: Nissl stain and Gallyas stain from the same sample. (Reused from Wang et al., 2018).
Finally, an alternative to label-free methods is tissue clearing, followed by labeling, e.g., with lipophilic dyes or immunohistochemistry of myelin-specific proteins, and imaging, e.g., with confocal fluorescence microscopy (CFM) or two-photon fluorescence microscopy (TPFM). Tissue clearing can be performed with Clear Lipid-exchanged Acrylamide-hybridized Rigid Imaging/Immunostaining/In situ hybridization-compatible Tissue-hYdrogel (CLARITY; Chung et al., 2013). Clearing involves infusing the tissue with hydrogel, which is then polymerized to act as a support structure for the tissue. Lipids can then be removed from the tissue, rendering it optically transparent while preserving the rest of its biomolecular content. Cleared tissue samples can be imaged without sectioning and, consequently, without the need for tile stitching or slice alignment procedures. Tissue clearing methods are an active area of research, with ongoing efforts to make them applicable to larger samples and to the higher myelin density of the human brain (Tomer et al 2014; Yang et al., 2014; Costantini et al., 2015, 2019; Hou et al., 2015; Murray et al., 2015; Park et al., 2019; Zhao et al., 2020). After clearing, it is possible to perform consecutive rounds of staining with different fluorescent dyes on the same tissue sample with System-Wide control of Interaction Time and kinetics of CHemicals (SWITCH; Murray et al., 2015). For the purpose of comparison to dMRI orientation estimates, clarified tissue is typically stained for neurofilaments (Stolp et al., 2018; Leuze, et al 2021). As opposed to label-free techniques like PLI and PSOCT, which acquire direct measurements of axonal orientations, here the orientations have to be computed from the fluorescence microscopy images by structure tensor analysis, similarly to the conventional histological stains of Section 5.1.2.
5.2.2. Comparison to dMRI
Qualitative comparisons of fiber orientation maps obtained with PLI and dMRI from the same samples have been performed in the human brainstem (Henssen et al., 2019). A quantitative validation study compared the in-plane dispersion of fiber orientations in the human corpus callosum, as estimated from histology, PLI, and dMRI in the same samples (Mollink et al., 2017). The authors reported correlation coefficients of r = 0.79 between dMRI and histology, and r = 0.6 between dMRI and PLI.
A study that performed voxel-wise comparisons of optic axis orientation measurements from PSOCT and principal eigenvectors of tensors derived from dMRI showed low average angular error but high variability (5.4°± 32.5°) in a human medulla oblongata (Wang et al., 2014b). A more recent study used PSOCT to evaluate the accuracy of dMRI orientation estimates obtained with different q-space sampling schemes (Cartesian, single- and multi-shell), spatial resolutions, and orientation reconstruction methods in human white-matter samples (Jones et al., 2020). The spatial resolution emerged as a key factor, with accuracy deteriorating as dMRI voxel size increased from 1 to 2 mm. In comparison, the benefit of increasing the number of directions from 128 to 514 and the maximum b-value from 12,000 to 40,000 s/mm2 was modest. A follow-up study showed that a 171-direction, undersampled Cartesian scheme can achieve both the accuracy of the fully sampled Cartesian scheme and the flexibility of multi-shell schemes (Jones et al., 2021). The best- and worst-case mean angular errors, among all sampling schemes and orientation reconstruction methods at the native resolution of the dMRI data, were 8.3°/15.1° in single-fiber areas, 18.7°/35.7° in a fiber branching area, 20.2°/42.2° in an interdigitated crossing area, and 15.7°/32.7° in a separable crossing area. Thus the branching and interdigitated crossing were particularly challenging fiber configurations for dMRI (Jones et al., 2020).
Two studies have used CFM to image brain tissue processed with CLARITY, and compare FODs extracted with 3D structure tensor analysis (see Section 5.1.2) to dMRI orientations in the same sample. The first study performed a qualitative comparison and showed moderate agreement between FODs from dMRI and those obtained from a variety of fluorescent dyes, including for neurofilaments (Stolp et al., 2018). The second study performed a quantitative comparison of FODs extracted from a neurofilament stain and dMRI orientations in the same human sample (Leuze et al., 2021). Angular errors of 19°± 15° were reported between the principal fiber orientations obtained from CLARITY microscopy and dMRI, in a mainly single-fiber area. This error is about twice as big as the errors previously reported in single-fiber areas (see above and 5.1.2) using 2D structure tensor analysis on myelin stains (Leergaard et al., 2010; Choe et al., 2012; Seehaus et al., 2015), 3D structure tensor analysis on myelin stains (Schilling et al., 2016; Schilling et al., 2018) or 2D orientations measured with PSOCT (Jones et al., 2020; Jones et al., 2021).
5.2.3. Limitations
Label-free optical imaging methods, like PLI and PSOCT, obtain direct measurements of axonal orientation angles. That is, no image processing operations like structure tensor analysis are necessary to estimate the fiber orientation vectors from the images. This is unlike methods that involve staining the tissue, whether conventionally (Section 5.1.1) or after clearing with CLARITY. Removing both the possible tissue shrinkage sustained during conventional histological staining (see Section 5.1.3) and the additional image processing step is the advantage of label-free methods like PLI and PSOCT.
However, like histological techniques, PLI requires tissue to be sectioned and mounted before imaging, which may introduce deformations. The importance of accurate cross-modal registration for mitigating histological distortions was discussed in Section 5.1.3. The typical section thickness used for PLI is greater than that commonly used for conventional histology, and this may lead to somewhat less severe distortions. Custom registration frameworks have been developed for registering PLI to MRI (Ali et al., 2018).
The advantage of PSOCT in this regard is that it images the superficial layer of tissue before sectioning rather than after. Thus, the PSOCT orientation and retardance maps do not suffer from such deformations and do not require any registration between slices. However, PSOCT scanning is at present much slower, which limits the sample sizes that can be imaged in a practical amount of time.
A possible concern that was discussed in the context of histological techniques (see Section 5.1.3), and that also applies to label-free imaging methods when in-plane orientations are measured, is whether evaluating the accuracy of dMRI orientations in 2D results in any bias. Encouragingly, the angular errors computed in single-fiber areas by PSOCT agree with those reported using conventional histological techniques either in 2D or in 3D (Section 5.1.2). Furthermore, the in-plane angular errors between dMRI and PSOCT orientations were not found to be associated with the magnitude of the through-plane component of the dMRI orientations (Jones et al., 2020). One approach that has been proposed to infer through-plane fiber orientations with PSOCT is to apply structure tensor analysis along the through-plane dimension of the stacked retardance maps (Wang et al., 2018). Another possibility is to infer the through-plane orientation from measurements of in-plane orientations with two or more light incidence angles (Ugryumova et al., 2006; Ugryumova et al., 2009). In PLI, a forward model of birefringence and fiber orientation measurements from multiple oblique views is used to infer 3D orientations directly (Axer et al., 2011b; Schmitz et al., 2018). These techniques, however, have not yet been used in dMRI validation studies.
In principle, processing with CLARITY should allow tissue to be imaged intact, i.e., without sectioning. However, as the clearing process removes lipids from the myelin and membranes, the tissue becomes softer, deforms, and expands. Importantly, all MRI scanning must be completed before clearing, as the latter eliminates MR contrasts (Leuze et al., 2017). Thus, tissue deformation and expansion induced by clearing would make accurate alignment to dMRI challenging. As a result, studies that performed voxel-wise comparisons to dMRI used a passive form of CLARITY (Tomer et al 2014; Yang et al., 2014). This approach reduces tissue expansion but is slow and can thus only be applied to tissue sections (e.g., a 1 cm2 area with 500 μm thickness in Leuze et al. (2021). In Leuze et al. (2017), a 315% increase in volume after one week of passive clearing was reported. Prior to microscopy, the clarified sections are placed in a refractive index matching solution that shrinks them back to approximately their initial size. After microscopy, affine registration is used to align sections to each other and/or to the dMRI volume (Stolp et al., 2018; Leuze et al., 2021).
A major challenge for all optical imaging techniques is scaling them to image the circuitry of the entire human brain at microscopic resolution. Cryo-sectioning and mounting sections with an area up to 15 × 10 cm2 and a thickness of 50 mm is well-known to result in section-unique, non-linear distortions. For PLI, where the brain is imaged after slicing, aligning large sections at the level of individual axons is difficult, even with extensive landmarks. For PSOCT, where each slice is cut after it is imaged, scaling up is a hardware problem, which will require the integration of a microtome that can handle an entire brain (frozen or embedded in solid materials) onto the OCT rig. For CLARITY processing, tissue volume is also not arbitrarily scalable in all directions, as the clearing solutions and dyes cannot penetrate an entire human brain. Deformations induced by clearing and sectioning once again make alignment of large slices at the level of individual axons a potentially insurmountable problem. Even if these technological hurdles are overcome in the coming years, optical imaging comes with staggering storage and computational requirements. For example, sampling a human brain volume of 1,200 cm3 with voxels sizes of 0.244 × 0.244 × 1 mm3 (TPFM), 1.3 × 1.3 × 60 mm3 (3D-PLI), or 3.5 × 3.5 × 15 mm3 (OCT) voxel sizes results in a total of 1016, 1013, or 1012 voxels, respectively. With multiple contrasts acquired and multiple subsequent processing steps, this leads to massive datasets that need to be transferred, stored, and analyzed. Access to supercomputing resources and specialized software will therefore be key for enabling fully digitized, high-throughput neuroanatomy at the microscale.
6. Validation of microstructure beyond fiber orientations
Microstructural models aim to interrogate tissue properties such as axon diameter, density, packing, and the degree of myelination, all of which are known to affect the diffusion of water molecules in the tissue (Beaulieu et al., 2002). These models are fit to the dMRI signal on a voxel-by-voxel basis, and the parameters of interest can then be averaged either over all voxels that intersect with a certain tract, or over consecutive cross-sections of the tract to generate an along-tract profile (Jones et al., 2005; O’Donnell et al., 2009; Bells et al., 2011; Colby et al., 2012; De Santis et al., 2014). This combination of microstructural modeling and tractography, sometimes referred to as tractometry, allows us to quantify differences in microstructure both between and along white-matter tracts.
To estimate microscopic tissue features from MR signals on order of millimetres, diffusion models rely on complex signal modelling with many strong assumptions (Jelescu and Budde, 2017). These assumptions are often violated in real tissue but they are necessary to make the models parsimonious enough to be fit to in vivo dMRI data. As a result, microstructure models also require validation, to assert the extent to which our MR parameters are sensitive to specific biological features of interest (Jelescu and Budde, 2017; Dyrby et al., 2018).
6.1. Methodology
Many of the methods discussed in Section 5 can also be used to validate microstructural models. Here, the validation strategy is inherently dependent on the tissue feature of interest (e.g., axon diameter, g-ratio, or the relative volume fractions of different microstructural compartments). Certain tissue features may require higher imaging resolutions, such as those obtained from micron-scale synchrotron x-ray computed tomography or electron microscopy.
Histological staining (Section 5.1) provides high specificity imaging of many tissue constituents, not only axons but also cell bodies (e.g., Nissl stain), glia (e.g., GFAP, which stains all glia, or CD68, which stains only activated microglia – a marker of inflammation) and proteins associated with pathology (e.g., pTDP-43 in ALS, Pallebage-Gamarallage et al, 2018). Analysis of histological slides include cell counting, characterization of cell morphology (e.g., Sholl 1953), extracting staining densities, or calculating the fraction of stained pixels over a local neighborhood.
Fluorescence microscopy (Section 5.2) allows more quantitative analyses, as, under certain conditions, fluorescence can be directly related to fluorophore concentration (Lichtman and Conchello, 2005). Further, fluorescent labeling allows for multiple fluorophores per tissue section, facilitating co-localization of multiple tissue features, and can be combined with tissue clearing and/or a wide range of microscopy methods to provide high resolution or 3D imaging. Together, these capabilities make fluorescence imaging a useful tool for quantifying cell or protein density, and the gross morphology of cells.
Label-free optical imaging methods (Section 5.2), such as PLI and PSOCT, can quantify not only fiber orientations but also the amount of myelin per pixel (Axer et al., 2011b; Wang et al., 2018; Mollink et al., 2019; see also Fig. 5). The latter is often indirectly associated with MR parameters sensitive to axons, e.g., fractional anisotropy (FA) from diffusion tensor imaging (DTI; Basser et al., 1994).
Micron-scale synchrotron x-ray computed tomography (microCT) is a non-destructive, 3D imaging technique that can provide micron resolution images of thick (~1cm cubed) tissue blocks (Foxley et al., 2020; Trinkle et al. 2021; Andersson et al., 2021). Here, osmium-stained tissue is rotated through a synchrotron x-ray beam, after which a high-resolution 3D volume is reconstructed from a series of 2D back-projections. MicroCT of neural tissue can capture complex, 3D cellular morphologies (Andersson et al., 2021), as well as detailed, long-range axonal projections (Foxley et al., 2020), making it a valuable, up-and-coming tool for microstructure validation. Furthermore, microCT can be combined with electron microscopy to provide multi-scale imaging of the same tissue (Foxley et al., 2020).
Electron microscopy (EM) can resolve nanometer-scale structures from tissue stained with heavy metals (typically osmium). It allows us to characterize the detailed morphology of neurons and glia, or fine anatomical structures such as layers of the myelin lamella, synapses on post-synaptic neurons, microtubules in the cytoskeleton or mitochondria within the axoplasm (Kasthuri et al., 2015). Methods for EM can vary both in terms of tissue processing (e.g., tape-based or block-face) and in terms of imaging (e.g., back-scattered or transmission EM) (Lichtman et al., 2014). In serial, block-face scanning EM (SBEM; Denk and Hostmann, 2004), the top face of the sample is first imaged (using back-scattered electron detection) and then sectioned in situ, using a microtome or focused ion beam. The process is then repeated to produce a series of well-aligned images. Alternatively, using the tape-based method (Kasthuri et al., 2015), the tissue block is first sectioned using an ultramicrotome and mounted onto tape, after which the sections are imaged serially by either transmission or back-scattered EM. Where the SBEM images exhibit little deformation or misalignment, tape-based serial sections can be rotated, stretched, or otherwise misaligned with respect to each other, making reconstruction of the 3D volume more challenging. This is counterbalanced by the more limited lateral resolution of SBEM compared to transmission EM. With the development of state-of-the-art, multibeam serial EM (Eberle and Zeidler, 2018), nanometer resolution images can now be acquired over tissue volumes comparable to a dMRI voxel (~mm).
6.2. Comparison to dMRI
Diffusion models can be used to extract parameters sensitive to a wide range of tissue features. For details on the plethora of competing dMRI microstructural models and their relative strengths and weaknesses, we refer the reader to the many excellent reviews on the topic (e.g., Jelescu and Budde 2017,Novikov et al. 2018, Alexander et al. 2019, Jelescu et al. 2020). Below we provide only a few, non-exhaustive examples where tissue features from microscopy have been related to dMRI parameters.
6.2.1. Density of cells, myelin, or other tissue features
(i). Validation of DTI indices:
Although it is arguably a signal model rather than biophysical model of the tissue, DTI is widely used due to its simplicity. Indices extracted from DTI, such as FA and mean/axial/radial diffusivity (MD/AD/RD), have been correlated with a variety of microscopy metrics related to myelin or cell density.
Histological stains:
Meta-analyses of studies that estimated myelin density from histology reveal that, in general, myelin correlates positively with FA and negatively with RD, whereas its relationship to AD or MD is less clear (Mancini et al., 2020; Lazari and Lipp, 2021). Inconsistencies in results across studies are likely related to the fact that DTI indices are influenced not only by myelin, but also a range of other factors, such as fibre morphology, density or dispersion. As an alternative to myelin content, a tissue anisotropy index computed by structure-tensor analysis of DiI-stained histological sections has also been found to correlate with FA in rat (Budde and Frank, 2012) and macaque (Khan et al., 2015). Furthermore, FA has been related to markers of neuroinflammation, where an increased density of CD68, a marker of activated microglia, was associated with reduced FA in traumatic brain injury (Soni et al., 2020).
Label-free optical imaging:
Retardance is a tissue property related to myelin content. A study that compared retardance from PSOCT to FA from DTI in the same human medulla oblongata sample reported correlation as high as r = 0.9 (Wang et al., 2014b). In an ALS study of the perforant path, retardance from PLI correlated positively with FA (r = 0.52) (Mollink et al., 2019). Another study showed moderate correlations between reflectivity and attenuation as measured with (non-PS) OCT and FA in mouse brain (Lefebvre et al., 2017).
Fluorescence imaging:
A study using CFM in the spinal cord of a pre- and post-symptomatic ALS mouse model found that decreases in FA and AD and increases in RD correlated with changes in axonal fluorescence intensity and membrane cellular markers (Gatto et al., 2018).
Tissue clearing:
A study that imaged clarified mouse brains with CFM or TPFM, showed positive correlations between FA and neurite density from two-photon microscopy, which were strong (r = 0.87) in medial lemniscus and less strong (r = 0.51) in caudate nucleus and putamen (Kamagata et al., 2016). Another study reported that the density of myelin basic protein immunofluorescence correlated strongly with FA and, in some cases, with RD (Chang et al., 2017). A study in mouse hippocampus found fluorescent staining for cell nuclei to be correlated with MD, RD, and AD; neurofilament staining to be correlated with MD and RD; and astrocyte staining to be correlated with FA (Stolp et al., 2018).
(ii). Validation of multi-compartment diffusion models:
These models typically estimate the signal fraction associated with different tissue features (e.g., compartments associated with axons, soma, or the extra-cellular space). Here, the intra-axonal signal fraction from various such models has been shown to correlate positively with histological estimates of myelin, a proxy for neurite density (Jespersen et al., 2010; Grussu et al., 2017). In the cortex, Nissl-stained histological maps of cell body density qualitatively mirror recent diffusion maps of cell soma density (Palombo et al., 2020). In comparison, the relationship between glia and diffusion parameters remains relatively unexplored, with few dMRI models accounting for a specific glia compartment. Intriguingly, the increased density of activated microglia, a marker of inflammation, has recently been related to the dispersion parameter of the neurite orientation dispersion and density imaging (NODDI) model (Yi et al., 2019), which is argued to be a marker for greater hindered diffusion in the extra-cellular space.
These MR signal fractions can then be converted to microscopic volume fractions by accounting for the T2 properties of the various compartments. This includes correcting for the substantial fraction of myelin, which is “MR-invisible” at the echo times of typical diffusion experiments due to its ultra-short T2 (~10ms, see Mackay et al., 1994). Accurate quantification of “volume fractions” typically requires higher resolution 3D imaging, such as from microCT or EM. When corrected, EM estimates of 30-50% intra-axonal space in the white matter translate to MR-visible fractions of 40-60% (Xu et al., 2014; Stikov et al., 2015; Jelescu et al., 2016; Lampinen et al., 2019), as is found in many diffusion models (Jelescu and Budde, 2017; Jespersen et al., 2010; Kelm et al., 2016).
6.2.2. Axon morphology
(i). Validation of axon caliber:
The introduction of human MRI scanners with ultra-high gradient strengths was a critical advance towards probing axon diameter in the living human brain (Burcaw et al., 2015; Huang et al., 2015; Huang et al., 2020; Veraart et al., 2020). This reinvigorated interest in validating dMRI-based estimates of axon caliber. High-resolution microscopy has been used to estimate axon diameters, or the axon diameter distribution over a given area, by fitting a circle or ellipse to the circumference of axons. It has shown that axons take tortuous trajectories through space, differ in their degree of myelination, have variable diameter along their length, and are characterized by both macro- and microscopic dispersion (Lee et al., 2019; Andersson et al., 2020). Early attempts to estimate axon diameters from dMRI, which used data acquired with older MRI gradient technology, often produced axon diameters up to an order of magnitude larger than those observed in microscopy (Assaf and Basser, 2005; Assaf et al., 2008; Barazany et al., 2009; Alexander et al., 2010). This discrepancy is now thought to be due to the dMRI signal from clinical-grade scanners lacking sensitivity to the intra-axonal space (Jelescu et al., 2020). Recent diffusion models, when applied to dMRI data collected with ultra-high gradients, provide estimates more in line with those from microscopy (Veraart et al., 2020). Further, many common diffusion models assume that axons are straight cylinders of fixed diameter, while the effect of complex axon morphologies on the diffusion signal is an area of active investigation (Budde and Frank, 2010; Nilsson et al., 2012; Fieremans et al., 2016; Ginsburger et al., 2018; Lee et al., 2019, 2020a,b; Brabec et al., 2020; Jelescu et al., 2020; Andersson et al., 2020; Andersson et al., 2021).
Histology:
Neurofilament-stained histological sections imaged at high resolution (~10 nm in-plane) can provide estimates of axon radii (Veraart et al., 2020). Using this method in fixed rat tissue, Veraart et al. (2020) estimated effective axon diameters of ~0.8-1.2 μm, which were closely aligned to, though slightly lower than, those estimated from a dMRI model using ultra-strong gradients (~1-1.4 μm).
MicroCT:
This technique can track 3D axons over some hundreds of microns to quantify along-fiber variations in axon diameter. Although so far limited to characterizing large diameter axons, Andersson et al found the axon caliber to be highly influenced by surrounding tissue features such as other fibers, cells, vacuoles and blood vessels (Andersson et al. 2021).
EM:
Wide axon diameters are further associated with the presence of mitochondria in EM data (Lee et al. 2020). The axon diameters estimated from EM data range from 0.1-10 μm, with the vast majority of axons having diameters below 3 μm (Aboitiz et al., ; Lee et al., 2019). Though dMRI microstructural models are often biased, i.e., overestimate axon diameters when compared to EM (Assaf and Basser, 2005; Assaf et al., 2008; Barazany et al., 2009; Alexander et al., 2010; Burcaw et al., 2015; Huang et al., 2015; Huang et al., 2020; Fan et al., 2020), they are able to replicate known variations across the brain (Fan et al., 2020), e.g., the low-high-low pattern of axon diameters across the corpus callosum (Barazany et al., 2009), which was previously demonstrated with EM (Aboitiz et al., 1992).
(ii) Validation of g-ratio:
Both microCT and EM data can provide estimates of the g-ratio, i.e., the ratio of the inner and outer (axon + myelin) diameter of the axon. These estimates can be used to validate MR indices that are sensitive to the g-ratio (Stikov et al., 2015; West et al. 2018; Mohammadi & Callaghan, 2021). Interestingly, a recent microCT study (Andersson et al., 2020) provides evidence for a fairly consistent myelin thickness along large axons, bar at the nodes of Ranvier, with g-ratio fluctuations being largely driven by variations in axon diameter.
6.3. Limitations
An important consideration for post mortem validation of tissue microstructure is that microscopy images of postmortem, fixed, processed tissue, may not be a faithful representation of the scanned or in vivo structure (Howard et al., 2019). Experimental animals typically undergo perfusion fixation at death, minimizing autolysis-related changes to the tissue microstructure such as the loosening and degradation of myelin (Hukkanen and Röyttä, 1987; Shepherd et al., 2009; Dyrby et al., 2018). In comparison, human tissue is typically immersion-fixed. As a result, the post mortem interval, i.e., the time between death and fixation, can be relatively long, leading to microstructure degradation (Shepherd et al., 2009), particularly for deep brain structures.
In addition, dMRI contrast differs post mortem vs. in vivo, which may require alterations to in vivo diffusion models. Formaldehyde fixation leads to the cross-linking of proteins, resulting in increased tissue rigidity and a reduction in diffusivity (Miller et al., 2011). This must be accounted for in diffusion microstructure models such as NODDI (Zhang et al., 2012), which assume fixed, pre-defined diffusivities for the tissue (Grussu et al., 2017). Furthermore, when applied to post mortem data, microstructural models frequently include a non-diffusing “dot-compartment” (Grussu et al., 2017; Palombo et al., 2020; Veraart et al., 2020), which represents immobilized water in fixed tissue. Though most studies provide evidence for this compartment (Stanisz et al., 1997; Alexander et al., 2010; Panagiotaki et al., 2010; Kaden et al., 2016; Veraart et al., 2020), others do not (Palombo et al., 2020). Consequently, best practice can include fitting both the in vivo “default” and ex vivo “dot-variant” models, and comparing the relative quality of the model fits (Palombo et al., 2020), e.g., using the corrected Akaike information criterion (Burnham and Anderson, 2002).
Validation studies should be wary of considering microscopy as a ground truth estimate of the tissue microstructure, rather than a biased approximation with its own sources of error (Howard et al., 2019). Firstly, the microscopy metric may be only semi-quantitative or indirectly linked to the feature of interest. For example, when stains such as DAB do not follow the Beer-Lambert law, the relationship between the stain density and chromogen concentration in a pixel is not linear. Consequently, the stain density is often considered only a proxy or semi-quantitative histology metric (Tolcos et al., 2016). Second, the microscopy may be biased to describing only a subset of the tissue microstructure. As each histology stain informs on only a subset of tissue features, consecutive slides may be differently stained to build a more complete description of the tissue. MicroCT and EM data may be biased towards large-diameter or myelinated axons (West et al., 2018; Andersson et al., 2020), which may confound validation of metrics associated with axon morphology. Third, tissue processing can lead to deformation of the tissue architecture. In tissue clearing, lipid removal relies on a process of tissue expansion and shrinkage, which may affect microstructural integrity. Tissue shrinkage is also a major concern for microCT and EM, which undergo the same tissue preparation. Unless a specific extra-cellular space preserving method is adopted (Korogod et al., 2015; Pallotto et al., 2015), EM images typically suggest little or no extra-cellular space, precluding EM-based validation of this compartment. In comparison, axonal volumes appear relatively unaffected (Korogod et al., 2015; Jelescu and Budde, 2017).
The non-selective nature of the osmium stain often used in microCT and EM imaging poses an additional challenge for the identification and segmentation of cells and other tissue features from the complex texture of the reconstructed 3D volume. The segmentation task is challenging for several reasons (Lichtman et al., 2014): (i) the stain is non-specific, hence different cell types must then be identified purely based on their morphology and/or localization with respect to other structures, (ii) the cells have complex morphology and are often intertwined, (iii) cellular processes often branch or fork, in which case two apparently separate structures in one image can in fact be part of the same cell, and (iv) in EM the in-plane and through-plane resolution of the non-isotropic images can differ by an order of magnitude (e.g., 3 × 3 × 30nm). Automated cell segmentation has greatly benefited from recent advances in machine learning approaches (Kleinnijenhuis et al., 2020; Abdollahzadeh et al., 2021), but some manual correction is often required for high precision (Kasthuri et al., 2015).
In high-resolution microscopy, the acquisition time and data storage often constrain the field of view that can be imaged. If a single cubic millimeter of tissue, i.e., one MRI voxel, were imaged with EM at nanometer resolution, it would yield several TB of data, and might take months or even years to image and analyze (Lichtman et al., 2014, Eberle and Zeidler, 2018). Consequently, nanometer EM techniques are often limited to characterizing small tissue blocks (50-100 μm3), which are sparsely sampled throughout the brain. Consequently, nanometer EM techniques are limited to characterizing small tissue blocks (50-100 μm3), which are sparsely sampled throughout the brain. The penetration of chemicals for tissue clearing currently limits the field of view in fluorescence imaging, as does the osmium-stain penetration in microCT (Trinkle et al., 2021). If the imaged block is not representative of the larger MRI voxel from which it is sampled, this may bias the comparison.
Microstructure validation studies are typically limited to small regions of interest. Future whole-brain MRI-microscopy comparisons would contribute significantly to the validation of along- and between-tract microstructural changes. Finally, it is important to remember that many dMRI microstructural indices are dependent on more than one feature of the underlying microstructure (e.g., FA depends on myelin content, fiber dispersion, etc.) Thus, with only a single microscopy contrast, we can often at best look for correlations between dMRI indices and microstructural features, rather than a measure of true accuracy of these indices. Future efforts to simultaneously analyze data from multiple microscopy contrasts will help to elucidate the unique contributions of different microstructural features to dMRI signals.
7. Discussion
In the previous sections we described a variety of methods for validating dMRI tractography, fiber orientations, and other microstructural properties of axon bundles in post mortem tissue. As should be clear by now, each of these methods has its own potential sources of errors and uncertainty. When faced with this fact, one may ask, “Is this really ground truth?” There are several important considerations here. First, these methods are not meant as push-button solutions for obtaining a correct answer. They should always be coupled with neuroanatomical expertise. The experienced anatomist can interpret the results of a validation study, place them in the context of centuries of knowledge on neuroanatomy, and ultimately evaluate the quality of the validation dataset itself. Second, small errors at the microscopic scale where these methods operate can still yield accurate results at the mesoscopic scale of dMRI. Third, there is great value in obtaining converging information from multiple sources of validation data. The fact that none of these validation methods are error-free or can provide ground truth on every cell in the brain does not mean that we should use none of these methods but that we should use many of them.
In comparison to in vivo neuroimaging studies, efforts on post mortem validation may appear to progress slowly, as data are collected on much smaller numbers of subjects, with time-consuming acquisition and post-processing. Nonetheless, we present here a growing body of knowledge, with several implications emerging for how dMRI data should be acquired and analyzed. For example, there is now accumulating evidence from tracer validation studies that probabilistic tractography has greater anatomical accuracy than deterministic tractography. This comes from studies that compared area-to-area connectivity matrices between dMRI tractography and existing tracer databases (Delettre et al., 2019; Girard et al., 2020), as well as studies that performed voxel-wise comparisons of dMRI tractography and tracer injections in the same NHP brains (Grisot et al., 2021; Maffei et al., 2021).
Furthermore, evidence on the limited benefit of very high b-values on the accuracy of ODFs and tractography is emerging from several independent sources, including histological staining (Schilling et al., 2018), PSOCT (Jones et al., 2020), and anatomic tracing (Ambrosen et al., 2020; Grisot et al., 2021). This does not necessarily mean that very high b-values do not contain useful information on fiber architectures. It may mean that existing methods for ODF reconstruction and tractography are not designed to take advantage of this information. This topic merits further investigation in the future. The same is true of converging evidence from PSOCT (Jones et al., 2020) and anatomic tracing (Grisot et al., 2021; Maffei et al., 2021) on the importance of resolving fiber configurations other than crossing, such as branching or turning, and the role that spatial resolution might play towards this end.
The studies that we have reviewed here offer a glimpse of the knowledge that can be gained by bridging the gap between whole-brain, mesoscopic-resolution MRI and microscopic-resolution imaging of smaller samples, ideally from the same brain. New technologies developed by the Connectome 2.0 project, discussed elsewhere in this issue (Huang et al., 2021), aim to push spatial resolution for both in vivo and ex vivo dMRI to the sub-mm level, thus narrowing this gap. Advanced computational methods will be necessary to improve alignment across modalities and overcome the differences in shape, dimensions, physical and morphological characteristics of the tissue at every step of data acquisition. A nested connectome reconstruction across scales, that combines the complementary virtues of many imaging techniques and utilizes machine learning approaches to predict missing information, will be advantageous for this purpose. For example, recent work used deep neural networks to predict fluorescence images of diverse cell and tissue structures from measurements of density, anisotropy, and orientation acquired with label-free imaging (Guo et al., 2020). Other examples include joint modeling of microscopy and dMRI, e.g., to overcome the degeneracy between fiber dispersion and radial diffusion in dMRI models (Howard et al., 2019), and training neural networks on paired optical imaging and dMRI data to infer complex fiber architectures directly from dMRI (Yendiki et al., 2020). Ultimately, the next frontier for the microscopic imaging modalities described in this review will be to use them not only to validate existing computational tools for inferring brain circuitry from mesoscopic dMRI, but to engineer the next generation of such tools.
Acknowledgments
A. Yendiki was supported by NIH grants R01-EB021265, R01-NS119911, P50-MH106435, and U01-EB026996. M. Aggarwal was supported by NIH grant R01-AG057991. M. Axer was supported by the European Union’s Horizon 2020 Framework Programme for Research and Innovation under the Specific Grant Agreement No. 945539 (“Human Brain Project” SGA3). A.F.D. Howard and the Wellcome Centre for Integrative Neuroimaging were supported by the Wellcome Trust (grants WT202788/Z/16/A and 203139/Z/16/Z). S.N. Haber was supported by NIH grants R01-MH045573 and P50-MH106435
References
- Abdollahzadeh A, Belevich I, Jokitalo E, Sierra A, Tohka J, 2021. DeepACSON automated segmentation of white matter in 3D electron microscopy. Commun. Biol [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aboitiz F, Scheibel AB, Fisher RS, Zaidel E, 1992. Fiber composition of the human corpus callosum. Brain Res. 598 (1–2), 143–153. [DOI] [PubMed] [Google Scholar]
- Adler DH, Pluta J, Kadivar S, Craige C, Gee JC, Avants BB, Yushkevich PA, 2014. Histology-derived volumetric annotation of the human hippocampal subfields in postmortem MRI. Neuroimage 84, 505–523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aggarwal M, Mori S, Shimogori T, Blackshaw S, Zhang J, 2010. Three-dimensional diffusion tensor microimaging for anatomical characterization of the mouse brain. Magn. Reson. Med 64, 249–261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aggarwal M, Zhang J, Pletnikova O, Crain B, Troncoso J, Mori S, 2013. Feasibility of creating a high-resolution 3D diffusion tensor imaging based atlas of the human brainstem: a case study at 11.7T. Neuroimage 74, 117–127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aggarwal M, Nauen DW, Troncoso JC, Mori S, 2015. Probing region-specific microstructure of human cortical areas using high angular and spatial resolution diffusion MRI. Neuroimage 105, 198–207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alexander DC, et al. , 2010. Orientationally invariant indices of axon diameter and density from diffusion MRI. Neuroimage 52 (4), 1374–1389. [DOI] [PubMed] [Google Scholar]
- Alexander DC, Dyrby TB, Nilsson M, Zhang H, 2019. Imaging brain microstructure with diffusion MRI: practicality and applications. NMR Biomed. 32 (4) John Wiley and Sons Ltd; 01-Apr. [DOI] [PubMed] [Google Scholar]
- Alho EJL, Fonoff ET, Di Lorenzo Alho AT, Nagy J, Heinsen H, 2021. Use of computational fluid dynamics for 3D fiber tract visualization on human high-thickness histological slices: histological mesh tractography. Brain Struct. Funct 226 (2), 323–333. [DOI] [PubMed] [Google Scholar]
- Ali S, Wörz S, Amunts K, Eils R, Axer M, Rohr K, 2018. Rigid and non-rigid registration of polarized light imaging data for 3D reconstruction of the temporal lobe of the human brain at micrometer resolution. Neuroimage 181, 235–251. [DOI] [PubMed] [Google Scholar]
- Alimi A, Deslauriers-Gauthier S, Matuschke F, Müller A, Muenzing SEA, Axer M, Deriche R, 2020. Analytical and fast fiber orientation distribution reconstruction in 3D-polarized light imaging. Med. Image Anal 65, 101760. [DOI] [PubMed] [Google Scholar]
- Ambrosen KS, et al. , 2020. Validation of structural brain connectivity networks: the impact of scanning parameters. Neuroimage 204, 116207. [DOI] [PubMed] [Google Scholar]
- Amunts K, Mohlberg H, Bludau S, Zilles K, 2020. Julich-brain: a 3D probabilistic atlas of the human brain’s cytoarchitecture. Science 369, 988. [DOI] [PubMed] [Google Scholar]
- Andersson M, Kjer HM, Rafael-Patino J, Pacureanu A, Pakkenberg B, Thiran JP, Ptito M, Bech M, Bjorholm Dahl A, Andersen Dahl V, Dyrby TB, 2020. Axon morphology is modulated by the local environment and impacts the noninvasive investigation of its structure-function relationship. In: Proceedings of the National Academy of Sciences of the United States of America, 117, pp. 33649–33659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andersson M, Pizzolato M, Kjer HM, Skodborg KF, Lundell H, Dyrby TB., 2021. Does powder averaging remove dispersion bias in diffusion MRI diameter estimates within real 3D axonal architectures? Neuroimage, 118718 Nov 9. [DOI] [PubMed] [Google Scholar]
- Arnts H, Kleinnijenhuis M, Kooloos JGM, Schepens-Franke AN, van Cappellen van Walsum AM, 2013. Combining fiber dissection, plastination, and tractography for neuroanatomy education: revealing the cerebellar nuclei and their white matter connections. Anat. Sci. Educ. [DOI] [PubMed] [Google Scholar]
- Assaf Y, Basser PJ, 2005. Composite hindered and restricted model of diffusion (CHARMED) MR imaging of the human brain. Neuroimage 27 (1), 48–58. [DOI] [PubMed] [Google Scholar]
- Assaf Y, Blumenfeld-Katzir T, Yovel Y, Basser PJ, 2008. AxCaliber: a method for measuring axon diameter distribution from diffusion MRI. Magn. Reson. Med 59 (6), 1347–1354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Assayag O, Grieve K, Devaux B, Harms F, Pallud J, Chretien F, Boccara C, Varlet P, 2013. Imaging of non-tumorous and tumorous human brain tissues with full–field optical coherence tomography. NeuroImage Clin 2, 549–557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Axer M, Amunts K, Gräßel D, Palm C, Dammers J, Axer H, Pietrzyk U, Zilles K, 2011a. A novel approach to the human connectome: ultra-high resolution mapping of fiber tracts in the brain. Neuroimage 54, 1091–1101. [DOI] [PubMed] [Google Scholar]
- Axer M, Gräßel D, Kleiner M, Dammers J, Dickscheid T, Reckfort J, Hütz T, Eiben B, Pietrzyk U, Zilles K, Amunts K, 2011b. High-resolution fiber tract reconstruction in the human brain by means of three-dimensional polarized light imaging. Front Neuroinform. 5, 34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Axer M, Strohmer S, Gräßel D, Bücker O, Dohmen M, Reckfort J, Zilles K, Amunts K, 2016. Estimating fiber orientation distribution functions in 3D-polarized light imaging. Front Neuroanat. 10, 40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aydogan DB, Jacobs R, Dulawa S, Thompson SL, Francois MC, Toga AW, Dong H, Knowles JA, Shi Y, 2018. When tractography meets tracer injections: a systematic study of trends and variation sources of diffusion-based connectivity. Brain struct. funct 223 (6), 2841–2858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Azadbakht H, et al. , 2015. Validation of high-resolution tractography against in vivo tracing in the macaque visual cortex. Cereb. Cortex 25 (11), 4299–4309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barazany D, Basser PJ, Assaf Y, 2009. In vivo measurement of axon diameter distribution in the corpus callosum of rat brain. Brain 132 (Pt 5), 1210–1220 May. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Basser PJ, Mattiello J, LeBihan D, 1994. MR diffusion tensor spectroscopy and imaging. Biophys. J 66 (1), 259–267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baydin S, Gungor A, Tanriover N, Baran O, Middlebrooks EH, Rhoton AL, 2016. Fiber tracts of the medial and inferior surfaces of the cerebrum. World Neurosurg.. [DOI] [PubMed] [Google Scholar]
- Beaulieu C, 2002. The basis of anisotropic water diffusion in the nervous system - a technical review. NMR Biomed. 15 (7–8), 435–455. [DOI] [PubMed] [Google Scholar]
- Bernard F, Lemee JM, Mazerand E, Leiber LM, Menei P, Ter Minassian A, 2020. The ventral attention network: the mirror of the language network in the right brain hemisphere. J. Anat 237 (4), 632–642 Oct. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bodian D, 1936. A new method for staining nerve fibers and nerve endings in mounted paraffin sections. Anat. Rec 65, 89–97. [Google Scholar]
- Böhringer HJ, Lankenau E, Stellmacher F, Reusche E, Hüttmann G, Giese A, 2009. Imaging of human brain tumor tissue by near-infrared laser coherence tomography. Acta Neurochir. (Wien) 151, 507–517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boppart SA, Brezinski ME, Pitris C, Fujimoto JG, 1998. Optical coherence tomography for neurosurgical imaging of human intracortical melanoma. Neurosurgery 43, 834–841. [DOI] [PubMed] [Google Scholar]
- Brabec J, Lasič S, Nilsson M, 2020. Time-dependent diffusion in undulating thin fibers: Impact on axon diameter estimation. NMR Biomed. 33 (3). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brodmann K, 1903. Bemerkungen zur untersuchung des nervensystems im polarisierten licht. J. Psychol. Neurol 2, 211–213. [Google Scholar]
- Brodmann K, 1909. Vergleichende Lokalisationslehre der Gross- Hirnrinde in ihren Prinzipien Dargestellt und Grund des Zelle- nbaues. Leipzig, Barth, Leipzig. [Google Scholar]
- Briggs RG, Chakraborty AR, Anderson CD, Abraham CJ, Palejwala AH, Conner AK, Pelargos PE, O’Donoghue DL, Glenn CA, 2019. Sughrue me. anatomy and white matter connections of the inferior frontal gyrus. Clin. Anat 32 (4), 546–556 May. [DOI] [PubMed] [Google Scholar]
- Briggs RG, Khan AB, Chakraborty AR, Abraham CJ, Anderson CD, Karas PJ, Bonney PA, Palejwala AH, Conner AK, O’Donoghue DL, Sughrue ME., 2020. Anatomy and white matter connections of the superior frontal gyrus. Clin. Anat 33 (6), 823–832 Sep. [DOI] [PubMed] [Google Scholar]
- Briggs RG, Lin YH, Dadario NB, Kim SJ, Young IM, Bai MY, Dhanaraj V, Fonseka RD, Hormovas J, Tanglay O, Chakraborty AR, Milligan TM, Abraham CJ, Anderson CD, Palejwala AH, Conner AK, O’Donoghue DL, Sughrue ME., 2021. Anatomy and white matter connections of the middle frontal gyrus. World Neurosurg. (21) S1878 Mar 17-875000413-7. [DOI] [PubMed] [Google Scholar]
- Budde MD, Frank JA, 2010. Neurite beading is sufficient to decrease the apparent diffusion coefficient after ischemic stroke. Proc. Natl. Acad. Sci. USA [DOI] [PMC free article] [PubMed] [Google Scholar]
- Budde MD, Frank JA, 2012. Examining brain microstructure using structure tensor analysis of histological sections. Neuroimage 63 (1), 1–10. [DOI] [PubMed] [Google Scholar]
- Burcaw LM, Fieremans E, Novikov DS, 2015. Mesoscopic structure of neuronal tracts from time-dependent diffusion. Neuroimage 114, 18–37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bürgel U, Mecklenburg I, Blohm U, Zilles K, 1997. Histological visualization of long fiber tracts in the white matter of adult human brains. J. Hirnforsch 38 (3), 397–404. [PubMed] [Google Scholar]
- Bürgel U, Schormann T, Schleicher A, Zilles K, 1999. Mapping of histologically identified long fiber tracts in human cerebral hemispheres to the MRI volume of a reference brain: position and spatial variability of the optic radiation. Neuroimage 10 (5), 489–499. [DOI] [PubMed] [Google Scholar]
- Bürgel U, Amunts K, Hoemke L, Mohlberg H, Gilsbach JM, Zilles K, 2006. White matter fiber tracts of the human brain: three-dimensional mapping at microscopic resolution, topography and intersubject variability. Neuroimage 29 (4), 1092–1105. [DOI] [PubMed] [Google Scholar]
- Burnham KP, Anderson DR, 2002. Model Selection and Inference: A Practical Information-theoretic Approach. Springer, New York. [Google Scholar]
- Calabrese E, Badea A, Coe CL, Lubach GR, Styner MA, Johnson GA., 2014. Investigating the tradeoffs between spatial resolution and diffusion sampling for brain mapping with diffusion tractography: time well spent? Hum. Brain Mapp 35 (11), 5667–5685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caminiti R, Borra E, Visco-Comandini F, Battaglia-Mayer A, Averbeck BB, Luppino G, 2017. Computational architecture of the parieto-frontal network underlying cognitive-motor control in monkeys. eNeuro 4 (1). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carriel V, Campos A, Alaminos M, Raimondo S, Geuna S, Pellicciari C, Biggiogera M, 2017. Staining methods for normal and regenerative myelin in the nervous system. Histochemistry of Single Molecules. Methods in Molecular Biology, 1560. Humana Press, New York, NY. [DOI] [PubMed] [Google Scholar]
- Caspers S, Axer M, Caspers J, Jockwitz C, Jütten K, Reckfort J, Grässel D, Amunts K, Zilles K, 2015. Target sites for transcallosal fibers in human visual cortex – a combined diffusion and polarized light imaging study. Cortex 72, 40–53. [DOI] [PubMed] [Google Scholar]
- Catani M, Howard RJ, Pajevic S, Jones DK., 2002. Virtual in vivo interactive dissection of white matter fasciculi in the human brain. Neuroimage 17 (1), 77–94. [DOI] [PubMed] [Google Scholar]
- Chang EH, et al. , 2017. The role of myelination in measures of white matter integrity: combination of diffusion tensor imaging and two-photon microscopy of CLARITY intact brains. Neuroimage. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen H, Liu T, Zhao Y, Zhang T, Li Y, Li M, Zhang H, Kuang H, Guo L, Tsien JZ, Liu T, 2015. Optimization of large-scale mouse brain connectome via joint evaluation of DTI and neuron tracing data. Neuroimage 115, 202–213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X, Sun YC, Zhan H, Kebschull JM, Fischer S, Matho K, Huang ZJ, Gillis J, Zador AM, 2019. High-throughput mapping of long-range neuronal projection using in situ sequencing. Cell 179 (3), 772–786 Oct 17e19.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choe AS, Gao Y, Li X, Compton KB, Stepniewska I, Anderson AW, 2011. Accuracy of image registration between MRI and light microscopy in the ex vivo brain. Magn. Reson. Imaging 29 (5), 683–692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choe A, Stepniewska I, Colvin D, Ding Z, Anderson A, 2012. Validation of diffusion tensor MRI in the central nervous system using light microscopy: quantitative comparison of fiber properties. NMR Biomed. 25 (7), 900–908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chung K, Wallace J, Kim SY, Kalyanasundaram S, Andalman AS, Davidson TJ, Mirzabekov JJ, Zalocusky K.a, Mattis J, Denisin AK, Pak S, Bernstein H, Ramakrishnan C, Grosenick L, Gradinaru V, Deisseroth K, 2013. Structural and molecular interrogation of intact biological systems. Nature 497, 332–337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colby JB, Soderberg L, Lebel C, Dinov ID, Thompson PM, Sowell ER, 2012. Along-tract statistics allow for enhanced tractography analysis. Neuroimage. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conturo TE, Lori NF, Cull TS, Akbudak E, Snyder AZ, Shimony JS, McKinstry RC, Burton H, Raichle ME, 1999. Tracking neuronal fiber pathways in the living human brain. Proc. Natl. Acad. Sci. USA vol. 96 (18), 10422–10427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Costantini I, Ghobril JP, Di Giovanna AP, Allegra Mascaro AL, Silvestri L, Mullenbroich MC, Onofri L, Conti V, Vanzi F, Sacconi L, Guerrini R, Markram H, Iannello G, Pavone FS, 2015. A versatile clearing agent for multi-modal brain imaging. Sci. Rep 5, 9808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Costantini I, Cicchi R, Silvestri L, Vanzi F, Pavone FS, 2019. In-vivo and ex-vivo optical clearing methods for biological tissues: review. Biomed. Opt. Express 10, 5251–5267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Côté MA, Girard G, Boré A, Garyfallidis E, Houde JC, Descoteaux M, 2013. Tractometer: towards validation of tractography pipelines. Med. Image Anal 17 (7), 844–857. [DOI] [PubMed] [Google Scholar]
- Daducci A, Canales-Rodriguez EJ, Descoteaux M, Garyfallidis E, Gur Y, Lin YC, et al. , 2014. Quantitative comparison of reconstruction methods for intra-voxel fiber recovery from diffusion MRI. IEEE Trans. Med. Imaging 33 (2), 384–399. [DOI] [PubMed] [Google Scholar]
- D’Arceuil HE, Westmoreland S, de Crespigny AJ, 2007. An approach to high resolution diffusion tensor imaging in fixed primate brain. Neuroimage 35, 553–565. [DOI] [PubMed] [Google Scholar]
- Dauguet J, et al. , 2007. Comparison of fiber tracts derived from in-vivo DTI tractography with 3D histological neural tract tracer reconstruction on a macaque brain. Neuroimage 37 (2), 530–538. [DOI] [PubMed] [Google Scholar]
- De Benedictis A, Nocerino E, Menna F, Remondino F, Barbareschi M, Rozzanigo U, Corsini F, Olivetti E, Marras CE, Chioffi F, Avesani P, Sarubbo S, 2018. Photogrammetry of the human brain: a novel method for three-dimensional quantitative exploration of the structural connectivity in neurosurgery and neurosciences. World Neurosurg. 115, e279–e291. [DOI] [PubMed] [Google Scholar]
- De Boer JF, Milner TE, van Gemert MJ, Nelson JS, 1997. Two-dimensional birefringence imaging in biological tissue by polarization-sensitive optical coherence tomography. Opt. Lett 22, 934–936. [DOI] [PubMed] [Google Scholar]
- De Castro I, Christoph Dde H, dos Santos DP, Landeiro JA, 2005. Internal structure of the cerebral hemispheres: an introduction of fiber dissection technique. Arq. Neuropsiquiatr 63, 252–258. [DOI] [PubMed] [Google Scholar]
- Delettre C, Messé A, Dell LA, Foubet O, Heuer K, Larrat B, Meriaux S, Mangin JF, Reillo I, de Juan Romero C, Borrell V, Toro R, Hilgetag CC, 2019. Comparison between diffusion MRI tractography and histological tract-tracing of cortico–cortical structural connectivity in the ferret brain. Netw. Neurosci 3 (4), 1038–1050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Denk W, Horstmann H, 2004. Serial block-face scanning electron microscopy to reconstruct three-dimensional tissue nanostructure. PLoS Biol. 2 (11), e329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Santis S, Drakesmith M, Bells S, Assaf Y, Jones DK., 2014. Why diffusion tensor MRI does well only some of the time: variance and covariance of white matter tissue microstructure attributes in the living human brain. Neuroimage 89 (100), 35–44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dohmen M, Menzel M, Wiese H, Reckfort J, Hanke F, Pietrzyk U, Zilles K, Amunts K, Axer M, 2015. Understanding fiber mixture by simulation in 3D polarized light imaging. Neuroimage 111, 464–475. [DOI] [PubMed] [Google Scholar]
- Donahue CJ, et al. , 2016. Using diffusion tractography to predict cortical connection strength and distance: a quantitative comparison with tracers in the monkey. J. Neurosci 36 (25), 6758–6770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dyrby TB, Søgaard LV, Parker GJ, Alexander DC, Lind NM, Baaré WF, Hay-Schmidt A, Eriksen N, Pakkenberg B, Paulson OB, Jelsing J, 2007. Validation of in vitro probabilistic tractography. Neuroimage 37 (4), 1267–1277. [DOI] [PubMed] [Google Scholar]
- Dyrby TB, Baaré WFC, Alexander DC, Jelsing J, Garde E, Søgaard LV, 2011. An ex vivo imaging pipeline for producing high-quality and high-resolution diffusion-weighted imaging datasets. Hum. Brain Mapp 32, 544–563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dyrby TB, Innocenti GM, Bech M, Lundell H, 2018. Validation strategies for the interpretation of microstructure imaging using diffusion MRI. Neuroimage 182, 62–79. [DOI] [PubMed] [Google Scholar]
- Dziedzic TA, Balasa A, Jeżewski MP, et al. , 2021. White matter dissection with the Klingler technique: a literature review. Brain Struct. Funct 226, 13–47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eberle AL, Zeidler D, 2018. Multi-beam scanning electron microscopy for high-through-put imaging in connectomics research. Front Neuroanat. 12, 112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edlow BL, Mareyam A, Horn A, Polimeni JR, Witzel T, Tisdall MD, Augustinack JC, Stockmann JP, Diamond BR, Stevens A, Tirrell LS, Folkerth RD, Wald LL, Fischl B, van der Kouwe A, 2019. 7 Tesla MRI of the ex vivo human brain at 100 micron resolution. Sci. Data 6, 244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Egemen E, Celtikci P, Dogruel Y, Yakar F, Sahinoglu D, Farouk M, Adiguzel E, Ugur HC, Coskun E, Güngör A, 2021. Microsurgical and tractographic anatomical study of transtemporal-transchoroidal fissure approaches to the ambient cistern. In: Oper Neurosurg., 20, pp. 189–197 Hagerstown. [DOI] [PubMed] [Google Scholar]
- Ehrenberg CG, 1849. Weitere Mittheilung über Resultate bei Anwendung des chromatisch-polarisirten Lichtes für mikroskopische Verhaltnisse. Ber. Akad. Wiss 1849, 55–76 [Google Scholar]
- Eichner C, Paquette M, Mildner T, Schlumm T, Pléh K, Samuni L, Crockford C, Wittig RM, Jäger C, Möller HE, Friederici AD, Anwander A, 2020. Increased sensitivity and signal-to-noise ratio in diffusion-weighted MRI using multi-echo acquisitions. Neuroimage 221, 117172. [DOI] [PubMed] [Google Scholar]
- Eickhoff S, Walters NB., Schleicher A, Kril J, Egan GF, Zilles K, Watson JDG, Amunts K, 2005. High-resolution MRI reflects myeloarchitecture and cytoarchitecture of human cerebral cortex. Hum. Brain Mapp 24, 206–215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan Q, Nummenmaa A, Witzel T, Zanzonico R, Keil B, Cauley S, Polimeni JR, Tisdall D, Van Dijk KRA, Buckner RL, Wedeen VJ, Rosen BR, Lawrence L, 2014. Wald.Brain Connect. 718–726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan Q, et al. , 2020. Axon diameter index estimation independent of fiber orientation distribution using high-gradient diffusion MRI. Neuroimage. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Felleman DJ, Van Essen DC, 1991. Distributed hierarchical processing in the primate cerebral cortex. Cereb. Cortex 11, 1–47. [DOI] [PubMed] [Google Scholar]
- Fieremans E, et al. , 2008. The design of anisotropic diffusion phantoms for the validation of diffusion weighted magnetic resonance imaging. Phys. Med. Biol 53 (19), 5405–5419. [DOI] [PubMed] [Google Scholar]
- Fieremans E, Burcaw LM, Lee HH, Lemberskiy G, Veraart J, Novikov DS, Apr. 2016. In vivo observation and biophysical interpretation of time-dependent diffusion in human white matter. Neuroimage 129, 414–427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flores-Justa A, Baldoncini M, JC PC, F SG, Martínez OA, González-López P, Á C, 2019. White matter topographic anatomy applied to temporal lobe surgery. World Neurosurg. 132, e670–e679 Dec. [DOI] [PubMed] [Google Scholar]
- Foxley S, Jbabdi S, Clare S, Lam W, Ansorge O, Douaud G, Miller K, 2014. Improving diffusion-weighted imaging of post-mortem human brains: SSFP at 7T. Neuroimage 102, 579–589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foxley S, et al. , 2020. Multi-modal imaging of a single mouse brain over five orders of magnitude of resolution. bioRxiv 2020.10.07.329789 Jan. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fraher JP, MacConaill MA, 1970. Fibre bundles in the CNS revealed by polarized light. J. Anat 106, 170. [PubMed] [Google Scholar]
- Fritz F, Foxley S, Sengupta S, Harms R, Caspers S, Zilles K, Tse D, Poser B, Miller K, Roebroeck A, 2016. Whole human brain diffusion MRI at 450μm post mortem with dwSSFP and a specialized 9.4T RF-coil. In: Proceedings of the ISMRM Annual Meeting. [Google Scholar]
- Fritz FJ, Sengupta S, Harms RL, Tse DH, Poser BA, Roebroeck A, 2019. Ultra--high resolution and multi-shell diffusion MRI of intact ex vivo human brains using kT-dSTEAM at 9.4T. Neuroimage 202, 116087. [DOI] [PubMed] [Google Scholar]
- Gallyas F, 1979. Silver Staining of Myelin by Means of Physical Development. Neurol. Res 1 (2), 203–209. [DOI] [PubMed] [Google Scholar]
- Gambetti P, Autilio-Gambetti L, Papasozomenos SC, 1981. Bodian’s silver method stains neurofilament polypeptides. Science 213, 1521–1522 (80-.). [DOI] [PubMed] [Google Scholar]
- Gatto RG, Li W, Gao J, Magin RL, 2018. In vivo diffusion MRI detects early spinal cord axonal pathology in a mouse model of amyotrophic lateral sclerosis. NMR Biomed.. [DOI] [PubMed] [Google Scholar]
- Gao Y, et al. , 2013. Validation of DTI tractography-based measures of primary motor area connectivity in the squirrel monkey brain. PLoS One 8 (10), e75065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ginsburger K, et al. , 2018. Improving the realism of white matter numerical phantoms: a step toward a better understanding of the influence of structural disorders in diffusion MRI. Front. Phys. [Google Scholar]
- Girard G, Caminiti R, Battaglia-Mayer A, St-Onge E, Ambrosen KS, Eskildsen SF, Krug K, Dyrby TB, Descoteaux M, Thiran JP, Innocenti GM, 2020. On the cortical connectivity in the macaque brain: a comparison of diffusion tractography and histological tracing data. Neuroimage 221, 117201. [DOI] [PubMed] [Google Scholar]
- Glickstein M, 2006. Golgi and Cajal: The neuron doctrine and the 100th anniversary of the 1906 Nobel Prize. Curr. Biol. [DOI] [PubMed] [Google Scholar]
- Goryainov SA, Kondrashov AV, Gol’dberg MF, Batalov AI, Sufianov RA, Zakharova NE, Pronin IN, Gol’bin DA, Zhukov VY, Dobrovol’sky GF, Shelyakin SY, Vorob’ev VN, Dadykin SS, Potapov AA, 2017. Long association tracts of the human white matter: an analysis of 18 hemisphere dissections and in vivo HARDI-CSD tractography. In: Zh Vopr. Neirokhir. Im. N. N. Burdenko, 81, pp. 13–25. doi: 10.17116/neiro201780713-25 English, Russian. [DOI] [PubMed] [Google Scholar]
- Grisot G, Haber SN, Yendiki A, 2021. Diffusion MRI and anatomic tracing in the same brain reveal common failure modes of tractography. Neuroimage 239, 118300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grussu F, et al. , 2017. Neurite dispersion: a new marker of multiple sclerosis spinal cord pathology? Ann. Clin. Transl. Neurol 4 (9), 663–679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guilfoyle DN, Helpern JA, Lim KO, 2003. Diffusion tensor imaging in fixed brain tissue at 7.0 T. NMR Biomed. 16, 77–81. [DOI] [PubMed] [Google Scholar]
- Guo SM, Yeh LH, Folkesson J, Ivanov IE, Krishnan AP, Keefe MG, Hashemi E, Shin D, Chhun BB, Cho NH, Leonetti MD, Han MH, Nowakowski TJ, Mehta SB, 2020. Revealing architectural order with quantitative label-free imaging and deep learning. eLife 9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutman DA, Magnuson M, Majeed W, Keifer OP, Davis M, Ressler KJ, Keilholz S, 2013. Mapping of the mouse olfactory system with manganese-enhanced magnetic resonance imaging and diffusion tensor imaging. Brain Struct Funct 218, 527–537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haber SN, Kim KS, Mailly P, Calzavara R, 2006. Reward-related cortical inputs define a large striatal region in primates that interface with associative cortical inputs, providing a substrate for incentive-based learning. J. Neurosci 26, 8368–8376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haynes WIA, Haber SN, 2013. The organization of prefrontal-subthalamic inputs in primates provides an anatomical substrate for both functional specificity and integration: implications for Basal Ganglia models and deep brain stimulation. J. Neurosci 33 (11), 4804–4814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hagmann P, Gigandet X, Meuli R, Kötter R, Sporns O, Wedeen VJ, 2008. Quantitative validation of MR tractography using the CoCoMac database. Proc. Intl. Soc. Mag. Reson. Med 16. [Google Scholar]
- Heilbronner SR, Haber SN., 2014. Frontal cortical and subcortical projections provide a basis for segmenting the cingulum bundle: implications for neuroimaging and psychiatric disorders. J. Neurosci 34 (30), 10041–10054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henssen D, Mollink J, Kurt E, van Dongen R, Bartels R, Grabetael D, Kozicz T, Axer M, Van Cappellen van Walsum AM, 2019. Ex vivo visualization of the trigeminal pathways in the human brainstem using 11.7T diffusion MRI combined with microscopy polarized light imaging. Brain Struct. Funct 224, 159–170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herculano-Houzel S, 2009. The human brain in numbers: a linearly scaled-up primate brain. Front. Hum. Neurosci 3, 31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herold C, Schlömer P, Mafoppa-Fomat I, Mehlhorn J, Amunts K, Axer M, 2018. The hippocampus of birds in a view of evolutionary connectomics. Cortex. [DOI] [PubMed] [Google Scholar]
- Honig MG, Hume RI, 1989a. Dil and diO: versatile fluorescent dyes for neuronal labelling and pathway tracing. Trends Neurosci. 12 (9), 340–341 333-5. [PubMed] [Google Scholar]
- Honig MG, Hume RI, 1989b. Carbocyanine dyes. Novel markers for labelling neurons. Trends Neurosci. 12 (9), 336–338. [PubMed] [Google Scholar]
- Horgos B, Mecea M, Boer A, Szabo B, Buruiana A, Stamatian F, Mihu CM, Florian IŞ, Susman S, Pascalau R, 2020. White matter dissection of the fetal brain. Front. Neuroanat 14, 584266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hou B, Zhang D, Zhao S, Wei M, Yang Z, Wang S, Wang J, Zhang X, iu B, Fan L, Li Y, Qiu Z, Zhang C, Jiang T, 2015. Scalable and DiI- compatible optical clearance of the mammalian brain. Front. Neuroanat 9, 1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howard AF, et al. , 2019. Joint modelling of diffusion MRI and microscopy. Neuroimage. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang D, Swanson EA, Lin CP, Schuman JS, Stinson WG, Chang W, Hee MR, Flotte T, Gregory K, Puliafito CA, Et A, 1991. Optical coherence tomography. Science 254, 1178–1181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang SY, Nummenmaa A, Witzel T, Duval T, Cohen-Adad J, Wald LL, McNab JA, 2015. The impact of gradient strength on in. vivo diffusion MRI estimates of axon diameter. Neuroimage 106, 464–472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang SY, Tian Q, Fan Q, Witzel T, Wichtmann B, McNab JA, Daniel Bireley J, Machado N, Klawiter EC, Mekkaoui C, Wald LL, Nummenmaa A, 2020. High-gradient diffusion MRI reveals distinct estimates of axon diameter index within different white matter tracts in the in vivo human brain. Brain Struct. Funct 225, 1277–1291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang SY, Witzel T, Keil B, Scholz A, Davids M, Dietz P, Rummert E, Ramb R, Kirsch JE, Yendiki A, Fan Q, Tian Q, Ramos-Llordén G, Lee HH, Nummenmaa A, Bilgic B, Setsompop K, Wang F, Avram AV, Komlosh M, Rosen BR, 2021. Connectome 2.0: Developing the next-generation ultra-high gradient strength human MRI scanner for bridging studies of the micro-, meso- and macro-connectome. Neuroimage 243, 118530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hukkanen V, Röyttä M, 1987. Autolytic changes of human white matter: an electron microscopic and electrophoretic study. Exp. Mol. Pathol. [DOI] [PubMed] [Google Scholar]
- Holl N, Noblet V, Rodrigo S, Dietemann JL, Mekhbi MB, Kehrli P, Wolfram-Gabel R, Braun M, Kremer S, 2011. Temporal lobe association fiber tractography as compared to histology and dissection. Surg. Radiol. Anat 33 (8), 713–722. [DOI] [PubMed] [Google Scholar]
- Iglesias JE, Modat M, Peter L, Stevens A, Annunziata R, Vercauteren T, Lein E, Fischl B, Ourselin S Alzheimer’s Disease Neuroimaging Initiative, 2018. Joint registration and synthesis using a probabilistic model for alignment of MRI and histological sections. Med. Image Anal 50, 127–144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Innocenti GM, Dyrby TB, Andersen KW, Rouiller EM, Caminiti R, 2017. The crossed projection to the striatum in two species of monkey and in humans: behavioral and evolutionary significance. Cereb. Cortex 27 (6), 3217–3230. [DOI] [PubMed] [Google Scholar]
- Jbabdi S, et al. , 2013. Human and monkey ventral prefrontal fibers use the same organizational principles to reach their targets: tracing versus tractography. J. Neurosci 33 (7), 3190–3201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jelescu IO, et al. , 2016. In vivo quantification of demyelination and recovery using compartment-specific diffusion MRI metrics validated by electron microscopy. Neuroimage. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jelescu IO, Budde MD, 2017. Design and validation of diffusion mri models of white matter. Front. Phys 5 November. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jelescu IO, Palombo M, Bagnato F, Schilling KG, 2020. Challenges for biophysical modeling of microstructure. J. Neurosci. Methods [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jespersen SN, et al. , 2010. Neurite density from magnetic resonance diffusion measurements at ultrahigh field: Comparison with light microscopy and electron microscopy. Neuroimage. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones DK, Simmons A, Williams SC, Horsfield MA, 1999. Non-invasive assessment of axonal fiber connectivity in the human brain via diffusion tensor MRI. Magn. Reson. Med 42 (1), 37–41. [DOI] [PubMed] [Google Scholar]
- Jones DK, Travis AR, Eden G, Pierpaoli C, Basser PJ, 2005. PASTA: Pointwise assessment of streamline tractography attributes. Magn. Reson. Med. [DOI] [PubMed] [Google Scholar]
- Jones R, Grisot G, Augustinack J, Magnain C, Boas DA, Fischl B, Wang H, Yendiki A, 2020. Insight into the fundamental trade-offs of diffusion MRI from polarization-sensitive optical coherence tomography in ex vivo human brain. Neuroimage 214, 116704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones R, Maffei C, Augustinack J, Fischl B, Wang H, Bilgic B, Yendiki A, 2021. High-fidelity approximation of grid- and shell-based sampling schemes from undersampled DSI using compressed sensing: Post mortem validation. Neuroimage 244, 118621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaden E, Kelm ND, Carson RP, Does MD, Alexander DC, 2016. Multi-compartment microscopic diffusion imaging. Neuroimage 139, 346–359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kamagata K, et al. , 2016. Quantitative histological validation of diffusion tensor MRI with two-photon microscopy of cleared mouse brain. Magn. Reson. Med. Sci. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kasthuri N, et al. , 2015. Saturated reconstruction of a volume of neocortex. Cell 162 (3), 648–661. [DOI] [PubMed] [Google Scholar]
- Kebschull JM, Garcia da Silva P, Reid AP, Peikon ID, Albeanu DF, Zador AM, 2016. High-throughput mapping of single-neuron projections by sequencing of barcoded RNA. Neuron 91 (5), 975–987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelm ND, West KL, Carson RP, Gochberg DF, Ess KC, Does MD, 2016. Evaluation of diffusion kurtosis imaging in ex vivo hypomyelinated mouse brains. Neuroimage. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khan AR, Cornea A, Leigland LA, Kohama SG, Jespersen SN, Kroenke CD, 2015. 3D structure tensor analysis of light microscopy data for validating diffusion MRI. Neuroimage 111, 192–203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kleinnijenhuis M (2014). Thesis: imaging fibres in the brain, chapter 2: a historical essay on connectional neuroanatomy. [Google Scholar]
- Kleinnijenhuis M, Johnson E, Mollink J, Jbabdi S, Miller KL., 2020. A semi-automated approach to dense segmentation of 3D white matter electron microscopy. bioRxiv doi: 10.1101/2020.03.19.979393, .03.19.979393 [Preprint]. Available from-doi.org/. [DOI] [Google Scholar]
- Klingler J, 1935. Erleichterung der makroskopischen Praeparation des Gehirns durch den Gefrierprozess. Schweiz. Arch. Neurol. Psychiatr 36, 247–256. [Google Scholar]
- Klingler J, Gloor P, 1960. The connections of the amygdala and of the anterior temporal cortex in the human brain. J. Comp. Neurol 115, 333–369. [DOI] [PubMed] [Google Scholar]
- Klüver H, Barrera EA, 1953. A method for the combined staining of cells and fibers in the nervous system. J. Neuropathol. Exp. Neurol 12 (4), 400–403. [DOI] [PubMed] [Google Scholar]
- Knösche TR, Anwander A, Liptrot M, Dyrby TB, 2015. Validation of tractography: comparison with manganese tracing. Hum. Brain Mapp 36 (10), 4116–4134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Korogod N, Petersen CCH, Knott GW, 2015. Ultrastructural analysis of adult mouse neocortex comparing aldehyde perfusion with cryo fixation. Elife. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuhlmann T, Ludwin S, Prat A, Antel J, Brück W, Lassmann H, 2017. An updated histological classification system for multiple sclerosis lesions. Acta Neuropathol. 133 (1), 13–24 Jan. [DOI] [PubMed] [Google Scholar]
- Lampinen B, et al. , 2019. Searching for the neurite density with diffusion MRI: challenges for biophysical modeling. Hum. Brain Mapp 40 (8), 2529–2545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latini F, Mårtensson J, Larsson EM, Fredrikson M, Åhs F, Hjortberg M, Aldskogius H, Ryttlefors M, 2017. Segmentation of the inferior longitudinal fasciculus in the human brain: a white matter dissection and diffusion tensor tractography study. Brain Res. 1675, 102–115. [DOI] [PubMed] [Google Scholar]
- Lazari A, Lipp I, 2021. Can MRI measure myelin? Systematic review, qualitative assessment, and meta-analysis of studies validating microstructural imaging with myelin histology. Neuroimage. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lebenberg J, érard ASH, Dubois A, Dauguet J, Frouin V, Dhenaina M, Hantraye P, Delzescaux T, 2010. Validation of MRI-based 3D digital atlas registration with histological and autoradiographic volumes: an anatomofunctional transgenic mouse brain imaging study. Neuroimage 51, 1037–1046. [DOI] [PubMed] [Google Scholar]
- Lefebvre J, Castonguay A, Pouliot P, Descoteaux M, Lesage F, 2017. Whole mouse brain imaging using optical coherence tomography: reconstruction, normalization, segmentation, and comparison with diffusion MRI. Neurophotonics. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee HH, et al. , 2019. Along-axon diameter variation and axonal orientation dispersion revealed with 3D electron microscopy: implications for quantifying brain white matter microstructure with histology and diffusion MRI. Brain Struct. Funct 224 (4), 1469–1488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee HH, Jespersen SN, Fieremans E, Novikov DS, 2020a. The impact of realistic axonal shape on axon diameter estimation using diffusion MRI. Neuroimage, 117228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee HH, Papaioannou A, Kim SL, Novikov DS, Fieremans E, 2020b. A time-dependent diffusion MRI signature of axon caliber variations and beading. Commun. Biol 3 (1), 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leemans A, et al. , 2005. Mathematical framework for simulating diffusion tensor MR neural fiber bundles. Magn. Reson. Med 53 (4), 944–953. [DOI] [PubMed] [Google Scholar]
- Leergaard TB, Bjaalie JG, Devor A, Wald LL, Dale AM, 2003. In vivo tracing of major rat brain pathways using manganese-enhanced magnetic resonance imaging and three-dimensional digital atlasing. Neuroimage 20 (3), 1591–1600. [DOI] [PubMed] [Google Scholar]
- Leergaard TB, White NS, De Crespigny A, Bolstad I, D’Arceuil H, Bjaalie JG, Dale AM, 2010. Quantitative histological validation of diffusion MRI fiber orientation distributions in the rat brain. PLoS One 5 (1), e8595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lehman JF, Greenberg BD, McIntyre CC, Rasmussen SA, Haber SN, 2011. Rules ventral prefrontal cortical axons use to reach their tar- gets: Implications for diffusion tensor imaging tractography and deep brain stimulation for psychiatric illness. J. Neurosci 31, 10392–10402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leuze CWU, Anwander A, Bazin P-L, Dhital B, Stüber C, Reimann K, Geyer S, Turner R, 2012. Layer-Specific Intracortical Connectivity Revealed with Diffusion MRI. Cereb. Cortex 24, 328–339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leuze C, et al. , 2017. The separate effects of lipids and proteins on brain MRI contrast revealed through tissue clearing. Neuroimage. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leuze C, Goubran M, Barakovic M, Aswendt M, Tian Q, Hsueh B, Crow A, Weber EMM, Steinberg GK, Zeineh M, Plowey ED, Daducci A, Innocenti G, Thiran JP, Deisseroth K, McNab JA, 2021. Comparison of diffusion MRI and CLARITY fiber orientation estimates in both gray and white matter regions of human and primate brain. Neuroimage 228, 117692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li M, Ribas EC, Wei P, Li M, Zhang H, Guo Q, 2020. The ansa peduncularis in the human brain: a tractography and fiber dissection study. Brain Res. 1746, 146978. [DOI] [PubMed] [Google Scholar]
- Lichtman J, Conchello JA., 2005. Fluorescence microscopy. Nat. Methods 2, 910–919. [DOI] [PubMed] [Google Scholar]
- Lichtman JW, Pfister H, Shavit N, 2014. The big data challenges of connectomics. Nat. Neurosci 17 (11), 1448–1454 28-Oct-. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin CP, Tseng WY, Cheng HC, Chen JH, 2001. Validation of diffusion tensor magnetic resonance axonal fiber imaging with registered manganese-enhanced optic tracts. Neuroimage 14 (5), 1035–1047. [DOI] [PubMed] [Google Scholar]
- Lin CP, Wedeen VJ, Chen JH, Yao C, Tseng WY, 2003. Validation of diffusion spectrum magnetic resonance imaging with manganese-enhanced rat optic tracts and ex vivo phantoms. Neuroimage 19 (3), 482–495. [DOI] [PubMed] [Google Scholar]
- Liptrot MG, Sidaros K, Dyrby TB, 2014. Addressing the path-length-dependency confound in white matter tract segmentation. PLoS One 9 (5), e96247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ludwig E, Klingler J, 1956. Atlas cerebri humani: der innere bau des gehirns dargestellt auf grund mackroskopischer praeparate. Basel 136 Switzerland: S. Karger.p. [Google Scholar]
- Mackay A, Whittall K, Adler J, Li D, Paty D, Graeb D, 1994. In vivo visualization of myelin water in brain by magnetic resonance. Magn. Reson. Med. [DOI] [PubMed] [Google Scholar]
- Maffei C, Jovicich J, De Benedictis A, Corsini F, Barbareschi M, Chioffi F, Sarubbo S, 2018. Topography of the human acoustic radiation as revealed by ex vivo fibers micro-dissection and in vivo diffusion-based tractography. Brain Struct. Funct 223 (1), 449–459 Jan. [DOI] [PubMed] [Google Scholar]
- Maffei C, Girard G, Schilling K, Aydogan B, Aduluru N, Zhylka A, Wu Y, Mancini M, Hamamci A, Sarica A, Telliac A, Baete S, Karimi D, Yeh F, Yildiz M, Gholipour A, Bihan-Poudec Y, Hiba B, Quattrone A, Quattrone A, Boshkovski T, Stikov N, Yap P-T, De Luca A, Pluim J, Leemans A, Prabhakaran V, Bendlin BB, Alexander A, Landman B, Canales-Rodriguez E, Barakovic M, Rafael-Patino J, Yu T, Rensonnet G, Schiavi S, Daducci A, Pizzolato M, Fischi-Gomez E, Thiran J-P, Dai G, Grisot G, Lazovski N, Puch A, Ramos M, Rodrigues P, Prchkovska V, Jones R, Lehman J, Haber S, Yendiki A, 2021. Insights from the irontract challenge: optimal methods for mapping brain pathways from multi-shell diffusion MRI. bioRxiv doi: 10.1101/2021.12.17.472836, 12.17.472836 [Preprint]. Available from. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magnain C, Augustinack JC, Reuter M, Wachinger C, Frosch MP, Ragan T, Akkin T, Wedeen VJ, Boas DA, Fischl B, 2014. Blockface histology with optical coherence tomography: a comparison with Nissl staining. Neuroimage 84, 524–533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magnain C, Augustinack JC, Konukoglu E, Frosch MP, Sakadzic S, Varjabedian A, Garcia N, Wedeen VJ, Boas DA, Fischl B, 2015. Optical coherence tomography visualizes neurons in human entorhinal cortex. Neurophotonics 2, 015004–015004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magnain C, Wang H, Sakadzic S, Fischl B, Boas DA, 2016. En face speckle reduction in optical coherence microscopy by frequency compounding. Opt. Lett 41, 1925–1928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magnain C, Augustinack JC, Tirrell L, Fogarty M, Frosch MP, Boas D, Fischl B, Rockland KS, 2019. Colocalization of neurons in optical coherence microscopy and Nissl-stained histology in Brodmann’s area 32 and area 21. Brain Struct. Funct 224, 351–362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maier-Hein KH, Neher PF, Houde JC., et al. , 2017. The challenge of mapping the human connectome based on diffusion tractography. Nat. Commun 8, 1349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Majka P, Wójcik DK, 2016. Possum - a framework for three-dimensional reconstruction of brain images from serial sections. Neuroinformatics 14 (3), 265–278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mancini M, Karakuzu A, Cohen-Adad J, Cercignani M, Nichols TE, Stikov N, 2020. An interactive meta-analysis of MRI biomarkers of Myelin. Elife. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mandonnet E, Sarubbo S, Petit L, 2018. The nomenclature of human white matter association pathways: proposal for a systematic taxonomic anatomical classification. Front. Neuroanat. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marchi V, Algeri G, 1885. Sulle degenerazioni descendenti consecutive a lesioni sperimentale in diverse zone della corteccia cerebrale. Riv. Freniat 11, 492–494. [Google Scholar]
- Markov NT, Ercsey-Ravasz MM, Ribeiro Gomes AR, Lamy C, Magrou L, Vezoli J, Misery P, Falchier A, Quilodran R, Gariel MA, Sallet J, Gamanut R, Huissoud C, Clavagnier S, Giroud P, Sappey-Marinier D, Barone P, Dehay C, Toroczkai Z, Knoblauch K, Van Essen DC, Kennedy H, 2014. A weighted and directed interareal connectivity matrix for macaque cerebral cortex. Cereb. Cortex 24, 17–36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martino J, Hamer PCDW, Vergani F, Brogna C, Lucas EM, Vazquez-Barquero A, Garcia-Porrero JA., Duffau H, 2011. Cortex-sparing fiber dissection: an improved method for the study of white matter anatomy in the human brain. J. Anat doi: 10.1111/j.1469-7580.2011.01414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martino J, et al. , 2013. Analysis of the subcomponents and cortical terminations of the perisylvian superior longitudinal fasciculus: a fiber dissection and DTI tractography study. Brain Struct. Funct 218, 105–121. [DOI] [PubMed] [Google Scholar]
- McNab JA, Jbabdi S, Deoni SCL, Douaud G, Behrens TEJ, Miller KL, 2009. High resolution diffusion-weighted imaging in fixed human brain using diffusion-weighted steady state free precession. Neuroimage 46, 775–785. [DOI] [PubMed] [Google Scholar]
- McNab JA, Edlow BL, Witzel T, Huang SY, Bhat H, Heberlein K, Feiweier T, Liu K, Keil B, Cohen-Adad J, Tisdall MD, Folkerth RD, Kinney HC, Wald LL., 2013. The human connectome project and beyond: initial applications of 300 mT/m gradients. Neuroimage 80, 234–245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Menzel M, Axer M, De Raedt H, Costantini I, Silvestri L, Pavone FS, Amunts K, Michielsen K, 2020. Toward a high-resolution reconstruction of 3D nerve fiber architectures and crossings in the brain using light scattering measurements and finite-difference time-domain simulations. Phys. Rev. X 10, 021002. [Google Scholar]
- Menzel M, André Reuter J, Gräßel D, Huwer M, Schlömer P, Amunts K, Axer M, 2021. Scattered light imaging: resolving the substructure of nerve fiber crossings in whole brain sections with micrometer resolution. arXiv e-prints. arXiv 2008.01037. (accepted by NeuroImage). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miklossy J, Van der Loos H, 1987. Cholesterol esther crystals in polarized light show pathways in the human brain. Brain Res. 426, 377–380. [DOI] [PubMed] [Google Scholar]
- Miller KL, McNab JA, Jbabdi S, Douaud G, 2012. Diffusion tractography of post–mortem human brains: optimization and comparison of spin echo and steady-state free precession techniques. Neuroimage 59, 2284–2297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller KL, Stagg CJ, Douaud G, Jbabdi S, Smith SM, Behrens TEJ, Jenkinson M, Chance SA, Esiri MM, Voets NL, Jenkinson N, Aziz TZ, Turner MR, Johansen-Berg H, McNab JA, 2011. Diffusion imaging of whole, post-mortem human brains on a clinical MRI scanner. Neuroimage 57, 167–181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Modo M, Hitchens TK, Liu JR, Richardson RM, 2016. Detection of aberrant hippocampal mossy fiber connections: ex vivo mesoscale diffusion MRI and microtractography with histological validation in a patient with uncontrolled temporal lobe epilepsy. Hum. Brain Mapp 37, 780–795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mohammadi S, Callaghan MF, 2021. Towards in vivo g-ratio mapping using MRI: unifying myelin and diffusion imaging. J. Neurosci. Methods 348, 108990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mollink J, van Baarsen KM, Dederen PJ, Foxley S, Miller KL, Jbabdi S, Slump CH, Grotenhuis JA, Kleinnijenhuis M, van Cappellen van Walsum AM, 2016. Dentatorubrothalamic tract localization with postmortem MR diffusion tractography compared to histological 3D reconstruction. Brain Struct. Funct 221 (7), 3487–3501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mollink J, Kleinnijenhuis M, Cappellen van Walsum AV, Sotiropoulos SN, Cottaar M, Mirfin C, Heinrich MP, Jenkinson M, Pallebage-Gamarallage M, Ansorge O, Jbabdi S, Miller KL, 2017. Evaluating fibre orientation dispersion in white matter: Comparison of diffusion MRI, histology and polarized light imaging. Neuroimage 157, 561–574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mollink J, et al. , 2019. White matter changes in the perforant path area in patients with amyotrophic lateral sclerosis. Neuropathol. Appl. Neurobiol 45 (6), 570–585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mori S, Crain BJ, Chacko VP, van Zijl PC, 1999. Three-dimensional tracking of axonal projections in the brain by magnetic resonance imaging. Ann. Neurol 45 (2), 265–269. [DOI] [PubMed] [Google Scholar]
- Morris DM, Embleton KV, Parker GJM, 2008. Probabilistic fibre tracking: differentiation of connections from chance events. Neuroimage 42, 1329–1339. [DOI] [PubMed] [Google Scholar]
- Murray E, Cho JH, Goodwin D, Ku T, Swaney J, Kim SY, Choi H, Park YG, Park JY, Hubbert A, McCue M, Vassallo S, Bakh N, Frosch MP, Wedeen VJ, Seung HS, Chung K, 2015. Simple, scalable proteomic imaging for high-dimensional profiling of intact systems. Cell 163, 1500–1514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neher PF, et al. , 2014. Fiberfox: facilitating the creation of realistic white matter software phantoms. Magn. Reson. Med 72 (5), 1460–1470. [DOI] [PubMed] [Google Scholar]
- Nieuwenhuys R, Broere CAJ, Cerliani L, 2015. A new myeloarchitectonic map of the human neocortex based on data from the Vogt-Vogt school. Brain Struct. Funct 220, 2551–2573. [DOI] [PubMed] [Google Scholar]
- Nilsson M, Lätt J, Ståhlberg F, Westen D, Hagslätt H, 2012. The importance of axonal undulation in diffusion MR measurements: a Monte Carlo simulation study. NMR Biomed. 25 (5), 795–805. [DOI] [PubMed] [Google Scholar]
- Nooij RP, Hoving EW, van Hulzen AL, Cornelissen FW, Renken RJ., 2015. Preservation of the optic radiations based on comparative analysis of diffusion tensor imaging tractography and anatomical dissection. Front Neuroanat 9, 96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Novikov DS, Fieremans E, Jespersen SN, Kiselev VG, 2018. Quantifying brain microstructure with diffusion MRI: theory and parameter estimation. NMR Biomed. e3998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Donnell LJ, Westin CF, Golby AJ, 2009. Tract-based morphometry for white matter group analysis. Neuroimage. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oh SW, Harris JA, Ng L, Winslow B, Cain N, Mihalas S, Wang Q, Lau C, Kuan L, Henry AM, Mortrud MT, Ouellette B, Nguyen TN, Sorensen SA, Slaughterbeck CR, Wakeman W, Li Y, Feng D, Ho A, Nicholas E, Hirokawa KE, Bohn P, Joines KM, Peng H, Hawrylycz MJ, Phillips JW, Hohmann JG, Wohnoutka P, Gerfen CR, Koch C, Bernard A, Dang C, Jones AR, Zeng H, 2014. A mesoscale connectome of the mouse brain. Nature 508 (7495), 207–214 Apr 10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pallebage-Gamarallage M, Foxley S, Menke RAL, et al. , 2018. Dissecting the pathobiology of altered MRI signal in amyotrophic lateral sclerosis: A post mortem whole brain sampling strategy for the integration of ultra-high-field MRI and quantitative neuropathology. BMC Neurosci. 19, 11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pallotto M, Watkins PV, Fubara B, Singer JH, Briggman KL, 2015. Extracellular space preservation aids the connectomic analysis of neural circuits. Elife. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palombo M, et al. , 2020. SANDI: A compartment-based model for non-invasive apparent soma and neurite imaging by diffusion MRI. Neuroimage. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Panagiotaki E, Hall MG, Zhang H, Siow B, Lythgoe MF, and Alexander DC, “High-fidelity meshes from tissue samples for diffusion MRI simulations,” in Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 2010, vol. 6362 LNCS, no. PART 2, pp. 404–411. [DOI] [PubMed] [Google Scholar]
- Park YG, Sohn CH, Chen R, McCue M, Yun DH, Drummond GT, Ku T, Evans NB, Oak HC, Trieu W, Choi H, Jin X, Lilascharoen V, Wang J, Truttmann MC, Qi HW, Ploegh HL, Golub TR, Chen SC, Frosch MP, Kulik HJ, Lim BK, Chung K, 2019. Protection of tissue physicochemical properties using polyfunctional crosslinkers. Nat. Biotechnol 37, 73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perrin M, et al. , 2005. Validation of q-ball imaging with a diffusion fibre-crossing phantom on a clinical scanner. Philoso. Trans. R. Soc. Lond. Ser. B Biol. Sci 360 (1457), 881–891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petrides M. Pandya DN. Boller F. Grafman J. 1994. Comparative architectonic analysis of the human and the macaque frontal cortex. In: Handbook of Neuropsychology, 9. Elsevier, Amsterdam, pp. 17–58 eds. [Google Scholar]
- Pfefferbaum A. Sullivan EV, Adalsteinsson E. Garrick T. Harper C. 2004. Post-mortem MR imaging of formalin-fixed human brain. Neuroimage 21, 1585–1595. [DOI] [PubMed] [Google Scholar]
- Poupon C, et al. , 2008. New diffusion phantoms dedicated to the study and validation of high-angular-resolution diffusion imaging (HARDI) models. Mag. Reson. Med 60 (6), 1276–1283. [DOI] [PubMed] [Google Scholar]
- Pujari VB, Jimbo H. Dange N, Shah A. Singh S. Goel A. 2008. Fiber dissection of the visual pathways: analysis of the relationship of optic radiations to lateral ventricle: a cadaveric study. Neurol. India 56 (2), 133–137. [DOI] [PubMed] [Google Scholar]
- Reckfort J. Wiese H. Pietrzyk U. Zilles K. Amunts K. Axer M. 2015. A multiscale approach for the reconstruction of the fiber architecture of the human brain based on 3D-PLI. Front. Neuroanat 9, 118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reese TG. Heid O. Weisskoff RM. Wedeen VJ. 2003. Reduction of eddy-current-induced distortion in diffusion MRI using a twice-refocused spin echo. Magn. Reson. Med 49, 177–182. [DOI] [PubMed] [Google Scholar]
- Roebroeck A, Sengupta S, Bastiani M, Schillak S, Tramm B, Waks M, Lataster A, Herrler A, Tse D, Poser B, 2015. High resolution MRI neuroanatomy in whole human brains post mortem with a specialized 9.4T RF-coil. In: Proceedings of the Organization for Human Brain Mapping. [Google Scholar]
- Roebroeck A. Miller KL. Aggarwal M. 2019. Ex vivo diffusion MRI of the human brain: Technical challenges and recent advances. NMR Biomed. 32, e3941–e3941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Romeis B. 1989. Mikroskopische Technik. Urban and Schwarzenberg Verlag, München. [Google Scholar]
- Safadi Z, Grisot G, Jbabdi S, Behrens T, Heilbronner SR, Mandeville J, Versace A, Phillips ML. Yendiki A, Haber SN. 2018. Functional segmentation of the internal capsule: Linking white matter abnormalities to specific connections. J. Neurosci 38 (8), 2106–2117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sarubbo S. Petit L. De Benedictis A. Chioffi F. Ptito M. Dyrby TB. 2019. Uncovering the inferior fronto-occipital fascicle and its topological organization in non-human primates: the missing connection for language evolution. Brain Struct Funct. [DOI] [PubMed] [Google Scholar]
- Seehaus A, Roebroeck A, Bastiani M, Fonseca L, Bratzke H, Lori N, Vilanova A, Goebel R, Galuske R, 2015. Histological validation of high-resolution DTI in human post mortem tissue. Front. Neuroanat 9, 98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Setsompop K, Kimmlingen R, Eberlein E, Witzel T, Cohen-Adad J, McNab JA, Keil B, Tisdall MD, Hoecht P, Dietz P, Cauley SF, Tountcheva V, Matschl V, Lenz VH, Heberlein K, Potthast A, Thein H, Van Horn J, Toga A, Schmitt F, Lehne D. Rosen BR. Wedeen V. Wald LL. 2013. Pushing the limits of in vivo diffusion MRI for the human connectome project. Neuroimage 80, 220–233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schilling K, Janve V, Gao Y, Stepniewska I, Landman BA, Anderson AW, 2016. Comparison of 3D orientation distribution functions measured with confocal microscopy and diffusion MRI. Neuroimage 129, 185–197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schilling K, Gao Y, Stepniewska I, Choe AS, Landman BA, Anderson AW, 2017a. Reproducibility and variation of diffusion measures in the squirrel monkey brain, in vivo and ex vivo. Magn. Reson. Imaging 35, 29–38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schilling K, Gao Y, Janve V, Stepniewska I, Landman BA, Anderson AW, 2017b. Can increased spatial resolution solve the crossing fiber problem for diffusion MRI? NMR Biomed. 30 (12), e3787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schilling KG, Janve V, Gao Y, Stepniewska I, Landman BA, Anderson AW, 2018. Histological validation of diffusion MRI fiber orientation distributions and dispersion. Neuroimage 165, 200–221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schilling KG. Gao Y. et al. 2019a. Anatomical accuracy of standard-practice tractography algorithms in the motor system - a histological validation in the squirrel monkey brain. Magn. Reson. Imaging 55, 7–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schilling KG. Nath V. et al. 2019b. Limits to anatomical accuracy of diffusion tractography using modern approaches. Neuroimage 185, 1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmahmann JD, Pandya DN, 2006. Fiber pathways of the brain. Oxford University Press, New York. [Google Scholar]
- Schmahmann JD, et al. , 2007. Association fibre pathways of the brain: Parallel observations from diffusion spectrum imaging and autoradiography. Brain 130 (3), 630–653. [DOI] [PubMed] [Google Scholar]
- Schmahmann JD., Smith EE, Eichler FS, Filley CM, 2008. Cerebral white matter neuroanatomy, clinical neurology, and neurobehavioral correlates. Ann. N.Y. Acad. Sci 1142, 266–309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmitz D, Muenzing SEA, Schober M, Schubert N, Minnerop M, Lippert T, Amunts K, Axer M, 2018. Derivation of fiber orientations from oblique views through human brain sections in 3D-polarized light imaging. Front. Neuroanat 12, 75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmued L, Slikker W, 1999. Black-gold: a simple, high-resolution histochemical label for normal and pathological myelin in brain tissue sections. Brain Res. 837 (1-2), 289–297 Aug 7. [DOI] [PubMed] [Google Scholar]
- Scholz A. Etzel R. May M. Mahmutovic M. Tian Q. Ramos-Llordén G. Bilgiç B. Witzel T, Stockmann JP, Mekkaoui C, Wald LL, Huang SY, Yendiki A, Keil B, 2021. A 48-channel receive array coil for mesoscopic diffusion-weighted MRI of human ex vivo brain on the 3T Connectome scanner. Neuroimage 238, 118256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schubert N, Axer M, Schober M, Huynh AM, Huysegoms M, Palomero-Gallagher N, Bjaalie JG, Leergaard TB, Kirlangic ME, Amunts K, Zilles K, 2016. 3D reconstructed cyto-, muscarinic M2 receptor, and fiber architecture of the rat brain registered to the Waxholm space Atlas. Front Neuroanat 10, 51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schubert N. Axer M. Pietrzyk U. Amunts K. Halefoğlu AM. 2018. 3D polarized light imaging portrayed: visualization of fiber architecture derived from 3D-PLI. In: High-Resolution Neuroimaging - Basic Physical Principles and Clinical Applications. IntechOpen, pp. 29–46. [Google Scholar]
- Sengupta S, Fritz FJ, Harms RL, Hildebrand S, Tse DHY, Poser BA, Goebel R, Roebroeck A, 2018. High resolution anatomical and quantitative MRI of the entire human occipital lobe ex vivo at 9.4T. Neuroimage 168, 162–171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shepherd TM, Flint JJ, Thelwall PE, Stanisz GJ, Mareci TH, Yachnis AT, Blackband SJ., 2009. Postmortem interval alters the water relaxation and diffusion properties of rat nervous tissue–implications for MRI studies of human autopsy samples. Neuroimage 44 (3), 820–826. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shinohara H. Liu X. Nakajima R. Kinoshita M. Ozaki N. Hori O. Nakada M. 2020. Pyramid-shape crossings and intercrossing fibers are key elements for construction of the neural network in the superficial white matter of the human cerebrum. Cereb. Cortex [DOI] [PubMed] [Google Scholar]
- Sholl DA, 1953. Dendritic organization in the neurons of the visual and motor cortices of the cat. J. Anat 87 (4), 387–406. [PMC free article] [PubMed] [Google Scholar]
- Sivukhina EV, Jirikowski GF, 2021. Oxytocin, but not arginine-vasopressin neurons project from the hypothalamus to amygdala in human: DII-based tracing study in postmortem brain. J. Chem. Neuroanat 111, 101882. [DOI] [PubMed] [Google Scholar]
- Soni N, Vegh V, To XV, Mohamed AZ, Borges K, Nasrallah FA, 2020. Combined diffusion tensor imaging and quantitative susceptibility mapping discern discrete facets of white matter pathology post-injury in the rodent brain. Front. Neurol. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stacho M. Herold C. Rook N. Wagner H. Axer M. Amunts K. Güntürkün O. 2020. A cortex-like canonical circuit in the avian forebrain. Science 369. [DOI] [PubMed] [Google Scholar]
- Stephan KE. Kamper L. Bozkurt A. Burns GA. Young MP. Kötter R. 2001. Advanced database methodology for the collation of connectivity data on the macaque brain (CoCoMac). Philos. Trans. R. Soc. Lond. B Biol. Sci 356 (1412), 1159–1186 Aug. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stanisz GJ, Szafer A, Wright GA, Henkelman RM, 1997. An analytical model of restricted diffusion in bovine optic nerve. Magn. Reson. Med. [DOI] [PubMed] [Google Scholar]
- Stikov N. et al. 2015. In vivo histology of the myelin g-ratio with magnetic resonance imaging. Neuroimage. [DOI] [PubMed] [Google Scholar]
- Stolp HB, et al. , 2018. Voxel-wise comparisons of cellular microstructure and diffusion-MRI in mouse hippocampus using 3D Bridging of Optically-clear histology with Neuroimaging Data (3D-BOND. Sci. Rep 8 (1), 4011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun SW, Neil JJ, Liang HF, He YY, Schmidt RE, Hsu CY, Song SK, 2005. Formalin fixation alters water diffusion coefficient magnitude but not anisotropy in infarcted brain. Magn. Reson. Med 53, 1447–1451. [DOI] [PubMed] [Google Scholar]
- Takata N, Kusayanagi K, Maruyama H, Eitai K, Abo M, Akiyama F, Tajima R, Inaba S, Tanaka KF, Mimura M, Sanaka K, 2018. Visualization of myelinated fiber bundles orientation during brain slice preparation by reflection polarized light microscopy. Microsc. Res. Tech 81, 1366–1373. [DOI] [PubMed] [Google Scholar]
- Takemura H. Palomero-Gallagher N. Axer M, Gräßel D. Jorgensen MJ. Woods R. Zilles K, 2020. Anatomy of nerve fiber bundles at micrometer-resolution in the vervet monkey visual system. eLife 9, e55444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang W, et al. , 2019. A connectional hub in the rostral anterior cingulate cortex links areas of emotion and cognitive control. eLife e43761, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tardif E, Clarke S, 2001. Intrinsic connectivity of human auditory areas: a tracing study with DiI. Eur. J. Neurosci 13 (5), 1045–1050. [DOI] [PubMed] [Google Scholar]
- Thal DR, Capetillo-Zarate E, Galuske RA, 2008. Tracing of temporo-entorhinal connections in the human brain: cognitively impaired argyrophilic grain disease cases show dendritic alterations but no axonal disconnection of temporo-entorhinal association neurons. Acta Neuropathol. 115, 175–183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomas C, et al. , 2014. Anatomical accuracy of brain connections derived from diffusion MRI tractography is inherently limited. Proc. Natl. Acad. Sci 111 (46), 16574–16579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tolcos M, Rowitch DH, Dean J, 2016. Oligodendrocytes: Cells of origin for white matter injury in the developing brain. Neuromethods. [Google Scholar]
- Tomer R, Ye L, Hsueh B, Deisseroth K, 2014. Advanced CLARITY for rapid and high--resolution imaging of intact tissues. Nat. Protoc (7) 1682–1697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trinkle S. Foxley S. Kasthuri N. 2021. La Rivière P. Synchrotron X-ray micro-CT as a validation dataset for diffusion MRI in whole mouse brain. Magn. Reson. Med 86 (2), 1067–1076 Aug. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Türe U. Yaşargil MG. Friedman a, H.. Al-Mefty O. 2000. Fiber dissection technique: lateral aspect of the brain. Neurosurgery 47, 426–427 417–26; discussion. [DOI] [PubMed] [Google Scholar]
- Tyszka JM, Frank LR, 2009. High-field diffusion MR histology: Image-based correction of eddy-current ghosts in diffusion-weighted rapid acquisition with relaxation enhancement (DW-RARE). Magn. Reson. Med 61, 728–733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uchihara T, 2007. Silver diagnosis in neuropathology: principles, practice and revised interpretation. Acta Neuropathol. 113, 483–499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ugryumova N, Gangnus SV, Matcher SJ, 2006. Three-dimensional optic axis determination using variable-incidence-angle polarization-optical coherence tomography. Opt. Lett 31, 2305–2307. [DOI] [PubMed] [Google Scholar]
- Ugryumova N, Jacobs J, Bonesi M, Matcher SJ, 2009. Novel optical imaging technique to determine the 3-D orientation of collagen fibers in cartilage: variable-incidence angle polarization- sensitive optical coherence tomography. Osteoarthr. Cartil 17, 33–42. [DOI] [PubMed] [Google Scholar]
- van den Heuvel MP. et al. 2015. Comparison of diffusion tractography and tract-tracing measures of connectivity strength in rhesus macaque connectome. Hum. Brain Mapp 36 (8), 3064–3075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Essen DC, Smith SM, Barch DM, Behrens TE, Yacoub E, Ugurbil K Consortium WU-Minn HCP Consortium, 2013. The WU-minn human connectome project: an overview. Neuroimage 80, 62–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veraart J. et al. 2020. Noninvasive quantification of axon radii using diffusion MRI. Elife 9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vogt O, 1903. Zur anatomischen gliederung des cortex cerebri. J. Psychol. Neurol 2, 160–180. [Google Scholar]
- Wakana S, Jiang H, Nagae-Poetscher LM, van Zijl PC, Mori S, 2004. Fiber tract-based atlas of human white matter anatomy. Radiology 230 (1), 77–87. [DOI] [PubMed] [Google Scholar]
- Wang H, Black AJ, Zhu J, Stigen TW, Al-Qaisi MK, Netoff TI, Abosch A, Akkin T. 2011. Reconstructing micrometer-scale fiber pathways in the brain: multicontrast optical coherence tomography based tractography. Neuroimage 58 (4), 984–992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang H, Zhu J, Akkin T, 2014a. Serial optical coherence scanner for large-scale brain imaging at microscopic resolution. Neuroimage 84, 1007–1017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang H, Zhu J, Reuter M, Vinke LN, Yendiki A, Boas DA, Fischl B, Akkin T, 2014b. Cross-validation of serial optical coherence scanning and diffusion tensor imaging: a study on neural fiber maps in human medulla oblongata. Neuroimage 100, 395–404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang H, Akkin T, Magnain C, Wang R, Dubb J, Kostis WJ, Yaseen MA, Cramer A, Sakadžić S, Boas D, 2016. Polarization sensitive optical coherence microscopy for brain imaging. Opt. Lett 41 (10), 2213–2216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang H, Magnain C, Wang R, Dubb J, Varjabedian A, Tirrell LS, Stevens A, Augustinack JC, Konukoglu E, Aganj I, Frosch MP, Schmahmann JD, Fischl B, Boas DA, 2018. as-PSOCT: volumetric microscopic imaging of human brain architecture and connectivity. Neuroimage 165, 56–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wehrl HF, Bezrukov I, Wiehr S, Lehnhoff M, Fuchs K, Mannheim JG, Quintanilla-Martinez L, Kohlhofer U, Kneilling M, Pichler BJ, Sauter AW, 2015. Assessment of murine brain tissue shrinkage caused by different histological fixatives using magnetic resonance and computed tomography imaging. Histol. Histopathol 30, 601–613. [DOI] [PubMed] [Google Scholar]
- Weiller C, Reisert M, Peto I, Hennig J, Makris N, Petrides M, Rijntjes M, Egger K, 2021. The ventral pathway of the human brain: a continuous association tract system. Neuroimage 234, 117977. [DOI] [PubMed] [Google Scholar]
- West KL, Kelm ND, Carson RP, Alexander DC, Gochberg DF, Does MD, 2018. Experimental studies of g-ratio MRI in ex vivo mouse brain. Neuroimage 167, 366–371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams JH, Mepham BL, Wright DH, 1997. Tissue preparation for immunocytochemistry. J. Clin. Pathol 50, 422–428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wysiadecki G, Clarke E, Polguj M, Haładaj R, Żytkowski A, Topol M, 2019. Klingler’s method of brain dissection: review of the technique including its usefulness in practical neuroanatomy teaching, neurosurgery and neuroimaging. Folia Morphol. 78 (3), 455–466 (Warsz; ). [DOI] [PubMed] [Google Scholar]
- Xu J, et al. , 2014. Mapping mean axon diameter and axonal volume fraction by MRI using temporal diffusion spectroscopy. Neuroimage. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamada M, Momoshima S, Masutani Y, Fujiyoshi K, Abe O, Nakamura M, Aoki S, Tamaoki N, Okano H, 2008. Diffusion-tensor neuronal fiber tractography and manganese-enhanced MR imaging of primate visual pathway in the common marmoset: preliminary results. Radiology 249 (3), 855–864. [DOI] [PubMed] [Google Scholar]
- Yang B, Treweek JB, Kulkarni RP, Deverman BE, Chen CK, Lubeck E, Shah S, Cai L, Gradinaru V, 2014. Single-cell phenotyping within transparent intact tissue through whole-body clearing. Cell 158 (4), 945–958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yendiki A, Jones R, Dalca A, Wang H, Fischl B, 2020. Towards taking the guesswork (and the errors) out of diffusion tractography. Proc. Intl. Soc. Mag. Res. Med. [Google Scholar]
- Yi SY, et al. , 2019. Detecting microglial density with quantitative multi-compartment diffusion MRI. Front. Neurosci. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeineh MM, Palomero-Gallagher N, Axer M, Grassel D, Goubran M, Wree A, Woods R, Amunts K, Zilles K, 2017. Direct visualization and mapping of the spatial course of fiber tracts at microscopic resolution in the human hippocampus. Cereb. Cortex 27, 1779–1794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang H, Schneider T, Wheeler-Kingshott CA, Alexander DC, 2012. NODDI: practical in vivo neurite orientation dispersion and density imaging of the human brain. Neuroimage 61 (4), 1000–1016. [DOI] [PubMed] [Google Scholar]
- Zhao S, Todorov MI, Cai R, Maskari RA, Steinke H, Kemter E, Mai H, Rong Z, Warmer M, Stanic K, Schoppe O, Paetzold JC, Gesierich B, Wong MN, Huber TB, Duering M, Bruns OT, Menze B, Lipfert J, Puelles VG, Wolf E, Bechmann I, Ertürk A, 2020. Cellular and molecular probing of intact human organs. Cell 180, 796–812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zemmoura I, Serres B, Andersson F, Barantin L, Tauber C, Filipiak I, Cottier J-P, Venturini G, Destrieux C, 2014. FIBRASCAN: a novel method for 3D white matter tract reconstruction in MR space from cadaveric dissection. Neuroimage 103, 106–118. [DOI] [PubMed] [Google Scholar]
- Zemmoura I, Blanchard E, Raynal PI, Rousselot-Denis C, Destrieux C, Velut S, 2016. How Klingler’s dissection permits exploration of brain structural connectivity? An electron microscopy study of human white matter. Brain Struct. Funct 221 (5), 2477–2486 Jun. [DOI] [PubMed] [Google Scholar]
Further reading
- Budde MD, Kim JH, Liang HF, Russell JH, Cross AH, Song SK, 2008. Axonal injury detected by in vivo diffusion tensor imaging correlates with neurological disability in a mouse model of multiple sclerosis. NMR Biomed.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dhital B, Reisert M, Kellner E, Kiselev VG, 2019. Intra-axonal diffusivity in brain white matter. Neuroimage 189, 543–550. [DOI] [PubMed] [Google Scholar]
- Fuster JM, 2001. The prefrontal cortex–an update: time is of the essence. Neuron 30 (2), 319–333. [DOI] [PubMed] [Google Scholar]
- Jones DK, Knösche TR, Turner R, 2013. White matter integrity, fiber count, and other fallacies: The do’s and don’ts of diffusion MRI. Neuroimage. [DOI] [PubMed] [Google Scholar]
- Nigel I, Lawes C, Barrick TR, Murugam V, Spierings N, Evans DR, Song M, Clark CA, 2008. Atlas-based segmentation of white matter tracts of the human brain using diffusion tensor tractography and comparison with classical dissection. Neuroimage 39, 62–79. [DOI] [PubMed] [Google Scholar]
- Nair G, Tanahashi Y, Hoi PL, Billings-Gagliardi S, Schwartz WJ, Duong TQ, 2005. Myelination and long diffusion times alter diffusion-tensor-imaging contrast in myelin-deficient shiverer mice. Neuroimage. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salo RA, Belevich I, Jokitalo E, Gröhn O, Sierra A, 2021. Assessment of the structural complexity of diffusion MRI voxels using 3D electron microscopy in the rat brain. Neuroimage. [DOI] [PubMed] [Google Scholar]
- Song S-K, Sun S-W, Ramsbottom MJ, Chang C, Russell J, Cross AH, 2002. Dysmyelination revealed through MRI as increased radial (but unchanged axial) diffusion of water. Neuroimage 17 (3), 1429–1436. [DOI] [PubMed] [Google Scholar]
- Torkildsen O, Brunborg LA, Myhr KM, Bø L, 2008. The cuprizone model for demyelination. Acta Neurol. Scand. Suppl 188, 72–76. [DOI] [PubMed] [Google Scholar]
- Yushkevich PA, Zhang H, Simon TJ, Gee JC, 2008. Structure-specific statistical mapping of white matter tracts. Neuroimage. [DOI] [PMC free article] [PubMed] [Google Scholar]