Cytokinesis machinery promotes cell dissociation from collectively migrating strands in confinement

Robert A Law; Alexander Kiepas; Habben E Desta; Emiliano Perez Ipiña; Maria Parlani; Se Jong Lee; Christopher L Yankaskas; Runchen Zhao; Panagiotis Mistriotis; Nianchao Wang; Zhizhan Gu; Petr Kalab; Peter Friedl; Brian A Camley; Konstantinos Konstantopoulos

doi:10.1126/sciadv.abq6480

. 2023 Jan 11;9(2):eabq6480. doi: 10.1126/sciadv.abq6480

Cytokinesis machinery promotes cell dissociation from collectively migrating strands in confinement

Robert A Law ^1,², Alexander Kiepas ^1,^2,^†, Habben E Desta ^1,^2,^†, Emiliano Perez Ipiña ^3,^†, Maria Parlani ⁴, Se Jong Lee ^1,², Christopher L Yankaskas ^1,², Runchen Zhao ^1,², Panagiotis Mistriotis ^1,^2,⁵, Nianchao Wang ^1,², Zhizhan Gu ^1,^2,^*, Petr Kalab ¹, Peter Friedl ^4,^6,⁷, Brian A Camley ^3,⁸, Konstantinos Konstantopoulos ^1,^2,^9,^10,^*

^¹Department of Chemical and Biomolecular Engineering, Johns Hopkins University, Baltimore, MD 21218, USA.

^²Johns Hopkins Institute for NanoBioTechnology, Johns Hopkins University, Baltimore, MD 21218, USA.

^³William H. Miller III Department of Physics and Astronomy, Johns Hopkins University, Baltimore, MD 21218, USA.

^⁴Department of Genitourinary Medical Oncology, The University of Texas MD Anderson Cancer Center, Houston, TX 77030, USA.

^⁵Department of Chemical Engineering, Auburn University, Auburn, AL 36849, USA.

^⁶Department of Cell Biology, Radboud Institute for Molecular Life Sciences, Radboud University Medical Center, Nijmegen, Netherlands.

^⁷Cancer Genomics Center, 3584 Utrecht, Netherlands.

^⁸Department of Biophysics, Johns Hopkins University, Baltimore, MD 21218, USA.

^⁹Department of Biomedical Engineering, Johns Hopkins University, Baltimore, MD 21218, USA.

^¹⁰Department of Oncology, Johns Hopkins University, Baltimore, MD 21205, USA.

^†

These authors contributed equally to this work as second authors.

Corresponding author. Email: konstant@jhu.edu (K.K.); zhizhan.gu@alumni.brown.edu (Z.G.)

Roles

Robert A Law: Conceptualization, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Supervision, Validation, Visualization, Writing - original draft, Writing - review & editing

Alexander Kiepas: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Project administration, Resources, Supervision, Validation, Visualization, Writing - original draft, Writing - review & editing

Habben E Desta: Conceptualization, Formal analysis, Investigation, Methodology, Resources, Validation

Emiliano Perez Ipiña: Data curation, Formal analysis, Methodology, Software, Validation, Visualization, Writing - original draft, Writing - review & editing

Maria Parlani: Conceptualization, Formal analysis, Investigation, Methodology, Project administration, Resources, Validation, Visualization, Writing - original draft, Writing - review & editing

Se Jong Lee: Data curation, Formal analysis, Investigation

Christopher L Yankaskas: Conceptualization, Formal analysis, Methodology, Writing - review & editing

Runchen Zhao: Formal analysis, Methodology, Software

Panagiotis Mistriotis: Conceptualization, Methodology, Resources, Writing - review & editing

Nianchao Wang: Formal analysis, Investigation, Validation

Zhizhan Gu: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Project administration, Resources, Supervision, Validation, Visualization, Writing - original draft, Writing - review & editing

Petr Kalab: Formal analysis, Investigation, Validation, Writing - review & editing

Peter Friedl: Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Visualization, Writing - original draft, Writing - review & editing

Brian A Camley: Conceptualization, Formal analysis, Funding acquisition, Methodology, Software, Writing - review & editing

Konstantinos Konstantopoulos: Conceptualization, Data curation, Funding acquisition, Methodology, Project administration, Resources, Supervision, Validation, Visualization, Writing - original draft, Writing - review & editing

PMCID: PMC9833664 PMID: 36630496

Abstract

Cells tune adherens junction dynamics to regulate epithelial integrity in diverse (patho)physiological processes, including cancer metastasis. We hypothesized that the spatially confining architecture of peritumor stroma promotes metastatic cell dissemination by remodeling cell-cell adhesive interactions. By combining microfluidics with live-cell imaging, FLIM/FRET biosensors, and optogenetic tools, we show that confinement induces leader cell dissociation from cohesive ensembles. Cell dissociation is triggered by myosin IIA (MIIA) dismantling of E-cadherin cell-cell junctions, as recapitulated by a mathematical model. Elevated MIIA contractility is controlled by RhoA/ROCK activation, which requires distinct guanine nucleotide exchange factors (GEFs). Confinement activates RhoA via nucleocytoplasmic shuttling of the cytokinesis-regulatory proteins RacGAP1 and Ect2 and increased microtubule dynamics, which results in the release of active GEF-H1. Thus, confining microenvironments are sufficient to induce cell dissemination from primary tumors by remodeling E-cadherin cell junctions via the interplay of microtubules, nuclear trafficking, and RhoA/ROCK/MIIA pathway and not by down-regulating E-cadherin expression.

Cytokinesis proteins promote leader cell dissociation by triggering RhoA/myosin IIA dismantling of E-cadherin junctions.

INTRODUCTION

Cell migration is broadly classified into two major categories: collective and single-cell migration (1). To date, most in vitro and in vivo cancer research studies have focused primarily on single-cell or semicollective (multicellular streaming) cell migration. The molecular understanding of single-cell migration mechanisms has offered insights into the dissemination of tumors that escape from lesions via the epithelial-to-mesenchymal transition (EMT) and cancer cells that migrate constitutively as individual cells, such as leukemias and lymphomas. However, invasive breast and squamous carcinoma cells often migrate collectively as a group by maintaining cell-cell contacts (1–3). Cancer cells can adopt different modes of migration orchestrated by both cell-autonomous and reactive mechanisms stimulated by the physical and biochemical microenvironment. Hence, they may flexibly interconvert between collective and single-cell migration programs to overcome complex physical barriers in the extracellular tissue space.

A key feature of collectively migrating cell sheets is the supracellular polarity of cells organized into leader cells, which sense the microenvironment and direct migration, and follower cells, which polarize leader cells via contact inhibition of locomotion (4). Leader cells exhibit asymmetric adhesive structures involving integrin-based focal adhesion connections with the extracellular matrix (ECM) at their leading edges and cadherin-containing adherens junctions at their trailing edges, which form cell-cell contacts with follower cells (4). Cadherins interact with the actin cytoskeleton via intracellular adaptor proteins and coordinate actomyosin contractility, multicellular polarity, and collective cell migration (5). On two-dimensional (2D) unconfined surfaces, collective cell migration is facilitated by low actomyosin contractility at sites of cell-cell contact (2). Moreover, loss or disruption of E-cadherin function results in the dissociation of single cells or a small cluster of cells from collectively migrating sheets on unconfined or locally free tissue spaces (3). In contrast, the down-regulation of E-cadherin in confinement results in a jamming transition from coordinated to uncoordinated collective migration (3).

Intravital microscopy studies show that tumor cells preferentially migrate along preexisting channel-like tracks created by various anatomical structures in vivo (6). These tracks are 100 to 600 μm in length and range from highly confining (≤3 μm in width) to larger than the individual tumor cell body (~30 μm) (7, 8). Lateral confinement, imposed by progressively narrower fibronectin-coated microstripes (from 100 μm down to 20 μm), enhanced the speed of Madin-Darby canine kidney migrating cell sheets (9). In line with these findings (9), a similar extent of confinement enhanced the directional persistence of neural crest cells, leading to more efficient collective migration in zebrafish and Xenopus embryos (10). On the other hand, decreasing the width of fibronectin-coated microstripes from 20 to 5 μm reduced lamellipodial protrusive forces and slowed down collective keratinocyte cell migration (11). While these previous in vitro models investigated the role of 2D lateral confinement in collective cell migration, it is noteworthy that cells in vivo are also confined in the dorsoventral direction (12). To determine how 3D-like confinement affects collective cell migration, we induced collective sheets of A431 epidermal and MCF-7 breast carcinoma cells to enter fibronectin-coated microchannels of prescribed length (400 μm) and height (10 μm) but different widths ranging from 2D-like unconfined channels (50 μm) to highly confining (6 μm) ones.

We found that 3D-like confinement induces cell dissociation from collectively migrating sheets via mechanisms resembling those controlling daughter cell separation in the final step of the mitotic process known as cytokinesis, whereby RhoA activation at the equatorial plasma membrane is required to promote the assembly of the contractile ring that drives the successful separation of cells (13). RhoA activation during cytokinesis is mediated by the evolutionarily conserved RhoA guanine nucleotide exchange factor (GEF) known as epithelial cell transforming 2 (Ect2), which is physically associated with RacGAP1, a component of the centralspindlin complex. Confinement mediates cell dissociation from cohesive ensembles by promoting intense myosin IIA (MIIA) localization to the cell-cell junction at the rear of leader cells. A mathematical model of this process suggested that fluctuating levels of myosin drive cell junction separation. We used small-molecule inhibitors, recombinant constructs, and optogenetic tools to define the role of the RhoA/Rho-associated protein kinase (ROCK)/MIIA pathway in cell dissociation. We identified that confinement activates RhoA via the polarization of GEF-H1 at the cell poles and the nuclear exit of the cytokinesis-regulatory proteins RacGAP1 and Ect2. The critical role of RacGAP1 and Ect2 nuclear exit in this process was corroborated by generating mutants lacking nuclear localization signals (NLSs). Collectively, our data reveal that the interplay of microtubules, nuclear trafficking, and RhoA/ROCK/MIIA pathway regulates cell-cell junctions in response to confining tissue microenvironments.

RESULTS

Confinement promotes the dissociation of leader cells from collectively migrating strands

The mouse dermis contains a complex network of collagen bundles, myofibers, blood vessels, and other anatomical structures, which can restrict the movement of migrating cells by generating confining channel-like tracks (7, 8). To investigate how confinement affects cell migration behavior in vivo, we implanted an orthotopic HT-1080 fibrosarcoma xenograft into the mouse dermis and monitored cells over time using longitudinal intravital multiphoton microscopy (14). HT-1080 cells invaded the surrounding tissue collectively but frequently migrated in a single-file line likely due to confinement imposed by the surrounding myofibers and their perimysium adjacent to aligned collagen fibrils and blood vessels (fig. S1A). Leader cells at the tip of collectively migrating strands exhibited substantial lateral deformation, as evidenced by reduced nuclear diameter and circularity (fig. S1, C and D). While leader and follower cells could push against surrounding structures to create space and remain collective (15), we also observed cell dissociation from collectively migrating strands (fig. S1B and movie S1). Cells that detached from collective strands remained squeezed, with no significant change in the nuclear area, as they navigated through confinement (fig. S1, C to E). These results suggest that physical confinement imposed by the surrounding tissue architecture may facilitate leader cell dissociation from collective strands.

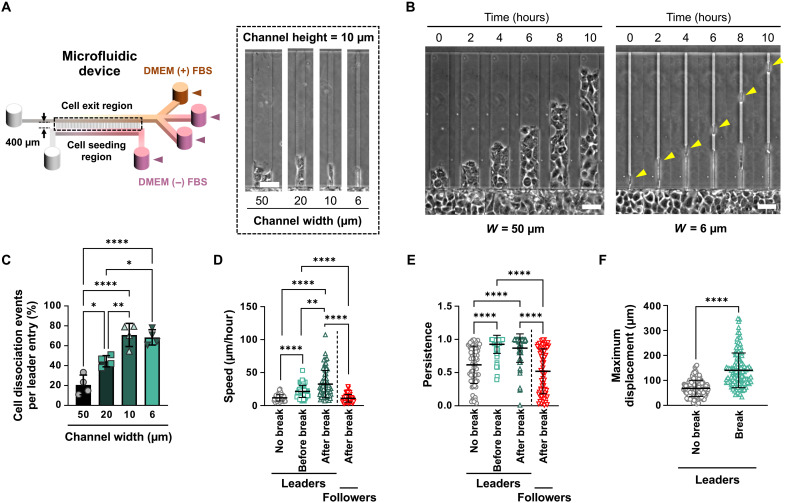
To delineate the effects of physical confinement on collective migration in vitro, we fabricated fibronectin-coated microchannels of defined length (L = 400 μm) and height (H = 10 μm) and varying widths (W). The width ranged from 50 μm, which recapitulates a 2D environment, to 6 μm, which simulates a highly confining microenvironment (Fig. 1A) (16, 17). In subsequent experiments, we chose to focus on A431 epidermal carcinoma cells, as these cells form tight cell-cell adhesions on 2D surfaces. Cells were seeded into microfluidic devices at a high density to form confluent monolayers and induced to migrate into channels in response to a chemotactic fetal bovine serum (FBS) gradient (18). Cells migrated collectively during their entry into channels irrespective of channel width. Only one leader cell existed in narrower (W = 10 or 6 μm) channels, while several leader cells were present along the migration front in wider channels (20 and 50 μm) (Fig. 1B, fig. S2A, and movie S2). Leader cells were defined as those whose leading edges were exposed to the empty microchannel space immediately ahead of them. Conversely, followers were attached to neighboring cells in their front and rear and confined by adjacent cells or the channel walls on the lateral sides.

Inside 50-μm-wide channels, cells primarily migrated collectively by maintaining cell-cell adhesions between leader and follower cells (Fig. 1B). For every leader cell that entered a wide channel, ~20% of them dissociated from the collective strand (Fig. 1C and fig. S2A). In marked contrast, about 70% of leader cells dissociated in narrower (W = 10 or 6 μm) channels (Fig. 1C). The majority (~75%) of all dissociation events in 6-μm-wide channels occurred during the first 10 to 12 hours of migration (fig. S2B). To validate our findings, we also tested MCF-7 breast cancer cells and found that collective strands of this cell type also exhibited greater leader cell dissociation with increasing confinement (fig. S2, C and D).

A431 leader cells that detached from their immediate followers migrated faster and more persistently than leader cells that remained attached to their follower strands (Fig. 1, D and E). Leader cells that eventually detached were ~2-fold faster and ~1.5-fold more persistent than their nondetaching counterparts before dissociation, suggesting that highly motile cells lead strands that exhibit leader cell dissociation. Along these lines, follower cells migrated significantly slower and less persistently following the detachment of leader cells (Fig. 1, D and E). Furthermore, dissociating leader cells penetrated markedly further into the microchannels (~141 μm) within the 10-hour experimental duration compared to nondissociating leader cells (~68 μm; Fig. 1F). Given the interplay between E-cadherin and integrin β1 in the regulation of directional collective migration and the polarization of cellular forces (19), we examined whether integrin β1 knockdown alters leader cell detachment. We found that A431 cells devoid of integrin β1 exhibited significantly fewer leader cell dissociations than scramble control (SC) cells (fig. S3, A and B). In line with previous work showing that chemotactic gradients alter the confined migration of single cells (18), we also observed that the presence of a 5% FBS gradient markedly facilitated leader cell detachment in confinement (fig. S3C). However, further increases in the gradient concentration from 5 to 10% or 20% had no additional effect on cell dissociation (fig. S3C). Together, our data indicate that confinement triggers the dissociation of leader cells from collectively migrating strands of A431 cells, resulting in the dissemination of primarily single leader cells with enhanced migratory characteristics.

E-cadherin engagement is required to maintain cell-cell junctions

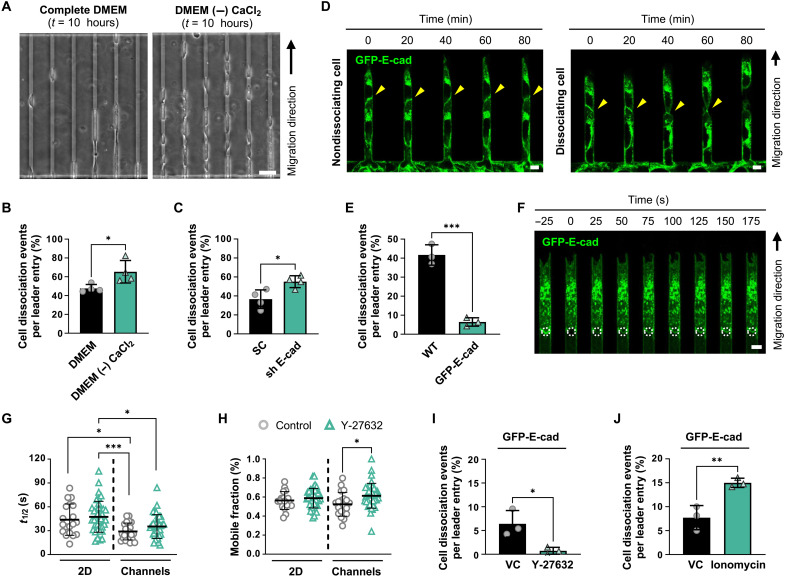
Loss of E-cadherin expression correlates with tumor dissemination, invasion, and EMT (20–22). We thus examined whether leader cell detachment in confining channels is due to disruption of E-cadherin–mediated cell-cell adhesion or confinement-induced loss of E-cadherin expression. Given that the dimerization and mechanical stabilization of E-cadherin junctions depend on Ca²⁺ (23), we used a calcium switch assay to probe the role of E-cadherin bond disruption in leader cell dissociation. To this end, after forming a monolayer just outside the channel entrances, cells were allowed to migrate into confining channels either in the presence of medium spiked with 1.8 mM CaCl₂ or Ca²⁺-free medium. Significantly more leader cell dissociations were observed in Ca²⁺-free than Ca²⁺-containing medium (Fig. 2, A and B), consistent with the notion that Ca²⁺-dependent E-cadherin adhesions oppose leader cell dissociation. To verify that E-cadherin engagement is required for cell-cell junction maintenance in A431 cells, we stably reduced its expression by ~50% using a short hairpin RNA (shRNA) construct (fig. S4A). In line with our Ca²⁺ depletion results, reducing E-cadherin expression significantly enhanced leader cell detachment relative to SC cells (Fig. 2C).

Fig. 2. — (A) Representative phase-contrast images of A431 WT cells after 10 hours of migration in confining (W = 6 μm) microchannels in the presence (complete DMEM) or absence of calcium [DMEM (−) CaCl₂]. (B) Percentage of A431 WT leader cells that detach in the presence or absence of CaCl₂. Data represent means ± SD for n ≥ 502 cells from four experiments. (C) Percentage of SC or E-cadherin shRNA leader cells that dissociate in confining microchannels. Data represent means ± SD for n ≥ 446 leader cells from four experiments. (D) Representative confocal images of GFP-E-cad–expressing A431 cells that fail to dissociate (left) or successfully dissociate (right) in confining microchannels. In both cases, E-cadherin is localized to the leader-follower junction (yellow arrowheads). (E) Percentage of WT and GFP-E-cad–expressing A431 leader cells that dissociate in microchannels. Data represent means ± SD for n ≥ 365 leader cells from three experiments. (F) Representative confocal images of GFP-E-cad following FRAP at a cell-cell junction (white dashed circles). (G and H) Half-lives (t_1/2) (G) and mobile fractions (H) of junctional E-cadherin recovery calculated from individual cell recovery curves in control and Y-27632–treated cells. Data represent means ± SD for n ≥ 18 leader cells from three to four experiments. (I) Percentage of GFP-E-cad–expressing A431 leader cells that dissociate in microchannels under vehicle control (VC) or Y-27632 treatment. Data represent means ± SD for n ≥ 246 cells from three experiments. (J) Percentage of GFP-E-cad–expressing A431 leader cells that dissociate in microchannels under VC or ionomycin treatment. Data represent means ± SD for n ≥ 316 cells from three experiments. Tests performed: Student’s t test (B, C, E, I, and J), one-way ANOVA after log transformation (G), or Kruskal-Wallis test (H). *P < 0.05, **P < 0.01, and ***P < 0.001. Scale bars, 50 μm (A) or 6 μm (D and F).

To visualize the spatiotemporal distribution of E-cadherin during confined migration, we ectopically expressed green fluorescent protein–E-cadherin (GFP-E-cad) in A431 cells (fig. S4B). GFP-E-cad was prominently localized to the cell-cell junction before detachment and was at least partially retained at the rear of dissociated leader cells (Fig. 2D). Overexpression of GFP-E-cad resulted in a marked reduction in leader cell detachment in confining channels relative to wild-type (WT) controls (Fig. 2E). Consistent with previous evidence (24), these data suggest that increased E-cadherin localization at the intercellular junctions and avidity-dependent increase in junctional strength reduce leader cell dissociation.

As a critical constituent of adherens junctions, E-cadherin undergoes dynamic regulation via endocytosis, proteolytic cleavage, and turnover (25). We thus examined whether confinement affects cell-cell junctional strength via the regulation of E-cadherin dynamics. Using fluorescence recovery after photobleaching (FRAP), we photobleached GFP-E-cad at cell-cell junctions and monitored recovery over time in the 2D seeding region and inside confining channels (Fig. 2F). Although the fraction of mobile E-cadherin remained relatively stable, the mobilized E-cadherin was much more dynamic in channels, as indicated by a ~1.5-fold decrease in half-lives (Fig. 2, G and H). These data suggest that confinement induces destabilization of E-cadherin–dependent cell-cell junctions to facilitate leader cell dissociation. Because junctional E-cadherin can be modulated by the RhoA/ROCK/MIIA pathway (26–28) and given that confinement increases RhoA activity in migrating cells (12), we sought to investigate the effects of modulating cell contractility on E-cadherin dynamics. FRAP analysis revealed that the ROCK inhibitor Y-27632 (20 μM) did not alter E-cadherin half-lives but moderately increased its mobile fraction (Fig. 2, G and H), suggesting that ROCK inhibition does not significantly affect E-cadherin dynamics. Nevertheless, ROCK inhibition suppressed the dissociation of GFP-E-cad–expressing leader cells in confinement (Fig. 2I). Conversely, ionomycin, which increases intracellular Ca²⁺ levels and stimulates cell contractility (29), doubled cell dissociation frequency (Fig. 2J). Together, these data suggest that the ROCK/myosin II pathway primarily supports leader cell dissociation by adding additional stress on cell-cell junctions.

Nonmuscle MIIA, but not MIIB, mediates leader cell dissociation in confinement

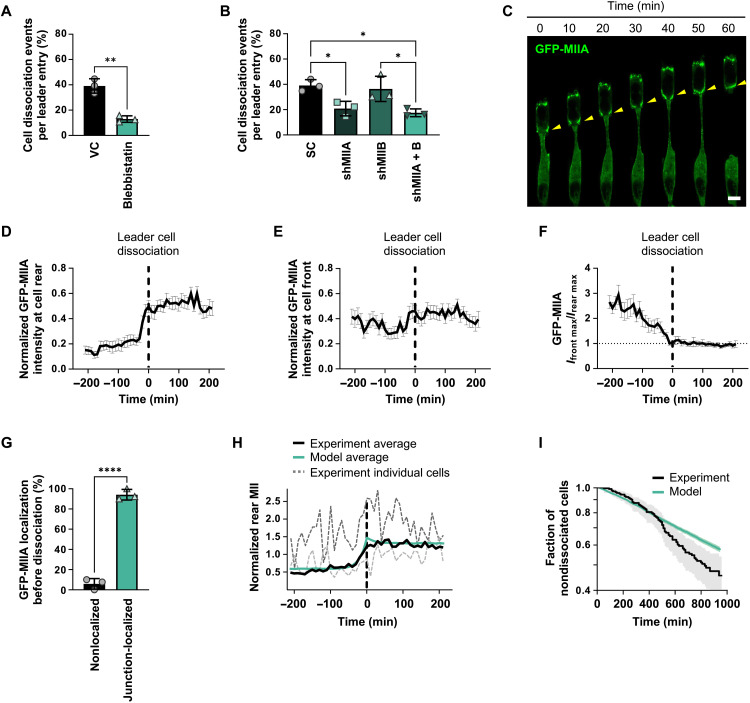
Owing to the central role of actomyosin in regulating epithelial tissue dynamics (30, 31), we next investigated the role of myosin II in cell dissociation by stimulating contractility in A431 WT cells via ionomycin treatment. In line with the findings using ectopically expressing GFP-E-cad A431 cells (Fig. 2J), this intervention also induced a pronounced increase in cell dissociation in WT cells (fig. S5A). On the other hand, inhibition of myosin II function via blebbistatin caused a marked reduction in cell detachment relative to vehicle control (Fig. 3A). To identify which myosin II isoform regulates leader cell dissociation, we generated stable MIIA and MIIB knockdowns using shRNA (fig. S5, B and C). shMIIA, but not shMIIB, markedly attenuated leader cell dissociation relative to SC cells; dual knockdown failed to suppress further the extent of dissociation relative to shMIIA cells (Fig. 3B). These data suggest that nonmuscle MIIA is the essential isoform regulating confinement-mediated junctional disruption.

Fig. 3. — (A) Percentage of A431 WT leader cells that dissociate in confining microchannels under blebbistatin treatment. Data represent means ± SD for n ≥ 309 cells from three experiments. (B) Percentage of A431 cells that dissociate in microchannels following single or dual MIIA/MIIB knockdown. Data represent means ± SD for n ≥ 390 cells from three experiments. (C) Representative confocal images of a dissociating A431 cell expressing GFP-MIIA. Yellow arrowheads indicate junctional MIIA recruitment. Scale bar, 6 μm. (D and E) Normalized peak intensity of GFP-MIIA at the rear (D) or front (E) of leader cells before and after cell detachment (t = 0 min, vertical dashed line) in microchannels. Data represent means ± SEM for n ≥ 30 cells from three experiments. (F) Ratio of peak GFP-MIIA intensity at the front (I_{front max}) and rear (I_{rear max}) of leader cells in microchannels. Vertical dashed line (t = 0 min) indicates dissociation. Data represent means ± SEM for n ≥ 30 cells from three experiments. P values were calculated relative to t = 0 min (see table S1). (G) Percentage of dissociated A431 leader cells that exhibited junctional GFP-MIIA recruitment preceding detachment. Data represent means ± SD for n ≥ 54 cells from three experiments. (H) Average normalized rear myosin concentration before and after cell detachment (t = 0 min, vertical dashed line). Gray dashed lines show two experimental traces of individual cells for reference. Myosin was normalized to the average front concentration. (I) Fraction of nondissociated cells as a function of time. Shaded areas represent the 95% confidence interval. Model parameters: m₁ = 2.23, α = 0.62 min⁻¹, γ = 32.46 min⁻¹, and ∆l = 79.09 arbitrary units. τ, σ, and m₀ are drawn from the posterior distribution (see fig. S6C). Tests performed: Student’s t test (A and G), one-way ANOVA (B), or Kruskal-Wallis (F). *P < 0.05, **P < 0.01, and ****P < 0.0001

Live-cell imaging using GFP-MIIA–expressing A431 cells revealed that MIIA accumulated at the front of leader cells and was nearly absent at cell-cell junctions between leader cells and their immediate followers in confinement for 1 to 3 hours before dissociation. During the period leading up to dissociation, GFP-MIIA progressively relocated from the lateral sides of leader cells and accumulated at their posterior, ultimately leading to dissociation (Fig. 3C). Quantitative analysis of the spatiotemporal localization of MIIA (fig. S5D) in multiple leader cells revealed that MIIA prominently localized to cell junctions immediately before cell dissociation and reached peak intensity at the time of detachment (t = 0 min; Fig. 3D). Moreover, MIIA remained concentrated at the rear as leader cells assumed a single-cell migration mode upon detachment (Fig. 3, C and D). Note that MIIA signal intensity at the leading edge was essentially unaltered before or after cell dissociation (Fig. 3E and table S1). Comparing the ratio of maximum MIIA front-to-rear intensities showed that MIIA was about threefold higher at the front relative to the rear ~3 hours before dissociation but decreased to 1 at the time of cell detachment (t = 0 min) and remained unchanged for 3 hours after dissociation (Fig. 3F and table S1). In nondetaching leader cells, MIIA intensity was consistently elevated at the leading relative to the trailing edge with no enrichment at the cell rear or front (fig. S5, E to G). Overall, MIIA accumulation at intercellular junctions between leader and follower cells preceded >90% of all dissociation events (Fig. 3G).

On the basis of these observations, we hypothesized that actomyosin contractile forces induce E-cadherin bond disruption via laterally imposed shearing forces. While the population average of MIIA fluorescence intensity at cell-cell junctions showed minimal fluctuations just before and after dissociation, individual cell measurements exhibited large changes in intensity (Fig. 3H and fig. S6A). In addition, dissociations occurred at widely varying times after entry into the channel (fig. S2B), which is a hallmark of a stochastic event. Both observations led us to hypothesize that fluctuations of myosin II at the rear of the leader cells drive cell dissociations. Our proposed mechanism is that myosin at the rear of the leader cell induces mechanical stress on the cell-cell junction (fig. S6B). Fluctuations in myosin levels can drive stress to a level that shrinks the cell-cell junction to a critical value and dismantles it. We propose a mathematical model for the cell-cell junction length that depends on the myosin II concentration at the junction (Materials and Methods). Fitting the model to observations of myosin dynamics and survival probability, we simulate myosin II levels as a function of time and the resulting dissociations. The model successfully described junctional myosin II rise before rupture, indicating that high levels of myosin II activity at the junction may be sufficient to drive rupture (Fig. 3H). To determine whether the model can capture when dissociations will occur, we computed the survival probability (fraction of cells undissociated) using the Kaplan-Meier estimator (Fig. 3I) in simulation and experiment. The model and data are in agreement for the first 6 hours, which suggests that dissociations are driven by myosin fluctuations (Fig. 3I). Note that the model underestimates rupture at longer times (Fig. 3I), suggesting that other factors outside our model description contribute to increased dissociation at distant time points. For example, the cell-cell junction in leader cells may experience greater tension at distant time points due to longer strands of follower cells. Nevertheless, the fact that the model exhibits good agreement for early times shows that dissociation driven by myosin fluctuations is consistent with our experimental observations. Our model shows that there is a quantitative link between myosin dynamics and rupture, which can be used to predict how survival depends on experimental interventions. Specifically, our mathematical model correctly predicts that increased RhoA/ROCK/myosin II contractility (fig. S5A) or decreased E-cadherin expression (Fig. 2C) promotes the dissociation of leader cells (fig. S6D). Conversely, decreasing myosin II (Fig. 3B) or increasing E-cadherin (Fig. 2E) expression reduces leader cell detachment in confinement (fig. S6D). Although several lines of evidence suggest the importance of myosin II in forming junctions and maintaining cell-cell cohesion (32, 33), we herein highlight the dynamic role of myosin, which can also facilitate junctional dismantling. These findings provide insights into a mechanism regulating cell dissociation by MIIA recruitment to trailing-end cell junctions of leader cells.

Confinement-induced RhoA activation mediates the contractile response preceding cell detachment

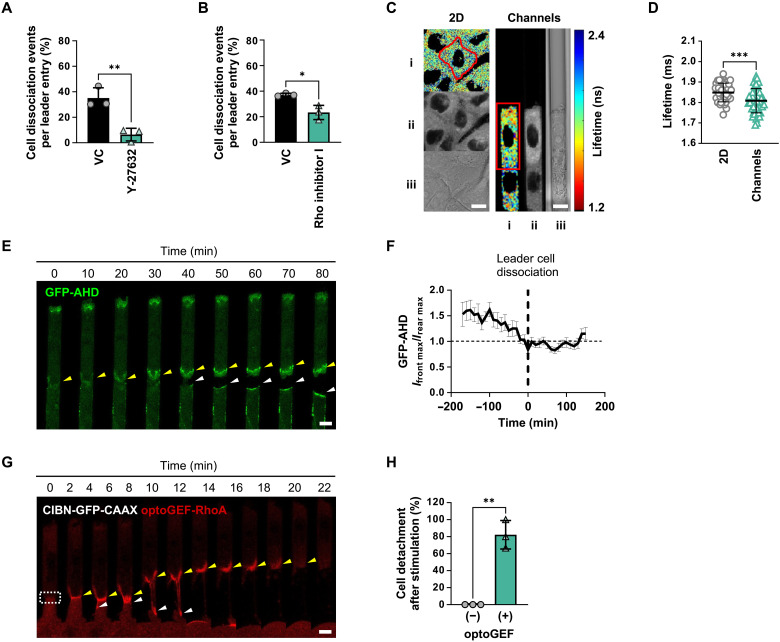
As myosin II contractility can be regulated by ROCK and RhoA, we examined their roles in confinement-induced cell dissociation by pharmacologically inhibiting them with Y-27632 and Rho inhibitor I, respectively. In line with our data using ectopically expressing GFP-E-cad cells (Fig. 2I), Y-27632 nearly eliminated WT cell dissociation (Fig. 4A). Moreover, Rho inhibitor I significantly reduced cell dissociation (Fig. 4B), indicating that RhoA regulates leader cell dissociation in confinement. To further delineate the role of RhoA in this process, we quantified its activity in collectively migrating cells in confinement and on 2D using the RhoA2G Förster resonance energy transfer (FRET) biosensor in conjunction with fluorescence lifetime imaging microscopy (FLIM) (34, 35). First, we verified sensor function in RhoA2G-expressing A431 cells in the presence or absence of lysophosphatidic acid (LPA), a known activator of RhoA. In accord with prior work (35), LPA treatment reduced donor fluorescence lifetimes (fig. S7A), corresponding to increased RhoA activity. Cells on 2D relative to attached leader cells in confinement displayed lower RhoA activity (Fig. 4, C and D). At the subcellular level, RhoA activity was elevated at the cell anterior compared to the cell-cell junction for confined leader cells still attached to follower strands (fig. S7B), which agrees with the preferential MIIA localization before leader cell dissociation (Fig. 3, C to G).

Fig. 4. — (A) Percentage of A431 WT leader cells that dissociate in confining microchannels under Y-27632 treatment. Data represent means ± SD for n ≥ 411 cells from three experiments. (B) Percentage of A431 WT leader cells that dissociate in microchannels under Rho inhibitor I treatment. Data represent means ± SD for n ≥ 375 cells from three experiments. (C) Heatmap of RhoA activity in cells on 2D (left) or in microchannels (right) imaged with FLIM-FRET. Images represent (i) lifetime, (ii) donor intensity, and (iii) differential interference contrast. (D) Donor fluorescence lifetime of RhoA activity in cells on 2D or in microchannels. Data represent means ± SD for n = 45 cells from three experiments. (E) Representative confocal images of a dissociating A431 leader cell expressing GFP-AHD. Yellow and white arrowheads indicate GFP-AHD recruitment to the junction between leader and follower cells, respectively. (F) Ratio of peak GFP-AHD intensity at the front (I_{front max}) and rear (I_{rear max}) of leader cells in confinement. Data represent means ± SEM for n ≥ 17 cells from three experiments. P values were calculated relative to t = 0 min (see table S2). (G) Representative confocal images of A431 cells expressing an optogenetic system used to control RhoA activation (CIBN-GFP-CAAX and optoGEF-RhoA). Dashed white box indicates the stimulation area. Yellow and white arrowheads indicate RhoA localization and activation at the junction between leader and follower cells, respectively. (H) Percentage of A431 leader cells that detach after optogenetic stimulation in cells transduced with both CIBN-GFP-CAAX and optoGEF-RhoA relative to cells transduced with CIBN-GFP-CAAX only. Data represent means ± SD for n ≥ 10 cells from three experiments. Tests performed: Student’s t test (A, B, D, and H) or one-way ANOVA followed by Dunnett’s test (F). *P < 0.05, **P < 0.01, and ***P < 0.001. Scale bars, 6 μm.

To visualize the spatiotemporal distribution of RhoA activity, we used GFP-tagged anillin homology domain (GFP-AHD), which binds directly to guanosine triphosphate (GTP)–loaded RhoA (36), as a live-cell reporter of active RhoA. Quantification of GFP-AHD intensity at the front (I_{front max}) and rear (I_{rear max}) of leader cells revealed that active RhoA was markedly higher at the cell anterior than posterior at 2 to 3 hours before leader cell dissociation (Fig. 4E). This ratio gradually reduced and reached unity at the time of dissociation (Fig. 4F and table S2), which mirrored the GFP-MIIA localization (Fig. 3F).

We next sought to determine whether RhoA activation at the cell-cell junction alone was sufficient to trigger leader cell dissociation. To address this question, we activated RhoA in a spatially controlled manner using the cryptochrome 2 (Cry2)–cryptochrome-interacting basic-helix-loop-helix (CIBN) light-gated dimerizer system (37, 38). This technology relies on the fusion of the catalytic domain of the RhoA-GEF activator to Cry2-mCherry (optoGEF-RhoA) and its GFP-labeled dimerization partner CIBN engineered to bind to the plasma membrane. Localization of optoGEF-RhoA to the plasma membrane via the CAAX anchor (CIBN-GFP-CAAX) promoted light-induced cortical activation of RhoA. Pulsing a 488-nm laser at the cell-cell junctions between the leader and follower cells in microchannels activated RhoA locally at the junction (Fig. 4G). In concert with our GFP-MIIA and GFP-AHD data (Figs. 3F and 4F), we found that localized activation of RhoA at the leader-follower cell junction was sufficient to induce detachment. As a control, we performed the same experiment using cells transduced with CIBN-GFP-CAAX in the absence of optoGEF-RhoA (−), which yielded 0% cell detachment after 1 hour compared to 82% in cells transduced with both plasmids (+) (Fig. 4H). Together, our data reveal a mechanism by which active RhoA localization to the posterior of migrating leader cells triggers detachment in confinement.

Confinement alters microtubule dynamics, which, in turn, results in GEF-H1–mediated leader cell dissociation

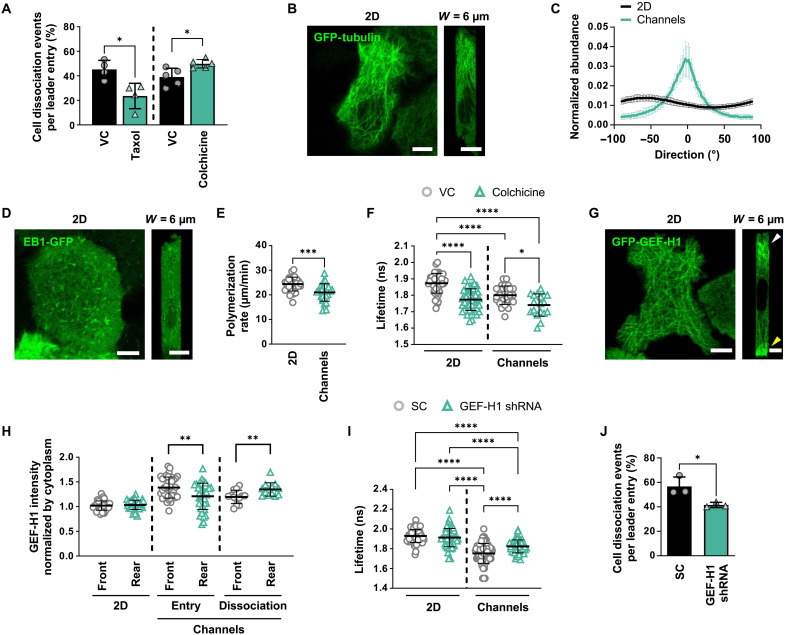
Because confinement alters microtubule dynamics (16), we examined the role of microtubules as potential mediators of confinement-induced cell dissociation. To this end, pharmacological interventions targeting microtubule stability indicated that stabilization of microtubules by taxol reduced leader cell dissociation in confinement, while inhibition of microtubule polymerization with colchicine yielded the opposite effect (Fig. 5A). These findings reveal the involvement of microtubules in regulating intercellular adhesion in confinement. To visualize how confinement alters the spatial distribution of microtubule networks in cells, we ectopically expressed GFP-tubulin in A431 cells (Fig. 5B). We observed that microtubules were organized isotropically in 2D, with roughly equal incidence of individual microtubule fibers extending in any direction (Fig. 5C). However, in confinement, the microtubule networks of leader cells were primarily oriented parallel with the axis of migration (0°), with other fibers distributed around this peak (Fig. 5, B and C, and table S3). These data align with the reported anisotropic orientation of cytoskeletal components of cells in different confining aspect ratios (39), indicating that cells reorient microtubule networks in response to confinement. To determine whether microtubule dynamics are also affected by confinement, we ectopically expressed end-binding protein 1–GFP (EB1-GFP), which binds to the growing (+) ends of microtubules (Fig. 5D). We found that microtubules polymerize slower in confining channels relative to 2D (Fig. 5E). These data show that confinement alters microtubule organization, and the polymerization/stability states of microtubules exert differential effects on leader cell detachment.

Fig. 5. — (A) Percentage of WT leader cells that dissociate in confining microchannels under taxol (n ≥ 369 cells, four experiments) or colchicine (n ≥ 514 cells, five experiments) treatment. Data represent means ± SD. (B and C) Representative confocal images (B) and directionality (C) of GFP-tubulin in cells on 2D or in microchannels. 0° is parallel to the direction of migration. Data represent means ± SD for n ≥ 32 cells from three experiments. (D) Representative confocal images of cells expressing EB1-GFP on 2D (left) or in microchannels (right). (E) Microtubule polymerization rates of EB1-GFP in cells on 2D and in microchannels. Data represent means ± SD for n = 30 cells from three experiments. (F) Donor fluorescence lifetime of RhoA activity following colchicine treatment of cells on 2D and in confinement. Data represent means ± SD for n ≥ 18 cells from three experiments. (G) Representative confocal images of cells expressing GFP-GEF-H1 on 2D (left) or in microchannels (right). (H) Mean intensity of GFP-GEF-H1 at the front and rear of cells on 2D, upon cell entry into confinement, and at the time of dissociation. Values were normalized to the mean intensity of the cytoplasm in each cell. Data represent means ± SD for n = 13 to 39 cells from five experiments. (I) Donor fluorescence lifetime of RhoA activity in SC or GEF-H1 shRNA cells on 2D and in confinement. Data represent means ± SD for n ≥ 43 cells from four experiments. (J) Percentage of SC or GEF-H1 shRNA leader cells that dissociate in confining microchannels. Data represent means ± SD for n ≥ 272 leader cells from three experiments. Tests performed: Student’s t test (A, E, H, and J) (during entry), Student’s t test after log transformation (H) (during dissociation), one-way ANOVA test (F and I), or two-way ANOVA (C) (see table S3). *P < 0.05, **P < 0.01, ***P < 0.001, and ****P < 0.0001. Scale bars, 6 μm. Cell model: A431.

It is well established that microtubules can regulate RhoA via the association or dissociation of GEFs, which are known activators of RhoA (40, 41). To investigate the interplay between microtubules and RhoA, we quantified how colchicine alters RhoA activity in collectively migrating cells using the RhoA2G biosensor (38). Colchicine reduced donor fluorescent lifetimes both in 2D and in confinement, thereby demonstrating that inhibition of microtubule polymerization increases RhoA activity (Fig. 5F). To investigate whether RhoA could also influence microtubule dynamics via a feedback loop, we treated cells with Rho inhibitor I and measured microtubule polymerization rates using ectopically expressing EB1-GFP A431 cells. This pharmacological intervention failed to alter microtubule polymerization rates both in 2D and confinement (fig. S8A), suggesting that microtubule destabilization is upstream of RhoA and unidirectionally promotes RhoA activity.

In view of these findings, we hypothesized that microtubule-dependent activation of RhoA occurs through the dissociation of microtubule-associated GEFs. Prior work has shown that GEF-H1 becomes active upon dissociation from microtubules, which can occur when microtubules become destabilized (42). Once free, GEF-H1 can activate RhoA through its known GEF activity, which has been confirmed with microtubule binding–deficient GEF-H1 mutants (43). To visualize how confinement alters the spatial distribution of GEF-H1, we ectopically expressed GFP-GEF-H1 in A431 cells (Fig. 5G). We observed a uniform distribution of GFP-GEF-H1 in cells on 2D. In contrast, GFP-GEF-H1 was polarized to the leading and trailing edges of leader cells in confinement (Fig. 5G). GEF-H1 preferentially polarized to the front of leader cells upon cell entry into confining channels (Fig. 5H and movie S3). However, at the time of dissociation, leader cells exhibited GEF-H1 enrichment at the cell rear (Fig. 5H). To test the potential involvement of GEF-H1 in cell dissociation from collectively migrating strands, we knocked down GEF-H1 with shRNA (fig. S8B) and found that GEF-H1 depletion reduced RhoA activity in leader cells compared to SC cells, resulting in a marked reduction in cell detachment (Fig. 5, I and J). Reducing GEF-H1 expression transiently with small interfering RNA (siRNA) also decreased leader cell dissociation relative to SC cells (fig. S8, C and D). Together, our data support a model in which confinement-induced microtubule destabilization releases and activates GEF-H1, which, in turn, promotes RhoA activation, thereby resulting in leader cell detachment.

Exit of nuclear Ect2 and RacGAP1 to the cytoplasm activates RhoA and promotes leader cell detachment in confinement

Cell-cell dissociation in confinement resembles aspects of the physiological process of cytokinesis during which daughter cells separate from one another. The success of cytokinesis depends on RhoA, whereby localized activation of RhoA at the equatorial plasma membrane facilitates the formation of the cytokinetic furrow and the assembly of the contractile ring that drives the separation of daughter cells (13). RhoA activation during cytokinesis is mediated by the evolutionarily conserved RhoA GEF known as Ect2, which is physically associated with RacGAP1, a component of the centralspindlin complex. Both Ect2 and RacGAP1 have been well studied within cytokinesis (13, 44); however, little is known about their nonmitotic functions and their role in collective cell migration. To probe the potential contributions of Ect2 and RacGAP1 to cell dissociation from collectively migrating cells in confinement, we knocked down Ect2 and RacGAP1 using siRNA (fig. S9, A and B). Both interventions led to a significant decrease in leader cell dissociation relative to SC cells (Fig. 6A), thereby implicating Ect2 and RacGAP1 as regulators of intercellular adhesion in confinement. Using A431 cells expressing the RhoA2G biosensor, we also determined that Ect2 or RacGAP1 depletion suppresses RhoA activity in confinement (Fig. 6B). These data reveal that Ect2 and RacGAP1 promote RhoA-dependent leader cell dissociation in confining microenvironments.

Fig. 6. — (A) Percentage of leader cells with Ect2 or RacGAP1 knockdown that dissociate in microchannels relative to SC. Data represent means ± SD for n ≥ 346 cells from three to four experiments. (B) Donor fluorescence lifetime of RhoA activity in Ect2 and RacGAP1 knockdown cells versus SC. Data represent means ± SD for n ≥ 28 cells from four experiments. (C and E) Representative confocal images of cells expressing GFP-Ect2 (C) or RacGAP1-GFP (E) migrating in microchannels. Images were pseudo-colored to aid visualization. Arrowheads indicate cytosolic enrichment (C) or depletion (E) at the leading (white) and trailing edge (yellow) of a leader cell before and after cell detachment (t = 0 min). (D, F, and G) Cytosolic intensity of GFP-Ect2 (D) or RacGAP1-GFP in the absence (F) or presence of importazole (G) in leader cells at the time of cell detachment compared to 1 hour before detachment. Data represent means ± SD for n = 36 (D), 29 (F), or 33 (G) cells from four experiments. (H) Percentage of WT leader cells that dissociate in microchannels under importazole treatment. Data represent means ± SD for n ≥ 411 cells from four experiments. (I and K) Representative confocal images of cells expressing RacGAP1 (WT or NLS mutant) (I) or Ect2 (HA-tagged or NLS mutant) (K) stained with Hoechst and phalloidin (actin). (J and L) Percentage of leader cell dissociation of cells expressing RacGAP1 (WT or NLS mutant) (J) or Ect2 (HA-tagged or NLS mutant) (L) in microchannels. Data represent means ± SD for n ≥ 171 cells from three experiments. Tests performed: unpaired Student’s t test (A, J, and L), Kruskal-Wallis (B), paired Student’s t test (D, F, and G), or Mann-Whitney (H). *P < 0.05, **P < 0.01, ***P < 0.001, and ****P < 0.0001. Scale bars, 6 μm (C and E) or 20 μm (I and K). Cell model: A431.

We next used A431 cells ectopically expressing GFP-Ect2 or RacGAP1-GFP to visualize the Ect2 and RacGAP1 distribution dynamics in confined cells. Ect2 was primarily localized to the nucleus before cell dissociation (Fig. 6C). However, a significant enrichment of cytosolic GFP-Ect2 was detected at the time point of cell-cell detachment (Fig. 6D), suggesting that Ect2 cytoplasmic accumulation might promote RhoA activation. On the other hand, cells migrating in confinement had higher cytoplasmic RacGAP1-GFP levels compared to cells on 2D (fig. S9C). Cytoplasmic RacGAP1-GFP levels started decreasing ~50 min before cell-cell dissociation (fig. S9D), while the nuclear intensity increased in parallel, indicating nuclear RacGAP1-GFP import (Fig. 6, E and F, and fig. S9, D to F). Leader cells that successfully detached exhibited nuclear RacGAP1-GFP translocation before dissociation, while leader cells that failed to separate maintained elevated RacGAP1-GFP cytoplasmic localization (fig. S9, G and H). These results suggest that the regulation of the cytoplasmic levels of both Ect2-GFP and RacGAP1-GFP has a critical role in controlling RhoA-dependent leader cell dissociation. However, when sufficient RhoA activation is reached and irreversibly commits the leader cell to the ensuing separation from followers, RacGAP1-GFP is reimported to the nuclei, explaining its seemingly paradoxical cytoplasmic decline at the point of detachment.

Both RacGAP1 (45) and Ect2 (46) contain NLSs recognized by the Ran-regulated importin-α/β complex, which is responsible for their primarily nuclear localization. To initially test the role of active nuclear import in the regulation of leader cell detachment, we first applied importazole, the small-molecule inhibitor of importin-β (47). Importazole treatment enhanced RacGAP1-GFP accumulation in the cytoplasm (Fig. 6G) with a corresponding reduction in RacGAP1-GFP nuclear intensity (fig. S9I), which induced a markedly higher percentage of cell detachment in confinement (Fig. 6H). To validate this finding, we sequestered RacGAP1 to the cytosol by generating A431 cells expressing RacGAP1 with a mutated NLS, which prevents its nuclear entry (45). Immunofluorescence confocal microscopy confirmed that the NLS mutant of RacGAP1-GFP was predominantly localized in the cytosol (Fig. 6I). The extent of cell dissociation was more pronounced in cells expressing NLS-mutant RacGAP1-GFP relative to WT controls (Fig. 6J). Similarly, cytoplasmic accumulation of Ect2 in cells expressing an NLS mutant of Ect2 (48) (Fig. 6K) promoted cell detachment relative to WT controls (Fig. 6L). Collectively, these data suggest that cytoplasmic accumulation of RacGAP1 and Ect2 controls cell detachment from collectively migrating cells in confinement by promoting RhoA activation.

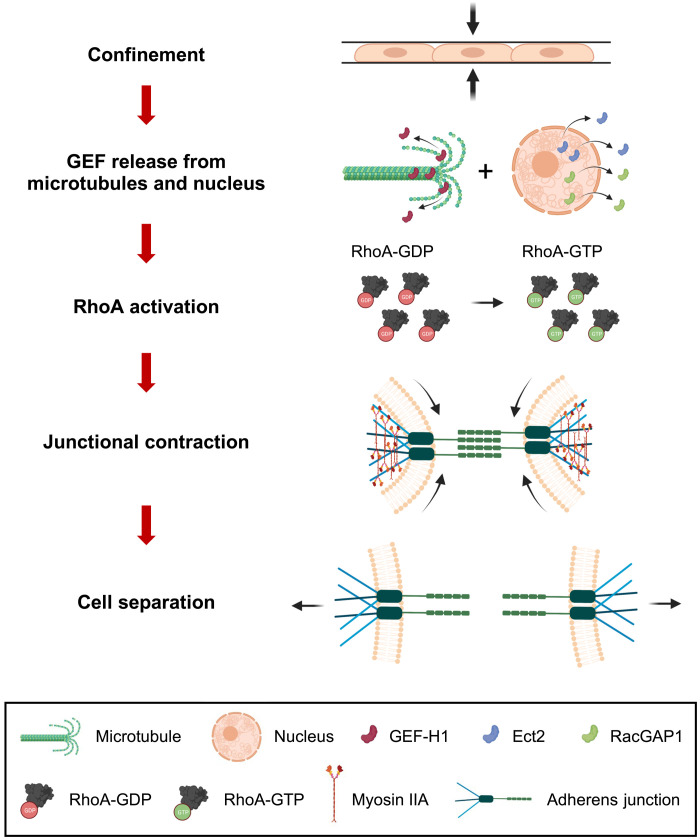
Together, our data reveal that physical confinement (W = 6 μm × H = 10 μm) of collectively migrating cells is sufficient to abrogate E-cadherin–dependent restriction of metastatic leader cell dissemination by inducing a RhoA/ROCK/MIIA mechanism via microtubule-associated GEF-H1 and the cytokinesis-regulatory proteins RacGAP1 and Ect2 (Fig. 7). Confinement alters the organization and dynamics of microtubules, which allows GEF-H1 to dissociate from these structures and activate RhoA. Concomitantly, confinement induces RacGAP1 localization to the cytoplasm where it also contributes to RhoA activation. To determine whether GEF-H1 and RacGAP1 independently contribute to leader cell dissociation, we knocked down both proteins simultaneously (fig. S10A). Depletion of both GEF-H1 and RacGAP1 impaired leader cell dissociation more profoundly than individual silencing of either protein (fig. S10B), suggesting that GEF-H1 and RacGAP1 cooperate to induce RhoA activation in collective cell strands migrating through confinement. Together, confinement induces cytosolic enrichment of Ect2 and RacGAP1, as well as GEF-H1 release from microtubules, which work together to promote leader cell detachment via downstream RhoA-mediated MIIA contractility.

Fig. 7. — Confinement induces slow microtubule polymerization, which increases the cytosolic fraction of unbound GEF-H1. Concurrently, Ect2 and RacGAP1 exit the nucleus. Together, these three proteins activate RhoA, which relocalizes to cell-cell junctions. Actomyosin contraction via ROCK and MIIA promotes junctional collapse, E-cadherin disengagement, and leader cell detachment.

DISCUSSION

Collective cell migration is a fundamental process critical for morphogenesis, wound healing, and tissue regeneration. Collective migration has also been observed during cancer cell dissemination out of the primary tumor. The maintenance of cell-cell contacts confers the advantage of suppressing reactive oxygen species–mediated cancer cell apoptosis and enhancing survival, thereby resulting in more efficient metastasis (49). While the role of collective cell migration in cancer progression (3, 49) and therapeutic resistance (15) is increasingly appreciated, it is currently unknown how confining geometries within the tissue microenvironment contribute to collective invasion or cell detachment and individualization. Using an in vitro microfluidic platform that mimics geometries encountered in vivo (H = 10 μm × W = 6 to 50 μm), we here demonstrate that physical confinement induces cell dissociation from a group of collectively migrating cancer cells. Specifically, tissue-like tracks equal to or less than 20 μm in width, which are naturally present in vivo along ECM fibers in the interstitial space, between epithelial and endothelial interfaces, and along or within blood vessels (6), promote the dissociation of leader cells. Leader cells that dissociate from cohesive ensembles move faster before they detach and maintain their elevated speed after detachment compared to nondetached leader cells, thereby resulting in deeper penetrations into the channels. These findings are in line with reports showing that leader cells are more metabolically active (50), produce greater traction forces (51), and exert higher protrusive forces (11). Our molecular data propose a model whereby confinement of collectively migrating cancer cells causes perturbations in microtubule assembly and exerts physical stress on the cell nucleus, which results in the release of GEF-H1 and translocation of nuclear proteins into the cytoplasm, respectively. GEF-H1, in conjunction with the cytokinesis-regulatory proteins RacGAP1 and Ect2, activates RhoA, which localizes to E-cadherin–based cell-cell junctions and triggers MIIA-mediated contraction, leading to junctional shrinkage and leader cell separation.

Down-regulation of E-cadherin via EMT promotes cancer cell dissemination and invasion (22, 52). However, epithelial cancer progression and metastasis can occur in the presence (22, 52) and absence (49, 53) of E-cadherin deregulation, and collective invasion can persist despite cadherin repression when cancer cells move in confined 3D tissue (3). Thus, we examined whether low versus high confinement represses or induces cancer cell dissociation from a cohesive ensemble, which simulates aspects of a primary tumor, in the absence of E-cadherin down-regulation. Our work illustrates that physical confinement enhances E-cadherin dynamics at cell-cell junctions, leading to the formation of more transient contacts that promote leader cell dissociation. The maintenance of E-cadherin expression levels allows dissociated leader cells to reform cell-cell contacts later to navigate the metastatic process successfully. Thus, cancer cell dissociation from a primary tumor in confining microenvironments does not require loss or down-regulation of E-cadherin but can be mechanically triggered.

Previous studies showed that leader cells initiate a global tug-of-war through E-cadherin junctions (51), which induces F-actin and phosphorylated myosin light chain accumulation at the basal side of collectively migrating cells (54). In accord with these findings, we show that MIIA localizes to cell-cell junctions and mediates leader cell dissociation. Myosin is functionally integrated with junctional complexes and can generate forces that rapidly dismantle junctions mechanically. This finding is further substantiated by a physics-based model assuming that myosin level fluctuations at intercellular junctions are responsible for cell dissociation. The model recapitulates both the observed increase in myosin II at the junction before dissociation and the probability of dissociation within the first 6 hours of channel entry by assuming that myosin II regulates cell-cell junction tension. It also successfully predicts how modulation of E-cadherin or myosin II alters cell dissociation. In line with the well-established role of RhoA as a crucial regulator of myosin II–dependent cell contractility, we show that confinement enhances RhoA activity in collectively migrating cells. Enrichment of active GTP-RhoA localization to cell-cell junctions is a prerequisite to leader cell detachment. Optogenetic activation of RhoA at the cell-cell border of a leader and a follower cell is sufficient to trigger cell dissociation. This finding aligns with data showing that local stimulation of RhoA activity induces local recruitment of actin and myosin (55), which provides the necessary force to dismantle adherens junctions.

RhoA activation is controlled by small guanosine triphosphatases (GTPases) that cycle between active GTP-bound and inactive guanosine diphosphate–bound conformations. In turn, GTPases are regulated by the opposing actions of GEFs and GTPase activating proteins (GAPs). In this work, we identified GEF-H1 as a critical mediator of leader cell dissociation in confining spaces. We found that confinement alters microtubule polymerization, which presumably results in GEF-H1 release from microtubules and subsequent RhoA activation. Upon cell entry into confining channels, GEF-H1 redistributes to the cell poles with a preferential enrichment at the cell leading edge. However, at the time of cell detachment, leader cells exhibit a more intense GEF-H1 signal at the trailing edge near cell-cell junctions. These findings are in concert with prior work showing that GEF-H1 promotes cell contractility via RhoA, ROCK, and myosin light chain following its dissociation from microtubules (56). Accordingly, GEF-H1 mutants deficient in microtubule binding promote higher RhoA activation than microtubule-bound forms (43). Notably, GEF-H1 has also been reported to associate with apical junctional complexes to mediate RhoA/ROCK-II–dependent but myosin light chain kinase–independent epithelial cell dissociation on 2D following calcium depletion (57). In marked contrast, we found that increasing Ca²⁺ influx with ionomycin enhances leader cell dissociation in confinement via RhoA/ROCK/myosin II–dependent pathway. Our data are in accord with numerous other studies showing that RhoA and calcium regulate myosin II contractility.

Localization of active RhoA to cell-cell junctions and subsequent myosin II–induced cell detachment in confinement are reminiscent of cytokinetic furrow formation and daughter cell detachment in cytokinesis. Ectopic activation of RhoA at the cell poles or cell equator via optogenetics is sufficient to induce the assembly of functional contractile rings independent of spindle position and cell cycle stage (58). The RhoA GEF Ect2 localizes to the equatorial membrane via RacGAP1 to regulate the activity and spatial distribution of RhoA during cytokinesis (59). However, in interphase cells, Ect2 and RacGAP1 can function independently to enhance RhoA activity (60). In light of these findings, we examined and established the involvement of both Ect2 and RacGAP1 in confinement-induced leader cell dissociation. We observed that Ect2, a predominantly nuclear GEF, is enriched in the cytoplasm before dissociation, which coincides with active RhoA accumulation at the cell-cell junction. On the other hand, RacGAP1 moves into the cytoplasm upon channel entry and begins to reenter the nucleus ~50 min before cell detachment. We postulate that this subcellular redistribution is initiated once a sufficient level of RhoA activity for dissociation has been achieved. Mechanical cues from the sufficiently weakened leader-follower cell junctions might trigger signaling that mediates RacGAP1 and Ect2 nucleocytoplasmic shuttling. Confining RacGAP1 to the cytoplasm through the use of a construct bearing an NLS mutation or via importin-β inhibition further increases leader cell detachment. Ectopic expression of Ect2 containing NLS mutations also enhances dissociation, consistent with its RhoA GEF activity. The availability of RacGAP1 and Ect2 for nucleocytoplasmic shuttling is defined primarily by their sizes and the presence of nuclear import or export localization signals. Although RacGAP1 and Ect2 harbor NLS (45, 46), no nuclear export signal (NES) motifs have been identified thus far. The molecular masses of both Ect2 (104 kDa) and RacGAP1 (71 kDa) are larger than the ~30- to 60-kDa range beyond which the passive diffusion through nuclear pore channels (NPCs) substantially diminishes. We speculate that three factors might be involved in controlling the nucleocytoplasmic localization of both proteins in leader cells. First, the nuclear import of RacGAP1 and Ect2 is likely driven by the energy-dependent nuclear import via the Ran-importin-β/importin-α pathway. Second, previous studies showed that instead of acting as a fixed size barrier, the NPC passive size exclusion limit is continuous over a range of cargo sizes and is affected by the cargo surface charge (61). Moreover, mechanical forces acting on the nucleus can affect nucleocytoplasmic shuttling of proteins (62). Third, as indicated by the recruitment of RacGAP1 to cytoplasmic Ras GTPase-activating-like protein IQGAP1 (IQGAP1) in migrating 2D cells (60), local cytoplasmic retention mechanisms are likely involved. Together, we hypothesize that, at a steady state, the balance of rapid active nuclear import and slow passive nuclear exit results in a primarily nuclear Ect2 and RacGAP1 localization. However, the collectively migrating leader cells dynamically regulate Ect2 and RacGAP1 availability for nucleocytoplasmic shuttling by altering their retention at cytoplasmic binding sites. Then, the cytoplasmic buildup of Ect2-binding partners and the depletion of RacGAP1 binders might drive the observed translocations. Future work will be needed to test this model and elucidate the precise molecular mechanisms of confinement-induced Ect2 and RacGAP1 nuclear trafficking in collectively migrating cells.

In summary, we show that physical confinement promotes RhoA localization to E-cadherin–based cell-cell junctions, which activates MIIA to induce leader cell detachment. We further demonstrate that RhoA/ROCK/MIIA activation is regulated by GEF-H1 and the cytokinesis-regulatory proteins Ect2 and RacGAP1 via the involvement of microtubules and nuclear trafficking, respectively. The functions of Ect2 and RacGAP1 in cell dissociation from collective strands were relatively unknown before this study. Thus, upstream mechanical triggers and downstream regulation of the nucleus are attractive targets for future studies of collective cell migration.

MATERIALS AND METHODS

Cell culture and pharmacological inhibitors

Human HT-1080 fibrosarcoma, A431 epidermoid carcinoma, MCF-7 breast cancer, and human embryonic kidney (HEK) 293T cells were obtained from the American Type Culture Collection and cultured in Dulbecco’s modified Eagle’s medium (DMEM) containing glucose (4.5 g/liter), l-glutamine, and sodium pyruvate (11995073, Gibco). Medium was supplemented with 10% heat-inactivated FBS (16140071, Gibco) and 1% penicillin-streptomycin (10,000 U/ml; 15140122, Gibco). Cells were maintained at 37°C with 5% CO₂. A431 cells expressing GFP-E-cad were a gift from V. Bruntons (EH4 2XR, University of Edinburgh, UK) (63). In select experiments, cells were treated with the following pharmacological agents: Y-27632 (20 μM; Y0503, Sigma-Aldrich), ionomycin (0.5 and 1 μM; I0634, Sigma-Aldrich), blebbistatin (50 μM; B0560, Sigma-Aldrich), Rho inhibitor I (1 μg/ml; CT04-A, Cytoskeleton Inc.), LPA (50 μM; L7260, Sigma-Aldrich), paclitaxel (taxol equivalent) (1 μM; P3456, Thermo Fisher Scientific), colchicine (125 μM; C9754, Sigma-Aldrich), and importazole (50 μM; SML0341, Sigma-Aldrich).

Cloning, lentivirus preparation, transduction, and transfection

Lentiviral shRNAs targeting integrin β1, E-cadherin (CDH1), and GEF-H1 (ARHGEF2) were generated by subcloning the following sequences into pLKO.1 puro (plasmid #8453, Addgene): ITGβ1_sense, 5′-CCG GGT TGT AGG AAG AGG GAT AAT ACT CGA GTA TTA TCC CTC TTC CTA CAA ATT TTT G-3′; ITGβ1_anti-sense, 5′-AAT TCA AAA ATT TGT AGG AAG AGG GAT AAT ACT CGA GTA TTA TCC CTC TTC CTA CAA C-3′; CDH1_sense, 5′-CCG GGC ACC CGG GAC AAC GTT TAT TCT CGA GAA TAA ACG TTG TCC CGG GTG TTT TTT G-3′; CDH1_anti-sense, 5′-AAT TCA AAA AAC ACC CGG GAC AAC GTT TAT TCT CGA GAA TAA ACG TTG TCC CGG GTG C-3′; ARHGEF2_sense, 5′-CCG GCG CTC TGT CCA TCG AAA CTT TCT CGA GAA AGT TTC GAT GGA CAG AGC GTT TTT G-3′; and ARHGEF2_anti-sense, 5′-AAT TCA AAA ACG CTC TGT CCA TCG AAA CTT TCT CGA GAA AGT TTC GAT GGA CAG AGC G-3′. Lentiviral shRNA targeting MIIA and MIIB was previously generated by subcloning target sequences into pLKO.1 puro or pLVTHM (plasmid #12247, Addgene) (12, 35).

GFP-GEF-H1 was a gift from R. Rottapel (University of Toronto, Toronto, ON) (64). A lentiviral version of GFP-GEF-H1 was created by adding Mlu I and Not I restriction sites to the coding sequence via polymerase chain reaction (PCR) amplification and subcloning into the lentiviral backbone pLV-EF1a-IRES-Puro (plasmid #85132, Addgene).

GFP-AHD (36) and RacGAP1-GFP plasmids were gifts from M. Glotzer (University of Chicago, Chicago, IL). A lentiviral version of GFP-AHD was created by adding Bam HI and Not I restriction sites to the coding sequence via PCR amplification and subcloning into the lentiviral backbone pLV-EF1a-IRES-Puro. A lentiviral version of RacGAP1-GFP was created by adding Eco RI and Not I restriction sites to the coding sequence via PCR amplification and subcloning into pLV-EF1a-IRES-Puro. GFP-Ect2 was a gift from A. Yap (University of Queensland, St Lucia, QLD, Australia) (26). A lentiviral version of GFP-Ect2 was created by adding Bam HI and Not I restriction sites to the coding sequence and subcloning into pLV-EF1a-IRES-Puro.

CIBN-GFP-CAAX and optoGEF-RhoA lentiviral plasmids were gifts from X. Trepat (Institute for Bioengineering of Catalonia, Barcelona, Spain) (37). Lentiviral plasmids for hemagglutinin (HA)–tagged WT Ect2 and NLS-mutant Ect2 were gifts from A. Cox (University of North Carolina at Chapel Hill, Chapel Hill, NC) (48). RacGAP1-NLS was a gift from T. Kitamura (University of Tokyo, Tokyo, Japan). A lentiviral plasmid for RacGAP1-NLS-GFP was created by exchanging the WT NLS sequence in RacGAP1-GFP with the mutated NLS sequence via PCR amplification and subcloning through Eco RI and Bst BI restriction sites. NLS-mCherry (plasmid #37354), GFP-MIIA (plasmid #11347), pLentiRhoA2G (plasmid #40179), L304-EGFP-Tubulin-WT (plasmid #64060), EB1-EGFP (JB131) (plasmid #39299), psPAX2 (plasmid #12260), and pMD2.G (plasmid #12259) were obtained from Addgene. A lentiviral plasmid for NLS-mCherry was created by subcloning the coding sequence into pLV-EF1a-IRES-Hygro (plasmid #85134, Addgene) using Bam HI and Eco RI restriction sites.

Transient knockdowns of scramble (sc-37007, Santa Cruz Biotechnology), ARHGEF2 (catalog no. 4392420, ID: s17546, Thermo Fisher Scientific), Ect2 (sc-35259, Santa Cruz Biotechnology), and RacGAP1 (sc-76335, Santa Cruz Biotechnology) siRNAs were performed with the Lipofectamine RNAiMAX Kit (13778075, Thermo Fisher Scientific) on ~70% confluent cells in six-well plates according to the manufacturer’s recommendations. Transient transfections of plasmids were performed with Lipofectamine 3000 (L3000008, Thermo Fisher Scientific) on ~70% confluent cells in six-well plates according to the manufacturer’s recommendations. Calcium phosphate transfection of HEK293T cells was used to generate lentiviruses. HT-1080 and A431 cells were incubated with polybrene (10 μg/ml) and virus-containing media for 24 hours to allow for infection. All cultured cells were routinely screened for mycoplasma using PCR.

HT-1080 sarcoma xenograft implantation and intravital imaging

Dorsal skin fold chambers were surgically implanted on 8- to 12-week-old female athymic nu/nu mice (obtained from the Department of Experimental Radiation Oncology, MD Anderson Cancer Center) as described in prior publications (15). Briefly, the surgery involved the implantation of an imaging window held by a titanium frame onto the back of the mouse. By a surgical procedure, one layer of the skin was removed at the front side of the chamber to expose the contralateral deep dermis. One day after surgery, three tumors were implanted per chamber by intradermally injecting HT-1080 cells stably expressing NLS-mCherry with a 30-gauge needle (2.5 × 10⁵ to 5 × 10⁵ cells in 2 to 4 μl), and the growing and invading tumors were monitored for up to 11 days. For intravital microscopy, mice were anesthetized with isoflurane (1 to 3% in oxygen) and secured on a temperature-controlled stage (37°C). Blood vessels were visualized by retro-orbital injection of Alexa Fluor 750–labeled 70-kDa dextran (2 mg per mouse; Thermo Fisher Scientific).

Tumor growth was monitored by intravital multiphoton microscopy, as previously described (15). The setup consisted of a LaVision TriM Scope II scanner with three titanium-sapphire lasers (Ti:Sa, Chameleon-XR, Coherent) and two optical parametric oscillator compact systems (OPO, APE/Coherent, tunable excitation wavelengths ranging between 800 and 1300 nm). Imaging was performed using an Olympus XLPLN25XWMP2 25×/1.05 numerical aperture (NA) water-immersion objective (2 mm, working distance). Multichannel images were acquired using up to three excitation wavelengths (880, 1090, and 1280 nm) in two consecutive scans. Emission was detected using up to five backward and/or two forward photomultipliers and the following band-pass filters: mCherry (ET595/40 nm), second-harmonic generation (SHG) (ET525/50 nm), and Alexa Fluor 750 (ET810/90 nm) (Chroma Technology Inc., Bellows Falls, VT). Sequential 3D volumes were acquired with a step size of 3 to 4 μm for up to 250 μm of penetration depth into the dermis. Time-lapse recording was performed for a maximum duration of 5 hours with a frame interval of 20 min. 3D stacks and time-lapses were reconstructed, stitched, and analyzed using ImageJ (National Institutes of Health, Bethesda, MD). Measurements of nuclear diameter, circularity, and cross-sectional area were obtained from multiple views of the three tumors implanted in two mice in two independent experiments. The tumors were imaged longitudinally 2 to 7 days after implantation. All animal studies were approved by the Institutional Animal Care and Use Committee (IACUC) of The University of Texas, MD Anderson Cancer Center, which is accredited by the Association for Assessment and Accreditation of Laboratory Animal Care (IACUC protocols 00001002).

Photolithography and device fabrication

Microfluidic devices consisting of an array of parallel microchannels of prescribed length (L = 400 μm) and height (H = 10 μm) but different widths (W = 50, 20, 10, and 6 μm) were fabricated from polydimethylsiloxane as previously described (16, 65). In select experiments, devices of prescribed dimensions (L × H × W = 400 μm × 10 μm × 6 μm) were fabricated and used. All channel heights were verified with a profilometer. Channels were coated with human fibronectin (20 μg/ml; F0895, Sigma-Aldrich) overnight at 4°C. Cells were induced to migrate through channels in response to a chemotactic gradient generated with 20% FBS. However, in fig. S3C, cells were allowed to migrate through channels in the presence of a 0, 5, 10, or 20% FBS gradient.

Microfluidic device seeding and live-cell imaging

Cells were harvested from culture flasks with 0.25% trypsin-EDTA (25200114, Gibco), centrifuged at 300g for 5 min, and resuspended at a concentration of 5 × 10⁷ cells/ml in serum-containing media. Back pressure was created in the microfluidic devices by adding media (20 μl) into the top two wells of the device to inhibit premature cell entry into the channels. Cell suspension (10 μl) was then added to the seeding channel inlet, creating a pressure-driven flow of cells across the length of the cell seeding region. As flowing cell suspension reached the outlet, additional cell suspension (10 μl) was added to the opposing side to arrest flow and allow cells to adhere to the ECM (fibronectin). Flow and balance steps were repeated at 5-min intervals until a homogeneous layer of evenly spaced cells was observed in the cell seeding region. Wells were then filled with serum-containing media, and the devices were incubated at 37°C with 5% CO₂ for ~2 hours until the seeded cells spread evenly into a monolayer. Immediately before imaging, a chemotactic gradient was created by filling the three bottom right wells with serum-free DMEM (containing only 1% penicillin-streptomycin) and the top right well with serum-containing DMEM (20% FBS with 1% penicillin-streptomycin). For select calcium-free experiments, the chemotactic gradient was established the same way but with media containing or lacking CaCl₂ (21068028, Gibco). Cells were imaged with phase contrast every 10 min for at least 10 hours using a Nikon Eclipse Ti inverted microscope (Nikon, Tokyo, Japan) equipped with automated controls (NIS-Elements, Nikon) and a 10×/0.45 NA objective. A temperature- and CO₂-controlled stage-top incubator (Tokai Hit, Shizuoka-hen, Japan) was used to maintain cells at 37°C with 5% CO₂.

Cell dissociation per leader cell entry quantification

Time-lapse videos were trimmed to 10 hours in ImageJ, and cell dissociations were manually counted. Leader cell dissociations were then normalized by the total number of cell strands that entered microchannels to obtain a measure of cell detachment as a function of leader cell entry. Any cell at the leading edge of a collectively migrating strand that entered a microchannel and experienced unoccupied channel space ahead of it was classified as a leader cell. Any cell that was completely surrounded on all sides by channel walls and/or other neighboring cells (i.e., no cell area exposed to free space) was classified as a follower cell.

In wider (W = 20 and 50 μm) channels, two to five leader cells per channel were typically observed during 10 hours of collective migration. A single leader cell detachment in a 50-μm-wide channel with a total of four leader cells (fig. S2A, left) yielded a cell dissociation per leader cell entry of 25%. In contrast, large clusters of detached cells (more than five cells) were scored as a single dissociation event and normalized to the total number of leader cells for the following reason: All leader cells were still functionally intact, and the resulting dissociation usually occurred as the result of a single “weak link” cell-cell junction (fig. S2A, right) as opposed to multiple synchronous leader cell detachments. The total number of cell dissociation events was then divided by the total number of leader cells that entered channels of the specified widths to yield the percentage of cell dissociation per leader cell entry for each channel width.

Cell migration tracking and maximum displacement analysis

Time-lapse microscopy images were trimmed to 10 hours (unless indicated otherwise) and tracked using the MTrackJ plugin in ImageJ as previously described (12). Briefly, cells were tracked from the time of complete entry into a microchannel until the leading edge of the cell reached the channel exit or the cell detached. Leader and follower cells were also tracked following detachment by initiating cell tracks immediately after leader cell dissociation until cells reached the exit or the experiment concluded. Custom codes were developed in MATLAB (MathWorks, Natick, MA) to calculate cell speeds and the maximum displacements of leader cells based on cell trajectory data from MTrackJ. Apoptotic cells and cells undergoing mitosis were uncommon but excluded from all analyses.

Actin staining and immunofluorescence

Human influenza HA-tagged WT Ect2 and NLS-mutant Ect2 cells, as well as RacGAP1-GFP WT and NLS-mutant RacGAP1-GFP cells, were plated on glass-bottom dishes (35 mm; D35-20-1.5-N, Cellvis) coated with human fibronectin (20 μg/ml) and incubated overnight at 37°C with 5% CO₂. The following day, cells were fixed with 4% paraformaldehyde (J19943K2, Thermo Fisher Scientific), permeabilized with 0.1 to 0.2% Triton X-100 (T9284, Millipore), and blocked with 2% bovine serum albumin (A9647, Sigma-Aldrich) containing 0.1 to 0.2% Triton X-100. WT and NLS-mutant Ect2 cells were incubated with anti–HA-Tag (1:875; 3724T, Cell Signaling Technology) antibody diluted in blocking buffer overnight at 4°C. Cells were subsequently washed with 1× phosphate-buffered saline and incubated with Alexa Fluor 488 (1:100; A11034, Thermo Fisher Scientific) secondary antibody, Hoechst (1:2500; BD Pharmingen), and rhodamine phalloidin (1:200; Invitrogen) diluted in blocking buffer for 1 hour at room temperature to visualize Ect2, nuclei, or actin, respectively. To visualize the subcellular localization of RacGAP1, WT and NLS-mutant RacGAP1-GFP cells were processed using the same protocol but with 1:1000 Hoechst and 1:1000 rhodamine phalloidin instead.

Confocal imaging

Fluorescently labeled cells were imaged on a Nikon A1 confocal microscope (Nikon, Tokyo, Japan) using a 60×/1.4 NA oil-immersion objective. Twelve-bit images were acquired at a resolution of 2048 × 2048, 1024 × 1024, 1024 × 128, or 512 × 512 pixels², where indicated. Cells were illuminated with 405-, 488-, and/or 561-nm lasers, where indicated. A temperature- and CO₂-controlled incubator (Tokai Hit, Shizuoka-hen, Japan) was used to maintain cells at 37°C with 5% CO₂ during live-cell time-lapse experiments.

FLIM imaging and quantification of RhoA FRET sensors

RhoA2G-expressing cells in microchannels were imaged using a confocal FLIM on a Zeiss LSM 780 confocal microscope equipped with a PicoQuant system and a 40×/1.1 NA water-immersion objective as previously described (12, 35). Cells were scanned at the resolution of 1024 × 1024 pixels² in 2D and 2000 × 200 pixels² in microchannels using a 440-nm diode laser pulsed at 32 MHz and controlled by a Sepia II module. A reflection plate diverted the emission to a 482 ± 35–nm filter and PicoQuant PMA-04 hybrid detector (Berlin, Germany). Time-correlated single-photon counting (TCSPC) PicoHarp 300 module and SymPhoTime 64 2.3 software (PicoQuant) were used to acquire the TCSPC FLIM data. A temperature- and CO₂-controlled incubator (Carl Zeiss, Jena, Germany) was used to maintain cells at 37°C with 5% CO₂ during live-cell time-lapse experiments. FLIM data were analyzed using SymPhoTime 64 2.3 as previously reported (35).

FRAP imaging and quantification

A431 cells expressing GFP-E-cad were seeded in devices and induced to migrate for 3 to 4 hours through microchannels in response to an FBS-generated chemotactic gradient. In select experiments, cells were treated with Y-27632 upon application of an FBS gradient. Cells in both the 2D seeding region and in microchannels were imaged with a Nikon A1 confocal microscope using a 60×/1.4 NA oil-immersion objective (512 × 512 pixels² for cells on 2D and 1024 × 128 pixels² for cells in channels) to examine the effects of confinement on protein dynamics. Regions of interest (ROIs) were drawn at GFP-E-cad junctions in both 2D and in microchannels to photobleach the fluorescence signal and measure junctional GFP-E-cad recovery. Images were acquired at 5-s intervals for 20 s before ROIs were stimulated with a 488-nm laser at 100% power for 1 s. Images were subsequently acquired at 5-s intervals for 3 to 4 min to observe fluorescence recovery. One ROI was photobleached per cell and per field of view to minimize cellular phototoxicity. The dimensions of all ROIs were conserved across experiments to avoid imaging artifacts.

Time-lapse videos were stabilized using the Correct 3D drift plugin in ImageJ to minimize movements due to stage drift. The plot z-axis profile tool was then used to measure fluorescence intensities over time at areas where the cell was photobleached (BL), a region of a neighboring cell that is unbleached for reference (RF), and at an unoccupied background space (BK). BK values were subtracted from both BL and RF values to obtain corrected intensity values at bleached and unbleached reference areas. The corrected BL values were then normalized to the corrected RF values to obtain normalized corrected bleach intensities (BL2). The online easyFRAP tool (66) was then applied to calculate mobile fractions and half-lives. To that end, the BL2 recovery data were individually trimmed to 120 to 150 s to obtain the maximal possible length of recovery while conforming to the requirement for single-exponential association fit with R² > 0.95. Any FRAP data not conforming to these requirements (indicative of cell or stage motion-driven artifacts during the acquisition) were excluded from the analyses. Mobile fractions and half-lives were averaged over three independent experiments.

GFP-MIIA and GFP-AHD intensity quantification

Cells expressing GFP-MIIA or GFP-AHD were seeded in microfluidic devices and imaged on a Nikon A1 confocal microscope overnight at 10-min intervals using a 60×/1.4 NA oil-immersion objective (1024 × 1024 pixels²). Time-lapse videos of GFP-MIIA and GFP-AHD cells were cropped in ImageJ and analyzed with a custom MATLAB code that performed ROI detection and line scanning to compute GFP intensity profiles over the entire body of leader cells over time. Maximum peak intensities were computed at the front and rear of cells for each interval, and total trajectories were then normalized according to overall maximum and minimum intensity values for each individual cell. Front-to-rear ratio was determined by dividing raw front intensity values by raw rear intensity values, yielding dimensionless values of front:rear intensity over time.

GFP-GEF-H1 intensity quantification

Cells expressing GFP-GEF-H1 were seeded in microfluidic devices and imaged on a Nikon A1 confocal microscope overnight at 30-min intervals using a 60×/1.4 NA oil-immersion objective (2048 × 2048 pixels²). At each time point, a 3D stack with six planes and 0.5-μm spacing was acquired. A single plane was chosen, and ROIs were manually drawn in ImageJ to outline the (i) nucleus, (ii) leading edge, (iii) trailing edge, and (iv) perimeter of each cell. The sum intensity of GFP-GEF-H1 within the nucleus was then subtracted from the whole-cell value and divided by the difference in area to obtain a measure of mean cytoplasmic intensity. Last, the mean intensity of GFP-GEF-H1 in the leading and trailing edges was normalized by the mean cytoplasmic intensity in each cell.

GFP-Ect2 and RacGAP1-GFP intensity quantification

Cells expressing GFP-Ect2 or RacGAP1-GFP were seeded in microfluidic devices and imaged on a Nikon A1 confocal microscope overnight at 10-min intervals using a 60×/1.4 NA oil-immersion objective (1024 × 1024 pixels²). Time points of leader cell dissociation were determined, and ROIs were drawn manually in ImageJ around cells excluding the nucleus to isolate the cytoplasmic fraction of GFP-Ect2 or RacGAP1-GFP, respectively. ROIs were drawn for the interval 1 hour before dissociation and at the exact time of dissociation. Intensities were then normalized to the initial GFP-Ect2 values. For single–time point analysis of RacGAP1 nuclear:cytoplasmic intensity, images were imported into Imaris (v.9.5.1, Bitplane AG, Zürich, Switzerland) to draw manual contours around the nucleus and perimeter of each cell. The sum intensity of RacGAP1-GFP within the nucleus was then subtracted from the whole-cell value to obtain a measure of cytoplasmic intensity.

To temporally quantify RacGAP1-GFP nuclear and cytosolic fractions, a custom MATLAB code was used to manually determine the cell boundary of leader cells and compute nuclear and cytosolic fractions via thresholding of the higher-intensity nucleus and subtracting it from the intensity of the entire cell while simultaneously quantifying both fraction intensities separately over time.

Optogenetic RhoA activation experiments

Cells expressing either CIBN-GFP-CAAX (green) alone or CIBN-GFP-CAAX (green) and optoGEF-RhoA (red) were induced to migrate for 3 to 4 hours before imaging on a Nikon A1 confocal microscope using a 60×/1.4 NA oil-immersion objective (1024 × 128 pixels²). Cells were then visualized with the 561-nm laser to avoid triggering dimerization prematurely with the 488-nm laser. ROIs were drawn around cell-cell junctions in channels and used for targeted stimulation with a 488-nm laser set at 1% power and pulsed for 1 s at 10-s intervals for 20 intervals. ROIs were then redrawn to accommodate for cell motion, and the pulsing was repeated until leader and follower cells completely separated or until the pulsing was repeated a maximum of 20 times and no detachment had occurred. For control cells expressing only CIBN-GFP-CAAX and not optoGEF-RhoA, cells were visualized with CellLight Plasma Membrane-RFP (red fluorescent protein) (BacMam 2.0; 1:40; C10608, Thermo Fisher Scientific), which was used in accordance with the manufacturer’s specifications. These control cells were pulsed for 12 rounds of 20 pulses, which was determined to be the average number of rounds required to cause cell-cell detachment for cells that were expressing both plasmids.

Microtubule orientation quantification

Images of cells expressing GFP-tubulin were acquired with a Nikon A1 confocal microscope using a 60×/1.4 NA oil-immersion objective (1024 × 1024 pixels²) to visualize the microtubule networks within cells in the 2D seeding region and in confining (W = 6 μm) microchannels. The Directionality plugin in ImageJ was used to calculate microtubule orientation. Briefly, the background was subtracted from images to aid the visualization of microtubule networks. Images were rotated to align the direction of migration with the 0° axis. An ROI was drawn around cells, and the plugin was run with 90 bin points to generate a histogram of microtubule amounts detected per bin point. Each bin point corresponds to 2°, allowing for the detection of microtubules oriented in all directions (±90° from zero axis).

EB1-GFP imaging and analysis

EB1-GFP stably transfected cells were imaged at 3-s intervals for 3 min on a Nikon A1 confocal microscope with a 60×/1.4 NA oil-immersion objective (512 × 512 pixels²) to measure microtubule polymerization rates in the 2D seeding region and in confining (W = 6 μm) microchannels. The MTrackJ plugin in ImageJ was used in conjunction with a custom MATLAB code to calculate the rates of microtubule growth by tracking the growing plus ends of polymerizing microtubules and analyzing the corresponding trajectories.

Western blotting

Western blots were performed as previously described (12, 67) using NuPAGE 3 to 8% tris-acetate (EA0375BOX, Thermo Fisher Scientific), 4 to 12% bis-tris (NP0336BOX, Thermo Fisher Scientific), or 4 to 12% tris-glycine gels (XP04125BOX, Thermo Fisher Scientific). The following primary antibodies were used: anti–integrin β1 (rabbit) (1:1000; 4706, Cell Signaling Technology), anti–E-cadherin (mouse) (1:100; ab1416, Abcam), anti-MIIA (rabbit) (1:1000; 3403S, Cell Signaling Technology), anti-MIIB (rabbit) (1:1000; 3404S, Cell Signaling Technology), anti-Ect2 (mouse) (1:500; sc-514750, Santa Cruz Biotechnology), anti-RacGAP1 (mouse) (1:100; sc-271110, Santa Cruz Biotechnology), and anti–GEF-H1 (55B6) (rabbit) (1:1000; 4076S, Cell Signaling Technology). β-Actin (1:10,000; 612656, BD Biosciences) or glyceraldehyde-3-phosphate dehydrogenase (1:5000; 2118, Cell Signaling Technology) were used as loading controls. The following secondary antibodies were used: anti-mouse immunoglobulin G (IgG) horseradish peroxidase (HRP)–linked antibody (1:2000; 7076S, Cell Signaling Technology) and anti-rabbit IgG HRP-linked antibody (1:2000; 7074S, Cell Signaling Technology).

Statistical analysis

Data represent means ± SD or means ± SEM for each condition from three or more experiments (reflecting independent biological replicas). For samples with more than eight data points, the D’Agostino-Pearson omnibus normality test was used to determine whether data were normally distributed. Datasets with Gaussian distributions were compared using Student’s t test (two-tailed) and one-way analysis of variance (ANOVA) followed by Tukey’s post hoc test (unless specified otherwise). The Shapiro-Wilk test was used to test for normality when the number of data points was ≤8. For non-Gaussian distributions, the nonparametric Mann-Whitney U test was used to compare two conditions, while the Kruskal-Wallis test followed by Dunn’s multiple comparison was used for more than two groups. Select experiments were analyzed using two-way ANOVA followed by Sidak’s comparison test. Statistical outliers were determined via a ROUT test, and all analyses were performed with GraphPad Prism 9 software. Statistical significance was identified as *P < 0.05, **P < 0.01, ***P < 0.001, and ****P < 0.0001.

Mathematical model

We implemented a mathematical model for the cell-cell junction length that depends on myosin concentration at the junction, building on the work of Curran et al. (68). We consider that the cell-cell junction behaves as a spring that relaxes with rate γ to its rest length l₀, and the cell-cell junction length l(t) can be described as

\frac{d}{d t} l (t) = - γ (l - l_{0}) - α m (t)

(1)

where m(t) is the myosin concentration at the junction and α is a parameter that regulates the myosin tension over the cell-cell junction. We describe the myosin concentration as fluctuating around a characteristic concentration m₀

\frac{d}{d t} m (t) = - \frac{1}{τ} (m - m_{0}) + σ ε (t)

(2)

where σ is the amplitude of the fluctuations and τ is the characteristic relaxation time. Fluctuations are produced by an uncorrelated Gaussian noise ε(t) with 〈ε(t)〉 = 0 and 〈ε(t)ε(t^′)〉 = δ(t − t^′). Cell dissociation takes place when the cell-cell junction shrinks to a critical value, l_c. Because we are mostly interested in how dissociation events are triggered, for simplicity, we assume that postdissociation myosin fluctuates around a new typical concentration value m₁ while the other parameters of the model remain the same.

Model fitting and simulations

We fit our model parameters (τ, γ, α, m₀, m₁, l₀, l_c) from two sources of data: the dynamics of myosin fluctuations at the junction near rupture and the distribution of rupture times (fig. S2B). Because our model only describes dissociation between a single leader cell and a trailing cell, we only considered single-cell dissociation data in our analysis and excluded cluster dissociation events. In comparing to the experimental data, we assume that the myosin concentration at the junction m(t) can be summarized by the value at the rear of the cell, as in Fig. 3D, extracted as shown in fig. S6A.

Model fitting consisted of two stages. First, the parameters for the rear predissociation myosin concentration were obtained using a Bayesian inference method. Using a Markov chain Monte Carlo method (69, 70), we obtained samples from the parameter posterior distributions from the likelihood of the discretized in time stochastic differential equation in Eq. 2 (see fig. S6C). Second, we fitted the remaining model parameters by implementing a simulation-based inference method (71). The method simulates data from the model and contrasts it with the observations, allowing us to infer probabilities and posterior distributions for the parameters. Because m₁ only depends on myosin after dissociation, it was fitted apart from the rest of the parameters. Then, the remaining parameters were obtained by fitting simultaneously the average myosin concentration 100 min before and after dissociation (Fig. 3H) and the survival curve up to 490 min (Fig. 3I). To do so, we use the compass search algorithm from Noisyopt (72) to minimize the mean square error of both curves at the same time. To standardize the variability in fluorescence intensity between different cells, myosin concentration was normalized by the cell’s mean myosin concentration at the front. Note that this normalization is different from the one used in Fig. 3 (D and E).

Numerical simulations from the model were implemented using the Euler-Maruyama method with integration time step ∆t = 2 min. Initial conditions were set such that myosin was equal to its mean concentration and the cell-cell junction was at rest with the tension coming from the myosin at equilibrium. Because cell dissociation occurs when the cell-cell junction shrinks a quantity of ∆l = l₀ − l_c, to reduce the number of parameters, we set l_c = 0 and l₀ = ∆l.

Acknowledgments

We thank Q. B. Smith (University of California, Irvine) for insightful discussions, input on schematic design, and editorial feedback and A. Amitrano for technical assistance. We also thank BioRender.com for providing the tools to create the schematic for the proposed mechanisms in this work.

Funding: This work was supported, in part, by a U54 CA 210173 (to K.K.), R01 GM142175 (to K.K. and P.F.), an NIH R01 CA183804 Supplement (to R.A.L.), and an NSF Graduate Research Fellowship DGE2139757 (to H.E.D.). P.F. was also supported by Cancergenomics.nl. E.P.I. and B.A.C. were supported, in part, by NIH R35GM142847. P.M. was supported, in part, by R35GM147101. A.K. was supported by postdoctoral fellowships from the Fonds de recherche du Québec–Nature et technologies and the Natural Sciences and Engineering Research Council of Canada.

Author contributions: Study conceptualization: R.A.L., Z.G., and K.K. Experimental methodological design (in vitro): R.A.L., A.K., H.E.D., S.J.L., C.L.Y., P.M., N.W., Z.G., P.K., and K.K. MATLAB codes: R.Z. Mouse experiments: M.P. and P.F. Mathematical modeling: E.P.I. and B.A.C. Visualization: R.A.L. and A.K. Supervision: B.A.C. (mathematical modeling), P.F. (mouse experiments), and K.K. (in vitro experiments). Writing (original draft): R.A.L., A.K., and K.K. Writing (review and editing): All authors.

Competing interests: The authors declare that they have no competing interests.

Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials.The code for the mathematical mode is available on Zenodo at https://doi.org/10.5281/zenodo.7474374.

Supplementary Materials

This PDF file includes:

Figs. S1 to S10

Tables S1 to S3

Click here for additional data file.^{(2.3MB, pdf)}

Other Supplementary Material for this : manuscript includes the following:

Movies S1 to S3

Click here for additional data file.^{(6.2MB, zip)}

View/request a protocol for this paper from Bio-protocol.

REFERENCES AND NOTES

1.P. Friedl, J. Locker, E. Sahai, J. E. Segall, Classifying collective cancer cell invasion. Nat. Cell Biol. 14, 777–783 (2012). [DOI] [PubMed] [Google Scholar]
2.C. Hidalgo-Carcedo, S. Hooper, S. I. Chaudhry, P. Williamson, K. Harrington, B. Leitinger, E. Sahai, Collective cell migration requires suppression of actomyosin at cell-cell contacts mediated by DDR1 and the cell polarity regulators Par3 and Par6. Nat. Cell Biol. 13, 49–58 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
3.O. Ilina, P. G. Gritsenko, S. Syga, J. Lippoldt, C. A. M. La Porta, O. Chepizhko, S. Grosser, M. Vullings, G. J. Bakker, J. Starruss, P. Bult, S. Zapperi, J. A. Kas, A. Deutsch, P. Friedl, Cell-cell adhesion and 3D matrix confinement determine jamming transitions in breast cancer invasion. Nat. Cell Biol. 22, 1103–1115 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
4.L. Qin, D. Yang, W. Yi, H. Cao, G. Xiao, Roles of leader and follower cells in collective cell migration. Mol. Biol. Cell 32, 1267–1272 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
5.M. Reffay, M. C. Parrini, O. Cochet-Escartin, B. Ladoux, A. Buguin, S. Coscoy, F. Amblard, J. Camonis, P. Silberzan, Interplay of RhoA and mechanical forces in collective cell migration driven by leader cells. Nat. Cell Biol. 16, 217–223 (2014). [DOI] [PubMed] [Google Scholar]
6.C. D. Paul, P. Mistriotis, K. Konstantopoulos, Cancer cell motility: Lessons from migration in confined spaces. Nat. Rev. Cancer 17, 131–140 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
7.B. Weigelin, G.-J. Bakker, P. Friedl, Intravital third harmonic generation microscopy of collective melanoma cell invasion: Principles of interface guide and microvesicle dynamics. IntraVital 1, 32–43 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
8.K. Wolf, S. Alexander, V. Schacht, L. M. Coussens, U. H. von Andrian, J. van Rheenen, E. Deryugina, P. Friedl, Collagen-based cell migration models in vitro and in vivo. Semin. Cell Dev. Biol. 20, 931–941 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
9.S. R. Vedula, M. C. Leong, T. L. Lai, P. Hersen, A. J. Kabla, C. T. Lim, B. Ladoux, Emerging modes of collective cell migration induced by geometrical constraints. Proc. Natl. Acad. Sci. U.S.A. 109, 12974–12979 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
10.A. Szabó, M. Melchionda, G. Nastasi, M. L. Woods, S. Campo, R. Perris, R. Mayor, In vivo confinement promotes collective migration of neural crest cells. J. Cell Biol. 213, 543–555 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
11.D. Mohammed, G. Charras, E. Vercruysse, M. Versaevel, J. Lantoine, L. Alaimo, C. Bruyère, M. Luciano, K. Glinel, G. Delhaye, O. Théodoly, S. Gabriele, Substrate area confinement is a key determinant of cell velocity in collective migration. Nat. Phys. 15, 858–866 (2019). [Google Scholar]
12.E. O. Wisniewski, P. Mistriotis, K. Bera, R. A. Law, J. Zhang, M. Nikolic, M. Weiger, M. Parlani, S. Tuntithavornwat, A. Afthinos, R. Zhao, D. Wirtz, P. Kalab, G. Scarcelli, P. Friedl, K. Konstantopoulos, Dorsoventral polarity directs cell responses to migration track geometries. Sci. Adv. 6, eaba6505 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
13.A. Basant, M. Glotzer, Spatiotemporal regulation of RhoA during cytokinesis. Curr. Biol. 28, R570–R580 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
14.S. Alexander, G. E. Koehl, M. Hirschberg, E. K. Geissler, P. Friedl, Dynamic imaging of cancer growth and invasion: A modified skin-fold chamber model. Histochem. Cell Biol. 130, 1147–1154 (2008). [DOI] [PubMed] [Google Scholar]
15.A. Haeger, S. Alexander, M. Vullings, F. M. P. Kaiser, C. Veelken, U. Flucke, G. E. Koehl, M. Hirschberg, M. Flentje, R. M. Hoffman, E. K. Geissler, S. Kissler, P. Friedl, Collective cancer invasion forms an integrin-dependent radioresistant niche. J. Exp. Med. 217, e20181184 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
16.E. M. Balzer, Z. Tong, C. D. Paul, W. C. Hung, K. M. Stroka, A. E. Boggs, S. S. Martin, K. Konstantopoulos, Physical confinement alters tumor cell adhesion and migration phenotypes. FASEB J. 26, 4045–4056 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
17.W.-C. Hung, S.-H. Chen, C. D. Paul, K. M. Stroka, Y.-C. Lo, J. T. Yang, K. Konstantopoulos, Distinct signaling mechanisms regulate migration in unconfined versus confined spaces. J. Cell Biol. 202, 807–824 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
18.Z. Tong, E. M. Balzer, M. R. Dallas, W.-C. Hung, K. J. Stebe, K. Konstantopoulos, Chemotaxis of cell populations through confined spaces at single-cell resolution. PLOS ONE 7, e29211 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
19.K. L. Mui, C. S. Chen, R. K. Assoian, The mechanical regulation of integrin-cadherin crosstalk organizes cells, signaling and forces. J. Cell Sci. 129, 1093–1100 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
20.T. T. Onder, P. B. Gupta, S. A. Mani, J. Yang, E. S. Lander, R. A. Weinberg, Loss of E-cadherin promotes metastasis via multiple downstream transcriptional pathways. Cancer Res. 68, 3645–3654 (2008). [DOI] [PubMed] [Google Scholar]
21.J. P. Thiery, H. Acloque, R. Y. Huang, M. A. Nieto, Epithelial-mesenchymal transitions in development and disease. Cell 139, 871–890 (2009). [DOI] [PubMed] [Google Scholar]
22.K. Vleminckx, L. Vakaet, M. Mareel, W. Fiers, F. van Roy, Genetic manipulation of E-cadherin expression by epithelial tumor cells reveals an invasion suppressor role. Cell 66, 107–119 (1991). [DOI] [PubMed] [Google Scholar]
23.B. Nagar, M. Overduin, M. Ikura, J. M. Rini, Structural basis of calcium-induced E-cadherin rigidification and dimerization. Nature 380, 360–364 (1996). [DOI] [PubMed] [Google Scholar]
24.G. R. Kale, X. Yang, J.-M. Philippe, M. Mani, P.-F. Lenne, T. Lecuit, Distinct contributions of tensile and shear stress on E-cadherin levels during morphogenesis. Nat. Commun. 9, 5021 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
25.A. P. Kowalczyk, B. A. Nanes, Adherens junction turnover: Regulating adhesion through cadherin endocytosis, degradation, and recycling. Subcell. Biochem. 60, 197–222 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
26.A. Ratheesh, G. A. Gomez, R. Priya, S. Verma, E. M. Kovacs, K. Jiang, N. H. Brown, A. Akhmanova, S. J. Stehbens, A. S. Yap, Centralspindlin and α-catenin regulate Rho signalling at the epithelial zonula adherens. Nat. Cell Biol. 14, 818–828 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
27.M. V. Rao, R. Zaidel-Bar, Formin-mediated actin polymerization at cell-cell junctions stabilizes E-cadherin and maintains monolayer integrity during wound repair. Mol. Biol. Cell 27, 2844–2856 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
28.W. Engl, B. Arasi, L. L. Yap, J. P. Thiery, V. Viasnoff, Actin dynamics modulate mechanosensitive immobilization of E-cadherin at adherens junctions. Nat. Cell Biol. 16, 587–594 (2014). [DOI] [PubMed] [Google Scholar]
29.S. Sakurada, N. Takuwa, N. Sugimoto, Y. Wang, M. Seto, Y. Sasaki, Y. Takuwa, Ca²⁺−dependent activation of Rho and Rho kinase in membrane depolarization-induced and receptor stimulation-induced vascular smooth muscle contraction. Circ. Res. 93, 548–556 (2003). [DOI] [PubMed] [Google Scholar]
30.T. Lecuit, A. S. Yap, E-cadherin junctions as active mechanical integrators in tissue dynamics. Nat. Cell Biol. 17, 533–539 (2015). [DOI] [PubMed] [Google Scholar]
31.S. Ohsawa, J. Vaughen, T. Igaki, Cell extrusion: A stress-responsive force for good or evil in epithelial homeostasis. Dev. Cell. 44, 284–296 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
32.M. L. Heuzé, G. H. N. Sankara Narayana, J. D’Alessandro, V. Cellerin, T. Dang, D. S. Williams, J. C. van Hest, P. Marcq, R. M. Mège, B. Ladoux, Myosin II isoforms play distinct roles in adherens junction biogenesis. ELife 8, e46599 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
33.A. M. Shewan, M. Maddugoda, A. Kraemer, S. J. Stehbens, S. Verma, E. M. Kovacs, A. S. Yap, Myosin 2 is a key Rho kinase target necessary for the local concentration of E-cadherin at cell-cell contacts. Mol. Biol. Cell 16, 4531–4542 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
34.R. D. Fritz, M. Letzelter, A. Reimann, K. Martin, L. Fusco, L. Ritsma, B. Ponsioen, E. Fluri, S. Schulte-Merker, J. van Rheenen, O. Pertz, A versatile toolkit to produce sensitive FRET biosensors to visualize signaling in time and space. Sci. Signal. 6, rs12 (2013). [DOI] [PubMed] [Google Scholar]
35.P. Mistriotis, E. O. Wisniewski, K. Bera, J. Keys, Y. Li, S. Tuntithavornwat, R. A. Law, N. A. Perez-Gonzalez, E. Erdogmus, Y. Zhang, R. Zhao, S. X. Sun, P. Kalab, J. Lammerding, K. Konstantopoulos, Confinement hinders motility by inducing RhoA-mediated nuclear influx, volume expansion, and blebbing. J. Cell Biol. 218, 4093–4111 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
36.A. J. Piekny, M. Glotzer, Anillin is a scaffold protein that links RhoA, actin, and myosin during cytokinesis. Curr. Biol. 18, 30–36 (2008). [DOI] [PubMed] [Google Scholar]
37.L. Valon, A. Marín-Llauradó, T. Wyatt, G. Charras, X. Trepat, Optogenetic control of cellular forces and mechanotransduction. Nat. Commun. 8, 14396 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
38.C. L. Yankaskas, K. Bera, K. Stoletov, S. A. Serra, J. Carrillo-Garcia, S. Tuntithavornwat, P. Mistriotis, J. D. Lewis, M. A. Valverde, K. Konstantopoulos, The fluid shear stress sensor TRPM7 regulates tumor cell intravasation. Sci. Adv. 7, eabh3457 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
39.J. V. Serbo, S. Kuo, S. Lewis, M. Lehmann, J. Li, D. H. Gracias, L. H. Romer, Patterning of fibroblast and matrix anisotropy within 3D confinement is driven by the cytoskeleton. Adv. Healthc. Mater. 5, 146–158 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
40.T. Wittmann, C. M. Waterman-Storer, Cell motility: Can Rho GTPases and microtubules point the way? J. Cell Sci. 114, 3795–3803 (2001). [DOI] [PubMed] [Google Scholar]
41.J. Birkenfeld, P. Nalbant, S.-H. Yoon, G. M. Bokoch, Cellular functions of GEF-H1, a microtubule-regulated Rho-GEF: Is altered GEF-H1 activity a crucial determinant of disease pathogenesis? Trends Cell Biol. 18, 210–219 (2008). [DOI] [PubMed] [Google Scholar]
42.A. S. Kashyap, L. Fernandez-Rodriguez, Y. Zhao, G. Monaco, M. P. Trefny, N. Yoshida, K. Martin, A. Sharma, N. Olieric, P. Shah, M. Stanczak, N. Kirchhammer, S. M. Park, S. Wieckowski, H. Laubli, R. Zagani, B. Kasenda, M. O. Steinmetz, H. C. Reinecker, A. Zippelius, GEF-H1 signaling upon microtubule destabilization is required for dendritic cell activation and specific anti-tumor responses. Cell Rep 28, 3367–3380.e3368 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
43.M. Krendel, F. T. Zenke, G. M. Bokoch, Nucleotide exchange factor GEF-H1 mediates cross-talk between microtubules and the actin cytoskeleton. Nat. Cell Biol. 4, 294–301 (2002). [DOI] [PubMed] [Google Scholar]
44.H. K. Matthews, U. Delabre, J. L. Rohn, J. Guck, P. Kunda, B. Baum, Changes in Ect2 localization couple actomyosin-dependent cell shape changes to mitotic progression. Dev. Cell 23, 371–383 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
45.T. Kawashima, Y. C. Bao, Y. Minoshima, Y. Nomura, T. Hatori, T. Hori, T. Fukagawa, T. Fukada, N. Takahashi, T. Nosaka, M. Inoue, T. Sato, M. Kukimoto-Niino, M. Shirouzu, S. Yokoyama, T. Kitamura, A Rac GTPase-activating protein, MgcRacGAP, is a nuclear localizing signal-containing nuclear chaperone in the activation of STAT transcription factors. Mol. Cell. Biol. 29, 1796–1813 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
46.D. R. Cook, M. Kang, T. D. Martin, J. A. Galanko, G. H. Loeza, D. G. Trembath, V. Justilien, K. A. Pickering, D. F. Vincent, A. Jarosch, P. Jurmeister, A. M. Waters, P. S. Hibshman, A. D. Campbell, C. A. Ford, T. O. Keku, J. J. Yeh, M. S. Lee, A. D. Cox, A. P. Fields, R. S. Sandler, O. J. Sansom, C. Sers, A. Schaefer, C. J. Der, Aberrant expression and subcellular localization of ECT2 drives colorectal cancer progression and growth. Cancer Res. 82, 90–104 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
47.J. F. Soderholm, S. L. Bird, P. Kalab, Y. Sampathkumar, K. Hasegawa, M. Uehara-Bingen, K. Weis, R. Heald, Importazole, a small molecule inhibitor of the transport receptor importin-beta. ACS Chem. Biol. 6, 700–708 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
48.L. P. Huff, M. J. Decristo, D. Trembath, P. F. Kuan, M. Yim, J. Liu, D. R. Cook, C. R. Miller, C. J. Der, A. D. Cox, The role of Ect2 nuclear RhoGEF activity in ovarian cancer cell transformation. Cancer 4, 460–475 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
49.V. Padmanaban, I. Krol, Y. Suhail, B. M. Szczerba, N. Aceto, J. S. Bader, A. J. Ewald, E-cadherin is required for metastasis in multiple models of breast cancer. Nature 573, 439–444 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
50.J. Zhang, K. F. Goliwas, W. Wang, P. V. Taufalele, F. Bordeleau, C. A. Reinhart-King, Energetic regulation of coordinated leader-follower dynamics during collective invasion of breast cancer cells. Proc. Natl. Acad. Sci. U.S.A. 116, 7867–7872 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
51.X. Trepat, M. R. Wasserman, T. E. Angelini, E. Millet, D. A. Weitz, J. P. Butler, J. J. Fredberg, Physical forces during collective cell migration. Nat. Phys. 5, 426–430 (2009). [Google Scholar]
52.A. K. Perl, P. Wilgenbus, U. Dahl, H. Semb, G. Christofori, A causal role for E-cadherin in the transition from adenoma to carcinoma. Nature 392, 190–193 (1998). [DOI] [PubMed] [Google Scholar]
53.P. J. Kowalski, M. A. Rubin, C. G. Kleer, E-cadherin expression in primary carcinomas of the breast and its distant metastases. Breast Cancer. Res. 5, R217–R222 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
54.G. F. Weber, M. A. Bjerke, D. W. DeSimone, A mechanoresponsive cadherin-keratin complex directs polarized protrusive behavior and collective cell migration. Dev. Cell. 22, 104–115 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
55.P. W. Oakes, E. Wagner, C. A. Brand, D. Probst, M. Linke, U. S. Schwarz, M. Glotzer, M. L. Gardel, Optogenetic control of RhoA reveals zyxin-mediated elasticity of stress fibres. Nat. Commun. 8, 15817 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
56.Y. C. Chang, P. Nalbant, J. Birkenfeld, Z. F. Chang, G. M. Bokoch, GEF-H1 couples nocodazole-induced microtubule disassembly to cell contractility via RhoA. Mol. Biol. Cell 19, 2147–2153 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
57.S. N. Samarin, A. I. Ivanov, G. Flatau, C. A. Parkos, A. Nusrat, Rho/Rho-associated kinase-II signaling mediates disassembly of epithelial apical junctions. Mol. Biol. Cell 18, 3429–3439 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
58.E. Wagner, M. Glotzer, Local RhoA activation induces cytokinetic furrows independent of spindle position and cell cycle stage. J Cell. Biol. 213, 641–649 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
59.O. Yuce, A. Piekny, M. Glotzer, An ECT2-centralspindlin complex regulates the localization and function of RhoA. J. Cell Biol. 170, 571–582 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
60.G. Jacquemet, D. M. Green, R. E. Bridgewater, A. von Kriegsheim, M. J. Humphries, J. C. Norman, P. T. Caswell, RCP-driven α5β1 recycling suppresses Rac and promotes RhoA activity via the RacGAP1-IQGAP1 complex. J. Cell Biol. 202, 917–935 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
61.S. Frey, R. Rees, J. Schünemann, S. C. Ng, K. Fünfgeld, T. Huyton, D. Görlich, Surface properties determining passage rates of proteins through nuclear pores. Cell 174, 202–217.e209 (2018). [DOI] [PubMed] [Google Scholar]
62.I. Andreu, I. Granero-Moya, N. R. Chahare, K. Clein, M. Molina-Jordan, A. E. M. Beedle, A. Elosegui-Artola, J. F. Abenza, L. Rossetti, X. Trepat, B. Raveh, P. Roca-Cusachs, Mechanical force application to the nucleus regulates nucleocytoplasmic transport. Nat. Cell Biol. 24, 896–905 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
63.M. Canel, A. Serrels, D. Miller, P. Timpson, B. Serrels, M. C. Frame, V. G. Brunton, Quantitative in vivo imaging of the effects of inhibiting integrin signaling via Src and FAK on cancer cell movement: Effects on E-cadherin dynamics. Cancer Res. 70, 9413–9422 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
64.D. Meiri, C. B. Marshall, D. Mokady, J. LaRose, M. Mullin, A. C. Gingras, M. Ikura, R. Rottapel, Mechanistic insight into GPCR-mediated activation of the microtubule-associated RhoA exchange factor GEF-H1. Nat. Commun. 5, 4857 (2014). [DOI] [PubMed] [Google Scholar]
65.C. D. Paul, D. J. Shea, M. R. Mahoney, A. Chai, V. Laney, W.-C. Hung, K. Konstantopoulos, Interplay of the physical microenvironment, contact guidance, and intracellular signaling in cell decision making. FASEB J 30, 2161–2170 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
66.G. Koulouras, A. Panagopoulos, M. A. Rapsomaniki, N. N. Giakoumakis, S. Taraviras, Z. Lygerou, EasyFRAP-web: A web-based tool for the analysis of fluorescence recovery after photobleaching data. Nucleic Acids Res. 46, W467–W472 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
67.P. Wang, F. Zhu, K. Konstantopoulos, The antagonistic actions of endogenous interleukin-1β and 15-deoxy-Δ12,14-prostaglandin J2 regulate the temporal synthesis of matrix metalloproteinase-9 in sheared chondrocytes. J. Biol. Chem. 287, 31877–31893 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
68.S. Curran, C. Strandkvist, J. Bathmann, M. de Gennes, A. Kabla, G. Salbreux, B. Baum, Myosin II controls junction fluctuations to guide epithelial tissue ordering. Dev. Cell 43, 480–492.e486 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
69.B. Carpenter, A. Gelman, M. D. Hoffman, D. Lee, B. Goodrich, M. Betancourt, M. Brubaker, J. Guo, P. Li, A. Riddell, Stan: A probabilistic programming language. J. Stat. Softw. 76, 1–32 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
70.M. D. Hoffman, A. Gelman, The No-U-Turn sampler: Adaptively setting path lengths in Hamiltonian Monte Carlo. J. Mach. Learn. Res. 15, 1593–1623 (2014). [Google Scholar]
71.K. Cranmer, J. Brehmer, G. Louppe, The frontier of simulation-based inference. Proc. Natl. Acad. Sci. U.S.A 117, 30055–30062 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
72.A. Mayer, T. Mora, O. Rivoire, A. M. Walczak, Diversity of immune strategies explained by adaptation to pathogen statistics. Proc. Natl. Acad. Sci. U.S.A. 113, 8630–8635 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Figs. S1 to S10

Tables S1 to S3

Click here for additional data file.^{(2.3MB, pdf)}

Movies S1 to S3

Click here for additional data file.^{(6.2MB, zip)}

[R1] 1.P. Friedl, J. Locker, E. Sahai, J. E. Segall, Classifying collective cancer cell invasion. Nat. Cell Biol. 14, 777–783 (2012). [DOI] [PubMed] [Google Scholar]

[R2] 2.C. Hidalgo-Carcedo, S. Hooper, S. I. Chaudhry, P. Williamson, K. Harrington, B. Leitinger, E. Sahai, Collective cell migration requires suppression of actomyosin at cell-cell contacts mediated by DDR1 and the cell polarity regulators Par3 and Par6. Nat. Cell Biol. 13, 49–58 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R3] 3.O. Ilina, P. G. Gritsenko, S. Syga, J. Lippoldt, C. A. M. La Porta, O. Chepizhko, S. Grosser, M. Vullings, G. J. Bakker, J. Starruss, P. Bult, S. Zapperi, J. A. Kas, A. Deutsch, P. Friedl, Cell-cell adhesion and 3D matrix confinement determine jamming transitions in breast cancer invasion. Nat. Cell Biol. 22, 1103–1115 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R4] 4.L. Qin, D. Yang, W. Yi, H. Cao, G. Xiao, Roles of leader and follower cells in collective cell migration. Mol. Biol. Cell 32, 1267–1272 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R5] 5.M. Reffay, M. C. Parrini, O. Cochet-Escartin, B. Ladoux, A. Buguin, S. Coscoy, F. Amblard, J. Camonis, P. Silberzan, Interplay of RhoA and mechanical forces in collective cell migration driven by leader cells. Nat. Cell Biol. 16, 217–223 (2014). [DOI] [PubMed] [Google Scholar]

[R6] 6.C. D. Paul, P. Mistriotis, K. Konstantopoulos, Cancer cell motility: Lessons from migration in confined spaces. Nat. Rev. Cancer 17, 131–140 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R7] 7.B. Weigelin, G.-J. Bakker, P. Friedl, Intravital third harmonic generation microscopy of collective melanoma cell invasion: Principles of interface guide and microvesicle dynamics. IntraVital 1, 32–43 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R8] 8.K. Wolf, S. Alexander, V. Schacht, L. M. Coussens, U. H. von Andrian, J. van Rheenen, E. Deryugina, P. Friedl, Collagen-based cell migration models in vitro and in vivo. Semin. Cell Dev. Biol. 20, 931–941 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R9] 9.S. R. Vedula, M. C. Leong, T. L. Lai, P. Hersen, A. J. Kabla, C. T. Lim, B. Ladoux, Emerging modes of collective cell migration induced by geometrical constraints. Proc. Natl. Acad. Sci. U.S.A. 109, 12974–12979 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R10] 10.A. Szabó, M. Melchionda, G. Nastasi, M. L. Woods, S. Campo, R. Perris, R. Mayor, In vivo confinement promotes collective migration of neural crest cells. J. Cell Biol. 213, 543–555 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R11] 11.D. Mohammed, G. Charras, E. Vercruysse, M. Versaevel, J. Lantoine, L. Alaimo, C. Bruyère, M. Luciano, K. Glinel, G. Delhaye, O. Théodoly, S. Gabriele, Substrate area confinement is a key determinant of cell velocity in collective migration. Nat. Phys. 15, 858–866 (2019). [Google Scholar]

[R12] 12.E. O. Wisniewski, P. Mistriotis, K. Bera, R. A. Law, J. Zhang, M. Nikolic, M. Weiger, M. Parlani, S. Tuntithavornwat, A. Afthinos, R. Zhao, D. Wirtz, P. Kalab, G. Scarcelli, P. Friedl, K. Konstantopoulos, Dorsoventral polarity directs cell responses to migration track geometries. Sci. Adv. 6, eaba6505 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R13] 13.A. Basant, M. Glotzer, Spatiotemporal regulation of RhoA during cytokinesis. Curr. Biol. 28, R570–R580 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R14] 14.S. Alexander, G. E. Koehl, M. Hirschberg, E. K. Geissler, P. Friedl, Dynamic imaging of cancer growth and invasion: A modified skin-fold chamber model. Histochem. Cell Biol. 130, 1147–1154 (2008). [DOI] [PubMed] [Google Scholar]

[R15] 15.A. Haeger, S. Alexander, M. Vullings, F. M. P. Kaiser, C. Veelken, U. Flucke, G. E. Koehl, M. Hirschberg, M. Flentje, R. M. Hoffman, E. K. Geissler, S. Kissler, P. Friedl, Collective cancer invasion forms an integrin-dependent radioresistant niche. J. Exp. Med. 217, e20181184 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R16] 16.E. M. Balzer, Z. Tong, C. D. Paul, W. C. Hung, K. M. Stroka, A. E. Boggs, S. S. Martin, K. Konstantopoulos, Physical confinement alters tumor cell adhesion and migration phenotypes. FASEB J. 26, 4045–4056 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R17] 17.W.-C. Hung, S.-H. Chen, C. D. Paul, K. M. Stroka, Y.-C. Lo, J. T. Yang, K. Konstantopoulos, Distinct signaling mechanisms regulate migration in unconfined versus confined spaces. J. Cell Biol. 202, 807–824 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R18] 18.Z. Tong, E. M. Balzer, M. R. Dallas, W.-C. Hung, K. J. Stebe, K. Konstantopoulos, Chemotaxis of cell populations through confined spaces at single-cell resolution. PLOS ONE 7, e29211 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R19] 19.K. L. Mui, C. S. Chen, R. K. Assoian, The mechanical regulation of integrin-cadherin crosstalk organizes cells, signaling and forces. J. Cell Sci. 129, 1093–1100 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R20] 20.T. T. Onder, P. B. Gupta, S. A. Mani, J. Yang, E. S. Lander, R. A. Weinberg, Loss of E-cadherin promotes metastasis via multiple downstream transcriptional pathways. Cancer Res. 68, 3645–3654 (2008). [DOI] [PubMed] [Google Scholar]

[R21] 21.J. P. Thiery, H. Acloque, R. Y. Huang, M. A. Nieto, Epithelial-mesenchymal transitions in development and disease. Cell 139, 871–890 (2009). [DOI] [PubMed] [Google Scholar]

[R22] 22.K. Vleminckx, L. Vakaet, M. Mareel, W. Fiers, F. van Roy, Genetic manipulation of E-cadherin expression by epithelial tumor cells reveals an invasion suppressor role. Cell 66, 107–119 (1991). [DOI] [PubMed] [Google Scholar]

[R23] 23.B. Nagar, M. Overduin, M. Ikura, J. M. Rini, Structural basis of calcium-induced E-cadherin rigidification and dimerization. Nature 380, 360–364 (1996). [DOI] [PubMed] [Google Scholar]

[R24] 24.G. R. Kale, X. Yang, J.-M. Philippe, M. Mani, P.-F. Lenne, T. Lecuit, Distinct contributions of tensile and shear stress on E-cadherin levels during morphogenesis. Nat. Commun. 9, 5021 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R25] 25.A. P. Kowalczyk, B. A. Nanes, Adherens junction turnover: Regulating adhesion through cadherin endocytosis, degradation, and recycling. Subcell. Biochem. 60, 197–222 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R26] 26.A. Ratheesh, G. A. Gomez, R. Priya, S. Verma, E. M. Kovacs, K. Jiang, N. H. Brown, A. Akhmanova, S. J. Stehbens, A. S. Yap, Centralspindlin and α-catenin regulate Rho signalling at the epithelial zonula adherens. Nat. Cell Biol. 14, 818–828 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R27] 27.M. V. Rao, R. Zaidel-Bar, Formin-mediated actin polymerization at cell-cell junctions stabilizes E-cadherin and maintains monolayer integrity during wound repair. Mol. Biol. Cell 27, 2844–2856 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R28] 28.W. Engl, B. Arasi, L. L. Yap, J. P. Thiery, V. Viasnoff, Actin dynamics modulate mechanosensitive immobilization of E-cadherin at adherens junctions. Nat. Cell Biol. 16, 587–594 (2014). [DOI] [PubMed] [Google Scholar]

[R29] 29.S. Sakurada, N. Takuwa, N. Sugimoto, Y. Wang, M. Seto, Y. Sasaki, Y. Takuwa, Ca²⁺−dependent activation of Rho and Rho kinase in membrane depolarization-induced and receptor stimulation-induced vascular smooth muscle contraction. Circ. Res. 93, 548–556 (2003). [DOI] [PubMed] [Google Scholar]

[R30] 30.T. Lecuit, A. S. Yap, E-cadherin junctions as active mechanical integrators in tissue dynamics. Nat. Cell Biol. 17, 533–539 (2015). [DOI] [PubMed] [Google Scholar]

[R31] 31.S. Ohsawa, J. Vaughen, T. Igaki, Cell extrusion: A stress-responsive force for good or evil in epithelial homeostasis. Dev. Cell. 44, 284–296 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R32] 32.M. L. Heuzé, G. H. N. Sankara Narayana, J. D’Alessandro, V. Cellerin, T. Dang, D. S. Williams, J. C. van Hest, P. Marcq, R. M. Mège, B. Ladoux, Myosin II isoforms play distinct roles in adherens junction biogenesis. ELife 8, e46599 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R33] 33.A. M. Shewan, M. Maddugoda, A. Kraemer, S. J. Stehbens, S. Verma, E. M. Kovacs, A. S. Yap, Myosin 2 is a key Rho kinase target necessary for the local concentration of E-cadherin at cell-cell contacts. Mol. Biol. Cell 16, 4531–4542 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R34] 34.R. D. Fritz, M. Letzelter, A. Reimann, K. Martin, L. Fusco, L. Ritsma, B. Ponsioen, E. Fluri, S. Schulte-Merker, J. van Rheenen, O. Pertz, A versatile toolkit to produce sensitive FRET biosensors to visualize signaling in time and space. Sci. Signal. 6, rs12 (2013). [DOI] [PubMed] [Google Scholar]

[R35] 35.P. Mistriotis, E. O. Wisniewski, K. Bera, J. Keys, Y. Li, S. Tuntithavornwat, R. A. Law, N. A. Perez-Gonzalez, E. Erdogmus, Y. Zhang, R. Zhao, S. X. Sun, P. Kalab, J. Lammerding, K. Konstantopoulos, Confinement hinders motility by inducing RhoA-mediated nuclear influx, volume expansion, and blebbing. J. Cell Biol. 218, 4093–4111 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R36] 36.A. J. Piekny, M. Glotzer, Anillin is a scaffold protein that links RhoA, actin, and myosin during cytokinesis. Curr. Biol. 18, 30–36 (2008). [DOI] [PubMed] [Google Scholar]

[R37] 37.L. Valon, A. Marín-Llauradó, T. Wyatt, G. Charras, X. Trepat, Optogenetic control of cellular forces and mechanotransduction. Nat. Commun. 8, 14396 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R38] 38.C. L. Yankaskas, K. Bera, K. Stoletov, S. A. Serra, J. Carrillo-Garcia, S. Tuntithavornwat, P. Mistriotis, J. D. Lewis, M. A. Valverde, K. Konstantopoulos, The fluid shear stress sensor TRPM7 regulates tumor cell intravasation. Sci. Adv. 7, eabh3457 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R39] 39.J. V. Serbo, S. Kuo, S. Lewis, M. Lehmann, J. Li, D. H. Gracias, L. H. Romer, Patterning of fibroblast and matrix anisotropy within 3D confinement is driven by the cytoskeleton. Adv. Healthc. Mater. 5, 146–158 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R40] 40.T. Wittmann, C. M. Waterman-Storer, Cell motility: Can Rho GTPases and microtubules point the way? J. Cell Sci. 114, 3795–3803 (2001). [DOI] [PubMed] [Google Scholar]

[R41] 41.J. Birkenfeld, P. Nalbant, S.-H. Yoon, G. M. Bokoch, Cellular functions of GEF-H1, a microtubule-regulated Rho-GEF: Is altered GEF-H1 activity a crucial determinant of disease pathogenesis? Trends Cell Biol. 18, 210–219 (2008). [DOI] [PubMed] [Google Scholar]

[R42] 42.A. S. Kashyap, L. Fernandez-Rodriguez, Y. Zhao, G. Monaco, M. P. Trefny, N. Yoshida, K. Martin, A. Sharma, N. Olieric, P. Shah, M. Stanczak, N. Kirchhammer, S. M. Park, S. Wieckowski, H. Laubli, R. Zagani, B. Kasenda, M. O. Steinmetz, H. C. Reinecker, A. Zippelius, GEF-H1 signaling upon microtubule destabilization is required for dendritic cell activation and specific anti-tumor responses. Cell Rep 28, 3367–3380.e3368 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R43] 43.M. Krendel, F. T. Zenke, G. M. Bokoch, Nucleotide exchange factor GEF-H1 mediates cross-talk between microtubules and the actin cytoskeleton. Nat. Cell Biol. 4, 294–301 (2002). [DOI] [PubMed] [Google Scholar]

[R44] 44.H. K. Matthews, U. Delabre, J. L. Rohn, J. Guck, P. Kunda, B. Baum, Changes in Ect2 localization couple actomyosin-dependent cell shape changes to mitotic progression. Dev. Cell 23, 371–383 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R45] 45.T. Kawashima, Y. C. Bao, Y. Minoshima, Y. Nomura, T. Hatori, T. Hori, T. Fukagawa, T. Fukada, N. Takahashi, T. Nosaka, M. Inoue, T. Sato, M. Kukimoto-Niino, M. Shirouzu, S. Yokoyama, T. Kitamura, A Rac GTPase-activating protein, MgcRacGAP, is a nuclear localizing signal-containing nuclear chaperone in the activation of STAT transcription factors. Mol. Cell. Biol. 29, 1796–1813 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R46] 46.D. R. Cook, M. Kang, T. D. Martin, J. A. Galanko, G. H. Loeza, D. G. Trembath, V. Justilien, K. A. Pickering, D. F. Vincent, A. Jarosch, P. Jurmeister, A. M. Waters, P. S. Hibshman, A. D. Campbell, C. A. Ford, T. O. Keku, J. J. Yeh, M. S. Lee, A. D. Cox, A. P. Fields, R. S. Sandler, O. J. Sansom, C. Sers, A. Schaefer, C. J. Der, Aberrant expression and subcellular localization of ECT2 drives colorectal cancer progression and growth. Cancer Res. 82, 90–104 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R47] 47.J. F. Soderholm, S. L. Bird, P. Kalab, Y. Sampathkumar, K. Hasegawa, M. Uehara-Bingen, K. Weis, R. Heald, Importazole, a small molecule inhibitor of the transport receptor importin-beta. ACS Chem. Biol. 6, 700–708 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R48] 48.L. P. Huff, M. J. Decristo, D. Trembath, P. F. Kuan, M. Yim, J. Liu, D. R. Cook, C. R. Miller, C. J. Der, A. D. Cox, The role of Ect2 nuclear RhoGEF activity in ovarian cancer cell transformation. Cancer 4, 460–475 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R49] 49.V. Padmanaban, I. Krol, Y. Suhail, B. M. Szczerba, N. Aceto, J. S. Bader, A. J. Ewald, E-cadherin is required for metastasis in multiple models of breast cancer. Nature 573, 439–444 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R50] 50.J. Zhang, K. F. Goliwas, W. Wang, P. V. Taufalele, F. Bordeleau, C. A. Reinhart-King, Energetic regulation of coordinated leader-follower dynamics during collective invasion of breast cancer cells. Proc. Natl. Acad. Sci. U.S.A. 116, 7867–7872 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R51] 51.X. Trepat, M. R. Wasserman, T. E. Angelini, E. Millet, D. A. Weitz, J. P. Butler, J. J. Fredberg, Physical forces during collective cell migration. Nat. Phys. 5, 426–430 (2009). [Google Scholar]

[R52] 52.A. K. Perl, P. Wilgenbus, U. Dahl, H. Semb, G. Christofori, A causal role for E-cadherin in the transition from adenoma to carcinoma. Nature 392, 190–193 (1998). [DOI] [PubMed] [Google Scholar]

[R53] 53.P. J. Kowalski, M. A. Rubin, C. G. Kleer, E-cadherin expression in primary carcinomas of the breast and its distant metastases. Breast Cancer. Res. 5, R217–R222 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R54] 54.G. F. Weber, M. A. Bjerke, D. W. DeSimone, A mechanoresponsive cadherin-keratin complex directs polarized protrusive behavior and collective cell migration. Dev. Cell. 22, 104–115 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R55] 55.P. W. Oakes, E. Wagner, C. A. Brand, D. Probst, M. Linke, U. S. Schwarz, M. Glotzer, M. L. Gardel, Optogenetic control of RhoA reveals zyxin-mediated elasticity of stress fibres. Nat. Commun. 8, 15817 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R56] 56.Y. C. Chang, P. Nalbant, J. Birkenfeld, Z. F. Chang, G. M. Bokoch, GEF-H1 couples nocodazole-induced microtubule disassembly to cell contractility via RhoA. Mol. Biol. Cell 19, 2147–2153 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R57] 57.S. N. Samarin, A. I. Ivanov, G. Flatau, C. A. Parkos, A. Nusrat, Rho/Rho-associated kinase-II signaling mediates disassembly of epithelial apical junctions. Mol. Biol. Cell 18, 3429–3439 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R58] 58.E. Wagner, M. Glotzer, Local RhoA activation induces cytokinetic furrows independent of spindle position and cell cycle stage. J Cell. Biol. 213, 641–649 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R59] 59.O. Yuce, A. Piekny, M. Glotzer, An ECT2-centralspindlin complex regulates the localization and function of RhoA. J. Cell Biol. 170, 571–582 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R60] 60.G. Jacquemet, D. M. Green, R. E. Bridgewater, A. von Kriegsheim, M. J. Humphries, J. C. Norman, P. T. Caswell, RCP-driven α5β1 recycling suppresses Rac and promotes RhoA activity via the RacGAP1-IQGAP1 complex. J. Cell Biol. 202, 917–935 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R61] 61.S. Frey, R. Rees, J. Schünemann, S. C. Ng, K. Fünfgeld, T. Huyton, D. Görlich, Surface properties determining passage rates of proteins through nuclear pores. Cell 174, 202–217.e209 (2018). [DOI] [PubMed] [Google Scholar]

[R62] 62.I. Andreu, I. Granero-Moya, N. R. Chahare, K. Clein, M. Molina-Jordan, A. E. M. Beedle, A. Elosegui-Artola, J. F. Abenza, L. Rossetti, X. Trepat, B. Raveh, P. Roca-Cusachs, Mechanical force application to the nucleus regulates nucleocytoplasmic transport. Nat. Cell Biol. 24, 896–905 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R63] 63.M. Canel, A. Serrels, D. Miller, P. Timpson, B. Serrels, M. C. Frame, V. G. Brunton, Quantitative in vivo imaging of the effects of inhibiting integrin signaling via Src and FAK on cancer cell movement: Effects on E-cadherin dynamics. Cancer Res. 70, 9413–9422 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R64] 64.D. Meiri, C. B. Marshall, D. Mokady, J. LaRose, M. Mullin, A. C. Gingras, M. Ikura, R. Rottapel, Mechanistic insight into GPCR-mediated activation of the microtubule-associated RhoA exchange factor GEF-H1. Nat. Commun. 5, 4857 (2014). [DOI] [PubMed] [Google Scholar]

[R65] 65.C. D. Paul, D. J. Shea, M. R. Mahoney, A. Chai, V. Laney, W.-C. Hung, K. Konstantopoulos, Interplay of the physical microenvironment, contact guidance, and intracellular signaling in cell decision making. FASEB J 30, 2161–2170 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R66] 66.G. Koulouras, A. Panagopoulos, M. A. Rapsomaniki, N. N. Giakoumakis, S. Taraviras, Z. Lygerou, EasyFRAP-web: A web-based tool for the analysis of fluorescence recovery after photobleaching data. Nucleic Acids Res. 46, W467–W472 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R67] 67.P. Wang, F. Zhu, K. Konstantopoulos, The antagonistic actions of endogenous interleukin-1β and 15-deoxy-Δ12,14-prostaglandin J2 regulate the temporal synthesis of matrix metalloproteinase-9 in sheared chondrocytes. J. Biol. Chem. 287, 31877–31893 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R68] 68.S. Curran, C. Strandkvist, J. Bathmann, M. de Gennes, A. Kabla, G. Salbreux, B. Baum, Myosin II controls junction fluctuations to guide epithelial tissue ordering. Dev. Cell 43, 480–492.e486 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R69] 69.B. Carpenter, A. Gelman, M. D. Hoffman, D. Lee, B. Goodrich, M. Betancourt, M. Brubaker, J. Guo, P. Li, A. Riddell, Stan: A probabilistic programming language. J. Stat. Softw. 76, 1–32 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R70] 70.M. D. Hoffman, A. Gelman, The No-U-Turn sampler: Adaptively setting path lengths in Hamiltonian Monte Carlo. J. Mach. Learn. Res. 15, 1593–1623 (2014). [Google Scholar]

[R71] 71.K. Cranmer, J. Brehmer, G. Louppe, The frontier of simulation-based inference. Proc. Natl. Acad. Sci. U.S.A 117, 30055–30062 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R72] 72.A. Mayer, T. Mora, O. Rivoire, A. M. Walczak, Diversity of immune strategies explained by adaptation to pathogen statistics. Proc. Natl. Acad. Sci. U.S.A. 113, 8630–8635 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

Cytokinesis machinery promotes cell dissociation from collectively migrating strands in confinement

Robert A Law

Alexander Kiepas

Habben E Desta

Emiliano Perez Ipiña

Maria Parlani

Se Jong Lee

Christopher L Yankaskas

Runchen Zhao

Panagiotis Mistriotis

Nianchao Wang

Zhizhan Gu

Petr Kalab

Peter Friedl

Brian A Camley

Konstantinos Konstantopoulos

Roles

Abstract

INTRODUCTION

RESULTS

Confinement promotes the dissociation of leader cells from collectively migrating strands

Fig. 1. Cell confinement directs the dissociation of highly motile leader cells.

E-cadherin engagement is required to maintain cell-cell junctions

Fig. 2. Junctional E-cadherin dynamics are enhanced in cells under confinement.

Nonmuscle MIIA, but not MIIB, mediates leader cell dissociation in confinement

Fig. 3. MIIA localization to cell-cell junctions is a prerequisite to leader cell detachment.

Confinement-induced RhoA activation mediates the contractile response preceding cell detachment

Fig. 4. Confinement promotes RhoA activation at cell-cell junctions to induce cell detachment.

Confinement alters microtubule dynamics, which, in turn, results in GEF-H1–mediated leader cell dissociation

Fig. 5. Confinement alters microtubule organization and dynamics, resulting in GEF-H1–mediated RhoA activation.

Exit of nuclear Ect2 and RacGAP1 to the cytoplasm activates RhoA and promotes leader cell detachment in confinement

Fig. 6. Ect2 and RacGAP1 regulate confinement-induced RhoA activation and leader cell dissociation.

Fig. 7. Schematic of the proposed mechanism for confinement-induced leader cell dissociation.

DISCUSSION

MATERIALS AND METHODS

Cell culture and pharmacological inhibitors

Cloning, lentivirus preparation, transduction, and transfection

HT-1080 sarcoma xenograft implantation and intravital imaging

Photolithography and device fabrication

Microfluidic device seeding and live-cell imaging

Cell dissociation per leader cell entry quantification

Cell migration tracking and maximum displacement analysis

Actin staining and immunofluorescence

Confocal imaging

FLIM imaging and quantification of RhoA FRET sensors

FRAP imaging and quantification

GFP-MIIA and GFP-AHD intensity quantification

GFP-GEF-H1 intensity quantification

GFP-Ect2 and RacGAP1-GFP intensity quantification

Optogenetic RhoA activation experiments

Microtubule orientation quantification

EB1-GFP imaging and analysis

Western blotting

Statistical analysis

Mathematical model

Model fitting and simulations

Acknowledgments

Supplementary Materials

This PDF file includes:

Other Supplementary Material for this : manuscript includes the following:

REFERENCES AND NOTES

Associated Data

Supplementary Materials

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases